Mode decomposition in DCB and ENF tests with geometric and material assymetry

1 Introducción

Una de las limitaciones más importantes de la utilización de materiales compuestos en forma de laminados es la ausencia de refuerzo en la dirección del espesor del laminado. Debido a impactos de baja energía o a defectos en la fabricación, pueden aparecer fallos en forma de deslaminaciones. En ausencia de refuerzo, las deslaminaciones pueden avanzar y provocar el fallo del laminado. Con el fin de caracterizar la energía necesaria para el avance de grieta, existen distintos ensayos en modos I y II, que son los modos fundamentales de avance de grietas interlaminares. El más habitual en modo I es el ensayo de Viga en Doble Voladizo (Double Cantilever Beam, DCB). En modo II el más utilizado es el ensayo de Flexión con Entalla Final (End Notched Flexure, ENF). Utilizando un útil de ensayo especial se obtiene una combinación de los anteriores, el ensayo de Flexión en Modo Mixto (Mixed Mode Bending, MMB). Estos ensayos se realizan habitualmente en casos en que los brazos de grieta son iguales. Además de la fractura interlaminar, se pueden utilizar también para determinar las propiedades de adhesivos con adherentes iguales. En el caso de un laminado en el que los brazos de grieta tengan distinto espesor o de una unión adhesiva bimaterial, la pérdida de simetría implica la aparición de modos combinados de fallo.

El ensayo DCB asimétrico (Asymmetric DCB, ADCB) ha sido analizado por diversos autores, analítica, numérica y experimentalmente. Según el criterio de descomposición de Williams [1], en este ensayo sólo existe modo I, pero modelos analíticos y numéricos detallados muestran la existencia de modo II.

En el presente trabajo se sigue el análisis de Williams en el sentido de que se aísla una rebanada diferencial cercana a la punta de grieta para determinar la diferencia de energía complementaria antes y depués del avance de grieta, incluyendo el efecto del cortante. En este artículo se denominará coenergía a la energía complementaria. Posteriormente se establecen los criterios para descomponer la tasa crítica de liberación de energía en modos I y II y se realizan comparaciones con modelos analíticos y numéricos previos en el caso de ADCB [2]. En el caso de ENF se aportan los resultados obtenidos de acuerdo al modelo propuesto.

2 Tasa de liberación de energía y zona cohesiva

La tasa de liberación de energía G es la energía necesaria para un avance infinitesimal de grieta dividida por la superficie de grieta generada. Analizando un sistema en equilibrio sometido a un sistema de fuerzas independientes ${\textstyle {F}_{i}}$, siendo ${\textstyle {\delta }_{i}}$ los desplazamientos de los puntos de aplicación de las fuerzas en la misma dirección, realizando un balance energético y suponiendo que la energía y la coenergía son diferenciales exactas se obtiene:

${\textstyle {\left({\frac {dC}{{dF}_{i}}}\right)}_{a}={\delta }_{i}\quad {\frac {1}{b}}{\left({\frac {dC}{da}}\right)}_{{F}_{i}}=}$$G$

(1)

siendo C la coenergía. La primera ecuación es el teorema de Engesser-Castigliano y permite determinar los desplazamientos. La segunda ecuación de (1) permite determinar la tasa de liberación de energía cuando C se expresa en función de las fuerzas aplicadas independientes.

Por otra parte, Rice definió la integral J como una integral independiente del camino en una curva cerrada que incluía la punta de grieta. Se demuestra además que ${\textstyle J=}$$G$ en el caso de comportamiento elástico del material. Teniendo en cuenta las tensiones y desplazamientos relativos en una zona próxima a la punta de grieta denominada zona cohesiva resulta:

${\textstyle J=G=\int _{0}^{{\delta }_{n}}\sigma \,d{\delta }_{n}+\int _{0}^{{\delta }_{t}}\tau \,d{\delta }_{t}}$

(2)

siendo ${\textstyle \sigma }$ la tensión normal de apertura, ${\textstyle {\delta }_{n}}$ el desplazamiento relativo asociado, ${\textstyle \tau }$ la tensión cortante y ${\textstyle {\delta }_{t}}$ el desplazamiento relativo asociado. Por lo tanto, la primera integral de la ecuación (2) representa la contribución del modo I y la segunda integral incluye la contribución de los modos II y III, aunque este último no se considera en el presente trabajo. La zona cohesiva está relacionada con diversos factores: plastificación debido a que las tensiones alcanzan el límite elástico, puenteo de fibras en la zona de grieta o aparición de microgrietas.

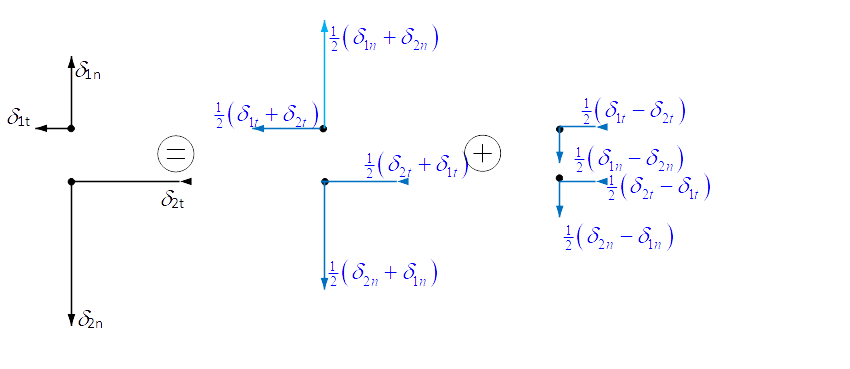
En caso de modos puros, únicamente existe un desplazamiento relativo como variable de estado. Los desplazamientos relativos ${\textstyle {\delta }_{n}}$ y ${\textstyle {\delta }_{t}}$ son la suma de los desplazamientos correspondientes a puntos homólogos de cada brazo de grieta, entendiendo como puntos homólogos aquellos que antes del avance de grieta eran un mismo punto. Por lo tanto, en el caso de que los desplazamientos de los puntos homólogos sean distintos, se podrán descomponer en una parte simétrica que realiza trabajo y una parte antisimétrica que no realiza trabajo y está asociada a un movimiento de sólido rígido, tal y como se muestra en la Figura 1.

Figura 1. Descomposición de desplazamientos.

Los planteamientos más razonables para realizar la descomposición de modos son:

1. El modo I puro se produce cuando el desplazamiento relativo tangencial en la parte simétrica es nulo, es decir:

${\textstyle {\delta }_{1t}+{\delta }_{2t}=0}$

(3)

En la parte simétrica de la Figura 1, los únicos desplazamientos que realizan trabajo son los correspondientes a modo I. Teniendo en cuenta únicamente la flexión y empotramiento perfecto de los brazos de grieta, esta condición es equivalente a que las deformaciones unitarias normales de puntos homólogos sean iguales. Los resultados obtenidos a partir de esta condición coinciden en flexión con los de la propuesta de Valvo [3] de descomposición de modos.

2. El modo II puro se produce cuando el desplazamiento relativo normal en la parte simétrica es nulo, es decir:

${\textstyle {\delta }_{1n}+{\delta }_{2n}=0}$

(4)

En la parte simétrica de la Figura 1, los únicos desplazamientos que realizan trabajo son los correspondientes a modo II. Teniendo en cuenta únicamente la flexión y empotramiento perfecto en los brazos de grieta la condición dada en la ecuación (4) es equivalente a que las curvaturas de los brazos de grieta sean iguales, es decir, la condición de Williams para modo II puro.

La condición dada en la ecuación (3) se considera más adecuada que la condición dada en la ecuación (4). El motivo es que en el cálculo de desplazamientos horizontales de (3) no intervienen fuerzas cortantes y el efecto de la zona local de la punta de grieta afecta mucho menos que en los desplazamientos verticales de (4). En este último caso, la determinación de desplazamientos verticales incluye el efecto del cortante y los desplazamientos debidos a la rotación de la punta de grieta.

3 Descomposición de modos en flexión y cortadura

3.1 Descripción del problema

La tasa de liberación de energía de deformación corresponde a la diferencia de coenergía antes y despúes del avance de grieta dividida entre la variación de longitud de grieta y del ancho, manteniendo constantes las fuerzas aplicadas, de acuerdo a la ecuación (1). Aunque la energía y coenergía de deformación son iguales en sistemas elásticos lineales sin deformaciones iniciales, las variables de estado de la energía son la longitud de grieta y los desplazamientos, mientras que las de la coenergía son la longitud de grieta y las fuerzas aplicadas.

Dado que la coenergía varía debido al crecimiento de grieta, se analiza un elemento de longitud Δa. Se tendrán en cuenta los momentos flectores y las fuerzas cortantes. La Figura 2 muestra los momentos flectores y fuerzas cortantes antes del avance de grieta.

Figura 2. Descomposición de desplazamientos.

El brazo superior se denomina 1 y el brazo inferior 2. Ambos brazos pueden ser de material y espesor diferente.

3.2 Momentos flectores en modo I y II

Considerando únicamente el efecto de la flexión, la energía complementaria ${\textstyle {C}_{a}}$ antes del avance de grieta viene dada por:

${\textstyle {C}_{af}={\frac {{\left({M}_{1}+{M}_{2}\right)}^{2}}{2D}}\Delta a}$

(5)

Donde ${\textstyle D}$ es la rigidez a flexión de toda la sección. Tras el avance de grieta, la energía complementaria ${\textstyle {C}_{d}}$ es:

${\textstyle {C}_{df}=\left({\frac {{M}_{1}^{2}}{2{D}_{1}}}+{\frac {{M}_{2}^{2}}{2{D}_{2}}}\right)\Delta a}$

(6)

Donde ${\textstyle {D}_{1}}$ y ${\textstyle {D}_{2}}$ son las rigideces a flexión de las partes 1 y 2, respectivamente. De acuerdo a la ecuación (1) la tasa crítica de liberación de energía es:

${\textstyle {G}_{f}={\frac {{C}_{df}-{C}_{af}}{b\left(\Delta a\right)}}=}$${\frac {1}{2bD}}\left[{M}_{1}^{2}{r}_{1}+{M}_{2}^{2}{r}_{2}-{\left({M}_{1}+{M}_{2}\right)}^{2}\right]$

(7)

Donde ${\textstyle {r}_{1}}$ y ${\textstyle {r}_{2}}$ son las relaciones entre rigideces a flexión. Aplicando el principio de superposición los momentos flectores de cada brazo de grieta se descomponen en los correspondientes a los modos de fractura I y II:

${\textstyle {\begin{matrix}{M}_{1}={M}_{1I}+{M}_{1II}\\{M}_{2}={M}_{2I}+{M}_{2II}\end{matrix}}}$

(8)

Sustituyendo la ecuación (8) en la ecuación (7) se puede escribir ${\textstyle G}$ en función de los momentos en modo I y II y por lo tanto se obtienen las tasas de liberación de energía correspondientes a cada modo:

${\textstyle {\begin{matrix}{G}_{IM}={\frac {1}{2bD}}\left[{M}_{1I}^{2}\left({r}_{1}-1\right)+{M}_{2I}^{2}\left({r}_{2}-1\right)-2{M}_{1I}{M}_{2I}\right]\\{G}_{IIM}={\frac {1}{2bD}}\left[{M}_{1II}^{2}\left({r}_{1}-1\right)+{M}_{2II}^{2}\left({r}_{2}-1\right)-2{M}_{1II}{M}_{2II}\right]\end{matrix}}}$

(9)

Por otra parte, la suma de términos que contienen productos de momentos en modos I y II deben ser nulos dado que los modos son independientes, es decir:

${\textstyle {M}_{1I}{M}_{1II}\left({r}_{1}-1\right)+{M}_{2I}{M}_{2II}\left({r}_{2}-\right.}$$\left.1\right)-\left({M}_{1I}{M}_{2II}+{M}_{1II}{M}_{2I}\right)=0$

(10)

Se supone ahora que los momentos de cada modo están relacionados según dos parámetros ${\textstyle {c}_{I}}$ y ${\textstyle {c}_{II}}$:

${\textstyle {\begin{matrix}{M}_{2I}={{c}_{I}M}_{1I}\\{M}_{2II}={{c}_{II}M}_{1II}\end{matrix}}}$

(11)

Sustituyendo la ecuación (11) en la ecuación (10):

${\textstyle \left({r}_{1}-1\right)+{c}_{I}{c}_{II}\left({r}_{2}-1\right)-}$$\left({c}_{II}+{c}_{I}\right)=0$

(12)

Utilizando la condición de descomposición de modos de la ecuación (3) se tiene la relación entre momentos de modo I:

${\textstyle {\frac {{M}_{1I}{h}_{1}}{2{D}_{1}}}=-{\frac {{M}_{2I}{h}_{2}}{2{D}_{2}}}}$

(13)

De la ecuación (16) se obtiene c_I y sustituyendo en (15) se obtiene c_II siendo:

${\textstyle {c}_{I}=-{\frac {{h}_{1}{r}_{1}}{{h}_{2}{r}_{2}}}}$ ${\textstyle {c}_{II}=}$${\frac {{h}_{1}{r}_{1}+{h}_{2}{r}_{2}\left({r}_{1}-1\right)}{{h}_{2}{r}_{2}+{h}_{1}{r}_{1}\left({r}_{2}-1\right)}}$

(14)

De las ecuaciones (11) y (14) se pueden obtener los momentos en los distintos modos:

${\textstyle {\begin{matrix}{M}_{1I}={\frac {{c}_{II}{M}_{1}-{M}_{2}}{{c}_{II}-{c}_{I}}}\\{M}_{1II}={\frac {{{M}_{2}-c}_{I}{M}_{1}}{{c}_{II}-{c}_{I}}}\end{matrix}}}$

(15)

Combinando las ecuaciones(15) con las ecuaciones (9) y pueden determinarse ${\textstyle {G}_{IM}}$ y ${\textstyle {G}_{IIM}}$.

El modelo presentado establece la condición de desplazamientos tangenciales cerca de la punta de grieta sin tener en cuenta la zona no agrietada cercana a la punta de grieta, que de acuerdo a Williams [4] y Maimí [5] influye en la descomposición de modos.

3.3 Fuerzas cortantes en modo I y II

La tasa de liberación de energía debida al cortante puede determinarse mediante un procedimiento análogo al anterior. Considerando únicamente el efecto del cortante, la coenergía ${\textstyle {C}_{a}}$ antes del avance de grieta viene dada por:

${\textstyle {C}_{aQ}={\frac {{\left({Q}_{1}+{Q}_{2}\right)}^{2}}{2S}}da}$

(16)

Donde ${\textstyle S}$ es la rigidez a cortante de toda la sección. Después del avance de grieta, la coenergía ${\textstyle {C}_{dQ}}$ es:

${\textstyle {C}_{dQ}=\left({\frac {{Q}_{1}^{2}}{2{S}_{1}}}+{\frac {{Q}_{2}^{2}}{2{S}_{2}}}\right)da}$

(17)

Donde ${\textstyle {S}_{1}}$ y ${\textstyle {S}_{2}}$ son las rigideces a flexión de las partes 1 y 2, respectivamente. La tasa crítica de liberación de energía es:

${\textstyle {G}_{Q}={\frac {1}{2bS}}\left[{Q}_{1}^{2}{t}_{1}+{Q}_{2}^{2}{t}_{2}-\right.}$$\left.{\left({Q}_{1}+{Q}_{2}\right)}^{2}\right]$

(18)

Donde ${\textstyle {t}_{1}}$ y ${\textstyle {t}_{2}}$ son las relaciones entre rigideces a cortante. Las fuerzas cortantes se descomponen en las correspondientes a los modos de fractura I y II:

${\textstyle {\begin{matrix}{Q}_{1}={Q}_{1I}+{Q}_{1II}\\{Q}_{2}={Q}_{2I}+{Q}_{2II}\end{matrix}}}$

(19)

Sustituyendo la ecuación (19) en la ecuación (18) se obtienen términos correspondientes a modo I, modo II y combinación de modos. Como en el caso de flexión, la suma de términos que incluyen combinación de modos debe anularse:

${\textstyle {Q}_{1I}{Q}_{1II}\left({t}_{1}-1\right)+{Q}_{2I}{Q}_{2II}\left({t}_{2}-\right.}$$\left.1\right)-\left({Q}_{1I}{Q}_{2II}+{Q}_{1II}{Q}_{2I}\right)=0$

(20)

Además, las fuerzas cortantes están relacionadas únicamente con modo I. Ello se puede ver aplicando cargas unitarias horizontales en puntos homólogos. Estas cargas unitarias generan derivadas de momentos flectores, pero no de fuerzas cortantes. En consecuencia, la suma de términos relacionados con modo II también deben ser nula:

${\textstyle {Q}_{1II}^{2}\left({t}_{1}-1\right)+{Q}_{2II}^{2}\left({t}_{2}-\right.}$$\left.1\right)-2{Q}_{1II}{Q}_{2II}=0$

(21)

Relacionando las fuerzas cortantes de los distintos modos según:

${\textstyle {\begin{matrix}{Q}_{2I}={{k}_{I}Q}_{1I}\\{Q}_{2II}={{k}_{II}Q}_{1II}\end{matrix}}}$

(22)

En el caso del cortante se tienen dos condiciones para determinar k_I y k_II, sin atender a condiciones de desplazamiento relativo. Sustituyendo (22) en las condiciones dadas en las ecuaciones (20) y (21) se obtienen dos ecuaciones con las incógnitas k_I y k_II, que para un único material son:

${\textstyle {k}_{I}=-1}$ ${\textstyle {k}_{II}={\frac {{h}_{2}}{{h}_{1}}}=}$$c$

(23)

Sustituyendo los resultados en la ecuación (18), la tasa crítica de liberación de energía debida al cortante queda:

${\textstyle {\begin{matrix}{G}_{IQ}={\frac {{Q}_{1I}^{2}}{2bS}}\left[{\frac {{c}^{2}+2c+1}{c}}\right]\\{G}_{IIQ}=0\end{matrix}}}$

(24)

4 ENSAYOS DCB y ENF

La Figura 3 muestra una configuración general válida para DCB y ENF. En el caso de DCB, las cargas son iguales y de sentido opuesto. Sin embargo, en ENF las cargas dependen de los espesores y de las propiedades de cada uno de los brazos. El empotramiento se establece sin tener en cuenta el giro que existe en el ensayo ENF o en cualquier ensayo DCB asimétrico. Dicho giro corresponde a una rotación de sólido rígido que afecta a toda la probeta y por lo tanto no afecta a la variación de coenergía antes y después del avance de grieta. Los momentos en la punta de grieta son M₁ =F₁a y M₂ =F₂a.

Figura 3. Configuración general para DCB y ENF.

En el ensayo ADCB, las fuerzas son ${\textstyle {F}_{1}=P}$, ${\textstyle {F}_{2}=}$$-P.$

Se analizan ahora las fuerzas F₁ y F₂ en el caso de un ensayo ENF asimétrico. Las reacciones globales no varían debido a la asimetría y se supone que la transferencia de cargas entre ambos brazos es una fuerza concentrada encima del apoyo. La zona no agrietada no se ve afectada por esta fuerza hiperestática que se denominará Y. Por lo tanto, en el caso de ENF las fuerzas de la Figura 3 son ${\textstyle {F}_{1}=}$$Y$, ${\textstyle {F}_{2}={\frac {P}{2}}-Y}$.

En los brazos 1 y 2, los momentos y fuerzas cortantes en la zona agrietada son:

${\textstyle {M}_{(1)}=Yx{\begin{matrix}&\end{matrix}}{Q}_{(1)}=Y}$

(25)

${\textstyle {M}_{(2)}=\left({\frac {1}{2}}P-Y\right)x{\begin{matrix}&\end{matrix}}{Q}_{(2)}=}$${\frac {1}{2}}P-Y$

(26)

El valor de la incógnita Y se obtiene imponiendo la condición:

${\textstyle {\frac {\partial C}{\partial Y}}=0}$

(27)

Sustituyendo los términos de flexión y cortadura, la ecuación (27) queda:

${\textstyle {\begin{matrix}\int _{0}^{a}{\frac {{M}_{\left(1\right)}{M}_{\left(1\right),Y}}{{D}_{1}}}dx+\int _{0}^{a}{\frac {{M}_{\left(2\right)}{M}_{\left(2\right),Y}}{{D}_{2}}}dx\\\int _{0}^{a}{\frac {{Q}_{\left(1\right)}{Q}_{\left(1\right),Y}}{{S}_{1}}}dx+\int _{0}^{a}{\frac {{Q}_{\left(2\right)}{Q}_{\left(2\right),Y}}{{S}_{2}}}dx\end{matrix}}}$

(28)

De la ecuaciones (25), (26) y (28), la fuerza hiperestática Y resulta ser:

${\textstyle Y={\frac {P}{2}}{\frac {{a}^{3}{D}_{2}^{-1}+3,6a{S}_{2}^{-1}}{{a}^{3}{D}^{-1}+3,6a{S}^{-1}}}}$

(29)

Siendo ${\textstyle {D}^{-1}=\left({D}_{1}^{-1}+{D}_{2}^{-1}\right)}$ y ${\textstyle {S}^{-1}=}$$\left({S}_{1}^{-1}+{S}_{2}^{-1}\right)$

Sin tener en cuenta el efecto del cortante, la ecuación (29) queda:

${\textstyle Y={\frac {P}{2}}{\frac {{D}_{2}^{-1}}{{D}^{-1}}}}$

(30)

Si los brazos de grieta son del mismo material, (30) queda:

${\textstyle Y={\frac {P}{2}}{\frac {1}{{1+c}^{3}}}}$

(31)

Cuando c = 1, ${\textstyle Y={\frac {P}{4}}}$, que es el valor utilizado en ENF simétrico.

Una vez obtenidas las fuerzas cortantes y momentos flectores que corresponden a cada modo, puede analizarse el efecto de la asimetría en la relación de modos I y II de fractura interlaminar.

5 Conclusiones

Se propone un planteamiento global para descomposición de modos para flexión y cortadura, aplicable a ensayos DCB y ENF asimétricos. En el caso de flexión, se imponen las siguientes condiciones:

1. La suma de términos con productos de modos I y II debe ser nula.

2. Para que exista modo I puro el desplazamiento relativo tangencial de puntos homólogos debe ser nulo.

En el caso de la cortadura las condiciones son:

1. La suma de términos con productos de modos I y II debe ser nula.

2. No existe modo II asociado a cortadura.

La tasa de liberación de energía se determina mediante la variación de energía complementaria o coenergía antes y después del avance de grieta en cada uno de los casos. Se deben determinar las rigideces equivalentes a flexión y cortadura en el caso de uniones adhesivas de dos materiales diferentes.

Es necesario contrastar las fórmulas obtenidas en el presente estudio con ejemplos numéricos de ensayos DCB y ENF asimétricos, con el fin de evaluar la idoneidad de las hipótesis realizadas.

Agradecimientos

Los autores agradecen a la Universidad del País Vasco (UPV/EHU) la financiación del Grupo de Investigación Mecánica de Materiales GIU 16/51 en la convocatoria de 2016.

Referencias

[1] J.G. Williams, International Journal of Fracture 36, pág. 101-119 (1988). DOI: 10.1007/BF00017790

[2] V.Mollón, J. Bonhomme, J. Viña, A. Argüelles, Polymer Testing 29, pág. 766-770 (2010). DOI: 10.1016/j.polymertesting.2010.04.001

[3] P.S. Valvo, Engineering Fracture Mechanics, 165, pág. 114-139 (2016). DOI: 10.1016/j.engfracmech.2016.08.010

[4] J.G. Williams, Procedia Engineering 114, pág 189–198 (2015). doi: 10.1016/j.proeng.2015.08.058

[5] P. Maimí, N. Gascons, L. Ripoll, J. Llobet, International Journal of Solids and Structures, 155, pág. 36-46 (2018). DOI: 10.1016/j.ijsolstr.2018.06.032