Clúster de PCs tipo Beowulf Utilizado en un Problema de Segmentación de Imágenes Médicas

Clúster de PCs tipo Beowulf Utilizado en un Problema de Segmentación de Imágenes Médicas

José Luis Fraga Almanza$^{1\ast }$, Carlos Eduardo Rodríguez García$^{1}$ Roberto Costancio Torres Ramírez$^{1}$

$^{1}$Facultad de Ciencias Físico Matemáticas, UAdeC

$^{\ast }$Autor por correspondencia: josefraga@uadec.edu.mx

Resumen

En este trabajo se muestran las etapas principales de la implantación de un Clúster tipo Beowulf, en la Facultad de Ciencias Físico Matemáticas de la Universidad Autónoma de Coahuila. En éste se implementó el algoritmo de agrupamiento de datos K-Means, con la finalidad de distribuir (no de paralelizar) el proceso de clasificación de píxeles en las imágenes. También se realizó un preprocesamiento para la selección de los centroides iniciales requeridos por el algoritmo para una mejor segmentación de imágenes, que como se mostrará logra mejores resultados para el análisis de imágenes digitales médicas, como la segmentación de las mamografías que buscan microcalcificaciones dentro de la mama, que las obtenidas al implantarse de forma secuencial.

Palabras clave: Clustering, K-Means, MPI4Py, Microcalcificaciones.

2 Introducción

El uso intensivo de las computadoras personales (PCs) para dar solución a problemas científicos se dio desde la década de los 70s del siglo pasado, y aun cuando las capacidades computacionales emergían de manera exponencial, la mayoría del equipo a pesar de ser útil, dadas las nuevas necesidades, se volvía rápidamente obsoleto. Esta situación originó la necesidad de diseñar y construir procesadores cada vez más rápidos, de bajo costo y redes tipo ethernet altamente eficientes, aprovechando los avances en la tecnología. Estos desarrollos favorecieron un cambio en la relación precio/prestación en favor del uso de un conjunto de PCs interconectadas a una red ethernet, en lugar de un único procesador de alta velocidad, para resolver un problema dado en común [1]. A este conjunto se le llamó clúster. En el año 1994, en la revista National Aeronautics and Space Administration (NASA), Becker y Sterling, presentaron el desarrollo de un tipo particular de clúster llamado Beowulf, [2], utilizando una metodología de multicomputadoras para aplicaciones paralelas/distribuidas (APD). Un clúster de este tipo consiste básicamente de un servidor y uno o más clientes (o esclavos) conectados por medio de una red ethernet y sin ningún hardware específico. En sus inicios el primer sistema operativo que se utilizó en este tipo de clústeres fue GNU/Linux, esto no quiere decir que sea el único, se pueden utilizar otros sistemas operativos incluyendo los privativos (Sun Solaris, HP-UX, Microsoft Windows y IBM AIX). Las características que tienen los sistemas operativos de código abierto [3], son la clave para que sean utilizados generalmente en los clústeres tipo Beowulf. En este trabajo se presentan las etapas y pasos que se realizaron para la instalación y configuración del clúster Beowulf utilizando el sistema operativo FreeBSD, que es un descendiente de la Berkeley Software Distribution (BSD) y derivado de UNIX, [4]. La implementación del clúster se llevó a cabo en la Facultad de Ciencias Físico Matemáticas (FCFM) de la Universidad Autónoma de Coahuila (UAdeC), con la finalidad de implementar el algoritmo K-Means para realizar el análisis de imágenes médicas, específicamente mamografías digitales que se usan para identificar microcalcificaciones en la misma.

3 Desarrollo del clúster tipo Beowulf

A continuación se presentan los pasos realizados, ver Figura 1, para la conexión y configuración de los elementos que forman el clúster tipo Beowulf de la FCFM de la UAdeC.

Pasos en el desarrollo del Clúster tipo Beowulf, FCFM, UAdeC. Fuente: Elaboración propia.

Figura 1: Pasos en el desarrollo del Clúster tipo Beowulf, FCFM, UAdeC. Fuente: Elaboración propia.

3.1 Adecuación del hardware actual

La FCFM de la UAdeC contaba con doce computadoras activas de tipo genéricas. Una de ellas se caracterizaba por tener una placa base marca Intel con un procesador intel core 2 duo, memoria RAM de 4GB y una capacidad de disco de 500GB. Estas características permitieron adecuarla para que funcionara como el nodo maestro, es decir, como la computadora donde se instalaron las librerías, el software y las configuraciones necesarias para la comunicación y réplica de flujos de datos a las once computadoras restantes que al contar con placas base Intel y tipo de procesador Xeon E5 de 16 núcleos, memoria RAM de 16GB y un disco de capacidad de 500GB, por lo que podían convertirse en los nodos esclavos que realizarán las tareas intensivas en la resolución del problema que tuvieran en común. También se contaba con una red ethernet de alta velocidad con un switch de la marca 3COM de 24 puertos con capacidad 10/100/1000Mbs y con módulos de fibra óptica, la cual permitió la interconexión del equipo maestro y los equipos esclavos. La instalación física de los equipos se realizó a través de un rack que cuenta con ventilación independiente de la marca Sun Microsystems. En la Figura 2 se muestran los equipos de cómputo conectados y listos para instalar el software requerido. Como respaldo de energía se cuenta con dos Smart-UPS 3000XL de la marca APC, que es en donde están conectados la mayor parte de los equipos del clúster.

Figura 2: Instalación física de los elementos del clúster de la FCFM de la UAdeC. Fuente: Elaboración propia.

La configuración física implica atornillar los equipos en el rack, conectar los cables de energía y los cables de red a las tarjetas de red de los equipos, pero también deben ser conectadas al switch principal, para formar la red ethernet que se utiliza en el clúster.

3.2 Red ethernet

Una vez que se preparó y adecuó el hardware como se indicó en la sección 3.1, se llevó a cabo la conexión. La configuración lógica de la red ethernet del clúster de la FCFM de la UAdeC es la comunicación entre el nodo maestro y los nodos esclavos, ésta se llevó a cabo por medio de direcciones del tipo Internet Protocol (IP) privadas (10.10.1.0/24). La conexión física y lógica de las PCs, es la parte medular del clúster. La conexión y configuración de red que se tiene actualmente se puede observar en la Figura 3, de esta manera el clúster realiza todas las tareas que se le envíen.

Red ethernet del clúster FCFM de la UAdeC. Fuente: Elaboración propia.

Figura 3: Red ethernet del clúster FCFM de la UAdeC. Fuente: Elaboración propia.

Los nodos del clúster deberán estar registrados en el archivo /etc/hosts del nodo maestro con sus respectivas direcciones IP y sus nombres (host name). De la misma manera que se configuró el nodo maestro, se debe hacer una configuración equivalente en todos y cada uno de los nodos esclavos, es preferible que se tenga instalado y configurado un servicio de DHCP para que la asignación de direcciones IPs en el clúster sea de manera dinámica (esto es realmente útil cuando se tiene una gran cantidad de nodos en el clúster).

3.3 Instalación del software

El software utilizado en el clúster es del tipo software libre. La instalación se hizo mediante el manejador de paquetes que en este caso se llama pkg, que es una herramienta de apoyo para llevar a cabo la tarea de descargar, instalar y configurar el programa requerido. Los lenguajes de programación escenciales en el clúster son C, C++ y Fortran, que están contenidos en el paquete llamado GNU Compiler Collection (GCC), el cual es utilizado para llevar a cabo instalaciones de software adicional, por ejemplo, cuando sólo se cuenta con su código fuente, pero también es utilizado por pkg para realizar tareas de configuración e instalación de dependencias requeridas por algún otro software adicional, la instalación se realiza de la siguiente manera:

pkg install lang/gcc

A continuación se presenta una lista que es un subconjunto de los lenguajes, programas y librerías que se requieren adicionalmente para llevar a cabo la segmentación de las imágenes digitales.

1. MPI
2. Linear Algebra Package (LAPACK)
3. Scalable LAPACK (ScaLAPACK)
4. Python
5. MPI4Py

MPI es un modelo de comunicación ampliamente usado en computación paralela y distribuida, en [5], se puede encontrar una buena introducción a este modelo de comunicación. Es un estándar que define la sintaxis y la semántica de las funciones, contenidas en una biblioteca de paso de mensajes diseñada para ser usada en programas que hagan uso de multiples procesadores. Se instala con la siguiente instrucción:

pkg install net/mpich

LAPACK es una colección de subrutinas escritas en FORTRAN que sirven para resolver problemas matemáticos y que son parte del álgebra lineal numérica. Las subrutinas de LAPACK se basan en otras subrutinas más sencilla que se conocen por la sigla BLAS (Basic Linear Algebra Subprograms). La instalación de LAPACK se hace de la siguiente forma:

pkg install math/lapack

ScaLAPACK es un conjunto de rutinas LAPACK rediseñadas para la computación paralela de memoria distribuida. Está diseñado para computación heterogénea y es portátil en cualquier computadora que admita MPI, depende de PBLAS de la misma forma que LAPACK depende de BLAS. La instalación se realiza de la siguente forma:

pkg install math/scalapack

Python es un lenguaje de programación de alto nivel, orientado a objetos, con una semántica dinámica integrada, es conocido por su gran variedad de usos, por ejemplo, inteligencia artificial, big data, cómputo científico, etc. La instalación es la siguiente.

pkg install py37-pip

Adicionalmente para la implementación del clúster es necesario instalar Python Intel, que es una distribución relativamente nueva de Python, desarrollada por Intel para la Deep Learning & Vision Tools. Los detalles de esta distribución de Python se pueden encontrar en [6]. La instalación se lleva a cabo mediante un archivo ejecutable llamado bash_setup_intel_python.sh, para detalles de instalación consultar en [6]. MPI4Py es un estándar de MPI para Pyhton, permite a los programas escritos en Python ejecutarse en computadoras con múltiples procesadores, en [7] se explica a detalle todo sobre éste modelo de programación en Python.

3.4 Administración básica del clúster

La tarea principal que se lleva a cabo en el uso del clúster es su administración, esto implica hacer lo siguiente.

• Crear cuentas de usuarios.
• Preparar el directorio Net File System (NFS): /export/aplicaciones.
• Monitorear el estado del clúster con Ganglia.

Las cuentas de usuario se crean utilizando el comando useradd de UNIX, previamente el administrador deberá crear los grupos de trabajo para dar una jerarquía adecuada en el clúster. En este caso existen los grupos: investigadores y alumnos, son grupos con ciertos privilegios ante el sistema operativo para poder clasificar los procesos enviados a los nodos esclavos. El NFS es un sistema que permite accesar localmente a un sistema de archivos que se encuentra en un dispositivo físico remoto, es decir, NFS permite tener acceso inmediato a los archivos de otra computadora como si fueran archivos de una computadora local. Este sistema utiliza los protocolos RPC (Remote Procedure Call), la preparación de su configuración en el nodo maestro que exporta el sistema de archivos permite definir quiénes pueden acceder al sistema de archivos y con qué privilegios (lectura, escritura, etc.). La configuración se realiza mediante la edición del archivo ubicado y llamado /etc/exports. La sintaxis básica de este archivo es como sigue:

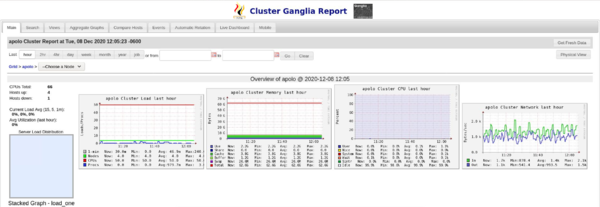
<sistema de archivos> <regla\_IP> (opciones). <regla\_IP> (opciones), 

donde sistema de archivos es el directorio asociado al sistema de archivos que se quiere exportar, regla_IP es una regla que define las IPs que se pueden montar de manera remota con NFS, el sistema de archivos y opciones definen en NFS los privilegios que se otorgarán. Para monitorear el estado del clúster se utiliza una interfaz web llamada Ganglia, es una herramienta que hace uso de un servidor web como Apache [8]. A continuación se muestra un ejemplo de Ganglia funcionando en el clúster de la FCFM de la UAdeC.

Figura 4: Ganglia, herramienta para monitoreo del clúster FCFM de la UAdeC. Fuente: Elaboración propia.

En la Figura 4 se observa en la parte superior un conjunto de pestañas que representan diferentes visualizaciones del clúster para observar el estado en que se encuentra su funcionamiento. También se muestra el nombre apolo que se le dió al clúster en su configuración, en la parte media se presentan algunas gráficas de diferentes elementos que conforman el clúster como lo es su memoria RAM, el CPU, el flujo de Red y otras más. En el ejemplo se muestra que en este momento se encuentran 66 procesadores activos en cuatro PCs y que un nodo no esta funcionando bien y por lo tanto Ganglia lo reporta como un nodo inactivo.

4 Problema de agrupamiento de datos

El agrupamiento de datos, es considerado uno de los problemas relevantes en el aprendizaje no supervisado [9]. Es decir, como en todos los problemas de este tipo, lo que se trata de hacer es encontrar grupos en un conjunto de datos. De manera más general, puede definirse el agrupamiento de datos como el proceso de organización de objetos que son muy similares de alguna manera, ver Figura 5.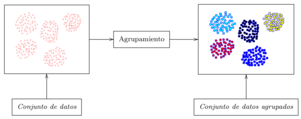

Figura 5: Agrupamiento de puntos en $\mathbb {R} ^{2}$. Fuente: Elaboración propia.

Definición 1: Dado un conjunto $D$ de datos con $n$ objetos en un espacio $m$-dimensional, agrupar datos es particionar los mismos en $k$ grupos tales que los puntos dentro de un grupo son más similares entre ellos que con otros grupos, dicha similitud se mide atendiendo a alguna función distancia.

4.1 El algoritmo K-Means

Una solución al problema de agrupamiento de datos se da al aplicar algoritmos de agrupamiento, como el K-Means. Este algoritmo tiene caractarísticas simples y una gran cantidad de variantes como se describe en [10]. A continuación se mencionan algunos aspectos del algoritmo K-Means implementado en el Clúster, para mayor detalle, consultar en [9,11]. Algoritmo K-Means Dado un conjunto de datos $D=\left\{x_{1},x_{2},\ldots ,x_{n}\right\}$ y un $k$ número de clústers a formar, entonces

1. Seleccionar un conjunto arbitrario o aleatorio de centroides iniciales en ${\textstyle D}$ para los ${\textstyle k}$ clústers: ${\textstyle c_{1},c_{2},\ldots ,c_{k}}$.
2. Para cada ${\textstyle x_{j}}$ de ${\textstyle D}$, encontar el centroide ${\textstyle c_{j}}$ más cercano a ${\textstyle x_{i}}$ y asignamos ${\textstyle x_{j}}$ al clúster ${\textstyle C_{j}}$

$C_{j}=\displaystyle {\underset {1\leq j\leq k}{\min }}||x_{i}-c_{j}||.$

3. Para cada uno de los clústers recalcular su centroide basado en los elementos que están contenidos en el clúster.
4. Repetir los pasos 2 y 3 hasta que

   $q_{j}=\sum \limits _{v\in \pi _{j}}\|a_{v}-m_{j}\|_{2}^{2}$

donde ${\textstyle q_{j}}$ es una partición de los ${\textstyle k}$ grupos.

${\begin{aligned}&{\underset {\Pi }{\hbox{min}}}&&Q(\Pi )=\sum \limits _{j=1}^{k}q_{j}=\sum \limits _{j=1}^{k}\sum \limits _{v\in \pi _{j}}\|a_{v}-m_{j}\|_{2}^{2}.\end{aligned}}$

El algoritmo K-Means proporciona agrupamientos buenos y malos. Enseguida se presenta un ejemplo de buen agrupamiento y otro de mal agrupamiento.

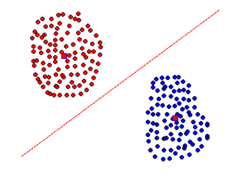
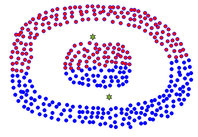
(a) Buen agrupamiento.	(b) Mal agrupamiento.
Figura 6: Ejemplos de agrupamiento de puntos en $\mathbb {R} ^{2}$ con K-Means. Fuente: Elaboración propia.

Se observa que en el caso del buen agrupamiento se puede trazar una recta que divida al plano en regiones, cada una de ellas conteniendo a uno de los grupos. En el caso de un mal agrupamiento es imposible trazar una recta con esas caracterísiticas. Esta es la clave para saber cuando K-Means dará un buen agrupamiento. A pesar de ser utilizado ampliamente en una gama de aplicaciones, el algoritmo K-Means no está exento de limitaciones. Algunos de los inconvenientes que presenta han sido ampliamente descritos en la literatura [12]. Existen técnicas o variantes de K-Means que intentan superar estas limitaciones, por ejemplo en el trabajo realizado por Fraga, Mederos y Madrid [13,14] se propone una variante a la hora de seleccionar los centroides iniciales, misma que se utiliza en este trabajo.

4.2 Imágenes en escala de grises

En una imagen digital a escala de grises, cada pixel puede definir solamente una tonalidad de gris (luminosidad) y el número de pixeles define la cantidad de información que contiene la imagen. Las tonalidades están comprendidas en el intervalo $[0,255]$ donde el tono negro es el valor de $0$ y el blanco es el valor de $255$, ver Figura 7. Una representación matemática de una imagen en escala de grises en una computadora puede definirse asociándole a cada pixel una terna $(x,y,t)$, donde $x$, $y$ representa la posición del pixel y $t$ su tonalidad, por lo tanto una imagen digital es un conjunto representado en tres dimensiones.

Figura 7: Escala de grises de 0 a 255. Fuente: [9].

Una imagen se representa por una matriz. En la Figura 8 se observa un ejemplo de una imagen digital en escala de grises, representada en la computadora.

$\rightarrow$ $\left[{\begin{array}{cccccccccc}248&253&255&0&7&2&0&255&253&255\\253&255&0&255&248&253&255&0&251&255\\1&0&255&250&255&255&247&249&0&3\\4&246&255&0&249&5&255&255&255&0\\3&255&248&2&255&0&246&251&249&0\\0&251&255&254&247&255&255&4&255&0\\6&255&244&251&255&255&0&0&251&9\\0&252&255&0&1&0&6&255&245&1\\255&3&254&255&252&254&255&238&1&255\\238&251&8&0&0&5&0&4&250&250\end{array}}\right]$

Figura 8: Representación de una imagen en una computadora. Fuente: Elaboración propia.

Si la imagen digital es de $m\times n$ entonces la representación de los datos para ser agrupados con K-Means es una matriz de orden $mn\times 3$ donde las primeras dos columnas son las posiciones $x$, $y$ en la matriz y la tercer columna es la tonalidad. De esta manera cada renglón de la matriz de datos representa un pixel de la imagen.

4.3 Segmentación de imágenes

La segmentación de imágenes es un tipo particular de agrupamiento de datos, en este sentido se puede utilizar K-Means y llevar a cabo este tipo de agrupamiento. Cada segmento o grupo de la imagen tiene las siguientes propiedades:

1. Las componentes ${\textstyle x}$ y ${\textstyle y}$ de cada pixel están cercanas entre sí, es decir, están cercanas geométricamente.
2. Las componentes ${\textstyle t}$ de cada pixel tienen tonos de gris cercanos entre sí.

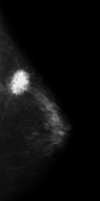
Figura 9: Imagen con resolución 1024Mp. Fuente: Proyecto en desarrollo, División de Ciencias Exactas y Naturales de la UNISON.

A continuación se presentan los resultados proporcionados por K-Means de la segmentación de la Figura 9 que tiene un tamaño de $1280\times 800$ pixeles, por lo tanto una matriz de tamaño $1024000\times 3$, dando distintos valores de $k$ y con centroides iniciales arbitrarios, esto es, aplicando el algoritmo K-Means sin hacer alguna selección especial de los centroides iniciales. Un preprocesamiento (selección de centroides iniciales de manera adecuada al problema) como el que se presenta en [14] fue utilizado posteriormente para segmentar la misma imagen, obteniendose resultados mucho más significativos que utilizando el algoritmo sin él, como se puede ver en la Figura 11.

(a) Valor de $k=3$.	(b) Valor de $k=4$.
Figura 10: Segmentación de mamografía con K-Means con centroides iniciales arbitrarios. Fuente: Elaboración propia.

Las segmentaciones obtenidas en la Figura10 significan, que se buscan dentro de la mamografía, tres y cuatro tonalidades diferentes en la escala de grises. Por ejemplo en la Figura 10a solo se aprecia el contorno color blanco de la mamografía y dos tonalidades diferentes en el fondo. En la Figura 10b se aprecia que dentro de la mamografía hay cuatro tonalidades diferentes, blanco, negro y dos tonalidades de tipo diferente de gris, sin embargo, esto no proporciona información relevante, ya que se busca la existencia de microcalcificaciones dentro de la mamografía. Por tal motivo, es necesario realizar el preprocesamiento descrito en [14], que realice una elección adecuada de los centroides iniciales, para así hacer evidente la existencia de microcalcificaciones dentro de la mamografía.

(a) Valor de $k=3$ y preprocesamiento.	(b) Valor de $k=4$ y preprocesamiento.
Figura 11: Mamografía segmentada con K-Means, eligiendo centroides iniciales adecuados. Fuente: Elaboración propia.

En las Figuras 11a y 11b se observan mayores detalles dentro de la mamografía segmentada, esto significa que la segmentación ha mejorado. En ellas se puede distinguir la existencia de microcalcificaciones, por ejemplo, en la Figura 11a esas microcalcificaciones son de color blanco dentro de la mama, es decir, tonalidades que pertenecen a un mismo grupo. Aumentar el valor de $k$ es encontrar más características (grupos) en la mamografía que se está segmentando. Esto no significa que incrementar el valor de $k$ hará mucho mejor la segmentación, eso dependerá del tipo de problema que se esté trabajando. Utilizando el mismo preprocesamiento pero ahora escribiendo una versión distribuida del programa con MPI4Py e implementado en el clúster de la FCFM, se obtiene la segmentación que se muestra en la Figura 12.

(a) $k=3$ y MPI4Py.	(b) $k=4$ y MPI4Py.
Figura 12: Segmentación de una mamografia con K-Means, en forma distribuida. Fuente: Elaboración propia.

La forma distribuida ha mejorado significativamente la segmentación en la mamografía. En las Figuras 12a y 12b se observa que las microcalcificaciones están en color blanco y en el resto de la mamografía se aprecian diferencias de tonalidades de grises dibujando patrones distintos. Esto se debe a la elección adecuada de los centroides iniciales y por que en cada nodo del clúster se calculan centroides iniciales diferentes. El nodo maestro obtiene un vector de centroides diferentes y siguiendo el preprocesamiento descrito en [14] se vuelve a realizar una nueva segmentación. El programa que realiza la segmentación con K-Means en forma distribuida en el clúster se llama segkmeanspreale.py que utiliza las bibliotecas OpenCV y Numpy, su diagrama de flujo es:

Diagrama de Flujo programa: segkmeanspreale.py. Fuente: Elaboración propia.

Figura 13: Diagrama de Flujo programa: segkmeanspreale.py. Fuente: Elaboración propia.

La biblioteca MPI4Py es utilizada para distribuir los procesos en el clúster con la instrucción from mpi4py import MPI y se comunica por medio de MPI.COMM_WORLD con todos los procesos enviados al clúster. El esquema de envió de procesos sería como se puede observar en la Figura 14.

Figura 14: Concepto de comunicación de procesos con MPI. Fuente: [7].

La ejecución del programa se realiza con: mpiexec -f archivonodos -n 4 python3 -i mamografia.jpg -k 3 Para más detalles de cómo distribuir un programa utilizando MPI4Py revisar [7], documento base para llevar acabo el experimento que se presenta en este trabajo.

5 Conclusiones

El experimento de la segmentación de la imagen de una mamografía digital con la finalidad de identificar microcalcificaciones en la mama, con resultados altamente satisfactorios permiten ver la gran utilidad y ventaja de tener un clúster como herramienta computacional de apoyo en el análisis de este tipo de imágenes médicas, ya que en un momento dado se podrían eliminar las biopsias que resultan ser procedimientos invasivos para los pacientes. La construcción de un clúster tipo Beowulf representó ser para la FCFM de la UAdeC, una inversión de muy bajo costo en recursos financieros, pero de una muy alta utilidad para los investigadores y alumnos, quienes podrán utilizarlo para realizar su trabajo. Con él se puede hacer búsquedas de soluciones a problemas complejos, es una opción económica, sustentable y generadora de conocimiento tanto para investigadores como para los alumnos. Las ventajas que tienen este tipo de clústeres es que no requieren de hardware especial, ya que están compuestos de piezas que se pueden encontrar fácilmente en el mercado y a un bajo costo. El software libre es una gran oportunidad de aprendizaje tanto para alumnos como para investigadores de la FCFM, ya que proporciona la libertad que necesita el usuario para no depender de un presupuesto económico, ni estar sujeto a términos y condiciones de uso como lo impone el software privativo. Con este tipo de sofware se cuenta con programas, librerias y compiladores especializados en el área del cómputo científico. Un hecho importante de los clústeres tipo Beowulf es que las soluciones obtenidas al utilizarlos, se logran a menor costo, y por tanto existe un gran impacto económico, lo que justifica seguir construyendo supercomputadoras de este tipo.

BIBLIOGRAFÍA

[1] Daillidis Christos. (2004) "Establishig Linux Clusters for high-performance computing". Naval Postgraduate School

[2] Sinisterra, María Mercedes and Díaz Henao, Tania Marcela and Ruiz López, Erik Giancarlo. (2012) "Clúster de balanceo de carga y alta disponibilidad para servicios web y mail", Volume 76. Informador Técnico 93

[3] Prieto, S.S. and Población, Ó.G. and TOME, A.G. (2004) "Unix y Linux. Guía práctica, 3a edición". RA-MA S.A. Editorial y Publicaciones

[4] Wikipedia. (2020) "Berkeley Software Distribution" https://es.wikipedia.org/wiki/Berkeley_Software_Distribution

[5] Hidrobo, Francisco and Hoeger, Herbert. (2005) "Introduccón a MPI" Centro Nacional de Cálculo Científico Universidad de los Andes

[6] Intel inside. (2020) "Intel Distribution for Python" https://software.intel.com/content/www/us/en/develop/tools/distribution-for-python.html

[7] Pajankar, Ashwin. (2017) "Parallel Programming in Python 3". Raspberry Pi Supercomputing and Scientific Programming: MPI4PY, NumPy, and SciPy for Enthusiasts. Apress 87–97

[8] Massie, Matt and Li, Bernard and Nicholes, Brad and Vuksan, Vladimir and Alexander, Robert and Buchbinder, Jeff and Costa, Frederiko and Dean, Alex and Josephsen, Dave and Phaal, Peter and Pocock, Daniel. (2012) "Monitoring with Ganglia". O'Reilly Media, Inc., 1st Edition

[9] Gan, Guojun and Ma, Chaoqun and Wu, Jianhong. (2007) "Data clustering: theory, algorithms, and applications", Volume 20. Society for Industrial and Applied Mathematics

[10] Anil K. Jain. (2010) "Data clustering: 50 years beyond K-means", Volume 31. Pattern Recognition Letters 8 651 - 666

[11] Eldén, Lars. (2007) "Matrix methods in data mining and pattern recognition". SIAM

[12] Pérez, J and Henriques, MF and Pazos, R and Cruz, L and Reyes, G and Salinas, J and Mexicano, A. (2007) "Mejora al algoritmo de agrupamiento K-means mediante un nuevo criterio de convergencia y su aplicación a bases de datos poblacionales de cáncer". II Taller Latino Iberoamericano de Investigación de Operaciones

[13] Fraga Almanza, José Luis. (2011) "El Algoritmo K-Means y algunas aplicaciones". Universidad Autónoma de Coahuila. Facultad de Ciencias Físico Matemáticas, UAdeC

[14] Fraga Almanza, José Luis and Mederos Madrazo, Boris de Jesús and Madrid de la Vega, Humberto. (2015) "Segmentación de imágenes en escala de grises con K-Means". Tópicos Recientes sobre Aplicaciones de las Matemáticas en México 47-59