Modelització del deflectòmetre d’impacte amb el mètode dels elements finits i les partícules

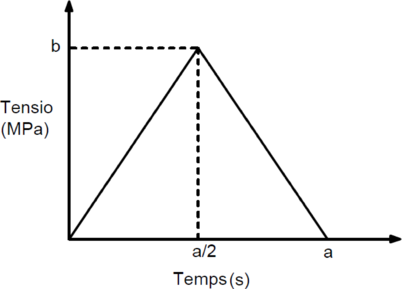
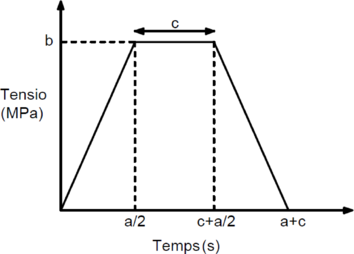
• Va bé que algú mostri esperit, - va dir-li Settembrini, mirant a l’aire melangiosament. Però es va revifar i, transigint gentilment, va continuar:

• En tot cas no crec que m’equivoqui en deduir de les seves paraules que ha escollit una professió tan fatigosa com honorable. Déu meu, jo sóc humanista, un homo humanus, no hi entenc gens, en qüestions de l’enginy, per més franc que sigui el respecte que em mereixen. Però sí que sóc capaç d’imaginar-me que, en la seva especialitat, la teoria exigeix un cap clar i penetrant, i la pràctica, un home sencer... No és així?

• Cert, és així, sí, en això estic completament d’acord – va respondre Hans Castorp, bo i procurant parlar involuntàriament amb una mica d’eloqüència –. Les exigències són colossals avui dia, no has de tenir gaire present que demanen molt rigor, altrament perdries de debò l’ànim. No, no és cap broma.

Thomas Mann, La muntanya màgica

Agraïments

Estic en deute amb diferents persones sense les quals no hauria estat possible aquest treball.

Vull donar les gràcies al meu professor i tutor, el Dr. Eugenio Oñate per haver-me brindat l’oportunitat de realitzar aquest treball al CIMNE.

També vull agrair molt sincerament la inestimable ajuda del Dr. Josep Maria Carbonell. Sense ell aquesta treball no hauria pas arribat a bon port.

Finalment vull agrair l’incalculable suport de la meva família, els meus pares i els meus germans Albert i Francesc. El deute és molt llarg i aquesta garlanda no en fa compliment.

Resum

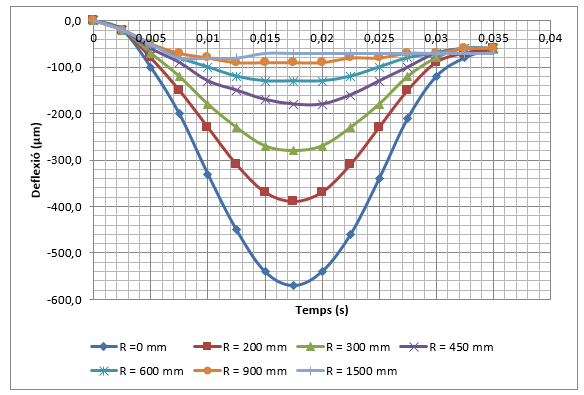
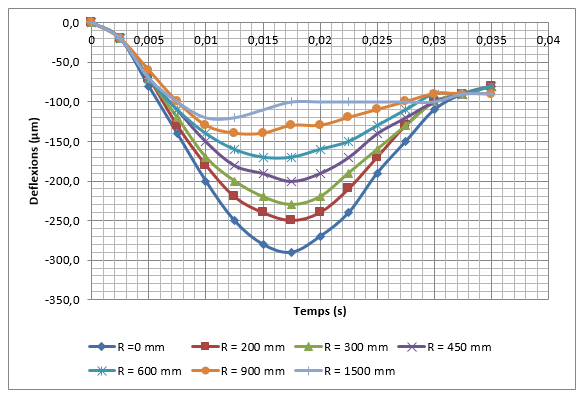
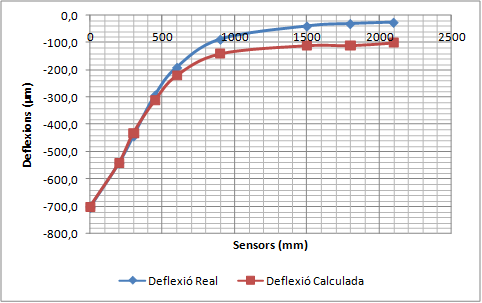
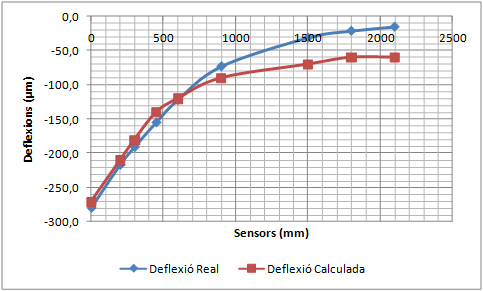
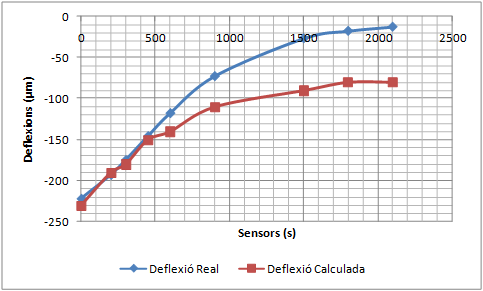
El deflectòmetre d’impacte segurament és l’aparell més utilitzat per realitzarassaigs no destructius dels ferms. Els enginyers utilitzen el deflectòmetre d’impacte per estimar els mòduls elàstics de les diferents capes que conformen el ferm assumint una aproximació quasi estàtica del fenomen. Amb la utilització del Mètode dels Elements Finits i les Partícules (PFEM), per una banda es pot simular l’impacte que provoca el deflectòmetre d’impacte sobre el ferm, i de l’altra validar el PFEM com a model axisimètric de resposta dinàmica d’un ferm.

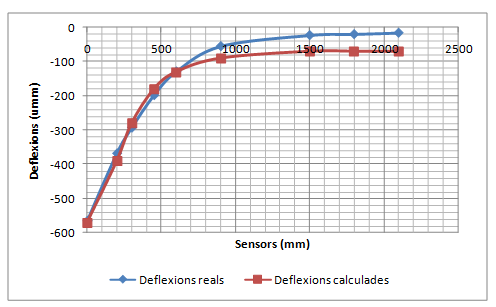
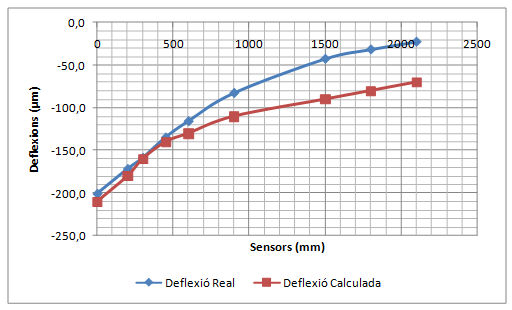
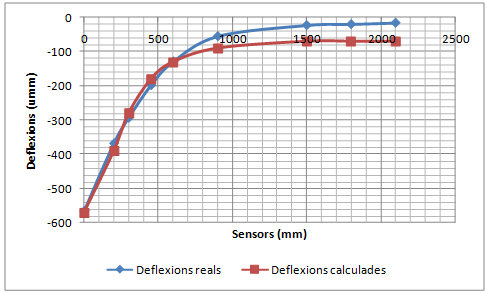
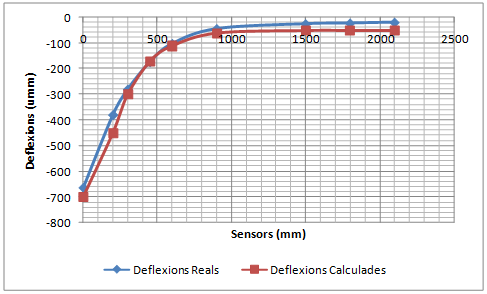
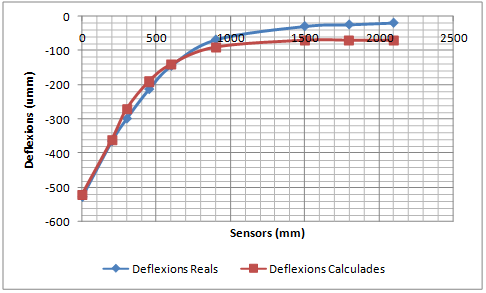
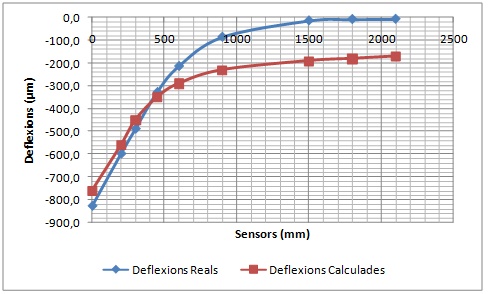
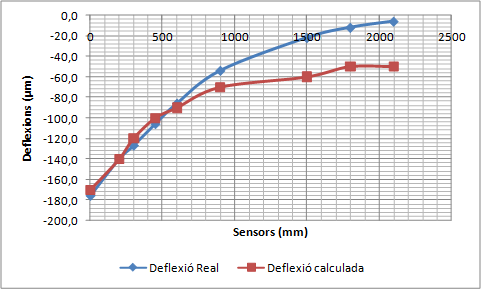
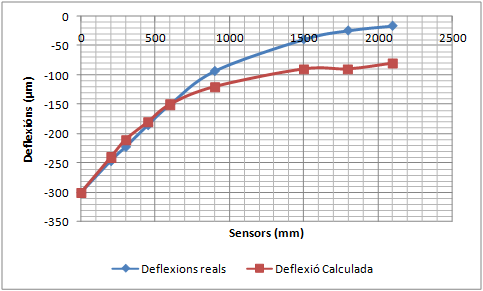
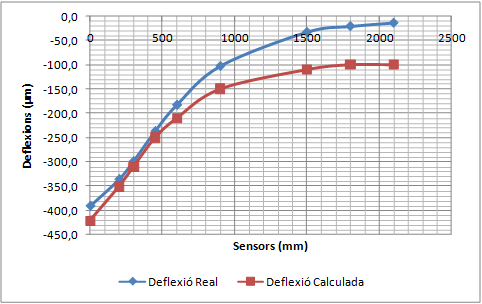
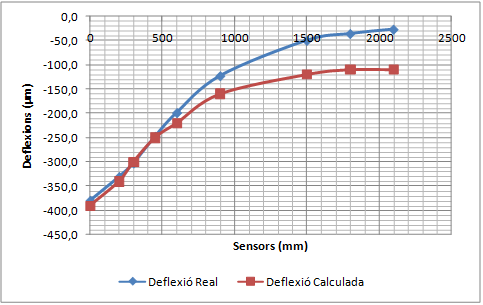
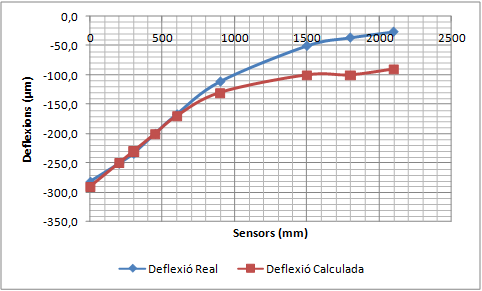
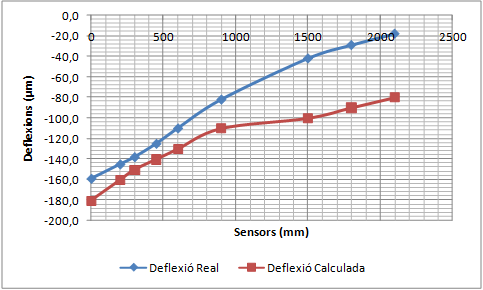
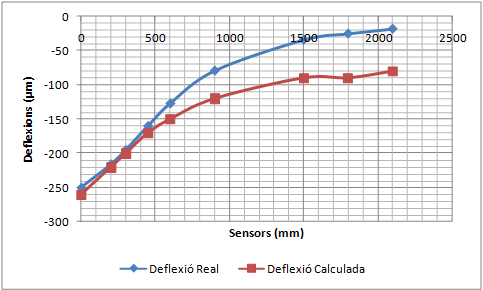
La validació consisteix a comparar la concavitat de deflexions mesurada pel deflectòmetre d’impacte amb la concavitat de deflexions calculada amb el PFEM utilitzant els mòduls elàstics que proporciona el càlcul invers.

Els capítols 2 i 3 inclouen el marc teòric en el qual es desenvolupa el treball. El capítol 2 inclou una introducció als ferms, presenta el concepte de deflexió, fa un repàs dels equips d’avaluació no destructiva i presenta un resum dels diferents mètodes existents per al càlcul de paviments flexibles. El capítol 3 és una introducció al Mètode dels Elements Finits i les Partícules.

El capítol 4 presenta els desenvolupaments dels objectius plantejats.

Per últim, es presenten unes consideracions finals, que inclouen les conclusions, possibles millores del programa d’ordinador emprat i propostes de futures línies d’investigació.

Els annexes inclouen els resultats de tots els casos calculats amb les taules i les gràfiques corresponents.

Abstract

The Falling Weight Deflectometer (FWD) is probably the most used device for the non-destructive testing of pavements. Engineers use the FWD for the estimation of the elastic modulus of the different layers which constitute the pavement assuming a quasi-static approach to the response. By using the Particle Finite Element Method (PFEM), one can on the one hand simulate the impact generated by the FWD on the pavement, and on the other validate the PFEM as an axysimmetric dynamic response model of a pavement.

The validation consists in comparing the deflection bowl measured by the FWD with that calculated with the PFEM using the elastic modulus obtained by the previous backanalysis.

Chapters 2 and 3 establish the framework in which this minor thesis is developed. Chapter 2 includes an introduction to pavements; presents the concept of deflection; reviews the different non-destructive testing devices and surveys the different available approaches to response models. Chapter 3 introduces the Particle Finite Elements Method.

In chapter 4, the developments of the previous objectives are presented.

Finally, final considerations are presented. They include the conclusions, proposals of improvements related with the used program and further lines of research.

In the annex, the results of the different calculated cases are included with all their graphics and tables.

1 Introducció i objectius

El deflectòmetre d’impacte s’adscriu al conjunt d’aparells pertanyents a la categoria d’equips d’auscultació estructural no destructiva de ferms. És un aparell que ha estat àmpliament acceptat per descriure i comprendre el comportament estructural dels ferms. El mode de funcionament consisteix a deixar caure una massa que impacte sobre una placa circular d’acer per aconseguir una força d’impacte sobre el ferm. L’aparell mesura la força d’impacte i els desplaçaments verticals del ferm (deflexions) a diverses distàncies de la càrrega al llarg del temps. Aquestes dades sovint s’han utilitzat pels enginyers per estimar el mòdul elàstic de les diferents capes que conformen un ferm. La majoria de vegades només tenen en compte els valors màxims de la càrrega d’impacte i de les deflexions, com si fossin les dades obtingudes d’un problema quasi-estàtic i posteriorment, amb models de ferms estàtics, s’obté l’estimació dels mòduls elàstics de les diferents capes del ferm (càlcul invers).

La comunitat científica ha discutit sobre la idoneïtat d’utilitzar models de ferms estàtics per obtenir els mòduls elàstics. Malgrat les opinions dels diferents estudiosos de la matèria, el fet que el deflectòmetre d’impacte es tracti d’un assaig purament dinàmic proporciona un argument sòlid a favor d’una anàlisi dinàmica.

La validesa dels mòduls elàstics obtinguts amb models de ferms estàtics sempre ha estat un tema de gran interès per part dels investigador i enginyers de ferms. La seva importància rau en aplicacions pràctiques com per exemple fer una estimació de la vida útil que li resta a un ferm o la necessitat de rehabilitar-lo.

Els objectius del present treball són els següents:

• Simular amb el Mètode dels Elements Finits i les Partícules (PFEM) la força d’impacte de l’assaig del deflectòmetre d’impacte.

• Realitzar una simulació dinàmica de les deflexions d’un ferm per validar el Mètode dels Elements Finits i les Partícules (PFEM) com a model de resposta d’un ferm. El procés de validació consistirà en comparar deflexions mesurades amb el deflectòmetre d’impacte amb les deflexions calculades amb el PFEM de casos ben diferents entre ells. Els mòduls elàstics necessaris per realitzar el càlcul directe amb el PFEM corresponen als valors proporcionats pel càlcul invers dels assaigs reals. Si les deflexions calculades coincideixen amb les deflexions mesurades, el PFEM queda validat com a model de resposta.

Els capítols 2 i 3 inclouen el marc teòric en el qual es desenvolupa el treball. El capítol 2 inclou una introducció als ferms, presenta el concepte de deflexió, fa un repàs dels equips d’avaluació no destructiva i presenta un resum dels diferents mètodes existents per al càlcul de paviments flexibles. El capítol 3 és una introducció al Mètode dels Elements Finits i les Partícules.

El capítol 4 presenta els desenvolupaments dels objectius plantejats.

Per últim, es presenten unes consideracions finals, que inclouen les conclusions, possibles millores del programa d’ordinador emprat i propostes de futures línies d’investigació.

Els annexes inclouen els resultats de tots els casos calculats amb les taules i les gràfiques corresponents.

2 Ferms de carretera

2.1 Introducció als paviments flexibles

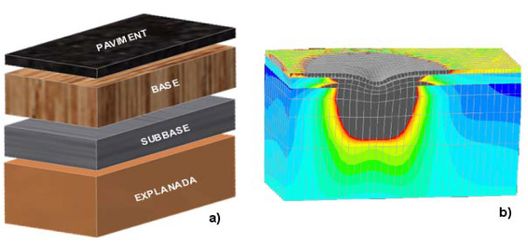
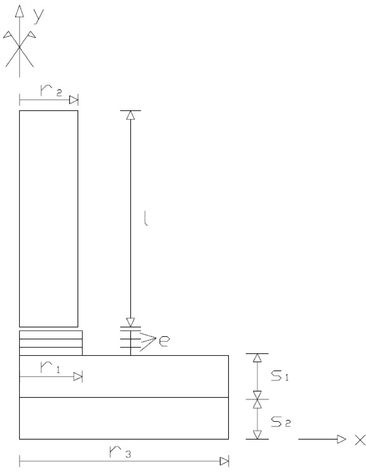
Els ferms de carretera són elements estructurals formats per un conjunt de capes superposades, relativament horitzontals i d’alguns centímetres d’espessor, de materials diversos, adequadament compactats, que recolzen sobre una esplanada obtinguda pel moviment de terres (veure Figura 2.1). La seva funció és proporcionar una superfície de rodadura segura, còmode i de característiques permanents que suportin les càrregues dinàmiques del trànsit durant un període de temps determinat. El mecanisme de funcionament consisteix a repartir les tensions imposades pel trànsit pesat, dissipant-les de manera que a l’esplanada només hi arribi una petita part de la tensió assumible per la seva capacitat portant. (Veure (1)).

Les esplanades, fins i tot les que estan dotades d’una major capacitat portant constituïdes per sòls granulars sense fins, només són capaces de suportar un trànsit lleuger i poc intens. L’acció de càrregues d’ordres de magnitud properes a 1 MPa, que són les que provoquen les rodes dels vehicles de transport col·lectiu de passatgers i de transport de mercaderies, provocarien amb prestesa deformacions inassumibles. Si a més a més s’hi suma el fet que la superfície seria lliscant i inestable en condicions de pluja i ple de pols en un ambient sec, la carretera no oferiria les prestacions de qualitat i seguretat exigibles.

Figura 2.1. Estructura (a) i funcionament (b) d’un ferm flexible de carretera

De les característiques que ha de complir el ferm, les característiques funcionals del paviment (capa de rodadura) que tenen una repercussió directe sobre els seus usuaris són:

• Proporcionar una superfície de rodadura segura, còmoda i de característiques permanents sota càrregues repetides de trànsit durant un període de temps raonable (la vida útil) que assegurin una bona adherència dels pneumàtics en qualsevol situació.

• Impermeabilitat per tal de protegir l’esplanada de la intempèrie, principalment pel problema que l’acció de l’aigua suposa sobre la resistència a l’esforç tallant dels sòls.

• Regularitat superficial, tant longitudinalment com transversalment. S’aconsegueix gràcies a una posta en obra adequada, malgrat el fet que la seva qualitat depèn directament de la qualitat assolida a les capes inferiors.

• Soroll de la rodadura limitat, tant a l’interior del vehicle (per protegir els usuaris) com a l’exterior (per minimitzar els nivells de contaminació acústica provocada en l’entorn). El soroll produït depèn principalment del contingut de buits del material i de la mida màxima de les partícules.

• Reflexió lluminosa, imprescindible per la conducció nocturna i el bon ús dels elements d’il·luminació, així com el bon contrast entre les marques viàries i el paviment.

• Aspecte estètic de la carretera.

Pel que fa als aspectes de durabilitat del ferm, s’han de garantir les següents característiques:

• Resistència front a les deformacions plàstiques.

• Resistència a l’envelliment per evitar fissures i despreniments.

• Resistència a la desintegració causada per l’acció de l’aigua.

• En ferms molt flexibles, especificació de la resistència a la fatiga. En vies de molt poc trànsit, s’exigeix que el ferm sigui deformable.

Les característiques estructurals dels ferms estan relacionades amb els materials empleats per fer cadascuna de les capes. La seva deformabilitat provoca discontinuïtats en les tensions i les deformacions en els plans de contacte entre dues capes diferents.

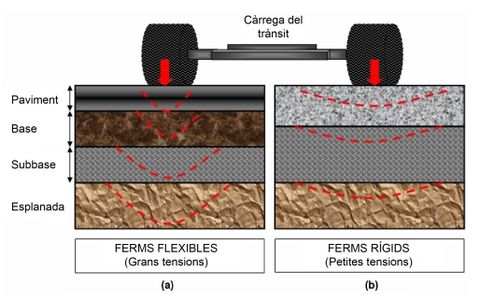
Els ferms de carretera es diferencien i es classifiquen segons els materials que els componen i la forma que tenen de distribuir els esforços i les deformacions generades pel trànsit. Tot i que bàsicament hi ha dos grans grups, els ferms flexibles i els ferms rígids (veure Figura 2.2), a continuació es presenta una relació dels principals tipus de ferms existents:

• Ferms flexibles, formats per una sèrie de capes constituïdes per materials amb una resistència a la deformació decreixent amb la profunditat. En general, tenen almenys una capa de trànsit bituminosa sobre capes granulars.

• Ferms semiflexibles o flexibles amb base bituminosa (que tenen un espessor de mescla bituminosa de 15 cm o més).

• Ferms semi-rígids, amb capes inferiors d’igual o major rigidesa que les superiors, formats per bases tractades o estabilitzades amb ciment o paviments bituminosos.

• Ferms inversos, en els quals entre el paviment bituminós i la capa tractada amb ciment s’interposa una capa granular per evitar la reflexió en superfície de les esquerdes produïdes per la retracció de la capa tractada.

• Ferms rígids, formats per un paviment de formigó sobre capes tractades o granulars. El paviment de formigó assegura la funció resistent del ferm. En els ferms rígids, les deflexions són gairebé inapreciables.

• Ferms mixtos, constituïts per una capa de formigó de baixa resistència i un paviment bituminós.

Figura 2.2 Estructura dels ferms flexibles (a) i dels ferms rígids (b) de carretera

Aquests grups de ferms, d’acord amb els materials utilitzats i els diferents espessors de les capes, tenen comportaments molt diferents en relació a la distribució de les tensions estàtiques un cop aplicades les càrregues dinàmiques del trànsit.

Sovint, els ferms semi-rígids i semiflexibles s’acostumen a incloure dins la categoria dels ferms flexibles perquè tenen unes capes superiors bituminoses anàlogues, però el seu comportament estructural és diferent, amb una menor deformabilitat sota una mateixa càrrega.

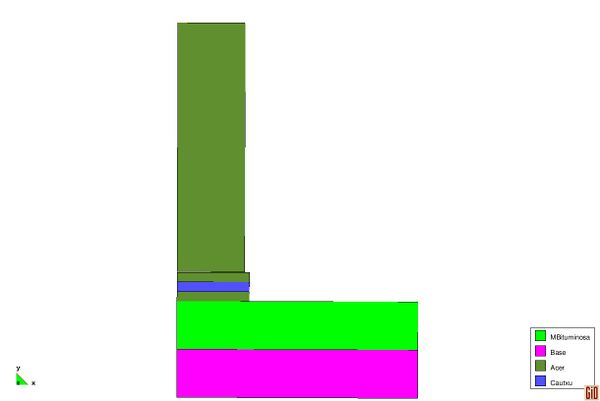
Els ferms flexibles, semiflexibles i semi-rígids estan formats per vàries capes anomenades de dalt a baix: paviment, base i subbase respectivament. Al seu torn, cadascuna d’aquestes capes pot estar formada per més d’una capa.

El paviment és la part superior del ferm i la que rep directament les sol·licitacions del trànsit. Des del punt de vista estructural, absorbeix els esforços horitzontals i part dels esforços verticals. Els paviments més comuns són els regs de graveta i les mescles bituminoses. Els regs de graveta s’utilitzen típicament en ferms de nova construcció per trànsits de baixa intensitat o per restaurar la textura de paviments ja existents. Les mescles bituminoses s’utilitzen en carreteres amb trànsits d’intensitat mitjana i alta. Quan l’espessor total del paviment és superior a 8 cm, generalment s’executa en dues capes: la capa de rodadura i la capa intermèdia. La capa de rodadura i la capa intermèdia tenen diferències de composició, sobretot en relació amb la resistència al poliment de l’àrid gros. Sovint la capa de rodadura és porosa per garantir que l’aigua de pluja s’infiltra ràpidament.

La base és la capa del ferm situada just sota el paviment. La seva raó de ser és estructural: s’encarrega d’absorbir la majoria dels esforços verticals. Per trànsits amb intensitats mitjanes i baixes s’utilitzen bases granulars amb graves i arenes triturades. En canvi, per trànsits amb intensitats elevades de vehicles pesats, s’utilitzen materials granulars tractats amb un lligant (bases de mescla bituminosa) o un conglomerant (bases de grava ciment).

La subbase és la capa del ferm situada sota la base i just sobre l’esplanada. En aquells casos en què l’esplanada tingui una alta capacitat portant, la subbase no és necessària. La seva funció és proporcionar a la base un suport uniforme i constituir una plataforma de treball adequada per a la seva posta en obra. Està constituïda per materials granulars com graves i arenes rodades o triturades.

En aquest treball es tractaran només ferms flexibles.

2.2 La deflexió com a paràmetre d’avaluació

Es defineix l’avaluació estructural dels ferms com la tècnica que proporciona un coneixement detallat de l’estat dels ferms, permetent efectuar una monitorització del seu comportament a través del temps d’un mode racional i econòmic.

La metodologia més emprada és l’auscultació estructural no destructiva, que ha anat variant al llarg del temps a mesura que progressaven els avenços tecnològics en matèria dels equips de medició desenvolupats. L’aparició de nous equips de medició cada cert temps ha permès una avaluació més sistemàtica dels paràmetres característics del ferm, assolint un elevat rendiment operacional que permet minimitzar l’afectació sobre la carretera.

Els resultats obtinguts i les mesures que s’atribueixen als sistemes d’auscultació estructural de ferms no són directes, sinó que s’obtenen de processar la informació obtinguda durant la feina de camp. Típicament en l’auscultació d’un ferm es mesuren deflexions.

S’entén per deflexió la deformació elàstica recuperada que produeix l’aplicació d’una càrrega tipus sobre la superfície d’un ferm, que constitueix una mesura de la seva capacitat portant. La deformació elàstica que experimenta un ferm sotmès al pas d’una càrrega és funció del tipus de ferm, del seu estat actual així com de l’equip de medició utilitzat i el mètode emprat. La mesura de la deflexió s’inscriu en el conjunt d’assaigs no destructius.

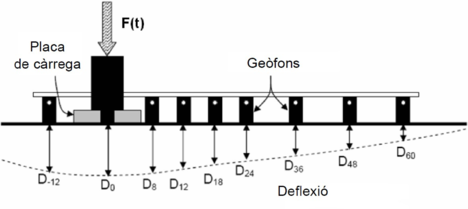
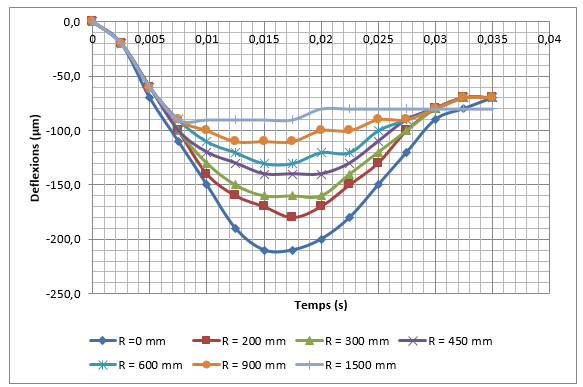
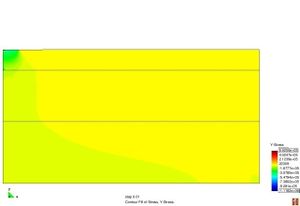
Quan s’aplica una càrrega sobre la superfície, no només es desplaça el punt situat just a sota de la càrrega, sinó que es desplaça tota una regió al voltant d’aquesta càrrega. Aquesta regió, en l’enginyeria de ferms es coneix com a concavitat de deflexions i es pot arriba a estendre fins a 2,5 metres des del centre de la càrrega.

Per determinar la concavitat de deflexions d’un ferm existeixen diferents models i equips. El funcionament bàsic consisteix a aplicar una càrrega sobre el ferm i a mesurar la deformació produïda sobre la seva superfície en diversos punts situats a diferents distàncies de la càrrega. En el passat, generalment es fixava un nivell de deflexió tolerable per una secció de ferm sota un trànsit determinat però actualment l’ús de la informació proporcionada per les mesures de les deflexions s’ha sofisticat. A dia d’avui, les mesures de les deflexions tenen diversos usos que es resumeixen a la següent llista:

• Identificació de les seccions dels ferms que són estructuralment uniformes.

• Identificació de les zones dèbil i/o deteriorades.

• Càlcul de la capacitat estructural.

• Disseny de la rehabilitació.

• Restriccions de càrrega.

• Procediments per permetre sobrecàrregues.

• Avaluació d’anomalies.

• Aplicació en els Sistemes de Gestió de Paviments (SGP).

D’altra banda, la deflexió i la concavitat de deflexions presenten les següents característiques:

• La deflexió màxima es produeix a l’eix de l’aplicació de la càrrega.

• La concavitat de deflexions presenta un valor màxim a l’eix de l’aplicació de la càrrega i les deflexions disminueixen el seu valor a mesura que s’allunyen de l’eix d’aplicació.

Coneguda la concavitat de deflexió es pot determinar el paràmetre conegut com a ÀREA, que és un valor geomètric que proporciona una idea de l’espessor i la capacitat de suport del model estructural d’un paviment. Sovint, la utilització de més d’un índex proporciona informació complementaria que permet realitzar una descripció més acurada del comportament del paviment.

2.3 Equips d’avaluació no destructiva

L’auscultació no destructiva dels ferms flexibles es defineix segons la classificació emprada. Les classificacions més importants es descriuen a la Taula 2.1.

Taula 2.1 Classificació dels mètodes d’avaluació estructural

Classificació	Descripció
1. Lloc on es realitzen les mesures	* Dins la concavitat * Fora de la concavitat
2. Forma d’aplicació de la càrrega	* Estàtica o en moviment lent * Vibració * Impacte * Propagació d’ones
3. Tipus de sensors	* Geòfons: mesuren la velocitat de desplaçament de la superfície del paviment. * Acceleròmetres: mesuren la desacceleració a la superfície del paviment. * Transformadors diferencials de voltatge lineal: mesuren els desplaçaments de la superfície del paviment

La classificació més emprada és la que té en compte la forma d’aplicar la càrrega. A continuació es realitza una descripció general de cadascun dels equips d’aplicació de la càrrega més utilitzats: la biga Benkelman, el deflectògraf Lacroix, els equips de càrrega per vibració, el deflectòmetre d’impacte, el deflectòmetre rodant, el deflectòmetre d’alta velocitat i els equips de medició d’ones.

2.3.1 Equips de càrrega estàtica o moviment lent

Són la primera generació, originada amb el desenvolupament de la Biga Benkelman durant els anys 50 o el deflectògraf Lacroix. Ambdós proporcionen la mesura de les deflexions en un punt sota una càrrega fixa o de moviment lent.

La biga Benkelman fou el primer equip adaptat de forma majoritària per a l’obtenció de deflexions seguint un procediment normalitzat. Està constituïda per un braç de palanca a l’extrem final del qual hi ha un comparador en què es mesura la deflexió produïda a l’extrem inicial, que se situa entre les dues rodes bessones d’un eix tipus de 13 tones. Els baixos rendiments de l’equip (lentitud de la presa de mesures, necessitat de molts operadors, alt cost operacional, etc) i les innovacions tecnològiques donaren pas a dues tendències dins dels equips de deflectometria: d’una banda es començà a treballar amb els equips d’impacte i de l’altra s’inicià el desenvolupament d’equips basats en el mateix principi de la biga Benkelman, però que permetessin una operació continua i mecanitzada amb millors rendiments. Com a conseqüència d’aquesta segona tendència es desenvolupà el deflectògraf Lacroix.

Figura 2.3 Biga Benkelman

El deflectògraf Lacroix consta bàsicament de dues bigues muntades sobre un camió que mesuren les deflexions provocades pel pas de l’eix posterior del vehicle, cada 3-5 metres, a una velocitat relativament reduïda (2-4 km/h), per la qual cosa pot provocar interferències en el trànsit.

Figura 2.4 Deflectògraf tipus Lacroix

També forma part dels equips de càrrega estàtica o moviment lent el curviàmetre, un equip semblant al deflectògraf de Lacroix però que permet realitzar les mesures a una velocitat de 18 km/h, que obté un radi de curvatura equivalent de la concavitat de deflexions.

2.3.2 Equips de càrrega per vibració

Aquests equips tenen més mobilitat i productivitat que els equips de tipus estàtics. Pretenen aconseguir representacions que s’acostin més a l’acció dels trànsit dels vehicles i ho fan aplicant càrregues dinàmiques vibratòries. D’altra banda, les deflexions es generen per fenòmens vibratoris, que imposen una força sinusoïdal dinàmica sobre un pes estàtic.

Aquests equips sempre apliquen una càrrega de compressió de magnitud variable sobre el paviment auscultat. La mesura de la deflexió s’obté amb geòfons, els quals es situen generalment a distàncies regulars del centre. A diferència dels equips estàtics, els equips de càrrega per vibració no requereixen un punt de referència específic.

2.3.3 Equips de càrrega per impacte

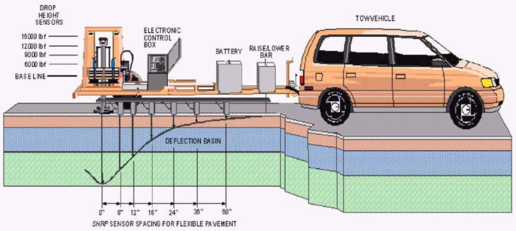
El desenvolupament dels equips tipus impacte (deflectòmetre d’impacte, en anglès conegut com a Falling Weight Deflectometer o FWD) va començar a mitjans dels anys 60 del segle XX, a Holanda i Dinamarca. Fins a mitjans dels anys 70 no començà la seva producció a nivell industrial, per part de les empreses Phoenix, Dynatest i KUAB. Durant els anys 80, la utilització del deflectòmetre d’impacte es generalitzà en un bon nombre de països. El principal avantatge del deflectòmetre d’impacte respecte dels equips tipus biga és que permeten registrar la forma de tota la concavitat de deflexions, no només la deflexió màxima central.

Aquests equips proporcionen una càrrega d’impacte considerable sobre la base superior del paviment. Els models de deflectòmetre d’impacte presenten detalls de disseny diferents depenent del fabricant. Això incideix en la forma de l’impuls de la càrrega, que pot variar segons el model utilitzat.

Figura 2.5 Deflectòmetre d’impacte Dynatest

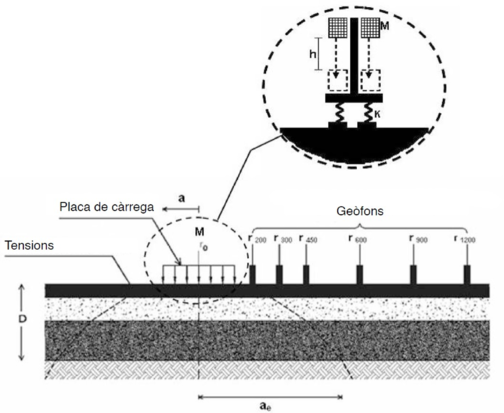
Generalment el deflectòmetre d’impacte es basa en un remolc d’eix senzill que pot ser remolcat per una furgoneta. L’equip consta de:

• Un sistema hidràulic que eleva la massa de l’assaig fins a una certa altura (modificable per l’operador) i la deixa caure sobre la placa de càrrega.

• Un conjunt de sensors que mesuren les deflexions. Nou sensors són suficients per descriure adequadament la concavitat de deflexions.

• Un odòmetre, que permet conèixer amb precisió la distància del punt de mesura a l’origen.

• Un ordinador.

• El comandament.

Figura 2.6 Esquema de l’equip complet d’un deflectòmetre d’impacte.

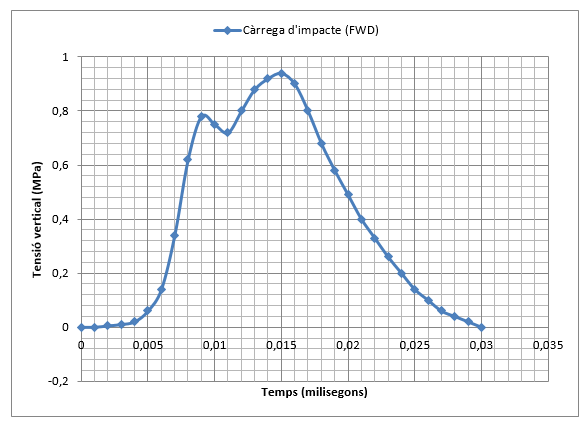
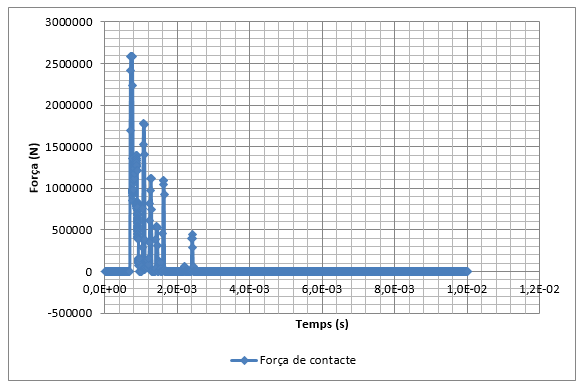
El principi general de funcionament del deflectòmetre d’impacte es basa en la generació d’un impuls de càrrega o força al llarg del temps, ${\textstyle F\left(t\right)}$ sobre el ferm amb una magnitud i una duració semblant a l’efecte que té el pas d’una roda d’un eix. A Espanya, aquesta magnitud correspon a un valor de 130 kN, unes 13 tones.

Figura 2.7 Impuls de càrrega d’un deflectòmetre d’impacte.

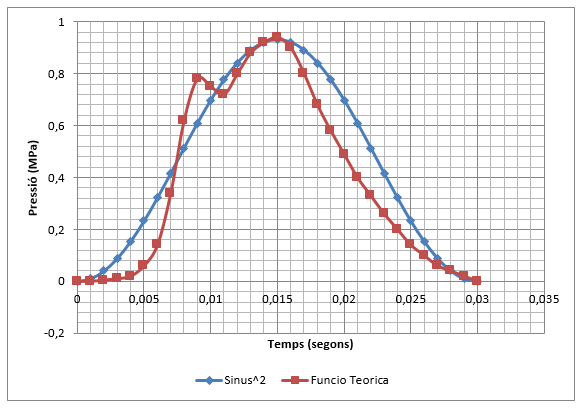
La generació de l’impuls sobre el paviment s’obté a partir de l’impacte provocat per la caiguda lliure d’una massa sobre un sistema d’amortiment instal·lat sobre una placa de càrrega. La massa ${\textstyle \left(M\right)}$ , el sistema d’amortiment ${\textstyle \left(k\right)}$ i l’altura de la caiguda ${\textstyle \left(h\right)}$ poden regular-se per tal d’obtenir la càrrega d’impacte desitjada sobre el ferm. Els sensors mesuren les deflexions verticals màximes del ferm sota el centre de la placa i a diferents distàncies del centre. Les dades obtingudes queden registrades a l’ordinador on són processades en temps real i són emmagatzemades en una base de dades. La majoria dels deflectòmetres d’impacte generen un impuls de càrrega amb un interval de temps entre l’origen i el màxim de la càrrega d’entre 5 i 30 milisegons, amb una duració total d’entre 20 i 60 milisegons (veure (2)). L’impuls de la càrrega generada pretén simular el pas d’un vehicle en moviment, tot i que no acaba de ser del tot representatiu. És per aquest motiu que s’han realitzat avenços considerables en el desenvolupament de nous equips: el deflectòmetre rodant i els deflectòmetre d’alta velocitat, basats en la utilització de sensors de raigs làser.

Figura 2.8 Esquema de la mesura de deflexions amb el deflectòmetre d’impacte.

El deflectòmetre rodant és un equip instal·lat en un vehicle que mesura contínuament la deflexió màxima del ferm sota una càrrega en moviment. Actualment l’equip permet realitzar mesures o bé a una velocitat màxima de 10 km/h amb càrregues de fins a 220 kN, o bé a una velocitat màxima de 32 km/h amb càrregues de fins a 40 kN per roda. Pel que fa al deflectògraf d’alta velocitat, realitza mesures contínues de deflexió en el rang de 20 a 70 km/h. Ambdós equips pretenen substituir els deflectòmetres d’impacte al futur i aspiren a poder prendre les mesures a les velocitats normals del trànsit.

Tot i que a Espanya es pren com a referència la deflexió mesurada amb la biga Benkelman, amb l’objectiu d’aplicar assaigs més reals, les deflexions es mesuren amb el deflectòmetre d’impacte i el deflectògraf Lacroix perquè són equips que permeten prendre mesures en punts específics interpretant posteriorment els resultats en relació a quatre aplicacions estructurals:

• Determinació de la capacitat portant a partir de l’aplicació de mètodes empírics. Les mesures efectuades amb el deflectòmetre d’impacte es poden utilitzar per determinar la capacitat de suport de ferms bituminosos i ferms de formigó. La capacitat de suport es pot avaluar de diferents maneres, utilitzant àbacs o programes informàtics. Això permet establir una classificació dels ferms en funció del seu estat estructural.

• Determinació dels mòduls de rigidesa. Les mesures del deflectòmetre d’impacte poden utilitzar-se per determinar els mòduls de rigidesa de les diferents capes del ferm:

• L’esplanada

• La base i l’esplanada

• El paviment bituminós, la base i l’esplanada

• El paviment de formigó, la base i l’esplanada

El càlcul invers del mòdul de rigidesa es realitza fent ús de criteris enginyerils. Si hi ha moltes capes, o es tracta de capes molt primes, és difícil calcular amb precisió els mòduls de rigidesa.

• Càlcul dels mòduls d’elasticitat per interpretacions futures. Els mòduls calculats a partir de les mesures del deflectòmetre d’impacte s’utilitzen per:

• Establir la contribució relativa del material granular i del material aglomerat a la resistència del ferm.

• Proporcionar una estimació suficientment precisa de la rigidesa de les capes per indicar l’existència de zones dèbils que necessiten ser tractades de forma especial o reemplaçades.

• Calcular tensions i deformacions a les diferents capes del ferm causades per la càrrega.

• Calcular la vida total de servei del ferm, combinant les tensions i les deformacions calculades amb corbes de fatiga o criteris de deformació i amb les dades històriques del trànsit.

• Determinar la vida residual del ferm a partir de la vida total i les previsions de trànsit a curt termini.

• Calcular els espessors de reforç del ferm, si la vida residual calculada és inferior a la vida de projecte requerida pel ferm.

• Identificar la qualitat estructural d’una capa crítica (o superfície de contacte entre capes).

• Càlcul de tensions i deformacions. Existeixen algoritmes de càlcul per determinar les tensions i les deformacions, basats en les relacions existents entre deflexions, tensions i deformacions, com ara pot ser el càlcul invers.

2.4 Equips de medició d’ones

Són els equips basats en l’anàlisi espectral d’ones superficials. Es tracta d’un mètode de prospecció geofísica basat en l’estudi de la propagació d’ones elàstiques a través del medi aplicant vibracions perpendiculars a la superfície dins d’una amplia gamma de freqüències. Dels equips que utilitzen aquesta tècnica actualment cal destacar l’Analitzador de Paviment Sísmic (Seismic Pavement Analyzer, SPA).

2.5 Mètodes comuns per al càlcul de paviments flexibles

El desenvolupament dels equips d’auscultació comentats anteriorment representen en certa manera la història del desenvolupament de tècniques de càlcul en l’anàlisi estructural de ferms. Amb el temps s’han anat desenvolupat tècniques més sofisticades per resoldre el càlcul estructural: determinar les propietats de les capes i els materials del ferm través de la interpretació de les deflexions obtingudes durant el treball de camp.

Els problemes de càlcul dels ferms formen part d’un tema delicat, deficientment resolt encara a dia d’avui. La solució obtinguda és molt sensible respecte petits canvis de la deflexió mesurada. D’altra banda, el plantejament matemàtic no té una solució única, cosa que dificulta més el problema matemàtic, que passa a tenir múltiples solucions.

La formulació del problema del càlcul estructural de ferms consta bàsicament de quatre aspectes:

• Models de càlcul directes i inversos. Descriuen el comportament d’un ferm en avaluació.

• Models de càrrega superficial, dels materials i de resposta dels ferms.

A continuació es descriuen les característiques generals de les diferents modelitzacions:

2.5.1 Models de càlcul directe i invers

Existeixen dos enfocaments per a l’anàlisi de ferms: una metodologia de càlcul directe i una altra de càlcul invers.

2.5.1.1 Càlcul directe

A partir dels valors dels mòduls de Young, els espessors de les capes del ferm i utilitzant programes informàtics que determinen les tensions i les deformacions, es pot comprovar si el ferm està ben dimensionat sota les hipòtesis preses. D’aquesta manera es realitza un càlcul directe.

El càlcul directe determina l’estat tensional (desplaçaments, deformacions i tensions, és a dir, ${\textstyle {\overline {u}},\,{\overline {\epsilon }},\,{\overline {\sigma }}}$), coneguts els espessors, els coeficients de Poisson de cada capa i el mòdul de Young ( ${\textstyle h,\,\nu ,\,E}$), proporcionant una solució única. Avui dia existeixen un gran número de programes informàtics que resolen les equacions diferencials que determinen l’estat tensional d’un ferm.

A continuació es presenten diferents models de resposta que fan un càlcul directe. Es defineix model de resposta com un algoritme computacional que proporciona la resposta d’una estructura sota l’acció d’una determinada càrrega en termes de tensions, deformacions i desplaçaments. Alguns dels diferents models de resposta desenvolupats són (veure (3)):

Semiespai de Boussinesq

El 1885 Boussinesq va solucionar les equacions de resposta d’un sòlid elàstic semi infinit. Les seves hipòtesis bàsiques foren:

• Equilibri estàtic

• Compatibilitat

• Llei de Hook

Tenint en compte aquestes hipòtesis, Boussinesq establí una equació diferencial de quart ordre que va solucionar per dues situacions diferents. La primera corresponia a l’acció d’una càrrega puntual i perpendicular a la superfície. La segona quan l’acció era una càrrega circular. En aquest segon cas només trobà la resposta en la línia definida pel centre de la càrrega.

Les solucions de Boussinesq permeten trobar les tensions, les deformacions i els desplaçaments del semiespai de Boussinesq quan la càrrega és puntual i dels punts corresponents a la línia definida pel centre de la càrrega circular quan la càrrega és circular.

Sistemes de capes

Quan el domini estudiat està format per un conjunt de capes, com és el cas d’un ferm de carretera, no existeixen solucions analítiques com les equacions de Boussinesq. Les diferents propostes per tractar sistemes elàstics de capes es divideixen en tres categories diferents:

• Mètode dels espessors equivalents: el 1949 Odemark va presentar un model simplificat per solucionar el problema dels sistemes de capes. Odemark transforma el sistema de capes en semiespais de Boussinesq on les solucions de Boussinesq són vàlides. Aquesta transformació es realitza calculant un “espessor equivalent” de manera que la rigidesa de cadascuna de les capes es manté.

• Models analítics de capes (Layered analytical models): generalment es basen en el treball de Burminster (1943). Es diu que tenen una solució exacte perquè resolen una equació diferencial de quart ordre donades les condicions de contorn utilitzant la integració numèrica. Són models que donen resposta (deformació i tensió) a qualsevol punt de l’estructura del paviment sota l’acció d’una càrrega induïda per una roda. Es considera que el paviment està format per un sistema multicapa, cada capa lineal, elàstica, i horitzontalment infinita. Originalment aquests models només permetien considerar capes lineals elàstiques i isotròpiques, càrregues circulars uniformes i adherència total entre capes, però actualment hi ha models que permeten considerar altres interaccions entre la roda i el paviment i comportaments diferents dels materials.

• Models d’elements finits: pertanyen a aquesta categoria els models basats en el mètodes dels elements finits. Aquest mètode assumeix que el continu es pot dividir en petits elements gràcies a una malla. Cada element es defineix amb un material diferent i el seu comportament. El comportament de cadascun dels elements es pot analitzar separadament i la contribució de les deformacions de tots i cadascun dels elements defineixen la deformació resultant de tota l’estructura. Aquest models permeten tenir en compte qualsevol equació constitutiva del material, contactes complexes entre la roda i el paviment, qualsevol forma geomètrica, etc. Les deformacions i les tensions es poden calcular a qualsevol punt de l’estructura. Cal distingir els mètodes bidimensionals (deformació plana, tensió plana), mètodes de simetria axial i mètodes tridimensionals.

El pas del “mètode dels espessors equivalents” als “models analítics de capes” i finalment als “models d’elements finits” suposen un augment de la complexitat tant en la definició del model com en els paràmetres a introduir que només es pot justificar si la resposta del model cada vegada s’ajusta més a la resposta real.

A continuació es presenten alguns dels models de resposta existents i se’n fa una petita descripció:

• AXIDIN: model d’elements finits axisimètric desenvolupat per a l’anàlisi de ferms sota càrregues dinàmiques. Es va desenvolupar principalment com a eina de recerca per la interpretació d’assaigs dinàmics i no destructius sobre ferms (deflectòmetre d’impacte).

• ELSYM5: model analític de capes axisimètric basat en el model LAYER5 desenvolupat per la University of California. Fa una anàlisi elàstica lineal. El model ELSYM5 assumeix que les capes són homogènies i s’estenen fins a l’infinit horitzontalment.

• WESLEA: model multicapa convencional que considera la linealitat elàstica de les diferents capes del ferm. Desenvolupat pel U.S. Army Waterways Experiment Station. Es poden arribar a definir fins a 5 capes isotròpiques.

• CAPA 3D: model d’elements finits tridimensional desenvolupat per la Structural Mechanics Section of TU Delft i sota desenvolupament continuat. Disposa d’un generador de malla i els corresponents preprocés i postprocés.

• KENLAYER: model de resposta de ferms que incorpora els seus comportaments no lineals i viscoelàstics. El model KENLAYER es basa en un model multicapa convencional elàstic amb una càrrega circular. El comportament no lineal i viscoelàstic es simula amb un procés iteratiu.

• MICHPAVE: model d’elements finits axisimètric no lineal desenvolupat el 1989 pel Department of Civil and Environmental Engineering of Michigan State University.

• SYSTUS: codi d’elements finits general desenvolupat per FRAMATOME. Inclou diverses possibilitats: anàlisis dinàmiques, anàlisis estàtiques, comportaments no lineals, grans deformacions, etc. També permet especificar el tipus d’interacció entre les diferents capes del ferm.

• VEROAD: programa multicapa que considera un comportament lineal i viscoelàstic. La teoria en què es fonamenta el programa és analítica i basada en el principi de correspondència. Aquest principi diu que un problema viscoelàstic en el domini temporal és un problema elàstic en el domini freqüencial. Això permet aplicar les transformades de Fourier a les parts depenents del temps (posició de la càrrega i propietats dels materials).

• APAS: Software desenvolupat per la Finnish Road Administration juntament amb NESTE Bitumen a Finlàndia. Permet calcular l’espessor de les capes d’un nou ferm o bé dissenyar rehabilitacions de ferms ja existents gràcies a les mesures del deflectòmetre d’impacte.

• BISAR: Model multicapa elàstic lineal que pot arribar a acceptar fins a 10 càrregues verticals.

• CIRCLY: software basat en un model multicapa i elàstic. Permet l’anàlisi d’un conjunt exhaustiu de diferents tipus de càrrega. Es va desenvolupar a partir del software CSIRO (Harrison, Wardle i Gerrard, 1972) i s’ha mantingut desenvolupant-se des de l’any que va néixer, el 1977.

• MMOPP: El Mathematical Model of Pavement Performance simula la deterioració d’un tram de carretera sota la influència d’una càrrega dinàmica, efectes climàtics i el temps. Es basa en un model elàstic multicapa convencional. El MMOPP té en compte la variació de la temperatura estacional i càrregues dinàmiques.

• NOAH: Model multicapa elàstic lineal convencional. El software inclou bases de dades de condicions de càrrega i propietats dels materials que l’usuari pot definir.

• VÄGDIM95: desenvolupat per ser un sistema de disseny de ferms user-friendly.

• VESYS-3PC-RD: originalment el programa VESYS fou desenvolupat per l’FHWA als Estats Units. Aquesta versió del VESYS fou adaptada a la University of Wuppertal (Alemanya) i permet calcular les profunditats de les roderes. Amb les modificacions corresponents, la nova versió permet estimar paràmetres dels materials a partir de resultats de tests de laboratori entre d’altres coses.

Aquest treball pretén fer un càlcul directe reproduint les condicions de l’assaig del deflectòmetre d’impacte amb un nou model de resposta axisimètric i dinàmic basat en el mètode dels elements finits i les partícules.

2.5.1.2 Càlcul invers

Tal i com ja s’ha comentat, quan s’ha d’estimar la capacitat estructural d’un ferm existent, es mesura el desplaçament vertical del paviment (deflexió) sota una càrrega coneguda. Per tal de poder realitzar el càlcul posterior, cal conèixer els espessors de les capes que conformen el ferm, així com els valors de la deflexió en el punt d’aplicació de la càrrega i en diversos punts allunyats del punt d’impacte. En definitiva, cal caracteritzar la concavitat de deflexions. Les dades necessàries són (deflexions, coeficients de Poisson ${\textstyle \nu ,}$ espessors ${\textstyle h}$). Posteriorment, a partir del càlcul invers, els valors de la deflexió s’utilitzen per determinar els mòduls de Young de cada capa, el seu estat tensional i les deformacions ( ${\textstyle E,\,{\overline {\sigma }},{\overline {\epsilon }}}$).

A diferència del càlcul directe, el càlcul invers no proporciona solucions exactes ni úniques. És necessari realitzar un procés iteratiu per ajustar la solució final als criteris de l’enginyeria de paviments. El càlcul invers es basa en el càlcul iteratiu de les deflexions superficials causades per l’impacte provocat pel deflectòmetre sobre l’estructura avaluada de forma que les deflexions mesurades concordin amb les deflexions calculades amb uns determinats valors dels mòduls de rigidesa, espessors de capa i coeficients de Poisson donats. L’objectiu és trobar el conjunt de mòduls que fan que les deflexions obtingudes per ordinador siguin el més semblants possible a les mesurades amb l’aparell.

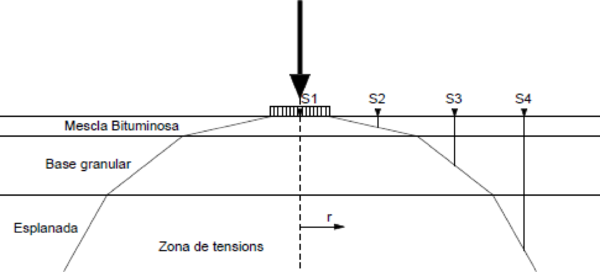
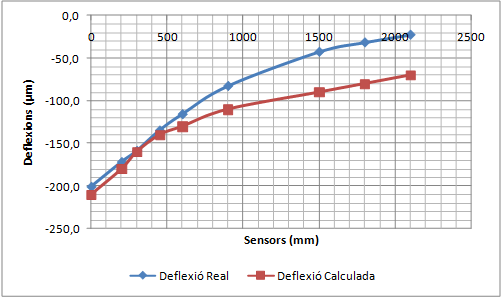
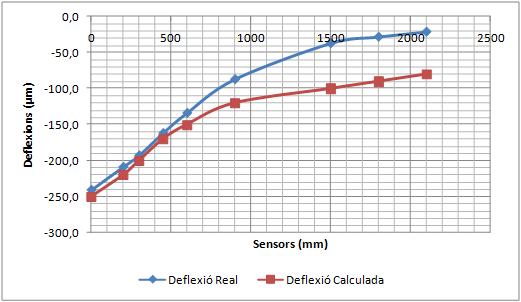
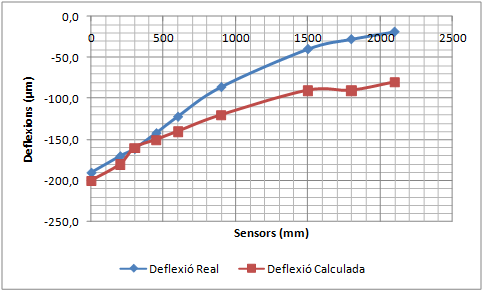
El procediment és el següent. La Figura 2.9 mostra un sistema de tres capes en el qual es mesuren les deflexions amb quatre sensors. S’assumeix de forma arbitrària que la distribució de càrregues a través de les capes és la representada per la línia definida a trossos. Com que el sensor número 4 és fora de la zona tensional de la capa de la mescla bituminosa i de la capa de la base granular, les deflexions del sensor depenen només del mòdul de l’esplanada. D’aquesta manera, aplicant el programa del sistema per capes, es pot obtenir un mòdul raonable per l’esplanada que faci que les deflexions mesurades pel sensor 4 coincideixin amb les calculades. La deflexió que registra el sensor número 3 depèn només del mòdul de la base i l’esplanada. Com que el mòdul de l’esplanada ja és conegut, es pot determinar el mòdul de la base variant-ne el rang, fins que les deflexions calculades coincideixin amb la deflexions calculades pel sensor número 3. Aplicant aquest mateix sistema es pot determinar el mòdul de la capa bituminosa.

Figura 2.9 Distribució de les tensions al ferm provocat pel deflectòmetre d’impacte.

Naturalment, l’explicació realitzada en el paràgraf anterior sobre l’afectació dels mòduls de les capes sobre les deflexions superficials és una simplificació. En realitat, la deflexió mesurada per qualsevol dels sensors depèn de tots els mòduls. Alguns mòduls tenen més influència i d’altres no tanta, però tots intervenen en el fenomen. De tota manera, per sistemes de tres capes sempre s’aplica aquest principi general: les deflexions dels sensors més allunyats del punt d’aplicació de la càrrega s’utilitzen per ajustar els mòduls de la capa inferior, els sensors de distàncies mitjanes s’utilitzen per ajustar els mòduls de la base i els sensors més propers per ajustar el mòdul de la capa superior.

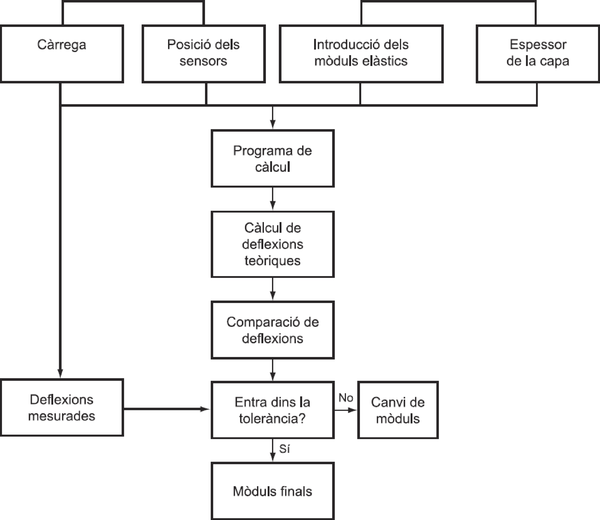
A partir de les dades de l’espessor de cada capa, els diferents coeficients de Poisson i dels diferents mòduls de rigidesa inicials, es calcula una primera concavitat de deflexions. El perfil obtingut es compara amb els resultats mesurats experimentalment (un dels criteris de comparació pot ser per exemple el criteri dels mínims quadrats). La comparació permet adoptar nous valors més aproximats del mòdul de rigidesa, es calcular una nova concavitat de deflexions i es compara de nou amb els resultats experimentals. Es realitzen les iteracions necessàries fins que la diferència entre els perfils de la deflexió mesurada i la deflexió calculada està per sota d’un cert llindar o bé les successives iteracions no suposen millores significatives de la solució.

Els programes de càlcul invers no serveixen per obtenir mòduls de les capes de qualsevol tipus de ferm. S’escapen del seu àmbit d’aplicació les capes molt primes, les capes amb rigideses molt diferents entre elles i les capes de rigideses molt semblants. Si s’introdueixen ferms amb algunes d’aquestes característiques, es poden obtenir resultats incoherents.

Dos exemples concrets de programes de càlcul emprats són els programes DYN i ELMOD.

El programa DYN calcula els mòduls d’elasticitat. Permet fer els càlculs de forma directa i de forma inversa. El mode directe consisteix a obtenir una concavitat de deflexions a partir dels mòduls d’elasticitat introduïts per l’usuari, mentre que el mode invers calcula els mòduls d’elasticitat de les diferents capes d’un ferm a partir de l’anàlisi de la concavitat de deflexions obtinguda amb el deflectòmetre d’impacte.

El programa ELMOD calcula els mòduls d’elasticitat de les diferents capes del ferm a partir de l’anàlisi de la concavitat de deflexions obtinguda amb el deflectòmetre d’impacte. Per fer-ho utilitza el model matemàtic plantejat inicialment per Westergaard el 1926 i desenvolupat posteriorment per Burmister el 1943, basat en el model dels espessors equivalents.

A part d’aquests dos programes existeixen altres programes per a la realització d’aquest càlcul. Una representació bàsica de les etapes de funcionament d’un programa de càlcul es visualitza a la Figura 2.10.

Figura 2.10 Etapes seguides per un programa de càlcul invers

També existeix la possibilitat de realitzar el càlcul invers iteratiu manualment i per interpolació.

2.5.2 Models de càrrega superficial, models dels materials i models de resposta dels ferms

La càrrega d’aplicació pot ser modelada com una càrrega estàtica, mòbil, vibratòria o d’impuls. La majoria d’algoritmes de càlcul invers utilitzen el model de càrrega estàtica perquè modelitzar càrregues dinàmiques o mòbils és molt més complex, requerint un major esforç de formulació i de càlcul.

La majoria d’algoritmes utilitzats en el càlcul invers assumeixen que els materials del ferm tenen un comportament elàstic lineal i són modelats sota una càrrega estàtica. És una simplificació perquè en realitat la majoria dels materials que conformen els ferms són de tipus granular i per tant no tenen una resposta lineal sota una càrrega de tipus dinàmic.

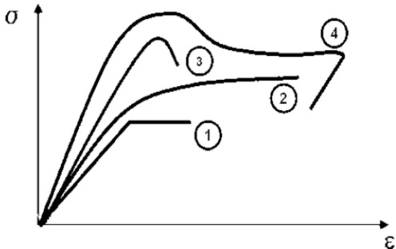
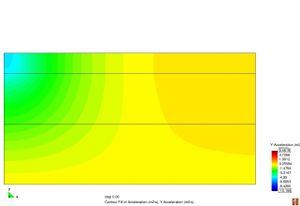
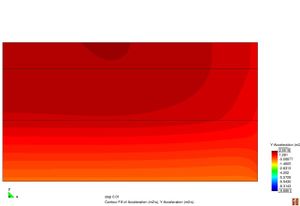
Conèixer els models de resposta dels materials que constitueixen el ferm és bàsic a l’hora de determinar les deflexions sota una càrrega d’assaig. La resposta d’un material es caracteritza segons la seva relació tensió–deformació. Els materials es poden classificar en quatre categories diferents segons la Figura 2.11.

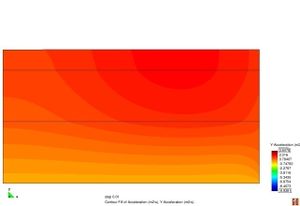
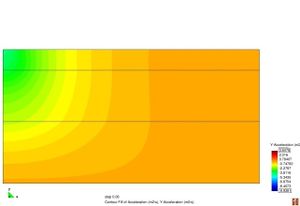
Figura 2.11 Models tensionals del comportament de paviments flexibles. (1) Lineal estàtic (2) Estàtic no lineal (3) Lineal dinàmic (4) No lineal dinàmic.

L’anàlisi lineal elàstic és el model més àmpliament utilitzat en la història de la interpretació del comportament dels ferms flexibles. En aquest treball, els materials també s’ha considerat que tenen un comportament elàstic lineal.

3 Introducció al PFEM

Tal i com s’ha comentat en el capítol (2.5.1 - Models de càlcul directe i invers), fins a dia d’avui s’han utilitzant diferents metodologies per a l’anàlisi i l’estudi de ferms. Aquest treball proposa la utilització del Mètode dels Elements Finits i les Partícules, conegut en anglès com Particle Finite Element Method (PFEM) per a la determinació dels esforços i les deformacions originades pel deflectòmetre d’impacte (FWD) tenint en compte la realitat dinàmica del fenomen. En aquest capítol es fa una breu introducció al Mètode dels Elements Finits i les Partícules (PFEM).

3.1 Mecànica dels medis continus en el PFEM

El Mètode dels Elements Finits i la Partícula (PFEM) pren com a base la teoria del Mètode dels Elements Finits (FEM) i la teoria de la mecànica dels medis continus. Aquest apartat conté un repàs dels punts més importants de la mecànica dels medis continus necessaris per la comprensió del PFEM. Es pot trobar una teoria estesa sobre la mecànica dels medis continus a (4) i una introducció al PFEM a (5).

3.1.1 Moviment i deformació

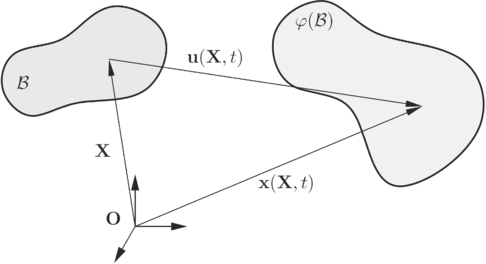
La configuració d’un cos ${\textstyle {B}_{t}}$ en un instant de temps ${\textstyle t}$ es defineix com el lloc geomètric de les posicions que ocupen a l’espai euclidià les partícules del medi continu. Existeix un cert instant ${\textstyle t=}$${t}_{0}$, que se l’anomena instant de referència. En aquest instant de temps es parla de la configuració de referència o configuració inicial ${\textstyle {B}_{{t}_{0}}}$.

La notació ${\textstyle X}$ indica les coordenades de la partícula en la configuració inicial, anomenades coordenades materials o lagrangianes. L’evolució de la posició espacial d’una partícula ${\textstyle X}$ segons el temps es defineix com:

$x={\mathit {\boldsymbol {\varphi }}}\left(X{\boldsymbol {,}}{\mathit {\boldsymbol {t}}}\right)x{\boldsymbol {(}}X{\boldsymbol {,}}{\mathit {\boldsymbol {t}}}{\boldsymbol {)}}$

(3.1)

on ${\textstyle x}$ indica les coordenades de la partícula ${\textstyle X}$ a l’instant ${\textstyle t}$, anomenades coordenades espacials o eulerianes. Per ${\textstyle t=}$$0$, s’obté la configuració de referència ${\textstyle {B}_{{t}_{0}}}$.

El vector desplaçament d’un punt material s’obté a partir de la diferència entre la posició actual i la posició original (veure la Figura 3.1):

$u\left(X{\boldsymbol {,}}t\right)={\boldsymbol {\varphi }}\left(X{\boldsymbol {,}}t\right)-$$X$

(3.2)

A partir de les derivades materials respecte del temps de l’equació (3.2) s’obtenen la descripció material de la velocitat i l’acceleració dels punts:

${\overset {\cdot }{u}}\left(X{\boldsymbol {,}}t\right)=v\left(X{\boldsymbol {,}}t\right)=$${\frac {\partial \varphi }{\partial t}}\left(X{\boldsymbol {,}}t\right)=$${\overset {\cdot }{\boldsymbol {\varphi }}}{\boldsymbol {(}}X{\boldsymbol {,}}t{\boldsymbol {)}}$

(3.3)

${\ddot {u}}\left(X{\boldsymbol {,}}t\right)=a\left(X{\boldsymbol {,}}t\right)=$${\frac {{\partial }^{2}\varphi }{\partial {t}^{2}}}\left(X{\boldsymbol {,}}t\right)=$${\ddot {\varphi }}\left(X{\boldsymbol {,}}t\right)={\overset {\cdot }{v}}{\boldsymbol {(}}X{\boldsymbol {,}}t{\boldsymbol {)}}$

(3.4)

Figura 3.1 Configuració de referència, configuració actual i vector desplaçament.

La deformació es refereix a l’estudi dels moviments relatius de les partícules. El tensor gradient de deformació és aquell que donat un element diferencial ${\textstyle {\boldsymbol {d}}X}$ en la configuració inicial ${\textstyle {B}_{{t}_{0}}}$ li fa correspondre el seu ${\textstyle {\boldsymbol {d}}x}$ en la configuració ${\textstyle {B}_{t}}$:

$\left\{{\begin{matrix}d{x}_{i}={\frac {\partial {x}_{i}}{\partial {X}_{j}}}d{X}_{j}\quad \,\forall i,j\in \left\{1,2,3\right\}\\{\boldsymbol {d}}x{\boldsymbol {=}}F{\boldsymbol {d}}X\end{matrix}}\right.$

(3.5)

L’equació (3.5) defineix el tensor gradient de deformació ${\textstyle F\left(X{\boldsymbol {,}}{\boldsymbol {t}}\right)}$ :

$F=Grad\varphi \left(X,t\right)=x\otimes \nabla$

(3.6)

D’una banda, per assegurar la continuïtat del medi continu durant la deformació, el tensor ${\textstyle F}$ no pot ser singular (cosa que assegura l’existència de la seva inversa). De l’altra, per garantir que no hi ha penetració, el jacobià de ${\textstyle F}$ ha de ser més gran que zero. En definitiva, s’ha de complir que ${\textstyle J=}$$det\left(F\right){\boldsymbol {>}}0$.

El tensor ${\textstyle F}$ admet una descomposició polar. És a dir, existeixen un tensor ortogonal ${\textstyle Q}$ i dos tensors simètrics ${\textstyle U}$ i ${\textstyle V}$ tals que:

$F=Q\cdot U=V\cdot Q$

(3.7)

El tensor gradient de deformació ${\textstyle F}$ s’utilitza per definir nous tensors que caracteritzen la deformació de maneres diferents, sobretot utilitzats en l’anàlisi de la mecànica dels medis continus no lineals. Alguns exemples es presenten a continuació.

El tensor C de Cauchy-Green per la dreta, en la configuració inicial, es defineix com:

$C={F}^{T}F$

(3.8)

El tensor de deformació E de Green-Lagrange es defineix com:

$E={\frac {\boldsymbol {1}}{\boldsymbol {2}}}\left(C-{\boldsymbol {1}}\right)$

(3.9)

El tensor d’Almansi es defineix com:

$e={\frac {1}{2}}\left(1-b\right)$

(3.10)

On el tensor b s’anomena tensor de Cauchy-Green per l’esquerra i es defineix com:

$b=F{F}^{T}$

(3.11)

El tensor d’Almansi i el tensor de Green-Lagrange es relacionen segons la següent expressió:

$E={F}^{T}eF$

(3.12)

3.1.2 Tensió

El tensor de tensions de Cauchy, representat per ${\textstyle {\mathit {\boldsymbol {\sigma }}}}$, és el tensor de tensions més conegut. Donada una direcció normal a la superfície, el tensor de tensions de Cauchy proporciona el vector de traccions corresponent a aquell punt de la superfície. La relació, en notació científica, és la següent:

$\left\{{\begin{matrix}\\t={\mathit {\boldsymbol {\sigma }}}^{\mathit {\boldsymbol {T}}}n\\\\\left\{{\begin{matrix}{t}_{1}\\{t}_{2}\\{t}_{3}\end{matrix}}\right\}=\left({\begin{matrix}{\sigma }_{11}&{\sigma }_{12}&{\sigma }_{13}\\{\sigma }_{21}&{\sigma }_{22}&{\sigma }_{23}\\{\sigma }_{31}&{\sigma }_{32}&{\sigma }_{33}\end{matrix}}\right)\left\{{\begin{matrix}{n}_{1}\\{n}_{2}\\{n}_{3}\end{matrix}}\right\}\end{matrix}}\right.$

(3.13)

A partir del principi de balanç del moment angular es pot demostrar que el tensor de tensions de Cauchy és un tensor simètric:

${\mathit {\boldsymbol {\sigma }}}={\mathit {\boldsymbol {\sigma }}}^{T}$

(3.14)

A partir del tensor de tensions de Cauchy es defineix el segon tensor de tensions de Piola-Kirchhoff S:

$S=J{F}^{-1}\sigma {F}^{-T}$

(3.15)

On ${\textstyle J}$ és el jacobià de F. S és simètric i referit a la configuració de referència. Té un paper important en la teoria de les lleis constitutives.

Sovint també s’utilitza el tensor de tensions de Kirchhoff ${\textstyle {\mathit {\boldsymbol {\tau }}}}$. Es defineix com l’operació endavant del segon tensor de tensions de Piola-Kirchhoff S a la configuració actual:

${\mathit {\boldsymbol {\tau }}}=FS{F}^{T}=J{\mathit {\boldsymbol {\sigma }}}$

(3.16)

3.1.3 Lleis de balanç

El principi de la conservació de la massa estableix que la massa d’un medi continu és constant. El balanç de la massa ${\textstyle m\,}$ d’un cos és:

$m=\int _{\partial B}^{}{\rho }_{0}dV=\int _{\partial \varphi \left(B\right)}^{}\rho dV$

(3.17)

On ${\textstyle {\rho }_{0}}$ és la densitat durant la configuració inicial i ${\textstyle \rho }$ és la densitat a la situació actual. La forma local material del principi de la conservació de la massa s’escriu:

${\rho }_{0}\left(X\right)={\rho }_{t}\left(X\right)\left|{F}_{t}\left(X\right)\right|=$${\rho }_{t}\left(X\right)J\quad \quad \forall X\in {V}_{0\,},\,\forall t$

(3.18)

De l’equació (3.18) es dedueix que:

$dv={\frac {{\rho }_{0}}{\rho }}dV=JdV$

(3.19)

L’equació de balanç del principi de la quantitat de moviment, en la seva forma local, i en coordenades espacials, s’escriu:

${\boldsymbol {\nabla }}\cdot {\mathit {\boldsymbol {\sigma }}}+\rho {\overline {b}}=\rho {\ddot {u}}\quad \quad \,\forall x\in V,\quad \forall t$

(3.20)

On ${\textstyle {\mathit {\boldsymbol {\sigma }}}}$ és el tensor de tensions de Cauchy, ${\textstyle \rho {\overline {b}}}$ són les forces màssiques per unitat de volum i ${\textstyle \rho {\ddot {u}}}$ són les forces de l’acceleració per unitat de volum. Prenent ${\textstyle {\ddot {u}}=}$$0$ s’obté l’equació d’equilibri utilitzada per fer anàlisis estàtics.

La forma local de l’equació de balanç del principi del moment angular, en coordenades espacials, adopta la següent forma:

${\mathit {\boldsymbol {\sigma }}}={\mathit {\boldsymbol {\sigma }}}^{T}$

(3.21)

Els mètodes numèrics es serveixen dels principis variacionals per resoldre els sistemes d’equacions diferencials en derivades parcials. És per aquest motiu que s’utilitza la forma feble de les equacions diferencials que governen el problema físic.

En el present treball no es considera el problema tèrmic.

3.1.4 Models constitutius

Matemàticament, el comportament d’un material es descriu a partir del seu model constitutiu. Amb els models constitutius adequats es poden representar el comportament de fluids, metalls, formigó, etc. L’equació constitutiva proporciona la tensió en funció de la deformació històrica del material. El model més general de l’elasticitat lineal de grans deformacions és el model de Kirchhoff:

$\left\{{\begin{array}{l}S=C:E\\{S}_{AB}={C}_{ABCD}{E}_{CD}\end{array}}\right.$

(3.22)

On ${\textstyle C}$ és un tensor de quart ordre de mòdul elàstic, constant si es tracta d’un material de Kirchhoff. Pel cas d’un material isòtrop, el tensor també ho ha de ser, i adopta la següent expressió:

$\left\{{\begin{matrix}C=\lambda 1\otimes 1+2\mu I\\{C}_{ijkl}=\lambda {\delta }_{ij}{\delta }_{kl}+\mu \left[{\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}\right]\quad i,j,k,l\in \left\{1,2,3\right\}\end{matrix}}\right.$

(3.23)

On ${\textstyle \lambda }$ i ${\textstyle \mu }$ són conegudes com les constants de Lamé.

Si es substitueix l’equació (3.23) a l’equació (3.22), la relació entre la tensió i la deformació es pot reescriure com:

$S=\lambda \left(trE\right)1+2\mu E$

(3.24)

Les constants de Lamé també es poden expressar en funció de dues constants que tenen més significat físic: el coeficient de Poisson ${\textstyle \nu }$ i el mòdul de Young ${\textstyle E}$ (mòdul de deformació longitudinal):

$\left\{{\begin{matrix}\lambda ={\frac {\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}}\\\mu ={\frac {E}{2\left(1+\nu \right)}}\end{matrix}}\right.$

(3.25)

Els materials que segueixen el model de Kirchhoff es caracteritzen per l’existència d’un potencial del qual es deriva la tensió.

3.1.5 Linealitzacions

Un cop definit el problema a resoldre, la geometria del problema, les equacions constitutives i certes condicions de contorn, comporten la no linealitat del problema. És per aquest motiu que caldrà linealitzar les equacions del problema. Sigui la següent funció de variable vectorial:

$G:\quad E\,\longrightarrow \quad F$ ${\textstyle x\longrightarrow G(x)}$

(3.26)

A partir de la sèrie de Taylor s’obté que:

$G\left({\overline {x}}+u\right)={\overline {G}}+{\overline {D}}G\cdot u+R$

(3.27)

On

${\overline {D}}G=DG\left({\overline {x}}\right)={\left.{\frac {\partial G\left(x\right)}{\partial x}}\right|}_{x{\boldsymbol {=}}{\overline {x}}}$

(3.28)

I la derivada direccional es defineix com:

${\left.{\frac {d}{d\epsilon }}\left[G\left({\overline {x}}+\epsilon u\right)\right]\right|}_{\epsilon =0}=$${\overline {D}}G\cdot u\,:={\boldsymbol {\Delta }}{\overline {G}}$

(3.29)

3.1.6 Discretització del continu

El domini ${\textstyle \varphi (B)}$ es subdivideix en ${\textstyle e}$ elements, de 1 a ${\textstyle {n}_{e}}$. Si el domini de cada element s’escriu com ${\textstyle {\Omega }_{e}}$, el domini total és la unió de tots els seus subdominis:

$\varphi \left(B\right)=\bigcup _{e=1}^{{n}_{e}}\varphi ({\Omega }_{e})$

(3.30)

Cada element té un cert número de nodes ${\textstyle {n}_{n}}$. Cada node té unes coordenades espacials en la configuració actual.

La interpolació de qualsevol variable ${\textstyle u}$ s’escriu gràcies als valors nodals i les funcions de forma. La manera estàndard d’expressar-ho és segons (1) i (3):

$u\left(X,t\right)=\sum _{I=1}^{{n}_{n}}{N}_{I}\left(X\right){u}_{I}\left(t\right)$

(3.31)

On ${\textstyle {N}_{I}\left(X\right)}$ són les funcions d’interpolació que compleixen:

${N}_{I}\left({X}_{J}\right)={\delta }_{IJ}$

(3.32)

Sent ${\textstyle {\delta }_{IJ}}$ la delta de Kronecker.

El FEM i el PFEM utilitzen el concepte de l’isoparametria per definir la geometria dels elements (veure (6)). Això vol dir que si es coneixen les coordenades ${\textstyle {x}_{1},{x}_{2},{x}_{3},\,\ldots ,{x}_{n}}$ de n punts qualssevol de l’element, es pot calcular la coordenada de qualsevol punt del mateix element, interpolant els valors de les coordenades conegudes. Aquesta interpolació es pot escriure de la forma següent:

$x={N}_{1}\left({\mathit {\boldsymbol {\xi }}}\right){x}_{1}+{N}_{2}\left({\mathit {\boldsymbol {\xi }}}\right){x}_{2}+\cdots +$${N}_{n}\left({\mathit {\boldsymbol {\xi }}}\right){x}_{n}=\sum _{I=1}^{{n}_{n}}{N}_{I}\left({\mathit {\boldsymbol {\xi }}}\right){x}_{I}$

(3.33)

Aquesta formulació és útil perquè permet conèixer la relació existent entre les coordenades cartesianes ${\textstyle x}$ i les coordenades naturals de les funcions de forma ${\textstyle {\mathit {\boldsymbol {\xi }}}}$. Per veure un exemple de la utilitat de la utilització de l’isoparametria s’exposa el cas del càlcul de les deformacions. Les deformacions s’obtenen com:

${\mathit {\boldsymbol {\epsilon }}}={\frac {du}{dx}}={\frac {d}{dx}}\left(\sum _{I=1}^{{n}_{n}}{N}_{I}\left({\mathit {\boldsymbol {\xi }}}\right){u}_{I}\right)=$$\sum _{I=1}^{{n}_{n}}\left({\frac {d{N}_{I}\left({\mathit {\boldsymbol {\xi }}}\right)}{dx}}\right){u}_{I}$

(3.34)

On tal i com indica (3.34), cal calcular la derivada de les funcions de forma respecte de les coordenades cartesianes. Es podrà determinar fàcilment gràcies a la interpolació isoparamètrica, expressada a l’equació (3.33):

${\frac {\partial N}{\partial {\mathit {\boldsymbol {\xi }}}}}={\frac {\partial x}{\partial {\mathit {\boldsymbol {\xi }}}}}{\frac {\partial N}{\partial x}}\Rightarrow {\frac {\partial N}{\partial x}}=$${\left[{\frac {\partial x}{\partial {\mathit {\boldsymbol {\xi }}}}}\right]}^{-1}{\frac {\partial N}{\partial {\mathit {\boldsymbol {\xi }}}}}$

(3.35)

3.2 Formulació del PFEM

3.2.1 Concepte de partícula

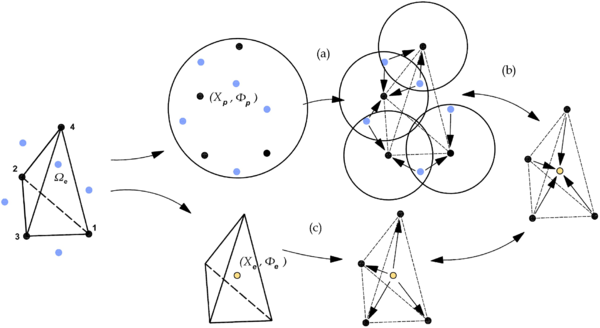
En el Mètode dels Elements Finits i les Partícules, la descripció del continu es realitza a partir d’un núvol de partícules (veure Figura 3.2). La filosofia del mètode es basa amb el fet que les partícules contenen tota la informació (desplaçaments, velocitats, acceleracions, deformacions, tensions, propietats del material, variables internes, etc), perquè s’utilitza per tractar problemes que tenen una morfologia molt variable, com per exemple problemes d’interacció entre fluids i estructures. D’aquesta manera, amb el conjunt de les dades associades a les partícules, és possible refer la situació inicial.

Figura 3.2 Definició d’un cos a partir d’un núvol de punts.

Les partícules formen part dels nodes d’una malla d’elements finits a partir de la qual es discretitza el medi continu. Cada vegada que es regenera la malla per realitzar la següent iteració, la informació de cada element s’obté a partir de les dades de les partícules que el defineixen.

Tot i que la majoria de vegades succeeix que les partícules coincideixen amb els nodes de la malla, no sempre és així. Hi ha situacions en què és necessari introduir més nodes a la malla o, contràriament, eliminar-ne. Per dotar amb la informació necessària els nous nodes, s’interpolen els valors de les partícules del voltant.

Per al càlcul, cal transferir la informació dels nodes als elements. Aquest és un pas crucial del qual depèn l’èxit de la simulació.

3.2.2 Formulació del continu pel PFEM

Les equacions necessàries per resoldre el problema amb la metodologia del PFEM s’han descrit anteriorment. S’obtenen de les lleis del balanç i s’expressen a partir d’equacions diferencials en derivades parcials (EDP’s).

Les equacions que cal utilitzar són les següents (expressades a partir de la descripció Lagrangiana del continu en la configuració actual ${\textstyle \varphi \left(B\right)}$ ):

Equació de la conservació de la massa:

$\rho \left(X,t\right)\cdot J\left(X,t\right)={\rho }_{0}(X,t)$

(3.36)

Equació de conservació de la quantitat de moviment:

${\frac {\partial {\sigma }_{ij}}{\partial {x}_{j}}}+\rho {b}_{i}=\rho {\ddot {u}}_{i}$

(3.37)

Equació de conservació del moment angular:

$\sigma ={\sigma }^{T}$

(3.38)

Equació constitutiva:

${\sigma }_{ij}=(1-d){C}_{ijkl}{E}_{kl}$

(3.39)

On ${\textstyle d}$ és la variable que caracteritza el dany, i ${\textstyle {E}_{kl}}$ és la part lineal del tensor de deformacions de Green-Lagrange. Notar que el PFEM admet la utilització de qualsevol llei constitutiva.

La forma integral de l’equilibri es representa a partir del principi dels treballs virtuals. Si es substitueix la interpolació de l’element finit al principi dels treball virtuals s’obté:

$r\left(u,t\right):=M{\ddot {u}}-{F}^{ext}\left(u,t\right)+{F}^{int}\left(u,t\right)=$$0$

(3.40)

Per solucionar l’equació (3.40) es necessita conèixer unes condicions inicials ( ${\textstyle {u}_{0},\,{\overset {\cdot }{u}}_{0},{\ddot {u}}_{0}}$) així com unes forces externes aplicades al domini físic.

En una anàlisi dinàmica utilitzant elements finits, la discretització del domini ${\textstyle \varphi \left({B}_{t}\right)}$ correspon a l'instant de temps ${\textstyle t}$. L’espai es discretitza segons els elements finits, i el temps s’expressa com la suma de petits passos de temps. La suma de tots els petits elements i de tots els petits passos de temps, proporciona la solució del medi continu al llarg del temps. Les característiques específiques del PFEM estan involucrades amb la manera de calcular les variables dels elements finits entre dos instants de temps diferents.

Durant el pas del temps, primerament cal actualitzar els valors de les variables de la configuració inicial a la nova configuració de referència. Es fa a partir de les equacions incrementals del moviment, presentats al següent apartat.

3.2.3 Equacions incrementals del moviment basat en les partícules:

L’objectiu és resoldre l’equació (3.40) en el temps. A mesura que el temps canvia, la posició del domini estudiat també va canviant. La funció ${\textstyle \varphi \left(X,t\right)}$ definida segons l’equació (3.1) descriu l’evolució de les partícules del cos.

Amb els elements finits, l’anàlisi dinàmica es divideix en passos de temps ${\textstyle \Delta t}$. La configuració actual del cos a l’instant ${\textstyle t}$, ${\textstyle {\varphi }_{t}\left({B}_{t}\right)}$ es pren com la configuració de referència per al temps ${\textstyle t+}$$\Delta t$, és a dir:

${B}^{t+\Delta t}={\varphi }_{t}\left({B}^{t}\right)$

(3.41)

Les variables físiques i mecàniques canvien cada vegada que la configuració de referència s'actualitza. L'actualització de les variables s'obté a partir d'una forma incremental:

${u}_{p}^{t+\Delta t}={u}_{p}^{t}+{{\mathit {\boldsymbol {\Delta }}}u}_{p}$

(3.42)

${S}_{p}^{t+\Delta t}={\sigma }_{p}^{t}+{{\mathit {\boldsymbol {\Delta }}}S}_{\mathit {\boldsymbol {p}}}$

(3.43)

On ${\textstyle S}$ és el segon tensor de tensions de Piola-Kirchhoff i ${\textstyle \sigma }$ és el tensor de tensions de Cauchy i el subíndex ${\textstyle p}$ indica el valor que la variable té a la partícula ${\textstyle p}$.

Els desplaçaments, les velocitats i les acceleracions són variables que s'expressen directament als nodes, i s'actualitzen just després d'haver-se calculat els nous desplaçaments. Si es tracta de partícules que no coincideixen amb nodes, es fa una interpolació.

Hi ha altres variables que representen característiques espacials, com per exemple variables constitutives, mesures de la tensió, etc. Cadascuna d'aquestes variables es calcula associada a cada element, concretament a partir dels seus punts d'integració, i un cop s'ha acabat la iteració, la informació es traspassa de nou a les partícules. Això provoca una pèrdua d'informació: les variables associades als elements són discontínues d'un element al del costat. Això vol dir que cada node té valors diferents segons quin sigui el seu element de referència. Les tensions en són un bon exemple.

Figura 3.3 La associació de les variables pot ser amb les partícules o els elements: (a) transferència de la informació de les partícules als nodes (b) transferència dels nodes a l’element (c) transferència de l’element als nodes

Perquè cada node tingui associat un valor de la tensió, es fa una interpolació amb els valors de les tensions dels elements que comparteixen el node en qüestió. Aquest procés introdueix una suavització de la variable tractada. Si més endavant, a partir dels valors de les tensions associats a les variables es vol recuperar la situació inicial, el resultat no coincideix. Aquesta suavització de la variable, posa en perill l'equilibri del sistema. En funció de l'algoritme implementat, l'efecte de la suavització és major o menor. Aquest és el motiu pel qual el traspàs de la informació dels nodes als elements i de nou als nodes és un punt delicat.

3.2.4 Assignació del material a les partícules

3.2.4.1 Assignació del material: dels elements a les partícules

La informació referent a les característiques del material també és informació associada als elements de la malla que cal traspassar als nodes. Cal diferenciar dos casos.

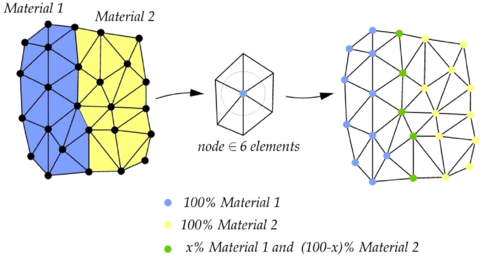
El primer cas correspon a un domini homogeni. Un cop creada la malla, a cada element se li associa el material corresponent. A continuació es passa la informació a les partícules. Totes les partícules tindran exactament les mateixes propietats.

El segon cas correspon a un domini heterogeni, que estigui format per més d'un material. Cada material tindrà les seves propietats. Feta la malla, s'associa a cada element el material que corresponent. Si l'heterogeneïtat no és causada per discontinuïtats en el material, hi haurà una regió de transició entre un material i el del costat. Aquesta transició es pot reproduir a partir d'un tractament especial de les partícules que comparteixen elements amb materials diferents. Hi ha dues opcions diferents:

• La primera opció és comptabilitzar els elements d'un material i els elements de l'altre, en contacte amb la partícula i assignar-li el material majoritari. Aquesta opció no és prou refinada i no és la que utilitza el programa.

• La segona opció consisteix a definir un percentatge de cada material depenent del volum definit pels elements representants de cada material en contacte amb la partícula.

Figura 3.4 Assignació del material dels elements a les partícules. El valor de x es determina a partir dels volums associats als elements del voltant de la partícula corresponent.

3.2.4.2 Assignació del material: de les partícules als elements.

Malgrat que la manera habitual de procedir és associar el material als elements de la malla i posteriorment traspassar les dades a les partícules, tal i com s'ha explicat a l'apartat anterior, hi ha una altra manera d'assignar el material que permet estendre el mètode a d'altres tipus de problemes com ara les interaccions entre sòlids i fluids. Es tracta que les partícules defineixin el material del domini.

Es parteix d'un núvol de partícules. Un cop s'ha construït la malla, s'han de dotar els elements de les seves propietats, informació que s'extreu de les partícules. L'assignació del material als elements es pot fer seguint qualsevol de les dues maneres següents:

• A partir de la combinació de les propietats dels materials assignats a les partícules que conformen l'element. Aquesta combinació proporciona un valor isotròpic de cada propietat de l'element.

• Assignar a l'element les propietats que són comunes a totes les partícules que defineixen l'element. D'aquesta manera no hi haurà cap mescla.

3.2.5 Algoritmes solució

Es poden escollir diferents algoritmes per solucionar les equacions no lineals associades als elements finits. En general, els mètodes emprats es diferencien entre mètodes explícits i mètodes implícits. Cadascun té els seus avantatges i els seus inconvenients.

3.2.5.1 Mètodes explícits

Amb els mètodes explícits no és necessari solucionar un sistema no lineal d'equacions a cada pas de temps. Són fàcils d'implementar perquè l'instant ${\textstyle {t}_{n+1}}$ depèn només de variables ja conegudes a l'instant ${\textstyle {t}_{n}}$. El principal escull és que els mètodes explícits són condicionalment estables: si el pas de temps supera un cert llindar, la solució es desestabilitza i divergeix. El llindar ve governat pel criteri de Courant. El mètode explícit més utilitzat és el mètode de les diferències centrades. Les velocitats i les acceleracions utilitzant aquest algoritme, són:

${\overset {\cdot }{u}}_{n}={\frac {\left({u}_{n+1}-{u}_{n-1}\right)}{2\Delta t}}$

(3.44)

${\ddot {u}}_{n}={\frac {\left({u}_{n+1}-2{u}_{n}+{u}_{n-1}\right)}{\Delta {t}^{2}}}$

(3.45)

On ${\textstyle {(\cdot )}_{n}}$, ${\textstyle {(\cdot )}_{n+1}}$ i ${\textstyle {(\cdot )}_{n-1}}$ són els valors de la variable als instants de temps ${\textstyle {t}_{n}}$, ${\textstyle {t}_{n}+}$$\Delta t$ i ${\textstyle {t}_{n}-\Delta t}$ respectivament.

Si es substitueixen els valors de ${\textstyle {\overset {\cdot }{u}}_{n}}$ i ${\textstyle {\ddot {u}}_{n}}$ a l’equació (3.40) i a més a més, s’hi inclou un terme d’amortiment, ${\textstyle C{\overset {\cdot }{u}}_{n}}$ ,la discretització de les equacions del moviment a l’instant de temps ${\textstyle {t}_{n}}$ serà:

$M\left[{u}_{n+1}-2{u}_{n}+{u}_{n-1}\right]+{\frac {\Delta t}{2}}C\left[{u}_{n+1}-\right.$$\left.{u}_{n-1}\right]-{\left(\Delta t\right)}^{2}\left({F}^{ext}\left({u}_{n}\right)-\right.$$\left.{F}^{int}\left({u}_{n}\right)\right)=0$

(3.46)

L’equació (3.46) es pot reescriure com segueix:

$\left(M+{\frac {\Delta t}{2}}C\right){u}_{n+1}={\left(\Delta t\right)}^{2}\left({F}_{n}^{ext}-\right.$$\left.{F}_{n}^{int}\right)+{\frac {\Delta t}{2}}C{u}_{n-1}+M\left[2{u}_{n}-{u}_{n-1}\right]$

(3.47)

on les matrius ${\textstyle M}$ i ${\textstyle C}$ són constants.

3.2.5.2 Mètodes implícits

Els mètodes implícits han de solucionar sistemes d'equacions no lineals cada instant de temps. Tenen un cost computacional molt més elevat que els mètodes explícits. Les derivades temporals de ${\textstyle {t}_{n}}$ depenen de quantitats que també depenen de ${\textstyle {t}_{n}}$ i de valors no coneguts a l’instant de temps ${\textstyle {t}_{n+\alpha }}$. El gran avantatge dels mètodes implícits és que poden ser incondicionalment estables.

L’equació a resoldre és la següent:

$0=r\left({u}_{n+1},{t}_{n+1}\right)=M{\ddot {u}}_{n+1}-{F}^{ext}\left({u}_{n+1},{t}_{n+1}\right)+$${F}^{int}\left({u}_{n+1},{t}_{n+1}\right)$

(3.48)

On ${\textstyle r\left({u}_{n+1},{t}_{n+1}\right)}$ és el vector residual. Les actualitzacions de les velocitats i les acceleracions, utilitzant la formulació clàssica del mètode de Newmark, són:

${u}_{n+1}={u}_{n}+\Delta t{\overset {\cdot }{u}}_{n}+{\left(\Delta t\right)}^{2}\left[\left({\frac {1}{2}}-\right.\right.$$\left.\left.\beta \right){\ddot {u}}_{n}+\beta {\ddot {u}}_{n+1}\right]$

(3.49)

${\overset {\cdot }{u}}_{n+1}={\overset {\cdot }{u}}_{n}+\Delta t\left[\left(1-\right.\right.$$\left.\left.\gamma \right){\ddot {u}}_{n}+\gamma {\ddot {u}}_{n+1}\right]$

(3.50)

La resolució del problema es fa a utilitzant el mètode de Newton-Raphson. A partir del teorema de Taylor es linealitza el conjunt d’equacions no lineals que representa l’equació (3.48):

$r\left({u}_{n+1}^{\nu },{t}_{n+1}\right)+{\frac {\partial r\left({u}_{n+1}^{\nu },{t}_{n+1}\right)}{\partial u}}\Delta u+$$O\left(\Delta {u}^{2}\right)=0$

(3.51)

on ${\textstyle \nu }$ indica el número d’iteracions realitzades. És a dir, ${\textstyle {u}_{n+1}^{\nu }}$ és el vector de desplaçaments a la iteració ${\textstyle \nu }$ al pas de temps ${\textstyle {t}_{n+1}=}$${t}_{n}+\Delta t$. L’equació linealitzada (3.51) es pot reescriure com:

$r-A\Delta u=0$

(3.52)

on l’increment del vector desplaçament a cada iteració ${\textstyle \nu }$ es calcula com:

${u}^{\nu +1}={u}^{\nu }+\Delta u$

(3.53)

i la matriu ${\textstyle A}$ es calcula com:

$A={\frac {\partial r}{\partial u}}$

(3.54)

El mètode de Newmark té característiques i ordres diferents segons els valors que es prenguin dels paràmetres ${\textstyle \beta }$ i ${\textstyle \gamma }$ . A l’hora d’escollir-los cal tenir en compte els casos següents:

• Per ${\textstyle \beta =0}$, ${\textstyle \gamma =0}$, es tracta del mètode explícit pur.

• Per ${\textstyle \beta =0}$, ${\textstyle \gamma ={\frac {1}{2}}}$, es tracta del mètode de les diferències centrades. És explícit i condicionalment estable.

• Per ${\textstyle \beta ={\frac {1}{4}}}$, ${\textstyle \gamma =}$${\frac {1}{2}}$, esdevé la regla del trapezi sense esmorteïment. Es tracta d’un mètode incondicionalment estable.

Pel que fa l’estabilitat, cal tenir en compte que:

• Per ${\textstyle \gamma \leq {\frac {1}{2}}}$, inestable.

• Per ${\textstyle \gamma \geq {\frac {1}{2}}}$, ${\textstyle \beta \leq {\frac {1}{4}}}$, condicionalment estable.

• Per ${\textstyle \gamma \geq {\frac {1}{2}}}$, ${\textstyle \beta \geq {\frac {1}{4}}}$, incondicionalment estable.

3.3 Procés de mallatge en el PFEM

En el PFEM el domini queda definit amb un núvol de partícules, a diferència del MEF, que queda definit amb un conjunt d’elements. La metodologia emprada pel procés de mallatge és la Delaunay Tessellation, que és un procediment útil per dividir un domini continu en subdominis (els elements).

Cada vegada que es calcula un pas de temps, s’actualitzen les variables de cada partícula. Les partícules hauran canviat la seva posició relativa a l’espai. De nou s’utilitzarà la Delaunay Tessellation per crear una nova malla per poder calcular el següent pas de temps.

3.3.1 Delaunay Tessellation

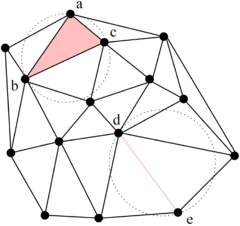
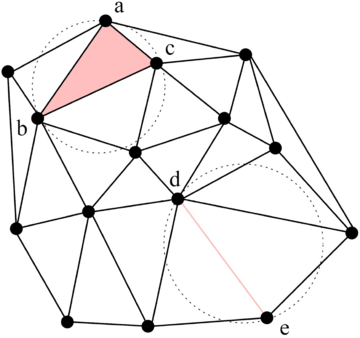
La Delaunay Tessellation, en el cas de dues dimensions, s’anomena Delaunay Triangulation. Es parla d’una circumferència buida si la circumferència circumscrita d’un triangle de la malla no conté cap vèrtex de cap altre triangle. La condició de Delaunay requereix que una xarxa de triangles és una triangulació de Delaunay si totes les circumferències circumscrites de tots els triangles són buides (veure Figura 3.5).

Aquest mateix concepte es pot estendre a espais de tres dimensions, substituint el concepte de circumferència circumscrita pel d’una esfera circumscrita a un tetràedre.

La condició de Delaunay té les següents dues propietats:

• Assegura que els angles de l’interior dels triangles siguin el més grans possible, o dit d’altra manera, assegura que l’angle més petit del triangle sigui el més gran possible.

• La triangulació forma l’envolupant convexa del conjunt de punts.

Figura 3.5 Exemple d’una Delaunay triangulation.

3.3.2 Alpha Shape

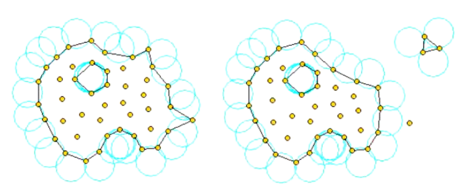
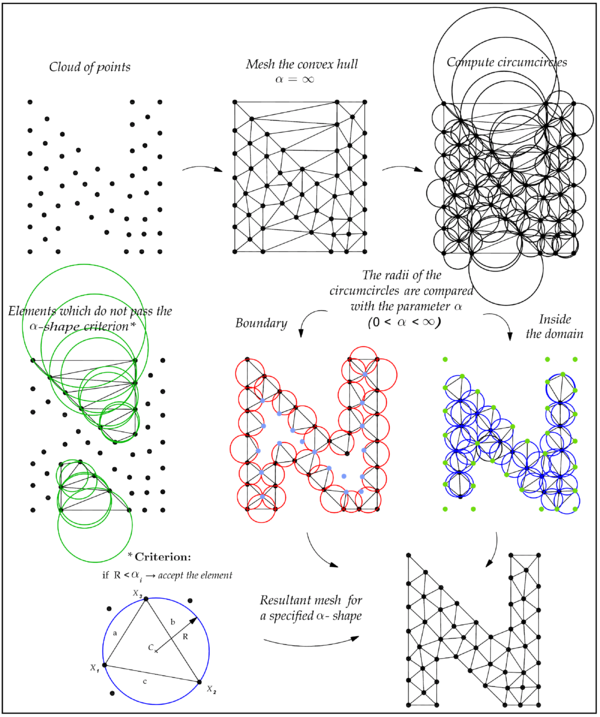
Una de les principals dificultats a l’hora de fer el mallatge del núvol de punts és la identificació correcta de la frontera del domini. El concepte Alpha Shape permet abordar aquesta dificultat. El paràmetre α representa el radi del cercle (2 dimensions) o l’esfera (3 dimensions) segons cada cas.

L’α-shape d’un conjunt de partícules és un politop que no té perquè ser ni convex ni connectat. El paràmetre α pren valors des de ${\textstyle \infty }$ fins a 0. Per un valor de ${\textstyle \alpha =}$$\infty$ , l’ α-shape correspon a la forma convexa, mentre que per un valor de ${\textstyle \alpha =}$$0$, l’ α-shape correspon només al conjunt de partícules. A mesura que el valor del paràmetre ${\textstyle \alpha }$ disminueix, l’α-shape va generant cavitats gradualment. Aquestes cavitats poden ser interiors o exteriors (veure Figura 3.6).

Figura 3.6 Exemple d’α-shapes d’un mateix núvol de punts, des de α = ${\textstyle {\mathit {\boldsymbol {\infty }}}}$ (forma convexe) fins a α = 0 (únicament el conjunt de partícules).

El concepte de l’α-shape es pot utilitzar juntament amb la Delaunay Tessellation. Primerament s’utilitza la tècnica de l’α-shape per obtenir les partícules que defineixen la frontera del domini (veure Figura 3.7). A continuació, s’aplica la Delaunay Tessellation dins dels politops.

Figura 3.7 Reconeixement de la frontera del domini d’un núvol de partícules emprant el concepte α-shape.

El concepte α-shape és útil per trobar la frontera d’un núvol de partícules uniformement distribuïdes a l’espai, però quan les partícules no estan uniformement distribuïdes, aquest sistema no funciona. Aquest problema es resol amb la utilització del concepte non-uniform α-shape. Utilitzant aquesta metodologia, el paràmetre ${\textstyle \alpha }$ s’adapta a les circumstàncies de cada malla. Això és molt útil en el PFEM, en què a cada pas de temps es defineix una nova malla de característiques diferents de la malla anterior.

S’associa a cada partícula un valor diferent del paràmetre α. Donada una partícula ${\textstyle j}$, el seu paràmetre ${\textstyle {\alpha }_{j}}$ es defineix com:

${\alpha }_{j}=\sum _{i=1}^{{n}_{b}}{\frac {\left|{x}_{i}-{x}_{j}\right|}{{n}_{b}}}$

(3.55)

On ${\textstyle {n}_{b}}$ és el número de partícules veïnes ${\textstyle i}$ i ${\textstyle {x}_{k}\,}$ són les posicions espacials de les partícules.

Cada valor ${\textstyle {\alpha }_{j}}$ es compara amb el radi Delaunay de la circumferència o de l’esfera que inclou la partícula. Això proporciona un criteri per determinar si s’accepta o es descarta l’element de la Delaunay Tessellation. Concretament, si el radi de la circumferència o esfera és més petit que el paràmetre ${\textstyle {\alpha }_{j}}$ associat a l’element, s’accepta l’element. En canvi, si és més gran, es descarta (veure Figura 3.8).

Figura 3.8 Exemple del procés de mallatge d’un núvol de punts en el PFEM.

3.3.3 Detecció del contacte

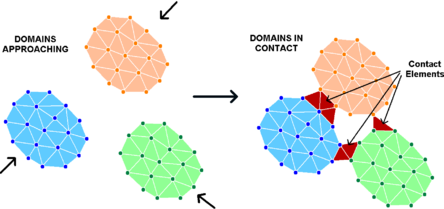
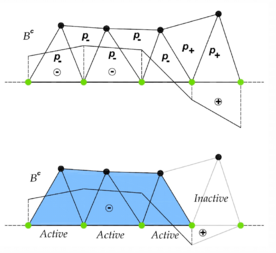
El PFEM permet modelar problemes en què interaccionen cossos diversos. La primera dificultat a superar és detectar el contacte entre dos cossos diferents. La identificació del contacte es realitza a partir del concepte α-shape. Cada partícula està caracteritzada amb una etiqueta que l’identifica amb un cos del problema. El mètode α-shape no distingeix els diferents cossos o subdominis i per tant, es fa un mallatge sense tenir-ho en compte. Quan les partícules de dos cossos s’aproximen, els α-shapes ajunten aquests dos cossos o subdominis per crear un nou domini més gran. La frontera detectada contindrà partícules dels diferents cossos. Entre els dos subdominis que entren en contacte i xoquen, es crea una interfase d’elements anomenats elements de contacte (veure Figura 3.9).

Figura 3.9 Amb el concepte de l’α-shape, la detecció del contacte entre diferents subdominis és automàtica. Es creen els anomenats elements de contacte.

El problema amb aquesta metodologia és que quan dos elements estan en contacte, es crea una malla d’interfase. Aquesta desavantatge es soluciona estenent l’estratègia de la detecció de la frontera a un nou esquema de mallatge.

3.3.3.1 Contracció de les fronteres

Per tal d’obtenir el contacte geomètric real, es pot realitzar una contracció de les fronteres abans de realitzar el mallatge de fora dels subdominis. Una compensació amb la distància adequada permet assegurar la posició de contacte real sense haver d’introduir cap capa d’elements de contacte que desvirtuï la geometria real.

Els elements de contacte existeixen i ocupen un espai a la geometria contreta, però no pas a la real. Tal i com es pot veure a la figura següent, l’algoritme és el següent: (a) primer es disposa de la geometria inicial que (b) es discretitza, (c) s’identifiquen les partícules que defineixen les fronteres dels dominis, (d) es defineixen les normals definides a les partícules dels contorns, (e) es contrau la geometria i finalment (f) es defineix la malla de l’interfase de contacte.

Figura 3.10 Algoritme de la contracció

3.4 Mecànica de contacte

3.4.1 Cinemàtica del contacte

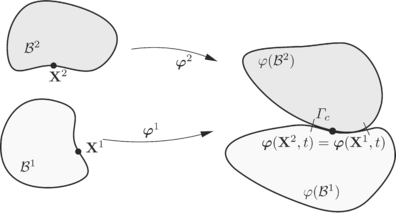
Siguin dos o més cossos ${\textstyle {B}^{\alpha }}$ que s’aproximen l’un a l’altre i que finalment acaben contactant a través d’alguna zona de les fronteres dels seus dominis ${\textstyle {\Gamma }_{c}}$. La Figura 3.11 mostra que dos punts ${\textstyle {X}^{1}}$ i ${\textstyle {X}^{2}}$, cadascun pertanyent a un cos diferent, poden ocupar la mateixa posició espacial a la configuració actual ${\textstyle \varphi \left({X}^{1}\right)=}$$\varphi \left({X}^{2}\right)$ . Cal formular unes condicions que descriguin el contacte corresponent a la configuració actual adequadament.

Figura 3.11 Deformació finita i contacte entre dos cossos.

Per determinar si existeix el contacte són necessaris dos passos: primerament una cerca global del contacte i a continuació un establiment de les relacions d’interacció. Les relacions d’interacció es caracteritzen per un contacte normal i un contacte tangencial. Les aproximacions clàssiques al fenomen del contacte admeten dues opcions: la condició d’impenetrabilitat o bé l’acceptació d’una petita penetració.

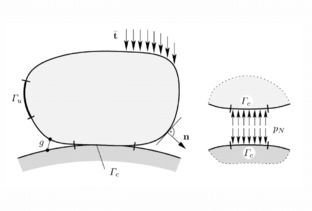
La teoria del contacte parteix de dos cossos elàstics ${\textstyle {B}^{\alpha }}$, ${\textstyle \alpha =}$$1\,,\,2$ cadascun ocupant el domini ${\textstyle {\Omega }^{\alpha }\subset {R}^{3}}$, ${\textstyle \alpha =}$$1\,,\,2$. La superfície fronterera del domini ${\textstyle {\Gamma }^{\alpha }}$ del cos ${\textstyle {\Omega }^{\alpha }}$ està dividida en tres parts: ${\textstyle {\Gamma }_{\sigma }^{\alpha }}$, que correspon a l’àrea de forces de superfície prescrites; ${\textstyle {\Gamma }_{u}^{\alpha }}$ que correspon a l’àrea en què els moviments estan prescrits; i finalment ${\textstyle {\Gamma }_{c}^{\alpha }}$ que correspon a l’àrea de contacte entre els dos cossos.

3.4.1.1 Contacte Normal

A partir de la Figura 3.12 es pot definir la condició d’impenetrabilitat, que es basa en la direcció normal:

$\left({x}^{2}-{x}^{1}\right)\cdot {n}^{1}\geq 0$

(3.56)

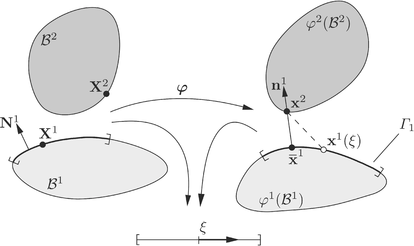
On ${\textstyle {x}^{\alpha }}$ són les coordenades de la configuració actual ${\textstyle \varphi \left({B}^{\alpha }\right)}$ dels cossos. La normal ${\textstyle {n}^{1}}$ s’associa al cos ${\textstyle {B}^{1}}$. Per trobar el punt on s’ha de calcular la normal, s’utilitza el criteri de la mínima distància. Aquest criteri assumeix que la frontera de contacte descriu, almenys localment, una regió convexa. Per tant, cada punt ${\textstyle {x}^{2}}$ de ${\textstyle {\Gamma }^{2}}$ es pot relacionar amb un punt ${\textstyle {\overline {x}}^{1}=}$${x}^{1}\left({\overline {\xi }}\right)$ de ${\textstyle {\Gamma }^{1}}$.

Figura 3.12 Configuració deformada de ${\textstyle B^{\alpha }}$ i mínima distància entre cossos

Aquesta correspondència es fa a partir de la distància mínima entre dos cossos, que es pot definir com:

${\hat {d}}^{1}\left({\xi }^{1},{\xi }^{2}\right)=\left\|{x}^{2}-{\overline {x}}^{1}\right\|=$$\mathrm {min} \,\left\{\left.{x}^{2}-{x}^{1}\left(\xi \right)\right|{x}^{1}\subseteq {\Gamma }^{1}\right\}$

(3.57)

Figura 3.13 Problema de la distància mínima

El paràmetre ${\textstyle {\mathit {\boldsymbol {\xi }}}=\left({\xi }_{1},{\xi }_{2}\right)}$ és la parametrització de la frontera ${\textstyle {\Gamma }^{1}}$. El vector ${\textstyle {n}^{1}}$ es defineix al punt ${\textstyle \left({\overline {\xi }}_{1},{\overline {\xi }}_{2}\right)}$ , que és el de mínima distància. Els vectors ${\textstyle {a}_{1}^{1}}$ i ${\textstyle {a}_{2}^{1}}$ són tangents a la superfície en el punt ${\textstyle \left({\overline {\xi }}_{1},{\overline {\xi }}_{2}\right)}$ . La condició ${\textstyle {n}^{1}\left({\overline {\xi }}_{1},{\overline {\xi }}_{2}\right)\cdot {a}_{\alpha }^{1}\left({\overline {\xi }}_{1},{\overline {\xi }}_{2}\right)=}$$0$ significa que el punt ${\textstyle {x}^{1}\left({\overline {\xi }}_{1},{\overline {\xi }}_{2}\right)}$ és la projecció ortogonal del punt ${\textstyle {x}^{2}}$ a la superfície en la configuració actual ${\textstyle {\varphi }^{1}\left({\Gamma }_{c}^{1}\right)}$ (veure Figura 3.13). El vector ${\textstyle {n}^{1}}$ es defineix com:

${n}^{1}={\frac {{a}_{1}^{1}\times {a}_{2}^{1}}{\left\|{a}_{1}^{1}\times {a}_{2}^{1}\right\|}}$

(3.58)

La restricció d’impenetrabilitat s’escriu com:

${g}_{N}=\left({x}^{2}-{\overline {x}}^{1}\right)\cdot {\overline {n}}^{1}\geq 0$

(3.59)

Mentre que la funció de penetració és:

${\overline {g}}_{N}=\left\{{\begin{matrix}\left({x}^{2}-{\overline {x}}^{1}\right)\cdot {\overline {n}}^{1}{\boldsymbol {\,\longrightarrow }}{\mathit {\boldsymbol {si}}}{\boldsymbol {\,}}\left({x}^{2}-{\overline {x}}^{1}\right)\cdot {\overline {n}}^{1}{\boldsymbol {<}}0\,\\0\end{matrix}}\right.$	(3.60)

3.4.1.2 Contacte tangencial

Per caracteritzar la component tangencial del contacte, hi ha dos casos diferents. El primer cas, conegut com a stick case, no permet el moviment tangencial d’un punt que està en contacte. El segon cas, conegut com a sliding case, considera el moviment tangencial del punt que està en contacte.

3.4.1.2.1 Condició stick

La condició stick significa que el punt no es pot moure tangencialment, com si estigués enganxat. Matemàticament, la condició stick es pot formular així:

${g}_{T}={g}_{T\alpha }\cdot {\overline {a}}^{\alpha }=0\quad \quad \quad on\quad \quad \quad {g}_{T\alpha }=$$\left({x}^{2}-{\overline {x}}^{1}\right)\cdot {\overline {a}}_{\alpha }^{1}$

(3.61)

On ${\textstyle {g}_{T}}$ denota el desplaçament relatiu en la direcció tangencial. S’imposa que sigui zero. En el cas de la condició stick, tant les condicions ${\textstyle {g}_{N}}$ com ${\textstyle {g}_{T}}$ es poden imposar d’una manera molt més senzilla:

${x}^{2}-{\overline {x}}^{1}=0$

(3.62)

3.4.1.2.2 Condició slip

Quan les superfícies dels dos cossos descriuen una deformació relativa, el canvi de punt ${\textstyle {x}^{2}}$ en relació a la seva projecció ${\textstyle {\overline {x}}^{1}}$ defineix un lliscament tangencial. Això vol dir que el punt solució que s’ha obtingut a partir del criteri de la mínima distància es mourà sobre la superfície.

En general, el camí que segueix un punt ${\textstyle {x}^{2}}$ sobre la superfície de referència no es coneix a priori. De fet, el camí seguit fins i tot pot definir una línia que es creui a si mateixa. L’única variable coneguda és el vector de la velocitat relativa. La integració de la velocitat relativa al llarg del temps proporcionarà el camí seguit per la partícula ${\textstyle {x}^{2}}$ sobre la superfície de referència. Es parteix de:

$d{g}_{T}={\overline {a}}_{\alpha }^{1}d{\xi }^{\,\,\alpha }={\overline {x}}_{,\alpha }^{1}d{\xi }^{\,\,\alpha }$

(3.63)

i la longitud del camí seguit es calcula com:

${g}_{T}=\int _{{t}_{0}}^{t}\left\|{\overset {\cdot }{\mathit {\boldsymbol {\xi }}}}^{\alpha }{\overline {x}}_{,\alpha }^{1}\right\|dt$

(3.64)

On ${\textstyle t}$ és el temps, utilitzat per parametritzar el camí seguit per la partícula ${\textstyle {x}^{2}}$. A més a més, s’ha utilitzat la següent igualtat: ${\textstyle {\overset {\cdot }{\mathit {\boldsymbol {\xi }}}}^{\alpha }dt=}$$d{\xi }^{\alpha }.$

3.4.1.3 Adaptació del contacte al PFEM

La restricció d’impenetrabilitat i la funció de penetració definides per l’equació (3.59) i l’equació (3.60) respectivament cal adaptar-les al PFEM. En el PFEM, el contacte s’activa abans que les superfícies dels cossos ${\textstyle {B}^{1}}$ i ${\textstyle {B}^{2}}$ entrin en contacte. Per tant, cal modificar la restricció i la funció degudament.

Es defineix un gap o distància predefinida ${\textstyle {\hat {g}}_{N}}$ que determinarà la distància a partir de la qual ja es considerarà el contacte entre els dos cossos. Aquesta distància serà funció de les alpha-shapes dels elements finits associats a la interfase de contacte.

La desigualtat que imposa la restricció d’impenetrabilitat adaptada al PFEM adopta la següent expressió:

${g}_{N}=\left({x}^{2}-{\overline {x}}^{1}\right)\cdot {\overline {n}}^{1}-{\hat {g}}_{N}\geq 0$

(3.65)

Mentre que la funció de penetració queda:

${\overline {g}}_{N}=\left\{{\begin{matrix}cert\,\longrightarrow si\,\left({x}^{2}-{\overline {x}}^{1}\right)\cdot {\overline {n}}^{1}{\boldsymbol {-}}{\hat {g}}_{N}{\boldsymbol {\,}}<0\,\\fals\,\longrightarrow en\,cas\,contrari\end{matrix}}\right.$

(3.66)

3.4.2 Problema de la frontera del contacte

La consideració més general és considerar la no penetrabilitat del contacte normal. Altres possibilitats consisteixen a introduir les equacions constitutives per descriure el tractament de les superfícies en contacte.

El fet d’imposar el contacte normal com a única restricció bàsicament requereix un bon compliment de les restriccions geomètriques. En aquest cas no és necessari especificar les relacions constitutives a la interfase de contacte. La pressió del contacte s’obté de la reacció a la superfície del contacte, que es dóna quan ${\textstyle {g}_{N}=}$$0$. Aleshores, el vector de la tensió s’expressa com:

${t}^{1}={\sigma }^{1}{\overline {n}}^{1}={p}_{N}^{1}{\overline {n}}^{1}+{t}_{T}^{1\beta }{a}_{\beta }^{1}$

(3.67)

On ${\textstyle {p}_{N}^{1}}$ és la component normal del vector de la tensió. La tensió tangencial ${\textstyle {t}_{T}^{1\beta }}$ és nul·la si no es considera la fricció. En absència de forces d’adhesió, la component normal ha de ser de compressió: ${\textstyle {p}_{N}<0}$. Els punts anteriors defineixen les condicions de Kuhn Tucker per al contacte:

${g}_{N}\geq 0,\,{p}_{N}\leq 0,\,{g}_{N}{p}_{N}=0$

(3.68)

Inicialment, per cada cos, l’equació de balanç de cadascun dels cossos en contacte ${\textstyle {B}^{\gamma }}$ amb ${\textstyle \gamma =}$$1,2$ serà:

Figura 3.14 Contacte entre dos sòlids

$div{\sigma }^{\gamma }+{\rho }^{\gamma }{\overline {b}}^{\gamma }=0$ ${\varphi }^{\gamma }={\overline {\varphi }}^{\gamma }\,en\,{\Gamma }_{\varphi }^{\gamma }$ ${t}^{\gamma }={\overline {t}}^{\gamma }\,en\,{\Gamma }_{\sigma }^{\gamma }$

(3.69)

On ${\textstyle {\overline {\varphi }}^{\gamma }}$ i ${\textstyle {\overline {t}}^{\gamma }}$ són valors prescrits. Quan els dos cossos entren en contacte, les condicions de contacte cinemàtiques passen a ser les condicions de Khun Tucker (veure l’equació (3.68)).

La forma dèbil de les equacions proporciona una desigualtat pel fet que les condicions de Khun Tucker s’expressen d’aquesta mateixa manera. Per al cas general, la forma dèbil és:

$\sum _{i=1}^{2}\int _{\varphi \left({B}^{\gamma }\right)}^{}{\sigma }^{\,\gamma }\cdot {\nabla }^{S}\left({\eta }^{\gamma }-{\varphi }^{\gamma }\right)dv\geq \sum _{i=1}^{2}\left(\int _{\varphi \left({B}^{\gamma }\right)}^{}{\rho }^{\gamma }{\overline {b}}^{\gamma }\cdot \left({\eta }^{\gamma }-{\varphi }^{\gamma }\right)dv-\int _{\varphi \left(\partial {B}_{\sigma }^{\gamma }\right)}^{}{\overline {t}}\cdot \left({\eta }^{\gamma }-{\varphi }^{\gamma }\right)d\Gamma \right)$

(3.70)

La deformació ${\textstyle \left({\varphi }^{1},{\varphi }^{2}\right)\in H}$ es satisfà per tot parell de funcions ${\textstyle \left({\eta }^{1},{\eta }^{2}\right)\in H}$ on ${\textstyle H}$:

$H=\left\{\left.\left({\eta }^{1},{\eta }^{2}\right)\in V\right|\left[{\eta }^{2}-\right.\right.$$\left.\left.{\hat {\eta }}^{1}\left({\overline {\xi }}^{1},{\overline {\xi }}^{2}\right)\right]\cdot {\overline {n}}^{1}\geq 0\right\}$

(3.71)

On ${\textstyle V}$ és el conjunt de les funcions de test. A causa de la desigualtat, de l’equació (3.61) es tracta d’un problema no lineal malgrat per al cas de l’elasticitat lineal.

3.4.3 Tractament de les restriccions del contacte

Existeixen diferents possibilitats a l’hora de d’incorporar les restriccions del contacte a la formulació variacional del contacte, amb o sense fricció. Els diferents mètodes compleixen les diferents equacions de restricció en la direcció normal de la interfase de contacte. Pel que fa a la part tangencial, s’utilitzen equacions constitutives quan es dóna el cas de moviment slip-stick.

La representació més simple assumeix que el contacte a la interfase és conegut. Aquesta assumpció permet solucionar la desigualtat (3.70). Quan el contacte de la interfase és conegut, la forma dèbil es pot reescriure com una igualtat:

$\sum _{\gamma =1}^{2}\left\{\int _{\varphi \left({B}^{\gamma }\right)}^{}{\sigma }^{\gamma }\cdot {\nabla }^{S}{\eta }^{\gamma }dv-\int _{\varphi \left({B}^{\gamma }\right)}^{}{\rho }^{\gamma }{\overline {b}}^{\gamma }\cdot {\eta }^{\gamma }dv-\int _{\varphi \left(\partial {B}_{\sigma }^{\gamma }\right)}^{}{\overline {t}}\cdot {\eta }^{\gamma }d\Gamma \right\}+$${C}_{C}=0$

(3.72)

${\textstyle {C}_{C}}$ representa la contribució del contacte associat al conjunt de restriccions actives, ${\textstyle {\eta }^{\gamma }\in V}$ és la funció de test (o de desplaçaments virtuals) i val zero a la frontera ${\textstyle {\Gamma }_{\varphi }^{\gamma }}$, on les deformacions són prescrites. A més, tal i com ja s’ha dit, s’assumeix que el contacte és actiu a la superfície ${\textstyle {\Gamma }_{C}\equiv \partial {B}_{C}}$.

Existeixen diferents propostes per a la formulació del terme ${\textstyle {C}_{C}}$, tot i que les més emprades són el mètode dels multiplicadors de Lagrange i el Penalty Method. Per al PFEM, s’ha desenvolupat una nova formulació que utilitza la malla creada durant la detecció del contacte entre els dos cossos i s’ha batejat com Continuum Constraint Method. Es basa en el potencial d’un domini continu fictici que treballa entre els dos cossos que han entrat en contacte. Quan la restricció en ${\textstyle \partial {B}_{C}}$ és activa, el terme del contacte de l’equació (3.72) es pot calcular com:

${C}_{C}^{CC}=\int _{\varphi \left({B}_{\sigma }^{c}\right)}^{}\left(P{\sigma }_{c}+T{\sigma }_{c}\right)\cdot {\nabla }^{S}{\eta }_{c}dv$

(3.73)

On el tensor ${\textstyle P}$ es calcula com ${\textstyle P=}$${\overline {n}}^{1}\otimes {\overline {n}}^{1}$, sent ${\textstyle {\overline {n}}^{1}}$la normal de la superfície de contacte en el punt situat a la mínima distància i el tensor ${\textstyle T}$ es calcula com ${\textstyle T=}$$\left(I-P\right)$ . La integració es realitza sobre el subdomini ocupat per la interfase de contacte entre els dos cossos en la configuració actual: ${\textstyle {B}_{\sigma }^{c}}$. Com que el tensor de tensions de Cauchy ${\textstyle {\sigma }_{c}}$ es pot escriure com:

${\sigma }_{c}=P{\sigma }_{c}+\left(I-P\right){\sigma }_{c}=\,P{\sigma }_{c}+$$T{\sigma }_{c}$

(3.74)

El terme del contacte de l’equació (3.73) es pot reescriure com:

${C}_{C}^{CC}=\int _{\varphi \left({B}_{\sigma }^{c}\right)}^{}{\sigma }_{c}\cdot {\nabla }^{S}{\eta }_{c}dv$

(3.75)

I representa el treball virtual intern per un domini continu.

3.4.4 Cerca del contacte

La detecció del contacte és un problema complex, especialment quan hi intervenen més de dos cossos. També els problemes de contacte estàtics de grans deformacions presenten dificultats per detectar-lo, perquè l’àrea de contacte pot canviar ràpidament d’un pas al següent a causa d’un increment de la càrrega.

Tradicionalment, la cerca del contacte es realitza amb dues fases. Primerament es realitza una cerca global d’objectes (subdominis) que possiblement poden entrar en contacte. En segon lloc, la determinació de parells d’objectes que interseccionen i per tant estan en contacte.

Aquestes fases corresponents a la cerca espacial, que requereixen algoritmes complicats, queden molt simplificades amb la utilització del PFEM. El contacte es detecta quan els subdominis són tan propers que permeten la generació dels elements de contacte entre els subdominis que interaccionen. La malla d’interfase s’anticipa al contacte.

3.4.4.1 Detecció del contacte i activació

Els elements de contacte apareixen abans que es produeixi el contacte real entre els subdominis. El que fan és anticipar la interacció entre els subdominis i definir un possible contacte. La detecció dels elements actius en el contacte físic es realitza després. Per cada element de contacte es segueix el següent algoritme:

1. Calcular la normal de la cara de l’element de contacte.

2. Calcular la distància normal ${\textstyle {d}_{i}^{n}}$ entre les superfícies de contacte.

3. Quan la distància normal ${\textstyle {d}_{i}^{n}}$ és més petita que la distància de contacte ${\textstyle {\hat {g}}_{N}}$, l’element de contacte es considera que és actiu.

El conjunt dels diferents elements de contacte defineixen l’àrea de la superfície en contacte. La distància de contacte ${\textstyle {\hat {g}}_{N}}$ es defineix a partir de la mida dels elements i es determina quan es genera la primera capa d’elements de contacte actius. El criteri per determinar ${\textstyle {\hat {g}}_{N}}$ comença amb la determinació del primer element de contacte actiu. A partir dels paràmetres α-shapes no uniformes associats a aquest element es defineix:

${d}_{act}={\frac {1}{n}}\sum _{i=1}^{n}{\alpha }_{i}$

(3.76)

On ${\textstyle {d}_{act}}$ és la distància normal associada al primer element actiu, ${\textstyle n}$ el número de nodes de l’element de contacte, i ${\textstyle {\alpha }_{i}}$ el paràmetre alpha-shape associat a cada node. L’activació del contacte queda definida per:

$\left\{{\begin{matrix}{d}_{i}^{n}\leq {d}_{act}\Rightarrow {\hat {g}}_{N}={d}_{i}^{n}\,;contacte\,actiu\\{d}_{i}^{n}>{d}_{act}\Rightarrow {\hat {g}}_{N}=0\,;sense\,contacte\end{matrix}}\right.$

(3.77)

El paràmetre per a la contracció es defineix com segueix:

${d}_{c}={\frac {{\hat {g}}_{N}}{2}}$

(3.78)

La distància de contacte ${\textstyle {\hat {g}}_{N}}$ és constant mentre el conjunt d’elements actius no canvia.

3.4.4.2 Compliment de les restriccions del contacte

En el PFEM s’utilitzen elements triangulars i tetràedres pel domini del contacte. Això permet definir un criteri senzill per activar o desactivar els elements de contacte. L’element de contacte es mantindrà actiu mentre la tensió mitjana dels punts d’integració sigui de compressió. Això es veu a la Figura 3.15.

Figura 3.15 Activació i desactivació dels elements de contacte i distribució de la pressió amb una aproximació lineal.

La contribució de tots els elements actius proporcionen la força global de compressió del contacte.

4 Resultats

4.1 Caracterització de les sol·licitacions del FWD

Típicament, l’enginyeria de ferms s’ha ocupat d’estudiar les tensions i les deformacions produïdes per càrregues estàtiques. Es consideren càrregues estàtiques aquelles càrregues que varien la seva magnitud des de zero fins als valors definitius tan lentament que les acceleracions que reben els elements de l’estructura són menyspreables. Un exemple molt senzill d’aquest tipus de càrregues són les que suporten els pilars d’un edifici de vivendes, que tarden a rebre el total de càrregues gravitacionals aproximadament dos anys, que és el temps que generalment es tarda des de la construcció de les columnes fins a l’habilitació de l’edifici.

Quan una càrrega s’aplica amb un període relativament curt de temps rep el nom de càrrega dinàmica. Les càrregues dinàmiques es distingeixen de les càrregues estàtiques perquè originen modificacions tant en la magnitud de les tensions com en les deformacions, la forma i el límit de ruptura dels materials. La deformació de ruptura dels materials sol·licitats dinàmicament es redueix considerablement. En canvi, el límit de fluència i la tensió de ruptura augmenten. Molts materials que sota l’acció de càrregues estàtiques tenen un comportament dúctil, sota càrregues dinàmiques tenen un comportament fràgil.

L’acció de càrregues dinàmiques produïdes per l’impacte d’un cos en moviment (per exemple l’impacte de les rodes d’un vehicle pesat per una carretera) pot originar en l’estructura (o en part d’ella) efectes vibratoris.

La determinació rigorosa de les tensions originades com a conseqüència de les càrregues dinàmiques resulta complexa. En el cas de les sol·licitacions estàtiques, les càrregues actuants poden determinar-se de forma molt més fiable que en el cas de les sol·licitacions dinàmiques, on es produeix la transferència d’una certa quantitat d’energia cinètica, la qual, a la pràctica és molt difícil de determinar.

Un altre efecte que juga un paper important en el procés de xoc és la dissipació de l’energia. És un fenomen difícil de quantificar.

La majoria de vegades els efectes dinàmics es quantifiquen experimentalment. A l’hora de realitzar els càlculs, s’utilitzen “càrregues estàtiques equivalents”, que no són altra cosa que càrregues fictícies que actuant estàticament produeixen el mateix efecte que les càrregues dinàmiques veritables. Aquestes càrregues estàtiques equivalents s’obtenen multiplicant les càrregues veritables per un “coeficient d’impacte” o un “coeficient dinàmic”. Aquest coeficient depèn de nombroses variables i la majoria de vegades es determina experimentalment.

Amb el deflectòmetre d’impacte s’aplica una càrrega al ferm que representa una roda d’un eix d’un vehicle pesat. Això correspon a una tensió vertical d’aproximadament 1000 kPa sobre un cercle de radi igual a 0,15 m, que és la dimensió de la placa de càrrega de l’aparell. En els càlculs convencionals estàtics s’aplica aquesta tensió màxima. En canvi, en els càlculs dinàmics, s’introdueix la dimensió temporal i per tant és important tenir en compte la forma de la càrrega al llarg del temps. Típicament, la funció de la càrrega d’impacte al llarg del temps adopta una forma com la de la Gràfica 4.1:

Gràfica 4.1 Caracterització de l’impuls de càrrega d’un deflectòmetre d’impacte.

La funció es caracteritza per una corba ascendent, una corba descendent i la presència de dos pics entremig. La Gràfica 4.1 presenta un primer pic inferior que el segon, però no sempre és així. De vegades el primer pic és més gran que el segon. La duració de l’impuls queda dins de l’interval típic de la duració de l’impacte d’un deflectòmetre d’impacte: entre els 20 i 60 milisegons, mentre que s’assoleix el valor màxim de la càrrega entre els 5 i els 30 milisegons. Una duració de 30 milisegons és molt comuna.

4.2 Simulació de l’impacte amb el PFEM

L’objectiu d’aquest apartat és determinar si la força d’impacte o impuls de càrrega aconseguida amb la simulació del Solid PFEM reprodueix la forma de l’impuls de càrrega real. Per simular una càrrega aproximada de 13/2 t, que correspon a la meitat de la càrrega per eix, es pot prendre una massa d’acer de ${\textstyle M=}$$250\,kg$ deixada caure d’una altura ${\textstyle h=25\,cm}$. D’aquesta manera es vol simular l’efecte al qual està sotmès la carretera pel pas d’un eix de 13 t passant a una velocitat de ${\textstyle 30\,km/h}$.

La geometria del problema es pot veure a la Figura 4.1.

Figura 4.1 Geometria del model d’un deflectòmetre d’impacte en la seva configuració inicial.

Tal i com es pot veure, una massa ${\textstyle M}$ cau des d’una altura ${\textstyle {h}_{1}}$ sobre una placa de càrrega de radi ${\textstyle {r}_{1}}$ que garanteix una distribució uniforme de les pressions de contacte. Aquesta placa de càrrega inclou un disc de goma d’un espessor mínim de ${\textstyle 5\,mm}$, situada entre dos discos d’acer. La placa de càrrega recolza sobre el ferm de la carretera. En aquest model (veure Figura 4.1), el ferm només inclou la capa corresponent a la mescla bituminosa i una part de la capa corresponent a la base.

Els valors geomètrics per la simulació realitzada, prenen els següents valors: ${\textstyle {r}_{1}=}$$0,15\,m$, ${\textstyle {r}_{2}=0,14\,m}$, ${\textstyle {r}_{3}=}$$0,5\,m$, ${\textstyle {s}_{1}=0,1\,m}$, ${\textstyle {s}_{2}=}$$0,1\,m$, ${\textstyle e=0,02\,m}$, ${\textstyle {h}_{1}=}$$0,25\,m$ i ${\textstyle l=0,517\,m}$.

És important dir que a la simulació només s’hi inclou una petita part del domini del ferm per no carregar excessivament el càlcul amb una malla més gran del compte. En aquest mateix sentit, per aconseguir que la simulació sigui més ràpida, en comptes de deixar caure la massa ${\textstyle M}$ amb una velocitat zero des d’una altura de ${\textstyle {h}_{1}=}$$0,25\,m$, es decideix deixar caure el pes des de només una altura de ${\textstyle {h}_{2}=}$$0,0015\,m$ amb una velocitat inicial igual a la que tindria el cos si hagués caigut des de ${\textstyle {h}_{1}=}$$0,25\,m$ a l’instant de passar per aquell punt. Cinemàticament:

${x}_{f}={x}_{0}+{v}_{0}\cdot t+{\frac {1}{2}}\cdot a\cdot {t}^{2}$

(4.1)

I tenint en compte que ${\textstyle {x}_{f}=0,25\,m}$, ${\textstyle {x}_{0}=}$$0,0015\,m$, ${\textstyle {v}_{0}=0\,m/s}$, ${\textstyle a=}$$9,81\,m/{s}^{2}$, el temps de caiguda serà:

$0,25=0,0015+{\frac {1}{2}}\cdot 9,81\cdot {t}^{2}$ $t=0,225084\,s$

(4.2)

La velocitat de la massa quan sigui a només ${\textstyle 0,0015\,m}$ d’impactar amb la placa de càrrega serà:

${v}_{f}={v}_{0}+a\cdot t$ ${v}_{f}=9,81\cdot 0,225084=2,208\,m/s$

(4.3)

La Figura 4.2 reprodueix les noves condicions inicials:

Figura 4.2 Geometria del model d’un deflectòmetre d’impacte amb les condicions inicials introduïdes en el model.

On la massa ${\textstyle M}$ parteix d’una altura sobre la placa de càrrega de ${\textstyle {h}_{2}=}$$0,0015\,m$ amb una velocitat inicial de ${\textstyle {v}_{0}=}$$-2,208\,m/s$.

La geometria del problema plantejat té una simetria axial, és a dir, es considera que la geometria i les propietats mecàniques del sòlid són independents de la coordenada circumferencial ${\textstyle \theta }$ (els anomenats sòlids de revolució). Tot i que el comportament és tridimensional, el seu estudi matemàtic es pot tractar com un problema bidimensional, utilitzant únicament les coordenades cartesianes. L’estudi de les estructures de revolució segueix pràcticament els mateixos passos que un problema bidimensional (veure (6)).

La geometria a introduir és la representada a la Figura 4.3.

Figura 4.3 Geometria segons el model axisimètric.

Per les condicions de contorn s’imposa que:

${u}_{x}=0\,en\,x=0$ ${u}_{x}=0\,en\,y=0$ ${v}_{y}=0\,en\,y=0$

(4.4)

Figura 4.4 Condicions de contorn imposades en el model axisimètric

Mentre que per les condicions inicials, tal i com s’ha dit anteriorment, s’imposa una velocitat inicial sobre la massa ${\textstyle M}$ de ${\textstyle {v}_{0}=}$$-2,208\,m/s$, tal i com indica la Figura 4.5.

Figura 4.5 Condicions inicials imposades en el model axisimètric

La següent taula recull els valors dels mòduls elàstics ${\textstyle E}$, els coeficients de Poisson ${\textstyle \nu }$ i les densitats ${\textstyle \rho }$ utilitzades per cadascun dels materials.

Material	Acer	Cautxú	Mescla Bituminosa	Base
$E\,(MPa)$	210.000	10	2.000	150
$\nu$	0,3	0,45	0,35	0,35
$\rho \,\left(kg/{m}^{3}\right)$	7.850	930	2.400	2.000

Els valors de l’amortiment introduïts pels materials del ferm són ( ${\textstyle \alpha =}$$0,36\,$ i ${\textstyle \beta =0,0026}$). (Veure 4.4-Amortiment, pàgina 82).

La Figura 4.6 mostra els materials emprats per cada part del domini.

Figura 4.6 Materials emprats

La malla emprada conté 6.958 nodes i 12909 elements triangulars. La placa d’impacte la malla respon a una forma estructurada de mida 0,0015 m. La base de la massa que entra en contacte amb la placa d’impacte també té elements triangulars d’aquesta dimensió. Aquesta zona s’ha mallat de manera molt fina per poder obtenir en detall l’evolució de la força de contacte al llarg del temps.

També cal comentar que el radi de la massa ${\textstyle M}$ ( ${\textstyle {r}_{2}=}$$0,14\,m$) és un pensament més petit que el radi de la placa d’impacte ( ${\textstyle {r}_{1}=}$$0,15\,m$) perquè d’aquesta manera s’evitaven problemes a l’hora de reproduir els elements de contacte.

Figura 4.7 Malla emprada

 <

Figura 4.8 Detall de la malla a la zona de la placa de càrrega

El pas de temps de la simulació ha estat de ${\textstyle \Delta t={10}^{-5}s}$ i la duració de ${\textstyle t=}$$0,01\,s$. L’evolució de la força de contacte entre la massa ${\textstyle M}$ i la placa de càrrega al llarg del temps es mostra a la Gràfica 4.2.

Gràfica 4.2 Evolució de la força d’impacte al llarg del temps

La distribució de les forces de contacte entre la massa ${\textstyle M}$ i la placa de càrrega en alguns instants de temps es pot veure a la Figura 4.9.

Figura 4.9 Seqüència de l’evolució de la força d’impacte distribuïda al llarg del temps.

L’evolució de la força d’impacte al llarg del temps obtinguda amb el Solid PFEM és una mala aproximació respecte la força d’impacte real definida a la Gràfica 4.1. No s’assembla ni en la intensitat màxima, ni en la durada ni tampoc en la forma. La Gràfica 4.2 mostra una força de contacte molt irregular en el temps, amb pics molt elevats i valors nuls entremig.

La duració total del contacte segons la simulació és de ${\textstyle 0,00176\,s}$, molt lluny de la duració real que pot valer entre 20 i 60 milisegons.

La distribució de la força de contacte entre la massa ${\textstyle M}$ i la placa de càrrega és molt irregular tan a nivell temporal com a nivell espacial. En el primer instant del contacte, adopta una forma triangular creixent amb el radi. Té sentit en tant que es tracta d’un model axisimètric, però un cop s’ha superat aquest instant, la distribució espacial és totalment irregular. Apareixen forces de contacte molt elevades en uns determinats punts, forces de contacte molt petites en d’altres punts, i una part on no hi ha cap contacte.

Algunes de les raons per les quals la simulació de l’impacte simulat amb el Solid PFEM no és satisfactòria són les següents:

• Si bé s’han modelat els materials amb lleis constitutives elàstiques lineals, la realitat és que la mescla bituminosa i el material que conforma la base del ferm, o el mateix cautxú es caracteritzen per tenir lleis viscoelàstiques. La utilització d’un model elàstic lineal amb amortiment per simular un model viscoelàstic no aconsegueix reproduir correctament l’impacte.

• En aquesta simulació dinàmica no s’ha introduït cap tipus d’amortiment a la massa ${\textstyle M}$ d’acer. El fet d’introduir un determinat amortiment provocava que les forces externes no quedaven igualades amb les forces internes i el programa era incapaç de convergir a una solució. El problema de no introduir cap amortiment és que un cop produït l’impacte, s’introdueix a la massa d’acer ${\textstyle M}$ una energia i provoca una ona que no s’atenua. Això provoca una mala simulació del contacte perquè aquestes petites oscil·lacions afecten en el manteniment del contacte amb la placa de càrrega.

Per tal de poder fer una anàlisi del ferm de la carretera s’opta per definir la funció que caracteritza la força d’impacte i introduir-la al codi.

4.3 Definició de la càrrega d’impacte

Com que la simulació de l’impacte amb el PFEM no ha donat uns resultats satisfactoris perquè no ha reproduït correctament la càrrega experimental de contacte, es decideix introduir al programa d’ordinador la funció experimental de l’impuls de càrrega.

L’impuls de càrrega proposat l’apartat 4.1 és una funció que queda definida a punts segons la Taula 4.1.

Temps (s)	Pressió (MPa)	Temps (s)	Pressió (MPa)
0	0	0,016	0,9
0,001	0,002	0,017	0,8
0,002	0,005	0,018	0,68
0,003	0,01	0,019	0,58
0,004	0,02	0,02	0,49
0,005	0,06	0,021	0,4
0,006	0,14	0,022	0,33
0,007	0,34	0,023	0,26
0,008	0,62	0,024	0,2
0,009	0,78	0,025	0,14
0,01	0,75	0,026	0,1
0,011	0,72	0,027	0,06
0,012	0,8	0,028	0,04
0,013	0,88	0,029	0,02
0,014	0,92	0,03	0
0,015	0,93	-	-

Taula 4.1 Definició a punts d’un exemple de funció de l’impuls de càrrega provocat per un deflectòmetre d’impacte.

Per tal d’obtenir-ne una expressió analítica, s’opta per definir una funció polinòmica a trossos que s’ajusti a la funció:

$f\left(t\right)=\left\{{\begin{matrix}{f}_{1}\left(t\right)\quad \quad \quad \quad \quad \quad \quad \quad \quad si\,t\in \left[0;0,001\right)\\{f}_{2}\left(t\right)\quad \quad \quad \quad \quad \quad \,\,si\,t\in \left[0,001;0,002\right)\\{f}_{3}\left(t\right)\quad \quad \quad \quad \quad \quad \,\,si\,t\in \left[0,002;0,006\right)\\{f}_{4}\left(t\right)\quad \quad \quad \quad \quad \quad \quad si\,t\in \left[0,006;0,01\right)\\{f}_{5}\left(t\right)\quad \quad \quad \quad \quad \quad \quad si\,t\in \left[0,01;0,015\right)\\{f}_{6}\left(t\right)\quad \quad \quad \quad \quad \quad \,si\,t\in \left[0,015;0,021\right)\\{f}_{7}\left(t\right)\quad \quad \quad \quad \quad \quad \quad si\,t\in \left[0,021;0,03\right)\end{matrix}}\right.$

(4.5)

On

${f}_{1}\left(t\right)=2\cdot t$ ${f}_{2}\left(t\right)=3\cdot t-0,001$ ${f}_{3}\left(t\right)=-308.333.333.347,987\cdot {t}^{5}+$$5.541.666.666,950680\cdot {t}^{4}-34.875.000,002138\cdot {t}^{3}+$$99.458,333341\cdot {t}^{2}-124,816667\cdot t+0,057$ ${f}_{4}\left(t\right)=2.416.666.667.075,22\cdot {t}^{5}-$$91.250.000.015,4563\cdot {t}^{4}+1.338.750.000,23072\cdot {t}^{3}-$$9.528.750,0016962\cdot {t}^{2}+33.058,8333395\cdot t-44,88$ ${f}_{5}\left(t\right)=-83.333.333.522,0703\cdot {t}^{5}+$$7.916.666.678,80078\cdot {t}^{4}-272.083.333,643556\cdot {t}^{3}+$$4.392.083,3372762\cdot {t}^{2}-33.857,8333583\cdot t+101,37$ ${f}_{6}\left(t\right)=138.888.887.584.008,0\cdot {t}^{6}-$$14.999.999.858.711,1\cdot {t}^{5}+672.222.215.865,765\cdot {t}^{4}-$$15.997.499.847,9146\cdot {t}^{3}+213.177.636,847916\cdot {t}^{2}-1.507.977,4854343\cdot t+$$4.424,5399568$ ${f}_{7}\left(t\right)=1.960.784.307.279,31\cdot {t}^{6}-$$310.143.287.116,198\cdot {t}^{5}+20.288.272.941,1516\cdot {t}^{4}-$$702.677.137,039046\cdot {t}^{3}+13.595.989,4494293\cdot {t}^{2}-139.489,459905\cdot t+$$594,1450335$

(4.6)

La següent taula mostra els valors utilitzats per determinar cadascun dels polinomis així com la regressió assolida:

Tram	r2	Valors emprats per definir la funció a trossos
${f}_{1}\left(t\right)$	1	${\textstyle t=}$$[0;0,001$]
${f}_{2}\left(t\right)$	1	$t=[0,001;0,002]$
${f}_{3}\left(t\right)$	1	$t=[0,001;0,006]$
${f}_{4}\left(t\right)$	1	$t=[0,005;0,01]$
${f}_{5}\left(t\right)$	1	$t=[0,01;0,015]$
${f}_{6}\left(t\right)$	1	${\textstyle t=}$$[0,015;0,021$]
${f}_{7}\left(t\right)$	0,9998781	${\textstyle t=}$$[0,020;0,030$]

Aquesta manera d’aproximar la càrrega real té alguns inconvenients. Es tracta d’un model complicat i laboriós. L’objectiu és reproduir amb el programa resultats experimentals que canvien lleugerament el valor de la pressió màxima i la forma de l’impuls de càrrega a cadascun dels assaigs. Per tant, no és eficient haver de fer un ajust complet d’aquestes característiques per cadascun dels casos perquè caldria, primerament fer l’ajust per la càrrega d’impacte corresponent a cada cas i en segon lloc introduir el nou ajust al codi cada vegada que es volgués reproduir un assaig diferent. A més a més, en aquest treball es desconeixen les formes exactes dels impulsos de càrrega. Per tant no es tenen prou paràmetres per ajustar els polinomis per cadascun dels casos.

Així doncs, es proposen models de l’impuls de la càrrega una mica simplificats que s’ajustin introduint tan sols dos o tres paràmetres la màxima intensitat de la càrrega.

La funció utilitzada en aquest treball és la funció sinusoïdal al quadrat, malgrat que les altres opcions també es podrien contemplar com a possibilitats a escollir i per tant també han estat programades.

4.3.1 Funció sinusoïdal al quadrat

Com a alternativa a l’aproximació polinòmica, es proposa una aproximació simplificada amb un sinus al quadrat. La seva expressió analítica és la següent:

$f\left(t\right)=P\cdot {sin}^{2}\left({\frac {\pi }{D}}\cdot t\right)$

(4.7)

On ${\textstyle P}$ correspon a la màxima tensió vertical assolida durant la força d’impacte i ${\textstyle D}$ és la durada total de l’impacte. És la funció escollida per simular els diferents casos dinàmics d’aquest treball. Per exemple, per aproximar amb la funció sinusoïdal al quadrat la càrrega d’impacte real proposada a l’apartat 4.3, només cal imposar que la durada de l’impacte sigui de ${\textstyle D=}$$0,03\,s$ i que la màxima tensió vertical prengui un valor de ${\textstyle P=}$$0,93\,MPa$. Així doncs, determinant només dos paràmetres diferents, la màxima tensió vertical i la durada de l’impacte, ràpidament queda definida la càrrega adequadament, facilitant molt la tasca que requeria fer-ne un ajust polinòmic per cada cas diferent.

La Gràfica 4.3 mostra la comparació entre una càrrega real i la corresponent proposta d’una funció sinusoïdal al quadrat.

Temps (s)	Pressió (MPa)	Temps (s)	Pressió (MPa)
0	0	0,016	0,9198
0,001	0,0102	0,017	0,8898
0,002	0,0402	0,018	0,8412
0,003	0,0888	0,019	0,7761
0,004	0,1539	0,02	0,6975
0,005	0,2325	0,021	0,6087
0,006	0,3213	0,022	0,5136
0,007	0,4164	0,023	0,4164
0,008	0,5136	0,024	0,3213
0,009	0,6087	0,025	0,2325
0,01	0,6975	0,026	0,1539
0,011	0,7761	0,027	0,0888
0,012	0,8412	0,028	0,0402
0,013	0,8898	0,029	0,0102
0,014	0,9198	0,03	0
0,015	0,93	-	-

Taula 4.2 Valors de l’impuls de càrrega sinusoïdal per alguns instants de temps.

Gràfica 4.3 Comparació entre la càrrega real del deflectòmetre d’impacte i la proposta de la funció amb un sinus al quadrat.

Malgrat que la forma proposada no coincideixi exactament amb la càrrega real, s’ha optimitzat tenint en compte els següents criteris:

• Amplitud de la càrrega

• Temps des de l’inici de la senyal fins que s’assoleix la càrrega màxima

• La superfície sota la corba (MPa·s), que suposa una mesura de la càrrega total rebuda.

• La duració total de la càrrega

4.3.2 Funció triangular

Una altra de les opcions seria utilitzar una funció triangular simètrica. De nou depèn només de dos paràmetres:

$f\left(t\right)=\left\{{\begin{matrix}{\frac {b}{\left({\frac {a}{2}}\right)}}\cdot t\quad si\,t\in \left[0,{\frac {a}{2}}\right]\\-{\frac {b}{\left({\frac {a}{2}}\right)}}\cdot t+2\cdot b\quad si\,t\in \left(\left.{\frac {a}{2}},a\right]\right.\end{matrix}}\right.$

(4.8)

On ${\textstyle a}$ és la duració total de l’impacte i ${\textstyle b}$ el valor de la màxima tensió vertical assolida, tal i com mostra la gràfica de la funció:

Gràfica 4.4 Funció triangular.

És una aproximació més simple i que ajusta pitjor la forma real de la càrrega.

4.3.3 Funció trapezoïdal

Una tercera proposta seria la utilització d’una funció trapezoïdal, una mica més elaborada que la funció triangular. Ara però, la funció, que continua sent simètrica, queda definida amb tres paràmetres:

$f\left(t\right)=\left\{{\begin{matrix}{\frac {2b}{a}}\cdot t\quad si\,t\in \left[\left.0,{\frac {a}{2}}\right)\right.\\b\quad \,\,si\,t\in \left[\left.{\frac {a}{2}},{\frac {a}{2}}+c\right)\right.\\-{\frac {2b}{a}}\cdot t+2b\left(1+{\frac {c}{a}}\right)\quad si\,t\in \left[{\frac {a}{2}}+c,a+c\right]\end{matrix}}\right.$

(4.9)

On ${\textstyle {\frac {a}{2}}}$ és la durada de la branca ascendent i també de la branca descendent de la funció, mentre que ${\textstyle c}$ és la durada en què la funció és constant. El paràmetre ${\textstyle b}$ indica la màxima tensió vertical assolida durant l’impacte. Naturalment, en aquest cas, la clau és determinar la duració del paràmetre ${\textstyle c}$.

Gràfica 4.5 Funció trapezoïdal

4.3.4 Funció sinusoïdal al quadrat composta

Una altra opció, més elaborada encara que la funció trapezoïdal, i que pren com a base la funció sinusoïdal, és aproximar la força d’impacte real amb dues funcions sinusoïdals al quadrat per tal de poder simular els dos pics existents. Per fer-ho cal definir una funció a trossos amb tres intervals:

$f\left(t\right)=\left\{{\begin{matrix}P\cdot {sin}^{2}\left({\frac {\pi }{D}}\cdot t\right)\,si\,t\in \left[0;s\right]\\P\cdot {sin}^{2}\left({\frac {\pi }{D}}\cdot t\right)+Q\cdot {sin}^{2}\left({\frac {\pi }{\hat {D}}}\cdot \left(t-s\right)\right)\,si\,t\in \left[s,D\right]\\Q\cdot {sin}^{2}\left({\frac {\pi }{\hat {D}}}\cdot \left(t-s\right)\right)\,si\,t\in \left[D,s+{\hat {D}}\right]\end{matrix}}\right.$

(4.10)

On ${\textstyle P}$ és la màxima tensió vertical assolida pel primer pic, ${\textstyle D}$ correspon a la duració del primer sumand sinusoïdal al quadrat, ${\textstyle Q}$ és la màxima tensió vertical assolida pel segon pic, ${\textstyle {\hat {D}}}$ correspon a la duració del segon sumand sinusoïdal al quadrat i ${\textstyle s}$ és la translació del segons sumand sinusoïdal en l’eix temporal. Gràficament:

Gràfica 4.6 Funció sinusoïdal al quadrat composta.

Per aconseguir una bona aproximació cal ajustar cinc valors: ${\textstyle P}$, ${\textstyle D}$, ${\textstyle Q}$, ${\textstyle {\hat {D}}}$ i ${\textstyle s}$. Tal i com ja passava amb l’aproximació polinòmica, per un costat és laboriós aproximar cada cas, i de l’altre, com que es desconeix la funció real, no és possible fer-ne un ajust perquè no es tenen les referències necessàries.

4.4 Amortiment

Si bé els materials que conformen el ferm (mescla bituminosa, base i esplanada) es caracteritzen per descriure’s amb lleis constitutives viscoelàstiques, aquest treball fa el supòsit que es tracten de materials elàstics lineals. Per simular un comportament viscoelàstic, s’utilitza un comportament elàstic lineal amb la presència d’amortiment.

A més a més, en una anàlisi estàtica, els paràmetres que s’han de tenir en compte són el mòdul d’elasticitat ${\textstyle E}$ i el coeficient de Poisson ${\textstyle \nu }$ . Ara bé, per a una anàlisi dinàmica, a més a més són necessaris la densitat ${\textstyle \rho }$ del material i el factor d’amortiment ${\textstyle C}$.

D’una banda, les densitats de les diferents capes que conformen els ferms són prou conegudes i relativament fàcils de determinar i de l’altra no canvien significativament durant la seva vida útil. La seva influència durant el procés de monitorització és irrellevant.

En canvi, el factor d’amortiment ${\textstyle C}$ té una influència important en el càlcul dinàmic elàstic. En un model dinàmic elàstic, l’energia transmesa al model pel deflectròmetre d’impacte no es dissipa, i això provocaria que el model entrés en una oscil·lació sense final. Per tant és necessari aplicar un factor que comptabilitzi el comportament viscoelàstic de l’estructura: el factor d’amortiment, també anomenat amortiment viscós o amortiment de Rayleigh. Aquest factor s’inclou a l’equació del moviment. Aquest factor d’amortiment és l’encarregat de dissipar l’energia i el responsable que l’amplitud de les vibracions lliures disminueixin amb el temps. L’amortiment viscós és el resultat de la combinació lineal de l’efecte de la massa i l’efecte de la rigidesa de l’estructura. Matemàticament, el factor d’amortiment s’escriu:

$C=\alpha M+\beta K$

(4.11)

On ${\textstyle M}$ i ${\textstyle K}$ són les matrius de massa i rigidesa respectivament. Els paràmetres ${\textstyle \alpha }$ i ${\textstyle \beta }$ es poden determinar segons el següent sistema d’equacions:

$\left\{{\begin{matrix}{\xi }_{1}={\frac {\alpha }{2{\omega }_{1}}}+{\frac {\beta {\omega }_{1}}{2}}\\{\xi }_{2}={\frac {\alpha }{2{\omega }_{2}}}+{\frac {\beta {\omega }_{2}}{2}}\end{matrix}}\right.$

(4.12)

On les variables ${\textstyle {\xi }_{1}}$ i ${\textstyle {\xi }_{2}}$ s’anomenen ratios d’amortiment i estan continguts en el rang entre el 2% i el 7%. El valor ${\textstyle {\omega }_{1}}$ representa el valor propi de freqüència més baixa, mentre que el valor ${\textstyle {\omega }_{2}}$ representa la màxima freqüència. La diferència entre ${\textstyle {\omega }_{1}}$ i ${\textstyle {\omega }_{2}}$ s’anomena rang d’interès. Els valors que es prenen de ${\textstyle {\omega }_{1}}$ i ${\textstyle {\omega }_{2}}$ tenen influència sobre la malla requerida. La dimensió de la malla escollida està en connivència amb els valors presos de ${\textstyle {\omega }_{1}}$ i ${\textstyle {\omega }_{2}}$.

La Gràfica 4.7, extreta de (7), és una gràfica mitjana de diferents ferms que permeten trobar valors inicials dels paràmetre d’amortiment. Donat un ràtio d’amortiment, permet determinar uns valors inicials per als paràmetres d’amortiment ${\textstyle \alpha }$ i ${\textstyle \beta }$ . Com que la Gràfica 4.7 caracteritza el conjunt del ferm, s’assignen els mateixos valors ${\textstyle \alpha }$ i ${\textstyle \beta }$ a totes les capes del ferm i no es poden establir valors per cadascuna d’elles.

Gràfica 4.7 Gràfica per valorar els paràmetres d’amortiment escollits.

Prenent un valor del ràtio d’amortiment ${\textstyle \xi ={\xi }_{1}=}$${\xi }_{2}=5\%$, ${\textstyle 5\%\in \left[2\%,\,7\%\right]}$ , que és un valor raonable, s’obté una freqüència mínima de ${\textstyle {\omega }_{1}=}$$4\,Hz$ i una freqüència màxima de ${\textstyle {\omega }_{2}=}$$35\,Hz$. Els valors ${\textstyle \alpha }$ i ${\textstyle \beta }$ s’obtenen resolent el sistema següent:

$\left\{{\begin{matrix}{\frac {5}{100}}={\frac {\alpha }{2\cdot 4}}+{\frac {\beta \cdot 4}{2}}\\{\frac {5}{100}}={\frac {\alpha }{2\cdot 35}}+{\frac {\beta \cdot 35}{2}}\end{matrix}}\right.$

(4.13)

D’on s’obté que ${\textstyle \alpha =0,36}$ i ${\textstyle \beta =}$$0,0026$.

4.5 Ubicació dels assaigs

La tesina d’especialitat “Análisis del empleo del deflectómetro de impacto para el control de la calidad de la construcción de firmes de carreteras”, d’Antonio García Velasco (veure (8)), realitza una auscultació amb el deflectòmetre d’impacte model PHOENIX VW2100 de la nova variant de Capellades. Es tracta d’una carretera de nova construcció sobre la qual s’han analitzat cadascuna de les fases de construcció del ferm. Concretament, s’han establert tres fases. El ferm final consta de la següent distribució:

• 6 cm de capa de rodadura

• 10 cm de capa intermèdia

• 10 cm de base

• 2 capes de 25 cm de capa granular

• Esplanada

Les tres capes de mescla bituminosa es consideren en el càlcul com una sola capa perquè el programa de càlcul invers que utilitza només admet tres capes diferents, que acaben corresponent a l’esplanada, la base i la mescla bituminosa. Els espessors de les capes dels ferms per cadascuna de les fases són els següents:

La primera fase auscultada:

• 10 cm de mescla bituminosa

• 50 cm de material granular

• Esplanada

La segona fase auscultada:

• 20 cm de mescla bituminosa

• 50 cm de material granular

• Esplanada

La tercera fase auscultada:

• 26 cm de mescla bituminosa

• 50 cm de material granular

• Esplanada

L’objectiu de l’estudi “Análisis del empleo del deflectómetro de impacto para el control de la calidad de la construcción de firmes de carreteras” és determinar, quan només es disposen de sis sensors o bé un programa de càlcul invers només admet la introducció de sis valors de deflexions, quina és la distribució que permet al càlcul invers proporcionar uns valors dels mòduls d’elasticitat de les capes del ferm més propers a la realitat. Els seus annexos recullen un conjunt de deflexions amb els corresponents mòduls d’elasticitat obtinguts amb el càlcul invers per cadascuna de les tres fases de la construcció de la variant de Capellades que serviran de dades per al present treball.

Aquest treball realitza un càlcul directe: es parteix dels espessors proporcionats per (8), els mòduls d’elasticitat corresponents a la distribució dels sensors més adequada segons (8) i els coeficients de Poisson adequats (veure (8) i (9)) per determinar els moviments ${\textstyle {\overline {u}}}$ (deflexions), les deformacions ${\textstyle {\overline {\epsilon }}}$ i les tensions ${\textstyle {\overline {\sigma }}}$.

4.6 Plantejament geomètric del problema

La geometria del problema plantejat té una simetria axial, tal i com ja passava quan es volia simular l’impacte.

Com que les càrregues exteriors també són de revolució, el desplaçament d’un punt de l’estructura té només components en la direcció radial ${\textstyle \left(x\right)}$ i axial ${\textstyle \left(y\right)}$ . L’estudi de les estructures de revolució segueix pràcticament els mateixos passos que un problema bidimensional. Si les càrregues no fossin de revolució, s’hauria de realitzar una anàlisi tridimensional (veure (6)).

Figura 4.10 Representació del problema en 3-D.

Així doncs, la geometria és:

Figura 4.11 Dimensions de la geometria del problema.

On les dimensions són: per la Fase 1, ${\textstyle {h}_{1}=0,1\,m}$, ${\textstyle {h}_{2}=}$$0,5\,m$ i ${\textstyle {h}_{3}=0,6\,m}$; per la fase 2, ${\textstyle {h}_{1}=}$$0,2\,m$, ${\textstyle {h}_{2}=0,5\,m}$ i ${\textstyle {h}_{3}=}$$0,6\,m$; i per la fase 3, ${\textstyle {h}_{1}=0,26\,m}$, ${\textstyle {h}_{2}=}$$0,5\,m$ i ${\textstyle {h}_{3}=0,6\,m}$. Per a les tres fases, ${\textstyle r=}$$0,15\,m$ i ${\textstyle l=2,5\,m}$.

Per les condicions de contorn s’imposa que:

${u}_{x}=0\,en\,x=0$ ${u}_{x}=0\,en\,y=0$ ${v}_{y}=0\,en\,y=0$

(4.14)

Figura 4.12 Condicions de contorn imposades.

Finalment, s’aplica la força sinusoïdal al quadrat amb el temps:

${\overline {F}}\left(t\right)=\left({\frac {{F}_{x}(t)}{{F}_{y}(t)}}\right)=\left({\frac {0}{f\left(t\right)}}\right)=$$\left({\frac {0}{P\cdot {sin}^{2}\left({\frac {\pi }{D}}\cdot t\right)}}\right)\quad on\quad t\in \left[0;D\right]\,\,$

(4.15)

En

$x\in \left[0;0,15\,\right]\,m$

I en

$y=\left\{{\begin{matrix}=1,2\,en\,Fase\,1\\=1,3\,en\,Fase\,2\\=1,36\,en\,Fase\,3\end{matrix}}\right.$

On ${\textstyle P}$ correspon a la màxima tensió vertical assolida durant la força d’impacte i ${\textstyle D}$ és la durada total de l’impacte.

La Figura 4.13 mostra la seqüència de diferents instants de la força d’impacte al llarg del temps. Concretament, de dalt a baix i d’esquerra a dreta, les imatges corresponen als instants ${\textstyle {t}_{1}=}$$0,0005\,s$, ${\textstyle {t}_{2}=0,005\,s}$, ${\textstyle {t}_{3}=}$$0,01\,s$, ${\textstyle {t}_{4}=0,015\,s}$, ${\textstyle {t}_{5}=}$$0,02\,s$, i ${\textstyle {t}_{6}=0,025\,s}$.

Figura 4.13 Seqüència de la força d’impacte al llarg del temps.

Cada capa queda caracteritzada per un mòdul d’elasticitat ${\textstyle E}$ i un coeficient de Poisson ${\textstyle \nu }$ . Seguint (5) i (6), es pren un únic coeficient de Poisson de valor ${\textstyle \nu =}$$0,35$ per totes les capes. En total s’han modelat un total de 18 casos, 6 per cadascuna de les fases. Seguint la codificació de (4), on el número indica el punt quilomètric i la lletra el carril sobre el qual s’ha realitzat l’assaig, els casos calculats són el següents:

FASE 1	FASE 2	FASE 3
3801_C	3825_R	4325_I
3875_C	3925_C	4075_D
3674_L	5700_L	6175_D
8125_L	7900_D	7150_D
8500_C	8475_C	8075_D
8550_L	8850_C	8275_C

Taula 4.3 Nomenclatura dels casos realitzats en el present treball.

Per la fase 1, els mòduls d’elasticitat de cada cas calculat són els següents:

Cas	3801_C	3674_L	3875_C	8125_L	8500_C	8550_L
Distribució	B	B	B	B	B	B
${\textstyle P}$ Pressió de contacte ${\textstyle (MPa)}$	0,707	0,749	0,721	0,693	0,707	0,721
${E}_{1}(MPa)$	2108	1659	2638	1517	5369	5404
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	177	130	207	207	175	127
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	152	129	137	59	70	102

Taula 4.4 Dades inicials dels casos analitzats corresponents a la Fase 1.

Per la fase 2, els mòduls d’elasticitat de cada cas calculat són els següents:

Cas	3825_R	3925_C	5700_L	7900_D	8475_C	8850_C
Distribució	C	C	C	C	C	C
${\textstyle P}$ Pressió de contacte ${\textstyle (MPa)}$	0,749	0,693	0,707	0,707	0,721	0,721
${E}_{1}(MPa)$	2884	5339	2973	2622	3584	5479
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	310	546	302	129	150	236
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	180	199	126	124	107	118

Taula 4.5 Dades inicials dels casos analitzats corresponents a la Fase 2

Per la fase 3, els mòduls d’elasticitat de cada cas calculat són els següents:

Cas	4325_I	4075_D	6175_D	7150_D	8075_D	8275_C
Distribució	D	D	D	D	D	D
${\textstyle P}$ Pressió de contacte ${\textstyle (MPa)}$	0,707	0,721	0,707	0,721	0,693	0,693
${E}_{1}(MPa)$	7958	4314	4030	6436	3523	4202
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	598	393	207	392	197	224
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	127	148	150	135	154	166

Taula 4.6 Dades inicials dels casos analitzats corresponents a la Fase 3.

Per la densitat de les diferents capes es prenen els mateixos valors per tots els casos i totes les fases. Els valors són els següents: per la capa superior, corresponent a la mescla bituminosa, es pren una densitat de ${\textstyle 2400\,kg/{m}^{3}}$, mentre que per la base i l’esplanada es pren el mateix valor de ${\textstyle 2000\,kg/{m}^{3}}$.

La màxima tensió vertical assolida durant la força d’impacte (el valor ${\textstyle P}$), és una dada de cada cas. La durada tota de l’impacte, ${\textstyle D}$, es fixa en ${\textstyle 0,030}$ segons. La durada de l’impacte és diferent de la durada de la simulació, que és de ${\textstyle 0,035}$ segons.

La malla del domini consisteix en una malla estructurada d’elements triangulars, d’una dimensió de 1 cm el costat de cada element. La malla dels casos de la Fase 1 consta de 60.000 elements i 30.371 nodes; la malla de la Fase 2 consta de 65.000 elements i 32.881 nodes, i finalment, la malla de la fase 3 consta de 68.000 elements i 34.387 nodes.

Figura 4.14 Malla emprada.

Figura 4.15 Detall de la malla emprada.

La introducció de dades en el programa Solid PFEM segueix la següent seqüència: introducció de la geometria a través del programa de preprocés GiD, definició dels diferents dominis, introducció de les condicions de contorn i les condicions inicials, introducció de les condicions de contorn (accions), definició dels materials, i finalment els aspectes relatius a l’eina de càlcul escollits han estat els següents:

• Simulació d’una durada de ${\textstyle 0,035\,s}$ llevat d’alguns casos en què ha estat de ${\textstyle 0,05\,s}$, amb un interval de temps ${\textstyle \Delta t=}$$0,0005\,s$.

• Simulation Type: SOLID

• Problem Type: Dynamic

• Time Integration: Implicit

• Equation System Solver: Direct

• Preconditioning: None

• Time Stepping: Alpha – Method

• Time Step ${\textstyle \beta }$ : 0,5

• Time Step ${\textstyle \gamma }$ : 0,25

• Time Step ${\textstyle \alpha -F}$: 0,0

• Time Step ${\textstyle \alpha -M}$: 0,01

Per acabar només cal definir i generar la malla més apropiada i procedir al càlcul de la simulació.

4.7 Casos calculats

Es presenten els resultats de tres casos diferents, un com a exemple representatiu per cadascuna de les tres fases. Aquests resultats inclouen una comparació entre la concavitat de deflexions reals i la concavitat de deflexions calculada i l’evolució de la deflexió al llarg del temps de cadascun dels punts corresponents als sensors de l’experiment real. Finalment s’hi adjunten una seqüència d’imatges que mostren l’evolució temporal tant de les acceleracions en la direcció Y com de les tensions en la component Y corresponents als instants de temps ${\textstyle {t}_{1}=}$$0,005$, ${\textstyle \,{t}_{2}=0,01}$, ${\textstyle \,{t}_{3}=}$$0,02$ i ${\textstyle \,{t}_{4}=0,03}$. La resta dels casos es poden consultar als annexes del treball. La Taula 4.7 mostra el temps de càlcul de cadascun dels casos amb el número de nodes i elements corresponents:

Fase	Casos	Duració de la simulació (s)	Temps de Càlcul (s)	Nº Nodes	Nº d'elements
1	3801_C	0,035	2472,87	30371	60000
1	3875_C	0,035	2457,58	30371	60000
1	3674_L	0,035	2156,13	30371	60000
1	8125_L	0,035	2102,58	30371	60000
1	8500_C	0,035	2634,68	30371	60000
1	8550_L	0,035	2498,75	30371	60000
2	3825_R	0,035	2319,12	32881	65000
2	3925_C	0,035	2340,01	32881	65000
2	5700_L	0,05	3432,95	32881	65000
2	7900_D	0,035	2835,58	32881	65000
2	8475_C	0,035	2889,33	32881	65000
2	8850_C	0,035	2937,45	32881	65000
3	4325_I	0,05	4431,96	34387	68000
3	4075_D	0,05	4246,72	34387	68000
3	6175_D	0,05	4419,73	34387	68000
3	7150_D	0,035	3497,65	34387	68000
3	8075_D	0,035	3506,83	34387	68000
3	8275_C	0,035	3456,56	34387	68000

Taula 4.7 Duració de cadascuna de la simulació, temps de càlcul requerit, número de nodes i número d’elements de la malla.

Els tres casos presentats són els següents: el cas 3801_C corresponent a la Fase 1, el cas 8850_C corresponent a la Fase 2 i el cas 4075_D corresponent a la Fase 3.

4.7.1 Cas 3801_C

El cas 3801_C, està conformat per una capa de mescla bituminosa de 0,1 m i un mòdul elàstic de 2108 MPa, una base de 0,5 m amb un mòdul elàstic de 177 MPa i una esplanada de 0,6 m amb un mòdul elàstic de 152 MPa. La màxima tensió vertical assolida és de 0,707 MPa.

Fase	1
Distribució	B
Pressió contacte ${\textstyle (MPa)}$	0,707
${E}_{1}(MPa)$	2108
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	177
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	152

La Taula 4.8 recull la posició dels sensors del deflectòmetre d’impacte respecte del punt on es produeix l’impacte (en mm), la deflexió mesurada per cadascun dels sensors (deflexió real), una aproximació de la deflexió mesurada amb els sensors a la desena superior i a la desena inferior (això es fa perquè la màxima precisió proporcionada pel PFEM és de 10 μm i d’aquesta manera s’acota el resultat experimental amb la precisió del PFEM), la deflexió calculada amb el PFEM obtinguda com la diferència entre la posició inicial (y₀) i la posició final (y_f), i finalment el percentatge per conèixer la precisió de la deflexió calculada. Aquest percentatge es calcula com el quocient entre el valor calculat de la deflexió i el valor mesurat de la deflexió multiplicat per cent.

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	566	369	294	199	130	56	24	21	17
Valor Super. (μm)	570	370	300	200	130	60	30	30	20
Valor Inferior (μm)	560	360	290	190	130	50	20	20	10
y0 (m)	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2
yf (m)	1,19943	1,19961	1,19972	1,19982	1,19987	1,19991	1,19993	1,19993	1,19993
y0-yf (μm)	570,0	390,0	280,0	180,0	130,0	90,0	70,0	70,0	70,0
% Limit Sup.	100,0	105,4	93,3	90,0	100,0	150,0	233,3	233,3	350,0
% Limit Inf.	101,8	108,3	96,6	94,7	100,0	180,0	350,0	350,0	700,0
% Real	100,7	105,7	95,2	90,5	100,0	160,7	291,7	333,3	411,8

Taula 4.8 Comparativa de les deflexions del cas 3801_C

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

Gràfica 4.8 Comparació entre les deflexions real i les deflexions calculades del cas 3801_C

Tal i com es pot observar a la Gràfica 4.8, les deflexions calculades s’ajusten molt bé fins a una distància de 600 mm respecte del punt on es produeix l’impacte. El valor de la deflexió a 900 mm, tot i que no s’ajusta amb la mateixa exactitud que els casos anteriors, encara preveu correctament l’ordre de magnitud de la deflexió mesurada amb el deflectòmetre d’impacte. A partir d’un metre de distància, les deflexions calculades fan previsions incorrectes, sobreestimant-ne el valor.

La Taula 4.9 mostra la deflexió assolida per cada sensor al llarg del temps.

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,2	1,2	0,0	1,2	0,0	1,2	0,0
0,0025	1,2	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
0,005	1,2	1,1999	-100,0	1,19992	-80,0	1,19993	-70,0
0,0075	1,2	1,1998	-200,0	1,19985	-150,0	1,19988	-120,0
0,01	1,2	1,19967	-330,0	1,19977	-230,0	1,19982	-180,0
0,0125	1,2	1,19955	-450,0	1,19969	-310,0	1,19977	-230,0
0,015	1,2	1,19946	-540,0	1,19963	-370,0	1,19973	-270,0
0,0175	1,2	1,19943	-570,0	1,19961	-390,0	1,19972	-280,0
0,02	1,2	1,19946	-540,0	1,19963	-370,0	1,19973	-270,0
0,0225	1,2	1,19954	-460,0	1,19969	-310,0	1,19977	-230,0
0,025	1,2	1,19966	-340,0	1,19977	-230,0	1,19982	-180,0
0,0275	1,2	1,19979	-210,0	1,19985	-150,0	1,19988	-120,0
0,03	1,2	1,19988	-120,0	1,19991	-90,0	1,19992	-80,0
0,0325	1,2	1,19992	-80,0	1,19993	-70,0	1,19994	-60,0
0,035	1,2	1,19994	-60,0	1,19994	-60,0	1,19994	-60,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,2	0,0	1,2	0,0	1,2	0,0	1,2	0,0
1,19998	-20,0	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
1,19994	-60,0	1,19995	-50,0	1,19995	-50,0	1,19995	-50,0
1,19991	-90,0	1,19992	-80,0	1,19993	-70,0	1,19992	-80,0
1,19987	-130,0	1,1999	-100,0	1,19992	-80,0	1,19992	-80,0
1,19985	-150,0	1,19988	-120,0	1,19991	-90,0	1,19992	-80,0
1,19983	-170,0	1,19987	-130,0	1,19991	-90,0	1,19993	-70,0
1,19982	-180,0	1,19987	-130,0	1,19991	-90,0	1,19993	-70,0
1,19982	-180,0	1,19987	-130,0	1,19991	-90,0	1,19993	-70,0
1,19984	-160,0	1,19988	-120,0	1,19992	-80,0	1,19993	-70,0
1,19987	-130,0	1,1999	-100,0	1,19992	-80,0	1,19993	-70,0
1,1999	-100,0	1,19992	-80,0	1,19993	-70,0	1,19993	-70,0
1,19993	-70,0	1,19993	-70,0	1,19993	-70,0	1,19993	-70,0
1,19994	-60,0	1,19994	-60,0	1,19994	-60,0	1,19993	-70,0
1,19994	-60,0	1,19994	-60,0	1,19994	-60,0	1,19993	-70,0

Taula 4.9 Evolució de les deflexions al llarg del temps del cas 3801_C

La Gràfica 4.9 és la representació de la Taula 4.9. Cada corba representa l’evolució de les deflexions al llarg del temps d’un sensor.

Gràfica 4.9 Evolució de les deflexions calculades al llarg del temps 3801_C

A la Gràfica 4.9 es pot observar com la corba que representa les deflexions al llarg del temps a 900 mm ofereix una forma de menys qualitat que les corbes que representen els punts més propers a l’impacte. Aquest fet era d’esperar perquè la deflexió màxima a 900 mm, tal i com ja s’ha comentat anteriorment, malgrat ser del mateix ordre de magnitud que la deflexió màxima calculada, és clarament superior.

La corba corresponent a 1500 mm no és correcte, tal i com ja passava amb les deflexions màximes dels sensors més allunyats.

Acceleracions en Y:

Tensions en Y:

4.7.2 Cas 8850_C

El cas 8850_C, està conformat per una capa de mescla bituminosa de 0,2 m (0,1 m més gruixuda que el cas anterior) i un mòdul elàstic de 5479 MPa (un valor de més del doble que el mòdul elàstic de la mescla bituminosa del cas anterior), una base de 0,5 m amb un mòdul elàstic de 236 MPa i una esplanada de 0,6 m amb un mòdul elàstic de 118 MPa. La màxima tensió vertical assolida és de 0,721 MPa, 0,014 MPa més gran que la del cas 3801_C.

Fase	2
Distribució	C
Pressió contacte ${\textstyle (MPa)}$	0,721
${E}_{1}(MPa)$	5479
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	236
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	118

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	282	251	234	200	167	111	50	36	26
Valor Superior (μm)	290	260	240	200	170	120	50	40	30
Valor Inferior (μm)	280	250	230	200	160	110	50	30	20
y0 (m)	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3
yf (m)	1,29971	1,29975	1,29977	1,2998	1,29983	1,29987	1,2999	1,2999	1,29991
y0-yf (μm)	290,0	250,0	230,0	200,0	170,0	130,0	100,0	100,0	90,0
% Limit Inf.	100,0	96,2	95,8	100,0	100,0	108,3	200,0	250,0	300,0
% Limit Sup.	103,6	100,0	100,0	100,0	106,3	118,2	200,0	333,3	450,0
% Real	102,8	99,6	98,3	100,0	101,8	117,1	200,0	277,8	346,2

Taula 4.10 Comparativa de les deflexions del cas 8850_C

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

Gràfica 4.10 Comparació entre les deflexions real i les deflexions calculades del cas 8850_C

Observant la Gràfica 4.10 es pot veure com les deflexions calculades amb el PFEM s’ajusten a les deflexions mesurades amb l’aparell fins a una distància de 1 metre. Més enllà d’aquesta distància les previsions no són correctes.

L’evolució de les deflexions al llarg del temps es recull a la Taula 4.11:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,3	1,3	0,0	1,3	0,0	1,3	0,0
0,0025	1,3	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
0,005	1,3	1,29992	-80,0	1,29993	-70,0	1,29993	-70,0
0,0075	1,3	1,29986	-140,0	1,29987	-130,0	1,29988	-120,0
0,01	1,3	1,2998	-200,0	1,29982	-180,0	1,29983	-170,0
0,0125	1,3	1,29975	-250,0	1,29978	-220,0	1,2998	-200,0
0,015	1,3	1,29972	-280,0	1,29976	-240,0	1,29978	-220,0
0,0175	1,3	1,29971	-290,0	1,29975	-250,0	1,29977	-230,0
0,02	1,3	1,29973	-270,0	1,29976	-240,0	1,29978	-220,0
0,0225	1,3	1,29976	-240,0	1,29979	-210,0	1,29981	-190,0
0,025	1,3	1,29981	-190,0	1,29983	-170,0	1,29984	-160,0
0,0275	1,3	1,29985	-150,0	1,29987	-130,0	1,29987	-130,0
0,03	1,3	1,29989	-110,0	1,2999	-100,0	1,2999	-100,0
0,0325	1,3	1,29991	-90,0	1,29991	-90,0	1,29991	-90,0
0,035	1,3	1,29992	-80,0	1,29992	-80,0	1,29992	-80,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,3	0,0	1,3	0,0	1,3	0,0	1,3	0,0
1,29998	-20,0	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
1,29993	-70,0	1,29993	-70,0	1,29994	-60,0	1,29993	-70,0
1,29989	-110,0	1,29989	-110,0	1,2999	-100,0	1,2999	-100,0
1,29985	-150,0	1,29986	-140,0	1,29987	-130,0	1,29988	-120,0
1,29982	-180,0	1,29984	-160,0	1,29986	-140,0	1,29988	-120,0
1,29981	-190,0	1,29983	-170,0	1,29986	-140,0	1,29989	-110,0
1,2998	-200,0	1,29983	-170,0	1,29987	-130,0	1,2999	-100,0
1,29981	-190,0	1,29984	-160,0	1,29987	-130,0	1,2999	-100,0
1,29983	-170,0	1,29985	-150,0	1,29988	-120,0	1,2999	-100,0
1,29986	-140,0	1,29987	-130,0	1,29989	-110,0	1,2999	-100,0
1,29988	-120,0	1,29989	-110,0	1,2999	-100,0	1,2999	-100,0
1,2999	-100,0	1,29991	-90,0	1,29991	-90,0	1,2999	-100,0
1,29991	-90,0	1,29991	-90,0	1,29991	-90,0	1,29991	-90,0
1,29992	-80,0	1,29992	-80,0	1,29991	-90,0	1,29991	-90,0

Taula 4.11 Evolució de les deflexions al llarg del temps del cas 8850_C

La representació gràfica de la Taula 4.11 es recull a la Gràfica 4.11:

Gràfica 4.11 Evolució de les deflexions calculades al llarg del temps 8850_C

A la Gràfica 4.11 es poden observar com el repeteixen el mateixos fenòmens del cas 3801_C:

• La corba que representa l’evolució de les deflexions al llarg del temps del sensor situat a 900 mm no és de la mateixa qualitat que les dels sensors més propers al punt d’impacte.

• La corba del sensor situat a 1500 mm no és correcte perquè el PFEM sobreestima les deflexions dels sensors més allunyats.

Acceleracions en Y:

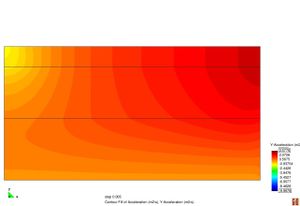
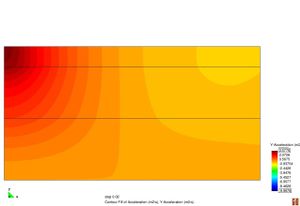
Tensions en Y:

4.7.3 Cas 4075_D

El cas 4075_D, està conformat per una capa de mescla bituminosa de 0,26 m (0,06 m més gruixuda que el cas 8850_C) i un mòdul elàstic de 4314 MPa, una base de 0,5 m amb un mòdul elàstic de 393 MPa i una esplanada de 0,6 m amb un mòdul elàstic de 148 MPa. La màxima tensió vertical assolida és de 0,721 MPa.

Fase	3
Distribució	D
Pressió contacte ${\textstyle (MPa)}$	0,721
${E}_{1}(MPa)$	4314
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	393
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	148

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	201	172	159	135	116	83	43	32	23
Valor Super. (μm)	210	180	160	140	120	90	50	40	30
Valor Inferior (μm)	200	170	150	130	110	80	40	30	20
y0 (m)	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36
yf (m)	1,35979	1,35982	1,35984	1,35986	1,35987	1,35989	1,35991	1,35992	1,35993
y0-yf (μm)	210,0	180,0	160,0	140,0	130,0	110,0	90,0	80,0	70,0
% Limit Sup.	105,0	105,9	106,7	107,7	118,2	137,5	225,0	266,7	350,0
% Limit Inf	100,0	100,0	100,0	100,0	108,3	122,2	180,0	200,0	233,3
% Real	104,5	104,7	100,6	103,7	112,1	132,5	209,3	250,0	304,3

Taula 4.12 Comparativa de les deflexions del cas 4075_D

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

Gràfica 4.12 Comparació entre les deflexions real i les deflexions calculades del cas 4075_D

La Gràfica 4.12 mostra com la concavitat de deflexions calculada amb el PFEM s’ajusta als valors mesurats amb el deflectòmetre d’impacte fins a un metre de distància. Més enllà, la previsió és incorrecte.

L’evolució de les deflexions al llarg del temps es recull a la Taula 4.13:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,36	1,36	0,0	1,36	0,0	1,36	0,0
0,0025	1,36	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
0,005	1,36	1,35993	-70,0	1,35994	-60,0	1,35994	-60,0
0,0075	1,36	1,35989	-110,0	1,3599	-100,0	1,3599	-100,0
0,01	1,36	1,35985	-150,0	1,35986	-140,0	1,35987	-130,0
0,0125	1,36	1,35981	-190,0	1,35984	-160,0	1,35985	-150,0
0,015	1,36	1,35979	-210,0	1,35983	-170,0	1,35984	-160,0
0,0175	1,36	1,35979	-210,0	1,35982	-180,0	1,35984	-160,0
0,02	1,36	1,3598	-200,0	1,35983	-170,0	1,35984	-160,0
0,0225	1,36	1,35982	-180,0	1,35985	-150,0	1,35986	-140,0
0,025	1,36	1,35985	-150,0	1,35987	-130,0	1,35988	-120,0
0,0275	1,36	1,35988	-120,0	1,3599	-100,0	1,3599	-100,0
0,03	1,36	1,35991	-90,0	1,35992	-80,0	1,35992	-80,0
0,0325	1,36	1,35992	-80,0	1,35993	-70,0	1,35993	-70,0
0,035	1,36	1,35993	-70,0	1,35993	-70,0	1,35993	-70,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,36	0,0	1,36	0,0	1,36	0,0	1,36	0,0
1,35998	-20,0	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
1,35994	-60,0	1,35994	-60,0	1,35994	-60,0	1,35994	-60,0
1,3599	-100,0	1,35991	-90,0	1,35991	-90,0	1,35991	-90,0
1,35988	-120,0	1,35989	-110,0	1,3599	-100,0	1,35991	-90,0
1,35987	-130,0	1,35988	-120,0	1,35989	-110,0	1,35991	-90,0
1,35986	-140,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35986	-140,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35986	-140,0	1,35988	-120,0	1,3599	-100,0	1,35992	-80,0
1,35987	-130,0	1,35988	-120,0	1,3599	-100,0	1,35992	-80,0
1,35989	-110,0	1,3599	-100,0	1,35991	-90,0	1,35992	-80,0
1,35991	-90,0	1,35991	-90,0	1,35991	-90,0	1,35992	-80,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0
1,35993	-70,0	1,35993	-70,0	1,35993	-70,0	1,35992	-80,0
1,35993	-70,0	1,35993	-70,0	1,35993	-70,0	1,35992	-80,0

Taula 4.13 Evolució de les deflexions al llarg del temps del cas 4075_D

La representació gràfica de la Taula 4.13 es recull a la Gràfica 4.13:

Gràfica 4.13 Evolució de les deflexions calculades al llarg del temps 4075_D

L’evolució de les deflexions al llarg del temps dels punts més allunyats del punt de l’impacte prenen formes més inexactes. Les deflexions del punt situat a 1500 mm són incorrectes.

Acceleracions en Y:

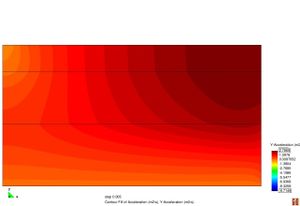
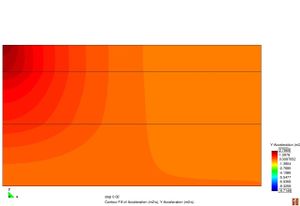
Tensions en Y:

4.7.4 Comparació entre casos

Les taules recollides en aquest apartat mostren, per cada cas, la semblança entre les deflexions reals mesurades amb els sensors del deflectòmetre d’impacte i les deflexions calculades amb el PFEM, expressada en forma de percentatge:

$\%={\frac {deflexi{\acute {o}}\,calculada}{deflexi{\acute {o}}\,mesurada\,FWD}}\cdot 100$

(4.16)

Els casos estan agrupats en les diferents fases.

Fase 1:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
3801_C	100,71	105,69	95,24	90,45	100	160,71	291,67	333,33	411,76
3875_C	98,48	98,63	90,30	89,20	96,55	132,35	241,38	291,67	368,42
3674_L	105,26	118,11	106,76	97,70	106,80	133,33	192,31	217,39	250
8125_L	91,90	93,65	92,02	106,71	135,51	267,44	1357,14	2250	2428,57
8500_C	96,83	94,78	94,17	98,80	110,66	156,25	312,5	378,38	433,33
8550_L	99,57	99,82	97,29	106,16	115,18	159,09	275	354,84	384,62
Mitjana	98,80	101,78	95,96	98,17	110,78	168,20	445	637,60	712,78

Taula 4.14 Comparació dels percentatges entre els diferents casos de la Fase 1

Els resultats mostren com les deflexions calculades corresponents a les distàncies de 0 mm, 200 mm, 300 mm i 450 mm prenen pràcticament els mateixos valors que les deflexions experimentals. Els percentatges mitjans de la Fase 1 d’aquestes quatre localitzacions són de 98,8% a 0 mm, de 101,78% a 200 mm, 95,96% a 300 mm i 98,17% a 450 mm. La deflexió del sensor situat a 600 mm del punt d’impacte pren, de mitjana, un valor de 110,78% respecte de la deflexió experimental, un percentatge lleugerament superior en comparació als valors corresponents a les posicions de 0 mm, 200 mm, 300 mm i 450 mm. El sensor corresponent a 900 mm arriba a un 168,20%, clarament per sobre de les localitzacions anteriors. A partir d’aquí les deflexions dels sensors situats a 1500 mm, 1800 mm i 2100 mm, fan una predicció incorrecta de les deflexions (445%; 637,60% i 712,78% respectivament), sobreestimant la deflexió mesurada amb el deflectòmetre d’impacte.

Fase 2:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
3825_R	96,43	96,77	94,24	90,32	98,36	123,29	225,80	285,71	400
3925_C	96,59	100	94,49	94,34	104,65	129,63	272,73	416,67	833,33
5700_L	100	97,56	94,59	97,30	100	129,03	230,77	375	500
7900_D	107,42	104,17	103,68	105,49	114,75	145,63	333,33	476,19	714,29
8475_C	102,63	102,72	99,01	100,81	110,55	130,08	240	305,56	407,41
8850_C	102,84	99,60	98,29	100	101,80	117,12	200	277,78	346,15
Mitjana	100,98	100,14	97,38	98,04	105,02	129,13	250,44	356,15	533,53

Taula 4.15 Comparació dels percentatges entre els diferents casos de la Fase 2

Les prediccions a 0 mm, 200 mm, 300 mm i 450 mm de la Fase 2 són pràcticament iguals que les de la Fase 1. A 0 mm s’obté un percentatge de 100,98%, a 200 mm de 100,14%, a 300 mm de 97,38% i a 450 mm de 98,04%. En comparació a la Fase 1, les prediccions de les deflexions aconseguides amb la Fase 2 milloren substancialment perquè les prediccions fetes a 600 mm i 900 mm milloren. A 600 mm s’obté un percentatge de 105,02% mentre que a la Fase 1 era del 110,78% (suposa una reducció de 5,76%, gairebé sis punts). A 900 mm s’obté un percentatge de 129,13%, mentre que a la Fase 1 era del 168,20% (suposa una reducció del 39,07%, quasi un 40%). A partir d’aquí, les previsions de les deflexions a 1500 mm, 1800 mm i 2100 mm tornen a ser incorrectes. Tot i que es torna a produir una sobreestimació de les deflexions mesurades amb l’aparell, és una sobreestimació menor en comparació a la Fase 1: a 1500 mm s’obté un percentatge de 250,44%, a 1800 mm de 356,15% i a 2100 mm de 533,53% (mentre que per a la Fase 1 s’obtenien: 445%; 637,6% i 712,78% respectivament, clarament per sobre).

Fase 3:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
4325_I	113,21	110,34	108,70	112	118,18	134,15	238,10	310,34	444,44
4075_D	104,48	104,65	100,63	103,70	112,07	132,53	209,30	250	304,35
6175_D	103,73	105,26	103,63	104,94	111,94	137,93	270,27	321,43	380,95
7150_D	105,26	105,88	99,38	105,63	114,75	139,53	225	321,43	421,05
8075_D	104	101,85	102,56	106,25	118,11	151,90	264,71	360	444,44
8275_C	103,60	98,45	102,86	102,74	118,64	150,68	333,33	444,44	615,38
Mitjana	105,71	104,41	102,96	105,88	115,62	141,12	256,78	334,61	435,10

Taula 4.16 Comparació dels percentatges entre els diferents casos de la Fase 3

Els resultats corresponents a la Fase 3 tornen a predir correctament els deflexions corresponents a les distàncies de 0 mm, 200 mm, 300 mm i 450 mm. Aquest cop, ho fa sobreestimant-ho molt lleugerament per sobre: a 0 mm li correspon un percentatge de 105,71%, a 200 mm de 104,41%, a 300 mm de 102,96% i a 450 mm de 105,88%. La deflexió corresponent als 600 mm es sobreestima i és superior als valors corresponents a les fases anteriors: 115,62% (mentre que a les fases 1 i fase 2 s’assolia un percentatge del 110,78% i 105,02%). A 900 mm s’obté un percentatge del 141,12%, millor que la Fase 1 (168,20%) però pitjor que la Fase 2 (129,13%). Finalment, les deflexions calculades a les distàncies de 1500 mm, 1800 mm i 2100 mm es tornen a sobreestimar. A 1500 mm s’obté un 256,78%, un pèl per sobre respecte del valor corresponent a la Fase 2 (250,44%). En canvi, a 1800 mm i a 2100 mm, tot i que també es sobreestimen les deflexions, ho fan en menor mesura que a la Fase 2. A 1800 mm s’obté un 334,61% i a 2100 un 435,10% (mentre que a la Fase 2 s’obtenen 356,15% i 533,53% respectivament).

5 Consideracions finals

5.1 Conclusions

Arrel dels resultats obtinguts al llarg d’aquest treball, es conclou que:

La simulació de l’impacte amb el PFEM no dóna resultats satisfactoris. La forma que pren la funció de l’impacte calculat, la seva magnitud així com la seva duració s’allunyen molt de la funció d’impacte del deflectòmetre d’impacte. Causes imputables a aquest fet són les següents:

• La mescla bituminosa i el material que conforma la base del ferm, o el mateix cautxú es caracteritzen per tenir lleis viscoelàstiques. La utilització d’un model elàstic lineal amb amortiment per simular un model viscoelàstic no aconsegueix reproduir correctament l’impacte.

• En la simulació dinàmica no s’ha introduït cap tipus d’amortiment a la massa ${\textstyle M}$ d’acer. El fet d’introduir un determinat amortiment provocava que les forces externes no quedessin igualades amb les forces internes i el programa era incapaç de convergir a una solució. El problema de no introduir cap amortiment és que un cop produït l’impacte, s’introdueix a la massa d’acer ${\textstyle M}$ una energia i provoca una ona que no s’atenua. Això provoca una mala simulació del contacte perquè aquestes petites oscil·lacions afecten en el manteniment del contacte amb la placa de càrrega.

La funció sinusoïdal al quadrat definida per aproximar la càrrega d’impacte d’un deflectòmetre d’impacte proporciona bons resultats. Les deflexions obtingudes així ho demostren.

La simulació dinàmica de les deflexions del ferm amb el PFEM proporciona resultats satisfactoris a una distància de fins a 1 metre respecte del punt on es produeix l’impacte. A més, es poden conèixer els valors de les acceleracions dels punts d’interès, cosa que els sensors dels deflectòmetres d’impacte no sempre permeten. El PFEM queda validat en aquest tram.

A partir d’una distància de 1 metre en endavant, les deflexions calculades no s’ajusten als valors mesurats amb el deflectòmetre d’impacte. El PFEM sobreestima els valors de les deflexions respecte els valors mesurats. L’error de la deflexió calculada creix amb la distància respecte de la força d’impacte. Aquest fet està en la línia de (10).

5.2 Possibles millores del programa

Alguns aspectes que es podrien millorar del programa són els següents:

• Augmentar el número de xifres significatives de les coordenades de posició dels nodes de la malla emprada fins a una resolució de 1 ${\textstyle \mu m}$.

• Millorar la sortida dels resultats perquè la seva extracció sigui menys feixuga per l’usuari i se’n pugui facilitar el tractament.

• Fer disponible més tipologies d’elements més enllà dels elements triangulars lineals.

5.3 Futures línies d’investigació

Com a futures línies d’investigació són interessants els següents punts:

• Estudiar les possibles conseqüències de variar els mòduls elàstics de les diferents capes del ferm.

• Determinar la influència que tenen els mòduls elàstics de la base i l’esplanada sobre les deflexions dels punts més allunyats de la càrrega d’impacte i determinar fins a quin punt són responsables de la sobreestimació produïda.

• Assignar valors dels paràmetres d’amortiment ajustats a cadascuna de les capes del ferm per intentar millorar les prediccions de les deflexions dels punts més allunyats de la càrrega d’impacte.

• Estudiar el mateix problema amb un model de tres dimensions en comptes d’un model axisimètric.

6 Bibliografia

1. Kraemer, Carlos, y otros. Ingeniería de carreteras (volumen II). Madrid : Mc Graw Hill, 2004. 84-481-3998-4.

2. CEDEX (Centro de Estudios y Experimentación de Obras Públicas). Armonización del uso del Deflectómetro de Impacto en Firmes. Parte 1. Firmes Flexibles. Madrid : Ministerio de Fomento, 1997. 84-7790-283-6.

3. AMADEUS. Advanced Models for Analytical Design of European Pavement Structures. 1999.

4. Oliver Olivella, Xavier i Agelet de Saracíbar Bosch, Carlos. Mecànica de medis continus per a enginyers. Barcelona : Edicions UPC, 2003. 84-8301-719-9.

5. Carbonell, J.M., Oñate, E. y Suárez, B. Modeling of Ground Excavation with the Particle Finite Element Method. Barcelona : CIMNE, 2010. 978-84-96736-85-6.

6. Oñate Ibáñez de Navarra, Eugenio. Cálculo de Estructuras por el Método de Elementos Finitos. Análisis estático lineal. Barcelona : CIMNE, 1995. 84-87867-00-6.

7. Norambuena Contreras, José. Análisis dinámico de los firmes de carretera. Santander : Universidad de Cantabria - GITECO, 2008.

8. Velasco, Antonio García. Análisis del empleo del deflectómetro de impacto para el control de la calidad de la construcción de firmes de carreteras. Tesina. Barcelona : ETSECCPB-UPC, 2000.

9. López, María Pilar. Determinación de las características mecánicas de las capas de los firmes flexibles mediante el empleo del deflectómetro de impacto. Tesina. Barcelona : ETSECCPB-UPC, 1999.

10. Verification of falling weight deflectometer backanalysis using a dynamic finite elements simulation. Loizos, Andreas y Scarpas, A. (Tom). 2, June de 2005, The International Journal of Pavement Engineering, Vol. 6, págs. 115-123.

11. ETSECCPB. Diccionari d'Enginyeria civil. Barcelona : Enciclopèdia Catalana, 2005. 84-412-1403-4.

12. Riba Romeva, Carles. Selección de materiales en el diseño de máquinas. Barcelona : Edicions UPC, 2008. 978-84-8301-738-8.

13. van Gurp, Christ. Characterization of seasonal influences on asphalt pavements with the use of falling weight deflectometers. Delft : TU Delft, 1995.

14. Al-Khoury, Rafid Ismail. Parameter Identification Technique for Layered Systems. 2002. 90-9016414-6.

15. Duvert, Audrey. Finite Element Simulation of Far Fiel Problems. s.l. : TU Delft, École Centrale de Nantes, 2000.

7 Annexes

7.1 Resultats dels casos

La següent taula mostra el conjunt de casos calculats:

FASE 1	FASE 2	FASE 3
3801_C	3825_R	4325_I
3875_C	3925_C	4075_D
3674_L	5700_L	6175_D
8125_L	7900_D	7150_D
8500_C	8475_C	8075_D
8550_L	8850_C	8275_C

Els següents valors són comuns a tots els casos:

$\alpha$	0,36
$\beta$	0,0026
$\nu$	0,35
${\rho }_{MB}\,(kg/{m}^{3})$	2400
${\rho }_{Base}(kg/{m}^{3})$	2000
${\rho }_{Explanada}(kg/{m}^{3})$	2000

7.1.1 Resultats dels casos corresponents a la Fase 1

7.1.1.1 Cas 3801_C

Mòduls d’elasticitat emprats:

Fase	1
Distribució	B
Pressió contacte ${\textstyle (MPa)}$	0,707
${E}_{1}(MPa)$	2108
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	177
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	152

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	566	369	294	199	130	56	24	21	17
Valor Super. (μm)	570	370	300	200	130	60	30	30	20
Valor Inferior (μm)	560	360	290	190	130	50	20	20	10
y0 (m)	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2
yf (m)	1,19943	1,19961	1,19972	1,19982	1,19987	1,19991	1,19993	1,19993	1,19993
y0-yf (μm)	570,0	390,0	280,0	180,0	130,0	90,0	70,0	70,0	70,0
% Limit Sup.	100,0	105,4	93,3	90,0	100,0	150,0	233,3	233,3	350,0
% Limit Inf.	101,8	108,3	96,6	94,7	100,0	180,0	350,0	350,0	700,0
% Real	100,7	105,7	95,2	90,5	100,0	160,7	291,7	333,3	411,8

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,2	1,2	0,0	1,2	0,0	1,2	0,0
0,0025	1,2	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
0,005	1,2	1,1999	-100,0	1,19992	-80,0	1,19993	-70,0
0,0075	1,2	1,1998	-200,0	1,19985	-150,0	1,19988	-120,0
0,01	1,2	1,19967	-330,0	1,19977	-230,0	1,19982	-180,0
0,0125	1,2	1,19955	-450,0	1,19969	-310,0	1,19977	-230,0
0,015	1,2	1,19946	-540,0	1,19963	-370,0	1,19973	-270,0
0,0175	1,2	1,19943	-570,0	1,19961	-390,0	1,19972	-280,0
0,02	1,2	1,19946	-540,0	1,19963	-370,0	1,19973	-270,0
0,0225	1,2	1,19954	-460,0	1,19969	-310,0	1,19977	-230,0
0,025	1,2	1,19966	-340,0	1,19977	-230,0	1,19982	-180,0
0,0275	1,2	1,19979	-210,0	1,19985	-150,0	1,19988	-120,0
0,03	1,2	1,19988	-120,0	1,19991	-90,0	1,19992	-80,0
0,0325	1,2	1,19992	-80,0	1,19993	-70,0	1,19994	-60,0
0,035	1,2	1,19994	-60,0	1,19994	-60,0	1,19994	-60,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,2	0,0	1,2	0,0	1,2	0,0	1,2	0,0
1,19998	-20,0	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
1,19994	-60,0	1,19995	-50,0	1,19995	-50,0	1,19995	-50,0
1,19991	-90,0	1,19992	-80,0	1,19993	-70,0	1,19992	-80,0
1,19987	-130,0	1,1999	-100,0	1,19992	-80,0	1,19992	-80,0
1,19985	-150,0	1,19988	-120,0	1,19991	-90,0	1,19992	-80,0
1,19983	-170,0	1,19987	-130,0	1,19991	-90,0	1,19993	-70,0
1,19982	-180,0	1,19987	-130,0	1,19991	-90,0	1,19993	-70,0
1,19982	-180,0	1,19987	-130,0	1,19991	-90,0	1,19993	-70,0
1,19984	-160,0	1,19988	-120,0	1,19992	-80,0	1,19993	-70,0
1,19987	-130,0	1,1999	-100,0	1,19992	-80,0	1,19993	-70,0
1,1999	-100,0	1,19992	-80,0	1,19993	-70,0	1,19993	-70,0
1,19993	-70,0	1,19993	-70,0	1,19993	-70,0	1,19993	-70,0
1,19994	-60,0	1,19994	-60,0	1,19994	-60,0	1,19993	-70,0
1,19994	-60,0	1,19994	-60,0	1,19994	-60,0	1,19993	-70,0

Acceleracions en Y:

Tensions en Y:

7.1.1.2 Cas 3674_L

Mòduls d’elasticitat emprats:

Fase	1
Distribució	B
Pressió contacte ${\textstyle (MPa)}$	0,749
${E}_{1}(MPa)$	1659
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	130
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	129

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	665	381	281	174	103	45	26	23	20
Valor Super. (μm)	670	390	290	180	110	50	30	30	20
Valor Inferior (μm)	660	380	280	170	100	40	20	20	20
y0 (m)	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2
yf (m)	1,1993	1,19955	1,1997	1,19983	1,19989	1,19994	1,19995	1,19995	1,19995
y0-yf (μm)	700,0	450,0	300,0	170,0	110,0	60,0	50,0	50,0	50,0
% Limit Sup.	104,5	115,4	103,4	94,4	100,0	120,0	166,7	166,7	250,0
% Limit Inf.	106,1	118,4	107,1	100,0	110,0	150,0	250,0	250,0	250,0
% Real	105,3	118,1	106,8	97,7	106,8	133,3	192,3	217,4	250,0

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,2	1,2	0,0	1,2	0,0	1,2	0,0
0,0025	1,2	1,19997	-30,0	1,19998	-20,0	1,19998	-20,0
0,005	1,2	1,1999	-100,0	1,19992	-80,0	1,19994	-60,0
0,0075	1,2	1,19977	-230,0	1,19984	-160,0	1,19988	-120,0
0,01	1,2	1,19961	-390,0	1,19975	-250,0	1,19982	-180,0
0,0125	1,2	1,19946	-540,0	1,19965	-350,0	1,19976	-240,0
0,015	1,2	1,19934	-660,0	1,19958	-420,0	1,19972	-280,0
0,0175	1,2	1,1993	-700,0	1,19955	-450,0	1,1997	-300,0
0,02	1,2	1,19934	-660,0	1,19958	-420,0	1,19971	-290,0
0,0225	1,2	1,19945	-550,0	1,19965	-350,0	1,19976	-240,0
0,025	1,2	1,1996	-400,0	1,19974	-260,0	1,19982	-180,0
0,0275	1,2	1,19976	-240,0	1,19984	-160,0	1,19988	-120,0
0,03	1,2	1,19987	-130,0	1,19991	-90,0	1,19993	-70,0
0,0325	1,2	1,19993	-70,0	1,19994	-60,0	1,19995	-50,0
0,035	1,2	1,19995	-50,0	1,19995	-50,0	1,19995	-50,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,2	0,0	1,2	0,0	1,2	0,0	1,2	0,0
1,19998	-20,0	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
1,19995	-50,0	1,19996	-40,0	1,19996	-40,0	1,19996	-40,0
1,19992	-80,0	1,19994	-60,0	1,19995	-50,0	1,19994	-60,0
1,19989	-110,0	1,19992	-80,0	1,19994	-60,0	1,19994	-60,0
1,19986	-140,0	1,19991	-90,0	1,19994	-60,0	1,19994	-60,0
1,19984	-160,0	1,1999	-100,0	1,19994	-60,0	1,19995	-50,0
1,19983	-170,0	1,19989	-110,0	1,19994	-60,0	1,19995	-50,0
1,19984	-160,0	1,1999	-100,0	1,19994	-60,0	1,19995	-50,0
1,19986	-140,0	1,19991	-90,0	1,19994	-60,0	1,19995	-50,0
1,19989	-110,0	1,19992	-80,0	1,19994	-60,0	1,19995	-50,0
1,19992	-80,0	1,19994	-60,0	1,19995	-50,0	1,19995	-50,0
1,19994	-60,0	1,19995	-50,0	1,19995	-50,0	1,19995	-50,0
1,19995	-50,0	1,19995	-50,0	1,19995	-50,0	1,19995	-50,0
1,19995	-50,0	1,19995	-50,0	1,19995	-50,0	1,19995	-50,0

Acceleracions en Y:

Tensions en Y:

7.1.1.3 Cas 3875_C

Mòduls d’elasticitat emprats:

Fase	1
Distribució	B
Pressió contacte ${\textstyle (MPa)}$	0,721
${E}_{1}(MPa)$	2638
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	207
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	137

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	528	365	299	213	145	68	29	24	19
Valor Super. (μm)	530	370	300	220	150	70	30	30	20
Valor Inferior (μm)	520	360	290	210	140	60	20	20	10
y0 (m)	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2
yf (m)	1,19948	1,19964	1,19973	1,19981	1,19986	1,19991	1,19993	1,19993	1,19993
y0-yf (μm)	520,0	360,0	270,0	190,0	140,0	90,0	70,0	70,0	70,0
% Limit Sup.	98,1	97,3	90,0	86,4	93,3	128,6	233,3	233,3	350,0
% Limit Inf.	100,0	100,0	93,1	90,5	100,0	150,0	350,0	350,0	700,0
% Real	98,5	98,6	90,3	89,2	96,6	132,4	241,4	291,7	368,4

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,2	1,2	0,0	1,2	0,0	1,2	0,0
0,0025	1,2	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
0,005	1,2	1,19991	-90,0	1,19992	-80,0	1,19993	-70,0
0,0075	1,2	1,19981	-190,0	1,19985	-150,0	1,19988	-120,0
0,01	1,2	1,1997	-300,0	1,19978	-220,0	1,19983	-170,0
0,0125	1,2	1,19959	-410,0	1,19971	-290,0	1,19978	-220,0
0,015	1,2	1,19951	-490,0	1,19965	-350,0	1,19974	-260,0
0,0175	1,2	1,19948	-520,0	1,19964	-360,0	1,19973	-270,0
0,02	1,2	1,1995	-500,0	1,19965	-350,0	1,19974	-260,0
0,0225	1,2	1,19958	-420,0	1,1997	-300,0	1,19977	-230,0
0,025	1,2	1,19969	-310,0	1,19978	-220,0	1,19982	-180,0
0,0275	1,2	1,1998	-200,0	1,19985	-150,0	1,19988	-120,0
0,03	1,2	1,19988	-120,0	1,19991	-90,0	1,19992	-80,0
0,0325	1,2	1,19992	-80,0	1,19993	-70,0	1,19993	-70,0
0,035	1,2	1,19993	-70,0	1,19994	-60,0	1,19994	-60,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,2	0,0	1,2	0,0	1,2	0,0	1,2	0,0
1,19998	-20,0	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
1,19994	-60,0	1,19994	-60,0	1,19995	-50,0	1,19994	-60,0
1,1999	-100,0	1,19992	-80,0	1,19992	-80,0	1,19992	-80,0
1,19987	-130,0	1,19989	-110,0	1,19991	-90,0	1,19991	-90,0
1,19984	-160,0	1,19988	-120,0	1,19991	-90,0	1,19992	-80,0
1,19982	-180,0	1,19987	-130,0	1,19991	-90,0	1,19992	-80,0
1,19981	-190,0	1,19986	-140,0	1,19991	-90,0	1,19993	-70,0
1,19982	-180,0	1,19987	-130,0	1,19991	-90,0	1,19993	-70,0
1,19984	-160,0	1,19988	-120,0	1,19991	-90,0	1,19993	-70,0
1,19987	-130,0	1,19989	-110,0	1,19992	-80,0	1,19993	-70,0
1,1999	-100,0	1,19991	-90,0	1,19992	-80,0	1,19993	-70,0
1,19992	-80,0	1,19993	-70,0	1,19993	-70,0	1,19993	-70,0
1,19994	-60,0	1,19994	-60,0	1,19993	-70,0	1,19993	-70,0
1,19994	-60,0	1,19994	-60,0	1,19993	-70,0	1,19993	-70,0

Acceleracions en Y:

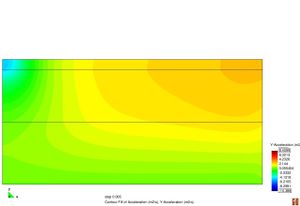
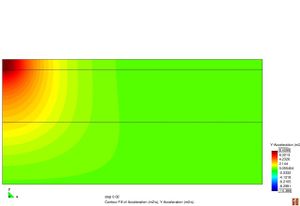
Tensions en Y:

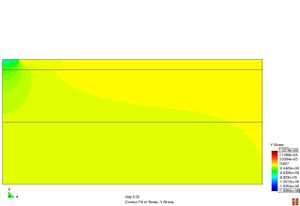
7.1.1.4 Cas 8125_L

Mòduls d’elasticitat emprats:

Fase	1
Distribució	B
Pressió contacte ${\textstyle (MPa)}$	0,693
${E}_{1}(MPa)$	1517
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	207
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	59

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	827	598	489	328	214	86	14	8	7
Valor Super. (μm)	830	600	490	330	220	90	20	10	10
Valor Inferior (μm)	820	590	480	320	210	80	10	8	7
y0 (m)	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2
yf (m)	1,19924	1,19944	1,19955	1,19965	1,19971	1,19977	1,19981	1,19982	1,19983
y0-yf (μm)	760,0	560,0	450,0	350,0	290,0	230,0	190,0	180,0	170,0
% Limit Sup.	91,6	93,3	91,8	106,1	131,8	255,6	950,0	1800,0	1700,0
% Limit Inf	92,7	94,9	93,8	109,4	138,1	287,5	1900,0	2250,0	2428,6
% Real	91,9	93,6	92,0	106,7	135,5	267,4	1357,1	2250,0	2428,6

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,2	1,2	0	1,2	0,0	1,2	0,0
0,0025	1,2	1,19997	-30	1,19997	-30,0	1,19998	-20,0
0,005	1,2	1,19988	-120	1,19989	-110,0	1,19991	-90,0
0,0075	1,2	1,19973	-270	1,19978	-220,0	1,19981	-190,0
0,01	1,2	1,19956	-440	1,19966	-340,0	1,19972	-280,0
0,0125	1,2	1,1994	-600	1,19955	-450,0	1,19963	-370,0
0,015	1,2	1,19929	-710	1,19948	-520,0	1,19958	-420,0
0,0175	1,2	1,19924	-760	1,19944	-560,0	1,19955	-450,0
0,02	1,2	1,19928	-720	1,19947	-530,0	1,19957	-430,0
0,0225	1,2	1,19938	-620	1,19954	-460,0	1,19962	-380,0
0,025	1,2	1,19953	-470	1,19965	-350,0	1,1997	-300,0
0,0275	1,2	1,19968	-320	1,19975	-250,0	1,19978	-220,0
0,03	1,2	1,19981	-190	1,19984	-160,0	1,19985	-150,0
0,0325	1,2	1,19987	-130	1,19988	-120,0	1,19988	-120,0
0,035	1,2	1,19988	-120	1,19989	-110,0	1,19989	-110,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,2	0,0	1,2	0,0	1,2	0,0	1,2	0,0
1,19998	-20,0	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
1,19991	-90,0	1,19992	-80,0	1,19992	-80,0	1,19992	-80,0
1,19984	-160,0	1,19985	-150,0	1,19986	-140,0	1,19986	-140,0
1,19977	-230,0	1,19979	-210,0	1,19981	-190,0	1,19982	-180,0
1,19971	-290,0	1,19974	-260,0	1,19978	-220,0	1,1998	-200,0
1,19967	-330,0	1,19972	-280,0	1,19977	-230,0	1,1998	-200,0
1,19965	-350,0	1,19971	-290,0	1,19977	-230,0	1,19981	-190,0
1,19966	-340,0	1,19972	-280,0	1,19978	-220,0	1,19983	-170,0
1,1997	-300,0	1,19975	-250,0	1,1998	-200,0	1,19984	-160,0
1,19975	-250,0	1,19979	-210,0	1,19982	-180,0	1,19985	-150,0
1,19981	-190,0	1,19983	-170,0	1,19984	-160,0	1,19985	-150,0
1,19986	-140,0	1,19986	-140,0	1,19986	-140,0	1,19985	-150,0
1,19988	-120,0	1,19988	-120,0	1,19987	-130,0	1,19985	-150,0
1,19989	-110,0	1,19988	-120,0	1,19987	-130,0	1,19985	-150,0

Acceleracions en Y

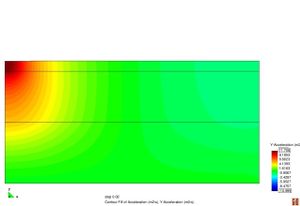
Tensions en Y

7.1.1.5 Cas 8500_C

Mòduls d’elasticitat emprats:

Fase	1
Distribució	B
Pressió contacte ${\textstyle (MPa)}$	0,707
${E}_{1}(MPa)$	5369
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	175
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	70

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	630	517	446	334	244	128	48	37	30
Valor Superior (μm)	630	520	450	340	250	130	50	40	30
Valor Inferior (μm)	630	510	440	330	240	120	40	30	30
y0 (m)	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2
yf (m)	1,19939	1,19951	1,19958	1,19967	1,19973	1,1998	1,19985	1,19986	1,19987
y0-yf (μm)	610	490,0	420,0	330,0	270,0	200,0	150,0	140,0	130,0
% Limit Inf.	96,8	94,2	93,3	97,1	108,0	153,8	300,0	350,0	433,3
% Limit Sup.	96,8	96,1	95,5	100,0	112,5	166,7	375,0	466,7	433,3
% Real	96,8	94,8	94,2	98,8	110,7	156,2	312,5	378,4	433,3

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,2	1,2	0,0	1,2	0,0	1,2	0,0
0,0025	1,2	1,19997	-30,0	1,19997	-30,0	1,19998	-20,0
0,005	1,2	1,19989	-110,0	1,1999	-100,0	1,19991	-90,0
0,0075	1,2	1,19977	-230,0	1,1998	-200,0	1,19982	-180,0
0,01	1,2	1,19964	-360,0	1,1997	-300,0	1,19974	-260,0
0,0125	1,2	1,19952	-480,0	1,1996	-400,0	1,19966	-340,0
0,015	1,2	1,19943	-570,0	1,19953	-470,0	1,1996	-400,0
0,0175	1,2	1,19939	-610,0	1,19951	-490,0	1,19958	-420,0
0,02	1,2	1,19942	-580,0	1,19953	-470,0	1,1996	-400,0
0,0225	1,2	1,1995	-500,0	1,19959	-410,0	1,19965	-350,0
0,025	1,2	1,19962	-380,0	1,19969	-310,0	1,19973	-270,0
0,0275	1,2	1,19974	-260,0	1,19978	-220,0	1,1998	-200,0
0,03	1,2	1,19983	-170,0	1,19985	-150,0	1,19986	-140,0
0,0325	1,2	1,19988	-120,0	1,19989	-110,0	1,19989	-110,0
0,035	1,2	1,1999	-100,0	1,1999	-100,0	1,1999	-100,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,2	0,0	1,2	0,0	1,2	0,0	1,2	0,0
1,19998	-20,0	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
1,19992	-80,0	1,19992	-80,0	1,19993	-70,0	1,19992	-80,0
1,19985	-150,0	1,19986	-140,0	1,19987	-130,0	1,19987	-130,0
1,19978	-220,0	1,19981	-190,0	1,19983	-170,0	1,19984	-160,0
1,19972	-280,0	1,19977	-230,0	1,19981	-190,0	1,19983	-170,0
1,19969	-310,0	1,19974	-260,0	1,1998	-200,0	1,19983	-170,0
1,19967	-330,0	1,19973	-270,0	1,1998	-200,0	1,19985	-150,0
1,19969	-310,0	1,19975	-250,0	1,19981	-190,0	1,19986	-140,0
1,19972	-280,0	1,19977	-230,0	1,19983	-170,0	1,19987	-130,0
1,19977	-230,0	1,19981	-190,0	1,19984	-160,0	1,19987	-130,0
1,19983	-170,0	1,19984	-160,0	1,19986	-140,0	1,19987	-130,0
1,19987	-130,0	1,19987	-130,0	1,19988	-120,0	1,19987	-130,0
1,19989	-110,0	1,19989	-110,0	1,19988	-120,0	1,19987	-130,0
1,1999	-100,0	1,19989	-110,0	1,19989	-110,0	1,19987	-130,0

Acceleracions en Y:

Tensions en Y:

7.1.1.6 Cas 8550_L

Mòduls d’elasticitat emprats:

Fase	1
Distribució	B
Pressió contacte ${\textstyle (MPa)}$	0,721
${E}_{1}(MPa)$	5404
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	127
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	102

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	703	541	442	292	191	88	40	31	26
Valor Superior (μm)	710	550	450	300	200	90	40	40	30
Valor Inferior (μm)	700	540	440	290	190	80	40	30	20
y0 (m)	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2	1,2
yf (m)	1,1993	1,19946	1,19957	1,19969	1,19978	1,19986	1,19989	1,19989	1,1999
y0-yf (μm)	700,0	540,0	430,0	310,0	220,0	140,0	110,0	110,0	100,0
% Limit Inf.	98,6	98,2	95,6	103,3	110,0	155,6	275,0	275,0	333,3
% Limit Sup.	100,0	100,0	97,7	106,9	115,8	175,0	275,0	366,7	500,0
% Real	99,6	99,8	97,3	106,2	115,2	159,1	275,0	354,8	384,6

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,2	1,2	0,0	1,2	0,0	1,2	0,0
0,0025	1,2	1,19997	-30,0	1,19997	-30,0	1,19998	-20,0
0,005	1,2	1,19989	-110,0	1,1999	-100,0	1,19991	-90,0
0,0075	1,2	1,19976	-240,0	1,1998	-200,0	1,19983	-170,0
0,01	1,2	1,19961	-390,0	1,19968	-320,0	1,19974	-260,0
0,0125	1,2	1,19946	-540,0	1,19957	-430,0	1,19965	-350,0
0,015	1,2	1,19935	-650,0	1,19949	-510,0	1,19959	-410,0
0,0175	1,2	1,1993	-700,0	1,19946	-540,0	1,19957	-430,0
0,02	1,2	1,19934	-660,0	1,19948	-520,0	1,19958	-420,0
0,0225	1,2	1,19944	-560,0	1,19956	-440,0	1,19964	-360,0
0,025	1,2	1,19958	-420,0	1,19967	-330,0	1,19973	-270,0
0,0275	1,2	1,19973	-270,0	1,19978	-220,0	1,19981	-190,0
0,03	1,2	1,19985	-150,0	1,19987	-130,0	1,19988	-120,0
0,0325	1,2	1,1999	-100,0	1,19991	-90,0	1,19992	-80,0
0,035	1,2	1,19992	-80,0	1,19992	-80,0	1,19992	-80,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,2	0,0	1,2	0,0	1,2	0,0	1,2	0,0
1,19998	-20,0	1,19998	-20,0	1,19998	-20,0	1,19998	-20,0
1,19992	-80,0	1,19993	-70,0	1,19993	-70,0	1,19993	-70,0
1,19986	-140,0	1,19988	-120,0	1,1999	-100,0	1,19989	-110,0
1,1998	-200,0	1,19984	-160,0	1,19988	-120,0	1,19987	-130,0
1,19975	-250,0	1,19981	-190,0	1,19986	-140,0	1,19988	-120,0
1,19971	-290,0	1,19979	-210,0	1,19986	-140,0	1,19988	-120,0
1,19969	-310,0	1,19978	-220,0	1,19986	-140,0	1,19989	-110,0
1,1997	-300,0	1,19978	-220,0	1,19987	-130,0	1,1999	-100,0
1,19974	-260,0	1,19981	-190,0	1,19987	-130,0	1,1999	-100,0
1,19979	-210,0	1,19984	-160,0	1,19988	-120,0	1,1999	-100,0
1,19985	-150,0	1,19987	-130,0	1,19989	-110,0	1,1999	-100,0
1,19989	-110,0	1,1999	-100,0	1,1999	-100,0	1,1999	-100,0
1,19992	-80,0	1,19992	-80,0	1,19991	-90,0	1,1999	-100,0
1,19992	-80,0	1,19992	-80,0	1,19991	-90,0	1,1999	-100,0

Acceleracions en Y

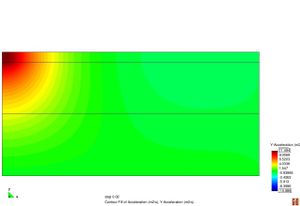
Tensions en Y

7.1.2 Resultats dels casos corresponents a la Fase 2

7.1.2.1 Cas 3825_R

Mòduls d’elasticitat emprats:

Fase	2
Distribució	C
Pressió contacte ${\textstyle (MPa)}$	0,749
${E}_{1}(MPa)$	2884
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	310
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	180

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	280	217	191	155	122	73	31	21	15
Valor Super. (μm)	280	220	200	160	130	80	40	30	20
Valor Inferior (μm)	280	210	190	150	120	70	30	20	10
y0 (m)	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3
yf (m)	1,29973	1,29979	1,29982	1,29986	1,29988	1,29991	1,29993	1,29994	1,29994
y0-yf (μm)	270,0	210,0	180,0	140,0	120,0	90,0	70,0	60,0	60,0
% Limit Sup	96,4	100,0	94,7	93,3	100,0	128,6	233,3	300,0	600,0
% Limit Inf	96,4	95,5	90,0	87,5	92,3	112,5	175,0	200,0	300,0
% Real	96,4	96,8	94,2	90,3	98,4	123,3	225,8	285,7	400,0

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,3	1,3	0,0	1,3	0,0	1,3	0,0
0,0025	1,3	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
0,005	1,3	1,29993	-70,0	1,29994	-60,0	1,29994	-60,0
0,0075	1,3	1,29988	-120,0	1,2999	-100,0	1,29991	-90,0
0,01	1,3	1,29983	-170,0	1,29986	-140,0	1,29987	-130,0
0,0125	1,3	1,29978	-220,0	1,29982	-180,0	1,29985	-150,0
0,015	1,3	1,29974	-260,0	1,2998	-200,0	1,29983	-170,0
0,0175	1,3	1,29973	-270,0	1,29979	-210,0	1,29982	-180,0
0,02	1,3	1,29974	-260,0	1,2998	-200,0	1,29983	-170,0
0,0225	1,3	1,29977	-230,0	1,29982	-180,0	1,29985	-150,0
0,025	1,3	1,29983	-170,0	1,29986	-140,0	1,29988	-120,0
0,0275	1,3	1,29988	-120,0	1,2999	-100,0	1,29991	-90,0
0,03	1,3	1,29992	-80,0	1,29993	-70,0	1,29993	-70,0
0,0325	1,3	1,29994	-60,0	1,29994	-60,0	1,29994	-60,0
0,035	1,3	1,29994	-60,0	1,29994	-60,0	1,29994	-60,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,3	0,0	1,3	0,0	1,3	0,0	1,3	0,0
1,29998	-20,0	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
1,29995	-50,0	1,29995	-50,0	1,29995	-50,0	1,29995	-50,0
1,29992	-80,0	1,29992	-80,0	1,29993	-70,0	1,29993	-70,0
1,29989	-110,0	1,29991	-90,0	1,29992	-80,0	1,29993	-70,0
1,29988	-120,0	1,29989	-110,0	1,29992	-80,0	1,29993	-70,0
1,29986	-140,0	1,29989	-110,0	1,29991	-90,0	1,29993	-70,0
1,29986	-140,0	1,29988	-120,0	1,29991	-90,0	1,29993	-70,0
1,29986	-140,0	1,29989	-110,0	1,29991	-90,0	1,29993	-70,0
1,29988	-120,0	1,2999	-100,0	1,29992	-80,0	1,29993	-70,0
1,2999	-100,0	1,29991	-90,0	1,29992	-80,0	1,29993	-70,0
1,29992	-80,0	1,29992	-80,0	1,29993	-70,0	1,29993	-70,0
1,29993	-70,0	1,29994	-60,0	1,29994	-60,0	1,29994	-60,0
1,29994	-60,0	1,29994	-60,0	1,29994	-60,0	1,29994	-60,0
1,29994	-60,0	1,29994	-60,0	1,29994	-60,0	1,29994	-60,0

Acceleracions en Y:

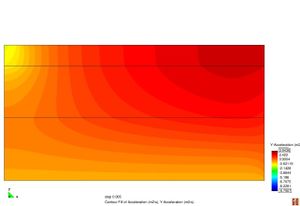
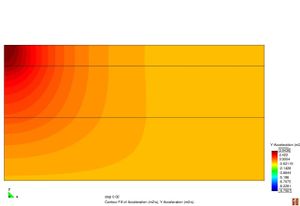
Tensions en Y:

7.1.2.2 Cas 3925_C

Mòduls d’elasticitat emprats:

Fase	2
Distribució	C
Pressió contacte ${\textstyle (MPa)}$	0,693
${E}_{1}(MPa)$	5339
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	546
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	199

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	176	140	127	106	86	54	22	12	6
Valor Super. (μm)	180	140	130	110	90	60	30	20	10
Valor Inferior (μm)	170	140	120	100	80	50	20	10	10
y0 (m)	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3
yf (m)	1,29983	1,29986	1,29988	1,2999	1,29991	1,29993	1,29994	1,29995	1,29995
y0-yf (μm)	170,0	140,0	120,0	100,0	90,0	70,0	60,0	50,0	50,0
% Limit Sup	100,0	100,0	100,0	100,0	112,5	140,0	300,0	500,0	500,0
% Limit Inf	94,4	100,0	92,3	90,9	100,0	116,7	200,0	250,0	500,0
% Real	96,6	100,0	94,5	94,3	104,7	129,6	272,7	416,7	833,3

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,3	1,3	0,0	1,3	0,0	1,3	0,0
0,0025	1,3	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
0,005	1,3	1,29995	-50,0	1,29995	-50,0	1,29995	-50,0
0,0075	1,3	1,29991	-90,0	1,29992	-80,0	1,29993	-70,0
0,01	1,3	1,29988	-120,0	1,2999	-100,0	1,29991	-90,0
0,0125	1,3	1,29986	-140,0	1,29988	-120,0	1,29989	-110,0
0,015	1,3	1,29984	-160,0	1,29987	-130,0	1,29988	-120,0
0,0175	1,3	1,29983	-170,0	1,29986	-140,0	1,29988	-120,0
0,02	1,3	1,29984	-160,0	1,29987	-130,0	1,29988	-120,0
0,0225	1,3	1,29986	-140,0	1,29988	-120,0	1,29989	-110,0
0,025	1,3	1,29988	-120,0	1,2999	-100,0	1,29991	-90,0
0,0275	1,3	1,29991	-90,0	1,29992	-80,0	1,29993	-70,0
0,03	1,3	1,29994	-60,0	1,29994	-60,0	1,29994	-60,0
0,0325	1,3	1,29995	-50,0	1,29995	-50,0	1,29995	-50,0
0,035	1,3	1,29995	-50,0	1,29995	-50,0	1,29995	-50,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,3	0,0	1,3	0,0	1,3	0,0	1,3	0,0
1,29998	-20,0	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
1,29995	-50,0	1,29996	-40,0	1,29996	-40,0	1,29995	-50,0
1,29993	-70,0	1,29994	-60,0	1,29994	-60,0	1,29994	-60,0
1,29992	-80,0	1,29993	-70,0	1,29993	-70,0	1,29994	-60,0
1,29991	-90,0	1,29992	-80,0	1,29993	-70,0	1,29994	-60,0
1,2999	-100,0	1,29991	-90,0	1,29993	-70,0	1,29994	-60,0
1,2999	-100,0	1,29991	-90,0	1,29993	-70,0	1,29994	-60,0
1,2999	-100,0	1,29991	-90,0	1,29993	-70,0	1,29994	-60,0
1,29991	-90,0	1,29992	-80,0	1,29993	-70,0	1,29994	-60,0
1,29992	-80,0	1,29993	-70,0	1,29994	-60,0	1,29994	-60,0
1,29993	-70,0	1,29994	-60,0	1,29994	-60,0	1,29995	-50,0
1,29995	-50,0	1,29995	-50,0	1,29995	-50,0	1,29995	-50,0
1,29995	-50,0	1,29995	-50,0	1,29995	-50,0	1,29995	-50,0
1,29995	-50,0	1,29995	-50,0	1,29995	-50,0	1,29995	-50,0

Acceleracions en Y:

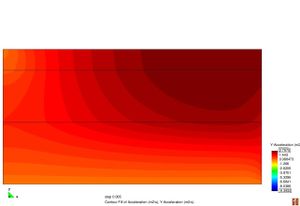
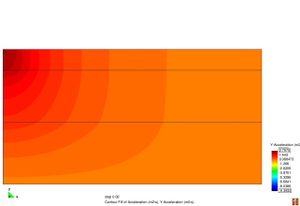
Tensions en Y:

7.1.2.3 Cas 5700_L

Mòduls d’elasticitat emprats:

Fase	2
Distribució	C
Pressió contacte ${\textstyle (MPa)}$	0,707
${E}_{1}(MPa)$	2973
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	302
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	126

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	300	246	222	185	150	93	39	24	16
Valor Super. (μm)	300	250	230	190	150	100	40	30	20
Valor Inferior (μm)	300	240	220	180	150	90	30	20	10
y0 (m)	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3
yf (m)	1,2997	1,29976	1,29979	1,29982	1,29985	1,29988	1,29991	1,29991	1,29992
y0-yf (μm)	300,0	240,0	210,0	180,0	150,0	120,0	90,0	90,0	80,0
% Limit Sup.	100,0	100,0	95,5	100,0	100,0	133,3	300,0	450,0	800,0
% Limit Inf	100,0	96,0	91,3	94,7	100,0	120,0	225,0	300,0	400,0
% Real	100,0	97,6	94,6	97,3	100,0	129,0	230,8	375,0	500,0

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,3	1,3	0	1,3	0,0	1,3	0,0
0,0025	1,3	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
0,005	1,3	1,29992	-80,0	1,29993	-70,0	1,29993	-70,0
0,0075	1,3	1,29986	-140,0	1,29988	-120,0	1,29989	-110,0
0,01	1,3	1,2998	-200,0	1,29983	-170,0	1,29984	-160,0
0,0125	1,3	1,29975	-250,0	1,29979	-210,0	1,29981	-190,0
0,015	1,3	1,29971	-290,0	1,29976	-240,0	1,29979	-210,0
0,0175	1,3	1,2997	-300,0	1,29976	-240,0	1,29979	-210,0
0,02	1,3	1,29971	-290,0	1,29977	-230,0	1,2998	-200,0
0,0225	1,3	1,29975	-250,0	1,2998	-200,0	1,29982	-180,0
0,025	1,3	1,2998	-200,0	1,29983	-170,0	1,29985	-150,0
0,0275	1,3	1,29986	-140,0	1,29987	-130,0	1,29988	-120,0
0,03	1,3	1,2999	-100,0	1,29991	-90,0	1,29991	-90,0
0,0325	1,3	1,29992	-80,0	1,29992	-80,0	1,29992	-80,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,3	0,0	1,3	0,0	1,3	0,0	1,3	0,0
1,29998	-20,0	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
1,29994	-60,0	1,29994	-60,0	1,29994	-60,0	1,29994	-60,0
1,29989	-110,0	1,2999	-100,0	1,29991	-90,0	1,29991	-90,0
1,29986	-140,0	1,29987	-130,0	1,29989	-110,0	1,29989	-110,0
1,29984	-160,0	1,29986	-140,0	1,29988	-120,0	1,2999	-100,0
1,29983	-170,0	1,29985	-150,0	1,29988	-120,0	1,2999	-100,0
1,29982	-180,0	1,29985	-150,0	1,29988	-120,0	1,29991	-90,0
1,29983	-170,0	1,29985	-150,0	1,29989	-110,0	1,29991	-90,0
1,29985	-150,0	1,29987	-130,0	1,29989	-110,0	1,29991	-90,0
1,29987	-130,0	1,29988	-120,0	1,2999	-100,0	1,29991	-90,0
1,29989	-110,0	1,2999	-100,0	1,29991	-90,0	1,29991	-90,0
1,29991	-90,0	1,29991	-90,0	1,29992	-80,0	1,29991	-90,0
1,29992	-80,0	1,29992	-80,0	1,29992	-80,0	1,29991	-90,0

Acceleracions en Y:

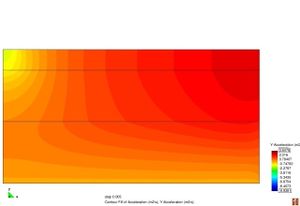
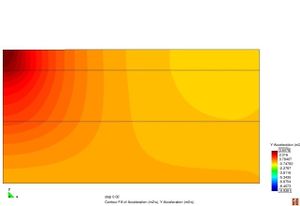
Tensions en Y:

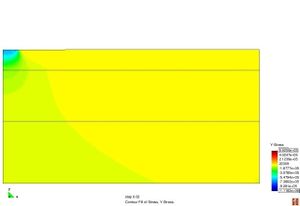
7.1.2.4 Cas 7900_D

Mòduls d’elasticitat emprats:

Fase	2
Distribució	C
Pressió contacte ${\textstyle (MPa)}$	0,707
${E}_{1}(MPa)$	2622
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	129
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	124

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	391	336	299	237	183	103	33	21	14
Valor Superior (μm)	400	340	300	240	190	110	40	30	20
Valor Inferior (μm)	390	330	290	230	180	100	30	20	10
y0 (m)	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3
yf (m)	1,29958	1,29965	1,29969	1,29975	1,29979	1,29985	1,29989	1,2999	1,2999
y0-yf (μm)	420,0	350,0	310,0	250,0	210,0	150,0	110,0	100,0	100,0
% Limit Inf.	105,0	102,9	103,3	104,2	110,5	136,4	275,0	333,3	500,0
% Limit Sup.	107,7	106,1	106,9	108,7	116,7	150,0	366,7	500,0	1000,0
% Real	107,4	104,2	103,7	105,5	114,8	145,6	333,3	476,2	714,3

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,3	1,3	0,0	1,3	0,0	1,3	0,0
0,0025	1,3	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
0,005	1,3	1,29991	-90,0	1,29992	-80,0	1,29992	-80,0
0,0075	1,3	1,29983	-170,0	1,29984	-160,0	1,29986	-140,0
0,01	1,3	1,29974	-260,0	1,29977	-230,0	1,2998	-200,0
0,0125	1,3	1,29966	-340,0	1,29971	-290,0	1,29974	-260,0
0,015	1,3	1,2996	-400,0	1,29967	-330,0	1,29971	-290,0
0,0175	1,3	1,29958	-420,0	1,29965	-350,0	1,29969	-310,0
0,02	1,3	1,2996	-400,0	1,29967	-330,0	1,29971	-290,0
0,0225	1,3	1,29965	-350,0	1,29971	-290,0	1,29975	-250,0
0,025	1,3	1,29973	-270,0	1,29977	-230,0	1,2998	-200,0
0,0275	1,3	1,29981	-190,0	1,29984	-160,0	1,29985	-150,0
0,03	1,3	1,29987	-130,0	1,29989	-110,0	1,29989	-110,0
0,0325	1,3	1,2999	-100,0	1,29991	-90,0	1,29991	-90,0
0,035	1,3	1,29991	-90,0	1,29991	-90,0	1,29991	-90,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,3	0,0	1,3	0,0	1,3	0,0	1,3	0,0
1,29998	-20,0	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
1,29993	-70,0	1,29993	-70,0	1,29993	-70,0	1,29993	-70,0
1,29987	-130,0	1,29988	-120,0	1,29989	-110,0	1,29989	-110,0
1,29982	-180,0	1,29984	-160,0	1,29987	-130,0	1,29987	-130,0
1,29978	-220,0	1,29982	-180,0	1,29985	-150,0	1,29987	-130,0
1,29976	-240,0	1,2998	-200,0	1,29985	-150,0	1,29988	-120,0
1,29975	-250,0	1,29979	-210,0	1,29985	-150,0	1,29989	-110,0
1,29976	-240,0	1,2998	-200,0	1,29986	-140,0	1,29989	-110,0
1,29979	-210,0	1,29982	-180,0	1,29987	-130,0	1,2999	-100,0
1,29983	-170,0	1,29985	-150,0	1,29988	-120,0	1,2999	-100,0
1,29986	-140,0	1,29988	-120,0	1,29989	-110,0	1,29989	-110,0
1,2999	-100,0	1,2999	-100,0	1,2999	-100,0	1,29989	-110,0
1,29991	-90,0	1,29991	-90,0	1,29991	-90,0	1,2999	-100,0
1,29991	-90,0	1,29991	-90,0	1,29991	-90,0	1,2999	-100,0

Acceleracions en Y:

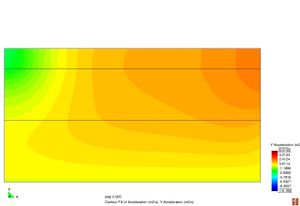
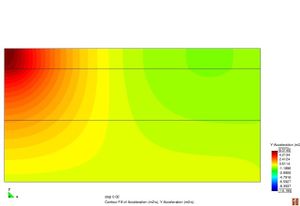
Tensions en Y:

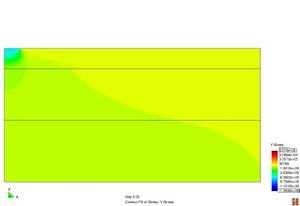
7.1.2.5 Cas 8475_C

Mòduls d’elasticitat emprats:

Fase	2
Distribució	C
Pressió contacte ${\textstyle (MPa)}$	0,721
${E}_{1}(MPa)$	3584
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	150
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	107

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	380	331	303	248	199	123	50	36	27
Valor Superior (μm)	380	340	310	250	200	130	50	40	30
Valor Inferior (μm)	380	330	300	240	190	120	50	30	20
y0 (m)	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3
yf (m)	1,29961	1,29966	1,2997	1,29975	1,29978	1,29984	1,29988	1,29989	1,29989
y0-yf (μm)	390,0	340,0	300,0	250,0	220,0	160,0	120,0	110,0	110,0
% Limit Inf.	102,6	100,0	96,8	100,0	110,0	123,1	240,0	275,0	366,7
% Limit Sup.	102,6	103,0	100,0	104,2	115,8	133,3	240,0	366,7	550,0
% Real	102,6	102,7	99,0	100,8	110,6	130,1	240,0	305,6	407,4

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,3	1,3	0,0	1,3	0,0	1,3	0,0
0,0025	1,3	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
0,005	1,3	1,29991	-90,0	1,29992	-80,0	1,29992	-80,0
0,0075	1,3	1,29983	-170,0	1,29985	-150,0	1,29985	-150,0
0,01	1,3	1,29975	-250,0	1,29978	-220,0	1,29979	-210,0
0,0125	1,3	1,29967	-330,0	1,29972	-280,0	1,29974	-260,0
0,015	1,3	1,29962	-380,0	1,29968	-320,0	1,29971	-290,0
0,0175	1,3	1,29961	-390,0	1,29966	-340,0	1,2997	-300,0
0,02	1,3	1,29962	-380,0	1,29968	-320,0	1,29971	-290,0
0,0225	1,3	1,29967	-330,0	1,29972	-280,0	1,29975	-250,0
0,025	1,3	1,29974	-260,0	1,29978	-220,0	1,2998	-200,0
0,0275	1,3	1,29982	-180,0	1,29984	-160,0	1,29985	-150,0
0,03	1,3	1,29987	-130,0	1,29988	-120,0	1,29988	-120,0
0,0325	1,3	1,2999	-100,0	1,2999	-100,0	1,2999	-100,0
0,035	1,3	1,29991	-90,0	1,29991	-90,0	1,29991	-90,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,3	0,0	1,3	0,0	1,3	0,0	1,3	0,0
1,29998	-20,0	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
1,29992	-80,0	1,29993	-70,0	1,29993	-70,0	1,29993	-70,0
1,29987	-130,0	1,29988	-120,0	1,29988	-120,0	1,29988	-120,0
1,29982	-180,0	1,29983	-170,0	1,29985	-150,0	1,29986	-140,0
1,29978	-220,0	1,2998	-200,0	1,29984	-160,0	1,29986	-140,0
1,29975	-250,0	1,29979	-210,0	1,29983	-170,0	1,29987	-130,0
1,29975	-250,0	1,29978	-220,0	1,29984	-160,0	1,29988	-120,0
1,29976	-240,0	1,29979	-210,0	1,29984	-160,0	1,29988	-120,0
1,29978	-220,0	1,29981	-190,0	1,29985	-150,0	1,29989	-110,0
1,29982	-180,0	1,29984	-160,0	1,29987	-130,0	1,29989	-110,0
1,29986	-140,0	1,29987	-130,0	1,29988	-120,0	1,29989	-110,0
1,29989	-110,0	1,29989	-110,0	1,29989	-110,0	1,29989	-110,0
1,2999	-100,0	1,2999	-100,0	1,2999	-100,0	1,29989	-110,0
1,29991	-90,0	1,2999	-100,0	1,2999	-100,0	1,29989	-110,0

Acceleracions en Y:

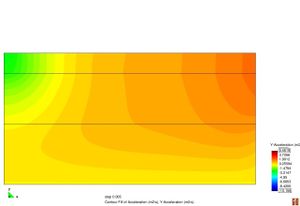
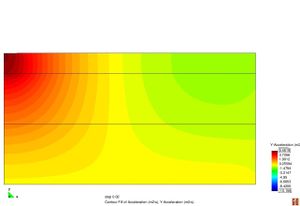
Tensions en Y:

7.1.2.6 Cas 8850_C

Mòduls d’elasticitat emprats:

Fase	2
Distribució	C
Pressió contacte ${\textstyle (MPa)}$	0,721
${E}_{1}(MPa)$	5479
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	236
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	118

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	282	251	234	200	167	111	50	36	26
Valor Superior (μm)	290	260	240	200	170	120	50	40	30
Valor Inferior (μm)	280	250	230	200	160	110	50	30	20
y0 (m)	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3	1,3
yf (m)	1,29971	1,29975	1,29977	1,2998	1,29983	1,29987	1,2999	1,2999	1,29991
y0-yf (μm)	290,0	250,0	230,0	200,0	170,0	130,0	100,0	100,0	90,0
% Limit Inf.	100,0	96,2	95,8	100,0	100,0	108,3	200,0	250,0	300,0
% Limit Sup.	103,6	100,0	100,0	100,0	106,3	118,2	200,0	333,3	450,0
% Real	102,8	99,6	98,3	100,0	101,8	117,1	200,0	277,8	346,2

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,3	1,3	0,0	1,3	0,0	1,3	0,0
0,0025	1,3	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
0,005	1,3	1,29992	-80,0	1,29993	-70,0	1,29993	-70,0
0,0075	1,3	1,29986	-140,0	1,29987	-130,0	1,29988	-120,0
0,01	1,3	1,2998	-200,0	1,29982	-180,0	1,29983	-170,0
0,0125	1,3	1,29975	-250,0	1,29978	-220,0	1,2998	-200,0
0,015	1,3	1,29972	-280,0	1,29976	-240,0	1,29978	-220,0
0,0175	1,3	1,29971	-290,0	1,29975	-250,0	1,29977	-230,0
0,02	1,3	1,29973	-270,0	1,29976	-240,0	1,29978	-220,0
0,0225	1,3	1,29976	-240,0	1,29979	-210,0	1,29981	-190,0
0,025	1,3	1,29981	-190,0	1,29983	-170,0	1,29984	-160,0
0,0275	1,3	1,29985	-150,0	1,29987	-130,0	1,29987	-130,0
0,03	1,3	1,29989	-110,0	1,2999	-100,0	1,2999	-100,0
0,0325	1,3	1,29991	-90,0	1,29991	-90,0	1,29991	-90,0
0,035	1,3	1,29992	-80,0	1,29992	-80,0	1,29992	-80,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,3	0,0	1,3	0,0	1,3	0,0	1,3	0,0
1,29998	-20,0	1,29998	-20,0	1,29998	-20,0	1,29998	-20,0
1,29993	-70,0	1,29993	-70,0	1,29994	-60,0	1,29993	-70,0
1,29989	-110,0	1,29989	-110,0	1,2999	-100,0	1,2999	-100,0
1,29985	-150,0	1,29986	-140,0	1,29987	-130,0	1,29988	-120,0
1,29982	-180,0	1,29984	-160,0	1,29986	-140,0	1,29988	-120,0
1,29981	-190,0	1,29983	-170,0	1,29986	-140,0	1,29989	-110,0
1,2998	-200,0	1,29983	-170,0	1,29987	-130,0	1,2999	-100,0
1,29981	-190,0	1,29984	-160,0	1,29987	-130,0	1,2999	-100,0
1,29983	-170,0	1,29985	-150,0	1,29988	-120,0	1,2999	-100,0
1,29986	-140,0	1,29987	-130,0	1,29989	-110,0	1,2999	-100,0
1,29988	-120,0	1,29989	-110,0	1,2999	-100,0	1,2999	-100,0
1,2999	-100,0	1,29991	-90,0	1,29991	-90,0	1,2999	-100,0
1,29991	-90,0	1,29991	-90,0	1,29991	-90,0	1,29991	-90,0
1,29992	-80,0	1,29992	-80,0	1,29991	-90,0	1,29991	-90,0

Acceleracions en Y:

Tensions en Y:

7.1.3 Resultats dels casos corresponents a la Fase 3

7.1.3.1 Cas 4325_I

Mòduls d’elasticitat emprats:

Fase	3
Distribució	D
Pressió contacte ${\textstyle (MPa)}$	0,707
${E}_{1}(MPa)$	7958
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	598
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	127

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	159	145	138	125	110	82	42	29	18
Valor Super. (μm)	160	150	140	130	110	90	50	30	20
Valor Inferior (μm)	150	140	130	120	110	80	40	20	10
y0 (m)	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36
yf (m)	1,35982	1,35984	1,35985	1,35986	1,35987	1,35989	1,3599	1,35991	1,35992
y0-yf (μm)	180,0	160,0	150,0	140,0	130,0	110,0	100,0	90,0	80,0
% Limit Sup.	120,0	114,3	115,4	116,7	118,2	137,5	250,0	450,0	800,0
% Limit Inf	112,5	106,7	107,1	107,7	118,2	122,2	200,0	300,0	400,0
% Real	113,2	110,3	108,7	112,0	118,2	134,1	238,1	310,3	444,4

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,36	1,36	0,0	1,36	0,0	1,36	0,0
0,0025	1,36	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
0,005	1,36	1,35994	-60,0	1,35994	-60,0	1,35994	-60,0
0,0075	1,36	1,35989	-110,0	1,35989	-110,0	1,3599	-100,0
0,01	1,36	1,35986	-140,0	1,35986	-140,0	1,35987	-130,0
0,0125	1,36	1,35983	-170,0	1,35985	-150,0	1,35985	-150,0
0,015	1,36	1,35982	-180,0	1,35984	-160,0	1,35985	-150,0
0,0175	1,36	1,35982	-180,0	1,35984	-160,0	1,35985	-150,0
0,02	1,36	1,35983	-170,0	1,35985	-150,0	1,35985	-150,0
0,0225	1,36	1,35984	-160,0	1,35986	-140,0	1,35987	-130,0
0,025	1,36	1,35987	-130,0	1,35988	-120,0	1,35988	-120,0
0,0275	1,36	1,35989	-110,0	1,3599	-100,0	1,3599	-100,0
0,03	1,36	1,35991	-90,0	1,35991	-90,0	1,35991	-90,0
0,0325	1,36	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0
0,035	1,36	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,36	0,0	1,36	0,0	1,36	0,0	1,36	0,0
1,35998	-20,0	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
1,35994	-60,0	1,35994	-60,0	1,35994	-60,0	1,35994	-60,0
1,3599	-100,0	1,3599	-100,0	1,3599	-100,0	1,35991	-90,0
1,35987	-130,0	1,35988	-120,0	1,35989	-110,0	1,3599	-100,0
1,35986	-140,0	1,35987	-130,0	1,35988	-120,0	1,3599	-100,0
1,35986	-140,0	1,35987	-130,0	1,35988	-120,0	1,3599	-100,0
1,35986	-140,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35986	-140,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35987	-130,0	1,35988	-120,0	1,35989	-110,0	1,35991	-90,0
1,35989	-110,0	1,35989	-110,0	1,3599	-100,0	1,35991	-90,0
1,3599	-100,0	1,3599	-100,0	1,35991	-90,0	1,35991	-90,0
1,35991	-90,0	1,35991	-90,0	1,35991	-90,0	1,35992	-80,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0

Acceleracions en Y:

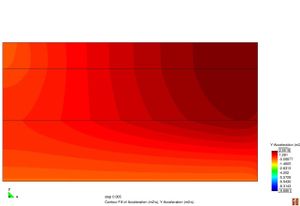
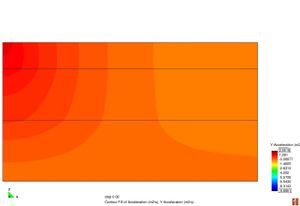
Tensions en Y:

7.1.3.2 Cas 4075_D

Mòduls d’elasticitat emprats:

Fase	3
Distribució	D
Pressió contacte ${\textstyle (MPa)}$	0,721
${E}_{1}(MPa)$	4314
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	393
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	148

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	201	172	159	135	116	83	43	32	23
Valor Super. (μm)	210	180	160	140	120	90	50	40	30
Valor Inferior (μm)	200	170	150	130	110	80	40	30	20
y0 (m)	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36
yf (m)	1,35979	1,35982	1,35984	1,35986	1,35987	1,35989	1,35991	1,35992	1,35993
y0-yf (μm)	210,0	180,0	160,0	140,0	130,0	110,0	90,0	80,0	70,0
% Limit Sup.	105,0	105,9	106,7	107,7	118,2	137,5	225,0	266,7	350,0
% Limit Inf	100,0	100,0	100,0	100,0	108,3	122,2	180,0	200,0	233,3
% Real	104,5	104,7	100,6	103,7	112,1	132,5	209,3	250,0	304,3

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,36	1,36	0,0	1,36	0,0	1,36	0,0
0,0025	1,36	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
0,005	1,36	1,35993	-70,0	1,35994	-60,0	1,35994	-60,0
0,0075	1,36	1,35989	-110,0	1,3599	-100,0	1,3599	-100,0
0,01	1,36	1,35985	-150,0	1,35986	-140,0	1,35987	-130,0
0,0125	1,36	1,35981	-190,0	1,35984	-160,0	1,35985	-150,0
0,015	1,36	1,35979	-210,0	1,35983	-170,0	1,35984	-160,0
0,0175	1,36	1,35979	-210,0	1,35982	-180,0	1,35984	-160,0
0,02	1,36	1,3598	-200,0	1,35983	-170,0	1,35984	-160,0
0,0225	1,36	1,35982	-180,0	1,35985	-150,0	1,35986	-140,0
0,025	1,36	1,35985	-150,0	1,35987	-130,0	1,35988	-120,0
0,0275	1,36	1,35988	-120,0	1,3599	-100,0	1,3599	-100,0
0,03	1,36	1,35991	-90,0	1,35992	-80,0	1,35992	-80,0
0,0325	1,36	1,35992	-80,0	1,35993	-70,0	1,35993	-70,0
0,035	1,36	1,35993	-70,0	1,35993	-70,0	1,35993	-70,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,36	0,0	1,36	0,0	1,36	0,0	1,36	0,0
1,35998	-20,0	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
1,35994	-60,0	1,35994	-60,0	1,35994	-60,0	1,35994	-60,0
1,3599	-100,0	1,35991	-90,0	1,35991	-90,0	1,35991	-90,0
1,35988	-120,0	1,35989	-110,0	1,3599	-100,0	1,35991	-90,0
1,35987	-130,0	1,35988	-120,0	1,35989	-110,0	1,35991	-90,0
1,35986	-140,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35986	-140,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35986	-140,0	1,35988	-120,0	1,3599	-100,0	1,35992	-80,0
1,35987	-130,0	1,35988	-120,0	1,3599	-100,0	1,35992	-80,0
1,35989	-110,0	1,3599	-100,0	1,35991	-90,0	1,35992	-80,0
1,35991	-90,0	1,35991	-90,0	1,35991	-90,0	1,35992	-80,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0
1,35993	-70,0	1,35993	-70,0	1,35993	-70,0	1,35992	-80,0
1,35993	-70,0	1,35993	-70,0	1,35993	-70,0	1,35992	-80,0

Acceleracions en Y:

Tensions en Y:

7.1.3.3 Cas 6175_D

Mòduls d’elasticitat emprats:

Fase	3
Distribució	D
Pressió contacte ${\textstyle (MPa)}$	0,707
${E}_{1}(MPa)$	4030
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	207
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	150

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	241	209	193	162	134	87	37	28	21
Valor Super. (μm)	250	210	200	170	140	90	40	30	30
Valor Inferior (μm)	240	200	190	160	130	80	30	20	20
y0 (m)	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36
yf (m)	1,35975	1,35978	1,3598	1,35983	1,35985	1,35988	1,3599	1,35991	1,35992
y0-yf (μm)	250,0	220,0	200,0	170,0	150,0	120,0	100,0	90,0	80,0
% Limit Sup.	104,2	110,0	105,3	106,3	115,4	150,0	333,3	450,0	400,0
% Limit Inf	100,0	104,8	100,0	100,0	107,1	133,3	250,0	300,0	266,7
% Real	103,7	105,3	103,6	104,9	111,9	137,9	270,3	321,4	381,0

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R = 0 mm	R = 0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,36	1,36	0	1,36	0,0	1,36	0,0
0,0025	1,36	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
0,005	1,36	1,35993	-70,0	1,35993	-70,0	1,35993	-70,0
0,0075	1,36	1,35987	-130,0	1,35988	-120,0	1,35989	-110,0
0,01	1,36	1,35982	-180,0	1,35984	-160,0	1,35985	-150,0
0,0125	1,36	1,35978	-220,0	1,35981	-190,0	1,35982	-180,0
0,015	1,36	1,35976	-240,0	1,35979	-210,0	1,35981	-190,0
0,0175	1,36	1,35975	-250,0	1,35978	-220,0	1,3598	-200,0
0,02	1,36	1,35976	-240,0	1,35979	-210,0	1,35981	-190,0
0,0225	1,36	1,35979	-210,0	1,35982	-180,0	1,35983	-170,0
0,025	1,36	1,35983	-170,0	1,35985	-150,0	1,35986	-140,0
0,0275	1,36	1,35987	-130,0	1,35988	-120,0	1,35989	-110,0
0,03	1,36	1,3599	-100,0	1,35991	-90,0	1,35991	-90,0
0,0325	1,36	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,36	0,0	1,36	0,0	1,36	0,0	1,36	0,0
1,35998	-20,0	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
1,35994	-60,0	1,35994	-60,0	1,35994	-60,0	1,35994	-60,0
1,35989	-110,0	1,3599	-100,0	1,3599	-100,0	1,35991	-90,0
1,35986	-140,0	1,35987	-130,0	1,35988	-120,0	1,35989	-110,0
1,35984	-160,0	1,35986	-140,0	1,35988	-120,0	1,35989	-110,0
1,35983	-170,0	1,35985	-150,0	1,35988	-120,0	1,3599	-100,0
1,35983	-170,0	1,35985	-150,0	1,35988	-120,0	1,35991	-90,0
1,35983	-170,0	1,35985	-150,0	1,35988	-120,0	1,35991	-90,0
1,35985	-150,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35987	-130,0	1,35988	-120,0	1,3599	-100,0	1,35991	-90,0
1,35989	-110,0	1,3599	-100,0	1,35991	-90,0	1,35991	-90,0
1,35991	-90,0	1,35991	-90,0	1,35991	-90,0	1,35991	-90,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35991	-90,0

Acceleracions en Y:

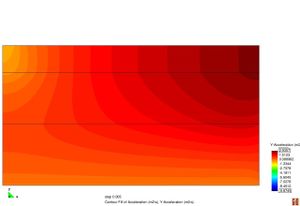
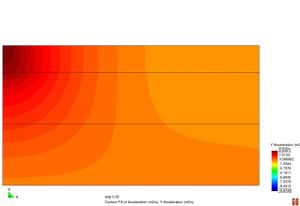
Tensions en Y:

7.1.3.4 Cas 7150_D

Mòduls d’elasticitat emprats:

Fase	3
Distribució	D
Pressió contacte ${\textstyle (MPa)}$	0,721
${E}_{1}(MPa)$	6436
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	392
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	135

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	190	170	161	142	122	86	40	28	19
Valor Superior (μm)	190	170	170	150	130	90	40	30	20
Valor Inferior (μm)	190	170	160	140	120	80	40	20	10
y0 (m)	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36
yf (m)	1,3598	1,35982	1,35984	1,35985	1,35986	1,35988	1,35991	1,35991	1,35992
y0-yf (μm)	200,0	180,0	160,0	150,0	140,0	120,0	90,0	90,0	80,0
% Limit Inf.	105,3	105,9	94,1	100,0	107,7	133,3	225,0	300,0	400,0
% Limit Sup.	105,3	105,9	100,0	107,1	116,7	150,0	225,0	450,0	800,0
% Real	105,3	105,9	99,4	105,6	114,8	139,5	225,0	321,4	421,1

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,36	1,36	0,0	1,36	0,0	1,36	0,0
0,0025	1,36	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
0,005	1,36	1,35993	-70,0	1,35994	-60,0	1,35994	-60,0
0,0075	1,36	1,35989	-110,0	1,35989	-110,0	1,35989	-110,0
0,01	1,36	1,35985	-150,0	1,35986	-140,0	1,35986	-140,0
0,0125	1,36	1,35982	-180,0	1,35984	-160,0	1,35985	-150,0
0,015	1,36	1,3598	-200,0	1,35983	-170,0	1,35984	-160,0
0,0175	1,36	1,3598	-200,0	1,35982	-180,0	1,35984	-160,0
0,02	1,36	1,35981	-190,0	1,35983	-170,0	1,35984	-160,0
0,0225	1,36	1,35983	-170,0	1,35985	-150,0	1,35986	-140,0
0,025	1,36	1,35985	-150,0	1,35987	-130,0	1,35987	-130,0
0,0275	1,36	1,35988	-120,0	1,35989	-110,0	1,3599	-100,0
0,03	1,36	1,35991	-90,0	1,35991	-90,0	1,35991	-90,0
0,0325	1,36	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0
0,035	1,36	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,36	0,0	1,36	0,0	1,36	0,0	1,36	0,0
1,35998	-20,0	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
1,35994	-60,0	1,35994	-60,0	1,35994	-60,0	1,35994	-60,0
1,3599	-100,0	1,3599	-100,0	1,35991	-90,0	1,35991	-90,0
1,35987	-130,0	1,35988	-120,0	1,35989	-110,0	1,3599	-100,0
1,35986	-140,0	1,35987	-130,0	1,35988	-120,0	1,3599	-100,0
1,35985	-150,0	1,35986	-140,0	1,35988	-120,0	1,3599	-100,0
1,35985	-150,0	1,35986	-140,0	1,35988	-120,0	1,35991	-90,0
1,35986	-140,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35987	-130,0	1,35988	-120,0	1,35989	-110,0	1,35991	-90,0
1,35988	-120,0	1,35989	-110,0	1,3599	-100,0	1,35991	-90,0
1,3599	-100,0	1,3599	-100,0	1,35991	-90,0	1,35991	-90,0
1,35991	-90,0	1,35991	-90,0	1,35991	-90,0	1,35992	-80,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0

Acceleracions en Y:

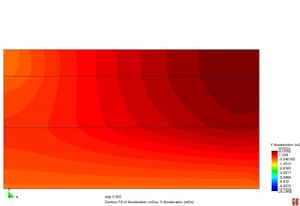
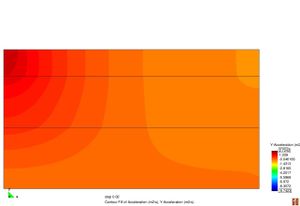
Tensions en Y:

7.1.3.5 Cas 8075_D

Mòduls d’elasticitat emprats:

Fase	3
Distribució	D
Pressió contacte ${\textstyle (MPa)}$	0,693
${E}_{1}(MPa)$	3523
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	197
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	154

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	250	216	195	160	127	79	34	25	18
Valor Superior (μm)	250	220	200	160	130	80	40	30	20
Valor Inferior (μm)	250	210	190	160	120	70	30	20	10
y0 (m)	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36
yf (m)	1,35974	1,35978	1,3598	1,35983	1,35985	1,35988	1,35991	1,35991	1,35992
y0-yf (μm)	260,0	220,0	200,0	170,0	150,0	120,0	90,0	90,0	80,0
% Limit Inf.	104,0	100,0	100,0	106,3	115,4	150,0	225,0	300,0	400,0
% Limit Sup.	104,0	104,8	105,3	106,3	125,0	171,4	300,0	450,0	800,0
% Real	104,0	101,9	102,6	106,3	118,1	151,9	264,7	360,0	444,4

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,36	1,36	0,0	1,36	0,0	1,36	0,0
0,0025	1,36	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
0,005	1,36	1,35993	-70,0	1,35993	-70,0	1,35993	-70,0
0,0075	1,36	1,35987	-130,0	1,35988	-120,0	1,35989	-110,0
0,01	1,36	1,35982	-180,0	1,35984	-160,0	1,35985	-150,0
0,0125	1,36	1,35978	-220,0	1,35981	-190,0	1,35982	-180,0
0,015	1,36	1,35975	-250,0	1,35979	-210,0	1,35981	-190,0
0,0175	1,36	1,35974	-260,0	1,35978	-220,0	1,3598	-200,0
0,02	1,36	1,35975	-250,0	1,35979	-210,0	1,35981	-190,0
0,0225	1,36	1,35978	-220,0	1,35981	-190,0	1,35983	-170,0
0,025	1,36	1,35982	-180,0	1,35985	-150,0	1,35986	-140,0
0,0275	1,36	1,35987	-130,0	1,35988	-120,0	1,35989	-110,0
0,03	1,36	1,3599	-100,0	1,35991	-90,0	1,35991	-90,0
0,0325	1,36	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0
0,035	1,36	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,36	0,0	1,36	0,0	1,36	0,0	1,36	0,0
1,35998	-20,0	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
1,35994	-60,0	1,35994	-60,0	1,35994	-60,0	1,35994	-60,0
1,35989	-110,0	1,3599	-100,0	1,35991	-90,0	1,35991	-90,0
1,35986	-140,0	1,35987	-130,0	1,35989	-110,0	1,35989	-110,0
1,35984	-160,0	1,35986	-140,0	1,35988	-120,0	1,3599	-100,0
1,35983	-170,0	1,35985	-150,0	1,35988	-120,0	1,3599	-100,0
1,35983	-170,0	1,35985	-150,0	1,35988	-120,0	1,35991	-90,0
1,35983	-170,0	1,35985	-150,0	1,35988	-120,0	1,35991	-90,0
1,35985	-150,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35987	-130,0	1,35988	-120,0	1,3599	-100,0	1,35991	-90,0
1,35989	-110,0	1,3599	-100,0	1,35991	-90,0	1,35991	-90,0
1,35991	-90,0	1,35991	-90,0	1,35991	-90,0	1,35991	-90,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35991	-90,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35991	-90,0

Acceleracions en Y:

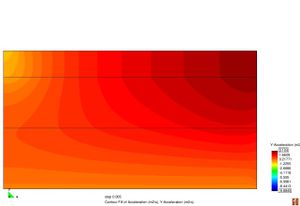
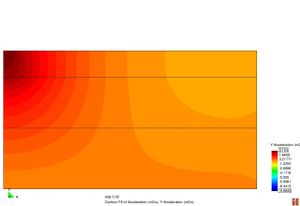
Tensions en Y:

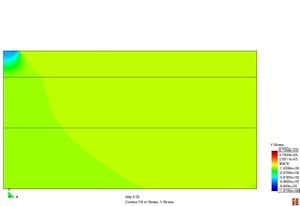
7.1.3.6 Cas 8275_C

Mòduls d’elasticitat emprats:

Fase	3
Distribució	D
Pressió contacte ${\textstyle (MPa)}$	0,693
${E}_{1}(MPa)$	4202
${\textstyle {E}_{2}}$ ${\textstyle (MPa)}$	224
${\textstyle {E}_{3}}$ ${\textstyle (MPa)}$	166

Comparació entre les deflexions mesurades amb el deflectòmetre d’impacte i les deflexions calculades:

Sensors a x (mm)	0	200	300	450	600	900	1500	1800	2100
Deflexió Real (μm)	222	193	175	146	118	73	27	18	13
Valor Superior (μm)	230	200	180	150	120	80	30	20	20
Valor Inferior (μm)	220	190	170	140	110	70	20	10	10
y0 (m)	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36	1,36
yf (m)	1,35977	1,35981	1,35982	1,35985	1,35986	1,35989	1,35991	1,35992	1,35992
y0-yf (μm)	230,0	190,0	180,0	150,0	140,0	110,0	90,0	80,0	80,0
% Limit Inf.	100,0	95,0	100,0	100,0	116,7	137,5	300,0	400,0	400,0
% Limit Sup.	104,5	100,0	105,9	107,1	127,3	157,1	450,0	800,0	800,0
% Real	103,6	98,4	102,9	102,7	118,6	150,7	333,3	444,4	615,4

Gràficament, la concavitat de deflexions mesurada comparada amb la calculada:

L’evolució de les deflexions al llarg del temps:

		R =0 mm	R =0 mm	R = 200 mm	R = 200 mm	R = 300 mm	R = 300 mm
Temps (s)	x0 (m)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
0	1,36	1,36	0,0	1,36	0,0	1,36	0,0
0,0025	1,36	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
0,005	1,36	1,35993	-70,0	1,35994	-60,0	1,35994	-60,0
0,0075	1,36	1,35988	-120,0	1,35989	-110,0	1,3599	-100,0
0,01	1,36	1,35984	-160,0	1,35986	-140,0	1,35987	-130,0
0,0125	1,36	1,3598	-200,0	1,35983	-170,0	1,35984	-160,0
0,015	1,36	1,35978	-220,0	1,35981	-190,0	1,35983	-170,0
0,0175	1,36	1,35977	-230,0	1,35981	-190,0	1,35982	-180,0
0,02	1,36	1,35978	-220,0	1,35981	-190,0	1,35983	-170,0
0,0225	1,36	1,35981	-190,0	1,35983	-170,0	1,35985	-150,0
0,025	1,36	1,35984	-160,0	1,35986	-140,0	1,35987	-130,0
0,0275	1,36	1,35988	-120,0	1,35989	-110,0	1,3599	-100,0
0,03	1,36	1,35991	-90,0	1,35992	-80,0	1,35992	-80,0
0,0325	1,36	1,35992	-80,0	1,35993	-70,0	1,35993	-70,0
0,035	1,36	1,35993	-70,0	1,35993	-70,0	1,35993	-70,0

R = 450 mm	R = 450 mm	R = 600 mm	R = 600 mm	R = 900 mm	R = 900 mm	R = 1500 mm	R = 1500 mm
xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)	xf (m)	x0-xf (μm)
1,36	0,0	1,36	0,0	1,36	0,0	1,36	0,0
1,35998	-20,0	1,35998	-20,0	1,35998	-20,0	1,35998	-20,0
1,35994	-60,0	1,35994	-60,0	1,35994	-60,0	1,35994	-60,0
1,3599	-100,0	1,35991	-90,0	1,35991	-90,0	1,35991	-90,0
1,35988	-120,0	1,35988	-120,0	1,3599	-100,0	1,3599	-100,0
1,35986	-140,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35985	-150,0	1,35987	-130,0	1,35989	-110,0	1,35991	-90,0
1,35985	-150,0	1,35986	-140,0	1,35989	-110,0	1,35991	-90,0
1,35985	-150,0	1,35987	-130,0	1,35989	-110,0	1,35992	-80,0
1,35986	-140,0	1,35988	-120,0	1,3599	-100,0	1,35992	-80,0
1,35988	-120,0	1,35989	-110,0	1,35991	-90,0	1,35992	-80,0
1,3599	-100,0	1,35991	-90,0	1,35991	-90,0	1,35992	-80,0
1,35992	-80,0	1,35992	-80,0	1,35992	-80,0	1,35992	-80,0
1,35993	-70,0	1,35993	-70,0	1,35993	-70,0	1,35992	-80,0
1,35993	-70,0	1,35993	-70,0	1,35993	-70,0	1,35992	-80,0

Acceleracions en Y:

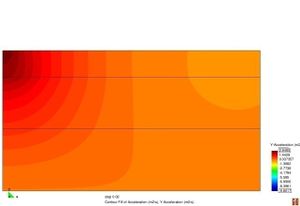
Tensions en Y: