Published in Comput. Methods Appl. Mech. Engrg., Vol. 194, pp. 907-932, 2005;
doi: 10.1016/j.cma.2003.08.012
Abstract
In this paper an assumed strain approach is presented in order to improve the membrane behaviour of a thin shell triangular element. The so called Basic Shell Triangle (BST) has three nodes with only translational degrees of freedom and is based on a Total Lagrangian Formulation. As in the original BST element the curvatures are computed resorting to the surrounding elements (patch of four elements). Membrane strains are now also computed from the same patch of elements which leads to a non-conforming membrane behaviour. Despite this non-conformity the element passes the patch test. Large strain plasticity is considered using a logarithmic strain-stress pair. A plane stress behaviour with an additive decomposition of elastic and plastic strains is assumed. A hyperplastic law is considered for the elastic part while for the plastic part an anisotropic quadratic (Hill) yield function with non-linear isotropic hardening is adopted. The element, termed CBST, has been implemented in an explicit (hydro-)code adequate to simulate sheet-stamping processes and in an implicit static/dynamic code. Several examples are given showing the good performance of the enhnaced rotation-free shell triangle.
1 Introduction
Development of efficient and robust shell finite elements for modelling large-scale industrial applications has been a field of constant research in the last thirty years. The continuining efforts of many scientists has focused in the direction of deriving simple elements (preferably triangles) applicable to large scale computation, typical of practical shell problems. Some recent successful shell triangles are reported in [1,2]. For a comprehensive review of shell elements see [3]. From the theoretical point of view Kirchhoff hypothesis are enough for the simulation of the essential aspects of most shells problems, including structures in civil, mechanical and naval engineering, sheet metal forming, crash-worthiness analysis and others. Due the well-known difficulties associated to continuity, “thick shell” approaches that need continuity only have been extensively used, although they are computationally more expensive due to the number of degrees of freedom necessary to obtain thin solutions with similar precision. The development of shell elements without transversal shear strains then collides with the need for C continuity, which is not simple to satisfy in general conditions and has led to the development of non-conforming approaches. Among the many options of this kind, the use of shell elements with only displacements as degrees of freedom (rotation-free) is very attractive from the computational point of view.
Few shell elements exists in the literature with only translations as degrees of freedom. They are generally based on non-conforming approaches. A state of the art can be found in Ref. [4]. Recently Cirak y Ortiz [5] have developed a conforming thin shell element, but it departs in some aspects from the standard finite element formulation. The use of rotation-free shell elements in large scale simulations of sheet metal forming processes is growing [6]-[9], specially in explicit integration codes.
In Ref. [10] we presented a thin shell triangular element with only displacements as degrees of freedom, based on a total lagrangian formulation. The element is an extension of the rotation-free Basic Shell Triangle (BST) originally developed by Oñate y Zárate [4] using an updated lagrangian formulation The element has three nodes and a linear approximation of the displacement field. The membrane part is identical to the standard constant strain triangle. The bending part is also constant and is computed from an integration over the element boundary using information from the deflection gradients of the adjacent elements. This leads to a non-conforming element for the bending part, but it converges to the right solution and is robust. The BST element has a very good performance in bending for structured meshes, but it is less accurate for non-structured grids. On the other hand, for membrane dominated problems, as is the case for most sheet metal forming simulations, it requires fine discretizations associated to the constant strain triangle behaviour.
In this paper an extension of the rotation-free BST element is presented. The displacement gradient terms needed for the membrane and bending strains are computed from the nodal displacements of a patch of element using a new procedure. This allows to improve the membrane behaviour and obtain a smoother curvature field. The outline of this paper is as follows. In sections 2 and 3 we introduce the kinematics of the shell and the constitutive models used in the numerical simulations. Sections 4 to 6 describe the finite element approximation, including the new proposal for the gradient evaluation from a patch of elements, the computation of the metric tensor and the curvatures and the derivation of the necessary element expressions for the computer implementation. Sections 7 and 8 sumarize the numerical experiments performed in the linear and non-linear range. Numerical results demonstrate the excellent performance of the enhanced three node rotation-free shell triangle.
2 Shell kinematics
A summary of the most relevant hypothesis related to the kinematic behaviour of the shell are presented. Further details may be found in the wide literature dedicated to this field [3].
Consider a shell with undeformed middle surface occupying the domain in with a boundary . At each point of the middle surface a thickness is defined. The positions and of any point in the undeformed and the deformed configurations can be respectively written as a function of the position of the middle surface and the normal at the point as
|
where are curvilinear local coordinates defined over the middle surface of the shell, and is the distance in the undeformed configuration of the point to the middle surface. The product is the distance of the point to the middle surface measured on the deformed configuration. This implies a constant strain in the normal direction associated to the parameter relating the thickness at the present and initial configurations, i.e.
|
|
A convective system is defined at each point as
|
|
(3) |
|
This can be particularized for the points on the middle surface as
|
This allows to introduce the covariant (first fundamental form) and contravariant metric tensors of the middle surface as
|
|
(8) |
|
|
(9) |
and the curvatures (second fundamental form) of the middle surface as
|
|
(10) |
The deformation gradient can be written as
|
|
(11) |
The product (where is the right stretch tensor, and the right Cauchy-Green deformation tensor) is
|
|
(12) |
where the derivatives of the thickness ratio have been neglected. Neglecting also the term associated to and introducing the definition of the covariant metric tensor at the middle surface and the curvatures gives
|
|
(13) |
Above expression shows that is non-zero at the original configuration for curved surfaces (). The changes of curvature of the middle surface are computed by
|
|
(14) |
For computational convenience the following approximate expression (which is exact for initially flat surfaces) will be adopted
|
|
(15) |
Above expression of is useful to compute different Lagrangian strain measures. An advantage of these measures is that they are associated to material fibres, what makes it easy to take into account material anisotropy. It is also useful to compute the eigen decomposition of as
|
|
(16) |
where and are the eigenvalues and eigenvectors of the right stretch tensor .
In order to treat plasticity at finite strains an adequate stress-strain pair must be used. The Hencky measures will be adopted here. The (logarithmic) strains are defined as
|
|
(17) |
Consistently, the Hencky stress tensor will be used as the stress measure. Using a total lagrangian formulation it is convenient to work with the the second Piola-Kirchhoff stresses () for the evaluation of the residual forces. We define the rotated tensors as
|
|
(18) |
where is the rotation tensor obtained from the eigenvectors of given by
|
|
(19) |
The relationship between the Hencky and Piola-Kirchhoff stresses is
|
|
(20) |
The second Piola-Kirchhoff stress tensor can be finally computed by
|
|
(21) |
The generalized stresses (forces and moments) are obtained by integrating across the original thickness the second Piola-Kirchhoff stress tensor using the actual distance to the middle surface for the evaluation of the bending moments, i.e.
|
With these values the weak form of the equilibrium equations can be written as
|
|
(23) |
where is the virtual curvature vector and is the virtual Green-Lagrange strain vector of the middle surface, with
|
|
(24) |
3 Constitutive models
In this section, a brief description of the constitutive models used in the numerical examples presented in Sections 7 and 8 is given. Two types of materials are described: an elastic-plastic material associated to thin rolled metal sheets and a hyper-elastic material for rubbers.
In the case of metals, where the elastic strains are small, the use of a logarithmic strain measure reasonably allows to adopt an additive decomposition of elastic and plastic components as
|
|
(25) |
A constant linear relationship between (plane) stresses and elastic strains is also adopted giving
|
|
(26) |
These constitutive equations are integrated using a standard return algorithm. The following Mises-Hill [11] yield function with non-linear isotropic hardening is adopted
|
|
(27) |
where and define the non-isotropic shape of the yield surface and the parameters and define its size as a function of the effective plastic strain .
The Mises-Hill yield function has the advantage of simplicity and it allows, as a first approximation, to treat rolled thin metal sheets with planar and transversal anisotropy.
For the case of rubbers, the Ogden [12] model extended to the compressible range is considered. The material behaviour is characterized by the strain energy density per unit undeformed volume of the form
|
|
(28) |
where is the bulk modulus of the material, is the determinant of , , and are material parameters, are real numbers such that and is a positive integer.
The stress measures associated to the principal logarithmic strains are denoted by . They can be computed noting that
|
|
(29) |
we define now
|
|
(30) |
which gives
|
|
(31) |
The values of , expressed in the principal strains directions, allow to evaluate the stresses in the convective coordinate system as
|
|
(32) |
We note that the Hencky stress tensor can be easily particularized for the plane stress case.
4 Interpolation functions and gradient evaluation
The starting point of the enhanced rotation-free of BST element is to discretize the shell surface with a standard 3-node triangular mesh. The difference with a standard finite element method is that for the computation of strains within an element, the configuration of the three adjacent triangular elements is used. Then at each triangle a patch of four elements, formed by the central triangle and the three adjacent ones is considered (see Figure 1.a). This allows to define a quadratic interpolation of the geometry from the position of the 6 nodes. In the isoparametric space, we keep the vertices of the 3-node master element (standard linear triangle) with the positions
- node 1:
- node 2:
- node 3:
and the three additional nodes that complete the patch with the positions
- node 4:
- node 5:
- node 6:
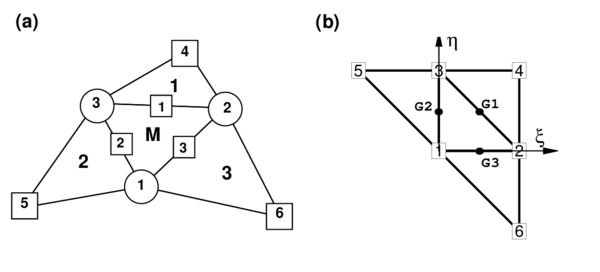
|
| Figure 1: Patch of four elements (a)in spacial coordinates (b)in natural coordinates |
It is possible to define now a set of (non-standard) quadratic shape functions over over the six node element as:
|
|
(33) |
This interpolation allows to compute the displacement gradients at selected points in order to use an assumed strain approach. The computation of the gradients is performed at three points over the boundary of the central element of the patch. These points are located at the mid-point of each side, denoted by G1, G2 and G3 in Figure 1.b. This election has the following characteristics.
- Gradients at these points depend only on the nodes pertaining to the two elements adjacent to the side. This can be easily verified by sampling the derivatives of the shape functions at each mid-side point.
- When gradients are computed at the common mid-side point from two adjacent elements, the same values are obtained, as the coordinates of the same four points are used. That is, the gradients at the mid-side points are independent of the element where they are computed. A side-oriented implementation of the finite element could lead to a unique evaluation of the gradients per side.
Next, some details of the implementation chosen are presented. We denote by and the orthogonal unit vectors over the tangent plane (undeformed configuration) associated to a conveniently selected local cartesian system. The cartesian derivatives of the shape functions are computed at the original configuration by the standard expression
|
|
(34) |
where the Jacobian matrix at the original configuration is
|
|
(35) |
With the previous definitions the deformation gradient on the middle surface, associated to an arbitrary spatial cartesian system and to the material cartesian system defined on the middle surface, is
|
|
(36) |
The covariant metric tensor can be computed from above expression as
|
|
(37) |
The component of can be used to compute any convenient membrane strain measures. For example the Green-Lagrange strain tensor is obtained by
|
|
(38) |
In the usual FEM matrix notation
|
|
(39) |
The virtual strains are obtained by the variation of above expression as
|
|
(40) |
In sides of elements where the adjacent element does not exist (i.e. at the boundaries of the shell), the gradient on that side is made equal to the gradient computed over the 3 nodes of the central element of the patch. From the definition of the gradients at the three mid-side points of the triangle, the element formulation can be interpreted as an assumed strain approach, where the metric tensor is interpolated over the element using the values computed on the sides by
|
|
(41) |
5 Computation of curvatures
Curvatures are assumed to be constant over the element. They are computed by performing an average over the central element as
|
|
(42) |
where ( is the original area of the element).
Integrating by parts Eq.(43), the following integral over the element boundary is obtained:
|
|
(43) |
The three distinct components of the curvature tensor are
|
|
(44) |
The numerical evaluation of the boundary integral in Eq.(44) results in a sum over the integration points on the element boundary which are, in fact, the same points used for the computation of the gradients in the membrane formulations, i.e.
|
|
(45) |
For the definition of , the linear interpolation over the central element is used. In this case the tangent plane components are (with and being the usual cartesian projections of the sides when area coordinates are used)
|
|
(46) |
|
|
(47) |
From these expressions it is also possible to compute in the original configuration the element area , the outer normals at each side and its lengths . Eq.(47) also allows to evaluate the thickness ratio in the deformed configuration and the actual normal . In Eq.(46), are the linear shape functions of the three node linear triangle [3].
As one integration point is used over each side, it is not necessary to distinguish between sides () and integrations points () any more. In this way the curvatures can be computed by:
|
In the original BST element [4,10] the gradient was computed as the average of the linear approximations over the two adjacent elements. In the new version, the gradient is computed at each side from the quadratic interpolation
|
|
(50) |
Note again than at each side the gradients depend only on the positions of the three nodes of the central triangle and of an extra node (), associated precisely to the side () where the gradient is computed.
An alternative form to express the curvatures, which is useful when their variations are needed, is to define:
|
|
(51) |
This gives
|
|
(52) |
This last expression allows to interpret the curvatures as the projections of the vectors over the normal of the central element. Direction t can be seen as a reference direction. If a different direction is chosen, at an angle with the former, this has an influence of order in the projection. This justifies Eq.(47) for the definition of t as a function exclusively of the three nodes of the central triangle, instead of the 6-node isoparametric interpolation.
5.1 Variation of the curvatures
From Eq.(52) the variation of the curvatures is obtained as
|
|
(53) |
The first term is crucial in the evaluation of the curvatures variation. The variations of are:
|
|
(54) |
where
|
|
(55) |
The variations of t can be computed as shown in the original BST element [10].
|
|
(56) |
leading to
|
|
(57) |
where are the contravariant base vectors in the central triangle
|
|
(58) |
We then have
|
|
(59) |
Substituting the last expression in Eq.(53), results
|
|
(60) |
where the projections of the vectors over the contravariant base vectors have been included
|
|
(61) |
These projections together with Eq.(52) allows to write
|
|
(62) |
5.2 Boundary conditions
Elements at the domain boundary, where an adjacent element does not exist, deserve a special attention. The treatment of essential boundary conditions associated to translational constraints is straightforward, as they are the natural degrees of freedom of the element. The conditions associated to the normal vector are crucial in this formulation. For clamped sides or symmetry planes, the normal vector must be kept fixed (clamped case), or constrained to move in the plane of symmetry (symmetry case). The former case can be seen as a special case of the latter, so we will consider symmetry planes only. This restriction can be imposed through the definition of the tangent plane at the boundary, including the normal to the plane of symmetry that does not change during the process.
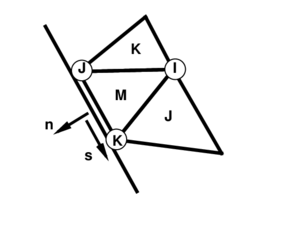
|
| Figure 2: Local cartesian system for the treatment of boundary conditions |
The tangent plane at the boundary is expressed in terms of two orthogonal unit vectors referred to as local-to-the-boundary cartesian system (see Figure 2) and defined as
|
|
(63) |
where vector is fixed while direction emerges as the intersection of the symmetry plane with the plane defined by the central element (). The plane (gradient) defined by the central element is
|
|
(64) |
the intersection of this plane with the plane of symmetry can be written in terms of the position of the nodes that define the side ( and ) and the original length of the side , i.e.
|
|
(65) |
That together with the outer normal to the side (resolved in the selected original convective cartesian system) leads to
|
|
(66) |
where the normal component of the gradient is
|
|
(67) |
In this way the contribution of the gradient at side to vectors results in
|
|
(68) |
The only difference with Eq.(54) necessary for the computation of the curvature variations, is that now the contribution from the gradient at side is
|
where the influence of variations in the length of vector has been neglected.
In the case of natural boundary conditions (either free or simple supported) the gradient at the sides is supposed to be equal to the gradient in the central element, similarly as in the membrane approach, i.e.
|
|
(71) |
Using Eq.(71), vectors and their variations can be easily computed. A second possibility is to make use of the natural boundary condition constraining the normal curvature to a zero value. In simple supported sides where the curvature along the side is zero, this leads to zero values for both bending moments.
6 Stiffness matrix evaluation
When a predictor-corrector scheme is used to trace the movement of the shell, the derivative (stiffness matrix) of the weak form of the momentum equations (23) is needed. As usual, material and geometric components are computed separately. The material part does not offer difficulties and it is computed from the integral
|
|
(72) |
where matrix includes:
a) a membrane part computed at each mid side point from
|
|
(73) |
Typically one integration point is used for computing the terms in .
b) a bending part which results from Eq.(60) that is constant over the element.
In Eq.(72), C is the elasticity matrix integrated in the thickness. If material non-linearity is considered, a layer wise numerical integration across the thickness is required This leads to the tangent or algorithmic elastic-plastic constitutive matrix .
6.1 Geometric stiffness (membrane part)
The geometric stiffness due to membrane forces results from computing
|
|
(74) |
This can be written as the sum of the contributions of the three sides, i.e.
|
|
(75) |
6.2 Geometric stiffness (bending part)
The geometric stiffness associated to bending moments is more involved. Its expression stems from
|
|
(76) |
Recalling expressions (51) and (52) it can be written
|
|
(77) |
where
|
|
(78) |
The first two terms lead to symmetric components. The second one can be expressed as
|
|
(79) |
Then, a first component of the geometric bending stiffness can be written as
|
|
(80) |
The last term in (78), can be obtained observing that (sum in and )
|
then
|
|
(82) |
|
|
(83) |
with
|
|
(84) |
where the covariant metric tensor at the middle surface has been used.
Denoting the sum
|
|
(85) |
the term
|
|
(86) |
results in
|
|
(87) |
The last expression (87) has components only in the nodes of the central element, which stems from the definition used for t.
Numerical experiments have shown that the bending part of the geometric stiffness is not so important and can be disregarded in the iterative process.
7 Numerical examples in the linear range
In this section, a summary of the results obtained in the assessment of the proposed element in the linear range are presented. In this first part of the numerical experiments, results have been obtained with a static/dynamic code that uses a implicit solution of the discretized equilibrium equations. In the examples, the original BST element [10] is compared with the enhanced version here proposed, denoted by CBST when a numerical integration is performed with three points, and CBST1 when only one integration point is used. Note that one integration quadrature is equivalent to averaging the metric tensors computed at each side.
7.1 Membrane patch test
The main objective of the present formulation is to obtain a (non conforming) membrane element with a similar performance than the linear strain triangle, that satisfies the patch test. To assess this, a square domain subjected to nodal forces associated to a constant stress state (in both directions and in shear) is considered. Figure 3 shows the patch of elements and the necessary nodal forces to obtain a uniform tensile stress in direction . Note that the nodal forces used correspond to the constant strain triangle, not to the linear one. For the distorted mesh shown, correct results are obtained using either 1 or 3 integration points.
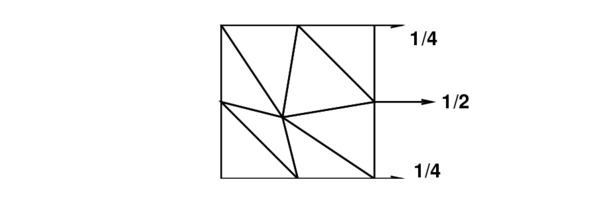
|
| Figure 3: Membrane patch test |
7.2 Bending patch test (torsion)
The element bending formulation does not allow to apply external bending moments (there are not rotational DOFs). Hence it is not possible to analyse a patch of elements under loads leading to a uniform bending moment. A uniform torsion can be considered if a point load is applied at the corner of a rectangular plate with two consecutive free sides and two simple supported sides. Figure 4 shows three patches leading to correct results both in displacements and stresses. All three patches are structured meshes. When the central node in the third patch is displaced from the center, the results obtained with the CBST element are not correct. The original element BST gives correct results in all cases, if natural boundary conditions are imposed in the formulation. If this is not the case, incorrent results are obtained even with structured meshes.
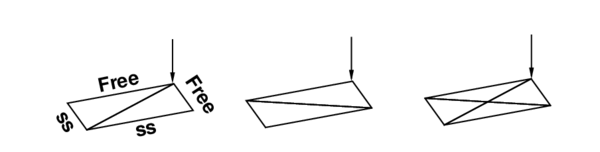
|
| Figure 4: Patch test for uniform torsion |
7.3 Cook's membrane problem
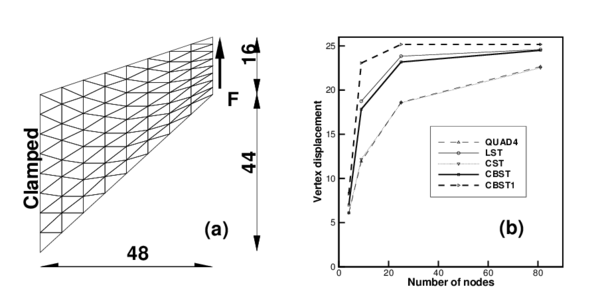
This example is used to assess the membrane performance of the CBST element and to compare it with the linear triangle (constant strain) and the quadratic triangle (linear strain). This example involves important shear energy and was proposed to assess the distortion capability of elements. Figure 5.a shows the geometry and the applied load. Figure 5.b plots the vertical displacement of the upper vertex as a function of the number of nodes in the mesh. In this figure results obtained with other isoparametric elements have been also plotted for comparison. They include the constain strain triangle (CST), the bilinear quadrilateral (QUAD4) and the linear strain triangle (LST). Note that in this membrane problem both the BST and the CST elements give identical results.
|
| Figure 5: Cook membrane problem (a) Geometry (b) Results |
From the plot shown it can be seen that the new element with three integration points (CBST) gives values slightly better that the constant strain triangle for the most coarse mesh (only two elements). However, when the mesh is refined, a performance similar to the linear strain triangle is obtained, that is dramatically superior that the former. On the other hand, if a one point quadrature is used (CBST1) the convergence in the reported displacement is notably better that for the rest of the elements.
7.4 Cylindrical roof
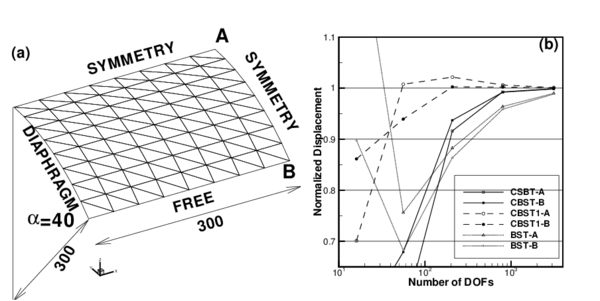
In this example an effective membrane interpolation is of primary importance. Hence this is good test to assess the new element. The geometry is a cylindrical roof supported by a rigid diaphragm at both ends and it is loaded by a uniform dead weight (see 6.a.). Only one quarter of the structure is modelled due to symmetry conditions. Unstructured and structured meshes are considered. In the latter case two orientations are possible (Figure 6 shows orientation B).
Tables 1, 2 and 3 present the normalized vertical displacements at the crown (point A) and in the midpoint of the free side (point B) for the two orientations of structured meshes and non-structured meshes. Values used for normalization are y that are quoted in reference [13].
|
| Figure 6: Cylindrical roof under dead weight. E=3 E, , Thickness =3.0, shell weight =0.625 per unit area. |
| Point-A | Point-B | |||||
| NDOFs | CBST | CBST1 | BST | CBST | CBST1 | BST |
| 16 | 0.65724 | 0.91855 | 0.74161 | 0.40950 | 0.70100 | 1.35230 |
| 56 | 0.53790 | 1.03331 | 0.74006 | 0.54859 | 1.00759 | 0.75590 |
| 208 | 0.89588 | 1.04374 | 0.88491 | 0.91612 | 1.02155 | 0.88269 |
| 800 | 0.99658 | 1.01391 | 0.96521 | 0.99263 | 1.00607 | 0.96393 |
| 3136 | 1.00142 | 1.00385 | 0.99105 | 0.99881 | 1.00102 | 0.98992 |
| Point-A | Point-B | |||||
| NDOFs | CBST | CBST1 | BST | CBST | CBST1 | BST |
| 16 | 0.26029 | 0.83917 | 0.40416 | 0.52601 | 0.86133 | 0.89778 |
| 56 | 0.81274 | 1.10368 | 0.61642 | 0.67898 | 0.93931 | 0.68238 |
| 208 | 0.97651 | 1.04256 | 0.85010 | 0.93704 | 1.00255 | 0.86366 |
| 800 | 1.00085 | 1.01195 | 0.95626 | 0.99194 | 1.00211 | 0.95864 |
| 3136 | 1.00129 | 1.00337 | 0.98879 | 0.99828 | 1.00017 | 0.98848 |
| Point-A | Point-B | |||||
| NDOFs | CBST | CBST1 | BST | CBST | CBST1 | BST |
| 851 | 0.97546 | 0.8581 | 0.97598 | 0.97662 | 1.0027 | 0.97194 |
| 3311 | 0.98729 | 0.9682 | 0.98968 | 0.98476 | 1.0083 | 0.98598 |
| 13536 | 0.99582 | 0.9992 | 1.00057 | 0.99316 | 0.9973 | 0.99596 |
Figure 6.b shows the normalized displacement of point-B over the structured meshes as a function of the number of degrees of freedom. An excelent convergence the CBST element can be seen. The version with only one integration point (CBST1) presents a behavior a little more flexible and converges from above. Table 3 shows that for non-structured meshes the element converges to the correct value but more slowly.
7.5 Open semi-espherical dome with point loads
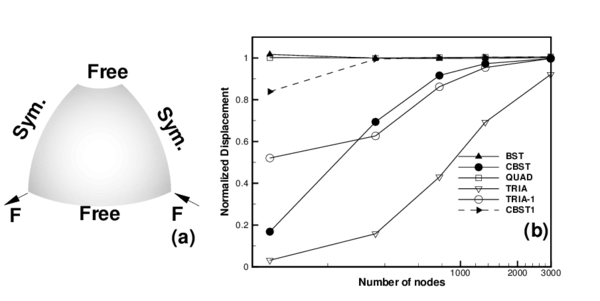
The main problem of finite elements with initially curved geometry is the so called membrane locking. The CBST element proposed has a quadratic interpolation of the geometry, then it may suffer from this problem. To assess this we resort to an example of inextensional bending. This is an hemispherical shell of radius and thickness with an 18 hole in the pole and free at all boundaries, subjected to two inward and two outward forces 90 apart. Material properties are and . Figure 7.a shows the discretized geometry (only one quarter of the geometry is considered due to symmetry).
|
| Figure 7: Pinched hemispherical shell with a hole, (a)geometry, (b)normalized displacement |
In Figure 7.b the displacements of the points under the loads have been plotted versus the number of nodes used in the discretization. Due to the orientation of the meshes chosen, the displacement of the point under the inward load is not the same as the displacement under the outward load, so in the figure an average (the absolute values) has been used. Results obtained with other elements have been included for comparison: two membrane locking free elements namely the original linear BST and a transverse shear-deformable quadrilateral (QUAD); a transverse shear deformable quadratic triangle (TRIA) [1] that is vulnerable to locking and an assumed strain version of this triangle (TRIA-1)[1] that alleviates membrane locking but does not eliminate it.
From the plotted results it can be seen that the CBST element presents membrane locking in bending dominated problems with initially curved geometries. This locking is much less severe than in a standard quadratic triangle and even than for the assumed strain version used for comparison. When only one integration point is used (CBST1 element) membrane locking disappears.
8 Non linear numerical examples
Results for examples with geometric and material non-linearities are presented next using the CBST1 element. Due to the features of the modelized problems, with strong nonlinearities associated to instabilities and frictional contact conditions, a code with explicit integration of the dynamic equilibrium equations has been used [14]. This code allows to obtain pseudo-static solutions throught dynamic relaxation.
8.1 Inflation of a sphere
The example is the inflation of a spherical shell under internal pressure. An incompressible Mooney-Rivlin constitutive material have been considered. The Ogden parameters are , , , , . Due to the simple geometry an analytical solution exists [15] (with ):
|
|
In this numerical simulation the same geometric and material parameters used in Ref. [16] have been adopted: and . The three meshes considered to evaluate convergence are shown in Figure 8.a. The value of the actual radius as a function of the internal pressure is plotted in Figure 8.b for the different meshes and is also compared with the analytical solution. It can be seen that with a few degrees of freedom it is possible to obtain an excellent agreement for the range of strains considered. The final value corresponds to a thickness radius ratio of .
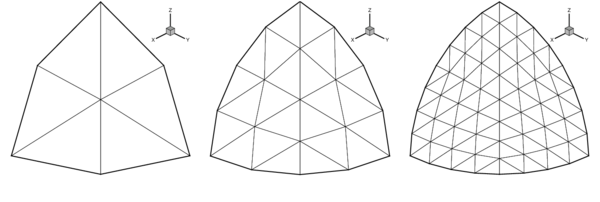
|
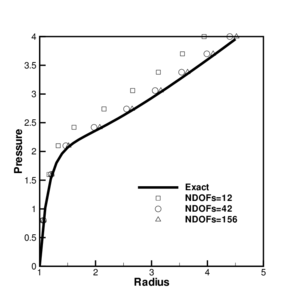
|
| Figure 8: Inflation of sphere of Mooney-Rivlin material. (a) Meshes used in the analysis (b) Change of radius as a function of the internal pressure. | |
8.2 Inflation of an air-bag
This example has also been taken from Ref.[16] where it is shown that the final configuration is mesh dependent due to the strong instabilities leading to a non-uniqueness of the solution. In [16] it is also discussed the important regularizing properties of the bending energy, that when disregarded leads to massive wrinkling in the compressed zones.
The air bag geometry is initially square with an undeformed diagonal of . The constitutive material is a linear isotropic elastic one with modulus of elasticity and Poisson's ratio . Only one quarter of the geometry has been modelled due to symmetry. Only the normal to the original plane is constrained along the boundaries. The thickness considered is and the inflation pressure is . Using a density , pressure is linearly incremented from 0 to the final value in .
With comparative purposes and also to backup the comments in Ref. [16] two analyses have been performed, a purely membranal one and one including bending effects. Figure 9 shows the final deformed configurations for three meshes with 289, 1089 and 4225 nodes. The top row corresponds to a full analysis including bending and the central row is a pure membrane analysis. The bottom row is also an analysis including bending where the mesh orientation has been changed.

|
| Figure 9: Inflation of a square air-bag . Deformed configurations for three different meshes with 800, 3136 and 12416 degrees of freedom. |
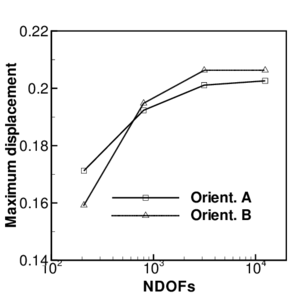
The top and bottom lines show the final shapes change according to the degree of discretization and mesh orientation due to instabilities and non uniqueness of the solution. The central row shows the noteworthy increment of wrinkles as the mesh is refined. Finally in Figure 10 presents the convergence of the maximum displacement of the central point as the mesh is refined.

|
| Figure 10: Inflation of a square air-bag. Convergence of the maximum displacement versus the number of degrees of freedom in the model. |
8.3 Deep drawing of a rolled sheet
The element performance in problems involving large strains and anisotropic plastic behaviour is assesed in a benchmark proposed in a recent NUMISHEET [17] meeting. This is the deep drawing of a circular mild steel sheet with a spherical punch of radius (). The original radius of the sheet () is (). The drawing depth is () is 85 mm () and the force over the blank holder is . The constitutive material of the rolled sheet is characterized by three tensile tests along three different directions respect to rolling direction () (Table 4). Note that the modellization requires to treat the material as transversally anisotropic, as this improves the deep drawability and if not considered leads to an early localized necking of the material. The yield function originally proposed by Hill[11] has been chosen for both associative and non-associative potential functions. For elastic-plastic problems a numerical integration along the thickness direction is necessary. This is accomplished here using four integration points.
| Thickness | Orientation | Yield | Tensile | n | r | ||
| respect to RD | stres | strength | (uniform) | (total) | |||
| [mm] | [] | [N/mm] | [N/mm] | [%] | [%] | - | - |
| 0 | 176 | 322 | 24 | 40 | 0.214 | 1.73 | |
| 0.98 | 45 | 185 | 333 | 22 | 39 | 0.203 | 1.23 |
| 90 | 180 | 319 | 23 | 44 | 0.206 | 2.02 |
Only one quarter of the geometry has been considered due to symmetry. Tools are modelized as rigid surfaces, the punch has been defined by 1439 points and 2730 triangles. For the die 744 points and 490 quadrilaterals have been used. Finally the blank holder has been discretized with 155 points and 120 quadrilaterals. Figure 11.a shows a perspective of the tools and Figure 11.a the final deformed sheet. The sheet has been modelled with 6370 3-node triangles and 3284 nodes (9274 DOFs).
|
| Figure 11: Deep drawing of a circular sheet. (a)geometry of the tools, (b)final deformed shape of the sheet. |
The reported results are associated to three different meridiands: A at 90 of the rolling direction, B: at 45 of the rolling direction and C: in the rolling direction. The numerical results are compared with a set of experimental values reported by Thyssen Krupp Stahl AG (who proposed the benchmark and supplied the sheet samples) [17]. It must be noted that there was a great dispersion in the experimental data send to NUMISHEET, so it is difficult to extract conclusions from a unique comparison. In any case the experimental data supplied seems to be consistent enought to have an idea if the numerical model gives reasonable results.
The first element of comparison associated to the planar anisotropy, are the different displacements (draw in) of the points in the boundary of the sheet. Table 5 shows the values obtained for the three reference meridians chosen.
| Draw in [mm] | |||
| Model | Section A | Section B | Section C |
| CBST1-Non Associative | 29.06 | 31.91 | 30.77 |
| CBST1-Associative | 27.08 | 31.36 | 28.95 |
| Experimental | 30.75 | 32.30 | 30.00 |
The values for the non-associative model are much like the experimental ones, those obtained with the associative model are a little lower. The largest draw-in is at the meridian at 45 of rolling direction ( B). In the numerial simulation the draw-in at meridian C is larger than in meridian A, while in the experimental results the latter are larger than the former. It should be reminded that other numerical results presented at NUMISHEET and most of the numerical simulations showed the same tendency of present values.
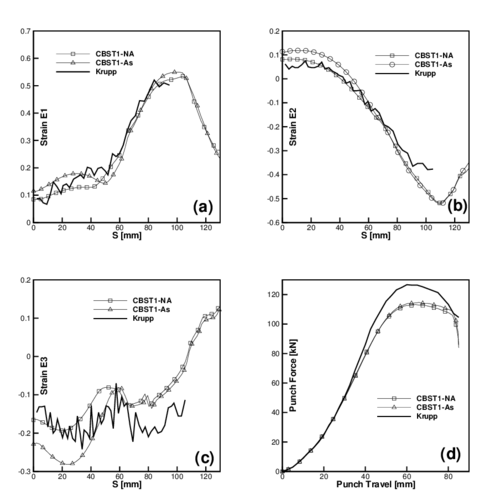
The experimental data supplied are the three logarithmic principal strains associated to the three meridians defined above. Here one strain at each meridian has been choosen for comparison. Figure 12.a shows the meridian strain () along meridian A (direction transversal to rolling); Figure 12.b shows the circunferencial strain () along meridian B and in Figure 12.c the thickness strain () along meridian C (rolling direction) has been plotted.
The experimental data show a saw-tooth profile (specially for the thickness strain) that is difficult to accept. These values are therefore not reliable point-wise but as a whole. Based on this fact and on the above mentioned differences between experimental values, it can be said that the present simulations agree quite well with the experimental values, specially when the non-associative plasticity model was used.
In the central part of the sheet the experimental data gives strains lower than the numerical simulation. It can be said that experimentally the sheet has better drawability. In the external zone there are less differences for in plane strains but for thickness strains they are larger. Experimentally thickness strains are more or less uniform between and what differs from present numerical simulations and also from other numerical simulations and experimental data presented at NUMISHEET [17].
Finally Figure 12 shows resistance to punch as a funtion of punch travel. In the final part simulation forces are smaller than experimental values. This may be due to an incorrect definition of friction with the tools.
From the present results it is difficult to draw definite conclusions about what should be improved in the numerical model due to all the factors involved, including the constitutive model, the thin shell theory, the contact treatment, the reliability of the experimental data of both the material characterization and the deep drawing, etc..
9 Conclusions
A membrane and bending non-conforming rotation-free shell finite element has been presented. The element pass the membrane patch test and the numerical experiments performed do not show problems. From the bending point of view the element is a little stiffer than the original BST element, but presents a smoother continuity of displacement gradients. Convergence rate in membrane dominated problems is similar to the linear strain triangle. Using three integration points the elements is vulnerable to membrane locking for initially curved surfaces. This locking effect dissapears when only one integration point is used, which the usual case for elastic-plastic problems and for any large scale simulation.
Acknowledgments
The first author is a member of the scientific staff of the Science Research Council of Argentina (CONICET). The support provided by grants of CONICET and Agencia Córdoba Ciencia S.E. is gratefully acknowledged.
Bibliography
[1] F.G. Flores, E. Oñate and F. Zárate “New assumed strain triangles for non-linear shell analysis”, Computational Mechanics, 17, 107-114, 1995.
[2] J.H. Argyris, M. Papadrakakis, C. Aportolopoulun and S. Koutsourelakis. The TRIC element. Theoretical and numerical investigation. Comput. Meth. Appl. Mech. Engrg., 182, 217–245, 2000.
[3] O.C. Zienkiewicz and R.L. Taylor. The finite element method. Solid Mechanics. Vol II, Butterworth-Heinemann, 2000.
[4] E. Oñate and F. Zárate, “Rotation-free plate and shell triangles”, Int. J. Num. Meth. Engng, 47, pp. 557–603, 2000.
[5] F. Cirak and M. Ortiz, Subdivision surfaces: A new paradigm for thin-shell finite element analysis, Int. J. Num. Meths in Engng, vol. 47, 2000, págs. 2039-2072.
[6] D.Y. Yang, D.W. Jung, L.S. Song, D.J. Yoo and J.H. Lee, “Comparative investigation into implicit, explicit and iterative implic/explicit schemes for simulation of sheet metal forming processes” NUMISHEET'93, A. Makinouchi, E. Nakamachi, E. Oñate and R.H. Wagoner (Eds.), RIKEN, pp. 35–42, Tokyo, 1993.
[7] M. Brunet and F. Sabourin, “Prediction of necking and wrinkles with a simplified shell element in sheet forming”, Int. Conf. of Metal Forming Simulation in Industry, Vol. II, pp. 27–48, B. Kröplin (Ed.), 1994.
[8] G. Rio, B. Tathi and H. Laurent, “A new efficient finite element model of shell with only three degrees of freedom per node. Applications to industrial deep drawing test”, in Recent Developments in Sheet Metal Forming Technoloy, Ed. M.J.M. Barata Marques, 18th IDDRG Biennial Congress, Lisbon, 1994.
[9] Rojek J., Oñate E. and Postek E ., Application of explicit FE codes to simulation of sheet and bulk metal forming processes Journal of the Materials Processing Thecnology, 41, págs. 620-627, 1998.
[10] F.G. Flores F.G. and E. Oñate A basic thin shell triangle with only translational DOFs for large strain plasticity, Int. J. Num. Meths in Engng, vol. 51, pp 57-83, 2001.
[11] R. Hill, “A Theory of the Yielding and Plastic Flow of Anisotropic Metals”, Proc. Royal Society London, vol. A193, pp. 281, 1948.
[12] R.W. Ogden “Large deformation isotropic elasticity: on the correlation of theory and experiments for incompressible rubberlike solids”, Proceedings of the Royal Society of London, vol. A326, pp. 565-584, 1972.
[13] H.C. Huang, Static and Dynamic Analysis of Plates and Shells, page 40, Springer-Verlag, Berlin, 1989.
[14] STAMPACK, A General Finite Element System for Sheet Stamping and Forming Problems, Quantech ATZ, Barcelona, Spain, 2003 (www.quantech.es).
[15] A. Needleman, Inflation of spherical rubber ballons, Int. J. of Solids and Structures, 13, 409–421, 1977.
[16] F. Cirak and M. Ortiz, Fully -conforming subdivision elements for finite deformations thin-shell analysis , Int. J. Num. Meths in Engng, vol. 51, 2001, 813-833.
[17] NUMISHEET'99, Fourth International Conference and Workshop on Numerical Simulation of 3D Sheet Forming Processes, NUMISHEET'99, J.C. Gelin and P. Picart (Eds.), BURS Edition, Besancon, France, 1999.
Document information
Published on 01/01/2005
DOI: 10.1016/j.cma.2003.08.012
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?