Abstract
In this work, the study of smoke fire transportation inside of a subway passenger platform is presented. The study includes a set of numerical simulations to observe the behavior of the smoke inside the platform. Two smoke transport simulations using the FDS program are also included. Subsequently, the development of a 3D - 1:100 scale model is described and it was used to perform an experimental observation of the phenomenon. The model was built by using a 3D printer which allowed to include more architectural details of the real scenario. The inclusion of these details allowed to observe qualitative similarity between the results of the simulation and the experimental work. Although there are clear differences between what could happen in a real scenario and what was observed in the scale model, it was identified that the model is an important complement to the simulations. In addition to the simulations, the use of this type of 3D models allows the observation of the phenomenon by different specialists such as firefighters, policeman, medical personnel, etc., in the same place and its intention is to provide a more interactive tool to the observation group, increasing the time devoted to the development of contingency actions and reducing the costs associated with the logistics of a real simulacrum. The model allows to better identify the strengths, opportunities, weaknesses and threats of the contingency procedures developed by the safety and hygiene groups and to make their corresponding adjustments if necessary.
Keywords: CFD, FDS, ANSYS-FLUENT, smoke, critical velocity, 3D print
1. Introduction
During a fire emergency in a subway platform, several specialized teams have to interact each other to ensure the safety of the passengers. At least 25 tasks and resources have been identified during an empirical study of emergency response [1]. They have to deal with a situation in which, the architectural distribution creates important differences in the behavior of the fire and smoke distribution [2] loss of visibility [3,4], as well as the ventilation characteristics [5]. The reaction procedure of the staff is intended to adequately manage the time that elapses until the last person is evacuated [6,7]. Passenger reactions to an emergency in subways have shown to be independent of their individual characteristics such as gender, educational level and for example; carrying-on luggage [8]. These kind of disasters involve a great human cost because in subterranean emergency scenarios, the possibilities for the passengers to leave or scape out of a critical location is quite compromised. The limited space for mobility, low visibility, presence of fresh air, etc., are some of the restrictions that a passenger can face in these situations. Therefore we propose the use of computer simulations together with observations in 3D scale models to increase the scope in the study of these phenomenon.
When designing subterranean installations, connections to atmospheric pressure are one of the most important issues that have to be considered. The location and size of the ventilation ports, external and internal weather conditions among others create set of variable air conditions. In the case of subway tunnels, convective flow currents enhance the generation of vortex in random locations even when the air velocity can be maintained constant along the tunnel by natural conditions or by means of a mechanical ventilation system. The emission of smoke close to a ventilation duct connected to the atmosphere does not always guarantee a safety condition because the atmospheric pressure creates an equilibrium between the internal and external pressures affected by the temperature and the resulting direction of the air flow in consequence is not easy to predict.
2. Materials and methods
This study is composed by several steps with the purpose of observing in a separate way the events occurring in a fire scenario. In these events, several physical situations are presented simultaneously, by dividing the sequence of them, interesting observations can be made to understand the complexity of the phenomenon when the equilibrium condition is reached. The temperature changes generated inside the platform will have a straight interaction with the ducts connected to atmospheric pressure, and finally addressing the transportation of the smoke. Therefore, the study was divided in three stages. The first stage was developed to validate the critical velocity calculation. The second one to simulate the smoke transportation phenomena and the third one describes the creation of the scaled model to observe and compare the displacement of the smoke with respect to the simulation.
2.1. First stage
The first stage considers the analysis of the flow velocity inside the platform when the critical velocity is injected from one side of the tunnel. There is not fire source in this case but only the air flow velocity of the calculation. The NFPA 130-7 provides important information to carry out the calculation of the critical velocity which is the velocity required to provide adequate ventilation conditions and to produce adequate smoke transportation in case of fire emergencies [9]. This critical velocity avoids also the backlayering effect in which the smoke in certain cases tends to move in a different direction of the one desired. To observe the flow pattern, a simplified theoretical 2D model was implemented in FORTRAN. This flow pattern was compared with the results obtained in ANSYS-FLUENT and in FDS programs by extracting only a sliced plane of each one. The observation of these results are very important during the selection and location process of commercial fans for subterranean installations.
2.2. Second stage
The second stage considers a 180 seconds fire simulation in FDS [10]. In this case, a totally developed fire of 5MW is located close to the center of the platform as in [11]. The evacuation of the smoke trough the natural ventilation ports is another interesting issue to observe in the simulation [12] and to notice the presence or not of the backlayering effect with the injection of the critical velocity [13-15]. It is not easy to predict the displacement of the smoke because at least 4 ventilation ducts connected to atmospheric pressure are close to the fire source. In one simulation, the air conditions are allowed to move freely. In a second simulation, the previously calculated critical velocity is injected from the left side of the platform and both results are compared.
2.3. Third stage
In the third stage, a 3D printed model was constructed to create a suitable observation experiment setup by using a Mendelmax printer and Polylactic Acid (PLA) as the deposition material with 0.2mm thickness layers. The stage has been developed with the purpose of re-creating the scenario to observe the smoke spread. Once the smoke output is constant, an exchange of temperatures within the platform is generated, these differences between the hot and cold gases, after some time, reach an equilibrium behavior creating a flow distribution (under free motion conditions). This equilibrium is directly related with the distance between the ventilation ducts because they are communicated through the platform and are directly affected by the atmospheric pressure. Once the ventilation system has been turned on, it will be possible to observe if the behavior is similar to the one observed in the simulations (stage 2), although in a real scenario many other factors will be presented and may differ from this experiment. Table 1 shows a list of all the analyzed cases in each stage of this study.
| Case No. | Program | Simulation type | Objective |
| 1 | Fortran | Air flow injection at critical velocity | Validation |
| 2 | ANSYS-FLUENT | Air flow injection at critical velocity | Validation |
| 3 | FDS | Air flow injection at critical velocity | Validation |
| 4 | FDS | Smoke transported at free motion condition | Observe and measure the free smoke movement |
| 5 | FDS | Smoke transported with the air flow at critical velocity | Observe and measure the influenced movement of the smoke |
| 6 | Experimental setup | Smoke transported in free motion | Observe experimental behavior with respect to the FDS simulations |
| 7 | Experimental setup | Smoke transported with the fans on | Observe experimental behavior with respect to the FDS simulations |
2.4. Description of the analysis scenario
In the presence of fire inside underground facilities, different parameters should be considered to handle the emergency situation and provide a suitable breading atmosphere for the users, it must be kept sustainable conditions for life. However, every subway systems have particular characteristics, they require specific solutions which relate internal and external conditions of the tunnel as an enclosed place with limited escape routes.
The analyzed platform considered has 15m depth from the sidewalk level and 150m in length, it has four ventilation ports (ducts) at the ceiling connected to atmospheric pressure and three passenger access towards the street. Figure 1 shows the dimensions and geometry considered for the 3D model. They were obtained by direct measurements of the platform creating a simplified geometry.
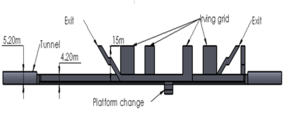
|
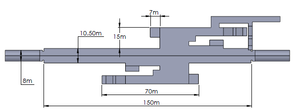
|
| (a) | (b) |
| Figure 1. 3D CAD geometry and dimensions a) lateral view and b) top view | |
2.5. Critical velocity calculation
During the backlayering effect, the ventilation conditions are not suitable to transport the smoke to a desired direction or exit. The critical velocity has become in one of the prime criteria for the designing of ventilation systems, especially in tunnel section [15]. In this study, the Kennedy model (Equations (1) up to (3)) were used to calculate the critical velocity in the subterranean scenario, where the value of the critical velocity is determined as a solution of the three equations of the Kennedy model [16-19].
|
|
(1) | |
|
|
(2) | |
|
|
(3) |
For the model, is a dimensionless constant value given by Equation (3), the Froude number considered for the calculation takes a value of 4.5 according to [20-22] and is a dimensionless slope factor; the average burning temperature was °K (96.2°C) which resulting values corresponds to the ones presented in [23]. The 5MW fire source was considered according with [24,25], and the remaining values considered for the critical velocity calculation are shown in Table 2 [26].
| Parameter | Value |
| Gravity acceleration (g) | 9.81 |
| Tunnel height (H) | 5.2 m |
| Slope | 0 % |
| Air density () | 1.176 |
| Specific heat of air (Cp) | 1.007 |
| Transverse section area (A) | 41.6 |
| Air temperature () | 300.15 °K (97 °C) |
| Critical velocity (Vc) | 1.464 |
3. General formulation
3.1. Theoretical analysis implemented in FORTRAN
The present analysis is based on the pressure-velocity coupling method, known as vorticity-stream function. The governing equations for the analysis consider an incompressible and Newtonian flow (2D), the mass conservation and momentum balance are given in Equations (4) and (5). The analysis considers a procedure step by step with respect to time, variable velocities (), density () and dynamic viscosity (μ):
|
|
(4) | |
|
|
(5) |
The vorticity - stream function () equations were discretized using the finite differences method where each node is used to describe the computer dominion (Equations (6) and (7)) [27]:
|
|
(6) | |
|
|
(7) |
Here, and corresponds to the velocities in the and directions (Equation (8)):
|
(8) |
After discretization of Equation (6), the following is obtained:
|
|
(9) |
|
|
(10) |
in which, the coefficients are:
|
|
(11) |
and for Equation (7):
|
|
(12) |
|
|
(13) |
The coefficients are:
|
|
(14) |
The model was constructed by considering a rectangular shape with 50 divisions in width and 275 divisions in length representing the top view of the passenger platform, the discretization was defined by considering a regular mesh with an equivalent and of 0.2m. This value was obtained by considering a physical real dimension of 10.5m for the width and 58m for the length of the model and used for the analysis of case 1. On the other hand, the resulting Reynolds number was in this case .
3.2. Boundary conditions in the theoretical model implemented in Fortran
Figure 2 (a) shows the distribution of boundary conditions in the 2D model (case 1). The resulting mesh arrangement is shown in Figure 2 (b). The figure represents the top view of an idealized duct; the control area, it is represented by a horizontal layer crossing along the center of the passenger platform. The location of each boundary condition is applied on each side by considering the Thom formulation and an idealized velocity profile [28].

|
| (a) |
|
| (b) |
| Figure 2. Top view of the theoretical model. (a) Boundary conditions applied to the FORTRAN model. (b) Resulting mesh |
3.3. Boundary conditions in ANSYS-FLUENT
This analysis (case 2) was carried out only to observe the flow stream along the platform at the critical velocity and compare with case 1. It considers the Finite Volume formulation allowing the discretization and solution of the differential equations. The resulting 3D model is shown in Figure 3, it is composed by a large rectangular shape representing the passenger platform, and four rectangular blocks were used to represent the natural ventilation ports. Another three slender blocks (tilted) were used to represent the stairs. The location of the areas connected to atmospheric pressure were identified as condition type 1. These includes the natural ventilation ports and passenger accesses. For the type 2 condition, 1.46m/s of air velocity was applied at the end of the tunnel (left side).
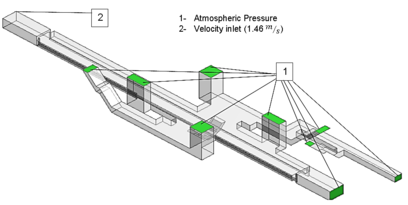
|
| Figure 3. Boundary conditions applied to the 3D ANSYS-FLUENT model |
Different mesh methods were tested until an excellent mesh quality range (qualification) was obtained according to [29]. The resulting model contains 284,816 nodes and 247,974 brick type elements as shown in Figure 4.
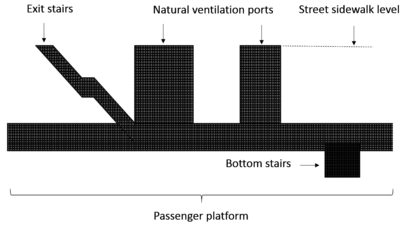
|
| Figure 4. Resulting CFD mesh, lateral view of the mesh showing the location of the exit stairs, the natural ventilation ports and the bottom stairs |
Table 3 shows the main parameters considered for the ANSYS-FLUENT simulation.
| Name | Selection/Value |
| Solution type | Pressure based |
| Velocity formulation | Absolute |
| Viscous model | k-ε standard |
| Air density | 1.164 kg/m |
| Dynamic viscosity | 1.86 e-05 kg/m.s |
| Inlet velocity | 1.464 m/s |
3.4. Boundary conditions in FDS
Fire Dynamic Simulator (FDS) was used to simulate the behavior of the calculated critical velocity in the platform [30-32]. The CAD modelling for this case was created considering the same dimensions of the previous case and the resulting model is shown in Figure 5. In this model, three case studies were considered, one was used to verify the development of the critical velocity named case 3. Case 4, includes the fire source in free motion and case 5 includes the fire source and the application of the critical velocity (location 2).
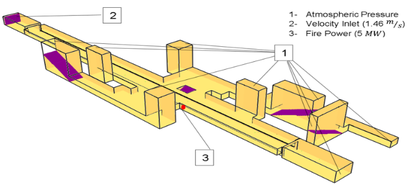
|
| Figure 5. Boundary conditions applied to the 3D FDS model |
For the FDS meshing, the total number of rectangular cells was 2,474,693, a simplified view of the resulting brick mesh is shown in Figure 6 (a) isometric view and a close view in Figure 6 (b).
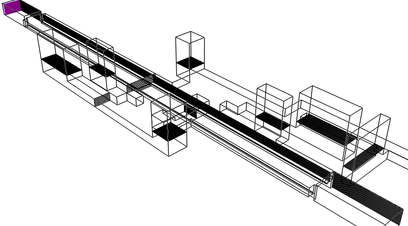
|
| (a) |
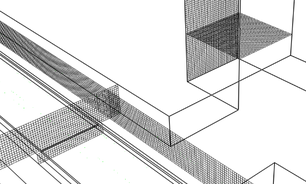
|
| (b) |
| Figure 6. Resulting mesh in FDS. (a) Isometric view of the passenger station. (b) Close view of mesh layers at the center of the passenger platform |
4. Results
The gathering of results was made by considering a horizontally oriented rectangular plane crossing along the model, located at 3.4m (height) from the floor level, in the middle of the platform, this plane was used to observe the flow contour plot similar to the one presented in [33] but in this case horizontally oriented.
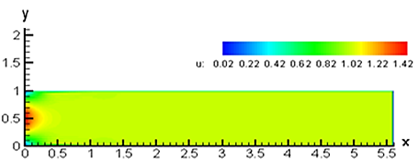
4.1. Case 1- Results obtained in FORTRAN
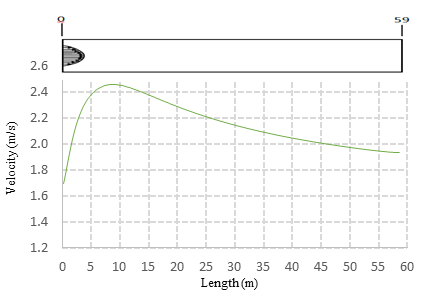
Figure 7 (a) shows a dimensionless scale of the resulting air velocity distribution. This results were scaled to the real dimensions and tracked through a crossing line at the middle of the plane as shown in Figure 7 (b).
|
| (a) |
|
| (b) |
| Figure 7. Velocity distribution along the idealized duct in FORTRAN. |
4.2. Case 2- Results obtained in ANSYS-FLUENT
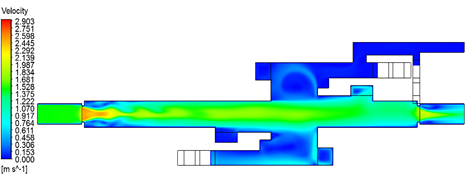
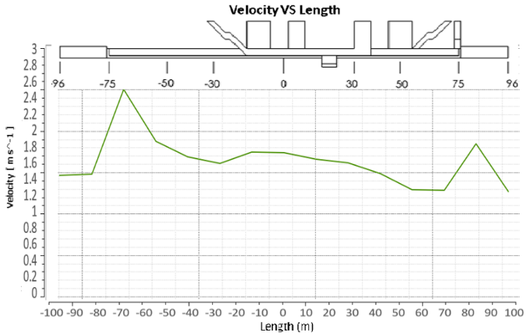
Figure 8 shows the resulting velocity contour obtained in ANSYS-FLUENT. The red frame represents the portion of the model analyzed in FORTRAN. An increment of the velocity is present at both ending sides of the model due to the reduction of the cross section area (-70m and 80m) between the tunnel and the passenger platform.
|
| (a) |
|
| (b) |
| Figure 8. Contour of velocity distribution (ANSYS-FLUENT) |
The results observed in Figure 8 shows that the maximum velocity is achieved at approximate 10m away from the location of the air injection. After that, the air reduces its velocity specially when achieving the passenger entrance area which is also in contact with the exit stairs. When the air crosses trough the natural ventilation ducts this velocity is also reduced. An interesting effect is then observed following this direction path. The air velocity suddenly increases when entering the tunnel at approximate 5m. This can be produced by the abrupt reduction of the cross section area between the passenger platform and the tunnel. This phenomenon indicates that special considerations have to be taken when stablishing the switching on and off of the mechanical ventilation fans because the architectural details of the construction directly affect the behavior of the flow.
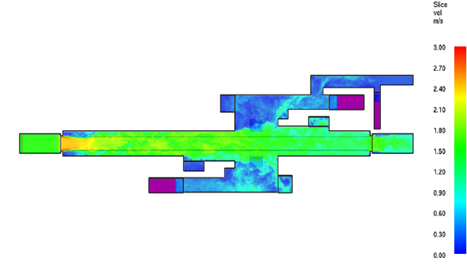
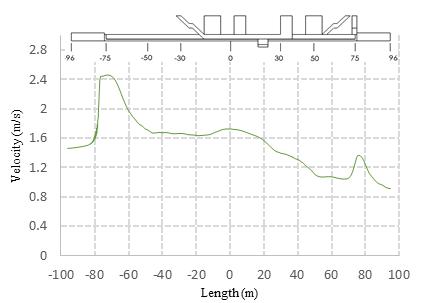
4.3. Case 3. Results obtained in FDS
Figure 9 shows the velocity contour obtained in FDS for case 3. The results present a similar behavior as in ANSYS-FLUENT.
|
| (a) |
|
| (b) |
| Figure 9. Contour of velocity distribution (FDS) |
4.4. Case 4 and 5. Comparison
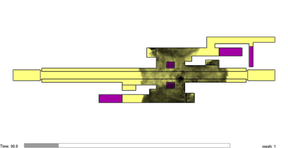
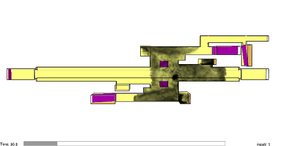
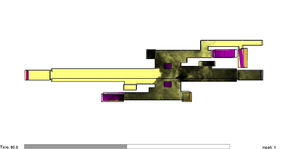
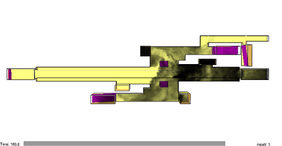
Case 4 corresponds to the simulation of the smoke evolution in free motion condition. The smoke moves only according to the influence of the temperature changes and atmospheric interactions. Case 5 presents the evolution of the smoke affected with an air velocity of 1.46 m/s. The evolution of the simulations is presented in Figure 10. From (a) to (c) corresponds to case 4 and figures (d) to (f) corresponds to case 5.
| Evolution of smoke for Case 4 | Evolution of smoke for Case 5 |
|
|
| (a) 30 sec. | (d) 30 sec. |
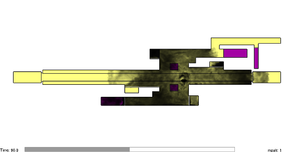
|
|
| (b) 90 sec. | (e) 90 sec. |

|
|
| (c) 180 sec. | (f) 180 sec. |
| Figure 10. Evolution of smoke transportation for cases 4 and 5. | |
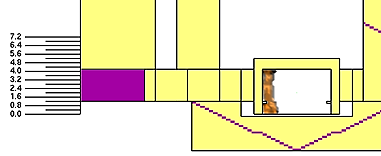
According to the calculation described in [34], the resulting flame height is in this case 6.07m which is higher than the top ceiling level as observed in Figure 11, and a safety distance for the passengers to be away from the fire source goes beyond 10m [35,36].
|
| Figure 11. Front view of the FDS model showing the flame height in contact with the ceiling, the scale on the left is a reference in meters |
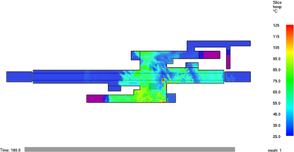
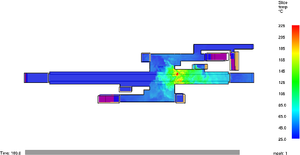
The difference of heat distribution for cases 4 and 5 after 3 minutes of fire evolution is presented in Figures 12 (a) and (b) for free motion, and (c) and (d) with the fans switched on. When the critical velocity is injected from the left side of the platform.
| Temperature distribution for case 4 | Temperature distribution for case 5 |
|
|
| (a) | (c) |
| (b) 180 sec. | (d) 180 sec. |
| Figure 12. Temperature distribution for cases 4 and 5 | |
The distribution of the heat is maintained above 35°C for more than 80m long in the free motion case with a maximum of 63°C. When the critical velocity is acting on the scenario, a notorious local increment in the temperature reaches more than 220°C. After approximately 10 meters this temperature drops to 100°C and 40meters away it falls down below 60°C. As in many fire situations, an increment in the air velocity can produce enrichment of the fire reaction.
5. Experimental setup
The use of the experimental setup is important because it allows to include more physical senses during the study of the phenomenon. Although the creation of the scaled model is not a straight way work, instead it has presented a series of challenges, because of that, a series of recommendations are described below.
5.1. Distribution and manufacturing of the setup
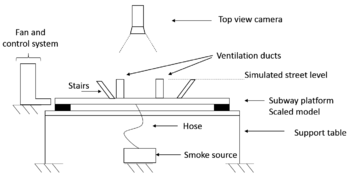
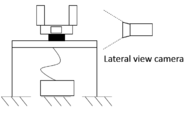
Figure 13 shows the distribution of the experimental setup, the scaled model is mounted on a support table. Apart from the 3D printing of the model, extra support equipment will be required to locate the camera systems depending on the shots or pictures that are required to obtain. Another important factor that must be carefully considered is the treatment of the filming (or photographs) in scaled scenarios. For this reason, an adequate lighting system will allow to obtain better pictures during the experiment. In this case, different attempts had to be made to obtain a suitable observation sequences.
|
|
| (a) | (b) |
| Figure 13. Distribution of the experimental setup and camera positions. (a) Lateral view. (b) Front view | |
For the creation of the scaled model, a series of modifications were considered in the original 3D CAD model in order to create the printable file. The modifications included the elimination of the ceiling and selected walls also. These layers will be next substituted with transparent glass to allow the observation of the smoke. The final CAD file is shown in Figure 14.
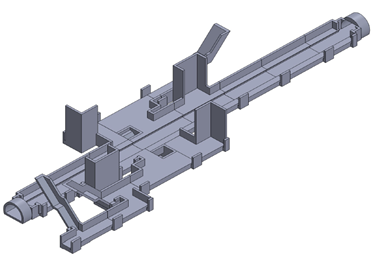
|
| Figure 14. 3D printable CAD file of the passenger platform |
It is possible to observe also that the model was divided in many sections to be finally assembled together. A series of mechanical supports were also included to provide rigid support and to hold in position the transparent layers. Previous prints were made to obtain the model shown in Figure 15.

|
| Figure 15. Previous 3D print for assembling validation |
In this case, this model allow us to validate the assembling process between all the sections and make corrections if needed. For convenience of this picture, the bottom stairs were located on top of the model upside down (number 11 in the picture). Once the entire model was validated, a 1:100 scaled model was finally printed. It is recommended to create a numbered map and list of all the pieces to avoid confusion during the assembling. In this form, the model can be easily transported to a preferred location for the experiments. Figure 16 shows the resulting assembled model, now the bottom stairs are properly located at the bottom face of the model.

|
| Figure 16. Resulting model for the experimental observations |
Finally, the transparent layers of the ceiling were installed. Figure 17 shows the final scenario constructed for the experiment. Prior to the experiment it was verified the room temperature (21°C), that there were no smoke leaks around the model and no external air currents also. An LCD digital gauge meter measure anemometer (GM8908) together with a regulated power supply connected to the fan motor were used to control the velocity of the air injected to the scaled model. After several trails, a velocity of 0.245 m/s was achieved. This value was calculated by using the critical velocity equation but replacing the corresponding scaled values (area, height, fire power, etc.).

|
| Figure 17. Final scenario constructed for the experiment |
5.2. Captured shots of the smoke
Besides of the top views captured during the experiments, a close lateral view in the location of the smoke source is also considered and presented in Figure 18. In this case, the ceiling reflect is observed on the top side of the picture. This is one of the issues that can appear during the close-up shots and have to be identified during the interpretation of results.

|
| Figure 18. Lateral view in the location of the smoke source |
5.3. Smoke displacement in free motion
Once the smoke has been injected into the setup, a free displacement of smoke was allowed. After 60 seconds, the internal equilibrium of the system was clearly achieved generating a flow pattern like the one shown in Figure 19. In the right side of the figure, the tendency of the smoke to move out of the platform in the same ventilation duct as the one observed in the FDS simulation can be observed.

|
| Figure 19. Top view of the flow of the smoke inside the platform after 60 seconds |
5.4. Smoke displacement with fans switched on
In Figure 20 (a) a top view of the smoke movement was captured when the fans were switched on. This is compared with the result obtained in the FDS simulation in Figure 20 (b). Similar displacement of the smoke was observed in both scenarios showing that the smoke leaves out in the same ventilation duct despite of the differences appreciated between the scaled model and the simulation.

|

|
| (a) | (b) |
| Figure 20. Top view of the comparison of smoke displacement between (a) the scaled scenario and (b) the FDS simulation when the equilibrium flow pattern was achieved | |
Figure 21 shows a lateral close view in the smoke emission zone in two different cases, a) when the fans are turned off and b) when the fans are turned on.

|

|
| (a) | (b) |
| Figure 21. Lateral view of the comparison of smoke displacement between (a) fans off and (b) fans on | |
Several differences with respect a real scenario can be observed also. For example, in a real fire source, the temperature of hot gases can maintain the smoke plume close to the ceiling for a longer distance than the one observed in picture 21 (a). The smoke displacement on the bottom stairs is another important difference. According to the fire source location, there exist the possibility of the passengers to use this bottom stairs to evacuate towards the opposite side of the platform. In the experiment the presence of smoke was observed there creating a dangerous situation in which passengers taking the bottom stairs could be facing the presence of smoke on top and bottom sides of this particular route as observed in the simulations.
7. Discussion
In Figure 10 (a) which corresponds to 30 seconds in the simulation, the smoke moves enough to reach the closest ventilation duct and leave the platform, which corresponds similarly in the experimental setup. There, the smoke starts to leave the platform in the same duct after 40 seconds from the beginning of the emission. It was observed that, even when the smoke reaches the same longitudinal distance in a similar time, it took at least 10 more seconds to the smoke of the experiment to ascend through the ventilation ducts, due to the wall roughness and size relation between simulation and experiment and this an important drawback to consider. Likewise, the reduced dimensions of the setup have an important influence in the temperature of the smoke. In the simulation, the smoke travels close to the ceiling of the platform and in the experimental setup, the smoke travels close to the floor which can be observed by comparing Figure 11 with Figure 21 (a). After 180 seconds of simulation, most of the smoke presents stagnation in the platform. In the experimental work, this was also observed even before the 180 seconds. The stagnation continued with the same behaviour for more than 5 minutes. The amount of smoke leaving the platform in both analyses of free motion is not enough to identify a smoke-free route towards the exit stairs. When the ventilation fans were switched on in the simulation, no flashback was observed but in the experimental setup, this behaviour is difficult to observe because the amount of air enclosed in the model is very sensitive to the smallest changes of air movements. The amount of smoke being emitted and the velocity of air injected to the model are two main sensitive variables not easy to control and they can create totally different flow patterns inside the platform.
The development of the 3D printed setup combined with computer simulations, allows to have better interaction with the phenomena but also with the development of emergency procedures. The implementation of a contingency plan is complex and expensive because it requires the time of coordinated interaction with different specialized personnel. For example, one of the initial steps during an emergency contingency considers the communication procedure between the security personnel and to the passengers advising the need of evacuation. It requires the interaction of internal and external groups affecting not only the subterranean service but also (in the case of Mexico City) the activation of the external emergency transport service, which can face issues related to the urban traffic or sudden obstructions of the streets [37]. Another important step in emergency contingency is related to the evacuation process. It would be easy to generate external obstructions in the streets near the stations during the evacuation process. External groups like fire fighters, police patrols, ambulances, etc., require in just that moment a free access to the stations. Mistakes in this procedures can conduct to several injuries or demands to the transport service. The setup helps also to create a better understanding of the subterranean distribution of the building. It reduces the chance to have situations in which, the emergency personal get lost inside the subterranean installation specially in long transfer platforms or the situations in which the arrival of the crew is not the one expected for example in an opposite or different doorway of the same platform. The amount of people on each platform, agglomeration of people at peak hours, size and complexity of the station, internal and external accessibility to the platform, location of extinguishers, etc., are elements that must be discussed and studied before the appearance of the emergency situations. Better designed 3D scaled models are a suitable complement because they create an interactive tool in which several crew members can observe and discuss about common topics and to identify weaknesses, strengths, opportunities, and threats of previously designed contingency plans. A wide variety of analysis scenarios can be observed in a very short time by changing the location of the smoke source (hose location) and probably not only for fire contingency. Several future work implementations can be applied in the setup from sophisticated control systems to special illumination for pattern recognition, image analysis algorithms, thermography or other technologies for intelligent support of firefighters that can be implemented also in real platforms.
8. Conclusions
According to the simulation, 1.46m/s is required to produce adequate smoke transportation of the 5MW fire source; no backlash was observed. This was an idealized case in which the velocity of air can be altered for example by the presence of the piston effect produced by trains traveling along the tunnels. These results consider just a limited case of study, for example in real cases, an increment of the velocity caused by external factors could produce an increment in the combustion also due oxygen enrichment towards the fire source. The results presented here correspond qualitatively to the ones presented in the literature with differences related to the power of fire considered in each investigation. The time it takes the smoke to occupy the entire platform can be used to calculate the available time the passengers have to evacuate the platform, in these situations the critical velocity plays an important role for the transportation of the smoke.
Acknowledgements
Authors acknowledge the Instituto Politécnico Nacional (IPN) and the Consejo Nacional de Ciencia y Tecnología (CONACYT) México for the support provided for this academic research.
References
[1] Li Q., Deng Y., Liu C., Zeng Q., Lu Y. Modeling and analysis of subway fire emergency response: An empirical study. Safety Science, 84:171–180, 2016.
[2] Gao R., Li A., Zhang Y., Luo N. How domes improve fire safety in subway stations. Safety Science, 80:94–104, 2015.
[3] Kang K. A smoke model and its application for smoke management in an underground mass transit station. Fire Safety Journal, 42:218–231, 2007.
[4] Tsukahara M., Koshiba Y., Ohtani H. Effectiveness of downward evacuation in a large-scale subway fire using Fire Dynamics Simulator. Tunnelling and Underground Space Technology, 26:573–581, 2011.
[5] Luo N., Li A., Gao R., Tian Z., Hu Z. Smoke confinement utilizing the USME ventilation mode for subway station fire. Safety Science 70:202–210, 2014.
[6] Zhilei W., Min H., Dayong X., Xuhai P. Simulation research on human evacuation in subway with a single point fire scenario. Procedia Engineering, 84:595–602, 2014.
[7] Roh J.S., Ryou H.S., Park W.H., Jang Y.J. CFD simulation and assessment of life safety in a subway train fire. Tunneling and Underground Space Technology, 24:447–453, 2009.
[8] Wang j.H., Yan W., Zhi Y., Jiang J.C. Investigation of the panic psychology and behaviors of evacuation crowds in subway emergencies. Procedia Engineering 135:128–137, 2016.
[9] NFPA 130: Standard for Fixed Guideway Transit & Passenger Rail Systems. 2007 Edition.
[10] Roh J.S., Ryou H.S., Park W.H., Jang Y.J. CFD simulation and assessment of life safety in a subway train fire. Tunnelling and Underground Space Technology, 24:447–453, 2009.
[11] Rie D.H., Hwang M.W., Kim S.J., Yoon S.W., Ko J.W., Kim H.Y. A study of optimal vent mode for the smoke control of subway station fire. Tunnelling and Underground Space Technology, 21:300–301, 2006.
[12] Zhang S., Yao Y., Zhu K., Li K., Zhang R., Lu S., Cheng X. Prediction of smoke back-layering length under different longitudinal ventilations in the subway tunnel with metro train. Tunnelling and underground space technology, 53:13-21, 2016.
[13] Zhang S., Cheng X., Yao Y., Zhu K., Li K., Lu S., Zhang R., Zhang H. An experimental investigation on blockage effect of metro train on the smoke back-layering in subway tunnel fires. Applied Thermal Engineering, 99:214–223, 2016.
[14] Weng M., Lu X., Liu F., Shi X., Yu L. Prediction of backlayering length and critical velocity in metro tunnel fires. Tunnelling and Underground Space Technology, 47:64–72, 2015.
[15] Li Y.Z., Lei B., Ingason H. Study of critical velocity and backlayering length in longitudinally ventilated tunnel fires. Fire Safety Journal, 45:361–370, 2010.
[16] Kashef A., Yuan Z., Lei B. Ceiling temperature distribution and smoke diffusion in tunnel fires with natural ventilation. Fire Safety Journal, 62:249–255, 2013.
[17] Chow W.K. On smoke control for tunnels by longitudinal ventilation. Fire and life safety, Tunnelling and Underground Space Technology, 13(3):271–275, 1998.
[18] Wu Y., Bakar M.Z.A. Control of smoke in tunnel fires using longitudinal ventilation systems - a study of the critical velocity. Fire Safety Journal, 35:363-390, 2000.
[19] Chen F. Smoke propagation in road tunnels. Applied Mechanics Reviews, 53(8):207-218, 2000.
[20] Kennedy W.D., Gonzalez J.A., Sanchez J.G. Derivation and application of the SES critical velocity equations. Transactions-American Society of Heating Refrigerating and Air Conditioning Engineers (ASHRAE), 102 Pt 2, 1996.
[21] Giachetti B., Couton D., Plourde F. Smoke spreading analyses in a subway fire scale model. Tunnelling and Underground Space Technology, 70:233-239, 2017.
[22] Tang F., Li L.J., Dong M.S., Wang Q., Mei F.Z., Hu L.H. Characterization of the bouyant flow stratification behaviours by Richardson (Froude) number in a tunnel fire with complex combination of longitudinal ventilation and ceiling extraction. Applied Thermal Engineering, 110:1021-1028, 2017.
[23] Klote J.H., Milke J.A., Turnbull P.G., Kashef A., Ferreira M.J. Handbook of smoke control Engineering. Atlanta, ASHRAE, ICC, SFPE & NFPA, USA, 2012.
[24] Stefopoulos E.K., Damigos D.G. Design of emergency ventilation system for an underground storage facility. Tunnelling and Underground Space Technology, 22(3):293–302, 2007.
[25] Hurley M.J. SFPE Handbook of Fire Protection Engineering. 5th edition, Springer, USA, 2016.
[26] NFPA 502: Standard for Road Tunnels, Bridges, and Other Limited Access Highways. 2011 Edition.
[27] Patankar S.V. Numerical heat transfer and fluid flow. Series in Computational Methods in Mechanics and Thermal Sciences, McGraw-Hill, USA, 1980.
[28] Thom A. The flow past circular cylinders at low speeds. Proc. Roy. Soc. London, A 141, 651-669, 1933.
[29] ANSYS FLUENT Meshing User's Guide. ANSYS Inc., Release 15.0, USA, 2013.
[30] McGrattan K., Klein B., Hostikka S., Floyd J. Fire dynamics simulator user’s guide (Version 5). NIST Special Publication 1019-5, USA, 2007.
[31] Lei W., Li A., Tai C. The effect of different fire source locations on the environment of a subway station. Procedia Engineering, 205:3721-3726, 2017.
[32] Lei W., Li A., Tai C. The effect of heat release rate on the environment of a subway station. Procedia Engineering 205:3717-3720, 2017.
[33] You H.Z., Faeth G.M., An investigation of fire impingement on a horizontal ceiling. NBS-GCR-81-304, National Bureau of standards, Washington D.C., USA, 1981.
[34] Wang B. Comparative research on FLUENT and FDS’s numerical simulation of smoke spread in subway platform fire. Procedia Engineering, 26:1065–1075, 2011.
[35] Klote J.H., Turnbull J.A., Kashef P.G., Ferreira M.J. Handbook of smoke control engineering. Atlanta ASHRAE, 2012.
[36] Deng J., Ma L., Wang Z., Xing Z., Wang W. Simulation study on critical velocity of longitudinal ventilation tunnel fire. Procedia Engineering, 52:67–71, 2013.
[37] Flores-Herrera L.A., Sandoval-Pineda J.M., Silva-Rivera U.S., Tamayo-Meza P.A., Rivera-Blas R. CFD simulation of obstructed ventilation ports in a subway tunnel section. International Journal of Simulation Modeling, 16(3):386-398, 2017.
Document information
Published on 08/02/19
Accepted on 15/03/18
Submitted on 29/10/17
Volume 35, Issue 1, 2019
DOI: 10.23967/j.rimni.2018.03.005
Licence: CC BY-NC-SA license