Circular causality and indeterminism in machines for design

Abstract

Presenting a hard-to-predict typography-varying system predicated on Nazi-era cryptography, the Enigma cipher machine, this paper illustrates conditions under which unrepeatable phenomena can arise, even from straight-forward mechanisms. Such conditions arise where systems are observed from outside of boundaries that arise through their observation, and where such systems refer to themselves in a circular fashion. It argues that the Enigma cipher machine is isomorphous with Heinz von Foersters portrayals of non-triviality in his non-trivial machine (NTM), but not with surprising human behaviour, and it demonstrates that the NTM does not account for spontaneity as it is observed in humans in general.

Keywords

System boundaries ; Design ; Predictability ; Enigma

1. Background

From the inside, it can be challenging to determine the scope, shape and development of the field one is operating in. Are the frontiers of architectural design research static, unvarying limits? Or are the frontiers of architectural design research changing borderlines, shifting according to modes, depths and directions of enquiry? To what extent do its design and research aspects overlap, and to what extent are design and research comparable or compatible? Do design and research have enough in common to be approached as equals, rendering insights into one of them applicable to the respective other? Are they viable models or metaphors for one another, or are they too different to allow such analogies between them? Answers to these questions, of course, depend much on what is meant by design and by research.

Understandings of design and research, of their methods, tools and standards, diverge considerably in different contexts. The argument presented here addresses design, design tools and research methods in reference to systemic boundaries and circular re-entry, and with regards to the notion of determinability in order to shine a critical light on those instances where design and design research are approached in terms of purely linear cause and effect. It is shown that conceptualisations of design (research) in terms of (natural-scientific or computational) linear causality may be unduly limited.

The argument below draws parallels between the designing human mind and a mechanical (cipher) machine. This is not to say that the mind is like a mechanism, or that mechanisms can act in the ways human minds do. The point made is merely that minds and some mechanisms are characterised by circular re-entry, which, in both cases, leads to indeterminable behaviour, i.e. novelty. Neither circular causality nor indeterminism, however, is recognised by natural-scientific reasoning.

2. System boundaries, input, output and re-entry

Computer-aided architectural designing is an endeavour in which the boundaries of systems are crossed. “System” is understood here as whatever set of elements an observer considers to act together, following a common goal. An observer may choose to regard the components that make up a computer as a system. Similarly, an observer may choose to regard the organs making up the organism of a designer as a system, or consider the designer and the computer together as a system. With these different ways of looking (Weinberg, 2001 ), the imaginary boundary that circumscribes what is regarded as a system changes, and what is considered as a system lies in the eyes of the observer. Sometimes there are physical boundaries containing what is regarded as a system, such as the skin of a designer and the case of a computer but this is coincidental. Designer and computer together may be regarded as one system contained by an imaginary, but without a physical boundary. Patterns in the widest sense crossing the imaginary boundaries of systems are, depending on perceived direction, called inputs and outputs.

A common example of systems whose boundaries are crossed by incoming inputs and by outgoing outputs is the behaviourist-type stimulus-response structure of the kind shown on the left-hand sides of Figure 1  ;  Figure 2 . This structure offers convenience in modelling various systemic relationships not only by way of abstraction and of being broadly applicable. It is also conveniently compatible with common basic tools of rational modern thought such as linear logic and syllogistic reasoning. Humans are frequently described as systems which, prompted by input, produce output. And, typically, so are computers. Alternatively, although this happens less frequently, an observer may also choose to view multiple systems (inter)acting together as one system which responds to input by producing output. Human–computer interaction in CAAD may be viewed in this way, along the lines of the following statement by Bateson (1972, p. 317) : “The computer is only an arc of a larger circuit which always includes a man and an environment from which information is received and upon which efferent messages from the computer have effect.” Other examples in the design context include the interactions between members of a design team, and the interaction between a designer and his or her sketching (Fischer, 2010 , p. 612).

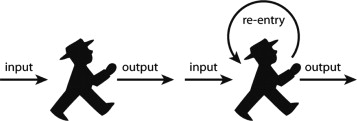
Figure 1. Human viewed as a linear stimulus–response system (left) and with the acknowledgement of circular self-reference (right).

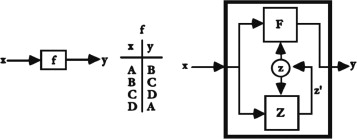
Figure 2. Trivial machine with truth table (left) and non-trivial machine (right), reproduced from Von Foerster (2003, pp. 310–311) .

Any of these systems – human, computer, human–human, human–computer and so on – is defined by an imaginary boundary projected by an observer. This imaginary boundary sets the system׳s interior apart from its exterior. If a human considers herself or himself as a system, then making (the interior self-affecting the exterior other) and learning (the exterior other affecting the interior self) constitute instances of outputs and inputs crossing boundaries. While cyclical relationships such as the ones observable in human–computer interaction are commonly dissected and broken up into pieces, it is uncommon to turn systems back on themselves to form closed loops. This is because modern culture appreciates systems which allow description in terms of linearly-causal logic and which offer predictable control in terms of defined states. Closed loop structures tend to be appreciated only where they facilitate control, typically in the form of negative feedback and error correction or of stable oscillation. Unpredictable fluctuations and out-of-control patterns tend to be unwelcome outside of artistic and experimental domains. They are rarely the subject of formal analysis, and attempts at their formal analysis are hampered by the linear nature of common tools of description. Nonetheless, the (designing) human mind must be acknowledged not merely as a static stimulus-response system, as a static translator between inputs and outputs, but as a system whose input channels are subjected to its own output. Contrary to the technologies it currently tends to develop, the human mind is subjected to what it itself produces and is thus changed by its own performance (see Figure 1 ).

As stated above, design, being at least in part out-of-control (Glanville, 2000 ), involves not only linear but also circular causality – between design team members, between designers and their sketches etc. (Fischer, 2010 ). Common algorithmic devices for generative, computer-based design likewise involve circular feedback such as the potentially circularly-causal relationship between any two cells in a cellular automata system, or the self-referential relationships in L-systems, in evolutionary algorithms and so on. Input–output operations can leave traces inside of (designing) systems equipped with suitable “internal state” memory. Such systems can therefore, in effect, become different systems through each of their operations. And through the interaction between input and/or output with given internal states, such machines can behave unpredictably. Systems of this kind will be explored and illustrated in the following, with special attention to the limits of purely mechanical or digital implementations in the design context.

The loop which is formed when human articulations feedback as an input to the human creative process allows expressions of the mind to re-enter into the mind where they may leave increasingly stable traces (Glanville, 1997 , p. 2), i.e. memory. This view was substantiated in Von Foerster (1950) ׳s interpretation of a previous study of human memory. In that previous study subjects had been asked to memorise random, meaningless syllables and to re-count as many of them as they could afterwards at regular intervals. Memory and progressive forgetting were shown to follow an exponential decay curve, which did not approach zero, but a number of syllabi greater than zero that the subjects were increasingly more likely to remember permanently. Von Foerster explains this with the human being capable of both input (listening) and output (speaking), and hence circular closure and re-entry of articulations. Thus, every re-counting of a remembered syllable (output) is also a new input which reinforces what is known. Repeated recalling thus leads to an eventually stable subset of remembered syllables.

Von Foerster (2003, p. 311) illustrated processes of this nature using his notion of the trivial machine (TM), which he juxtaposed to his notion of the non-trivial machine (NTM). Somewhat comparable to Turing׳s (1937, p. 231ff.) proposal of the Turing Machine, von Foerster describes both the TM and the NTM as minimal hypothetical machines not for the purpose of implementation, but for the purpose of illustrating ideas. He describes both TM and NTM as basic input–output (stimulus-response) systems, each being a mechanism connected to an input channel and an output channel. The TM predictably translates inputs into corresponding outputs, so that an external observer can, after a period of observation, establish clear causal relationships between possible inputs and resulting outputs, for example in the form of a “truth table” as shown on the left of Figure 2 . A complete truth table is a reliable model for predicting the TM׳s output responses to given inputs, irrespectively of how long the machine has been in operation. In contrast, the NTM contains means to memorise a machine state (labelled z on the right of Figure 2 ). This state co-determines the machine׳s output together with its input. At the same time, the state may change with each input–output operation. This results in a vast number of possible input–output mappings which can easily exceed the quantitative limits of what an external observer can determine analytically, i.e. derive predictive capabilities from Glanville (2003, p. 99) . The NTM׳s history of input–output translations can be said to leave traces in the machine, which in effect turns into a different machine through and for each of its own operations. An outside observer cannot easily establish a reliable truth table by which outputs resulting from given inputs can be predicted.

Von Foerster׳s presentations of the NTM changed slightly from presentation to presentation, in particular with regards to that which brings about state changes in the machine. According to Von Foerster (1970, p. 139) the transitions of internal states depend on the machine׳s previous state and on its input, according to Von Foerster (1972, p. 6) internal state transitions depend on the machine׳s previous output, and according to Von Foerster (1984, p. 10) internal state transitions depend again on the machine׳s previous state and on its input.

Another description of non-triviality offered by von Foerster is the image of a schoolboy who displays non-trivial behaviour by responding to a maths or history problem with an unexpected answer. Similar to the mechanistic portrayal of non-triviality, the anthropomorphic portrayal changes slightly from one presentation to the next. In Sander (1999) and Pruckner (2002) the schoolboy responds to the problem “2 times 2” with the result “green”. In Von Foerster (2003, p. 311) he responds to problem “2 times 3” with the answer “green” or with the answer “Thats how old I am”. In Von Foerster (1972, p. 6) he responds to the question When was Napoleon born? with the answer “Seven years before the Declaration of Independence.” Von Foerster deplores the state of educational systems in which school children who offer such unexpected responses are deemed insufficiently trivialised, and therefore trained more until they produce the desired answers reliably.

The distinction between the trivial and the non-trivial behaviour deserves attention in general and in particular in our field because in every encounter the choice between both metaphors determines much of the ethical stance one takes towards others, tools, buildings etc. Virtually all of our science and technology corresponds to the principle of the trivial machine in the sense that a given input is expected to always reliably lead to the same output. Multiple computers are, put simply, expected to always have the same response in the face of the same task or problem. Stereotypical engineers, managers and representatives of other professions, be they allied with architecture or not, are likewise expected to arrive at the same results when presented with the same input. In the education of these professions this aspiration to the ideal of the trivial machine is enforced with the principle of scientific repeatability. Multiple stereotypical engineers tasked with the same structural analysis problem, or the same engineer tasked with the same structural analysis problem twice should reliably arrive at the same results, i.e. fulfil expectations predictably and reliably. Briefing multiple architectural designers with the same project brief, in contrast, makes sense only if variety among multiple responses is desired. Briefing the same architectural designer with the same task twice will also lead to two different outcomes because the second time around, one would be facing a different architect one who was subjected to her/his own first design process and outcome, which left traces in her/him and thus changed her/him. In this sense, and in the sense of Heraclitus statement that “No man ever steps in the same river twice, for it׳s not the same river and he׳s not the same man”, one cannot design (or learn, for that matter) the same thing twice.

Von Foerster explains convincingly that neither NTM nor schoolboy permits analytical determination from the perspective of a human observer. He does not, however, address the possible conclusion that NTM and unpredictable human are therefore to be taken as isomorphous. He calls for humans to be perceived as non-trivial (Von Foerster, 1972 , p. 6), without addressing the question of whether the NTM would be capable of giving the answers given by the schoolboy.

3. Variety and automated production

Surprising variety (in the cybernetic sense: number of choices available) and reliable predictability are, paradoxically both for better and for worse, essential human needs and human characteristics (Fischer, 2010 , p. 611). We experience this paradox in numerous contexts in which we enjoy both stimulating variety in expression as well as economic and organisational benefits of uniformity. In shaping our products and environments, the advantages offered by predictably uniform (hence interchangeable) prefabricated components famously gave rise to assembly-line based production since the early days of industrial production; and it is part and parcel of architectural construction today. Having been introduced to architecture with uniform building elements, prefabrication brought along with it sameness at the scales of component repetition. At small scales of component repetition, such as that of clay bricks (Fischer, 2007 ), interchangeability may be appreciated for allowing flexibility and subtle texture. At larger scales such as that of floor plans or whole buildings as found in Platenbau developments (Hopf and Meier, 2011 ), repetitive sameness is criticised for being monotonously boring or even socially detrimental. Aiming at repeatable input–output relationships, early computer applications in our field focussed on predictable input–output relationships, leading to criticisms of applying the computer as a “fancy drawing board” (Dantas, 2010, p. 161 ) and of valuing it as an equivalent to “an army of clerks” (Alexander, 1965 ). In architecture and in other industries, there are now tendencies acting against monotonous sameness. Referred to as customisation approaches (Gilmore et al., 1997 ), these tendencies are increasingly aided by computational (generative, parametric etc.) techniques that allow increasing of variety via circular feedback. The development of typography follows a similar pattern. Moveable type introduced economic benefits along with monotonous sameness to book printing. Using type wheels and the like, typewriters, teletypes and computer printers achieved similar predictable sameness and cost-efficiency also in documents produced in small numbers. Contextual variations such as ligatures have been introduced to mechanical typesetting. Some contemporary computer typefaces go further and achieve “organic”, “random” or “handwritten” appearances by introducing randomness to curve paths or by providing sets of alternative glyphs for the same characters.

4. Enigma cipher machine

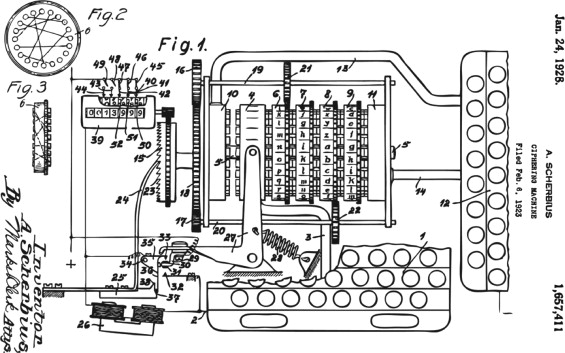
With these working principles, the NTM is essentially isomorphous with the Enigma machine (Scherbius, 1928 ; Fischer, 2012 ) which was used to encipher and to decipher communications in Nazi Germany before and during World War II (this relationship between NTM and Enigma machine was previously suggested by Tessmann, 2008 , p. 55). Looking somewhat like a typewriter, the Enigma machine was used to encrypt and to decrypt text messages by substituting letters with a replacement mechanism that changes systematically as the machine is used. It takes its input via a qwertz keyboard (label 1 in Figure 3 ) with typically 26 keys, and offers its output via typically 26 lamps which are also arranged in a qwertz layout (label 12 in Figure 3 ). Pressing any key closes an electrical circuit which travels across a set of cylindrical rotors each of which contains a different irregularly-connected wiring, leading to the illumination of a lamp with a different letter. Before it closes a circuit each keystroke also results in the change of the internal state of the machine by way of rotating one or more of the rotors by one twenty-sixth of a full rotation so that the combined irregular wiring changes for each letter that is enciphered or deciphered. Additionally, a plug board allows the swapping of pairs of letters using patch cables. Much like von Foerster׳s NTM, the Enigma machine translates input characters to output characters, with every translation resulting in a re-mapping of the set of accepted input characters to the set of available output characters. The Enigma machine demonstrates that the NTM is implementable as a physical device, which is very challenging to determine analytically from the perspective of an external observer.

Figure 3. Schematic diagram of Enigma machine (from Scherbius, 1928 ).

Pressing a key will activate one of the lamps, apparently at random, according to selection of cylinders and their current orientation. Additionally, each keystroke results in the rotation of the first cylinder by one of 26 rotation positions, after 26 keystrokes, the second cylinder will also rotate by one position and so forth, somewhat in the fashion of the digit cylinders in a mechanical odometer. Thus, each keystroke results in a new wiring between keyboard and lamps coming into effect for the subsequent keystroke. In other words: use of the machine leaves a trace in it, changing the wiring of the machine, and hence the cipher, progressively. (Due to the symmetrical setup of the wiring going into the cylinders and back out through the same cylinders, the same machine setup can be used both to cipher and to decipher. The identical setup is achieved by referring to a secret timetable based code book of which both ends must hold a copy.) To an outside observer the input-to-output mapping of the Enigma machine is extremely difficult to determine, while it is perfectly determinable to those who developed it and who have a good understanding of its setup and inner workings. With inner workings of this kind the Enigma machine shares key characteristics of designing, making it a useful metaphor for the purpose of showing how designing is a relatively straight-forward process when viewed from the inside perspective but mysterious and wonderful when viewed from the outside perspective.

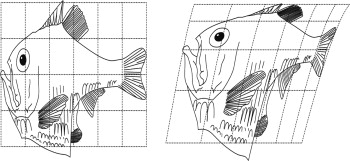
Figure 4. Fish transformations based on Thompson (1992, pp. 1053–1093) .

5. A typographical metaphor

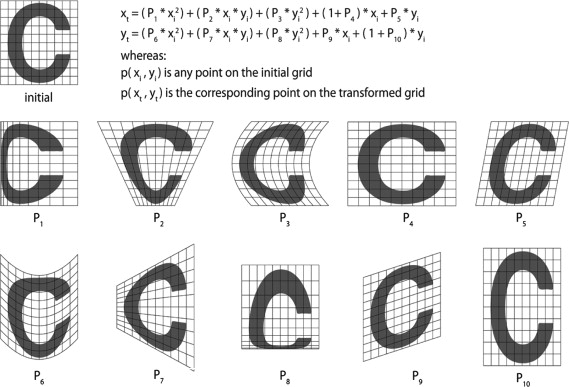
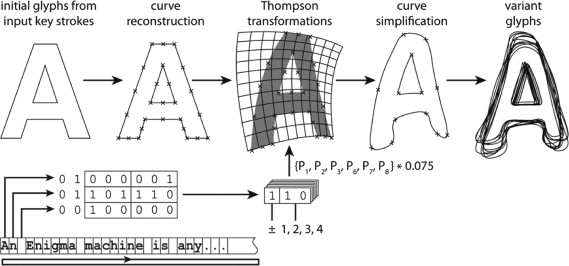
The illustration presented here is a piece of software predicated on the Enigma machine and implemented as a VBA script controlling Rhino3D. Glyph renderings of characters input via keyboard are distorted dynamically and individually, with the use of a “private key” string stored inside the system. Somewhat akin to the (de)ciphering process of the Enigma machine, each key that is typed, modelled, transformed and rendered changes the internal state of the system (leaves a trace in it) to change the way the following glyph is distorted. In contrast to common computer typefaces, glyphs of same characters are unpredictably variant. As a point of departure, the system uses the typeface Helvetica to derive initial glyph outline curves for each typed character. The system then applies a combination of six (Thompson, 1992 ) transformations (see Figure 5 ) to these outline curves.

Figure 5. Quadratic functions and Thompson transformations based on parametric variation.

Thompson transformations (parametric “warping” based on quadratic functions, Wilkinson, 2005 , pp. 223–224) as illustrated in Figure 3 allow positive and negative transformations based on parameters P1–P10. Of these, the presented generative system uses the six parameters P1, P2, P3, P6, P7 and P8. Parameters P4, P9 and P10 are ignored while P5 can be toggled manually, providing an “italics” option. Parametric input for the six Thompson transformations performed by the system is derived from the ASCII bit patterns of characters of a “private key” string, which is “rotated” by three characters with each input keystroke. Any ASCII string of any length can be used for this purpose (Figure 6 ).

Figure 6. Key operations of glyph-variation based on “private key” string.

Once a key is pressed, the first three characters of the “private key” string are converted to their respective ASCII bit patterns and the six last bits of each are used to produce two factors out of the set −4, −3, −2, −1, 1, 2, 3, 4, which are multiplied with a scaling factor (0.075 gives a good effect) to produce a total of six parameters (see Figure 4 ).

Following parametric Thompson transformations, the resulting glyph outline curves are simplified by reducing their numbers of control points, resulting in casual looking, “blobby” glyphs. These are variant with identical characters being shown as different glyphs (see the bottom line of Figure 7 ). Overall, the resulting types are nevertheless largely consistent and recognisable as members of the same typographical style, which I call Polymorph. The generative system includes a rudimentary automatic kerning function, the performance of which is also visible in the bottom line of Figure 7 . The top line of Figure 5 shows the typeface Helvetica. The middle line shows the hand-drawn, Helvetica-inspired typeface YWFT HLLVTKA Round, each character of which looks irregular, while identical characters are rendered with the same glyphs.

Figure 7. Helvetica (top), YWFT HLLVTKA round (middle) and polymorph (bottom).

Just as the Enigma machine׳s cipher output is enigmatic and unpredictable to outsiders such as wartime enemies, the glyph transformations generated by the described system are unlikely to be predictable to outsiders of the system. Nevertheless, both systems are perfectly determinable and appear straight-forward to those aware of both systems׳ setups and of the ways in which the performances of both systems leave traces within them, changing their internal states, thus in effect leading to new inner workings with each operation. Designers, articulating and (re-)considering ideas can be seen as embodying a similar, non-trivial re-entry structure which, similarly, can appear either surprising and unpredictable or straight-forward and traceable depending on an observer׳s inside or outside perspective.

6. Observations

Some processes are linear, predictable and seem causal while others involve circularity appear unpredictable. The difference can be shown with the distinction between the trivial machine and the non-trivial machine. Like the Enigma machine, instances of designing can be viewed as circular systems (Glanville, 1992 ; Fischer, 2010  ;  Gänshirt, 2011 ) which display the structure and quality of the non-trivial machine. It was demonstrated here that circular re-entry affecting the internal state of a system is a sufficient condition of indeterminability, and for systems characterised by circular re-entry to transcend the narrow notion of linear cause and effect typically applied to (digital) technology and natural-scientific research. The wonder and surprise offered by indeterminable systems depend on their interior workings evading observation (Fischer, 2008 ). Design is, on the inside, concerned with what is unpredictable to outsiders. It hence corresponds to the non-trivial machine. Science, always on the outside, is concerned with prediction and hence corresponds to the trivial machine. This poses a challenge to scientific researchers aiming to research into designing objectively, somewhat comparable to the challenge of cryptography that leaves outsiders mystified while insiders understand. Design processes can be appreciated and understood on the subjective inside. Objective scientific description, though, is required to approach design from the outside.

Von Foerster׳s TM, his NTM, and the Enigma machine share the trait that, the question of predictability notwithstanding, the varieties of acceptable inputs, of available internal states, and of their sets of possible outputs is predefined by the makeup of the machine in question. These varieties are finite and do not change through the machines operations. The Enigma machine, for example, can neither be expected to cope with unforeseen inputs that are not supported in its set of acceptable input characters, nor to spontaneously transcend its set of available outputs to include for example Chinese characters, let alone previously unknown characters. Similarly, neither the NTM, nor the TM, can be expected to accept and to process inputs other than those these machines were set up to accept and to process or to offer outputs other than those they were designed to offer.

The human mind is different in this respect (and obviously in other respects, too¹ ). It has the capability of accepting previously not accepted inputs, and of expressions beyond the range of expected outputs as illustrated by the statement “2 × 2=grün”. More overtly, nonetheless evident in human learning, the mind also modulates its repertoire of internal attitudes towards inputs it encounters, i.e. its range of internal states. In other words, our nervous system has the capability of amplifying the variety of ranges of inputs it accepts, of its internal states, and of outputs it can be expected to offer. The TM׳s, the NTM׳s and the Enigma machine׳s clearly specified, constant input, internal state, and output varieties are typical of digital technology (Fischer, 2011 ), which is developed and used precisely for the predictable control it offers, at the expense, as Glanville (2009, p. 119) argues, of variety. Fixes varieties in technical systems are established by a kind of observer (matchmaker) who intentionally brings system together to serve purposes by way of control (Fischer, 2011 ). The human mind, in contrast, can actively modulate these varieties. It can, for instance, refuse to answer a yes-or-no question in those terms or answer an arithmetic problem by naming a colour. Giving a human an arithmetic problem to solve implicitly aims to reduce that humans input and output variety to the language of arithmetic and numbers within which a response may then be evaluated. A humans concession to answer in terms of mathematics and numbers constitutes a reduction of that humans output variety. A surprising (i.e. substantially or formally incorrect) answer will then likely be dismissed as wrong, regardless of whether the contemplations that led to it have value. On such grounds Dostoyevsky׳s (2009, p. 25) underground man can be dismissed when he states: “I admit that twice two makes four is an excellent thing, but if we are to give everything its due, twice two makes five is sometimes a very charming thing too.”

Drawing a mutually-exclusive distinction between the trivial and the non-trivial, however, von Foerster places both his mechanistic and his anthropomorphic portrayal of non-triviality in the same category, suggesting that humans are a subset of, and hence isomorphous with, non-trivial machines. While the human nervous system and non-trivial mechanisms share some characteristics, they are set apart by others, rendering them not isomorphous. Mechanistic systems such as the Enigma machine, most critically, do not share the human capability to reduce and to amplify the variety of ranges of accepted inputs, of internal states, and of expectable outputs (to make new and to drop old distinctions). As a model for human inventiveness von Foersters mechanistic description of the NTM is therefore crude at best.

While at a theoretical level the argument presented here shines a critical light on those instances where design and design research are approached in terms of purely linear cause and effect, it also offers a path forward for future research into digital design tools and computational creativity: reduction and amplification of input and output channel variety are well within the scope of technical implementability (consider digital sound or image input and output based on different sampling rates and resolutions). As a next step in the presented line of enquiry, the potential of changing input and output channel variety in systems allowing for circular re-entry will be investigated with regards to the potential for novelty generation.

References

1. Alexander, 1965 C. Alexander; The question of computers in design; Landscape, 14 (3) (1965), pp. 6–8
2. Bateson, 1972 G. Bateson; Steps to an Ecology of Mind; University of Chicago Press, Chicago (1972)
3. Dantas, 2010 Dantas, J.R., 2010. The end of Euclidean geometry or its alternate uses in computer design. In: Proceedings of SIGraDi. Bogot, Colombia, pp. 161–164.
4. Dostoyevsky, 2009 F. Dostoyevsky; Notes from the Underground; Hacket, Indianapolis (2009)
5. Fischer, 2007 T. Fischer; Rationalising bubble trusses for batch production; Autom. Construc., 16 (2007), pp. 45–53
6. Fischer, 2008 T. Fischer; Obstructed Magic; W. Nakpan (Ed.), et al. , Proceedings of CAADRIA2008, Pimniyom Press, Chiang Mai (2008), pp. 609–618
7. Fischer, 2010 T. Fischer; The interdependence of linear and circular causality in CAAD research: a unified model; B. Dave (Ed.), et al. , Proceedings of CAADRIA2010, CUHK (2010), pp. 609–618
8. Fischer, 2011 T. Fischer; When is analog? When is digital?; Kybernetes, 40 (7,8) (2011), pp. 1004–1014
9. Fischer 2012 Fischer, T., 2012. Design Enigma. A typographicalmetaphor for epistemological processes, including designing, In: Fischer T. et al., (Eds.), Proceedings of CAADRIA 2012, Hindustan University, Chennai, 679–688.
10. Gänshirt, 2011 C. Gänshirt; Werkzeuge für Ideen; Birkhäuser, Basel (2011)
11. Gilmore et al., 1997 H.G. Gilmore, B.J. Pine II; The four faces of mass customization; Harvard Bus. Rev. (January–February) (1997), pp. 91–101
12. Glanville, 1992 R. Glanville; CAD abusing computing; B. Martens (Ed.), et al. , CAAD Instruction: The New Teaching of an Architect? eCAADe Proceedings, Barcelona (1992), pp. 213–224
13. Glanville, 1997 R. Glanville; A ship without a rudder; Ranulph Glanville, Gerard de Zeeuw (Eds.), Problems of Excavating Cybernetics and Systems, BKS+, Southsea (1997)
14. Glanville, 2000 R. Glanville; The value of being unmanageable: variety and creativity in cyberspace; Hubert Eichmann, Josef Hochgerner, Franz Nahrada (Eds.), Netzwerke, Falter Verlag, Vienna (2000)
15. Glanville 2009 Glanville, R., 2009. The Black Boox Vol. III: 39 Steps, Echoraum; Vienna.
16. Glanville, 2003 R. Glanville; Machines of wonder; Cybern. Hum. Know., 10 (3,4) (2003), pp. 91–105
17. Hopf and Meier, 2011 S. Hopf, N. Meier; Plattenbau Privat; 60 Interieurs, Nicolai, Berlin (2011)
18. Pruckner, 2002 Pruckner, M., 2002. 90 Jahre Heinz von Foerster. Die Praktische Bedeutung seiner Wichtigsten Arbeiten (DVD), Malik Managment Zentrum, St. Gallen.
19. Sander, 1999 Sander, K., 1999. In: Sander, K. (Ed.), Heinz von Foerster: 2×2=grün (CD), supposeé, Küln.
20. Scherbius, 1928 Scherbius, A., 1928. Ciphering Machine. US Patent No. 1.657.411.
21. Tessmann, 2008 Tessmann, O., 2008. Collaborative Design Procedures for Architects and Engineers (Ph.D. thesis), University of Kassel, Books on Demand, Noderstedt.
22. Thompson, 1992 D.W. Thompson; On Growth and Form; (The Complete Revised Edition)Dover Publications, New York (1992)
23. Turing, 1937 Turing, A.M., 1937. On computable numbers, with an application to the Entscheidungsproblem. In: Proceedings of the London Mathematical Society, vol. 42, Ser. 2, pp. 230–265.
24. Wilkinson, 2005 L. Wilkinson; The Grammar of Graphics; (2nd ed.)Springer, New York (2005)
25. Von Foerster, 1950 Von Foerster, H., 1950. Quantum mechanical theory of memory. In: von Foerster, H. (Ed.), Cybernetics: Transaction of the Sixth Conference, Josiah Macy Jr. Foundation, NY.
26. Von Foerster, 1970 H. Von Foerster; Molecular ethology, an immodest proposal for semantic clarification; G. Ungar (Ed.), Molecular Mechanisms in Memory and Learning, Plenum Press, New York (1970), pp. 213–248
27. Von Foerster, 1972 H. Von Foerster; Perception of the future and the future of perception; Instr. Sci., 1 (1) (1972), pp. 31–43
28. Von Foerster, 1984 H. Von Foerster; Principles of self-organization in a socio-managerial context; H. Ulrich, G.J.B. Probst (Eds.), Self-Organization and Management of Social Systems, Springer, Berlin (1984), pp. 2–24
29. Von Foerster, 2003 H. Von Foerster; Understanding Understanding; Springer, New York (2003)
30. Weinberg, 2001 G.M. Weinberg; An Introduction to General Systems Theory; Dorset House, NY (2001)

Notes

1. Obviously the differences between simple hypothetical or physical mechanisms and the human nervous system with all its complexity and subtlety are vast.