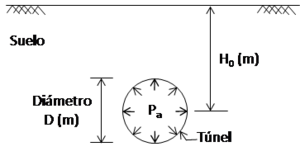Diseño de túneles usando Elementos Finitos 2D y 3D y la influencia de los parámetros mecánicos y geométricos para el diseño

ABSTRACT

In practice, tunnels design uses analytical methods and numerical models. The last methods are because tunnels need solutions that provide a high level of security given their complexity and civil use. In this paper the study of the influence of the geometric and the mechanical soil properties on the tunnel displacements is presented, when it is used the finite element method (FEM) in two (2D) and three (3D) dimensions. Validation of results was through of the displacements comparison with an elastic analytical method. The constitutive model used was the Mohr-Coulomb and the soil parameters are of a soil in Mexico. Results shows a convergence towards a similar behavior for the elastic case and a difference when a perfect elasto-plastic behavior is considered in design. As fundamental conclusions, it is observed that it is possible to speed up the time using the 2D-FEM method, as well as the feasibility of quickly reviewing a 3D tunnel using a 2D program.

Key words: Finite elements; two-dimensions; three-dimensions; tunnels.

1. Introducción

Durante la excavación de túneles, los cambios del tipo suelo inicialmente caracterizado son un común denominador. En ese sentido, conocer una respuesta rápida de los desplazamientos y del comportamiento del túnel se vuelve imperativo para no detener la construcción, debido a los altos costos que esto representa. Los métodos analíticos han sido eficientes a la hora de realizar los diseños de túneles [1] y [2]. De igual forma Broms y Bennermark [3] adaptaron métodos para el estudio de excavaciones verticales y Peck [4] estableció conceptos para el ademado de los túneles, así como para determinar los asentamientos superficiales. sin embargo, el uso de herramientas numéricas, se ha vuelto indispensable para llevar a cabo diseños apegados a las condiciones reales [5] y [6] y de igual forma se ha establecido el uso de métodos de confiabilidad para garantizar un mejor diseño [7]. La ventaja de los estudios numéricos es debido a que los modelos constitutivos de estos programas son más adecuados para reproducir las condiciones naturales del suelo. Sin embargo, el uso de estas herramientas además de su costo, requiere de un alto nivel de conocimientos, aunado a que el analista o diseñador debe conocer en gran medida la posible respuesta que se puede esperar de estas obras. Aunado a lo anterior, la variabilidad de parámetros del suelo y por la complejidad de los túneles, éstos frecuentemente se analizan de forma particular y específica. Lo anterior concluye en una gran inversión de tiempo y de recursos humanos, debido a los cambios que se presentan frecuentemente en la construcción, por lo que es necesario que se recurra muchas veces a continuar la construcción sin analizar nuevamente con detalle la obra en cuestión. Por otro lado, el software comercial ofrece la posibilidad de diseñar en dos dimensiones (2D) y en tres dimensiones (3D), siendo éstos últimos los que se consideran los más adecuados a la realidad, ya que se puede analizar con más detalle el avance de la obra. Sin embargo, el análisis en 3D ocupa de una inversión mayor en todos los sentidos, tanto en tiempo como en recursos humanos y por supuesto en la inversión de equipo adecuado a los procesos numéricos que se deben resolver al modelar en 3D. En cuanto a las teorías de análisis, el análisis elástico ha sido utilizado con más frecuencia que teorías más complejas que consideren la plasticidad, a las que sin duda debe migrar el diseño de túneles. Bajo estas observaciones, en este artículo se presenta de una forma sencilla, la influencia que tienen los parámetros del suelo y geométricos a la hora de modelar un túnel en condiciones elásticas.

2. Consideraciones para el estudio

2.1. Parámetros del suelo

El suelo se modelo con la teoría de Mohr-Coulomb, considerando un comportamiento elástico. Los parámetros del suelo se muestran en la Tabla 1.

Tabla 1. Parámetros de suelo, modelo constitutivo Mohr-Coulomb en condiciones elásticas.

Suelo	c (kPa)	Φ (-)	γ (kN/m3)	E (kN/m2)	ν (-)
1	12	22	17.4	5 000 15 000 10 000 24 000	0.35
2	12	22	16	20 000	0.3

2.2. Modelo analítico para validación del modelo 2D

Se llevó a cabo un análisis paramétrico usando una ecuación analítica y se realizaron comparaciones con los resultados numéricos en 2D. Esta comparación permitió migrar a los modelos 3D. El método analítico se basa en la teoría elástica [8], la que se utiliza frecuentemente para el diseño de túneles. Entre las soluciones que se usaban desde unos inicios para excavaciones circulares (ver Figura 1), se considera la siguiente expresión [9]:

${\textstyle \delta =\left(\gamma {\,H}_{o}-{P}_{a}\right){\frac {\left(1+\nu \right)D}{2E}}}$

(1)

En donde:

δ es el desplazamiento en la periferia del túnel; γ es el peso específico del túnel; H_o es la profundidad a partir de la superficie del terreno al centro del túnel; P_a es el esfuerzo radial en la periferia del túnel; ν es la relación de Poisson; D es el diámetro del túnel y E es el módulo elástico del suelo. La Figura 1 muestra el esquema de un túnel circular y la presión Pa aplicada en la modelación.

Figura 1. Esquema de un túnel circular.

2.3. Modelos numéricos FEM

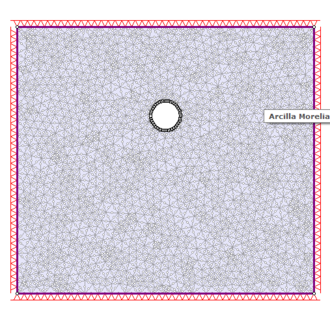
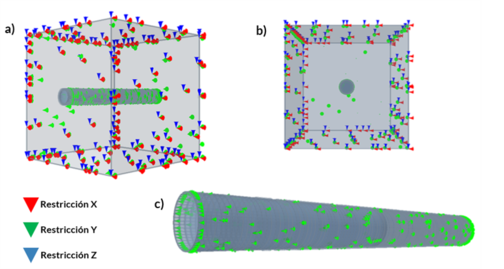
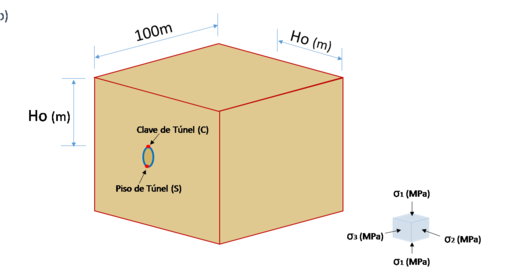
Para los modelos en Elementos Finitos (FEM), se usaron mallas con geometrías dependiendo del radio o de la forma del túnel analizado. Se consideró una densidad de la malla “fina” en la periferia del túnel para garantizar resultados adecuados, así como fronteras en el sentido vertical alejadas del túnel y en algunos casos también en el sentido horizontal. Las condiciones de frontera son: cero desplazamientos en las caras vertical y horizontal (–x y –y) para los casos 2D (ver Figura 2), y cero desplazamientos en la dirección –z para los casos 3D (ver Figura 3), lo que permitió llevar a cabo la comparación entre los diferentes modelos. La presión radial Pa se disminuyó linealmente en la periferia del túnel, partiendo de un esfuerzo in situ para simular un proceso de excavación. la Figura 4 presenta un esquema y la nomenclatura usada en los modelos 3D. El diámetro del túnel es de D=10m para todos los casos.

Figura 2. Modelo numérico 2D y nomenclatura usada en los modelos 3D.

Figura 3. a) Modelo numérico 3D, b) restricciones y c) simulación del avance en la excavación.

Figura 4. Modelo 3D y nomenclatura usada en las simulaciones FEM.

3. Resultados y discusión

En esta sección, se presenta la influencia de los parámetros de diseño usados en las modelaciones numéricas, como es la profundidad de la excavación (H₀), el peso específico del suelo (γ), el módulo de rigidez del suelo (E), así como la geometría de la malla generada automáticamente en un programa comercial de Elementos Finitos (MEF). Se presenta la comparación con un método analítico.

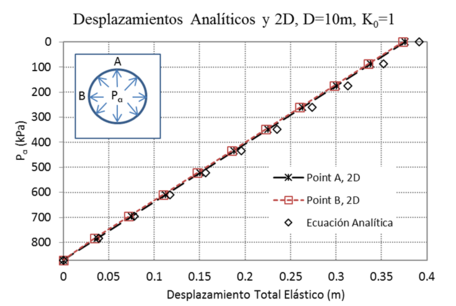
Los resultados obtenidos aplicando la ecuación (1) se presentan en la Figura 5, en donde se observan los desplazamientos totales en la periferia del túnel (rombos), considerando una disminución lineal de la presión P_a hasta que ésta llega a cero. De igual forma se observan los desplazamientos obtenidos en el RS2® [10] en 2D, tomados en los puntos A y B (ver Figura 5), marcados con cruces y cuadrados respectivamente. Para este caso las soluciones concuerdan bastante bien, lo que permitió validar los modelos numéricos y migrar a los modelos 3D que se presentan posteriormente.

Cabe mencionar que la Pa en los resultados, alcanza de forma idealizada hasta un valor igual a cero. Además, para este caso la malla se extendió hasta una profundidad de H_o=50m, tomando como base el diámetro D=10m. En la práctica esta profundidad podría no ser congruente. Sin embargo, para la finalidad del modelo numérico los resultados presentan desplazamientos muy cercanos a la teoría elástica, lo que pudiese considerarse para el diseño de túneles profundos. Además, la simulación que se llevó a cabo no considera el peso propio del material, de lo contrario debido al valor de H_o los desplazamientos del túnel se ven influenciados por la columna del suelo.

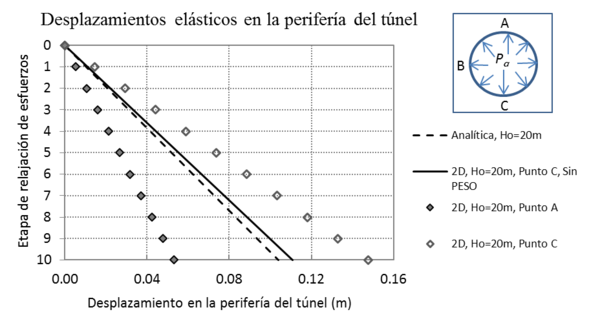
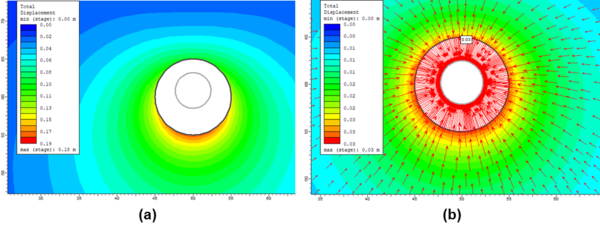
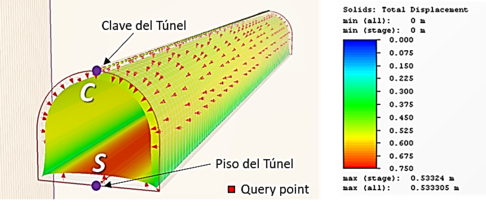
Las Figura 6 presenta los resultados para un H_o=20m. En este caso se simularon las dos condiciones, tomando en cuenta el peso propio del material y la condición en la que se toman esfuerzos constantes en toda la malla. En la Figura 6 se puede observar que para el caso en donde se toma en cuenta el peso propio del material (símbolos en rombo), el desplazamiento para el piso del túnel (rombos vacíos) es más grande que el analítico y se presenta un desplazamiento menor en la clave del túnel (rombos rellenos). Para el caso en donde se considera un promedio de los esfuerzos en la malla en función de la profundidad del túnel, los desplazamientos son muy parecidos a la respuesta analítica elástica (líneas punteada y continua). La Figura 7 se presentan las cinemáticas de desplazamientos (a) para el caso simulado en 2D considerando el peso propio del material y (b) sin considerar el peso del material en la influencia de los desplazamientos, se observan igualmente los vectores de desplazamiento.

Figura 5. Desplazamientos analíticos y 2D obtenidos en la periferia del túnel (Suelo 1).

Figura 6. Desplazamientos analíticos y 2D obtenidos en la periferia del túnel (Suelo 2).

Figura 7. Cinemática de desplazamientos 2D (a) con peso, (b) sin peso (Suelo 2).

Figura 8. Longitud de excavación vs Desplazamientos en los puntos A y C para dos tipos de secciones de túneles: circulares y en herradura (Suelo 1).

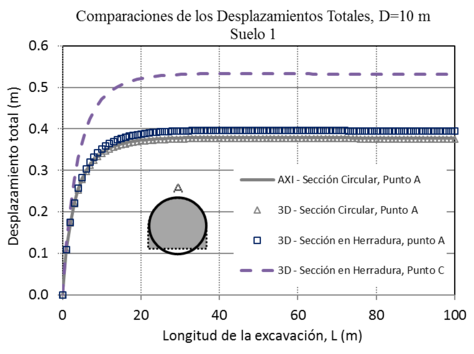
La Figura 8 muestra los desplazamientos generados en el punto A para las condiciones de un túnel circular en 3D y en axisimetría usando los programas RS3® [11] y RS2® respectivamente. Los dos valores son iguales (triángulos y línea continua). Por otro lado, se observa que para el caso de los túneles en herradura se observan mayores desplazamientos, por lo que corresponde a la zona más desfavorable del túnel (línea discontinua). De la misma forma se observa que los desplazamientos en la clave de la herradura, son cercanos a los obtenidos para los túneles circulares (cuadrados vacíos). Es importante señalar, que para una cierta longitud de excavación (L), los desplazamientos se estabilizan presentándose los máximos para todos los casos, independientemente que la excavación siga avanzando. Para comparar los resultados de los túneles circulares y en herradura se recurrió a un artificio geométrico, en el que se hizo coincidir a las dos claves de los túneles y las áreas son equivalentes. La figura 9, presenta la cinemática de desplazamientos generada para un túnel en herradura.

Figura 9. Cinemática de desplazamientos 3D para un túnel con sección en herradura (Suelo 1).

Figura 10. Longitud de excavación vs Desplazamientos Normalizados para una sección de túnel circular (Suelo 1).

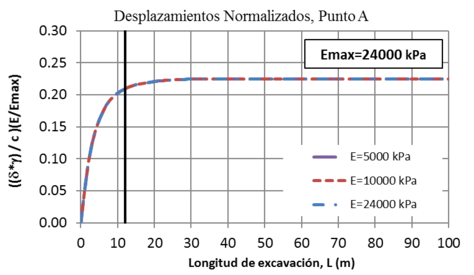
La Figura 9 presenta los desplazamientos (δ) normalizados respecto al peso específico (γ), la cohesión del suelo (c), y una variación en los módulos elásticos del suelo (E), tomando como máximo un valor de un suelo rígido (Emax= 24 000 kPa). Se observa que las curvas concuerdan muy bien entre ellas. De igual forma se observa que hay una longitud (L) en la que los desplazamientos se estabilizan (L≅ 10m) a pesar de que la longitud de excavación continúe avanzando.

Figura 11. Longitud de excavación vs Desplazamientos para una sección de túnel circular.

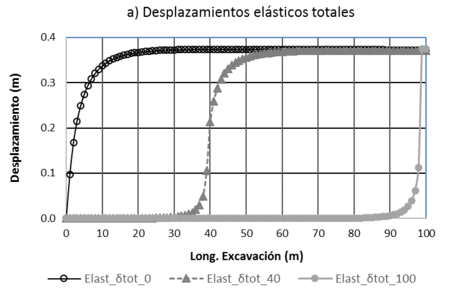
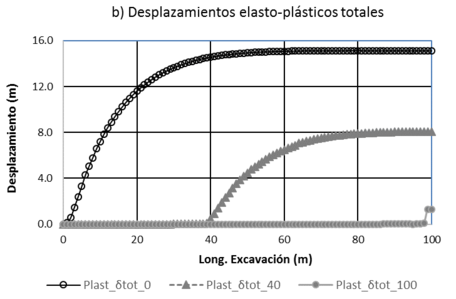
La Figura 11 presenta los resultados entre las respuestas 3D de un análisis elástico y un análisis elasto-plástico perfecto: Para simular este comportamiento, se repiten los valores mecánicos de resistencia al corte mostrados en la Tabla 1 en el programa. Al utilizar un modelo constitutivo con un comportamiento diferente, se observa que la respuesta en términos de desplazamientos cambia inmediatamente (ver 11a y 11b). Cabe mencionar que los desplazamientos generados para un comportamiento elasto-plástico perfecto están fuera de la realidad, debido a que en este modelo se utilizó un valor de P_a=0 kPa. Es importante mencionar que la finalidad de este análisis únicamente corresponde a conocer la diferencia numérica en respuestas con respecto al modelo constitutivo señalado, por lo que es requerido hacer más análisis para un diseño real. Además las tres líneas en cada gráfica de la Figura 11, representan diferentes avances de excavación en el túnel, observándose por ejemplo que para el avance a L=40 m (Elast_δtot_40 y Plast_δtot_40), las dos respuestas numéricas en términos de desplazamientos son diferentes para el caso plástico en las diferentes longitudes de excavación, a diferencia de los desplazamientos elásticos, comportamiento en el cual a partir de una cierta longitud de excavación, los desplazamientos son iguales. Lo anterior nos lleva a la conclusión de que es muy importante definir los modelos constitutivos en todas las obras de una forma adecuada, y más tratándose de obras complejas como lo son los túneles.

4. Conclusiones

De los resultados obtenidos, se concluye que es posible replicar los resultados obtenidos a partir de soluciones analíticas simples con modelos numéricos y que a partir de estos resultados se puede migrar a modelos más complejos como es el caso 3D. El replicar estos modelos permite validar los diseños simples.

De igual forma se observa que la influencia de los parámetros considerando condiciones elásticas se puede normalizar, observándose la misma tendencia para los resultados en 3D. De igual forma se presenta una longitud de excavación, para la que los desplazamientos elásticos numéricos alcanzan un máximo, por lo que también se concluye, que en los primeros metros los desplazamientos son menores debido a la relajación de esfuerzos iniciales.

Cuando se realiza un modelo elasto-plástico perfecto, el comportamiento es muy diferente al comportamiento elástico, mostrándose además una variación en los desplazamientos a medida que avanza la excavación del túnel. Este hecho permite concluir que la elección del modelo constitutivo debe de hacerse con sumo cuidado, en función de la obra y de su complejidad.

El diseño de túneles es complejo, tratar de generalizar un comportamiento es difícil. Sin embargo, se pueden inducir respuestas esperadas a partir de modelos más simples y que concuerdan con teorías usadas en la práctica común de la Ingeniería. Por otro lado, usar teorías más complejas, permite obtener resultados más adaptados a la realidad.

Finalmente, los modelos numéricos representan un área de oportunidad para el diseño, aun cuando correspondan a modelos 2D. Conocer bien el funcionamiento de los programas, así como los modelos constitutivos con los que se puede modelar, evita gastos innecesarios, así como accidentes y errores fatales.

Referencias

[1] Terzaghi, K. (1942). Shield tunnels of the Chicago subway. Journal of the Boston Society Civil Engineers, Vol. 29, 163-210.

[2] Terzaghi, K. (1946). Rock defects and loads on tunnel support. In R.V. Proctor and T.L. White (editors), Rock Tunneling with Steel Supports, Commercial Shearing and Stamping Co., Youngstown, Ohio, U.S.A., Section 1, 15-99.

[3] Broms, B.B., Bennermark, H. (1967). Stability of clay at vertical opening. J. Soil Mech. Found. Div. ASCE 93(1), 71-94.

[4] Peck, R.B. (1969). Deep excavations and tunneling in soft ground. State of the Art Report, Proceedings of the 7th International Conference on Soil Mechanics and Foundations Engineering, Mexico, 225-325.

[5] Vlachopoulos, N. and Diederichs, M. (2014). Appropriate uses and practical limitations of 2D numerical analysis of tunnels and tunnel support response. Geotechnical and Geological Engineering, Vol. 32(2), 469-488, Springer. doi: 10.1007/s10706-014-9727-x.

[6] Equihua-Anguiano, L.N., Rubio-Saldaña, I., Orozco-Calderon, M., Arreygue-Rocha, E., and Chavez-Negrete, C. (2018)Equivalent FEM Meshes from Axisymmetric (AXID) to Three (3D) Dimensions Applied to Tunnels in Clay Springer International Publishing AG, part of Springer Nature 2019 S. Shu et al. (eds.), New Developments in Materials for Infrastructure Sustainability and the Contemporary Issues in Geo-environmental Engineering, Sustainable Civil Infrastructures, https://doi.org/10.1007/978-3-319-95774-6_2.

[7] Celestino, T. B., Aoki, N., Silva, R, M., Gornes, R.A.M.P., Bortolucci, A. A., and Ferreira, D. A. (2006). “Evaluation of tunnel support structure reliability.” Safety in the Underground Space - Proceedings of the ITA-AITES 2006 World Tunnel Congress and 32nd ITA General Assembly, Elsevier, Seoul, Korea, doi.org/10.1016/j.tust.2005.12.028.

[8] Tamez-González, E., Rangel-Núñez, J. L., and Holguín, E. (1997). Diseño Geotécnico de Túneles, TGC Geotecnia S.A. de C.V., Ciudad de México, México.

[9] Deere, D.U, Peck, R.B., Monsees, J.E., and Schmidt, B. (1969). Design of Tunnel Liners and Support Systems. Final Report. Department of Civil Engineering. University of Illinois, Urbana. For office of High Speed Transportation, U.S. Department of Transportation. Contract No. 3-0152.

[10] RS2 Version 9 Modeler, Version 9.020 64-bit, 2D finite element analysis for rock & soil, Copyright© 1990-2016, Rocscience Inc., Toronto, Ontario, Canada, www.rocscience.com.

[11] RS3 Version 1.017 64-bit, 3D finite element analysis for rock & soil, Copyright© 2013-2015, Rocscience Inc., Toronto, Ontario, Canada, www.rocscience.com.