Geometric proportions: The underlying structure of design process for Islamic geometric patterns

Abstract

This paper discusses geometric proportions which serve as a design tool, especially for Islamic pattern design. The key role of geometry in Islamic patterns is discussed with relation to proportions which act as the underlying structure of the design process. Evaluations based on spatial structure and esthetic criteria are integrated into the conceptual phase of the design process. Proportions serve two objectives; firstly, in pattern design, proportions are strongly linked to geometry, which can be viewed as a self-guiding method of esthetically proven design. Secondly, geometric proportions regulate primarily the order of patterns; while at the same time they mediate between the two poles of order and diversity as well as among different esthetic levels. This paper analyzes geometric principles and design features of traditional Islamic patterns, involving geometric proportion analysis. It also describes the syntheses of Islamic patterns from the perspectives of Islamic cosmology, philosophy and metaphysics of geometry, which can be seen as following a pre-established principle of geometric and proportional design with high accuracy and great precision. Furthermore, the underlying relationship between cosmology and geometry is manifested in Islamic patterns where geometry acts as the vocabulary underpinning the pattern language. These findings support the argument that geometry was independently discovered and applied by Islamic culture as a universal language, constituting one of the most important multicultural symbols in design.

Keywords

Geometry ; Proportions ; Islamic patterns

1. Introduction

The word geometry refers to the science of properties and relations of magnitudes such as points, lines, surfaces, or solids in space and the way the parts of a particular object fit together (Concise Oxford English Dictionary, 1999 ). Geometry is well known based on two Greek words “geo”, meaning the earth, and “metry”, meaning to measure. So geometry literally means “the measurable earth” or “earthly measurements”. Geometry, according to Plato, can also refer to the science of stereo-metry or “spatial measurements”. The very laws of how things are allowed to be by the “Divine will” are the laws of “Harmony of Being”. Tradition holds that, as engraved over the entrance to Platos Academy, “Only he who is familiar with geometry shall be admitted here” (Critchlow, 1976 ).

Geometry has existed in many buildings and design forms across centuries. The first confirmed record of geometric knowledge and its relationship to astronomy, human and music can be traced back to the ancient Greeks, in particular, Pythagoras and Plato. However, prior to the Greeks, many old civilizations have left clear geometric footprints by applying sacred geometry in their constructions. The prehistoric carved stones found in Scotland representing the Platonic Solids.¹ can be dated back to over a thousand years earlier than the Greeks.² The Greeks may well have been the first to have offered geometry to the public, but they were, by no means, the first to realize it (Critchlow, 1987 ; Hecht, 1988 ; Critchlow, 1987 ).

Geometric ratios and proportions existed and were employed in the design of ancient sacred and ceremonial sites in all traditional civilizations. They were invariably built with dimensions that incorporate mathematical numbers, constants and ratios such as the “golden/sacred mean”, and the use of geometries based on proportional roots, proportional rectangles and Pythagorean triangle (Pennick, 1994 ). For example, Christian cathedrals incorporated symbolic geometry, while the design of Hindu and Buddha temples was based on sacred geometry. In Islamic art, geometric elements have been employed since its origin and were used to create unique geometric formations, serving as the underlying structure of Islamic design process.

Geometry or proportional geometry is a sacred art form due to its fundamental association with the Creations principal laws. The visual expression of the order of these laws is best represented through the discipline of geometry. Geometry is both quantitative and qualitative in nature. Its quantitative dimension regulates the order and construction of design forms. Its qualitative nature sets the proportions of design forms and represents an expression of the order of the universe as a visual representation of the truth. Each figure or geometric shape, when seen from the perspective of its symbolic meaning, represents an echo of unity and a reflection of the values and principles within the larger frame beyond that unity (universal unity) (Ardalan and Bakhtiar, 2000 ). Seyyid Hossein Nasr argued that geometry and rhythm manifest a doctrine of unity which is central to Islam, upon which Islamic art developed based on mathematical ratios and proportions which represent the very heart of Islam (Critchlow, 1976 ).

Geometry is the blueprint of the Creation and the generator of all forms. It is a science that deals with numbers in space on four basic levels: the first one is arithmetic (pure numbers), i.e., any measurement or proportion is a geometrical measurement. The second level is numbers in space which represent proportional geometry. They reflect the meanings and “Ideas”. The third level is numbers in time, which is the foundation of music. The fourth level is numbers in space and time which represent the cosmology of the universe. Geometry explores and explains the patterns that unify and reveal the structure of the Creation within all natural patterns of growth or movement and their conformity with geometric shapes. All life forms emerge out of timeless geometric codes. Viewing and contemplating these codes allow us to understand the wisdom of the inner workings of the universe in order to fully comprehend and appreciate its beauty based on the concept of proportions. Ikhwan Al-Safa wrote, “One of our aims… consists of demonstrating clearly that the whole world is composed in conformity with arithmetical, geometrical, and musical relations. There, we have explained in detail the reality of universal harmony” (Nasr, 1978 ).

Geometric proportions in architectural patterns represent a design language, as words do in a spoken language. They determine the frameworks within which elements may be arranged into a pattern, a relation between one element and another, and a proportional relation within one element. They address and reflect the natural laws that govern the basic harmonies of nature, being describable by means of mathematics and geometry.

Islamic art favors geometry because of its intelligible aspect. Geometry possesses abstraction and the capacity to express and reveal objectively immutable and spiritual truths. Geometry involves proportions and prime roots that are considered the most beautiful proportions (the proportions of beauty). As such, beauty, for the Muslim artists, is objective and self-expression of truths, which is the essential nature of beauty as Plato stated, “Beauty is the splendor of the truth” (Burckhardt, 1987 ).

The language of Islamic design springs primarily from the abstract. Therefore, geometry in general and geometrical proportion in particular carry great importance in the design process of Islamic art, presented in its primary elements, geometry, biomorphic forms, and calligraphy, which are all based on and ruled by the underlying geometric laws (proportions). It follows that the Islamic design principles are reflected in geometry. In other words, geometry plays a central role in Islamic design.

This paper examines Islamic pattern design, which can be viewed as a key method of expressing Islamic cosmological esthetics. In addition to representing cosmological and philosophical structures at the level of form, geometric patterns can also be seen as efficient and powerful representations of some of the central concepts that characterize Islamic debates on the divine nature. Islamic pattern was developed as visual tools for contemplating the underlying mathematical nature of the universe, leading to the nature of beauty, by virtue of Gods creation of the universe (the nature of the divine itself).

2. Geometric proportional systems

In architecture dating back to prehistory, particularly in Islamic arts and architecture, the most important geometric proportional systems are: the proportions of the golden mean and the primary three proportional roots √2, √3 and √5, on which all Islamic arts and architectural forms, especially their geometric pattern design, are based.

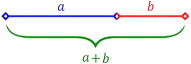
The golden mean proportion is a proportional system whereby two elements are related to each other by a set proportion. Two segments of a line not equal to each other are related in a proportion: a/b=(a+b)/a (Figure 1 ). It is this unique point that divides the single line into segments with qualitative proportions. It is a reflection of multiplicity within unity in terms of geometry. If the line is divided into equal halves, the two segments would be a monotonous repetition of one and the same thing, neither multiplicity nor unity within the geometry.

Figure 1. The golden mean proportion: a/b=(a+b)/A=1.61803.

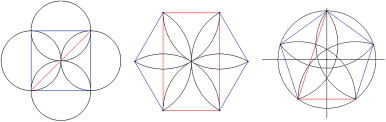
The proportional rectangles or the proportional roots are based on the geometry of the polygons.

For example, the square includes √2,³ the hexagon includes √3, and the pentagon includes the golden mean which numerically equals to [(√5+1)/2]=1.61803 (Figure 2 ; Hambidge, 1920 ; El-Said, 2001 )

Figure 2. The proportional roots: (a) the √2 proportion, (b) the √3 proportion, and (c) the golden mean (Phi) proportion.

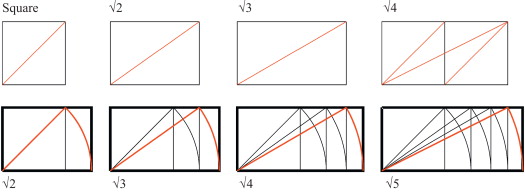
Figure 3 shows the successive constructions of the root proportions in proportional rectangles based on the diagonal of the square.

Figure 3. The root proportions based on the square.

The Muslim artists created these geometric proportions from the circle of Unity. As one of the most common shapes in nature, it was reflected symbolically in the signs of the Creation, just like the sun being one of the signs of divinity (the universal symbol) (Guenon, 1995 ; Figure 4 ). The circle is an obvious example of a basic geometry, constituting all the proportional geometries inherent in traditional architecture.

Figure 4. Unity in multiplicity and multiplicity in unity primary circle symbolizing wholeness, completion, unity and infinity.

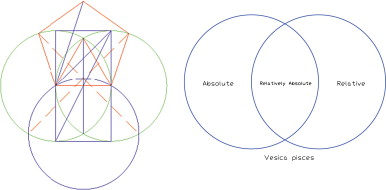
The circle of Unity is the most significant form, for it contains a circumference revolving around a fixed center. It is therefore extremely important to understand that all other geometric shapes can be determined from a circle, from which come the full polygons, including series of roots and proportions. Figure 5 shows a symbolic relationship between the absolute and the relative, represented by two circles overlapped. This construction is known as the Vesica Pisces. The realm enclosed within this overlap is, according to Frithjof Schuon, the “Relatively Absolute” (Schuon, 2003 ). The absolute represents the metaphysical and the relative represents illusion. The geometric proportions within the “Relatively Absolute” sphere indicate that it is connected to truth. The Vesica Pisces is one of the key starting blocks from which sacred geometry was applied in the geometric matrix used for the design in all religious buildings.

Figure 5. Roots and the golden mean within the Vesica.

Within the Vesica Pisces realms, the primary proportional roots, i.e., √2, √3, and √5, as well as the golden mean, are illustrated, all of which are found within the realm of the “Relatively Absolute”. When the drawing is further intersected by straight lines, an equilateral triangle, a hexagon, a pentagon, a square and so on, have emerged.

The sacred mean or Phi (Φ ), the divine proportion, and also golden section or golden ratio, is one of the key-stones of sacred geometry. The mathematics of the golden ratio proportion is generated by the formula (√5+1/2) (or 1:1.618).

The mathematics of the golden ratio is related to Leonardo Fibonacci, the founder of the “Fibonacci sequence”, a numerical series found frequently in the natural world (Lawlor, 1989 ). It simply follows the rule that the next number is the sum of the previous two numbers, as follows: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 etc. If we divide any number in the Fibonacci sequence by the one before it, for example 144/89, or 89/55, the answer is always close to 1.61803, which is the value of the golden ratio. The Fibonacci sequence, or the description of the golden mean features can be seen everywhere in the forms of nature, music, and the arts. One of the mathematical products of the sacred mean is the spiral, commonly found in nature (Rawles, 1997  ;  Schneider, 1994 ; Figure 6 ).

Figure 6. Spirals, the mathematical products of “Fibonacci sequence” and the sacred mean.

Proportional geometry regulates primarily the order of design process. It is needed to create the micro cosmos by which we acknowledge beauty in design forms. The beauty of proportions is based on the simple geometry of regular polygons with a set of ratios of side lengths to diagonals (such as √2, √3, √4, √5 and …), which can be translated into the design process.

These geometric proportions are used to quantify esthetic qualities. This process is, to a great extent, based on objective facts. Judgments on beauty versus ugliness can be based on systematic arguments characterized by unifying principles or patterns. They can be achieved by means of algorithms of visual math as an objective ground which can be founded on geometry and proportions, which are part of their elementary pillars. As Aristotle stated, beauty is to “maintain the just measure” (Lawlor, 1989 ). Beauty in proportions has a key function in constituting them because it forms the underlying structure of order versus diversity, establishing systematic design principles.

The objective criteria of beauty revealed by means of geometric analysis aim to establish sets of design tools, which would increase, rather than restrain, the freedom of design, and to find a system path to a design language that includes beauty rather than systematically excludes it.

3. Geometry in man, nature, and cosmos

Geometry is an unseen presence in Islamic art and architecture. It is the visual means by which human mind can comprehend the order and harmony inherent in the Creation. It is the visual representation of the mathematical patterns found everywhere in man, nature, and cosmos. These patterns, with their esthetic and philosophical values, are found within all aspects of Islamic design process.

The understanding of geometry as an underlying part of our existence is nothing new. In fact, the golden mean and other forms of geometric proportions can be seen imbedded in man, nature, and the universe, either represented as micro or macro cosmos.

Since ancient times, there has been a deep interest in forms that are considered to incorporate within their intrinsic relationships mathematical and geometrical proportions (universal truth). It was believed that these geometries were derived from the basic laws of the universe. Kepler stated the belief that geometry is underpinning the cosmos, which was based on Platos ideas that God created the universe according to a geometric plan—“God geometrizes continually” (Lawlor, 1989 ). The structure of the universe is determined by and revealed as certain mathematical and geometric constants which represent a confirmation that proportions are the underlying fabric of nature. This can be seen in man, nature, and cosmos. Beyond this discipline, it was believed that these geometries were based on the Creation itself (sacred) and, by incorporating them in music, art and architecture, the fruits from these fields would have a harmony of proportions and a special sacred character—“harmony of being”. By studying or contemplating these geometric proportions, an understanding could be obtained towards the sacred truth.

3.1. Man

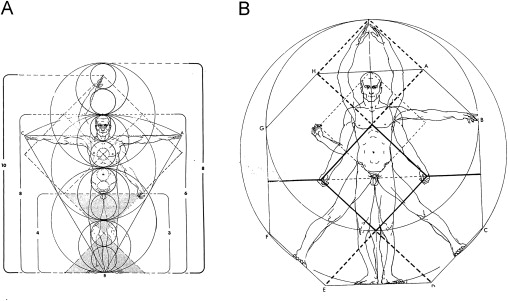
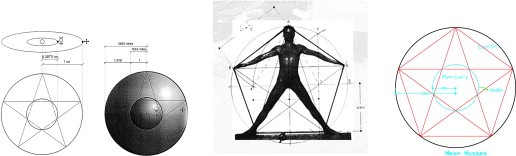
Geometric proportions are one of the definitive geometric qualities of life itself. According to the Holy Quran, man has within himself all what is reflected in the universe—“the best proportions”. Man is the core of Gods creatures; he possesses the most harmonious proportions, reflecting of the Divine harmony of being (Lings, 1976 ; Guenon, 1994 ). “We have indeed created man in best of forms”–proportions– (The Holy Quran, Chapter 95, verse 4 ). Leonardo da Vinci illustrated the mathematical proportions of human body, showing that human being exhibits clearly golden mean proportions in his body based on ratios of 1.618. The Vitruvian Man drawn by Leonardo Da Vinci is based on Vitruvius, who had written that human proportions should have a relationship in architecture. Vitruvius believed that if human proportions could be incorporated into buildings, they would become perfect in their geometry. According to Vitruvius, the distance from fingertip to fingertip should be the same as that from head to toe. The sacred mean rules can be seen in the ratios of body parts throughout the human body. Man reflects these principles in a language of sacred geometry (Guenon, 1995 ; Figure 7 ).

Figure 7. Vitruvian man, with proportions based on the sacred mean (Critchlow, 1976 ).

According to Robert Lawlor, “The human body contains in its proportions all the important geometric geodesic measures and functions… the proportions of ideal man are at the center of a circle of invariant cosmic relationships” (Lawlor, 1982 ).

3.2. Nature

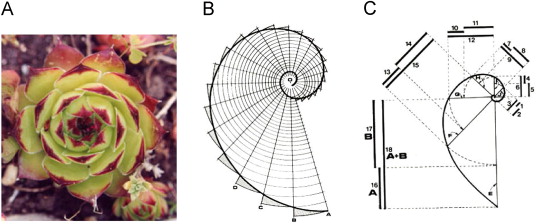
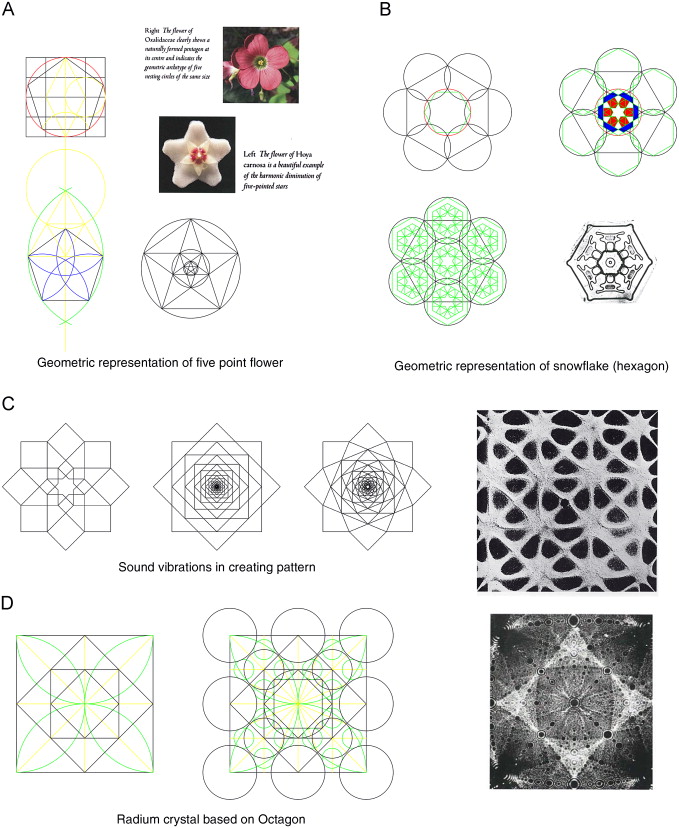
The study of geometric proportions has its roots in the study of nature and matter (Skinner, 2009 ). Many forms observed in nature can be related to geometry. For example, the snowflake crystals and honey cells construct hexagonal geometries. Radium crystal and sound vibrations that carry sound information are based on √2 proportions, showing the octagonal geometry. Flowers in nature tend to have a variety of geometries, although their variety seems to be infinite. Four, five, and six pointed geometries seem to be more common in nature. There are many plants and other aspects of nature which exhibit the form of spiraling geometry, which is related to Fibonacci proportions based on the golden mean. Thus the golden mean is the “fingerprint” of the Creation (Figure 8 ).

Figure 8. Geometric proportions in nature (Singer, 2008 ).

3.3. Cosmos

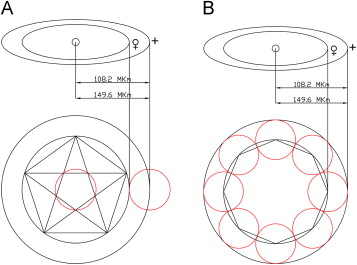
The mathematical harmony of the universe can be seen from the proportions of the planets in our solar system. For example, the ratio of the sacred mean can be seen in the rotations of the Venus and the Earth around the Sun in that for each five years that the Earth rotates around the Sun, the Venus rotates around it eight times. The connection between 5 and 8, both of which are Fibonacci numbers, is the golden mean proportion (8/5=1.6). The result of this motion is that the Venus “draws” a pentagon around the sun every eight years (Skinner, 2009 ; Figure 9 A).

Figure 9. Proportions of the Venus' and the Earths mean orbits are based on the sacred mean (Martineau, 2001 ).

Figure 9 B shows that a circle is drawn, which represents the Venus' mean orbit. A pentagon is constructed inside it and a small circle placed through the arm-crossing points. The radius of this small circle divides the radius of the large one into golden sections and can be used to space the Venus' orbit from the Earths orbit. It can be seen from the agreement between eightfold and fivefold geometries that eight touching circles are drawn from the Venus' mean orbit. In turn, the circumference circle is enclosing these eight circles, defining the Earths mean orbit (Martineau, 2001 ; Figure 9 C).

The conclusion from these diagrams shows that, mathematically speaking, the ratio of the mean orbits of the Venuss to the Earth is √2 proportion. The geometric representation of these orbits creates the golden mean proportion.

The same proportions can be observed between the Earth and the Mercury. Two circles defined by the arm-crossing points of the pentagon are both the Earths and the Mercurys mean orbit. Their sizes are their relative physical bodies (Martineau, 2001 ; Figure 10 ).

Figure 10. Proportions of the Mercurys and the Earths mean orbits are based on the sacred mean (Martineau, 2001 ).

Sacred geometry describes the assertions of a mathematical order of the intrinsic nature of the universe. Scientists see the same geometric and mathematical patterns as arising directly from natural principles. “Traditional art has rules that apply to cosmic laws and universal principles”. (Schuon, 1984 )

These and other similarities are seen in sacred geometry to serve as the further proof of the cosmic significance of geometric forms. Islamic architecture is created based on the essential harmonies of nature together with various symbolic meanings and theories of perfect proportions. The designers based their geometrical vocabulary on what they have seen in the nature around them, in an attempt to develop a codified series of proportions which may improve our psychological comfort with buildings (Skinner, 2009 ).

It has been proposed that the understanding of sacred geometry was extended into time and space. We may never know for sure whether such geometry was identified first from the observation of natural formations, or alternatively, it came as a result of an intellectual quest. However, whichever it would be, it is clear that these mathematical codes derived from nature began to be applied in the design of many important man-made structures.

Geometry constitutes a graphic description of the universe. Geometric analysis is an attempt to understand the causes and the reality of the nature, the principles governing existence, the material universe, and the perception of physical phenomena, as well as to analyze human behaviors.

God speaks through these forms. Virgin nature was the first book, which made the Truth visible. “From the bosom of nature, man seeks to transcend nature and nature herself can be an aid in this process, provided man can learn to contemplate her, not as an independent domain of reality but as a mirror reflecting a higher reality, a vast panorama of symbols which speaks to man and has meaning for him”. (Nasr, 1997 )

Geometry is the very basis of our reality. Therefore, we live in a coherent world governed by underlying laws. They are always manifested in our world. The golden mean and proportional roots govern the proportion of our world, which can be found in the proportions of all living and nonliving forms.

4. Geometric proportions as a tool of design: study model

Geometric proportions are used by Muslim designers as the most valuable tool of design process to produce ordered patterns that govern esthetic beauty in designed spaces, surfaces and objects. They present us the “Principles of Nature” in their own language. By applying the golden mean (Phi) and the root proportions, geometric patterns are produced to be applied to the fields of building crafts, such as tiles, mosaic, plaster and wood, as well as to the field of book art.

By diminishing the polygon contained in the circle of Unity toward the center until the stars, which control the shape of the pattern, appear, the Muslim artists preserve the esthetics of these proportions and grant them exquisite beauty at a higher level than direct, material expression.

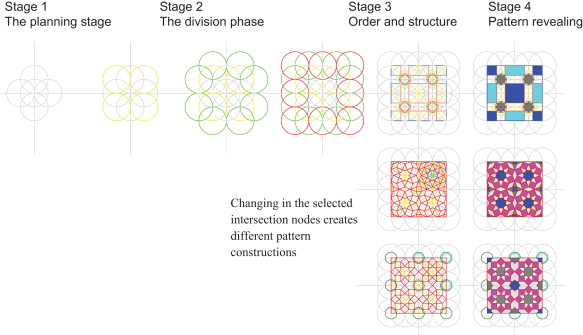
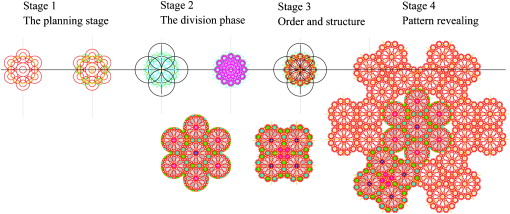
The system of geometric design starts from the circle (the basic unit), from which the pattern starts to unfold, creating harmonious divisions of the circle in four stages:

• The planning stage: starting by determining the proportional systems based on the unit pattern structure within the circle of Unity. The decision is based on the symbolic meanings underlying the geometric pattern and its relation to micro–macro cosmos.
• The division phase: construction of the basic geometric pattern.
• Pattern order and structure: initiating the crossing lines to create the artistic shape of the pattern on natural junctions formed by those lines. This gives rise to a series of points that can be used in the development of patterns. This type of framework forms the driving geometry for the relatively simple Islamic patterns with which we are familiar.
• Desired pattern revealing: establishing the geometric variations of the pattern and defining its boarder lines. It is derived from all the vital proportion systems based on a single unit. The process can be repeated indefinitely, presenting the same center everywhere and nowhere. It is ratio, rather than measurement, that determines the relative lengths of crucial dimensions.

The infinitely repeating geometrical patterns and the rules of geometric construction are a reflection of the unchanging laws of God. They are based on esthetic proportions as seen in the rhythm of the Creation and can be presented according to the design process in the following study models.

4.1. Fourfold to eightfold pattern

The two simplest geometric constructions which form the basis for many of the patterns to be found in Islamic decorations are the constructions of four and eight pointed geometries respectively. These relatively simple geometrical constructions are easy to develop by connecting various intersections, forming the basis for a variety of pattern making.

Figure 11 shows how this kind of geometric patterns develops when they are added together following the basic rules created by the selection process. By illustrating how small changes can affect the overall pattern according to the types of pattern and how they are achieved by simple changes, it is possible to see how a very small differentiation can produce a dramatically different overall pattern.

Figure 11. Construction stages of four pointed patterns.

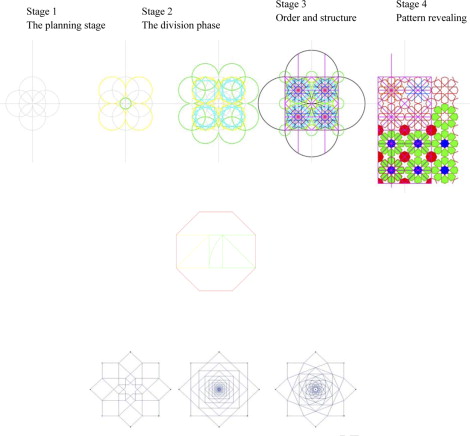
Figure 12 illustrates the construction of eight pointed geometry based on subdividing the square and √2 rectangles. The octagon, associated with the eight directions of space, is a symbol of the divine throne and its application within architecture is reflected in a Moroccan ceramic (Zilij) panel and in the harmonic diminishing of the eight-fold star in the Alhambra Palace, The Hall of The Abencerrajes, and the Hall of the Two Sisters (Figure 13 ).

Figure 12. Construction stage of eight pointed patterns based on √2 proportions.

Figure 13. Applications of the octagon based on eight pointed patterns in architecture “And the angels will be on its sides, and eight will, that Day, bear the throne of thy Lord above them” (The Holy Quran , Chapter 69, verse 17).

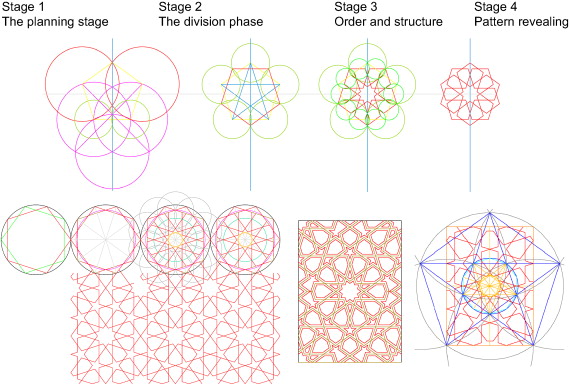
4.2. Fivefold to tenfold pattern

This part of geometric study shows a construction of the geometric panel based on proportional geometry. Its esthetic advantage is related to the golden section, showing one of the many ways to apply the geometry to form different patterns using a variety of materials.

Figure 14  ;  Figure 15 show the construction systems of a five-to-tenfold pattern which appears on the body of Salah Al-Din wooden Minbar (Pulpit) at Al-Aqsa mosque (Jerusalem), on a wooden door from Mumluk period (Cairo) and on a frontispiece at a Mamluk Quran. Ten pointed geometry lends itself to a wide variety of design possibilities through relatively small variations in the underlying relationships and to the creation of different patterns at different scales as a unified design.

Figure 14. Construction of a five-to-tenfold pattern based on the golden mean proportion.

Figure 15. Applications of a five-to-tenfold pattern based on the golden mean proportion.

4.3. Sixfold to twelvefold pattern

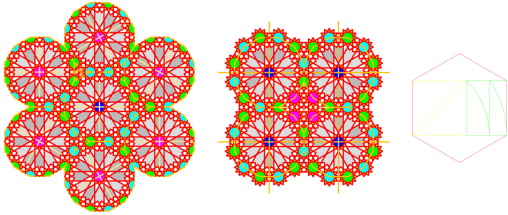
Twelve pointed geometry can be constructed from six pointed geometry. The hexagon is one of the most important forms in Islamic geometry. It is simple to construct, it has the capability of producing, by means of repetition, an overall coverage of a surface, it contains the important relationship of √3 proportions, and it bears a strong similarity to the circle, a symbol of the Creation in Islam.

Figure 16 is a study based on variations of the panels of ceramic tile. Their underlying geometry is based on the relationships between the circles containing the 6–12 pointed geometry, which is derived from the central six-pointed rose and a combination of a square, a lozenge and a triangle.

Figure 16. A study of 6–12 pointed patterns.

The complexity is introduced on a relatively simple basis by applying colors and doubling of the structure lines while employing the technique of cutting the tiles in such a way as to imply the interweaving of the running lines.

The pattern is both logical and rhythmical, i.e., both mathematical and melodious, which is the most significant characteristics of the spirit of Islam, showing its balancing—“unity in multiplicity” or “multiplicity in unity” within a series of regular geometrical figures contained within a circle, or a series of regular polyhedral contained within a sphere (Burkhardt, 1986  ;  Burckhardt, 1987 ).

Figure 17 shows how a relatively simple pattern based on six-pointed geometry might be developed into so many potential choices for the designer, which accounts for the great number of design variations that are possible.

Figure 17. Potential variations of 6–12 pointed patterns based on the same structure as in Figure 16 based on √3 proportions.

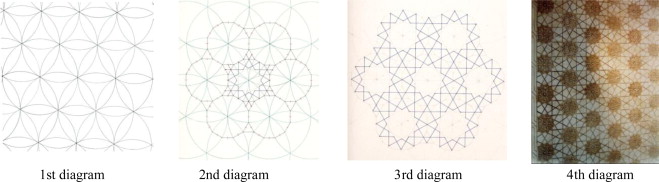
It is surprising that how many variations can be made from a simple geometric shape. Figure 18 illustrates a pattern based on a study using six-fold geometry. The first diagram illustrates the basic construction, beginning with the development from a circle. The second one shows the six pointed divisions. It is these selections shown in the third diagram that create the possibility for different patterns to evolve. The fourth is the result of this drawing and selecting process.

Figure 18. Analysis stages: example of step by step unfolding of the pattern.

The Ikhwan Al-Safa (the Brothers of Purity) stressed the important symbolism of number six, regarding number 6 as a perfect number. The number 6 consists of 1×2×3; at the same time also 1+2+3. Any number with this quality is considered a perfect number. Also, it was on the sixth day of the Creation that God created man. There are six directions of space as well. The six-sided hexagon is therefore a symbol of the universal man ( Ardalan and Bakhtiar, 2000 ).

Figure 18 shows the significant study on tile patterns and their underlying geometry, particularly the visual strength of the geometric structure in the application of these patterns. The construction of such natural geometries forms the basis upon which artisans on building sites set out their designs and work.

Figure 19 shows the applications of 6–12 pointed patterns based on √3 proportions in a wooden panel and a paper based geometric stars (medallion).

Figure 19. Applications of 6–12 pointed patterns

These studies illustrate only a small number of numerous possibilities out of the variations of proportional patterns based on simple polygon geometries. The ways of altering the relationship between the elements of these geometries appear to be relatively simple. However, every decision results in diversified complex patterns that are quite different from each other.

Islamic patterns, by their very nature, do not have any direction underlain in their geometry. Rather, they tend to be formed in fields with no apparent ending. The framing of patterns tends to be controlled by proportion systems. In other words, it is an objectively intellectual qualitative geometry, reflecting Truth in space. Ibn Khaldun states: “Geometry enlightens the intellect and sets ones mind right. All its proofs are very clear and orderly. It is hardly possible for errors to enter into geometric reasoning, because it is well arranged and orderly. Thus the mind that constantly applies itself to geometry is unlikely to fall into error”. (Ibn Khaldun, 1958 )

5. Conclusion

We can conclude that proportion is a characteristic of (traditional) Islamic patterns, serving as a tool of self-guiding process for esthetically proven design. Muslim builders knew of the autonomy or “inner laws” in constructing spaces and patterns. The relations among various parts can be seen everywhere in ancient buildings. In other words, buildings were designed with particular care, exhibiting mastery in pattern design of their spaces and surfaces.

Geometric proportions regulate the order of patterns based on mathematical ratios, which is influential in understanding the universe, man and nature; these proportions are, by their nature, the essential ingredients in sacred geometry, as Pythagoreans stated that these harmonic ratios render music in a balanced pattern.

Geometric proportion is strongly linked to Islamic cosmology, philosophy and metaphysical dimensions. It brings meanings and spiritual exercises for the viewer, deconstructing the meanings underpinning the geometric framework. As such, the viewer is more than an observer; he or she is a participant in the establishment of a strong link with geometry symbolizing man, nature and cosmos.

The geometry as well as its rhythm shown in Islamic patterns illustrates an infinite variety, permitting and encouraging contemplative reflections. It is one of the most powerful forms of sacred art It is a source of contemplation that allows our minds to wander and contemplate the infinite. These patterns were developed with strict geometric rules, relating to the understanding of natural forms based on geometric ratios in the cosmos, set as the prime mover behind design.

References

1. Ardalan and Bakhtiar, 2000 Nader Ardalan, Laleh Bakhtiar; The Sense of Unity: The Sufi Tradition in Persian Architecture; Kazi Publications (2000) p. 21
2. Burckhardt, 1987 Titus Burckhardt; Mirror of the Intellect; State University of New York Press, New York, USA (1987) p. 219,227
3. Burkhardt, 1986 Titus Burkhardt; Sacred Art in East and West: Its Principles and Methods; Perennial Books, Indiana, USA (1986) p. 101
4. Concise Oxford English Dictionary, 1999 Concise Oxford English Dictionary; Oxford University Press Inc., USA (1999)
5. Critchlow, 1976 Keith Critchlow; Islamic Patterns: An Analytical and Cosmological Approach; Schocken Books, Thames and Hudson, London, UK (1976) p. 4,9
6. Critchlow, 1987 Keith Critchlow; Order in Space: A Design Source Book; Thames and Hudson, USA (1987) p. 9
7. El-Said, 2001 Isasam El-Said; Islamic Art and Architecture: The Systems of Geometric Design; Garnet Publishing Ltd., UK (2001) p. 15
8. Guenon, 1995 Rene Guenon; The Reign of Quantity and the Sign of the Times; Sophia Perennis, Ghent (1995) p. 8,170
9. Guenon, 1994 Rene Guenon; The Great Triad; South Asia Books, New York, USA (1994) p. 23
10. Hambidge, 1920 Jay Hambidge; The Elements of Dynamic Symmetry; Yale University Press, NewHaven, USA (1920) p. 23
11. Hecht, 1988 Laurence Hecht; Mysterium microcosmicum: the geometric basis for the periodicity of the elements; 21st Century Science (1988), p. 18
12. Ibn, 1958 Khaldun Ibn; The Muqaddimah Franz Rosenthal; Pantheon Books, New York, USA (1958) 378
13. Lawlor, 1989 Robert Lawlor; Sacred Geometry: Philosophy and Practice; Thames and Hudson, New York (1989) p. 3,48,82,92
14. Lings, 1976 Martin Lings; The Quranic Art of Calligraphy and Illumination; Tajir Trust, London (1976) p. 13
15. Martineau, 2001 John Martineau; A Little Book of Coincidence; Walker and Company, New York, U.S.A (2001) p. 15,21
16. Nasr, 1978 Sayyed Hussein Nasr; An Introduction to Islamic Cosmological Doctrines, Thames and Hudson, UK (1978) p. 45
17. Nasr, 1997 Seyyid Hossein Nasr; Man and Nature; ABC International Group, Chicago, USA (1997) p. 95
18. Pennick, 1994 Nigel Pennick; Sacred Geometry—Symbolism and Purpose in Religious Structures; Capall Bann Publishing, San Francisco, USA (1994) p. 67
19. Rawles, 1997 Bruce Rawles; Sacred Geometry Design Sourcebook; Elysian Publishing, Eagle Point, Oregon (1997) p. 87
20. Schneider, 1994 Michael Schneider; A Beginners Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art and Science; Harper Collins, New York (1994) p. 10
21. Frithjof, 2003 Frithjof Schuon; Survey of Metaphysics and Esoterism; World Wisdom, Indiana, USA (2003) p. 48
22. Schuon, 1984 Frithjof Schuon; The Transcendent Unity of Religions; Quest Books, USA (1984) p. 62
23. Singer, 2008 Lynette Singer; The Minbar of Saladin: Reconstructing a Jewel of Islamic Art; Thames and Hudson, London, UK (2008) p. 110
24. Skinner, 2009 Stephen Skinner; Sacred Geometry: Deciphering the Code; Sterling, New York (2009) p. 7,91,107
25. The Holy Quran The Holy Quran. Chapter 95, verse 4 (95:4).

Notes

1. The “Platonic solids” are the names given to the five three-dimensional solids—tetrahedron , hexahedron, octahedron, dodecahedron, and icosahedrons—(perfect shapes) formed when dividing a sphere based on the exact shape and angle. For the Greeks, these five solids were the core patterns of physical creation. They were seen as the archetypal patterns behind the four elements (earth, air, fire, and water), while the fifth was held to be the pattern behind the life force itself, the ether.

2. Small carved stones found in Scotland conform to the five Platonic solids, which suggest an association with this mathematical principle.

3. √2 proportion is that of the internationally used “A” paper sizes—A4 , the most commonly used, being 210 mm×297 mm.