Robust topology optimization of continuum structures using Monte Carlo method and Kriging models

Resumen

El objetivo de este trabajo es presentar una nueva metodología eficiente y precisa llamada Monte Carlo y Kriging (MCK) para la optimización de topología robusta. El objetivo es minimizar el valor esperado de la compliance considerando la existencia de incertidumbre con cargas concentradas. La incertidumbre en la carga puede presentarse en la magnitud, en la dirección y/o en la posición. La evaluación de la función objetivo se realiza utilizando el método de simulación de Monte Carlo en combinación con un modelo Kriging. Para estimar el valor esperado de la compliance, se transforma el problema probabilístico en otro determinístico sujeto a múltiples estados de carga mediante el Método de Monte Carlo pero empleando un reducido número de evaluaciones del modelo de simulación. Para ello es necesario construir un modelo Kriging del modelo de simulación a partir de una pequeña muestra obtenida con un hipercubo latino del espacio de diseño y predecir la compliance en cada uno de los puntos utilizados por la simulación de Monte Carlo. Dos ejemplos demuestran la precisión y eficiencia del algoritmo. Para verificar el algoritmo propuesto, los problemas también se resuelven mediante el método de Monte Carlo estándar.

Palabras clave: Optimización de topología robusta, incertidumbre de la carga, método de Monte Carlo, modelos Kriging.

Abstract

The aim of this paper is to introduce an efficient and accurate new approach called Monte Carlo and Kriging (MCK) to robust topology optimization. The objective is to minimize the expected value of compliance under concentrated loading uncertainty. The loading uncertainty may occur in magnitude, direction and/or position. The Monte Carlo simulation method and Kriging model are used to evaluate the objective function. To evaluate the expected value of compliance the probabilistic problem is transformed into a multiple loading deterministic one using of Monte Carlo method but with a reduced evaluations number of simulation model. A small sample obtained with a Latin Hypercube is used to build a Kriging model of the simulation model. This is utilized to estimate the compliance in those points used by Monte Carlo simulation method. Two problems are solved to demonstrate the efficiency and accuracy of the approach. The examples are solved again using a standard Monte Carlo simulation to check the proposed approach.

1. Introducción

La optimización estructural ha experimentado un importante crecimiento en las últimas décadas debido a aplicaciones numéricas que permiten automatizar el proceso de diseño. La optimización estructural se puede dividir en tres categorías: tamaño, forma y topología. La optimización de topología es la que mejores resultados aporta, ya que proporciona una mayor libertad a la hora de obtener nuevos diseños conceptuales.

La optimización de topología tiene como objetivo encontrar la mejor distribución de material a partir de la forma y la localización de las cavidades para un dominio de diseño dado. Desde el trabajo original de Bendsoe y Kikuchi [1], la optimización de topología ha experimentado un rápido crecimiento, siendo los métodos más utilizados: el Método de homogeneización [1], el Método SIMP (Solid Isotropic Material with Penalization) [2], el método ESO (Evolutionary Structural Optimization) [3], y el método SA (Simulated Annealing) [4]. En los últimos años han surgido nuevas metodologías como el método LSM (Level Set Method) [5] y el método ITD (Isolines Topology Design) [6]. Una revisión actual sobre los avances realizados en optimización de topología se puede encontrar en Deathon y Grandhi [7]. En el campo industrial, la optimización de topología ha demostrado ser una herramienta potente, aplicándose a un extenso rango de disciplinas físicas tales como la transferencia de calor [8], la acústica [9], la mecánica de fluidos [10], el diseño de materiales [11], etc. También, la optimización de topología se ha convertido en una parte fundamental de muchos softwares como ABAQUS, Genesis, OptiStruct, Permas, ANSYS, etc.

En la mayoría de los casos, el problema de optimización se estudia desde un punto de vista determinista, lo que se denomina como optimización de topología determinista (Deterministic Topology Optimization, DTO), donde los diseños son obtenidos sin considerar de forma explícita la influencia de las diversas fuentes de incertidumbre (o variabilidad) presentes en la realidad, tales como variaciones en las cargas, en las propiedades de material, en la geometría, en las condiciones de contorno, etc. Así pues, una formulación determinista puede afectar al rendimiento y operatividad de la estructura, ya que los diseños óptimos obtenidos solo tienen un comportamiento óptimo bajo condiciones operativas cercanas a los valores utilizados en el proceso de optimización. Tradicionalmente, el efecto de las incertidumbres se ha tenido en cuenta mediante la incorporación de factores de seguridad dentro de la formulación; sin embargo, esta técnica heurística puede conducir a estructuras conservadoras o poco eficientes.

Con objeto de obtener estructuras menos sensibles, más racionales y con un mayor rendimiento ante condiciones reales, en los últimos años ha tomado un gran interés el desarrollo de formulaciones capaces de incluir explícitamente aquellas fuentes de incertidumbre que puedan provocar cambios significativos en el comportamiento y en el rendimiento de la estructura. De forma general, se pueden distinguir dos formulaciones, la optimización de topología basada en fiabilidad y la optimización de topología robusta.

En la optimización de topología basada en fiabilidad (Reability-Based Topology Optimization, RBTO) el problema de optimización se formula como la minimización de una función objetivo determinista sujeta a restricciones de tipo incierto, donde las restricciones son expresadas a través de probabilidades o modos de fallo. Existe una extensa literatura sobre RBTO, pero aquí solo se recogen algunos de los modos de fallo que han sido considerados como estados críticos en deformación [12, 13], en rigidez [14, 15], y en frecuencias naturales [13, 14]. También se han empleado técnicas diferentes para estimar de modo preciso y eficaz los modos de fallo, tales como los métodos FORM y SORM (First and Second Order Reliability Methods) [16], el método de simulación de Monte Carlo [14], el método PMA (Performance Measure Approach) [13], el método RSM (Response Surface Method) [15] y el método SRSM (Stochastic Response Surface Method) [17].

La optimización de topología robusta (Robust Topology Optimization, RTO), se formula como la minimización de una función objetivo probabilística sujeta a una serie de restricciones deterministas. La función objetivo probabilística más popular es la suma ponderada de la media y la desviación estándar de la compliance [18-25], aunque también se utiliza el valor esperado de la compliance [26, 27]. Otra alternativa consiste en tratar el problema como una optimización multiobjetivo [28], donde se optimiza de forma simultanea los objetivos en conflicto (el valor esperado y la desviación estándar) mediante un frente de Pareto (conjunto de óptimos de Pareto, entendiendo como óptimo una solución tal que no existe otra que mejore el valor del objetivo sin deteriorar el resto).

Aunque las dos formulaciones incluyen la aleatoriedad o la incertidumbre dentro del proceso de optimización, difieren básicamente en que RBTO se centra en satisfacer criterios de fiabilidad de eventos extremos mientras que RTO se centra en reducir la variación de la respuesta estructural ante las fluctuaciones diarias. De modo que RBDO se asocia con el daño inducido por fallo y RTO con el gasto derivado de una pobre calidad en el rendimiento estructural.

En la actualidad, la mayoría de los trabajos publicados en RTO, tratan las incertidumbres en la carga [18, 20, 23-27], aunque algunos de estos consideran también las incertidumbres en las propiedades del material [29, 30] y en la geometría [19, 22, 30].

En este trabajo se utiliza la formulación RTO centrada en las incertidumbres en la carga, ya que pequeñas variaciones en sus parámetros pueden provocar grandes cambios en la respuesta estructural. Conti et al. [31] proponen una metodología donde se combina LSM con técnicas de programación estocástica para la optimización de estructuras con incertidumbre en cargas concentradas. Chen et al. [18] proponen una metodología donde integran LSM con una formulación robusta, no solo para considerar la incertidumbre en cargas concentradas, sino también para cargas distribuidas. Las cargas concentradas se modelan como variables aleatorias estadísticamente independientes, mientras que las cargas distribuidas se modelan como campos aleatorios. La alta dimensionalidad del campo aleatorio se transforma en un conjunto finito de variables aleatorias estadísticamente independientes mediante un método espectral como el desarrollo de Karhunen-Loeve. Finalmente, los momentos estadísticos de la compliance se evalúan mediante el método UDR (Univariate Dimension Reduction) en los puntos de cuadratura de Gauss. Dunning y Kim [26] presentan un método analítico para minimizar el valor esperado de la compliance, con incertidumbre en la magnitud y en la dirección de la carga, usando complejas derivadas numéricas. En el caso más desfavorable, el problema RTO se transforma en otro de 3n+1 estados de carga, siendo n el número de cargas con incertidumbre. Sin embargo, la metodología se limita a variables aleatorias estadísticamente independientes definidas mediante distribuciones normales. Dunning y Kim [20] amplían la metodología anterior incorporando la desviación estándar de la compliance en la función objetivo. Zhao y Wang [27] proponen una metodología para evaluar el valor esperado de la compliance, que permite utilizar cualquier tipo de función de probabilidad continua para describir la incertidumbre. Para obtener los momentos estadísticos utilizan el método de Monte Carlo y la descomposición de matrices. Zhao et al. [25] presentan un método para la optimización de topología considerando incertidumbre en la carga, utilizando el método de colocación estocástico para obtener los momentos estadísticos. Los puntos de colocación y sus respectivos pesos se determinan mediante la cuadratura del producto tensorial completo y la cuadratura dispersa de Smolyak, respectivamente.

Todas las metodologías descritas anteriormente transforman el problema RTO en otro sujeto a múltiples estados de carga deterministas en donde los momentos estadísticos se calculan evaluando repetidamente la respuesta para cada uno de los estados de carga. A menudo, el coste computacional del análisis es elevado, por lo que la evaluación de la función objetivo de forma precisa y eficiente es crucial en este tipo de problemas.

Actualmente se usan metamodelos (modelos aproximados), tales como el método RSM [32], los modelos RBF (Radial Basis Function) [33], el método ANNs (Artificial Neural Networks) [34] o los modelos Kriging [35], para reducir el elevado coste computacional asociado con el cálculo de los momentos estadísticos y de los modelos de simulación. Debido a la capacidad para interpolar exactamente los valores de la respuesta en los puntos de muestreo y la flexibilidad para capturar cualquier tipo de comportamiento no lineal, los modelos Kriging son especialmente adecuados para aproximar simulaciones con un elevado coste computacional. Los modelos Kriging se han utilizado con éxito tanto en optimización basada en fiabilidad [36, 37] como en optimización robusta [38, 39], aunque todavía no se han utilizado para RTO de estructuras continuas. La aplicación de modelos Kriging para el diseño óptimo robusto de estructuras articuladas puede verse en Martínez y Martí [40].

En este trabajo se propone una nueva metodología RTO, eficiente y precisa, que permite minimizar el valor esperado de la compliance considerando la existencia de incertidumbre en cargas concentradas. La incertidumbre en la carga puede presentarse en la magnitud, la dirección, la posición o una combinación de ellas, pudiendo ser descrita por cualquier tipo de función de densidad de probabilidad (probability density function, pdf). La evaluación de la función objetivo se realiza utilizando el método de simulación de Monte Carlo en combinación con un modelo Kriging. El objetivo es poder estimar el valor esperado de la compliance de forma precisa, transformando el problema RTO en otro sujeto a múltiples estados de carga mediante el método de simulación de Monte Carlo, pero empleando un número reducido de evaluaciones del modelo de simulación. Para ello, se debe construir un modelo Kriging del modelo de simulación a partir de una pequeña muestra obtenida usando un hipercubo latino del espacio aleatorio y obtener la respuesta estructural en los puntos de muestreo utilizados por la simulación de Monte Carlo. La metodología propuesta en este trabajo permite reducir el coste computacional, sobre todo en los casos donde existe un elevado número de cargas con incertidumbre. La metodología se ha aplicado a problemas bidimensionales, utilizando el método SIMP, aunque se pueden utilizar otros métodos de optimización de topología.

El trabajo se ha organizado en cinco apartados: en el apartado 1 se realiza una revisión del estado del arte sobre el problema RTO. En el apartado 2 se describen los fundamentos teóricos usados para el desarrollo de la metodología propuesta: formulación del problema RTO usando el método SIMP, incertidumbres consideradas, método de simulación de Monte Carlo y modelos Kriging. En el apartado 3 se presenta la metodología y el algoritmo propuesto. En el apartado 4 se muestran los resultados obtenidos para dos ejemplos, y en el apartado 5 se presentan las conclusiones.

2. Fundamentos teóricos

2.1. Formulación RTO con el método SIMP

El objetivo principal de este trabajo es considerar la existencia de incertidumbre en la magnitud, la dirección y/o la posición de cargas concentradas en el problema de optimización de topología utilizando el método SIMP.

El método SIMP fue presentado por Bendsøe [41] y posteriormente desarrollado por Zhou y Rozvany [42]. Actualmente es una de las técnicas más extendidas dentro de los métodos de optimización de topología basados en densidad. La idea básica del método consiste en determinar la mejor distribución de material. Para ello, se discretiza el dominio inicial mediante un conjunto de elementos finitos y se utiliza la densidad de cada elemento ${\textstyle ({\rho }_{e})}$ como variable de diseño para indicar su estado, si es vacío ${\textstyle {\rho }_{e}}$= 0 y si es material ${\textstyle {\rho }_{e}}$=1. Para evitar densidades intermedias y alcanzar soluciones del tipo 0/1, el método SIMP utiliza una ley de interpolación con penalización:

${E}_{e}={E}_{min}+\left(E-{E}_{min}\right){\rho }_{e}^{p}$

(1)

donde ${\textstyle E}$ es el módulo de elasticidad para el material sólido, ${\textstyle {E}_{min}}$ es el módulo de elasticidad para el material vacío y el exponente ${\textstyle p}$ es un factor de penalización, siendo habituales valores ${\textstyle p\geq 1}$. Para evitar inestabilidades numéricas, normalmente se considera que ${\textstyle {E}_{min}}$= ${\textstyle \,E\times ({10}^{-3}\,a\,{10}^{-6})}$.

La relación entre la fuerza aplicada a una estructura y el desplazamiento que induce en la dirección de esta es el término conocido como la compliance ${\textstyle C}$.

$C={\boldsymbol {u}}^{\boldsymbol {T}}{\boldsymbol {f}}$

(2)

donde ${\textstyle {\boldsymbol {u}}}$ es el vector de desplazamientos y ${\textstyle {\boldsymbol {f}}}$ el vector de cargas en los nodos. La aplicación del teorema de Clayperon proporciona una relación entre la compliance ${\textstyle \left(C\right)}$ y la energía elástica de deformación ${\textstyle U}$

$C=2U$

(3)

Por lo que, el valor de la compliance se puede utilizar para determinar el nivel de energía de deformación contenido en la estructura. La compliance proporciona un valor matemático útil y preciso del grado de optimalidad de una estructura, con respecto a la rigidez del conjunto. De forma que minimizar la energía elástica de deformación total de la estructura, minimiza la compliance y de este modo se maximiza la rigidez estructural.

En este trabajo, para poder obtener una estructura óptima robusta, se ha utilizado el valor esperado de la compliance [26, 27], aunque también se puede utilizar una suma ponderada del valor esperado y de la desviación estándar de la compliance. De este modo, el problema RTO se puede formular como minimizar el valor esperado de la compliance ${\textstyle ({\mu }_{C})}$ (Ec. 4.1) sujeto a una ecuación de equilibrio (Ec. 4.2), una restricción de desigualdad (Ec. 4.3) y una de doble desigualdad (Ec. 4.4):

Minimizar:	${\mu }_{C}=E\left[C\left({\boldsymbol {\rho }},{\boldsymbol {z}}\right)\right]=\int _{}^{}C\left({\boldsymbol {\rho }},{\boldsymbol {z}}\right)P\left({\boldsymbol {z}}\right)d{\boldsymbol {z}}$	(4.1)	(4)
sujeto a:	${\boldsymbol {K}}\left({\boldsymbol {\rho }}{\mathit {\boldsymbol {,}}}{\boldsymbol {z}}\right){\boldsymbol {\,u}}\left({\boldsymbol {\rho }}{\mathit {\boldsymbol {,}}}{\boldsymbol {z}}\right)=$${\boldsymbol {f}}({\boldsymbol {z}})$	(4.2)
	${\textstyle V-{V}_{max}}$ ≤ 0	(4.3)
	${\boldsymbol {0}}\leq {\boldsymbol {\rho }}\leq {\boldsymbol {1}}$	(4.4)

donde:

${\boldsymbol {\rho }}$	es el vector de las variables de diseño (densidades de los elementos),
${\boldsymbol {z}}$	es el vector de las variables aleatorias,
$C\left({\boldsymbol {\rho }},{\boldsymbol {z}}\right)$	es la compliance de la estructura,
$P\left({\boldsymbol {z}}\right)$	es la función de densidad de probabilidad que caracteriza la variable aleatoria ${\textstyle {\boldsymbol {z}}}$,
${\boldsymbol {K}}\left({\boldsymbol {\rho }}{\mathit {\boldsymbol {,}}}{\boldsymbol {z}}\right)$	es la matriz de rigidez global,
${\boldsymbol {u}}\left({\boldsymbol {\rho }}{\mathit {\boldsymbol {,}}}{\boldsymbol {z}}\right)$	es el campo de desplazamientos para un vector de fuerzas ${\textstyle {\boldsymbol {f}}\left({\boldsymbol {z}}\right),}$
$V$	es el volumen,
${V}_{max}$	es el volumen máximo admisible.

El problema de optimización (Ec. 4) se puede resolver mediante OC (Optimality Criteria), SLP (Sequencial Linear Progamming), MMA (Method of Moving Asymptotes), etc. [43]. Por simplicidad, el problema se ha resuelto utilizando el Método OC, donde la densidad de cada elemento ${\textstyle {\rho }_{e}}$ se actualiza mediante un esquema heurístico [44]:

${\rho }_{e}^{nuevo}=\left\{{\begin{matrix}\mathrm {max} \,\left(0,{\rho }_{e}-m\right)\\\mathrm {min} \,\left(1,{\rho }_{e}+m\right)\\{\rho }_{e}{B}_{e}^{\eta }\end{matrix}}\right.$ ${\begin{matrix}si\quad {\rho }_{e}{B}_{e}^{\eta }\,\leq \mathrm {max} \,\left(0,{\rho }_{e}-m\right)\,\,\\si\quad {\rho }_{e}{B}_{e}^{\eta }\,\geq \,\mathrm {min} \,\left(1,{\rho }_{e}+m\right)\\otro\,caso\end{matrix}}$

(5)

donde ${\textstyle m}$ es un límite de movimiento, ${\textstyle \eta =}$$0,5$ es un coeficiente de amortiguamiento y ${\textstyle {B}_{e}}$ es la condición de optimalidad:

${B}_{e}={\frac {-{\frac {\partial {\mu }_{C}}{\partial {\rho }_{e}}}}{\lambda {\frac {\partial V}{\partial {\rho }_{e}}}}}$

(6)

siendo ${\textstyle \lambda }$ el multiplicador de Lagrange que garantiza que se satisface la restricción de volumen, cuyo valor se determina usando un algoritmo de bisección.

La sensibilidad de la función objetivo ${\textstyle ({\mu }_{C})}$ y del volumen ( ${\textstyle V}$) con respecto a las variables de diseño se han determinado como:

${\frac {\partial {\mu }_{C}}{\partial {\rho }_{e}}}={\frac {\partial E\left[C\left({\boldsymbol {\rho }},{\boldsymbol {z}}\right)\right]}{\partial {\rho }_{e}}}=$$E\left[{\frac {\partial C\left({\boldsymbol {\rho }},{\boldsymbol {z}}\right)}{\partial {\rho }_{e}}}\right]$	(7)
${\frac {\partial V}{\partial {\rho }_{e}}}={v}_{e}$	(8)

De este modo, la sensibilidad del valor esperado de la función objetivo es igual a la media de la sensibilidad de la compliance, y la sensibilidad del volumen es igual al volumen del elemento ${\textstyle \left({v}_{e}\right)}$ .

Se conoce que los diseños obtenidos usando el método SIMP, pueden presentar soluciones dependientes de la malla (una malla fina puede producir diseños nuevos, en lugar de optimizar los obtenidos con una malla más gruesa), así como una alternancia de elementos sólidos y vacíos ordenados en forma de tablero de ajedrez [45] si no se utiliza algún esquema de regularización.

En general, los métodos para la restricción de la densidad en problemas de optimización de topología se dividen en tres grupos [46-52]: (1) métodos para la independencia de la malla, que se subdividen en filtros de sensibilidades y de densidades; (2) métodos de restricción como el control de perímetro, el control por gradiente local, y la penalización regularizada; y (3) otros métodos como la parametrización de ondas, el campo fase, y las curvas de nivel. Estos esquemas tienen ventajas e inconvenientes y probablemente todavía el esquema ideal no ha sido desarrollado.

Los diseños obtenidos introduciendo un filtro de densidad pueden contener densidades intermedias, lo que dificulta la interpretación del diseño. Por ello, las densidades intermedias, también, se pueden tratar mediante técnicas de proyección a 0/1 [48-51]. Para evitar soluciones dependientes de la malla y patrones del tipo tablero de ajedrez, se ha utilizado en este trabajo el filtro propuesto por Sigmund [49]. Este filtro modifica las sensibilidades de los elementos a partir del promedio ponderado de las sensibilidades de los elementos situados en el entorno cercano, Ec. 9.

${\frac {\hat {{\partial \mu }_{C}}}{\partial {\rho }_{e}}}={\frac {1}{{\rho }_{e}\sum _{i=1}^{N}{\hat {{H}_{i}}}}}\sum _{i=1}^{N}{\hat {{H}_{i}}}{\rho }_{i}{\frac {\partial {\mu }_{C}}{\partial {\rho }_{i}}}$

(9)

donde el operador convolución (factor de ponderación) ${\textstyle {\hat {{H}_{i}}}}$ se define como:

${\hat {{H}_{i}}}={r}_{min}-d\left(e,i\right)$ $\left\{i\in N\right\},k=1,\cdots ,N$

(10)

donde el operador ${\textstyle d\left(e,i\right)}$ se define como la distancia entre el centro del elemento ${\textstyle k}$ y el centro del elemento ${\textstyle i}$. El operador convolución ${\textstyle {\hat {{H}_{i}}}}$ es cero fuera del área del filtro. El operador convolución para el elemento ${\textstyle i}$ disminuye linealmente con la distancia al elemento ${\textstyle e}$, lo que significa que en lugar de utilizar las sensibilidades reales ${\textstyle {\frac {\partial {\mu }_{C}}{\partial {\rho }_{i}}}}$ se utilizan las sensibilidades filtradas ${\textstyle {\frac {\hat {{\partial \mu }_{C}}}{\partial {\rho }_{e}}}}$. Merece la pena resaltar que: (1) cuando el ${\textstyle {r}_{min}}$ (radio de filtro con centro en el elemento ${\textstyle e}$) tiende a cero la sensibilidad filtrada converge a la real; (2) que todas las sensibilidades son iguales (caso de una distribución uniforme de material) cuando el valor de ${\textstyle {r}_{min}}$ tiende a infinito; y (3) que este filtro es puramente heurístico pero produce resultados muy similares a los obtenidos usando control por gradiente local, su implementación es sencilla y solo conlleva un pequeño gasto computacional extra.

Apuntar que en este trabajo para la consecución de la optimización de topología se ha utilizado una versión modificada de la implementación del método SIMP “99 líneas en Matlab” realizada por Sigmund [44].

2.2. Incertidumbres

En este trabajo se consideran las incertidumbres de cargas concentradas. Las cargas se definen por medio de cuatro variables: magnitud (F), dirección (θ), posición respecto al eje x (S_x) y posición con respecto al eje y (S_y), cada una de las cuales pueden presentar o no incertidumbre. Cualquiera de las variables anteriores que presente incertidumbre se caracteriza mediante una pdf.

La totalidad de los trabajos sobre RTO de estructuras continuas encontrados en la bibliografía [18, 20, 23-27] utilizan métodos que requieren adoptar la hipótesis de que las variables aleatorias consideradas son independientes. Aunque esta hipótesis no se cumple en una gran cantidad de casos, los problemas resueltos hasta el momento se han realizado con variables aleatorias independientes. Esta decisión ha permitido, entre otras cosas, la comparación de sus resultados con los existentes en la bibliografía. En trabajos posteriores se analizará el efecto que la dependencia entre las variables aleatorias puede introducir en los parámetros del modelo Kriging.

2.3. Método de simulación de Monte Carlo

El método de simulación Monte Carlo es un método numérico no determinístico, usado para aproximar expresiones matemáticas que resultan costosas si se evalúan con exactitud. El método se llamó así en referencia al Casino de Monte Carlo, por ser la ruleta un generador simple de números aleatorios.

El uso del método de Monte Carlo, como herramienta de investigación, proviene del trabajo realizado en el desarrollo de la bomba atómica durante la Segunda Guerra Mundial en el Laboratorio Nacional de Los Álamos en EE. UU. Su origen se establece en 1949, cuando por primera vez aparece en el título de un artículo de Metropolis y Ulam [53], en el cual se denomina como un método “estadístico numérico para aproximar expresiones matemáticas complejas y costosas de evaluar con exactitud”. Hoy en día, el método de Monte Carlo se utiliza en el desarrollo de reactores nucleares, cromodinámica cuántica, radioterapia, comportamiento de radiación en la atmósfera terrestre, flujos de tráfico, evolución estelar, cálculos y predicciones económicas, búsqueda de petróleo, etc.

La idea del método de Monte Carlo consiste en crear un modelo matemático del sistema que se quiere analizar, identificando aquellas variables que tienen un carácter aleatorio. Una vez determinadas estas variables, se lleva a cabo un diseño de experimentos consistente en generar una muestra para dichas variables aleatorias, y analizar el modelo de simulación para los valores generados.

En este trabajo se utiliza el método de Monte Carlo para evaluar el valor esperado de la compliance (Ec. 4.1). Para ello, el primer paso consiste en identificar las variables aleatorias. Como se ha mencionado, la incertidumbre puede darse en la magnitud, la dirección, la posición respecto al eje x, y la posición respecto al eje y de la carga. Estas variables se consideran estadísticamente independientes. A partir de ellas se genera aleatoriamente una muestra de diseño del espacio multidimensional ${\textstyle {\boldsymbol {Z}}=}$${\left({\boldsymbol {z}}_{\mathit {\boldsymbol {1}}}{\boldsymbol {,\,z}}_{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {,\ldots ,\,}}}{{\boldsymbol {\,z}}_{\mathit {\boldsymbol {i}}}{\mathit {\boldsymbol {,\ldots ,\,}}}{\boldsymbol {z}}}_{{\mathit {\boldsymbol {N}}}_{\mathit {\boldsymbol {MC}}}}\right)}^{T}$, uniformemente distribuida según la pdf con ${\textstyle {\mathit {\boldsymbol {z}}}_{\mathit {\boldsymbol {i}}}\,\in \,{R}^{s}}$, donde la dimensión s es igual al número de variables aleatorias consideradas. Así pues, si se considera que hay una única carga con magnitud y dirección aleatoria, la muestra será ${\textstyle {\boldsymbol {z}}_{\mathit {\boldsymbol {i}}}=}$$\left({F}_{i},\,{\theta }_{i}\right)$ para i = 1,…, N_MC, siendo N_MC el tamaño de la muestra. A partir de la evaluación de la muestra se estima el valor esperado de la compliance, transformando la integral definida en la Ec. 4.1 en la expresión:

${\mu }_{C}\cong {\frac {1}{{N}_{MC}}}\sum _{i=1}^{{N}_{MC}}{C}_{i}\left({\boldsymbol {\rho }},{\boldsymbol {z}}_{\mathit {\boldsymbol {i}}}\right)$

(11)

Esta ecuación permite transformar el problema robusto en otro sujeto a múltiples estados de carga deterministas, siendo necesario evaluar repetidamente el modelo de simulación de la estructura para cada una de las N_MC muestras.

Según Rubinstein y Kroese [54] el método de simulación de Monte Carlo es la metodología más precisa para la estimación de momentos estadísticos de alto orden dimensional, lo que permite: (1) resolver problemas cuya solución es difícil o imposible de resolver, (2) estudiar la interacción entre las diferentes variables aleatorias del problema, y (3) evaluar los momentos estadísticos sin necesidad de modificar el modelo de simulación. Sin embargo, su mayor inconveniente es el elevado coste computacional, el cual es proporcional al tamaño de la muestra. La precisión de la estimación depende del tamaño de la muestra; en concreto, según el teorema del límite central, para ${\textstyle {N}_{MC}}$ grandes, el promedio de la muestra tiene distribución aproximadamente normal con media igual a la media de la variable original y desviación estándar la de la variable dividida por la raíz cuadrada de ${\textstyle {N}_{MC}}$. Así, la desviación estándar de la variable se puede estimar por medio de la desviación estándar de la muestra (Ec. 12):

$\sigma ={\sqrt {{\frac {1}{{N}_{MC}}}\left(\sum _{i=1}^{n}{{C}_{i}\left({\boldsymbol {\rho }},{\boldsymbol {z}}_{\mathit {\boldsymbol {i}}}\right)}^{2}-{{\mu }_{C}}^{2}\right)}}$

(12)

Actualmente se han desarrollado alternativas para mejorar la eficiencia numérica, tales como el muestreo por importancia, el muestreo estratificado, etc. [55].

En este trabajo se ha utilizado el método de simulación de Monte Carlo, ya que permite resolver el problema como una suma ponderada de múltiples estados de carga deterministas, donde la precisión del método solo depende del tamaño de la muestra y no de la dimensionalidad del problema, lo que resulta muy útil en problemas con una alta dimensionalidad.

2.4. Metamodelos

Los metamodelos (modelos de modelos) se utilizan para sustituir a un modelo de simulación cuya evaluación tiene un alto coste computacional. Estos metamodelos pueden utilizarse, entre otras aplicaciones, para acelerar el proceso de optimización y para realizar visualizaciones y exploraciones del espacio de diseño óptimo. En la literatura especializada existe una gran variedad de metamodelos, tales como las superficies de respuesta [32], los modelos Kriging [56], las funciones de base radial [57], o las redes neuronales [58]. De entre las diferentes técnicas de metamodelos, los modelos Kriging han alcanzado una gran popularidad en los últimos años, debido a: 1) su gran flexibilidad para aproximar respuestas con alto grado de no linealidad [59]; 2) ser especialmente adecuados para aproximar simulaciones con un elevado coste computacional; 3) que en su formulación se imponen las condiciones para que el modelo sea un estimador lineal insesgado de los valores interpolados, y 4) proporcionan información estadística del error cometido en la predicción [60, 61].

2.4.1. Modelos Kriging

Los modelos Kriging surgieron en los años 50 para estimar las reservas en las minas de oro de Sudáfrica por el ingeniero minero Daniel Krige y el estadista Herbert Shichel. Posteriormente, Matheron adoptó el trabajo original realizado por Daniel Krige y formuló matemáticamente la mayor parte de los conceptos teóricos [61].

Los modelos Kriging están basados en la interpolación estocástica, utilizando un modelo de regresión que considera la correlación existente entre éste y las observaciones para construir un modelo aproximado ${\textstyle {\hat {y}}({\mathit {\boldsymbol {x}}})}$, computacionalmente menos costoso que el modelo de simulación ${\textstyle y\left({\boldsymbol {x}}\right)\,}$ [35].

A continuación se presentan los aspectos fundamentales de los modelos Kriging para una sola respuesta y(x). La generalización para múltiples respuestas ( ${\textstyle {y}_{l}\left({\boldsymbol {x}}\right),\,l=}$$1,\ldots q)$, y otros detalles de la formulación, puede verse en [56].

Dados un conjunto de m puntos de diseño ${\textstyle S={\left[{s}_{1}\ldots {s}_{m}\right]}^{T}\,con\,\,{s}_{i}\in {R}^{n}}$ y sus respuestas ${\textstyle Y=}$${\left[{y}_{1}\ldots {y}_{m}\right]}^{T}$, el modelo Kriging ${\textstyle {\hat {y}}\left({\boldsymbol {x}}\right)}$ expresa la respuesta y(x) para un vector de entrada n-dimensional ${\textstyle {\boldsymbol {x}}\in {R}^{n}\,}$ como una realización de un modelo de regresión ${\textstyle F}$ y una función aleatoria (proceso estocástico):

${\hat {y}}\left({\boldsymbol {x}}\right)=F\left({\boldsymbol {\beta ,x}}\right)+$$z\left({\boldsymbol {x}}\right)$

(13)

Como modelo de regresión se utiliza una combinación lineal de p funciones elegidas previamente ${\textstyle {f}_{j}}$:

$F\left({\boldsymbol {\beta ,x}}\right)={\beta }_{1}{f}_{1}\left({\boldsymbol {x}}\right){\boldsymbol {+\ldots +\,}}{\beta }_{p}{f}_{p}\left({\boldsymbol {x}}\right)=$${\boldsymbol {f}}{\left({\boldsymbol {x}}\right)}^{T}{\boldsymbol {\beta }}$

(14)

siendo ${\textstyle {{\boldsymbol {f}}\left({\boldsymbol {x}}\right)}^{T}=}$$\left[{f}_{1}\left({\boldsymbol {x}}\right){\mathit {\boldsymbol {\ldots }}}{f}_{p}\left({\boldsymbol {x}}\right)\right]$ las funciones base y ${\textstyle \,{\boldsymbol {\beta }}{\mathit {\boldsymbol {\,}}}}$ el vector de parámetros de regresión.

El proceso aleatorio z se supone que tiene media cero y covarianza:

$E\left(z\left({\boldsymbol {w}}\right),z\left({\boldsymbol {x}}\right)\right)={\sigma }^{2}R\left(\theta ,{\boldsymbol {w}},{\boldsymbol {x}}\right)$

(15)

entre z(w) y z(x), donde ${\textstyle {\sigma }^{2}}$ es la varianza del proceso para la respuesta y ${\textstyle R\left(\theta ,{\boldsymbol {w}},{\boldsymbol {x}}\right)}$ el modelo de correlación con parámetros ${\textstyle \theta }$ .

El valor verdadero de la función para un punto x puede ponerse en la forma:

$y\left({\boldsymbol {x}}\right)=F\left({\boldsymbol {\beta ,x}}\right)+$$\alpha \left({\boldsymbol {\beta ,x}}\right)$

(16)

donde ${\textstyle \alpha \left({\boldsymbol {\beta ,x}}\right)}$ es el error de la aproximación. La hipótesis es que con una elección adecuada de ${\textstyle {\boldsymbol {\beta }}}$ el error es del tipo “ruido blanco” en la región de interés de la aproximación.

Para el conjunto S de puntos de diseño se tiene el vector F de respuestas:

${\boldsymbol {F}}={\left[f({s}_{1})\ldots f({s}_{m})\right]}^{T}$

(17)

con f(x) definido en la Ec. 14. Se define R como la matriz de correlaciones del proceso estocástico entre los z en los puntos de diseño:

${R}_{ij}=R\left(\theta ,{s}_{i},{s}_{j}\right),\quad i,j=1,...,m$

(18)

Para un punto x no introducido, sea:

${\boldsymbol {r}}\left(x\right)={\left[R\left(\theta ,{s}_{1},x\right)\ldots \,R\left(\theta ,{s}_{m},x\right)\right]}^{T}$

(19)

el vector de correlaciones entre las z en los puntos de diseño y el punto x.

Se considera el estimador lineal:

${\hat {y}}\left({\boldsymbol {x}}\right)=\,{\boldsymbol {c}}^{T}{\boldsymbol {Y}}$

(20)

con c = c(x) ${\textstyle \in {R}^{m}}$. El error es:

${\hat {y}}\left({\boldsymbol {x}}\right)-y\left({\boldsymbol {x}}\right)=\,{\boldsymbol {c}}^{T}{\boldsymbol {Y-}}y\left({\boldsymbol {x}}\right)=$${\boldsymbol {c}}^{T}\left({\boldsymbol {F\beta +Z}}\right)-\left({{\mathit {\boldsymbol {f}}}\left({\boldsymbol {x}}\right)}^{T}{\boldsymbol {\beta +z}}\right)=$${\boldsymbol {c}}^{T}{\boldsymbol {Z-z+}}{\left({\boldsymbol {F}}^{T}{\boldsymbol {c}}{\mathit {\boldsymbol {-f(}}}{\boldsymbol {x}}{\mathit {\boldsymbol {)}}}\right)}^{T}{\boldsymbol {\beta }}$

(21)

donde ${\textstyle {\boldsymbol {Z}}={\left[{z}_{1}\ldots \,{z}_{m}\right]}^{T}}$ son los errores en los puntos de diseño. Para mantener el estimador insesgado se exige la condición:

${\boldsymbol {F}}^{\mathit {\boldsymbol {T}}}{\boldsymbol {c}}\left({\boldsymbol {x}}\right){\mathit {\boldsymbol {=f(x)}}}$

(22)

Con esta condición el error cuadrático medio del estimador de la Ec. 20 es:

$\varphi \left({\mathit {\boldsymbol {x}}}\right)=E\left[{\left({\hat {y}}\left({\boldsymbol {x}}\right)-y\left({\boldsymbol {x}}\right)\right)}^{2}\right]=$$E\left[{\left({\boldsymbol {c}}^{T}{\boldsymbol {Z-z}}\right)}^{2}\right]=E\left[{\boldsymbol {z}}^{2}+\right.$$\left.{\boldsymbol {c}}^{T}{\mathit {\boldsymbol {Z}}}{\boldsymbol {Z}}^{T}{\boldsymbol {c}}-\right.$$\left.2{\boldsymbol {c}}^{T}{\boldsymbol {Zz}}\right]={\sigma }^{2}\left(1+{\boldsymbol {c}}^{T}{\boldsymbol {Rc-2}}{\boldsymbol {c}}^{T}{\boldsymbol {r}}\right)$

(23)

La función Lagrangiana para el problema de minimizar el error ${\textstyle \varphi }$ con respecto a c, sujeto a las restricciones de la Ec. 21 es:

$L\left({\boldsymbol {c}}{\mathit {\boldsymbol {,}}}{\boldsymbol {\lambda }}\right)=$${\sigma }^{2}\left(1+{\boldsymbol {c}}^{T}{\boldsymbol {Rc-2}}{\boldsymbol {c}}^{T}{\boldsymbol {r}}\right)-$${\boldsymbol {\lambda }}^{T}\left({\boldsymbol {F}}^{T}{\boldsymbol {c}}{\mathit {\boldsymbol {-f}}}\right)$

(24)

El gradiente de la Ec. 24 con respecto a c es:

${L}^{'}\left({\boldsymbol {c}}{\mathit {\boldsymbol {,}}}{\boldsymbol {\lambda }}\right){\mathit {\boldsymbol {=2}}}{\sigma }^{2}\left({\boldsymbol {Rc-r}}\right)-$${\boldsymbol {F\lambda }}$

(25)

y a partir de las condiciones de primer orden necesarias para la optimalidad, se obtiene el sistema de ecuaciones:

$\left[{\begin{matrix}{\boldsymbol {R}}&{\boldsymbol {F}}\\{\boldsymbol {F}}^{T}&{\mathit {\boldsymbol {0}}}\end{matrix}}\right]\left[{\begin{matrix}{\boldsymbol {c}}\\{\tilde {\boldsymbol {\lambda }}}\end{matrix}}\right]=$$\left[{\begin{matrix}{\boldsymbol {r}}\\{\boldsymbol {f}}\end{matrix}}\right]$

(26)

donde ${\textstyle {\tilde {\boldsymbol {\lambda }}}=-{\frac {\boldsymbol {\lambda }}{2{\sigma }^{2}}}}$.

La solución del sistema de ecuaciones de la Ec. 26 es:

${\begin{matrix}{\tilde {\boldsymbol {\lambda }}}={\left({\boldsymbol {F}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {F}}\right)}^{-1}\left({\boldsymbol {F}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {r-f}}\right)\\{\boldsymbol {c}}={\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}\left({\boldsymbol {r-F}}{\tilde {\boldsymbol {\lambda }}}\right)\end{matrix}}$

(27)

Sustituyendo la Ec. 27 en la Ec. 20, y teniendo en cuenta que la matriz R es simétrica, y por lo tanto también lo es su inversa R^-1, se obtiene:

${\begin{matrix}{\tilde {y}}({\boldsymbol {x}})={\left({\boldsymbol {r-F}}{\tilde {\boldsymbol {\lambda }}}\right)}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {Y}}\\={\boldsymbol {r}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {Y-}}{\left({\boldsymbol {F}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {r-f}}\right)}^{T}{\left({\boldsymbol {F}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {F}}\right)}^{-1}{\boldsymbol {F}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {Y}}\end{matrix}}$

(28)

La solución de mínimos cuadrados para el problema de regresión ${\textstyle {\boldsymbol {F\beta \cong Y}}}$ es:

${\boldsymbol {\beta }}^{\mathit {\boldsymbol {\ast }}}={\left({\boldsymbol {F}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {F}}\right)}^{-1}{\boldsymbol {F}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {Y}}$

(29)

Al sustituir la Ec. 29 en la Ec. 28 se obtiene la expresión final del estimador:

${\begin{matrix}{\tilde {y}}({\boldsymbol {x}})={\boldsymbol {r}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {Y-}}{\left({\boldsymbol {F}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}{\boldsymbol {r-f}}\right)}^{T}{\boldsymbol {\beta }}^{\mathit {\boldsymbol {\ast }}}\\={\boldsymbol {f}}^{T}{\boldsymbol {\beta }}^{\mathit {\boldsymbol {\ast }}}{\mathit {\boldsymbol {+}}}{\boldsymbol {r}}^{T}{\boldsymbol {R}}^{\mathit {\boldsymbol {-1}}}\left({\boldsymbol {Y}}{\mathit {\boldsymbol {-}}}{\boldsymbol {F}}{\boldsymbol {\beta }}^{\mathit {\boldsymbol {\ast }}}\right)\end{matrix}}$

(30)

Si se sustituye uno de los puntos de diseño (s_i) en la Ec. 30 se obtiene que ${\textstyle {\tilde {y}}\left({s}_{i}\right)=}$$y\left({s}_{i}\right)$ , lo que demuestra que los modelos Kriging pasan por todos los puntos de diseño.

Modelos de regresión. Los modelos de regresión considerados son polinomios de orden 0, 1 y 2 (tabla 1).

Tabla 1. Modelos de regresión con polinomios de orden 0, 1 y 2.

Orden polinomio	Número de funciones	Funciones base
Constante (orden 0)	p = 1	f1(x) = 1
Lineal (orden 1)	p = n+1	f1(x) = 1, f2(x) = x1,…, fn+1(x) = xn
Cuadrática (orden 2)	p = 0,5(n+1)(n+2)	f1(x) = 1, f2(x) = x1,…, fn+1(x) = xn fn+2(x) = x12,…, f2n+1(x) = x1x2 f2n+2(x) = x22,…, f3n(x) = x2xn fp(x) = xn2

Modelo de correlación. El modelo de correlación utilizado es el exponencial generalizado:

$R\left(\theta ,{\boldsymbol {w}},{\boldsymbol {x}}\right)=\mathrm {exp} \,\left(-\sum _{l=1}^{q}{\theta }_{l}{\left|{\boldsymbol {x}}_{il}-{\boldsymbol {x}}_{jl}\right|}^{{p}_{l}}\right),\quad 0\leq {p}_{l}\leq 2$

(31)

Este modelo tiene la propiedad que si ${\textstyle {\boldsymbol {x}}_{i}=}$${\boldsymbol {x}}_{\boldsymbol {j}}$ la correlación es 1, y si | ${\textstyle {\boldsymbol {x}}_{i}-}$${\boldsymbol {x}}_{j}$| tiende a ∞, la correlación tiende a cero. El parámetro θ_l determina la rapidez con la que la correlación “cae” a medida que se mueve en la dirección coordenada l, y el exponente ${\textstyle {p}_{l}\,determina\,la\,suavidad\,de\,la\,funci{\acute {o}}n\,en\,la\,direcci{\acute {o}}n\,coordenada\,l.}$

Las funciones de correlación y de regresión más adecuadas dependen de las características de la función a aproximar. En este trabajo se han considerado los modelos de regresión de orden cero, uno y dos de la Tabla 1, en combinación con el modelo de correlación exponencial generalizado. En general, la elección de las funciones de correlación y regresión se puede realizar “a priori”, en base al conocimiento que se tenga de las funciones a aproximar, o en base al error cuadrático medio (Root Mean Square Error, RMSE) y al coeficiente de determinación (R²). Estos dos indicadores se obtienen utilizando las respuestas del modelo de simulación (y(x)) para una muestra de validación (x_v) de tamaño m_v:

$RMSE={\sqrt {\frac {\sum _{i=1}^{{m}_{v}}{\left({y}_{i}\left({\boldsymbol {x}}_{v}\right)-{\hat {y}}_{i}\left({\boldsymbol {x}}_{v}\right)\right)}^{2}}{{m}_{v}}}}$	(32)
${R}^{2}=1-{\frac {\sum _{i=1}^{{m}_{v}}{\left({y}_{i}\left({\boldsymbol {x}}_{v}\right)-{\hat {y}}_{i}\left({\boldsymbol {x}}_{v}\right)\right)}^{2}}{\sum _{i=1}^{{m}_{v}}{\left({y}_{i}\left({\boldsymbol {x}}_{v}\right)-{\overline {y}}_{i}\left({\boldsymbol {x}}_{v}\right)\right)}^{2}}}$	(33)

donde ${\textstyle {\overline {y}}_{i}\left({\boldsymbol {x}}_{v}\right)}$ es la media de los valores obtenidos, con el modelo de simulación, para la muestra de validación.

En este trabajo, el modelo Kriging se ha utilizado para estimar el valor esperado de la compliance (Ec. 11) a partir de un diseño de experimentos con un tamaño de población mucho menor que el de la muestra original (N_{K <<} N_MC). Para ello, primero se genera una población mediante un hipercubo latino ${\textstyle {\boldsymbol {S}}=}$${\left({\boldsymbol {s}}_{\mathit {\boldsymbol {1\,}}}{\boldsymbol {s}}_{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {\ldots \,}}}{\boldsymbol {s}}_{{\mathit {\boldsymbol {N}}}_{\mathit {\boldsymbol {k}}}}\right)}^{T}$, donde la dimensión s es igual al número de variables aleatorias consideradas. A continuación, se analiza el modelo de simulación, obteniendo la compliance para cada uno de los puntos ${\textstyle {\boldsymbol {C}}=}$${\left({C}_{1}\,{C}_{2}\ldots \,{C}_{{N}_{K}}\right)}^{T}$. A partir del espacio de diseño y la respuesta estructural, se ajustan los parámetros del modelo Kriging ${\textstyle {\hat {y}}({\boldsymbol {S,C}})}$ de modo que aproxime de la mejor forma posible el modelo de simulación. Una vez se ha generado el modelo Kriging, se predice la compliance en los puntos de muestreo del método de Monte Carlo
${\textstyle {\hat {\boldsymbol {C}}}=}$${\left({\hat {C}}_{1}\,{\hat {C}}_{2}\ldots \,{\hat {C}}_{{N}_{MC}}\right)}^{T}$ y a partir de estos, se evalúa el valor esperado de la compliance ${\textstyle {\,{\hat {\mu }}}_{C}}$:

${\hat {\mu }}_{C}\cong {\frac {1}{n}}\sum _{i=1}^{n}{\hat {C}}_{i}\left({\boldsymbol {\rho }},{\boldsymbol {z}}_{\mathit {\boldsymbol {i}}}\right)$

(34)

Para generar el modelo Kriging se ha utilizado la toolbox DACE [62], muy utilizada como así se recoge en la bibliografía [63-65].

3. Algoritmo de optimización

En este apartado se describe el algoritmo para la optimización de topología robusta de estructuras continuas bidimensionales considerando la existencia de incertidumbre en cargas concentradas. La incertidumbre de la carga se puede presentar en la magnitud, la dirección y/o la posición de la misma. Estas variables aleatorias se consideran estadísticamente independientes. La función objetivo a minimizar es el valor esperado de la compliance. Para su evaluación de forma precisa, pero con un reducido número de evaluaciones, se combina el método de Monte Carlo con el modelo Kriging. A continuación se describen los pasos en los que se ha dividido el algoritmo:

1. Definir las características del dominio inicial de la estructura (número de elementos en la dimensión x, número de elementos en la dimensión y, propiedades del material, regiones optimizables y no optimizables, etc.).

2. Definir los parámetros de la optimización (fracción de volumen, factor de penalización, radio de filtro, tamaño de la muestra (N_MC), tamaño del diseño de experimentos (N_K), etc.).

3. Definir las características de las cargas con incertidumbre (número de cargas con incertidumbre, identificar variables de la carga con aleatoriedad, pdf para cada una de las variables).

4. Generar una muestra uniformemente distribuida de modo aleatorio según las pdfs ${\textstyle {\boldsymbol {Z}}=}$${\left({\boldsymbol {z}}_{\mathit {\boldsymbol {1\,}}}{\mathit {\boldsymbol {\,}}}{\boldsymbol {z}}_{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {\ldots \,}}}{\boldsymbol {z}}_{{\mathit {\boldsymbol {N}}}_{\mathit {\boldsymbol {MC}}}}\right)}^{T}$ de tamaño N_MC.

5. Generar el modelo Kriging utilizando la toolbox DACE.

5.1. Diseño de experimentos mediante hipercubo latino con un tamaño de población de N_k puntos, ${\textstyle {\boldsymbol {S}}=}$${\left({\boldsymbol {s}}_{\mathit {\boldsymbol {1\,}}}{\mathit {\boldsymbol {\,}}}{\boldsymbol {s}}_{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {\ldots \,}}}{\boldsymbol {s}}_{{\mathit {\boldsymbol {N}}}_{\mathit {\boldsymbol {k}}}}\right)}^{T}$.

5.2. Obtener la compliance, usando el modelo de simulación, ${\textstyle {\boldsymbol {C}}=}$${\left({C}_{1}\,{C}_{2}\ldots \,{C}_{{N}_{k}}\right)}^{T}$ para la muestra generada ${\textstyle {\left({\boldsymbol {s}}_{\mathit {\boldsymbol {1\,}}}{\mathit {\boldsymbol {\,}}}{\boldsymbol {s}}_{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {\ldots \,}}}{\boldsymbol {s}}_{{\mathit {\boldsymbol {N}}}_{\mathit {\boldsymbol {K}}}}\right)}^{T}}$.

5.3. Ajustar los parámetros del modelo Kriging a partir de la muestra generada y su compliance ${\textstyle {\hat {y}}({\mathit {\boldsymbol {S}}}{\boldsymbol {,C}})}$.

6. Estimar la respuesta estructural ${\textstyle {\hat {\boldsymbol {C}}}=}$${\left({\hat {C}}_{1}\,{\hat {C}}_{2}\ldots \,{\hat {C}}_{{N}_{MK}}\right)}^{T}$ para cada uno de los puntos de la muestra Monte Carlo ${\textstyle {\boldsymbol {Z}}=}$${\left({\boldsymbol {z}}_{\mathit {\boldsymbol {1\,}}}{\mathit {\boldsymbol {\,}}}{\mathit {\boldsymbol {z}}}_{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {\ldots \,}}}{\boldsymbol {z}}_{{\mathit {\boldsymbol {N}}}_{\mathit {\boldsymbol {MC}}}}\right)}^{T}$ a partir del modelo Kriging.

7. Evaluar el valor esperado de la compliance ${\textstyle \left({\hat {\mu }}_{C}\right)}$ y la sensibilidad de la compliance usando las Ec. 11 y Ec. 7, respectivamente.

8. Actualizar la distribución de las densidades mediante la Ec. 5.

9. Si no se cumple el criterio de parada volver al punto 5. En caso contrario parar. Como criterio de parada se ha utilizado que la diferencia de compliance entre la iteración actual y la anterior sea inferior a un nivel mínimo de cambio.

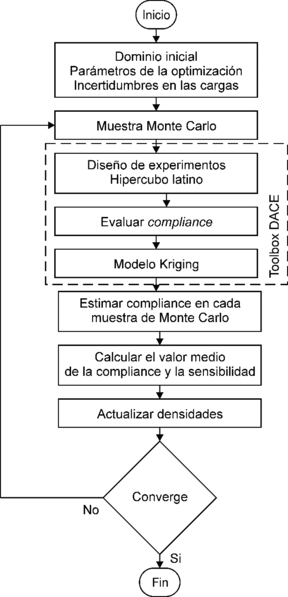
En la Figura 1 se muestra un diagrama de flujo del algoritmo de optimización.

Figura 1. Diagrama de flujo. Algoritmo para la RTO considerando incertidumbre en la carga con el método de Monte Carlo con Kriging.

4. Ejemplos

En este apartado se pretende mostrar la validez del algoritmo propuesto, al que se denomina MCK (Monte Carlo con Kriging), mediante la resolución de dos ejemplos, una viga en voladizo y una T-invertida. Para los dos ejemplos el módulo de Young es de 1 para una región sólida y de 10^-6 para una región vacía, el coeficiente de Poisson ν = 0,3. El tipo de elemento finito utilizado es cuadrado lineal de tamaño unidad. Para la optimización con SIMP se utiliza un factor de penalización p = 3 y un radio de filtro r = 2. El sistema de unidades es coherente.

Con objeto de validar el algoritmo MCK, las soluciones obtenidas se han comparado con las obtenidas utilizando el método de simulación de Monte Carlo, que denominaremos MC. La precisión del método se determina a partir del error relativo ${\textstyle {E}_{r}}$:

${E}_{r}={\frac {\left({{\mu }_{C}}_{\left(MC\right)}-{{\mu }_{C}}_{\left(MCK\right)}\right)}{{{\mu }_{C}}_{\left(MC\right)}}}\,\,100$

(35)

donde ${\textstyle {{\mu }_{C}}_{(MC)}}$ y ${\textstyle {{\mu }_{C}}_{(MCK)}}$ es el valor esperado de la compliance obtenida con MC y MCK, respectivamente. Por otro lado, la eficiencia del método se determina mediante ahorro en tiempo computacional ${\textstyle {E}_{t}}$:

${E}_{t}={\frac {\left({t}_{\left(MC\right)}-{t}_{\left(MCK\right)}\right)}{{t}_{\left(MC\right)}}}\,\,100$

(36)

donde ${\textstyle {t}_{(MC)\,}}$ y ${\textstyle {t}_{(MCK)}}$ son los tiempos medios por iteración con MC y MCK, respectivamente.

En los dos ejemplos se han utilizado funciones base de orden cero para el modelo de regresión. Las funciones de base de orden cero son las más utilizadas en la bibliografía y constituyen el denominado Ordinary Kriging. Para el modelo de correlación se ha adoptado el modelo exponencial generalizado, con p_l = 1 y adoptando el mismo parámetro ${\textstyle {\theta }_{l}\,}$ para todas las direcciones coordenadas, lo que lo convierte en un modelo exponencial isótropo.

4.1. Viga en voladizo

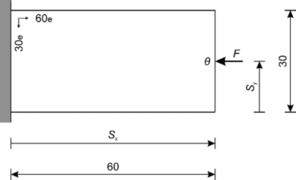
El primer ejemplo para mostrar el efecto de considerar la existencia de incertidumbre en la magnitud, dirección y/o posición de la carga, es una viga en voladizo (Figura 2), la cual es optimizada mediante 6 configuraciones de carga (Tabla 2). La posición de la carga se define mediante dos variables S_x y S_y con respecto a la longitud y al ancho del dominio inicial. La carga se define mediante el módulo F y la dirección θ. En la optimización se utiliza una restricción de volumen de ${\textstyle ({V}_{f}/{V}_{0})=}$ 0,3, siendo ${\textstyle {V}_{f}}$ el volumen final y ${\textstyle {V}_{0}}$ el volumen inicial.

Figura 2. Viga en voladizo. Dominio de diseño y carga aplicada.

Para las variables con incertidumbre que definen la carga (F, θ, S_x, S_y), se han considerado pdf de variables aleatorias normales N(𝜇; 𝜎) de media 𝜇 y desviación estándar 𝜎, y con truncamiento por la izquierda y por la derecha para las variables S_x y S_y. Las variables sin incertidumbre se han definido mediante su valor nominal.

La configuración de carga 1 hace referencia a la optimización determinista; las configuraciones de carga 2, 3 y 4 hacen referencia a RTO donde solo se tiene en cuenta la incertidumbre en la magnitud, la dirección y la posición de la carga, respectivamente; la configuración de carga 5 hace referencia a una RTO donde se considera la existencia simultánea de incertidumbre en la magnitud y dirección de la carga; y la configuración de carga 6 hace referencia a una RTO donde se considera la existencia simultánea de incertidumbre en la magnitud, la dirección y la posición de la carga. Los parámetros utilizados para describir las pdfs que caracterizan la incertidumbre en la magnitud y la dirección de la carga son los utilizados por Dunning et al. [26]. Lógó [66] describe la incertidumbre de la posición de la carga mediante una pdf normal, pero no detalla los parámetros para su caracterización. En este trabajo la incertidumbre en la posición de la carga se define mediante una función normal, cuyos parámetros han sido elegidos de manera que la carga pueda situarse a lo largo de todo el borde lateral, pero con una mayor probabilidad de situarse sobre el centro.

Tabla 2. Viga en voladizo. Parámetros de las configuraciones analizadas.

Configuración	F	θ (rad)	Sx 0 ≤ Sx ≤ 1	Sy 0 ≤ Sy ≤ 1	NMC	Nk
1	1	0 rad	1	0,5	-	-
2	N(1,0; 0,5)	0 rad	1	0,5	10000	10
3	1	N(0,0; 0,25)	1	0,5	10000	10
4	1	0 rad	1	NT(0,5; 0,17)	10000	10
5	N(1,0; 0,5)	N(0,0; 0,25)	1	0,5	10000	10
6	N(1,0; 0,5)	N(0,0; 0,25)	1	NT(0,5; 0,17)	10000	10

Configuración 1: Optimización determinista

La configuración 1 corresponde al caso determinista, donde todas las variables se han caracterizado por su valor nominal. La solución es una barra recta horizontal (Figura 3), obteniendo un valor para la compliance de 16,67. Sin embargo, si se analiza la topología determinista considerando las incertidumbres de los casos 2, 3, 4, 5 y 6, el valor esperado de la compliance aumenta a 15,45; 275,73; 450,77; 926,13 y 1763,91, respectivamente. Estos valores demuestran que la topología óptima determinista se puede comportar de forma poco fiable ante la presencia de cargas inciertas. Los valores esperados de la compliance para los casos 2, 3 y 4 revelan como la incertidumbre en la posición tiene una mayor influencia en el comportamiento estructural que la incertidumbre en la dirección, y como éstas tienen una mayor influencia que la incertidumbre en la magnitud.

Figura 3. Viga en voladizo. Diseño óptimo determinista.

Configuración 2: Incertidumbre en la magnitud de la carga

Para la configuración 2 se realiza la RTO considerando la existencia de incertidumbre en la magnitud de la carga. En la Figura 4, se muestra que la solución coincide con la obtenida para el diseño determinista ya que esta disposición es la que proporciona una mayor rigidez para cargas horizontales. El valor esperado de la compliance usando MC y MCK es de 14,19 y 13,78 respectivamente, lo que supone un error relativo del 2,88%. El tiempo computacional medio por iteración con MC y MCK es de 11389,4 y 6,81 segundos, respectivamente, lo que supone un ahorro del 99,94%.

(a)	(b)
Figura 4. Viga en voladizo. Diseño óptimo robusto considerando incertidumbre en la magnitud de la carga. (a) MC, (b) MCK.

Configuración 3: Incertidumbre en la dirección de la carga

Para la configuración 3 se realiza la RTO considerando la existencia de incertidumbre en la dirección de la carga. Los diseños obtenidos (Figura 5) pasan de ser una barra horizontal, como en el caso de la optimización determinista, a ser dos barras inclinadas. El ángulo entre las barras depende del valor de la desviación estándar de la dirección de la carga, ya que cuanto mayor sea, mayor es la componente vertical de la fuerza. El valor esperado de la compliance con MC y MCK es de 27,68 y 29,96, respectivamente, lo que supone un error relativo del 2,60%. El tiempo computacional medio por iteración usando MC y MCK es de 20638,5 y 12,99 segundos, respectivamente, lo que supone un ahorro del 99,93%.

(a)	(b)
Figura 5. Viga en voladizo. Diseño óptimo robusto considerando incertidumbre en la dirección de la carga. (a) MC, (b) MCK.

Configuración 4: Incertidumbre en la posición de la carga

Para la configuración 4 se realiza la RTO considerando la existencia de incertidumbre en la posición de la carga. Los diseños obtenidos (Figura 6) presentan una amplia zona con material en el extremo derecho del dominio, debido a las diferentes posiciones en las que puede situarse la carga. El valor esperado de la compliance es de 25,58 y 24,93 usando MC y MCK, respectivamente, lo que supone un error relativo del 2,54%. El tiempo computacional medio por iteración usando MC y MCK es de 10763,3 y 6,64 segundos, respectivamente, lo que supone un ahorro del 99,93%.

(a)	(b)
Figura 6. Viga en voladizo. Diseño óptimo robusto considerando incertidumbre en la posición de la carga. (a) MC, (b) MCK.

Configuración 5: Incertidumbre en la magnitud y en la dirección de la carga

Para la configuración 5 se realiza la RTO considerando la existencia simultánea de incertidumbre en la magnitud y la dirección de la carga. Los diseños obtenidos (Figura 7) están constituidos por dos barras inclinadas, debido a que la influencia de la incertidumbre en la dirección de la carga es mucho más importante que la incertidumbre en la magnitud. El valor esperado de la compliance con MC y MCK es de 25,04 y 24,82, respectivamente, lo que supone un error del 0,87%. El tiempo computacional medio por iteración usando MC y MCK es de 16646,8 y 7,12 segundos, respectivamente, suponiendo un ahorro del 99,95%.

(a)	(b)
Figura 7. Viga en voladizo. Diseño óptimo robusto considerando incertidumbre en la magnitud y dirección de la carga. (a) MC, (b) MCK.

Configuración 6: Incertidumbre en la magnitud, en la dirección y en la posición de la carga

Para la configuración 6 se realiza la RTO considerando de forma simultánea la existencia de incertidumbre en la magnitud, en la dirección y en la posición de la carga. En la Figura 8 se muestran las soluciones obtenidas. Las topologías presentan una disposición que viene determinada por la incertidumbre en la posición de la carga al ser ésta la que mayor influencia tiene sobre el problema. El valor esperado de la compliance con MC y MCK es de 52,13 y 49,96, respectivamente, lo que supone un error del 4,16%. El tiempo computacional medio por iteración usando MC y MCK es de 16162,5 y 7,02 segundos, respectivamente, lo que supone un ahorro del 99,95%.

(a)	(b)
Figura 8. Viga en Voladizo. Diseño óptimo robusto considerando incertidumbre en la magnitud, en la dirección y en la posición de la carga. (a) MC, (b) MCK.

A través de las configuraciones estudiadas, se puede concluir que: (1) las soluciones óptimas obtenidas usando RTO se comportan de forma más eficiente que la topología determinista ante la presencia de incertidumbres en la carga, (2) el algoritmo MCK proporciona soluciones igual de precisas que usando MC, y (3) el ahorro en tiempo computacional es como mínimo del 99,9% siendo el error en todos los casos estudiados inferior al 5%.

4.2. T-invertida

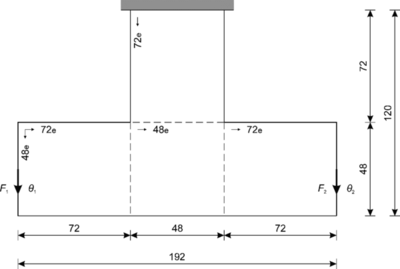
El segundo ejemplo es una estructura en forma de T invertida, las dimensiones del dominio de diseño se muestran en la Figura 9. La estructura está fija en su extremo superior, y sujeta a dos cargas concentradas F₁ y F₂, de magnitud y dirección inciertas, aplicadas en los puntos medios de los extremos laterales. La estructura se ha optimizado bajo condiciones de carga determinista y considerando incertidumbres en la magnitud y en la dirección de la carga. Tanto para la optimización determinista, como para la optimización robusta, se ha utilizado una fracción de volumen de (V_f /V_o) = 0,5. Con este ejemplo se pretende demostrar el efecto de variar los parámetros de las pdfs que caracterizan las cargas. Para ello, se han estudiado dos configuraciones, donde las variables aleatorias se describen mediante las distribuciones normales recogidas en la Tabla 3. En la configuración 1 se han utilizado los parámetros usados por Dunning et al. [26], y en la configuración 2 se ha aumentado el valor de la desviación estándar de las direcciones de las cargas.

Figura 9. Estructura T-invertida. Dominio de diseño y cargas aplicadas.

Tabla 3. T-invertida. Parámetros de las configuraciones estudiadas.

Configuración	F1	θ1	F2	θ2	NMC	Nk
1	N(5,0; 0,5)	N(0,0; 0,25)	N(5,0; 0,5)	N(0,0; 0,25)	10000	10
2	N(5,0; 0,5)	N(0,0; 0,5)	N(5,0; 0,5)	N(0,0; 0,5)	10000	10

La optimización determinista produce un diseño con un valor de compliance igual a 2786 (Figura 10). Si la topología óptima determinista obtenida se analiza considerando la existencia de incertidumbres en la magnitud y en la dirección de ambas cargas, el valor esperado de la compliance aumenta hasta 6792 y 7451, para la configuración 1 y 2, respectivamente. En el caso de realizar una RTO usando MCK se obtienen unos valores esperados para la compliance de 3328 y 3677, para la configuración 1 y 2, respectivamente. Al igual que en el primer ejemplo, se demuestra que los diseños obtenidos usando una formulación RTO se comportan mejor ante la existencia de incertidumbre que los diseños obtenidos mediante una formulación determinista.

Figura 10. Estructura T-invertida. Diseño óptimo determinista.

En las figuras 11 y 12 se muestran los diseños obtenidos usando MC y MCK, para la configuración 1 y 2, respectivamente. Estos diseños son muy similares a los obtenidos en la solución determinista salvo por las barras superiores centrales, las cuales pasan de estar inclinadas a verticales y reforzadas con crucetas. Esta disposición se debe a la componente horizontal de la fuerza, originada al considerar incertidumbre en la dirección de la misma. Además, se puede observar como al aumentar la desviación estándar en la dirección de la carga, el refuerzo de las crucetas también aumenta para proporcionar mayor rigidez lateral (Figuras 11b y 12b).

Para determinar la precisión y eficiencia del algoritmo MCK, las soluciones se han comparado con las obtenidas usando MC. El valor esperado de la compliance, usando MC para las configuraciones 1 y 2, es de 3341 y de 3742, lo que supone un error relativo de 0,38 y 1,71%, respectivamente. Por otro lado, el tiempo medio por iteración para la configuración 1 usando MCK es de 48 segundos, mientras que usando MC es de 99387, lo que supone un ahorro de tiempo del 99,95%. Para la configuración 2, el tiempo medio por iteración usando MCK es de 53 segundos, mientras que usando MC es de 114411, lo que supone un ahorro de tiempo del 99,95%.

(a)	(b)
Figura 11. Estructura T-invertida. Diseño óptimo robusto considerando incertidumbre en la magnitud y dirección de la carga para la configuración 1 ( ${\textstyle {\sigma }_{\theta }=}$$0,25).\,$ (a) MC, (b) MCK.
(a)	(b)
Figura 12. Estructura T-invertida. Diseño óptimo robusto considerando incertidumbre en la magnitud y dirección de la carga para la configuración 2 ( ${\textstyle {\sigma }_{\theta }=}$$0,5)$. (a) MC, (b) MCK.

5. Conclusiones

En este trabajo se presenta un algoritmo, denominado Monte Carlo con Kriging (MCK), para la optimización de topología robusta considerando la existencia de incertidumbres en las cargas. Para ello, el problema de RTO se ha formulado de forma probabilista, tomando como función objetivo el valor esperado de la compliance. En cada iteración, el valor esperado de la compliance se evalúa por medio del método de simulación de Monte Carlo en combinación con un modelo Kriging. El algoritmo propuesto puede generalizarse a otros tipos de optimización de topología determinista y a problemas tridimensionales.

La precisión y eficiencia del método se ha demostrado mediante dos ejemplos. En estos ejemplos, las cargas se definen por medio de cuatro variables, la magnitud (F), la dirección (θ), la posición respecto al eje x (S_x) y la posición con respecto al eje y (S_y), que pueden ser aleatorias. Las variables no aleatorias se caracterizan por su valor nominal, y las variables aleatorias se caracterizan mediante funciones de densidad de probabilidad normales, aunque el algoritmo permite utilizar cualquier otro tipo de pdf. Los ejemplos estudiados demuestran que:

1. El algoritmo MCK propuesto proporciona diseños casi tan precisos como los obtenidos usando el método de simulación de Monte Carlo estándar, pero de forma mucho más eficiente. Esto es debido a que el método MCK propuesto solo necesita realizar N_K análisis del modelo de simulación, en vez de los N_MC necesarios con el método de Monte Carlo (N_K = 10 << N_MC = 10000). Además, el número de evaluaciones con el método propuesto es independiente del número de cargas inciertas, siendo muy útil cuando el problema presenta una alta dimensionalidad.

2. El valor esperado de la compliance para los diseños obtenidos mediante una formulación robusta es menor que el valor para el diseño obtenido mediante una formulación determinista ante la existencia de incertidumbre en la carga. Esto demuestra también la importancia de incorporar la existencia de incertidumbre en el proceso de optimización de topología.

Los ejemplos también muestran el efecto de considerar diferentes fuentes y niveles de incertidumbre:

3. En el ejemplo 1 se demuestra que la incertidumbre en la posición de la carga tiene una mayor influencia que la incertidumbre en la dirección, y que estas a su vez tienen mayor influencia que la magnitud.

4. En el ejemplo 2, se muestra como el diseño robusto se adapta al nivel de incertidumbre.

Agradecimientos

Los autores agradecen el apoyo financiero del Ministerio de Economía y Competitividad a través del proyecto de investigación “Sistema integrado de diseño óptimo robusto de topología de estructuras (DPI2011-27939-C02-01)”, el cual ha permitido la realización de esta investigación.

Referencias

[1] Bendsøe M.P., Kikuchi N. Generating optimal topologies in structural design using a homogenisation method. Comp. Meth. Appl. Mech. Engng., 71:197-224, 1988.

[2] Rozvany G.I.N., Zhou M., BirkerT. Generalized shape optimization without homogenization. Struct. Optim., 4:250-254, 1992.

[3] Xie Y.M., Steven G.P. A simple evolutionary procedure for structural optimization. Comput. Struct., 49(5):885-896, 1993.

[4] Kirkpatrick S., Gellat C.D., Vecchi M.P. Optimization by simulated annealing. Science, 220(4598):671-680, 1983.

[5] Sethian J.A. Level set method and fast marching methods. 2nd Ed. New york, Cambridge University Press, 1999.

[6] Victoria M., Martí P., Querin O.M. Topology design of two-dimensional continuum structures using isolines. Comput. Struct., 87:101-09, 2009.

[7] Deaton J.D., Grandhi R.V. A survey of structural and multidisciplinary continuum topology optimization: post 2000. Struct. Multidisc. Optim., 49:1-38, 2014.

[8] Anflor C.T.M., Marczak R.J. Topological sensitivity analysis for two-dimensional heat transfer problems using the boundary element method. Optimization of Structures and Components, 43:11-33, 2013.

[9] Dühring M.B., Jensen J.S., Sigmund O. Acoustic design by topology optimization. J. Sound Vib., 317(3-5):557-575, 2008.

[10] Abdelwahed M., Hassine M., Masmoudi M. Optimal shape design for fluid flow using topological perturbation technique. J. Math. Anal. Appl., 356(2):548-563, 2009.

[11] Radman A., Huang X., Xie Y.M. Topological optimization for the design of microstructures of isotropic cellular materials. Eng. Optim., 45(11):1331-1348, 2013.

[12] Jung H.S., Cho S. Reability-based topology optimization of geometrically nonlinear structures with loading and material uncertainties. Finite Elem. Anal. Des., 41(3):311-331, 2004.

[13] Kim C., Wang S., Bae K-r, Moon H., Choi K.K. Reliability-based topology optimization with uncertainties. J. Mech. Sci. Tech., 20(4):494-504, 2006.

[14] Mogami K., Nishiwaki S., Izui K., Yoshimura M., Kogiso N. Reliability-based structural optimization of frame structures for multiple failure criteria using topology optimization techniques. Struct. Multidisc. Optim., 32(4):299-311, 2006.

[15] Yoo K.S., Eom Y.S., Park J.Y., Im M.G., Han S.Y. Reliability-based topology optimization using successive standard response surface method. Finite Elem. Anal. Des., 47(7):843-849, 2011.

[16] Kharmanda G., Olhoff N., Mohamed A., Lemaire M. Reliability-based topology optimization. Struct. Multidis. Optim., 26(5):295-307, 2004.

[17] Zhao Q., Chen X., Ma Z.D., Lin Y. Reliability-based topology optimization using stochastic response surface method with sparse grid design. Math. Probl. Engng., 2015:13, 2015.

[18] Chen S., Chen W., Lee S. Level set based robust shape and topology optimization under random field uncertainties. Struct. Multidisc. Optim., 41:507524, 2010.

[19] Chen S., Chen W. A new level-set based approach to shape and topology optimization under geometric uncertainty. Struct. Multidisc. Optim., 44:1-18, 2011.

[20] Dunning P.D., Kim H.A. Robust topology optimization: minimization of expected and variance of compliance. AIAA Journal, 51(11):2656-64, 2013.

[21] Schevenels M., Lazarov B.S., Sigmund O. Robust topology optimization accounting for spatially varying manufacturing errors. Comput. Methods Appl. Mech. Engrg., 200:3613-3627, 2011.

[22] Jansen M., Lombaert G., Diehl M., Lazarov B.S., Sigmund O., Schevenels M. Robust topology optimization accounting for misplacement of material. Struct. Multidisc. Optim., 47:317-33, 2013.

[23] Zhao J., Wang C. Robust topology optimization under loading uncertainty based on linear elastic theory and orthogonal diagonalization of symmetric matrices. Comput. Methods Appl. Mech. Engrg., 273:204-18, 2014.

[24] Zhao J., Wang C. Robust structural topology optimization under random field loading uncertianty. Struct. Multidisc. Optim., 50:517-22, 2014.

[25] Zhao Q., Chen X., Ma Z.D., Lin Y. Robust topology optimization based on stochastic collocation methods under loading uncertainties. Math. Probl. Engng., 1:1-14, 2015.

[26] Dunning P.D., Kim H.A., Mullineux G. Introducing loading uncertainty in topology optimization. AIAA Journal, 49:760-768, 2011.

[27] Zhao J., Wang C. Robust topology optimization of structures under loading uncertainty. AIAA Journal, 52(2):398-407, 2014.

[28] García-Lopez N.P., Sanchez-Silva M., Medaglia A.L., Chateauneuf A. An improved robust topology optimization approach using multiobjective evolutionary algorithms. Comput. Struct., 125:1-10, 2013.

[29] Tootkaboni M., Asadpoure A., Guest J. Topology optimization of continuum structures under uncertainty: a polynomial chaos approach. Comp. Methods Appl. Mech. Engrg., 201-204:263-275, 2012.

[30] Lazarov B.S., Schevenels M., Sigmund O. Topology optimization considering material and geometric uncertainties iusing stochastic collocations methods. Struct. Multidisc. Optim., 46:597-612, 2012.

[31] Conti S., Held H., Pach M., Rumpf M., Schultz R. Shape optimization under uncertainty: a sctochastic programming perspective. SIAM J. Optim., 19(4):1610-32, 2009.

[32] Myers H., Montgomery D.C. Response surface methodology: process and product optimization using designed experiments. 2nd edition, John Wiley & Sons, New York, USA, 2002.

[33] Powell M. The theory of radial basis function approximation in 1990. In Advances in Numerical Analysis, Vol.2: Wavelets, Subdivision Algorithms and Radial Basis Functions, W. Light (Ed.). Oxford University Press, Oxford, UK, 1992.

[34] Papadrakakis M., Lagaros N., Tsompanakis Y. Structural optimization using evolution strategies and neural networks. Comp. Meth. in Appl. Mech. Engrg., 156(1-4):309-333, 1998.

[35] Martin J.D., Simpson T.W. Use of Kriging models to approximate deterministic computer models. AIAA Journal, 43(4):853-863, 2005.

[36] Dubourg V., Sudret B., Bourine J.-M. Reliability-based design optimization using Kriging surrogates and subset simulation. Struct. Multidisc. Optim., 44:673-690, 2011.

[37] Chen Z., Peng S., Li X., Qiu H., Xiong H., Gao L., Li P. An important boundary sampling method for reliability-based design optimization using Kriging model. Struct. Multidisc. Optim., 52:55-70, 2015.

[38] Lee K.H., Kang D.H. A robust optimization using the statistics base on Kriging metamodel. J. Mech. Sci. Techn., 20(8):1169-1182, 2006.

[39] Jurecka F. Robust design optimization based on metamodeling techniques. Technische Universität München, München, 2007.

[40] Martínez J., Martí P. Diseño óptimo robusto utilizando modelos Kriging: aplicación al diseño óptimo robusto de estructuras articuladas. Rev. Int. Mét. Num. Cálc. Diseño Ing., 30(2):97-105, 2014.

[41] Bendsøe M.P. Optimal shape design as a material distribution problem. Struct. Optim., 1:193-202, 1989.

[42] Zhou M., Rozvany G. The COC algorithm. Part II: topological, geometry and generalized shape optimization. Comput. Methods Appl. Mech. Engrg., 89:197-224, 1991.

[43] Svanberg K. The method of moving asymptotes - a new method for structural optimization. Int. J. Numer. Meth. Engrg., 24:359-373, 1987.

[44] Sigmund O. A 99 line topology optimization code written in Matlab. Struct. Multidisc. Optim., 21:120-127, 2001.

[45] Sigmund O., Peterson J. Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Multidisc. Optim., 16:68-75, 1998.

[46] BrunsT.E., Tortorelli D.A. Topology optimization of non-linear elastic structures and compliant mechanisms. Comput. Methods. Appl. Mech. Engrg., 190(26-27):3443-3459, 2001.

[47] Bourdin B. Filters in topology optimization. Int. J. Numer. Meth. Engrg., 50:2143-2158, 2011.

[48] Guest J.K., Prévost J.H., Belytschko T. Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int. J. Numer. Meth. Engrg., 61(2):238-254, 2004.

[49] Sigmund O. Morphology-based black and white filters for topology optimization. Struct. Multidisc. Optim., 33(4-5):401-424, 2007.

[50] Xu S., Cai Y., Cheng G. Volume preserving nonlinear density filter based on heaviside functions. Struct. Multidisc. Optim., 41:495-505, 2010.

[51] Kawamoto A., Matsumori T., Yamakasi S., Nomura T., Kondoh T., Nishiwaki S. Heaviside projection based topology optimization by a pde-filtered scalar function. Struct. Multidisc. Optim., 44(1):19-24, 2008.

[52] Lazarov B.S., Sigmung O. Filers in topology optimization based on Helmholtz type differential equations. Int. J. Numer. Methods Engrg., 86(6):765-781, 2011.

[53] Metropolis N., Ulam S. The Monte Carlo method. J. Amer. Statist. Assoc., 44(247):335-341, 1949.

[54] Rubinstein R.Y., Kroese D.P. Simulation and the Monte Carlo method. 2nd Edition, John Wiley & Sons, 2008.

[55] Schuceller G.I. Developments in stochastic structural mechanics. Arch. Appl. Mech., 75:755-773, 2006.

[56] Krige D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. Journal of the Chemical, Metallurgical and Mining Society of South Africa, 52:119-139, 1951.

[57] Nakayama H., Arakawa M., Sasaki R. Simulation based optimization using computational intelligence. Optimiz. Eng., 3:201-214, 2002.

[58] Papadrakakis M., Lagaros N.D., Tsompanakis Y. Structural optimization using evolution strategies and neural networks. Comput. Methods. Appl. Mech. Engrg., 156:309-333, 1998.

[59] Jin R., Du X., Chen W. The use of metamodeling techniques for optimization under uncertainty. Struct. Multidisc. Optim., 25:99-116, 2003.

[60] Jones D.R. A taxonomy of global optimization methods based on response surfaces. J. Global Optimization, 21:345-383, 2001.

[61] Matheron G. Principles of geostatistics. Economic Geology, 58(8):1246-1266, 1963.

[62] Lophaven N., Nielsen H.B., Sondergaard J. Aspects of the Matlab toolbox DACE. Technical Report, Informatics and Mathematical Modelling, Technical University of Denmark, DTU, Richard Petersens Plads, Lyngby, 2002.

[63] Echard B., Gayton N., Lemaire M. AK-MCS: An active learning realiability method combining Kriging and Monte Carlo simulation. Struct. Saf., 33(2):145-154, 2011.

[64] Kaymaz I. Application of Kriging method to structural reliability problems. Struct. Saf., 27(2):133-151, 2005.

[65] Kleijnen J.P.C. Kriging metamodeling in simulation: a review. Eur. J. Oper. Res., 192(3):707-716, 2009.

[66] Lógó J. SIMP type topology optimization procedure considering uncertain load position. Civil Engineering, 56(2):213-219, 2012.