Resumo
No presente artigo apresenta‐se um estudo numérico sobre a evolução do estado de tensão geomecânico induzido pela passagem de tráfego ferroviário. O modelo numérico proposto é baseado na formulação 2,5D apoiada no MEF‐PML, permitindo a consideração da interação do sistema composto pelo comboio, via‐férrea e maciço de fundação. Para o caso de estudo proposto, as alterações do estado de tensão são sistematizadas sob a forma de trajetórias de tensão. Perante os resultados alcançados é possível reconhecer a grande influência da velocidade de circulação do comboio e da presença de irregularidades na via no comportamento da via‐férrea. Tirando partido dos conhecimentos adquiridos com a realização dos estudos paramétricos referidos, verifica‐se a adequabilidade de um ensaio laboratorial –ensaio torsional com cilindro vazado– na simulação das complexas trajetórias de tensão induzidas no solo de fundação pela passagem do tráfego ferroviário. Os resultados obtidos permitem perspetivar a simulação em laboratório dessa ação, através de um carregamento cíclico, com o objetivo de estudar a acumulação de dano nas amostras.
Abstract
In this paper, a numerical study of the geomechanical stress state evolution induced by the railway traffic is presented. The numerical model is based on a 2.5D formulation with the ability to account for the dynamic train‐track interaction. For the case study, the stress state evolution is systematized in the form of stress paths. The results obtained allow to recognize the great influence of the train speed and the presence of irregularities in the track for the behavior of the railway track. Based on the knowledge acquired during the implementation of previous parametric studies, the adequacy of the hollow cylinder torsional test to simulate the complex stress paths induced in the ground of the traffic railway is evaluated. The results obtained allow to put in perspective the simulation of these loads in laboratory, with the aim of studying the damage accumulation in the specimens.
Palavras‐chave
Linha férrea ; Modelo numérico ; Trajetórias de tensão ; Interação dinâmica veículo‐via ; Ensaio laboratorial
Keywords
Railway ; Numerical model ; Stress paths ; Train‐track dynamic interaction ; Laboratorial test
1. Introdução
O desempenho estrutural de vias‐férreas encontra‐se diretamente relacionado com o nível de tensões que são transmitidas ao maciço de fundação, através das camadas de desgaste superiores, devendo ser reduzidas a um nível aceitável para evitar a rápida degradação da estrutura ferroviária. A avaliação destas tensões é um processo complexo e que ainda está muito dependente de processos empíricos [1] and [2] . A avaliação numérica da evolução do estado de tensão geomecânico na estrutura sujeita ao tráfego ferroviário é deste modo um passo importante para uma sistematização dos processos de dimensionamento e previsão do comportamento da estrutura a curto/longo prazo.
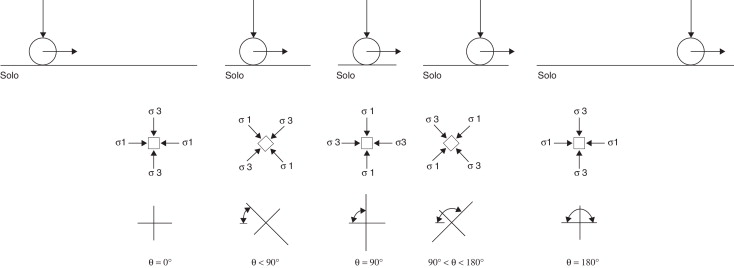
Nos últimos tempos diversos autores se têm debruçado sobre este tema, de modo a aprofundar o conhecimento sobre o mesmo [3] , [4] , [5] and [6] . Um dos fenómenos que contribui para o aumento do grau de complexidade são as sucessivas rotações das direções de tensões principais num dado elemento do solo, à medida que os vários eixos do comboio passam sobre este. Admitindo um estado de tensão hidrostático (σ1 = σ3 = σx = σz) a rotação das direções principais de tensão está apenas dependente das tensões dinâmicas induzidas pelo carregamento. Assim, no início do carregamento, quando este se encontra a uma distância tal que não induz incrementos de tensão no ponto em análise, as tensões principais σ1 e σ3 apresentam igual valor entre si, tal como representado na figura 1 . Com a aproximação da carga ao elemento do solo, a direção de tensão principal σ1, admitida inicialmente como horizontal, começa a rodar no sentido horário tornando‐se na tensão máxima. No exato momento em que a carga se encontra sobre o elemento a direção da tensão principal σ1 é vertical (θ = 90°) e aqui a tensão tangencial τxz anula‐se. Com o afastamento da carga do elemento considerado, a direção da tensão principal máxima σ1 roda de novo até atingir a direção horizontal, situação verificada quando a carga está suficientemente afastada de tal modo que o seu efeito torna‐se desprezável. A partir deste instante as tensões principais σ1 e σ3 igualam‐se novamente. Em suma, pode concluir‐se que as direções de tensão principais rodam 180° durante o ciclo de aproximação e afastamento da carga.
|
|
|
Figura 1. Representação esquemática da rotação da direção das tensões num dado elemento do solo devido à movimentação de um eixo do comboio ao longo do plano longitudinal (θ representa o ângulo de rotação da direção de tensão principal σ1 em relação à horizontal). |
As referidas rotações apresentam um carácter tridimensional, ocorrendo tanto no plano longitudinal, como anteriormente analisado, como nos planos transversais (a menos que o ponto de análise se encontre no plano de simetria da via), provocando um agravamento das deformações permanentes no solo em comparação com uma análise que não entre em linha de conta com esta especificidade, conforme diversos estudos já realizados [7] and [8] .
A avaliação da evolução do estado de tensão recorrendo a modelos numéricos de caráter bidimensional (2D), como a realizada por Yang et al. [5] , apresenta o inconveniente de apenas permitir a consideração da rotação da direção das tensões principais no plano longitudinal, sendo a análise limitada unicamente a pontos sob o plano de simetria da via. A juntar a esta limitação há ainda a considerar o facto de o amortecimento por radiação não ser adequadamente descrito pelos modelos bidimensionais uma vez que a aplicação de uma carga pontual à superfície de um maciço é um problema claramente tridimensional, originando a propagação de ondas com frente de onda claramente distinta da identificada em meios bidimensionais. Assim sendo, um modelo deste tipo não é capaz de considerar de uma forma correta esta atenuação da amplitude das vibrações [9] .
O recurso a modelos tridimensionais será uma alternativa natural de forma a ultrapassar as referidas limitações. Chen et al. [3] e Tao et al. [6] apresentam modelos tridimensionais analíticos na análise às alterações do estado de tensão, ultrapassando, ainda que parcialmente, as limitações enumeradas para os modelos bidimensionais. Contudo, os modelos analíticos são bastante limitados, só sendo possível a sua aplicação mediante determinadas simplificações do problema, nomeadamente no que concerne à sua geometria. Já Powrie et al. [4] recorre a um modelo tridimensional numérico tirando partido das potencialidades de uma malha de elementos finitos na discretização da estrutura ferroviária. No entanto, a utilização de uma malha deste tipo pode ser um fator dissuasivo da sua utilização devido à maior morosidade do processo de cálculo. Ressalva‐se, ainda, que o modelo numérico tridimensional apresentado em Powrie et al. [4] é um modelo que considera a aplicação das cargas do comboio de uma forma estática, não sendo capaz de simular os efeitos de movimento da ação, bem como a inerente excitação dinâmica. De uma forma geral, os modelos numéricos tridimensionais tendem a apresentar uma maior utilidade no estudo de pontos singulares da via, como zonas de transição, pois nos troços onde seja plausível considerar a estrutura como invariante e infinita ao longo da direção longitudinal, a adoção de modelos numéricos baseados no conceito 2,5D pode apresentar uma clara vantagem para a realização dos estudos paramétricos. Este conceito alia a rapidez de processamento de cálculo com a consideração da tridimensionalidade existente no problema, sendo claramente uma mais‐valia para este tipo de análises [10] , [11] , [12] and [13] .
A aplicação do conceito 2,5D, nas condições inumeradas anteriormente, apenas exige a discretização da secção transversal do problema, visto que se tira partido da transformada de Fourier em relação às variáveis tempo e espaço (na direção longitudinal). Esta combinação de procedimentos permite obter a resposta tridimensional do problema, repetida para diferentes números de onda/frequências.
No sentido de avaliar e interpretar as alterações do estado de tensão devidas ao tráfego ferroviário o presente artigo apresenta, numa primeira fase, o modelo de cálculo numérico adotado, o qual se baseia no conceito 2,5D adaptado ao método dos elementos finitos. De seguida apresenta‐se um caso de estudo para o qual é desenvolvido um conjunto de análises paramétricas, atendendo à interação dinâmica entre a via‐férrea e o maciço de fundação, bem como ao problema da interação entre o comboio e a via. Estes estudos paramétricos envolvem a avaliação da influência da velocidade de circulação, da posição geométrica dos pontos do solo considerados na análise e da ocorrência de irregularidades na via na evolução do estado de tensão sob a ação do tráfego ferroviário. Por fim apresenta‐se de uma forma sucinta o Ensaio Laboratorial de Cilindro Vazado com o objetivo de se avaliar a adequabilidade do mesmo na simulação das trajetórias características da alteração do estado de tensão devido à ação de uma carga móvel, comparativamente às obtidas nos estudos paramétricos realizados.
2. Modelo numérico
2.1. Considerações gerais
A modelação numérica de vibrações induzidas por tráfego ferroviário constitui um problema complexo para o qual concorrem vários aspetos, nomeadamente: i) o carácter móvel da ação; ii) a existência de um meio com fronteiras não definidas, correspondendo ao maciço de fundação; iii) o carácter tridimensional do problema; iv) o facto da fonte de excitação abranger uma gama de frequências muito alargada.
Apesar da complexidade exposta no ponto anterior, têm‐se verificado nos últimos anos avanços significativos nesta matéria, sendo várias as publicações sobre as melhores técnicas de modelação numérica do problema, referindo‐se a título de exemplo os seguintes trabalhos nos quais é apresentada uma resenha das mais atuais técnicas [9] , [13] , [14] , [15] and [16] .
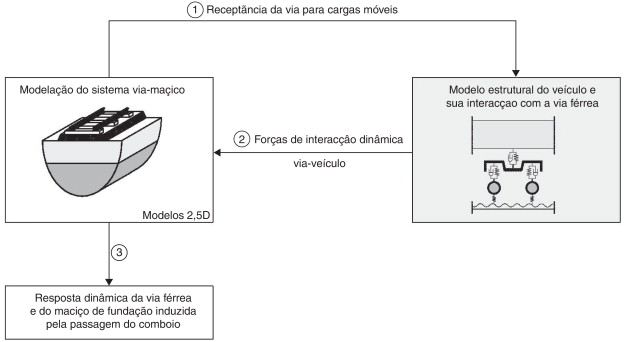
No presente trabalho é adotado um modelo numérico subestruturado, o qual é dividido em 2 submodelos, respeitantes ao veículo e ao remanescente meio, cuja interação dinâmica é garantida no total respeito das condições de compatibilidade de deslocamentos e equilíbrio de forças ao nível dos pontos de contacto entre os 2 domínios, como aliás se ilustra na figura 2 .
|
|
|
Figura 2. Fluxograma representativo da interação entre os vários módulos do modelo de cálculo proposto. |
Nos pontos seguintes apresenta‐se uma descrição sucinta dos principais pressupostos e particularidades dos modelos adotados para cada um dos meios.
2.2. Modelação da via – maciço de fundação
O carácter tridimensional dos problemas em questão levanta consideráveis dificuldades computacionais inerentes à grande dimensão dos domínios em estudo, sendo por isso necessário o desenvolvimento de ferramentas numéricas, especialmente concebidas e/ou adaptadas, para a análise de estruturas com desenvolvimento infinito, como pode geralmente ser admitido para as infraestruturas ferroviárias [13] and [17] . Atendendo a esta particularidade das infraestruturas ferroviárias, a análise do domínio tridimensional (via e maciço subjacente) pode ser realizada através do método dos elementos finitos 2,5D [18] , até porque, nessas circunstâncias é possível concluir que a estrutura é quase bidimensional e o carregamento é tridimensional. O principal conceito do método reside, assim, em resolver o problema através de uma metodologia intermédia entre o bidimensional e o tridimensional. Tratando‐se de um método baseado nos elementos finitos, apresenta como grande vantagem o recurso a técnicas transformadas que permitem uma drástica redução do número de graus de liberdade já que apenas a secção transversal do problema necessita de ser discretizada por elementos finitos.
Deste modo, e supondo que a resposta da estrutura é linear, a análise pode ser desenvolvida no domínio da frequência/número de onda, sendo aplicadas transformadas de Fourier em relação ao tempo e ao espaço na direção de desenvolvimento da via. Neste contexto, as grandezas transformadas (ação e resposta) passam a ser função das imagens de Fourier da direção espacial x e do tempo, t, sendo designadas, respetivamente, por número de onda e frequência angular, e representadas por k1 e ω. Este procedimento implica que apenas 2 das direções que caracterizam o meio tridimensional se mantenham no domínio não transformado, sendo por isso o plano descrito por essas direções discretizado através de elementos finitos (ver fig. 3 ).
|
|
|
Figura 3. Modelo 2,5D. |
A formulação do método dos elementos finitos 2,5D é em tudo semelhante à formulação de um modelo por elementos finitos bidimensional, com exceção do facto de cada nó ter 3 graus de liberdade e das entidades envolvidas se encontrarem no domínio transformado. Deste modo, procedendo à transformação das variáveis e discretização do plano ZY, chega‐se à seguinte equação de equilíbrio para cada elemento finito:
|
|
( 1) |
em que B representa a matriz das derivadas das funções de forma; N representa a matriz das funções de forma; D é a matriz de elasticidade; ρ é a massa volúmica; pn e un representam as forças e os deslocamentos nodais, respetivamente.
Seguindo a nomenclatura habitual do método dos elementos finitos, podem definir‐se as matrizes de rigidez e de massa, tal como indicado nas equações (2) e (3), respetivamente.
|
|
( 2) |
|
|
( 3) |
A matriz B é determinada através do produto do operador diferencial L pela matriz N , a qual agrupa as funções de forma do elemento finito. Dado que a direção x é submetida a uma operação de transformação para o número de onda k1 , as derivadas relativas a essa mesma direção são avaliadas de modo analítico, sendo então o operador L dado por:
|
|
( 4) |
Sem embargo do conjunto de vantagens inerentes à aplicação do MEF, nomeadamente na análise de geometrias complexas, cabe referir a limitação intrínseca do método quando o objeto de análise se prende com problemas de geodinâmica e respetiva simulação das fronteiras oriundas da truncatura do domínio. Com efeito, o MEF é na sua génese um método para o estudo de sistemas confinados, onde as condições de fronteira estejam totalmente definidas. Se em análises estáticas esta dificuldade é facilmente contornável através da consideração de fronteiras a distâncias suficientemente afastadas da zona de interesse do problema, o mesmo não ocorre na análise dinâmica, sendo fundamental a utilização de procedimentos especiais para o tratamento das fronteiras artificiais.
Existem diferentes métodos para lidar com as condições de radiação que devem ser cumpridas nas fronteiras artificiais, indo desde métodos globais, como a aplicação de modelos baseados na interação entre método dos elementos de contorno/método dos elementos finitos [12] and [13] , até métodos locais, tais como fronteiras absorventes [19] and [20] , método dos elementos infinitos [20] , [21] and [22] , ou métodos das camadas absorventes (perfect matched layers – PML ) [14] . Os métodos locais, embora apresentando um grau de acuidade inferior ao verificado nos métodos globais, têm como vantagem o facto de serem, regra geral, mais simples do ponto de vista da implementação numérica. Entre os diferentes métodos inumerados, destaca‐se o PML pela elevada acuidade alcançada por este método conjugada com a simplicidade de implementação apresentada.
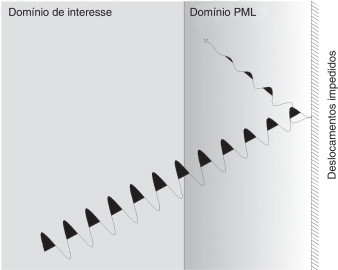
O fundamento do PML reside na aplicação de uma camada exterior ao domínio de interesse, também ela discretizada por elementos finitos, que permita a atenuação da onda incidente sem que no entanto se verifique qualquer tipo de reflexão no contacto entre os 2 domínios. Deste modo, o PML deverá ser absorvente e não refletivo, como aliás se ilustra na figura 4 .
|
|
|
Figura 4. Representação esquemática da atenuação da onda ao incidir na camada de PML. |
A combinação das 2 condições anteriormente mencionadas é alcançada através de uma passagem das coordenadas dos nós do domínio respeitante ao PML para o domínio complexo, mantendo‐se a equação governativa do problema e, por esse modo, evitando‐se reflexões espúrias na fronteira entre os 2 domínios em análise.
Atendendo ao expresso no parágrafo anterior, pode então proceder‐se a uma mudança de referencial geométrico do domínio descrito pelo PML para o domínio complexo. Tal relação é dada pelas seguintes funções de mudança de referencial, apenas aplicáveis à direção y e z , tanto mais que a direção x é transformada para o domínio do número de onda:
|
|
( 5) |
|
|
( 6) |
em que λy e λz são as funções de transformação nas direções y e z , respetivamente. Relativamente às derivadas das coordenadas nodais é também possível alcançar a seguinte relação:
|
|
( 7) |
|
|
( 8) |
As referidas funções são derivadas através da continuidade da solução para além do domínio de interesse, tendo presente o cuidado de corresponderem a uma solução suave de modo a evitar reflexões espúrias no interior do domínio correspondente ao PML. Segundo Lopes et al. [14] os requisitos para tais funções são compreendidos adotando funções com a seguinte configuração:
|
|
( 9) |
|
|
( 10) |
em que k0 é uma constante (Lopes et al. [14] recomendam k0 = 20); Hy e Hz correspondem à espessura da camada absorvente nas direções y e z , respetivamente; k corresponde ao comprimento de onda propagante ao longo da secção transversal do problema, o qual é dado por:
|
|
( 11) |
em que Cs é a velocidade de propagação das ondas de corte no terreno.
Por último, refira‐se que sistema global de equações é completamente definido após a assemblagem das matrizes de rigidez dinâmica, tanto dos elementos finitos como dos elementos PML, e da introdução das condições de fronteira de Neumann e de Dirichlet. Os resultados obtidos após a resolução do sistema de equações encontram‐se no domínio transformado, exigindo uma dupla transformada de Fourier inversa para converter a solução para o domínio do espaço/tempo, remetendo‐se o leitor para as seguintes referências bibliográficas onde poderá encontrar informação complementar: [10] , [23] and [24] .
2.3. Modelação do veículo
A ação dinâmica induzida pelo tráfego ferroviário é devida a diferentes mecanismos, os quais, no contexto da análise de vibrações induzidas por tráfego, são geralmente divididos entre mecanismos de excitação quasi‐estática e de excitação dinâmica [25] . A excitação quasi‐estática deve‐se ao movimento das cargas correspondentes ao peso próprio do comboio por eixo. Este tipo de excitação apresenta magnitude constante ao longo do tempo e o carácter dinâmico da resposta é apenas induzido pela variação temporal dos campos de tensão e deformação experimentados num ponto fixo do domínio. Em contraponto com a excitação quasi‐estática, a excitação dinâmica deve‐se às forças verticais de inércia que se geram no veículo. Este mecanismo de excitação pode ter diferentes causas, sendo as mais habituais as irregularidades geométricas ou de rigidez da via e as próprias imperfeições das rodas do comboio.
Como é evidente, a consideração do mecanismo quasi‐estático é simples, pois não ocorre nenhum fenómeno de interação dinâmica entre o material circulante e a via‐férrea. Porém, a mesma conclusão não pode ser generalizada para o caso da excitação dinâmica. A consideração deste tipo de excitação é muito mais complexa sendo necessário atender à interação entre 2 estruturas distintas (comboio e restante meio) e em que uma delas tem posição geométrica móvel. No contexto do presente artigo apenas se considera o mecanismo de excitação dinâmica devido às imperfeições geométricas da via‐férrea. Assim sendo, a compatibilidade de deslocamentos entre o comboio e a via, admitindo a linearidade do sistema, é estabelecida através da seguinte equação:
|
|
( 12) |
em que c representa a velocidade de circulação, ai é a posição geométrica da roda i no instante t = 0, e Δu corresponde à irregularidade geométrica da via identificada pela roda i , no instante temporal t .
Procedendo à transformação do perfil de irregularidades da via para o domínio do número de onda e atendendo às características geométricas do comboio e respetiva velocidade de circulação, as forças de interação dinâmica no domínio da frequência são dadas por [26] :
|
|
( 13) |
em que N é o vetor das forças de interação associadas a cada eixo do comboio e à irregularidade com comprimento de onda λ=2πc/Ω.
As matrizes Kv e A representam a resposta dinâmica do comboio e da via face à força dinâmica gerada pela irregularidade, respetivamente. Os termos da matriz A são dados por:
|
|
( 14) |
em que uG_Carril é o deslocamento do carril, no domínio transformado face a uma ação unitária que se move com a velocidade c e oscila em torno da frequência Ω. Relativamente às variáveis ai e aj , estas correspondem à posição dos eixos i e j do comboio para o instante temporal t = 0 s.
Por sua vez, a matriz Kv representa a matriz de rigidez dinâmica do veículo, devidamente condensada de modo a atender aos graus de liberdade que estão em contacto com a via (rodas ou eixos, no caso do modelo plano). Esta matriz é tanto mais complexa quanto mais elaborado for o modelo adotado para o comboio [27] , encontrando‐se uma explicação detalhada da sua elaboração nas seguintes referências bibliográficas: [9] , [13] , [27] , [28] and [29] .
Como se compreende para o cálculo da matriz A é necessário o recurso ao modelo de simulação do terreno e via‐férrea. Por sua vez, o resultado do modelo de interação, advindo da equação 13, é utilizado novamente no modelo de simulação do terreno e via‐férrea para a simulação da resposta dinâmica do sistema face à passagem de tráfego ferroviário.
3. Caso de estudo
3.1. Descrição geral
O caso de estudo aqui apresentado, para o qual se procede a um estudo teórico da evolução do estado de tensão geomecânico, adota as características geométricas e geomecânicas existentes no troço ferroviário da Linha do Norte incorporado no Campo Experimental do Carregado [9] e considera as características do comboio Alfa‐Pendular para a modelação do material circulante.
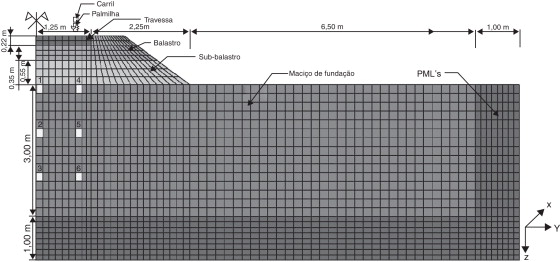
No que diz respeito à secção transversal da via, esta é exposta na figura 5 , podendo ser visualizadas as distintas camadas constituintes da via‐férrea.
|
|
|
Figura 5. Malha de elementos finitos 2,5D adotada no estudo em causa (x ‐ direção de desenvolvimento da via‐férrea). |
Uma chamada de atenção para o facto de as travessas serem consideradas como um elemento contínuo, tal como está subjacente no conceito 2,5D presente no modelo numérico apresentado anteriormente. Para tal, os elementos finitos que constituem a travessa apresentam uma lei constitutiva que os define como se se tratassem de elementos ortotrópicos [23] . No plano transversal são utilizadas as propriedades mecânicas das travessas, considerando‐se um comportamento elástico das mesmas. Na direção longitudinal, uma vez que no espaço entre travessas o material existente é o constituinte da camada de balastro, a rigidez do meio é considerada igual ao módulo de Young desse material. Esta solução foi devidamente testada em Alves Costa et al. [23] , com resultados satisfatórios.
Na modelação da secção transversal retira‐se partido das condições de simetria do problema, obtendo‐se uma assinalável redução do esforço computacional exigido. As várias camadas constituintes da estrutura ferroviária são discretizadas em elementos finitos e a camada envolvente do maciço da fundação representa às condições fronteira modeladas recorrendo à metodologia dos PML [14] .
Relativamente às propriedades geomecânicas dos diferentes constituintes da via‐férrea, estas encontram‐se presentes na tabela 1 . Desde já se refere que as propriedades adotadas para o maciço de fundação são compatíveis com uma velocidade de propagação das ondas S igual a 150 m/s, de acordo com as seguintes expressões:
|
|
( 15) |
|
|
( 16) |
| Rigidez | Coef. de Poisson | Amortecimento | Massa | |
|---|---|---|---|---|
| Carril | EIr = 6,45 MPa | (–) | (–) | mr = 64 kg/m |
| Palmilhas | Kp = 600 KN/mm | (–) | Cp = 22,5 KNs/mm | (–) |
| Travessas | E = 30.000 MPa | ν = 0,20 | ξ = 0,01 | ρ = 1.833,3 kg/m3 |
| Balastro | E = 97 MPa | ν = 0,12 | ξ
0,061 |
ρ = 1.591 kg/m3 |
| Sub‐balastro | E = 212 MPa | ν = 0,30 | ξ = 0,054 | ρ = 1.913 kg/m3 |
| Maciço de Fundação | E = 127,4 MPa | ν = 0,49 | ξ = 0,03 | ρ = 1.900 kg/m3 |
Por outro lado, o comboio adotado nos estudos efetuados foi, tal como referido anteriormente, o comboio Alfa‐Pendular (fig. 6 ). Este comboio é capaz de atingir velocidades de 220 km/h, sendo esta a velocidade máxima do sistema ferroviário português, e é composto por um total de 6 carruagens (apresenta um plano de simetria). As características mecânicas e o modelo estrutural utilizado na sua modelação podem ser encontrados em Alves Costa [9] . Refira‐se que o modelo adotado compreende a simulação das suspensões primária e secundária, bem como das principais massas do veículo (massa não suspensa, massa semi‐suspensa e massa suspensa) [20] .
|
|
|
Figura 6. Geometria do comboio Alfa‐Pendular [9] . |
Como referido anteriormente e com o objetivo de se tirar partido das imensas potencialidades do modelo numérico adotado, é apresentado seguidamente um estudo incidente sobre a evolução do estado de tensão para diferentes elementos do maciço de fundação.
3.2. Influência do mecanismo quasi‐estático
Numa primeira fase, os estudos elaborados apenas consideram a influência do mecanismo quasi‐estático nas alterações induzidas ao estado de tensão, ou seja, não se tem em conta a interação existente entre a via e o comboio, sendo simulado através de um conjunto de cargas móveis de magnitude constante e em consonância com a distribuição do peso pelos diferentes eixos. Estes estudos são efetuados para vários pontos do maciço de fundação, conforme assinalados na figura 5 .
Com os elementos assinalados pretende‐se a elaboração de um estudo acerca da evolução do estado de tensão em função da profundidade e da distância ao plano de simetria da via. As alterações ao estado de tensão serão apresentadas sob a forma de trajetórias de tensão e representadas num diagrama p‐q , em que p corresponde ao valor da tensão média e q ao valor da tensão de desvio, sendo definidos pelas equações (17) e (18).
|
|
( 17) |
|
|
( 18) |
onde as variáveis σ1 , σ2 e σ3 representam as componentes de tensão principais [30] .
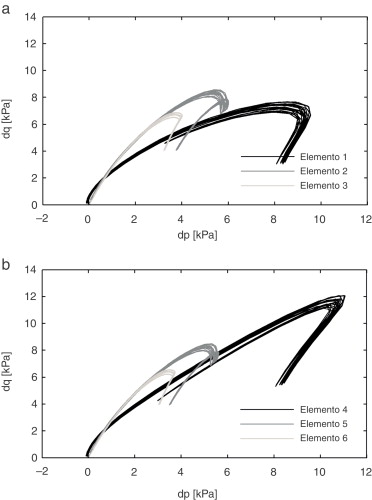
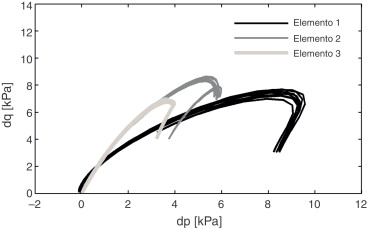
Assim, e considerando os 2 alinhamentos verticais que contêm, respetivamente, os Elementos 1, 2 e 3 (Alinhamento 1) e os Elementos 4, 5 e 6 (Alinhamento 2), identificados na figura 5 , observe‐se a evolução das trajetórias de tensão em profundidade através da análise da figura 7 , para uma velocidade de 30 m/s.
|
|
|
Figura 7. Evolução das trajetórias de tensão em profundidade com a passagem do comboio Alfa‐Pendular a uma velocidade de 30 m/s: a) Alinhamento 1; b) Alinhamento 2. |
A evolução das trajetórias de tensão apresentadas na figura 7 está diretamente relacionada com a geometria do comboio. O afastamento entre os vários eixos deste origina ciclos carga‐descarga com diferentes configurações. De modo a simplificar a interpretação destes ciclos, apresenta‐se de seguida a simulação da passagem de algumas partes do comboio isoladas, para os elementos situados no plano de simetria da via. Inicialmente apresentam‐se as trajetórias correspondentes à passagem dos 2 primeiros eixos do comboio (um bogie), seguindo‐se a simulação da passagem do primeiro veículo (4 eixos) e por fim, as trajetórias correspondentes à passagem de 2 veículos completos.
Como se pode observar através da figura 8 , as trajetórias de tensão representadas, correspondentes à simulação da passagem dos 2 primeiros eixos do comboio, apresentam um comportamento característico, notando‐se para os vários elementos um crescimento da tensão de desvio incremental (dq ) com a passagem do primeiro eixo. Após a passagem deste, ocorre algum alívio em que a tensão de desvio apresenta diminuição, de maior significância para os elementos mais próximos da superfície. Porém, como o segundo eixo se encontra próximo do primeiro não há lugar a uma descarga completa, até porque, como se pode observar, a diminuição da tensão média incremental (dp ) é reduzida senão mesmo inexistente. Quando o segundo eixo passa sobre o elemento observa‐se um novo incremento de tensão de desvio, atingindo‐se de novo um máximo. Por fim, à medida que este se afasta da secção em estudo, ocorre uma descarga completa das trajetórias de tensão.
|
|
|
Figura 8. Evolução das trajetórias de tensão em profundidade com a passagem dos 2 primeiros eixos do comboio (Alinhamento 1, V = 30 m/s). |
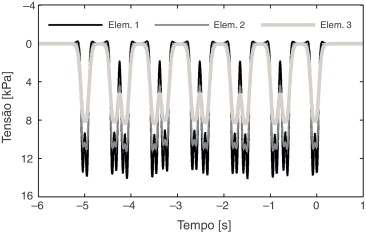
Chama‐se a atenção do leitor que o facto da diminuição da tensão de desvio, após a passagem do primeiro eixo, ser mais significativa nos elementos mais próximos da superfície resulta da degradação das tensões em profundidade. Este facto tem como consequência a não distinção dos eixos pertencentes a um dado bogie do comboio, por estes se encontrarem relativamente próximos, tal como representado na figura 9 para o Elemento 3. Assim, o ciclo carga‐descarga associado aos 2 eixos não apresenta uma redução da tensão de desvio tão evidente como a verificada nos elementos mais à superfície.
|
|
|
Figura 9. Evolução da tensão normal σz em profundidade (Alinhamento 1, V = 30m/s). |
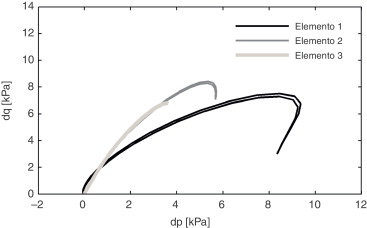
A figura 10 apresenta as trajetórias de tensão referentes à simulação da passagem de um veículo completo do comboio (4 eixos, divididos em 2 bogies).
|
|
|
Figura 10. Evolução das trajetórias de tensão em profundidade com a passagem do primeiro veículo do comboio (Ainhamento 1, V = 30 m/s). |
Como se pode observar, as principais diferenças que se notam em relação à figura 8 resumem‐se, praticamente, a haver um novo ciclo de carga‐descarga, correspondente à simulação da passagem do segundo bogie do primeiro veículo. Esta observação permite constatar que o afastamento dos 2 bogies considerados é suficientemente elevado para que não se verifique, em termos de alterações do estado de tensão, interação entre os efeitos induzidos pelos bogies individualmente. Como é evidente, esta conclusão é dependente da velocidade de circulação, carecendo por isso de cuidado na sua extrapolação.
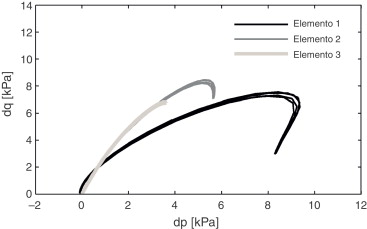
Relativamente à simulação da passagem de 2 veículos consecutivos, as trajetórias de tensão apresentam um novo padrão, como se pode observar na figura 11 .
|
|
|
Figura 11. Evolução das trajetórias de tensão em profundidade com a passagem dos 2 primeiros veículos do comboio (Alinhamento 1, V = 30 m/s). |
Com efeito, observa‐se que entre a passagem do fim do primeiro veículo e os 2 primeiros eixos do segundo, as trajetórias de tensão exibem um comportamento distinto do observado até então. De facto, é nesta transição entre os veículos que surge um desvio do padrão de comportamento observado anteriormente, ou seja, a geometria do comboio é um fator fulcral na trajetória dos ciclos carga‐descarga.
O ciclo de carga e descarga associado aos 2 primeiros eixos do segundo veículo apresenta algumas particularidades, verificando‐se uma mudança significativa do padrão de evolução em profundidade e na trajetória do ciclo carga‐descarga associado à passagem deste bogie. A interferência causada nas trajetórias de tensão deve‐se à posição geométrica dos eixos em questão. De facto a posição próxima entre os bogies adjacentes aos 2 veículos consecutivos faz com que a trajetória correspondente à passagem do último bogie da primeira carruagem não apresente um ciclo carga‐descarga completo, com uma considerável redução da tensão de desvio para os elementos a maiores profundidades.
Face às exposições efetuadas anteriormente, é agora mais facilmente interpretada a figura 7 , a qual representa as trajetórias de tensão implícitas à passagem da totalidade do comboio Alfa‐Pendular, cuja geometria foi apresentada anteriormente. Comparando as trajetórias de tensão referentes à simulação da passagem do comboio por completo e as obtidas com a simulação da passagem de apenas 2 veículos, conclui‐se que as primeiras apresentam a mesma configuração das segundas, com a particularidade de ostentarem uma repetição dos ciclos de carga‐descarga em virtude do número de veículos constituintes do comboio. Assim, pode‐se concluir que a análise da passagem de 2 veículos é suficiente para a avaliação completa das trajetórias de tensão, isto no caso de se considerar a geometria do comboio Alfa‐Pendular.
Uma avaliação quantitativa aos resultados anteriores é sintetizada na tabela 2 , na qual se indicam os valores máximos dos incrementos de tensão de desvio e de tensão média para cada elemento e a correspondente razão de tensão, ou seja, o quociente entre a primeira e a segunda.
| Elemento | 1 | 2 | 3 |
|---|---|---|---|
| Alinh. 1 | |||
| dqmáx [KPa] | 7,68 | 8,56 | 6,88 |
| dpmáx [KPa] | 9,55 | 6,00 | 4,02 |
| Razão de Tensão | 0,80 | 1,43 | 1,71 |
| Elemento | 4 | 5 | 6 |
|---|---|---|---|
| Alinh. 2 | |||
| dqmáx [KPa] | 12,09 | 8,48 | 6,57 |
| dpmáx [KPa] | 11,06 | 5,62 | 3,74 |
| Razão de tensão | 1,09 | 1,51 | 1,76 |
Os valores obtidos para o quociente denominado «Razão de tensão» permitem constatar que à medida que se evolui em profundidade os decréscimos nos incrementos de tensão média são mais significativos que os da tensão de desvio, o que revela que o solo ainda apresenta um grau de distorção considerável.
Comparando os valores para os 2 casos analisados, verifica‐se que seguem a mesma tendência de aumento da razão de tensão, sendo a maior diferença, como não poderia deixar de ser, verificada nos elementos situados mais próximo da superfície. Assim, o acréscimo de tensões de desvio é mais pronunciado para o caso do Elemento 4 em virtude de este se encontrar próximo da superfície e fora do plano de simetria, implicando a existência de tensões tangenciais nos 3 planos normais e, por consequente, um maior grau de distorção.
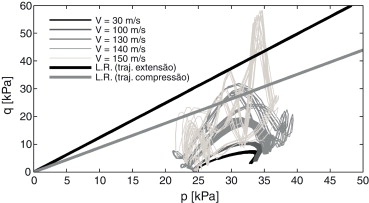
Sem embargo do anteriormente referido, reconhece‐se que a velocidade de circulação do comboio constitui um aspeto determinante para a evolução do estado de tensão no maciço. Assim sendo, de forma a avaliar o comportamento do solo da fundação para diferentes velocidades de circulação do comboio, são simuladas velocidades bastante superiores à considerada anteriormente, próximas da sua velocidade crítica (para um cenário homogéneo, a velocidade crítica do sistema via‐maciço é próxima da velocidade de propagação das ondas S[9] ), conforme se pode observar na figura 12 . Recorde‐se que o valor da velocidade de propagação das ondas S admitido para o maciço de fundação foi igual a 150 m/s sendo que, apesar do comboio Alfa‐Pendular e esta linha férrea em particular não estarem preparados para este nível de velocidades, as mesmas são plausíveis de ser atingidas, como se comprova pela velocidade de 574,5km/h (aproximadamente 160 m/s) atingida pelo TGV na linha Paris‐Estrasburgo.
|
|
|
Figura 12. Evolução das trajetórias de tensão para diferentes velocidades de circulação do comboio Alfa‐Pendular (Elemento 1). |
Adicionalmente, de forma a dotar estes estudos de elementos adicionais de análise, tem‐se em consideração o estado de tensão inicial. Para a geração deste estado considerou‐se um estado de tensão geostático em consonância com um coeficiente de impulso em repouso K0 igual a 1,0 (k0 = 1,0). Esta simplificação permite uma maior facilidade na leitura dos resultados. Na figura 12 são apresentadas ainda 2 linhas de rotura (L.R.) indicativas, correspondentes a trajetórias de extensão e de compressão, considerando um solo com ângulo de atrito de valor igual a 31° e o critério de rotura de Mohr‐Coulomb. Realça‐se que os critérios de cedência que se apresentam são meramente indicativos, pois a análise é efetuada no domínio da elasticidade.
Conforme é possível observar na figura 12 , a partir do momento em que a velocidade do comboio se aproxima da velocidade crítica do sistema via‐maciço começam a surgir comportamentos contrastantes com o padrão verificado nos vários ciclos carga‐descarga existentes nas velocidades mais reduzidas, não sendo mais possível a identificação dos mesmos.
Este aumento de complexidade deve‐se em grande medida aos efeitos de amplificação dinâmica originados nas elevadas velocidades de circulação, sendo que para velocidades mais reduzidas, o caráter dinâmico do problema deve‐se apenas à variação temporal da posição geométrica do carregamento e, como tal, os efeitos de amplificação dinâmicos tornam‐se displicentes.
Além do aumento de complexidade das trajetórias de tensão também são notórios os elevados incrementos de tensão de desvio que se verificam, em contraste com a pequena variação da tensão média. Este acontecimento é responsável pela rápida aproximação das trajetórias de tensão da superfície de rotura.
Sintetizando, é possível retirar algumas ilações dos estudos paramétricos apresentados anteriormente: i) a evolução das trajetórias de tensão em profundidade mostra um aumento na razão de tensão e um maior grau de distorção para os elementos afastados do plano de simetria; ii) as alterações do estado de tensão verificadas são mais pronunciadas para maiores velocidades; iii) o acréscimo da velocidade de circulação acarreta a geração de efeitos dinâmicos que se traduzem num aumento significativo na tensão de desvio; iv) a configuração das trajetórias de tensão sofre profundas alterações, aumentando o nível de complexidade da sua análise, com o aumento da velocidade.
3.3. Influência do mecanismo dinâmico
À semelhança dos estudos paramétricos realizados anteriormente, elaborados considerando unicamente a influência do mecanismo quasi‐estático na geração de vibrações, seguidamente avaliar‐se‐á a influência do mecanismo de excitação dinâmico na resposta do maciço de fundação face à passagem de tráfego ferroviário.
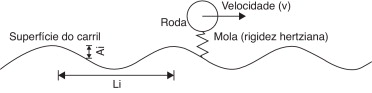
A fonte de geração de forças dinâmicas entre o veículo e a via, admitida no presente estudo, está relacionada com a presença de irregularidades ao longo do carril (fig. 13 ). A presença destas implicará a geração de forças dinâmicas ao nível do veículo, originando alterações no estado de tensão. De forma a simplificar a modelação destas irregularidades, considerar‐se‐ão diferentes perfis, gerados através de uma função sinusoidal, que em notação complexa apresenta a seguinte forma:
|
|
( 19) |
|
|
|
Figura 13. Idealização das irregularidades do carril e interação roda‐carril (adaptado de [5] ). |
onde Ai corresponde à amplitude da irregularidade e ki (ki = 2π/Li ) é o número de onda, sendo Li o comprimento de onda.
Neste estudo optou‐se pela investigação de 5 perfis de irregularidades, expostos na tabela 3 , cobrindo o intervalo típico de variações da geometria do carril de acordo com os estudos realizados por Selig and Waters [2] e apresentados em Yang et al. [5] .
| Li [m] | Ai [mm] | |
|---|---|---|
| Perfil 1 | 30,0 | 5,0 |
| Perfil 2 | 7,5 | 2,5 |
| Perfil 3 | 1,5 | 0,3 |
| Perfil 4 | 1,1 | 0,2 |
| Perfil 5 | 0,5 | 0,1 |
De forma a sistematizar a influência deste mecanismo na alteração do estado de tensão avaliam‐se, em função do perfil de irregularidades em análise, os coeficientes de majoração das tensões para uma velocidade de circulação igual a 70 m/s. A avaliação destes coeficientes tem por base de comparação os resultados dos incrementos de tensão para o caso de circulação do comboio a uma velocidade muito reduzida (10 m/s) e na ausência de irregularidades nos carris (consideração apenas do mecanismo quasi‐estático). Este caso pretende retratar uma situação base em que os efeitos dinâmicos sejam reduzidos ao mínimo. Para a velocidade de 70 m/s são avaliados os incrementos de tensão considerando primeiramente apenas a influência do mecanismo quasi‐estático (f = 0 Hz) e seguidamente a influência dos mecanismos quasi‐estático e dinâmico para diferentes frequências de excitação induzidas pelas irregularidades (diferentes perfis de irregularidades). Os coeficientes de majoração de tensões referidos resultam da divisão dos incrementos calculados para a velocidade de 70 m/s pelos incrementos obtidos para a situação base.
Neste estudo considera‐se a avaliação dos referidos coeficientes para o valor máximo dos incrementos de tensão normal σz , de tensão de desvio (dq ) e da tensão média (dp ). As Tabela 4 and Tabela 5 apresentam a informação necessária à sua avaliação e o respetivo valor, para os Elementos 1 e 4 indicados na figura 5 .
| V = 10 m/s | V = 70 m/s | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequência (f = V/Li ) [Hz] | |||||||||||||
| 0 Hz | 0 Hz | 2.3 Hz | 9.3 Hz | 46.7 Hz | 63.6 Hz | 140 Hz | |||||||
| [kPa] | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | |
| dpmáx | 9,39 | 9,61 | 1,02 | 9,94 | 1,06 | 11,21 | 1,19 | 17,73 | 1,89 | 26,95 | 2,87 | 26,00 | 2,77 |
| dqmáx | 7,51 | 8,43 | 1,12 | 8,80 | 1,17 | 12,08 | 1,61 | 18,95 | 2,52 | 32,79 | 4,37 | 19,51 | 2,60 |
| dσz,máx | 14,01 | 14,66 | 1,05 | 15,31 | 1,09 | 17,73 | 1,27 | 24,25 | 1,73 | 31,14 | 2,22 | 23,86 | 1,70 |
| V = 10 m/s | V = 70 m/s | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequência (f = V/Li ) [Hz] | |||||||||||||
| 0 Hz | 0 Hz | 2.3 Hz | 9.3 Hz | 46.7 Hz | 63.6 Hz | 140 Hz | |||||||
| [kPa] | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | [kPa] | Coef. de Maj. | |
| dpmáx | 11,07 | 11,09 | 1,00 | 11,59 | 1,05 | 13,07 | 1,18 | 19,74 | 1,78 | 29,39 | 2,65 | 22,35 | 2,02 |
| dqmáx | 11,33 | 12,91 | 1,14 | 13,47 | 1,19 | 16,66 | 1,47 | 22,20 | 1,96 | 30,25 | 2,67 | 22,52 | 1,99 |
| dσz,máx | 18,76 | 19,19 | 1,02 | 20,04 | 1,07 | 23,03 | 1,23 | 32,83 | 1,75 | 43,23 | 2,30 | 31,69 | 1,69 |
Uma primeira análise às Tabela 4 and Tabela 5 permite constatar que, considerando unicamente o efeito do aumento da velocidade de circulação de 10 m/s para 70 m/s, os coeficientes de majoração de tensões são pouco significativos, ou seja, os efeitos de amplificação dinâmica para esta gama de velocidades são praticamente negligenciáveis. Recorde‐se que para estes 2 casos apenas se considera a influência do mecanismo quasi‐estático na geração de alterações no estado de tensão
Quando considerado o efeito do mecanismo dinâmico, para as várias frequências de excitação da carga em consonância com os perfis de irregularidades considerados, os incrementos de tensões no solo sofrem importantes majorações. De facto, a consideração de imperfeições geométricas da via origina incrementos de tensões que aumentam com a «frequência de passagem» até um máximo que se situa no intervalo entre 60‐70 Hz. Este pico está relacionado com a ressonância das massas não suspensas do comboio que ocorre para valores dentro deste intervalo de frequências, tal como constatado em Alves Costa et al. [27] . Todavia na gama de frequências mais reduzidas a influência do mecanismo dinâmico é pouco significativa, podendo mesmo ser desprezável quando considerados grandes comprimentos de onda na definição das irregularidades.
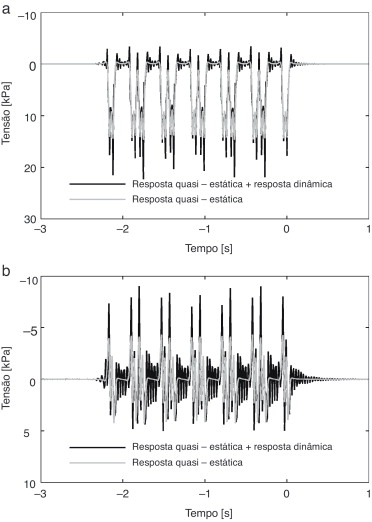
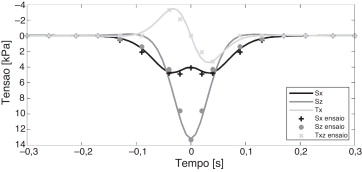
A título exemplificativo ilustra‐se na figura 14 a evolução temporal dos incrementos de tensão σz e τxz no Elemento 1 (ver fig. 5 ) para a velocidade de 70 m/s e considerando 2 situações distintas: i) apenas o mecanismo quasi‐estático; ii) a combinação do mecanismo quasi‐estático com o mecanismo dinâmico em consonância com o perfil de irregularidades 5 (ver tabela 3 ).
|
|
|
Figura 14. Representação dos incrementos de tensão no Elemento 1 ao longo do tempo, considerando a influência apenas do mecanismo de excitação quasi‐estático e a atuação conjunta dos mecanismos dinâmico e quasi‐estático (perfil 3 de irregularidades e V = 70m/s): a) σz ; b) τxz . |
Para a frequência de excitação considerada, esta figura permite a perceção da ocorrência de contínuas oscilações do estado de tensão entre a passagem dos diferentes bogies do comboio. Este facto deve‐se à consideração do mecanismo de excitação dinâmico, apesar de o aspeto típico das curvas dos componentes de tensão se manterem praticamente inalteradas. Estas oscilações começam a ser notadas momentos antes da passagem do primeiro eixo, propagando‐se durante alguns instantes após a passagem do último eixo do comboio (vibração livre). Na tensão tangencial τxz são ainda percetíveis as sucessivas alterações de sinal, correspondentes a sucessivas rotações na direção das tensões principais. Estas rotações provocam consecutivas distorções no solo, sendo presumivelmente responsáveis pela acumulação de deformação permanente.
Em suma, com os estudos efetuados compreende‐se a pertinência de uma análise considerando a interação do sistema via‐veículo, com maior relevância para elevadas velocidades e frequências de oscilação da carga na ordem dos 60‐70 Hz, nas condições de análise admitidas.
4. Ensaio laboratorial
4.1. Apresentação do ensaio
O estudo apresentado nas secções anteriores permitiu escrutinar as trajetórias de tensão induzidas no maciço pelo tráfego ferroviário. Estas trajetórias, obtidas em regime elástico e considerando unicamente a influência do mecanismo de excitação quasi‐estático, podem ser encaradas como indicativas para uma análise experimental da resposta do solo face a ações cíclicas. Assim, a possibilidade de realização de um ensaio laboratorial que permita a simulação destas trajetórias é um passo fulcral na avaliação e quantificação da acumulação de deformação permanente induzida pelo tráfego ferroviário na estrutura.
O ensaio a adotar deverá ser capaz de simular o comportamento do solo do maciço de fundação através da aplicação de inúmeros ciclos de carga‐descarga e permitir a simulação da rotação da direção de tensões principais. Deste modo, a escolha recai sobre o ensaio torsional com cilindro vazado, perspetivando‐se neste potencialidades para responder às condições referidas [4] .
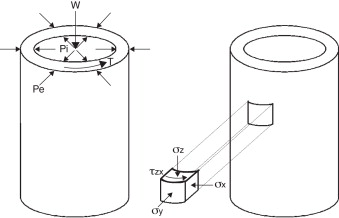
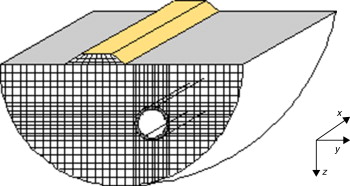
A forma da amostra de solo utilizada no referido ensaio (cilíndrica e oca) permite um esquema de carregamento composto por diversas forças, conforme se pode observar na figura 15 : carga vertical (W ), momento torsor (T ) e pressões exteriores e interiores (pe e pi , respetivamente). A conjugação destas distintas forças permite o controlo do valor das tensões representadas, para um elemento infinitesimal da amostra.
|
|
|
Figura 15. Esquema do carregamento aplicado e tensões originadas num elemento infinitesimal da amostra. |
As tensões referidas podem ser calculadas de forma analítica através de considerações de equilíbrio [4] , [31] and [32] . Assim, e de acordo com Powrie et al. [4] , as várias tensões podem ser obtidas através das seguintes expressões analíticas simplificadas:
|
|
( 20) |
|
|
( 21) |
|
|
( 22) |
|
|
( 23) |
correspondendo re e ri ao valor dos raios exterior e interior da amostra, respetivamente.
De acordo com a exposição efetuada até ao momento é possível a perceção que a principal limitação deste ensaio diz respeito à impossibilidade de imposição de tensões tangenciais nos planos xy e yz , o que confere ao ensaio apenas a possibilidade de simular as trajetórias de tensão em pontos sob o plano de simetria da via, tal como verificado ao longo dos estudos paramétricos efetuados anteriormente. Apesar desta limitação, do ponto de vista funcional, as potencialidades deste ensaio são assinaláveis na simulação dos fenómenos de rotação da direção das tensões principais devido à passagem de tráfego ferroviário, para pontos do terreno na referida disposição geométrica.
4.2. Simulação das trajetórias de tensão
Como referido inicialmente, pretende‐se averiguar a exequibilidade da simulação das trajetórias de tensão obtidas numericamente através do ensaio laboratorial, tirando partido das expressões analíticas deduzidas para este ensaio.
O estudo numérico é realizado considerando a simulação de uma carga elementar de valor igual a 130 kN (aproximadamente a carga de um eixo do comboio Alfa‐Pendular), deslocando‐se sobre os carris. Considere‐se ainda a análise referente ao Elemento 1 (ver fig. 5 ), situado no plano de simetria. Através de simulações numéricas avaliou‐se a evolução das tensões normais σx , σy e σz e da tensão tangencial τxz com a passagem da carga elementar descrita, que se apresentam na fig. 16 .
|
|
|
Figura 16. Comparação dos resultados obtidos numericamente com os obtidos através da simulação analítica do ensaio. |
As soluções analíticas das várias componentes de tensão são avaliadas através das expressões deduzidas para o ensaio através da admissão de sucessivos escalões de carga, conforme indicado na tabela 6 . Refere‐se ainda que os valores de incrementos das cargas aplicadas na simulação do ensaio procuram atender à gama de valores máximos e de resolução do equipamento desenvolvido na Universidade de Southampton (Reino Unido) em colaboração com a GSD Instruments Ltd. [8] .
| Tempo [s] | Pe [kPa] | Pi [kPa] | T [kN.m] | W [kN] |
|---|---|---|---|---|
| –0,17 | 0 | 0 | 0 | 0 |
| –0,13 | 0,25 | 0 | 0 | 0 |
| –0,09 | 1 | 0,25 | 0 | 0 |
| –0,04 | 4 | 3,5 | –0,0055 | 0 |
| –0,02 | 4,5 | 4,25 | –0,0035 | 0,1 |
| 0 | 5,25 | 6 | 0 | 0,17 |
| 0,02 | 4,5 | 4,25 | 0,0035 | 0,1 |
| 0,04 | 4 | 3,5 | 0,0055 | 0 |
| 0,09 | 1 | 0,25 | 0 | 0 |
| 0,13 | 0,25 | 0 | 0 | 0 |
| 0,17 | 0 | 0 | 0 | 0 |
Analisando a figura 16 , que representa a comparação dos resultados obtidos com as 2 análises (numérica e analítica), verifica‐se uma assinalável semelhança quer na tendência quer no conteúdo das curvas representativas das várias componentes de tensão. De facto, com esta simples simulação os resultados obtidos estão dentro das espectativas criadas, ou seja, há uma semelhança aceitável entre as 2 análises.
Refere‐se ainda que, devido ao facto do elemento do solo em estudo se situar no plano de simetria, a tensão normal σy é sempre uma tensão principal, motivo pelo qual o interesse da sua representação não é tão significativo quanto o das restantes tensões apresentadas e, portanto, a mesma não se encontra representada.
Recorda‐se que esta análise tem apenas como objetivo avaliar a possibilidade do ensaio laboratorial simular as alterações ao estado de tensão, tendo‐se verificado, na opinião do autor, essa possibilidade. Ressalva‐se a particularidade do não cumprimento da resolução do aparelho de ensaio referido no que toca às pressões a aplicar, de modo a alcançar uma simulação mais próxima da obtida numericamente. No entanto, esta mesma resolução está dependente das especificações próprias do equipamento analisado, existindo outros que se adaptam melhor a esta característica [32] .
Por fim, é conveniente referir que o estudo efetuado apenas tem em conta o mecanismo de excitação quasi‐estático na simulação das trajetórias de tensão. A consideração da influência do mecanismo dinâmico implicaria considerar a ação de forças dinâmicas induzidas por este mecanismo no carregamento. Esta ocorrência introduziria grandes contrastes no sistema de carregamento ao longo dos sucessivos escalões de carga, acarretando sérias dificuldades na sua definição.
5. Conclusões
No presente artigo foram avaliadas as alterações do estado de tensão provocadas pelo tráfego ferroviário, sendo o conhecimento do modo como essas alterações se processam uma mais‐valia para uma correta interpretação dos fenómenos em causa. De salientar que a utilização do modelo numérico 2,5D FEM‐PML revelou‐se fundamental, de forma a permitir reproduzir o comportamento tridimensional do problema com uma economia considerável em termos computacionais.
Os estudos efetuados considerando a distinção entre os mecanismos de excitação quasi‐estático e dinâmico permitiram a perceção da sua influência individual. Relativamente aos estudos elaborados tendo por base o primeiro mecanismo referido, há a referir que para níveis de velocidades afastados da velocidade crítica do solo, o comportamento deste a curto prazo não levanta problemas de maior. Porém, caso a velocidade se aproxime da velocidade crítica de circulação, assiste‐se a uma incremento considerável tanto da tensão média como da tensão de desvio podendo mesmo acarretar a plastificação do solo. Sem embargo, mesmo para velocidades de circulação inferiores à velocidade crítica, a degradação das capacidades resistentes dos elementos constituintes da via com a repetição de inúmeros ciclos carga‐descarga, pode implicar consequências nefastas para o comportamento estrutural desta. A realização de estudos laboratoriais considerando o ensaio laboratorial abordado poderá ser um bom método de identificação de leis de acumulação de deformação permanente na via, de forma a prever o seu comportamento a longo prazo. Salienta‐se ainda que quando consideradas velocidades próximas da velocidade crítica do solo é necessário levar em consideração os efeitos de amplificação dinâmica ocorrentes, pois estes efeitos acarretam graves consequências para o comportamento da via‐férrea.
A conservação geométrica da via‐férrea constituiu um parâmetro ao qual das administrações ferroviárias devem atentar. Conforme demonstrado, a presença de irregularidades nos carris, sobretudo de baixos comprimentos de onda, é responsável por elevadas majorações dos incrementos de tensão transmitidos à via aquando da passagem dos comboios, podendo induzir a sua degradação precoce, acarretando elevados custos de manutenção.
Conflito de interesses
Os autores declaram não haver conflito de interesses.
Agradecimentos
Os autores do presente artigo agradecem à FCT‐ Fundação para a Ciência e Tecnologia pelo apoio financeiro prestado, nomeadamente através do projeto de investigação ‐ PTDC/ECM/114505/2009.
Bibliografia
- [1] E. Fortunato; Renovação de Plataformas Ferroviárias. Estudos relativos à capacidade de carga, in Departamento de Engenharia Civil.; Universidade do Porto, Porto (2005)
- [2] E. Selig, J. Waters; Track Geotechnology and Substructure Management; T. Telford, London (1994)
- [3] Chen, Y.M., C.J. Wang, Y.P. Chen, and B. Zhu, Characteristics of stresses and settlement of ground induced by train. Environmental Vibrations – Takedemira (ed.), 2005.
- [4] W. Powrie, L.A. Yang, C.R.I. Clayton; Stress changes in the ground below ballasted railway track during train passage. Proceedings of the Institution of Mechanical Engineers; Part F: Journal of Rail and Rapid Transit, 221 (2) (2007), pp. 247–261
- [5] L.A. Yang, W. Powrie, J.A. Priest; Dynamic stress analysis of a ballasted railway track bed during train passage; Journal of Geotechnical and Geoenvironmental Engineering, 135 (5) (2009), pp. 680–689
- [6] Y. Tao, J. Zhou, X. Wen; The characteristics of dynamic stress in foundation soil cause by train load (2011)
- [7] S.F. Brown; Soil mechanics in pavement engineering; Geotechnique, 46 (3) (1996), pp. 383–426
- [8] P.J. Gräbe, C.R.I. Clayton; Effects of principal stress rotation on permanent: Deformation in rail track foundations; Journal of Geotechnical and Geoenvironmental Engineering, 135 (4) (2009), pp. 555–565
- [9] P. Alves Costa; Vibrações do sistema via‐maciço induzidas por tráfego ferroviário. Modelação numérica e validação experimental, in Departamento de Engenharia Civil.; Faculdade de Engenharia da Universidade do Porto, Porto (2011)
- [10] Y.B. Yang, H.H. Hung; A 2.5D finite/infinite element approach for modelling viscoelastic body subjected to moving loads; International Journal for Numerical Methods in Engineering, 51 (2001), pp. 1317–1336
- [11] S. François, M. Schevenels, P. Galvín, G. Lombaert, G. Degrande; A 2.5D coupled FE‐BE methodology for the dynamic interaction between longitudinally invariant structures and a layered halfspace; Computer Methods in Applied Mechanics and Engineering, 199 (23–24) (2010), pp. 1536–1548
- [12] P. Galvín, S. François, M. Schevenels, E. Bongini, G. Degrande, G. Lombaert; A 2.5D coupled FE‐BE model for the prediction of railway induced vibrations; Soil Dynamics and Earthquake Engineering, 30 (12) (2010), pp. 1500–1512
- [13] P. Alves Costa, R. Calçada, A. Silva Cardoso; Track‐ground vibrations induced by railway traffic: In‐situ measurements and validation of a 2.5D FEM‐BEM model; Soil Dynamics and Earthquake Engineering, 32 (1) (2012), pp. 111–128
- [14] P. Lopes, P. Alves Costa, R. Calçada, A. Silva Cardoso; Modeling of vibrations in tunnels using the finite element method with perfectly matched layers, in First International Conference on Railway Technology: Research; J. Pombo (Ed.), Development and Maintenance, Las Palmas de Gran Canaria, Spain (2012)
- [15] G. Lombaert, G. Degrande; Ground‐borne vibration due to static and dynamic axle loads of InterCity and high‐speed trains; Journal of Sound and Vibration, 319 (3–5) (2009), pp. 1036–1066
- [16] P. Galvín, A. Romero, J. Domínguez; Fully three‐dimensional analysis of high‐speed train‐track‐soil‐structure dynamic interaction; Journal of Sound and Vibration, 329 (2010), pp. 5147–5163
- [17] S. Gupta, M. Hussein, G. Degrande, H. Hunt, D. Clouteau; A comparison of two numerical models for the prediction of vibrations from underground railway traffic; Soil Dynamics and Earthquake Engineering, 27 (7) (2007), pp. 608–624
- [18] Y.B. Yang, H.H. Hung; Soil vibrations caused by underground moving trains; Journal of Geotechnical and Geoenvironmental Engineering, 134 (11) (2008), pp. 1633–1644
- [19] J. Lysmer, R.L. Kuhlemeyer; Finite dynamic model for infinite media; Journal of Engineering Mechanics Division, 95 (1969), pp. 859–877
- [20] P. Alves Costa, R. Calçada, J. Couto Marques, A. Silva Cardoso; A 2.5D finite element model for simulation of unbounded domains under dynamic loading; in 7th European Conference on Numerical Methods in Geotechnical Engineering, NUMGE, Trondheim, Norway (2010)
- [21] Y.B. Yang, S.R. Kuo, H.H. Hung; Frequency‐independent infinite elements for analysing semi‐infinite problems; International Journal for Numerical Methods in Engineering, 39 (20) (1996), pp. 3553–3569
- [22] P. Bettess; Infinite Elements; Phenshaw Press (1992)
- [23] P. Alves Costa, R. Calçada, A. Silva Cardoso, A. Bodare; Influence of soil non‐linearity on the dynamic response of high‐speed railway tracks; Soil Dynamics and Earthquake Engineering, 30 (4) (2010), pp. 221–235
- [24] X. Sheng, C.J.C. Jones, D.J. Thompson; Prediction of ground vibration from trains using the wavenumber finite and boundary element methods; Journal of Sound and Vibration, 293 (3–5) (2006), pp. 575–586
- [25] L. Auersch; The excitation of ground vibration by rail traffic: Theory of vehicle‐track‐soil interaction and measurements on high‐speed lines; Journal of Sound and Vibration, 284 (1–2) (2005), pp. 103–132
- [26] J. Bitzenbauer, J. Dinkel; Dynamic interaction between a moving vehicle and an infinite structure excited by irregularities ‐ Fourier transforms solution; Archive of Applied Mechanics, 72 (2–3) (2002), pp. 199–211
- [27] P. Alves Costa, R. Calçada, A.S. Cardoso; Influence of train dynamic modelling strategy on the prediction of track‐ground vibrations induced by railway traffic; Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 226 (4) (2012), pp. 434–450
- [28] X. Sheng, C.J.C. Jones, D.J.A. Thompson; Comparison of a theoretical model for quasi‐statically and dynamically induced environmental vibration from trains with measurements; Journal of Sound and Vibration, 267 (3) (2003), pp. 621–635
- [29] W. Zhai, Z. Cai; Dynamic interaction between a lumped mass vehicle and a discretely supported continuous rail track; Computers and Structures, 63 (5) (1997), pp. 987–997
- [30] V. Dias da Silva; Mecânica e Resistência dos Materiais.; E. Editora, Coimbra (1995)
- [31] A. Sayão; Behaviour of sand under general stress paths in the hollow cylinder torsional device, in Faculty of Graduate Studies – Department of Civil Engineering; University of British Columbia, Columbia (1989)
- [32] S. Sivathayalan, V. Manmatharajan, P. Logeswaran; Hollow cylinder torsional shear tests to evaluate the role of principal stress directions on cyclic resistance; in Pan‐Am CGS Geotechnical Conference., Ontario, Canada (2011)
Document information
Published on 01/06/15
Accepted on 13/02/14
Submitted on 20/06/13
Volume 31, Issue 2, 2015
DOI: 10.1016/j.rimni.2014.02.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?
![Geometria do comboio Alfa‐Pendular [9].](/wd/images/8/85/Draft_Content_106436184-1-s2.0-S0213131514000248-gr6.jpg)