Cálculo de daño en pavimentos mediante un análisis hidro-mecánico de pavimentos flexibles

Abstract. A hydro-mechanical analysis of a pavement is presented in which the variation of the water content is considered for the estimation of modulus of elasticity of the layers of soil in the pavement. To do this, the Richards differential equation and equilibrium in the axi-symmetric condition are solved simultaneously, considering a non-linear elasticity that depends on the suction and stress state in the soil. With this type of analysis, it is possible to quantify the variation of the damage with respect to time and visualize the deterioration of the pavement structures. It is considered a practical case in which the increase in damage is quantified in function of the variation of environmental conditions and conclusions are obtained.

Resumen. Se presenta un análisis hidro-mecánico de un pavimento en el que se consideran la variación de las condiciones de contenido de agua para la determinación del módulo de elasticidad de las capas de suelo en el pavimento. Para ello se soluciona la ecuación diferencial de Richards y de equilibrio en condición axi-simétrica de manera simultánea, considerando una elasticidad no lineal que depende de la succión y del estado de esfuerzos en el suelo. Con este tipo de análisis es posible cuantificar la variación del daño con respecto al tiempo y visualizar el deterioro de las estructuras de pavimento. Se considera un caso práctico en el cual se cuantifica el incremento del daño en función de la variación de las condiciones ambientales y se obtienen conclusiones.

Palabras clave: Análisis de Pavimentos, flujo de agua en suelos, daño en pavimentos

1 Introducción

La estructura de pavimentos está sometida a las solicitaciones del tránsito vehicular y clima; en particular la temperatura y el contenido de agua afectan los módulos con los cuales se realiza el análisis de esfuerzos y deformaciones de los pavimentos. Dentro de las metodologías mecanicistas de diseño de pavimentos, el estado de esfuerzos y deformaciones se relaciona con el número de repeticiones para la falla [1]. El comportamiento esfuerzo deformación de la carpeta asfáltica depende de la temperatura y falla por agrietamiento, el de las capas de suelo depende del contenido de agua y fallan por deformación permanente. Si cambian las condiciones anteriores la respuesta del pavimento varía. En el caso en que los módulos de resiliencia disminuyan el daño es mayor, esto sucede cuando la temperatura de la carpeta asfáltica aumenta y cuando existe infiltración de agua hacia las capas de suelo o un incremento en el nivel de aguas freáticas.

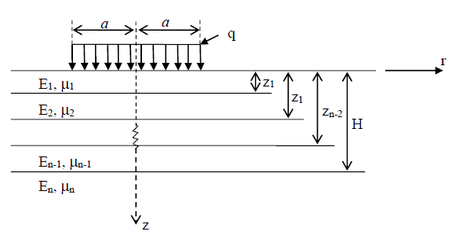
Los análisis de pavimentos se pueden realizar con la teoría de elasticidad multicapa de Burmister [2].Debido a las condiciones de contorno de la carga (neumático) se utiliza un análisis simplificado axi-simétrico alternativo al de tres dimensiones [1, 2]. En la Fig. 1 se presenta el sistema multicapa axi-simétrico simplificado que usualmente se utiliza para los análisis de pavimentos flexibles. En la Fig. 1, ${\textstyle a}$, es el radio del área cargada que representa la llanta del vehículo, q, el esfuerzo uniforme de la llanta (presión de inflado) y z las distancias a las capas de interés. Existe un número ${\textstyle n}$ de capas que tienen propiedades ${\textstyle E\,y\,\mu }$ . La teoría de Burmister considera que el módulo de elasticidad es constante, pero en la realidad depende del estado de esfuerzos y de las condiciones climáticas.

Alternativamente, se puede utilizar el método de los elementos finitos para resolver las ecuaciones diferenciales que resultan del problema elástico lineal en condiciones axi-simétricas que se plantea [3][4]. Como se menciona el clima afecta el comportamiento de los materiales con los que se construye un pavimento. En este estudio sólo se toma en cuenta la influencia de la variación de los contenidos de agua en las capas de suelo. Para ello en necesario solucionar la ecuación de Richards [5], para suelos parcialmente saturados.

Fig. 1. Sistema Multicapa simplificado para el análisis de pavimentos flexibles [1].

Con la solución de ambas ecuaciones diferenciales de manera simultánea, es posible estimar como varía el daño en pavimento cuando este está sometido a cambios en su contenido de agua, debido a la infiltración e incremento de nivel de agua freática.

2 Análisis de pavimentos

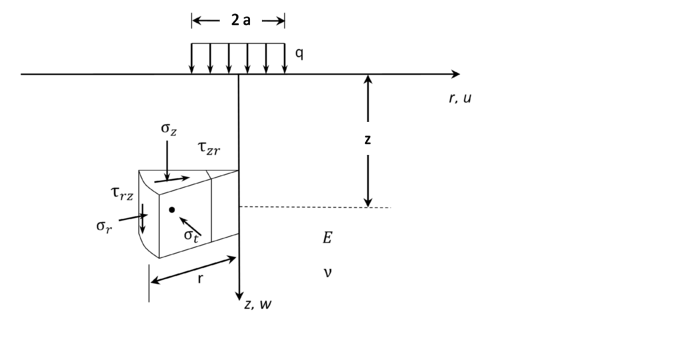
En la Fig. 2 se presenta el estado de esfuerzos en un punto en una condición axi-simétrica. El estado de esfuerzos es tridimensional, pero se puede estudiar con el uso de dos coordenadas (r, z) si las cargas exteriores se consideran axi-simétricas y generan desplazamientos en direcciones radial (u) y axial (w) [6].

Fig. 2. Componentes de los esfuerzos de una sección axi-simétrico.

2.1 Teoría de la elasticidad en condiciones axi-simétricas

De las ecuaciones de equilibrio en condenadas cilíndricas [7], se puede deducir las ecuaciones de equilibrio para problemas axi-simétricos. Debido a la simetría axial u y w son independientes de la coordenada ${\textstyle \theta }$ [6], por tanto, las ecuaciones de equilibrio se simplifican a dos ecuaciones que son:

${\frac {\partial \left(r\,{\sigma }_{r}\right)}{\partial r}}{\frac {1}{r}}-{\frac {{\sigma }_{\theta }}{r}}+$${\frac {\partial {\tau }_{rz}}{\partial z}}+{F}_{r}=0$ ${\frac {\partial \left(r{\tau }_{rz}\right)}{\partial r}}{\frac {1}{r}}+{\frac {{\partial \sigma }_{z}}{\partial z}}+$$Fz=0$

(1)

Donde ${\textstyle {\sigma }_{r}}$ y ${\textstyle {\sigma }_{z}}$ son los esfuerzos en las direcciones ${\textstyle r}$ y ${\textstyle z}$ , ${\textstyle {\sigma }_{\theta }}$ en la dirección circunferencial, ${\textstyle {\tau }_{rz}}$ es el esfuerzo de corte y ${\textstyle {F}_{r}}$ y ${\textstyle {F}_{z}}$ son las fuerzas de peso propio en las direcciones ${\textstyle r}$ y ${\textstyle z}$. Las correspondientes deformaciones quedan definidas por las siguientes ecuaciones:

${\epsilon }_{r}={\frac {\partial u}{\partial r}}$ ${\epsilon }_{z}={\frac {\partial w}{\partial z}}$ ${\gamma }_{rz}={\frac {\partial u}{\partial r}}+{\frac {\partial w}{\partial z}}$ ${\epsilon }_{\theta }={\frac {u}{r}}$

(2)

La ecuación constitutiva de acuerdo con la teoría de la elasticidad queda definida por:

$D={\frac {E}{\left(1+\nu \right)\left(1-2\nu \right)}}\left[{\begin{matrix}1-\nu &\nu &\nu &0\\\nu &1-\nu &\nu &0\\\nu &\nu &1-\nu &0\\0&0&0&{\frac {1-2\nu }{2}}\end{matrix}}\right]$

(3)

Donde ${\textstyle E}$ es el módulo de elasticidad y ${\textstyle \nu }$ es el coeficiente de Poisson.

En el análisis de pavimentos se utiliza el módulo de resiliencia ( ${\textstyle {M}_{r}}$) como módulo de elasticidad y se define como:

$M_{r}={\frac {\sigma _{d}}{\varepsilon _{r}}}$

(4)

Donde ${\textstyle {\sigma }_{d}={\sigma }_{1}-{\sigma }_{3}}$, es el esfuerzo desviador y ${\textstyle \varepsilon _{r}}$, es la deformación recuperable después de cien ciclos de carga y descarga.En los protocolos de ensayo del módulo de resiliencia [8] se utilizan combinaciones de esfuerzo de confinamiento ( ${\textstyle {\sigma }_{3}}$) y esfuerzo desviador cíclico para obtener los Mr, en distintas condiciones de esfuerzos. Existen ecuaciones de ajuste clásicas como la siguiente:

$E={k}_{1}\,{P}_{a}{\left({\frac {\theta }{{P}_{a}}}\right)}^{{k}_{2}}{\left({\frac {{\tau }_{oct}}{{P}_{a}}}+1\right)}^{{k}_{3}}$

(5)

Donde ${\textstyle {P}_{a}}$ es la presión atmosférica, ${\textstyle \theta }$ es la suma de los esfuerzos principales ${\textstyle =}$${\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}$, ${\textstyle {\tau }_{oct}}$ el esfuerzo octaédrico ${\textstyle =}$$1/3{\sqrt {{\left({\sigma }_{1}-{\sigma }_{2}\right)}^{2}+{\left({\sigma }_{1}-{\sigma }_{3}\right)}^{2}+{\left({\sigma }_{2}-{\sigma }_{3}\right)}^{2}}}$ y k₁, k₂, k₃ son parámetros experimentales. La ecuación (4) es propuesta por la guía empírico-mecanicista de diseño de pavimentos (MEPDG 2008). Si el módulo de resiliencia depende del estado de esfuerzos, se debe de resolver el análisis de esfuerzos de manera iterativa, correspondiendo a un análisis con elasticidad no lineal. Debido a la no linealidad de la ecuación (5), la convergencia de los análisis de esfuerzos se complica. Para los análisis presentados se usa la ecuación lineal utilizada por Huang [1], que se reproduce enseguida:

$E={E}_{0}\left(1+\beta \,\theta \right)$

(6)

Donde, ${\textstyle \beta }$ es una constante de ajuste y ${\textstyle {E}_{0}}$ es el módulo de resiliencia para el caso de que el invariante ${\textstyle \theta }$ tenga un valor de cero. La ecuación anterior no introduce demasiado error ya que los esfuerzos de compresión que se presentan en la base son mayores a cero debido al confinamiento que ejerce la carpeta.

2.2 Teoría de flujo de agua

Las capas de suelo de un pavimento están conformadas de suelos compactados. El proceso de compactación condiciona a los suelos a estar en estado de saturación parcial, con tres fases (aire, agua y sólidos). Los análisis de flujo de agua en pavimentos se resuelven en términos de succión matricial o presión negativa de agua. La succión está definida como

$s={u}_{a}-{u}_{w}$

(7)

Donde

${\textstyle {u}_{a}}$ es la presión del aire que se encuentra en los poros

${\textstyle {u}_{w}}$, es la presión del agua que está en los poros

El flujo de agua se resuelve tomando como base la ley de Darcy, que es válida suelos parcialmente saturados y se escribe como:

${v}_{x}=-{k}_{x}{\frac {\partial h}{\partial x}}$

(8)

Donde

${\textstyle {v}_{x}}$ es la velocidad del agua

${\textstyle {k}_{x}}$ es la conductividad hidráulica

${\textstyle {\frac {\partial h}{\partial x}}}$ es el gradiente hidráulico en la dirección ${\textstyle x}$

${\textstyle h=z+{\frac {{u}_{w}}{{\gamma }_{w}}}}$ es la carga hidráulica total

En suelos parcialmente saturados la ecuación diferencial de flujo transitorio que gobierna el flujo de agua es la ecuación de Richards [5]. La formulación clásica se considera en dos o tres dimensiones. La versión de dos dimensiones se puede reescribir para resolverla de manera simultánea con las ecuaciones de teoría de la elasticidad axi-simétrica, antes mencionadas. Para este caso la ecuación de Richards se escribe como:

${\frac {\partial }{\partial z}}\left({k}_{z}\left(s\right)\left(1+{\frac {1}{{\gamma }_{w}}}{\frac {\partial {u}_{w}}{{\partial }_{z}}}\right)\right)+$${\frac {\partial }{\partial r}}\left({\frac {{k}_{r}\left(s\right)}{{\gamma }_{w}}}{\frac {\partial {u}_{w}}{\partial r}}\right)+$${\frac {k}{r}}{\frac {1}{{\gamma }_{w}}}{\frac {\partial {u}_{w}}{\partial r}}\,={m}_{w}{\frac {\partial {u}_{w}}{\partial t}}$

(9)

Donde ${\textstyle {m}_{w}}$ es el módulo de almacenamiento y queda determinado por la ecuación:

${m}_{w}={\frac {\partial {\theta }_{w}}{\partial s}}$

(10)

Donde ${\textstyle {\theta }_{w}}$ se obtiene de la curva de retención del suelo. Se puede utilizar la ecuación de Van Genuchten [9], que queda definida por la siguiente ecuación:

$\theta n\left(s\right)={\frac {1}{{\left({\left(\alpha \,s\right)}^{n}+1\right)}^{m}}}$

(11)

Donde

${\textstyle {\theta }_{n}={\frac {{\theta }_{w}-{\theta }_{r}}{{\theta }_{s}-{\theta }_{r}}}}$ el contenido de agua normalizado

${\textstyle {\theta }_{r}}$ es el contenido volumétrico de agua residual

${\textstyle {\theta }_{s}}$ es el contenido volumétrico saturado de agua

${\textstyle \alpha }$ es un parámetro de ajuste relacionado con el valor de entrada de aire (1/kPa)

${\textstyle n,\,m}$ son parámetros de ajuste, y ${\textstyle m=1-}$${\frac {1}{n}}$

La conductividad hidráulica en un suelo parcialmente saturado depende de la succión a la que se encuentra el suelo y se adopta el modelo de Van Genuchten - Mualem [9][10] para conductividad hidráulica,

$k\left({\theta }_{n}\right)={k}_{s}{\sqrt {{\theta }_{n}}}{\left(1-{\left(1-{\theta }_{n}^{1/m}\right)}^{m}\right)}^{2}$

(12)

Donde ${\textstyle {k}_{s}}$ es la conductividad saturada del suelo y ${\textstyle m}$ se describe en la ecuación (11) de la curva característica.

El módulo de elasticidad se puede hacer dependiente de la succión. Una de las ecuaciones de ajuste es la de Liang [11] en términos de esfuerzos efectivos,

$E={k}_{1}\,{P}_{a}{\left({\frac {{\theta }_{b}+\chi \left({u}_{a}-{u}_{w}\right)}{{P}_{a}}}\right)}^{{k}_{2}}{\left({\frac {{\tau }_{oct}}{{P}_{a}}}+1\right)}^{{k}_{3}}$

(13)

Donde

${\textstyle {\theta }_{b}={\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}={\sigma }_{1}+}$$2{\sigma }_{3}$ es el invariante,

${\textstyle {\tau }_{oct}={\frac {1}{3}}{\sqrt {{\left({\sigma }_{1}-{\sigma }_{2}\right)}^{2}+{\left({\sigma }_{1}-{\sigma }_{3}\right)}^{2}+{\left({\sigma }_{2}-{\sigma }_{3}\right)}^{2}}}}$ es el esfuerzo octaédrico de corte

${\textstyle {\sigma }_{1},{\sigma }_{2},\,{\sigma }_{3}}$ son los esfuerzos principales

${\textstyle {k}_{1},{k}_{2},{k}_{3}}$ son parámetros de ajuste

${\textstyle \chi }$ es el parámetro de esfuerzos efectivos de Bishop que depende del grado de saturación del suelo cuyo valor oscila entre 0 y 1.

${\textstyle {P}_{a}}$ es la presión atmosférica (101.325 kPa)

La ecuación (13) es una modificación de la ecuación (5), la cual toma en cuenta el parámetro de esfuerzos efectivo de Bishop, ${\textstyle \chi }$ . Está ecuación fue desarrollada originalmente para suelos cohesivos.

Para los análisis que se presentan en este artículo se utiliza una modificación de la ecuación (6). Agregando el efecto de la succión por medio de la modificación lineal del parámetro ${\textstyle E{}_{0}}$ en función de la succión. La ecuación siguiente es la que se utiliza,

${E}_{0}={E}_{s0}+{\beta }_{s}s$

(14)

Donde ${\textstyle {E}_{s0}}$ valor es del módulo con succión cero, ${\textstyle {\beta }_{s}}$ es una constante que da la variación del módulo con respecto a la succión.

2.3 Análisis de pavimento y cálculo de daño

2.3.1 Definición del problema.

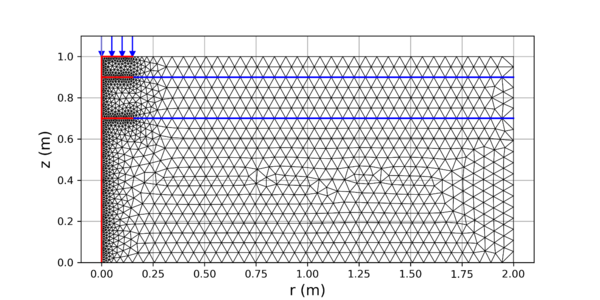
En este caso se analiza la estructura axi-simétrica del pavimento flexible que se presenta en la Fig. 3. La estructura tiene un espesor de carpeta de concreto asfáltico de 10 cm, un espesor de base de 20 cm y un espesor de subrasante de 70 cm. La carga aplicada corresponde a un eje equivalente de 8.2 ton aproximadamente. Las condiciones de frontera están esquematizadas mediante triángulos para restringir los desplazamientos en la dirección z y r, y círculos para restringir los desplazamientos solo en la dirección r en el eje de simetría.

Fig. 3. Sección de pavimento para análisis

Las propiedades de las capas de base y de subrasante dependen de los estados de esfuerzos y de la succión de acuerdo con la ecuación (14) y se presentan en la Tabla 1. La carpeta asfáltica se considera que tiene un comportamiento lineal con un módulo elástico de 3,000,000 kPa y con una relación de Poisson de 0.4.

Tabla 1. Parámetros para el análisis hidro-mecánico

Parámetro	Base	Subrasante
${\textstyle {E}_{s0}}$ (kPa)	80,843	34,200
$\beta$	0.0025	0.0035
${\beta }_{s}$	0.5	5

Los parámetros de la curva de retención y conductividad hidráulica se presentan en la Tabla 2,

Tabla 2. Parámetros hidráulicos usados

Parámetro	Carpeta	Base	Subrasante
${\theta }_{s}$	0.2	0.35	0.45
${\theta }_{r}$	0.01	0.05	0.05
$n$	1.4	7.35	1.4
${\textstyle \alpha }$ (1/kPa)	0.1	1.53	0.1
${\textstyle {k}_{s}}$ (m/hr)	0.01	3	0.1

La simulación considera cuatro etapas:

1. De 0 a 50 hrs. Equilibrio inicial con un nivel de aguas freáticas localizado a una profundidad de 5 m. La idea es considerar un equilibrio del nivel freático después de una temporada de secas, la succión que se obtiene es la condición de referencia para el daño cuando se presentan los cambios de contenido de agua subsecuentes. En la modelación, esta variación se introduce mediante una condición de frontera de succión (condición de Dirichlet) en la parte inferior, que varía con el tiempo.

2. De 50 a 74 hrs. Se introduce una infiltración de agua en la superficie del pavimento con una velocidad de 0.85 mm/h. Se implementa con una condición de Neumann en la parte superior.

3. De 74 a 100 hrs. Se elimina la infiltración y se equilibra nuevamente con las nuevas condiciones.

4. De 100 a 300 hrs. Se eleva el nivel de aguas freáticas a 3.5 m de profundidad.

2.3.2 Análisis de resultados.

Se utilizó el programa FlexPDE 7.0® para solucionar las ecuaciones diferenciales. Es una herramienta que utiliza los elementos finitos para solucionar cualquier sistema de ecuaciones diferenciales, con sus variables dependientes, en función del tiempo y toma en cuenta la no linealidad de las ecuaciones. El programa FlexPDE utiliza un método de Newton-Rapson Modificado para la solución del sistema no-lineal; el cual toma un paso de Newton por cada paso del tiempo, y las no-linealidades se manejan adaptando el tamaño de paso en el tiempo.  Se utilizaron triángulos, con un orden de interpolación cuadrático, para la malla de elementos finitos; se tienen un total de 2737 elementos. La malla se presenta en la Fig. 4, se puede notar que existe un mayor número de elementos en la zona del eje de axi-simetría y las interfaces (zonas con líneas rojas). Es en la zona donde se requiere estimar las deformaciones de tensión y de compresión, además del muestreo de la presión del agua en la base y subrasante.

Fig. 4. Malla utilizada para la solución del problema

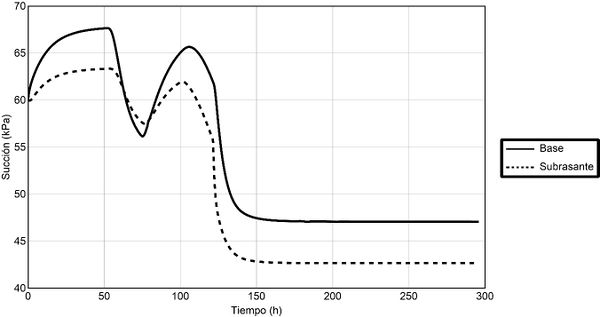
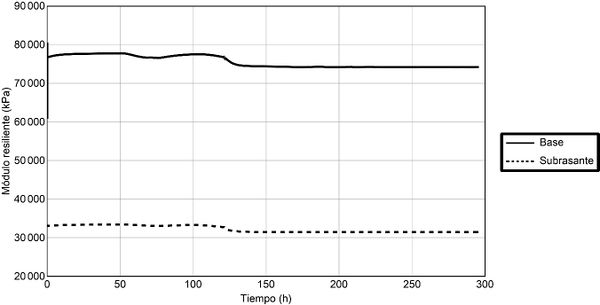
El problema se resolvió considerando las cuatro etapas mencionadas. Con el objetivo de ver como varían la succión y los módulos de resiliencia cuando se somete el pavimento a variaciones de las condiciones de frontera, se presentan dos gráficas donde se muestra la historia en el eje de simetría y en el centro de las capas de base y subrasante (ver Fig. 4 y Fig. 5). Si se analiza la Fig. 4, se puede verificar que en la primera etapa de la simulación la succión se equilibra hasta llegar a 67.5 y 63 kPa para la base y subrasante respectivamente. En el periodo de infiltración (segunda etapa) la succión disminuye en mayor medida en la base (11.6 kPa) que en la subrasante (5.8 kPa). En la tercera etapa el suelo tiende a secarse (aumenta la succión), y por último en la etapa cuatro se eleva el nivel de aguas freáticas y como resultado, la succión de la capa subrasante queda en 43 kPa aproximadamente.

Fig. 5. Variación de la succión respecto al tiempo, medido a media altura de las capas de base y subrasante.

De manera simultánea se presenta la variación de los módulos de resiliencia en los puntos antes mencionados (Ver Fig. 5). Se puede notar que cuando la succión aumenta los módulos aumentan y viceversa.

Fig. 6. Variación del Módulo resiliente respecto al tiempo, medido a media altura de las capas base y subrasante.

El número de repeticiones que resiste el pavimento por agrietamiento de la carpeta ( ${\textstyle {N}_{f}}$) y por deformación permanente ( ${\textstyle {N}_{d}}$) se puede calcular con las siguientes ecuaciones [1],

${N}_{f}={f}_{1}{\left({\varepsilon }_{r}\right)}^{-{f}_{2}}{\left({E}_{1}\right)}^{-{f}_{3}}$

(16)

${N}_{d}={f}_{4}{\left({\varepsilon }_{z}\right)}^{{f}_{5}}$

(17)

donde ${\textstyle {\epsilon }_{r}}$ es la deformación unitaria de tensión en la fibra inferior de la carpeta, ${\textstyle {E}_{1}}$ el módulo de elasticidad de la carpeta, ${\textstyle {\epsilon }_{z}}$ es la deformación de compresión en la fibra superior de la subrasante, ${\textstyle {f}_{1},{f}_{2},{f}_{3},{f}_{4}}$ y ${\textstyle {f}_{5}}$ parámetros de ajuste. El instituto del asfalto de Estados Unidos propone que estos parámetros sean 0.0796, 3.291, 0.854, 1.365x10^-9 y 4.477 respectivamente [1].

En el análisis del daño que se presenta se toma como referencia la succión de equilibrio al final de la primera etapa (50 hrs), condición de referencia de temporada de secas. Se calculó el número de repeticiones que soporta la estructura de pavimento por deformación permanente ( ${\textstyle {N}_{d}}$) y por fatiga de la carpeta ( ${\textstyle {N}_{f}}$). Se definió el daño que causa una pasada como,

${D}_{i}={\frac {1}{N}}$

(18)

Donde ${\textstyle N}$ toma el valor de ${\textstyle {N}_{d}}$ o ${\textstyle {N}_{f}}$ dependiendo del análisis que se realice, deformación permanente o fatiga. El daño que se causa con las condiciones iniciales se consideró como 1 y se realizaron los cálculos necesarios para ver la variación del daño por deformación permanente y agrietamiento. Los resultados de presentan en la Fig. 7, se observa muy claro como el daño aumenta cuando la succión disminuye (ver Fig. 5). Para este caso el daño final es mayor en ambos casos: 12.5% y 5.7 % por deformación permanente y agrietamiento respecto a la condición inicial.

Fig. 7. Daño por eje equivalente relativo

3 Conclusiones

La solución simultánea de las ecuaciones diferenciales de flujo y de equilibrio ayuda a la cuantificación del daño en las estructuras de pavimento de manera más precisa. El tema no es sencillo ya que las ecuaciones involucradas son no-lineales. Pero en la actualidad es posible solucionarlas con herramientas numéricas como los elementos finitos y con ello realizar mejores diseños. Para llevar estos análisis a la práctica es importante establecer las condiciones de frontera hidráulicas a las que la estructura estará expuesta, que dependen del clima y la profundidad del nivel de agua freática de la zona. Se necesita realizar más trabajo para establecer condiciones de frontera simplificadas generales para condiciones de diseño correspondientes a la práctica.

4 Referencias

[1] Huang, Y.H. (2004). Pavement Analysis and Design. Pearson Prentice Hall

[2] Burmister, D. M. (1945). The general theory of stresses and displacements in layered soil systems. III. Journal of applied Physics, 16(5), 296-302.

[3] Duncan, J. M., Monismith, C. L., & Wilson, E. L. (1968). Finite element analysis of pavements. Highway Research Record, 228, 18-33.

[4] Liu, P., Wang, D., & Oeser, M. (2017). Application of semi-analytical finite element method to analyze asphalt pavement response under heavy traffic loads. Journal of traffic and transportation engineering (English edition), 4(2), 206-214.

[5] Richards, L. A. (1931). Capillary conduction of liquids through porous mediums. physics, 1(5), 318-333.

[6] Oñate, E., (1995). Cálculo de estructuras por medio de elementos finitos. Análisis estático lineal. Centro Internacional de Métodos Numéricos en Ingeniería.

[7] Hamidzadeh, H. R., & Jazar, R. N. (2010). Vibrations of thick cylindrical structures. New York: Springer.

[8] AASHTO-T 307. (2003). Determining the resilient modulus of soils and aggregate materials. Standard specifications for transportation materials and methods of sampling and testing.

[9] Van Genuchten MT (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci Soc Am J, 44(5):892–8.

[10] Mualem Y (1976). A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour Res;12(3):513–22.

[11] Vanapalli, S. K., & Han, Z. (2014). Application of the unsaturated soil mechanics in the design of pavements. In Proceedings of the 6th International Conference on Unsaturated Soils, Sydney, Australia (pp. 1799-1805).