Semianalytical method for contact mechanic among shaft and bearing of a submarine vehicle

Resumen

En el presente trabajo, se estudia y analiza el mejor ajuste del eje del propulsor de un vehículo sumergible a su chumacera, mediante el estudio de la geometría de contacto entre dichos elementos. Para realizar este estudio, se ha aplicado un método semianalítico, basado en las normas de la cuadratura de los principales valores de Cauchy, el método de la secante, y un método numérico para la determinación del mapa tensional de las superficies en contacto entre el eje y la chumacera. Asumiendo que existen imperfecciones de micras en el mecanizado de las superficies en contacto, estas son una causa posible de daños subsuperficiales que favorecen fallos por picaduras (pitting ) o la formación y el crecimiento de las grietas por fatiga. Estos fallos afectan no solo el buen rendimiento propulsivo, sino también las condiciones de estanqueidad, con los consiguientes riesgos que ello supone para la integridad del buque. Los resultados permiten establecer los criterios de diseño en función de los módulos de Young, así como un mecanizado correcto y el ajuste de holguras posterior del sistema eje-chumacera, con lo cual se mejorala fiabilidad de dichos elementos.

Summary

The present study analyzes the best attachment of the propeller shaft of a submersible to his bearing, studying geometry of contact between those elements. A semi-analytical method based on the rules of the quadrature of the main values of Cauchy, the secant method and a numerical method for determining a tension map have been applied to the study of the contact surfaces between shaft and bearing. It is assumed that there are imperfections in the order of microns when machining the contact surfaces, which can produce subsurface damage that is possible, linked to pitting and the growth of fatigue cracks. Such failures not only will influence on the proper propulsive performance, but also on the watertightness conditions, which is related to the risk of ship integrity loss. The results let us to set design criteria, which account for the Youngs module and the importance of an adequate machining and further adjustment of clearances on the shaft-bearing system, thus improving the reliability of such elements.

Palabras clave

Eje ; Chumacera ; Mecánica del contacto ; Hertz ; Método semianalítico ; Ajuste ; Estanqueidad

Keywords

Shaft ; Bearing ; Contact mechanics ; Hertz ; Semianalytical method ; Adjustment ; Watertightness

Nomenclatura

a- Semiancho de contacto

a₀- Semiancho de contacto de Hertz

a^NK- Coeficientes de la función de aproximación

ci- Coeficientes de Gauss

dk- Coeficientes de la función de aproximación

p (x ) - Distribución de presiones en deformación plana

p_max- Presión máxima

p₀- Presión máxima de Hertz

P- Presión total

P₀- Carga predeterminada de diseño

F(x)- Fuerza total

ø- Diámetro en mm

E- Módulo de Young

ν- Coeficiente de Poisson

x- Variación de la posición en el eje X

s- Distancia de actuación de la carga sobre el semiespacio elástico

U_z(x)- Variación de la geometría de la superficie contacto

R- Radio equivalente entre eje y chumacera

R₁- Radio eje

R₂- Radio chumacera

t- Variable adimensional

δ- Diferencia de radios en la zona de contacto

U₁- Desplazamiento vertical eje

U₂- Desplazamiento vertical chumacera

V₁- Desplazamiento horizontal eje

V₂- Desplazamiento horizontal chumacera

Q(f; c)- Integral de Valores Principales de Cauchy

τ_max- Tensión cortante máxima

τ₀- Tensión cortante máxima para contacto hertziano

τ_max- Tensión máxima

z- Distancia de actuación sobre el espesor de la chumacera

1. Introducción

La línea del eje de la hélice o propulsor de un vehículo sumergible o submarino tiene la función principal de transmitir la potencia de la maquinaria propulsora a la hélice o propulsor. En general, el eje está sometido a importantes esfuerzos axiales y de torsión, a pares vibratorios y a fluctuaciones en las cargas hidrodinámicas que pueden generar problemas de fatiga. Además, el ajuste y el mecanizado correctos del eje y la chumacera alargan el período útil de funcionamiento y disminuyen el riesgo de fallo por fatiga superficial o picadura. Las consecuencias de un fallo en la instalación propulsora son muy graves, tanto desde el punto de vista de la integridad del buque como elemento estanco, como desde el punto de vista del coste de los propios equipos implicados (chumaceras, bocinas, reductoras, etc.), y requieren entrar el buque al dique para repararlo [1]  and [2] .

Un problema frecuente derivado de la desalineación del eje del propulsor con la chumacera es el daño que los elementos de apoyo pueden provocar en las zonas de contacto de la chumacera. Y, al no poderse añadir elementos amortiguadores (que añadirían imprecisión al apoyo), las tensiones de contacto pueden ser elevadas y llegar, en algunos casos, a desgastar e incluso a deformar parte de dicho elemento, lo cual ocasiona un daño muy costoso que compromete la seguridad del buque.

El contacto eje-chumacera se enmarca dentro de lo que se puede denominar contacto hertziano[3] . Este tipo de contacto se utiliza cuando el área de contacto es pequeña, en comparación con la dimensión de los cuerpos, y tradicionalmente ha servido para estudiar la mayoría de los tipos de contacto que se producen entre sólidos. Con la teoría de Hertz, se pueden realizar estudios diversos, como la deformación plástica de los materiales dúctiles, la evolución del daño de fractura en las capas de revestimiento [4] , el contacto entre materiales duros y frágiles [5] y la deformación que se produce a través de un contacto esférico.

En cuanto al desarrollo de las ecuaciones basadas en el contacto hertziano, que estudian y analizan el mejor ajuste entre superficies cilíndricas, cabe destacar los trabajos de Ciavarella y Decuzzi [6] , y de To y He [7] , que dan una buena respuesta a la teoría de Hertz para zonas de contacto pequeñas y grandes holguras.

Una alternativa a los estudios anteriores es utilizar el método de elementos finitos (MEF). Dentro de este enfoque, las discretizaciones necesarias en la zona de contacto se mejoraron con el uso de herramientas de mallado automático y métodos de descomposición de dominios en pequeñas deformaciones, estudiados por Belgacen et al.[8]  and [9] . Ambos trabajos utilizan una variante de la técnica de descomposición en el dominio no conforme. Desde este enfoque, el problema de aproximación resulta adecuado para obtener una solución discreta. Posteriormente, Hild y Laborde [10] propusieron un análisis de errores para comprobar la precisión de los métodos de desigualdad variacional, y la formulación mixta equivalente, y este último resultó más favorable que el primero, al reducir el error hasta la mitad.

Dentro de las grandes deformaciones, en que está permitido el deslizamiento de los nodos o elementos de contacto sobre los elementos del otro cuerpo en contacto, cabe destacar el trabajo de Simo et al.[11] , que propusieron una formulación basada en segmentos de contacto en el contexto de una interpolación bilineal para el campo de desplazamientos. Posteriormente, Papadopoulos y Taylor [12] introdujeron la formulación de penalización mixta para aproximar las inecuaciones variacionales con el fin de obtener una solución estática para los problemas de contacto con grandes deformaciones. Más recientemente, la formulación Mortar combina métodos de elementos finitos que utilizan espacios de funciones polinomiales de aproximación de diferente grado, o uniones con mallas que no comparten con los elementos adyacentes los nodos o caras, también llamadas mallas no conformes , para la resolución de problemas de contacto no lineal, sobre los cuales se han realizado distintos estudios [13] , [14]  and [15] . Además, los trabajos relacionados con el MEF han ido evolucionando a medida que ha aumentado la capacidad de computación de los ordenadores, que han llegado a solucionar problemas cada más complejos, donde se desarrollan modelos de fricción acoplados termomecánicamente, como los realizados por Hueber y Wolhlmuth [16] y Temizer [17] . En un trabajo más reciente, Sitzmann et al.[18] profundizan en la necesidad de combinar distintos modelos para considerar el efecto de la rugosidad mediante el estudio de leyes de contacto constitutivas en términos de multiplicadores de Lagrange. Los resultados teóricos de este trabajo muestran muy buena concordancia con los obtenidos experimentalmente.

Por otro lado, los sistemas eje-cojinete, como los utilizados en los sistemas eje-chumacera de los submarinos, han sido objeto de investigación en la última década. Entre estos, cabe destacar el estudio realizado por Albers et al.[19] , que analiza la influencia de distintos parámetros en el comportamiento del sistema de contacto friccional mediante el MEF y el modelado de rugosidades mediante un algoritmo de optimización. En la misma línea, Rezaei et al.[20] han implementado una formulación mixta Lagrangiana-Euleriana y la ecuación de Archard para determinar la evolución local del desgaste y su influencia en las simulaciones realizadas en problemas de contacto entre el eje y el cojinete. Esta evolución local en cada nodo de contacto fue añadida en el remallado adaptativo del MEF. Los resultados obtenidos por el MEF se aproximaban mucho a los obtenidos experimentalmente. Aguirrebeitia et al.[21] construyeron un modelo de elementos finitos multiparamétrico, con el fin de verificar la validez de los resultados de un modelo teórico, para obtener la capacidad de carga estática de guías de cojinete de cuatro contactos. Más recientemente, Lostado-Lorza et al.[22] han presentado una metodología para mejorar el diseño y la optimización de rodamientos de rodillos cónicos, basada en la combinación del MEF con técnicas de regresión basadas en el descubrimiento de conocimiento en base de datos (KDD), para predecir la relación de contacto en función de las cargas que actúan.

Aunque los resultados presentados en estos últimos trabajos son bastante precisos, y pese a haberse reducido el número de simulaciones con el uso de las técnicas de regresión mencionadas, el inconveniente principal del MEF sigue siendo su coste computacional, especialmente cuando resulta necesario un refinamiento de la malla en la zona de contacto entre los elementos objeto de estudio y se combina con otros métodos iterativos para modelar el efecto de las rugosidades o de los microdeslizamientos en la zona de contacto, a parte de los problemas de convergencia que pueden surgir por la aparición de discontinuidades, que dificultan la reconexión entre los nodos de las superficies en contacto.

Además, el problema se complica cuando el área de contacto es muy ancha, es decir, cuando el semiancho de contacto es del orden de magnitud del radio, en que las aproximaciones de Rudolph Hertz no son válidas en la mayoría de los casos. Una alternativa al MEF es utilizar métodos semianalíticos, que estudian el contacto entre los elementos de fijación y la pieza en procesos de mecanizado para distintas geometrías de apoyo y apriete, con perfiles geométricos compuestos por tramos curvos y rectos. Estos trabajos arrojaron unos resultados muy próximos a los obtenidos por la teoría de Hertz y a los del MEF, pero presentaban un coste computacional muy reducido [23]  and [24] .

En el problema de contacto entre el eje y la chumacera, el estado tensional en la subsuperficie es generado por la distribución de presiones en la superficie, y este depende del intervalo de separación entre los dos cuerpos y la fuerza con que se presiona uno contra otro. En otras palabras, el estado tensional depende de la holgura entre el radio del eje y el radio de la chumacera, así como del nivel de rugosidad alcanzado en su mecanizado. Dependiendo de la carga a que esté sometido y a las condiciones de operación, podría alcanzar una tensión tal de cortadura en la subsuperficie que rebasara la tensión de fatiga admisible, lo cual originaría una grieta subsuperficial que posteriormente se podría prolongar hasta la superficie y provocar, incluso, el desprendimiento de material. Las normas seguidas por las diferentes sociedades de clasificación (American Bureau of Shipping, Lloyds Register of Shipping, Bureau Veritas, Det Norske Veritas y Germanischer Lloyd) [25] , [26] , [27] , [28]  and [29] determinan el radio del eje y la chumacera o bocina, simplemente estableciendo su criterio de diseño, en unas relaciones empíricas basadas en la potencia entregada al eje, las revoluciones por minuto y la resistencia a la tracción mínima del material, sin profundizar en los problemas que son estudiados por la mecánica clásica de contacto.

El propósito de este trabajo es estudiar y analizar el mejor ajuste del eje de un vehículo sumergible a su chumacera, mediante el estudio de la geometría de contacto entre dichos elementos, a partir de la aplicación de un método semianalítico, basado en las normas de la cuadratura de los principales valores de Cauchy, el método de la secante y un método numérico, obteniendo la representación de un mapa tensional, basado en los modelos estudiados por Johnson [3] , aplicado a las superficies del eje y la chumacera. En primer lugar, se obtiene la distribución superficial de presión y un mapa tensional con la determinación de sus máximos. El método semianalítico se compara con el método de Hertz y con los resultados obtenidos por el MEF, para distintos valores de holgura entre eje y chumacera, con el fin de comprobar su validez. Posteriormente, se obtiene la curva de tensión máxima en la chumacera, que será útil para mejorar las tolerancias del eje y la chumacera. Finalmente, se determinará en qué rangos se encuentra la presión máxima, para poder garantizar una vida a fatiga superficial del eje y conocer una evolución máxima del desgaste. Los resultados presentados en este trabajo ofrecen la información necesaria para mejorar el diseño de dichos elementos y comprender la importancia de un buen ajuste, de la elección de las dimensiones geométricas del sistema eje-chumacera y de los materiales resistentes, así como el control del nivel de rugosidad que se debe alcanzar en su proceso de fabricación por mecanizado.

La consecución de este objetivo se apoya en la comparación de tres métodos: a ) la teoría de Hertz, cuyas expresiones son conocidas; b ) la teoría planteada mediante el contacto cilíndrico aproximándola a una parábola, basada en un trabajo presentado por Ciavarella [6] , y c ) la teoría del contacto basada en la separación mostrada en la ecuación (15), que representa un eje dentro de un cilindro y se deduce de la figura 5 . Esta última no utiliza la aproximación parabólica, sino la expresión exacta de separación, según la figura 5 . Esta solución se denomina en el presente trabajo contacto tipo placa o interior bicilíndrico . El desarrollo de las expresiones de ambas teorías basadas en el contacto cilíndrico se expone en el apartado titulado “Deducción de ecuaciones”.

2. Planteamiento del problema

Las consecuencias de un fallo en la instalación propulsora son muy graves, tanto desde el punto de vista de la integridad del buque como elemento estanco, como desde el punto de vista del coste de los propios equipos implicados (chumaceras, bocinas, reductoras, etc.), y requiere la reparación del buque mediante su entrada al dique para la alineación y el taqueado completo de toda la instalación propulsora.

Contrariamente a lo que puede parecer a primera vista, una alineación correcta de los ejes no es aquella en que todos los cojinetes de apoyo de la instalación son colineales, sino aquella en que los puntos de apoyo tienen su posición bien definida y situada. Además, es muy importante, desde el punto de vista del diseñador, conocer cuáles son los valores óptimos en cuanto a la geometría y a las características de los materiales elegidos. Las sociedades de clasificación, mediante formulaciones empíricas, exigen realizar cálculos para determinar las dimensiones geométricas del eje y la chumacera, así como su alineación, que permitan determinar las posiciones adecuadas de los cojinetes, con el objetivo principal de alcanzar unos valores aceptables, tanto de los esfuerzos como de su distribución, a lo largo de toda la línea de ejes. Pese a ello, los criterios de diseño de las geometrías más adecuadas y la elección de los materiales deben sustentarse en unos valores críticos de tolerancias, que han de determinarse con precisión mediante este método semianalítico, que disminuye el número de las operaciones que hay que realizar y simplifica el cálculo de las mismas, frente a otros métodos de cálculo, como el MEF, que posibiliten el ajuste más fino posible, para mejorar la eficiencia mecánica, lo cual se traducirá en una disminución de las vibraciones –que son, en definitiva, fuentes de ruido que transmiten al medio su potencia sonora– y favorecerá el alargamiento de su vida útil.

El caso que se va a estudiar es un caso de deformación plana, en el cual se determinará la influencia de la holgura, desde el punto de vista conceptual, y de los índices de tolerancia en la fabricación, en lo relativo a la distribución de presiones de contacto del conjunto eje-chumacera.

Cuando se trabaja con ajustes finos, como suele ser el caso del ajuste eje-chumacera, el semiancho de contacto es elevado y, por tanto, la aproximación parabólica de Hertz resulta insuficiente. Para superar este inconveniente, se ha realizado primero una aproximación cilíndrica de contacto, manteniendo el concepto de cilindro equivalente de Hertz, y se ha utilizado la geometría de aproximación eje-agujero, que prescinde del concepto de cilindro equivalente. Este último es el método semianalítico que se propone en este trabajo.

Para demostrar la utilidad del nuevo método, inicialmente se ha partido de unos valores fijados previamente en el caso de un vehículo sumergible, asumiendo que el elemento de apoyo, la chumacera, es de un material que tiene un comportamiento linealmente elástico (bronce al estaño CuSn₁₂ , con un módulo de Young de 110 KN/mm² y un coeficiente de Poisson ν de 0,31), con un radio interior de partida, que variará en función del radio del eje del propulsor y de la holgura existente entre ambos, y una longitud de apoyo de 700 mm, y que el eje del propulsor es de un material mucho más rígido (acero de alta resistencia, cuyo módulo de Young es de 205 KN/mm² y cuyo radio es 230 mm). Se estudian, por un lado, la influencia de la holgura en el comportamiento mecánico del sistema, con diez casos de estudio, partiendo de un valor inicial de holgura entre radios de 4 mm, que va disminuyendo progresivamente, tal como se muestra en la tabla 1 . Se obtendrán principalmente como resultados los valores comparativos obtenidos al resolver dicho método con la expresión propuesta en la teoría de Hertz [1] , basada en un trabajo presentado por Ciavarella [11] , y la ecuación propuesta en este trabajo.

Tabla 1. Situaciones de estudio analizados para diferentes holguras

Casos	Holgura entre radios
1	4,000 mm
2	2,000 mm
3	1,000 mm
4	0,500 mm
5	0,250 mm
6	0,125 mm
7	0,063 mm
8	0,031 mm
9	0,016 mm
10	0,008 mm

Además, se resuelven dos casos de semiancho de contacto (el de mayor y el de menor zona de contacto), realizados por el MEF, con el fin de demostrar que el método semianalítico presentado ofrece suficiente precisión. Una vez demostrada la utilidad de este nuevo método, se resuelven tres casos, basados en los índices de tolerancia (IT) según la ISO 286-1988, tal como se aplican en los estándares de diseño en ingeniería, siendo ø460H16/h16 (chumacera/eje) y ø460H4/h4 los casos que se han elegido, el último de los cuales es el más exigente en cuanto a tolerancias de fabricación. Los índices de tolerancia que no incluyen piezas de gran precisión se hallan entre IT4 e IT18. El nivel de calidad del acabado superficial, o nivel de tolerancia exigido, está relacionado directamente con las alturas del perfil de rugosidad, que están presentes en la superficie de la pieza tras el proceso de mecanizado. Estas han de ser menores que el valor de tolerancia que se quiere obtener.

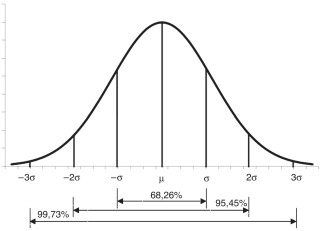
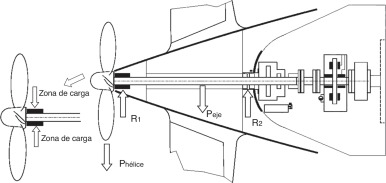
Con el fin de realizar un análisis representativo de las situaciones que podrían darse en los casos reales de fabricación, relativos a los valores de rugosidad que se pueden alcanzar para cada nivel de tolerancia estudiado, se han estimado aleatoriamente 40 situaciones posibles. Mediante la función de distribución normal inversa en una hoja de cálculo, se han simulado las variaciones debidas que se podrían dar como casos de incertidumbre en el mecanizado de las piezas a que se ha hecho referencia, como efecto de la rugosidad encontrada en la superficie del material, aplicando una desviación estándar definida para cada caso, suponiendo que las 40 situaciones posibles se hallan distribuidas normalmente, por lo cual se establece una cantidad media igual a la inicial (μ) y una desviación estándar σ, de manera que, si se le resta y se le suma a la cantidad media 3 veces σ, se obtiene el 99,74% del área bajo la curva de la distribución, tal como se muestra en la figura 1 . Se ha partido de una carga de diseño inicial P₀ , calculada a partir de las reacciones estáticas debidas al peso del propulsor y del eje, como se muestra en la figura 2 , y se ha obtenido una carga de 6.190 kg por metro lineal. El tipo de contacto es circular y se corresponde con el resuelto por la teoría de Hertz. Esta teoría, junto con el MEF, será utilizada como modelo de validación de los resultados obtenidos por el método semianalítico desarrollado en el presente trabajo.

Figura 1. Distribución 6σ (campana gaussiana).

Figura 2. Reacciones debidas al peso del conjunto eje-propulsor.

En la tabla 2 , se indican los valores geométricos de rugosidad de uno de los casos estudiados de IT, ø460H16/h16.

Tabla 2. Situaciones de estudio analizados para ø eje 460 holgura 2 mm

Casos	Radio Eje [mm]	Radio Chumacera [mm]	Casos	Radio Eje [mm]	Radio Chumacera [mm]
1	227,9476	231,8854	21	228,1735	232,0358
2	227,8924	231,8723	22	227,9287	231,8862
3	228,0344	232,0548	23	227,8320	232,0420
4	227,9605	231,8531	24	228,0340	231,9878
5	228,1972	232,0507	25	227,9558	232,0567
6	227,9596	232,0880	26	228,1126	232,0160
7	228,0388	231,8235	27	227,9894	232,0182
8	228,0437	232,0590	28	227,8893	231,9446
9	228,0346	231,9643	29	228,0375	231,8803
10	228,0617	232,0146	30	228,2948	231,9442
11	227,9243	231,9531	31	227,7928	232,0842
12	228,0082	232,0952	32	227,9742	232,0012
13	228,0827	232,0187	33	227,9871	232,1161
14	228,1145	232,0040	34	227,8811	231,8998
15	227,9036	231,9944	35	228,0738	231,9677
16	227,8970	231,9852	36	227,9947	231,9992
17	227,9061	231,9382	37	227,9568	232,0523
18	227,9242	232,0844	38	228,0500	232,0221
19	227,8404	231,7594	39	228,0903	232,1351
20	228,1012	232,0777	40	227,8271	232,0304

Como consecuencia de la variación de los radios del conjunto eje-chumacera para cada uno de los casos de la tabla 2 , se obtienen distintas distribuciones de la presión de contacto para diferentes semianchos a. Partiendo de la carga de diseño inicial P₀ , y utilizando la metodología que se describe a continuación, se resuelven los problemas planteados de tolerancias en el diseño del eje de cola de un vehículo sumergible.

3. Deducción de las ecuaciones

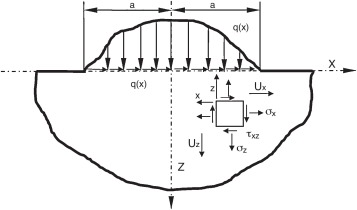
Por tanto, partimos de las ecuaciones de la mecánica del contacto, para el problema bidimensional de una distribución de presiones p (x), sobre un semiespacio elástico [3] (representado en la figura 3 ), donde a son los semianchos de contacto; U_x y U_z , los desplazamientos tangencial y normal a la superficie, y p (x) y q (x), las distribuciones de presión normal y tangencial, respectivamente.

Figura 3. Sección transversal del semiespacio elástico.

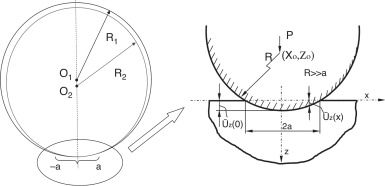
En el caso particular de contacto entre el apoyo del eje del propulsor y la chumacera, la fuerza de fricción es muy pequeña, comparada con las fuerzas de apriete normal, de modo que se puede despreciar la distribución tangencial de presiones q (x) y, debido a la alta rigidez del eje con respecto a la chumacera, se puede asumir que el desplazamiento normal del semiespacio elástico (chumacera), U’_z (x) (siendo U’_z   =  dU_z /dx), sigue la geometría del eje, es decir, se suponen las condiciones de contorno iniciales de clase II establecidas por Johnson [3] (v. fig. 4 ). Por tanto, las ecuaciones que rigen el contacto se reducen a:

$\int _{-a}^{a}{\frac {p(s)}{x-s}}ds={\frac {\pi \cdot E}{2}}U_{z}^{'}(x)$

( 1)

Figura 4. Eje-chumacera. Detalle del contacto circular con un radio equivalente.

3.1. Primera solución basada en la teoría de Hertz para contacto cilíndrico

Dentro de los límites de integración de estas ecuaciones acopladas, aparece un punto de singularidad cuando a  = x , y es por ello que se denominan ecuaciones integrales singulares .

En el caso de la parábola de contacto cilíndrico:

$U_{z}\left(x\right)=U_{o}-{\frac {x^{2}}{2\cdot R}}$

( 2)

$U_{z}^{'}\left(x\right)=-{\frac {x}{R}}$

( 3)

donde R es el radio equivalente del cilindro en contacto con una placa plana o un interior bicilíndrico, y U_z , como se ha anotado anteriormente, es el desplazamiento en z entre las dos superficies en contacto

$si{\mbox{ }}x\ll entonces\left\{tan{\frac {x}{R_{1}}}\approx {\frac {x}{R_{1}}}\right\}y\left\{cos{\frac {x}{R_{1}}}\approx 1\right\}\rightarrow U_{z}^{'}\left(x\right)=-{\frac {R_{2}-R_{1}}{R_{1}^{2}}}x$

$R_{1}\approx R_{2}\rightarrow U_{z}^{'}\left(x\right)=-{\frac {1}{R_{eq}}}\cdot x$

${\mbox{Hipótesis}}{\mbox{ }}{\mbox{de}}{\mbox{ }}{\mbox{radio}}{\mbox{ }}{\mbox{equivalente}}\equiv R_{eq}={\frac {1}{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}}}={\frac {R_{2}R_{1}}{R_{2}-R_{1}}}$

La ecuación (1) se puede describir mediante los valores principales de Cauchy de primera clase, que pueden resolverse a través de la solución propuesta por Söhngen (1954) o Mikhlin (1948) [3] , que se puede simplificar si la región cargada es simétrica, la cual queda expresada del siguiente modo:

$p\left(x\right)={\frac {1}{\pi ^{2}{\sqrt {a^{2}-x^{2}}}}}\left(C+\int _{-1}^{a}{\frac {{\sqrt {a^{2}-s^{2}}}\cdot {\frac {\pi E}{2R}}s}{x-s}}ds\right)$

( 4)

donde E es el módulo de Young equivalente y a es el semiancho de contacto.

Aplicando la condición de Boussinesq, cuando la derivada U ́_z (x) es finita en toda la zona de contacto, el valor de la presión cae gradualmente a 0 en los extremos de la misma. A partir de esta condición (p(x ) = 0 para x  = ±a ), se obtiene la constante C de la expresión (4) y, operando convenientemente, se llega a la expresión (20), que será fundamental para obtener la distribución de presiones a partir del semiancho de contacto a , y la geometría del apoyo U ́_z (x) en el desarrollo matemático que se describe a continuación

$p\left(a\right)=p\left(-a\right)=0$

( 5)

para que el denominador común no sea infinito, haciendo un cambio de variable:

$t=-s$

( 6)

$t\cdot dt=-s\cdot ds$

( 7)

$C=-\int _{-a}^{a}{\frac {{\sqrt {a^{2}-s^{2}}}\cdot {\frac {\pi E}{2R}}}{x-s}}ds=\int _{-a}^{a}{\frac {\sqrt {a^{2}-t^{2}}}{x+t}}\cdot {\frac {\pi E}{2R}}\cdot tdt$

( 8)

P (x ) es simétrica si U ́_z (x ) es antisimétrica.

Si se realiza este otro cambio de variable:

$s=a\cdot t$

( 9)

$s\cdot ds=a^{2}\cdot t\cdot dt$

( 10)

la ecuación (8) queda expresada del modo siguiente:

$C={\frac {\pi E}{2R}}\int _{-1}^{1}{\frac {a^{3}\cdot t\cdot {\sqrt {1-t^{2}}}}{a\left(1-t\right)}}dt={\frac {\pi E}{2R}}a^{2}\int _{-1}^{1}t\cdot {\sqrt {\frac {1+t}{1-t}}}dt$

( 11)

$p\left(x\right)={\frac {Ea^{2}}{2\pi R{\sqrt {a^{2}-x^{2}}}}}\left(\int _{-a}^{a}{\frac {t{\sqrt {1-t^{2}}}}{{\frac {x}{a}}-t}}dt+{\frac {\pi }{2}}\right)$

( 12)

De igual manera, es necesario evaluar otra función antisimétrica. En el presente trabajo, se han desarrollado las ecuaciones que posteriormente se resuelven mediante los métodos propuestos.

4. Segunda solución sin aproximaciones parabólicas

Si se utilizase la ecuación del cilindro sin aproximaciones parabólicas, se obtendrían las ecuaciones siguientes:

$\left(U_{z}-R\right)^{2}+x^{2}=R^{2}$

( 13)

$p\left(x\right)={\frac {E\cdot a^{2}}{2\pi {\sqrt {a^{2}-x^{2}}}}}\left(\int _{-1}^{1}{\frac {t{\sqrt {1-t^{2}}}}{\sqrt {R^{2}-a^{2}t^{2}}}}dt-\left.\int _{-1}^{1}{\frac {t{\sqrt {1-t^{2}}}}{(1-t){\sqrt {R^{2}-a^{2}t^{2}}}}}dt\right)\right.$

( 14)

Al resolver dichas ecuaciones mediante la metodología propuesta, se obtienen resultados en que las curvas de presión se asemejan a las obtenidas por el método de Hertz, para semianchos de contacto pequeños (a  < <) y holguras grandes (h  > >), siendo a el semiancho de contacto y h la holgura entre el eje y la chumacera. Este resultado es lógico debido a que el arco de una circunferencia se asemeja a una parábola, cuando el ángulo del sector es pequeño. La teoría de Hertz establece, como hipótesis de partida, que los cuerpos se comportan como sólidos elásticos semiinfinitos, sometidos a presiones distribuidas sobre la superficie circular de contacto y donde el área de contacto es pequeña, en comparación con las dimensiones de los cuerpos. Es decir, el semiancho de contacto a es, como máximo, la centésima parte del radio del cilindro.

5. Tercera solución por deducción geométrica en contacto de tipo placa o interior bicilíndrico

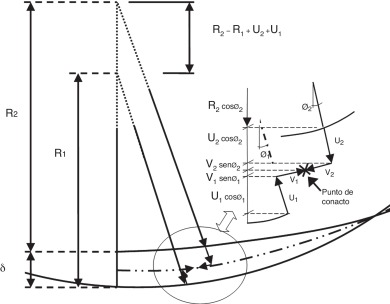
En la figura 5 , se muestra en detalle la región de contacto de tipo placa o interior bicilíndrico, para poder plantear las ecuaciones que conduzcan a la obtención de la expresión del método semianalítico expuesto en la subsección anterior, y que coincide con Hertz cuando a es muy pequeño.

Figura 5. Eje-chumacera. Detalle de los desplazamientos en la región de contacto.

Es preciso recordar que la teoría de Hertz muestra una curva de distribución de presiones diferente cuando los valores de a no son tan bajos, es decir, a ≈ R /100, sino que son del orden de magnitud del radio. En la figura 5 , los puntos 1 y 2 son los pertenecientes a los dos cuerpos que acaban estando en contacto, eje y chumacera, es decir, coinciden después de haber aplicado la presión. Por tanto, los ángulos θ₁ y θ₂ son los ángulos de posición de los puntos 1 y 2, respectivamente, cuando los sólidos sin deformar aún no han entrado en contacto. Por otro lado, U₁ y U₂ son los desplazamientos radiales de los puntos 1 y 2, respectivamente, y V₁ y V₂ son los desplazamientos tangenciales. Teniendo en cuenta la geometría descrita por esta figura, y realizando un sumatorio de desplazamientos en sentido radial, se puede obtener el desplazamiento producido en la región de contacto a través de la ecuación (15)

${\begin{array}{l}\displaystyle R_{2}cos\phi _{2}+U_{2}cos\phi _{2}+V_{2}sin\phi _{2}=R_{2}+\delta -R_{1}\left(1-cos\phi _{1}\right)-\\\displaystyle -U_{1}cos\phi _{1}+V_{1}sin\phi _{1}\end{array}}$

( 15)

${\textstyle si\left\{{\begin{array}{c}\phi _{2}=\phi _{1}=\phi \\V_{1}=V_{2}=0\end{array}}\right\}}$ , la ecuación queda expresada de la forma siguiente:

$R_{2}\left(1-cos\phi \right)-R_{1}\left(1-cos\phi \right)+\delta -\left(U_{1}+U_{2}\right)cos\phi =0$

( 16)

$U_{2}\left(x\right)=\left(R_{2}-R_{1}\right)\left({\frac {1-cos\phi }{cos\phi }}\right)+\delta$

( 17)

Asumiendo que el eje puede considerarse rígido con respecto a la chumacera y despreciando δ por ser de un orden de magnitud muy inferior en comparación con la diferencia de radios, se tiene:

$U_{1}=0$

$x{\mbox{ }}Circunferencial\rightarrow x=R_{2}\cdot \phi$

( 18)

$U_{2}\left(x\right)=\left(R_{2}-R_{1}\right)\left({\frac {1}{cos{\frac {x}{R_{1}}}}}-1\right)+\delta$

( 19)

Y, realizando la derivada, se obtiene la expresión siguiente:

${\begin{array}{l}\displaystyle U^{'}\left(x\right)=\left(R_{2}-R_{1}\right)\left({\frac {-{\frac {1}{R_{1}}}sin{\frac {x}{R_{1}}}}{cos^{2}\left({\frac {x}{R_{1}}}\right)}}\right)={\frac {\left(R_{2}-R_{1}\right)}{R_{1}}}\left({\frac {-sin{\frac {x}{R_{1}}}}{1-sin^{2}\left({\frac {x}{R_{1}}}\right)}}\right)=\\\displaystyle =\left(1-{\frac {R_{2}}{R_{1}}}\right){\frac {tan{\frac {x}{R_{1}}}}{cos{\frac {x}{R_{2}}}}}\end{array}}$

( 20)

$U^{'}\left(x\right)=\left({\frac {R_{1}}{R_{2}}}-1\right){\frac {tan{\frac {x}{R_{1}}}}{cos{\frac {x}{R_{1}}}}}$

( 21)

$p\left(x\right)={\frac {E\cdot a^{2}}{2\pi {\sqrt {a^{2}-x^{2}}}}}\left[\int _{-1}^{1}{\frac {U^{'}(t){\sqrt {1-t^{2}}}}{t-1}}dt+\int _{-1}^{1}{\frac {U^{'}(t){\sqrt {1-t^{2}}}}{t-{\frac {x}{a}}}}dt\right]$

( 22)

Posteriormente, se introduce el siguiente cambio de variable:

$ds=a\cdot dt$

( 23)

$x-s=-a\left(t-{\frac {x}{a}}\right)$

( 24)

Finalmente, se obtiene la expresión que proporciona la distribución de presión de contacto, expresada en función de la restricción geométrica descrita anteriormente, y la elasticidad en la zona de contacto, suponiendo un semiancho de contacto a

${\begin{array}{l}\displaystyle p\left(x\right)={\frac {E\cdot a\cdot \left({\frac {R_{chum}}{R_{e}je}}-1\right)}{2\pi \left(1-\nu ^{2}\right){\sqrt {a^{2}-x^{2}}}}}\left[\int _{-1}^{1}{\frac {tan\left({\frac {a\cdot t}{R_{e}je}}\right){\sqrt {1-t^{2}}}}{cos\left({\frac {a\cdot t}{R_{e}je}}\right)\cdot \left(t-{\frac {x}{a}}\right)}}dt-\right.\\\left.\displaystyle -\int _{-1}^{1}{\frac {tan\left({\frac {a\cdot t}{R_{e}je}}\right){\sqrt {1-t^{2}}}}{cos\left({\frac {a\cdot t}{R_{e}je}}\right)\cdot \left(t-1\right)}}dt\right]\end{array}}$

( 25)

La primera de las integrales mostradas es resuelta siguiendo a Mikhlin, mientras que la segunda integral impropia se resuelve por aproximaciones, ya que el límite está en 1, donde el valor de la función se hace infinito.

6. Metodología

La metodología que se sigue para obtener el semiancho de contacto a , la distribución de presiones que satisfaga la condición de que la carga total sea P₀ , y las restricciones geométricas junto con las ecuaciones de contacto expresadas en la ecuación (25), consta de distintas etapas. Por un lado, se necesita un método numérico para resolver el valor principal de Cauchy de la primera integral de la expresión (25), ya que su singularidad (x/a ) se encuentra dentro de los límites de integración. El método utilizado para esta integración fue elaborado por Hasegawa [30] . Por otro lado, es preciso integrar la función de presión para obtener la fuerza total, lo cual se realiza mediante la cuadratura de Legendre. Como la fuerza total es un dato del problema, el ajuste del semiancho de contacto a para que la integral de la presión sea la fuerza total se realiza mediante el método de la secante. Como resultado de la combinación de estos métodos, se obtiene el semiancho de contacto y, a partir de este, la distribución de presiones, la presión máxima y el mapa tensional en la subsuperficie.

7. Cuadratura del valor principal de Cauchy

El método desarrollado se estructura siguiendo la secuencia que se expone a continuación, para poder resolver el problema planteado y determinar la distribución de presiones sobre la chumacera.

En primer lugar, se calculan las integrales impropias mostradas en la expresión (25), que son valores principales de Cauchy, suponiendo un semiancho de contacto a y aplicando el método automático de cuadratura desarrollado por Hasegawa et al.[30]  and [31] . Este método permite aproximar integrales de valor principal de Cauchy del tipo que se muestra en la ecuación (26)

$Q\left(f:c\right)=\int _{-1}^{1}{\frac {f(t)}{t-c}}\delta t{\mbox{ }}-1<c<1$

( 26)

El cálculo de esta integral, se realiza aproximando la función f (t) mediante una suma de polinomios de Chebyshov, que permite eliminar la singularidad calculando los coeficientes mediante una metodología similar a la transformada rápida de Fourier, tal como se describe en [23] .

Por tanto, la fórmula de integración aproximada se puede expresar:

${\begin{array}{c}Q\left(f:c\right)\approx Q_{N}\left(f:c\right)\\Q_{N}\left(f:c\right)=2\sum _{k=0}^{{\frac {N}{2}}-1^{'}}d_{k}/(1-4k^{2})+f\left(c\right)log\left({\frac {1-c}{1+c}}\right)\end{array}}$

( 27)

donde la comilla superior ‘denota que el primer término del sumatorio está dividido por dos. Los coeficientes d_k se calculan utilizando la siguiente relación recurrente:

$d_{k+1}-2cd_{k}+d_{k-1}=2a_{K}^{N},{\mbox{ }}k=N,N-1,\ldots .,1{\mbox{.}}$

( 28)

donde los coeficientes ${\textstyle a_{K}^{N}}$ , pertenecientes a los polinomios de Chebyshov, se calculan mediante la fórmula siguiente:

$a_{k}^{N}={\frac {2}{N}}\sum _{j=0}^{N}f(cos\pi j/N)cos(\pi kj/N).{\mbox{ }}0\leq k\leq N{\mbox{.}}$

( 29)

8. Cuadratura de Legendre

El valor de la carga total P , que se ejerce en el contacto entre el eje y la chumacera, se calcula integrando la distribución de presiones mediante la cuadratura de Legendre de 10 puntos, mostrada en la ecuación siguiente:

$P=\int _{-a}^{a}p\left(x\right)dx\approx \sum _{i=1}^{n}c_{i}p(x_{i})$

( 30)

9. Método de la secante

Una vez resuelta la ecuación (30), y para poder resolver la ecuación (25), es necesario determinar, tal como se describe en [24] , el semiancho de contacto a y la derivada de la superficie del elemento de fijación U’_z (x ). Puesto que se pretende calcular el contacto para una carga P₀ predeterminada por las condiciones de diseño establecidas para la propulsión del buque, el semiancho de contacto a , que depende de la geometría y la fuerza total, se calcula mediante el método de la secante haciendo nula la función F (a):

$F\left(a\right)=\int _{-1}^{a}p\left(x,a\right)dx-P_{0}=0$

( 31)

9.1. Método numérico para la determinación del mapa tensional

Finalmente, para obtener el mapa tensional en la subsuperficie debido al contacto entre la herramienta y la pieza, se ha utilizado el algoritmo desarrollado por Estrems et al . [32] , basado en la discretización de una distribución de presiones como superposición de distribuciones triangulares, que se resuelve mediante las ecuaciones siguientes:

$\sigma _{x}={\frac {P_{0}}{\pi \cdot a}}\left(\left(x-a\right)\theta _{1}+\left(x+a\right)\theta _{2}-2x\theta -2z\cdot ln{\frac {r_{1}r_{2}}{r^{2}}}\right)$

( 32)

$\sigma _{z}={\frac {P_{0}}{\pi \cdot a}}\left(\left(x-a\right)\theta _{1}+\left(x+a\right)\theta _{2}-2x\theta \right)$

( 33)

$\tau _{xz}=-{\frac {P_{0}\cdot z}{\pi \cdot a}}\left(\theta _{1}+\theta _{2}-2\theta \right)$

( 34)

$r_{1}={\sqrt {\left(x-a\right)^{2}+z^{2}}};{\mbox{ }}r_{2}={\sqrt {\left(x+a\right)^{2}+z^{2}}}{\mbox{ }};{\mbox{ }}r^{2}=x^{2}+z^{2}$

( 35)

$tan\theta _{1}={\frac {z}{x-a}};{\mbox{ }}tan\theta _{2}={\frac {z}{x+a}};{\mbox{   }};{\mbox{ }}tan\theta ={\frac {z}{x}};$

( 36)

Una vez resueltas estas ecuaciones, se obtiene el valor de las tensiones en una matriz de puntos a partir de la cual puede realizarse la representación gráfica del mapa tensional, representando las líneas con idéntica tensión tangencial principal mediante interpolación. De este mapa, se obtienen también los valores máximos de la tensión tangencial y su localización. La representación gráfica de los mapas tensionales se ha realizado mediante el programa de ordenador MATLAB^© 2013, a partir de valores de la tensión cortante principal en una matriz de puntos.

10. Resultados y discusión

Primeramente, con objeto de validar el método propuesto comparándolo con la teoría de Hertz, se muestran en la tabla 3 los resultados de tensión cortante máxima principal para diferentes holguras entre el radio del eje y la chumacera, obtenidos mediante tres métodos, la teoría de Hertz, la de contacto cilíndrico [6] y la basada en el contacto cilíndrico con expresión exacta de separación, denominada, en este caso, de contacto de tipo placa o interior bicilíndrico . En dicha tabla, se muestran los valores obtenidos de semiancho de contacto a , la diferencia porcentual entre el método basado en un contacto de tipo placa o interior bicilíndrico con Hertz y el basado en un contacto cilíndrico con Hertz, así como los valores adimensionales máximos de las tensiones tangenciales.

Tabla 3. Diferencia entre los 3 métodos

Holgura (diferencia de radios) [mm]	Radio Eje [mm]	Radio Chumacera [mm]	a (semiancho) met. Placa [mm]	a (semiancho) Hertz [mm]	a (semiancho) met. Cilind. [mm]	% Dif. Met. Aprox. Placa- Hertz	% Dif. Met. Aprox. Cilin.- Hertz	τao-Placa	τao-Hertz	τao-Cilíndrica
4,000	230,000	234,000	5,812	5,792	5,857	0,35%	1,12%	0,29392098	0,294239692	0,293905458
2,000	230,000	232,000	8,289	8,208	8,338	0,98%	1,56%	0,293937033	0,294239692	0,293905456
1,000	230,000	231,000	11,942	11,825	11,980	0,98%	1,29%	0,293970986	0,294239692	0,293905456
0,500	230,000	230,500	17,045	16,874	17,095	1,00%	1,29%	0,294038953	0,294239692	0,293905455
0,250	230,000	230,250	24,248	24,013	24,356	0,97%	1,41%	0,294175609	0,294239692	0,293905455
0,125	230,000	230,125	34,219	34,008	34,483	0,62%	1,38%	0,294443334	0,294239692	0,293905455
0,063	230,000	230,063	48,069	48,109	48,759	−0,08%	1,33%	0,294966348	0,294239692	0,293905455
0,031	230,000	230,031	67,128	68,075	68,990	−1,41%	1,33%	0,296009726	0,294239692	0,293905455
0,016	230,000	230,016	92,612	96,305	97,572	−3,99%	1,30%	0,297990503	0,294239692	0,293905455
0,008	230,000	230,008	125,189	136,213	138,009	−8,81%	1,30%	0,301669133	0,294239692	0,293905455

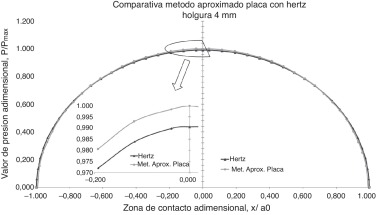
Se puede observar que los resultados obtenidos por el método semianalítico con geometría de tipo placa o interior bicilíndrico propuesto en este trabajo son muy próximos a los obtenidos mediante la teoría de Hertz (por ejemplo, 0,35% de error en el cálculo del semiancho a para el caso de holgura de 4 mm), cuando las zonas de contacto son pequeñas y las holguras, grandes. Se observa, además, que dicho error se incrementa significativamente a medida que la holgura disminuye. Por otro lado, el método basado en el contacto cilíndrico posee un error algo mayor para cualquier holgura propuesta con respecto a Hertz.

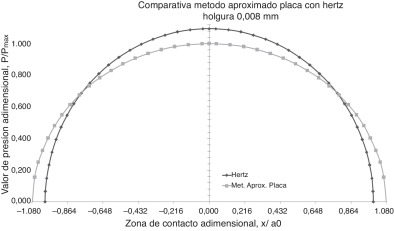
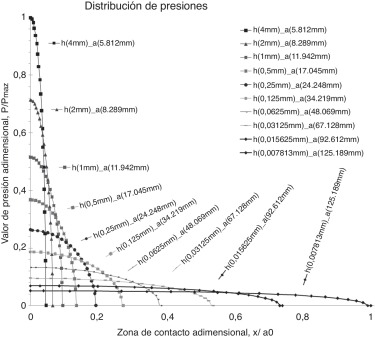
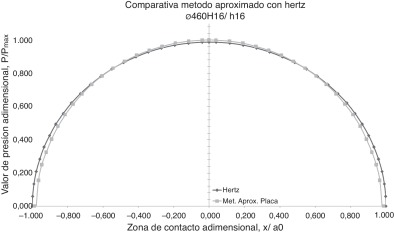
Además, la figura 6 muestra gráficamente la variación del semiancho de contacto a , con respecto a la holgura h , y en las Figura 7  and Figura 8 se representa la comparación de la distribución de presiones obtenida con respecto a la teoría de Hertz y el método propuesto en este trabajo, para los casos correspondientes a los dos extremos de los diez casos propuestos (es decir, ø_eje 460 con holgura máxima de 4 mm y mínima de 0,0078 mm). Se puede apreciar claramente la similitud en el primer caso, y una clara diferencia en el segundo. En la figura 8 , se observa una mayor diferencia cuando la holgura es pequeña.

Figura 6. Valores del semiancho a [mm] con respecto a la holgura h [mm].

Figura 7. Distribución de presiones. Perfil circular. Comparación con Hertz. Holgura de 4 mm.

Figura 8. Distribución de presiones. Perfil circular. Comparación con Hertz. Holgura de 0,0078 mm.

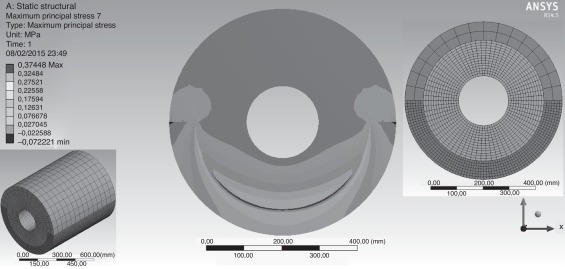
Por otro lado, debido a esta diferencia en el caso de h  =  0,0078 mm, se ha considerado conveniente utilizar, además, el MEF con el fin de contrastar los resultados obtenidos mediante el método semianalítico con el contacto de tipo placao interior bicilíndrico propuesto. Para ello, se ha empleado el software ANSYS R14.5®, donde se han modelizado las piezas en 3 D, dividiendo la chumacera en dos partes mediante el plano XZ, siguiendo con un mallado en cuadrículas de 10 mm de tamaño.

El contacto existente entre el eje y la chumacera se ha modelado con el tipo de contacto Bonded (multiple to multiple) , para la zona de contacto de piezas, y el tipo No separation (multiple to multiple) para la zona de unión de las dos piezas que forman la chumacera (zonas de pieza superior e inferior). Los elementos que forman el “par de contacto” han sido del tipo TARGE 170 para la superficie objeto y CONTA 174 para la superficie de contacto. En la figura 9 , se puede observar el resultado de las tensiones principales máximas considerando un plano XY en la zona de contacto, así como la amplia extensión que ocupa el semiancho de contacto en la zona de presión máxima (representado de color gris oscuro).

Figura 9. Eje-chumacera. Detalle de las tensiones en la región de contacto para una holgura de 0,0078 mm y detalle del mallado.

En la tabla 4 , se muestran los resultados comparativos del método propuesto, Hertz y el MEF para los dos casos de holgura mencionados. Se observa que la diferencia entre el método propuesto y el MEF está por debajo del 2% para la predicción de la tensión máxima.

Tabla 4. Diferencia entre MEF, Hertz y método propuesto para las holguras 0.0078 mm y 4 mm

Holgura (diferencia de radios) [mm]	Radio Eje [mm]	Radio Chumacera [mm]	A (semiancho) met. Placa [mm]	A (semiancho) Hertz [mm]	A (semiancho) MEF [mm]	P(x) [N/mm2] Hertz	P(x) [N/mm2] Placa	τao-Placa	τao-Placa [N/mm2]	τao-Hertz	τao-Hertz [N/mm2]	τao-MEF [N/mm2]
4	230,000	234,000	5,812	5,792	5,871	26,0163965	26,217881	0,29392098	7,70598529	0,29423969	7,65505649	7,6425
0,0078125	230,000	230,008	125,189	136,213	132,020	1,21579002	1,2576891	0,30166913	0,37940598	0,29423969	0,35773368	0,37448

Para poder comparar las curvas de presión obtenidas mediante los diferentes métodos estudiados, se han adimensionalizado la presión total P y la dimensión x con respecto a la referencia definida por los valores máximos de presión P₀ y semiancho de contacto a₀ , respectivamente. Estos han sido obtenidos a partir de todos los valores aleatorios generados en cada caso de estudio. De esta forma, se ha obtenido la gráfica de la figura 10 , que representa (P/P₀ ) con respecto a (x/a₀ ) en cada uno de los diez casos de holgura planteados en la tabla 1 . Se observa, además, que el pico de presión en a   =  0 aumenta a medida que disminuye el semiancho de contacto a y, por tanto, la fuerza por unidad de longitud distribuida.

Figura 10. Curvas de distribución de presiones adimensionalizadas para diferentes holguras.

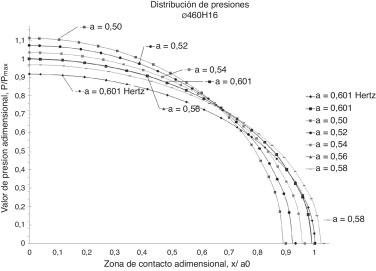
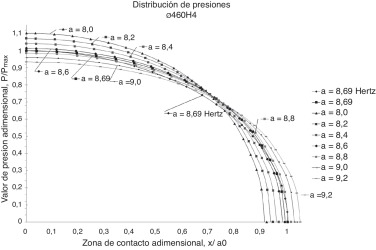
Una vez validada la idoneidad de este nuevo método, basado en un contacto de tipo placa o interior bicilíndrico, se muestran los resultados del problema de ingeniería propuesto como ejemplo, relativo a los índices de tolerancia aplicados en el diseño. De igual manera, en las Figura 11  and Figura 12 , se representan dos casos correspondientes al extremo de menor exigencia (ø460H16/h16) y al de mayor exigencia (ø460H4/h4). El primer caso, IT16 (Ajustes de superficies libres), tiene un ancho de tolerancia de 4.000 μm, mientras que, para un IT4, se exige una tolerancia de 20 μm.

Figura 11. Distribución de presiones. Perfil circular. Comparación con Hertz. ø460H16/h16 (holgura grande).

Figura 12. Distribución de presiones. Perfil circular. Comparación con Hertz. ø460H4/h4 (holgura pequeña).

Se puede observar, de forma análoga a lo expuesto anteriormente a propósito de la diferencia de holguras, que el IT define una holgura determinada. La figura 11 representa, para el caso IT16, las curvas obtenidas mediante Hertz, y el método de aproximación propuesto de contacto de tipo placa o interior bicilíndrico, del valor de presión adimensionalizada P/P_máx (donde P_máx es el valor de pico de presión máxima, que representa el área encerrada bajo las curvas de presión). La diferencia entre las dos gráficas es del 0,33% para todo el intervalo de contacto, si bien alcanza los valores más altos en los extremos, con una relación a/R de 0,25, y la diferencia aumenta conforme disminuye el índice de tolerancia. En el caso de IT4, la diferencia es de 6,81%, con un a /R de 3,59. Lógicamente, como consecuencia de las hipótesis establecidas por Hertz para elaborar su teoría, los errores o diferencias en los resultados entre ambos métodos aumentan a medida que aumenta la relación a/R , como también sucede en [6] .

A modo de ejemplo, en la tabla 5 se presentan los valores obtenidos de semiancho de contacto y los máximos de tensión tangencial adimensionalizada (tensión equivalente subsuperficial cortante), para el caso IT4 ø460H4/h4, tanto para el método propuesto como para el basado en la teoría de Hertz. De forma análoga, se han calculado los 40 casos de holgura para cada IT propuesto. Se aprecia que la tensión máxima tangencial, mostrada adimensionalmente, varía en función de la holgura en el caso del método propuesto. En cambio, aplicando la teoría de Hertz, el comportamiento es totalmente independiente con respecto a la variación de la holgura, con lo cual se pierde precisión cuando la holgura es mínima.

Tabla 5. Valores de semiancho “a” para los 40 situaciones de estudio de IT4 ø460H4/h4

Casos	Radio Eje[mm]	Radio Chumacera [mm]	a (semiancho) met. Aprox Placa [mm]	τao. Met. Placa [adim]	A (semiancho) Hertz [mm]	Tao Hertz [adim]	Casos	Radio Eje [mm]	Radio Chumacera [mm]	a (semiancho) met. Aprox Placa [mm]	τao. Met. Placa [adim]	a (semiancho) Hertz [mm]	Tao Hertz [adim]
1	229,9900	230,0108	81,1606	0,2972	83,3446	0,2942	21	229,9886	230,0098	80,6265	0,2971	82,7326	0,2942
2	229,9907	230,0103	83,5388	0,2974	86,0091	0,2942	22	229,9904	230,0101	83,2816	0,2974	85,7312	0,2942
3	229,9899	230,0101	82,4044	0,2973	84,7701	0,2942	23	229,9914	230,0097	86,2974	0,2977	89,1060	0,2942
4	229,9905	230,0094	85,0228	0,2976	87,6146	0,2942	24	229,9912	230,0112	82,7351	0,2973	85,1406	0,2942
5	229,9903	230,0104	82,5738	0,2973	84,9643	0,2942	25	229,9902	230,0093	84,4981	0,2975	87,0457	0,2942
6	229,9898	230,0097	83,0233	0,2974	85,4520	0,2942	26	229,9901	230,0094	84,2618	0,2975	86,7903	0,2942
7	229,9905	230,0100	83,7884	0,2974	86,2787	0,2942	27	229,9905	230,0104	83,0072	0,2974	85,4346	0,2942
8	229,9907	230,0104	83,3388	0,2974	85,7930	0,2942	28	229,9902	230,0103	82,6174	0,2973	85,0135	0,2942
9	229,9899	230,0096	83,3520	0,2974	85,8072	0,2942	29	229,9900	230,0099	82,9190	0,2974	85,3393	0,2942
10	229,9901	230,0100	82,8475	0,2974	85,2620	0,2942	30	229,9890	230,0102	80,4801	0,2971	82,5648	0,2942
11	229,9898	230,0101	82,1072	0,2973	84,4295	0,2942	31	229,9894	230,0090	83,4955	0,2974	85,9623	0,2942
12	229,9904	230,0107	82,2461	0,2973	84,5887	0,2942	32	229,9891	230,0105	80,3540	0,2971	82,4202	0,2942
13	229,9901	230,0103	82,3163	0,2973	84,6692	0,2942	33	229,9899	230,0102	82,2029	0,2973	84,5392	0,2942
14	229,9902	230,0107	81,7870	0,2973	84,0625	0,2942	34	229,9908	230,0108	82,7679	0,2973	85,1760	0,2942
15	229,9901	230,0098	83,4604	0,2974	85,9243	0,2942	35	229,9893	230,0097	82,0502	0,2973	84,3642	0,2942
16	229,9897	230,0090	84,0432	0,2975	86,5541	0,2942	36	229,9901	230,0102	82,5540	0,2973	84,9415	0,2942
17	229,9898	230,0088	84,7671	0,2975	87,3364	0,2942	37	229,9889	230,0099	80,9154	0,2972	83,0636	0,2942
18	229,9910	230,0090	86,9665	0,2977	89,8889	0,2942	38	229,9905	230,0104	82,9385	0,2974	85,3604	0,2942
19	229,9905	230,0100	83,6059	0,2974	86,0816	0,2942	39	229,9892	230,0107	80,1470	0,2971	82,1830	0,2942
20	229,9897	230,0103	81,7208	0,2973	83,9867	0,2942	40	229,9904	230,0100	83,4996	0,2974	85,9667	0,2942

A continuación, las Figura 13  and Figura 14 presentan las curvas de distribución de presiones adimensionalizadas (P /P₀ ), en función del semiancho de contacto a para los casos de estudio ø460H16/h16 y ø460H4/h4. Se aprecia, igual que en la figura 10 , cómo aumenta el valor máximo del pico de presión en a   =  0.

Figura 13. Curvas de distribución de presiones para diferentes semianchos de contacto a [ø460H16].

Figura 14. Curvas de distribución de presiones para diferentes semianchos de contacto a [ø460H4].

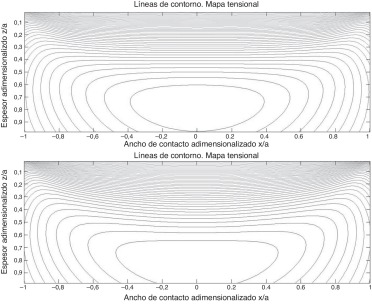
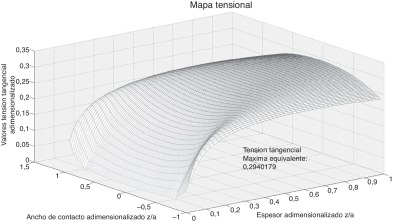
La figura 15 representa las líneas de contorno del mapa de tensiones, de los resultados obtenidos por el método de Hertz y por el método aproximado propuesto con contacto de tipo placa o interior bicilíndrico, para el caso de una holgura de 0,0078 mm. Se ha escogido este caso porque es el que mayor diferencia presenta entre ambos métodos, obtenido a partir del semiancho de contacto crítico. Esta representación permite establecer los valores máximos de tensión equivalente subsuperficial cortante, a partir de un espesor dado de chumacera, y se observa que los valores máximos se encuentran distantes de la superficie. Aplicando el método de Hertz, la tensión máxima tangencial tiene un valor adimensionalizado de 0,2942 y está localizado en un semiancho de contacto adimensionalizado de x/a  = 0 y un espesor adimensionalizado de z/a  = 0,76. Para el método aproximado, la tensión máxima tangencial tiene un valor adimensionalizado de 0,3017 y está localizado en x/a  = 0 y z/a  = 0,84. La figura 16 representa en 3 D estas mismas líneas de tensión para el método aproximado con contacto de tipo placa o interno bicilíndrico.

Figura 15. Líneas de contorno. Mapa tensional. Arriba: Método de Hertz/Abajo: Método aproximado con contacto de tipo placa.

Figura 16. Mapa tensional. Método aproximado con contacto de tipo placa o interno bicilíndrico.

Por tanto, siguiendo el criterio de Tresca, con las tensiones tangenciales máximas obtenidas para todos los casos de estudio, se puede conocer si las geometrías de estudio superan la tensión tangencial máxima permitida para dicho material. En este caso, se puede incurrir en un fallo del material, al sobrepasar el límite elástico, y producir daños permanentes en la chumacera o eje de cola del submarino. Un criterio ampliamente aceptado establece, como límite de resistencia a la fatiga, el que toma la mitad del valor del límite de fluencia, expresado por:

$\tau _{max}={\frac {\sigma _{Y}}{2}}=S_{e}^{'}$

( 37)

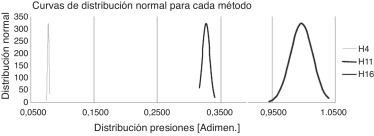
Una vez obtenidos los resultados de los 40 casos de los 3 IT previstos –ø460H16/h16 (chumacera/eje), ø460H11/h11 y ø460H4/h4)–, mediante una hoja de cálculo se puede establecer la media, la desviación estándar y la distribución normal a dichos valores y se pueden representar las curvas adimensionalizadas de distribución con el límite de resistencia establecido, cuyo valor es 1. Los valores que excedan dicho valor pueden incurrir en fallo por fatiga. En la figura 17 , se muestra el ejemplo que se acaba de describir.

Figura 17. Distribuciones normales de las tensiones equivalentes subsuperficiales cortantes para IT4, IT11 e IT16.

Por tanto, se aprecia que, a mayor índice de tolerancia IT, los valores de tensión aumentan, y es necesario mejorar las tolerancias de mecanizado para disminuir la holgura, y así evitar posibles daños subsuperficiales en la chumacera.

11. Conclusiones

El procedimiento de análisis que se ha presentado es una forma rápida y eficiente, en cuanto a número de cálculos y sencillez de implementación, para realizar un estudio local de las tensiones de contacto en los apoyos entre el eje de cola y la chumacera en un submarino, tanto para índices de tolerancia altos como para índices de tolerancia bajos, que requieren un ajuste y un mecanizado con mayor precisión. El método propuesto, basado en el contacto plano, ha sido validado con los resultados obtenidos mediante métodos de precisión contrastada y reconocida, como son el método de Hertz y el MEF. Los resultados demuestran que el método propuesto presenta una precisión suficiente, con un menor coste computacional (con tiempos de cálculo de pocos segundos y sin necesidad de preproceso, mallado y selección de elementos de contacto como en el MEF). Por ello, se presenta como una alternativa para el cálculo de casos de contacto entre el eje y la chumacera, donde solo es necesario realizar una implementación mediante MATLAB^® 2013, y el uso de una hoja de cálculo.

El método presentado incluye un análisis estadístico en el cual se refleja la pérdida de fiabilidad con el aumento de los índices de tolerancia en la fabricación. Mediante un ejemplo, se muestra cuál es el riesgo de aparición de fatiga superficial para un diseño concreto, cuyos componentes han sido mecanizados con diversos índices de tolerancia. Se muestra que, a mayor precisión de los componentes, se puede disminuir la holgura, lo cual se traduce en un mayor ciclo de vida. Esta herramienta permite, pues, establecer requerimientos de tolerancia a componentes de tipo eje-chumacera, y otros que se pueden dar en el sector de la automoción y en el aeronáutico.

Agradecimientos

Este trabajo es resultado del proyecto de investigación 08779/PI/08, financiado por la Fundación Séneca, de la Agencia de Ciencia y Tecnología de la Región de Murcia, en el marco del II PCTRM 2007-2010.

Referencias

1. [1] Foncubierta A. Importancia de la alineación de ejes propulsores en buques. Infomarine: Actualidad y tecnología de la industria naval y marítima. N° 200, pp: 71-72 (2012).
2. [2] T. Lamb (Ed.), Ship Design and Construction, Vol. II, SNAME Publ (2004)
3. [3] K.L. Johnson; Contact Mechanics; Cambridge University Press, Cambridge (1985)
4. [4] Y.-G. Jung, S. Wuttiphan, I.M. Peterson, B.R. Lawn; Damage modes in dental layer structures; J. Dent. Res., 78 (4) (1999), pp. 887–897
5. [5] H. Chai, B.R. Lawn, S. Wuttiphan; Fracture modes in brittle coatings with large interlayer modulus mismatch; J. Mater. Res., 14 (9) (1999), pp. 3805–3817
6. [6] M. Ciavarella, P. Decuzzi; The state of stress induced by the plane frictionless cylindrical contact. I. The case of elastic similitary; Int. J. of Solids and Structures., 38 (5) (2001), pp. 4507–4523
7. [7] Q.D. To, Q.-C. He; On the conforming contact problem in a reinforced pin-loaded structure with a non-zero second Dundurśconstant; Int. J. of Solids and Structures., 45 (2008), pp. 3935–3950
8. [8] F.B. Belgacem, P. Hild, P. Laborde; Approximation of the unilateral contact problem by the mortar finite element method; Comptes Rendus de l’Academie des Sciences Series I Mathematics., 324 (1) (1997), pp. 123–127
9. [9] F.B. Belgacem, P. Hild, P. Laborde; Extension of the mortar finite element method to a variational inequality modeling unilateral contact; Mathematical Models and Methods in Applied Sciences., 9 (2) (1999), pp. 287–303
10. [10] P. Hild, P. Laborde; Quadratic finite element methods for unilateral contact problems; Applied Numerical Mathematics, 41 (3) (2002), pp. 401–421
11. [11] J.C. Simo, P. Wriggers, R.L. Taylor; A perturbed Lagrangian formulation for the finite element solution of contact problems; Computer methods in applied mechanics and engineering, 50 (2) (1985), pp. 163–180
12. [12] P. Papadopoulos, R.L. Taylor; A mixed formulation for the finite element solution of contact problems; Computer Methods in Applied Mechanics and Engineering, 94 (3) (1992), pp. 373–389
13. [13] C. Hager, S. Hüeber, B. Wohlmuth; A stable energy conserving approach for frictional contact problems based on quadrature formulas; Internat J. Numer. Methods Engrg., 73 (2008), pp. 205–225
14. [14] M. Gitterle, A. Popp, M. Gee, W. Wall; Finite deformation frictional Mortar contact using a semi-smooth Newton method with consistent linearization; Internat. J. Numer. Methods Engrg., 84 (2010), pp. 543–571
15. [15] T. Dickopf, R. Krause; Efficient simulation of multi-body contact problems on complex geometries: a flexible decomposition approach using constrained minimization; Internat. J. Numer. Methods Engrg., 77 (2009), pp. 1834–1862
16. [16] S. Hüeber, B. Wohlmuth; Thermomechanical contact problems on non-matching meshes; Comput. Methods Appl.Mech. Engrg., 198 (2009), pp. 1338–1350
17. [17] I. Temizer; Thermomechanical contact homogenization with random rough surfaces and microscopic contact resistance; Tribol. Int., 44 (2) (2011), pp. 114–124
18. [18] S. Sitzmann, K. Willner, B.I. Wohlmuth; A dual Lagrange method for contact problems with regularized frictional contact conditions: Modelling micro slip; Computer Methods in Applied Mechanics and Engineering., 285 (2015), pp. 468–487
19. [19] A. Albers, L. Nowicki, H. Enkler; Development of a method for the analysis of mixed friction problems; Applied Mechanics and Engineering, 11 (3) (2006), p. 479
20. [20] A. Rezaei, W. Van Paepegem, P. De Baets, W. Ost, J. Degrieck; Adaptive finite element simulation of wear evolution in radial sliding bearings; Wear., 296 (1) (2012), pp. 660–671
21. [21] J. Aguirrebeitia, M. Abasolo, R. Avilés, I.F. de Bustos; General static load-carrying capacity for the design and selection of four contact point slewing bearings: Finite element calculations and theoretical model validation; Finite Elements in Analysis and Design, 55 (2012), pp. 23–30
22. [22] R. Lostado-Lorza, R. Escribano-García, R. Fernández-Martínez, M. Illera-Cueva, B.J. Mac Donald; Combination of the Finite Element Method and Data Mining Techniques to Design and Optimize Bearings; International Joint Conference SOCO’14-CISIS’14-ICEUTE’14, Springer International Publishing, Bilbao (España) (2014), pp. 165–174
23. [23] M. Estrems, J.J. Hernández, F. Faura; Análisis numérico de geometrías de contacto entre pieza y apoyo en máquinas herramienta; II Congreso CIMNE-CIMAT Vol. 2, Guanajuato (México). (2002), pp. 1141–1150
24. [24] H.T. Sánchez, M. Estrems, J.J. Hernández, F. Faura; Desarrollo de un método semianalítico para el estudio del contacto entre los elementos de fijación y la pieza en procesos de mecanizado; Rev. Int. Mét. Num. Cálc. Dis. Ing., 20 (1) (2004), pp. 33–54
25. [25] ABS. Guidance notes on Ship Vibration. American Bureau of Shipping , (2006).
26. [26] LRS. LRS Rules. Lloyds register of Shipping , Pt5, Ch6, (2006).
27. [27] BV. BV Rules for the Classification of Steel Ships Bureau Veritas , PtC, (2010).
28. [28] DNV. DNV Rules for Classification of Ships Det Norske Veritas , Pt4, (2009).
29. [29] GL. GL Rules and Guidelines Germanischer Lloyd , Pt1, (2014).
30. [30] T. Hasegawa, T. Torii; An automatic quadrature for Cauchy Principal Values Integrals; Mathematics of Computation, 56 (56) (1991), pp. 741–754 194
31. [31] Sánchez, H. T. Desarrollo e integración de métodos de análisis de sistemas de sujeción en Máquinas-Herramienta. Tesis doctoral Cap.4 91-118, (2003).
32. [32] M. Estrems, F. Faura, J.I. Pedrero; Desarrollo de un método numérico para la determinación del mapa tensional en la zona de contacto entre dos cuerpos; Rev. Int. Mét. Num. Cálc. Dis. Ing., 16 (4) (2000), pp. 455–470