Resumen
La teoría de conjuntos difusos ofrece un puente entre el procesamiento simbólico y el numérico que permite el uso de conceptos cualitativos útiles en el proceso de toma de decisiones relacionadas con la gestión del riesgo sísmico y, en general, con la gestión del riesgo de desastres. Su utilización en la evaluación del riesgo sísmico es necesaria en el caso en que los datos para aplicar un método de evaluación convencional del riesgo no estén disponibles o sean insuficientes. Una posible solución, considerada en este artículo, consiste en sustituir la información que falta por la opinión de expertos y en procesar las variables cualitativas y las calificaciones lingüísticas que se obtengan de dichas opiniones en lugar de valores numéricos. El procesamiento se realiza utilizando la teoría de conjuntos difusos. Para lograr una gestión eficaz, el riesgo se debe definir como las posibles consecuencias físicas, económicas, sociales y ambientales que pueden ocurrir en un período de tiempo determinado debido a fenómenos peligrosos. Desde esta perspectiva holística, y utilizando la teoría de conjuntos difusos, el método numérico propuesto calcula un nivel de riesgo físico y un nivel de agravamiento relacionado con las condiciones de fragilidad social y falta de resiliencia, para determinar un nivel de riesgo total. En el artículo se incluyen 2 ejemplos de aplicación del método propuesto y los resultados obtenidos se comparan con los correspondientes a un método convencional de evaluación holística.
Abstract
The fuzzy set theory offers a bridge between the symbolic and numerical processing, allowing managing qualitative concepts useful in the decision-making process related to the seismic risk management and, in general, to the disaster risk management. Its use in the seismic risk evaluation is necessary in the cases where the data required to apply a conventional method of assessing risk are not available or are insufficient. One possible solution, considered in this article, is to replace the missing information by expert opinions and to process the resulting qualitative variables and linguistic qualifications instead of numerical values. This process is based on the fuzzy set theory. In order to achieve an effective management, the risk must be defined as the potential physical, economic, social and environmental consequences which occur due to hazards in a given period of time. From this holistic perspective and using the fuzzy set theory, the proposed numerical method calculates a level of the physical risk and level of the aggravating conditions related to social fragility and to the lack of resilience, to determine a total risk level. In the article are included two examples of application of the proposed method and the obtained results are compared with those corresponding to a conventional method of holistic evaluation.
Palabras clave
Conjuntos difusos ; Inteligencia computacional ; Enfoque holístico ; Evaluación del riesgo ; Riesgo sísmico ; Vulnerabilidad socioeconómica
Keywords
Fuzzy sets ; Soft computing ; Holistic approach ; Risk evaluation ; Seismic risk ; Socio-economic vulnerability
1. Introducción
Los grandes avances en cuanto a hardware y software computacional han permitido el desarrollo de nuevos métodos no convencionales de procesamiento de datos y simulación. Uno de estos métodos es la inteligencia computacional o artificial (soft computing o artificial intelligence , en inglés), que es un enfoque emergente de la computación que tiene un paralelo notable con la capacidad de la mente humana de razonar y de aprender en un ambiente de incertidumbre e imprecisión [1] . Las principales herramientas de la inteligencia computacional son la lógica difusa, la computación neuronal y los algoritmos genéticos. Las principales características del procesamiento numérico en el marco de la inteligencia computacional son: a) utilización de conocimientos y opiniones de expertos; b) uso de modelos computacionales inspirados en la biología; c) aplicación de técnicas de optimización; d) utilización del cálculo numérico; e) incorporación de modelos de aprendizaje libre; f) procesamiento de un gran volumen de datos que lleva a resultados sintéticos, y g) fiabilidad [2] .
Un conjunto difuso es un conjunto sin un límite definido, es decir, la transición entre «pertenecer al conjunto» y «no pertenecer al conjunto» es gradual; esta transición suave es caracterizada por una función de pertenencia. Las funciones de pertenencia definen para cada elemento X el grado en que X pertenece a un conjunto determinado. Esta función toma valores en el intervalo [0,1], siendo 1 el valor correspondiente a la máxima pertenencia. Los conjuntos definidos de forma imprecisa o difusa juegan un papel importante en el pensamiento humano, particularmente en los dominios del reconocimiento de patrones, de la comunicación de la información y de la abstracción [2] , [3] , [4] and [5] .
El razonamiento con lógica difusa no es exacto, puesto que se hace de acuerdo con premisas e implicaciones difusas y las conclusiones que se obtienen son igualmente difusas [6] . Para dar una base conceptual a este razonamiento se introdujo el concepto de variable lingüística [4] , cuyos valores son palabras u oraciones en un lenguaje natural o artificial.
La motivación para el uso de palabras o de oraciones en lugar de números es la existencia de variables que involucran grandes imprecisiones que impiden su caracterización mediante valores numéricos [6] . Los conjuntos difusos, con sus funciones de pertenencia, dan flexibilidad a la modelización utilizando expresiones lingüísticas, tales como «mucho», «poco», «leve», «severo», «escaso», «suficiente», «caliente», «frío», «joven», «viejo», etc. Estos conjuntos surgieron de la necesidad de solucionar problemas complejos con información imprecisa, para los cuales la matemática y la lógica tradicionales no son suficientes. La lógica difusa permite trasladar sentencias sofisticadas del lenguaje natural a un formalismo matemático.
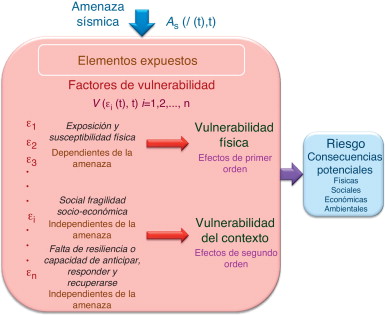
En este artículo proponemos la utilización de la teoría de los conjuntos difusos en el campo de la evaluación del riesgo sísmico. Dicho riesgo se puede definir como las posibles consecuencias económicas, sociales y ambientales de un evento sísmico que puede ocurrir en un período determinado de tiempo. En el pasado, el riesgo sísmico se ha definido de una manera fragmentaria, de acuerdo a cada disciplina científica involucrada en su evaluación [7] , y en las últimas décadas se han desarrollado varias metodologías que evalúan el riesgo desde diferentes perspectivas. Contrariamente a esta visión fragmentaria, en este trabajo hemos optado por realizar una evaluación multidisciplinar que tenga en cuenta, por una parte, el daño físico esperado en las estructuras e infraestructuras, el número de víctimas y las pérdidas económicas (efectos estos denominados de primer orden en el esquema de la figura 1 ), pero también las condiciones relacionadas con la fragilidad social y la falta de resiliencia de las comunidades que favorecen que se produzcan efectos de segundo orden cuando un terremoto golpea un centro urbano [8] , [9] , [10] , [11] and [12] . Este enfoque, denominado holístico, está esquematizado conceptualmente en la figura 1 .
|
|
|
Figura 1. Marco conceptual de un enfoque holístico para la evaluación del riesgo de desastres. I es la intensidad del evento, V es la vulnerabilidad y ɛi son los factores de vulnerabilidad [6] , [7] , [8] , [9] , [10] , [11] , [12] and [13] . |
Desde el marco conceptual de la evaluación holística del riesgo de la figura 1 se puede observar que el riesgo es función de un conjunto de factores de vulnerabilidad ɛi , algunos de ellos caracterizando la vulnerabilidad física y otros que conforman las condiciones de vulnerabilidad del contexto. La vulnerabilidad física caracteriza la susceptibilidad de los elementos expuestos a sufrir daño, teniendo en cuenta las intensidades potenciales, I , de los sismos en un período de tiempo t . La vulnerabilidad del contexto depende de la fragilidad social y de la falta de resiliencia de los sistemas urbanos propensos a desastres.
En estudios anteriores ha sido habitual evaluar el riesgo únicamente en términos físicos, dado que la vulnerabilidad social es difícil de evaluar cuantitativamente [14] , [15] and [16] . Sin embargo, también existen estudios que han conseguido tener en cuenta no solo los aspectos físicos de riesgo, sino también los aspectos no técnicos, que incluyen la capacidad económica de la comunidad, la capacidad de autoprotección de la población, la estructura social y sus niveles de organización y la gobirnanza, entre otros, es decir, realizan una evaluación holística del riesgo [9] , [10] , [11] , [12] , [17] and [18] . En estos estudios, la evaluación holística se ha llevado a cabo mediante el uso de indicadores compuestos y su objetivo primordial era obtener los resultados en una forma que permitiera guiar la toma de decisiones en la gestión de riesgos, ayudando a identificar las zonas críticas de una ciudad y su vulnerabilidad desde la perspectiva de diferentes disciplinas.
Como alternativa, en el presente artículo, en la integración de los datos y en la modelización de la vulnerabilidad y del riesgo se utilizan enfoques más avanzados, con base en la lógica difusa y en los sistemas expertos que permiten trabajar directamente con los valores cualitativos de los datos. Este tratamiento numérico proporciona una herramienta más flexible en los casos en que la información no está disponible o está incompleta, pero preservando el marco conceptual, holístico, de las metodologías anteriores. De esta manera, la información que no esté disponible puede ser sustituida por la opinión cualitativa de expertos locales del área urbana estudiada.
2. Método convencional para la evaluación holística del riesgo sísmico
La evaluación holística del riesgo con base en indicadores permite calcular un índice de riesgo total, RT , que se obtiene afectando el índice de riesgo físico, RF , por medio de un coeficiente F que depende de las condiciones de fragilidad socioeconómica y de la falta de resiliencia de la comunidad [9] , [10] , [11] , [12] , [17] and [18] .
|
|
( 1) |
La ecuación ( 1) es conocida en el ámbito de la evaluación del riesgo de desastres como la ecuación de Monchos. El riesgo físico, RF , es evaluado utilizando la siguiente ecuación:
|
|
( 2) |
donde FRFk son los factores del riesgo físico, wRFk son los pesos de dichos factores y p es el número total de factores considerados en el cálculo. El coeficiente F depende de la suma ponderada de un conjunto de factores agravantes asociados a la fragilidad socioeconómica de la comunidad, FFSi , y a la falta de resiliencia del contexto expuesto, FFRj:
|
|
( 3) |
siendo wFSi y wFRj los pesos de cada uno de estos factores, y m y n los números totales de descriptores de la fragilidad social y la falta de resiliencia, respectivamente.
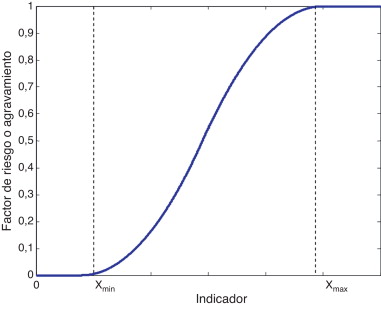
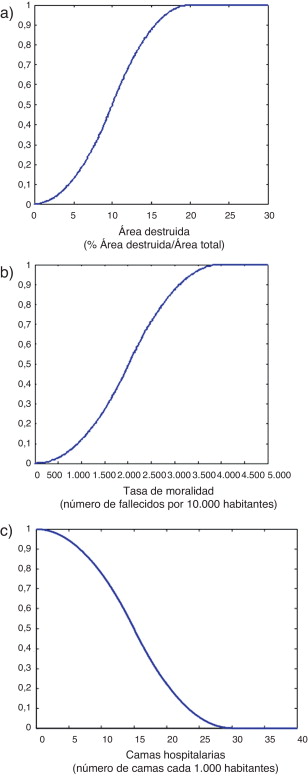
Los descriptores del riesgo físico, de fragilidad y de falta de resiliencia utilizados en la evaluación holística del riesgo tienen distintas unidades. Para estandarizar el valor bruto de los descriptores, transformándolos en valores conmensurables, en los estudios anteriores [9] , [10] , [11] , [12] , [18] and [19] se ha optado por el uso funciones de transformación que tienen el patrón que se muestra en la figura 2 . Dichas funciones tienen como objetivo el cálculo de los factores de riesgo físico, FRFk , y de los factores agravantes, FFSi y FFRj , a partir de sus correspondientes descriptores. En el modelo de función de transformación de la figura 2 , en el eje x se representan los valores de los descriptores, X , mientras que el valor del factor (de riesgo físico o de agravamiento) está en el eje y , tomando valores entre 0 y 1. Los valores límites, Xmin y Xmax , se definen teniendo en cuenta la opinión de expertos y la información existente sobre desastres pasados. En el caso de los descriptores de falta de resiliencia, la función tiene forma decreciente, de modo que el mayor valor del indicador de un menor valor de agravamiento. La figura 3 muestra algunos ejemplos de funciones de transformación utilizadas.
|
|
|
Figura 2. Modelo para las funciones de transformación. |
|
|
|
Figura 3. Ejemplos de funciones de transformación: a) área destruida; b) tasa de mortalidad, y c) camas hospitalarias. |
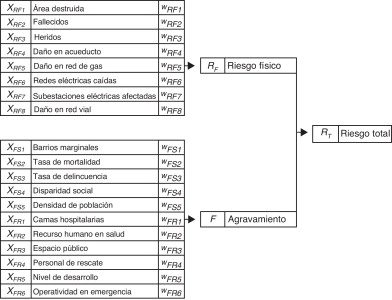
La figura 4 muestra el proceso de cálculo del índice de riesgo total, RT , para las diferentes zonas de análisis del área urbana, las cuales pueden ser distritos, municipalidades, comunas o localidades. En el procedimiento de evaluación holística original, los descriptores de riesgo físico, XRFk , se han obtenido a partir de evaluaciones previas del riesgo físico realizadas en la zona urbana. Los descriptores de agravamiento, XFSi y XFRj , se obtienen utilizando las bases de datos existentes sobre la zona urbana estudiada. Los descriptores incluidos en la figura 4 fueron seleccionados como los más significativos para cada categoría; sin embargo, pueden ser cambiados por otros de acuerdo con la disponibilidad de información para cada caso de estudio.
|
|
|
Figura 4. Descriptores del riesgo sísmico físico, de la fragilidad social y de la falta de resiliencia, sus pesos y el cálculo del riesgo total. |
Los pesos de los factores del riesgo físico, wRFk , y los pesos de los factores de la fragilidad social y la falta de resiliencia, wFSi y wFRj , se calculan por medio del proceso analítico jerárquico [9] , [12] and [19] .
La robustez de esta metodología ha sido estudiada evaluando la incertidumbre de los valores y la sensibilidad a cambiar los valores de los pesos y las funciones de transformación [17] and [18] .
3. Método numérico propuesto para la evaluación holística del riesgo sísmico
Para resolver el problema de evaluación holística del riesgo se propone un método alternativo al convencional descrito en la sección 2. Su objetivo es proporcionar una herramienta más flexible en los casos en que la información requerida por el método convencional original no esté disponible o sea incompleta; en tales casos se utiliza la opinión de expertos y los conjuntos difusos en lugar de índices. Al igual que en el método original, los pesos son asignados mediante la aplicación del proceso analítico jerárquico [19] .
Los descriptores utilizados y la secuencia de los cálculos son similares a los del proceso original descrito en la figura 4 . Sin embargo, en el método propuesto, los descriptores de riesgo físico —que se debían obtener a partir de estudios anteriores— y los descriptores de agravamiento —que eran información obtenida de bases de datos— pueden ser sustituidos por la opinión de expertos locales. Es decir, ahora la evaluación puede partir de calificaciones lingüísticas en lugar de valores numéricos. Usando calificaciones como «muy bajo», «bajo», «medio», «alto» y «muy alto», los descriptores son evaluados para calcular el riesgo total en la ciudad.
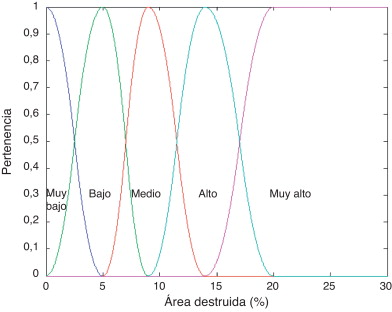
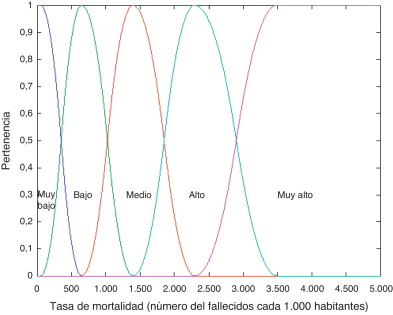
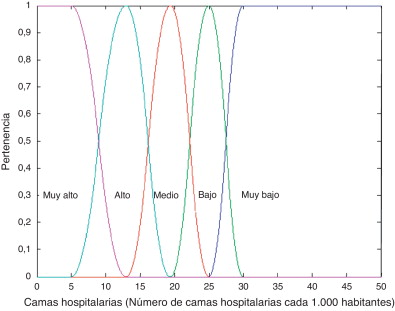
La calificación para cada descriptor es obtenida por medio de conjuntos difusos; el nivel de riesgo físico se denomina LRFi , y el nivel de agravamiento se denomina LFj . Para cada descriptor se definen, basándose en la opinión de expertos, funciones de pertenencia para los 5 niveles de riesgo físico, μLRF , y de agravamiento, μLF . Se dan aquí 3 ejemplos. La figura 5 muestra las funciones de pertenencia para los conjuntos difusos que corresponden al descriptor de riesgo físico «área destruida», XRF1 . La figura 6 muestra las funciones de pertenencia para los niveles de agravamiento correspondientes al descriptor de fragilidad social «tasa de mortalidad», XFS2 . Asimismo, la figura 7 muestra las funciones de pertenencia para los niveles de agravamiento correspondientes al descriptor de falta de resiliencia «camas hospitalarias», XFR1 .
|
|
|
Figura 5. Funciones de pertenencia para los niveles de riesgo físico de «área destruida». |
|
|
|
Figura 6. Funciones de pertenencia para los niveles de agravamiento de «tasa de mortalidad». |
|
|
|
Figura 7. Funciones de pertenencia para los niveles de agravamiento de «camas hospitalarias». |
Si se dispone de información en forma de escenarios de pérdidas potenciales, así como de información sobre la fragilidad social y la falta de resiliencia del centro urbano, se pueden usar estos valores; concretamente, al comparar dichos valores con la abscisa del centroide de la función de pertenencia de cada nivel, se define un nivel de riesgo o de agravamiento. Si esta información no existe, se asigna a cada descriptor el nivel de riesgo físico o de agravamiento mediante la opinión de expertos.
Usando las funciones de pertenencia, a partir de las calificaciones dadas al grupo de descriptores se obtiene un índice y una calificación de riesgo mediante la unión de los descriptores y la posterior defusificación, aplicando el método del centroide de área.
La unión de las calificaciones de los descriptores de riesgo físico, μRF(XRF) , se define como el máximo de las funciones de pertenencia μ , ponderadas con los pesos , correspondientes al nivel de riesgo LRF de cada descriptor XRFk .
|
|
( 4) |
donde μRFk es la función de pertenencia del descriptor de riesgo físico k para el nivel LRF , y wRFk es el peso de cada descriptor. El índice de riesgo físico, RF , se calcula como la abscisa del centroide del área bajo la curva calculada mediante la ecuación (4).
|
|
( 5) |
De acuerdo con el índice calculado se asigna un nivel de riesgo físico mediante variables lingüísticas.
El coeficiente de agravamiento, F , se evalúa mediante un proceso similar, partiendo de la unión de las calificaciones de los descriptores de fragilidad social y falta de resiliencia μ(XFS ,XFR). Las funciones de pertenencia, μ , son ponderadas con los pesos , correspondientes al nivel de agravamiento LF de cada descriptor XFSi y XFRj ,
|
|
( 6) |
|
|
( 7) |
donde μLFi es la función de pertenencia del descriptor de agravamiento al nivel LF , y wFSi y wFRj son los pesos de cada descriptor.
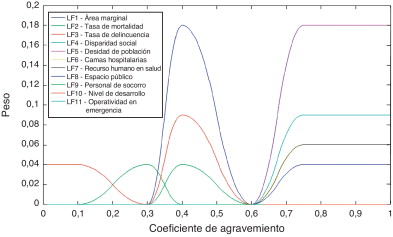
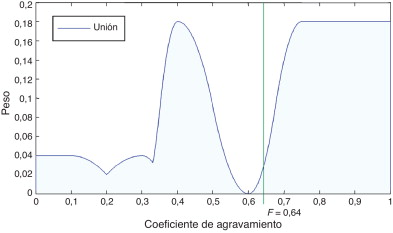
En las Figura 8 and Figura 9 se ejemplifica el proceso de cálculo del coeficiente de agravamiento mediante el método numérico propuesto. La figura 8 muestra las calificaciones de los descriptores de fragilidad social y de falta de resiliencia ponderadas por los pesos correspondientes. La figura 9 muestra la unión de las funciones de pertenencia ponderadas. El proceso de desfusificación consiste en el cálculo de la abscisa de la superficie obtenida.
|
|
|
Figura 8. Funciones de pertenencia ponderadas para el cálculo del coeficiente de agravamiento. |
|
|
|
Figura 9. Cálculo del coeficiente de agravamiento, unión y desfusificación. |
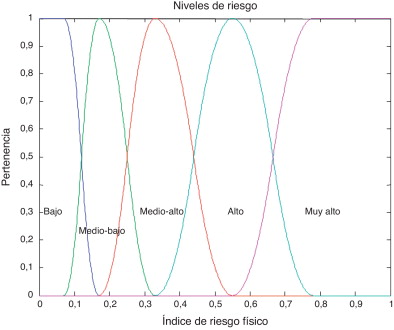
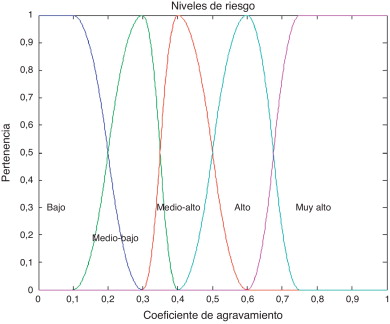
Las Figura 10 and Figura 11 muestran las funciones de pertenencia usadas para obtener los niveles de riesgo y agravamiento a partir de los índices calculados.
|
|
|
Figura 10. Funciones de pertenencia para los niveles de riesgo (bajo , medio-bajo , medio-alto , alto y muy alto ). |
|
|
|
Figura 11. Funciones de pertenencia para los niveles de agravamiento (bajo , medio-bajo , medio-alto , alto y muy alto ). |
Finalmente, el riesgo total, RT , se calcula aplicando a las calificaciones de riesgo físico y agravamiento obtenidas una base de reglas lógicas difusa que consiste en una colección de reglas lógicas del tipo «SI-ENTONCES». Dicho cálculo es el más frecuentemente utilizado en las aplicaciones prácticas [2] , [3] , [4] , [5] and [6] y su uso es necesario cuando las dependencias entre las variables son imprecisas o cuando no se requiere un alto grado de precisión [3] . En este caso, los niveles de riesgo/agravamiento que se utilizan son: «bajo», «medio-bajo», «medio-alto», «alto» y «muy alto». La base de reglas difusas utilizada se muestra en la tabla 1 .
| Agravamiento | |||||
|---|---|---|---|---|---|
| Riesgo físico | Bajo | Medio-bajo | Medio-alto | Alto | Muy alto |
| Bajo | Bajo | Bajo | Medio-bajo | Medio-bajo | Medio-bajo |
| Medio-bajo | Medio-bajo | Medio-bajo | Medio-alto | Medio-alto | Medio-alto |
| Medio-alto | Medio-alto | Medio-alto | Alto | Alto | Muy alto |
| Alto | Alto | Alto | Muy alto | Muy alto | Muy alto |
| Muy alto | Muy alto | Muy alto | Muy alto | Muy alto | Muy alto |
Aplicando la base de reglas lógicas de la tabla 1 se agrava el riesgo físico. Por ejemplo: SI se tiene un nivel de riesgo físico «bajo» y un nivel de agravamiento «alto», ENTONCES se obtendrá un nivel de riesgo total «medio-bajo». Otro ejemplo de aplicación: SI el nivel de riesgo físico es «medio-alto» y el nivel de agravamiento es «muy alto», ENTONCES el nivel de riesgo total será «muy alto».
Obviamente, los resultados obtenidos aplicando la metodología propuesta y la original no coincidirán, pero el propósito de este artículo tampoco era este. La intención era proponer un método de evaluación holística del riesgo de una ciudad que sirva para comenzar a identificar las áreas de más riesgo total del área urbana, pero en los casos en los que existe poca información o la información es de dudosa calidad. Y, en realidad, esta es la situación que se vive en la gran mayoría de las zonas urbanas.
4. Casos de estudio
4.1. Barcelona, España
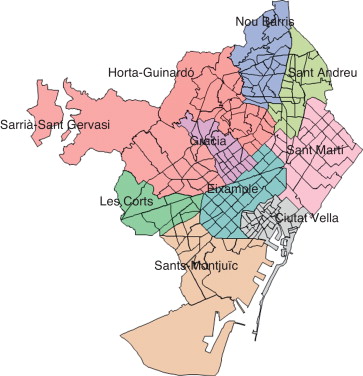
La ciudad de Barcelona está subdividida en 10 distritos y 248 zonas estadísticas pequeñas (ZEP) (fig. 12 ). El riesgo físico se calculó utilizando un escenario de riesgo sísmico probabilista [20] , [21] , [22] , [23] and [24] considerando las 248 ZEP. El agravamiento es calculado para cada distrito.
|
|
|
Figura 12. División administrativa de la ciudad de Barcelona. |
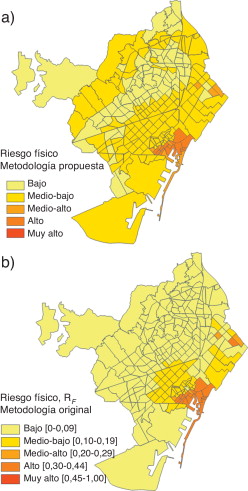
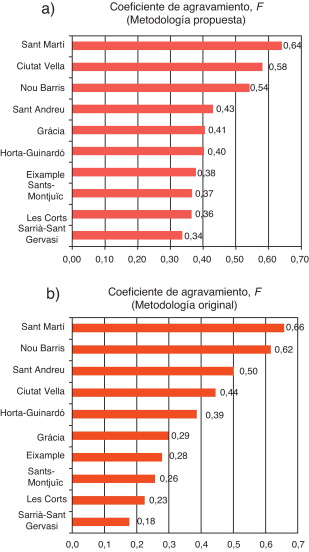
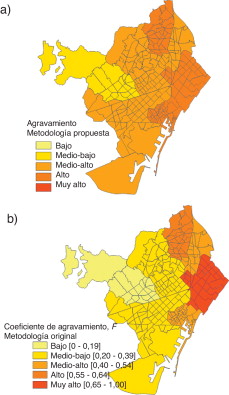
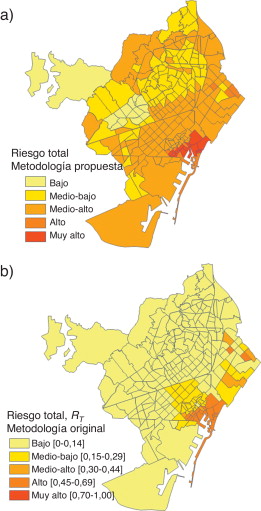
La figura 13 presenta los resultados para el nivel de riesgo físico obtenidos para las 248 ZEP de Barcelona; la mayor parte de la ciudad presenta un nivel «medio-bajo» (142 ZEP) y «bajo» (85 ZEP) de riesgo físico; 8 zonas en los distritos de Sant Martí y Ciutat Vella presentan nivel «medio-alto» y 13 zonas del distrito de Ciutat Vella presentan un nivel «alto» de riesgo físico sísmico. Las Figura 14 and Figura 15 muestran los resultados obtenidos para el coeficiente de agravamiento y su correspondiente nivel para cada uno de los distritos de Barcelona. La peor situación, según estos resultados, es para el distrito de Sant Martí, mientras que el distrito con el menor agravamiento es el de Sarrià-Sant Gervasi. Los niveles de riesgo total obtenidos se presentan en la figura 16 , donde se observa como la mayor parte de Barcelona (136 ZEP) tiene un nivel medio-alto de riesgo total y 77 ZEP tienen un nivel medio-bajo.
|
|
|
Figura 13. Niveles de riesgo físico para Barcelona: a) metodología propuesta; b) metodología original [12] , [13] and [17] . |
|
|
|
Figura 14. Coeficiente de agravamiento calculado para los distritos de Barcelona: a) metodología propuesta; b) metodología original [12] , [13] and [17] . |
|
|
|
Figura 15. Nivel de agravamiento calculado para los distritos de Barcelona: a) metodología propuesta; b) metodología original [12] , [13] and [17] . |
|
|
|
Figura 16. Niveles de riesgo total para Barcelona: a) metodología propuesta; b) metodología original [12] , [13] and [17] . |
Comparando los resultados obtenidos aplicando la metodología convencional original y la propuesta se observa que, cuando se aplica la metodología propuesta, el riesgo físico presenta niveles más altos y que se producen mayores diferencias entre los niveles de riesgo calculado en las diferentes zonas de la ciudad.
Por otro lado, los niveles de agravamiento tienen, en general, un nivel mayor que los obtenidos con la metodología original, excepto en el caso de los distritos de Sant Martí, Sant Andreu y Nou Barris, que muestran el mismo nivel de agravamiento en el caso de las 2 metodologías. La clasificación de los distritos de acuerdo con el coeficiente de agravamiento es similar en las 2 metodologías. Por consiguiente, el nivel de riesgo total tiene una tendencia similar al riesgo físico: tiene niveles más altos y muestra mayores diferencias entre las zonas de la ciudad.
Por las diferencias observadas entre los resultados obtenidos con las 2 metodologías, se puede afirmar que la metodología propuesta da una buena primera visión holística del riesgo sísmico de Barcelona, permitiendo identificar las zonas mas problemáticas.
4.2. Bogotá, Colombia
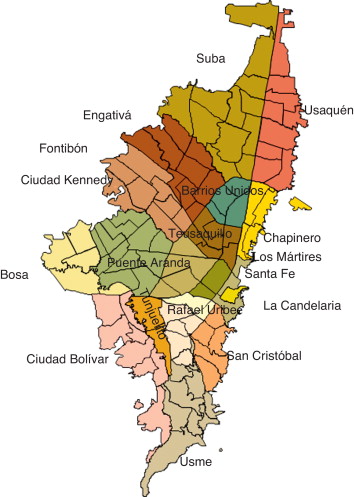
Bogotá está dividida en 20 localidades, las cuales presentan claras competencias en financiamiento y aplicación de recursos. En la simulación realizada se han tenido en cuenta 19 de ellas, ya que la localidad Sumapaz corresponde a un área rural (fig. 17 ). Estas localidades se subdividen en 117 unidades más pequeñas llamadas unidades de planeamiento zonal (UPZ).
|
|
|
Figura 17. División político-administrativa de la ciudad de Bogotá (Colombia). |
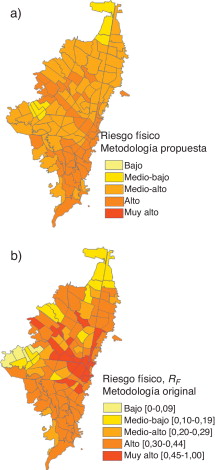
La figura 18 muestra los resultados calculados para los niveles de riesgo físico para las 117 UPZ de Bogotá considerando un escenario de riesgo sísmico existente [25] . La mayor parte de la ciudad presenta un nivel de riesgo físico medio-alto (64 UPZ) o alto (41 UPZ).
|
|
|
Figura 18. Niveles de riesgo físico obtenidos para Bogotá: a) metodología propuesta; b) metodología original [12] , [13] and [17] . |
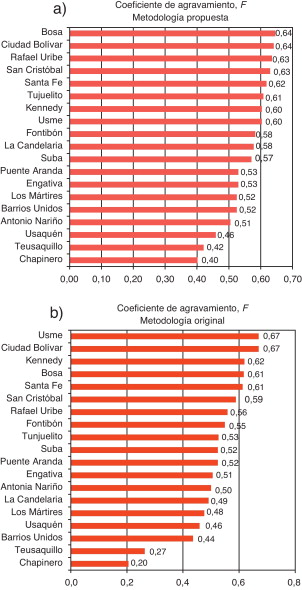
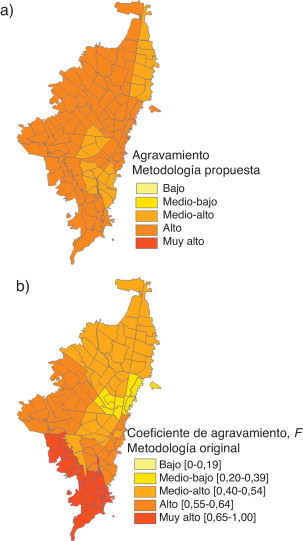
Las Figura 19 and Figura 20 muestran los resultados para el coeficiente de agravamiento para las diferentes localidades de la ciudad. Se observa que las localidades de la ciudad tienen niveles de agravamiento medio alto (las localidades de Antonio Nariño, Chapinero, Usaquén y Teusaquillo) y alto (las demás).
|
|
|
Figura 19. Clasificación del coeficiente de agravamiento calculado para las localidades de Bogotá: a) metodología propuesta; b) metodología original [12] , [13] and [17] . |
|
|
|
Figura 20. Coeficiente de agravamiento obtenido para las localidades de Bogotá: a) metodología propuesta; b) metodología original [12] , [13] and [17] . |
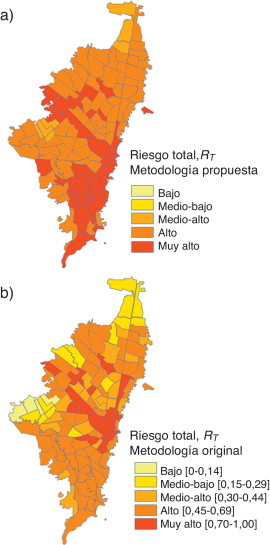
En el caso de Bogotá, algunos de los resultados obtenidos con la metodología basada en conjuntos difusos alcanzan un nivel de riesgo mayor que el nivel obtenido con la metodología original. La clasificación de las localidades de acuerdo con el coeficiente de agravamiento es similar para las 2 metodologías. El riesgo total presenta valores más altos con la metodología basada en conjuntos difusos (fig. 21 ); el nivel de riesgo total es alto en 64 UPZ, mientras que 41 UPZ es muy alto.
|
|
|
Figura 21. Nivel de riesgo total para Bogotá: a) metodología propuesta; b) metodología original [12] , [13] and [17] . |
De la comparación de resultados obtenidos con las 2 metodologías, se puede afirmar que la metodología propuesta da una buena aproximación holística del riesgo sísmico de Bogotá, permitiendo identificar las zonas que son más problemáticas, manteniendo la clasificación de los resultado obtenidos.
5. Conclusiones
En este artículo se propone una metodología para la evaluación holística del riesgo sísmico que utiliza la teoría de los conjuntos difusos. La metodología permite considerar el efecto del riesgo sísmico físico así como su agravamiento por condiciones socioeconómicas y de falta de resiliencia de la zona urbana estudiada; los resultados que se obtienen son el nivel de riesgo físico, el nivel de agravamiento y el nivel de riesgo total. La metodología propuesta es útil en aquellos casos en los que la información necesaria para aplicar el método de evaluación holística del riesgo con base en indicadores no está disponible o es insuficiente. En tales casos, la información que falta es sustituida por la opinión de expertos y es procesada mediante la utilización de conjuntos difusos. A pesar de que el modelo y el método de cálculo propuestos no pueden proporcionar resultados tan precisos como en el caso en que se dispone de datos suficientes y de calidad, el presente método facilita la gestión integral del riesgo por parte de los actores involucrados en la toma de decisiones acerca de la reducción del riesgo.
Los resultados obtenidos con la metodología propuesta en este artículo parten de datos subjetivos, por lo que, en cierta forma, los resultados obtenidos también tienen un cierto grado de subjetividad. Por esto, es importante resaltar que si la zona urbana estudiada cuenta con buena información en cantidad, calidad y detalles y si esta está disponible, es recomendable utilizar la metodología convencional original para la evaluación holística del riesgo propuesta anteriormente [9] , [12] and [24] . La metodología que se propone aquí da un primer paso hacia una evaluación holística en aquellos casos en que no se disponga de toda la información necesaria. La similitud en las clasificaciones del coeficiente de agravamiento obtenido con las 2 metodologías para las zonas administrativas en las que se subdivide una ciudad nos indica que la metodología basada en conjuntos difusos proporciona una buena aproximación.
El método propuesto se ha aplicado en este trabajo a la evaluación holística del riesgo sísmico de las ciudades de Barcelona (España) y Bogotá (Colombia). Los resultados obtenidos han demostrado que el método es robusto y permite identificar los aspectos y las características más relevantes del riesgo sísmico de las ciudades, sin la necesidad de un análisis o interpretación adicional de resultados. Dichos resultados permiten concluir que, en general, el riesgo físico es mayor en Bogotá que en Barcelona, lo que refleja la amenaza sísmica medio-alta en el caso de Bogotá y la amenaza sísmica medio-baja de Barcelona. El nivel de agravamiento es, en promedio, un nivel más bajo en Barcelona que en Bogotá y, finalmente, el riesgo total es notablemente más alto en Bogotá que en Barcelona.
Agradecimientos
Los autores agradecen al Ministerio de Economía y Competitividad de España, proyecto «Enfoque integral y probabilista para la evaluación del riesgo sísmico en España» (CGL2011-29063), y a la Comisión Europea, proyecto «Designing Safer Urban Spaces (DESURBS)». Se agradece también al proyecto INTERREG: POCTEFA 2007-2013/73/08.
Bibliografía
- [1] L.A. Zadeh; Fuzzy Logic, Neural Networks and Soft Computing, CS 294-4 Course Announcement, 1993; University of California at Berkeley, Berkeley, CA (1992)
- [2] J.S.R. Jang, C.T. Sun, E. Mizutani; Neuro-Fuzzy and Soft Computing. A Computational Approach to Learning and Machine Intelligence; Prentice-Hall, London, UK (1997)
- [3] L.A. Zadeh; Fuzzy sets; Information and Control, 8 (1965), pp. 338–353
- [4] Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning, Inf. Sci. Part I, 1975;8:199-249. Part II, 1975;8:301-357. Part III, 1975;9:43-80.
- [5] L.A. Zadeh; Fuzzy logic and the calculi of fuzzy rules and fuzzy graphs: a précis; Multiple Valued Logic, 1 (1996), pp. 1–38
- [6] D. Rutkowska; Neuro-Fuzzy Architectures and Hybrid Learning; Physica Verlag, Heidelberg, Alemania (2002)
- [7] O.D. Cardona; The need for rethinking the concepts of vulnerability and risk from a holistic perspective: a necessary review and criticism for effective risk management; G. Bankoff, G. Frerks, D. Hilhorst (Eds.), Mapping Vulnerability: Disasters, Development and People, Earthscan Publishers, London, UK (2004)
- [8] O.D. Cardona, J.E. Hurtado; Holistic Seismic Risk Estimation of a Metropolitan Center; Proceedings of 12th World Conference of Earthquake Engineering, January-February 2000, Auckland, New Zeland (2000)
- [9] M.L. Carreño, O.D. Cardona, A.H. Barbat; Urban seismic risk evaluation: a holistic approach; Nat. Hazards, 40 (2007), pp. 132–137
- [10] O.D. Cardona, A.H. Barbat; El Riesgo Sísmico y su Prevención, Cuaderno Técnico 5; Calidad Siderúrgica, Madrid (2000)
- [11] O.D. Cardona; Estimación holística del riesgo sísmico utilizando sistemas dinámicos complejos [tesis doctoral]; Barcelona, España, Departamento de Ingeniería del Terreno, Cartografía y Geofísica, Universidad Politécnica de Cataluña (2001)
- [12] M.L. Carreño; Técnicas innovadoras para la evaluación del riego sísmico y su gestión en centros urbanos: Acciones ex ante y ex post [tesis doctoral]; Departamento de Ingeniería del Terreno, Cartografía y Geofísica, Universidad Politécnica de Cataluña, Barcelona, España (2006)
- [13] M.L. Carreño, O.D. Cardona, A.H. Barbat; Disaster risk management performance index; Nat. Hazards, 41 (2007), pp. 1–20
- [14] A.H. Barbat, U. Mena, F. Yépez; Evaluación probabilista del riesgo sísmico en zonas urbanas; Rev. int. métodos numér. cálc. diseño ing., 14 (1998), pp. 247–268
- [15] A.H. Barbat, F. Yépez Moya, J.A. Canas; Damage scenarios simulation for risk assessment in urban zones; Earthq. Spectra, 2 (1996), pp. 371–394
- [16] F. Yépez, A.H. Barbat, J.A. Canas; Simulación de escenarios del daño sísmico en zonas urbanas; Rev. int. métodos numér. cálc. diseño ing., 12 (1996), pp. 331–358
- [17] A.H. Barbat, M.L. Carreño, O.D. Cardona, M.C. Marulanda; Evaluación holística del riesgo sísmico en zonas urbanas; Rev. int. métodos numér. cálc. diseño ing., 27 (2011), pp. 3–27
- [18] M.C. Marulanda, O.D. Cardona, A.H. Barbat; Robustness of the holistic seismic risk evaluation in urban centers using the USRi; Nat. Hazards, 49 (2009), pp. 501–516
- [19] T.L. Saaty, L.G. Vargas; Prediction, Projection, and Forecasting: Applications of the Analytical Hierarchy Process in Economics, Finance, Politics, Games, and Sports; Kluwer Academic Publishers, Boston, MA (1991)
- [20] J. Irrizari, N. Lantada, L.G. Pujades, A.H. Barbat, X. Goula, T. Susagna, et al.; Ground-shaking scenarios and urban risk evaluation of Barcelona using the risk-UE capacity spectrum based method; Bull. Earthq. Eng., 9 (2011), pp. 441–466
- [21] A.H. Barbat, L.G. Pujades, N. Lantada, R. Moreno; Performance of buildings under earthquakes in Barcelona, Spain; Comput.-Aided Civil Infrastruct. Eng., 21 (2006), pp. 573–593
- [22] A.H. Barbat, L.G. Pujades, N. Lantada, R. Moreno; Seismic damage evaluation in urban areas using the capacity spectrum method: Application to Barcelona; Soil Dyn. Earthq. Eng., 28 (2008), pp. 851–865
- [23] N. Lantada, L.G. Pujades, A.H. Barbat; Vulnerability index and capacity spectrum based methods for urban seismic risk evaluation. A comparison; Nat. Hazards, 51 (2009), pp. 501–524
- [24] A.H. Barbat, M.L. Carreño, L.G. Pujades, N. Lantada, O.D. Cardona, M.C. Marulanda; Seismic vulnerability and risk evaluation methods for urban areas. A review with application to a pilot area; Struct. Infrastruct. Eng., 6 (2010), pp. 17–38
- [25] Centro de Estudios sobre Desastres y Riesgos CEDERI, Universidad de los Andes; Escenarios de riesgo y pérdidas por terremoto para Bogotá, D.C.; Alcaldía Mayor de Bogotá, Dirección de Prevención y Atención de Emergencias, DPAE, Bogotá, Colombia (2005)
Document information
Published on 01/03/14
Accepted on 29/10/12
Submitted on 10/08/12
Volume 30, Issue 1, 2014
DOI: 10.1016/j.rimni.2012.10.002
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?