Abstract
The Discrete Element Method has been used to simulate fracture dynamics beacuse its inherent capacity to reproduce multi-body interaction, but in the case of elasticity mechanics the microparameters of the numerical model, required to replicate the properties of the material, are difficult to calibrate. On the other hand, damage models based on finite element strategies can easily reproduce the properties of the media but they can not simulate the dynamics of multiple fractures.
We propose a numerical approach, the Discrete Volume Method, to simulate fracture of brittle materials without the disadvantages mentioned, by combining the benefits of variational formulations and the numerical convenience of discrete element method to capture the dynamics of cracks. The Discrete Volume Method does not have microparameters, since the displacements are computed using the material properties and the fracture mechanism is controlled by an auxiliary damage field.
Within this work we discuss a numerical strategy to solve the elasticity problem upon unstructured and non conforming meshes, allowing all kinds of flat-faced elements (polygons in 2D and polyhedra in 3D). The core of the formulation relies on two numerical procedures the Control Volume Function Approximation (CVFA), and the polynomial interpolation in the neighborhood of the control volumes, which is used to solve the surface integrals resulting from applying the divergence theorem. By comparing the estimated stress against the analytical stress field of the well known test of an infinite plate with a hole, we show that this conservative approach is robust and accurate. A similar strategy is used to get the damage field solution.
In order to coupling both fields, displacement and damage, we use a finite increment arrangement for reducing the resdidual of elastic equation within each time step.
We develop a numerical formulation for time discretization based on the analytical solution of the differential equation resulting from assuming a continuous variation of internal forces of the system between time steps.
Finally, we show the effectiveness of the methodology by performing numerical experiments and comparing the solutions with published results.
The present investigation was sponsored by a CONACYT scolarship from the Mexican government and the TCAiNMaND project, an IRSES Marie Curie initiative under the European Union 7th Framework Programme.
In addition, the author want to express his gratitude to friends and mentors at CIMNE for all his support and shared wisdom, to friends at CIMAT for being always available for discussing the topics of this work and for his insightful commments and illuminating explanations about mathematical concepts, to Dr. Arturo Hernández for his support in promoting and divulging our discoveries in several conferences, and to Dr. Rafael Herrera for his priceless comments about numerical procedures and observations about the splines used here.
And last but not least, I want to thank to my beloved wife, Jimena, for all his support, tremendous patience and unconditional love since the beginning of this project, and to my Champion for teaching me every day how valuable is life. If angels exist, I already have a pair in my life.
1 Introduction
1.1 Problem definition
One of the main aims in engineering is creating tools, structures and systems to enhance the quality of life in our society. In the course of the creation process, the design stage is critical for the final outcome. During this stage the engineer have to predict the prototype response when interacting with the physical world. Many of the observed phenomena in the physical world, such as solid mechanics, fluid dynamics, heat diffusion, and others, can be described with Partial Differential Equations (PDEs) by assuming time and space as a continuum.
Computational Continuum Mechanics (CCM) is the area dedicated to develop numerical methods and heuristics to solve these PDEs. Most of the methods can be classified into these two families: weighted residual and conservative methods. The Galerkin formulations are popular and widely used weighted residual methods, such as the Finite Element Method (FEM), which is a well established technique in Computational Solid Mechanics (CSM). Alternatively, the Finite Volume Method (FV) and the Control Volume Function Approximation (CVFA) are common approaches of conservative methods. The main difference between both families is that weighted residuals methods do not conserve quantities locally, but globally instead, resulting in linear systems with commendable numerical properties (symmetrical and well-conditioned matrices, for example). Nevertheless, due to its conservative nature, the second group is more attractive for fluid structure interaction ([1,2]) and multiphysics simulations ([3,4]), where several PDE-solvers must be coupled. For that reason, in recent years FV has been subject of interest for solving CSM problems.
Most of the CSM non-linear strategies depend on the accuracy of the estimated stress field for the elasticity problem, such as those for plasticity and damage (see [5,6]). Hereafter we refer as elasticity-solver to the numerical computation that calculates the displacement and stress fields for a given domain and boundary conditions.
In industrial design it is critical to predict the cracks on materials in order to prevent a major failure on the whole system, especially in automotive, aeronautic and civil structures, where human lives can be lost. The three most important features that should be predicted with accuracy are the crack's morphology, tip's nucleation and evolution of the existing tips.
There are two main approaches to predict these cracks' features, the variational formulation which assumes a continuum where the crack is approximated by means of a function, and the multi-body system where the cracks emerges naturally by the separation of the rigid bodies. The first approach estimates the internal mechanics of materials with high accuracy, and the second approach is more suitable to capture the dynamics of systems where the initial continuum is broken apart into several subdomains.
The main objective of this work is to describe a numerical method to predict cracks by combining the accuracy and efficency of variational formulations and the ability to capture the dynamics of multibody systems.
1.2 State of the art
The prediction and analysis of brittle fracture is an intense research area with applicability to a wide range of industrial problems, such as the failure mechanism of structures, the fracking process, the detonations impact upon structures and the rock cutting. Moreover, the prevention of cracks is a main requirement in structural designs.
In his influential papers, Oñate et al [7,8], propose a FV format for structural mechanics based on triangular meshes, discussing the cell vertex scheme, the cell centred finite volume scheme and its corresponding mixed formulations, showing that the cell centred strategy produces the same symmetrical global stiffness matrix that FEM using linear triangular elements. Analogously, Bailey et al [9,10], develop a similar approach, but using quadrilateral elements to produce cell-centred volumes. Even though, the shapes of the volumes in both formulations are completely defined by the FEM-like mesh (triangular or quadrilateral) and it is not possible to handle arbitrary polygonal shapes, as we might expect when the mesh elements are produced by cracks.
Slone et al [11] extends the investigation of [7] by developing a dynamic solver based on an implicit Newmark scheme for the temporal discretization, with the motivation of coupling an elasticity-solver with his multi-physics modelling software framework, for later application to fluid structure interaction.
Another remarkable algorithm is the proposed by Demirdzic et al [12,13,14,15,16] The numerical procedure consists in decoupling the strain term into the displacement Jacobian and its transpose in a cell-centred scheme. The Jacobian is implicitly estimated by approximating the normal component of each face as the finite difference with respect to the adjacent nodes, while the Jacobian transpose is an explicit average of Taylor approximations around the same adjacent nodes. This decoupling produces a smaller memory footprint than FEM because the stiffness matrix is the same for all the components. The solution is found by solving one component each iteration in a coordinate descent minimization. This line of work has shaped most of the state of the art techniques in FV for coupling elasticity-solvers to Computational Fluid Dynamics (CFD) via finite volume practices (usually associated to CFD), such as the schemes proposed by [17,18,19]. However, this segregated algorithm may lead to slow convergence rates when processing non-linear formulations, for example, when it is required to remove the positive principal components of the stress tensor in phase-field damage formulations [20]. In addition, if some non-linear strategy requires multiple iterations of the linear elasticity-solver, such as finite increments in damage models, the nested iterations will increase the processing requirements for simple problems. To circumvent this drawback Cardiff et al [21] presents a fully block coupled direct solution procedure, which does not require multiple iterations, at expense of decomposing the displacement Jacobian of any arbitrary face into a) the Jacobian of the displacement normal component, b) the Jacobian of the displacement tangential component, c) the tangential derivative of the displacement normal component and d) the tangential derivative of the displacement tangential component. This decomposition complicates the treatment of the stress tensor in the iterative non-linear solvers mentioned before for plasticity and damage.
A generalized finite volume framework for elasticity problems on rectangular domains is proposed by Cavalcante et al [22]. They use higher order displacement approximations at the expense of fixed axis-aligned grids for discretization.
Nordbotten [23] proposes a generalization of the multi-point flux approximation (MPFA), which he names multi-point stress approximation (MPSA). The MPSA assembles unique linear expressions for the face average stress with more than two points in order to capture the tangential derivatives. The stress field calculated with this procedure is piece-wise constant.
In this work, we propose an elasticity-solver based on CVFA techniques (see [24,25]), using piece-wise polynomial interpolators for solving the surface integrals on the volumes boundaries. The polynomials degree can be increased without incrementing the system degrees of freedom, which make this method more suitable for non-linear models and dynamic computations. Furthermore, this algorithm can handle polygonal/polyhedral, unstructured and non conforming meshes, and does not require the decomposition of the stress tensor.
There are remarkable methodologies to solve the non-linear behaviour of brittle fracture using FEM, such as the damage models proposed in [26,27,28,29,30,31], the phase-field approaches to estimate the fracture surface described in [20,32,33] and the models of Extended FEM (XFEM) explained in [34,35,36]. However, these methods can not easily handle large displacements of the resulting sub-bodies after the fracture, such as the fragments blown up by a detonation. The Element Deletion Method could deal with these large displacements (see [37,38]), but none of these techniques can manage the collision between multiples bodies and the self-collision of boundaries.
The Discrete Element Method (DEM) has been used to solve problems involving granular material with success (as presented in [39,40,41]), since it can handle discontinuities in the domain without special considerations. DEM defines the interaction mechanism of multiple rigid-spheres (disks in 2D), such interaction is characterized by a set of micro-parameters which pretend to emulate the material properties. In order to approximate a continuum behaviour, the discrete elements are linked with cohesive bonds to its adjacent neighbours in the initial discretization. The fracture emerges when the cohesive bonds are broken systematically, this occurs if the force applied to them is superior to some threshold (which is a micro-parameter), a complete review of DEM is in [42,43,44,45,46].
There are two major challenges when we are working with the continuum using DEM. The first challenge is the approximation of the material properties with the microparameters, there are techniques to calculate these from a given material, as the proposed in [42], but none of these proposals proofs that the resulting behaviour of the body corresponds to the material properties. The second challenge is the computation of the system, due to the huge quantity of discrete elements (billions for some engineering problems) and the tiny time steps to maintain the numerical stability (a large time step could produce overlapping discrete elements and the wrong evolution of the displacements).
To handle these challenges, Oñate [45] proposes a DEM/FEM formulation with an underlying DEM discretization which is enabled when the finite elements are completely damaged, but this approach is expensive almost as much as the simple DEM. Zárate [47] proposes a FEM/DEM coupling scheme for fast computing simulations, but it requires the same microparameters than DEM. In the literature exists similar schemes to couple atomistic and continuum models [48,49,50,51,52], but all of them need microparameters to fix the interface between the discrete and the continuum model, and require small enough time steps to make the computation slow.
The Discrete Volume Method (DVM) aims to reduce the computational effort to perform a simulation of brittle fracture without the need of microparameters. The strategy is to solve the elasticity problem using the Control Volume Function Approximation method (CVFA), introduced in [53,24,25], on a coarse mesh and utilize an auxiliary damage field to refine the mesh in the damaged zones, separating the control volumes adjacent to completely damaged faces during the fracture process. The control volumes are named discrete volumes because them can be isolated from the domain.
DVM exploits the accuracy and robustness of CVFA and the ability to create cracks and handle multiple collisions of DEM.
2 Mathematical formulation
2.1 Continuum mechanics
We consider an arbitrary body, , with boundary . The displacement of a point at time is denoted by . We assume small deformations and deformation gradients, and the infinitesimal strain tensor, denoted , is given by
|
|
(2.1) |
Since we assume isotropic linear elasticity, the elastic energy density is defined
|
|
(2.2) |
where and are the Lamé parameters characterizing the material. These parameters are related with Young's modulus, , and Poisson's ratio, , by the following equivalences
|
|
(2.3) |
and
|
|
(2.4) |
where for plane stress analysis, and for plane strain and 3D cases.
The stress components are given by the partial derivative of the elastic energy density with respect to the corresponding strain component
|
|
(2.5) |
to simplify the notation, we use the fourth order tensor, , to map the strain field to the stress field
|
|
(2.6) |
where is the Kronecker delta. This tensor is symmetric, (major symmetry), (minor symmetry), and positive definite. The equation (2.5) is equivalent to
|
|
(2.7) |
where using the summation convention over repeated indices. Furthermore, since the strain tensor is symmetric, we can simplify the tensorial product to
|
|
(2.8) |
where is the identity matrix, defined in tensorial notation.
To model the loss of stiffness and the rupture of the material we use the damage field, denoted , which goes to one in the failure zones and it is equal to zero in the rest of the domain, as illustrated in Figure 1. We redefine the elastic energy density, , to consider the damage field effects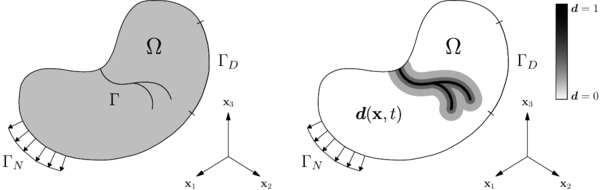
|
| Figure 1: The left side shows the body with an internal fracture, denoted , under boundary conditions. The right side shows the damage field approximation of the fracture surface. |
|
|
(2.9) |
where is the energy contribution due to tension, calculated with the positive part of the principal strains, denoted , and is the energy contribution due to compression, calculated with the negative part of the principal strains, denoted . To simplify the notation we use and . The principal strains are calculated through a spectral decomposition of the strain tensor
|
|
(2.10) |
where is the diagonal matrix containing the principal strains, denoted , and is conformed by their orthonormal eigenvectors. The positive and negative contributions are defined by
|
where
|
with . The equation (2.14) implies
|
|
(2.15) |
Observe that if there is not damage, , the energy density of the equation (2.9) is equivalent to the elastic energy density of the equation (2.2). The energy contribution due to tension is obtained from
|
|
(2.16) |
using the equation (2.15), the contribution due to compression is given by
|
|
(2.17) |
The stress of equation (2.5) is now calculated as
|
|
(2.18) |
developing the derivatives, the stress is expressed as
|
|
(2.19) |
and rearranging the terms we obtain
|
|
(2.20) |
From here, we are going to use the symbol to refer the linear elastic stress.
Observe that for the equation (2.20) is equal to (2.8), however for we have only the compression contribution.
2.2 Fracture mechanics
According to Griffith's theory of brittle fracture (see [20]), the energy required to create a unit area of fracture surface, , is equal to the critical fracture energy density, denoted , also known as critical energy release rate. The potential energy of the body, , is given by the sum of the elastic energy and the fracture energy
|
|
(2.21) |
Since we do not know the fracture surface, we use a crack surface density function, , to estimate the contribution of such surface in terms of the damage
|
|
(2.22) |
The damage field decays exponentially when goes away from the crack surface (see the work of Miehe [32,33]), this behaviour is given by the following differential equation
|
|
(2.23) |
where is a length scale parameter to control the smooth approximation of the crack. We take (2.23) as the Euler equation of the general form of the variational calculus problem
|
|
(2.24) |
to obtain
|
|
(2.25) |
By substituting (2.25) into (2.22) we approximate the fracture energy without a priori knowledge of the fracture surface, , with an integral over the entire domain, ,
|
|
(2.26) |
2.3 Formulation of the equations of motion
Replacing (2.26) into (2.21) we get the potential energy using only integrals over the domain ,
|
|
(2.27) |
The kinetic energy of the body is given by
|
|
(2.28) |
where is the density and is the velocity. Observe that the kinetic energy is unaffected by the damage field, resulting in a mass conservative scheme. The potential and kinetic energies defines the Lagrangian of the discrete fracture problem as
|
|
(2.29) |
Expanding the terms we have
|
|
(2.30) |
According to the principle of least action (see [33]), the displacement field is obtained from the following minimization
|
|
(2.31) |
and the damage field is given in a similar calculation
|
|
(2.32) |
Using the Euler-Lagrange equations to solve the minimization problems we get the strong form equations of motion
|
These equations of motion should be solved to found the displacement and damage fields.
The cracking process is irreversible, , this condition is enforced introducing a strain history field, , in the strong form equations of motion, which satisfies the Kuhn-Tucker conditions for loading and unloading
|
In this work the strain history field is defined as the maximum elastic energy density due to tension from to current time
|
|
(2.35) |
where is the dummy time variable.
Replacing the elastic energy density due to tension, , by the strain history field, , in (2.33.b) we get the system to be solved
|
The displacement field satisfies the time-dependent Neumann conditions given by upon the boundary and Dirichlet conditions given by upon the boundary , where . The damage gradient must be zero along the external boundary, . These conditions could be imposed by means of
|
The initial state of the system is characterized by
|
The strain history field, , could be used to model initial fracture surfaces (see appendix A of [20]).
2.4 Volumes definition
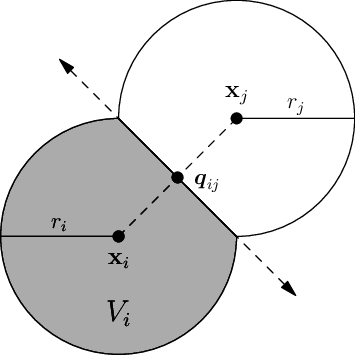
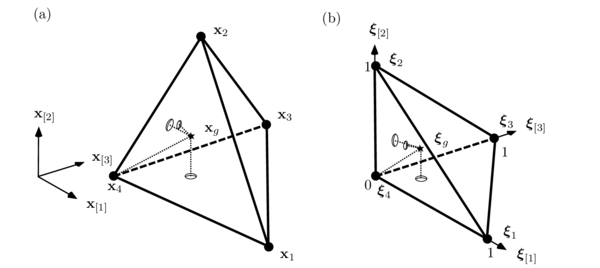
For a given set of centroids, denoted , the discrete volumes are spheres (disks in 2D) with radii truncated by planes orthogonal to the line connecting the centroids and at the following point
|
|
(2.39) |
the point is in the middle of and if is equal to . Formally, the discrete volumes of the partition are defined by
|
|
(2.40) |
Figure 2 helps to visualize the discrete volume defined by the equation (2.40). The left side of Figure 3 illustrates the domain of the discrete volume with respect to the remaining volumes , and the right side shows the discrete volumes forming a continuum in the domain, .
|
| Figure 2: The discrete volumes, , are defined by its radii and the planes orthogonal to the lines connecting the centroids and at the point , for all . |
The mass of the volumes is time-invariant and its center of mass is assumed to be the centroid. To enforce these assumptions, we associate a mass, denoted , an initial density, , and an initial volume, , to the discrete volumes, such quantities are calculated as
|
|
(2.41) |
Then, the density associated to the discrete volumes at any time, denoted , is given by
|
|
(2.42) |
Figure 4 shows the density of calculated from (2.42) for three cases.
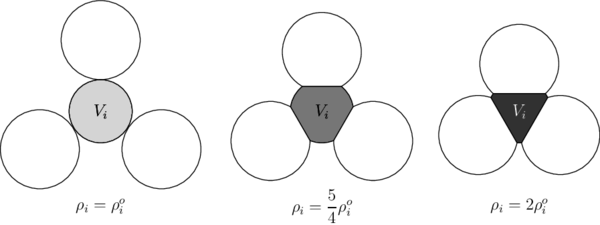
|
| Figure 4: The density is updated depending on the current volume of the sphere (disk in 2D) in order to conserve the mass. |
The integrals over the faces of the discrete volumes requires the normal of their surface, , but only the shared faces have a constant normal, the integrals on the curved faces are considered with a Neumann condition equal to zero, since such faces are not interacting with other discrete volumes,
|
|
(2.43) |
We want to remark that the elastic energy is transferred from one volume to its neighbours through the shared faces and the size of such faces has a non-linear behaviour with respect to the distance between its adjacent centroids. Most of the methodologies dealing with discrete bodies, such as the Discrete Element Method, assumes that this behaviour is linear. Figure 5 shows the surface area of the face shared by two discrete volumes with the same radius as a function of the distance between their centroids.
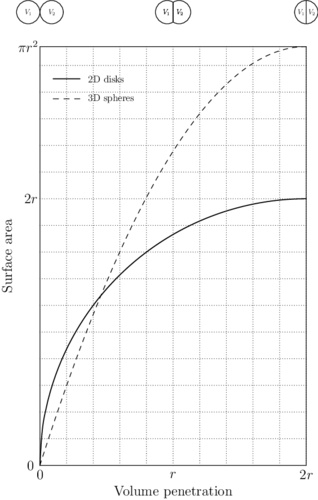
|
| Figure 5: The curves shows the surface area of the face shared by two discrete volumes with the same radius as a function of their distance, also referred as penetration. |
3 First equation of motion
On this chapter we go into the details of the numerical procedure by discussing the discretization with CVFA, the control volumes integration, the subfaces integrals, the simplex-wise polynomial approximation, the pair-wise polynomial approximation, the homeostatic splines used within the shape functions, the linear system assembling, how to impose boundary conditions, and two special cases of the formulation.
For the sake of legibility, in some parts of the text we unfold the matrices only for the bidimensional case, but the very same procedures must be followed for the 3D case.
3.1 Discretization of domain into control volumes
The domain is discretized into control volumes, denoted , using the Control Volume Function Approximation (CVFA) proposed by Li et al [24,25]. The partition of is defined by
|
|
(3.1) |
where the boundary of each control volume, , is composed by flat faces, denoted ,
|
|
(3.2) |
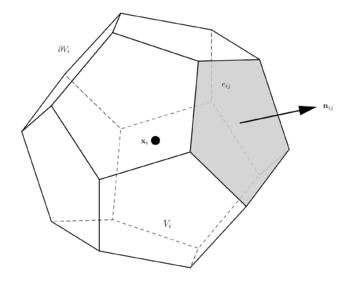
|
| Figure 7: The boundary of the three dimensional control volume is subdivided into flat faces, denoted . The unit vector is normal to the face . |
Every control volume must have a calculation point
|
|
(3.3) |
which is used to estimate the displacement field. Such a point is the base location to calculate the stiffness of the volume. In the volumes adjacent to the boundary , it is convenient to establish the calculation point over the corresponding boundary face,
|
|
(3.4) |
in order to set the Dirichlet condition directly on the point.
3.2 Control volumes integration
In this chapter we will focus our attention on the spatial discretization and numerical treatment of the stress term in first equation of motion (2.36.a), for simplicity assume , later we will remove this assumption.
We begin by integrating the stress divergence over the control volume
|
|
(3.5) |
using the divergence theorem we transform the volume integral into a surface integral over the volume boundary
|
|
(3.6) |
The evaluation of the surface integrals is based on the approximation of the displacement field inside the neighborhood of the volume, denoted ,
|
|
(3.7) |
making use of a group of piece-wise polynomial interpolators, denoted . We are going to discuss these interpolators later in this section.
For that reason, the displacement field is decoupled from the stress tensor by using the strain (2.1) and stress (2.8) definitions. Taking advantage of the stress tensor symmetry , we rewrite the stress normal to the boundary as
|
|
(3.8) |
where is the face orientation matrix and is the engineering stress vector. Developing the stress definition (2.8) component-wise we can decompose it into the constitutive matrix, denoted , and the engineering strain vector, denoted , as follows
|
then the components of the strain vector are retrieved from the equation (2.1), and it is decomposed into the matrix differential operator and the displacement function .
|
|
(3.11) |
Summarizing the equations (3.8), (3.10) and (3.11) we have
|
|
(3.12) |
where is the stiffness of the volume boundary.
Once the displacement field is decoupled, we rewrite the equation (3.6) as
|
|
(3.13) |
Using the fact that the control volume boundary is divided into flat faces, as in equation (3.2), we split the integral (3.13) into the sum of the flat faces integrals
|
|
(3.14) |
Notice that the face orientation along the flat face, denoted , is constant. Furthermore, if the control volumes are considered to be made of a unique material and the flat faces to be formed by pairs of adjacent volumes, then the constitutive matrix along the flat face, denoted , is also considered constant. The matrix is estimated from the harmonic average of the Lamé parameters assigned to the adjacent volumes, where and are the properties of the volume ,
|
|
(3.15) |
With and we simplify the equation (3.14) as
|
|
(3.16) |
where is the strain integral along the flat face ,
|
|
(3.17) |
The accuracy of the method depends on the correct evaluation of this integral.
3.3 Calculating face integrals
The surface integrals along the flat faces are calculated using an auxiliary piece-wise polynomial approximation of the displacement field. This approximation is based on the simplices (triangles in 2D or tetrahedra in 3D) resulting from the Delaunay triangulation of the calculation points from the neighborhood of . The Delaunay triangulation is the best triangulation for numerical interpolation, since it maximizes the minimum angle of the simplices, which means that its quality is maximized as well. We define the neighborhood of volume as the minimum set of calculation points such that the simplices intersecting does not change if we add another calculation point to the set. Observe that the neighborhood does not always coincide with the set of calculation points in volumes adjacent to , as in most of the FV formulations. Once the neighborhood is triangulated, we ignore the simplices with angles smaller than degrees, and the simplices formed outside the domain, which commonly appear in concavities of the boundary . The local set of simplices resulting from the neighborhood of is denoted . Figure 8 illustrates the difference between (a) the simplices resulting from the triangulation of the calculation points in adjacent volumes and (b) those resulting from the triangulation of the proposed neighborhood .
The face is subdivided into subfaces, denoted ,
|
|
(3.18) |
these subfaces result from the intersection between and the control volume . Figure 8.b illustrates six key points of this approach, 1) the simplices are used to create a polynomial interpolation of over the boundary of the control volume, 2) most of the faces are intersected by several simplices, such faces must be divided into subfaces to be integrated, 3) some few faces are inside a single simplex, as illustrated in the face formed by and , 4) there are volumes that require information of non-adjacent volumes to calculate its face integrals, such as requires , 5) the dependency between volumes is not always symmetric, which means that if requires does not implies that requires , and 6) non conforming meshes are supported, as shown in the faces formed by , , , and .
The integral (3.17) is now rewritten in terms of the subfaces
|
|
(3.19) |
Each subface is bounded by a simplex, where the displacement , and it derivatives, , are a polynomial interpolation. Hence the integrals in equation (3.19) are solved exactly by using the Gauss-Legendre quadrature with the required number of integration points, denoted , depending on the polynomial degree,
|
|
(3.20) |
Most of the cases, the displacement is interpolated inside the simplices, but in some geometrical locations these can not be created, in consequence, the displacement is interpolated pair-wise using the volumes adjacent to the subface . We discuss both strategies in the following subsections.
3.4 Simplex-wise polynomial approximation
In the general case, the simplices are formed by points. The points forming the simplex that is bounding the subface are denoted , and its displacements .
The shape functions used for the polynomial interpolation are defined into the normalized space. A point in such space is denoted , its component is denoted , and the point forming the simplex is expressed . The nodes of the normalized simplex are given by the origin, , and the standard basis vectors,
|
|
(3.21) |
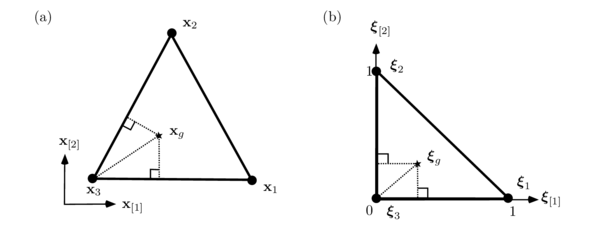
|
| Figure 10: (a) The simplex formed by the points , and in the original space contains an interior point that is mapped to (b) into the normalized 2D-simplex formed by the points , and . |
|
| Figure 11: (a) The 3D-simplex formed by the points , , and in the original space contains an interior point that is mapped to (b) into the normalized 3D-simplex formed by the points , , and . |
The shape functions, denoted , are used to interpolate the displacement field inside the normalized simplex. Such functions are non-negative and are given by
|
where is the homeostatic spline, which is the simplest polynomial defined in the interval that have derivatives equal to zero in the endpoints of the interval. We will discuss this spline later.
The set of shape functions is a partition of unity, which means that the sum of the functions in the set is equal to one into the interpolated domain
|
|
(3.23) |
furthermore, these functions are equal to one in its corresponding node, which implies that
|
The gradients of the shape functions with respect to the normalized space are denoted . The norm of the sum of such gradients is zero
|
|
(3.26) |
which means that there are not numerical artifacts into the strain field.
Any point inside the simplex can be formulated as a function of a point in the normalized space, , by using the shape functions and the points forming the simplex
|
|
(3.27) |
In order to calculate the normalized point, denoted , associated to the integration point , we use the shape functions definitions to rewrite the equation (3.27) in matrix form
|
where is the vector resulting from evaluating the spline for component-wise, and is the distortion matrix given by the concatenation of the following column vector differences
|
|
(3.30) |
Now, from equation (3.29) we retrieve the point as
|
|
(3.31) |
and solving for we obtain
|
|
(3.32) |
where is the inverse function of applied component-wise to the product of the matrix-vector operation.
Similar to the approximation in equation (3.27), within the simplex enclosing the subface , the displacement field evaluated at is defined as,
|
|
(3.33) |
Hence, when calculating the quadrature of equation (3.20), the strain evaluated at the integration point is given by
|
where captures the deformation at , and is the vector with the concatenated displacement components of the points forming the simplex.
In order to calculate the deformation matrix , we require the derivatives of the shape functions with respect to , denoted . These derivatives are calculated by solving the linear systems resulting from the chain rule
|
|
(3.36) |
where is the geometric jacobian evaluated at . This jacobian relates both spaces, captures the distortion of the simplex, and is derivated from equation (3.27),
|
|
(3.37) |
The gradients of the shape functions with respect to inside the sum are obtained straightforward once we have the spline first derivative . Notice that the geometric jacobian is equivalent to the distortion matrix if and only if the homeostatic spline is .
3.5 Pair-wise polynomial approximation
Since we are not making any assumption about the volumes distribution through the mesh, neither about the internal location of its calculation points, then we have to deal with portions of the mesh that are no covered by any simplex. Figure 12 illustrates the two most common cases. The first case takes place in meshes where the calculation points of volumes contiguous to the boundary are in the interior of such volumes, producing subfaces not intersected by any simplex, and the second case occurs when elongated sections of the domain are discretized with a queue of aligned volumes, where each volume has only two neighbors on opposite faces and no simplex can be formed.
In such cases, the displacement field within the subface is a pair-wise polynomial approximation between the adjacent volumes, and , regardless the dimension
|
|
(3.38) |
where and are the shape functions, and is the normalized projection of the integration point into the vector which goes from to , denoted
|
|
(3.39) |
When calculating the quadrature of equation (3.20), the pairwise strain is given by
|
This pairwise approximation must be used only when necessary because it can not capture the deformation orthogonal to .
3.6 Homeostatic spline
The homeostatic spline is a function of a single variable defined from to , denoted , and curved by the parameter , which indicates the level of smoothness. This spline is the simplest polynomial with derivatives equal to zero at the endpoints and . The polynomial degree is given by , and such a polynomial requires integration points to calculate the exact integral in equation (3.20) using the Gauss-Legendre quadrature.
When designing this spline, we wanted to gain accuracy by building a piece-wise bell-shaped interpolation function around the calculation points, inspired on the infinitely smooth kernels used in other numerical techniques. Therefore, we force the derivatives of the polynomial to be zero over such points in order to homogenize the function. For that reason, we use the term homeostatic spline when referring to this spline.
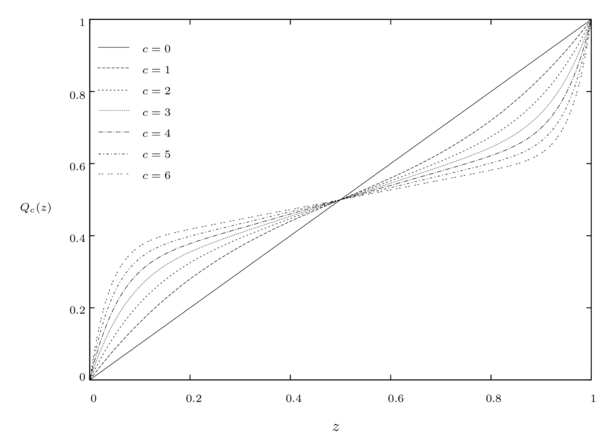
To fulfill the smoothness requisites commented before, we solved a linear system for calculating the coefficients of the polynomial. The equations of this system were obtained by forcing the derivatives to be zero at the endpoints. Once we solved the coefficients for the first twenty polynomials, from to , we found out that the first half of such coefficients are null, and the entire polynomial can be calculated directly as
|
|
(3.43) |
where is the not null coefficient
|
|
(3.44) |
is the number of factors needed to calculate
|
|
(3.45) |
and is accumulation of the coefficients for normalizing the spline
|
|
(3.46) |
The first derivative is simply calculated as
|
|
(3.47) |
Table 1 shows the polynomials resulting from low values of and Figure 14 depicts (a) the evolution of the spline as we increase the smoothness parameter from to , and (b) the evolution of it first derivative.
| Smoothness | Homeostatic spline |

|
| Figure 14: (a) The evolution of the homeostatic spline from to illustrates the smoothness requirements at the endpoints of each spline and its (b) first derivatives. |
Since the derivatives of the homeostatic spline (3.43) are zero at the endpoints of the interval , the inverse function is not defined in that points. However, we estimate a pseudo-inverse within this interval, , by finding the coefficients of a polynomial of the same degree, , such that the endpoints coincide with the spline and the first derivative at the midpoint is equivalent to the inverse of the spline first derivative, that is
|
|
(3.48) |
The higher derivatives in the midpoint are forced to be zero. Once we calculated the coefficients for the first twenty polynomials, from to , we found out that the pseudo-inverse can be approximated directly from the following formulae
|
|
(3.49) |
where is the coefficient for , and is the factor that distinguish higher order coefficients. Such terms are calculated as
|
|
(3.50) |
respectively. Figure 15 exhibits the curves for the first seven levels of smoothness. The null higher derivatives requirement is noticeable at the midpoint.
|
| Figure 15: Curves of the pseudo-inverse for the first seven levels of smoothness. The slope at the midpoint exposes the null higher derivatives requirement when increasing the polynomial order. |
3.7 Assembling volume's equation
By using the simplex-wise (3.35) or the pair-wise (3.42) approximation, the strain face integral (3.19) is reformulated as
|
|
(3.51) |
then, the volume equilibrium equation (3.16) is
|
|
(3.52) |
reordering the terms we obtain
|
|
(3.53) |
where the matrix
|
|
(3.54) |
is the stiffness contribution at the integration point , within the subface when integrating the volume. Observe that the stiffness matrix is rectangular and the resulting global stiffness matrix is asymmetric.
3.8 Boundary conditions
The Neumann boundary conditions are imposed over the volume faces intersecting the boundary, by replacing the corresponding term in the sum of equation (3.14) with the integral of the function provided in (2.37.a),
|
|
(3.55) |
The Dirichlet conditions are imposed over the volumes calculation points by fixing the displacement as it is evaluated in the function given in (2.37.b),
|
|
(3.56) |
Since the Dirichlet conditions are imposed directly on the calculation points, these points must be located along the face which intersects the boundary with the condition .
3.9 Special cases
By making some considerations, we identify two special cases where the calculations can be simplified, in order to increase the performance of the total computation, at the expense of losing control over the volumes shape. These cases are 1) the Voronoi mesh assumption and 2) the FV-FEM correlation.
In the first case, we assume that the initial mesh is equivalent to the Voronoi diagram and that the Voronoi centres correspond to the calculation points . Hence, the subdivision of the neighborhood is already given by the Delaunay triangulation which is dual to the Voronoi mesh, as illustrated in Figure 18.a. Moreover, the integrals of subfaces using pair-wise approximations can be exactly integrated with the midpoint rule, since the faces are orthogonal to the vector joining the calculation points , and the derivatives along the subface are constants.
In the second case, the initial mesh is generated from a FEM-like triangular mesh and the approximations are assumed to be linear. In such a case, the calculation points are defined to be the nodes of the triangular mesh, and the volume faces are created by joining the centroids of the triangles with the midpoint of the segments, as presented in Figure 18.b. This particular version is equivalent to the cell-centred finite volume scheme introduced by Oñate et al [7], who proved that the global linear system produced by this FV scheme is identical to that produced by FEM if the same mesh is used.
4 Second equation of motion
In this chapter we will focus on the numerical treatment of the second equation of motion (2.36.b), this equation describes the damage mechanics within the physical system by considering the potential energy produced by tensile stress.
As discussed in the mathematical formulation, the damage field is a smooth approximation of the fracture surface, a benefit of this approach is that fracture morphology is completely defined by the solution of this equation and we do not have to track the crack propagation with auxiliary checking procedures neither to check for new crack nucleations. However, it is important to be aware about the effects over the stress field produced by the scale length parameter which controls the smoothness of damage field solution. We observe that a length parameter proportional to the average size of control volumes, denoted , produces accurate results, these mesh size is taken as
|
|
(4.1) |
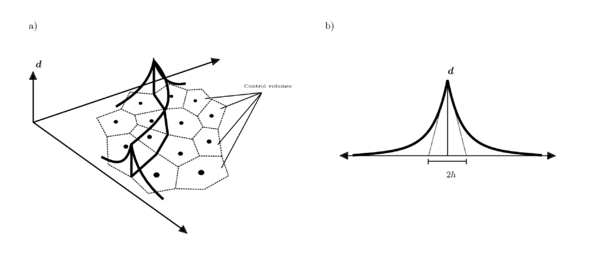
|
| Figure 19: a) Damage field above control volumes shows how the crack arises along volumes boundaries. b) Scale length parameter controls the smoothness of the damage field. |
For assembling the system of equations We will follow a similar path to that used in the first equation of motion by using the same partition and interpolators, simple-wise and pair-wise approximations also apply for the damage field.
4.1 Discretization
We start by integrating the strong form equation of motion (2.36.b) over the control volumes of the partition ,
|
|
(4.2) |
using the divergence theorem on the second integral we get
|
|
(4.3) |
Since is a material property, we assume that it is constant along the control volume, and dividing the first integral in two terms we obtain
|
|
(4.4) |
In order to solve volume integrals involving the strain history field, we use the following partition of the control volume
|
|
(4.5) |
The surface integral is solved along subfaces defined in (3.18), and the remaining volume integrals are solved using partition (4.5),
|
|
(4.6) |
The damage field is estimated using the same shape functions, (3.22.a) and (3.22.b), that we use for the displacement field,
|
where is the point corresponding to in the normalized space, is the vector containing the shape functions evaluated at , and is the vector containing the estimation of the damage field at the nodes forming the simplex. The gradient of the damage field is given by
|
|
(4.9) |
where is calculated from the chain rule in (3.36). Now the equation is fully discretized, the next step is to solve the integrals.
4.2 Assembling system of equations
The first integral in equation (4.6) is approximated using the midpoint rule,
|
|
(4.10) |
where is the damage estimated at calculation point . Due to the simple nature of polygonal subvolumes , we can always reduce them to simplices in order to use the Gauss-Legendre quadrature to solve the volume integrals, in 2D is straightforward,
|
where is the number of points in the quadrature, and is the strain history field evaluated with the strain information of the simplex corresponding to subface . Last but not least, we solve the surface integral that unfolds the damage gradient defined in (4.9), using again Gauss-Legendre quadrature
|
where is the matrix containing the derivatives of the shape functions evaluated at . For simplicity, the matrix notation in previous equation shows only values for 2D case.
Substituting, equations (4.10), (4.12), (4.13) and (4.17) into (4.6) we get
|
|
(4.19) |
The damage of the face produced by excesive loads is captured by vector
|
|
(4.20) |
on the other hand, the potential energy to create new crack surfaces is captured by
|
|
(4.21) |
Now we can rewrite the damage equation (4.19) for the control volume as follows
|
|
(4.22) |
Since damage is not a physical quantity, there is no damage flow between the system and the exterior, for that reason all the Neumann conditions are null, and Dirichlet conditions can be numerically set, but in our formulation these are defined in the initial strain history field .
5 Time discretization
In this chapter we will remove the assumption done in equation (3.5) about null acceleration, , and we will discuss in detail the discretization of time derivatives.
A common approach to approximate these derivatives in dynamic stress analysis is a staggered scheme by means of Finite Differences (FD), such as in [11], [34] and [52]. The simplicity of FD makes easy the incorporation of spatial non-linear phenomena, for instance fracture and damage, nevertheless FD does not consider the stress state within its approximation and we are forced to use tiny time steps to diminish spurious stress waves that produce undesired artifical internal forces.
In this work we build a customized numerical scheme considering the time variation of internal forces in order to get an approximation capable of performing bigger and more accurate time steps.
5.1 Time variation
In order to analyze the dynamic component of elasticity equation (2.36.a) we define the stress state of control volume as a function of time,
|
|
(5.1) |
with the intention of considering internal forces in the approximation,
|
|
(5.2) |
Equation (5.2) is an ordinary differential equation that can be solved analytically for a time step with the following Dirichlet conditions
|
We assume that temporal variation of the internal forces is given by
|
|
(5.4) |
where is the stress state calculated at , is the stress state which will be estimated at time , and is the shape function modelling time variation between concecutive stress states. This shape function has only two constraints and , for that reason we use as a normalizer in equation (5.4). In the discussion of this chapter we utilize “stress state” and “internal forces” as synonyms to refer the same term in equation (5.1).
Figure 21 illustrates the variation of the stress state in terms of the shape function that is used as interpolator between the value at two contiguous time steps.
5.2 Analytical solution
Using the asumption in (5.4), we get the analytical solution of the equation (5.2) for the interval by means of the Laplace transform (see appendix A for details),
|
|
(5.5) |
where is the velocity at time , and is the convolution between the spline and the function , as defined in appendix A.
By setting the second boundary condition, , into the analytical solution (5.5), we can find the velocity required to fulfill both Dirichlet conditions
|
|
(5.6) |
where is the convolution evaluated at . Thus, we replace equation (5.6) into (5.5) to get the analytical solution in terms of the known Dirichlet conditions
|
|
(5.7) |
now we can obtain the analytical time derivative (velocity),
|
|
(5.8) |
where is the time derivative of . Since the analytical solution (5.5) requires the initial conditions (displacement and velocity), we calculate the initial velocity by using equation (5.8) for a previous time interval ,
|
|
(5.9) |
where and . Finally, we replace equation (5.9) into (5.5) in order to get an analytical solution for as a function of two history system states,
|
|
(5.10) |
evaluating such an equation at , denoted , and rearranging the terms we get a numerical approximation dependent of the convolution of choosen spline,
|
|
(5.11) |
observe that even in the simplest case this approximation is more accurate than simple central finite differences applied directly on equation (5.2), because it takes into account variable time steps and the time variation of the system internal forces.
5.3 Numerical scheme
The analytical solution (5.11) of the ordinary differential equation (5.2) can be used to generate a family of numerical approximations, these approximations has a similar structure but distinct coefficients that depend on the shape function used for time variation of stress state. In this work we explore distinct families of functions in order to get a continuous stress state in contiguous time steps.
5.3.1 Harmonic oscillator sensibility
In order to select a good shape function for stress time variation we used the harmonic oscillator to measure the sensibility of the numerical scheme to distinct shape functions. The harmonic oscilator differential equation is
|
|
(5.12) |
where is the stiffness of the system, is the mass of the body and is the one-dimensional displacement. The analytical solution of equation (5.12) is
|
|
(5.13) |
where is the oscillation amplitude, the oscillation frequency and the phase, such constants are calculated in terms of material properties
|
with and as initial displacement and initial velocity respectively. In our numerical tests, the one dimensional stress state, denoted , is assumed to be
|
|
(5.17) |
For simplicity, in this sensibility analysis we used a constant time step .
5.3.1.1 Central Finite Differences
By using a central finite differences scheme, equation (5.12) can be rewritten as
|
|
(5.18) |
and the solution for next time step is calculated from
|
To measure the relative error with respect to analytical solution, we used (5.20) to compute the solution in the interval . To make evident the numerical drawbacks of FD we utilized a big enough . In Figure 22 we show the experiment results in four plots, the first one shows the displacement against time with a solid line for analytical solution and a dashed line for the numerical one, in this plot is clear that the system is loosing energy through time, no matter how small is the system will always loose energy proportionally to the time step. The second plot shows the phase space (solid line is analytical solution), which is velocity against displacement, in this plot we see the closing spiral when displacement and velocity decreases. The third plot shows the total energy in the system to emphasize that it is loosing energy, while total energy of analytical solution (solid line) remains constant. The fourth plot shows the cumulative relative error for distinct , such an error remains almost consant for since the numerical system looses all its energy in the first few time steps. In this plot we compute the comulative error as
|
|
(5.21) |
5.3.1.2 Linear spline
If we choose a linear shape function, , in order to set a constant variation of the internal forces in the interval , the convolution and its time derivative are given by
|
|
(5.22) |
respectively, and the resulting numerical scheme 5.11 is
|
|
(5.23) |
by applying the assumption of constant time steps, we reduce previous equation to
|
|
(5.24) |
then we use this numerical approximation to solve the harmonic oscillator and we get
|
|
(5.25) |
and the numerical solution is given by
|
|
(5.26) |
for displacement and
|
|
(5.27) |
for velocity.
In our experiments we used the same than with Finite Differences. Figure 23 shows the experimental results in four plots, analytical solution is the solid line and numerical results are depicted with a dashed line. In the first plot we show the direct numerical solution, displacement vs time, and we see how the system gains energy through time, reducing time step alleviates the problem but it does not solve it, since the artificial energy increasing is proportional to the time step. The second plot shows the phase space, which is velocity against displacement, here we observe how the artificial generated energy creates an opening spiral producing greater waves as the simulation moves in time. The third plot reflects how the total energy in the system grows with respect to time. The fourth plot shows the cumulative relative error (5.21) in the interval with respect to . From here we noticed that for this scheme is slightly better than Finite Differences, and for both schemes are useless in long term simulations, at least that we use a numerical mechanism to rebalance the energy (dampers for instance).
5.3.1.3 Numerical equilibrium
Using the general scheme in (5.11) and considering constant time steps, , we define a numerical approximation for harmonic oscillator in terms of the convolution and its derivative
|
|
(5.28) |
then the solution for displacement is
|
|
(5.29) |
and the velocity is given by
|
|
(5.30) |
In equation (5.29), observe that by choosing , we get a convolution of and a convolution derivative of , which produces the very same numerical scheme that finite differences in (5.20).
Notice that no matter which shape function we choose, the convolution evaluated at always have the form of and its derivative the form of , where and are variations of and respectively. From this fact we will use as an optimization variable for minimizing the error, and we set for simplificate the formula (since is not involved in the minimization). Now we simplify equation (5.29) as
|
|
(5.31) |
With previous equation and using the same that we use in previous numerical tests, we calculate as
|
|
(5.32) |
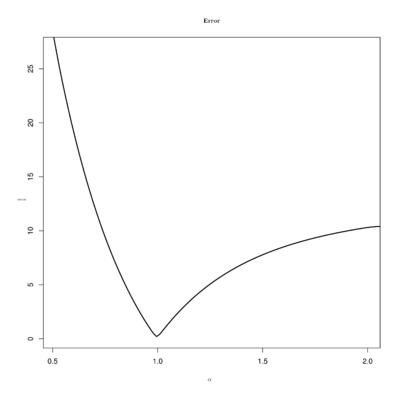
|
| Figure 24: The plot shows the cumulative relative error of equation (5.21) as a function of the optimization variable . It is clear that the minimum is in . The error curve is asymptotic to zero in the left and converges to some constant to the right. |
Since is the proportion of in convolution derivative, , from this experiment we found out that
|
Examples of energy state of conditions (5.33) and (5.35) can be observed in Figures 22 and 23 respectively.
In our experiments we notice that the variation of has a little impact on the results, but values of produce smaller oscillations of total energy than . For that reason, we constrain our search of shape functions to those functions that produce and .
Figure 25 shows experimental results with same of the numerical scheme resulting from taking and (value of is arbitrary chosen only for plotting purposes), which implies that and . The results are displayed in the same format that previous experiments of harmonic oscillator, the analytical solution is the solid line, the numerical solution is the dashed line, and we have 4 plots to show the curves of displacement vs time, the phase space (velocity vs displacement), the total energy and the error when moving . In this plots we can appreciate the stability of the system, which have little oscillations of the total energy.
5.3.2 Trigonometric shape function
In order to build our numerical time discretization, we propose this trigonometric shape function shown in Figure 21
|
|
(5.36) |
The appendix B discuss another proposals based on polynomials that produces accurate results, nevertheless this trigonometric function introduces less artificial energy that impact results in long term simulations.
The convolution corresponding to (5.36) is
|
|
(5.37) |
and its derivative is
|
|
(5.38) |
although when we evaluate at and we obtain
|
|
(5.39) |
as expected by previous discussion in this section. Notice that plots in Figure 25 were produced with , and for this shape function we have
|
|
(5.40) |
that produces almost identical plots.
5.3.3 Dynamic stress analysis
Considering discretized stress equation (3.53) into this numerical scheme, we have that
|
|
(5.41) |
replacing (5.36) into such stress equation we get our final numerical system for the first equation of motion (2.36.a)
|
|
(5.42) |
If we choose a constant time step, , we can simplify the equation to
|
|
(5.43) |
The results shown in this work use the trigonometric time variation with fixed length time steps, although our software supports automatic (variable) time steps.
5.3.4 Time step calculation
Numerically speaking, the time step is bounded by the maximum propagation speed of stress waves, denoted , which means that should be small enough to capture the stress state. Using the solution of the one dimensional wave equation, can be estimated as
|
|
(5.44) |
where and are material properties. This equation implies that in order to reproduce stress waves numerically, the following relation should be satisfied
|
|
(5.45) |
where is the Courant number and is the average area of control volumes. In this work we use Courant numbers proposed by [17] for stress analysis. At the beginning of simulation we use , but when damage field starts producing failures (interfering with stress analysis), we use a smaller Courant number to produce more accurate results and better conditioned sytems of equations.
6 Coupled system
In this chapter we will discuss in detail how the discretized versions of both equations of motion, (5.42) and (4.22), are coupled in a segregated approach. We will take first equation of motion as a cornerstone of the numerical scheme, since displacements and internal forces are first class fields in the physical system, while the damage field is an auxiliary abstraction to approximate fracture surface.
6.1 Residual minimization
Due to the fact that a single time step can release enough energy to create wide crack surfaces, the numerical structure can become unstable. In order to make small changes in stress field to produce numerically manageable systems we dose internal forces in equation (5.42) into finite increments,
|
|
(6.1) |
where coefficient is given by
|
|
(6.2) |
thus displacement and damage fields at time are calculated by computing finite increments. Each finite increment is solved by minimizing residual
|
|
(6.3) |
The displacement corresponding to finite increment , referred as , is the accumulation of displacement increments in residual minimization, denoted . Residual is minimized using Newton-Raphson iteration [41], starting with
|
|
(6.4) |
Such numerical scheme is composed by the linear systems in equations (5.42) and (4.22),
|
where superindex indicates the iteration within the residual minimization for solving finite increment . Finally, minimization finish when residual converges. We have two criteria for detecting convergence, the first one consist in checking if residual norm is small enough
|
|
(6.8) |
and the second criterion consist in checking that the derivative of the norm of the residual with respect to the iterations is approximately zero
|
|
(6.9) |
which means that solution is not changing any more in concecutive iterations. In order to estimate this derivative we calculate a linear regression of (with respect to ) of the fifty previous iterations, and we take the slope coefficient as the derivative.
6.2 Discrete Fracture
The fracture between the control volume and the volume adjacent to its face is produced when such face satisfies
|
|
(6.10) |
The condition is reached when the damage field is enable along all the face, this means that we consider a fracture when the face is completely damaged. Thus the control volumes could be separated from their adjacent control volumes due to this fracture mechanism, and for that reason, the title of the monograph is the Discrete Volume Method.
The discrete volumes are integrated with the CVFA method, considering discrete faces as continuum faces completely damaged, , when calculating the damaged strain equation (3.17). All the faces which not appear in the initial discretization are treated as discrete faces, this allows the collision of separated bodies and the self-collision of the body boundaries. New discrete faces arise from the fracture process.
7 Results
In this chapter we will discuss the following numerical experiments: plate with a hole to compare elasticity solver against analytical solution, stress wave in a bar to compare dynamic solver against published results, perfored strip under tension for fracture due to direct tension, three point bending bar test to compare our solver with lab experiments, brazilian test to analyze fracture due to indirect tensile strain, compressive test to verify cracking patterns against those produced with similar numerical methods, four point notched bar test for analyzing fracture mode II, Three point bending bar with asymmetric perforations test to evaluate sensibility of crack morphology, notched plate under shear to contrast our results with those of other authors, dynamic shear loading, and dynamic crack branching to demonstrate multicrack generation.
For each test we review the material properties, the geometrical description of the body, the configuration of boundary conditions, the numerical parameters and other considerations. We also provide figures to portray the specification of each experiment.
We use LU decomposition to solve both systems of equations (elasticity and damage), the displacement field requires memory to store a vector per discrete volume, whereas that damage field only requres a floating point number (double precision) per node. The discrete volumes are numbered using a nested dissection technique [54] before assembling the systems in order to reduce the fill-in in LU decomposition. In our experiments, initial meshes were generated with a central Voronoi-cells procedure.
7.1 Plate with a hole
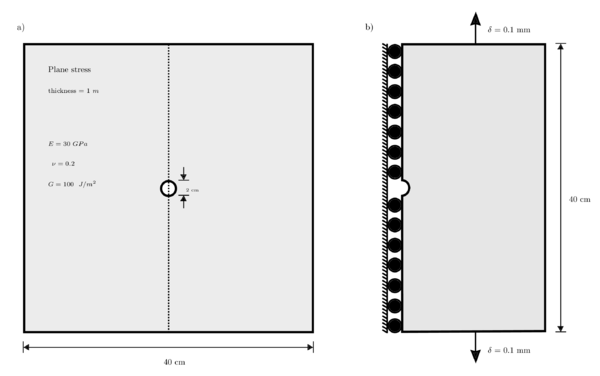
In order to test the numerical performance of the proposed method for solving the first equation of motion, we use the well known analytical experiment of an infinite plate with a circular hole in the origin (see [55]). In such a experiment, the plate is stretched along the horizontal axis with a uniform tension of from each side, as is shown in Figure 26. The material is characterized by the Poisson's ratio, , and Young modulus, . Plane stress is assumed with thickness equivalent to the unity. The dimensions of the computational domain are and .The analytical solution is given by the following formulae
|
where the polar coordinates,
|
|
(7.4) |
![(a) Polygonal mesh used for comparison of numerical results. (b) Level sets of σ[11] between 0 to 30 ~~kPa. (c) Level sets of σ[22] between -10 and 6 ~~kPa. (d) Level sets of σ[12] between -10 and 2 ~~kPa.](/wd/images/thumb/4/44/Draft_Samper_795975371_1569_monograph-picture-ccae4f.png/600px-Draft_Samper_795975371_1569_monograph-picture-ccae4f.png)
|
| Figure 27: (a) Polygonal mesh used for comparison of numerical results. (b) Level sets of between to . (c) Level sets of between and . (d) Level sets of between and . |
The Dirichlet conditions are imposed on the bottom and left side of the computational domain as is shown in Figure 27.b. Next in order, the analytic stress of equations (7.1), (7.2) and (7.3) is imposed as Neumann condition over the top and right side of the computational domain.
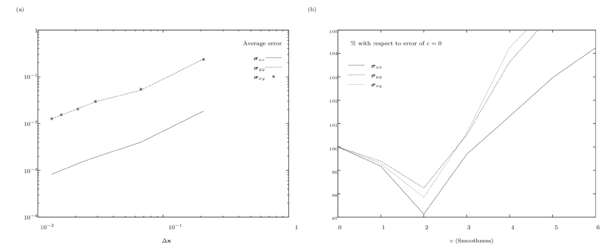
Figure 28.a presents the averaged error as a function of mesh size, denoted , as we might expect, the error is proportional to the mesh refinement. For a mesh of 628 volumes, Figure 28.b shows the percentage of the error with respect to the error of , for different smoothing levels, correspond the linear interpolator. Observe that the error of the stress field does not decreases significantly in the first three levels of smoothness, this is because we do not increase the degrees of freedom of the linear system (is the same mesh), although we built a better field description, which can be useful when solving non-linear formulations. The increasing error after is produced by floating point truncation, since implies computing integrals for polynomials of order or higher.7.2 Stress wave in a bar
This experiment consists in analyzing the pattern of a stress wave in a long bar to assess performance of time discretization developed in this work.
We assume plane stress with a thickness of , and we choose a smoothness . The material properties are those of steel, elasticity modulus , Poisson's ratio and density . The size of the bar is long and wide. The initial displacement and velocity at the interior of the bar are null. Figure 29 illustrates the geometrical distribution and numerical parameters.The bar is fixed from right side and is pushed from left side at time , this produces a propagation of the stress wave at speed of sound through the bar, that for steel is
|
|
(7.5) |
when the stress wave arrives to the fixed side, it is reflected in reverse direction, at this moment perpendicular waves resulting from Poisson's effect start interfering with our frontal wave. Figure 30 shows the bubble formed by stress wave after time , when frontal wave is reflected, as predicted by [17]. This bubble is the contour of , where
|
|
(7.6) |
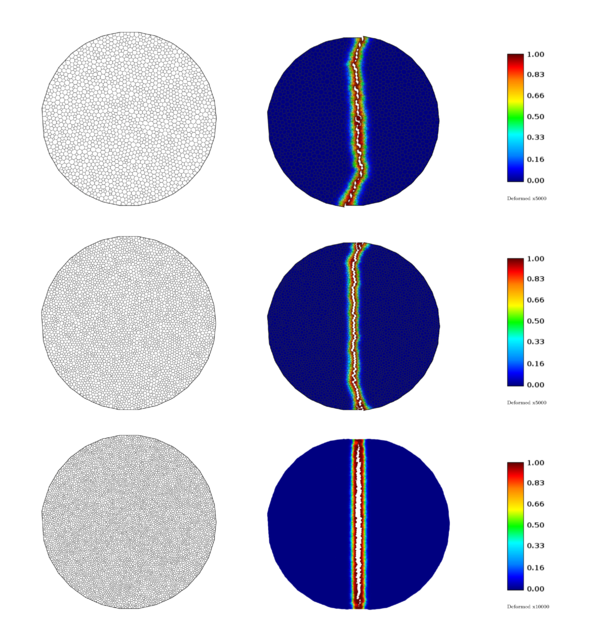
7.3 Perfored strip under tension
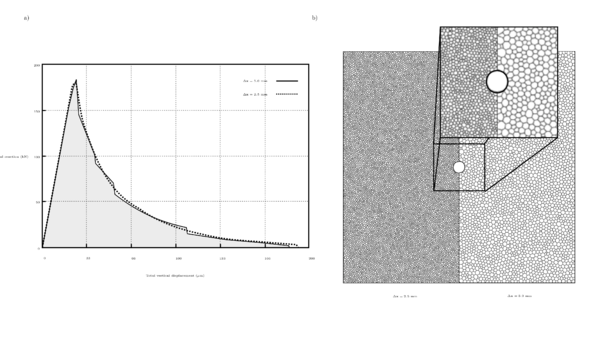
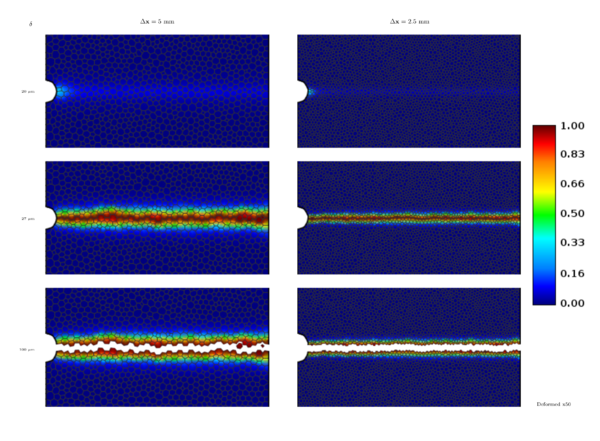
This test involves a perfored strip under tension, the stress field induces a fracture around the perforation because its tensions are greater there than in the rest of the domain. The goal of this experiment is producing a pure mode I failure. The strip is a perfect square of each side and perforation has a radius of . We assume plane stress with thikness = , and perform a quasi-static analysis with 100 finite increments, using a smoothness . Taking advantage of the symmetry we analyze only the right half of the body by imposing symmetry conditions. In the experiment, the strip is pulled apart vertically with an equivalent displacement from top and bottom . The material properties are Young modulus , Poisson's ratio and energy release rate . In order to compare our results to those published by [26], we discretize the strip in two distinct meshes with average size of (12277 volumes) and (3281 volumes). Figure 31 depicts a) the geometrical specifications and material properties, and b) the portion used for numerical analysis, where symmetry conditions were imposed.The numerical experiment is performed in meshes exposed in Figure 32. Fracture location coincides in both meshes, such fracture corresponds to an horizontal line in the middle of the strip. Curves shown in Figure 32 are similar to those published by [26]. The area under curve obtained with mesh size is equal to , whereas that theoretical energy released by fracture is
|
|
(7.7) |
|
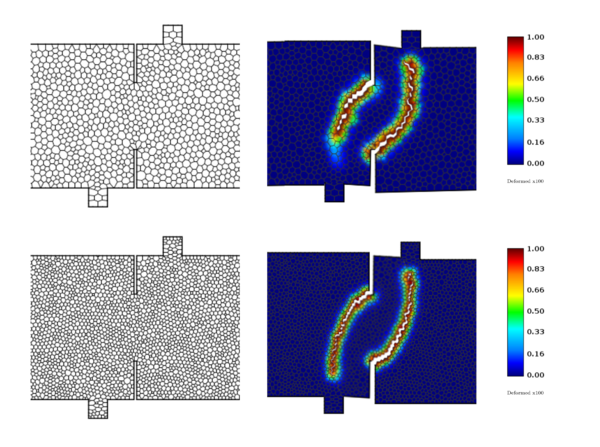
| Figure 33: First column illustrates damage field and discretization for mesh mm with x50 deformation factor, and second column shows same damage field but in discretization of mesh mm |
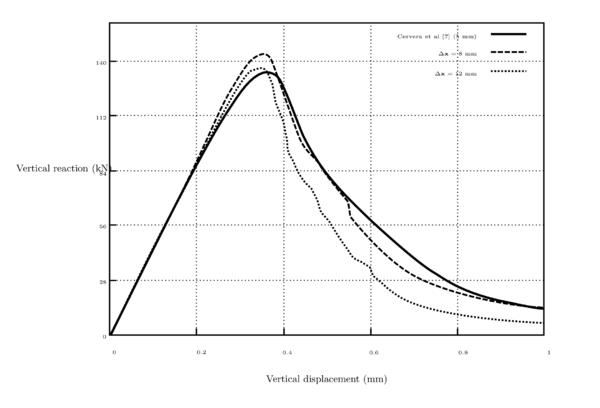
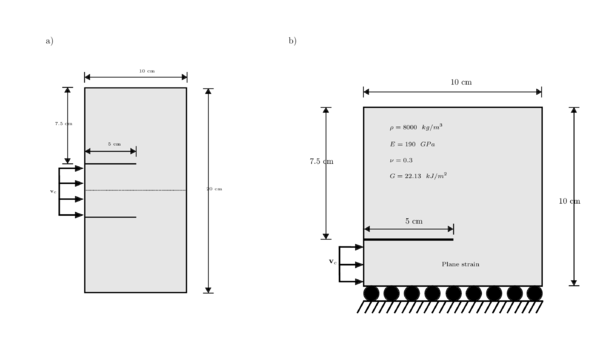
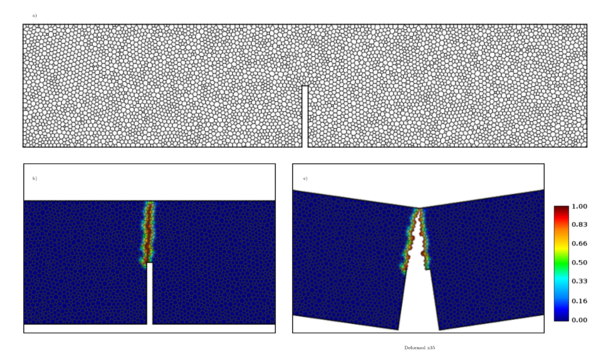
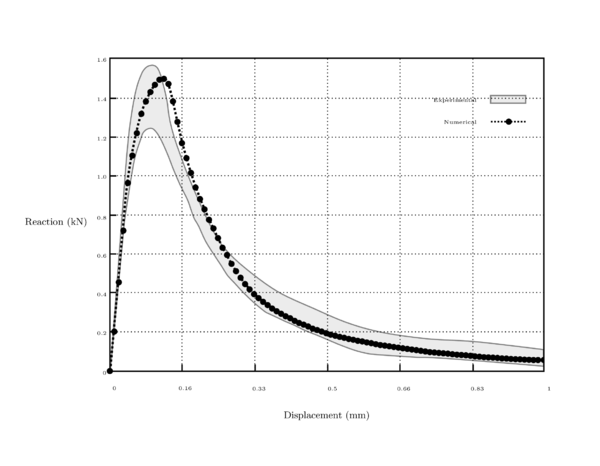
7.4 Three point bending bar
In this example we have a bar with size of long and wide, a vertical notch from center to bottom. The material has elasticity modulus , Poisson's modulus and energy release rate . The bar is vertically displaced, , from top to bottom. Figure 34 depicts geometrical specification, material properties, numerical parameters and boundary conditions.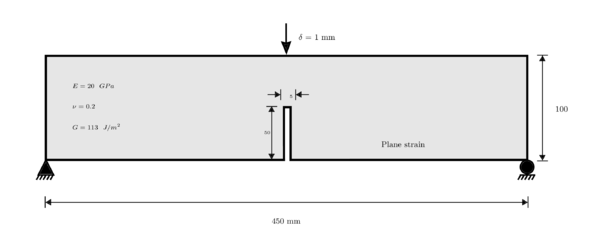
|
| Figure 34: Three point bending bar. Geometrical specification, material properties, numerical parameters and boundary conditions. |
|
| Figure 35: Three point bending bar. a) Partition used in numerical analysis with average size (5297 discrete volumes). b) Damage field and c) Deformation scaled with a factor of x35. |
|
| Figure 36: Three point bending bar. Reaction (load) vs displacement, gray area corresponds to experimental results, whereas that dashed line and black dots are related to numerical analysis. |
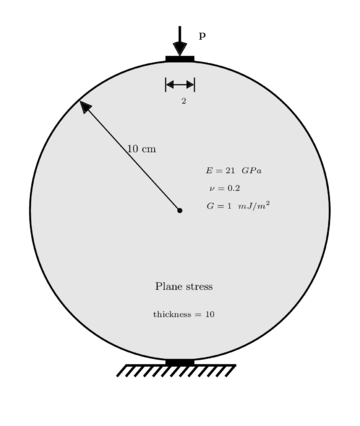
7.5 Brazilian test
The brazilian tensile strength (BTS) test was designed to assess strength of brittle materials [57]. This experiment consists in compressing a disk to generate, by Poisson's effect, indirect tensions to produce a vertical fracture. The disk has a radius of and is fixed to the bottom from a plain side (circular chord) of and is pushed from top to bottom using another plain side in the top of . The material has elasticity modulus , Poisson's ratio , and energy release rate . We assume plane stress with thickness of in a quasi-static analysis using 100 finite increments and smoothness . Within this experiment (see [57]), vertical stress is given by
|
|
(7.8) |
|
| Figure 37: Brazilian test. Geometry is described by a disk with radius and thickness of , assuming plane stress. Material properties and boundary conditions for quasi-static analysis are displayed. |
|
| Figure 38 |
7.6 Four point notched bar
This test is intended to produce a mode II failure and it is selected because its geometry has two initial crack tips at the end of the notches, where stress field has its highest values. The experiment consists in bar with size of long and wide with two vertical notches in the middle, onte from top and one from bottom. The bar is fixed to two boxes of that work as main support, the first one is close to the bottom-right corner, and the second is close to the top-left corner. The bar is pushed from top to bottom by displacing a small box next to the right of the centered upper notch, whereas that a second displaced box (same ) is pushing from bottom to top next to the left of the centered lower-notch. The material properties are elasticity modulus , Poisson's ratio , and energy release rate . Figure 39 depicts geometrical specification, position of notches and supports, material properties, and boundary conditions.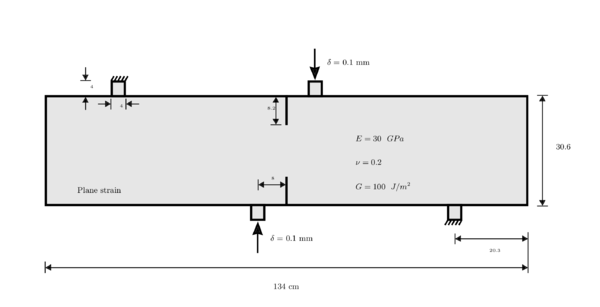
|
| Figure 39: Four point bending bar. Geometry specification, material properties, numerical parameters and boundary conditions. |
7.7 Three point bending bar with asymmetric perforations
The three point bending bar with asymmetric perforations is the classical example of fracture mechanics in brittle materials, this experiment was proposed by [58]. This test consists in a bar with size of long and wide, it has three perforations in left half with radius, these perforations are horizontally aligned and have a vertical separation of . The bar has a vertical notch long in the bottom-left quadrant. Such a bar is fixed from one point close to the bottom-left corner, vertical displacement is forbidden in a point close to the bottom-right corner, and a vertical displacement . Plane stress is assumed, thickness = 1, in a quasi-static analysis using 100 finite increments and smoothness . The material properties are those of PMMA, Polymethyl-methacrylate (also known as acrylic glass or plexiglas). We choose the average Poisson's ratio and according to [58] Young modulus is psi, which corresponds to . For numerical experiments, material properties must be transformed from units based on meters to units based on inches, or when defining the geometry and boundary conditions inches must be transformed to meters. Figure 42 depicts geometrical specifications, material properties and boundary conditions.
|
| Figure 42: Three point bending bar with asymmetric perforations. Geometrical specification, material properties and boundary conditions. |

|
| Figure 43: Three point bending bar with asymmetric perforations. Damage field obtained. |
![Experimental results obtained by Bittencourt et al [58].](/wd/images/thumb/2/2e/Draft_Samper_795975371_5598_monograph-asym_notched_3point_bending_published.png/168px-Draft_Samper_795975371_5598_monograph-asym_notched_3point_bending_published.png)
|
| Figure 44: Experimental results obtained by Bittencourt et al [58]. |
7.8 Notched plate under shear
This test is intended to demonstrate rupture by shear displacement, it consists in plate with an horizontal notch from left side to the center. The plate is fixed from bottom and is displaced from top to the right. The material properties are Young modulus , Poisson's ratio and energy release rate . Numerical analysis is performed assuming plane strain and using 100 finite increments and smoothness . Figure 45 illustrates a) the geometrical specification, material properties and boundary conditions, whereas that b) shows the damage field obtained with displacements scaled 1000.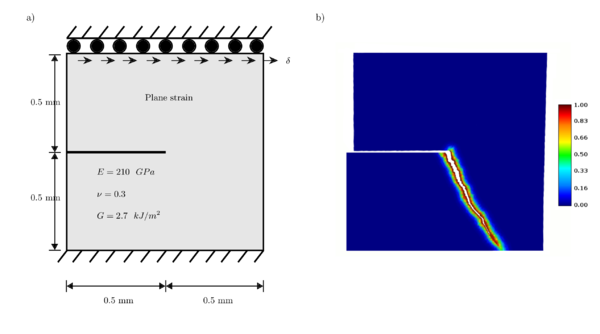
|
| Figure 45: Notched plate under shear, a) the geometrical specification, material properties and boundary conditions, and b) damage field obtained with displacements scaled 1000. |
7.9 Dynamic shear loading
This test consists in a bar with size of height and width, it has to horizontal notches symmetrical to the horizontal line that splits geometry in two halves, these notches goes from left side to central vertical line. Material properties are Young's modulus , Poisson's ratio , density and energy release rate . We simulate a projectile impacting the left side in between the notches at a velocity of
|
|
(7.9) |
|
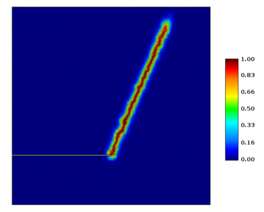
| Figure 47: Damage field obtained in dynamic shear loading test. |
7.10 Dynamic crack branching
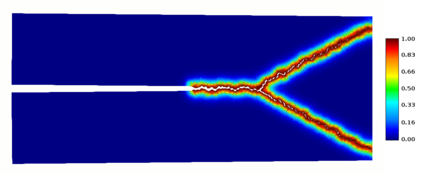
This experiment was proposed by [33] to generate a dynamic crack branching. It consists of a bar with size of long and wide. A horizontal notch is inserted from left side to center to produce an initial crack. Material properties are Young's modulus , Poisson's ratio , density and energy release rate . The bar is being pulled apart from top and bottom with a pressure of . The right side can not be displaced horizontally but it can over the vertical, the middle point of this side is completely fixed. For numerical analysis we assume plane strain using 100 finite increments and smoothness . Although the geometry and boundary conditions are vertically symmetric, we perform the analysis over the whole domain. Figure 48 shows numerical and geometrical specification, material properties and boundary conditions.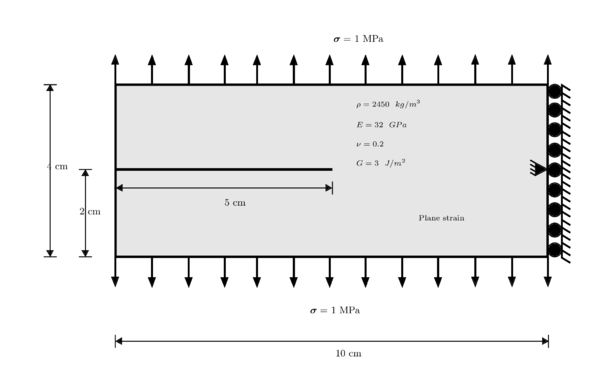
|
| Figure 48: Geometrical specification, numerical parameters, material properties and boundary conditions for dynamic crack branching experiment. |
|
| Figure 49: Damage field obtained int dynamic crack branching experiment. Displacements are scaled up a factor of 1000 |
8 Conclusions
In this work we proposed a numerical technique for simulating the mechanics of brittle fracture by using an alternative definition of the elastic potential energy that involves a damage field to decrease energy due to tensile strain over the fractured surface. Such damage field is a smooth approximation of the crack morphology, with a value of one to describe fractured surfaces and zero for the rest of the elastic body. In the mathematical formulation the total potential energy is determined by the contribution of the elastic potential energy and the potential energy of the body to nucleate new cracks. The elastic potential energy is charaterized by the sum of the elastic energy due to compression plus the elastic energy due to tension, the second term is scaled by a quadratic expression of the damage field, nullifying it when damage is equal to one. The potential energy to generate new cracks is related with the length of the existing cracks and the energy release rate, a material property. A bigger crack increases the potential energy to propagate it. The equations of motion are obtained from the solution of the variational problem for minimizing the Lagrangian of our system, that is, finding the optimal displacement and damage fields for reducing the difference between the potential and the kinetic energy of the body.
The solution of the system is calculated by applying finite increments, with an inner loop within each time step until reaching equilibrium of elasticity equation. That is solving elasticity equation and using the computed displacement field to solve the damage equation, in the next iteration we use damage field estimation to solve again elasticity equation, repeating the process until the residual norm is zero in first equation of motion.
In order to solve the partial differential equations we employ a numerical technique to discretize the body using unstructured and non conforming meshes formed by elements of any arbitrary polygonal/polyhedral shape. The elastic solver is based on a finite volume formulation that, using the divergence theorem, represent the volume integral of the stress divergence in terms of the surface integral of the stress over the volume boundary. Since the stress term is calculated directly on the boundary of the control volumes, this strategy can be used in our fracture formulation where volumes are treated as indivisible components and the rupture occurs across the volumes boundaries. The damage solver follows a similar approach, but considering volume integrals of damage field apart of the surface integral resulting of applying divergence theorem to damage diffusive term. Control volume boundary is divided into flat faces for considering the normal unit vector as a constant. Conforming and non-conforming meshes are processed without distinction. Both fields, displacement and damage, are a piece-wise polynomial approximation surrounding the volumes, built on the top of the simplices resulting from the Delaunay triangulation of the volume neighborhood. A pair-wise polynomial interpolation is used for neighborhoods where the simplices are exceedinlgy distorted or it can not be formed.
On the other hand, time discretization is based on the analytical solution, obtained by means of Laplace transform, of the ordinary differential equation resulting from assuming a continuous variation in time of the stress state.
In spatial discretization, we introduced the homeostatic splines and its pseudo-inverses for higher order polynomial interpolations without the necessity of increasing the discretization points, but adding a computational cost for numerical integration. The rate of increasing computational cost is greater than the rate of decreasing numerical error when choosing high degree homeostatic splines. This situation makes computationally expensive smoothness of solution at nodes.
In time discretization, we propose a trigonometric shape function to describe time variation of stress state, which produces an energy-stable numerical scheme and tolerates bigger time steps than methods based on simply finite differences. Leaving aside the stability of the method, choosing big time steps will increase the number of iterations of the finite increments strategy performed in every time step. In the results presented here we use a Courant number of 0.05 as a reasonable trade-off.
Finally we present numerical experiments for the well known plate with a hole to compare our elasticity solver against analytical solution, stress wave in a bar to compare our dynamic solver against published results, perfored strip under tension for checking fracture due to direct tension, three point bending bar test to compare our solver with lab experiments of fracture due to tensile strain, brazilian test to analyze fracture due to indirect tensile strain comparing our results against published by other authors, a compressive test to verify cracking patterns against those produced with similar numerical methods, four point notched bar test for analyzing fracture mode II, three point bending bar with asymmetric perforations to evaluate sensibility of crack morphology, notched plate under shear to contrast our results with those of other authors, dynamic shear loading, and dynamic crack branching to demonstrate multicrack generation.
In future work, we would like to analize numerical results of 3D tests, to explore adaptable meshes in order refine elements if damage is likely to occur, and to investigate the response of the system to shock wave impacts, such as those produced by detonations. Furthermore, it is possible to track position and stress state of each discrete volume and we would like to develop a contact interface for interacting with classical Discrete Element formulations. We also would like to develop a similar mathematical formulation for topology optimization problems, by redefining the elastic potential energy in terms of a solidification field that predicts the optimal shape of an elastic body to the given boundary conditions.
Appendix A. Analytical solution for time
In order to get an accurate approximation of the temporal derivative in the interval , we replace the stress state function of time into the differential equation (5.2),
|
|
(A.1) |
stress function is defined in equation (5.4). Reordering terms we have
|
|
(A.2) |
with initial conditions
|
|
(A.3) |
In order to solve (A.2) by means of Laplace Transform
|
|
(A.4) |
we change from time domain in equation (A.2) to frequency domain
|
|
(A.5) |
where is the frequency variable, is the Laplace transform of ,
|
|
(A.6) |
and the Laplace transform of acceleration term includes initial conditions (A.3)
|
|
(A.7) |
We can rewrite equation (A.5) as
|
|
(A.8) |
and applying the inverse Laplace transform, , we obtain
|
|
(A.9) |
where is a convolution. Such convolution is defined as
|
|
(A.10) |
and it derivative is
|
|
(A.11) |
where is the integration variable. Developing previous definitions we get
|
Finally, analytical solution of (A.2) is equation (A.9) and it is completely dependent of the shape function . This solution is used for building an accurate numerical squeme for discretizing time.
Appendix B. Polynomial shape functions for time
The analytical solution (5.11) of equation (5.2) is used to generate numerical schemes for time discretization, these approximations has a similar structure but distinct coefficients that depend on the shape function used for time variation of stress state. In this appendix we propose two families of polynomial functions in order to get a continuous stress state in contiguous time steps, such polynomial functions meet the condition of for producing stable schemes in terms of total energy.
The first polynomial family is defined by
|
|
(B.1) |
where is the polynomial order. The first three functions generated by this equation are shown in Table 2 and Figure 50 depicts the curves.
| Shape function | Convolution | |
| 1 | ||
| 2 | ||
| 3 |
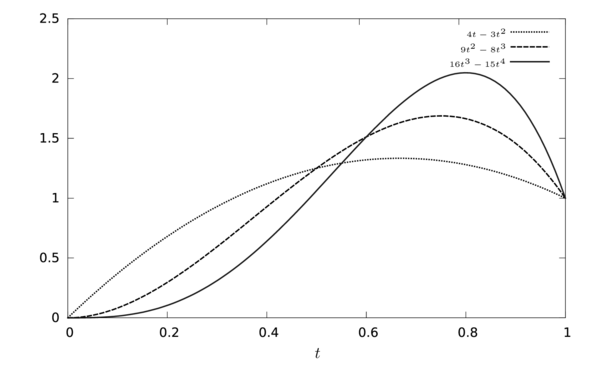
|
| Figure 50: Curves for first few polynomials generated with equation (B.1) |
The second polynomial family is given by
|
|
(B.2) |
where is the polynomial order. The first few functions generated by this equation are shown in Table 3 and Figure 51 depicts the curves.
| Shape function | Convolution | |
| 1 | ||
| 2 |
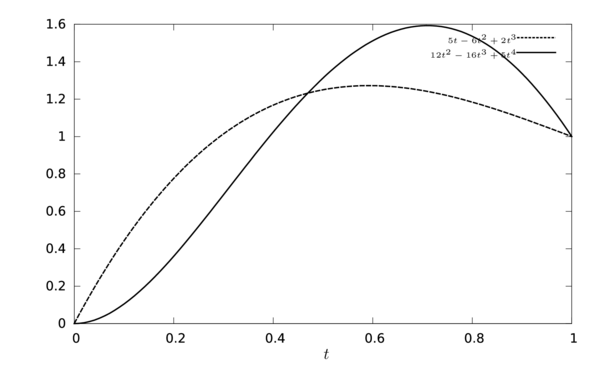
|
| Figure 51: Curves for first few polynomials generated with equation (B.2) |
Bibliography
[1] A.K. Slone and K. Pericleous and C. Bailey and M. Cross. (2002) Dynamic fluid-structure interaction using finite volume unstructured mesh procedures, Volume 80. Elsevier. Computers and Structures 371-390
[2] A.K. Slone and K. Pericleous and C. Bailey and M. Cross and C. Bennett. (2004) A finite volume unstructured mesh approach to dynamic fluid-structure interaction: an assessment of the challenge of predicting the onset flutter, Volume 28. Elsevier. Applied Mathematical Modeling 211-239
[3] C. Bailey and G. A. Taylor and M. Cross and P. Chow. (1999) Discretisation procedures for multi-physics phenomena, Volume 103. Elsevier. Journal of Computational and Applied Mathematics 3-17
[4] M. Souli and A. Ouahsine and L. Lewin. (2000) ALE formulation for fluid-structure interaction problems, Volume 190. Elsevier. Computer Methods in Applied Mechanics and Engineering 659-675
[5] J. Lubliner and J. Oliver and S. Oller and E. Oñate. (1989) A Plastic-Damage model for concrete, Volume 25. Elsevier. International Journal of Solids and Structures 299-326
[6] Francisco Armero and S. Oller. (2000) A general framework for continuum damage models. I. Infinitesimal plastic damage models in stress space, Volume 37. Elsevier. International Journal of Solids and Structures 7409-7436
[7] E. Oñate and M. Cervera and C. Zienkiewicz. (1994) A finite volume format for structural mechanics, Volume 37. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering 181-201
[8] S. R. Idelsohn and E. Oñate. (1994) Finite volumes and finite elements: Two 'Good Friends', Volume 37. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering 3323-3341
[9] Y. D. Fryer and C. Bailey and M. Cross and C. H. Lai. (1991) A control volume procedure for solving the elastic stress-strain equations on an unstructured mesh, Volume 15. Elsevier. Applied Mathematical Modeling 639-645
[10] C. Bailey and M. Cross. (1995) A Finite Volume procedure to solve elastic solid mechanics problems in three dimensions on an unstructured mesh, Volume 38. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering 1757-1776
[11] A. K. Slone and C. Bailey and M. Cross. (2003) Dynamic solid mechanics using finite volume methods. Elsevier. Applied Mathematical Modeling 69-87
[12] I. Demirdzic and D. Martinovic. (1993) Finite volume method for thermo-elasto-plastic stress analysis, Volume 109. Elsevier. Computer Methods in Applied Mechanics and Engineering 331-349
[13] I. Demirdzic and S. Muzaferija. (1994) Finite volume methods for stress analysis in complex domains, Volume 137. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering 3751-3766
[14] I. Demirdzic and S. Muzaferija and M. Peric. (1997) Benchmark solutions of some structural analysis problems using finite-volume method and multigrid acceleration, Volume 40. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering 1893-1908
[15] I. Bijelonja and I Demirdzic and S. Muzaferija. (2005) A finite volume method for large strain analysis of incompressible hyperelastic materials, Volume 64. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering 1594-1609
[16] I. Bijelonja and I. Demirdzic and S. Muzaferija. (2006) A finite volume method for incompressible linear elasticity, Volume 195. Elsevier. Computer Methods in Applied Mechanics and Engineering 6378-6390
[17] H. Jasak and H. G. Weller. (2000) Application of the finite volume method and unstructured meshes to linear elasticity, Volume 48. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering 267-287
[18] Z. Tukovic and A. Ivankovic and A. Karac. (2012) Finite-volume stress analysis in multi-material linear elastic body. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering
[19] Tian Tang and Ole Hededal and Philip Cardiff. (2015) On finite volume method implementation of poro-elasto-plasticity soil model. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering
[20] M. J. Borden and C. V. Verhoosel and M. Scott and T. J. R. Hughes and C. M. Landis. (2012) A phase-field description of dynamic brittle fracture. Elsevier. Computer Methods in Applied Mechanics and Engineering 217-220
[21] P. Cardiff and Z. Tukovic and H. Jasak and A. Ivankovic. (2016) A block-coupled Finite Volume methodology for linear elasticity and unstructured meshes. Elsevier. Computers and Structures 100-122
[22] Marcio A. A. Cavalcante and Marek-Jerzy Pindera. (2012) Generalized Finite-Volume Theory for Elastic Stress Analysis in Solid Mechanics - Part I: Framework. The American Society of Mechanical Engineers. Journal of Applied Mechanics
[23] Jan Martin Nordbotten. (2014) Cell-centered finite volume discretizations for deformable porous media. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering
[24] B. Li and Z. Chen and G. Huan. (2003) Control volume function approximation methods and their applications to modeling porous media flow. Elsevier. Advances in water resources 435-444
[25] B. Li and Z. Chen and G. Huan. (2004) Control volume function approximation methods and their applications to modeling porous media flow II: the black oil model. Elsevier. Advances in water resources 99-120
[26] M. Cervera and M. Chiumenti. (2006) Mesh objective tensile cracking via a local continuum damage model and a crack tracking technique. Elsevier. Computer Methods in Applied Mechanics and Engineering
[27] M. Cervera and L. Pela and R. Clemente and P. Roca. (2010) A crack-tracking technique for localized damage in quasi-brittle materials. Elsevier. Engineering Fracture Mechanics
[28] M. Cervera and M. Chiumenti and R. Codina. (2011) Mesh objective modeling of cracks using continuous linear strain and displacement interpolations. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering
[29] A. D. Hanganu and E. Oñate and A. H. Barbat. (2002) A finite element methodology for local/global damage evaluation in civil engineering structures. Elsevier. Computers and Structures 1667-1687
[30] E. Oñate. (2000) Desarrollos y aplicaciones de modelos de fractura en la escuela de ingenieros de caminos de barcelona. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Universidad Politécnica de Catalunya
[31] E. Oñate and J. Rojek. (2004) Combination of discrete element and finite element methods for dynamic analysis of geomechanics problems. Elsevier. Computer Methods in Applied Mechanics and Engineering 3087-3128
[32] C. Miehe and M. Hofacker and F. Welschinger. (2010) A phase field model for rate independent crack propagation: robust algorithmic implementation based on operator splits. Elsevier. Computer Methods in Applied Mechanics and Engineering
[33] C. Miehe and M. Hofacker and F. Welschinger. (2010) Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Elsevier. Computer Methods in Applied Mechanics and Engineering
[34] J. Hoon Song and H. Wang and T. Belytschko. (2007) A comparative study on finite element methods for dynamic fracture. Computational Mechanics
[35] N. Moes and T. Belytschko. (2002) Extended finite element method for cohesive crack growth. Elsevier. Engineering Fracture Mechanics 813-833
[36] G. Zi and T. Belytschko. (2003) New crack-tip elements for XFEM and applications to cohesive cracks. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering 2221-2240
[37] L. Mishnaevsky and S. Shmauder. (1998) FE-simulation of crack growth using a damage parameter and the cohesive zone concept. In ECF 12- Fracture from defects, Proc. 12th European Conference on Fracture. London, EMAS 2, 1053-1059.
[38] L. Mishnaevsky and N. Lippmann and S. Shmauder. (2003) Computational modeling of crack propagation in real microstructures of steels and virtual testing of artificially designed materials. International Journal of Fracture
[39] P. Cundall and O. Strack. (1979) A discrete numerical method for granular assemblies, Volume 1. Geotechniques 47-65
[40] J. Rojek and F. Zarate and C. Agelet and C. Gilbourne and P. Verdot. (2004) Discrete element modelling and simulation of sand mould manufacture for the lost foam process. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering
[41] O. C. Zienkiewicz and R. L. Taylor. (2005) The Finite Element Method. For Solid and Structural Mechanics. Elsevier
[42] J.P. Morris and M.B. Rubin and G.I. Blocka and M.P. Bonnera. (2006) Simulations of fracture and fragmentation of geologic materials using combined FEM/DEM analysis. International Journal of Impact Engineering 463-473
[43] A. Munjiza. (2004) The combined finite-discrete element-method. John Wiley & sons
[44] D. Potyondy and P. Cundall. (2004) A bonded-particle model for rock. Elsevier. International Journal of rock mechanics and mining sciences 1329-1364
[45] J. Rojek and E. Oñate. (2007) Multiscale analysis using a coupled discrete/finite element model. Interaction and Multiscale Mechanics
[46] E. Oñate and C. Labra and F. Zárate and J. Rojek. (2012) Modelling and simulation of the effect of blast loading on structures using an adaptive blending of discrete and finite element methods. Taylor & Francis group. Risk Analysis, Dam Safety, Dam Security and Critical Infrastructure Management
[47] Francisco Zárate and Eugenio Oñate. (2015) A simple FEM-DEM technique for fracture prediction in materials and structures, Volume 2. Springer. Computational Particle Mechanics 301-314
[48] E. B. Tadmor and M. Ortiz and R. Phillips. (1996) Quasicontinuum analysis of defects in solids, Volume 73. Philosophical Magazine A. 1529-1563
[49] E. B. Tadmor and Rob Phillips. (1996) Mixed Atomistic and Continuum Models of Deformation in Solids, Volume 12. Americal Chemical Society 4529-4534
[50] Gregory J. Wagner and W. K. Liu. (2003) Coupling of Atomistic and Continuum Simulations using a Bridging Scale Decomposition. Journal of Computational Physics
[51] S.P. Xiao and T. Belytschko. (2004) A bridging domain method for coupling continua with molecular dynamics. Computer Methods in Applied Mechanics and Engineering
[52] Mei Xu and Ted Belytschko. (2004) Conservation properties of the bridging domain method for coupled molecular/continuum dynamics. John Wiley & Sons, Ltd. International Journal for Numerical Methods in Engineering
[53] Z. Chen and G. Huan and B. Li. (2003) Modeling 2D and 3D horizontal wells using CVFA. Comm. Math. Sci.
[54] Richard Lipton and Donald Rose and Robert Endre Tarjan. (1979) Generalized nested dissection, Volume 16. SIAM. Journal on Numerical Analysis 346-358
[55] S. P. Timoshenko and J. N. Goodier. (1970) Theory of Elasticity. McGraw-Hill, 3 Edition
[56] Jan Gerrit Rots. (1988) Computational Modeling of Concrete Fracture. Technische Universiteit Delft
[57] Jose Rafael Capua Proveti and Gerard Michot. (2006) The Brazilian test: a tool for measuring the toughness of a material and its brittle to ductile transition. International Journal of Fracture 455-460
[58] T. N. Bittencourt. (1996) Quasi-automatic simulation of crack propagation for 2D LEFM problems, Volume 55. Elsevier. Engineering Fracture Mechanics 321-334
Document information
Published on 31/05/19
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?
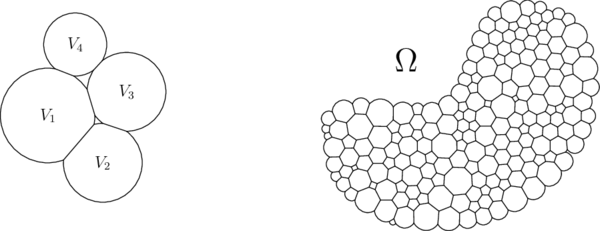

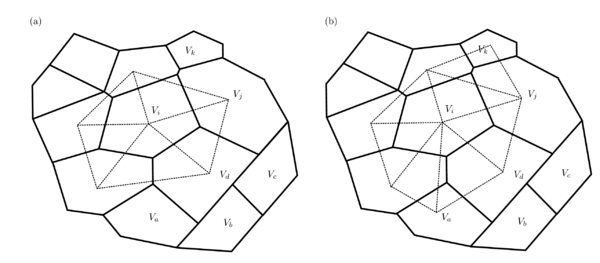
![(a) Blue shaded volume Vi is being integrated. The integral over the subface eijk is calculated using the polynomial approximation of shaded simplex. The integration point must be mapped to (b) Normalized space [-1,1] in order to use the Gauss- Legendre quadrature.](/wd/images/thumb/2/2f/Draft_Samper_795975371_1088_monograph-picture-2d816e.png/600px-Draft_Samper_795975371_1088_monograph-picture-2d816e.png)
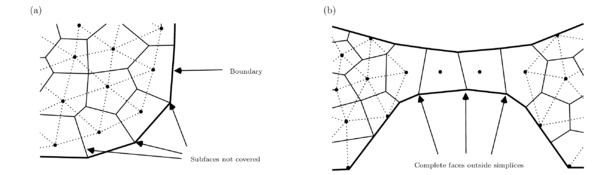
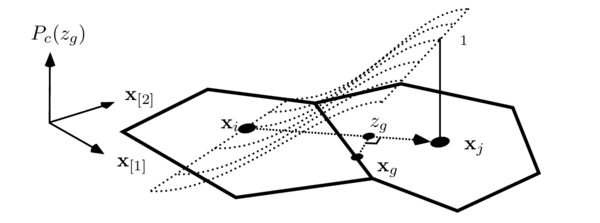
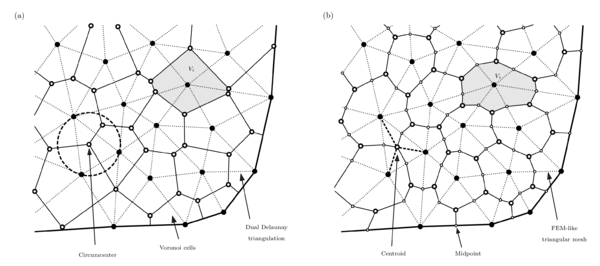
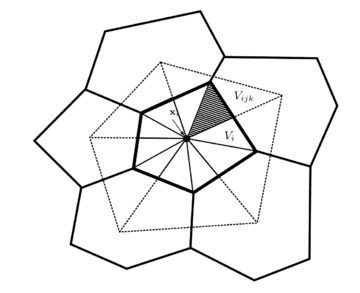
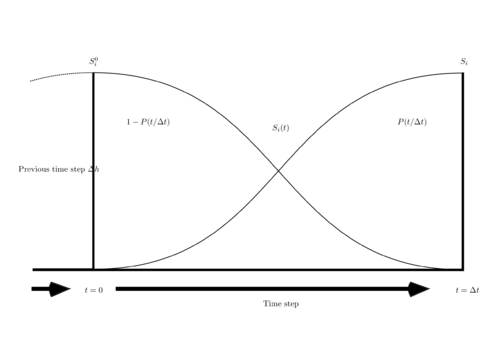
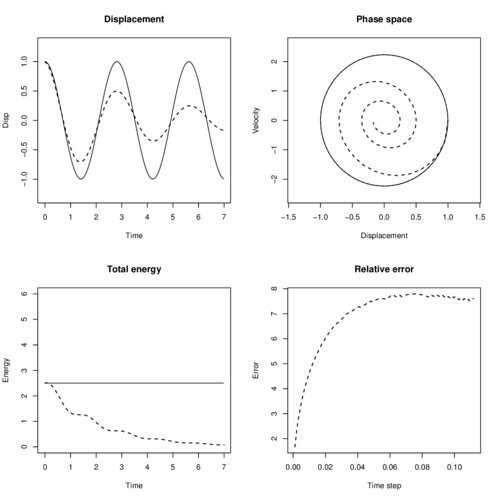
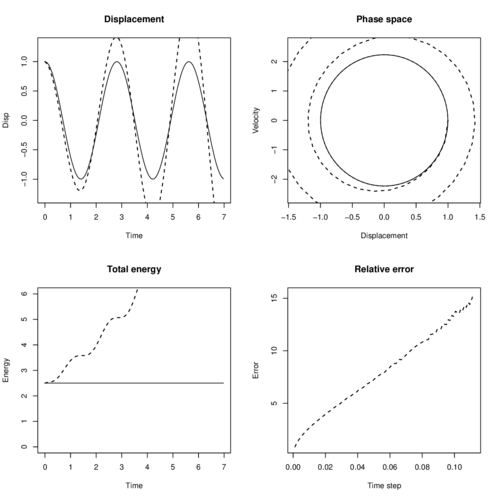
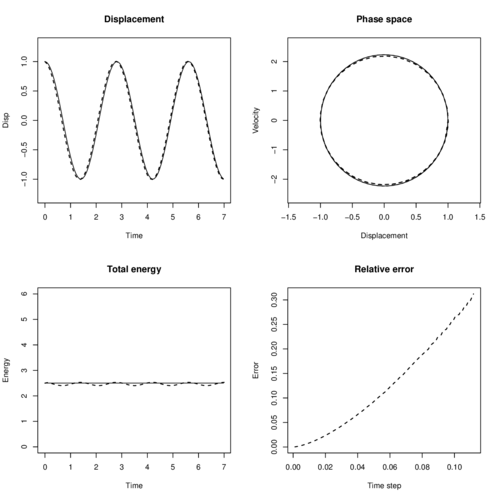
![(a) Infinite plate with a hole being stretched along the horizontal axis with a force of f[1]=10 ~~kPa from each side. (b) Computational domain, a= 0.5m and b=2m, with axysymmetrical assumptions used to test the numerical method. The polar coordinates, r and θ, for calculating the analytical stress field.](/wd/images/thumb/9/94/Draft_Samper_795975371_3611_monograph-picture-a9059f.png/600px-Draft_Samper_795975371_3611_monograph-picture-a9059f.png)