Resumen
Cuando una estructura de hormigón armado queda expuesta a la acción del fuego se producen, tanto en el hormigón como en el acero, un conjunto de fenómenos físico-químicos que pueden comprometer la estabilidad de la misma. Entre los procesos más importantes destaca el de eclosión (spalling). Se considera que las posibles causas del spalling pueden ser un elevado crecimiento de la presión en los poros (spalling hidráulico) o un exagerado aumento de las tensiones de compresión debidas a la dilatación térmica restringida. Para poder tener en cuenta en el análisis el spalling hidráulico es necesario considerar un modelo que tenga en cuenta la componente hídrica del hormigón.
En esta monografía se presenta un modelo higro-termo-mecánico que permite representar el comportamiento general del hormigón armado expuesto a elevadas temperaturas y en particular simular el fenómeno de spalling.
Se parte de proponer un marco termodinámico consistente a partir del cual se derivan las variables de estado que se utilizan posteriormente para el desarrollo de las ecuaciones de gobierno del problema. Asimismo se proponen modelos constitutivos para el comportamiento mecánico del hormigón y del acero.
Una vez establecidos las ecuaciones de gobierno del problema se describen los aspectos numéricos para su resolución. Para la integración espacial del problema se utiliza el Método del los Elementos Finitos y para la integración temporal el Método de Diferencias Finitas. Se propone un esquema iterativo en bloque para el tratamiento del acoplamiento. Se ha desarrollado un programa de cálculo diseñado especialmente para materializar la metodología numérica propuesta en esta monografía.
Para la validación del modelo propuesto se presentan ejemplos en los que se comparan los resultados obtenidos numéricamente con resultados experimentales.
Finalmente, se presentan un conjunto de ejemplos que muestran la capacidad del modelo propuesto para captar el comportamiento general de una estructura de hormigón armado expuesta al fuego y en especial el fenómeno de spalling.
Capítulo 1 Introducción
1-1 Generalidades
Un fuego no deseado es una fuerza destructiva que causa cada año muchas pérdidas de vidas humanas y enormes pérdidas de bienes materiales. Las personas en cualquier lugar del mundo desean que sus hogares y lugares de trabajo sean lo suficientemente seguras al efecto destructivo del fuego. Desafortunadamente, pueden ocurrir incendios en cualquier tipo de construcción en el momento menos esperado.
Desde 1922 se vienen realizando investigaciones sobre el efecto del fuego sobre el hormigón y las estructuras de hormigón. Hasta hace aproximadamente una década, las investigaciones se concentraban en el comportamiento de hormigones de resistencias normales y los ingenieros empleaban principalmente métodos prescriptivos de diseño para asegurar la estabilidad estructural frente al fuego por un periodo suficiente de tiempo que permita a las personas abandonar el edificio y permitir al servicio de bomberos extinguir el fuego. Desde entonces, ha habido dos grandes desarrollos en la tecnología del hormigón:
1-) El creciente uso de nuevos tipos de hormigones, tales como, los hormigones autocompactantes y hormigones de alta resistencia en edificios, túneles y puentes, han permitido el diseño de estructuras cada vez más esbeltas, cuya microestructura, mucho más compacta que los hormigones convencionales, modifica el comportamiento al fuego desfavorablemente.
2-) La progresiva aceptación de la evaluación del comportamiento y diseño de las estructuras basándose en cálculos de ingeniería.
Las estructuras de hormigón tienen la reputación de tener un buen comportamiento frente al fuego. Un gran número de edificios de hormigón que han sufrido graves incendios han sido perfectamente reparados y puestos nuevamente en servicio. El hormigón posee un conjunto de propiedades que le confieren una excelente resistencia al fuego en comparación con otros materiales como el acero. Entre las propiedades más importantes del hormigón se pueden citar:
- Material no combustible.
- Baja conductividad térmica.
- La pasta de cemento en el hormigón genera, cuando se calienta, una reacción endotérmica reduciendo de esta manera el aumento de temperatura.
- La humedad contenida en el hormigón genera al evaporarse una reacción endotérmica, reduciendo también el aumento de temperatura.
A nivel estructural, la necesidad de desarrollo de nuevos métodos de evaluación para el ingeniero surge de la limitación inherente en los tradicionales métodos prescriptivos. Varios países ya han desarrollados códigos basados en las prestaciones (Reino Unido, Suecia, Noruega, Nueva Zelanda y Australia) y otros países están en proceso de conseguirlo. Este nuevo planteamiento permite al ingeniero aportar ideas innovadoras en aras de mejorar la seguridad estructural ante el fuego.
La respuesta del hormigón como material y como estructura frente a un fuego real depende de la naturaleza del fuego que puede ser muy variable. La característica principal de la acción del fuego sobre una estructura de hormigón es la curva temperatura-tiempo impuesta sobre su superficie. Los parámetros más relevantes de dicha curva son:
- La velocidad de calentamiento influye en el desarrollo de gradientes de temperatura, humedad y presión de poros. Esta tasa de calentamiento se ve aumentada en el caso de aparición de llamaradas.
- El nivel máximo de temperatura influye en la naturaleza de los cambios físico-químicos que se dan en el material y a partir de estos en sus propiedades.
- La duración del fuego influye en el desarrollo de temperatura dentro de la masa de hormigón.
- El proceso de enfriado tiene un efecto distinto sobre el material dependiendo si se trata de un enfriamiento con agua o natural.
1-2 Escenarios de fuego
Cuando se evalúa la resistencia al fuego de una estructura de hormigón, independientemente del método de evaluación adoptado (experimental o teórico), el primer paso es el modelado del fuego real por medio de un escenario de fuego realista y conservador. Dichos modelos se pueden clasificar en tres categorías:
a-) Curva nominal de fuego
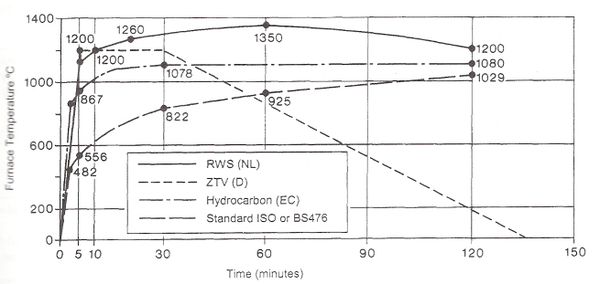
Las curvas nominales idealizan fuegos que no tienen en cuenta factores como la distribución de la temperatura o la cantidad de material combustible, sino que por el contrario, consideran una temperatura de gas uniforme en cada compartimiento expuesto al fuego. Estas curvas fueron establecidas a partir de la experiencia en fuegos reales y se enmarcab en tres categorías dependiendo de la aplicación: Edificios, plataformás offshore y petroquímicas, túneles. En el caso de edificios la curva nominal más utilizada a efectos de evaluar la resistencia al fuego de estructuras es la curva de fuego ISO 834 (ISO 834, 1975). La Figura 1-1 presenta algunos ejemplos de curvas nominales.
b-) Curvas paramétricas en edificios o fuegos “naturales”
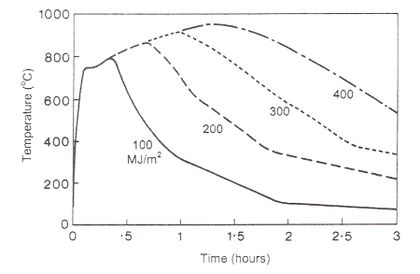
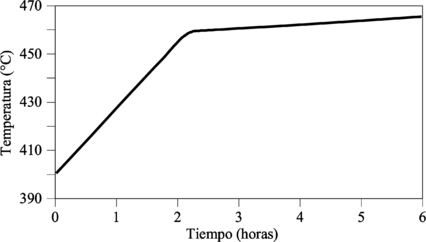
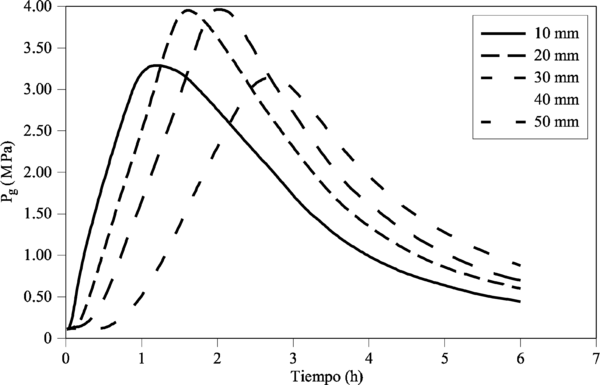
Las curvas de fuego paramétricas describen un completo conjunto de curvas tiempo-temperatura para diferentes cargas y factores de abertura. Al igual que la anterior sigue considerando una temperatura de gas uniforme en el compartimento sometido al fuego pero tienen en cuenta otros factores como la cantidad y tipo de combustibles, ventilación, inercia térmica de las paredes y pisos, etc. Estas curvas tienen tanto una rama de calentamiento como de enfriamiento. A pesar de constituir una mejora respecto de las curvas de fuego nominales, no son muy prácticas para su utilización experimental en hornos de calentamiento. El elemento más difícil de controlar es la rama de enfriamiento. Por otro lado las curvas paramétricas son muy apropiadas para el cálculo. Dichas curvas mejoran la precisión en la predicción del comportamiento respecto de las curvas nominales. En la Figura 1-2 se representan ejemplos de este tipo de curvas.
c-) Modelos multi-zona y CFD
Los modelos multi-zona y de mecánica de fluidos computacional (CFD) son los más avanzados. Estos modelos resuelven las ecuaciones de conservación de energía y masa para cada zona o elemento. Estos modelos se utilizan principalmente con fines de investigación. Los modelos de dos-zonas se utilizan en varios países (Luxemburgo, Francia, Suecia) en las etapas de diseño y asumen una temperatura constante en la capa de humo mientras que los modelos CFD simulan un escenario más realista de variación espacial de la temperatura aunque difícilmente se utilizan para evaluar el impacto del fuego sobre los elementos estructurales.
1-3 Evaluación de la respuesta al fuego
1-3-1 Antecedentes
La base de la mayor parte de la legislación actual, en materia de evaluación de la respuesta al fuego, es el tradicional ensayo al fuego estándar, en el cual un elemento constructivo separado del entorno del edificio, es colocado en un horno y expuesto a un fuego estándar prescrito (ISO 834). Se establecen los requerimientos que dicho elemento constructivo debe cumplir, para soportar esta carga térmica por un cierto período de tiempo. Dicho tiempo se estima de manera más o menos arbitraria en relación al tiempo necesitado por las personas para escapar del edificio. En primer lugar, estos requerimientos se establecen a efectos de garantizar la seguridad de los ocupantes, los vecinos y la brigada de bomberos. En segundo lugar se establecen requerimientos para proteger las inversiones o minimizar pérdidas económicas.
Es claramente aparente, que la mayoría de los códigos de edificación existentes son predominantemente de naturaleza prescriptiva, o sea, que los códigos prescriben soluciones o dan herramientas analíticas para verificar que la solución propuesta cumple con los requerimientos. Además, la mayoría de la legislación está basada en el concepto de prevención, el cual se materializa estableciendo los requerimientos para que el fuego se mantenga dentro del compartimiento donde comenzó por un período de tiempo suficientemente largo. Este período de tiempo se expresa comúnmente en minutos y se incrementa a intervalos de 30 minutos, cubriendo desde 30 a 120 minutos.
El rápido calentamiento resultante del fuego puede causar grandes variaciones volumétricas debidos a dilataciones térmicas, así como retracción térmica y fluencia lenta asociadas con la pérdida de humedad. Estos cambios de volumen, sumados a la degradación de las propiedades mecánicas, pueden generar grandes tensiones internas que conduzcan tanto a la creación de fisuras como a la de grandes fracturas. En algunas situaciones cuando el calentamiento por fuego es particularmente rápido, puede ocurrir el llamado fenómeno de spalling explosivo del hormigón. El spalling explosivo puede dar lugar a una significativa pérdida de sección de hormigón. El ingeniero proyectista debe asegurar que todos estos factores combinados no afecten a la estructura en sus funciones de separación y de capacidad portante por un cierto periodo de tiempo.
En cuanto a las funciones de separación de la estructura deben valorarse dos criterios: integridad y aislamiento. El criterio de integridad establece ciertos valores límites para asegurar que la estructura no permita la penetración de llamás o de gases calientes a través de brechas o fisuras. El criterio de aislamiento establece valores límites para el aumento de temperatura en el lado no expuesto de una estructura sometida a un fuego nominal: 140°C en promedio y 180°C en picos locales.
En cuanto a las funciones de capacidad portante, está simplemente limitada por el colapso bajo la carga aplicada. Todos los modos de fallo relevantes tales como: fallo por flexión, fallo por cortante, fallo por pandeo y fallo por anclaje, deben ser evaluados.
1-3-2 Niveles de evaluación estructural
De acuerdo con el Eurocódigo 2, una estructura puede evaluarse en tres niveles dependiendo de su creciente complejidad y tamaño:
a-) Evaluación de un miembro aislado
Si la resistencia al fuego es establecida en forma experimental, generalmente se analizan elementos aislados debido a las limitaciones de tamaño de los hornos de ensayo. Uno de los inconvenientes de este tipo de evaluación es la apropiada elección de las condiciones de contorno a colocar en dichos elementos aislados.
b-) Evaluación de una subestructura
Una manera de resolver el problema de la determinación de las condiciones de contorno apropiadas es analizar una subestructura. El Eurocódigo 2 establece que la estructura global debería ser dividida en subestructuras de manera tal que la interacción de las deformaciones térmicas durante el fuego pueda ser aproximada por apoyos y condiciones de contorno independientes del tiempo. Si bien el análisis de una subestructura es más exacto que el análisis de un simple elemento, la determinación de la subdivisión no es una tarea trivial.
c-) Evaluación de la estructural global
El método más exacto de predicción de la respuesta estructural es a través de la evaluación de la estructura completa por un ensayo a escala completa o por modelado. Los efectos de redistribución de esfuerzos y de restricción a las expansiones térmicas se tienen en cuenta. La principal desventaja de este tipo de análisis es, obviamente, su complejidad y elevado costo.
1-3-3 Métodos de evaluación de la resistencia al fuego
La resistencia al fuego de estructuras de hormigón puede evaluarse por medio de los cuatro métodos siguientes:
a-) Ensayos estándar de fuego
El ensayo al fuego de un elemento estructural o de una subestructura representa la opción más cara en comparación con métodos de cálculo o de datos tabulados. Este tipo de ensayos usualmente se restringen al análisis de elementos aislados con dimensiones tales que permitan utilizar los hornos de calentamiento disponibles. De esta manera surge el problema de la correcta determinación de las condiciones de contorno a efectos de que el elemento estructural ensayado en forma aislada pueda reproducir su situación real dentro de la estructura global. Por otro lado la exactitud del ensayo es muy sensible a los dispositivos experimentales y los métodos utilizados, por lo que existe un gran esfuerzo por parte de los comités internacionales de diferentes países para armonizar los ensayos de laboratorio
Asimismo pueden realizarse ensayos a gran escala, pero tal como se comentó anteriormente son de un costo y complejidad tan elevados que raramente se realizan.
b-) Datos tabulados
La práctica de ingeniería actual se basa en la aplicación de códigos de datos tabulados en los que el ingeniero diseña en función de unos requerimientos predeterminados basados en los tipos de ocupación y riesgo al fuego. Este tipo de método de evaluación a pesar de ser muy sencillo de aplicar es el menos exacto comparado con otros métodos analíticos, de manera tal que el nivel de seguridad obtenido puede variar significativamente. Los requerimientos de resistencia al fuego se establecen en función del comportamiento de elementos estructurales expuestos a un fuego estándar ISO 834. Esto significa que un elemento estructural debería ser diseñado para resistir 30, 60, 90 o 120 minutos. Sin haber clases intermedias. En consecuencia, si un elemento resiste hasta 59 minutos de exposición debe catalogarse como de tipo R30 de resistencia al fuego.
En particular el Eurocódigo 2 proporciona tablas especificando dimensiones mínimás y distancias al eje de la armadura para resistencias al fuego que van desde media hora a cuatro horas para vigas, columnas y losas. Los datos también distinguen si se trata de construcciones simplemente apoyadas o continuas en elementos trabajando a flexión.
c-) Cálculos simplificados
La distribución de temperatura en un elemento estructural expuesto al fuego puede conocerse a partir de datos de la literatura para casos similares o por medio de un análisis térmico. Una vez conocida dicha distribución se puede realizar un análisis simplificado utilizando la propuesta primeramente introducida por Anderberg (Anderberg, 1976) y actualmente presentada en el Eurocódigo 2. En dicho método se propone que el espesor del hormigón de árido silíceo dañado corresponde con la profundidad de la isoterma de 500°C en la zona de compresión de la sección transversal. Para otros tipos de áridos deben utilizarse otro valor para la isoterma. Se considera que el hormigón dañado (o sea que superan la temperatura crítica de 500°C) no contribuyen a resistir tensiones y que la parte restante de la sección transversal conserva las propiedades mecánicas iniciales.
e-) Cálculos avanzados
La mayoría de programás de ordenador dedicados a analizar las estructuras de hormigón expuestas al fuego pueden clasificarse como termo-mecánicos. La mayoría de estos tipos de modelos consisten básicamente en sendos programás térmico y mecánico separados, de manera tal que el campo de temperaturas obtenido como resultado del programa térmico es introducido dentro del programa mecánico en cada paso de tiempo a efectos de calcular las deformaciones y tensiones en cada punto. Los programás térmicos y mecánicos están generalmente desacoplados. Esto significa que si la estructura desarrolla fisuras que modifican el flujo de calor esto no se verá reflejado en el análisis térmico. Dichos programás son capaces de predecir con razonable exactitud los desplazamientos de vigas y columnas expuestas al fuego. Para tales aplicaciones, los relativamente simples modelos termo-mecánicos ofrecen una relación precisión- costo computacional muy razonable a efectos de predecir la resistencia al fuego de vigas y columnas tras una o dos horas de exposición al fuego.
No obstante, los modelos termo-mecánicos son incapaces de predecir fenómenos relacionados con el flujo de humedad y el desarrollo de presión en los poros durante el calentamiento, tales como el spalling explosivo. Cuando el contenido de humedad en el hormigón es importante, es necesario un modelo con una componente hídrica. Surgen entonces los modelos higro-termo-mecánicos que tienen en cuenta todos estos aspectos de una manera más completa. Debido a su complejidad, actualmente existen pocos códigos de ordenador con este tipo modelos para el análisis de estructuras expuestas al fuego.
1-4 Modos de fallo al fuego
Cuando se evalúa la capacidad portante de una estructura de hormigón expuesta al fuego deberían considerarse todos los modos de fallo relevantes. Dependiendo de la distribución de carga, la historia de calentamiento y el tipo de estructura, pueden ocurrir los siguientes tipos de fallo:
- Fallo por flexión
- Fallo por compresión y pandeo
- Fallo por anclaje
- Fallo por cortante o torsión
- Fallo por spalling
1-4-1 Fallo por flexión
El fallo por flexión es el tipo fallo más común para miembros estructurales horizontales tales como vigas o losas en una dirección. Una hipótesis de cálculo aceptada es que los momentos flectores causan tensiones de tracción en las barras de acero y tensiones de compresión en el hormigón. Los momentos positivos causan tensiones de tracción en la armadura inferior y tensiones de compresión en el hormigón de la parte superior. Los momentos negativos generan tensiones de tracción en la armadura superior y tensiones de compresión en el hormigón de la parte inferior. Considerando que solo la parte inferior esta expuesta al fuego, el fallo puede ocurrir tanto por ruptura de la armadura inferior como en el caso de momentos positivos o por aplastamiento del hormigón en la zona de compresión común en el caso de momentos negativos cerca de los apoyos. La armadura inferior cercana a los apoyos también puede fallar por excesiva rotación de la sección. Se ha demostrado mediante ensayos que las losas apoyadas en cuatro lados tienen un comportamiento más bien de membrana trabajando a tracción que de flexión.
1-4-2 Fallo por compresión y pandeo
El fallo por pandeo es el más relevante en el caso de elementos verticales tales como columnas y paredes. Debido al calentamiento de la estructura, el módulo de Young y la resistencia del hormigón y del acero disminuyen reduciendo de esta manera la resistencia al pandeo y la capacidad portante a flexión. La combinación de una reducción de resistencia y de rigidez conduce finalmente a un fallo por pandeo. De la misma manera elementos de hormigón armado trabajando a flexo-compresión pueden fallar por agotamiento de la resistencia en la zona comprimida debido a la disminución de resistencia con la temperatura.
1-4-3 Fallo por anclaje
El fallo por anclaje puede ocurrir si las tensiones en las armaduras no pueden desarrollarse sobre la longitud disponible para la adherencia de las mismas. En este caso la armadura se arranca. En las estructuras de hormigón con aceros dulces y sin pretensar, el fallo por anclaje es muy raro. Por el contrario, en el caso de estructuras pretensadas que utilizan armadura pretesa, el fallo por anclaje puede gobernar el comportamiento estructural
1-4-4 Fallo por cortante o torsión
El fallo por cortante y por torsión no es común en las estructuras de hormigón expuestas al fuego. Las tensiones de cortante se transfieren principalmente cerca del centro de la sección transversal, la cual es una zona relativamente fría. A pesar de eso el fallo por cortante o torsión puede ocurrir especialmente en el caso de estructuras sin armadura de cortante.
1-4-5 Fallo por spalling
En algunas situaciones cuando el calentamiento por fuego es particularmente rápido, puede ocurrir el llamado spalling explosivo del hormigón. El spalling explosivo puede dar lugar a una significativa pérdida de sección de hormigón reduciendo drásticamente la capacidad portante de la estructura. En el año 1996, el “Túnel del Canal de la Mancha” que conecta Inglaterra y Francia con un túnel ferroviario, sufrió un incendio que expuso la estructura a un fuego de 10 horas de duración con una temperatura de 700°C (ver Figura 1-4). El fuego destruyo partes de los anillos de hormigón del túnel por spalling explosivo en una longitud de varios cientos de metros. Los daños fueron valorados en 250 millones de euros y el tiempo de reparación fue de 6 meses.
Varias soluciones tecnológicas han sido desarrolladas para brindar a la estructura una protección pasiva o activa contra el spalling. Entre dichas soluciones, la adición de fibras de polipropileno en el hormigón ha demostrado ser muy eficiente.
1-5 Objetivos
El objetivo general de la monografía es desarrollar un modelo general para el análisis de estructuras de hormigón armado expuestas al fuego que sea capaz de predecir los fenómenos relacionados con el transporte de humedad y aumento de la presión en los poros, tales como el spalling explosivo.
Los objetivos específicos relacionados con el desarrollo de dicho modelo son los siguientes:
- 1) Proponer un marco termodinámico para el hormigón expuesto a elevadas temperaturas dentro del contexto de la mecánica de los medios porosos no saturados.
- 2) Proponer un modelo higro-termo-mecánico para el hormigón expuesto a elevadas temperaturas que permita simular el fenómeno de spalling.
- 3) Desarrollar una herramienta numérica para la aplicación de los modelos propuestos. Para el desarrollo de dicha herramienta numérica se ha escogido el marco brindado por la teoría general del Método de los Elementos Finitos.
1-6 Contenidos de la monografía
Esta monografía se ha organizado en diez capítulos y un anexo, cubriendo los siguientes contenidos:
En el Capítulo 2 se describen los aspectos más importantes del comportamiento de ambos materiales, hormigón y acero, expuestos a grandes temperaturas. Primeramente se describen los cambios que se desarrolla en la microestructura del hormigón al aumentarse la temperatura. Luego describen la evolución de algunas propiedades mecánicas con la temperatura tales como resistencia a compresión, resistencia a tracción, módulo de Young, energía de fractura, deformaciones de dilatación y deformaciones inducidas por tensiones. Seguidamente se describe la evolución de algunas propiedades higro-térmicas tales como conductividad, calor específico, permeabilidad intrínseca, transporte de humedad. También se describe el fenómeno de spalling exponiendo cuáles son los dos mecanismos que intentan explicarlo: spalling debido a dilataciones térmicas restringidas y spalling debido al aumento de la presión de poros. Por último, se realiza una breve descripción del comportamiento mecánico de la barras de acero al someterse a temperaturas elevadas.
En el Capítulo 3 se describen brevemente los distintos modelos que pueden encontrarse en la literatura, que intentan predecir el comportamiento del hormigón expuesto a elevadas temperaturas. En primer lugar, se describen los modelos comúnmente utilizados para el estudio de las estructuras de hormigón expuestas al fuego, los modelos termo-mecánicos desacoplados. En segundo lugar, se describen los modelos más complejos que pueden encontrarse en la literatura, los modelos higro-termo-mecánicos acoplados. Por último, se describen un tipo de modelo que representa una simplificación del modelo anterior, los modelos higro-termo-mecánicos semi acoplados.
En el Capítulo 4 se realizará un breve resumen de la teoría de la mecánica de medios porosos no saturados. Primeramente se describen las hipótesis básicas de esta teoría. Luego se repasan los conceptos clásicos de la mecánica del continuo pero aplicados al medio poroso no saturado, tales como las relaciones cinemáticas, ecuaciones de balance (masa, momentum y entropía), ecuaciones de estado para fluidos, ecuaciones constitutivas y ecuaciones de transporte de masa y calor. Asimismo se describen los distintos tipos de porosidades utilizadas en la teoría.
En el Capítulo 5 se desarrolla un modelo higro-termo-mecánico para el hormigón expuesto a elevadas temperaturas. Primeramente se establecen las hipótesis básicas del modelo propuesto. Seguidamente se presentan las bases termodinámicas del modelo donde se deducen las ecuaciones de estado para las tensiones, porosidad y entropía. Luego se desarrollan las ecuaciones de gobierno del problema higro-termo-mecánico acoplado: ecuación de balance de masa de aire seco, ecuación de balance de especies de agua, ecuación de balance de entropía y ecuación de balance de momentum. Seguidamente se realiza la definición de las variables de daño mecánico y daño térmico, describiendo sus leyes de evolución. Por ulútimo, se definen las deformaciones de fluencia transitoria y sus leyes de evolución.
En el Capítulo 6 se describe como se ha tenido en cuenta la armadura de acero en el presente trabajo. Se detallan las hipótesis de la teoría clásica de mezclas y se plantea su utilización para la consideración de la contribución de la armadura de acero al comportamiento del hormigón armado. Por último, se propone un algoritmo de integración de la ecuación constitutiva de la armadura expuesta a elevadas temperaturas.
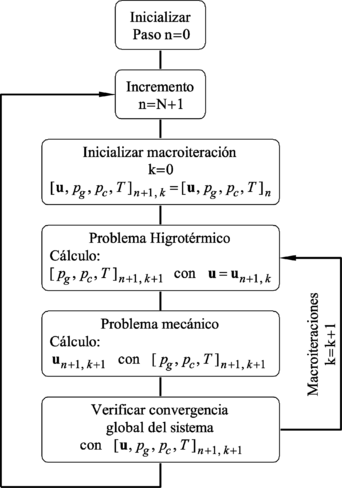
En el Capítulo 7 se presenta un esquema de análisis de problemás higro-termo-mecánico acoplados. Primeramente se plantea la resolución numérica del problema higro-térmico utilizando el Método de los Elementos Finitos para la integración espacial y el Método de diferencias finitos para la integración temporal. Seguidamente se plantea la resolución del problema mecánico utilizando también el Método de los Elementos Finitos. Por último, se plantea un algoritmo iterativo para tratar el problema acoplado.
En el Capítulo 8 se presentan un conjunto de ejemplos de validación del modelo propuesto. Primeramente se presenta un ejemplo de validación de las variables higro-térmicas obtenidas del modelo propuesto. Seguidamente se presenta un ejemplo de validación de las variables termo-mecánicas obtenidas del modelo propuesto.
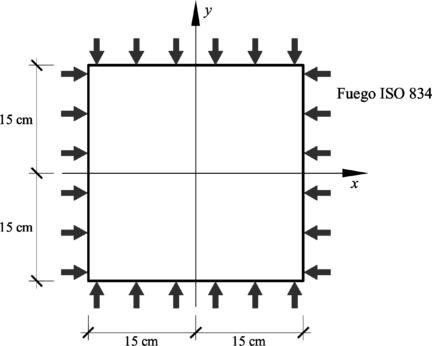
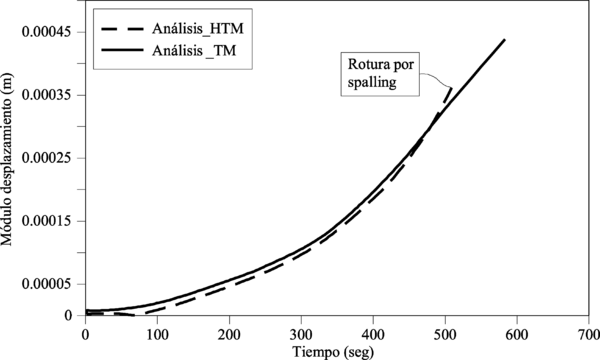
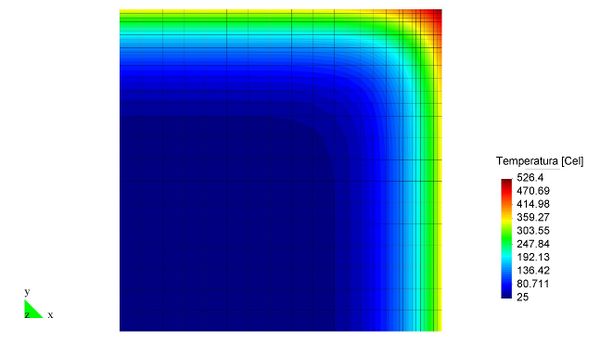
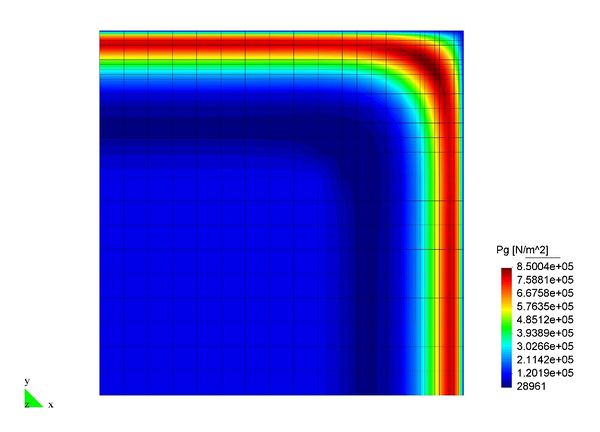
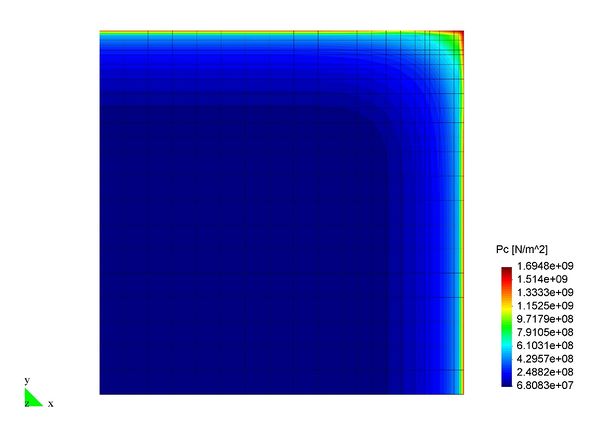
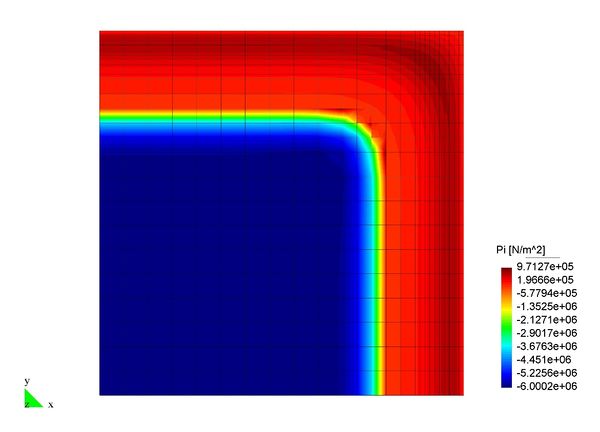
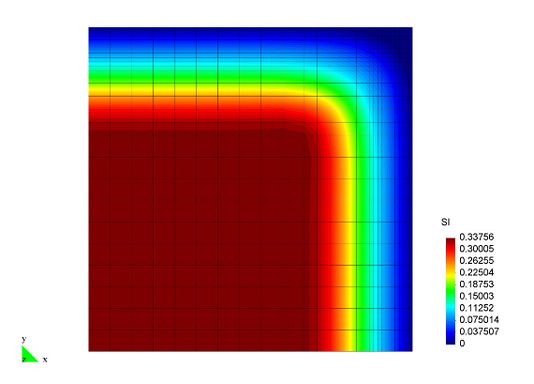
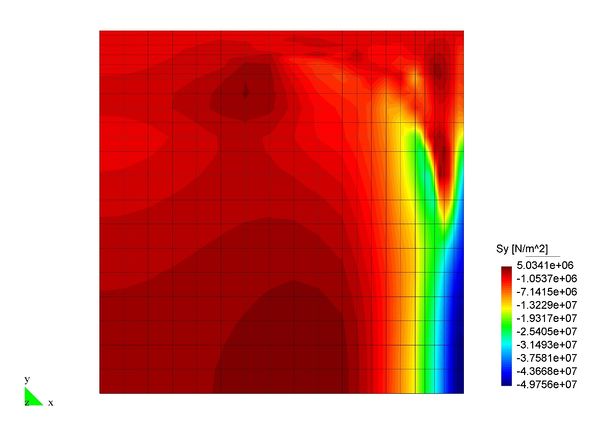
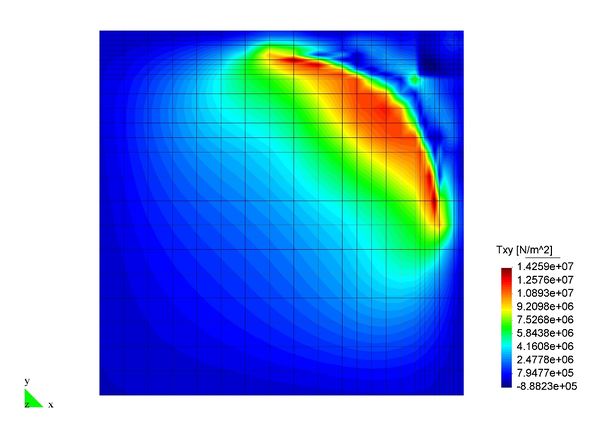
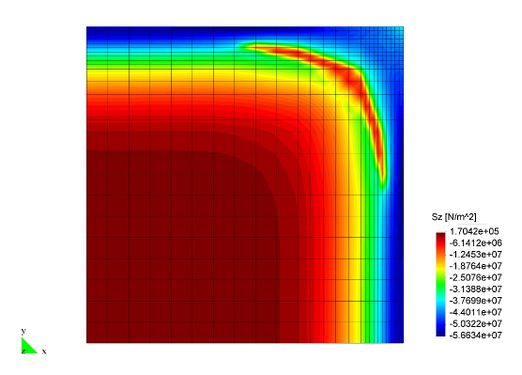
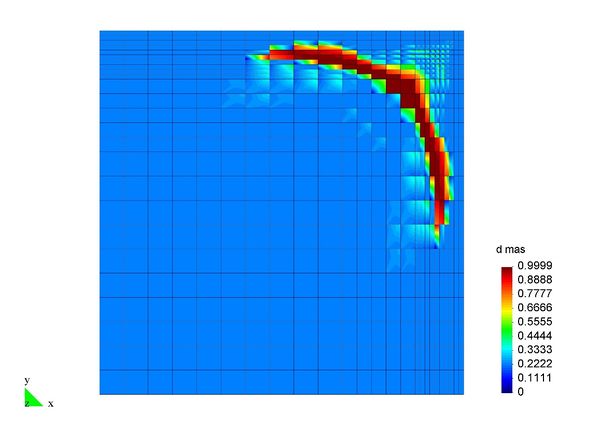
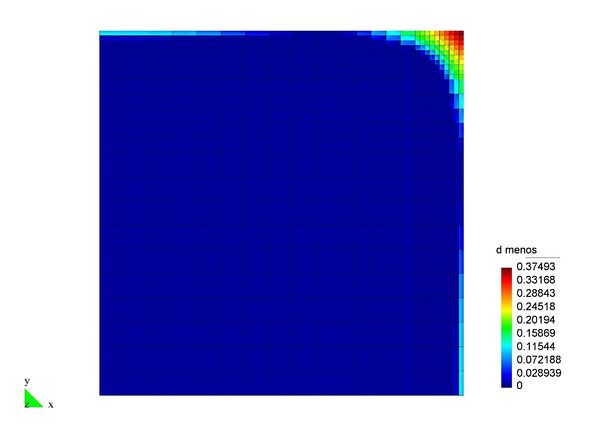
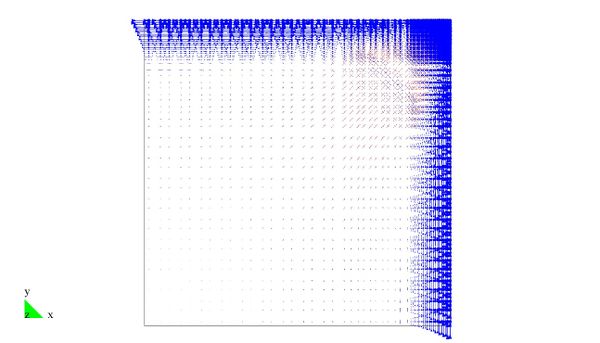
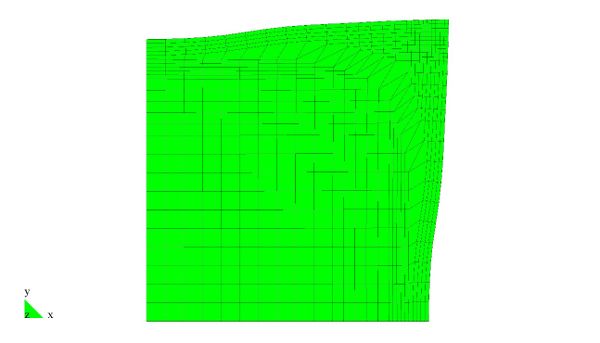
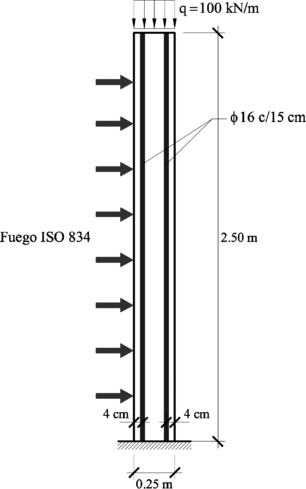
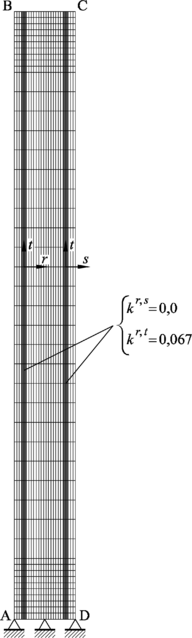
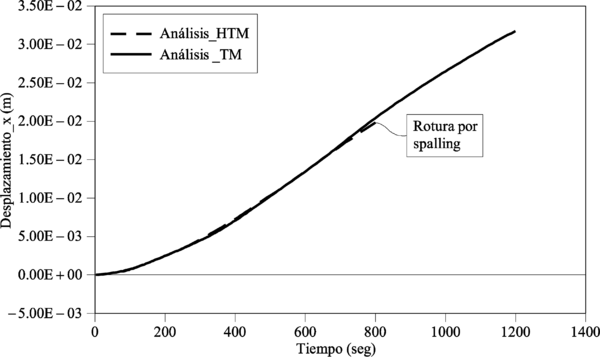
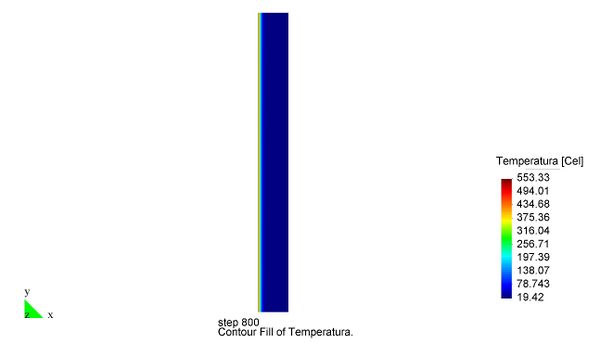
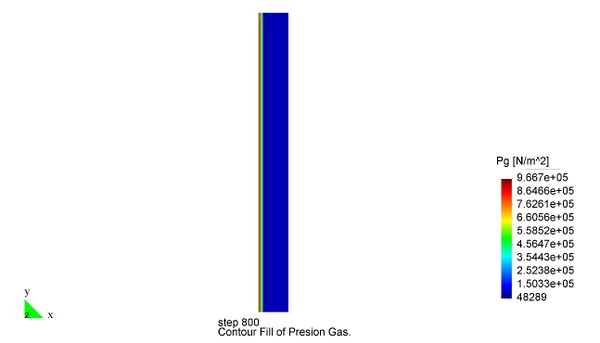
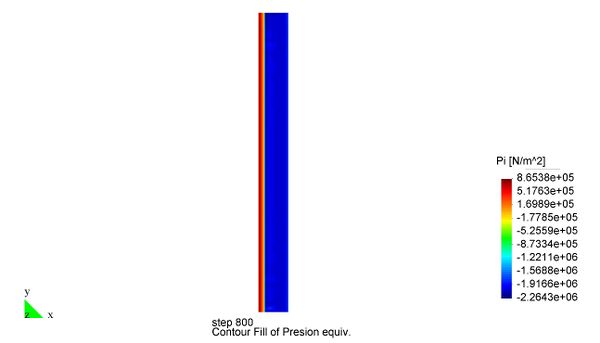
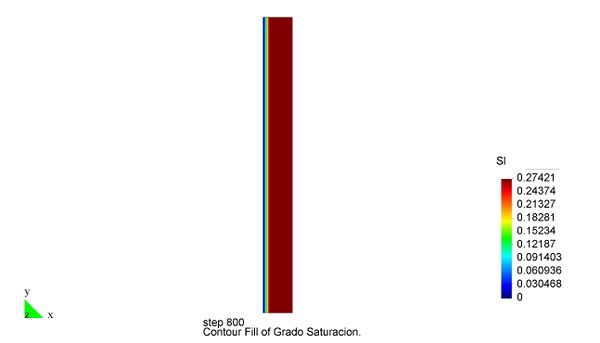
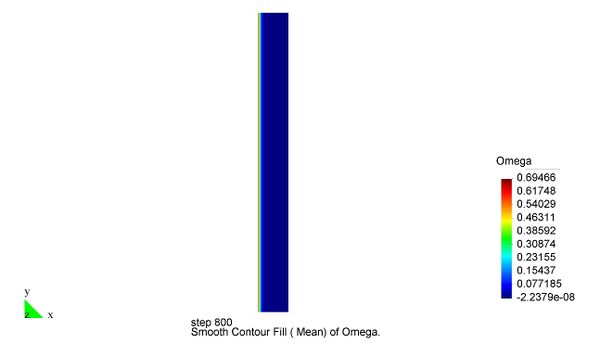
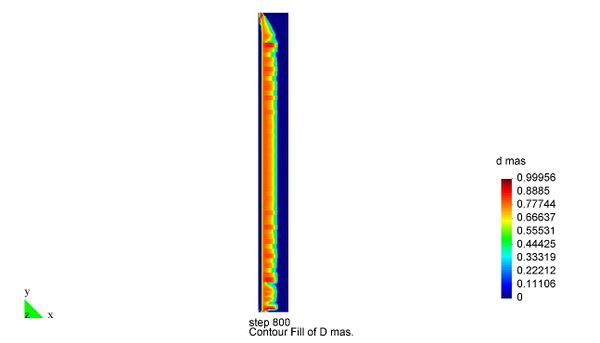
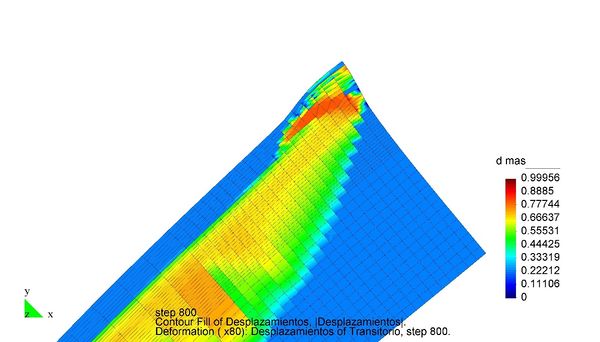
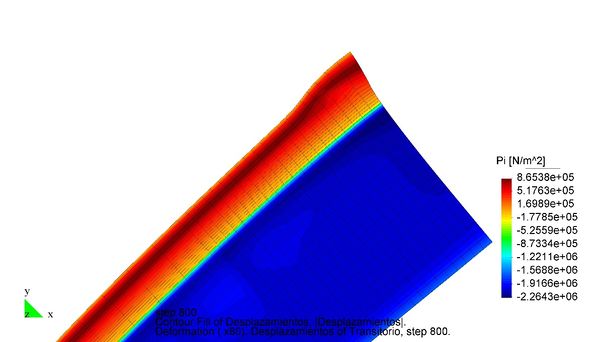
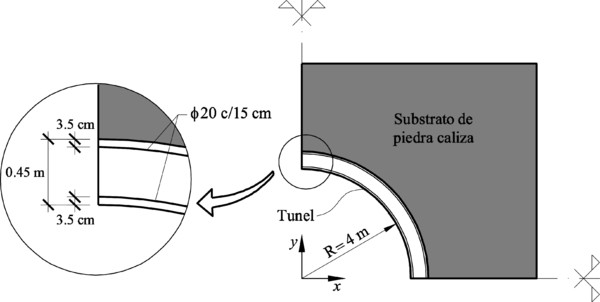
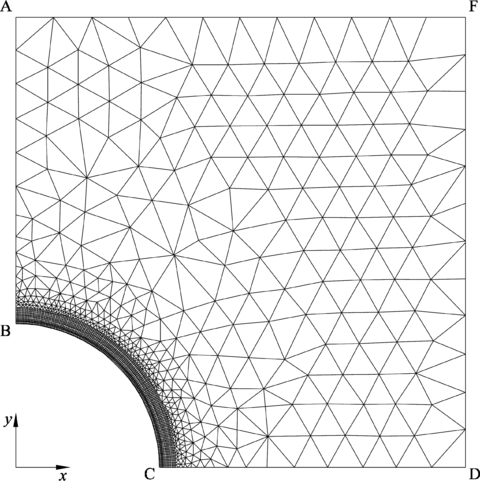
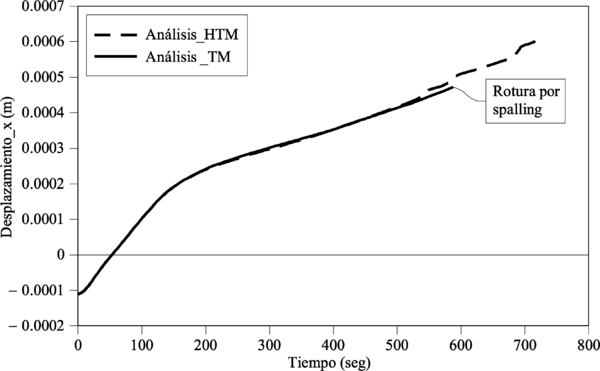
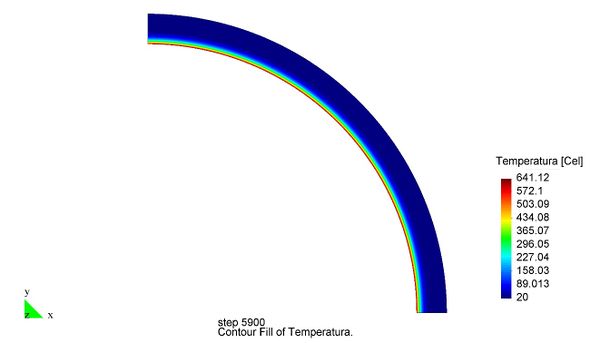
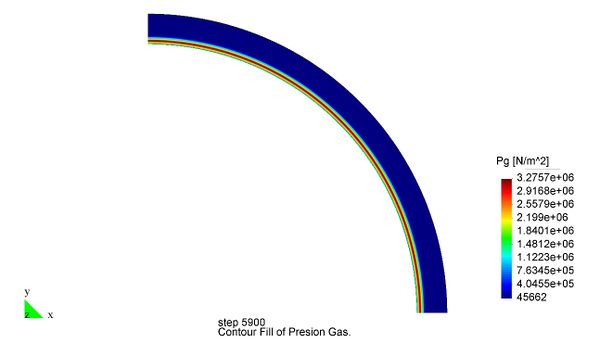
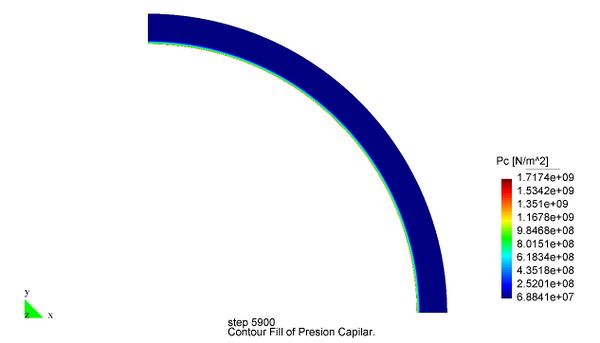
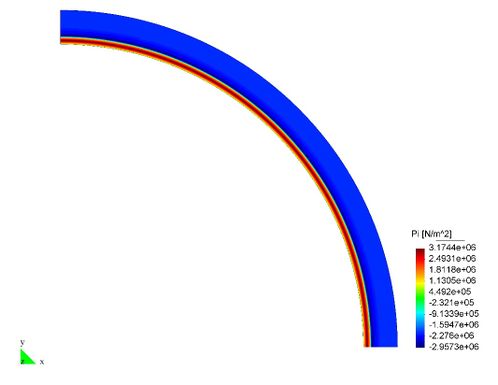
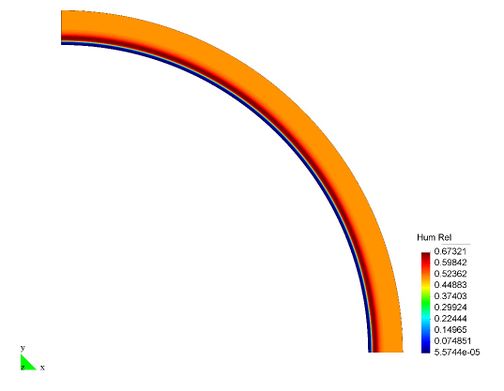
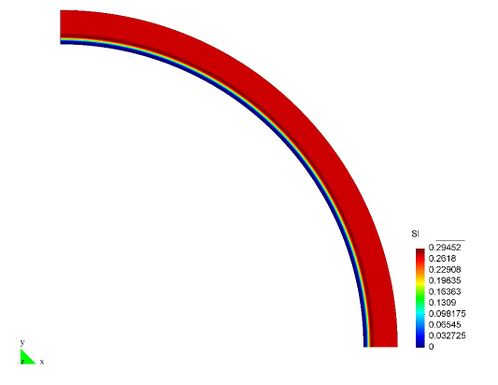
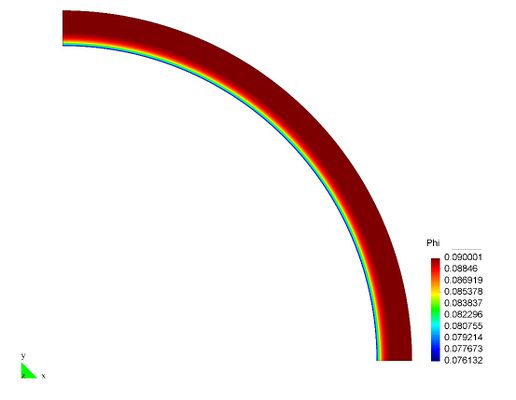
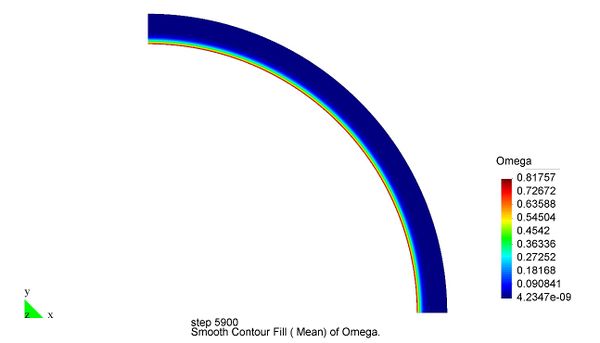
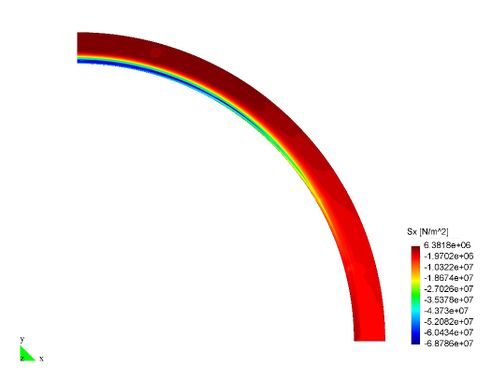
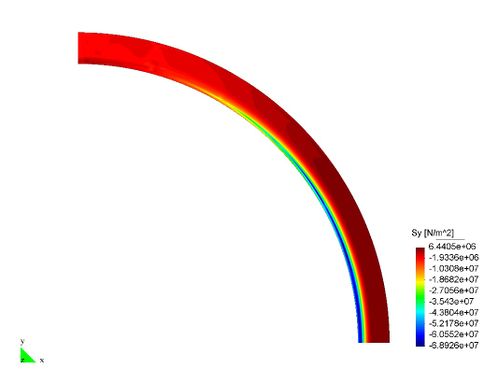
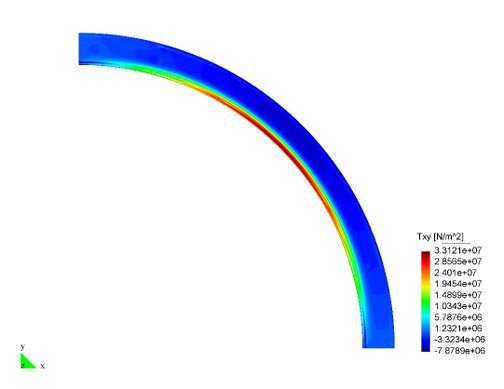
En el Capítulo 9 se presentan tres ejemplos de aplicación del modelo higro-termo-mecánico para el hormigón expuesto a elevadas temperaturas desarrollado en esta monografía. En el primer ejemplo se analiza un pilar cuadrado de hormigón armado expuesto a un fuego estándar en sus cuatro lados en el que puede verse claramente cómo se produce el fenómeno de spalling. En el segundo ejemplo se analiza el comportamiento de un muro de hormigón armado expuesto por una cara. En el tercer ejemplo se analiza el comportamiento al fuego de una sección transversal de un túnel de hormigón armado cuyas características son similares al del Túnel Canal que une Francia con el Reino Unido.
Finalmente, en el Capítulo 10 se presentan las conclusiones extraídas, las aportaciones realizadas y las futuras líneas de investigación que pueden desprenderse de este trabajo.
En el Anexo 1 primeramente se realiza el desarrollo algebraico para la obtención de la matriz tangente consistente para el modelo mecánico. Seguidamente se proponen las ecuaciones y valores para los distintos parámetros definidos en el modelo propuesto.
Capítulo 2 Propiedades y comportamiento de los materiales expuestos a elevadas temperaturas
2-1 Propiedades y comportamiento del hormigón a elevadas temperaturas
Cuando se expone al hormigón a elevadas temperaturas, éste experimenta un conjunto de transformaciones y reacciones en su composición química, estructura física y contenido de agua. Estos cambios ocurren en primer lugar en la pasta de cemento endurecido, pero en algunos casos pueden ocurrir en el agregado. Tales cambios se reflejan en cambios en las propiedades físicas y mecánicas del hormigón asociado con el aumento de temperatura. A temperaturas de hasta 800°C, las reacciones toman principalmente la forma de deshidratación y de pérdida de humedad. Entre los 600 y 900°C, puede ocurrir la descarbonatación de los carbonatos, si el hormigón contiene áridos calcáreos. Por encima de los 1200°C y hasta los 1300°C, algunos componentes del hormigón comienzan a fundirse. Por encima de los 1300°C el hormigón se ha fundido completamente.
Las barras de acero de refuerzo de hormigón también sufren cambios en sus propiedades mecánicas asociados al aumento de la temperatura.
2-1-1 Hidratación y deshidratación de la pasta de cemento Pórtland
El hormigón consiste en la unión de pasta de cemento hidratado y áridos. Las propiedades del hormigón son determinadas por las propiedades de sus componentes y las interfaces entre ellos. El principal ingrediente de una mezcla de hormigón es el cemento Pórtland, sus principales componentes son los siguientes:
Silicato tricálcico 3CaO.SiO2 C3S
Silicato dicálcico 2CaO.SiO2 C2S
Aluminato tricálcico 3CaO.Al2O3 C2A
Aluminoferrita tetracálcico 4CaO.Al2O3Fe2O3 C4AF
Los principales productos de la hidratación de la pasta de cemento Pórtland son el hidrato de silicato cálcico compuesto esencialmente de 3CaO. 2SiO2.3H2O3 (gel de tobermonita) y hidróxido de calcio (CH), ambos productos resultantes de la reacción de C3S y C2S con agua. Las reacciones de hidratación pueden escribirse como sigue:
2C3S + 6H C3S2H3 + 3CH
2C2S + 4H C3S2H3 + CH
Harmathy (1970) mostró que la deshidratación de la pasta de cemento comienza tan pronto como la desorción del agua evaporable se completa (alrededor de 105°C), y continúa ininterrumpidamente hasta la alrededor de los 800°C. El hidrato de silicato cálcico (CSH) se descompone principalmente en β–silicato dicálcico (β-C2S), β-wallastonita (β-CS) y agua (H), y el hidróxido cálcico (CH) descompone en oxido cálcico © y agua. Harmathy describe estas reacciones de la deshidratación de la pasta de cemento como sigue
C1.62SH1.5 [(1- ξCSH) C1.62 SH1.5 + 0.62ξCSHC2S++ 0.38ξCSHCS]+1.5 ξCSH H↑
CH [(1 - ξCH) CH + ξCH C] + ξCH H↑
Donde ξCSH y ξCH son las variables de progreso de la deshidratación de CSH y para la deshidratación de CH, respectivamente. Estas variables son funciones únicamente de la temperatura. La flecha indica que el agua abandona el sistema. Harmathy estimó el grado y la tasa de conversión del gel de tobermonita (CSH) y el hidróxido cálcico (CH) en una idealizada pasta de cemento.
2-1-2 Pérdida de tres tipos de agua en la pasta de cemento Portland
Powers y Brownyard (1948) dividen en tres categorías los diferentes tipos de agua en la pasta de cemento endurecida como sigue,
- Agua no-evaporable (sólida): Incluye todo tipo de agua de constitución, incluyendo el agua de cristalización y el agua químicamente combinada.
- Agua de gel (líquida): Agua evaporable, ubicada en los intersticios de gel por absorción o por otras fuerzas del tipo de van der Waals.
- Agua libre y agua capilar (líquida): Agua utilizada en la mezcla original de cemento, y agua evaporable ubicada en los poros capilares principalmente por condensación capilar.
Powers y Brownyard (1948) sugieren los siguientes valores para las densidades de los tres tipos de agua anteriormente mencionados:
- Agua no evaporable: ρ=1220kgm3
- Agua de gel: ρ=1110kgm3
- Agua libre y agua capilar: ρ=1000kgm3
Con el aumento de temperatura, la pasta de cemento primeramente pierde el agua evaporable retenida por fuerzas capilares, luego el agua retenida por las fuerzas de Van der Waals en los poros del gel. Harmathy (1970, 1993) trata la desorción del agua evaporable como una reacción que tiene lugar alrededor de los 100°C. El esquema de la reacción es el siguiente,
H20 (l) (1 - ξW) H20 (l) + ξW H20 (g)↑
Donde ξW es la variable de progreso para la evaporación del agua evaporable, y (l) y (g) significan fases líquida y gaseosa (vapor), respectivamente. La flecha indica que el vapor de agua abandona el sistema.
Cuando la temperatura alcanza 105°C, solamente existe agua no evaporable. Un posterior aumento en la temperatura causa una gradual descomposición del gel de CSH, y alrededor de 500°C, una rápida descomposición de CH. Debido a que la reacción de deshidratación se acompaña por pérdida de masa, los ensayos termogravimétricos ofrecen un conveniente medio para determinar las variables de progreso de la reacción en función de la temperatura.
2-1-3 Comportamiento del hormigón
El hormigón sufre una serie de cambios al aumentar de temperatura. Entre estas transformaciones se encuentran la pérdida de peso por calcinación y los cambios de color.
En la Figura 2-1 se observa una micrografía de las distintas transformaciones en el hormigón.
Pueden darse dos tipos de comportamientos totalmente diferentes en la pasta de cemento cuando la misma se encuentra sellada (se conserva la humedad bajo ciertas condiciones hidrotérmicas) o cuando se encuentra no-sellada (se permite el secado). El hormigón ubicado en la superficie puede considerarse bajo condición no-sellada. Por otro lado el hormigón en el interior del elemento estructural puede considerarse como sellado.
Una muestra de hormigón en condición sellada al calentarse por encima de 100ºC sufre en la pasta de cemento un conjunto de reacciones hidrotérmicas, las cuales generan significativos cambios en su microestructura fisicoquímica. La naturaleza de los cambios de fase que tienen lugar en la pasta de cemento depende de la relación C/S, la temperatura y la presión.
A continuación se detallan las distintas transformaciones que se dan en el hormigón al aumentar la temperatura (Khoury, 1992) en condición no-sellada:
- De 20 a 80ºC se produce un incremento en la hidratación de la pasta del cemento. Asimismo se produce una lenta pérdida del agua capilar y una reducción de las fuerzas cohesivas al expandirse el agua.
- A 100ºC se produce un marcado incremento (100 veces) en la permeabilidad del agua.
- Entre 80ºC y 200ºC, se incrementa la velocidad de pérdida de agua capilar y comienza la del agua físicamente ligada.
- Entre 80ºC y 850ºC, se produce la pérdida del agua químicamente ligada.
- A 150ºC se produce el pico del primer estado de descomposición del silicato cálcico hidratado (CSH).
- A 300ºC se produce un marcado incremento de la porosidad y la microfisuración.
- A 350ºC se produce rotura de algunos áridos como las gravas de rió.
- A 374ºC es el punto crítico del agua a partir del cual la presencia de agua libre deja de ser posible. Como se comentará más adelante, el efecto favorable de la humedad, puede ser contraproducente en incendios que se desarrollan muy deprisa y que hacen aumentar rápidamente la temperatura en el hormigón, provocando el fenómeno de “spalling” o desprendimiento explosivo de los recubrimientos. Esto es debido a que el agua interior, al tratar de evaporarse, crea unas fuertes tensiones internas.
- Entre 400ºC y 600ºC, se produce una disociación del Ca(OH)2 en CaO y agua.
- A 573ºC se produce una transformación en áridos cuarcíticos y arenas.
- Entre 550ºC y 600ºC, se produce un marcado incremento de los efectos térmicos.
- A 700ºC se produce la descarbonatación del CaCO3 en CaO y CaO2.
- A 720ºC se produce el segundo pico de la descomposición del silicato cálcico hidratado (CSH) en y .
- A 800ºC comienzan las ligaduras cerámicas la cual reemplaza a las ligaduras hidráulicas.
- A 1060ºC comienzan a fundir algunos constituyentes.
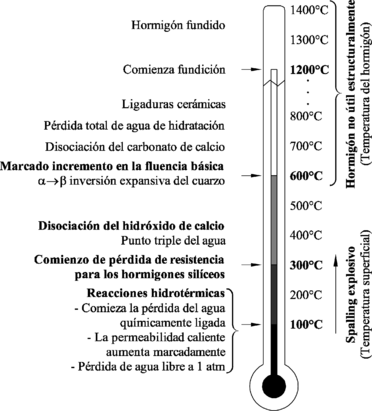
En la Figura 2-2 se presenta un esquema de todos estos procesos.
Es importante darse cuenta de que el hormigón una vez que se enfría a temperatura ambiente no vuelve a alcanzar su resistencia inicial a compresión. Su resistencia residual fc,θ,20ºC depende de la temperatura máxima que haya alcanzado durante la fase de calentamiento.
2-3 Propiedades mecánicas del hormigón a elevadas temperaturas
2-3-1 Módulo de elasticidad
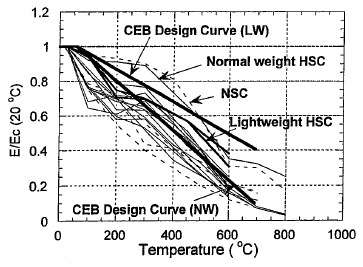
El módulo de elasticidad se ve notoriamente afectado por la temperatura. La Figura 2-3 muestra las relaciones de los módulos de elasticidad-temperatura obtenidas de ensayos para hormigones normales y livianos. El módulo de elasticidad disminuye con el aumento de temperatura.
El grado de disminución del módulo de elasticidad depende del tipo de agregado utilizado. Hormigones con áridos de piedra caliza, los cuales son químicamente muy estables, indican una menor reducción en el módulo de elasticidad comparados con hormigones de áridos cuarzíticos (Bazant y Kaplan, 1996).
2-3-2 Módulo de Poisson
Según los estudios experimentales de Marechal’s (1972b), el módulo de Poisson decrece casi linealmente con el aumento de la temperatura. El módulo de Poisson para un hormigón con áridos cuarzíticos reduce de 0.27 a temperatura ambiente a 0.10 a 400ºC. Esto se debe al ablandamiento de la microestructura resultante de la ruptura de las ligaduras debidas al calentamiento (Bazant y Kaplan, 1996).
2-3-3 Resistencia a compresión
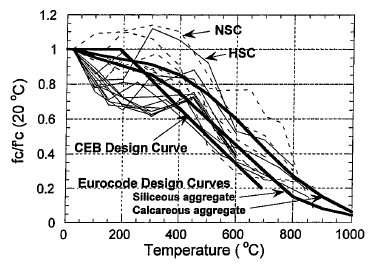
La resistencia a la compresión del hormigón disminuye con el aumento de temperatura. Uno de los principales factores que afectan a la resistencia a la compresión del hormigón expuesto a elevadas temperaturas es el tipo de áridos. Por ejemplo los hormigones de áridos calcáreos muestran una menor reducción en la resistencia a la compresión a temperaturas elevadas que los hormigones de áridos silíceos. Otros de los factores es la relación agregado-cemento, cuanto menor es dicha relación, menor será la reducción de la resistencia a compresión.
Phan (1996) compiló y comparó los datos experimentales de diez ensayos materiales, reportados por varios investigadores, para el hormigón a elevadas temperaturas. La Figura 2-4 muestra las relaciones de la resistencia a compresión-temperatura para ensayos en hormigones de peso normal. Phan divide en tres los estados de resistencia a compresión en relación a la temperatura:
- Estado inicial de pérdida de resistencia: Entre la temperatura ambiente y los 100 o 200ºC.
- Estado de estabilización: Entre 100-200ºC y los 400-450ºC.
- Estado permanente de pérdida de resistencia: Comienza a los 400-450 ºC.
2-3-4 Resistencia a tracción
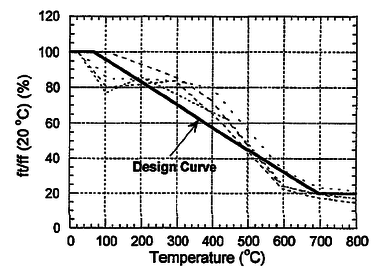
La resistencia a la tracción del hormigón disminuye con la temperatura. La resistencia a la tracción es mucho más sensible a los efectos de la temperatura que la resistencia a la compresión.
El tipo de agregado tiene una gran influencia sobre la resistencia a tracción del hormigón expuesto a elevadas temperaturas. El decrecimiento de la resistencia a tracción en áridos calcáreos es dos veces más alto que en el caso de los áridos silíceos.
Hormigones con bajo contenido de cemento tienen una reducción de resistencia menor que los hormigones con alto contenido.
En la Figura 2-4 se muestran los ensayos Thelardersson (1971) y se muestra una curva de diseño propuesta por el CEB Bulletin D’ Information N°208.
2-3-5 Coeficiente de dilatación térmica
Al estar el hormigón formado por áridos y por la pasta de cemento, el coeficiente de dilatación térmica depende de las características de estos dos materiales.
La pasta de cemento endurecida inicialmente se expande con el calentamiento hasta aproximadamente los 150ºC. Entre los 150 y 300º la pasta de cemento no expande mas, y comienza a contraer entre los 300 y 800ºC (Bazant y Kaplan 1996).
Los áridos muestran una expansión térmica casi lineal entre los 25 y 800ºC.
La expansión térmica del hormigón a elevadas temperaturas se encuentra principalmente influenciada por los áridos, debido a que los áridos ocupan entre el 60 y 80% del volumen del hormigón. Los hormigones generalmente se expanden con la temperatura, a pesar de que la pasta de cemento endurecida pueda contraerse entre los 150 y 300ºC. La expansión de los áridos generalmente predomina sobre la contracción de la pasta de cemento y el resultado neto es la expansión del hormigón (Bazant y Kaplan 1996).
2-3-6 Energía de fractura
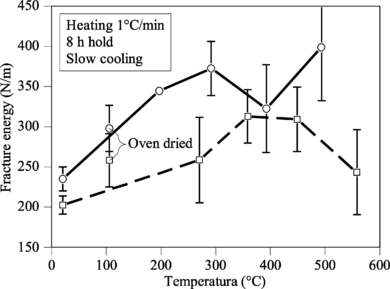
Se encuentran muy pocos datos en la literatura de la evolución con la temperatura de la energía de fractura . Este parámetro es muy importante para el control de la evolución de la fisuración con la temperatura.
Nielsen y Bićanic (2003) analizan la energía de fractura residual de un conjunto de vigas de hormigón con áridos basalticos de alta resistencia y de hormigón normal de grava. La tendencia de ambos tipos de hormigones es muy parecida hasta 400-500ºC, a partir del cual la energía de fractura residual del hormigón de grava comienza a decrecer al hacerse extensivo el daño térmico. En la Figura 2-6 se muestran los resultados experimentales comentados.
2-3-7 Deformaciones térmicas inducidas por tensiones
Las deformaciones térmicas inducidas por carga (LITS) se determinan indirectamente como la diferencia entre la deformación medida durante el primer calentamiento sin carga y aquella bajo carga (excluyendo la deformación elastoplástica inicial). Por tanto, las LITS representan las deformaciones que se desarrollan cuando el hormigón es calentado por primera vez bajo carga y esencialmente incluyen:
- Fluencia básica (basic creep).
- Fluencia por secado (drying creep).
- Fluencia térmica de transición (transitional thermal creep, ttc).
- Deformaciones elásticas
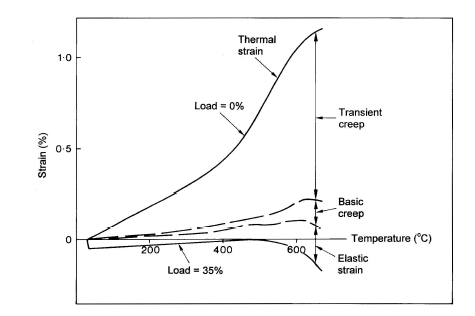
Las LITS solo se dan con tensiones de compresión. La combinación de la fluencia térmica de transición y la fluencia por secado es usualmente llamado fluencia transitoria (transient creep) y constituye la componente de deformación más grande tal como muestra la Figura 2-5.
La fluencia transitoria parece ser particular del hormigón y ocurre solamente durante el primer calentamiento a una temperatura determinada, pero no durante el enfriamiento o recalentamiento posterior bajo carga. Este fenómeno se produce en la pasta de cemento y está relacionado con las complejas transformaciones físico-químicas que ocurren en CSH durante el primer calentamiento. Las LITS de hormigones conteniendo diferentes áridos pero con la misma relación de volumen total, resultan muy similares a pesar de que sus deformaciones térmicas son muy diferentes.
Es importante resaltar que cualquier análisis de tensiones que ignore las LITS dará resultados muy erróneos.
2-4 Propiedades higro-térmicas del hormigón a elevadas temperaturas
2-4-1 Calor específico
El calor específico es la cantidad de calor por unidad de masa, requerida para modificar la temperatura del hormigón en un grado.
El calor específico a presión constante, cp, se define como sigue (Harmathy y Allen, 1973):
|
|
(2.1) |
donde H es la entalpía, T es la temperatura y p la presión. Si el calentamiento va acompañado de reacciones químicas, la entalpía es función del grado de conversión de reactantes en productos y de la temperatura. La expresión anterior resulta:
|
|
(2.2) |
donde ξ (0≤ξ≤1) es el grado de conversión de los reactantes en productos, y ![]() es conocido como calor específico aparente. El primer término de la derecha representa la contribución de calor sensible al calor específico para un determinado grado de conversión, y el segundo término representa la contribución del calor latente al calor específico.
es conocido como calor específico aparente. El primer término de la derecha representa la contribución de calor sensible al calor específico para un determinado grado de conversión, y el segundo término representa la contribución del calor latente al calor específico.
En el caso de la pasta de cemento Pórtland, las dos reacciones a elevadas temperaturas más importantes son la deshidratación del gel de tobermonita (CSH) en silicato β–dicálcico y β–wollastonita (β-CS), y la deshidratación del hidróxido de calcio (CH) en oxido de calcio. Investigaciones realizadas por Harmathy (1970) muestran que la contribución de calor latente al calor específico es muy importante en rango completo de la deshidratación (de 100 a 850ºC), y el valor del calor específico aparente es varias veces más grande que calor sensible debido a la absorción de calor en la reacción de deshidratación.
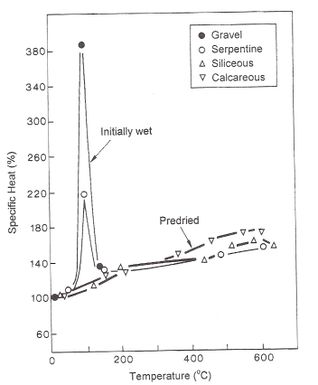
Harmarthy y Allen (1973) reportan los resultados de datos experimentales en diferentes tipos de hormigones. En general, el calor específico parece bastante insensible al tipo de agregado utilizado y a las proporciones de las mezclas. El calor específico de varios hormigones es de aproximadamente 0.80 kJ/kgK a 25 ºC y se incrementa a valores entre 1.0 y 1.5 kJ/kgK a 650ºC.
El contenido de humedad tiene un fuerte efecto sobre el calor específico del hormigón a temperaturas por debajo de 200ºC. Para hormigones saturados, el calor específico muestra un rápido y temporal aumento en temperaturas de alrededor de 100ºC debido a la vaporización del agua libre.
2-4-2 Conductividad térmica
La conductividad térmica se define como la relación de la tasa de flujo de calor y el gradiente de temperatura. La conductividad térmica de hormigones ordinarios a temperaturas normales se ubica entre 1.4 y 3.6 W/m K.
Harmathy (1970) estima la conductividad térmica de un hormigón secado en horno a temperaturas de hasta 1000ºC. Si bien los valores no están sujetos a grandes variaciones, en general la conductividad térmica disminuye con el aumento de temperatura.
Debido a que la conductividad térmica de la pasta de cemento no varía ampliamente, la conductividad térmica de los áridos determina principalmente la del hormigón (Harmathy 1970).
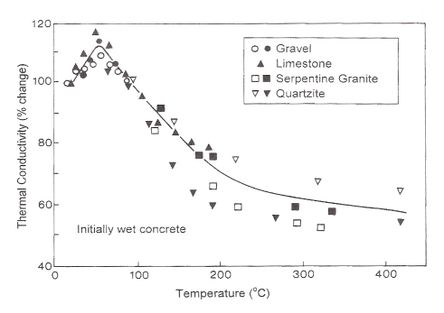
La conductividad térmica del hormigón es influenciada por su contenido de humedad. El agua aumenta su conductividad térmica de 0.6 W/m K para 20ºC a 0.69 W/m K para 130ºC. Para calentamiento más allá de los 100ºC hay una significante reducción en la conductividad térmica del hormigón debido a la reducción del contenido de humedad.
En la Figura 2-9 se muestra el efecto de la temperatura sobre la conductividad térmica.
2-4-3 Permeabilidad intrínseca del hormigón
El coeficiente de permeabilidad del hormigón a temperaturas normales esta influenciado por la capilaridad de los poros, la cual es gobernada por la relación agua/cemento y por el grado de hidratación.
El coeficiente de permeabilidad del hormigón aumenta con el aumento de temperatura. Para temperaturas por encima de 100ºC, la permeabilidad del hormigón aumenta por dos órdenes de magnitud (Chapman 1976, Chapman y England 1977, Bazant y Thounguthai 1977).
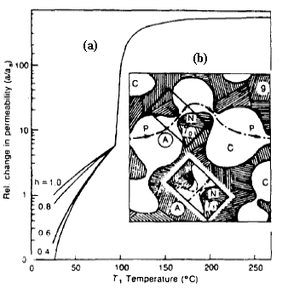
Bazant y Thounguthai (1978) reportan la dependencia de la permeabilidad con la temperatura, mostrando el salto de dos órdenes de magnitud cuando la temperatura supera los 100 ºC que se comento anteriormente (Figura 2.10a). Ellos explican el fenómeno de la siguiente manera,
- El flujo de humedad esta gobernado por cuellos (“N” en la Figura 2.10b) en el flujo pasante de la pasta de cemento.
- Un calentamiento por encima de 100ºC causa un suavizado de la superficie rugosa del poro y un ensanchamiento de los cuellos, dando lugar a un aumento en la permeabilidad.
Greathead (1986) midió la importancia del curado y los posteriores tratamientos higro-térmicos sobre la permeabilidad del hormigón. Las principales conclusiones son las siguientes:
- El coeficiente de permeabilidad es dramáticamente afectado por el tipo de curado y los posteriores tratamientos higro-térmicos.
- La permeabilidad cambia siete órdenes de magnitud entre un curado continuo con agua y un secado severo a 600ºC.
- El valor más bajo de la permeabilidad es de 1x10-21 m2 para un curado con agua a temperatura ambiente.
2-4-4 Transporte de humedad y presión de poros
El transporte de humedad en el hormigón está gobernado por dos tipos de flujos:
- Flujo inducido por presión: El flujo se produce desde una región con alta presión a una región de baja presión debido al gradiente de presión.
- Flujo difusivo: El flujo se produce de una región de alta concentración de humedad a una región de baja concentración de humedad debido al gradiente de concentración de humedad.
Cuando el hormigón se calienta, la presión en los poros aumenta debido a la existencia de agua en los mismos. La importancia de aumento de presión en los poros depende de la temperatura y el contenido de humedad. Con un aumento de temperatura y/o de contenido de humedad la presión aumentará.
2-4-5 Spalling del hormigón
El spalling del hormigón es un fenómeno natural, en el cual al aumentarse la temperatura se genera fuerzas en el interior del elemento de hormigón que causan la desintegración de la capa superficial de hormigón. El spalling del hormigón implica la separación y rotura, a veces violenta, de partículas o trozos de varios tamaños de la superficie.
El spalling del hormigón puede ser atribuido a dos mecanismos:
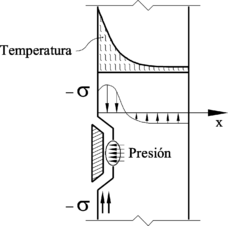
- Spalling debido a dilataciones térmicas restringidas (Bazant 1997): Esta hipótesis considera que el spalling resulta de dilataciones térmicas restringidas cercanas a la superficie calentada. Las tensiones de compresión generadas son liberadas por una fractura frágil en el hormigón que da lugar al spalling (Figura 2-11).
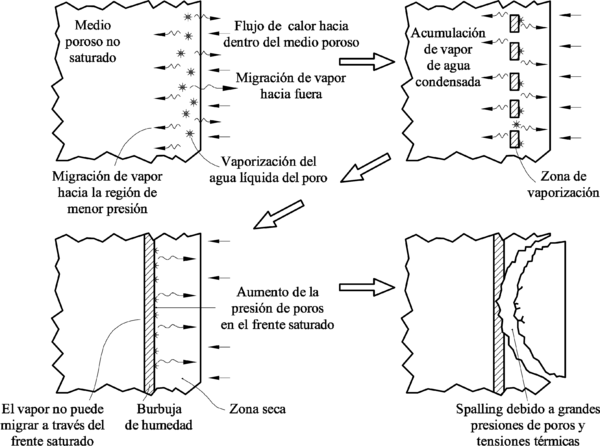
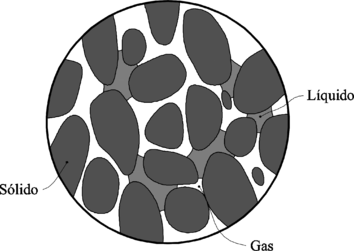
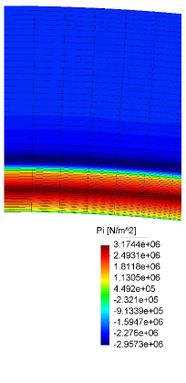
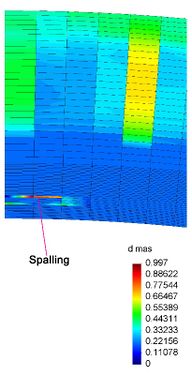
- Spalling debido a un aumento en la presión en los poros (Harmathy 1965, Smith 1978): Esta hipótesis queda definida por el proceso conocido como spalling por taponamiento de humedad (moisture clog spalling) esquematizado en la Figura 2-12. Los materiales porosos como el hormigón contienen agua líquida libre, agua absorbida (bound water), agua vaporizada, y aire en los espacios de los poros. Durante una carga térmica importante, el flujo de calor dentro del material conduce a un aumento en la temperatura del esqueleto sólido y el agua en los poros. Cuando el agua en los poros alcanza una temperatura suficientemente alta comienza a vaporizar. Al vaporizar el agua la presión en los poros aumenta. Al aumentar la presión en la zona de vaporización se produce un gradiente de presión entre dicha zona y regiones de menor presión como la superficie exterior y en partes más profundas de la pieza. También, debido a que la temperatura del agua en los poros aumenta, la expansión térmica de la fase líquida contribuye a aumentar aún más la presión en los poros. Como el vapor migra debido a un gradiente de presión, éste escapará a la atmósfera, o viajará hacia el interior de la pieza llegando a zonas de menor temperatura y condensando. Esta migración de vapor aliviará la presión en los poros en la zona de vaporización pero también incrementará el nivel de saturación en la zona de condensación. A medida que el vapor que migra condensa, añadiendose al agua líquida de los poros en las zonas más frías. A medida que este ciclo de vaporización-migración-condensación continua, el aumento de agua líquida en los poros irá aumentando a llegar a formar una capa completamente saturada. Un vez que dicha capa se forma, el agua de poros vaporizada se ve impedida de migrar hacia el interior de la pieza de hormigón debido al frente de saturación. De esta manera el vapor se ve forzado a migrar a las regiones secas para escapar a la atmósfera. Si la permeabilidad del material es suficientemente baja o la velocidad de calentamiento es suficientemente alta, el agua vaporizada no será capaz de escapar lo suficientemente rápido para evitar el aumento de la presión de los poros. El spalling ocurre cuando la resistencia a tracción se supera por una elevada presión en los poros.
Es lógico pensar que el verdadero mecanismo que produce el spalling será una combinación de los dos procesos anteriormente comentados.
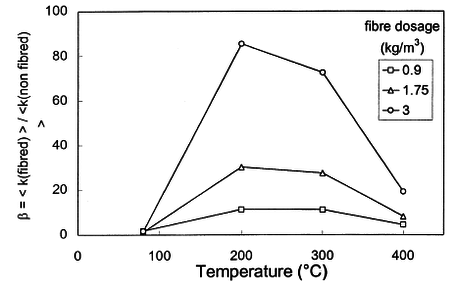
El añadido de fibras de polipropileno (FP) es una forma de evitar el evitar el spalling. Las FP tienen un notable efecto sobre el aumento de la presión de los poros durante el calentamiento: Para un hormigón con un contenido de fibra de 3 kg/m3 la presión en los poros llega a reducirse por un factor de 4 respecto de un hormigón sin fibras (Kalifa et al. 2001). Las FP funden a los 170 ºC (el spalling se da entre 190 y 250ºC) y son parcialmente absorbidas por la matriz de cemento, dejando libre un camino para el flujo de vapor. Por tanto las fibras contribuyen a la creación de una red más permeable que la matriz, que permite la migración al exterior del vapor y resulta en una reducción de presión en los poros.
2-5 Propiedades y comportamiento de las barras de acero a elevadas temperaturas
2-5-1 Generalidades
A diferencia del hormigón, el acero como material tiene muy poca resistencia al fuego. Esto se debe a que las propiedades mecánicas del acero caen muy bruscamente al aumentar su temperatura por efecto del fuego. Es por eso que todos los códigos de edificación recomiendan proteger la armadura con cierto recubrimiento mínimo, el cual se relaciona directamente con el tiempo de resistencia al fuego esperado.
A continuación se describen el efecto de la temperatura sobre las propiedades mecánicas más importantes de las barras de acero.
2-5-2 Módulo de elasticidad
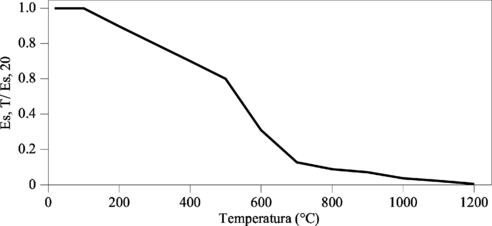
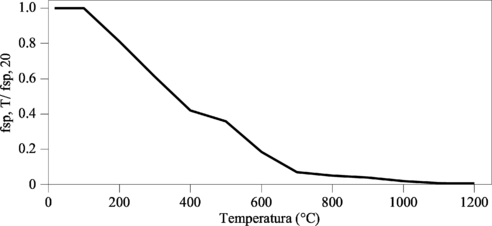
El módulo de elasticidad del acero disminuye con la temperatura. El valor del módulo de elasticidad se mantiene constante hasta 100ºC a partir de donde muestra un marcado descenso. En la Figura 2-13 se muestra la variación del módulo de elasticidad con la temperatura propuesta en Eurocode 2 (1995) para barras laminadas en caliente.
2-5-3 Resistencia a tracción
La resistencia a tracción disminuye con la temperatura. Su valor se mantiene constante hasta 400ºC a partir de donde cae abruptamente. En la Figura 2-14 se muestra la variación de la resistencia a tracción con la temperatura propuesta en Eurocode 2 (1995) para barras laminadas en caliente.
2-5-4 Límite elástico
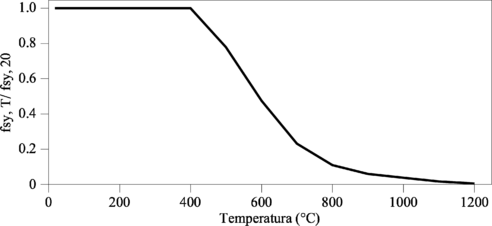
El límite elástico también disminuye con la temperatura. En la Figura 2-15 se muestra la variación del límite elástico con la temperatura propuesta en Eurocode 2 (1995) para barras laminadas en caliente.
2-5-5 Dilatación térmica
La dilatación térmica de las barras de acero aumenta con la temperatura. En Eurocode 2 (1995) se propone la siguiente formula referida a la longitud a 20 ºC:
|
|
(2.3) |
2-5-6 Relación tensión-deformación
La relación tensión-deformación a elevadas temperaturas depende de si las condiciones de ensayos son transitorias o en estado de régimen permanente. Las condiciones transitorias reflejan mejor la realidad de una situación de una estructura expuesta al fuego. En condiciones transitorias, la velocidad de calentamiento tiene cierta influencia debido a la deformación de fluencia (creep). Pero debido a que dicha deformación de fluencia es pequeña, la velocidad de calentamiento comúnmente utilizada en los ensayos es de 10ºC/min.
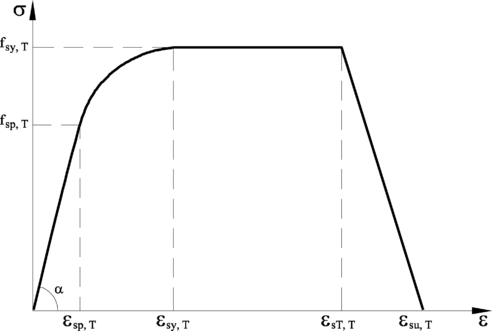
A pesar de que se han propuesto muchos modelos matemáticos para la relación tensión-deformación la mayoría se basa en el conjunto de ensayos realizados por Kirby y Preston (1988). El modelo propuesto por los Eurocódigos es bien aceptado. En dicho modelo la relación tensión-deformación para el acero consiste en una línea recta seguida de una relación elíptica y luego una meseta.
En la Figura 2-16 se presenta gráficamente el modelo propuesto en Eurocode 2 (1995) y su descripción matemática se presenta a continuación:
|
|
(2.4) |
donde es el módulo de elasticidad, es el límite de proporcionalidad, es la resistencia a tracción y los parámetros a, b y c se definen en el código mencionado.
Capítulo 3 Revisión de modelos para el análisis del hormigón a elevadas temperaturas
3-1 Introducción
Hasta el momento se han desarrollado muchos modelos que intentan analizar distintos aspectos del comportamiento del hormigón expuesto a elevadas temperaturas. Dichos modelos pueden dividirse de la siguiente manera:
- Modelos termo-mecánicos desacoplados.
- Modelos higro-térmicos-mecánicos semi acoplados.
- Modelos higro-termo-mecánicos acoplados.
3-2 Modelos termo-mecánicos desacoplados
3-2-1 Modelo Ulm, Coussy, Bazant (1999a)
En Ulm, Coussy, Bazant (1999) se desarrolla un modelo macroscópico del material para el hormigón calentado rápidamente. El hormigón es considerado como medio poroso compuesto por un esqueleto y tres fases fluidas que llenan el espacio poroso (agua, vapor y aire seco). La deformación observable es la del esqueleto sólido, denotada como . La fisuración se considera con el enfoque continuo de la elastoplasticidad por medio de un conjunto de variables como el tensor de deformación plástica y la variable de endurecimiento/ablandamiento plástico , las cuales modelan los cambios irreversibles en el esqueleto asociado a la fisuración. La masa de cemento hidratado se denota como , la cual es igual pero con signo opuesto a la masa deshidratada expelida en forma de líquido desde los microporos del gel de cemento al espacio de los poros capilares. Se considera al sistema elemental como cerrado con respecto a las fases fluidas que llenan el espacio de los macroporos.
Para formular el acoplamiento entre deshidratación, temperatura, y deformación, se utiliza el marco de los medios porosos reactivos (Coussy 1995). Para esto, se considera la energía de disipación de el material poroso reactivo cerrado, la cual se expresa como,
|
|
(3.1) |
donde el punto denota derivada temporal, es el tensor de tensiones macroscópico, es la entropía y es la energía libre (Helmholtz) por unidad de volumen. La energía libre es una función de las variables de estado, las cuales definen el estado de energía del sistema elemental. Las siguientes variables de estado son la temperatura absoluta y la deformación como variables de estado externas, y las variables plásticas y como variables de estado internas. La masa hidratada también es parte del conjunto de variables de estado internas. Se supone que la energía tiene la siguiente forma
|
|
(3.2) |
donde es un potencial reducido y es energía congelada relacionada con el endurecimiento/ablandamiento quimio-plástico. Reemplazando (3.1) en (3.2) se tiene
|
|
(3.3) |
|
|
(3.4) |
siendo,
|
|
(3.5) |
|
|
(3.6) |
donde es la tasa de disipación de energía asociada con la deformación plástica (incluyendo el endurecimiento/ablandamiento plástico); es la tasa de disipación de energía asociada con el proceso de deshidratación, es la fuerza termodinámicamente conjugada con la el endurecimiento o ablandamiento plástico y es la fuerza termodinámicamente conjugada con la masa deshidratada.
El enfoque energético permite derivar los efectos cruzados quimio-térmicos y quimio-mecánicos a partir de las simetrías de Maxwell de los potenciales y . En particular, para el proceso de deshidratación los acoplamientos se presentan de la siguiente manera
|
|
(3.7) |
La primera relación tiene en cuenta los efectos de calor latente relacionados a la deshidratación, y la segunda tiene en cuenta la dependencia de la fuerza con la masa hidratada . A partir de las ecuaciones (3.7) , las ecuaciones de estado (3.5) y (3.6) se obtienen por diferenciación en la siguiente forma incremental:
|
|
(3.8) |
|
|
(3.9) |
|
|
(3.10) |
|
|
(3.11) |
En estas ecuaciones,
- es el tensor de rigidez tangente. Este se considera función de la masa hidratada, o sea , la que para el caso isótropo toma la siguiente expresión
|
|
(3.12) |
Siendo el tensor unitario de segundo orden y tensor unitario de cuarto orden
- es la tensión de compresión inducida por el cambio de temperatura . Este tensor se relaciona con el tensor de coeficientes de dilatación térmica , por la expresión . Para el caso isótropo se reduce a .
- es el tensor de segundo orden de acoplamiento entre las propiedades elásticas y la masa hidratada . Los términos en los que aparece el tensor no son considerados, por considerar su rango de importancia más allá del entorno de temperatura de interés en Ulm, Coussy, Bazant (1999).
- es el coeficiente de acoplamiento quimio-plástico.
- es el coeficiente de endurecimiento plástico.
- es el calor específico por unidad de volumen a deformación constante.
- es el calor latente de deshidratación con signo cambiado.
- es una constante de equilibrio del proceso de deshidratación considerado.
No considerando las fuentes externas de calor, la ecuación de balance de calor queda
|
|
(3.13) |
donde es el vector de flujo de calor. Remplazando la (3.9) en la (3.13) se tendrá
|
|
(3.14) |
donde es el módulo volumétrico.
En la expresión anterior para los casos de interés práctico se pueden hacer varias simplificaciones:
- El término debido a que las deformaciones elásticas son de un orden muy pequeño .
- El término puede despreciarse debido a la baja ductilidad de los materiales cementicios.
Finalmente, adoptando para la conducción de calor la ley de Fourier, la ecuación de calor (3.14) quedará
|
|
(3.15) |
donde es el coeficiente de conductividad y es el operador laplaciano.
La evolución de la masa hidratada se relaciona con una variable conocida como grado hidratación
|
|
(3.16) |
Este grado de hidratación se relaciona con la evolución del módulo de elasticidad con la temperatura, indicando de esta manera una proporcionalidad entre el volumen de los productos de hidratación y las propiedades elásticas del hormigón.
|
|
(3.17) |
Los cambios irreversibles en el esqueleto sólido asociados con la microfisuración se consideran dentro del marco de la quimio-plasticidad (Coussy y Ulm 1996).
3-2-2 Modelo Luccioni, Figueroa, Danesi (2003)
El modelo esta basado en la hipótesis de elasticidad desacoplada. De acuerdo con esta hipótesis, la densidad de energía libre puede suponerse formada por dos partes independientes: una parte termo-elástica y otra termo-plástica. Un tercer miembro debido al daño térmico es también incluido
|
|
(3.18) |
donde es la densidad de energía libre por unidad de volumen, es la densidad de energía libre termo-elástica por unidad de volumen, es la densidad de energía libre termo-plástica por unidad de volumen, es la densidad de energía libre de termo-daño por unidad de volumen, es el tensor de deformación elástica, ![]() es el tensor de deformación,
es el tensor de deformación, ![]() es el tensor de deformaciones plástico, es la variable de daño térmico, es un conjunto de variables internas plásticas, es una medida de temperatura, es la variable de daño térmico que representa una medida de el deterioro producido por altas temperaturas tal que
es el tensor de deformaciones plástico, es la variable de daño térmico, es un conjunto de variables internas plásticas, es una medida de temperatura, es la variable de daño térmico que representa una medida de el deterioro producido por altas temperaturas tal que
|
|
(3.19) |
Se adopta la siguiente expresión para la densidad de energía libre termo-elástica
|
|
(3.20) |
donde ![]() es el tensor constitutivo secante afectado por el daño mecánico y por el proceso de daño térmico, y es la temperatura de referencia.
es el tensor constitutivo secante afectado por el daño mecánico y por el proceso de daño térmico, y es la temperatura de referencia.
El tensor constitutivo secante tiene en cuenta un daño mecánico escalar y un daño térmico isótropo caracterizado por la variación en el módulo elástico y el coeficiente de Poisson como función de la variable de daño térmico. Se propone la siguiente expresión para el tensor constitutivo secante
|
|
(3.21) |
donde y son el módulo elástico y el coeficiente de Poisson afectados por el proceso de daño térmico que puede ser obtenido de ensayos. es el tensor de acoplamiento termo-elástico que representa la tensión inducida por unidad de temperatura por restricción de la dilatación térmica y se puede expresar como
|
|
(3.22) |
representa el tensor de coeficientes de dilatación que en el caso isótropo puede escribirse, . es el calor específico o cantidad de calor requerida para aumentar la temperatura en 1 y puede obtenerse como sigue
|
|
(3.23) |
La otra parte plástica de la densidad de energía libre puede escribirse como
|
|
(3.24) |
donde es el tensor de endurecimiento plástico que depende del daño térmico.
La disipación total por unidad de volumen puede escribirse como sigue
|
|
(3.25) |
donde es el tensor de tensiones, es la entropía específica, es flujo de calor por conducción y son las coordenadas espaciales.
El cumplimiento de la desigualdad de Clausius Duhem se garantiza si
|
|
(3.26) |
Además la disipación mecánica y térmica son ambas negativas
|
|
(3.27) |
|
|
(3.28) |
La ecuación de conservación de calor puede obtenerse combinando la primera y la segunda ley de la termodinámica. Suponiendo la ley de Fourier para la conducción de calor, se tendrá
|
|
(3.29) |
donde los términos entre paréntesis presentan el acoplamiento termo-mecánico, los cuales son despreciados en Luccioni, Figueroa, Danesi (2003). Además
|
|
(3.30) |
|
|
(3.31) |
siendo el calor latente del daño térmico , es la conductividad, y es las fuentes de calor distribuidas por unidad de volumen.
La evolución del daño térmico se evalúa suponiendo que la relación entre la reducción del módulo elástico respecto de su valor el inicial es proporcional a la variable de daño térmico. Las curvas experimentales que relacionan el módulo de elasticidad con la temperatura pueden utilizarse para expresar la siguiente relación:
|
|
(3.32) |
3-3 Modelos higro-térmicos-mecánicos semi acoplados
3-3-2 Introducción
Se han desarrollado varios modelos higro-térmicos para analizar la evolución de las presiones de poros y de las temperaturas al someter al hormigón a la acción del fuego. Entre estos modelos se encuentran los trabajos de Bazant yThonguthai (1978, 1979), Ahmed y Hurst (1995, 1997a, 1997b) y Tenchev, Li y Purkiss (2001a, 2001b). Estos modelos permiten predecir el campo de temperaturas y de presiones de poros, no obstante no permiten analizar la resistencia mecánica del hormigón.
En Tenchev y Purnell (2005) se acopla la solución del problema higro-térmico planteada en Tenchev, Li y Purkiss (2001a, 2001b) con el modelo constitutivo de daño mecánico propuesta por Ortiz (1985).
3-3-2 Modelo Bazant Thonguthai (1978, 1979)
En Bazant Thonguthai (1978,1979) se desarrollan un modelo unidimensional y bidimensional con su respectiva solución numérica con el método de los elementos finitos, para predecir la presión en los poros para el hormigón calentado. La teoría se basa en las propiedades termodinámicas del agua y tiene en cuenta el enorme cambio en la permeabilidad y en la absorción isotérmica con la temperatura, como así también los cambios en el espacio de poros debido a la temperatura y presión.
El acoplamiento del transporte de humedad y calor en el hormigón calentado se expresa por el vector de flujo másico de humedad , y por el vector de flujo de calor , como una combinación lineal de los gradientes de la presión de poros y de temperatura
|
|
(3.33) |
|
|
(3.34) |
En la cual es la permeabilidad (m s-1), es la conductividad térmica y la aceleración de la gravedad.
La condición de conservación de masa se escribe como
|
|
(3.35) |
En la cual es el contenido de agua libre (masa de toda el agua por m3 de hormigón, no vinculada químicamente), y es la masa del agua libre que se libera dentro de los poros por deshidratación.
|
|
(3.36) |
Donde es la densidad del hormigón, es la capacidad calórica isobárica del hormigón incluyendo el agua combinada químicamente pero excluyendo su agua libre, es la capacidad calórica del agua libre más el calor de absorción de las capas de agua absorbida en las paredes de los poros, es la capacidad calórica del agua líquida.
Las condiciones de contorno para el transporte de calor y humedad en la superficie son
|
|
(3.37) |
|
|
(3.38) |
donde es el vector unitario de la normal exterior a la superficie, y son la presión parcial y la temperatura del entorno adyacente, y son los valores de y de la superficie del hormigón, la pérdida de calor debida a el calor latente de la humedad de vaporización en la superficie, y son la emisividad superficial para la humedad y el calor, respectivamente ( y representa el caso un hormigón perfectamente sellado y perfectamente aislado, y representa el caso de transmisión perfecta de humedad y calor).
3-3-3 Modelo Ahmed y Hurst (1995, 1997a, 1997b)
Ahmed y Hurst (1995, 1997a, 1997b) desarrollan un modelo matemático y computacional, simulando el acoplamiento del transporte de masa y calor y los procesos relacionados en el hormigón expuesto a elevadas temperaturas. Se obtiene un conjunto de tres ecuaciones diferenciales acopladas, teniendo en cuenta la conservación de masa, momentun y energía, e incluyendo los efectos de los procesos de evaporación y deshidratación en el fenómeno de transporte. El modelo permite predecir la temperatura, contenido de humedad y presión en los poros.
Las siguientes hipótesis y consideraciones se aplican para la simulación numérica,
- El hormigón es un sistema poroso multifase.
- La movilidad del líquido es despreciable comparada con la de la mezcla gaseosa.
- El vapor de agua, el aire y su mezcla gaseosa siguen la ley universal de los gases ideales.
- La presión de saturación del vapor del agua libre está dada por la ecuación de Clausius-Clayperon.
- El contenido local de humedad en equilibrio (agua libre en los poros) se relaciona con la presión de vapor relativa y la temperatura en el hormigón a través de una relación constitutiva expresada como un conjunto de curvas de absorción isotérmicas .
- Se considera la descomposición térmica del agua químicamente ligada, la cual se determina por análisis termogravimétricos.
- Se tienen en cuenta los mecanismos de evaporación /condensación del agua contenida en el medio poroso.
- Se consideran la conducción de calor, la transferencia convectiva y difusiva de masa y calor a través del medio poroso.
- La transferencia convectiva de calor y masa está generada por un gradiente de presión en los poros, el transporte difusivo por una gradiente de concentración de masa, y la transferencia de calor por un gradiente de temperatura.
La ecuación de conservación de masa de vapor de agua es:
|
|
(3.39) |
La ecuación de conservación de masa para la mezcla gaseosa de vapor de agua y aire es
|
|
(3.40) |
La tasa de evaporación de agua por unidad de volumen del medio poroso , esta dada por
|
|
(3.41) |
La ecuación de conservación de energía es:
|
|
(3.42) |
El término de evaporación deshidratación en la ecuación de energía, se define como
|
|
(3.43) |
donde es la densidad efectiva del medio poroso, es la densidad del vapor de agua, es la densidad de la mezcla gaseosa, es la fracción de volumen de la mezcla gaseosa en el medio poroso, es el coeficiente de permeabilidad, es la presión en los poros de la mezcla gaseosa en el medio poroso, es la fracción molar de agua de la mezcla gaseosa, la difusividad modificada de la mezcla gaseosa, el calor específico efectivo, Cpg el calor específico de la mezcla gaseosa, Cpa el calor específico del aire en la mezcla gaseosa, es la temperatura absoluta, es el tiempo, la coordenada espacial, la conductividad térmica efectiva, la tasa de la masa de evaporación por unidad de volumen de medio poroso, es el calor latente de evaporación, es el calor latente de evaporación y deshidratación, es el contenido de agua libre en los poros, es el contenido de agua químicamente ligada.
Las condiciones iniciales se dan a partir de una distribución uniforme de temperatura, presión en los poros y contenido de humedad en el hormigón en el instante inicial. Las condiciones de contorno para simular losas de hormigón expuestas al fuego, son de exposición al fuego de un lado y a condiciones ambientales del otro. Las condiciones de contorno a ambos lados de la losa pueden especificarse como sigue,
Superficie expuesta al fuego :
|
|
(3.44) |
|
|
(3.45) |
|
|
(3.46) |
Superficie no expuesta al fuego :
|
|
(3.47) |
|
|
(3.48) |
|
|
(3.49) |
Donde es el coeficiente de transferencia de calor total, es el coeficiente de transferencia de masa, es el peso molecular de vapor de agua en la mezcla gaseosa, coeficiente de difusividad, presión atmosférica, temperatura del fuego, temperatura ambiente, fracción molar de vapor de agua de la mezcla gaseosa en la zona expuesta al fuego, fracción molar de vapor de agua de una mezcla gaseosa del ambiente.
Las ecuaciones diferenciales de gobierno de conservación de masa y energía (3.39), (3.40) y (3.42) se resuelven usando las técnicas numéricas por un esquema implícito completo de diferencias finitas.
3-3-4 Modelo Thenchev, Li y Purkiss (2001a, 2001b)
En Thenchev, Li y Purkiss (2001a, 2001b) se propone un modelo higro-térmico para el análisis del hormigón expuesto al fuego. A partir de las leyes básicas de conservación de masa y de energía se obtiene el sistema acoplado de ecuaciones diferenciales para el transporte de calor y de masa.
-Ecuación de conservación de energía:
|
|
(3.50) |
El termino “ ” representa la tasa de cambio de la energía acumulada por unidad de volumen; es la capacidad calórica efectiva del hormigón cuando este se considera un mezcla de esqueleto sólido, agua y gas. El termino “ ” representa la energía difundida por conducción ( es la conductividad térmica efectiva). El termino “ ” representa la energía transmitida por convección. El termino “ ” representa la energía requerida por evaporación del agua líquida ( es el calor latente de evaporación y es la tasa de evaporación). El termino “ ” representa la energía combinada requerida para la liberación de agua ligada por deshidratación del esqueleto sólido y eventualmente su evaporación si las condiciones termodinámicas son tales que agua en estado líquido no puede existir. es la densidad de agua químicamente ligada por unidad de volumen de hormigón; ; es el calor específico de deshidratación del agua ligada; cuando , el agua químicamente ligada se libera como agua líquida o cuando el agua ligada se libera como vapor.
-Ecuación de conservación de agua líquida:
|
|
(3.51) |
El termino “ ” representa la tasa de cambio de contenido de agua líquida en una unidad de volumen de hormigón, el termino “ ” representa masa de agua transmitida por convección ( es el flujo de agua líquida), el termino “ ” representa la pérdida de masa por evaporación y el termino “ ” representa la masa ganada por deshidratación del agua químicamente ligada.
-Ecuación de conservación de agua líquida:
|
|
(3.52) |
donde es la fracción volumétrica de la mezcla de gases y es el flujo de vapor de agua.
-Ecuación de conservación de agua líquida:
|
|
(3.53) |
donde es el flujo de aire seco.
Los flujos másicos son:
|
|
(3.54) |
|
|
(3.55) |
|
|
(3.56) |
donde es la densidad de la fase i por unidad de volumen de la mezcla de gases, es el coeficiente de difusión entre el aire seco y vapor de agua y son la velocidades.
Las velocidades de la mezcla de gases y de agua líquida se supone que se relacionan con los correspondientes gradientes de presiones de poros a través de la formula de Darcy:
|
|
(3.57) |
donde es la permeabilidad intrínseca del hormigón, es la permeabilidad relativa de la fase i, es la presión y es la viscosidad dinámica. Los subíndices de las fases son = , = , = y = .
No se realiza ninguna distinción entre agua líquida libre en los poros y el agua absorbida en la superficies de los poros. El flujo del agua líquida se considera como el promedio de esos flujos.
Se supone que el aire y vapor de agua responden a la ley de gases ideales. El equilibrio entre vapor de agua y contenido de agua líquida se asume que está gobernado por las curvas de absorción (Bazant Thonguthai 1978, 1979)
Luego de la eliminación de la tasa de evaporación queda planteado un sistema de tres ecuaciones diferenciales en las variables .
3-3-5 Modelo Thenchev y Purnell (2005)
En Thenchev y Purnell (2005) se considera que para modelar concretamente el spalling en el hormigón expuesto a elevadas temperaturas es necesario tener en cuenta la aparición de fisuras paralelas a la dirección de carga de compresión uniaxial. El modelo constitutivo propuesto por Ortiz (1985) permite predecir la aparición de fisuras verticales debido a la acción de cargas de compresión. En dicho modelo se considera al hormigón como una mezcla de áridos y mortero. Pueden predecirse tensiones transversales de tracción bajo la acción de cargas de compresión debido a la interacción entre agregado y mortero, y también al posterior daño en este último.
En el trabajo Thenchev y Purnell (2005) se mejora el modelo de Ortiz (1985) para tener en cuenta el efecto de las altas temperaturas y la dependencia de las propiedades de los materiales con la temperatura.
Utilizando las presiones de poros obtenidas con el modelo de Thenchev, Li y Purkiss (2001a, 2001b) se introducen en el modelo mecánico antes comentado como fuerzas de masa. La magnitud de dichas fuerzas de masa se calculan a partir de los gradientes de la presiones de poros:
|
|
(3.58) |
donde es el coeficiente de Biot.
Es importante remarcar que en este modelo el campo de presiones y temperaturas está débilmente acoplado con el de desplazamientos. Una variación de presiones y temperaturas pude modificar las deformaciones, y consecuentemente la fisuración en el cuerpo. Por el contrario una variación en el campo de deformaciones o de fisuración en el cuerpo no altera el campo de presiones y temperaturas.
3-4 Modelos higro-térmo-mecánicos acoplados
3-4-1 Modelo Gawin, Pesavento y Schrefler (1999, 2003)
En este modelo el hormigón es tratado como un sistema multifásico donde los vacíos del esqueleto se llena parcialmente con una fase líquida y parcialmente con una fase gaseosa. La fase líquida consiste en agua físicamente ligada o absorbida (bound water) la cual está presente en rango completo de contenidos de agua del medio, y agua capilar o agua libre la cual aparece cuando el contenido de agua excede el llamado punto de saturación del sólido Sssp, o sea el límite superior de la región higroscópica del contenido de humedad. La fase gaseosa, o sea el aire húmedo, es una mezcla de aire seco (parte no-condensable) y vapor de agua (gas condensable), y se asume que se comporta como un gas ideal.
El modelo completo consiste en las siguientes ecuaciones de balance: masa del esqueleto sólido, masa de aire seco, masa de las especies del agua (ambas líquida y gaseosa, teniendo en cuenta los procesos de cambios de fase: evaporación-condensación, absorción-deabsorción y hidratación-deshidratación), entalpía del medio completo ( se consideran el calor latente de los cambios de fase y los efectos térmicos de los procesos de hidratación y deshidratación), momentum lineal del sistema multifásico. Las ecuaciones de balance se completan con un apropiado conjunto de ecuaciones de estado y constitutivas, así como relaciones termodinámicas.
Para describir unívocamente el estado del hormigón a elevadas temperaturas, se necesitan cuatro variables de estado primarias: la presión del gas , la presión capilar , la temperatura y desplazamiento de la matriz sólida , así como también tres variables que describen el avance de los procesos de deshidratación y deterioro: el grado de deshidratación , el parámetro de daño termo-químico , y el parámetro de daño mecánico . Todas la otras cantidades físicas que caracterizan al hormigón húmedo y sus constituyentes pueden encontrase por medio de ecuaciones de estado y relaciones termodinámicas (Gawin, Pesavento y Schrefler, 2003)
El modelo completo consiste en siete ecuaciones: dos ecuaciones de balance de masa, una ecuación de balance de energía (entalpía), una ecuación de balance de momento lineal y tres ecuaciones de evolución. Las ecuaciones del modelo para el caso del esqueleto incompresible, expresadas en términos de las variables de estado primarias, luego de introducir las relaciones constitutivas (Gawin, Pesavento y Schrefler 2003), toman la siguiente forma final:
- Ecuación de balance de entalpía del medio multifásico:
|
|
(3.59) |
Donde el término fuente del vapor de agua se expresa por,
|
|
(3.60) |
- Ecuación de conservación de momento lineal del medio multifásico:
|
|
(3.61) |
Con definida por:
|
|
(3.62) |
- Ecuación de conservación del aire seco (incluyendo el balance de masa del esqueleto sólido):
|
|
(3.63) |
- Ecuación de conservación de las especies del agua (líquido y vapor) incluyendo el balance de masa del esqueleto sólido:
|
|
(3.64) |
- La ecuación de evolución del proceso de deshidratación :
|
|
(3.65) |
- Ecuación de evolución del daño termo-químico,
|
|
(3.66) |
Siendo el módulo de elasticidad inicial a la temperatura sin cargar y es la temperatura ambiente (20°C).
- Ecuación de evolución del daño mecánico, d(t) (Gawin, Pesavento y Schrefler 2003).
El daño mecánico del hormigón se considera siguiendo el modelo escalar isótropo de Mazars.
Para cerrar el modelo son necesarias las condiciones iniciales y de contorno. Las condiciones iniciales especifican los campos completos de las variables de estado primarias en el instante , en el dominio completo analizado y en su contorno ,
|
|
(3.67) |
Las condiciones de contorno (BCs) pueden ser de tipo Dirichlet sobre
|
|
(3.68) |
También pueden ser de tipo de Cauchy (BCs mixtas) sobre :
|
|
(3.69) |
donde es el vector normal apuntando hacia el gas del entorno exterior, son respectivamente, los flujos impuestos de aire seco, vapor y calor, y es la tracción impuesta, ![]() y
y ![]() son la concentración másica de vapor de agua y la temperatura en un campo lejano sin perturbar de fase gaseosa, es la emisividad de la superficie, el la constante de Stefan-Boltzmann, mientras que y son los coeficientes de intercambio convectivo de masa y calor. Las condiciones de contorno, con solamente los flujos impuestos se llaman BCs de Neuman. Las condiciones de contorno puramente convectivo para intercambio de humedad y calor se llaman BCs de Robin.
son la concentración másica de vapor de agua y la temperatura en un campo lejano sin perturbar de fase gaseosa, es la emisividad de la superficie, el la constante de Stefan-Boltzmann, mientras que y son los coeficientes de intercambio convectivo de masa y calor. Las condiciones de contorno, con solamente los flujos impuestos se llaman BCs de Neuman. Las condiciones de contorno puramente convectivo para intercambio de humedad y calor se llaman BCs de Robin.
3-4-2 Modelo Mounajed y Obeid (2004)
En Mounajed y Obeid (2004) se desarrolla un modelo basado en la teoría de la Mecánica de Medios Porosos (Coussy 1995). Se establecen las siguientes hipótesis en el modelo,
- El medio poroso consiste en tres fases, fase sólida (índice s), fase líquida (índice l) conteniendo solamente agua pura, y fase gaseosa (índice g) conteniendo una mezcla de aire seco (índice a) y vapor de agua (índice v).
- El medio poroso se considera homogéneo, isótropo y se supone que tiene un comportamiento termo-poro-elástico no lineal.
- La evolución del sistema es cuasiestática.
- Las transformaciones del esqueleto se consideran infinitesimales.
- La fase gaseosa se comporta como una mezcla ideal de gases perfectos.
- La matriz sólida se considera químicamente inerte.
- Se tiene en cuenta el cambio de fase líquido-vapor que se desarrolla en el medio poroso.
- No se consideran los fenómenos de histéresis de las curvas de absorción.
- Las leyes de conducción de calor y de masa de fluidos se consideran desacopladas.
Las ecuaciones de gobierno del problema de evolución cuasiestático en el comportamiento termo-poro-elástico no-lineal son:
Ecuaciones de conservación
1- Ecuación de conservación de momento lineal:
|
|
(3.70) |
2- Ecuación de conservación de masa de fluidos:
|
|
(3.71) |
|
|
(3.72) |
|
|
(3.73) |
3- Ecuación de conservación de calor
|
|
(3.74) |
Ecuaciones de comportamiento
1-Ley de Darcy para la transferencia del líquido
|
|
(3.75) |
2- Ley de Fick para la transferencia del vapor y aire seco
|
|
(3.76) |
|
|
(3.77) |
3- Ley de transferencia de Fourier
|
|
(3.78) |
4- Ecuaciones de estado del comportamiento termo-poro-elástico no lineal
|
|
(3.79) |
|
|
(3.80) |
|
|
(3.81) |
5- Leyes de cambio de estado líquido-vapor
Se supone que el cambio de fase se produce sin disipación y está gobernado por la ley de Clapeyron generalizada:
|
|
(3.82) |
Variables independientes del modelo
Las variables del modelo son las siguientes: el campo de desplazamientos , la temperatura y las presiones intersticiales . Las tres presiones intersticiales son interdependientes entre sí de la siguiente manera:
|
|
(3.83) |
Consecuentemente, se eligen solo dos presiones intersticiales independientes: la presión total de gas y la presión capilar .
Capítulo 4 Mecánica de medios porosos no saturados
4-1 Introducción
Tal y como ya se ha comentado, las temperaturas elevadas en el hormigón inducen importantes modificaciones en su micro-estructura debidos a los procesos físico-químicos que se desarrollan.
Entre los efectos más importantes del aumento elevado de temperatura en el hormigón se han mencionado (Luccioni et al, 2003):
- Deshidratación de la pasta de cemento.
- Incremento de la porosidad.
- Modificación del contenido de humedad.
- Expansión térmica.
- Aumento de la presión de poros.
- Pérdida de resistencia.
- Fisuración debida a deformaciones térmicas restringidas.
- Fluencia térmica.
- Retracción.
- Spalling.
Para tratar de tener en cuenta todos estos fenómenos en el análisis de estructuras de hormigón expuestas al fuego es necesario desarrollar un modelo higro-termo-mecánico (Gawin et al, 2003). Los modelos termo-mecánicos tradicionales (Luccioni et al., 2003, Ulm et al., 1999a) que no tienen en cuenta la componente hídrica, no pueden considerar la presión en los poros como uno de los motivos del fenómeno de spalling (Mssad, 2005).
Para desarrollar un modelo de estas características es necesario considerar al hormigón como un material poroso (Ulm et al, 2004). El modelo higro-termo-mecánico desarrollado en este trabajo se basa en el marco teórico de la mecánica de medios porosos no saturados (Coussy 1995, 2004).
En este capítulo se realizará un breve resumen de la teoría de la mecánica de medios porosos no saturados (Coussy 1995, 2004).
4-2 Enfoque contínuo de los medios porosos no saturados
El medio poroso no saturado se compone de un esqueleto y un espacio poroso. Este espacio poroso se llena de tres fases fluidas: agua líquida, vapor de agua y aire seco. En general se considera al vapor de agua y al aire seco como una mezcla ideal de gases dando lugar a la fase de aire húmedo. El medio poroso se trata como la superposición de tres continuos, el continuo del esqueleto, el continuo del agua líquida y el continuo del aire húmedo. De esta manera cualquier partícula infinitesimal del medio se trata como la superposición de tres partículas materiales (Figura 4-1). La primera es la partícula del esqueleto formado por la matriz y el espacio poroso interconectado vacío de fluidos. Las otras dos partículas se asocian a las fases fluidas de agua líquida y aire húmedo.
4-3 Deformación del esqueleto
La deformación de esqueleto es la deformación única que eventualmente puede observarse. El esqueleto se deforma cuando se somete a la acción de fuerzas externas y cuando varía la presión en las fases fluidas. La descripción de esta deformación no difiere de la que se realiza en un sólido continuo estándar.
En el instante se considera una configuración inicial para el esqueleto. En esta configuración una partícula del esqueleto se ubica por su vector posición de componentes. , referido a un sistema de ejes coordenados Cartesianos de base ortonormal . En el instante el esqueleto ha deformado y se encuentra en la configuración actual. En esta configuración la partícula cuyo vector posición inicial era se ubica ahora en el vector posición actual de componentes . Luego se escribe
|
|
(4.1) |
donde los índices repetidos se suman. En lo que sigue se adopta dicha convención, y estará referida a un sistema coordenado cartesiano.
Gradiente de deformación y transporte de un vector . En la configuración inicial se considera un vector material infinitesimal uniendo la partícula ubicada en a la partícula próxima ubicada en . Después de la deformación pasa a ser uniendo las mismás partículas de esqueleto con sus nuevas posiciones, y (Figura 4-2). El vector puede ser obtenido de por diferenciación de (4.1)
|
|
(4.2) |
o en forma equivalente
|
|
(4.3) |
donde
|
|
(4.4) |
en (4.4) denota el operador nabla relativo a la configuración inicial. se conoce como tensor gradiente de deformación. Este tensor transporta cualquier vector material a su deformado . Su inversa y su transpuesta se definen respectivamente como,
|
|
(4.5) |
y satisface
|
|
(4.6) |
Gradiente de deformación y desplazamiento. Sea el vector de desplazamientos de una partícula para la cual sus posiciones iniciales y finales son respectivamente y . Luego se define
|
|
(4.7) |
De las definiciones (4.4) y (4.7) el tensor gradiente de deformación puede expresarse como función del vector de desplazamientos de acuerdo a:
|
|
(4.8) |
donde es el delta de Kronecker.
Transporte de un elemento de volumen. El volumen infinitesimal actual es igual al producto compuesto
|
|
(4.9) |
donde (sin suma). La linealidad del producto compuesto con respecto a los vectores permite escribir
|
|
(4.10) |
Como consecuencia cualquier volumen material inicial transforma en el volumen material a través de la relación
|
|
(4.11) |
donde es el Jacobiano de la transformación.
Transporte de un elemento de superficie. Se considera una superficie material , orientada según la normal unitaria . Con motivo de la deformación se transforma en la superficie material , orientada según la normal unitaria . Debido a que y no son vectores materiales, estos no están relacionados en la deformación. Sea cualquier vector material en la configuración inicial. El cilindro material de volumen inicial se transforma en el cilindro material de volumen (Figura 4-3). De acuerdo a (4.11) se tiene
|
|
(4.12) |
Debido a que (4.12) es válida para cualquier vector , se deduce que
|
|
(4.13) |
Sea cualquier vector vinculado a la configuración actual y sea el vector asociado vinculado a la configuración inicial y definido en tal manera que el flujo de a través de coincide con el flujo de a través de . Luego se escribe
|
|
(4.14) |
A partir de (4.13) y (4.14) se deduce
|
|
(4.15) |
Integrando (4.14) sobre los volúmenes y relacionados por la deformación, seguido del uso del teorema de la divergencia y la relación (4.11), se obtiene la valiosa identidad
|
|
(4.16) |
Tensor de deformación. La deformación induce cambios en las longitudes de los vectores materiales y en los ángulos entre ellos. El tensor de deformaciones de Green-Lagrange mide dichos cambios por medio de la cuantificación de la variación del producto escalar de dos vectores materiales y transformados en la deformación a y respectivamente. Se tiene
|
|
(4.17) |
Utilizando (4.5) puede expresarse a en función del gradiente de deformación de acuerdo a:
|
|
(4.18) |
Asimismo utilizando (4.8) puede expresarse a como función de los desplazamientos de acuerdo a:
|
|
(4.19) |
|
|
(4.20) |
Porosidades Eulerianas y Lagrangeanas. Dado un elemento infinitesimal de volumen en la configuración actual, se define a como la porosidad Euleriana, tal que, el volumen que ocupan los fluidos en dicha configuración es . Debido a que el elemento material de volumen cambia con la deformación, la porosidad no cuantificará apropiadamente el cambio de volumen del espacio poroso vinculado al volumen material inicial . En contraste con la porosidad Euleriana , la cual se refiere al volumen actual , el cambio en el espacio poroso eventualmente se captura mejor por medio de la porosidad Lagrangeana , la cual refiere el volumen de poros actual al volumen inicial de acuerdo a:
|
|
(4.21) |
siendo el Jacobiano de la deformación tal que y es el tensor gradiente de deformación.
Transformaciones infinitesimales y tensor de deformaciones infinitesimales. En muchos problemás se puede realizar una aproximación de primer orden de la teoría finita bajo la condición de transformaciones infinitesimales, o sea
|
|
(4.22) |
En el límite de las transformaciones infinitesimales la configuración actual e inicial se juntan, tal que el operador puede ser usado sin necesidad de un subíndice que lo refiera a una configuración particular, o sea .
Bajo la condición (4.22) el tensor de deformaciones de Green-Lagrange se reduce al tensor de deformaciones infinitesimales
|
|
(4.23) |
Utilizando la aproximación de transformaciones infinitesimales, (4.8) se escribe como
|
|
(4.24) |
Se define a como la dilatación volumétrica del esqueleto, de manera tal que (4.11) se reescribe como
|
|
(4.25) |
La dilatación volumétrica macroscópica observable que experimenta el esqueleto se debe al cambio en la porosidad y a la dilatación volumétrica de la matriz sólida, sin embargo esta última no es directamente accesible a partir de experimentos macroscópicos. Análogamente a (4.25) puede describirse la evolución del volumen ocupado por la matriz sólida
|
|
(4.26) |
El volumen ocupado por la matriz sólida se relacionan con el volumen total a partir de la relaciones
|
|
(4.27) |
Combinado (4.26) y (4.27) se deduce la expresión de balance de volumen
|
|
(4.28) |
4-4 Derivada material referida a cada partícula
La descripción de la deformación del esqueleto por medio del tensor gradiente de deformación es por naturaleza una descripción Lagrangeana. Los campos son funciones del tiempo y del vector posición que localiza la partícula en la configuración inicial. Esta última no varía con el tiempo y la cinemática del esqueleto resulta en una simple derivada temporal.
En contraste con la Lagrageana, la descripción Euleriana involucra solamente a la configuración actual, sin referencia a la configuración inicial. Este enfoque se realiza utilizando el campo de velocidades de la partícula coincidente en el instante con el punto geométrico ubicado en . La partícula puede ser una partícula del esqueleto , una partícula de agua líquida . En el instante , se aplica la misma descripción Euleriana debido a que el continuo del esqueleto, el continuo del agua líquida y el continuo del aire húmedo se funden en la misma configuración actual.
La consideración de las distintas descripciones (Lagrangeana y Euleriana) de las propiedades del medio poroso lleva a diversas definiciones de las derivadas temporales de dichas propiedades.
Un concepto muy utilizado en la mecánica de medios continuos clásica es el de la derivada material. Esta última se refiere a la variación de la propiedad respecto al tiempo siguiendo a una partícula material específica del medio continuo.
Debido a que en el medio poroso no saturado coexisten tres medios continuos, debe definirse la derivada material referida a las partículas materiales de dichos continuos. Dado un campo , se denota la derivada material del campo referida a la partícula como .
A continuación se repasan las expresiones de la derivada material de algunas propiedades.
Derivada material de un vector material
|
|
(4.29) |
Derivada material de un volumen material
|
|
(4.30) |
Derivada material de un campo
|
|
(4.31) |
Derivada material de una integral de volumen de un campo
|
|
(4.32) |
4-5 Porosidades parciales y grado de saturación
El espacio poroso es llenado por tres fluidos: agua en estado líquido (índice l), vapor de agua (índice v) y aire seco (índice a). Se define la porosidad total ![]() y las porosidades parciales
y las porosidades parciales ![]() y
y ![]() como
como
|
|
(4.33) |
donde denota el volumen de una partícula del medio poroso, denota el volumen de poros existente en , denotan respectivamente los volúmenes de líquido, vapor y aire seco que hay en dicha partícula.
Se define al grado de saturación ![]() del fluido
del fluido ![]() como
como
|
(4.34) |
Se define a ![]() como la densidad intrínseca y a
como la densidad intrínseca y a ![]() el contenido de masa de fluido, ambos relacionados al fluido
el contenido de masa de fluido, ambos relacionados al fluido ![]()
|
(4.35) |
Se considera que el vapor de agua y el aire seco ocupan el mismo espacio poroso formando una mezcla ideal de gases constituyendo la fase gaseosa (índice g)
|
|
(4.36) |
4-6 Balance de masa
4-6-1 Ecuaciones Eulerianas de continuidad
Sean y la densidades mesoscópicas o intrínsecas de la matriz sólida y del fluido respectivamente, de manera tal que y representan respectivamente las masas de esqueleto y del fluido contenidas en el volumen material . De acuerdo con esto, y representan respectivamente las densidades macroscópicas o aparentes del esqueleto y del fluido .
Cuando no se producen cambios en la masa del esqueleto (deshidratación de la matriz sólida) ni en la del fluido (cambios de fase de las especies acuosas) contenido en el volumen , el balance de masa se puede expresar como
|
|
(4.37) |
|
|
(4.38) |
Aplicando (4.32) a (4.37) y (4.38) se obtiene
|
|
(4.39) |
|
|
(4.40) |
y las ecuaciones Eulerianas de continuidad
|
|
(4.41) |
|
|
(4.42) |
4-6-2 Ecuaciones Lagrangeanas de continuidad
Sea la masa del fluido que atraviesa el elemento diferencial de superficie orientado según una normal n entre los instantes y . Luego se puede escribir
|
|
(4.43) |
donde es el vector Euleriano de flujo relativo de masa del fluido . Debido a que la cantidad es el volumen infinitesimal de fluido que atraviesa la superficie del esqueleto en el instante infinitesimal de tiempo , el vector de flujo relativo de masa de fluido , , se define consistentemente como (Figura 4-4)
|
|
(4.44) |
donde es el vector de filtración del fluido . Usando la definición (4.44) es posible referir el balance de masa del fluido al movimiento del esqueleto reordenando la ecuación de continuidad del fluido de la siguiente manera
|
|
(4.45) |
Las expresiones Lagrangeanas del balance de masa de fluido se puede obtener introduciendo el contenido de masa Lagrangeano de fluido actual por unidad de volumen inicial . Este último se relaciona al contenido de masa Euleriano de fluido actual por unidad de volumen actual de acuerdo a:
|
|
(4.46) |
Utilizando (4.21) y (4.46) se obtiene la relación
|
|
(4.47) |
donde representa la porosidad Lagrangeana.
Sea el vector Lagrangeano vinculado a la configuración inicial y relacionado al vector a través de la relación
|
|
(4.48) |
donde las superficies y corresponden a la deformación del esqueleto. De esta manera, utilizando las expresiones (4.14) a (4.16) se obtiene la formula de transporte siguiente
|
|
(4.49) |
Sustituyendo (4.46) y (4.49) en (4.45) remultiplicando por , y utilizando (4.30), se obtiene la ecuación Lagrangeana de continuidad del fluido
|
|
(4.50) |
En adelante se adoptará la hipótesis de transformaciones infinitesimales. De esta manera la ecuación (4.50) se reescribe como
|
|
(4.51) |
Si en las expresiones de conservación de masa de las fases fluidas (4.51), se tienen en cuenta el proceso de cambio de fase de líquido a vapor se tendrá
|
|
(4.52) |
|
|
(4.53) |
|
(4.54) |
donde es la tasa de transformación de líquido a vapor por unidad de volumen y es el vector de flujo relativo relacionado al fluido .
La expresión Lagrangeana de balance de masa del esqueleto se obtiene remplazando (4.21) en (4.39)
|
|
(4.55) |
Operando sobre la expresión (4.55) y teniendo en cuenta (4.21), se tiene
|
|
(4.56) |
Adoptando nuevamente la hipótesis de transformaciones infinitesimales, se puede suponer que . Asimismo de la ecuación (4.24) se deduce que . De esta manera la ecuación (4.56) se reescribe como
|
|
(4.57) |
Si se tiene en cuenta en la expresión de conservación de masa del esqueleto los procesos de deshidratación de la masa del sólido se obtiene la siguiente expresión para la variación temporal de la porosidad Lagrageana
|
|
(4.58) |
donde es la tasa de deshidratación de la masa del sólido. Esta tasa puede obtenerse experimentalmente a partir de ensayos termogravimétricos (Harmathy y Allen, 1973).
En la expresión (4.58) aparece la variación temporal de la densidad de la matriz sólida , dicha variación se puede obtener suponiendo la siguiente expresión funcional para (Gawin et al., 2003)
|
|
(4.59) |
|
|
(4.60) |
donde representa el primer invariante del tensor de tensiones efectivas. El tensor de tensiones efectivas se define como
|
|
(4.61) |
Se asume la siguiente relación para la variación temporal del primer invariante del tensor de tensiones efectivas (Gawin et al., 2003)
|
|
(4.62) |
donde es el módulo volumétrico del esqueleto, es el módulo volumétrico de la matriz sólida y es el coeficiente de dilatación térmica de la matriz sólida.
La expresión (4.60) puede rescribirse de la siguiente manera (Gawin et al., 2003)
|
|
(4.63) |
donde
|
|
(4.64) |
Remplazando (4.62) en (4.63) y la expresión resultante en (4.58) se obtiene
|
|
(4.65) |
4-7 Balance de la cantidad de movimiento
Denotando a la tensión total por y despreciando los términos dinámicos (aproximación cuasiestática), el balance de la cantidad de movimiento total (del medio poroso en conjunto) se expresa como:
|
|
(4.66) |
donde es la densidad de masa total del material poroso, es el vector de fuerza másicas.
Adoptando nuevamente la hipótesis de transformaciones infinitesimales se puede escribir a la densidad de la masa total como
|
|
(4.67) |
donde es la densidad de la matriz sólida, es la densidad del agua en estado líquido y es la densidad del aire húmedo.
4-8 Ecuaciones de estado de los fluidos
La primera ley de la termodinámica aplicada a los fluidos indica que en cualquier evolución de un sistema material desde un estado de equilibrio homogéneo a otro, la variación de la energía interna del último es la suma del trabajo mecánico de las fuerzas externas sobre el sistema y del calor externo suministrado. De esta manera la primera ley se expresa de la siguiente manera
|
|
(4.68) |
donde es la energía interna específica (por unidad de masa) relacionado al fluido ![]() ; representa el trabajo mecánico infinitesimal aplicado sobre fluido
; representa el trabajo mecánico infinitesimal aplicado sobre fluido ![]() por la presión en el cambio infinitesimal de volumen , y es el suministro infinitesimal externo de calor.
por la presión en el cambio infinitesimal de volumen , y es el suministro infinitesimal externo de calor.
La segunda ley aplicada a los fluidos indica que existe una función aditiva llamada entropía tal que la variación de entropía en cualquier evolución de un sistema material desde un estado de equilibrio homogéneo a otro, es igual al suministro externo de entropía. Se asume que existe una escala universal de temperatura absoluta positiva tal que el suministro infinitesimal externo de entropía se define como el suministro infinitesimal externo de calor dividido por la temperatura absoluta. Por tanto excluyendo las transformaciones irreversibles la segunda ley puede escribirse como
|
|
(4.69) |
donde es la entropía específica del fluido ![]() y es la temperatura absoluta.
y es la temperatura absoluta.
Combinando (4.68) y (4.69) se obtiene el siguiente balance de energía
|
|
(4.70) |
La expresión (4.70) es válida para cualquier evolución del fluido ![]() desde un estado homogéneo a otro. Como consecuencia y constituyen un conjunto completo de variables de estado independientes tal que:
desde un estado homogéneo a otro. Como consecuencia y constituyen un conjunto completo de variables de estado independientes tal que:
|
|
(4.71) |
La ecuación (4.71) actúa como las ecuaciones de estado del fluido ![]() donde la energía interna actúa como un potencial que vincula el conjunto de variables termodinámicas de estado al conjunto conjugado .
donde la energía interna actúa como un potencial que vincula el conjunto de variables termodinámicas de estado al conjunto conjugado .
Las ecuaciones de estado pueden invertirse parcialmente con respecto al par de variables conjugadas , por la introducción de la entalpía específica
|
|
(4.72) |
de manera tal que las ecuaciones de estado toman la siguiente forma alternativa
|
|
(4.73) |
Del mismo modo las ecuaciones (4.71) pueden invertirse parcialmente con respecto al par de variables conjugadas . Introduciendo la energía libre de Helmholtz específica
|
|
(4.74) |
tal que
|
|
(4.75) |
Finalmente las ecuaciones (4.71) pueden invertirse totalmente. Introduciendo la entalpía libre específica
|
|
(4.76) |
de donde se obtiene
|
|
(4.77) |
La entalpía libre específica también se conoce como potencial de Gibbs.
4-9 Balance de energía y entropía del material poroso
En el contexto de transformaciones infinitesimales y cuasiestáticas, despreciando las fuentes externas de calor, la ecuación de balance de energía (primera ley de la termodinámica) del material poroso se escribe como
|
|
(4.78) |
donde ![]() es la densidad de energía interna total por unidad de volumen,
es la densidad de energía interna total por unidad de volumen, ![]() es el tensor de deformaciones,
es el tensor de deformaciones, ![]() es el vector de flujo de calor total, y
es el vector de flujo de calor total, y ![]() es la entalpía específica relacionada al fluido
es la entalpía específica relacionada al fluido ![]() .
.
La segunda ley de la termodinámica aplicada al medio poroso no saturado se expresa como
|
|
(4.79) |
donde ![]() es la densidad de entropía total por unidad de volumen y
es la densidad de entropía total por unidad de volumen y ![]() es la entropía específica relacionada al fluido
es la entropía específica relacionada al fluido ![]() . Combinando la primera ley (4.78) y la segunda ley (4.79) se obtiene la siguiente relación fundamental de la disipación total
. Combinando la primera ley (4.78) y la segunda ley (4.79) se obtiene la siguiente relación fundamental de la disipación total
|
|
(4.80) |
donde es la disipación relacionada al esqueleto, y ![]() y
y ![]() son las disipaciones relacionadas con el transporte de masa de fluido y de calor respectivamente.
son las disipaciones relacionadas con el transporte de masa de fluido y de calor respectivamente.
Las expresiones de cada una de estas disipaciones son las siguientes
|
|
(4.81) |
|
|
(4.82) |
|
|
(4.83) |
donde ![]() es el gradiente del potencial de Gibbs (entalpía libre especifica)
es el gradiente del potencial de Gibbs (entalpía libre especifica) ![]() relacionada al fluido
relacionada al fluido ![]() tomando a temperatura constante, y
tomando a temperatura constante, y ![]() es la energía libre total.
es la energía libre total.
Debido a la naturaleza tan variada de las disipaciones , ![]() y
y ![]() , se realiza la hipótesis de desacoplamiento de la disipación, en la cual la desigualdad (4.80) se sustituye por las siguientes tres
, se realiza la hipótesis de desacoplamiento de la disipación, en la cual la desigualdad (4.80) se sustituye por las siguientes tres
|
|
(4.84) |
El balance de entropía se expresa finalmente en forma de ecuación térmica
|
|
(4.85) |
donde representa la disipación mecánica y actúa como una fuente espontánea de calor.
4-10 Ecuaciones constitutivas de los fluidos
Las ecuaciones constitutivas del esqueleto son independientes de la naturaleza y de las ecuaciones constitutivas de los fluidos que llenan el medio poroso. Esto se debe a que solo se consideran fuerzas de contacto entre el esqueleto y los fluidos de manera tal que éstos últimos ejercen presiones sobre las paredes internas de la red porosa. De la misma manera las ecuaciones constitutivas de los fluidos son independientes de las del esqueleto.
Diferenciando las ecuaciones de estado (4.77) se obtiene
|
|
(4.86) |
es el módulo volumétrico tangente del fluido ![]() , es el coeficiente de dilatación térmica tangente del fluido
, es el coeficiente de dilatación térmica tangente del fluido ![]() , es el calor específico tangente a presión constante.
, es el calor específico tangente a presión constante.
A temperatura ambiente el agua líquida dentro de los poros en general se considera como un fluido incompresible, por lo que se considera que y en la ecuación (4.86), obteniéndose
|
|
(4.87) |
donde el índice 0 denota valores de referencia.
No obstante, a elevadas temperaturas la densidad del agua disminuye con el aumento de temperatura en forma apreciable. A partir de la expresión (4.86) se deduce una expresión para el coeficiente de dilatación térmica tangente del líquido :
|
|
(4.88) |
Así mismo, en general se consideran al vapor de agua y al aire seco como gases ideales
|
|
(4.89) |
donde es la masa molar del gas considerado y es la constante de los gases ideales.
La mezcla ideal de gases que forman el vapor de agua y el aire seco también se comporta como un gas ideal
|
|
(4.90) |
Diferenciando (4.89) y comparando la ecuación resultante con (4.86) se identifica
|
|
(4.91) |
Suponiendo que es una constante, se puede integrar la segunda ecuación de (4.86) para obtener
|
|
(4.92) |
4-11 Cambio de fase en el medio poroso
La posible disipación asociada al cambio de fase de líquido a vapor tendría la siguiente expresión
|
|
(4.93) |
El equilibrio termodinámico local entre líquido y vapor requiere que la disipación sea nula. Por tanto se tiene que
|
|
(4.94) |
Asumiendo que el equilibrio líquido-vapor se mantiene a través de la evolución y teniendo en cuenta las ecuaciones de estado de los fluidos desarrolladas en el apartado 4.8, diferenciando (4.94) se obtiene
|
|
(4.95) |
Integrando (4.95) se obtiene la conocida ley de Kelvin
|
|
(4.96) |
donde es la presión de saturación de vapor a la temperatura .
Si el líquido es agua, la relación se identifica eventualmente con la humedad relativa
|
|
(4.97) |
4-12 Ecuaciones de estado del esqueleto
Utilizando las ecuaciones de balance de masa (4.52) a (4.54), teniendo en cuenta la expresión (4.94), es posible rescribir de la (4.81) de la siguiente forma
|
|
(4.98) |
Se definen a y como la energía libre y la entropía del esqueleto
|
|
(4.99) |
Teniendo en cuenta las expresiones (4.35)y (4.99), conjuntamente con las ecuaciones de estado de los fluidos desarrolladas en el apartado 5.2.4 aplicadas a cada fluido , puede expresarse como
|
|
(4.100) |
Tal como se definió anteriormente, y representan respectivamente la energía libre y la entropía del medio poroso completo contenido en el volumen . Por tanto y representan respectivamente la energía libre y la entropía del esqueleto, habida cuenta de que este último además de la matriz porosa incluye las interfaces entre los distintos componentes. Más aún las interfaces fluido-fluido y sólido-fluido, poseen su propia energía y entropía interfacial
Se considera que los fluidos que llenan el medio poroso son agua líquida , y aire húmedo (mezcla de vapor de agua y aire seco) . El agua líquida es el fluido que presenta mayor afinidad con el sólido, con un ángulo de contacto menor a (ver Figura 4-5).
Se define a como la energía libre por unidad de superficie de interfase entre la matriz sólida y el fluido . La entropía superficial en la interfase es . En forma similar se define a como la energía libre relacionada a la interfase entre el agua líquida y el aire húmedo. Cuando la energía libre de una interfase depende solamente de la temperatura, ésta se eventualmente se identifica con la tensión superficial ejercida a lo largo de la interfase. Teniendo en cuenta los comentarios anteriores y el carácter aditivo de la energía, se puede escribir
|
|
(4.101) |
donde representa la energía libre de la matriz sólida por unidad de volumen del medio poroso completo , representa la energía interfacial total por unidad de volumen de medio poroso , la cual se expresa como
|
|
(4.102) |
De acuerdo con la expresión (4.102), la completa saturación con respecto al agua líquida es considerada convencionalmente como el estado de referencia cero de toda la energía interfacial dado que .
Debido a que el espacio poroso se llena solamente con agua líquida y aire húmedo (), y teniendo en cuenta la definición (4.34) del grado de saturación , es posible rescribir (4.100) en la siguiente forma equivalente
|
|
(4.103) |
donde es la presión de fluido promedio o equivalente de poros definida por
|
|
(4.104) |
mientras que se define como la presión capilar macroscópica ejercida en la interfase entre los dos fluidos
|
|
(4.105) |
En el caso de transformaciones infinitesimales la porosidad puede reemplazarse por (Coussy, 2007), con lo cual la expresión (4.103) se reescribe como
|
|
(4.106) |
En la expresión (4.104) de la presión equivalente de poros se asume que la zona ocupada por el agua líquida se encuentra bien separada de la zona ocupada por el gas, siendo el aporte de cada presión proporcional al grado de saturación del agua líquida . Esta hipótesis no se cumple en el caso de materiales cementicios en el que dentro de cada poro se comporten zonas ocupadas por el agua líquida y el por gas fundamentalmente para valores bajos del grado de saturación . Una expresión mejorada de la presión equivalente de poros más adecuada para materiales cementicios como el hormigón se propone en Coussy ,2007 y Gawin et al, 2003:
|
|
(4.107) |
En Gawin et al. ,2003 se propone como expresión de la función a:
|
|
(4.108) |
donde es el limite superior de la región higroscópica. En este trabajo se considerará que el valor de es de 0.25 que corresponde para una temperatura de 20°C con una humedad relativa del 45%.
4-13 Ecuaciones constitutivas para la termoporoelasticidad no saturada
En el caso particular de un comportamiento termoporoelástico la disipación en la expresión(4.106) es cero
|
|
(4.109) |
De esta manera las ecuaciones de estado de la termoporoelasticidad no saturada, puede escribirse en la siguiente forma
|
|
(4.110) |
En el caso indeformable e isotérmico donde , y , las ecuaciones de estado (4.110) pueden reducirse como
|
|
(4.111) |
De este modo la presión capilar depende exclusivamente del grado de saturación
|
|
(4.112) |
La curva de como función de se conoce como curva de presión capilar o curva de retención. Dicha curva se determina experimentalmente.
A partir de (4.101) se observa que en el caso indeformable e isotérmico, la energía libre del esqueleto se reduce a la energía interfacial , de esta manera (4.111) se reescribe como
|
|
(4.113) |
Utilizando la curva de presión capilar e integrando (4.113) se obtiene la expresión de la energía interfacial como función del grado de saturación
|
|
(4.114) |
Para el caso indeformable pero no isotérmico, la presión capilar depende tanto de como de ,
|
|
(4.115) |
Una expresión comúnmente utilizada para la curva de retención (4.115) es la siguiente
|
|
(4.116) |
donde
|
|
(4.117) |
Para el caso del hormigón se puede utilizar y (Grasberger y Meschke, 2004; Baroghel-Bouny et al., 1999). Asimismo para la función puede utilizarse (Pruess, 1987; Olivella y Gens, 2000)
|
|
(4.118) |
La energía interfacial puede determinarse a partir de la identificación experimental de la variación de la curva de presión capilar con la temperatura,
|
|
(4.119) |
Para abordar el caso general de la termoporoelasticidad no saturada, o sea deformable y no isotérmico, una primera aproximación consiste en suponer válida (4.115) para el caso deformable. Sustituyendo (4.115) en la tercera de las ecuaciones de estado (4.110) y luego integrando, se puede expresar a como
|
|
(4.120) |
De acuerdo con (4.120), la energía libre de la matriz sólida se expresa separadamente de la energía interfacial , y además sus variables de estado son , y solamente y no del grado de saturación .
Sustituyendo (4.120) en (4.103) y utilizando la tercera de las ecuaciones de estado (4.110) se tiene
|
|
(4.121) |
donde se define como la entropía de la matriz sólida
|
|
(4.122) |
A partir de la expresión (4.121) se puede rescribir las ecuaciones de estado para termoporoelasticidad no saturada en la forma
|
|
(4.123) |
Utilizando la transformación de Legendre siguiente
|
|
(4.124) |
la ecuación (4.121) se reescribe como
|
|
(4.125) |
De (4.125) se deriva otra forma alternativa para las ecuaciones de estado para termoporoelasticidad no saturada, la cual permite tener a la presión equivalente de poros como variable de estado y no a la porosidad
|
|
(4.126) |
4-14 Conducción de calor y masa
4-14-1 Ley de Fourier
El vector de flujo de calor total ![]() que aparece en la ecuación térmica (4.85), se determina a partir de la ley de Fourier
que aparece en la ecuación térmica (4.85), se determina a partir de la ley de Fourier
|
|
(4.127) |
siendo la conductividad térmica.
4-14-2 Ley de Darcy
La ley de Darcy toma la siguiente expresión para el caso de agua líquida
|
|
(4.128) |
Asimismo, para el caso del aire y el vapor de agua la ley de Darcy se expresa como
|
|
(4.129) |
|
|
(4.130) |
siendo la permeabilidad intrínseca del esqueleto, la permeabilidad relativa del gas, es la permeabilidad relativa del gas dentro del medio y es la viscosidad dinámica de la fase gaseosa.
Permeabilidades relativas
En la literatura hay varias expresiones matemáticas utilizadas para definir las permeabilidades relativas. Entre las más utilizadas se encuentran:
1-) van Genuchten:
Primeramente van Genuchten deriva una fórmula para la permeabilidad relativa del líquido (van Genuchten, 1980). Asimismo Luckner et al. (1989) derivan una expresión para la permeabilidad relativa del gas.
|
|
(4.131) |
|
|
(4.132) |
donde toma el mismo valor que en la curva de retensión.
2-) Potencia generalizada:
Estas expresiones son muy utilizadas en medios porosos no saturados en general (Gawin et al., 1999)
|
|
(4.133) |
|
|
(4.134) |
donde y toman valores entre 1 y 3. Típicamente se les asigna el valor de 3.
4-14-2 Ley de Fick
Cuando un fluido es una mezcla de vapor y aire, el vapor se transporta a través de dos procesos: por advección, como un componente de la mezcla y por difusión molecular a través del gas. El proceso de advección esta gobernado por la ley de Darcy (4.130). El proceso de difusión esta gobernado por la ley de Fick, la cual define que el vector de flujo de masa es proporcional al gradiente de la concentración molar del aire
|
|
(4.135) |
|
|
(4.136) |
donde y son respectivamente los coeficientes de difusión efectiva de aire y vapor dentro de los poros del medio
|
|
(4.137) |
|
|
(4.138) |
donde es la llamada tortuosidad que tiene en cuenta el recorrido real en la difusión de las moléculas dentro del medio poroso, , y .
El vector de flujo de masa de aire y el vector de flujo de masa de vapor que aparecen respectivamente en las ecuaciones (4.53) y (4.54), están determinados por una combinación de la ley de Darcy para la mezcla ideal de aire-vapor y de la ley de Fick para la difusión de cada componente en dicha mezcla. De esta manera, se obtiene las siguientes expresiones para los flujos de masa de aire y de vapor
|
|
(4.139) |
|
|
(4.140) |
Capítulo 5 Modelo higro-termo-mecánico para el hormigón expuesto a elevadas temperaturas
5-1 Introducción
En este trabajo se considerará al hormigón como un medio poroso no saturado. A partir del marco teórico de la mecánica de medios porosos no saturados (Coussy 1995, 2004) presentado en el capítulo anterior, se desarrolla un modelo higro-termo-mecánico para el hormigón expuesto a elevadas temperaturas.
En el modelo propuesto se establecen las siguientes hipótesis iniciales:
- Existe equilibrio térmico entre las fases. Esto significa que se considera que todas las fases presentes en el hormigón (sólido, agua líquida, vapor de agua y aire seco) se encuentran a la misma temperatura.
- Se supone que el esqueleto sólido experimenta pequeñas deformaciones y pequeña velocidad de deformaciones.
- Se considera que el tensor de deformaciones totales se divide en una componente elástica, una componente asociada a deformaciones de fluencia básica y una componente de deformaciones de fluencia térmica transitoria.
|
|
(5.1) |
- Se supone que la matriz sólida tiene un comportamiento elástico lineal y que todo el comportamiento mecánico no-lineal del medio poroso se debe a un aumento de porosidad y fisuración del esqueleto.
- Se asume que la porosidad total se divide en una componente inicial, una componente elástica y otra componente asociada al proceso de deshidratación.
|
|
(5.2) |
- La concentración de vapor está en equilibrio con la fase líquida. La ley de Kelvin (Coussy, 2004) expresa dicha concentración.
- Los procesos que involucran una evolución del daño térmico son irreversibles.
Es importante notar que en la expresión (5.1) no se ha incluido explícitamente a la deformación de retracción como una componente más de la deformación total. Sin embargo la deformación de retracción se tiene en cuenta implícitamente por medio de la tensión que actúa en el esqueleto sólido (tensión efectiva del esqueleto sólido) la cual resulta de compresión cuando la presión de poros es positiva (ver expresión (5.108) más adelante).
5-2 Bases termodinámicas
Los complejos mecanismos de acoplamiento higro-termo-mecánico que se producen a nivel micro estructural se describen a nivel macroscópico a partir de variables de estado. Para el modelo presentado en este trabajo, la función de energía libre de la matriz sólida depende de tres variables externas y de cuatro variables internas :
|
|
(5.3) |
donde
- es el tensor de deformaciones infinitesimales,
- es el tensor de deformaciones inelásticas, siendo el tensor de deformaciones de fluencia básica y el tensor de deformaciones de fluencia térmica transitoria,
- son las variables de daño mecánico isótropo a tracción y compresión respectivamente, tal que ,
- es la variable de daño térmico que representa una medida del deterioro producido por la altas temperaturas, tal que .
Si se extiende la expresión (4.121) valida para el caso termoporoelástico, al caso termoporoelástico con daño se tendrá
|
|
(5.4) |
Partiendo de esta expresión y aplicando el método de Coleman, se obtienen las siguientes ecuaciones de estado
|
|
(5.5) |
Debido a que resulta más conveniente tener a la presión equivalente de poros como variable de estado y no a la porosidad, se utiliza la siguiente función de energía
|
|
(5.6) |
Se puede observar que utilizando la función de energía , el modelo también presenta tres variables externas y cuatro variables internas . Para este caso la expresión de la disipación mecánica del esqueleto se expresa como
|
|
(5.7) |
Asimismo las ecuaciones de estado serán las siguientes
|
|
(5.8) |
A partir de (5.8) se pueden plantear las siguientes relaciones de simetría de Maxwell
|
|
(5.9) |
Se propone la siguiente expresión para la función de energía
|
|
(5.10) |
donde
- es la parte elástica de la función de energía
|
|
(5.11) |
siendo es el tensor de tensiones iniciales, el tensor de constantes elásticas para el esqueleto en su estado original y es el tensor de tensiones efectivas el cual esta definido por
|
|
(5.12) |
donde es el tensor de deformaciones elásticas y es el tensor de deformaciones térmicas que para un material isótropo esta definido por
|
|
(5.13) |
siendo el coeficiente de dilatación volumétrica del esqueleto.
El tensor de tensiones efectivas puede descomponerse en una componente positiva y otra negativa (Faria et al. 1998 y 2004)
|
|
(5.14) |
La función incluye la parte de acoplamiento termo-mecánico de la función de energía .
- es la contribución térmica a la función de energía
|
|
(5.15) |
siendo es el calor específico del esqueleto, la temperatura de referencia y es el calor latente de las reacciones químicas del proceso de deshidratación en el esqueleto.
- es la parte de la función de energía relacionada con la humedad
|
|
(5.16) |
siendo la porosidad inicial, la presión equivalente de poros inicial, es la inversa del módulo de Biot secante para el material degradado y representa la variación de la porosidad que provoca una variación unitaria de la presión equivalente de poros . La parte de la porosidad asociada al proceso de deshidratación se la considera función del daño térmico .
- es la parte de acoplamiento higro-mecánico de la función de energía
|
|
(5.17) |
siendo el tensor de Biot secante que representa la variación de tensión producida por un incremento unitario de la presión equivalente de poros . Para el caso isótropo se puede escribir .
- es la parte de acoplamiento higro-térmico de la función de energía
|
|
(5.18) |
siendo el coeficiente de dilatación térmica volumétrica relacionado a la porosidad, y representa la variación de la porosidad que provoca una variación unitaria de la temperatura .
A partir de la ecuaciones (5.8) y (5.10) y se puede obtener las expresiones explicitas para las ecuaciones de estado
|
|
(5.19) |
|
|
(5.20) |
|
|
(5.21) |
donde es la entropía inicial de la matriz sólida.
La disipación del esqueleto (5.7) se expresa como
|
|
(5.22) |
donde , y .
Diferenciado las ecuaciones (5.19)-(5.21) se obtienen las expresiones diferenciales de las ecuaciones de estado
|
|
(5.23) |
|
|
(5.24) |
|
|
(5.25) |
donde
es el tensor de constantes elásticas secante del esqueleto,
son tensores de segundo orden que describen los mecanismos de acoplamiento entre la tensión total y la evolución del daño mecánico a tracción y compresión respectivamente,
es un tensor de segundo orden que describe los mecanismos de acoplamiento entre la evolución del daño térmico y la tensión total,
es un coeficiente escalar de acoplamiento asociado al cambio de la porosidad debido a la evolución del daño mecánico a tracción,
es un coeficiente escalar de acoplamiento asociado al cambio de la porosidad debido a la evolución del daño térmico.
es el calor latente del daño térmico,
y son los calores latentes del daño mecánico a tracción y compresión respectivamente.
Algunos autores (Grasberge y Meschke, 2004) consideran despreciable los acoplamientos asociados al cambio de porosidad debido a las evoluciones del daño mecánico. Esta suposición se basa en considerar que en materiales cementícios el proceso de fisuración es mucho más rápido que el proceso de microdifusión de líquido dentro de los espacios de fisuras recién generados. Si bien resulta discutible extender esta idea al caso de poros con aire húmedo a alta presión, en este trabajo se considerará por simplicidad,
|
|
(5.26) |
De esta manera (5.24) se reescribe como
|
|
(5.27) |
5-3 Identificación de los parámetros termoporoelásticos
Los coeficientes termoporoelásticos y propuestos en la función de energía representa propiedades del esqueleto a nivel macroscópico. Para determinar una expresión a dichos coeficientes es necesario relacionarlos con propiedades de la matriz (Coussy, 2007).
La tensión macroscópica media es el promedio de las tensiones microscópicas tal que se puede escribir
|
|
(5.28) |
donde es la tensión media de la matriz en la mesoescala.
La deformación media se relaciona con la deformación de la matriz sólida a través de la expresión (4.28)
|
|
(5.29) |
donde es la tensión media de la matriz en la mesoescala.
Asumiendo que la matriz se comporta como un material elástico lineal e isótropo, puede escribirse
|
|
(5.30) |
donde es el módulo volumétrico de la matriz sólida.
Bajo un estado de condiciones isotérmicas y libre de tensiones iniciales las expresiones (5.19) y (5.20) puede escribirse como
|
|
(5.31) |
|
|
(5.32) |
donde es el módulo volumétrico secante del medio poroso
|
|
(5.33) |
Para establecer las relaciones buscadas se realizan los siguientes desarrollos,
1-) Coeficiente de Biot :
Suponiendo que se puede plantear
|
|
(5.34) |
con lo que se deduce
|
|
(5.35) |
2-) Módulo de Biot :
Suponiendo que se puede plantear
|
|
(5.36) |
Con lo que se deduce que
|
|
(5.37) |
Luego a partir de (5.37) se deriva
|
|
(5.38) |
|
|
(5.39) |
con lo que se concluye
|
|
(5.40) |
3-) El coeficiente de dilatación térmica volumétrica relacionado a la porosidad :
La ecuación (5.21) se puede expresar en función de la tensión volumétrica en vez de la deformación volumétrica de la siguiente manera
|
|
(5.41) |
donde es el calor específico a tensión constante del esqueleto sólido. Debido al bajo valor del coeficiente de dilatación se considerará .
En forma semejante a la expresión (5.41) se plantea
|
|
(5.42) |
Donde es la entropía de la matriz sólida, es el calor específico a tensión constante de la matriz sólida y es el calor latente de las reacciones químicas del proceso de deshidratación en la matriz sólida.
Teniendo en cuenta el carácter aditivo de la entropía se puede escribir
|
|
(5.43) |
Remplazando (5.28) en (5.41) quedará
|
|
(5.44) |
Teniendo en cuenta (5.43) se establecen las siguientes relaciones:
|
|
(5.45) |
Similares expresiones a (5.35), (5.40) y (5.45) se obtienen en (Coussy 1995, 2004; Grasberger y Meschke, 2004).
Si se analiza la expresión (5.35) obtenida para el coeficiente de Biot, se puede deducir que para un módulo volumétrico de la matriz sólida , el módulo de Biot , recuperando de esta manera la expresión de la tensión efectiva de Terzaghi muy utilizada en la Mecánica de Suelos
|
|
(5.46) |
Teniendo en cuenta la hipótesis inicial de que la matriz sólida es elástica lineal , la variación del coeficiente de Biot estará dada por la variación del módulo volumétrico secante del esqueleto , el cual tiene la expresión (5.33). Es interesante observar que para el caso totalmente degradado, se vuelve a obtener la expresión de Terzaghi
|
|
(5.47) |
En el apartado 4-6-2 se dedujo la expresión (4.65) para la variación de la porosidad a partir del principio de conservación de masa del esqueleto. Teniendo en cuenta las expresiones (5.35), (5.40) y (5.45), la expresión (4.65) resultará
|
|
(5.48) |
Si se compara la ecuación (5.48) con (5.27) se establece que:
|
|
(5.49) |
De la expresión (5.49) se puede deducir que en el modelo propuesto se supone que el incremento de la masa producto del proceso de deshidratación provoca exclusivamente un incremento de porosidad en el esqueleto sólido. Estableciendo esta consideración, la expresión obtenida para el incremento de porosidad a partir de la ecuación de conservación de masa y la obtenida a partir de la diferenciación de las ecuaciones de estado son equivalentes.
5-4 Selección de las variables de estado del modelo
Se denominan variables de estado a un subconjunto de variables termodinámicas en función de las cuales se pueden definir todas las demás. También se las conoce como variables independientes o libres. Una correcta selección de las variables de estado es de vital importancia para conseguir una adecuada resolución numérica del modelo matemático resultante.
Como variables de estado termo-mecánicas la temperatura y el vector de desplazamientos del esqueleto sólido , son las opciones más naturales. No obstante la selección de una variable de estado relacionada con la humedad no resulta tan evidente. Existen varias posibilidades termodinámicamente equivalentes: masa o volumen del contenido de humedad, presión de vapor, humedad relativa y presión capilar.
Es importante recordar que a temperaturas por encima del punto crítico del agua (374.15 °C), solo existe agua en estado gaseoso (vapor) y que por tanto ya no se encuentra agua libre (capilar) en los poros del hormigón. Debido a esto el uso de la presión capilar como variable de estado relacionada con la humedad deja de tener sentido físico para temperaturas por encima del punto crítico del agua.
En Gawin et al. (2003) se realiza una extensa discusión de las posibles variables de estado relacionadas con la humedad. En dicha referencia se concluye que la elección más apropiada es la presión capilar pero con una interpretación física distinta para el rango de temperaturas superiores al punto crítico del agua (Gawin et al., 2002). En este rango de temperaturas se considera a la presión capilar como el potencial termodinámico del agua físicamente absorbida.
En resumen las variables de estado consideradas en el presente modelo son las siguientes: la presión del gas , la presión capilar , la temperatura y el vector de desplazamientos del esqueleto sólido .
5-5 Ecuaciones de gobierno
5-5-1 Ecuaciones de transporte de masa
Si en la ecuación de conservación de masa de agua líquida (4.52) se tiene en cuenta el proceso de deshidratación se tiene
|
|
(5.50) |
Sumando las ecuaciones (5.50) y (4.53) se obtienen las ecuación de balance de las especies de agua (líquido y vapor), la cual junto a la ecuación (4.54) forman las ecuaciones de balance de masa de las fases fluidas
|
|
(5.51) |
|
|
(5.52) |
Teniendo en cuenta (4.47) se obtiene
|
|
(5.53) |
|
|
(5.54) |
|
|
(5.55) |
Debido a que se ha considerado que la densidad del agua líquida a elevadas temperaturas varía con la temperatura, de la expresión (4.88) se deduce que
|
|
(5.56) |
Considerando al vapor de agua y al aire seco como gases ideales, a partir de (4.89) se obtiene
|
|
(5.57) |
Para expresar la presión de vapor en función de las variables de estado , y , se utiliza la ley de Kelvin (4.96) y (4.105)
|
|
(5.58) |
Luego la variación temporal de la presión de vapor tendrá la siguiente expresión
|
|
(5.59) |
donde
|
|
(5.60) |
|
|
(5.61) |
|
|
(5.62) |
Teniendo en cuenta (5.58) y que , la presión de aire seco se puede expresar en función de las variables de estado , y
|
|
(5.63) |
Asimismo, la variación temporal de la presión de aire seco será
|
|
(5.64) |
A partir de la curva de retención (4.115) se puede obtener una expresión funcional para el grado de saturación
|
|
(5.65) |
De esta última expresión se deduce
|
|
(5.66) |
Teniendo en cuenta (4.107) se puede expresar la expresión de la variación temporal de la porosidad (5.27) en función de las variables de estado
|
|
(5.67) |
donde,
|
|
(5.68) |
|
|
(5.69) |
De las expresiones (4.130) y (4.128) se obtienen los vectores de flujo de masa de agua líquida y vapor de agua
|
|
(5.70) |
El término de la expresión (5.70) se desarrolla como
|
|
(5.71) |
A partir de (5.58) se deduce que
|
|
(5.72) |
Reemplazando (5.72) en (5.71) se tiene
|
|
(5.73) |
Reemplazando (5.73) en (5.70) se tiene
|
|
(5.74) |
Con un desarrollo similar se obtiene la expresión de la masa de aire seco
|
|
(5.75) |
A partir de las expresiones (5.53) a (5.75) se reescriben las ecuaciones (5.51) y (5.52) de la siguiente manera
|
|
(5.76) |
|
|
(5.77) |
Las expresiones (5.76) y (5.77) pueden reescribirse en un formato más adecuado para su resolución numérica
|
|
(5.78) |
|
|
(5.79) |
donde,
5-5-2 Ecuación de balance de entropía
Para obtener la ecuación de balance de entropía para el caso de un material termo-poroelástico con daño (mecánico y térmico) se parte de la ecuación de balance de energía (4.78), que se reescribe
|
|
(5.80) |
Teniendo en cuenta (4.99) y (4.101) la densidad de energía interna total por unidad de volumen ![]() resulta
resulta
|
|
(5.81) |
Luego la derivada temporal de ![]() será
será
|
|
(5.82) |
Teniendo en cuenta (4.76), la entalpía específica del fluido se escribe como
|
|
(5.83) |
A partir de la expresión anterior y teniendo en cuenta (4.77), el termino que aparece en (5.80) resulta
|
|
(5.84) |
donde .
Considerando que ![]() y que
y que ![]() , teniendo en cuenta las ecuaciones de balance de masa de las fases fluidas (5.50), (4.53) y (4.54), el termino
, teniendo en cuenta las ecuaciones de balance de masa de las fases fluidas (5.50), (4.53) y (4.54), el termino ![]() resulta
resulta
|
|
(5.85) |
Remplazando (5.85) en (5.84), y la expresión resultante en (5.80), considerando que y que la disipación del proceso de evaporación es nula ![]() , se obtiene
, se obtiene
|
|
(5.86) |
donde la disipación relacionada con el transporte masa de fluido esta dada por la (4.83).
Teniendo en cuenta que ![]() y
y ![]() , el término
, el término ![]() de (5.86), puede rescribirse como
de (5.86), puede rescribirse como
|
|
(5.87) |
Teniendo en cuenta que para transformaciones infinitesimales la porosidad puede reemplazarse por , la expresión (5.87) quedará
|
|
(5.88) |
De (4.119) se deduce que
|
|
(5.89) |
Remplazando (5.88) y (5.89) en (5.86) se tiene
|
|
(5.90) |
donde ![]() se define por (4.122).
se define por (4.122).
Utilizando la expresión (5.6) y teniendo en cuenta (4.122), la expresión (5.90) se reescribe como
|
|
(5.91) |
donde ![]() , y
, y ![]() se define en (5.22).
se define en (5.22).
Utilizando las ecuaciones de balance de masa de las fases fluidas (5.50), (4.53) y (4.54), y asimismo las ecuaciones de estado (4.87) y (4.92) en el tercer termino del primer miembro de la ecuación (5.91) se tendrá
|
|
(5.92) |
Desarrollando el cuarto término de la ecuación (5.91) se obtiene
|
(5.93) |
Utilizando las ecuaciones de estado (4.87) y (4.92) se puede obtener las expresiones de ![]() para cada fluido
para cada fluido
|
|
(5.94) |
Sustituyendo (4.127), (5.25), (5.92), (5.93) y (5.94) en (5.91) y desarrollando algebraicamente se obtiene
|
|
(5.95) |
donde
- ![]() es el calor específico efectivo del medio poroso (esqueleto sólido y las fases fluidas)
es el calor específico efectivo del medio poroso (esqueleto sólido y las fases fluidas)
|
|
(5.96) |
En la expresión anterior el término para los valores de porosidades típicas del hormigón tiene poca influencia por lo que se lo despreciará.
- representa a la tasa de energía de disipación asociada al proceso de deshidratación. El término es la parte relacionada con la deshidratación esqueleto sólido, y el término es la parte relacionada con la energía que se genera debida a la aparición de agua como producto del proceso de deshidratación
- representa a los siguientes términos,
|
|
(5.97) |
- representa la tasa de energía consumida en el proceso de evaporación de la fase de agua líquida. El término representa el calor latente de vaporización a la temperatura T y a presión del líquido .
- representa la tasa de energía consumida en el proceso de deshidratación. El primer término de esta expresión aparece en la ecuación de balance de entropía (5.95) como un término sumidero de calor por unidad de volumen. El segundo término de la misma aparece también como un término sumidero y representa la tasa de energía almacenada en el agua que surge como producto del proceso de deshidratación.
La tasa de deshidratación de la masa del sólido , puede expresarse en función del daño térmico . Asimismo la variación temporal del daño térmico se puede relacionar con la variación temporal de la temperatura, tal como se expresa en (5.111). Finalmente la tasa de deshidratación de la masa del sólido , se expresa de la siguiente manera,
|
|
(5.98) |
La ecuación (5.95) puede simplificarse analizando la importancia relativa de cada uno de sus términos.
Se llamará al coeficiente que multiplica a y al coeficiente que multiplica a
|
|
(5.99) |
|
|
(5.100) |
Se puede demostrar que dentro del rango de temperaturas analizado se cumple que . El coeficiente decrece exponencialmente con la presión capilar y la temperatura.
Se puede deducir que para el rango de presiones de gas encontradas habitualmente en este tipo de análisis , la variación de temperatura debido al término es despreciable .
La influencia del término también es pequeña. Para el rango de temperaturas y presiones capilares típicas de este tipo análisis , la variación de temperatura debido al término es despreciable .
El término se relaciona con la variación temporal de la temperatura por medio de (5.98). De esta manera la expresión , puede incluirse como un término más en la expresión (5.96) del calor específico efectivo del medio poroso . Debido a que en la determinación experimental de , el factor es tenido en cuenta de forma natural, no se lo incluirá al mismo como un termino adicional de .
Por último y contienen términos asociados a la disipación del esqueleto y de los fluidos que también se los considerará despreciables (Ulm et al., 1999a).
Finalmente la ecuación de balance de entropía quedará
|
|
(5.101) |
La expresión de la tasa de transformación de líquido a vapor se determina a partir de (4.53)
|
|
(5.102) |
La expresión (5.101) puede reescribirse de una forma más apropiada para su resolución numérica
|
|
(5.103) |
donde
5-5-3 Ecuaciones de balance de la cantidad de movimiento
Sustituyendo la ecuación (5.19) en (4.66) se obtiene
|
|
(5.104) |
5-5-4 Condiciones iniciales y de contorno
Para que el modelo quede bien planteado es necesario indicar las condiciones iniciales y de contorno.
Las condiciones de contorno para problemás higro-termo-mecánicos están bien establecidas y son bastante comunes en todos los modelos presentes en la literatura. No obstante al elegir a la presión capilar como variable estado, la definición de una condición de contorno adecuada para esta variable no resulta tan evidente. En este trabajo se seguirá las condiciones de contorno propuestas en Gawin et al. (2003)
Las condiciones iniciales especifican el campo completo para las variables de estado en el instante , en el dominio completo analizado y en su contorno
|
|
(5.105) |
Las condiciones de contorno pueden ser de tipo Dirichlet sobre
|
|
(5.106) |
O bien pueden ser de tipo Cauchy sobre
|
|
(5.107) |
donde es el vector normal unitario apuntando hacia el exterior, son respectivamente los flujos impuestos de aire, vapor, agua líquida y térmico, el vector tensión impuesto, y son la densidad de vapor de agua y la temperatura en el ambiente exterior, es el factor de visión de la radiación, es la constante de Stefan-Boltzmann, es la absorción de la superficie, es la emisividad de la llama asociada con el fuego, es la emisividad de la superficie y finalmente y son los coeficientes de intercambio convectivo de calor y masa respectivamente.
5-6 Definición del daño termomecánico
El hormigón es un material que posee un comportamiento mecánico muy complejo y marcadamente no lineal. Algunos de los fenómenos más importantes que debería contemplar un modelo mecánico son (Prato, 1999):
- 1) La diferencia entre los comportamientos a tracción y compresión, lo que se traduce en resistencias y curvas tensión-deformación muy distintas para dichos fenómenos.
- 2) El aumento de resistencia para estados de tensiones bi o tridimensionales, respectos de la resistencia unidimensional.
- 3) La aparición de deformaciones plásticas en la descarga a compresión.
- 4) La dependencia del comportamiento de la velocidad de carga.
- 5) La recuperación de rigidez al pasar de tracción a compresión debido al cierre de fisuras.
Algunas de las formulaciones más difundidas que se encuentran en la literatura para predecir el comportamiento mecánico no lineal del hormigón se corresponden con modelos hipoelásticos, hiperelásticos, plásticos, viscoplásticos, basados en la mecánica de fractura y de daño continuo.
El modelo mecánico presentado en este trabajo se basa en la teoría del daño continuo. Desde su presentación por Kachanov (1958) la teoría del daño continuo se ha convertido en una herramienta muy atractiva para describir el deterioro progresivo del hormigón.
Luego del trabajo de Kachanov (1958) han surgido muchas variantes tales como las investigaciones de Krajcinovic y Fonseka (1981), Fonseca y Krajcinovic (1981), Chaboche (1988a, 1988b), Lubliner et al. (1989), Mazars y Pijaudier-Cabot (1989), Faria et al. (1998, 2004).
En este trabajo se utiliza un modelo de daño isótropo. La variable de daño, asociada al daño mecánico y a la degradación térmica se interpreta como la densidad superficial de los defectos en el hormigón y se definirá como la relación entre el área ocupada por la microfisuras y el área total (Kachanov, 1958). Esta definición de la variable de daño implica que es un parámetro cuyo incremento es siempre positivo, debido a que el área de las microfisuras aumenta en forma continua hasta la ruptura del material.
De esta manera el daño térmico en el hormigón se considera como una posterior disminución del área resistente efectiva (Nechnech et al., 2002). En la Figura 5-1 se presenta un esquema de los procesos de daño mecánico y térmico. El proceso de daño térmico está gobernado por la variable , la cual provoca una disminución de dicha área resistente efectiva pero de manera independientemente del daño mecánico (Nechnech et al., 2002).
Despreciando el tensor de tensiones iniciales , se puede rescribir la ecuación constitutiva (5.19) de la siguiente manera
|
|
(5.108) |
donde es la tensión efectiva del esqueleto sólido.
La tensión efectiva definida en (5.12) pueden reescribirse de la siguiente manera
|
|
(5.109) |
donde es la tensión efectiva neta.
5-7 Caracterización del daño térmico
El daño térmico representa una medida del grado de deshidratación del hormigón. La evolución de esta variable interna puede obtenerse indirectamente (Ulm et al., 1999a) a través de los efectos de la deshidratación, tal como pueden ser los cambios en el módulo de rigidez y en la resistencia del material. Entre las propiedades mecánicas del hormigón la más sensible a los efectos de las altas temperaturas es el módulo de elasticidad.
Se asume que el tiempo característico de proceso de deshidratación es despreciable comparado con el tiempo característico de la conducción de calor en estructuras de hormigón. Asimismo, se considera que el proceso de deshidratación es irreversible. De esta manera, el daño térmico puede ser expresado como una función de la máxima temperatura alcanzada.
Se supone que la relación entre el módulo elástico a cierta temperatura máxima y el módulo elástico a temperatura ambiente es proporcional a la variable de daño térmico . A partir de curvas experimentales que relacionan el módulo de elasticidad con la temperatura puede expresarse dicha relación como
|
|
(5.110) |
donde es la temperatura ambiente.
De (5.110) se obtiene la relación entre la evolución del daño térmico y la variación de la temperatura
|
|
(5.111) |
Como función del módulo de elasticidad respecto de la temperatura puede tomarse la utilizada en Willam et al. (2005)
|
|
(5.112) |
Los datos experimentales disponibles de la evolución de las propiedades higro-termo-mecánicas de los materiales (resistencia, rigidez, calor específico, etc.) debida a la degradación térmica, se la relacionan con la temperatura. Debido a que el proceso de degradación térmica se considera irreversible, es conveniente que la evolución de dichas de propiedades se relacione con la temperatura máxima alcanzada. Una forma alternativa es expresar dicha evolución en función del daño térmico . Las expresiones (5.110) y (5.112) permiten relacionar la temperatura máxima alcanzada con el daño térmico en forma biunívoca.
|
|
(5.113) |
|
|
(5.114) |
Es importante notar que la expresión (5.114) es válida solo para el rango . Esta situación no es un limitante debido que para un daño térmico del orden de se corresponde con una temperatura mayor a , siendo dicha temperatura difícilmente alcanzable en la práctica.
Finalmente, a partir de la expresión (5.114) es posible relacionar con el daño térmico a cualquier propiedad higro-termo-mecánicas cuya evolución esté referida a la temperatura. En este trabajo todas las propiedades térmicas, hídricas y mecánicas susceptibles de evolucionar con la degradación térmica se referirán al daño térmico.
5-8 Caracterización del daño mecánico
El modelo de daño isótropo escogido para este trabajo utiliza dos variables escalares para caracterizar el daño local a tracción y a compresión respectivamente. Este tipo de modelo tiene la ventaja de tener una formulación muy simple, pero con una gran capacidad de predicción para captar el comportamiento no lineal global del hormigón. Además el modelo puede ser implementado en función de las deformaciones, lo que conlleva a un algoritmo casi explícito de integración de la ecuación constitutiva. De esta manera se evita un excesivo coste computacional en la resolución de problemás transitorios a gran escala como es el caso del análisis de estructuras de hormigón armado expuestas al fuego.
El modelo presentado en este trabajo representa una variante del modelo presentado en Prato (1999) para el comportamiento mecánico del hormigón a edades tempranas. Dicho modelo permite capturar la regradación de la rigidez bajo al alternancia del signo de la tensión (daño unilateral).
Tal como se comento, el hormigón es un material que se comporta de manera muy diferente a tracción y a compresión. Debido a esto resulta necesario introducir dos variables de daño escalar y que tienen en cuenta los procesos de degradación mecánica a tracción y compresión respectivamente.
Dada la definición de la tensión dada en (5.19) debe verificarse
|
|
(5.115) |
5-8-1 Tensiones efectivas
Para poder identificar las contribuciones del tensor de tensiones efectivas a la degradación mecánica de tracción y compresión, se lo descompone en una parte positiva y otra negativa respectivamente. En lo que sucesivo se utilizan el superíndice para designar componente de tracción y superíndice para las componentes de compresión.
Utilizando la misma descomposición del tensor de tensiones que la presentada en Faria et al. (1998, 2004) se tiene,
|
|
(5.116) |
|
|
(5.117) |
donde el símbolo representa los paréntesis de Macaulay , es la tensión principal iésima de , representa el vector unitario correspondiente a la dirección principal iésima de y el símbolo denota producto tensorial.
5-8-2 Criterios de daño
Para poder distinguir entre los procesos de carga, descarga y recarga, así como la evolución de las variables , es necesario definir una norma del tensor de deformaciones o alternativamente del tensor de tensiones efectivas (netas modificadas). Esta norma se conoce también como deformación equivalente y se utiliza para comparar distintos estados de deformación. Esta deformación equivalente se normaliza con la resistencia pico a efectos de poder comparar diferentes estados de deformaciones con distintos grados de daño térmico. Debido a que la variable interna de daño se ha definido con una componente de tracción y otra de compresión, resulta necesario especificar dos deformaciones equivalentes normalizadas: una deformación equivalente normalizada de tracción y otra deformación equivalente normalizada de compresión . En el presente trabajo se utilizan las siguientes deformaciones equivalentes normalizadas (Prato, 1999; Faria et al. 1998, 2004)
|
|
(5.118) |
|
|
(5.119) |
Donde son los parámetros de normalización dependientes del daño térmico para deformaciones equivalentes de tracción y compresión respectivamente, y son la tensión octaédrica normal y la tensión octaédrica cortante obtenidas de . es una propiedad del material que depende de las resistencias uni y bidimensional del hormigón trabajando a compresión, que según los ensayos de Kupfer (1969) se encuentran entre 1.16 y 1.2.
La definición de la deformación equivalente normalizada a compresión (5.119) se inspira en el criterio de daño de Drucker-Prager, donde el parámetro determina el ángulo del cono.
Con las definiciones de las deformaciones equivalentes normalizadas se definen, dos criterios de daño separadas y , para tracción y compresión respectivamente
|
|
(5.120) |
|
|
(5.121) |
Las variables y son parámetros que definen los umbrales instantáneos normalizados del daño, los cuales controlan el tamaño de la superficies de daño que expanden en forma monótona.
Pueden calcularse los parámetros de normalización de las deformaciones equivalentes , de manera tal que los valores iniciales de los umbrales instantáneos del daño tomen valores unitarios (Faria et al., 1998)
|
|
(5.122) |
|
|
(5.123) |
donde son las resistencias pico a tracción y compresión respectivamente, es la relación entre las tensiones que indican el comienzo del comportamiento no lineal y las resistencias pico, y es el módulo de Young a temperatura ambiente. En este trabajo se supondrá que los parámetros son constantes en todo el análisis.
De esta manera los criterios de daño quedan definidos en un espacio normalizado de deformaciones elásticas, dando a lugar superficies de daño que no dependen del daño térmico del material. Esta característica interesante del presente modelo es utilizada en Prato (1999) pero en el contexto de superficies de daño dependientes del grado de envejecimiento del hormigón.
El parámetro puede calcularse a partir de ensayo de compresión uni y bidimensionales. En Faria et al. (1998) se calcula el siguiente valor de este parámetro
|
|
(5.124) |
donde es la tensión que indica el inicio del comportamiento no lineal en un ensayo a compresión biaxial.
5-8-3 Leyes de evolución
Las leyes de evolución del umbral del daño, se definen a partir de las condiciones de carga, descarga y recarga las cuales respetan las llamadas relaciones de Kuhn-Tucker
|
|
(5.125) |
donde el punto denota derivada temporal ().
En situación de carga la condición de persistencia y las relaciones (5.120) y (5.121) conducen a
|
|
(5.126) |
Integrando esta relación para un instante genérico , se llega a la siguiente expresión explicita de los valores actuales de la variables internas
|
|
(5.127) |
donde es el umbral que indica el limite del dominio elástico lineal.
Los indicies de daño y se definen explícitamente en función de los valores instantáneos de los umbrales de daño. Se proponen las siguientes funciones
|
|
(5.128) |
donde son funciones positivas de las variables .
Dado que los indicies de daño y deben verificar la relación (5.115), en vista a (5.128) equivale a:
|
|
(5.129) |
Para que la disipación del esqueleto sólido sea siempre positiva para cualquier proceso termomecánico, según la expresión (5.22) debe cumplirse que , lo que según (5.128) equivale a,
|
|
(5.130) |
Se proponen las siguientes funciones
|
|
(5.131) |
|
|
(5.132) |
donde , y son parámetros del material.
De la expresión (5.131) se deduce que se considera que para el régimen de tracción la rama de ablandamiento aparece inmediatamente después de alcanzarse el límite elástico de material . Esta hipótesis se utiliza comúnmente para el comportamiento a tracción.
Para obtener el parámetro debe tenerse en cuenta que deben cumplirse los requisitos de objetividad de la malla. Si se utiliza del método de los elementos finitos en el marco de los modelos locales, es necesario introducir una longitud característica (Oliver, 1989), la cual depende del tamaño (volumen o área) de la malla utilizada para la discretización espacial. Igualando la relación con la energía específica total disipada cualquier proceso mecánico (se consideran procesos en los cuales se mantienen constantes la temperatura y las variables hídricas), donde es la energía de fractura a tracción (considerada como una propiedad del material), se puede calcular el parámetro (Oliver et al., 1990; Faria et al., 1998)
|
|
(5.133) |
donde .
El parámetro se puede obtenerse teniendo en cuenta el valor que toma la variable para la resistencia pico , obtenida de un ensayo a compresión uniaxial. Sabiendo que cuando se alcanza la resistencia pico se cumple que se obtiene
|
|
(5.134) |
Teniendo en cuenta que en vista a la ecuación (5.128) se cumple que
|
|
(5.135) |
Remplazando la expresión (5.134) en (5.132) y esta a su vez en la (5.135), teniendo en cuenta que , se obtiene tras operar
|
|
(5.136) |
Para obtener el parámetro se procede de manera similar al caso del parámetro , obteniéndose
|
|
(5.137) |
donde es la energía de fractura a compresión (considerada como una propiedad del material).
En las expresiones (5.133) y (5.137) aparece el factor que algunos autores lo definen como la longitud característica del material (Nielsen y Bićanic, 2003) por ser una propiedad del material y tener unidades de longitud.
Estos parámetros deben determinarse experimentalmente. El parámetro más difícil de determinar es la evolución de la energía de fractura con la temperatura. Debido a la complejidad de este tipo de ensayos solo existen datos de energía de fractura residuales, o sea luego de un proceso de calentamiento-enfriamiento. En cuanto la energía de fractura a tracción existen varios datos experimentales en la literatura (Nielsen y Bićanic, 2003). De esta manera el parámetro puede determinarse para cada instante del proceso de degradación térmica.
En cuanto a la energía de fractura a compresión existen muy pocos datos experimentales a temperatura ambiente y ninguno a altas temperaturas. Por simplicidad se considerará que dicho el factor se mantiene constante para todo el proceso de degradación térmica.
|
|
(5.138) |
De esta manera los parámetros y resultan constantes.
Esta misma hipótesis se utiliza en Prato (1999) pero a efectos de modelar los procesos de envejecimiento en el hormigón, el cual puede considerarse como el fenómeno inverso del modelo proceso de degradación térmica presentado en este trabajo.
5-9 Deformaciones inelásticas
5-9-1 Deformaciones de fluencia térmica transitoria
Tal como se mencionó en el Capítulo 2, las deformaciones de fluencia térmica transitoria aparecen cuando el material bajo carga se calienta por primera vez.
Para determinar la magnitud de las deformaciones de fluencia térmica transitoria Anderberg y Thelandersson (1976) proponen una fórmula uniaxial muy sencilla
|
|
(5.139) |
donde es la tensión efectiva neta (sin incluir el daño mecánico ni el térmico), es el valor actual del coeficiente dilatación térmica lineal, es la resistencia a compresión a temperatura ambiente, y es un parámetro del material que oscila entre 1.8 y 2.35.
Es importante observar que en la formula (5.139) la dependencia de la tensión efectiva neta , se basa en la idea de que el mecanismo se produce sobre la parte del material que no ha degradado.
Posteriormente en Thelanderson (1987) se generaliza la fórmula para el caso multiaxial y en Heinfling et al. (1997) se la incluye dentro de un modelo termo-elastoplástico. En presente trabajo se utiliza la siguiente expresión para las deformaciones de fluencia térmica transitoria (Nechnech et al. 2002)
|
|
(5.140) |
donde es el tensor de cuarto orden siguiente
|
|
(5.141) |
siendo y parámetros que se ajustan con ensayos de fluencia transitoria.
5-9-2 Deformaciones de fluencia básica
Las deformaciones de fluencia básica son importantes solo en los casos en que altas temperaturas se mantengan en forma sostenida durante mucho tiempo. En general, en el caso de estructuras de hormigón armado bajo fuego, el tiempo de exposición es del orden de horas, con lo cual las deformaciones de fluencia básica son muy pequeñas comparadas con el resto de deformaciones.
En este trabajo las deformaciones de fluencia básica se considerarán despreciables.
|
|
(5.142) |
5-9-3 Actualización de la tensión efectiva neta
En el Apartado 5-8 se describió el proceso de actualización de la tensión efectiva. Dicha actualización involucra el conocimiento de la tensión efectiva neta modificada en el instante . Dicha tensión se relaciona con la tensión efectiva neta de la siguiente manera.
|
|
(5.143) |
A partir (5.108), se obtiene la expresión de la tensión efectiva neta en el instante
|
|
(5.144) |
donde
|
|
(5.145) |
Debido a que la tensión efectiva neta es función de la deformación de fluencia térmica transitoria , la cual según la expresión (5.140) depende a su vez , es necesario realizar cierta manipulación algebraica para actualizar su valor.
Expresando (5.140) en forma incremental se obtiene la expresión de la deformación de fluencia térmica transitoria en el instante
|
|
(5.146) |
donde .
Remplazando (5.146) en (5.144), se deduce una nueva expresión para la tensión efectiva neta en el instante
|
|
(5.147) |
donde
|
|
(5.148) |
|
|
(5.149) |
En la expresión (5.148) representa el tensor identidad simétrico de cuarto orden
|
|
(5.150) |
En el caso de un material elástico lineal e isótropo, el tensor de constantes elásticas tiene la siguiente expresión
|
|
(5.151) |
Donde y son las constantes de Lamé a temperatura ambiente, las cuales se relacionan con el módulo de Young y el coeficiente de Poisson de la siguiente manera
|
|
(5.152) |
|
|
(5.153) |
En este trabajo se considera que el coeficiente de Poisson se mantiene constante para todo el proceso de daño térmico.
Remplazando la expresión (5.151) en la (5.148) se obtiene una expresión explícita para el tensor
|
|
(5.154) |
donde
|
|
(5.155) |
|
|
(5.156) |
A partir de (5.154) puede calcularse la inversa de la matriz que toma la siguiente expresión
|
|
(5.157) |
5-10 Integración de la ecuación constitutiva
Hasta el momento se han descrito todos los ingredientes del modelo constitutivo termo-mecánico propuesto. Primeramente se ha descrito la ecuación constitutiva (5.108) que vincula la parte positiva y la negativa de la tensión efectiva con la tensión efectiva del esqueleto sólido . Se han descrito también las leyes de evolución de las variables de daño y . Por último se han descrito las deformaciones de fluencia térmica transitoria con su ley de evolución. Con todos estos ingredientes el modelo constitutivo de daño escalar presentado en este trabajo permite obtener la tensión efectiva del esqueleto sólido actualizada en forma explícita (Faria et al., 1998).
En el Cuadro 1 se presenta un algoritmo para la obtención de la tensión efectiva del esqueleto sólido . Primeramente se inicializan las variables internas del modelo , , y la deformación de fluencia térmica transitoria . Luego para cada nuevo paso de tiempo partiendo de la deformación total y la nueva temperatura , se actualizan las variables internas , , y se calcula la tensión efectiva del esqueleto sólido actualizada .
| CUADRO 5-1 |
| Algoritmo de integración de la ecuación constitutiva termo-mecánica del hormigón. |
| Paso
1-) , , , , , y Paso 2-) Evaluar , , y calcular 3-) 4-) 5-) 6-) Descomponer en y 7-) Calculo de y 8-) Actualización de : Si Sino 9-) Actualización de : Si Sino 10-) Actualización de y : y 11-) Calcular |
Capítulo 6 Consideración de la armadura
6-1 Introducción
Hasta el momento solo se ha desarrollado un modelo constitutivo para hormigón expuesto a elevadas temperaturas. No obstante en la mayoría de construcciones (edificios, puentes, túneles, etc.) el hormigón se encuentra comúnmente reforzado con barras de acero. El hormigón es un material con una gran resistencia a compresión y baja a tracción que se complementa con el acero que posee una elevada resistencia tanto a compresión como a tracción. De esta manera la integración de estos dos materiales ofrece una respuesta estructural optimizada dando lugar a un nuevo material conocido como hormigón armado.
Para el modelado numérico del hormigón armado se pueden utilizar diferentes tipos de escalas. En Cox y Herrmman, (1998) se describen tres tipos de escalas de análisis que se detallan a continuación (ver Figura 6-1):
- Escala de resalto: Incluyen usualmente una discretización explícita del corrugado de las barras. Una de las dificultades que presenta el modelado con este tipo de escala, es que su tamaño puede ser mucho menor que el elemento de volumen representativo (RVE) del hormigón. El RVE ser define como la región mínima donde un material puede considerarse homogéneo. En el caso del hormigón algunos áridos pueden ser mucho más grandes que el resalto de las barras perdiéndose de esta manera la hipótesis de homogeneidad.
- Escala intermedia: A esta escala se la denomina también escala de la barra. Tanto el hormigón como las barras se tratan como medios continuos y la interacción mecánica de los resaltos se considera homogenizada. De esta manera el fenómeno de adherencia se modela con una capa de elementos finitos adyacente a la barra.
- Escala de miembro: En esta escala se incluye tanto un miembro estructural o la estructura completa. Se requiere una cuidadosa selección del tipo de elementos y la discretización. En este tipo de modelo las barras se consideran homogenizadas o distribuidas en el elemento. Típicamente en esta escala las barras se consideran que poseen un comportamiento unidimensional.
En este trabajo se utilizará como escala de análisis la escala de miembro descrita anteriormente. Como técnica de homogenización o distribución de las barras de acero se utilizará la teoría de mezclas (Truesdell y Toupin, 1960). Dicha teoría permite considerar el comportamiento del material compuesto (hormigón armado) a partir de los modelos constitutivos de los materiales constituyentes (hormigón y acero). La teoría de mezclas se basa en las siguientes hipótesis:
- En cada volumen infinitesimal de material compuesto participan todos los materiales constituyentes.
- Cada componente aporta al comportamiento del material compuesto de forma proporcional a su participación volumétrica.
- El volumen ocupado por cada componente es menor que el volumen total del compuesto.
- Todos los materiales componentes tienen la misma deformación, definiendo la llamada ecuación de compatibilidad de deformaciones.
A partir de las dos primeras hipótesis se deduce que cada material constituyente del compuesto tiene una distribución homogénea, definida por su coeficiente de participación volumétrica el cual se define como:
|
|
(6.1) |
donde representa el volumen infinitesimal del material compuesto y el volumen infinitesimal del material componente i.
La última de las hipótesis determina la ley de compatibilidad de las deformaciones, expresa como:
|
|
(6.2) |
donde y son los tensores deformación del material compuesto y del material componente i respectivamente.
A partir de esta teoría se puede demostrar que el tensor de tensiones del material compuesto se expresa como (Linero, 2006):
|
|
(6.3) |
donde representa el tensor de tensiones del material constituyente i determinado en función del tensor de deformaciones y el vector de variables internas del material constituyente i.
En este trabajo se considerará que el material compuesto hormigón armado formado por una matriz de hormigón y dos paquetes de barras de refuerzo orientadas en las direcciones y (ver Figura 6-2).
De esta manera la expresión (6.3) quedará
|
|
(6.4) |
donde , y son los coeficientes de participación volumétrica de la matriz de hormigón, el refuerzo en la dirección y del refuerzo en la dirección respectivamente; y , y son los tensores de tensiones del hormigón, el refuerzo en la dirección y del refuerzo en la dirección respectivamente.
En general no se trabajará con cuantías geométricas de armaduras muy elevadas por lo que puede suponerse que . De esta manera la ecuación (6.4) quedará planteada como
|
|
(6.5) |
6-2 Modelo constitutivo de las barras de refuerzo a elevadas temperaturas
Para el modelo constitutivo de las barras de refuerzo se tendrán en cuenta las siguientes hipótesis adicionales:
- Las barras tienen un comportamiento axial en la dirección de su eje:
|
|
(6.6) |
donde y son las tensiones axiales para las barras con direcciones y respectivamente.
- Se considera adherencia perfecta entre las barras de acero y el hormigón circundante.
- Se desprecia el efecto pasador de las barras.
- Se considera un modelo constitutivo de plasticidad con endurecimiento isótropo no-lineal (Simo y Hughes, 1998).
En el cuadro 6-1 se presentan los elementos del modelo constitutivo termo-mecánico adoptado para las barras de acero.
| CUADRO 6-1 |
| Modelo constitutivo termo-mecánico para las barras de acero. |
| 1-) Relación tensión deformación
donde es el módulo de elasticidad del acero, es la dilatación térmica y es la deformación plástica. 2-) Reglas de flujo
3-) Condición de fluencia
4-) Condiciones complementarias de Kuhn-Tucker
5-) Condición de consistencia
|
Las deformaciones en la dirección de las barras pueden determinarse en función del tensor de deformaciones del material compuesto a partir de la siguiente relación
|
|
(6.7) |
La tensión límite se determina a partir de la expresión (2.4):
|
|
(6.8) |
Puede observarse que la variable interna de endurecimiento/ablandamiento se halla en el espacio de las deformaciones totales y no en el espacio de las deformaciones plásticas como es común en este tipo de modelos (Simo y Hughes, 1998).
El aporte de las barras de refuerzo al tensor constitutivo tangente del material compuesto se puede evaluar por la siguiente expresión (Linero, 2006):
|
|
(6.9) |
donde y son los módulos elásticos tangentes para las barras con direcciones y respectivamente. Dichos módulos elásticos tangentes pueden determinarse a partir de la siguiente expresión (Eurocode 2 ,1995):
|
|
(6.10) |
En el cuadro 6-2 se presenta un algoritmo de integración del modelo constitutivo presentado.
| CUADRO 6-2 |
| Algoritmo de integración de la ecuación constitutiva termo-mecánica de las barras de acero |
| 1-) Base de datos:
Para 2-) Dado el campo de deformaciones y de temperaturas se calcula:
3-) Calcular la tensión elástica de prueba
4-) Verificar carga plástica 4-1) Si 4-2)
5-) Algoritmo de retorno
|
Capítulo 7 Planteamiento Numérico
7-1 Planteamiento del problema higro-termo-mecánico
El análisis de una estructura de hormigón armado expuesta al fuego involucra diferentes problemás interdependientes. La clasificación más natural de dichos problemás es la siguiente:
- Problema térmico
- Problema de transporte de humedad
- Problema mecánico.
El problema térmico reside en la determinación de la distribución de temperaturas en la estructura y su evolución en el tiempo debida a las fuentes externas de calor. La ecuación que representa este problema es la (5.103). La variable de estado correspondiente es la temperatura .
El problema de transporte de humedad consiste en la determinación de la distribución de humedad y presión de poros en la pieza en estudio conjuntamente con su evolución temporal. Las ecuaciones que representan este problema son las (5.78) y (5.79). Las variables de estado correspondiente son la presión de gas y la presión capilar .
Por último, el problema mecánico consiste en la evaluación del campo de tensiones y deformaciones que verifican las condiciones del equilibrio y de compatibilidad a lo largo del proceso en estudio. La ecuación que representa este problema es la (5.104).
En la Figura 7-1 se presenta un diagrama esquemático de las interacciones que pueden presentarse entre los tres problemás mencionados (Prato, 1999).
La interacción 1 (problema térmico problema de transporte de humedad) tiene lugar debido a que las propiedades hídricas dependen de la temperatura. Asimismo el proceso de deshidratación producto del aumento de temperatura introduce cierta agua adicional en forma líquida o de vapor (dependiendo de la temperatura) en los poros variando de esta manera el problema de transporte de humedad.
La interacción 2 (problema de transporte de humedad problema térmico) se debe a que el movimiento de fluidos (aire seco, vapor de agua y agua líquida) genera una transmisión de calor convección. Además el movimiento de agua líquida provoca variaciones en el calor latente de evaporación.
La interacción 3 (problema mecánico problema de transporte de humedad) se genera ya que la deformaciones provocan variaciones en la porosidad modificando de esta manear la capacidad de almacenamiento de los poros. De la misma manera la fisuración modifica algunas de las propiedades hídricas como la permeabilidad.
La interacción 4 (problema de transporte de humedad problema mecánico) se debe a la presión equivalente de poros interviene directamente en la ecuación de equilibrio térmico.
La interacción 5 (problema térmico problema mecánico) se genera debido a que la variación de temperatura provoca deformaciones térmicas que a su vez dan lugar a tensiones. Asimismo la variación de temperatura provoca una evolución de las propiedades mecánicas del material.
La interacción 6 (problema mecánico problema térmico) tiene lugar cuando la energía consumida en la disipación mecánica se incluye en la ecuación de balance térmico. Este efecto se ha despreciado en este trabajo. No obstante la interacción mencionada se da indirectamente a través del problema de transporte de humedad.
7-2 Estrategias de solución del problema acoplado
El análisis higro-termo-mecánico de una estructura de hormigón expuesta al fuego implica la resolución del sistema de ecuaciones formado por las expresiones (5.78), (5.79), (5.103) y (5.104). Debido a las interacciones comentas en el apartado anterior el problema planteado es acoplado.
La resolución del problema consiste en encontrar el valor que toman las variables de estado para cada instante de tiempo. Para resolver dicho problema pueden plantearse distintas estrategias.
Una primera estrategia consiste en resolver el sistema de ecuaciones en forma conjunta, dando lugar al llamado esquema monolítico. En problemás bidimensionales esta estrategia involucra seis variables nodales . La principal desventaja de este tipo de estrategia es que el sistema de ecuaciones resultantes es de gran tamaño. De esta manera el tiempo computacional para la resolución de cada sistema de ecuaciones es muy elevado. Por otro lado se destacan como ventajas la velocidad de convergencia de la solución y la claridad de la formulación. El estudio de la estabilidad de este esquema es similar al de los problemás transitorios desacoplados (Bathe, 1996; Zienkiwicz y Taylor, 2004b).
Una segunda estrategia es el esquema iterativo en bloque. Esta estrategia consiste en resolver cada uno de los tres problemás (transporte de humedad, térmico y mecánico) en forma alternada e iterativa hasta lograr la convergencia global del problema para cada paso de tiempo. De esta manera se consigue reducir el tamaño de las matrices y el tiempo computacional de cálculo de cada sistema disminuye. El análisis de la estabilidad de este procedimiento es muy complicado. No obstante en la práctica un planteo condicionalmente estable es posible y competitivo si el tamaño del paso de tiempo esta más restringido por cuestiones de convergencia que de estabilidad (Cervera et al., 1996). La estabilidad en el tiempo también dependerá de la tolerancia exigida para la convergencia global del problema. Como caso limite, si no se chequea la convergencia global, tal como es el caso de la estrategia staggered, dará lugar a un planteo condicionalmente estable o en algunos casos incondicionalmente inestables. En el límite opuesto, si en este tipo de esta estrategia se itera hasta conseguir la convergencia global del problema las características de estabilidad de este procedimiento serán semejantes al del esquema monolítico (Cervera et al., 1996).
Una alternativa intermedia a las dos planteadas, es resolver los problemás de transporte de humedad y térmico en forma conjunta dando lugar a un nuevo problema llamado higro-térmico. Para este nuevo problema el número de variables nodales solo se eleva a tres . De esta manera el tamaño de las matrices del sistema no aumenta en forma exagerada pero la velocidad de convergencia se mejora notablemente. Luego se procede en forma semejante a la explicada en la segunda estrategia. Por cada paso de tiempo existe un ciclo de macroiteraciones hasta lograr la convergencia global del problema. En cada macroiteración se resuelven en forma secuencial el problema higro-térmico y el mecánico. Dichos problemás necesitan a su vez iteraciones debido a su carácter no-lineal. En la Figura 7-2 se representa un esquema de la estrategia propuesta.
7-3 Problema higro-térmico
7-3-1 Ecuaciones de gobierno del problema higro-térmico
El problema higro-térmico queda definido por la ecuación (5.79), de conservación de masa de aire seco, la ecuación (5.78), de conservación de masa de especies de agua, y la ecuación (5.103), de balance de entropía. Dichas ecuaciones se pueden compactar en una única ecuación vectorial de la siguiente manera:
|
|
(7.1) |
donde,
, ,
, ,
Las condiciones iniciales (5.105) se reformulan como
|
|
(7.2) |
donde,
Asimismo, las condiciones de contorno (5.106) y (5.107) se reescriben como
|
|
(7.3) |
|
|
(7.4) |
donde,
, ,
7-3-2 Forma débil de las ecuaciones higro-térmicas
La forma débil de las ecuaciones de gobierno del problema higro-térmico se obtiene aplicando el método de los residuos ponderados. Multiplicando a las ecuaciones (7.1) y (7.4) por las funciones de peso que satisfacen las condiciones de Dirichlet (7.3) en el contorno , se obtiene
|
|
(7.5) |
Integrando por partes el segundo termino de la ecuación (7.5), se tiene
|
|
(7.6) |
Sustituyendo la expresión (7.6) en la (7.5), se llega a
|
|
(7.7) |
7-3-3 Integración temporal del problema higro-térmico
Para la integración en el tiempo de la ecuación (7.7) se utilizará el esquema llamado Euler hacia atrás (backward Euler). Dicho esquema resulta incondicionalmente estable. Las derivadas temporales se expresarán entonces como
|
|
(7.8) |
donde es el vector de variables de estado higro-térmicas evaluados respectivamente en los instantes de tiempo y y es el incremento de tiempo utilizado para integración temporal.
El esquema de Euler hacia atrás consiste en evaluar la expresión (7.7) en el instante de tiempo . De esta manera
|
|
(7.9) |
7-3-4 Integración espacial del problema higro-térmico
La integración espacial de las ecuaciones de gobierno del problema higro-térmico se realiza por medio del método de los elementos finitos (Zienkiewicz y Taylor, 2004a y 2004b). Discretizando el dominio en elementos finitos bi o tridimensionales de nodos, las variables de estado higro-térmicas de cada elemento se expresan en función de sus valores nodales de la forma tradicional como
|
|
(7.10) |
donde,
Los vectores gradiente en cada elemento se obtienen como
|
|
(7.11) |
donde,
siendo
Utilizando para las funciones de peso la misma interpolación que la de la variable (Método de Galerkin), se puede expresar la ecuación (7.9) en la siguiente forma matricial
|
|
(7.12) |
donde,
,
,
7-3-5 Tratamiento de la no-linealidad del problema higro-térmico
La expresión (7.12) representa una ecuación no-lineal. Uno de los métodos más populares para resolución de problemás no-lineales es el de Newton-Rapshon. En el método de Newton-Rapshon se parte del vector de residuos
|
|
(7.13) |
Para que exista equilibrio, dicho vector debe ser nulo. En general no resulta inmediatamente nulo, y es necesario aplicar un método iterativo. Por tanto, para cada iteración , se plantea que una aproximación a la solución exacta de la siguiente manera
|
|
(7.14) |
|
|
(7.15) |
La expresión (7.15) representa un sistema de ecuaciones linealizado, el cual puede resolverse planteando
|
|
(7.16) |
donde
En cada iteración se actualiza la variable por medio de (7.14). El procedimiento iterativo continúa hasta que se satisfaga cierto criterio de convergencia en la solución.
En este trabajo se propone el siguiente criterio de convergencia.
|
|
(7.17) |
donde , y son las normás de las componentes del vector de residuos asociadas a , y respectivamente:
|
|
(7.18) |
, y representan la suma de la norma de las componentes de los flujos externos más la norma de las componentes de los flujos reactivos asociadas a , y respectivamente:
|
|
(7.19) |
7-3 Problema mecánico
7-3-1 Ecuaciones de gobierno del problema mecánico
El problema mecánico esta definido por la ecuación (5.104) que se reescribe como:
|
|
(7.20) |
donde el tensor de tensiones efectivas esta definido por (5.108).
Las condiciones iniciales del problema mecánico están dadas por la expresión (5.105d) para desplazamientos:
|
|
(7.21) |
Asimismo se supone que se parte de un estado inicial en el que las tensiones efectivas y las tensiones totales son nulas:
|
|
(7.22) |
Es importante comentar que la presión de equivalente de poros inicial hace referencia a un estado inicial distinto del comienzo del análisis objeto de este trabajo. En general se considera que y corresponde al inicio de la etapa de fraguado en la que el medio poroso se encuentra totalmente saturado .
Las condiciones de contorno (5.106d) y (5.107d) se reescriben como
|
|
(7.23) |
|
|
(7.24) |
7-3-2 Forma débil de las ecuaciones equilibrio mecánico
Utilizando el principio de los trabajos virtuales puede obtenerse la siguiente expresión integral totalmente equivalente a las ecuaciones de equilibrio mecánico descritas en el apartado anterior (Malvern, 1983):
|
|
(7.25) |
donde y son los vectores de desplazamientos y deformaciones virtuales respectivamente, es el vector de fuerzas másicas, y representa el vector de tensiones totales:
|
|
(7.26) |
siendo el vector de tensiones efectivas.
La expresión (7.26) se desarrolla como
|
|
(7.27) |
y
|
|
(7.28) |
7-3-3 Discretización espacial de las ecuaciones equilibrio mecánico
Discretizando el dominio en elementos finitos bi o tridimensionales de nodos, los desplazamientos se expresan en función de sus valores nodales de la forma tradicional como
|
|
(7.29) |
donde para problemás bidimensionales:
y para problemás tridimensionales
El vector de deformaciones totales se relaciona con el vector de desplazamientos nodales a través de la expresión (Oñate, 1995):
|
|
(7.30) |
donde para problemás bidimensionales
y para problemás tridimensionales
Reemplazando las ecuaciones (7.29) y (7.30) en (7.25) y desarrollando se llega a (Oñate, 1995)
|
|
(7.31) |
La expresión (7.26) se puede reescribir como
|
|
(7.32) |
donde
|
|
(7.33) |
y
|
|
(7.34) |
7-3-4 Tratamiento de la no-linealidad del problema mecánico
Debido a que la dependencia de los desplazamientos con las tensiones efectivas es no-lineal, la expresión (7.32) representa una ecuación no-lineal. Utilizando nuevamente el método de Newton-Rapshon se plantea la expresión (7.32) del residuo para el paso de tiempo :
|
|
(7.35) |
Para que ser cumpla la condición de equilibrio mecánico en cada paso de tiempo el vector de residuo debe ser nulo. Para hallar los desplazamientos que hagan nulo a dicho vector de residuos es necesario aplicar nuevamente un proceso iterativo. Por tal motivo se linealiza la expresión (7.35), planteando para cada iteración la siguiente aproximación
|
|
(7.36) |
|
|
(7.37) |
La expresión (7.37) representa un sistema de ecuaciones lineales que se resuelve planteando
|
|
(7.38) |
donde es la matriz de rigidez tangente definida en el apartado A5-1.
En cada iteración se actualizan los desplazamientos por medio de (7.36). El proceso iterativo continúa hasta que se satisfaga cierto criterio de convergencia en la solución. Dicho criterio de convergencia puede establecerse tanto en fuerzas como en desplazamientos (Crisfield, 1991).
7-4 Implementación numérica
El modelo higro-termo-mecánico desarrollado en este trabajo para el análisis de estructuras de hormigón armado expuesta al fuego se ha implementado numéricamente. El resultado es un programa de cálculo llamado HTM_Concrete (Hygro_Thermo_Mechanical_Concrete). Este programa fue preparado para funcionar dentro del entorno grafico ofrecido por el programa GiD.
El programa solo se ha implementado para la resolución de problemás bidimensionales, aunque la formulación desarrollada también incluye problemás tridimensionales.
Debido al esquema iterativo en bloque adoptado para la resolución, el programa desarrollado puede resolver los siguientes problemas: Mecánico, Térmico, Higro-Térmico, Termo-Mecánico e Higro-Termo-Mecánico.
El programa permite la visualización de los siguientes resultados:
1-) Problema Higro-Térmico:
- Mapa de colores e isolíneas de las temperaturas.
- Mapa de colores e isolíneas de las presiones de gas, capilar, de vapor, de aire seco y equivalente de poros.
- Mapa de colores e isolíneas del daño térmico.
- Mapa de colores e isolíneas de la masa de aire seco, masa de vapor, masa de de agua líquida y masa de agua total.
- Mapa de colores e isolíneas de la porosidad, grado de saturación y humedad relativa.
- Gráficos de evolución en el tiempo de las variables mencionadas.
2-) Problema Mecánico:
- Mapa de colores e isolíneas de los desplazamientos.
- Mapa de colores e isolíneas de las deformaciones totales, térmicas y de fluencias térmica transitoria.
- Mapa de colores e isolíneas de las tensiones en el hormigón.
- Mapa de colores e isolíneas de las tensiones en las barras de acero.
- Mapa de colores e isolíneas del los parámetros de daño mecánico.
- Diagrama de vectores de tensiones principales.
- Diagrama de vectores de reacciones.
- Gráficos de evolución en el tiempo de las variables mencionadas.
Capítulo 8 Ejemplos de validación
8-1 Introducción
En los capítulos anteriores se ha presentado un modelo higro-termo-mecánico para el análisis de estructuras de hormigón armado expuestas al fuego. También se ha descrito la implementación numérica del modelo propuesto en un código de elementos finitos.
Para analizar la capacidad de predicción del modelo desarrollado es necesario realizar algún tipo de validación del mismo. En general para validar un modelo numérico se realiza una comparación con resultados experimentales. Por razones obvias dichos ensayos siempre se realizan sobre probetas o elementos estructurales pequeños y no sobre estructuras completas. Si la herramienta numérica desarrollada es capaz de reproducir con suficiente aproximación los resultados experimentales obtenidos, se confía que también será capaz de predecir el comportamiento de estructuras más complejas.
Debido a la complejidad del fenómeno analizado es necesario realizar varias pruebas de validación. En la literatura se puede encontrar muchos ensayos experimentales en los cuales solo se monitoriza los desplazamientos y las temperaturas de probetas o elementos estructurales al ser sometidos a una carga de fuego nominal. Por otro lado existen muy pocos resultados experimentales de presión de poros en piezas sometidas a altas temperaturas. Debido a esto, en este trabajo se proponen dos ejemplos de validación. En el primer ejemplo se intentará validar la capacidad de predicción de las variables mecánicas obtenidas con el modelo. En el segundo ejemplo se pretende validar la precisión de las variables higro-térmicas obtenidas con el modelo.
8-2 Ejemplo de validación termo-mecánico
Se propone como ejemplo la reproducción numérica de los resultados experimentales del comportamiento de una losa de hormigón armado realizados Minne y Vandamme (1982). Dicho ensayo también se describe en Nechnech et al. (2002).
La geometría de la losa se describe en la Figura 8-1. Se trata de una losa simplemente apoyada trabajando en una dirección. La losa está sometida a dos cargas puntales de en los cuartos extremos de la luz. La armadura se ubica en la parte inferior con un recubrimiento de 3.5cm.
Para el análisis numérico de la losa se han utilizado elementos finitos cuadriláteros de 4 nodos en estado plano de tensiones. La discretización adoptada se representa en la Figura 8-2. La armadura inferior se distribuye en una sola fila de elementos finitos con un coeficiente de participación volumétrica .
Las propiedades termomecánicas del hormigón de la losa se indican en la Tabla 8-1. Las propiedades mecánicas de la losa se muestran en la Tabla 8-2. Los bordes inferior y superior se someten a las condiciones de contorno convectivas y radiactivas que se indican en la Tabla 8-3. La temperatura inicial del análisis es de .
| Propiedad | Valor |
| Módulo de Young | |
| Módulo de Poisson | |
| Resistencia compresión uniaxial | |
| Resistencia compresión biaxial | |
| Resistencia tracción | |
| Calor específico |
Variación según Figura 8-3 |
| Conductividad térmica |
Variación según Figura 8-3 |
| Propiedad | Valor |
| Módulo de Young | |
| Limite de proporcionalidad | |
| Resistencia a tracción |
| Borde | Variables | Valores y coeficientes |
| Inferior | ISO 834
Convectivo Radiactivo y | |
| Superior |
Convectivo Radiactivo y |
En la Figura 8-4 se muestra la evolución en el tiempo de los desplazamientos obtenidos a partir del modelo propuesto y del ensayo experimental.
Se puede observar que el modelo propuesto es capaz de reproducir tanto los valores máximos como la tendencia de los resultados experimentales.
8-3 Ejemplo de validación de variables higro-térmicas
Para validar las variables higro-térmicas (temperatura y presión de gas) que ofrece el modelo se propone comparar los resultados del mismo con los valores obtenidos en la campaña experimental realizada por Kalifa et al. (2000).
En la campaña experimental antes mencionada se ha aplicado una carga térmica sobre una de las caras de una pieza prismática de hormigón de medidas . Los laterales de la pieza se encontraban aislados térmicamente por bloques cerámicos. La fuente de calor la proveía un radiador de que cubre la superficie de la pieza y esta ubicado a de esta. La temperatura del radiador fue de . La configuración del ensayo se esquematiza en la Figura 8-5.
La pieza fue instrumentada mediante seis galgas termopares durante el hormigonado para medir temperaturas y presiones simultáneamente. Cinco de las galgas fueros ubicadas en la zona central de , a distancias de 10, 20, 30, 40 y 50 respectivamente de la superficie caliente.
Las propiedades del hormigón de la pieza ensayada se describen en la Tabla 8-4. Las condiciones iniciales del ensayo se detallan en la Tabla 8-5.
| Propiedad | Valor |
| Módulo de Young | |
| Módulo de Poisson | |
| Resistencia compresión uniaxial | |
| Resistencia compresión biaxial | |
| Resistencia tracción | |
| Calor específico | Eurocode 2, 1995 |
| Conductividad térmica | Kalifa et al., 1998. |
| Permeabilidad intrínseca |
| Propiedad | Valor |
| Grado de saturación | |
| Presión de gas | |
| Temperatura | |
| Porosidad |
Debido a la capa de aire que existe entre en el radiador y la superficie de la muestra, es difícil establecer de forma exacta las condiciones de contorno a la que esta sometida la pieza. Dicha capa de aire produce cierto efecto de enfriamiento generando que la temperatura de sobre la superficie de la pieza sea menor que la del radiador. Asimismo los coeficientes de radiación y convección irán variando a lo largo del tiempo. En Gawin et al. (2002) se analiza numéricamente este mismo ensayo. En dicho trabajo se proponen coeficientes de radiación y convección constantes y las condiciones de contorno descritas en la Tabla 8-6.
| Borde | Variables | Valores y coeficientes |
| AB |
|
Variación según Figura 8-6 Convectivo Radiactivo y |
| CD |
|
Convectivo Radiactivo y |
| P1 | ||
| P1 |
Para el estudio numérico se realizará un análisis higro-termo-mecánico. Se supondrá que la pieza esta bajo un estado plano de deformaciones. Se analiza una sección transversal de . Se han utilizado elementos finitos cuadrilátero de cuatro nodos. La discretización adoptada se muestra en la Figura 8-7.
La evolución de las temperaturas con el tiempo obtenidas con la simulación numérica se muestran en la Figura 8-9 la cual puede compararse con los resultados experimentales mostrados en la Figura 8-8. Analizando ambas figuras se observa que la correlación entre los resultados experimentales y numéricos es excelente. En general la predicción numérica de la temperatura es muy buena. Esto último se debe a que la determinación experimental de los parámetros que condicionan el problema térmico (conductividad y calor específico) muestra muy poca dispersión (Kalifa et al., 1998). Esta característica no se repite para las variables hídricas (permeabilidad).
La evolución de las presiones de gas con el tiempo obtenidas con la simulación numérica se muestra en la Figura 8-11, la cual puede compararse con los resultados experimentales mostrados en la Figura 8-10. El acuerdo entre los resultados experimentales y numéricos es bastante bueno en cuanto a los valores máximos y la tendencia general. El valor del resultado experimental de la presión de gas a la profundidad de 30mm no se corresponde con la tendencia creciente del resto de profundidades. En Kalifa et al. (2000) se sugiere que este efecto puede deberse a la aparición de una fisura muy cerca de la galga a 30mm de profundidad. Si fuera posible evitar esta perturbación en la lectura de la galga por la presencia de una fisura las presiones mostrarían un máximo y luego descenderían tal como se muestra en los resultados numéricos.
Capítulo 9 Ejemplos de aplicación
9-1 Introducción
En el capítulo anterior se han presentado dos ejemplos de validación del modelo higro-termo-mecánico del hormigón expuesto a elevadas temperaturas que se desarrollo en este trabajo. Dichos ejemplos de validación han mostrado una buena correlación con los resultados experimentales, y puede utilizarse para el análisis de estructuras más complejas. En este capítulo se presenta un conjunto de ejemplos de aplicación del modelo propuesto.
9-2 Pilar de 30cmx30cm
Cuando un incendio afecta a una estructura de edificación es muy común que los pilares sufran spalling dejando al descubierto las armaduras. Si el pilar está muy armado, las barras de acero representan una parte importante del mecanismo resistente. En este caso el efecto del fuego directo sobre las barras conduce rápidamente al colapso del pilar.
En este ejemplo se intenta reproducir el fenómeno de spalling en un pilar cuadrado de 30cmx30cm. Para el análisis se considera que la sección transversal del pilar se encuentra bajo un estado plano de deformaciones. La geometría del pilar se representa en la Figura 9-1.
Por simplicidad y aplicando condiciones de simetría se ha considerado solamente un cuarto de pilar. La discretización adoptada se representa en la Figura 9-2.
Las propiedades del material utilizadas en la simulación se muestran en la Tabla 9-1. Las condiciones iniciales y de contorno se muestran en las Tablas 9-2 y 9-3 respectivamente.
| Propiedad | Valor |
| Módulo de Young | |
| Módulo de Poisson | |
| Resistencia compresión uniaxial | |
| Resistencia compresión biaxial | |
| Resistencia tracción | |
| Calor específico | |
| Conductividad térmica | |
| Permeabilidad intrínseca |
| Propiedad | Valor |
| Humedad relativa | |
| Presión de gas | |
| Temperatura | |
| Porosidad |
| Borde | Variables | Valores y coeficientes |
| AB
y BC |
|
Curva ISO 834 Convectivo Radiactivo y |
| AD | ||
| DC |
Para estudiar el comportamiento de este pilar se han realizado dos tipos de análisis: termo-mecánico (TM) e higro-termo-mecánico (HTM). La evolución en el tiempo del desplazamiento del punto B para ambos tipos de análisis se muestra en la Figura 9-3. En esta figura se puede observar que los desplazamientos obtenidos con un análisis TM son prácticamente idénticos a los obtenidos con un HTM. El análisis HTM presenta un fallo anticipado por efecto del spalling hidráulico.
En las Figuras 9-4 - 9-18 se presentan los resultados obtenidos del análisis higro-termo-mecánico en el final de la simulación.
Los resultados muestran la aparición de una fisura por spalling a aproximadamente 1.5cm de profundidad. En este caso el spalling se debe principalmente a las tensiones por efecto de la dilatación. En la Figura 9-17 se muestra como se generan tensiones de compresión paralelas a las superficies expuestas al calor. Estas tensiones representan en el hormigón dos bielas comprimidas. Dichas bielas al unirse en el punto B generan una componente de tracción en la dirección de la diagonal. Cuando estas tensiones de tracción superan la resistencia a tracción del hormigón se genera el spalling. La presión de poros genera un aumento de tensiones de tracción produciendo un fallo anticipado.
9-2 Muro cortafuego
Los muros cortafuegos son los últimos medios para limitar una pérdida catastrófica debida a un incendio una vez que hayan fallado los restantes dispositivos de seguridad. Actualmente las instalaciones industriales modernas tienen grandes áreas para procesos y para el correcto almacenamiento de los productos. Para reducir el peligro en caso de incendio cada área puede delimitarse por los muros cortafuegos. La misión de éstos muros será la prevención de la propagación del calor, las llamás y el humo de una zona a otra.
En este ejemplo se presenta el análisis de un muro cortafuego de hormigón armado expuesto al fuego. Se trata de un muro de 25cm de espesor expuesto en una de sus caras a una curva nominal de fuego ISO 834. La geometría del muro se representa en la Figura 9-19.
Se supondrá que el muro se encuentra bajo un estado de deformación plana. Para la simulación numérica se utilizarán elementos finitos cuadriláteros de cuatro nodos. La discretización adoptada se muestra en la Figura 9-20.
Las propiedades del material utilizadas en la simulación se muestran en la Tabla 9-4. Las condiciones de contorno e iniciales se muestran en las Tablas 9-5 y 9-6 respectivamente.
| Propiedad | Valor |
| Módulo de Young | |
| Módulo de Poisson | |
| Resistencia compresión uniaxial | |
| Resistencia compresión biaxial | |
| Resistencia tracción | |
| Calor específico | Eurocode 2, 1995 |
| Conductividad térmica | Eurocode 2, 1995 |
| Permeabilidad intrínseca |
| Borde | Variables | Valores y coeficientes |
| AB |
|
Curva ISO 834 Convectivo Radiactivo y |
| CD |
|
Convectivo Radiactivo y |
| AD |
| Propiedad | Valor |
| Humedad relativa | |
| Presión de gas | |
| Temperatura | |
| Porosidad |
Se han realizado análisis TM y HTM. La evolución en el tiempo del desplazamiento horizontal del punto C para ambos tipos de análisis se muestra en la Figura 9-21. Al igual que en ejemplo anterior los desplazamientos obtenidos con un análisis TM son prácticamente idénticos a los obtenidos con un HTM. Nuevamente el análisis HTM presenta un fallo anticipado por efecto del spalling hidráulico.
En las Figuras 9-22 - 9-40 se presentan los resultados obtenidos del análisis HTM en el final de la simulación.
Analizando los resultados obtenidos se puede observar que la causa del fallo es la aparición de una fisura por spalling en la parte superior aproximadamente a 2 cm de la cara expuesta. En este caso la principal causa del spalling es la presión de poros. En la Figura 9-38 se superpone la presión equivalente de poros sobre la deformada. Se observa que la zona más abierta de la fisura coincide con los valores máximos de la presión equivalente de poros.
9-2 Túnel circular
Tal como se comentó en el Capítulo 1, el 18 de noviembre de 1996 que tuvo un incendio en el “Túnel del Canal de la Mancha” que generó un daño muy importante en el recubrimiento de hormigón del túnel debido al fenómeno de spalling explosivo. Han habido varios estudios que intentaron explicar el motivo de este fenómeno de spalling explosivo en dicho túnel. Uno de los trabajos más destacados es el realizado por Ulm et. alt. (1999b). En dicho trabajo se expone que la causa principal del spalling explosivo es el aumento de las tensiones de compresión originadas por las dilataciones térmicas restringidas. Dichas tensiones de compresión pueden aumentar hasta alcanzar la resistencia de compresión la cual se encuentra reducida por efecto del daño térmico. En el trabajo mencionado se realiza un análisis TM donde se muestra el aumento de tensiones de compresión en planos paralelos a la cara expuesto al fuego.
En este ejemplo se intenta reproducir el trabajo de Ulm et. alt. (1999b) pero realizando un análisis HTM para evaluar si en este caso la presión de poros es relevante en el fenómeno de spalling. En la Figura 9-41 se muestra la geometría de un cuarto de túnel.
Se supondrá que el túnel se encuentra bajo un estado de deformación plana. Para la simulación numérica se utilizarán elementos cuadriláteros de cuatro nodos para la zona de recubrimiento de hormigón y elementos triangulares de tres nodos para la zona de substrato de piedra caliza. La discretización adoptada se muestra en la Figura 9-42.
Las propiedades del material utilizadas en la simulación se muestran en la Tabla 9-7. Se ha supuesto que el hormigón responde al comportamiento constitutivo de daño isótropo con dos variables escalares de daño que ha sido desarrollado en este trabajo. Asimismo se ha supuesto que el substrato de piedra caliza se comporta como termo-elástico.
Las condiciones de contorno e iniciales se muestran en las Tablas 9-8 y 9-9 respectivamente.
| Propiedad | Hormigón | Piedra caliza |
| Módulo de Young | ||
| Módulo de Poisson | ||
| Resistencia compresión uniaxial | - | |
| Resistencia compresión biaxial | - | |
| Resistencia tracción | - | |
| Calor específico | Eurocode 2, 1995 | Eurocode 2, 1995 |
| Conductividad térmica | Eurocode 2, 1995 | Eurocode 2, 1995 |
| Permeabilidad intrínseca |
| Borde | Variables | Valores y coeficientes |
| BC |
|
Curva ISO 834 Convectivo Radiactivo y |
| AB | ||
| CD |
| Propiedad | Hormigón | Piedra calíza |
| Humedad relativa | ||
| Presión de gas | ||
| Temperatura | ||
| Porosidad |
Al igual que en los ejemplos anteriores se ha realizado un análisis TM y otro HTM. En la Figura 9-43 se presenta un gráfico comparando la respuesta obtenida con ambos tipos de análisis. En esta figura se observa que nuevamente el spalling conduce al fallo anticipado de la pieza.
En las Figuras 9-44 - 9-57 se presentan los resultados obtenidos del análisis HTM.
Analizando los resultados se puede observar que la causa de spalling es un efecto combinado de la presión de poros y las tensiones térmicas. En las Figuras 9-58 y 9-59 se muestra la evolución de las tensiones circunferenciales y longitudinales . Estas tensiones generan un estado de compresión biaxial que alcanza la resistencia para una temperatura dada. La resistencia desciende rápidamente al entrar en la rama de ablandamiento del material. Este efecto es que el se expone como explicación del spalling explosivo en Ulm et. alt. (1999b). No obstante la presión de poros juega un papel muy importante al generar tensiones de tracción que aumentan hasta generar repentinas fisuras de tracción tal como se muestra en la Figura 9-60.
Capítulo 10 Conclusiones
10-1 Conclusión
En este trabajo se presenta una metodología numérica, basada en la técnica de los Elementos Finitos, capaz de modelar el comportamiento higro-termo-mecánico del hormigón armado expuesto al fuego.
Las conclusiones extraídas a lo largo de la elaboración de esta Monografía son las siguientes:
- Se ha propuesto un marco termodinámico para el hormigón expuesto a elevadas temperaturas dentro del contexto de la mecánica de los medios porosos no saturados.
Para el desarrollo de dicho marco termodinámico se ha propuesto el daño térmico como variable interna que controla el proceso de deshidratación. Las propiedades higro-termo-mecánicas cuya evolución está referida a la temperatura máxima alcanzada se las ha relacionado con el daño térmico. De esta manera la función de energía queda expresada de manera clara y elegante.
A partir de este marco se ha podido tratar de forma consistente los complicados procesos irreversibles que se producen en el hormigón a elevadas temperaturas, asegurando de esta manera que la disipación total sea siempre positiva.
También gracias a este marco se han calculado las variables de estado que se han utilizado para el desarrollo de las ecuaciones de gobierno. Particularmente en el desarrollo de la ecuación de balance de entropía, los términos de calor latente de evaporación, calor latente de deshidratación y transmisión de calor por convección de fluidos han surgido de manera natural.
Se ha realizado una identificación de los parámetros termoporoelásticos del modelo con propiedades termo-mecánicas de la mesoescala. A partir de esta identificación se ha podido relacionar la expresión de la variación de la porosidad obtenida como variable de estado del marco termodinámico propuesto con la obtenida de plantear el principio de conservación de masa del esqueleto sólido. De esta manera se demuestra que ambas maneras de obtener una expresión para variación de porosidad son totalmente equivalentes.
- A partir de las variables de estado obtenidas del marco termodinámico y de las ecuaciones de gobierno del problema queda planteado un modelo higro-termo-mecánico para el hormigón expuesto a elevadas temperaturas.
Como variables de estado del modelo se han elegido la temperatura, la presión de gas, la presión capilar y los desplazamientos.
El comportamiento mecánico del hormigón presentado en este trabajo se basa en la teoría del daño continuo. Se propone un modelo de degradación con dos variables internas escalares que representan el daño a tracción y compresión respectivamente. De esta manera se consigue un modelo constitutivo que, a pesar de ser bastante sencillo, es capaz de representar globalmente el comportamiento no lineal del hormigón y reproducir fenómenos como el ablandamiento por deformación y regradación de rigidez bajo alternancia del signo de la tensión. A la degradación mecánica de la rigidez se le añade la degradación térmica caracterizada por la variable de daño mecánico. El modelo se formula en un formato normalizado permitiendo incorporar los fenómenos de disminución de resistencia y rigidez debidos a la degradación térmica de una manera natural y simple. Asimismo se incorporan al modelo las deformaciones de fluencia térmica transitoria de una manera sencilla proponiendo una expresión para su evolución en función de la tensión efectiva neta. El resultado final es un modelo implementado en función de la deformaciones lo cual conduce a un algoritmo explícito para la integración del tensor de tensiones en el tiempo. Asimismo se ha desarrollado una expresión para la matriz tangente algorítmica.
Para representar el aporte de la armadura a la resistencia mecánica se ha considerado al hormigón armado como un material compuesto y se ha desarrollado un modelo constitutivo basado en la teoría de mezclas. Esta teoría ha permitido considerar el aporte de cada grupo de barras al comportamiento del material compuesto de una forma proporcional a su participación volumétrica. Particularmente se ha supuesto que las barras de acero responden a un modelo constitutivo termo-mecánico basado en un comportamiento plástico con endurecimiento isótropo no-lineal. Se considera también la evolución del módulo de Young y la resistencia con la temperatura.
- Para la aplicación de los modelos propuestos se ha desarrollado una metodología numérica basada en el Técnica de los Elementos Finitos. El resultado final es un programa de cálculo para el análisis higro-termo-mecánico del hormigón armado expuesto a elevadas temperaturas. Este programa fue preparado para funcionar dentro del entorno grafico ofrecido por el programa GiD, disfrutando de su potencialidad para la generación de mallas y la visualización de resultados.
Para el tratamiento del acoplamiento se ha elegido el uso de un esquema iterativo en bloque, en el que se resuelven el problema higro-térmico y el mecánico de manera alternada e iterativa hasta lograr la convergencia global del problema para cada paso de tiempo.
- Para evaluar la capacidad de predicción del modelo numérico propuesto se han realizado ejemplos de validación. En dichos ejemplos, se han comparado los resultados numéricos obtenidos del modelo propuesto con resultados experimentales. En todos los casos la correlación obtenida ha sido bastante buena.
- Se han realizado un conjunto de ejemplos de aplicación. En dichos ejemplos ha quedado demostrada la capacidad del modelo propuesto para capturar el comportamiento general de una estructura de hormigón armado expuesta al fuego, y en especial el fenómeno de spalling.
Como ejemplo más destacado está el análisis del comportamiento al fuego un túnel de características similares al Túnel-Canal de la Mancha. En dicho ejemplo se demuestra que en este caso particular tanto la presión de poros como las tensiones producidas por deformaciones térmicas restringidas, han sido causas del spalling que ha sufrido el túnel.
10-2 Aportaciones
Las principales aportaciones que se han realizado en este trabajo son las siguientes:
- Definición de una expresión para la función energía a partir de la cual se ha desarrollado el marco termodinámico propuesto. Dicha función se separa en un conjunto de términos energéticos que se identifican con cada uno de los procesos higro-termo-mecánicos que se producen al someterse al hormigón a elevadas temperaturas.
- En el modelo se ha tenido en cuenta la compresibilidad del esqueleto sólido dando lugar a un coeficiente de Biot distinto de uno.
- Se propone una reformulación de un modelo de degradación que permite incorporar no solo los fenómenos de disminución de resistencia y rigidez debidos a la degradación térmica, sino también una longitud característica del material variable con la temperatura.
- Se ha considerado en el análisis el aporte de la armadura al comportamiento mecánico. Esto constituye una novedad para los modelos higro-termo-mecánicos de estructuras de hormigón expuestas a elevadas temperaturas.
- Se ha utilizado con éxito un esquema iterativo en bloque para el tratar el acoplamiento. Este tipo de esquema es particularmente atractivo para la resolución de grandes problemas en los que el tamaño de las matrices es mucho más reducido que en el caso de esquemas monolíticos.
- La consideración de dos variables de daño, una positiva y otra negativa, para las tensiones de tracción y compresión respectivamente, ha permitido identificar más claramente la zona donde se produce spalling.
10-3 Futuras líneas de investigación
A partir del estudio desarrollado en esta Monografía se desprenden algunas posibles futuras líneas de investigación que se describen a continuación:
- El modelo propuesto necesita mayor validación experimental. Los parámetros del modelo se han tomado a partir de datos de la bibliografía. No obstante existe una gran discrepancia entre las distintas referencias, principalmente en cuanto a parámetros como la permeabilidad intrínseca, módulo de elasticidad, energía de fractura, etc.
- Se debe continuar la investigación para lograr mayor robustez en la implementación numérica. El modelo presenta algunos problemás numéricos para ciertos casos particulares como es el caso de valores bajos de la energía de fractura y presiones de aire seco tendiendo a cero.
- En el trabajo presentado no se ha considerado la influencia de la fisuración sobre la permeabilidad. La consideración de este fenómeno se traduce en una mayor presición en la determinación de las presiones de poros. Asimismo, resulta de gran interés el modelado del efecto de la adición de fibras de propileno en el hormigón.
- El modelo se ha implementado solo para elementos finitos bidimensionales pero puede extenderse en forma natural al caso tridimensional. También resulta accesible la extensión del modelo al caso de pórticos tridimensionales y láminas debido al esquema iterativo en bloque adoptado. En este caso se debe realizar alguna hipótesis cinemática adicional en el problema higro-térmico como la suponer porosidad constante.
- Se pueden incorporar otros fenómenos como armaduras deslizantes y la inclusión de la variación de humedad en la fluencia transitoria (drying creep).
- El modelo higro-termo-mecánico desarrollado para el caso del hormigón expuesto a elevadas temperaturas puede extenderse al comportamiento del hormigón en edades tempranas.
Anexo 1
A1-1 Matriz tangente consistente para el modelo mecánico
Para obtener la matriz tangente consistente para el modelo mecánico propuesto, es necesario diferenciar la ecuación constitutiva (5.108) respecto al tiempo
|
|
(11.1) |
La derivada temporal de los tensores se determina según Faria et al. (2000) como
|
|
(11.2) |
|
|
(11.3) |
donde
|
|
(11.4) |
siendo la función de Heaviside, y son respectivamente los autovalores y autovectores del tensor .
En las ecuaciones (11.2) y (11.3) se ha considerado que la temperatura ya ha sido actualizada y por tanto el daño térmico se mantiene constante.
Remplazando la expresión (5.149) en (5.147), y luego diferenciando se obtiene la derivada temporal de
|
|
(11.5) |
donde
A partir de (5.128) se deduce la derivada temporal de los parámetros de daño
|
|
(11.6) |
con
|
|
(11.7) |
Teniendo en cuenta la expresión (5.126) y utilizando (5.118) se obtiene
|
|
(11.8) |
En forma semejante, utilizando (5.119) se tiene
|
|
(11.9) |
siendo
|
|
(11.10) |
|
|
(11.11) |
donde es el segundo invariante de la parte desviadora del tensor de tensiones efectivas modificadas netas.
Finalmente, a partir de las expresiones anteriores se determina la matriz tangente consistente
|
|
(11.12) |
con
|
|
(11.13) |
|
|
(11.14) |
|
|
(11.15) |
A1-2 Parámetros del modelo
A1-2-1 Densidad del agua líquida
Se supondrá que el agua líquida es incompresible. Sin embargo a elevadas temperaturas la densidad del agua puede variar sensiblemente. La variación de la densidad del agua con la temperatura se considera teniendo en cuenta a Gawin et al. (1999):
|
|
(11.16) |
donde es la densidad del agua a la temperatura de referencia y es el coeficiente de expansión térmica. El coeficiente cambia de manera no lineal con la temperatura, no obstante por simplicidad se considerará un valor promedio de .
A1-2-2 Densidad de la matriz sólida
Se supondrá que la densidad de la matriz sólida tiene un valor constante de .
A1-2-3 Parámetros termoporoelásticos
Los parámetros termoporoelásticos , y definidos en las ecuaciones (5.35), (5.40) y (5.45) varían con los parámetros del daño mecánico y y con el daño térmico . Asimismo dependen del módulo volumétrico de la matriz sólida , el cual se ha supuesto constante. Para obtener un valor aproximado de se puede utilizar la siguiente expresión:
|
|
(11.17) |
donde es el coeficiente de Biot para el material sin dañar. A modo ilustrativo un hormigón con una relación tiene un coeficiente de Biot de aproximadamente (Ulm et al., 2004)
El coeficiente de dilatación de la matriz sólida se lo considera aproximadamente igual que el coeficiente de dilatación del medio poroso (Coussy, 2004). A efectos de la ecuación (5.45) se considerará que .
A1-2-4 Evolución de la resistencia mecánica
Para determinar la evolución de las resistencias del hormigón a compresión y a tracción con el daño térmico se toma del Eurocode 2 (1995). A partir de dicha referencia y de la expresión (5.113) se obtiene la Tabla A1-1:
| Agregado Silíceo | Agregado Calcáreo | |||
| 20 | 0.0 | 1 | 1 | 1.0 |
| 100 | 0.14 | 1 | 1 | 0.8 |
| 200 | 0.29 | 0.95 | 0.97 | 0.6 |
| 300 | 0.41 | 0.85 | 0.91 | 0.4 |
| 400 | 0.51 | 0.75 | 0.85 | 0.2 |
| 500 | 0.59 | 0.6 | 0.74 | 0.0 |
| 600 | 0.66 | 0.45 | 0.6 | 0.0 |
| 700 | 0.71 | 0.3 | 0.43 | 0.0 |
| 800 | 0.76 | 0.15 | 0.27 | 0.0 |
| 900 | 0.80 | 0.08 | 0.15 | 0.0 |
| 1000 | 0.83 | 0.04 | 0.06 | 0.0 |
| 1100 | 0.85 | 0.01 | 0.02 | 0.0 |
| 1200 | 0.87 | 0.0 | 0.0 | 0.0 |
A1-2-5 Masa deshidratada
La evolución de la de masa de hormigón deshidratado se puede calcular a partir de ensayos termogravimétricos y dilatométricos (Harmathy y Allen, 1973). En la tabla A1-1 se muestra la evolución de con el daño térmico , para un hormigón con agregado silíceo y para otro con agregado calcáreo.
Para evaluar la tasa de la masa de hormigón deshidratado se utiliza la siguiente formula incremental:
|
|
(11.18) |
| Agregado Silíceo | Agregado calcáreo | ||
|
|
| ||
| 20 | 0 | 0.0 | 0.0 |
| 50 | 0.06 | 0.0 | 0.0 |
| 100 | 0.14 | 0.0 | 0.0 |
| 150 | 0.22 | 0.014 | 0.014 |
| 200 | 0.29 | 0.028 | 0.019 |
| 250 | 0.35 | 0.037 | 0.028 |
| 300 | 0.41 | 0.042 | 0.037 |
| 350 | 0.46 | 0.047 | 0.0425 |
| 400 | 0.51 | 0.056 | 0.056 |
| 450 | 0.55 | 0.065 | 0.065 |
| 500 | 0.59 | 0.084 | 0.084 |
| 550 | 0.63 | 0.093 | 0.103 |
| 600 | 0.66 | 0.112 | 0.136 |
| 650 | 0.69 | 0.136 | 0.182 |
| 700 | 0.71 | 0.182 | 0.280 |
| 750 | 0.74 | 0.243 | 0.561 |
| 800 | 0.76 | 0.383 | 0.650 |
| 850 | 0.78 | 0.393 | 0.654 |
| 900 | 0.80 | 0.393 | 0.654 |
| 950 | 0.81 | 0.397 | 0.654 |
| 1000 | 0.83 | 0.397 | 0.654 |
| 1200 | 0.87 | 0.397 | 0.654 |
A1-2-6 Deformación térmica
La deformación térmica se toma del Eurocode 2 (1995). A partir de dicha referencia y de la expresión (5.113) se obtiene la Tabla A1-3:
| Agregado Silíceo | Agregado Calcáreo | ||
| 20 | 0.0 | 0.0 | 0.0 |
| 100 | 0.14 | 0.00110 | 0.00049 |
| 200 | 0.29 | 0.00216 | 0.00119 |
| 300 | 0.41 | 0.00350 | 0.00206 |
| 400 | 0.51 | 0.00525 | 0.00318 |
| 500 | 0.59 | 0.00756 | 0.00463 |
| 600 | 0.66 | 0.01055 | 0.00650 |
| 700 | 0.71 | 0.01437 | 0.00888 |
| 800 | 0.76 | 0.01437 | 0.01184 |
| 805 | 0.761 | 0.01400 | 0.01200 |
| 900 | 0.79 | 0.01400 | 0.01200 |
| 1000 | 0.82 | 0.01400 | 0.01200 |
| 1200 | 0.87 | 0.01400 | 0.01200 |
A1-2-7 Calores específicos
El calor específico del esqueleto sólido se toma de del Eurocode 2 (1995). A partir de dicha referencia y de la expresión (5.113) se obtiene la Tabla A1-4:
| 20 | 0.0 | 2.07 |
| 100 | 0.14 | 2.07 |
| 115 | 0.17 | 2.1 |
| 200 | 0.29 | 2.25 |
| 300 | 0.41 | 2.33 |
| 400 | 0.51 | 2.40 |
| 500 | 0.59 | 2.38 |
| 600 | 0.66 | 2.36 |
| 700 | 0.71 | 2.33 |
| 800 | 0.76 | 2.31 |
| 900 | 0.80 | 2.29 |
| 1000 | 0.83 | 2.27 |
| 1100 | 0.85 | 2.25 |
| 1200 | 0.87 | 2.22 |
Para el calor específico del agua líquida se toma un valor constante de .
El calor específico del aire varía con la temperatura de la siguiente manera (Çengel y Boles, 2003):
|
|
(11.19) |
Por su parte, el calor específico de vapor de agua varía con la temperatura con la siguiente ley (Çengel y Boles, 2003):
|
|
(11.20) |
A1-2-8 Presión de saturación de vapor
La ecuación para la presión de saturación de vapor como función de la temperatura que se presenta fue desarrollada por Saul y Wagner (1987):
|
|
(11.21) |
donde es la presión crítica del agua, es la temperatura crítica del agua y la variable .
A1-2-9 Masas molares y constante universal de los gases
La masa molar del vapor de agua y del aire toman respectivamente los valores y (Çengel y Boles, 2003).
La constante universal de los gases toma el valor (Çengel y Boles, 2003).
A1-2-10 Calor latente de vaporización
Durante un proceso de cambio de fase la presión y la temperatura son propiedades dependientes y con una relación definida por la expresión (11.21). Debido a que en el proceso de vaporización se ha supuesto que no hay disipación, las energías de Gibbs son iguales . Por tanto se verifica que:
|
|
(11.22) |
A la expresión se la llama entalpía de vaporización o calor latente de vaporización.
En la Tabla A1-5 se muestra la evolución del calor latente de vaporización con la temperatura (Çengel y Boles, 2003).
| 20 | 2454.1 |
| 50 | 2382.7 |
| 75 | 2321.4 |
| 100 | 2257.0 |
| 125 | 2188.5 |
| 150 | 2114.3 |
| 175 | 2032.4 |
| 200 | 1940.7 |
| 225 | 1836.5 |
| 250 | 1716.2 |
| 275 | 1574.9 |
| 300 | 1404.9 |
| 330 | 1238.6 |
| 350 | 893.4 |
| 360 | 720.3 |
| 370 | 441.6 |
| 374.14 | 0.0 |
A1-2-11 Calor latente del daño térmico
Tal como ya se ha indicado, el calor latente del daño térmico tiene la siguiente expresión:
|
|
(11.23) |
A partir de la expresión (5.10) y (5.15) se deduce
|
|
(11.24) |
donde
|
|
(11.25) |
|
|
(11.26) |
|
|
(11.27) |
Analizando las expresiones (11.25), (11.26) y (11.27) se puede observar que el único término relevante es el asociado a , por tanto el calor latente del daño térmico quedará como:
|
|
(11.28) |
En la literatura hay muy pocos datos experimentales de este calor latente de deshidratación, fundamentalmente debido a la complejidad de los ensayos requeridos para su determinación. En Kanema et al., 2007 se propone un valor de .
A1-2-12 Permeabilidad intrínseca
En Gawin et al. (2003) se desarrolla una expresión para la permeabilidad intrínseca dependiente de la temperatura, la presión de gas y de la variable de daño :
|
|
(11.29) |
donde es la permeabilidad intrínseca inicial, y los parámetros , , y toman los siguientes valores:
|
|
(11.30) |
La permeabilidad intrínseca inicial depende del tipo de hormigón que se utilice, tomando valores de aproximadamente para hormigones normales y de para hormigones de alta resistencia.
En el presente trabajo no se considerará la dependencia del la fisuración sobre la permeabilidad intrínseca, por lo que se tomará al parámetro .
Referencias
Ahmed, G. N. y Hurst, J.P. (1995) Modelling the thermal behaviour of concrete slabs subjected to the ASTM E119 standard fire conditions, Journal of Fire Protection Engineering, 7, 125-132.
Ahmed, G. N. y Hurst, J.P. (1997a) Coupled heat and mass transfer phenomena in siliceous aggregate concrete slabs subjected to fire, Fire and Materials, 21, 161-168.
Ahmed, G. N. y Hurst, J.P. (1997b) An analytical approach for investigating the causes of spalling of high-strength concrete at elevated temperatures, International Workshop of Fire Perfomance of High-Strength Concrete, NIST Special Publication 919, Phan, L.T., Carino, N.J., Duthinh, D. and Garboczi, E. eds., National Institute of Standards and Technology, Gaithersburg, Maryland, 95-108.
Anderberg, Y. (1997) Spalling phenomena of HPC and OC, International Workshop of Fire Perfomance of High-Strength Concrete, NIST Special Publication 919, Phan, L.T., Carino, N.J., Duthinh, D. and Garboczi, E. eds. National Institute of Standards and Technology, Gaithersburg, Maryland, 69-73.
Anderberg, Y. y Thelandersson, S. (1976) Stress and deformation characteristic of concrete at high temperature. Bulletin 54, Lund Institute of Technology, Sweden.
Baroghel-Bouny, V., Mainguy, M., y Lassabatère, T., Coussy, O. (1999) Characterization and identification of equilibrium and transfer moisture properties for ordinary and high-perfomace cementitious materials, Cement and Concrete Research, 29, 1225-1238.
Bathe, K.J. (1996) Finite Element Procedures, Prentice Hall, New Jersey, USA.
Bazant Z.P. (1997) Analysis of pore pressure, thermal stress and fracture in rapidly heated concrete, International Workshop of Fire Perfomance of High-Strength Concrete, NIST Special Publication 919, Phan, L.T., Carino, N.J., Duthinh, D. and Garboczi, E. eds. National Institute of Standards and Technology, Gaithersburg, Maryland, 155-164.
Bazant Z.P. y Kaplan,M.F. (1996) Concrete at high temperature: material properties and mathematical models. London: Longman Group Limited.
Bazant Z.P. y Thonguthai, W. (1978) Pore pressure and driving of concrete at high temperature, Journal of Engineering Mechanics Division, Proceedings of the American Society of Civil Engineers, 104, 1059-1079.
Bazant Z.P. y Thonguthai, W. (1979) Pore pressure in heated concrete walls: theoretical prediction, Magazine of Concrete Research, 31, 67-76.
Çengel Y. y Boles M. (2003) Termodinámica. 4ta edición. McGraw Hill. México D.F.
Cervera, M., Codina, R. y Galindo, M. (1996) On the computacional efficiency and implementation of block-iterative algorithms for nonlinear coupled problems. International Journal for Computer-Aided Engineering and Software. 13,4-30.
Chaboche, J. (1988a) Continuum damage mechanics. Part I: general concepts. ASME Journal of Applied Mechanics, 55, 59-64.
Chaboche (1988b) Continuum damage mechanics. Part II: damage growth, crack initiation, and crack growth. ASME Journal of Applied Mechanics, 55, 65-72.
Chapman, D. A. (1976) A Study of the Movement of Moisture in and from Concrete at Elevated and Non-uniform Temperatures, Ph. D. Thesis, King’s College, University of London.
Chapman, D. A. y England, G.L. (1977) Effects of moisture migrations on shrinkage, pore pressures and other concrete properties, Transactions of the 4th International Conference on Structural Mechanics in Reactor Technology, San Francisco.
Comites Euro-International du Beton (1991) Fire design of Concrete Structures – in accordance with CEB/FIB Model Code 90 (Final Draft). CEB Bulletin D’Information N° 208. Laussane. Suiza.
Cox, J. V. y Herrmann, L. R. (1998) Development of a plasticity bond model for steel reinforcement. Mechanics of Cohesive-Frictional Material, 3, 155-180
Fib (2007) Fire design of concrete structures - materials, structures and modelling. FIB Bulletin N° 38.
Coussy, O. (1995) Mechanics of porous continua, John Wiley & Sons, Chichester.
Coussy, O.(2004) Poromechanics, John Wiley & Sons, Chichester.
Coussy, O. (2007) Revisiting the constitutive equations of unsaturated porous solids using a Lagrangian saturation concept, International Journal for Numerical and Analytical Methods in Geomechanics, 31(15), 20-39.
Crisfield, M.A. (1991) Non-linear finite element analysis of solids and structures, John Wiley & Sons, Chichester.
Linero, D. L. (2006) Un modelo del fallo material en el hormigón armado, mediante la metodología de discontinuidades fuertes de continuo y la teoría de mezclas. Tesis doctoral . Departamento de Resistencia de Materiales y Estructures en la Ingeniería. UPC.
Ellingwood, B. , Lin, T.D. (1991) Flexure and shear behaviour of concrete beams during fires, J. Struct. Eng., ASCE, 117(2), 440-458.
Eurocode 2 (1995), Design of concrete structures, Part 1-2: General rules- structural fire design, ENV 1992-1-2.
Faria, R., Oliver, J., y Cervera, M. (1998) A strain-based plastic viscous-damage model for massive concrete structures. Int. J. Solids and Structures, 35(14), 1533-1558.
Faria, R., Oliver, J., y Cervera, M. (2000) On isotropic scalar damage models for the numerical analysis of concrete structures. CIMNE, 198.
Faria, R., Oliver,J., y Cervera, M. (2004) Modelling material failure in concerte structures under cyclic actions. J. Struct. Eng., ASCE, 130(12), 1997-2005.
Fonseca, G. y Krajcinovic, D. (1981) The continuum damage theory of brittle materials. Part II: uniaxial and plane response mode. ASME Journal of Applied Mechanics, 48, 816-824.
Gawin D., Majorana C., Pesavanto F., y Schrefler B. (1998) A fully coupling multiphase model of higro-thermo-mechanical behaviour of concrete at high temperature. In: Computational Mechanics, New Trends and Applications. Barcelona, Spain, CIMNE; 1-19.
Gawin D., Majorana C., y Schrefler B. (1999) Numerical analysis of hygro-thermal behaviour and damage of concrete at high temperature. Mechanics of cohesive-frictional materials, 4, 37-74.
Gawin D., Pesavanto F., y Schrefler B. (2002) Modelling of higro-termal behaviour and damage of concrete at temperature above the critical point of water, Int. J. Numer. Anal. Methods Geomech., 26, 537-562.
Gawin D., Pesavanto F., y Schrefler B. (2003) Modelling of higro-termal behaviour of concrete at high temperature with thermo-chemical and mechanical material degradation, Comput. Methods Appl. Mech Engrg., 192, 1731-1771.
Grasberger, S. y Meschke, G. (2004) Thermo-higro-mechanical degradation of concrete: From coupled 3D material modelling to durability-oriented multifield structural analyses, Materials and Structures, 37, 244-256.
Gustaferro, A.H., Abrams, M.S. y Salse, E.A.B. (1971). Fire-resistance of prestressed concrete beams, study C: structural behaviour during fire test, Portland Cement Associations, Research and Development Bulletin.
Haksever, A. y Anderberg Y(1981) Comparison between measured and computed structural response of some reinforced concrete columns in fire. Fire Safety Journal -1982,4, 293-297.
Harmathy, T.Z. (1965) Effect of moisture on the fire endurance of building elements, In Moisture in Materials in Relation to Fire Tests, ASTM Special Technical Publications 385, American Society for Testing and Materials, Philadelphia, 74-95.
Harmathy, T.Z. (1970) Thermal properties of concrete at elevated temperatures, ASTM Journal of Materials, 5, 47-74.
Harmathy, T.Z. y Allen, L. W. (1973) Thermal properties of selected masonry unit concretes, Journal of American Concrete Institute, 70, 132-142.
Harmathy, T.Z. (1993) Fire Safety Design and Concrete, Longman Scientific & Technical, U.K.
Heinfling G., Reynouard, J.M., y Merabet O., Duval C.A. Thermo-elastic-plastic model for concrete at elevated temperatures including cracking and thermo-mechanical interaction strains. In: Owen, D.R., Oñate, E., Hinton, E. editors. Computational plasticity: fundamentals and applications, Vol. 2. Barcelona, Spain: CIMNE, 1493-1498.
Huang Z. y Platten A.( 1997) Non-linear finite element analysis of planar reinforced concrete members subjected to fires. ACI Structural Journal, 94(3), 272-82.
Huang, Z. y Platten, A., Roberts J. (1996) Non-linear finite element model to predict temperature histories within reinforced concrete in fires. Building and Environment, 31(2), 109-118.
ISO 834 (1975) Fire Resistance Test-Elements of building construction. International Standard 834, 1975-11-01.
Kachanov, L.M. (1958) Time of rupture process under creep conditions. Izvestia Akademii Nauk, Otd Tech Nauk; 8,26-31.
Kalifa, P., Chéné, G., Gallé, C. (2001) High temperature behaviour of HPC with polypropylene fibres. From spalling to microstructure. Cement and Concrete Research, 30, 1487-1499.
Kalifa, P., Menneteau, F.-D., Quenard, D. (2000) Spalling and pore pressure in HPC at high temperatures. Cement and Concrete Research, 30, 1915-1927.
Kalifa, P., Tsimbrovska, M., Baroghel-Bouny, V. (1998) High-Perfomance concrete at elevated temperatures- an extensive experimental investigation of thermal and hygral properties and microestructure. In P.C. Aïtcin, Y. Delagrave (Eds.), Proceedings of International Symposium on High-Perfomance and Reactive Powder Concretes, Sherbrooke (Canada), 127-143.
Kanema, M., Morais, M V G., Noumowe, A., Gallias, J L. y Cabrillac, R. (2007) Experimental and numerical studies of thermo-hydrous transfers in concrete exposed to high temperature. Heat and Mass Transfer, 44(2), 149-164-
Khoury, G.A. (1992) Compresive strength of concrete at high temperatures: a reassessment. Magazine of Concrete Research, 44(161), 291-309.
Kirby, B.R. y Preston, R.R. (1988). High temperatures properties of hot-rolled structural steels for use in fire engineering design studies. Fire Safety Journal, 13(1), 27-37.
Krajcinovic, D. y Fonseka, G. (1981) The continuum damage theory of brittle materials. Part I: general theory. ASME Journal of Applied Mechanics, 48, 809-815.
Kupfer, H., Hilsdorf, H., y Rusch, H. (1969) Behaviour of concrete under biaxial stress. J. Am. Concr. Inst., 66(8), 656-666.
Lie T.T. y Irwin RJ. (1993) Method to calculate the fire resistance of reinforced concrete columns with rectangular cross section. ACI Structural Journal, 90(1), 52-60.
Lin, T.D., Ellingwood, B. y Piet, O. (1998), Flexural and shear behaviour of reinforced concrete beams during fire test, Portland Cement Associations, Research and Development Bulletin, Repor No. NBS-GCR-87-536, Centre for Fire Research, National Bureau of Standards, Washington.
Lubliner, J., Oliver, J., Oller, S., y Oñate, E. (1989) A plastic-damage model for concrete. International Journal of Solids and Structures, 25(3), 299-326.
Lubliner, J., (1990) Plasticity theory, MacMillam Publishing, USA.
Luccioni, B.M., Figueroa M.I., y Danesi R.F. ( 2003) Termo-mechanics model for concrete exposed to elevated temperatures. Engineering Structures, 25, 729-742.
Luckner, L. , van Genuchten, M. Th. y Nielsen, D.R. (1989) A consistent set of parametric models for the two-phase flow of immiscible fluids in the subsurface, Water Resources Research, 25(10), 2187-2193.
Marlvern, L. E., (1983) Introduction to the mechanics of continuous medium. Prentice-Hall, California.
Marechal, J.C. (1972a) Thermal conductivity of thermal expansion coefficients of concrete as a function of temperature and humidity, in International Seminar on Concrete for Nuclear Reactors, ACI Special Publication 34, Vol. 2, American Concrete Institute, Detroit, 1047-1057.
Marechal, J.C. (1972b) Variations of the modulus of elasticity and Poisson’s ration with temperature, in International Seminar on Concrete for Nuclear Reactors, ACI Special Publication 34, Vol. 1, American Concrete Institute, Detroit, 495-503.
Mazars, J. y Pijaudier-Cabot, G. (1989) Continuum damage theory. Applications to concrete. ASCE Journal of Engineering Mechanics, 115(2), 345-365.
Minne, R. y Vandamme, M. (1982) Resistance of reinforced concrete floor slabs against fire. Cement , 34, 642-646 (en alemán).
Mounajed G. y Obeid W. (2004) A new coupling F.E. model for the simulation of thermal hidro-mechanical behaviour of concrete at high temperatures. Materials and Structures, 37, 422-432.
Msaad, Y., Bonnet, G., y Coussy, O. (2005) The spalling of heated concrete. Comparison between thermal and hydraulic spalling. Creep, Shrinkage and Durability of Concrete Structures (Proc. Concreep 7), G. Pijaudier-Cabot, B. Gérard, P. Acker eds.,Lavoisier, Nantes, Francia, 491-496.
Mustapha KN. (1994) Parametric study of the behaviour of reinforced concrete columns in fire. Ph. D thesis, Aston University.
Nechnech, W., Meftah, F., y Reynouard, J.M. (2002) An elasto-plastic damage model for plain concrete subjected to high temperatures. Engineering Structures, 24, 597-611.
Nielsen, C.V. y Bićanic, N. (2003) Residual fracture energy of high-perfomance and normal concrete subject to high temperatures. Materials and Structures. 36, 515-521.
Olivella, S. y Gens, A. (2000) Vapour Transport in Low Permeability Unsaturated Solis with capillary effects, Transport in Porous Media, 40, 219-241.
Oliver, J. (1989) A consistent characteristic length for smeared cracking models. International Journal for Numerical Methods in Engineering 28, 461-474.
Oliver, J., Cervera, M., Oller, S., y Lubliner, J. (1990) Isotropic damage models and smeared crack analysis of concrete. Proceedings of 2nd International Conference on Computer Aided Analysis and Design of Concrete Structures, Zell am See, 945-957.
Oñate, E. (1995) Calculo de Estructuras por el Método de Elementos Finitos. Análisis estático lineal, CIMNE, Barcelona.
Phan, L.T. (1996) Fire Performance of High-Strength Concrete: A report of the State-of-the-Art, NISTIR 5934, National Institute of Standards and Technology, Gaithersburg, Maryland.
Powers, T.C. y Brownyard, T.L., (1948) Studies of the physical properties of hardened Portland cement paste, Research Department Bulletin 22, Research Laboratories Cement Associations.
Prato, T. (1999) Comportamiento mecánico del hormigón a edades termpranas, modelización y aplicaciones. Tesis Doctoral, Universitat Politècnica de Catalunya.
Pruess, K. (1987), TOUGH User’s Guide, Lawrence Berkeley Laboratory.
Simo, J. y Hughes, T. H. R. (1998) Computational inelasticity. New York. Springer-Verlag.
Saul, A. y Wagner, W. (1989) A fundamental equation for covering the range from melting line to 1273 K at pressure up to 25000 MPa, Journal for Physical and Chemical Reference Data, Vol. 18, 1537-1564.
van Genuchten (1980) A closed-form equations for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Am. Proc., 44, 892-898.
Terro MJ. (1998) Numerical modelling of the behaviour of concrete structures in fire. ACI Structural Journal, 95(3/4), 183-193.
Thelandersson, S. (1971) Effect of High Temperature on Tensile Strength of Concrete. Division of Structural Mechanics and Concrete Construction, Institute of Technology, Neostyled, 27.
Thelandersson, S. (1987) Modelling of combined thermal and mechanical action in concrete. J. Engng Mech, ASCE, 113(6), 893-906.
Truesdell, C. y Toupin, R. (1960) The classical field theories. Berlin
Ulm, F.-J, Coussy, O. y Bazant, Z.P. (1999a) The “Chunnel” fire I: Chemoplastic softening in rapidly heated concrete, Journal of Engineering Mechanics, 125, 272-282.
Ulm, F.-J, Acker, P. y Levy, M. (1999b) The “Chunnel” fire II: Analysis of concrete damage, Journal of Engineering Mechanics, 125, 283-289.
Ulm, F.-J., Constantinides, G., yHeukamp, F.H., (2004) Is concrete a poromechanics material? Materials and Structures, 37(265), 43-58.
Wickström, U. (1979) A computer program for temperature analysis of structures exposed to fire. Report No. 79-2, Lund Institute of Technology, Lund Sweden.
Willam, K., Rhee, I., y Xi, Y. (2005) Thermal degradation of Heterogeneous Concrete Materials, Journal of Materials in Civil Engineering, 17 (3), 276-285.
Zienkiwicz, O. C. y Taylor, R. L. (2004a) El método del los elementos finitos. Las bases, Vol. 1, CIMNE, Barcelona.
Zienkiwicz, O. C. y Taylor, R. L. (2004b) El método del los elementos finitos. Mecánica de Sólidos, Vol. 2, CIMNE, Barcelona.
Document information
Published on 01/01/2009
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?