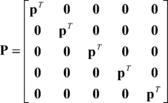Abstract
In this paper a study is performed on application of two recovery methods, i.e. Superconvergent Patch Recovery (SPR) and the Recovery by Equilibrium of Patches (REP), to plate problems. The two recovery methods have been recognized to give similar results in adaptive solutions of two dimensional stress problems. While the former applies a least square fit over a set of values at the so called superconvergent points, the latter does not need any knowledge of such points and thus has a wider application especially in non-linear problems. The formulation of REP is extended to Reissner-Mindlin plate problems. The convergence rates of the recovered fields of the gradients obtained from application of the two methods are compared using series of regular triangular and rectangular meshes for thick and thin plate solution cases. Assumed strain formulation based elements, i.e. the elements formulated by Mixed Interpolation of Tensorial Components, as well as conventional from of elements based on selective integration schemes are employed for the study.
In order to investigate the possibility of any improvement in the results by adding equilibrium constraints to SPR, as some authors suggest for simple two-dimensional problems, some weighted forms of such conditions are designed and added to the formulation. Comprehensive study has been given first by varying the weight terms to obtain the best enhanced results and then using the optimal values to investigate the effects of the constraints on the rate of convergence. It is observed that despite of the cost of this approach, due to the coupling of the gradient terms, no significant improvement is achieved.
Keywords: Recovery, Plate, Error Estimate, Superconvergent
1. INTRODUCTION
One important category of problems in engineering is of plates under lateral loads. Numerical solution of thin/thick plates has so far received a considerable attention by many researchers. Finite element method has been recognized as the most powerful numerical method for solution of this class of problems. To achieve a desired level of accuracy, adaptive procedures are usually employed. From two major parts of an adaptive finite element procedure, i.e. error estimation and mesh generation, here we focus on the first part.
For two dimensional problems, error estimation has now reached to a rather mature level and a rich literature is available for the subject. Two forms of approaches are sought by engineers. The first approach initiated by pioneering work due to Babuška and Rheinboldt is categorized as residual based error estimates [1]. The second approach introduced by Zienkiewicz and Zhu, known as ZZ estimate, falls in the category of recovery based error estimates [2]. For practical engineering problems, however, Babuška and co-workers, in a series of papers [3-5], showed that the most effective error estimates are those based on recovery methods, especially ZZ estimate utilizing Superconvergent Patch Recovery method (SPR) proposed in [6]. Success of a recovery based estimate, as proven in [7], is in debt to superconvergent property of the recovery method. To construct a recovered gradient field exhibiting superconvergent property in SPR a polynomial is fitted over a set of sampling points known to be best in a patch of elements surrounding a node. For the choice of patches, around singularities and other special cases, the reader can consult to reference 8 for further details. Another superconvergent method, which was later introduced in [9] and called Recovery by Equilibrium in Patches (REP), basically utilizes patches of elements as well. The method uses a weighted form of equilibrium equations to produce the recovered fields of the gradients. The method was later improved, in [10], and proven to pass the robustness test introduced by Babuška and co-workers in [3-5]. Unlike the SPR method which needs some information for superconvergent points over the elements, REP does not require any knowledge of such points. A combined formulation was later given in [11] in which the functionals used in SPR and REP were added together in order to make use of advantages of both methods. Such combined method, however, still needs some information at sampling points.
Unlike simple two dimensional problems, few studies can be found for errors in finite element solutions using mixed formulations such as the one is used in Reissner-Mindlin theory. In the category of residual based error estimates, recent researches by Weinberg and Carstensen can be found in the literature [12,13]. In the category of recovery based error estimates, however, some more studies can be traced. The pioneering work is due to Zienkiewicz and Zhu [14] who used an early version of the estimator. Later in a study by Lee et al [15] the recovered fields of stresses were obtained by application of SPR procedure augmented with some equilibrium constraints. The methodology is similar to the ones employed by Wiberg and Abdulwahab [16,17], and Blacker and Belytschko [18] for two dimensional stress analyses.
In order to pave the way for application of recovery based error estimates to plate problems, some investigations were performed by Zhang [19,20] aiming at giving a mathematical proof for existence of superconvergent points in some linear rectangular plate elements. The study was performed on a type of four node elements introduced by Bathe and co-workers [21-23] using an approach somewhat similar to reference 5. An overall conclusion of the study is that superconvergent property exists, at least, for interior elements and thus application of SPR can be promising.
In a research by Lee and Hobbs, application of ZZ estimate using SPR was studied through an adaptive procedure [24]. The elements employed in the study were those introduced by Huang and Hinton [25,26] and the recovery used was the augmented form of SPR suggested in [15]. Similar study can be seen in [27] for shell problems using elements introduced by Sze [28].
In another study on plate problems by Okstad et al in [29], statically admissible fields of smoothed stresses were used in SPR procedure to recover the stresses. Using such statically admissible fields is, in fact, equivalent to strictly satisfy the equilibrium constraints which are usually added to the functional and thus the study can be considered as a special case for similar studies [15, 24, 27]. Another kind of recovery method suitable for application of ZZ estimate can be found in literature for shell problems [30].
In this paper two forms of studies are given to demonstrate the applicability of SPR and REP (original/improved) to plate problems. In one form of study we shall compare the results obtained from application of the methods to series of regular meshes of elements. This, of course, requires extension of REP formulation to plate problems. For the finite element solutions a set of assumed strain elements introduced in [21-23] are employed. Both thick and thin plate problems will be examined here.
In another form of study we shall investigate the possibility of any improvement of the results by adding some weighted equilibrium constraints to the original form of SPR. Several types of constraints, including those suggested in [15-18] , are tested. During our studies we shall also give an answer to the common question regarding the role of the weights of the constraints on the accuracy and the convergence rate of the solutions.
The layout of the paper is as follows. In the second section of the paper, the mathematical model of Reissner-Mindin plate theory is given. The finite element formulation is then described followed by the assumption made for the elements used. The recovery procedures are formulated in the third section during which we shall extend the formulation of REP to plate problems. In order to study the effects of adding constraints on the recoveries, the definitions are given in section four. In section five we shall present the numerical results for each part of the study using some benchmark problems. The conclusions are given as the last section of this paper.
2. THE MODEL PROBLEM
Plates are usually formulated as special cases of three-dimensional problems assuming specific variation for in-plane displacement components i.e.
|
(1) |
and a general form for the third one as
|
(2) |
Where ![]() and
and ![]() are the components of the rotation vector of the mid-plane normal,
are the components of the rotation vector of the mid-plane normal, ![]() , and
, and ![]() is a suitable function in
is a suitable function in ![]() direction (see [31,32] for more recent formulations). In a Reissner-Mindlin type of formulation the variation of in-plane displacement is assumed to be linear in the transverse direction, i.e.
direction (see [31,32] for more recent formulations). In a Reissner-Mindlin type of formulation the variation of in-plane displacement is assumed to be linear in the transverse direction, i.e. ![]() , and the differences between the rotations of the mid-plane and those of its normal constitute the shear deformations. Thus
, and the differences between the rotations of the mid-plane and those of its normal constitute the shear deformations. Thus
|
(3) |
or in a more compact form;
|
(4) |
The bending strains are evaluated from the rotation of the mid-plane i.e.
|
(5) |
or in an operational form
|
(6) |
Stress-strain relations in a plate formulation are usually defined in a resultant from as
|
(7) |
so that ![]() ,
, ![]() while
while ![]() and
and ![]() being the bending and shear elasticity moduli in plate problems, i.e.
being the bending and shear elasticity moduli in plate problems, i.e.
|
(8) |
Where E, ![]() ,
, ![]() and
and ![]() are Young’s modulus, Poisson’s ratio, plate thickness and shear correction factor, respectively ( in this study). It should be noted that expressions (8) are obtained from a plane stress assumption made in Reissner-Mindlin formulation. More specifically, if one starts from (1) and (2) and uses a general three dimensional elasticity modulus, then the bending elasticity modulus will be different. In such a formulation a hierarchic model should be used instead of Reissner-Mindlin model. The reader may consult to reference 33 for more details.
are Young’s modulus, Poisson’s ratio, plate thickness and shear correction factor, respectively ( in this study). It should be noted that expressions (8) are obtained from a plane stress assumption made in Reissner-Mindlin formulation. More specifically, if one starts from (1) and (2) and uses a general three dimensional elasticity modulus, then the bending elasticity modulus will be different. In such a formulation a hierarchic model should be used instead of Reissner-Mindlin model. The reader may consult to reference 33 for more details.
The differential equilibrium equations may be written as:
|
(9) |
Now substituting relations (4) and (7) into (9), the equilibrium equations may be written in terms of displacement components as
|
(10) |
These equations could also be driven, for instance, from minimization of the following functional
|
|
(11) |
In the case of presence of traction at boundaries, corresponding potential terms are added to the right hand side of (11). The minimization is usually performed with the knowledge of the essential and natural boundary conditions as listed in Table 1.
| Boundary | Essential conditions | Natural Conditions |
| Free | ------------------------- | |
| Clamped | ------------------------------ | |
| Hard-simply supported | ||
| Soft-simply supported |
2.1 FINITE ELEMENT FORMULATION OF PLATES
The finite element solution starts with discritization of the domain and using shape functions for interpolation of the displacement and rotation nodal values:
|
(12) |
Here ![]() and
and ![]() are two sets of suitable shape functions written in matrix forms. Introducing the interpolated displacement and rotation fields into the functional of (11) and minimizing the result with respect to nodal values of the variables, the finite element formulation is derived as two sets of equations
are two sets of suitable shape functions written in matrix forms. Introducing the interpolated displacement and rotation fields into the functional of (11) and minimizing the result with respect to nodal values of the variables, the finite element formulation is derived as two sets of equations
|
|
(13) |
and
|
|
(14) |
or in a more compact form
|
|
(15) |
In which , , and matrices ![]() and
and ![]() are arranged accordingly so that
are arranged accordingly so that
|
(16) |
Due to ![]() nature of the functional, Lagrangian shape functions are usually chosen for the solution. However, such a scheme leads to the so-called “shear locking” effect when thin plates are to be solved. Several remedies have been suggested for overcoming the problem leading to introduction of several kinds of plate elements. In the next section we shall briefly overview those which have been used in this paper.
nature of the functional, Lagrangian shape functions are usually chosen for the solution. However, such a scheme leads to the so-called “shear locking” effect when thin plates are to be solved. Several remedies have been suggested for overcoming the problem leading to introduction of several kinds of plate elements. In the next section we shall briefly overview those which have been used in this paper.
2.2 THE ELEMENTS USED
The locking effect resulting from the application of Reissner-Mindlin formulation to thin plates is overcome by employing special integration schemes or introducing enhanced shear strain fields. Some of the well-adopted kinds of such remedies are explained here.
2.2.1 Reduced and selective integration schemes
It is well understood that a quick remedy for locking effect, when using conventional Lagrangian shape-functions, is to use an integration scheme with one order less than the full form. However, if such a scheme is used for all terms in Equation (15), due to some zero energy modes, a sort of instability may happen in the solution process. Therefore selective integration scheme is usually recommended. One of the conventional elements used in this paper is bilinear quadrilateral element for which we shall employ ![]() and
and ![]() Gauss quadrature rules for flexural and shear terms of (15), respectively. Similarly, for quadratic quadrilaterals ( 9 node elements)
Gauss quadrature rules for flexural and shear terms of (15), respectively. Similarly, for quadratic quadrilaterals ( 9 node elements) ![]() integration points for flexural, and
integration points for flexural, and ![]() integration points for shear terms will be used.
integration points for shear terms will be used.
2.2.2 Assumed strain formulations
Another remedy for the so called “locking” effect is using assumed variations for shear strains across the elements. Several forms of such elements can be found in literature. Here we shall employ the elements proposed in [21-23]. This class of elements consists of both quadrilateral and triangular elements having similar forms of formulations and has been shown to be robust. The formulations are based on interpolation of shear strains at some sampling points on the edges of the elements. This procedure is called Mixed Interpolation of Tensorial Components, MITC, and the elements are named with the acronym followed by a number associate with the number of nodes in the elements.
MITC4 element
In this type of element the transverse displacement and the two components of the rotation are interpolated by simple linear Lagrangian shape functions and the variations for the shearing strains are assumed as
Where ![]() ,
, ![]() ,
, ![]() and
and ![]() are determined from strains at four edge points, with normalized coordinates (
are determined from strains at four edge points, with normalized coordinates ( ![]() 0,
0, ![]() 1) and (
1) and ( ![]() 1,
1, ![]() 0), in terms of nodal displacements and rotations. The
0), in terms of nodal displacements and rotations. The ![]() matrix in (15) is arranged accordingly.
matrix in (15) is arranged accordingly.
MITC9 element
In this type of element a set of eight-node-based shape functions is used for interpolation of transverse displacement. For rotational components two sets of nine-node-based quadratic shape functions are used. The following forms are assumed for variations of shearing strains
| |
Where the ten parameters ![]() to
to ![]() and
and ![]() to
to ![]() are determined from eight shear strains at eight sampling points, with normalized coordinates (
are determined from eight shear strains at eight sampling points, with normalized coordinates (![]() 1,
1, ![]()
![]() ) and (
) and (![]()
![]() ,
, ![]() 1), in terms of nodal values and two additional conditions as
1), in terms of nodal values and two additional conditions as
|
(17) |
Having found the parameters, the ![]() matrix in (15) is arranged accordingly.
matrix in (15) is arranged accordingly.
MITC7 element
In this triangular element the transverse displacement is interpolated by a set of six-node-based shape functions using conventional area coordinates. The two components of rotation are interpolated by two sets of seven-node-based shape functions with the seventh ones, associated with the middle node, being as bubble functions. The variations of shearing strains are assumed as following expressions
with ![]() and
and ![]() being appropriate local orthogonal coordinates. The eight parameters in above expressions are evaluated in terms of shear strains at six sampling points on the edges, located at (
being appropriate local orthogonal coordinates. The eight parameters in above expressions are evaluated in terms of shear strains at six sampling points on the edges, located at ( ![]() /6)
/6) ![]() from the vertexes, and additional conditions similar to Equation (17).
from the vertexes, and additional conditions similar to Equation (17).
3. THE RECOVERY METHODS
In this paper we shall compare performances of two recovery methods, proven to be superconvergent in two dimensional problems, when applied to plate problems. The superconvergent patch recovery method SPR proposed by Zienkiewicz and Zhu [6] has been proven to be robust and sufficiently accurate for error estimation. Asymptotic rate of convergence of such an estimate has been studied and compared with other estimates in a series of papers by Babuška and coworkers [3-5]. In this method some sampling points, known to be best at each element, are used and a polynomial is fitted on a group of such points in a patch of elements constructed around a vertex node. Position of the sampling points is known for some simple quadrilateral and triangular elements in two dimensional problems. However, no information is generally available for such points in other kinds of elements.
Another superconvergent recovery method called as Recovery by Equilibrium in Patches REP was introduced in [9] and shown to have the same accuracy as SPR. This method does not need any information of sampling points. A polynomial is fitted to the gradient values through the equilibrium equations in a manner consistent with the FEM formulation - i.e. the weight form of equilibrium equations. The robustness patch test introduced by Babuška and coworkers [4,5] were applied to the REP and the robustness of the results was compared with those of SPR (see [10]). It was shown that both methods exhibit the same asymptotic rate of convergence and robustness index.
Here we introduce the general form of the recovery methods for application to plate problems.
3.1 THE SUPERCONVERGENT PATCH RECOVERY METHOD
It is well understood that in some simple elements there exist some points where the rate of convergence of the gradients is more than the nominal value of rate in a FEM solution. The locations and other features of such points received a considerable attention in the past two decades. In superconvergent patch recovery method, these points are used as sampling points in a patch of elements constructed on a vertex node. A new continuous distribution of each gradient component is considered as a complete polynomial of order equal to that of the interpolation functions.
For instance ![]() , as a representative of the stresses in a FEM solution, is defined as a polynomial with unknown coefficients as
, as a representative of the stresses in a FEM solution, is defined as a polynomial with unknown coefficients as
|
(18) |
with ![]() and
and ![]() being two vectors containing the polynomial components and the coefficients, respectively. Summation of the errors between the continuous and discontinuous fields of the stress component is then defined as a norm
being two vectors containing the polynomial components and the coefficients, respectively. Summation of the errors between the continuous and discontinuous fields of the stress component is then defined as a norm
|
(19) |
and minimized with respect to the unknown coefficients. The result of the minimization is vector ![]() as
as
|
(20) |
The value of the recovered stress at the patch node (the vertex node supporting the patch) is calculated by substitution of (20) in (18) and inserting the node coordinates in the polynomial
|
(21) |
The reader is referred to references 6 and 7 for more details. For nodes on the edges of the elements, an interpolation is performed between the recovered values of the stresses from the corresponding continuous fields at the two vertex nodes supporting the edge. The final form of the continuous stress field over the whole domain is constructed by interpolation of the nodal stress values.
|
(22) |
For nodes on the boundaries, it is recommended to use the information from the nearest internal patch instead of construction of the patch at the node.
For application of SPR to plate bending problems we shall directly recover the bending moments and shear stress resultants instead of the corresponding stresses by replacing ![]() , in Equations (18) to (20), with the components of
, in Equations (18) to (20), with the components of ![]() and
and ![]() in (7).
in (7).
For the choice of sampling points in this paper, ![]() and
and ![]() gauss points have been chosen for linear and quadratic quadrilateral elements, respectively. For quadratic triangular elements 3 gauss points, at the middle of the edges, have been used as superconvergent points. It may be noticed that such choices for sampling points are ideal for recovery of the bending moment components since the FEM bending moments are calculated through direct differentiation of the rotation field which is of continuity. This of course corresponds with the original idea of SPR in two dimensional plane stress/strain problems. However, for formulations using enhanced fields of shear stresses/strains, as the case for MITC elements, ambiguities arise in selection of sampling points and thus the need of a separate study is felt in this regard. However, as a reasonable choice for sampling points of shear stresses, we have used the same points as those employed for bending moments because of two reasons. First, it can be observed that information needed for an enhanced field is basically extracted from the derivatives of a field (e.g. see Equation (17)). Note that the final information at the sampling points to be used in the recovery is obtained from the enhanced field. Secondly, using similar sampling points for different stress components speeds up the procedure since the coefficient matrix to be inverted in (20) will be identical for all components.
gauss points have been chosen for linear and quadratic quadrilateral elements, respectively. For quadratic triangular elements 3 gauss points, at the middle of the edges, have been used as superconvergent points. It may be noticed that such choices for sampling points are ideal for recovery of the bending moment components since the FEM bending moments are calculated through direct differentiation of the rotation field which is of continuity. This of course corresponds with the original idea of SPR in two dimensional plane stress/strain problems. However, for formulations using enhanced fields of shear stresses/strains, as the case for MITC elements, ambiguities arise in selection of sampling points and thus the need of a separate study is felt in this regard. However, as a reasonable choice for sampling points of shear stresses, we have used the same points as those employed for bending moments because of two reasons. First, it can be observed that information needed for an enhanced field is basically extracted from the derivatives of a field (e.g. see Equation (17)). Note that the final information at the sampling points to be used in the recovery is obtained from the enhanced field. Secondly, using similar sampling points for different stress components speeds up the procedure since the coefficient matrix to be inverted in (20) will be identical for all components.
From above discussion the motive of using another form of recovery method, insensitive to the choice of sampling points, becomes clear. In the next subsection we shall use another recovery which does not exploit information at sampling points.
3.2 THE RECOVERY BY EQUILIBRIUM OF PATCHES
The idea of the REP method was inspired from the fact that both finite element stress field and the exact one satisfy a weighted form of the equilibrium equations. This is usually expressed as the following orthogonality condition
|
|
(23) |
Due to the discontinuity in , the condition can be applied, losing no generality, at each vertex node supporting a patch of elements. However, applying such a condition, solely, may not lead to recover any new stress values. If the exact stresses are replaced with some polynomial based stresses then application of (23) to errors of such stress fields, at all nodes in the patch, may lead to construction of the new stress fields. In that case, the orthogonality condition will be one of the applied equations. This leads us to write approximately
|
|
(24) |
It can be seen that the right hand side of Equation (24) is in fact the nodal force vector of the patch and helps the patch to maintain in an equilibrium state. The procedure resembles to the solution of a system, as small as a patch, using a set of piecewise continuous weight functions and a set of generalized coordinates as the polynomial terms. The formulation can be written for strain or even displacement field.
The method was initially proposed in [9] and then the improved version was given in [10]. In following subsections, we shall extend the formulation for application to plate bending problems.
3.2.1 The original form of REP
Writing the equilibrium equations in a weighted from as (24) implies that the new fields of all the stress components should be calculated in a coupled system of equations. Therefore Equation (18) is rewritten in a matrix form
|
|
(25) |
Where in plate problems, with five components for stresses, and are
|
(26) |
Now in view of Equation (15), the equilibrium equations of (24) can be written as:
|
|
(27) |
or
|
(28) |
It is clear that for general forms of patches, the number of the equations and the unknowns are not necessarily equal. Thus the following functional is defined
|
(29) |
and minimized with respect to ![]() as
as
|
(30) |
This results to
|
(31) |
For some patch configurations, matrix ![]() may still become ill-conditioned. In such cases
may still become ill-conditioned. In such cases ![]() can be evaluated as
can be evaluated as
|
(32) |
That is the result of minimization of the following functional
|
(33) |
In above, ![]() and
and ![]() have the same expressions as
have the same expressions as ![]() and
and ![]() but the integrals are written over each element area.
but the integrals are written over each element area.
The procedure continues by calculation of the nodal values for stresses and interpolation of these values by the shape functions. This latter part of the method is similar to that of the SPR, stated in the previous subsection, both for inside nodes and those on the boundaries.
3.2.2 The improved form of REP
In reference 10 it has been shown that the formulation given for original REP loses robustness for meshes with high aspect ratios. The sensitivity to aspect ratio is eliminated if we write both the finite element and the recovered stress vectors, ![]() and
and ![]() , as:
, as:
|
(34) |
and substitute in Equation (27) to obtain
|
(35) |
and split the equilibrium equations which ends up to
|
(36) |
In above we have
|
(37) |
or
|
(38) |
Appropriate columns in ![]() matrix may be selected, for nonzero terms only, to minimize the procedure cost.
matrix may be selected, for nonzero terms only, to minimize the procedure cost.
The split of equilibrium equations, in fact, leads to uncouple the system of equations making the procedure cheaper. Thus for each component of stresses we can write
|
|
(39) |
or
|
(40) |
Now, defining a functional as Equation (29) for each component and minimizing it with respect to the unknowns, the polynomial coefficients for the recovered solution are evaluated
|
(41) |
It can be seen that this type of formulation provides more equations when compared to the original form and thus gives better results for robustness tests. This enables us to apply the method to the boundary patches where usually the information for application of SPR is not sufficient. Despite of this, here we shall compare the performances of the two recoveries without using boundary patches.
4. ADDING SOME EQUILIBRIUM CONSTRAINTS
Several reports have so far been published on investigation of possible improvement in performance of SPR when augmented with equilibrium constraints. These studies are mainly in two dimensional problems and focus on increasing accuracy and convergence rate of the recovered values. The reader may refer to series of papers written by Wiberg and Abdulwahab [16,17], Blacker and Belytschko [18] for application of such constraints to plane stress/strain problems. For plate problems, Lee and Hobbs [24] emphasized on adding equilibrium constraints to the functional (19), similar to the work of Lee et al [15], to improve the stability of the recovery process. A rather similar constraint, strictly satisfied for the polynomials used, has also been suggested by Okstad et al in [29]. In this paper we shall present a rather comprehensive study on possibility of any improvement in accuracy, stability and rate of convergence of the results when SPR (or REP) is augmented with equilibrium constraints.
4.1 EQUILIBRIUM CONSTRAINTS ON SPR
Four forms of constraints are added to the functional used for SPR and the results for each case are distinguished with the acronym followed by a number.
SPR1
In this form we add conditions (9) in square forms to the functional used for SPR
|
|
(42) |
In which ![]() and
and ![]() are suitable weights and
are suitable weights and
|
(43) |
Where and are defined as (26). In above, the superscript ![]() is used for finite element solutions.
is used for finite element solutions.
Operators and are applied to and as bellow
|
|
(44) |
and
|
|
(45) |
Now minimization of ![]() with respect to
with respect to ![]() leads to the following matrix equation
leads to the following matrix equation
|
(46) |
where
|
|
(47) |
and
|
|
(48) |
Similar constraint has been recommended in [15,24] using ![]() and
and ![]() .
.
SPR2
Instead of requiring shear stress resultants ![]() to be close to the derivatives of recovered moments
to be close to the derivatives of recovered moments ![]() , one may apply the equilibrium conditions to the recovered values of
, one may apply the equilibrium conditions to the recovered values of ![]() and
and ![]() both. This simply means that the polynomial coefficients in
both. This simply means that the polynomial coefficients in ![]() are interrelated. The following functional is then defined
are interrelated. The following functional is then defined
|
|
(49) |
Here we note that
|
|
(50) |
Therefore matrices ![]() and
and ![]() in (46), after minimization of the functional, take the form of
in (46), after minimization of the functional, take the form of
|
|
(51) |
and
|
|
(52) |
This latter form of constraints seems to be more reasonable since less information is used from enhanced shear stresses which are not so reliable.
SPR3
Although many authors have used integral forms of equilibrium constraints, a point-wise approach for satisfaction of such conditions may have better interpretation. This is because the exact solution is not necessarily a polynomial but of course may be written as a truncated Taylor series in a tiny area around a point, e.g. patch node. Thus considering the patch node as a point where an enhanced solution is sought, we add to ![]() a set of point-wise constraints as
a set of point-wise constraints as
|
|
(53) |
Here again, minimization with respect to ![]() gives a matrix equation as (46) with
gives a matrix equation as (46) with ![]() and
and ![]() being
being
|
|
(54) |
and
|
|
(55) |
It can be seen that in the case of presence of concentrated load, this form of collocated constraints may not be used since the load intensity, ![]() , is not defined. The reader will notice that in the case of existence of a point load on a node, due to the presence of discontinuity in the stress field, the node should be excluded from the nominated ones for patch construction in all forms of stress recovery methods using patches of elements.
, is not defined. The reader will notice that in the case of existence of a point load on a node, due to the presence of discontinuity in the stress field, the node should be excluded from the nominated ones for patch construction in all forms of stress recovery methods using patches of elements.
SPR4
As the last version of the constraints, we shall use the equilibrium relations between shear stress resultants and bending moments to make links between the recovered shear stress resultants and the derivatives of the bending moments from the standard finite element solution. The motive of using such links is the fact that the FEM results for bending moments are not only more accurate than the shear stress resultants but also are of more convergence rate. Therefore, we examine the following form of constraints
|
|
(56) |
For evaluation of ![]() one may interpolate
one may interpolate ![]() through evaluation of the nodal values, by a simple averaging, and compute the first derivatives. Minimization of
through evaluation of the nodal values, by a simple averaging, and compute the first derivatives. Minimization of ![]() with respect to
with respect to ![]() leads to
leads to
|
|
(57) |
and
|
|
(58) |
Where
|
(59) |
In the section of numerical results, we shall give a study on accuracy of the recovered stresses when ![]() and
and ![]() take different values.
take different values.
4.2 CONSTRAINTS ON REP, (REP1)
Although REP procedure is in fact application of a weighted form of equilibrium operator to the recovered stress fields, we shall add only a set of constraints, on its original form, as Equation (42) with ![]() replaced with
replaced with ![]() in (29). The derivation of the relations is omitted here.
in (29). The derivation of the relations is omitted here.
5. NUMERICAL STUDY
To study the performances of the recovery methods, two main approaches available in literature may be employed. The first approach uses benchmark problems with exact solutions to demonstrate the accuracy of the recovered solutions. The idea supporting such an approach is to generalize the conclusions to wider range of problems though no proof is given. Majority of studies on error estimators fall within this form of approach [2,6,7,9,15-18,24,27,29].
In the second approach, asymptotic behaviors of the error estimators are studied. Although such a study does not play the role of a proof, but the mathematical basis is much stronger and the range of application is much wider than the first approach. Pioneering works by Babuška and coworkers for two-dimensional heat and plane stress/strain problems fall within this form of approach [3-5]. The methodology presented in these studies was later used to test the performance of REP in reference 10.
For plate bending problems, however, application of the second approach requires generalization of the methodology for mixed solution methods such as Reissner-Mindlin formulation, which is beyond the scopes of this paper. The reader may consult to references 19 and 20 for the mathematical model and benchmark examples performed for linear rectangular elements.
While using the first approach, problems with smooth exact solutions are needed. Here the term “smooth” indicates that no singularity is expected in the exact stress field. Searching for benchmarks in plate bending problems with perfect smooth exact solutions is not an easy task. In fact in many problems, especially in thin plates, boundary layer effect induced by shear forces at the edges of the plate plays the role of singularity. But, since such a boundary layer is just seen in transverse shear stresses and has small effect on bending stresses, it is neglected when the plates are designed for bending stresses.
|
|
| (a) | (b) |
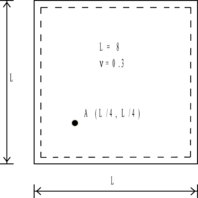
Figure 1. A simply supported square; for thick plate solution and for thin plate solution (a) the domain (b) typical uniform meshes of quadrilateral, solid lines, and triangular, dash lines, used.
In this paper a square plate, shown in Figure 1, with hard simply supports under uniform pressure is considered as a benchmark problem. Depending on the thickness of the plate, the exact solution is given with assumption of thick or thin plate formulation. Fourier series is usually used for both cases expressing the plate deflection as follows
|
(60) |
with ![]() and
and ![]() being the plate dimensions and
being the plate dimensions and ![]() representing a series of coefficients to be determined from the solution process. For thin plate solution, the deflection assumed above is directly substituted in to the governing differential equation derived from Kirchhoff assumptions. The solution is straightforward. For thick plate solution, however, some similar expressions for
representing a series of coefficients to be determined from the solution process. For thin plate solution, the deflection assumed above is directly substituted in to the governing differential equation derived from Kirchhoff assumptions. The solution is straightforward. For thick plate solution, however, some similar expressions for ![]() and
and ![]() are needed
are needed
|
(61) |
The solution may be found in reference 34.
In this section we shall present two series of results obtained for the thick and thin plates. The first series is of comparison between the performances of the two recovery methods SPR and REP. The second series will be given to demonstrate the performances of the recovery methods when the equilibrium constraints in Section 4 are applied.
The comparisons will be made by evaluation of relative norms of errors. Some norms used in this section are as follows
|
(62) |
|
(63) |
|
(64) |
For recovered values we define
|
(65) |
|
(66) |
|
(67) |
Thus the associative relative error norms are defined as
|
(68) |
The finite element solutions are obtained on uniform meshes of square elements and triangular elements with regular pattern.
5.1 Comparison between SPR and REP
Thick plate solution
The plate shown in Figure 1 has been solved with as a case of thick plate problems. The results of errors and the rates of convergence are reported in Tables 2-12 and Figures 2-4.
Table 2. Point-wise errors (percent) of ![]() at point A, MITC4.
at point A, MITC4.
| h | FEM | SPR | REP-old | REP |
| 2.0
1.0 0.5 0.333 0.222 C.R. |
45.60
14.11 5.71 3.62 2.34 1.351 |
28.10
4.72 1.69 0.75 0.33 2.018 |
23.72
3.83 1.38 0.61 0.27 2.034 |
26.97
4.48 1.60 0.71 0.32 2.025 |
Table 3. Point-wise errors (percent) of ![]() at point A, MITC4.
at point A, MITC4.
| h | FEM | SPR | REP-old | REP |
| 2.0
1.0 0.5 0.333 0.222 C.R. |
37.18
21.97 10.63 7.14 4.78 0.933 |
17.18
4.68 0.87 0.38 0.17 2.015 |
6.37
1.13 0.26 0.11 0.05 2.207 |
16.46
4.44 0.83 0.37 0.16 2.107 |
Table 4. Point-wise errors (percent) of at point A, MITC4.
| h | FEM | SPR | REP-old | REP |
| 2.0
1.0 0.5 0.333 0.222 C.R. |
86.00
35.62 16.26 10.61 6.98 1.143 |
30.76
4.45 0.34 0.15 0.07 2.791 |
10.54
1.93 0.22 0.11 0.05 2.398 |
46.44
3.73 0.21 0.09 0.04 3.191 |
Table 5. Point-wise errors (percent) of ![]() at point A, MITC7.
at point A, MITC7.
| h | SPR | REP-old | REP |
| 2.0
1.0 0.666 C.R. |
1.942
0.102 0.019 4.216 |
8.872
2.587 1.351 1.713 |
1.437
0.06 0.02 3.882 |
Table 6. Point-wise errors (percent) of ![]() at point A, MITC7.
at point A, MITC7.
| h | SPR | REP-old | REP |
| 2.0
1.0 0.666 C.R. |
1.042
0.162 0.033 3.154 |
1.757
2.277 1.403 --- |
1.169
0.084 0.010 4.325 |
Table 7. Point-wise errors (percent) of at point A, MITC7.
| h | SPR | REP-old | REP |
| 2.0
1.0 0.666 C.R. |
1.600
0.066 0.013 4.367 |
1.821
3.394 5.515 |
4.508
0.429 0.084 3.625 |
Table 8. Relative error norms for thick plate solution using MITC9 elements.
| FEM | SPR | REP-old | REP | |
| h | Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
| 2.00
1.33 1.00 .667 .533 .400 C.R. |
8.12 5.02 7.63
3.55 2.12 3.32 1.90 1.16 1.79 0.77 0.52 0.73 0.47 0.34 0.45 0.24 0.21 0.75 2.180 1.981 2.157 |
4.53 5.54 4.74
1.42 2.29 1.63 0.61 1.26 0.78 0.18 0.56 0.29 0.10 0.36 0.18 0.004 0.21 0.10 2.938 2.036 2.406 |
8.58 10.33 8.94
2.63 3.79 2.89 1.16 1.97 1.35 0.37 0.84 0.49 0.20 0.53 0.29 0.009 0.31 0.16 2.803 2.182 2.647 |
6.76 5.23 6.49
2.23 2.08 2.20 0.99 1.77 1.03 0.32 0.52 0.36 0.53 0.34 0.21 0.007 0.20 0.11 2.809 2.041 2.544 |
Table 9. Point-wise errors (percent) of ![]() at point A, MITC9.
at point A, MITC9.
| h | FEM | SPR | REP-old | REP |
| 2.0
1.0 0.666 0.400 C.R. |
10.59
3.73 1.33 0.375 2.075 |
0.815
0.078 0.016 0.002 3.707 |
1.884
0.078 0.010 0.0006 5.007 |
1.036
0.180 0.044 0.0079 3.032 |
Table 10. Point-wise errors (percent) of ![]() at point A, MITC9.
at point A, MITC9.
| h | FEM | SPR | REP-old | REP |
| 2.0
1.0 0.666 0.400 C.R. |
16.38
2.08 0.49 0.046 3.644 |
5.31
0.206 0.029 0.003 4.617 |
16.47
0.395 0.062 0.008 4.705 |
5.51
0.253 0.049 0.005 4.299 |
Table 11. Point-wise errors (percent) of at point A, MITC9.
| h | FEM | SPR | REP-old | REP |
| 2.0
1.0 0.666 0.400 C.R. |
29.19
2.91 0.81 0.28 2.878 |
2.713
0.106 0.014 0.002 4.489 |
10.91
0.895 0.289 0.044 3.420 |
3.32
0.101 0.010 0.002 4.648 |
Table 12. Relative error norms for thick plate solution using conventional 9 node elements.
| FEM | SPR | REP-old | REP | |
| h | Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
| 2.00
1.33 1.00 .667 .533 .400 C.R. |
3.21 7.85 4.48
1.48 3.69 2.09 0.85 2.14 1.21 0.38 0.97 0.54 0.25 0.62 0.35 0.14 0.35 0.20 1.955 1.938 1.945 |
3.96 5.14 4.21
1.28 2.17 1.49 0.56 1.20 0.73 0.17 0.54 0.28 0.09 0.35 0.17 0.04 0.20 0.09 2.896 2.011 2.360 |
8.26 8.22 8.25
2.58 3.04 2.68 1.12 1.60 1.23 0.34 0.71 0.44 0.18 0.46 0.25 0.07 0.26 0.13 2.923 2.150 2.592 |
6.15 4.97 5.94
2.06 2.10 2.07 0.92 1.21 0.98 0.29 0.55 0.35 0.15 0.36 0.21 0.06 0.21 0.10 2.829 1.974 2.532 |
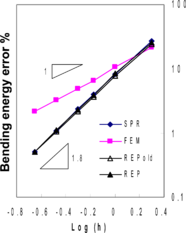
Figure 2 demonstrates the performances of SPR and REP when MITC4 elements are used. As expected, the average rate of convergence for FEM solution is close to unity while those of the recovery methods are more meaning that the recovery methods are superconvergent similar to simple two-dimensional problems. It can be seen that the convergence rates for the recovery methods are similar, though small differences are observed. Point-wise errors at point ![]() in Figure 1 are given in Tables 2 to 4. Nearly the same rates of convergence as energy norms are observed indicating that all points in the domain have similar rates of convergence.
in Figure 1 are given in Tables 2 to 4. Nearly the same rates of convergence as energy norms are observed indicating that all points in the domain have similar rates of convergence.
|
|

|
| (a) | (b) | (c) |
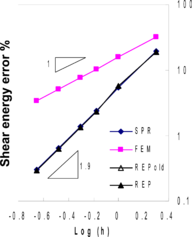
Figure 2. Relative error norms for thick plate solution using MITC4 elements; (a) error for bending stresses , (b) error for shear stresses , (c) total error .
Similar conclusions may be made from the results of Figure 3 where conventional linear elements are used.
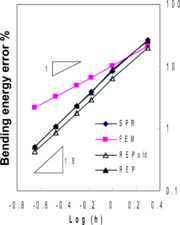
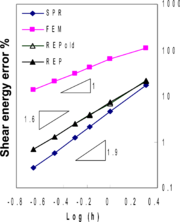
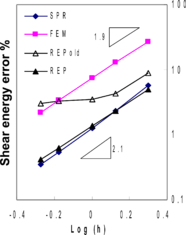
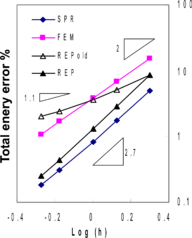
Rather surprising results can be seen in Figure 4 where the thick plate solution has been obtained using MITC7 elements. None of the recovery methods appear to be fully superconvergent in terms of energy norms, though they exhibit more convergent rates when compared to FEM solution, especially for bending stresses. It can be seen that REP-old, due to instability, fails to be superconvergent but the improved version of REP retains to be semi-superconvergent, similar to SPR. However, looking at Tables 5 to 7 for point-wise errors at ![]() , it can be concluded that the main reason for semi-superconvergent behavior lies in the treatment of boundary patches since the point-wise results show quite good superconvergent (or ultraconvergent) effects except for REP-old. In this paper, the recovered gradients at boundary nodes, for both SPR and two versions of REP, are obtained through extrapolation of information from closest inside patch. We note that, although in the improved form of REP there is no restriction for applying the formulation to a local boundary patch, no boundary patch has been used in this paper in order to compare REP and SPR in similar situations.
, it can be concluded that the main reason for semi-superconvergent behavior lies in the treatment of boundary patches since the point-wise results show quite good superconvergent (or ultraconvergent) effects except for REP-old. In this paper, the recovered gradients at boundary nodes, for both SPR and two versions of REP, are obtained through extrapolation of information from closest inside patch. We note that, although in the improved form of REP there is no restriction for applying the formulation to a local boundary patch, no boundary patch has been used in this paper in order to compare REP and SPR in similar situations.
|
|

|
| (a) | (b) | (c) |
Figure 3. Relative error norms for thick plate solution using conventional 4 node elements; (a) error for bending stresses , (b) error for shear stresses , (c) total error .
|
|
|
| (a) | (b) | (c) |
Figure 4. Relative error norms for thick plate solution using MITC7 elements; (a) error for bending stresses , (b) error for shear stresses , (c) total error .
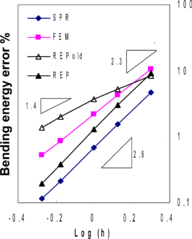
A similar conclusion can be made for quadratic elements MITC9. Table 8 demonstrates the performances of the recovery methods for this class of elements. Here again, when using energy norms, superconvergence is lost in recovered shear stresses, though the recovered bending stresses still exhibit better behavior. Similar conclusions for quadratic triangular elements are also valid here since the point-wise errors in Tables 9 to 11 demonstrate good superconvergent/ultraconvergent effects.
The results for conventional nine node elements, shown in Table 12, exhibit nearly the same behavior as MITC9 elements.
Thin plate solution
The plate shown in Figure 1 has been solved with as a case of thin plate problems. The results of errors and the rates of convergence are reported in Tables 13 and 14 and Figures 5 and 6.
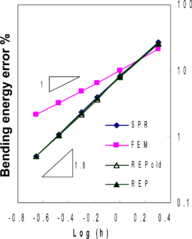
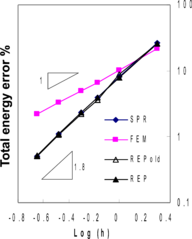
The summery of the results for a set of solutions using MITC4 elements is reported in Figure 5. Similar results have been obtained for the recovery methods. Both shear and bending stresses norms exhibit superconvergent effect. The reader may note that the errors in the figure are relative quantities and do not clearly show the contribution of each part of the energy in the total energy error. However, similarity between Figures (5-a) and (5-c) reveals that the contribution of shear part is very small. In thin plate formulation, the bending stresses have a prominent role in the plate behavior and thus the shear stresses are of less importance.
|

|
|
| (a) | (b) | (c) |
Figure 5. Relative error norms for thin plate solution using MITC4 elements; (a) error for bending stresses , (b) error for shear stresses , (c) total error .
Table 13 shows results obtained when MITC7 elements are used. Rather good results have been obtained for bending stress norms. The errors for shear stress norms from FEM solution show that the shear stress field obtained is not so accurate and when the element size decreases the convergence rate expected for FEM solution is not retrieved. It is worthwhile to note that the element was invented to solve the locking effect in thin plate formulation and thus the accuracy of the shear stresses is of no importance. However, it can be seen that both SPR and REP are able to recover the shear stress field with reasonable convergence rate, though the original form of REP fails to produce convergent results.
Table 13. Relative error norms for thin plate solution using MITC7 elements.
| FEM | SPR | REP-old | REP | |
| h | Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
| 2.00
1.33 1.00 .667 .533 C.R. |
29.25 26.40 29.25
18.04 25.63 18.04 13.11 25.97 13.11 8.51 23.62 8.51 6.75 22.77 6.75 1.109 0.112 1.489 |
14.29 16.28 14.29
6.97 12.31 6.98 4.22 10.48 4.23 2.30 7.96 2.10 1.43 6.63 1.43 1.741 0.679 1.740 |
30.83 27.79 30.83
29.21 36.51 29.22 25.06 53.50 25.07 24.08 81.12 24.09 21.69 88.10 21.69 0.266 - 0.266 |
29.84 17.18 29.84
14.46 12.98 14.46 8.85 10.92 8.85 4.24 8.39 4.24 2.83 7.10 2.83 1.781 0.668 1.735 |
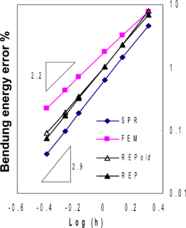
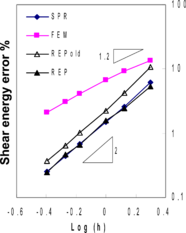
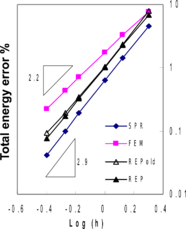
Performance of quadratic quadrilateral plate elements MITC9 has been shown in Figure 6. It can be seen that, similar to thick plate solution cases, all recovery methods produce semi-superconvergent results.
|
|
|
| (a) | (b) | (c) |
Figure 6. Relative error norms for thin plate solution using MITC9 elements; (a) error for bending stresses , (b) error for shear stresses , (c) total error .
Convergence rate obtained for stress resultants at point A , for all above cases, is reported in Table 14. Among the results for different types of elements in this table, those of MITC9 are notable which show ultraconvergence rates. Similar convergences were seen in Tables 9 to 11 for thick plate solution. Ultraconvergence of SPR was first reported by Zienkiewicz and Zhu in reference 6 in two dimensional plane stress/strain problems. The effect was later proven by Zhang [35] for quadrilateral elements. Also, ultraconvergence of REP was shown in reference 9 for two dimensional problems.
Table 14. Rate of convergence of stresses at point A - Thin plate solution using different types of elements.
5.2 Application of the equilibrium constraints
In this part we shall investigate the possibility of any improvement in the accuracy or the rate of convergence of the results when the constraints described in Section 4 are applied.
To proceed towards our investigation, we need to choose proper values for the weights used for the constraints in the functionals (42), (49), (53) and (56). This, in fact, needs a separate study which we shall present the results prior to study on the rates of convergence.
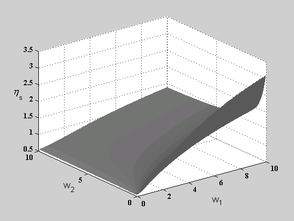
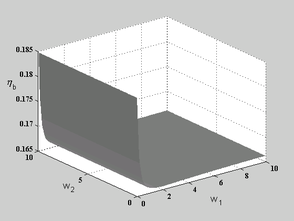
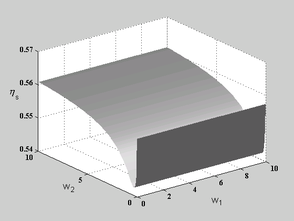
Figures 7 depicts the variation of relative errors, to be interpreted as the accuracy in a thick plate solution, with respect to variation of ![]() and
and ![]() for SPR1 type of constraints when a mesh of
for SPR1 type of constraints when a mesh of ![]() quadratic elements (MITC9) is used. The figures clearly show that no major improvement happens when the constraints are applied. Although an optimal value can be recognized for
quadratic elements (MITC9) is used. The figures clearly show that no major improvement happens when the constraints are applied. Although an optimal value can be recognized for ![]() , the solution is not much sensitive to the values of the weights.
, the solution is not much sensitive to the values of the weights.
|
|
| (a) | (b) |
Figure 7. Variation of relative errors with respect to variation of weight factors, and , for thick plate solution using MITC9 elements and when SPR1 recovery is applied; (a) variation of error norm for bending stresses , (b) variation of error norm for shear stresses .
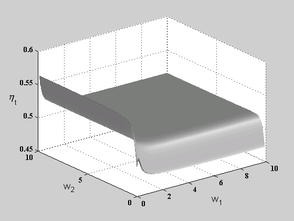
For SPR2 type of constraints, Figure 8 shows that the solution is only sensitive to ![]() but the accuracy deteriorates while
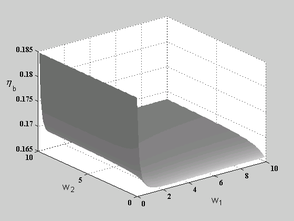
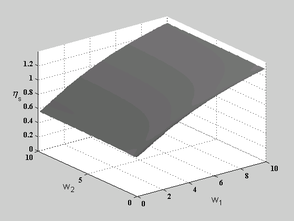
but the accuracy deteriorates while ![]() increases. This means that enforcing the recovered shear and bending stresses to be interrelated, in an integral form, will not lead to better results (viz. functional (49)). The optimal values, though not recognizable from the figures, are less than unity. Here again, no major improvement can be seen in the figures.
increases. This means that enforcing the recovered shear and bending stresses to be interrelated, in an integral form, will not lead to better results (viz. functional (49)). The optimal values, though not recognizable from the figures, are less than unity. Here again, no major improvement can be seen in the figures.
|
|
| (a) | (b) |
Figure 8. Variation of relative errors with respect to variation of weight factors, and , for thick plate solution using MITC9 elements and when SPR2 recovery is applied; (a) variation of error norm for bending stresses , (b) variation of error norm for shear stresses .
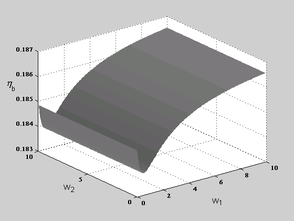
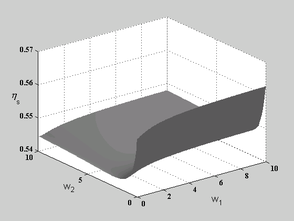
Figure 9 depicts the results for SPR3 type of formulation where point-wise forms of constraints have been used. Although, here again, the improvement is not significant, optimal values can be found for ![]() and
and ![]() . This means that adding point-wise constraints may lead to slightly better results.
. This means that adding point-wise constraints may lead to slightly better results.
|
|
| (a) | (b) |
Figure 9. Variation of relative errors with respect to variation of weight factors, and , for thick plate solution using MITC9 elements and when SPR3 recovery is applied; (a) variation of error norm for bending stresses , (b) variation of error norm for shear stresses .
For SPR4, just the shear energy norm has been selected to demonstrate the results since in functional (56) the constraints have been applied to recovered shear stresses only. Figure 10 shows that relating the recovered shear stresses to derivatives of bending moment does not improve the results. Similar conclusion is made from Figure 11 for constraints on REP1.
So far we have shown that adding equilibrium constraints to original form of SPR does not much improve the accuracy of the solution. This implicitly means that the recovered fields of stresses, obtained from the original form, are very close to equilibrium state.
Now, we are ready to examine the effect of constraints on the convergence rate of the recovered solution. For each case we have chosen the optimal values for ![]() and
and ![]() from the previous study. The results for the energy norms are reported in Tables 15 to 18 for thin and thick plate solutions. To perform the study we compare the rates in Figure 2, for original form of SPR, with those of Table 15 for thick plate solution using MITC4 elements. No significant change can be seen in the convergence rates. Among the four forms of SPR the second one, SPR2, shows a slight increase in the shear energy norm rate.
from the previous study. The results for the energy norms are reported in Tables 15 to 18 for thin and thick plate solutions. To perform the study we compare the rates in Figure 2, for original form of SPR, with those of Table 15 for thick plate solution using MITC4 elements. No significant change can be seen in the convergence rates. Among the four forms of SPR the second one, SPR2, shows a slight increase in the shear energy norm rate.
Table 15. Relative error norms for thick plate solution using MITC4 elements. A comparison between various forms of constraints on SPR.
| SPR1 | SPR2 | SPR3 | SPR4 | |
| h | Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
| 2.00
1.00 .667 .500 .333 .222 C.R. |
26.79 18.99 25.48
8.67 4.97 8.35 3.96 2.37 3.71 2.34 1.36 2.19 1.10 0.63 1.02 0.51 0.30 0.47 1.806 1.886 1.814 |
26.80 37.78 29.23
8.60 9.51 8.93 3.96 3.76 3.92 2.34 1.92 2.26 1.10 0.78 1.04 0.51 0.34 0.48 1.807 2.147 1.873 |
26.80 19.34 25.54
8.53 5.06 8.34 3.96 2.40 3.72 2.34 1.38 2.19 1.10 0.64 1.03 0.51 0.31 0.47 1.807 1.888 1.814 |
26.71 19.12 25.43
8.87 4.99 8.55 3.96 2.38 3.71 2.34 1.37 2.19 1.10 0.64 1.02 0.51 0.30 0.47 1.805 1.887 1.813 |
Table 16. Relative error norms for thick plate solution using MITC9 elements. A comparison between various forms of constraints on SPR.
| SPR1 | SPR2 | SPR3 | SPR4 | |
| h | Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
| 2.00
1.33 1.00 .667 .533 .400 C.R. |
4.27 5.46 4.52
1.34 2.23 1.56 0.58 1.23 0.75 0.18 0.54 0.28 0.09 0.35 0.17 0.04 0.20 0.09 2.922 2.050 2.404 |
4.15 7.89 5.08
1.31 2.77 1.69 0.56 1.40 0.80 0.17 0.58 0.30 0.09 0.37 0.18 0.04 0.21 0.10 2.926 2.245 2.446 |
4.55 5.63 4.77
1.43 2.33 1.64 0.61 1.28 0.79 0.19 0.56 0.30 0.10 0.36 0.18 0.04 0.21 010 2.922 2.044 2.411 |
4.53 5.47 4.72
1.42 2.25 1.62 0.61 1.24 0.77 0.18 0.55 0.29 0.10 0.35 0.18 0.04 0.20 0.10 2.938 2.043 2.417 |
Table 17. Relative error norms for thin plate solution using MITC4 elements. A comparison between various forms of constraints on SPR.
| SPR1 | SPR2 | SPR3 | SPR4 | |
| h | Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
| 2.00
1.00 .667 .500 .333 .222 C.R. |
26.80 18.73 25.80
8.25 4.66 8.24 3.95 2.35 3.95 2.33 1.36 2.33 1.09 0.64 1.09 0.50 0.31 0.50 1.808 1.874 1.808 |
26.81 37.67 26.81
8.31 8.46 8.31 3.95 3.72 3.93 2.33 1.90 2.33 1.09 0.78 1.09 0.50 0.34 1.60 1.808 2.142 1.808 |
26.80 19.07 26.80
8.38 4.87 8.38 3.96 2.39 3.96 2.34 1.38 2.34 1.09 0.65 1.09 0.50 0.31 0.50 1.901 1.875 1.808 |
26.73 19.11 26.73
8.15 4.81 8.15 3.95 2.37 3.95 2.33 1.37 2.33 1.09 0.64 1.09 0.50 0.31 0.50 1.807 1.874 1.807 |
Table 18. Relative error norms for thin plate solution using MITC9 elements. A comparison between various forms of constraints on SPR.
| SPR1 | SPR2 | SPR3 | SPR4 | |
| h | Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
Bend. Shear Total
|
| 2.00
1.33 1.00 .667 .533 .400 C.R. |
4.34 6.15 4.34
1.38 2.64 1.38 0.60 1.50 0.60 0.18 0.69 0.18 0.09 0.44 0.09 0.04 0.25 0.04 2.912 1.981 1.904 |
4.24 8.45 4.24
1.34 3.13 1.34 0.58 1.65 0.58 0.18 0.71 0.18 0.09 0.45 0.09 0.04 0.26 0.04 2.918 2.163 2.910 |
4.57 6.15 4.57
1.47 2.64 1.47 0.64 1.49 0.64 0.19 0.68 0.19 0.10 0.44 0.10 0.04 0.25 0.04 2.891 1.985 2.885 |
4.54 6.08 4.54
1.45 2.61 1.45 0.63 1.48 0.63 0.19 0.68 0.19 0.10 0.44 0.10 0.04 0.25 0.04 2.905 1.980 2.897 |
The same conclusion can be made for thick and thin plate solutions, reported in Tables 16 to 18, when they are compared to those of Tables 8, Figures 5 and 6, respectively.
It can clearly be seen that adding some equilibrium constraints, has almost no effect on the results of SPR for both accuracy and the rate of convergence. Here we have not reported the results for triangular elements since the same conclusion is also made for this class of elements.
To complete our studies, we report the results of a constrained form of REP as Table 19 (see subsection 4.2). Here the original form of REP has been used since the formulation is written in a couple form and thus additional constraints does not increase the computational cost siginificantly. Since REP formulation is, in fact, based on a weighted form of equilibrium, as expected, no improvement is seen in the results of Table.
| h | Bend. Shear Total
|
| 2.00
1.33 1.00 .667 .533 .400 C.R. |
7.60 9.09 7.90
2.44 3.33 2.64 1.11 1.76 1.26 0.37 0.79 0.48 0.21 0.52 0.29 0.10 0.31 0.02 2.710 2.106 2.423 |
6. CONCLUSIONS
In this paper the formulation of two recovery methods, proven to be superconvergent in two dimensional problems i.e. SPR and REP, have been extended and applied to plate problem using Reissner-Mindlin type of formulation. The elements used are basically those which have been recently proposed in [21-23] for eliminating “locking” effect, namely the series of MITC elements. The study has been performed on a benchmark problem used for both thick and thin cases.
Comparison of the results for SPR and REP shows that the improved version of REP gives similar results to those of SPR, though it does not require superconvergent sampling points. The original form of REP sometimes fails to give convergent results, however, in some point wise results it shows ultraconvergent rates.
For MITC4 elements, both SPR and REP, show nearly full superconvergent behavior for energy norms as well as point-wise values.
For quadratic elements MITC7 and MITC9, however, SPR and REP show semi-superconvergent behavior for energy norms but much better convergence rates are seen for point-wise values. This implies that, for these types of elements, the recovery procedures are very sensitive to the treatment of the boundary patches. In this paper for recovered values at boundaries we have extrapolated the values obtained from the closest interior patches for both SPR and REP.
The results obtained for thick and thin plate solutions basically exhibit similar rate of convergence and the accuracy for bending stresses. For shear stresses, however, the results of thick plate solution show superconvergent effect though those of thin plate solution, especially for MITC7 do not show the desired effects. We notice that, for this type of elements, although the finite element solution is poor regarding accuracy and convergence rate, the element can successfully eliminate the “locking” effect. Moreover, we note that the shearing part of the energy in thin plate solution, compared to bending part, is very small and has little contribution in an adaptive procedure. This means that this element, also, can effectively be used in adaptive procedures for thick and thick plate solutions, using recovery based estimates.
In another attempt we have investigated the effects of some equilibrium constraints on the results of SPR procedure. The constraints have been designed in integral and point-wise forms. The study consists of two parts. First the improvement in the accuracy of the recovered field has been examined and then a study has been performed on the effects of the constraints on the convergence rate. No significant improvement can be seen in the results regarding both accuracy and the convergence rate. This implies that the application of the uncoupled form of SPR leads to best results.
In this paper we have not applied boundary constraints to the recovery procedures. We believe that this can be a subject of another paper. Some other plate formulations, e.g. Kirchhoff type for thin plates, may also be used to examine the convergence rate of the recovery methods. In such formulations, determination of sampling points for SPR plays an important role and thus requires a separate study.
References
[1] Babuška, I. and Rheinboldt, W.C., “A posteriori error estimates for the finite element method’, International Journal for Numerical Methods in Engineering, Vol. 12, pp. 1597-1615, 1978.
[2] Zienkiewicz, O.C. and Zhu, J.Z., “ A simple error estimator and adaptive procedure for practical engineering analysis”, International Journal for Numerical Methods in Engineering, Vol. 24, pp. 337-357, 1987.
[3] Babuška, I., Strouboulis, T., Upadhyay, C.S., Gangaraj, S.K, and Copps, K., “ An objective criterion for assessing the reliability of a-posteriori error estimators in finite element computations”, USACM bulletin, Vol. 7, No. 2, pp. 4-15, 1994.
[4] Babuška, I., Strouboulis, T., Upadhyay, “ A model study of the quality of a posteriori error estimates for linear elliptic problems. Error estimation in the interior of patchwise uniform grids of triangles”, Computer Methods in Applied Mechanics and Engineering, Vol. 114, pp. 307-378, 1994.
[5] Babuška, I., Strouboulis, T., Upadhyay, C.S., Gangaraj, S.K, and Copps, K., “ Validation of a posteriori error estimators by numerical approach”, International Journal for Numerical Methods in Engineering, Vol. 37, pp. 1073-1123, 1994.
[6] Zienkiewicz, O.C. and Zhu, J.Z., “ The superconvergent patch recovery and a posteriori error estimates. Part I: The recovery technique”, International Journal for Numerical Methods in Engineering, Vol. 33, pp. 1331-1364, 1992.
[7] Zienkiewicz, O.C. and Zhu, J.Z., “ The superconvergent patch recovery and a posteriori error estimates. Part II: Error estimates and adaptivity”, International Journal for Numerical Methods in Engineering, Vol. 33, pp. 1365-1382, 1992.
[8] Zienkiewicz, O. C. and Taylor, R. L., “The finite element method”, 5th edition, Butterworth-Heineman, 2000.
[9] Boroomand, B. and Zienkiewicz, O.C. “ Recovery by equilibrium in patches (REP)”, International Journal for Numerical Methods in Engineering, Vol. 40, pp. 137-164, 1997.
[10] Boroomand, B. and Zienkiewicz, O.C. “ An improved REP recovery and the effectivity robustness test”, International Journal for Numerical Methods in Engineering, Vol. 40, pp. 3247-3277, 1997.
[11] Lo, S.H. and Lee, C.K., “ On using different recovery procedures for the construction of smoothed stress in finite element method”, International Journal for Numerical Methods in Engineering, Vol. 43, pp. 1223-1252, 1998.
[12] Weinberg, K., “ An adaptive finite element approach for a mixed Reissner-Mindlin plate formulation”, Computer Methods in Applied Mechanics and Engineering, Vol. 190, pp. 4999-5008, 2001
[13] Carstensen, C., Weinberg, K., “ Adaptive mixed finite element method for Reissner-Mindlin plate”, Computer Methods in Applied Mechanics and Engineering, Vol. 190, pp. 6895-6908, 2001.
[14] Zienkiewicz, O.C. and Zhu, J.Z., “ Error estimates and adaptive refinement to plate bending problems”, International Journal for Numerical Methods in Engineering, Vol. 28, pp. 2839-2853, 1989.
[15] Lee, S.H., Blacker, T. and Belytschko, T., “ On derivative recovery techniques for ![]() plate problems”, Engineering Computations, Vol. 11, pp. 495-512, 1994.
plate problems”, Engineering Computations, Vol. 11, pp. 495-512, 1994.
[16] Wiberg, N-E. and Abdulwahab, F. “ Patch recovery based on superconvergent derivatives and equilibrium”, International Journal for Numerical Methods in Engineering, Vol. 36, pp. 2703-2724, 1993.
[17] Wiberg, N-E. and Abdulwahab, F., “ Enhanced superconvergent patch recovery incorporating equilibrium and boundary conditions”, International Journal for Numerical Methods in Engineering, Vol. 37, pp. 3417-3440, 1994.
[18] Blacker, T. and Belytschko, T., “ Superconvergent patch recovery with equilibrium and conjoint interpolation enhancemenet”, International Journal for Numerical Methods in Engineering, Vol. 37, pp. 517-536, 1994.
[19] Zhang, Z and Zhang, S., “ Derivative superconvergence of rectangular finite elements for the Reissner-Mindlin plate”, Computer Methods in Applied Mechanics and Engineering, Vol. 134, pp. 1-16, 1996.
[20] Zhang, Z., “ Superconvergence in projected –shear plate-bending finite element methods”, Numerical Methods for Partial Differential Equation, Vol. 14, pp. 367-386, 1998.
[21] Bathe, K.J. and Dvorkin, E.N., “ A four-node plate bending element based on Mindlin/Reissner plate theory and mixed interpolation”, International Journal for Numerical Methods in Engineering, Vol. 21, pp. 367-383, 1985.
[22] Bathe, K.J. and Dvorkin, E.N., “ A formulation of general shell element- The use of mixed interpolation of tensorial components”, International Journal for Numerical Methods in Engineering, Vol. 22, pp. 697-722, 1986.
[23] Bathe, K.J., Bucalem, M.L. and Brezzi, F., “ Displacement and stress convergence of our MITC plate bending elements”, Engineering Computations, Vol. 7, pp. 291-302, 1990.
[24] Lee C.K. and Hobbs, R.E. “ Automatic adaptive refinement for plate bending problems using Reissner-Mindlin plate bending elements”, International Journal for Numerical Methods in Engineering, Vol. 41, pp. 1-63, 1998.
[25] Hinton, E. and Huang, H.C., “ A family of quadrilateral Mindlin plate elements with substitute shear strain fields”, Computers and Structures, Vol. 23, pp. 409-431,1986.
[26] Huang, H.C., Hinton, E., “ A nine node Lagrangian Mindlin plate element with enhanced shear interpolation”, Engineering Computation, Vol. 1, pp. 369-379, 1984.
[27] Lee, C.K., Sze, K.Y and Lo, S.H., “ On using degenerated solid shell elements in adaptive refinement analysis”, International Journal for Numerical Methods in Engineering, Vol. 45, pp. 627-659, 1999.
[28] Sze, K.Y. “ An explicit hybrid-stabilized 9-node Lagrangian shell elements”, Computer Methods in Applied Mechanics and Engineering, Vol. 117, pp. 361-379, 1994.
[29] Okstad, K.M., Kvamsdal, T.K. and Mathisen, K.M., “ Superconvergent patch recovery for plate problems using statically admissible stress resultant fields”, International Journal for Numerical Methods in Engineering, Vol. 44, pp. 697-727, 1999.
[30] Yazdani, A.A., Riggs, H.R. and Tessler, A., “ Stress recovery and error estimation for shell structures”, International Journal for Numerical Methods in Engineering, Vol. 47, pp. 1825-1840, 2000.
[31] Reddy, J.N. and Barbero, E.J., “ A plate bending element based on a generalized laminate plate theory”, International Journal for Numerical Methods in Engineering, Vol. 28, pp. 2275-2292, 1989.
[32] Barbero, E.J. and Reddy, J.N., “ An accurate determination of stresses in thick laminates using a generalized plate theory”, International Journal for Numerical Methods in Engineering, Vol. 29, pp. 1-14, 1990.
[33] Babuška, I., Likang, Li, “The problem of plate modeling: Theoretical and computational results”, Computer Methods in Applied Mechanics and Engineering, Vol. 100, pp. 249-273, 1992.
[34] Dobyns, A.L., “ Analysis of simply-supported orthotropic plates subject to static and dynamic loads”, AIAA Journal, Vol. 19, pp. 642-650, 1981.
[35] Zhang, Z., “Ultraconvergence of the patch recovery technique II”, Mathematical Computation, Vol. 69, pp. 141-158, 2000.
Document information
Published on 05/07/18
Submitted on 05/07/18
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?