A novel technique for mitigating motion artifacts in 3D brain imaging systems

Abstract

Over the past several years,there have been substantial improvements in the area of three-dimensional (3D) cone-beam Computed Tomography (CT) imaging systems. Nevertheless, more improvement is needed to detect and mitigate motion artifacts in the clinical follow-up of neurological patients with multiple sclerosis, tumors, and stroke, etc., in which failure to detect motion artifacts often leads to misdiagnosis of disease. In this paper, we propose a marker-based innovative approach to detect and mitigate motion artifacts in 3D cone-beam brain CT systems without using any external motion tracking sensors. Motion is detected by comparing the motion-free ideal marker projections and the corresponding measured marker projections. Once motion is detected, motion parameters (six degrees-of-freedom of motion) are estimated using a numerical optimization technique. Artifacts, caused by motions, are mitigated in the back projection stage of the 3D reconstruction process by correcting the position of every reconstruction voxel according to the estimated motion parameters. We refer to this algorithm as the MB_FDK (Marker-based Feldkemp–Davis–Kress) algorithm. MB_FDK has been evaluated on a modified 3D Shepp–Logan phantom with a range of simulated motion. Simulation results demonstrate a quantitative and qualitative validation of motion detection and artifact mitigation techniques.

Keywords

Three-dimensional CT ; Brain imaging ; FDK algorithm ; Cone-beam CT ; Motion detection ; Motion artifacts ; Mitigating motion artifacts

1. Introduction

In a brain CT imaging system, even with substantial head restraint, some amount of motion is inevitable, especially in less cooperative patients like children, traumatic patients and elderly people with Parkinson type diseases, which make it difficult to control head movement  [1]  and [2] . Head motion during 3D brain CT imaging studies can adversely affect the reconstructed image through distortion, loss of resolution and other related artifacts  [3] . Many researchers have attempted to eliminate motion artifacts from the two-dimensional reconstruction process  [4] , [5] , [6] , [7]  and [8] , but methods for compensating motion artifacts in 3D brain CT systems have been studied to a comparatively limited degree. Moreover, the existing techniques have not found wide clinical acceptance because of their design complexities, lack of accuracy, and problems with implementation. Therefore, it is imperative to detect and eliminate motion artifacts in 3D brain CT systems for diagnostic purposes.

Over the past few years, several methods have been reported to detect and correct head motion artifacts using external sensors. Goldstein et al.  [9] proposed a device that uses a triad of three incandescent lights affixed on the patient’s head while viewed by two position sensitive detectors. Fulton et al.  [10] and Beache et al.  [11] also proposed similar approaches that use an infrared reflector, while using a mechanical motion tracker comprised of a base which houses the electronics and a multiple-jointed light weight arm. On the other hand, several other approaches, solely based on sinogram/linogram information, such as the motion correction method, based on cross-correlation of the summed horizontal and vertical sinogram of successive projection  [12] , and motion estimation based upon a parabolic fitting of the peak of the correlation function of the sinogram/linograms of projection  [13]  and [14] , have been proposed and evaluated in the literature. It must be noted that motion detection using external sensors could cause systematic biases in the reconstructed images  [15] and Sinogram/Linogram approaches suffer from the common disadvantages of depending upon resolution, sampling, and noise characteristics, as well as the activity distribution of the scanned data set  [9] . Moreover, the sinogram approach often fails to detect motion in cases of abrupt and large variations in head movement. Therefore, to overcome the existing shortcomings, we have proposed a marker-based system to detect and mitigate motion artifacts in 3D brain imaging systems. Unlike using only the sinogram/linogram information of the projections, our proposed marker-based system uses four suitable markers (which have a high attenuation constant and are attached to the head surface) to detect head motion. Without using any external optical motion tracking sensors, six degrees of freedom head motion parameters are estimated using a numerical optimization technique. Mitigation of motion artifacts is achieved using the MB_FDK algorithm, which uses estimated motion parameters in a back projection stage. The proposed method uses the OSCaR-02  [16] implementation steps for efficient FDK-based 3D reconstruction. In this paper, we have adopted the modified X-ray projection equation of the 3D Shepp–Logan phantom [3]  and [17] , to simulate all possible forms of real life head motion (rotation and translation) during the data acquisition process. We have tested our MB_FDK algorithm on a modified 3D Shepp–Logan phantom with a range of simulated motion. Simulation results validate our motion detection and artifacts mitigation technique.

This paper is organized as follows. In Section  2 , for the completeness of this paper, we give a brief description of the FDK-based 3D reconstruction process. In Section  3 , we elaborately describe the proposed marker-based head motion measurement system. In Section  4 , we describe the proposed MB_FDK algorithm. In Section  5 , we give a detailed simulation of our marker-based system. In Section  6 , with the help of simulation outcomes, a quantitative and qualitative validation of our marker-based motion detection and artifacts mitigation approach is given. And, finally, a brief conclusion is drawn in Section  7 .

2. FDK-based 3D reconstruction in circular cone-beam tomography

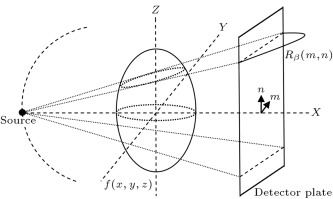
In 3D computer tomography, a 3D image of the internal structure of an object, ${\textstyle f(x,y,z)}$ , can be created from the X-ray projections taken around the object. The circular cone-beam CT system, as shown in Figure 1 , has been widely used in 3D tomography. In circular cone-beam CT systems, a source from one end of the object radiates a beam of X-rays through the entire object. A detector at the other end of the object collects the incident rays and creates an X-ray projection of the object. The source–detector pair are rotated in a circular orbit about the ${\textstyle Z}$ -axis by angle ${\textstyle \beta }$ , where ${\textstyle \beta }$ varies from 0° to 360°, with a suitable step size, with respect to the ${\textstyle Y}$ -axis. At every source–detector position (${\textstyle \beta }$ ), the entire 3D object is illuminated with the source, and the X-ray projection is created on the detector plate. The X-ray projection, sometimes called the sum of the ray integrals, is denoted by ${\textstyle R_{\beta }(m,n)}$ , where (${\textstyle m,n}$ ) represents the horizontal and vertical positions of the detector plate. For our simulation, we have used 360 projections (i.e. ${\textstyle \beta }$ of step size ${\textstyle 1{\mbox{°}}}$ ) and (${\textstyle m,n}$ ) of size (256, 256). The Feldkamp–Davis–Kress (FDK) algorithm is the most widely used algorithm for cone-beam volume reconstruction  [18] . Because of its simple one-dimensional filtration and parallel implementation, the FDK algorithm and its variations can be implemented efficiently. The FDK algorithm falls into the framework of the well-known Filtered Back Projection (FBP)  [19] . In practice, the cone-beam data acquired by the flat panel detector are row-wisely filtered with a suitable reconstruction filter and followed by a 3D back projection for volume reconstruction.

Figure 1. Circular cone-beam CT system.

3. Marker-based system

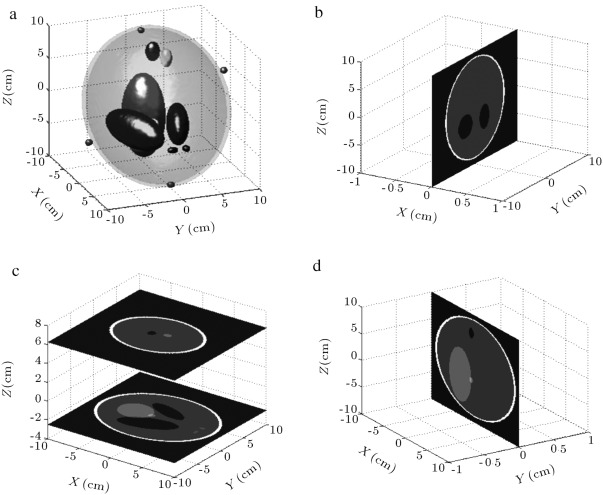
The idea behind our marker-based system is to detect head motion and mitigate motion artifacts without using any external motion tracking sensors. The proposed system, which is implemented in a circular cone-beam CT assembly, as shown in Figure 1 , uses four markers (with high attenuation constant) to detect rotational and translational parameters (six degrees of freedom) of motion. Using a suitable head band or a suitable fixture, markers can be attached to the head surface in such a way that that their positions (3D coordinates) will be linearly independent and their projections on the X-ray detector plate will never cross each other in cases of any practical head motion. The relative distances between the markers are known and always remain constant in cases of any head motion. The modified 3D Shepp–Logan phantom, as shown in Figure 2 , is used for our simulation. The model consists of four spherical markers and ten superimposed ellipsoids with different attenuation coefficients (CT values). The geometric locations, sizes and CT values of the ellipsoids are listed in Table 1 . CT values of each of the ellipsoid mimics the soft tissue, bone and other matters located in the head  [20] . One to one correspondence between the markers and their corresponding projections are ensured by carefully choosing the vertical location of the markers. In our marker-based system, the number of markers and their linear independence are the two necessary conditions for finding the motion parameters.

Figure 2. (a) A 3D version of the Shepp–Logan phantom with markers. (b) Axial slices at ${\textstyle Z=-2.5}$ and 6.25 cm. (c) Coronal slice. (d) Sagittal slice.

Table 1. Parameters of the modified 3D Shepp–Logan phantom.

	Center coordinate (cm)			Half axis (cm)			Rotation angle (${\textstyle {\mbox{°}}}$ )			CT value
	${\textstyle x_{o}}$	${\textstyle y_{o}}$	${\textstyle z_{o}}$	${\textstyle a}$	${\textstyle b}$	${\textstyle c}$	${\textstyle \varphi }$	${\textstyle \psi }$	${\textstyle \xi }$	${\textstyle \rho }$
Markers	0	0	9.25	0.25	0.25	0.25	0	0	0	5000
	7.25	0	3.25	0.25	0.25	0.25	0	0	0	5000
	0	−7.25	−3.25	0.25	0.25	0.25	0	0	0	5000
	−0.75	0.75	−9.25	0.25	0.25	0.25	0	0	0	5000
Ellipsoids	0	0	0	6.90	9.20	9.00	0	0	0	1000
	0	0	0	6.62	8.74	8.80	0	0	0	−800
	−2.2	0	−2.5	4.10	1.60	2.10	108	0	0	−200
	2.2	0	−2.5	3.10	1.10	2.20	72	0	0	−200
	0	3.5	−2.5	2.10	2.50	5.00	0	0	0	100
	0	1.0	−2.5	0.46	0.46	0.46	0	0	0	100
	−0.8	−6.5	−2.5	0.46	0.23	0.20	0	0	0	100
	0.6	−6.5	−2.5	0.46	0.23	0.20	90	0	0	100
	0.6	−1.05	6.25	0.56	0.40	1.00	90	0	0	100
	0	1.0	6.25	0.56	0.56	1.00	0	0	0	100

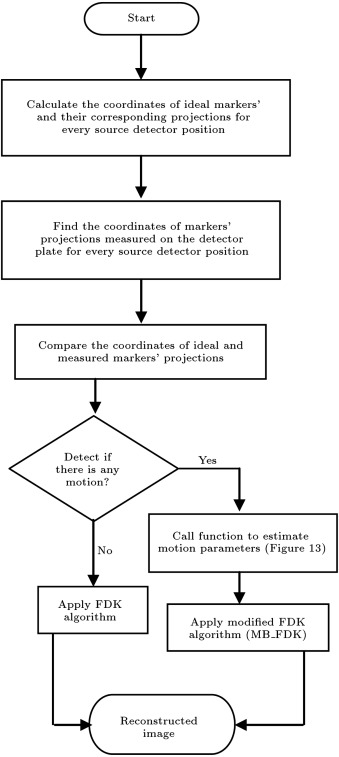
The flowchart of Figure 3 shows the kernel of our Marker-Based Motion Detection (MBMD) and MB_FDK based artifacts mitigation approach. The first step in our motion detection is to calculate the coordinates motion-free ideal markers and their corresponding projections for one complete revolution (which is elaborately discussed in Section  5 ). In case of any head motion during the CT scan, the markers and their corresponding projections will shift from their ideal positions. However, the relative distances between the markers will always remain constant, as they are on a rigid body structure. The new positions of the marker projections are known from the detector plate but the new positions of the markers are no longer known. In our proposed marker-based system, the new positions of the shifted markers are estimated by an iterative numerical optimization technique which minimizes the differences between the known relative distances between the motion-free markers and the corresponding relative distances between the estimated marker positions. Once the new positions of the shifted markers are known, the motion parameters can easily be calculated from the coordinates of shifted markers and their corresponding ideal positions. The estimated motion parameters are then used in our MB_FDK algorithm to mitigate motion artifacts.

Figure 3. Kernel of the marker-based system.

3.1. Illustration of the MBMD system

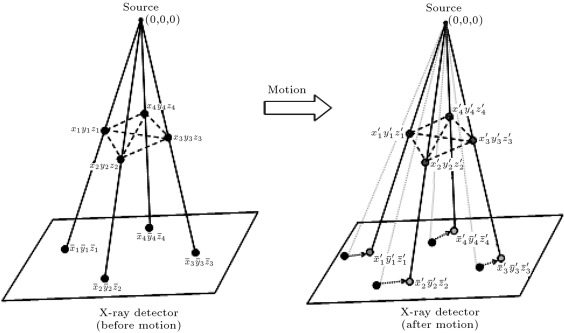
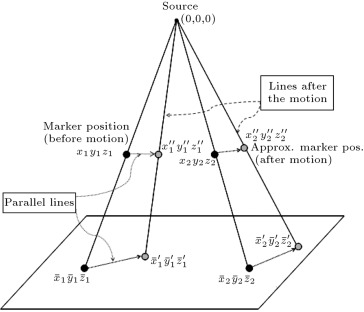
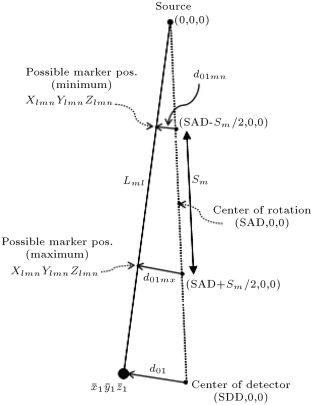
In order to make our calculation easier, the source, detector and the marker coordinates are represented in the same coordinate system, as shown in Figure 4 , where the source is considered as the origin of the coordinate system. Our proposed MBMD system is illustrated step by step in the following section:

Figure 4. MBMD system showing source, detector, markers and their corresponding projections before and after motion.

• We have four points, (${\textstyle x_{i}y_{i}z_{i}}$ , where ${\textstyle i=1,2,3,4}$ ), which we call markers (Figure 4 ), in the three-dimensional coordinate system. Suppose we know the coordinates of motion-free ideal markers. (The method of finding the coordinates of motion-free ideal markers is elaborately discussed in Section  5 .)
• From one point in space (0, 0, 0), which we call the X-ray source, we draw four lines (Eq. (1) ) through the four markers. These lines will intersect a plane, which we call the X-ray detector. We know the coordinates of four intersection points, ${\textstyle ({\overline {x}}_{i}{\overline {y}}_{i}{\overline {z}}_{i},where\quad i=1,2,3,4)}$ , which we call marker projections on the detector plate (as shown in Figure 4 (before motion)). By using a forward projection of the phantom (as elaborately discussed in Section  5 ), we can find the coordinates of motion-free ideal marker projections:

${\frac {x}{y}}={\frac {{\overline {x}}_{i}}{{\overline {y}}_{i}}}{\mbox{,}}\quad {\frac {y}{z}}={\frac {{\overline {y}}_{i}}{{\overline {z}}_{i}}}{\mbox{.}}$

( 1)

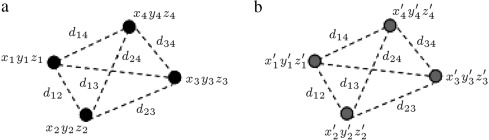
• Now, the four points (markers) are shifted because of motion. The coordinates of the shifted markers, ${\textstyle (x_{i}^{'}y_{i}^{'}z_{i}^{'})}$ , are no longer known. The only thing we know is that the relative distances (Eqs.  and  ) between the markers remain constant (Figure 5 ), since they are attached on a solid body (Figure 1 ):

${\sqrt {(x_{i}-x_{j})^{2}+(y_{i}-y_{j})^{2}+(z_{i}-z_{j})^{2}}}=d_{ij}{\mbox{,}}$

( 2)

for ${\textstyle \forall j>i}$ ,

Figure 5. Relative distances between markers. (a) Before motion; (b) after motion.

where, ${\textstyle i=1,2,3\quad and\quad j=2,3,4}$ .

• Now, if we draw four lines (Eq. (4) ) from the source through these four shifted markers, they will intersect the same plate, X-ray detector, in four new points, ${\textstyle ({\overline {x}}_{i}^{'}{\overline {y}}_{i}^{'}{\overline {z}}_{i}^{'}\quad where\quad i=1,2,3,4)}$ . We know the coordinates of these four intersection points, as shown in Figure 4 (after motion).

${\frac {x}{y}}={\frac {{\overline {x}}_{i}^{'}}{{\overline {y}}_{i}^{'}}}{\mbox{,}}\quad {\frac {y}{z}}={\frac {{\overline {y}}_{i}^{'}}{{\overline {z}}_{i}^{'}}}{\mbox{.}}$

( 4)

• Our goal is to find the coordinates of the shifted markers, ${\textstyle (x_{i}^{'}y_{i}^{'}z_{i}^{'}\quad where\quad i=1,2,3,4)}$ , from the information described in 1–4.

In other words, our problem boils down to calculating the coordinates of the four shifted markers from six relative distances (Euclidean distances) between the markers and four straight lines (linear in ${\textstyle x,y}$ and ${\textstyle z}$ ) equations (i.e. calculating marker positions from six non-linear and four linear equations). This system of equation is solved numerically by the following iterative optimization technique.

3.2. Numerical optimization

The first step in our numerical optimization technique is to find the approximate positions of shifted markers, (${\textstyle x_{i}^{''}\quad y_{i}^{''}z_{i}^{''}}$ , where ${\textstyle i=1,2,3,4}$ ). As shown in Figure 6 , the approximate position of the shifted marker 1 can be found by drawing a line (which is parallel to the line between the ideal marker 1’s projection ${\textstyle ({\overline {x}}_{1}{\overline {y}}_{1}{\overline {z}}_{1})}$ and the shifted marker 1’s projection${\textstyle ({\overline {x}}_{1}^{'}{\overline {y}}_{1}^{'}{\overline {z}}_{1}^{'})}$ from its ideal position ${\textstyle (x_{1}y_{1}z_{1})}$ to the shifted line. The intersection point, ${\textstyle (x_{1}^{''}y_{1}^{''}z_{1}^{''})}$ , is the approximate position of the shifted marker 1. The generalized formula for finding the approximate positions of the shifted markers is given by Eq. (5)

$z_{i}^{''}={\frac {K_{i2}\pm {\sqrt {K_{i2}^{2}-4K_{i1}K_{i3}}}}{2K_{i3}}}\lbrace {\begin{array}{cc}+if&z_{i}is~positive\\-if&z_{i}is~negative\end{array}}$

( 5)

where:

$i=1,2,3,4{\mbox{,}}$

Figure 6. Approximate coordinates of markers after motion.

After finding the approximate marker positions, (${\textstyle x_{i}^{''}y_{i}^{''}z_{i}^{''}}$ ), we need to calculate the relative distances, ${\textstyle d_{ij}^{''}}$ , between them:

$d_{ij}^{''}={\sqrt {(x_{i}^{''}-x_{j}^{''})}}^{2}+(y_{i}^{''}-y_{j}^{''})^{2}+(z_{i}^{''}-z_{j}^{''})^{2}{\mbox{,}}$

( 6)

for ${\textstyle \forall j>i}$ ,

where, ${\textstyle i=1,2,3}$ and ${\textstyle j=2,3,4}$ .

If these relatives distances, ${\textstyle d_{ij}^{''}}$ , are close to the ${\textstyle d_{ij}}$ (relative distances between the ideal marker positions), then our approximation is good. Otherwise, we need to vary the positions of the approximate marker positions along their corresponding shifted lines until their relative distances become very close to ideal distances, ${\textstyle d_{ij}}$ . With the help of a flow chart, this iteration process is explained in detail in Section  5 .

Once we reach within our error limit (in other words when ${\textstyle \sum _{ij}abs(d_{ij}^{''}-d_{ij})\leq Error}$ ), we can claim:

$x_{i}^{''}=x_{i}^{'}{\mbox{,}}\quad y_{i}^{''}=y_{i}^{'}{\mbox{,}}\quad z_{i}^{''}=z_{i}^{'}\quad {\mbox{where  }}i=1,2,3,4{\mbox{.}}$

( 7)

After finding the shifted marker positions, ${\textstyle (x_{i}^{'}y_{i}^{'}z_{i}^{'})}$ , we can easily extract the motion parameters from the following  [17] :

$[{\begin{array}{cccc}x_{1}&x_{2}&x_{3}&x_{4}\\y_{1}&y_{2}&y_{3}&y_{4}\\z_{1}&z_{2}&z_{3}&z_{4}\\1&1&1&1\end{array}}]=[{\begin{array}{cccc}r_{11}&r_{12}&r_{13}&t_{xe}\\r_{21}&r_{22}&r_{23}&t_{ye}\\r_{31}&r_{32}&r_{33}&t_{ze}\\0&0&0&1\end{array}}]\times [{\begin{array}{cccc}x_{1}^{'}&x_{2}^{'}&x_{3}^{'}&x_{4}^{'}\\y_{1}^{'}&y_{2}^{'}&y_{3}^{'}&y_{4}^{'}\\z_{1}^{'}&z_{2}^{'}&z_{3}^{'}&z_{4}^{'}\\1&1&1&1\end{array}}]{\mbox{,}}$

( 8)

where:

$r_{11}=cos\alpha _{e}cos\vartheta _{e}{\mbox{;}}\quad r_{21}=sin\alpha _{e}cos\vartheta _{e}{\mbox{,}}$

Estimated six degrees of freedom of motion are:

$\alpha _{e}{\mbox{—rotation about  }}z(yaw){\mbox{,}}$

Since the marker coordinates are linearly independent for any form of practical motion, the solution of Eq. (8) will always exist.

4. Marker-based Feldkemp–Davis–Kress algorithm (MB_FDK)

The idea behind the MB_FDK algorithm is to mitigate motion artifacts by correcting the position of every reconstruction voxel in the back-projection stage, according to the motion information acquired in the previous section. The first step in the MB_FDK algorithm is to find the location of the source–detector pair where motion occurred. The location of motion can be detected by continuously comparing the coordinates of ideal and measured marker projections. The next step in the MB_FDK algorithm is to find the estimated motion parameters corresponding to the location of motions. After finding the location of motions (${\textstyle \beta _{m}}$ ) and the estimated motion parameters, the necessary coordinate transformation, consisting of the transformation matrix ${\textstyle [T]}$ (which consists of the rotational parameters of motion) of Eq. (9) and a translation operation (which consists of the translational parameters of motion), can be done on the reconstruction grid, so that the contribution of every projection will be placed in its corresponding grid location during the reconstruction process.

$[T]=[{\begin{array}{ccc}T_{11}&T_{12}&T_{13}\\T_{21}&T_{22}&T_{23}\\T_{31}&T_{32}&T_{33}\end{array}}]{\mbox{,}}$

( 9)

where:

$T_{11}=cos\Theta cos\Omega {\mbox{,}}$

In case of motion:

$\Theta =-\vartheta _{e}{\mbox{;}}\quad \Psi =-\delta _{e}{\mbox{;}}\quad \Omega =-\alpha _{e}{\mbox{;}}$

Otherwise:

$\Theta =0{\mbox{;}}\quad \Psi =0{\mbox{;}}\quad \Omega =0{\mbox{;}}$

In this research, the following OSCaR-02 based implementation steps are adopted for efficient implementation of our MB_FDK algorithm. Modification of the FDK algorithm starts at step (9) . In step (9) , each projection is examined to find if there is motion. In case of motion, the rotational parameters of matrix ${\textstyle [T]}$ are replaced by the estimated parameters (rotational) of motion, followed by the necessary coordinate transformation in step (10) . The whole idea is to correct the position of the reconstruction grid so that during backprojection, the contribution of every projection will be placed in its corresponding position.

Steps to implementing the MB_FDK algorithm:

• Input Projection data ${\textstyle R_{\beta }(m,n)}$ ,
• Input ${\textstyle SDD}$ , ${\textstyle SAD}$ and desired reconstruction grid ${\textstyle (x,y,z)}$ ,
• for all projection angles ${\textstyle \beta }$ , do,
• ${\textstyle {\tilde {R}}_{\beta }(m,n)=R_{\beta }(m,n)\times {\frac {SDD}{\sqrt {SDD^{2}+m^{2}+n^{2}}}}}$ % rescaling where ${\textstyle m,n=[-12.8:0.1:12.8]}$ ;
• for all detector rows ${\textstyle m}$ , do,
• ${\textstyle Q_{\beta }(m,n)={\tilde {R}}_{\beta }(m,n){_{\ast }}h(m)}$  % filtering where ${\textstyle h(m)=\int _{-W}^{W}\vert \omega \vert e^{j\omega m}d\omega }$ ,
• end for,
• for all reconstruction voxels ${\textstyle (x_{p},y_{q},z_{r})}$ , do,
• if ${\textstyle \beta =\beta _{m}}$ , then;

$\Theta =-\vartheta _{e}{\mbox{;}}\quad \Psi =-\delta _{e}{\mbox{;}}\quad \Omega =-\alpha _{e}{\mbox{;}}$

End:

$[{\begin{array}{c}x_{p}\\y_{q}\\z_{r}\end{array}}]=[{\begin{array}{ccc}T_{11}&T_{12}&T_{13}\\T_{21}&T_{22}&T_{23}\\T_{31}&T_{32}&T_{33}\end{array}}][{\begin{array}{c}x_{p}-T_{x}\\y_{q}-T_{y}\\z_{r}-T_{z}\end{array}}]{\mbox{.}}$

• for all reconstruction voxels ${\textstyle (x_{p},y_{q},z_{r})}$ , do
• ${\textstyle U\leftarrow SAD+x_{p}sin\beta -y_{q}cos\beta \quad \%}$ backprojection stage
• ${\textstyle p^{'}=(SAD/U)(x_{p}cos\beta +y_{q}sin\beta )}$
• ${\textstyle \zeta =(SAD/U)z_{r}}$
• ${\textstyle f(x_{p},y_{q},z_{r})=f(x_{p},y_{q},z_{r})+(SAD^{2}/U^{2})\quad Q_{\beta }(p^{'},\zeta )}$
• end for
• end for.

5. Simulation of the marker-based system

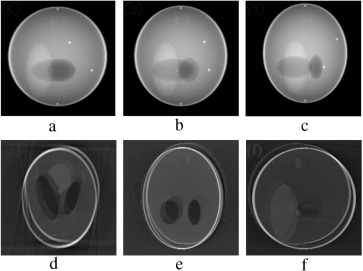
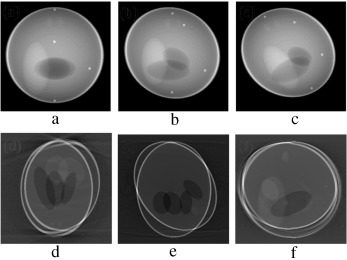
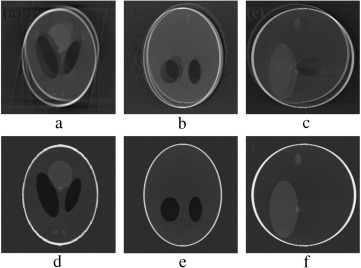
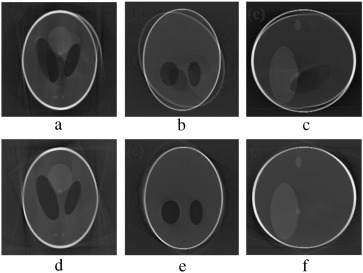
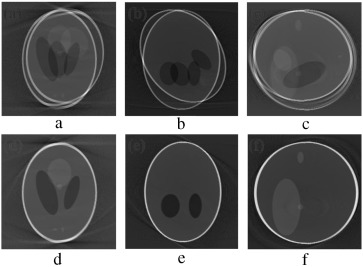
In order to validate the functionality of our proposed Marker-Based Motion Detection (MBMD) and artifacts mitigation technique (MB_FDK algorithm), we need to first simulate motion artifacts using our modified 3D Shepp–Logan phantom. For simulating motion artifacts, we need to perturb the 3D Shepp–Logan phantom during data acquisition time. Using the modified X-ray projection equation  [17] , which incorporated three translational ${\textstyle (t_{x},t_{y},t_{z})}$ and three rotational (roll, pitch, yaw ) parameters of motion, we simulated several abrupt and gradual variations of motion on the 3D Shepp–Logan phantom. The cone-beam parameters listed in Table 2 are used for our simulation. For abrupt variation of motion, we perturbed the 3D Shepp–Logan phantom with three different types of motion (translational, rotational, and rotational & translational combined) in three different test cases. Some of the images of motion corrupted projections and the axial, coronal and sagittal slices of the reconstructed volume of the above cases are plotted in Figure 7 , Figure 8  and Figure 9 . For gradual variation of motion, we varied each parameter of motion separately in six different test cases. For gradual translational motion corruption cases, we gave ±6 mm of perturbation with a step size of ±1 mm. For gradual rotational motion corruption cases, we gave perturbation of ±5° with a step size of ±1°. The axial, coronal and sagittal slices of the gradual motion corrupted cases (+ perturbation only) are plotted in Figure 10a  and Figure 10b . Figure 10a  and Figure 10b show the motion artifacts created in the reconstructed image due to the gradual perturbation given to the 3D Shepp–Logan phantom during data acquisition time. In Figure 10a , the 1st row shows the artifacts occurred due to the perturbation of +6 mm with a step size of +1 mm along the ${\textstyle X}$ -axis given. The 2nd and 3rd rows show the artifacts created due to the similar perturbation given to the phantom along the ${\textstyle Y}$ and ${\textstyle Z}$ axes, respectively. In Figure 10b , the 1st row shows the motion artifacts (artifacts dominant in the axial slice) occurred due to the rotational perturbation of 5° (clock-wise) with a step size of 1° given about the ${\textstyle Z}$ -axis (yaw). The 2nd row shows the motion artifacts (artifacts dominant in the sagittal slice) occurred due to the same rotational perturbation about the ${\textstyle Y}$ -axis (pitch). The 3rd row shows the artifacts (artifacts dominant in the coronal slice) occurred due to the rotational variation of similar motion about the ${\textstyle X}$ -axis (roll). From Figure 7 , Figure 8 , Figure 9 , Figure 10a  and Figure 10b , it can be observed that head motion during data acquisition time resulted in doubling, ghosting, blurring and loss of resolution artifacts in the reconstructed images.

Table 2. Geometric parameters chosen for the cone-beam CT system.

Description of parameters	Symbol	Values
Source to detector distance	SDD	2000 cm
Source to axis distance	SAD	1600 cm
Detector size	25.6×25.6cm2
No. of rows and columns in detectror	Nrow,Ncol	256, 256
Pixel lenth in m direction	dm	0.1 cm
Pixel length in n direction	dn	0.1 cm
Reconstruction voxel volume	0.08×0.08×0.08cm3

Figure 7. (a–c) Projection at ${\textstyle 160{\mbox{°}}}$ , ${\textstyle 180{\mbox{°}}}$ and ${\textstyle 200{\mbox{°}}}$ source position. (d–f) Axial, coronal and sagittal slices of the translational motion corrupted reconstructed volume.

Figure 8. (a–c) Projection at ${\textstyle 260{\mbox{°}},270{\mbox{°}}}$ and ${\textstyle 280{\mbox{°}}}$ source position. (d–f) Axial, coronal and sagittal slices of the rotational motion corrupted reconstructed volume.

Figure 9. (a–c) Projection at ${\textstyle 160{\mbox{°}},180{\mbox{°}}}$ and ${\textstyle 200{\mbox{°}}}$ source position. (d–f) Axial, coronal and sagittal slices of the translational and rotational motion corrupted reconstructed volume.

Figure 10a. Motion artifacts occurred due to translational varaiation of gradual motion.

Figure 10b. Motion artifacts occurred due to rotational varaiation of gradual motion.

The next step in our simulation is to develop an image processing tool to extract the coordinates of the marker projections from the detector plate (Figure 11 a). Using some basic image processing techniques (as shown in Figure 11 b–f), we can easily find the coordinates of the marker projections. First, we need to segment the marker projections using some suitable edge filter. In Figure 11 b, an “edge” function with a “Sobel” filter is used to segment the marker projections. Then, segmented marker projections are dilated with a suitable dilation function (Figure 11 c). Then, the segmented dilated markers projections are filled with a “fill” function (Figure 11 d). Then, a “clear border” function is used to remove the lighter structure from the edges of the segmented dilated filled marker projections, as shown in Figure 11 e. In the final step, as shown in Figure 11 f, an “erosion” function is used to convert the clear bordered marker projection into a square size marker projection. The center of the squared marker projection is the coordinates of the marker projection.

Figure 11. Finding coordinates of markers projection. (a) X-ray projection of the phantom with markers. (b) Binary gradient mask of markers projection. (c) Dilated gradient mask. (d) Binary image with filled holes. (e) Cleared border image. (f) Eroded segmented image.

The first step of our MBMD system is to find the coordinates of motion-free markers (${\textstyle x_{i}y_{i}z_{i}}$ , where ${\textstyle i=1,2,3,4}$ ) and their corresponding projections for every source–detector position (i.e   to find ${\textstyle {\overline {x}}_{i\beta }{\overline {y}}_{i\beta }{\overline {z}}_{i\beta }}$ , where ${\textstyle i=1,2,3,4}$ and ${\textstyle \beta =1{\mbox{°}}}$ to ${\textstyle 360{\mbox{°}}}$ with a step size of ${\textstyle 1{\mbox{°}}}$ ). If (${\textstyle x_{i}y_{i}z_{i}}$ ) are known, we can easily find ${\textstyle ({\overline {x}}_{i\beta }{\overline {y}}_{i\beta }{\overline {z}}_{i\beta })}$ by using the relative velocity between the 3D object and the source–detector pair and the forward projection operation. In our simulation, (${\textstyle x_{i}y_{i}z_{i}}$ ) is calculated from the first set of measured marker projections (assuming the first set of projection is not corrupted by motion. Otherwise, we need to choose a motion-free next set of projections) and the known relative distances between the markers ${\textstyle (d_{ij})}$ . Since the X-rays travels in a straight line, every marker must lie on the line connecting its projection and the source. However, the maximum possible length of a line segment whose marker can take a possible position can be found by using the geometry, as shown in Figure 12 . Where line segment, ${\textstyle S_{m}}$ , on the central X-ray line represents the maximum possible diameter (about 18 cm) of the human head. The parallel lines, ${\textstyle d_{01mx}}$ and ${\textstyle d_{01mn}}$ (which are parallel to the line ${\textstyle d_{01}}$ ), are drawn from the ends of ${\textstyle S_{m}}$ to the X-ray line connecting the projection of marker 1 ${\textstyle ({\overline {x}}_{1}{\overline {y}}_{1}{\overline {z}}_{1})}$ and the source, to find the maximum possible line segment, ${\textstyle L_{m1}}$ , for marker1. We need to find the maximum possible line segments ${\textstyle (L_{mi},i=1,2,3,4)}$ for all the other markers. Next, considering every point on ${\textstyle L_{mi}}$ (we choose 5000 points of equal interval for our simulation) as a potential candidate for possible marker position, we iteratively calculate the relative distances between markers until we get the distances close to the known relative distances. In other words, when ${\textstyle \sum _{ij}abs(d_{ij}^{I}-d_{ij})\leq Error}$ , where ${\textstyle d_{ij}^{I}}$ are the relative distances in the iteration, we can claim that we have found the coordinates of motion-free ideal markers ${\textstyle (x_{i}y_{i}z_{i})}$ , where ${\textstyle i=1,2,3,4}$ . This technique of finding marker coordinates is, however, a computational intensive process. Once ${\textstyle (x_{i}y_{i}z_{i})}$ is known, we can apply the MBMD technique to find the coordinates of shifted markers with less number of iterations.

Figure 12. Geometry showing maximum possible line segment ${\textstyle L_{m1}}$ for marker1.

After finding the coordinates of motion-free ideal markers, we can use the following (Eq. (10) ) to find the coordinates of 360 sets of motion-free ideal marker projections, ${\textstyle {\overline {x}}_{i\beta }{\overline {y}}_{i\beta }{\overline {z}}_{i\beta }}$ (i.e. for one complete revolution with ${\textstyle \beta }$ of step size ${\textstyle 1{\mbox{°}}}$ ).

${\overline {x}}_{i\beta }=SDD{\mbox{;}}\quad {\overline {y}}_{i\beta }={\frac {SDD}{x_{i\beta }}}y_{i\beta }{\mbox{;}}\quad {\overline {z}}_{i\beta }={\frac {SDD}{x_{i\beta }}}z_{i\beta }{\mbox{,}}$

( 10)

where:

$i=1,2,3,4\quad {\mbox{and}}\quad \beta =1,2,\ldots ,360{\mbox{°}}{\mbox{,}}$

( 11)

where ${\textstyle \beta }$ , in this case, is the rotation of the phantom about the ${\textstyle Z}$ -axis in the counter clock-wise direction (center of rotation is ${\textstyle SAD}$ ), while it is assumed that the source–detector pair is fixed at some location (whereas, in practical situations the 3D object remains fixed and the source–detector pair rotates in a clock-wise direction).

Once the coordinates of motion-free ideal marker projections are known, we can detect motion by comparing the coordinates of ideal and measured marker projections. For any source–detector location, if:

$[\sum _{i=1\cdots 4}{\sqrt {({\overline {x}}_{i\beta }-{\underset {i\beta }{\overset {'}{\overline {x}}}})^{2}+(y_{i\beta }-{\underset {i\beta }{\overset {'}{\overline {y}}}})^{2}+({\overline {z}}_{i\beta }-{\underset {i\beta }{\overset {'}{\overline {z}}}})^{2}}}]\geq 2{\mbox{  pixel width ,}}$

where ${\textstyle ({\overline {x}}_{i\beta }^{'}{\overline {y}}_{i\beta }^{'}{\overline {z}}_{i\beta }^{'})}$ are the coordinates of measured marker projections at location ${\textstyle \beta }$ , we can claim that motion has occurred at that location. Motion could also be detected from the correlations between the measured adjacent projections  [3]  and [21] . However, in motion detection, in cases of small and gradual variations of motion, the correlation-based technique may produce erroneous results since the correlations between adjacent projections could be corrupted by noise factors (such as, quantum noise, detector blurring and additive system noise) inherent in CT systems.

After detecting motion, we can apply the following MBMD iteration steps (as shown in Figure 13 ) to find the parameters of motion. To estimate the motion parameters efficiently, we choose some approximated line segment, ${\textstyle L}$ , on the shifted line around ${\textstyle (x_{i}^{''}y_{i}^{''}z_{i}^{''})}$ , for our iteration. ${\textstyle L}$ could be chosen based on the distance between ideal and shifted marker projections. After choosing ${\textstyle L}$ , we divide ${\textstyle L}$ into ${\textstyle N}$ equal parts for our iteration. Obviously, large values of ${\textstyle N}$ will produce better accuracy. The iteration is performed in several stages. In the first stage, using ${\textstyle L}$ , we try to find the closest possible coarse solution (i.e. coordinate of the shifted marker position). After getting the closest possible coarse marker positions, we choose a smaller length, half of the previous length (${\textstyle L/2}$ ), around the estimated coarse marker position, and divide it again by ${\textstyle N}$ equal parts for the next iteration. The process is repeated until we reach the desired Error Margin   (we used ${\textstyle Error~Margin=0.001,N=150}$ and ${\textstyle L=2cm,3.5cm}$ and 5 cm for translational, rotational and combined motion corrupted cases, respectively). If the process did not converge, then we need to increase ${\textstyle L}$ and the number of iterations.

Figure 13. Flowchart showing the iteration steps to find motion parameters.

6. Results and discussions

The performance of our proposed MBMD system is tested with all the above mentioned abrupt and gradual motion corrupted cases. In the first stage of verification, to validate the accuracy and linearity of the MBMD system, all six parameters of motion are tested separately with all gradual motion variations of motion, as shown in Figure 10a  and Figure 10b . For testing translational motion parameters, the 3D Shepp–Logan phantom is perturbed with a range of axial, lateral, and vertical motion parameters, individually, in three separate test scans.

Similarly, for testing rotational motion parameters, the phantom is perturbed with a range of roll, pitch, and yaw motion parameters, individually, in three separate test scans. For a translational motion case, the range of motion is −6 to 6 mm (step size 1 mm). For a rotational motion case, the range of motion is ${\textstyle -5{\mbox{°}}}$ –${\textstyle 5{\mbox{°}}}$ (step size ${\textstyle 1{\mbox{°}}}$ ). The results of our simulation are given in Table 3  and Table 4 . A comparison of the results with the well known Goldstain et al.  [9] optical sensor-based method is also given in Table 5 , where we have compared the slopes and the square correlation coefficient (${\textstyle R^{2}}$ ) of the best-fit lines through the data points. The results demonstrate that the system is linear, with most slopes being within 1% of unity. The rms deviations of the MBMD data from the best-fit straight lines are less then ${\textstyle 0.01{\mbox{°}}}$ for all rotation angles (${\textstyle \pm 5{\mbox{°}}}$ ) and less than 0.02 mm for the translations (±6 mm). The rms deviation from the actual input is less than ${\textstyle 0.02{\mbox{°}}}$ and 0.03 cm for rotation and translation, respectively. The simulation results of square correlation coefficients (${\textstyle R^{2}}$ ) of the best-fit lines through the data points demonstrate that the MBMD estimated data represent real data values much better than the Goldstein method.

Table 3. Comparisons of actual and estimated motion parameters (gradual translational motion).

Given perturbation (mm)	Estimated translational parameters
	Axial  ${\textstyle t_{xe}}$  (cm)	Lateral  ${\textstyle t_{ye}}$  (cm)	Vertical  ${\textstyle t_{ze}}$  (cm)
−6	−0.59808381	−0.60000249	−0.600003494
−5	−0.49556849	−0.50000177	−0.500001563
−4	−0.39872641	−0.40000117	−0.400002244
−3	−0.29873347	−0.30000069	−0.300001959
−2	−0.20126088	−0.20000034	−0.200001423
−1	−0.09872502	−0.10000006	−0.100001914
6	0.591496241	0.59999740	0.600002707
5	0.506999841	0.49999814	0.499996288
4	0.398761345	0.39999876	0.399997933
3	0.298754976	0.29999927	0.299999372
2	0.20129369	0.19999943	0.199998645
1	0.09875782	0.10000027	0.100000237

Table 4.

Comparisons of actual and estimated motion parameters (gradual rotational motion).

Given perturbation (deg)	Estimated rotational parameters
	Pitch (${\textstyle \vartheta _{e}^{o}}$ )	Roll (${\textstyle \delta _{e}^{o}}$ )	Yaw (${\textstyle \alpha _{e}^{o}}$ )
5	4.999757176	4.999644164	4.999632368
4	3.999668822	3.999715694	3.999856623
3	2.999866406	2.999787158	3.000001165
2	1.999954318	1.999858563	1.999896659
1	1.000011001	0.999929726	0.999914649
−1	−0.999957721	−0.999927445	−0.999956344
−2	−1.999987967	−1.999856576	−2.000110147
−3	−2.999837262	−2.999785288	−2.999971054
−4	−3.999698384	−3.999713789	−3.999880524
−5	−4.999768471	−4.999642071	−4.999851566

Table 5. Simulation results showing linearity and accuracy of MBMD system.

Motion	Slope		${\textstyle R^{2}}$
	Goldstein	MBMD	Goldstein	MBMD
Axial	0.983±0.004	0.9999±0.00337	0.99987	0.99989
Lateral	0.993±0.003	1.0000±0.00019	0.99998	1.00000
Vertical	1.004±0.002	1.0000±0.00030	0.99987	1.00000
Roll	0.990±0.002	0.9999±0.00001	0.99996	0.99999
Pitch	0.904±0.011	1.0000±0.00005	0.99904	1.00000
Yaw	0.991±0.009	1.0000±0.00010	0.99944	0.99995

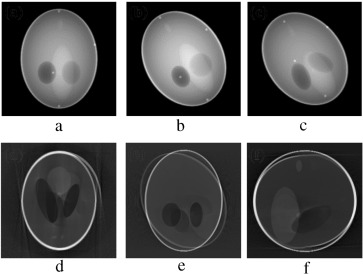
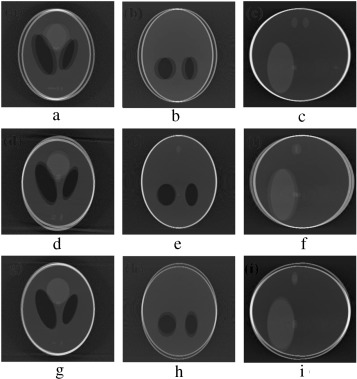
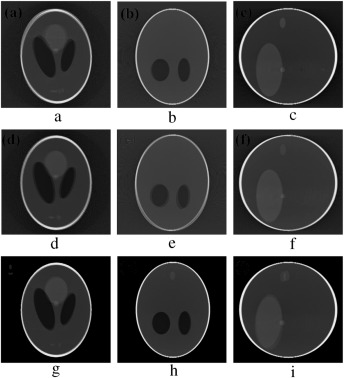
In the second stage of verification, the performance of our proposed marker-based estimator is tested with all the abrupt motion-corrupted cases of Figure 7 , Figure 8  and Figure 9 . Simulation results of actual and estimated motion parameters are listed in Table 6 , Table 7  and Table 8 . Estimated translation motion parameters are within 1.5% of actual values, and estimated rotational parameters are within 0.1% of actual values. Now, to demonstrate the efficacy of our proposed artifact mitigation technique, we apply the estimated motion parameters to the back-projection stage of the MB_FDK algorithm to reconstruct the 3D volume from the above different cases of motion corrupted projection data sets. In Figure 14 , Figure 15  and Figure 16 , we plotted the axial, coronal and sagittal slices taken from the reconstructed volume of different gradual rotational motion corrupted cases and motion artifacts compensated cases, side by side. From these figures, it can be observed that the motion artifacts originated from the gradual variations of motion have significantly been reduced by the MB_FDK approach. In Figure 17 , Figure 18  and Figure 19 , we plotted the axial, coronal and sagittal slices taken from the reconstructed volume of abrupt motion corrupted cases and motion artifacts compensated cases, side by side. From these plots it can also be inferred that the MB_FDK approach has significantly reduced the motion artifacts originated from the abrupt and large variations of motion.

Table 6. Comaprisons of estimated and actual motion parameters (translational motion corrupted case).

	Motion parameters	${\textstyle \beta =200}$	${\textstyle \beta =220}$	${\textstyle \beta =240}$
Estimated	txe  (cm)	0.2015	0.1900	0.1907
	tye  (cm)	5.6112e−010	0.4000	0.4000
	tze  (cm)	−5.1085e−009	−3.8690e−008	0.8000
	Pitch (ϑeo)	5.3459e−007	−8.9305e−007	−6.2537e−006
	Roll (δeo)	−8.4938e−008	8.5328e−006	−2.9586e−005
	Yaw (αeo)	−2.8764e−009	6.6432e−007	−2.4038e−006
Actual	tx  (cm)	0.2	0.2	0.2
	ty  (cm)	0.0	0.4	0.4
	tz  (cm)	0.0	0.0	0.8
	Pitch (ϑo)	0.0	0.0	0.0
	Roll (δo)	0.0	0.0	0.0
	Yaw (αo)	0.0	0.0	0.0

Table 7. Comaprisons of estimated and actual motion parameters (rotational motion corrupted case).

	Motion parameters	${\textstyle \beta =260}$	${\textstyle \beta =270}$	${\textstyle \beta =280}$
Estimated	txe  (cm)	0.0072	−0.0585	−0.0041
	tye  (cm)	3.7148e−009	−1.0912e−006	2.5090e−007
	tze  (cm)	−1.1130e−008	1.5781e−006	−2.0241e−007
	Pitch (ϑeo)	4.4109e−007	29.9988	29.9999
	Roll (δeo)	15.0001	14.9993	14.9999
	Yaw (αeo)	1.1443e−007	5.8719e−006	24.9989
Actual	tx  (cm)	0.0	0.0	0.0
	ty  (cm)	0.0	0.0	0.0
	tz  (cm)	0.0	0.0	0.0
	Pitch (ϑo)	0.0	30.00	30.00
	Roll (δo)	15.00	15.00	15.00
	Yaw (αo)	0.0	0.0	25.00

Table 8. Comaprisons of estimated and actual motion parameters (combined motion corrupted case).

	Motion parameters	${\textstyle \beta =160}$	${\textstyle \beta =180}$	${\textstyle \beta =200}$
Estimated	txe  (cm)	1.0036	0.9945	1.0037
	tye  (cm)	1.7047e−009	2.0000	2.0000
	tze  (cm)	−5.1528e−009	9.5482e−008	1.5000
	Pitch (ϑeo)	2.2245e−007	20.0009	20.0010
	Roll (δeo)	15.0000	14.9999	15.0000
	Yaw (αeo)	5.7943e−008	−2.9808e−007	24.9991
Actual	tx  (cm)	1.0	1.0	1.0
	ty  (cm)	0.0	2.0	2.0
	tz  (cm)	0.0	0.0	1.5
	Pitch (ϑo)	0.0	20.00	20.00
	Roll (δo)	15.00	15.00	15.00
	Yaw (αo)	0.0	0.0	25.00

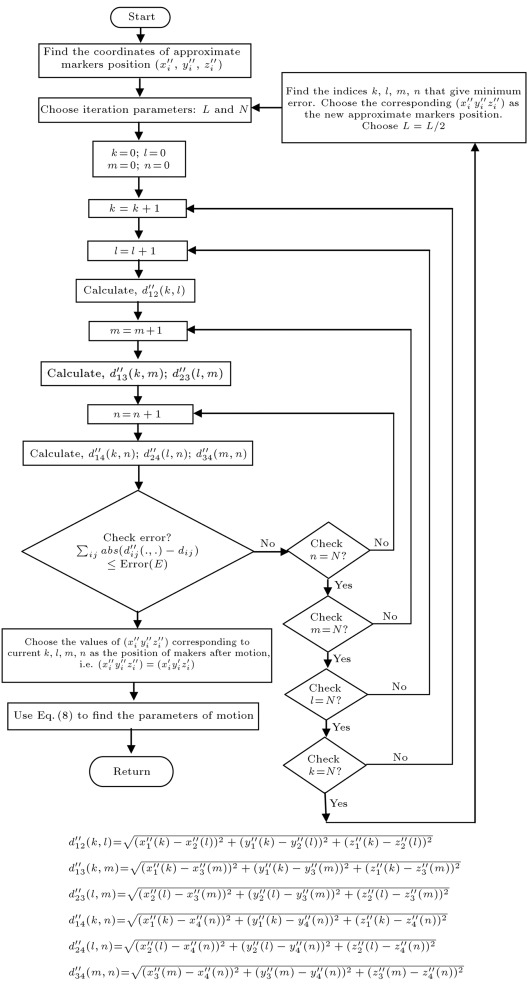
Figure 14. (a–c) Motion-free axial, coronal and sagittal slices. (d–f) Axial, coronal and sagittal slices of the gradual yaw motion corrupted case. (g–i) Same slices after motion compensation.

Figure 15. (a–c) Axial, coronal and sagittal slices of the gradual pitch motion corrupted case. (d–f) Same slices after motion compensation.

Figure 16. (a–c) Axial, coronal and sagittal slices of the gradual roll motion corrupted case. (d–f) Same slices after motion compensation.

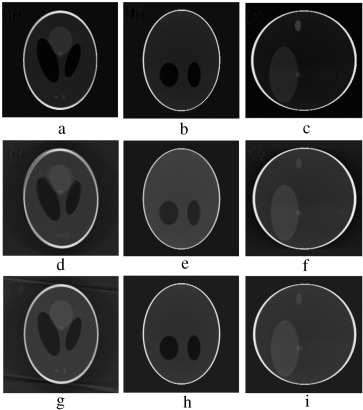
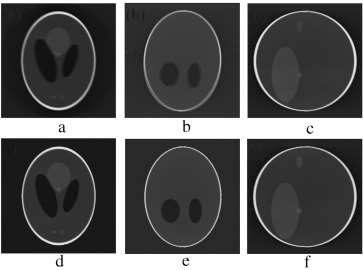
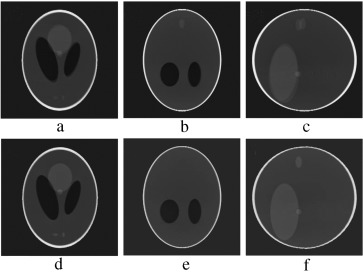
Figure 17. (a–c) Axial, coronal and sagittal slices of the translational motion corrupted case. (d–f) Same slices after motion compensation.

Figure 18. (a–c) Axial, coronal and sagittal slices of the rotational motion corrupted case. (d–f) Same slices after motion compensation.

Figure 19. (a–c) Axial, coronal and sagittal slices of combined rotational and translational motion corrupted case. (d–f) Same slices after motion compensation.

In order to assess the accuracy of our MB_FDK based motion artifacts correction approach, the motion-free study is treated as gold standard. We particularly choose the axial slice at ${\textstyle z=-2.5cm}$ for our comparison. The Mean Square Error (MSE) of the motion artifacts compensated cases and uncompensated cases (normalized) are calculated, with respect to motion-free slices (normalized). Since the abrupt variation of motion produced significant motion artifacts, we chose to compare the MSE of the abrupt motion corrupted case and artifacts compensated case with that of the ideal case. For combined motion corruption cases, the marker-based approach has reduced the MSE in the axial slice from 0.0155 (without motion correction) to 0.0051, i.e. by a factor of 3.0341, while for abrupt translational motion corrupted cases, the MB_FDK has reduced the MSE from 0.0103 (without motion correction) to 0.0035 and for rotational motion corrupted cases from 0.0073 to 0.0047.

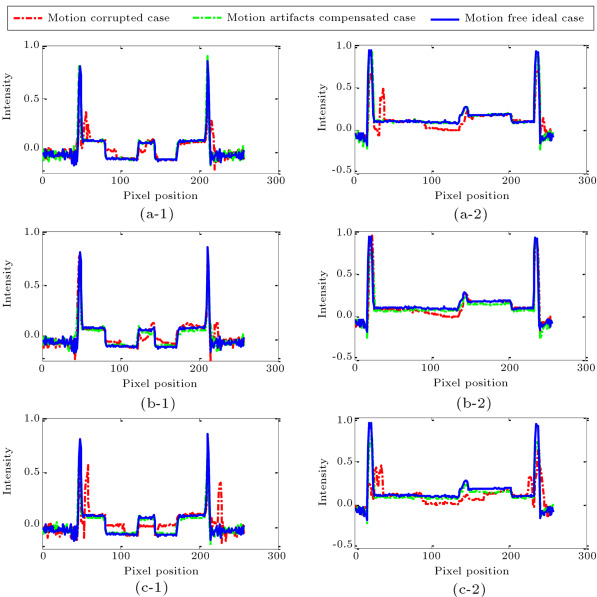
The improvement in accuracy can also be observed in the intensity profiles of translational, rotational and combined motion corrupted cases as shown in Figure 20 (a)–(c), respectively. In the left column of Figure 20 , we compared one pixel wide intensity profiles (where ${\textstyle Y}$ fixed at 129th position and ${\textstyle X}$ varies from 1 to 256) taken from the axial slices (at ${\textstyle z=-2.5cm}$ ) of the motion corrupted cases, artifacts compensated cases and motion-free ideal cases. In the 2nd column, we compared similar one pixel intensity profiles for ${\textstyle X}$ fixed at the 131st position and ${\textstyle Y}$ positions varied from 1 to 256. Figure 20 (a)-1 & (a)-2, (b)-1 & (b)-2 and (c)-1 & (c)-2 represent the translational, rotational and combined motion corrupted cases, respectively. We chose the particular ${\textstyle X}$ and ${\textstyle Y}$ positions so that maximum intensity variation could be observed. From Figure 20 , it is evident that motion artifacts compensation using the marker-based approach has resulted in intensity profiles very close to that of motion-free cases.

Figure 20. Comparisons of one pixel wide intensity profiles taken from the axial slices (at ${\textstyle z=-2.5cm}$ ) of motion-free ideal case, motion corrupted case and MB_FDK based motion artifacts mitigated case. (Left column: intensity profiles at ${\textstyle y=129th}$ position. Right column-intensity profiles at ${\textstyle x=131st}$ position.) (a)-1 & (a)-2 Translational motion corrupted cases is compared with the motion-free ideal case and artifacts compensated case. (b)-1 & (b)-2 Rotational motion corrupted case is compared with the motion-free ideal case and artifacts compensated case. (c)-1 & (c)-2 Combined motion corrupted case is compared with the motion-free ideal case and artifacts compensated case.

7. Conclusion

In this paper, we have designed and implemented a mathematical model of an innovative marker-based system to compensate motion artifacts in a FDK-based 3D cone-beam brain imaging system. Without using any external motion tracking sensor, the MBMD can estimate six degrees-of-freedom of motion parameters for any form of possible head motion. Motion artifacts are compensated for using the MB_FDK algorithm (which uses the estimated motion parameters in the backprojection stage of the FDK algorithm). Simulation results demonstrate that the MB_FDK has the necessary accuracy, resolution, and range. The MB_FDK method could also tackle abrupt and large variations of head motion. Most of the existing 3D CT motion artifacts mitigation techniques (where non-linear curve fitting and linear interpolations are widely used) are validated either on physical phantoms or on humans  [22]  and [23] . Since we had no access to a practical 3D CT scanner system, we could not compare our artifacts mitigation technique with the existing motion artifacts mitigation techniques. Instead, we used synthetic data-set from the Shepp–Logan head phantom which is an acceptable mechanism for evaluating CT algorithms in the medical imaging community. One important advantage of using synthetic data set is that we can generate any form of motion artifacts and compare the motion artifacts compensation techniques with the motion-free ideal data set. Another important advantage of our MB_FDK technique over the existing 3D motion artifacts mitigation techniques is that we do not use any curve fitting or linear interpolation techniques, which often fail to tackle large or abrupt variations of head motion. In future, efforts will be made to implement our marker-based system on practical CT systems.

References

1. [1] N.C. Linney, P.H. Gregson; Organ motion detection in ct images using opposite rays in fan-beam projection systems; IEEE Trans. Med. Imaging, 20 (2001), pp. 1109–1922
2. [2] M.V. Green, J. Seidel, S.D. Stein, T.E. Tedder, K.M. Kempner, C. Jertzman, T.A. Zeffiro; Head movement in normal subjects during simulated PET brain imaging with and without head restraint; J. Nucl. Med., 35 (9) (1994), pp. 1538–1546
3. [3] U. Bhowmik, R.R. Adhami; Correlation and support vector machine based motion artifacts mitigation in 3D computer tomography; J. X-ray Sci. Technol., 20 (2) (2012), pp. 141–160
4. [4] Ritchie, C.J. “Methods for reducing motion artifacts in computed tomography scans of the chest”, Ph.D. Dissertation, Univ. Washington, Seattle (1993).
5. [5] D.P. Boyd, M.J. Lipton; Cardiac computed tomography; Proc. IEEE, 71 (1983), pp. 298–307
6. [6] Crawford, C.R., Godwin, J.D. and Pelc, N.J. “Reduction of motion artifacts in computed tomography”, Proc. IEEE Engineering Medicine and Biology Society , 11, pp. 485–486 (1989).
7. [7] Crawford, C.R. and Pelc, N.J. “Method for reducing motion induced artifacts in projection imaging”, US Patent, 4 994 965 (1991).
8. [8] M. Menke, M.S. Atkins, K.R. Buckley; Compensation methods for head motion detected during PET imaging; IEEE Trans. Nucl. Sci., 43 (1996), pp. 310–317
9. [9] R. Goldstein, E. Margaret, W. Dube; A head motion measurement system suitable for emission computed tomography; IEEE Trans. Med. Imaging, 16 (1) (1997), pp. 17–27
10. [10] R.R. Fulton, S. Eberl, S.R. Meikle, M. Braun; A practical 3D tomographic method for correcting patient head motion in clinical SPECT; IEEE Trans. Nucl. Sci., 46 (3) (1999)
11. [11] Beach, R.D., Gifford, H.C., Shazeeb, S., Bruyant, P.P., Feng, B., Gennert, M.A., Nadella, S. and King, M.A. “Stereo infrared tracking to monitor and characterize rigid-body motion and respiration during cardiac SPECT imaging: progress towards robust clinical utilization”, Proc. of IEEE Nuclear Science Symp. Conf. Rec., 3, pp. 1731–1735 (Oct. 23–29, 2005).
12. [12] S. Sarkar, M.A. Oghabian, I. Mohammadi, A. Mohammadpour, A. Rahmim; A linogram/sinogram cross-correlation method for motion correction in planar and SPECT imaging; IEEE Trans. Nucl. Sci., 54 (1) (2007)
13. [13] L. Weiguo, R. Mackie; Tomographic motion detection and correction directly in Sinogram space; Phys. Med. Biol., 47 (2002), pp. 1267–1284
14. [14] Ens, S., Müller, J., Kratz, B. and Buzug, T.M. “Sinogram-based motion detection in transmission computed tomography”, Proc. 4th European Congress for Medical and Biomedical Engineering , Springer IFMBE Series, 22, pp. 505–508 (2008).
15. [15] A. Rahmim, P. Bloomfield, S. Houle, M. Lenox, C. Michel, K.R. Buckley, T.J. Ruth, V. Sossi; Motion compensation in histogram-mode and list-mode EM reconstruction: beyond the event-driven approach; IEEE. Trans. Nucl. Sci., 51 (2004), pp. 2588–2596
16. [16] Rezvani, N., Arullah, D., Jackson, K., Mosley, D. and Siewerdsen, J. “An open source cone-beam CT reconstruction tool for imaging research”, Poster, AAPM (2007).
17. [17] Bhowmik, U. “Marker-based head motion measurement system to mitigate motion artifacts in 3D cone-beam tomography”, Ph.D. Dissertation, University of Alabama in Huntsville (2012).
18. [18] L. Feldkamp, L. Davix, J. Kress; Practical cone- beam algorithm; J. Opt. Soc. Amer., A1 (1984), pp. 612–619
19. [19] A.C. Kak, M. Slaney; Principle of Tomographic Imaging; IEEE Press (1999)
20. [20] L.A. Shepp, B.F. Logan; The Fourier reconstruction of a head section; IEEE Trans. Nucl. Sci., 21 (1974), pp. 21–43
21. [21] Bhowmik, U. and Adhami, R.R. “Motion artifacts compensation in FDK based 3D cone-beam tomography using correlation of X-ray projections”, Proceedings of The International Conference on Image Processing, Computer Vision & Pattern Recognition , IPCV 2011, pp. 407–413, Las Vegas, USA (July 18–21, 2011).
22. [22] I. Ali, S. Ahmad, N. Alsbou, D.M. Lovelock, S. Kriminski, H. Amols; Correction of image artifacts from treatment couch in cone-beam CT from kV on-board imaging; J. X-ray Sci. Technol., 19 (2011), pp. 321–332
23. [23] Li Liang, Xing Yuxiang, Chen Zhiqiang, Zhang Li, Kang Kejun; A curve-filtered FDK (C-FDK) reconstruction algorithm for circular cone-beam CT; J. X-ray Sci. Technol., 19 (2011), pp. 355–371