Exact solution for thermal boundary layer in Casson fluid flow over permeable shrinking sheet with variable wall temperature and thermal radiation

Abstract

An analysis of thermal boundary layer in the flow of Casson fluid over a permeable shrinking sheet with variable wall temperature and thermal radiation is made. Using similarity transformations, self-similar nonlinear ODEs are obtained from the governing equations. Dual exact solutions of transformed velocity and energy equations are obtained. From the plotted results it can be observed that the temperature inside the boundary layer decreases with Casson parameter and wall mass transfer parameter in first solution and it increases in second solution. Whereas, temperature decreases for larger values of Prandtl number, radiation parameter and power-law exponent for inverse variation along the sheet in both solutions and it enhances with power-law exponent for direct variation along the surface. Also, thermal boundary layer thickness reduces with stronger thermal radiation and inverse variation of wall temperature along the surface and it becomes thicker with direct variation of wall temperature. The rate of heat transfer is less with increasing values of power-law exponent for direct variation along the sheet and for inverse variation it is higher. In graphical representation of temperature field, temperature overshoot is observed in certain cases. So, in some situations heat absorption at surface occurs instead of heat transfer from surface.

Keywords

Thermal boundary layer; Casson fluid; Shrinking sheet; Exact dual solutions; Variable wall temperature; Thermal radiation

1. Introduction

The boundary layer flow due to a shrinking sheet is emerged as an interesting problem in fluid dynamics. The shrinking sheet flows occur in some practical situations, such as, for rising shrinking balloon and it is very useful in packaging of bulk products. The heat transfer plays a vital role in the flow due to shrinking. Miklavčič and Wang [1] demonstrated that the steady flow of Newtonian fluid over a shrinking sheet is possible only when the adequate amount of mass suction through the porous sheet is applied. Actually, the mass suction suppresses the generated vorticity due to shrinking inside the boundary layer and maintains boundary layer flow. Later, Fang and Zhang [2] explained the influence of external magnetic field on the shrinking sheet flow and found that the strong magnetic field guarantees the steady boundary layer flow. Thereafter, the Newtonian fluid flow past a shrinking sheet is investigated by many researchers [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14] and [15] under various physical aspects.

On the other hand, Hayat et al. [16], [17] and [18] discussed the non-Newtonian fluid flows over a shrinking sheet. In reality, the majority of the fluids appeared in the technological processes shows non-Newtonian fluid properties [19], [20], [21], [22], [23], [24] and [25]. So, the studies of non-Newtonian flows are very crucial in technological point of view. Some significant investigations on the shrinking sheet flow of non-Newtonian fluids were reported by Ishak et al. [26] and [27], Yacob et al. [28] and [29] and Rosali et al. [30]. Later, Nadeem et al. [31] investigated MHD flow of a Casson fluid over an exponentially shrinking sheet. Recently, Bhattacharyya et al. [32] and [33] discussed the flow dynamics of Casson fluid over stretching/shrinking sheet with and without effect of magnetic field.

The thermal radiation effect on the boundary layer flow is relevant in many engineering problems because of its applications especially in high temperature engineering processes. Heat radiation effect is important in controlling the quality of the final product as it affects the rate cooling. Due to the above fact, important works on thermal radiation effect had been done by some researchers, viz., Hossain and Takhar [34], Elbashbeshy [35], Mukhopadhyay [36], Mukhopadhyay et al. [37] Akbar et al. [38] and Bhattacharyya [39]. The radiation effects on the boundary layer flow of Newtonian fluid and heat transfer over shrinking sheet were investigated by Bhattacharyya and his co-workers [40], [41] and [42] and Ali et al. [43]. The radiation effect becomes more interesting when the wall temperature distribution is variable. Pal et al. [44] showed the effect of thermal radiation on convection–dissipation heat transfer over stretching/shrinking sheet with variable surface temperature.

But very little is known about the simultaneous effects of radiation and variable wall temperature on the boundary layer flow of non-Newtonian fluid and heat transfer. So, the effects of thermal radiation and the variable surface temperature on the thermal boundary layer of Casson fluid flow over a shrinking sheet are still unknown. The significance of heat radiation effects on the heat flow when wall temperature is variable motivates us to study this paper. Hence, in the present paper the heat transfer in boundary layer flow of non-Newtonian Casson fluid over a shrinking sheet with variable wall temperature and thermal radiation is investigated. Similarity transformations are used and the exact solutions for velocity and temperature distributions are obtained.

2. Flow analysis

Consider the steady two-dimensional incompressible flow of Casson fluid bounded by a shrinking sheet at y = 0, the flow being confined in y > 0. We assume also that the rheological equation of state for an isotropic and incompressible flow of a Casson fluid can be written as follows (see Nakamura and Sawada [45]):

${\tau }_{ij}={\begin{array}{c}\left({\mu }_{B}+p_{y}/{\sqrt {2\pi }}\right)2e_{ij}{\mbox{,}}\quad \pi >{\pi }_{c}\\\left({\mu }_{B}+p_{y}/{\sqrt {2{\pi }_{c}}}\right)2e_{ij}{\mbox{,}}\quad \pi <{\pi }_{c}{\mbox{,}}\end{array}}$

(1)

where μ_B is plastic dynamic viscosity of the non-Newtonian fluid, p_y is the yield stress of fluid, π is the product of the component of deformation rate with itself, namely, π = e_ije_ij, e_ij is the (i, j)-th component of the deformation rate and π_c is critical value of π based on non-Newtonian model.

Under these conditions the boundary layer equations for the steady flow of Casson fluid may be written as follows [33]:

${\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}=$$0{\mbox{,}}$

(2)

$u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}=$$\upsilon \left(1+{\frac {1}{\beta }}\right){\frac {{\partial }^{2}u}{\partial y^{2}}}{\mbox{,}}$

(3)

where u and v are the velocity components in x and y directions respectively, υ is the kinematic fluid viscosity, ρ   is the fluid density, ${\textstyle \beta ={\mu }_{B}{\sqrt {2{\pi }_{c}}}/p_{y}}$ is the non-Newtonian (Casson) parameter.

The boundary conditions for the velocity components are

$u=-U_{w}{\mbox{,}}\quad v=-v_{w}\quad \quad {\mbox{at}}\quad \quad y=$$0{\mbox{;}}u\rightarrow 0\quad \quad {\mbox{as}}\quad \quad y\rightarrow \infty {\mbox{,}}$

(4)

where U_w = cx is shrinking velocity of the sheet with c(>0) being the shrinking constant. Here v_w is the wall mass transfer velocity with v_w > 0 for mass suction and v_w < 0 for mass injection.

The following similarity transformations are introduced:

$\psi ={\sqrt {\upsilon {xU}_{w}}}\quad f(\eta )\quad {\mbox{and}}\quad \eta =$$y{\sqrt {\frac {U_{w}}{\upsilon x}}}{\mbox{,}}$

(5)

where ψ   is the stream function defined in the usual notation as ${\textstyle u={\frac {\partial \psi }{\partial y}}\quad \quad {\mbox{and}}\quad \quad v=}$$-{\frac {\partial \psi }{\partial x}}$ and η is the similarity variable.

In view of the relations in (5), the Eq. (2) satisfies automatically and the Eq. (3) reduces to the following self-similar equation:

$\left(1+{\frac {1}{\beta }}\right)f^{'''}+{ff}^{''}-$$f^{{'}2}=0{\mbox{,}}$

(6)

where primes denote differentiation with respect to η.

The boundary conditions become

$f(\eta )=S{\mbox{,}}f^{'}(\eta )=-1\quad \quad {\mbox{at}}\quad \quad \eta =$$0{\mbox{;}}f^{'}(\eta )\rightarrow 0\quad \quad {\mbox{as}}\quad \quad \eta \rightarrow \infty {\mbox{,}}$

(7)

where S = v_w/(cυ)^1/2 is wall mass transfer parameter with S > 0 (i.e. v_w > 0) for mass suction and S < 0 (i.e. v_w < 0) for mass injection.

3. Heat transfer analysis

To know the behaviour of temperature distribution in the abovementioned flow field, the following energy equation using boundary layer approximation (neglecting viscous dissipation) needs to be solved:

$u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}=$${\frac {\kappa }{\rho c_{p}}}{\frac {{\partial }^{2}T}{\partial y^{2}}}-$${\frac {1}{\rho c_{p}}}{\frac {\partial q_{r}}{\partial y}}{\mbox{,}}$

(8)

where T is the temperature, κ is the thermal conductivity, c_p is the specific heat and q_r is the radiative heat flux.

The appropriate boundary conditions are

$T=T_{w}=T_{\infty }+T_{0}x^{n}\quad \quad {\mbox{at}}\quad \quad y=$$0{\mbox{;}}T\rightarrow T_{\infty }\quad \quad {\mbox{as}}\quad \quad y\rightarrow \infty {\mbox{,}}$

(9)

where T_w is the variable temperature along the sheet, T_∞ is the free stream temperature assumed to be constant, T₀ is a constant depended on the thermal properties of the fluid and n is a power-law exponent.

Using Rosseland approximation for radiation [46], q_r = −(4σ/3k₁)∂T⁴/∂y is obtained, where σ is the Stefan–Boltzmann constant and k₁ is the absorption coefficient. We presume that the temperature variation within the flow is such that T⁴ may be expanded in a Taylor’s series. Expanding T⁴ about T_∞ and neglecting higher order terms we get, T⁴ = 4T³_∞T − 3T⁴_∞.

Now Eq. (8) reduces to

$u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}}=$${\frac {\kappa }{\rho c_{p}}}{\frac {{\partial }^{2}T}{\partial y^{2}}}+$${\frac {16\sigma T_{\infty }^{3}}{3k_{1}\rho c_{p}}}{\frac {{\partial }^{2}T}{\partial y^{2}}}{\mbox{.}}$

(10)

Next, the dimensionless temperature θ is introduced as

$\theta (\eta )={\frac {T-T_{\infty }}{T_{w}-T_{\infty }}}{\mbox{.}}$

(11)

Using the relations in (5) and (11), the Eq. (10) reduces to

$(3R+4){\theta }^{''}+3RPr[f{\theta }^{'}-{nf}^{'}\theta ]=$$0{\mbox{,}}$

(12)

where primes denote differentiation with respect to η, Pr = c_pμ/κ is the Prandtl number and R = κ^∗k₁/4σT_∞³ is the thermal radiation parameter.

The boundary conditions for θ are obtained from (9) as follows:

$\theta (\eta )=1\quad \quad {\mbox{at}}\quad \quad \eta =$$0{\mbox{;}}\theta (\eta )\rightarrow 0\quad \quad {\mbox{as}}\quad \quad \eta \rightarrow \infty {\mbox{.}}$

(13)

4. Solution procedure

Exact closed form solutions of Eqs. (6) and (12) with the boundary conditions (7) and (13) will be obtained.

Let us assume that the solution of Eqs. (6) with (7) has the form [2]${\textstyle f(\eta )=a+{be}^{-\lambda \eta }}$, where a, b and λ(>0) are constants.

Substituting in Eqs. (6) and (7), the following is obtained:

$b={\frac {1}{\lambda }}{\mbox{,}}\quad a=S-{\frac {1}{\lambda }}\quad \quad {\mbox{and}}\quad \quad \lambda =$${\frac {S\pm {\sqrt {S^{2}-4(1+1/\beta )}}}{2(1+1/\beta )}}{\mbox{.}}$

(14)

Now the closed form solution is obtained as

$f(\eta )=S-{\frac {1}{\lambda }}+{\frac {1}{\lambda }}e^{-\lambda \eta }$

${\mbox{i}}.{\mbox{e}}.{\mbox{,}}\quad f(\eta )=S-{\frac {2(1+1/\beta )}{S\pm {\sqrt {S^{2}-4(1+1/\beta )}}}}+$${\frac {2(1+1/\beta )}{S\pm {\sqrt {S^{2}-4(1+1/\beta )}}}}e^{-{\frac {S\pm {\sqrt {S^{2}-4(1+1/\beta )}}}{2(1+1/\beta )}}\eta }{\mbox{.}}$

(15)

So, ${\textstyle f^{'}(\eta )=-e^{-{\frac {S\pm {\sqrt {S^{2}-4(1+1/\beta )}}}{2(1+1/\beta )}}\eta }}$ and ${\textstyle f^{''}(0)=\lambda ={\frac {S\pm {\sqrt {S^{2}-4(1+1/\beta )}}}{2(1+1/\beta )}}}$.

For physically feasible solution of the steady Casson fluid flow λ be positive, the steady flow is possible only if wall mass suction parameter S(>0) satisfies the following:

$S^{2}\geqslant 4(1+1/\beta ){\mbox{.}}$

(16)

The similarity solution is unique if ${\textstyle S^{2}=4(1+1/\beta )}$, it is of dual nature if ${\textstyle S^{2}>4(1+1/\beta )}$ and no similarity solution exists for ${\textstyle S^{2}<4(1+1/\beta )}$.

Substituting the solution of the velocity field, the Eq. (12) becomes

${\theta }^{''}+{\frac {3RPr}{\left(3R+4\right)}}\left(S-\right.$$\left.{\frac {1}{\lambda }}+{\frac {1}{\lambda }}e^{-\lambda \eta }\right){\theta }^{'}+$${\frac {3nRPr}{\left(3R+4\right)}}e^{-\lambda \eta }\theta =$$0{\mbox{.}}$

(17)

Now, a new variable ${\textstyle \epsilon ={\frac {3RPr}{(3R+4){\lambda }^{2}}}e^{-\lambda \eta }}$ is introduced and so the Eq. (17) reduces to

$\epsilon {\frac {{\partial }^{2}\theta }{\partial {\epsilon }^{2}}}+$$(h-\epsilon ){\frac {\partial \theta }{\partial \epsilon }}-$$g\theta =0{\mbox{,}}$

(18)

where ${\textstyle h=1-{\frac {3RPr}{\lambda (3R+4)}}(S-{\frac {1}{\lambda }})}$ and ${\textstyle g=-n}$.

The boundary conditions are

$\theta \left({\frac {3RPr}{(3R+4){\lambda }^{2}}}\right)=$$1\quad \quad {\mbox{and}}\quad \quad \theta (0)=0{\mbox{.}}$

(19)

Therefore, the solution for Eq. (18) is given by

$\theta (\epsilon )=A_{1}M(g{\mbox{,}}h{\mbox{,}}\epsilon )+$$A_{2}{\epsilon }^{1-h}M(g+1-h{\mbox{,}}2-h{\mbox{,}}\epsilon )$

(20)

where M   is the confluent hypergeometric function of the first kind or Kummer function with ${\textstyle A_{1}}$ and ${\textstyle A_{2}}$ arbitrary being constants.

Using (19) and submitting h and g we obtain from (20)

$\theta (\epsilon )={\frac {{\left({\frac {(3R+4){\lambda }^{2}\epsilon }{3RPr}}\right)}^{{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right)}M\left({\frac {3RPr}{(3R+4)\lambda }}(S-{\frac {1}{\lambda }})-n{\mbox{,}}1+{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right){\mbox{,}}\epsilon \right)}{M\left({\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right)-n{\mbox{,}}1+{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right){\mbox{,}}{\frac {3RPr}{(3R+4){\lambda }^{2}}}\right)}}{\mbox{.}}$

Then the temperature solution becomes

$\theta (\eta )={\frac {e^{-{\frac {3RPr}{\left(3R+4\right)}}\left(S-{\frac {1}{\lambda }}\right)\eta }M\left({\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right)-n{\mbox{,}}1+{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right){\mbox{,}}{\frac {3RPr}{(3R+4){\lambda }^{2}}}e^{-\lambda \eta }\right)}{M\left({\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right)-n{\mbox{,}}1+{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right){\mbox{,}}{\frac {3RPr}{(3R+4){\lambda }^{2}}}\right)}}{\mbox{.}}$

(21)

The wall temperature gradient is given as

$-{\theta }^{'}(0)={\frac {3RPr}{\left(3R+4\right)}}\left(S-\right.$$\left.{\frac {1}{\lambda }}\right)+{\frac {3RPr}{(3R+4)\lambda }}\left({\frac {{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right)-n}{1+{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right)}}\right){\frac {M\left(1+{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right)-n{\mbox{,}}2+{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right){\mbox{,}}{\frac {3RPr}{(3R+4){\lambda }^{2}}}\right)}{M\left({\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right)-n{\mbox{,}}1+{\frac {3RPr}{(3R+4)\lambda }}\left(S-{\frac {1}{\lambda }}\right){\mbox{,}}{\frac {3RPr}{(3R+4){\lambda }^{2}}}\right)}}{\mbox{.}}$

5. Results and discussion

To visualize the effects of various physical parameters on the velocity and temperature fields the exact solutions are plotted in some figures.

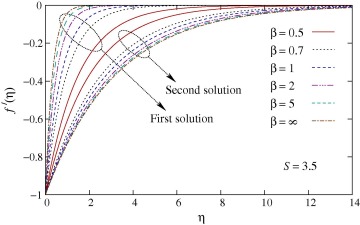
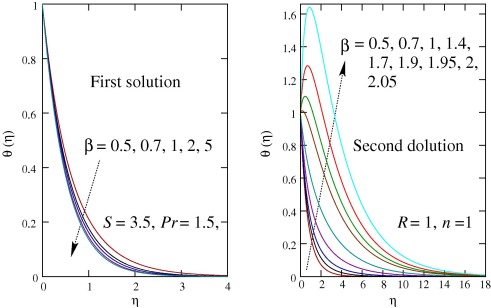
The effects of Casson parameter β on the velocity and temperature profiles are presented in Figs. 1 and 2, respectively. The velocity f′(η) at a point increases with β for first solution and the effect of β is opposite for second solution. Also, the velocity boundary layer thickness decreases with increasing values of β for first solution and it increases for second solution. Similarly, the thermal boundary layer thickness decreases with β for first solution and increases for second solution. Moreover, it is important to note that for large values of β temperature overshoot is observed in second solution. For second solution, it occurs because of the reverse heat flow near the wall, i.e., heat transfers from ambient fluid to the sheet.

Figure 1. Effect of β on the velocity profiles f′(η).

Figure 2. Effect of β on the temperature profiles θ(η).

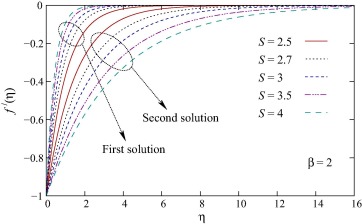
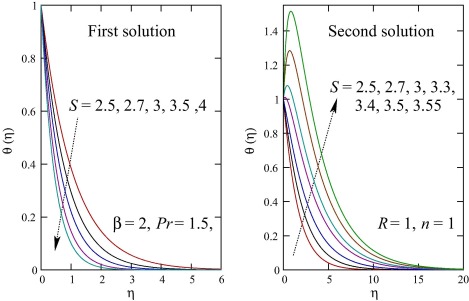
The dimensionless velocity and temperature profiles for various values of wall mass transfer parameter are depicted in Figs. 3 and 4, respectively. Similar to that of Casson parameter, it is observed that for increasing mass suction (S > 0) the velocity and thermal boundary layer thicknesses reduce for first solution and those become thicker for second solution. For stronger mass suction temperature overshoot is obtained in second solution only.

Figure 3. Effect of S on the velocity profiles f′(η).

Figure 4. Effect of S on the temperature profiles θ(η).

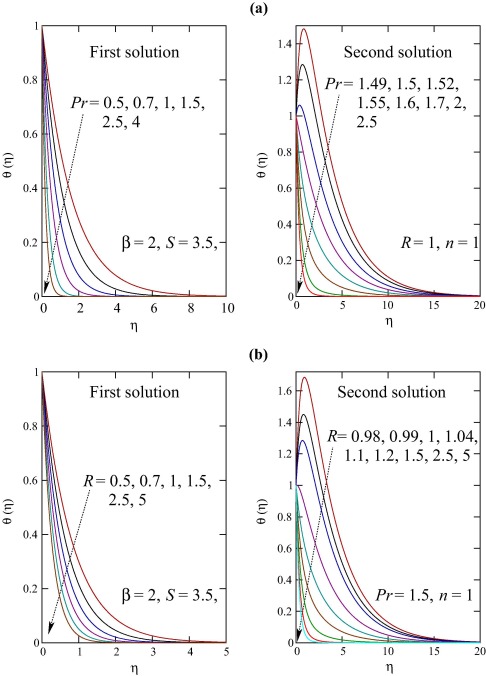
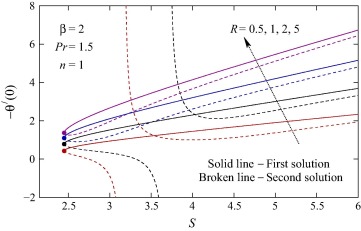
In Fig. 5, the temperature profiles for various values of the Prandtl number Pr and the radiation parameter R are plotted. Due to increase in the Prandtl number the temperature at a point decreases and the thermal boundary layer thickness reduces. Similar effects are noticed for the variation in R. In both cases, it is worth noting that for smaller values of Pr and R thermal overshoots are found in second solution.

Figure 5. (a) Effect of Pr and (b) Effect of R on the temperature profiles θ(η).

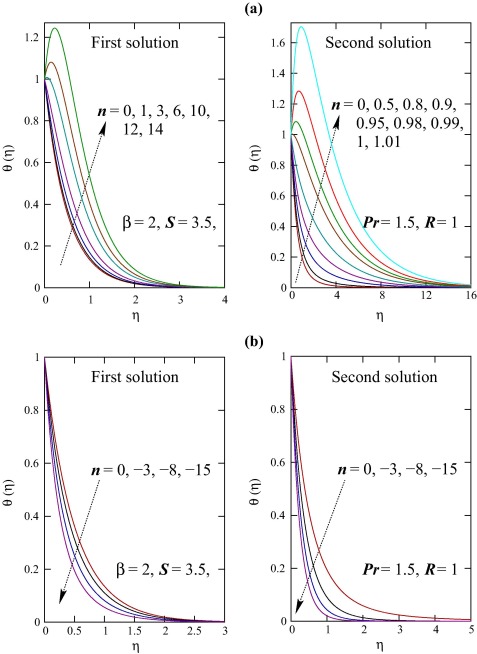
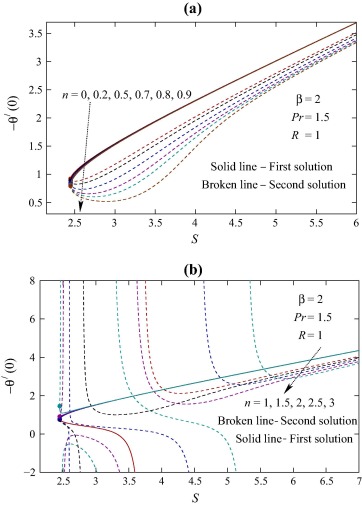
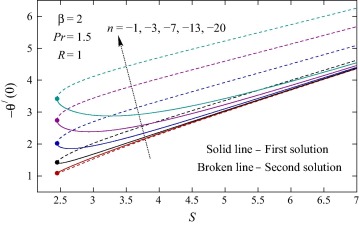
The variations in dimensionless temperature profiles for different values of power-law index n are exhibited in Fig. 6. When the wall temperature directly varies with the distance along the sheet, i.e., when n > 0 the temperature in the flow field increases with n for both solutions. On the other hand, for inverse variation of wall temperature (n < 0) with the distance along the sheet, the temperature decreases with the increasing magnitude of n. More importantly, thermal overshoot is viewed in some situations for direct variation (n > 0) in first solution (for large n) and in addition, for second solution the overshoot is always found (even for small n). The thermal overshoot implies that there heat transfers from the ambient fluid to the surface, i.e., heat absorption.

Figure 6. Effect of n (a. n positive and b. n negative) on the temperature profiles θ(η).

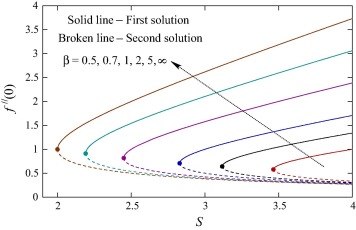
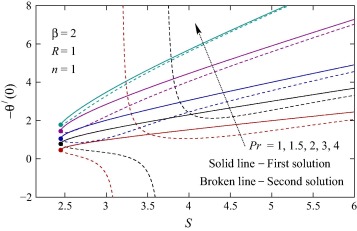
The quantities f″(0) and −θ′(0) related to the local skin friction coefficient and wall temperature gradient (rate of heat transfer) respectively are plotted in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 and also presented in Table 1 and Table 2 for several values involved parameters. The value of f″(0) increases with Casson parameter β and wall mass transfer parameter S for first solution and it decreases for both parameter in second solution ( Fig. 7). Consequently, the local skin friction coefficient increases (decreases) for first (second) solution. The quantity −θ′(0) related to the wall temperature gradient increases with Casson parameter, wall mass transfer parameter, Prandtl number and radiation parameter, which implies that the rate of heat transfer increases. For some values of wall mass transfer parameter the values of −θ′(0) are negative, which means heat absorption occurs in some situations. The heat absorption is found for higher values β and smaller values of Pr and R. Whereas, when β, Pr and R (2, 1.5 and 1 respectively) are fixed, the heat absorption is observed when n ⩾ 1 (approximately). Also, the values of −θ′(0) decrease with increasing values of n (>0, i.e., for direct variation) and the reduction is very prominent for second solution while minor effect is found for first solution. For inverse variation, i.e., for n < 0 the value of −θ′(0) increases with the magnitude of n. In addition to the abovementioned figures, two tables ( Table 1 and Table 2) are presented to show the effects and to demonstrate the current results.

Figure 7. Values of f″(0) against S for various values of β.

Figure 8. Values of −θ′(0) against S for various values of β.

Figure 9. Values of −θ′(0) against S for various values of Pr.

Figure 10. Values of −θ′(0) against S for various values of R.

Figure 11. Values of −θ′(0) against S for various values of n(>0).

Figure 12. Values of −θ′(0) against S for various values of n(<0).

Table 1. Values of f″(0) for various values of β and S.

β	S	3	3.5	4	4.5	5	5.5	6
0.5	1st	–	0.66667	1.00000	1.22871	1.43426	1.62867	1.81650
	2nd	–	0.50000	0.33333	0.27129	0.23241	0.20467	0.18350
1	1st	1.00000	1.39039	1.70711	2.00000	2.28078	2.55425	2.82288
	2nd	0.50000	0.35961	0.29289	0.25000	0.21922	0.19575	0.17712
2	1st	1.57735	2.00000	2.38743	2.75831	3.11963	3.47481	3.82574
	2nd	0.42265	0.33333	0.27924	0.24169	0.21370	0.19186	0.17426
5	1st	2.10391	2.59561	3.06110	3.51277	3.95602	4.39367	4.82737
	2nd	0.39609	0.32105	0.27223	0.23723	0.21065	0.18967	0.17263
∞	1st	2.61803	3.18614	3.73205	4.26556	4.79129	5.31174	5.82843
	2nd	0.38197	0.31386	0.26795	0.23444	0.20871	0.18826	0.17157

Table 2. Values of −θ′(0) for various values of β, Pr, R, n, and S.

β	Pr	R	n	S	3	3.5	4	4.5	5	5.5	6
0.5	1.5	1	1	1st	–	1.15415	1.78223	2.23840	2.64831	3.03443	3.40597
				2nd	–	0.96380	1.31949	1.82664	2.29774	2.72924	3.13457
1				1st	1.27345	1.77480	2.18333	2.56113	2.92315	3.27560	3.62169
				2nd	0.73385	0.95647	1.47881	2.00401	2.45817	2.87018	3.25974
2				1st	1.52040	1.92819	2.30189	2.65958	3.00804	3.35056	3.68898
				2nd	0.32261	−0.70403	2.40233	2.18650	2.54154	2.93656	3.31900
5				1st	1.61279	1.99439	2.35484	2.70420	3.04682	3.38496	3.71995
				2nd	3.22798	1.50380	1.73848	2.15325	2.57610	2.97424	3.35358
∞				1st	1.66269	2.03187	2.38537	2.73016	3.06950	3.40514	3.73817
				2nd	1.38753	1.37235	1.73036	2.17636	2.60288	2.99914	3.37629
2	1			1st	0.99025	1.26781	1.52010	1.76066	1.99449	2.22400	2.45053
				2nd	−0.80381	1.33692	1.06088	1.20424	1.47168	1.77028	2.05714
	2			1st	2.01310	2.55825	3.05796	3.53609	4.00169	4.45919	4.91110
				2nd	1.06965	1.76075	2.44503	3.02919	3.56267	4.06967	4.56004
	3			1st	2.84541	3.68883	4.45800	5.19025	5.90053	6.59641	7.28221
				2nd	2.21600	3.18540	4.04281	4.83436	5.58781	6.31684	7.02906
	4			1st	3.47592	4.63497	5.69264	6.69557	7.66446	8.61041	9.54002
				2nd	3.28267	4.50579	5.59699	6.61968	7.60148	8.55648	9.49280
	1.5	0.5		1st	0.94112	1.20701	1.44838	1.67838	1.90185	2.12113	2.33754
				2nd	−0.87748	1.28930	1.00366	1.12463	1.37276	1.66002	1.93920
		2		1st	2.10581	2.67945	3.20506	3.70779	4.19721	4.67803	5.15289
				2nd	1.19420	1.92145	2.61176	3.21212	3.76638	4.29513	4.80745
		5		1st	2.66733	3.43777	4.14111	4.81156	5.46258	6.10093	6.73044
				2nd	1.95648	2.86601	3.67156	4.40980	5.10981	5.78567	6.44502
		1	0	1st	1.54501	1.94247	2.31174	2.66703	3.01401	3.35553	3.69323
				2nd	1.17786	1.60393	2.02243	2.41719	2.79388	3.15840	3.51452
			0.5	1st	1.53090	1.93439	2.30624	2.66293	3.01076	3.35285	3.69096
				2nd	0.91515	1.35857	1.83537	2.27052	2.67138	3.05198	3.41989
			0.8	1st	1.52413	1.93044	2.30349	2.66083	3.00907	3.35143	3.68974
				2nd	0.66089	1.06784	1.65305	2.16096	2.58978	2.98369	3.36019
			1.5	1st	1.51406	1.92405	2.29874	2.65702	3.00586	3.34866	3.68728
				2nd	1.21697	1.03657	1.36012	1.86543	2.36534	2.80620	3.21008
			2	1st	1.51255	1.92215	2.29688	2.65527	3.00424	3.34716	3.68589
				2nd	0.39617	0.25604	−0.01527	−5.69389	2.68637	2.70790	3.09406
			2.5	1st	1.51663	1.92270	2.29638	2.65438	3.00321	3.34608	3.68481
				2nd	−0.33990	−8.39716	1.86128	1.58297	1.94817	2.47395	2.95479
			−1	1st	1.58224	1.96368	2.32588	2.67735	3.02200	3.36198	3.69862
				2nd	1.53217	1.92956	2.30223	2.65980	3.00822	3.35071	3.68911
			−3	1st	1.68316	2.02275	2.36521	2.70566	3.04353	3.37903	3.71255
				2nd	2.02040	2.38722	2.72287	3.04648	3.36491	3.68109	3.99638
			−7	1st	1.94372	2.18707	2.47789	2.78750	3.10559	3.42774	3.75187
				2nd	2.69807	3.03843	3.34503	3.63955	3.92964	4.21866	4.50821
			−13	1st	2.38533	2.49594	2.70212	2.95568	3.23538	3.53043	3.83488
				2nd	3.43725	3.76094	4.04923	4.32443	4.59458	4.86339	5.13272
			−20	1st	2.90145	2.89304	3.00878	3.19541	3.42562	3.68375	3.96031
				2nd	4.11493	4.42893	4.70643	4.96992	5.22765	5.48348	5.73944

6. Conclusions

The heat transfer in boundary layer flow of Casson fluid past a shrinking sheet with variable wall temperature and thermal radiation effect is investigated. The transformed self-similar nonlinear ordinary differential equations are obtained and then those are solved analytically. It is found that the velocity increases (decreases) with Casson parameter and wall mass transfer parameter for first (second) solution and the effect is opposite for the temperature. Consequently, the thermal boundary layer thickness decreases with Casson parameter and wall mass transfer parameter for first solution and it increases for second solution. On the other hand, the thermal boundary layer thickness reduces with the Prandtl number and the radiation parameter for both solutions. The local skin friction coefficient increases with Casson parameter and wall mass transfer parameter for first solution and the effect is reverse for second solution. The rate of heat transfer decreases with increasing values of power-law exponent for direct variation along the sheet and for inverse variation it increases. Importantly, heat absorption is found for second solution and in certain cases for first solution.

Acknowledgements

The authors express their sincere thanks to the esteemed referees for their constructive suggestions. One of the authors, K. Bhattacharyya gratefully acknowledges the financial support of National Board for Higher Mathematics (NBHM), Department of Atomic Energy, Government of India, for pursuing this work. G.C. Layek would like to acknowledge the assistance and support received from UGC, DSA-I in the Department of Mathematics, The University of Burdwan.

References

1. [1] M. Miklavčič, C.Y. Wang; Viscous flow due a shrinking sheet; Q. Appl. Math., 64 (2006), pp. 283–290
2. [2] T. Fang, J. Zhang; Closed-form exact solution of MHD viscous flow over a shrinking sheet; Commun. Nonlinear Sci. Num. Simulat., 14 (2009), pp. 2853–2857
3. [3] T. Hayat, Z. Abbas, T. Javed, M. Sajid; Three-dimensional rotating flow induced by a shrinking sheet for suction; Chaos, Solitons Fractals, 39 (2009), pp. 1615–1626
4. [4] K. Bhattacharyya; Boundary layer flow and heat transfer over an exponentially shrinking sheet; Chin. Phys. Lett., 28 (2011), p. 074701
5. [5] K. Bhattacharyya, I. Pop; MHD Boundary layer flow due to an exponentially shrinking sheet; Magnetohydrodynamics, 47 (2011), pp. 337–344
6. [6] C.Y. Wang; Stagnation flow towards a shrinking sheet; Int. J. Non-Linear Mech., 43 (2008), pp. 377–382
7. [7] T.R. Mahapatra, S.K. Nandy, A.S. Gupta; Momentum and heat transfer in MHD stagnation-point flow over a shrinking sheet; ASME J. Appl. Mech., 78 (2011), p. 021015
8. [8] K. Bhattacharyya, S. Mukhopadhyay, G.C. Layek; Slip effects on boundary layer stagnation-point flow and heat transfer towards a shrinking sheet; Int. J. Heat Mass Transf., 54 (2011), pp. 308–313
9. [9] Y.Y. Lok, A. Ishak, I. Pop; MHD stagnation-point flow towards a shrinking sheet; Int. J. Num. Meth. Heat Fluid Flow, 21 (2011), pp. 61–72
10. [10] K. Bhattacharyya; Dual solutions in boundary layer stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet; Int. Commun. Heat Mass Transf., 38 (2011), pp. 917–922
11. [11] K. Bhattacharyya; Dual solutions in unsteady stagnation-point flow over a shrinking sheet; Chin. Phys. Lett., 28 (2011), p. 084702
12. [12] H. Rosali, A. Ishak, I. Pop; Stagnation point flow and heat transfer over a stretching/shrinking sheet in a porous medium; Int. Commun. Heat Mass Transf., 38 (2011), pp. 1029–1032
13. [13] K. Bhattacharyya, K. Vajravelu; Stagnation-point flow and heat transfer over an exponentially shrinking sheet; Commun. Nonlinear Sci. Num. Simul., 17 (2012), pp. 2728–2734
14. [14] K. Bhattacharyya; Heat transfer in unsteady boundary layer stagnation-point flow towards a shrinking sheet; Ain Shams Eng. J., 4 (2013), pp. 259–264
15. [15] Y. Khan, A. Hussain, N. Faraz; Unsteady linear viscoelastic fluid model over a stretching/shrinking sheet in the region of stagnation point flows; Sci. Iran., 19 (2012), pp. 1541–1549
16. [16] T. Hayat, T. Javed, M. Sajid; Analytic solution for MHD rotating flow of a second grade fluid over a shrinking surface; Phys. Lett. A, 372 (2008), pp. 3264–3273
17. [17] T. Hayat, Z. Abbas, N. Ali; MHD flow and mass transfer of a upper-convected Maxwell fluid past a porous shrinking sheet with chemical reaction species; Phys. Lett. A, 372 (2008), pp. 4698–4704
18. [18] T. Hayat, S. Iram, T. Javed, S. Asghar; Shrinking flow of second grade fluid in a rotating frame: an analytic solution; Commun. Nonlinear Sci. Num. Simul., 15 (2010), pp. 2932–2941
19. [19] S. Nadeem, R.U. Haq, N.S. Akbar, C. Lee, Z.H. Khan; Numerical study of boundary layer flow and heat transfer of Oldroyd-B nanofluid towards a stretching sheet; PLoS ONE, 8 (2013), p. e69811
20. [20] S. Nadeem, R.U. Haq, N.S. Akbar, Z.H. Khan; MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet; Alex. Eng. J., 52 (2013), pp. 577–582
21. [21] N.S. Akbar, S. Nadeem, R.U. Haq, Z.H. Khan; Numerical solutions of magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet; Indian J. Phys., 87 (2013), pp. 1121–1124
22. [22] R. Mehmood, S. Nadeem, N.S. Akbar; Non-orthogonal stagnation point flow of a micropolar second grade fluid towards a stretching surface with heat transfer; J. Taiwan Inst. Chem. Eng., 44 (2013), pp. 586–595
23. [23] S. Nadeem, R. Mehmooda, N.S. Akbar; Non-orthogonal stagnation point flow of a nano non-Newtonian fluid towards a stretching surface with heat transfer; Int. J. Heat Mass Transf., 57 (2013), pp. 679–689
24. [24] S. Nadeem, R. Mehmood, N.S. Akbar; Nanoparticle analysis for non-orthogonal stagnation point flow of a third order fluid towards a stretching surface; J. Comput. Theor. Nanosci., 10 (2013), pp. 2737–2747
25. [25] S. Nadeem, R.U. Haq, Z.H. Khan; Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles; J. Taiwan Inst. Chem. Eng., 45 (2014), pp. 121–126
26. [26] A. Ishak, Y.Y. Lok, I. Pop; Stagnation-point flow over a shrinking sheet in a micropolar fluid; Chem. Eng. Commun., 197 (2010), pp. 1417–1427
27. [27] A. Ishak, Y.Y. Lok, I. Pop; Non-Newtonian power-law fluid flow past a shrinking sheet with suction; Chem. Eng. Commun., 199 (2012), pp. 142–150
28. [28] N.A. Yacob, A. Ishak, I. Pop; Melting heat transfer in boundary layer stagnation-point flow towards a stretching/shrinking sheet in a micropolar fluid; Comput. Fluids, 47 (2011), pp. 16–21
29. [29] N.A. Yacob, A. Ishak; Micropolar fluid flow over a shrinking sheet; Meccanica, 47 (2012), pp. 293–299
30. [30] H. Rosali, A. Ishak, I. Pop; Micropolar fluid flow towards a stretching/shrinking sheet in a porous medium with suction; Int. Commun. Heat Mass Transf., 39 (2012), pp. 826–829
31. [31] S. Nadeem, R.U. Haq, C. Lee; MHD flow of a Casson fluid over an exponentially shrinking sheet; Sci. Iran., 19 (2012), pp. 1550–1553
32. [32] K. Bhattacharyya, T. Hayat, A. Alsaedi; Analytic solution for magnetohydrodynamic boundary layer flow of Casson fluid over a stretching/shrinking sheet with wall mass transfer; Chin. Phys. B, 22 (2013), p. 024702
33. [33] K. Bhattacharyya, T. Hayat, A. Alsaedi; Exact solution for boundary layer flow of Casson fluid over a permeable stretching/shrinking sheet; ZAMM (J. Appl. Math. Mech.), 94 (2014), pp. 522–528
34. [34] M.A. Hossain, H.S. Takhar; Radiation effect on mixed convection along a vertical plate with uniform surface temperature; Int. J. Heat Mass Transf., 31 (1996), pp. 243–248
35. [35] E.M.A. Elbashbeshy; Radiation effect on heat transfer over a stretching surface; Can. J. Phys., 78 (2000), pp. 1107–1112
36. [36] S. Mukhopadhyay; Effect of thermal radiation on unsteady mixed convection flow and heat transfer over a porous stretching surface in porous medium; Int. J. Heat Mass Transf., 36 (2009), pp. 3261–3265
37. [37] S. Mukhopadhyay, K. Bhattacharyya, G.C. Layek; Steady boundary layer flow and heat transfer over a porous moving plate in presence of thermal radiation; Int. J. Heat Mass Transf., 54 (2011), pp. 2751–2757
38. [38] N.S. Akbar, S. Nadeem, R.U. Haq, Z.H. Khan; Radiation effects on MHD stagnation point flow of nano fluid towards a stretching surface with convective boundary condition; Chin. J. Aeronaut., 26 (2013), pp. 1389–1397
39. [39] K. Bhattacharyya; MHD stagnation-point flow of Casson fluid and heat transfer over a stretching sheet with thermal radiation; J. Thermodyn., 2013 (2013), p. 169674
40. [40] K. Bhattacharyya; Effects of radiation and heat source/sink on unsteady MHD boundary layer flow and heat transfer over a shrinking sheet with suction/injection; Front. Chem. Sci. Eng., 5 (2011), pp. 376–384
41. [41] K. Bhattacharyya, G.C. Layek; Effects of suction/blowing on steady boundary layer stagnation-point flow and heat transfer towards a shrinking sheet with thermal radiation; Int. J. Heat Mass Transf., 54 (2011), pp. 302–307
42. [42] K. Bhattacharyya, S. Mukhopadhyay, G.C. Layek, I. Pop; Effects of thermal radiation on micropolar fluid flow and heat transfer over a porous shrinking sheet; Int. J. Heat Mass Transf., 55 (2012), pp. 2945–2952
43. [43] F.M. Ali, R. Nazar, N.M. Arifin, I. Pop; Unsteady flow and heat transfer past an axisymmetric permeable shrinking sheet with radiation effect; Int. J. Num. Meth. Fluids, 67 (2011), pp. 1310–1320
44. [44] D. Pal, G. Mandal, K. Vajravelu; MHD convection–dissipation heat transfer over a non-linear stretching and shrinking sheets in nanofluids with thermal radiation; Int. J. Heat Mass Transf., 65 (2013), pp. 481–490
45. [45] M. Nakamura, T. Sawada; Numerical study on the flow of a non-Newtonian fluid through an axisymmetric stenosis; ASME J. Biomech. Eng., 110 (1988), pp. 137–143
46. [46] M.Q. Brewster; Thermal Radiative Transfer Properties; John Wiley and Sons (1972)