Abstract
This paper proposes a smart fault detection, classification and location (SFDCL) methodology for transmission systems with multi-generators using discrete orthogonal Stockwell transform (DOST). The methodology is based on synchronized current measurements from remote telemetry units (RTUs) installed at both ends of the transmission line. The energy coefficients extracted from the transient current signals due to occurrence of different types of faults using DOST are being utilized for real-time fault detection and classification. Support vector machine (SVM) has been deployed for locating the fault distance using the extracted coefficients. A comparative study is performed for establishing the superiority of SVM over other popular computational intelligence methods, such as adaptive neuro-fuzzy inference system (ANFIS) and artificial neural network (ANN), for more precise and reliable estimation of fault distance. The results corroborate the effectiveness of the suggested SFDCL algorithm for real-time transmission line fault detection, classification and localization.
Keywords
Remote telemetry units (RTUs) ; Global positioning system (GPS) ; Transmission control center (TCC) ; Discrete orthogonal Stockwell transform (DOST)
1. Introduction
Power system networks across the globe are transforming to smart grids with complex infrastructure. Exhilarating advancements in computational and digital communication technologies have paved the way for smart protection strategies like wide area protection systems (WAPS) for maintaining stable uninterrupted operation of smart grids [1] , [2] and [3] . Real time smart fault detection, classification and localization of the transmission line faults are the vital elements of WAPS. The development of global positioning system (GPS) synchronized remote telemetry units (RTUs) and high speed fiber optic links capable of transferring information over long distances with a sufficient channel capacity has paved the way for communication aided smart strategies for transmission line protection schemes. This has motivated researchers across the globe for developing smart techniques for transmission line protection in recent years [4] , [5] , [6] , [7] and [8] .
Numerous methodologies for detecting, classifying and locating the transmission line faults in real time are reported in literature. Major contributions are reported here. Reference [9] proposed a wavelet multi-resolution analysis for fault classification in transmission lines fed at two ends. Although the methodology can classify the type of fault occurred, the phases involved in the fault were not discriminated. Reference [10] presented a fuzzy set based fault classification methodology for adaptive relaying; however, the proposed method was not capable of classifying LLL faults. Impedance based fault location technique based on one-end measurement was given in reference [11] . But the accuracy of the algorithm was seriously affected by fault resistance. This method calculates the fault location by measuring the impedance seen from the relay end to the fault point. Traveling wave based approach for fault location was presented in reference [12] . Yet the suggested technique was computationally intensive. Real time fault classification and location methodology based on Adaptive Neuro-Fuzzy Inference System (ANFIS) considering the outcome of power swing was proposed in reference [13] . Artificial neural network (ANN) based fault location approach was presented in reference [14] . However tedious training is demanded for the glide slope to achieve acceptable accuracy. Reference [15] proposed a Thevenins equivalent system model based fault location technique. But the proposed approach was not studied for three-phase faults and two-phase to ground faults. The wavelet MRA technique has been taken over in reference [16] for real time transmission line fault detection and classification. Yet the proposed access was limited to fixed fault distances owing to very low sampling frequencies. Besides the approach requires zero-sequence elements to be estimated distinctly. Reference [17] presents a fault location technique based on estimating impedance from voltage and current measurements at the relay point with the aid of mathematical model of the transmission line system. Yet the suggested technique was highly vulnerable to model errors.
This paper proposes a novel smart fault detection, classification and location (SFDCL) methodology for detection, classification and location of all types of fault that occurred on a transmission line fed from both ends. The proposed methodology deploys DOST on synchronously measured current signals from both ends of the transmission line. The current energy coefficients of the transient fault current extracted using DOST are found to have hidden information pertaining to the type and location of the transmission line fault that occurred. Support vector machine (SVM) has been employed for estimating the location of the fault from the exacted features. The most substantial interest of this theme is that the proposed methodology can accurately discover, classify and locate all transmission line faults that occurred at any fault inception angle (FIA). The following sections are organized as follows: Section 2 illustrates the proposed SFDCL methodology with a key insight into time-frequency analysis using DOST. Detection and classification of transmission line fault are discussed in Section 3 . Section 4 depicts the fault location approach with various case studies. Section 5 discusses the results of the case studies conducted and Section 6 concludes the research work presented.
2. Proposed SFDCL methodology
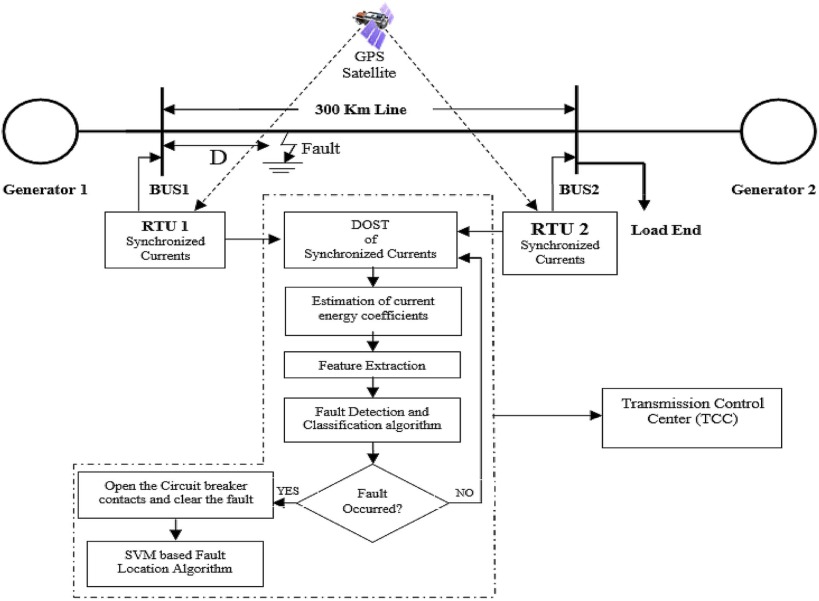
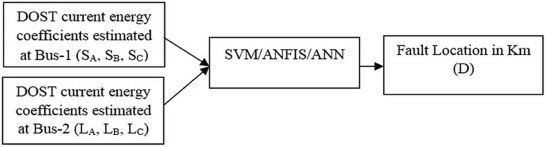
The proposed SFDCL methodology utilizes GPS enabled RTUs at both terminals of the transmission line for acquiring synchronous current measurements. The synchronously measured current signals are transferred to the TCC by means of high speed broadband communication system. Acquired synchronous current samples are analyzed through DOST in TCC and the frequency coefficients extracted are found to have concealed information regarding the type and localization of the fault. This operational procedure has been elucidated in Fig. 1 for better clarity.
|
|
|
Fig. 1. Block diagram of the proposed methodology. |
This section has been arranged as follows: analysis of synchronous current signals using DOST has been illustrated in Section 2.1 .
2.1. Time-frequency analysis using DOST
Founded along the hypothesis presented in reference [18] , [19] and [20] , by applying DOST to the current signals (measured at generator buses) of transmission lines, features have been drawn out. These features are used for fault detection, classification and location on a 300 km transmission line. To shorten the lengths of paper, condensed explanation of DOST has been made.
DOST is an orthogonal set of base functions that localizes the frequency spectrum and retains the advantageous phase properties of the Stockwell transform. Better clarity in the representation can be achieved through transforming N-point input time series transforms to N-point time-frequency representation with the aid of orthonormal transformation. Also, each point of the representation is linearly independent from any other point [18] , [19] and [20] .
Thus DOST representation can be specified as the inner products between a time series h [kT] and the basis functions defined as a part of [kT], as (1)–(2) [19] and [20] .
|
|
( 1) |
|
|
( 2) |
where ν is the frequency variable indicative of the center of a frequency band; β is indicative of frequency resolution; and τ is the time variable indicating the time localization.
2.1.1. Difference between DOST and S-transform (ST)
References [18] , [19] and [20] and [21] clearly define the difference between DOST and ST. Although DOST and the ST establish a time-frequency picture of the input signal, DOST delivers a perfectly non-redundant picture while ST has a very smooth redundant picture. The non-redundancy in the time-frequency framework facilitates DOST to be more efficient than ST. DOST differs in operation from ST such that at lower frequencies of the input signal DOST samples at smaller rate and in higher rate for higher frequencies. The high efficiency and faster operation compared to ST enable the DOST to be a stark alternative for digital relaying in transmission lines.
2.1.2. Feature extraction for fault analysis using DOST
Time-frequency information derived from DOST of the fault current samples has been deployed for the proposed SFDCL methodology in a modish way. The technique of extracting features for a doubly fed transmission line is illustrated in this section. It is assumed that both generator buses are equipped with GPS synchronized RTUs. The synchronized current measurements sampled at 5 kHz from both generator buses (BUS1 and BUS 2) are passed through DOST for feature extraction. From the three dimensional information of current frequency-time-magnitude data gathered from DOST, the data related to second and third harmonies are filtered away. Recent research findings [13] and [21] substantiate the dominancy of the second and third harmonics in the current waveform during transmission line faults. This is the motivation to extract second and third harmonic data from DOST of fault currents.
Equation (3) gives the formula for calculating DOSTAvg value, where DOST100 and DOST150 are the sum of fault currents, energy coefficients obtained from second and third harmonic component of the DOST matrix for the respective phase. Using this, the respective DOSTavg values are can be calculated for phases A, B and C at both buses (BUS 1 and BUS 2). DOSTnormal stands for the sum of the current energy coefficients obtained from fundamental component of the current signal during normal operating conditions for the respective phase. The DOSTnormal values can be calculated for phases A, B and C at both buses during normal operating conditions. Using Equations (4) , (5) , (6) , (7) , (8) and (9) SA , SB , SC , LA , LB and LC values are calculated. From the features extracted through DOST, current energy coefficients (SA , SB , SC , LA , LB , and LC ) are useful in real time fault detection and classification.
|
|
( 3) |
|
|
( 4) |
|
|
( 5) |
|
|
( 6) |
|
|
( 7) |
|
|
( 8) |
|
|
( 9) |
3. Detection and classification of transmission line faults
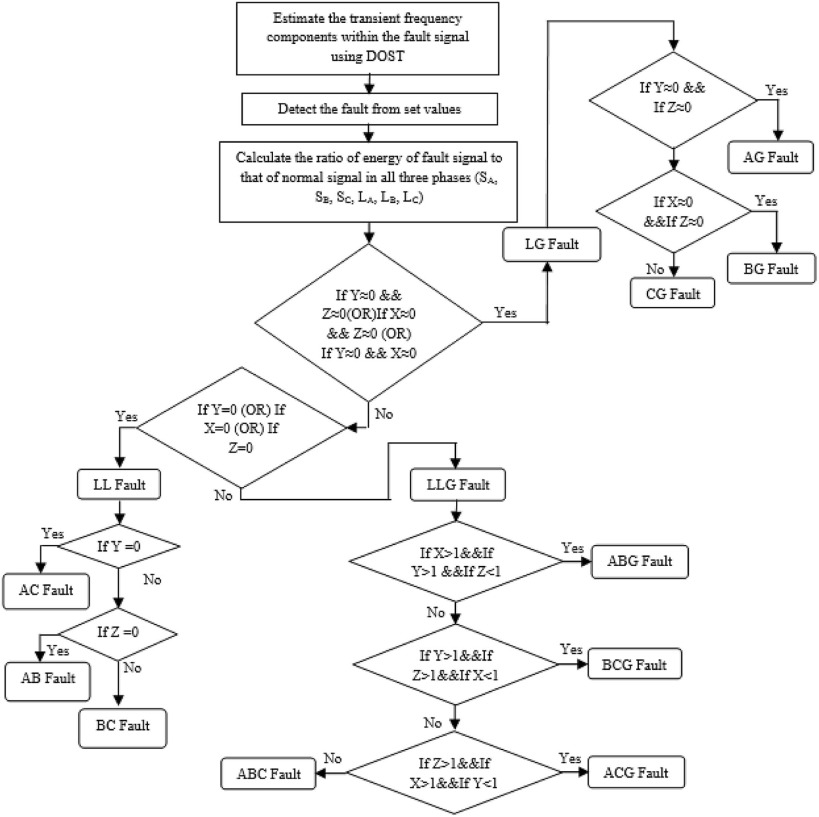
The proposed SFDCL methodology deploys the current energy coefficients, as illustrated in the preceding section, for real time transmission line fault detection and classification. The methodology of fault detection and classification has been presented as a flowchart in Fig. 2 . The methodology starts with estimation of frequency components within the fault signal using DOST. Fault detection is achieved with the help of set values as described in the following sections. Fault classification is achieved using the ratio of energy of three-phase fault signals to that of normal three-phase signal. These ratios are denoted as given in Equations (4) , (5) , (6) , (7) , (8) and (9) . The notations adopted in the flowchart are calculated as given in equations (10) , (11) and (12) . The classification of each type of fault is illustrated with case studies in the following section.
|
|
( 10) |
|
|
( 11) |
|
|
( 12) |
|
|
|
Fig. 2. Flow chart of proposed fault detection and classification methodology using DOST. |
3.1. Single line to ground (L-G) faults
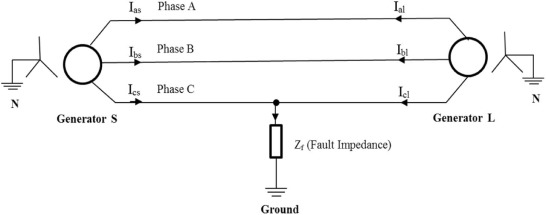
A 300 km long three-phase transmission line fed at both ends by generators S and L is shown in Fig. 3 . Ias , Ibs and Ics are the line currents from generator-S. Similarly that from generator-L are Ial , Ibl and Icl . An LG fault condition in C-phase (CG fault) with a fault impedance of Zf is created as shown in Fig. 3[22] , [23] , [24] and [25] .
|
|
|
Fig. 3. CG fault. |
During the fault condition,
|
|
( 13) |
Therefore . These conditions are taken to classify CG fault, as applied in the algorithm indicated in Fig. 2 . In a similar way for BG fault, . For AG fault, .
3.2. Line to line (L-L) faults
The 300 km transmission line shown in Fig. 3 is opted in this case study but with LL fault. L-L fault involving “B” and “C” phases (BC fault) with a fault impedance of Zf is shown in Fig. 4 . At the fault point, the subsequent conditions must be fulfilled.
|
|
( 14) |
|
|
|
Fig. 4. BC fault. |
Therefore, , so . These conditions are taken to classifying BC fault, as applied in the algorithm indicated in Fig. 2 . Similarly, for AB fault, . The same rule applies for CA fault.
3.3. Double line to ground (L-L-G) faults
The 300 km transmission line shown in Fig. 3 is opted in this case study but with LLG fault. LLG fault involving phases “B” and “C” (BCG fault) through the fault impedance Zf is shown in Fig. 5 . At the fault point, the subsequent conditions must be fulfilled.
|
|
( 15) |
|
|
|
Fig. 5. BCG fault. |
Therefore, X is minimum for BCG fault and hence this condition is taken for classifying BCG fault as given in the algorithm shown in Fig. 2 . Similarly for CAG and ABG faults are classified, using the fault classification algorithm as shown Fig. 2 .
3.4. Fault classification algorithm
It is confirmed through several case studies [7] , [8] , [13] and [14] that the FIA has considerable influence on the phase current and therefore on DOST output. As the signals are periodic, the effect of FIA ranging from 0° to 180° has been studied in this paper. The proposed fault classification algorithm proceeds as follows.
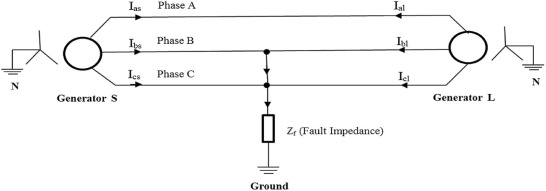
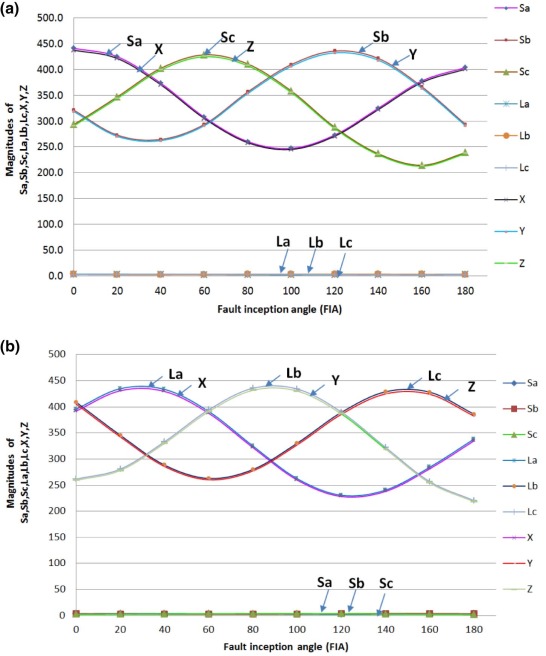
When any of the conditions (X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0 (or) X = 0 (or) Y = 0 (or) Z = 0) are satisfied, then the fault can be either LG (or) LL fault. This can be certified from mathematical analysis as shown in previous sections and simulation results as indicated in Fig. 6 (a) and Fig. 6 (b).
|
|
|
Fig. 6. (a) Influence of fault inception angle for AG Fault at 10 km and (b) influence of fault inception angle for AG fault at 290 km. |
If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0) is satisfied, then it can be concluded as LG fault. Fig. 6 (a) shows the influence of FIA for AG (LG) fault at 10 km. Fig. 6 (b) shows the influence of the FIA for LG (AG) fault at 290 km. From the figures, it is detected that Y ≅ 0 & Z ≅ 0, then it indicates that it is an AG fault. In a similar fashion, if X ≅ 0 and Y ≅ 0, then it is LG (CG) fault, and if Z ≅ 0 and X ≅ 0, then it is LG (BG) fault. Both Fig. 6 (a) and Fig. 6 (b) present the efficiency of the proposed algorithm for faults at two ends of the transmission line. Since the methodology is working at both ends, it will be effectively working for any distance between the two buses of the transmission line.
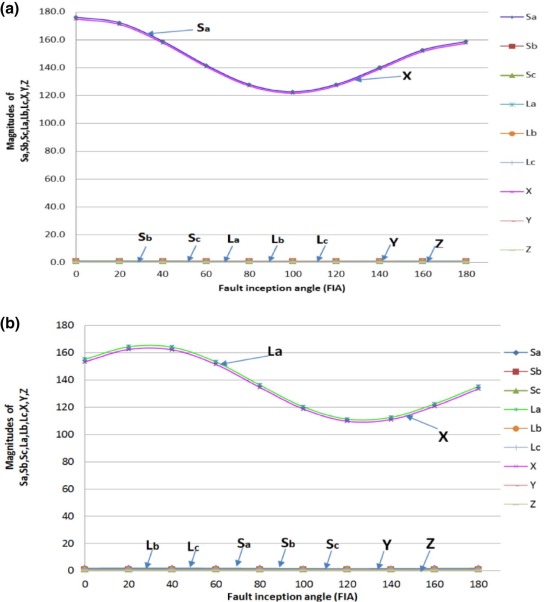
If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0) is not satisfied but if one of the conditions (i.e. X = 0 (or) Y = 0 (or) Z = 0) is satisfied, then it is LL fault. Fig. 7 (a) and Fig. 7 (b) show the influence of the FIA for LL fault at a length of 10 km and 290 kilometer. Simulation results shown in both figures indicate that the value of Z = 0 and X, Y ≠ 0 on both ends of the transmission line. Because both X and Y are not equal to zero and Z = 0, then it indicates that it is an LL (AB) fault. In a like fashion, if X equal to zero, then it is BC fault and if Y equal to zero then it is CA fault.
|
|
|
Fig. 7. (a) Influence of fault inception angle for AB fault at 10 km and (b) influence of fault inception angle for AB fault at 290 km. |
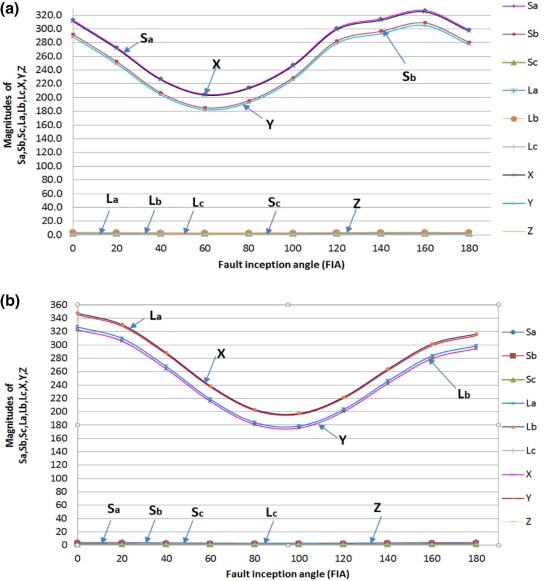
If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0 (or) X = 0 (or) Y = 0 (or) Z = 0) is not satisfied, then it can be decided as LLG (or) LLL fault. Discrimination between these two types of faults is such that, if any one of the conditions (X > 1, Y > 1 and Z < 1 (or) Y > 1, Z > 1 and X < 1 (or) Z > 1, X > 1 and Y < 1) is satisfied, then it can be categorized as an LLG fault. The effect of the FIA on LLG (ABG) fault involving phase ‘an’ at a distance of 10 km and 290 km is shown in Fig. 8 (a) and Fig. 8 (b) respectively. From the mathematical analysis given in the previous sections and simulation results, it is seen that X, Y, Z ≠ 0 and if X > 1, Y > 1 and Z < 1. It indicates the presence of ABG fault. Similarly X, Y, Z ≠ 0 and Y > 1, Z > 1 and X < 1, then it shows the presence of BCG fault. If X, Y, Z ≠ 0 and Z > 1, X > 1 and Y < 1 then it shows the presence of CAG fault. If none of the above conditions are achieved, then it can be considered as LLL (ABC) fault.
|
|
|
Fig. 8. (a) Influence of fault inception angle for ABG fault at 10 km and (b) influence of fault inception angle for ABG fault at 290 km. |
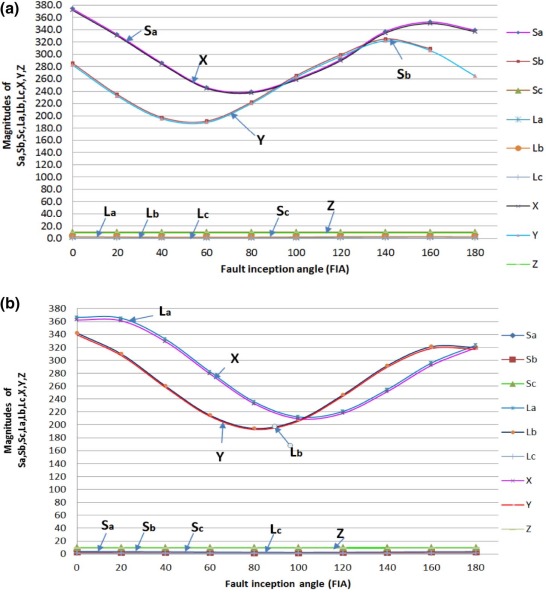
If X, Y, Z ≠ 0 and X > 1, Y > 1 and Z > 1, then it is LLL (ABC) fault. The outcome of the FIA on LLL (ABC) fault involving phase ‘a’ and ‘b’ at 10 km and 290 km distances is as presented in Fig. 9 (a) and Fig. 9 (b). From the mathematical analysis applied in the previous sections and simulation effects, it is visualized that in a case having X, Y, Z ≠ 0 and X > 1, Y > 1 and Z > 1, it shows the presence of LLL (ABC) fault. In a similar manner, all faults can be categorized using the suggested classification technique.
|
|
|
Fig. 9. (a) Influence of FIA for ABC fault at 10 km and (b) influence of FIA for ABC fault at 290 km. |
4. Location of transmission line fault
The current energy coefficients estimated from current measurements are observed to have hidden information related to the location of the transmission line fault. Numerous simulation studies have been done on a 300 kilometer transmission line by creating faults at every 5 km one at a time in different FIAs and different fault impedances to generate a data set for training SVM. Block diagram representation of proposed fault location methodology is shown in Fig. 10 .
|
|
|
Fig. 10. Block diagram of proposed fault location methodology. |
4.1. Fault location identification using the SVM fault location system
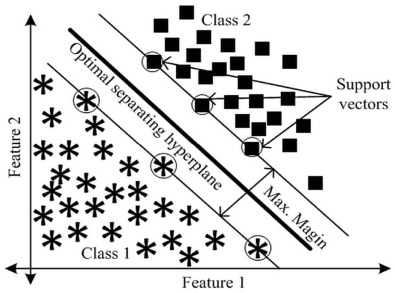
The SVM fault location system has been deployed for estimating the position of the fault that occurred on the transmission line from the features extracted through DOST. SVM is a statistical learning theory based computational learning method in which input vectors are nonlinearly mapped into a high dimensional feature space where an optimal hyper plane is found out to classify the input parameters. This hyperplane maximizes the generalization power of the classifier. For linearly separable data, this hyperplane that separates the data can be determined as in (16) [21] , [26] , [27] and [28] .
|
|
( 16) |
where “x” is the n-dimensional input samples, “w” is the n-dimensional vector and “b” is a scalar. The optimal separating hyperplane that maintains maximum margin from the nearest data can be found by working out the following convex quadratic optimization problem as given in (17).
Minimize:
|
|
Subject to:
|
|
( 17) |
where ξj is the slack variable and C is the error penalty. Classification of input data ready by means of optimal separating hyperplane is illustrated in Fig. 11 .
|
|
|
Fig. 11. SVM classification of data based on optimal hyperplane. |
For nonlinear classification tasks the data to be classified are mapped onto a high-dimensional feature space using kernel function. In this high-dimensional feature space the linear classification is possible. A nonlinear vector function, , is utilized to map the “n”-dimensional input vector “x” into the “m” dimensional feature space. The linear decision function in dual form is given by (10) [21] , [27] and [28] .
|
|
( 18) |
For estimating fault location, the SVM fault location system has to be trained with input–output data set. The current energy coefficients acquired through DOST (SA , SB , SC, LA , LB and LC ) for numerous fault locations with various FIAs on a 300 km transmission line form the input data set. The location of the fault corresponding to each set of data in the input data set forms the output data set. Multi-class was opted with a kernel function set as ‘rbf’ (i.e. radial basis function) and sigma as 0.8. After successful training, the SVM fault location system can accurately predict the location of the fault for any type of fault that occurred on the transmission line.
4.2. Fault location identification using ANFIS fault location system
ANFIS fault location system has been utilized for calculating the location of the fault that occurred on the transmission line from the features extracted through DOST. ANFIS syndicates the professional human knowledge in terms of fuzzy rules and adaptive learning capability through neural networks [22] and [23] . ANFIS fault location system learns the transmission line system using fuzzy inference system (FIS) from the input–output data of system response. The least square method is utilized for adjusting membership functions (MF) for linear systems, and the same is achieved through back-propagation descent method for nonlinear systems. This paper employs FIS model developed by Takagi–Sugeno–Kang, known as the Sugeno model using the input–output data [22] , [23] , [24] and [25] .
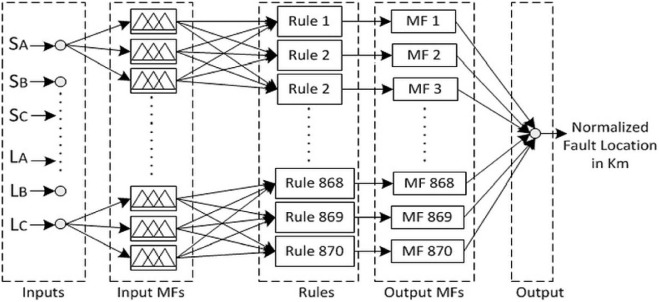
The current energy coefficients acquired through DOST (SA , SB , SC, LA , LB , and LC ) form the input data set for ANFIS fault location system. From this input data, the output variable is predicted, which is the distance of fault location in kilometers. The input–output dataset has been generated from extensive simulation studies performed on a 300 km transmission line by creating all types of faults one at a time with different locations and inception angles of the fault. The ANFIS fault location system is developed for the input–output dataset generated through case studies using hybrid learning method as an optimization tool. The trained model generated 870 rules and MFs from the input–output database. After successful training of the ANFIS fault location system using the input–output database, any fault location within 300 kilometer of the transmission line can be computed for any type of a fault condition. The architecture of the proposed scheme is depicted in Fig. 12 . The architecture consists of input set, input membership functions, rules, output membership functions and output set as shown in Fig. 12 . Membership function defines how each point in input space is mapped to membership value [22] , [23] , [24] and [25] . The input membership function is quantized into three linguistic variables such as LOW (L), MEDIUM (M), and HIGH (H). From 870 rules, the same number of output MFs are generated, which are connected to a common output node that delivers normalized fault location in kilometers.
|
|
|
Fig. 12. Architecture of proposed ANFIS fault location system. |
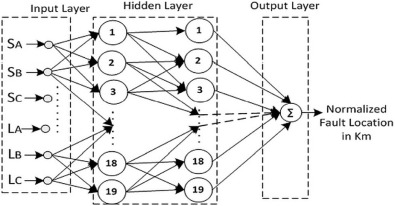
4.3. Fault location identification using the ANN fault location system
An ANN fault location system is likewise aimed to estimate the location of fault that occurred on a 300 km transmission line. Features extracted from DOST of fault current samples have been utilized for training the ANN fault location system. ANN consists of a number of processing units called “neurons” in different layers to achieve high computational power [29] and [30] . The same input–output data set utilized in training ANFIS fault location system has been employed for training ANN fault location system. A feed-forward neural network with one input layer consisting of six neurons, one output layer with one neuron and two hidden layers that consist of 19 neurons each has been opted for the study [30] and [31] . This structure has been chosen based on empirical knowledge acquired from training and testing of various neural network architectures. The current energy coefficients derived from DOST and the fault distance (normalized between zero and one by dividing the actual distance by 300) form the input and target respectively. The ANN fault location system is then trained for the input-target set using back-propagation algorithm, and the error was found to be decreased after 3,000 epochs. After completion of model training, the ANN fault location system is ready to calculate any type of fault condition within 300 km of the transmission line. The architecture of the proposed ANN fault location system is depicted in Fig. 13 .
|
|
|
Fig. 13. Architecture of proposed ANN fault location system. |
5. Results and discussion
DOST based fault classification methodology and SVM assisted fault location approach discussed in the preceding sections are studied on a 400 kV, 3-phase, 300 km transmission line fed by generators at both ends. The generators are modeled with positive and negative sequence source impedances of (0.45 + 0.5j Ω) per phase and a zero sequence source impedance of (0.675 + 0.75j Ω) per phase. The transmission line is modeled with positive and negative sequence values of resistance, inductance, and capacitance of 2.34Ω, 95.10mH, and 1.24µF per phase per 100 km, respectively. The zero sequence values of the same parameters are taken to be 38.85Ω, 325.08mH, and 0.845µF, respectively. Real and reactive power loading in the transmission line is taken to be 1,000 MW and 40 MVAR respectively [13] .
The system has been developed and simulated in a MATLAB/SIMULINK environment. All types of faults have been created one at a time at numerous locations in the transmission line at different FIA and fault impedance and the fault currents are acquired at a sampling frequency of 5 kHz. The sampled current signals are then analyzed using DOST and current energy coefficients (SA , SB , SC , LA , LB and LC ) for each phase are calculated. The estimated coefficients are then transferred to fault classification and fault location algorithms. The results of the case studies performed for validating fault classification methodology are exemplified in Table 1 , Table 2 , Table 3 and Table 4 . The efficacy of the proposed fault location methodology achieved in the case studies has been exemplified in Table 5 . A comparative study has been performed to validate the superiority of SVM over ANN and ANFIS for estimating the fault distance.
| Fault type | Distance in km | FIA | SA | SB | SC | LA | LB | LC | If Y ≈ 0 && Z ≈ 0 (or) X ≈ 0 && Z ≈ 0 (or) Y ≈ 0 && X ≈ 0 (Y/N) | If Y ≈ 0 && Z ≈ 0 (Y/N) | If X ≈ 0 && Z ≈ 0 (Y/N) | If Y ≈ 0 && X ≈ 0 (Y/N) | Type of fault classified |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AG | 30 | 0 | 44.7 | 1.1 | 0.9 | 1.21 | 1.03 | 0.93 | Y | Y | N | N | LG (AG) |
| AG | 60 | 20 | 15.56 | 1.04 | 0.96 | 1.32 | 1.01 | 0.97 | Y | Y | N | N | LG (AG) |
| AG | 90 | 40 | 8.02 | 1.03 | 0.97 | 1.50 | 1.00 | 0.99 | Y | Y | N | N | LG (AG) |
| AG | 120 | 60 | 6.94 | 1.02 | 0.98 | 1.77 | 0.99 | 1.00 | Y | Y | N | N | LG (AG) |
| AG | 150 | 80 | 5.42 | 1.01 | 0.99 | 2.18 | 0.98 | 1.00 | Y | Y | N | N | LG (AG) |
| AG | 180 | 100 | 2.6 | 1.00 | 1 | 5.94 | 0.98 | 1.02 | Y | Y | N | N | LG (AG) |
| AG | 210 | 120 | 2.15 | 0.99 | 1.01 | 7.60 | 0.97 | 1.02 | Y | Y | N | N | LG (AG) |
| AG | 240 | 140 | 1.9 | 0.98 | 1.02 | 9.27 | 0.96 | 1.03 | Y | Y | N | N | LG (AG) |
| AG | 270 | 160 | 1.76 | 0.95 | 1.05 | 30.0 | 0.94 | 1.07 | Y | Y | N | N | LG (AG) |
| AG | 300 | 180 | 2.01 | 0.84 | 1.27 | 622.8 | 0.86 | 1.31 | Y | Y | N | N | LG (AG) |
| Fault type | Distance in km | FIA | SA | SB | SC | LA | LB | LC | If Y ≈ 0 &&Z ≈ 0 (or) X ≈ 0&&Z ≈ 0 (or) Y ≈ 0&&X ≈ 0 (Y/N) | If Z = 0 (or) X = 0 (or) Y = 0 (Y/N) | If Z = 0 (Y/N) | If X = 0 (Y/N) | If Y = 0 (Y/N) | Type of fault classified |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AB | 30 | 0 | 109.8 | 97.6 | 1 | 2.191 | 4.033 | 1 | N | Y | Y | N | N | LL (AB) |
| AB | 60 | 20 | 38.21 | 31.04 | 1 | 2.312 | 4.375 | 1 | N | Y | Y | N | N | LL (AB) |
| AB | 90 | 40 | 18.2 | 13.14 | 1 | 2.425 | 4.742 | 1 | N | Y | Y | N | N | LL (AB) |
| AB | 120 | 60 | 10.56 | 9.7 | 1 | 2.714 | 5.335 | 1 | N | Y | Y | N | N | LL (AB) |
| AB | 150 | 80 | 7.356 | 4.274 | 1 | 3.632 | 7.653 | 1 | N | Y | Y | N | N | LL (AB) |
| AB | 180 | 100 | 5.951 | 3.402 | 1 | 8.103 | 9.702 | 1 | N | Y | Y | N | N | LL (AB) |
| AB | 210 | 120 | 5.243 | 3.069 | 1 | 12.38 | 16.9 | 1 | N | Y | Y | N | N | LL (AB) |
| AB | 240 | 140 | 4.832 | 2.927 | 1 | 29.43 | 35.67 | 1 | N | Y | Y | N | N | LL (AB) |
| AB | 270 | 160 | 4.388 | 2.688 | 1 | 92.26 | 102.5 | 1 | N | Y | Y | N | N | LL (AB) |
| AB | 300 | 180 | 3.904 | 2.365 | 1 | 759.2 | 787.5 | 1 | N | Y | Y | N | N | LL (AB) |
| Fault type | Distance in km | FIA | SA | SB | SC | LA | LB | LC | If Y ≈ 0 && Z ≈ 0 (or) X ≈ 0 && Z ≈ 0 (or) Y| ≈ 0 && X ≈ 0 (Y/N) | If Z = 0 (or) X = 0 (or) Y = 0 (Y/N) | If X > 1 && Y > 1 && Z < 1 (Y/N) | If Y > 1 && Z > 1 &&X < 1 (Y/N) | If X > 1 && Z > 1 && Y < 1 (Y/N) | Type of fault classified |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ABG | 30 | 0 | 123.4 | 93.1 | 1 | 2.741 | 3.421 | 0.98 | N | N | Y | N | N | LLG (ABG) |
| ABG | 60 | 20 | 42.96 | 29.31 | 1 | 2.999 | 3.653 | 0.991 | N | N | Y | N | N | LLG (ABG) |
| ABG | 90 | 40 | 20.21 | 12.58 | 1 | 3.253 | 3.918 | 0.995 | N | N | Y | N | N | LLG (ABG) |
| ABG | 120 | 60 | 11.48 | 6.83 | 1 | 3.686 | 4.457 | 0.997 | N | N | Y | N | N | LLG (ABG) |
| ABG | 150 | 80 | 7.643 | 4.669 | 1 | 4.728 | 6.777 | 0.998 | N | N | Y | N | N | LLG (ABG) |
| ABG | 180 | 100 | 5.896 | 3.69 | 1 | 8.329 | 8.914 | 0.992 | N | N | Y | N | N | LLG (ABG) |
| ABG | 210 | 120 | 5.058 | 3.576 | 1 | 13.84 | 16.31 | 0.992 | N | N | Y | N | N | LLG (ABG) |
| ABG | 240 | 140 | 4.589 | 3.357 | 1 | 31.67 | 35.43 | 0.998 | N | N | Y | N | N | LLG (ABG) |
| ABG | 270 | 160 | 4.176 | 3.055 | 1 | 98.18 | 103.3 | 0.997 | N | N | Y | N | N | LLG (ABG) |
| ABG | 300 | 180 | 3.641 | 2.737 | 1 | 806.9 | 897.7 | 0.978 | N | N | N | Y | N | LLG (ABG) |
| Fault type | Distance in km | FIA | SA | SB | SC | LA | LB | LC | If Y ≈ 0 && Z ≈ 0 (or) X ≈ 0 && Z ≈ 0 (or) Y ≈ 0 && X ≈ 0 (Y/N) | If Z = 0 (or) X = 0 (or) Y = 0 (Y/N) | If X > 1 && Y > 1 && Z < 1 (Y/N) | If Y > 1 && Z > 1 && X < 1 (Y/N) | If X > 1 && Z > 1 && Y < 1 (Y/N) | Type of fault classified |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ABC | 30 | 0 | 146.8 | 107.5 | 94.6 | 4.049 | 3.069 | 2.777 | N | N | N | N | N | LLL (ABC) |
| ABC | 60 | 20 | 54.4 | 35.17 | 41.62 | 4.886 | 3.273 | 3.931 | N | N | N | N | N | LLL (ABC) |
| ABC | 90 | 40 | 26.1 | 17.35 | 25.3 | 5.664 | 3.849 | 5.682 | N | N | N | N | N | LLL (ABC) |
| ABC | 120 | 60 | 13.92 | 11.44 | 17.2 | 6.398 | 5.238 | 8.156 | N | N | N | N | N | LLL (ABC) |
| ABC | 150 | 80 | 9.186 | 10.94 | 15.98 | 7.36 | 8.179 | 11.49 | N | N | N | N | N | LLL (ABC) |
| ABC | 180 | 100 | 5.33 | 7.675 | 8.3 | 9.312 | 14.04 | 16.06 | N | N | N | N | N | LLL (ABC) |
| ABC | 210 | 120 | 4.05 | 6.6 | 5.71 | 14.48 | 25.85 | 23.07 | N | N | N | N | N | LLL (ABC) |
| ABC | 240 | 140 | 3.59 | 5.597 | 3.85 | 30.29 | 52.91 | 37.12 | N | N | N | N | N | LLL (ABC) |
| ABC | 270 | 160 | 3.393 | 4.55 | 2.74 | 95.42 | 140 | 82.03 | N | N | N | N | N | LLL (ABC) |
| ABC | 300 | 180 | 3.292 | 3.538 | 2.12 | 851.6 | 976.3 | 562.6 | N | N | N | N | N | LLL (ABC) |
| Fault type | SA | SB | SC | LA | LB | LC | Actual distance in km | ANN distance in km | ANFIS distance in km | SVM distance in km | ANN %error | ANFIS %error | SVM %error |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AG | 320.7 | 1.22 | 0.831 | 1.358 | 1.177 | 0.824 | 5 | 25.63 | 6.88 | 5 | 6.88 | 0.628 | 0.1 |
| 24.43 | 1.054 | 0.943 | 1.257 | 1.022 | 0.959 | 45 | 65.29 | 33.59 | 45 | 6.76 | −3.804 | −0.1 | |
| 8.342 | 1.03 | 0.973 | 1.557 | 1.001 | 0.991 | 90 | 110.2 | 91.83 | 90 | 6.73 | 0.611 | 0.1 | |
| 4.55 | 1.017 | 0.988 | 2.188 | 0.99 | 1.006 | 135 | 141.66 | 137.27 | 135 | 2.22 | 0.758 | 0.1 | |
| 3.057 | 1.006 | 1 | 3.653 | 0.98 | 1.018 | 180 | 170.26 | 176.5 | 180 | −3.25 | −1.168 | −0.1 | |
| 2.314 | 0.989 | 1.015 | 8.193 | 0.965 | 1.034 | 225 | 206.33 | 224.63 | 225 | −6.22 | −0.122 | −0.1 | |
| 2.04 | 0.788 | 1.3 | 724.939 | 0.8 | 1.356 | 300 | 286.07 | 295.45 | 300 | −4.64 | −1.515 | −0.2 | |
| ABG | 551.58 | 420.65 | 1 | 2.36 | 2.93 | 0.96 | 5 | 47.9 | −4.49 | 5 | 14.3 | −3.164 | −0.2 |
| 72.17 | 53.83 | 1 | 3.06 | 3.77 | 0.99 | 45 | 167.34 | 28.4 | 45 | 40.78 | −5.535 | −0.2 | |
| 25.67 | 18.44 | 1 | 4.45 | 5.23 | 0.99 | 90 | 182.95 | 100.03 | 90 | 30.984 | 3.342 | 0.1 | |
| 13.55 | 9.42 | 1 | 7.09 | 7.88 | 1 | 135 | 187.06 | 147.3 | 135 | 17.353 | 4.099 | 0.1 | |
| 8.59 | 5.8 | 1 | 12.91 | 13.55 | 1 | 180 | 189.85 | 171.41 | 180 | 3.285 | −2.863 | −0.1 | |
| 6.05 | 4 | 1 | 29.67 | 29.4 | 1 | 225 | 195.08 | 209.21 | 225 | −9.972 | −5.263 | −0.2 | |
| 4.55 | 2.99 | 0.99 | 118.37 | 111.3 | 1 | 270 | 219.03 | 294.48 | 270 | −16.989 | 8.158 | 0.1 | |
| 3.77 | 2.64 | 0.91 | 925.55 | 955.31 | 0.97 | 300 | 282.48 | 259.55 | 300 | −5.838 | −13.485 | −0.2 | |
| AB | 448.07 | 422.45 | 1 | 1.83 | 3.51 | 1 | 5 | 4.42 | 10.974 | 5 | −0.19 | 1.99 | 0.1 |
| 65.02 | 56.04 | 1 | 2.46 | 4.42 | 1 | 45 | 42.4 | 50.435 | 45 | −0.87 | 1.81 | 0.1 | |
| 23.89 | 18.69 | 1 | 3.65 | 6.02 | 1 | 90 | 85.39 | 92.436 | 90 | −1.54 | 0.81 | 0.1 | |
| 12.94 | 9.28 | 1 | 5.94 | 8.92 | 1 | 135 | 133.13 | 133.928 | 135 | −0.62 | −0.36 | −0.1 | |
| 8.4 | 5.58 | 1 | 11.03 | 15.03 | 1 | 180 | 181.35 | 178.565 | 180 | 0.45 | −0.48 | −0.1 | |
| 4.02 | 2.28 | 1 | 830.59 | 863.48 | 1 | 300 | 299.12 | 294.979 | 300 | −0.29 | −1.67 | 0.1 | |
| ABC | 660.68 | 493.16 | 424.36 | 3.48 | 2.59 | 2.44 | 5 | 4.45 | −6.13 | 5 | −0.18 | −3.71 | −0.1 |
| 84.77 | 62.87 | 54.14 | 4.46 | 3.43 | 3.02 | 45 | 45.62 | 37.41 | 45 | 0.21 | −2.53 | −0.2 | |
| 28.68 | 22.51 | 17.94 | 6.24 | 5 | 4.1 | 90 | 88.07 | 109.41 | 90 | −0.64 | 6.47 | 0.1 | |
| 14.37 | 11.82 | 8.96 | 9.45 | 7.95 | 6.08 | 135 | 136.49 | 142.1 | 135 | 0.5 | 2.37 | 0.1 | |
| 8.61 | 7.57 | 5.38 | 16.27 | 14.48 | 10.34 | 180 | 180.25 | 167.59 | 180 | 0.08 | −4.14 | 0.1 |
5.1. Proposed classification algorithm
Synchronized fault currents from both ends of the transmission line are transmitted to TCC using RTU and GPS technology. Then current energy coefficients on two ends of the line are acquired through DOST, viz., SA , SB , SC , LA , LB , and LC of the original fault currents of three phases Ia , Ib and Ic are being calculated in TCC. These DOST features are utilized for fault classification. Various types of faults were created at different FIA, fault distance and fault resistance. Fault resistance assumed in all line faults are 0.1Ω and in all ground faults are 0.001Ω. The results contained in Table 1 , Table 2 , Table 3 and Table 4 validate the efficacy of the proposed fault classification algorithm for different fault conditions.
The results contained in Table 1 validate the proposed fault classification algorithm for AG fault for various fault distances as well as various FIA. When AG fault occurs at a distance of 90 km from generator-1 (from BUS1) and has an FIA of 40°, the SA , SB , SC , LA , LB and LC values are calculated using DOST. Then it is checked If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0) is satisfied or not. From the data, it is shown that the above said condition is satisfied, and then it is further investigated out of the above three conditions which condition is satisfied. If the results indicate Y (0) and Z (0), then the fault was classified to be AG fault. If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0) is satisfied and If X ≅ 0 and Z ≅ 0 is satisfied, then it is BG fault. Similarly If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0) is satisfied and If X ≅ 0 and Y ≅ 0 is satisfied, then it is CG fault. Similarly BG and CG faults can also be validated. Because of the page limit, the outcomes have not been presented here.
If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0) is not satisfied and if one of the conditions (i.e. X = 0 (or) Y = 0 (or) Z = 0) is satisfied, then it is classified as LL fault. The results contained in Table 2 validate the efficiency of the fault classification method for L-L (AB) faults at different fault conditions. When AB fault occurs at a distance of 180 km from generator 1 (from BUS1) with an FIA of 100°, the SA , SB , SC , LA , LB and LC values are calculated using DOST and it is checked. If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0) is not satisfied, but Z = 0 and X, Y ≠ 0, then fault was classified to be AB fault. If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0) is not satisfied and If X = 0 and Y, Z ≠ 0 is satisfied, then it is BC fault. Similarly If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0) is not satisfied and If Y = 0 and X, Z ≠ 0 is satisfied, then it is CA fault. Similarly BC and CA faults can also be validated. However, because of the page limit, the outcomes have not been presented here.
If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0 (or) X = 0 (or) Y = 0 (or) Z = 0) is not satisfied, then it can be concluded as LLG (or) LLL fault. The discrimination between these two types of faults is such that, if any one of the conditions (X > 1, Y > 1 and Z < 1(or) Y > 1, Z > 1 and X < 1 (or) Z > 1, X > 1 and Y < 1) is satisfied, then it can be classified as an LLG fault. The results contained in Table 3 and Table 4 validate the efficacy of the proposed fault classification algorithm for LL-G and LLL faults. For example, Table 3 validates the fault classification method for ABG fault for different fault conditions. When ABG fault occurs at a distance of 300 km from generator 1 and with FIA of 180°, the SA , SB , SC , LA , LB and LC values are calculated using DOST. Then it is checked; If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0 (or) X = 0 (or) Y = 0 (or) Z = 0) is not satisfied but X > 1, Y > 1 and Z < 1 satisfied, then it is classified as ABG fault. If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0 (or) X = 0 (or) Y = 0 (or) Z = 0) is not satisfied but Y > 1, Z > 1 and X < 1 satisfied, then it is classified as BCG fault. Similarly If one of the conditions (i.e. X ≅ 0 and Y ≅ 0 (or) Y ≅ 0 and Z ≅ 0 (or) Z ≅ 0 and X ≅ 0 (or) X = 0 (or) Y = 0 (or) Z = 0) is not satisfied but Z > 1, X > 1 and Y < 1 satisfied, then it is classified as CAG fault. If none of the above settings are satisfied, it can be considered as ABC fault. These events were tabulated for different fault conditions in Table 3 and Table 4 for ABG and ABC faults respectively. Similarly BCG and CAG faults can also be corroborated. Thus, from the results, the proposed classification algorithm seems to be capable for real time digital relaying operation.
5.2. Proposed location algorithm
The current energy coefficients (SA , SB , SC , LA , LB , and LC ) extracted through DOST of fault currents have been utilized for estimating the location of the transmission line fault. The proposed fault location methodology has been implemented using machine intelligence techniques like SVM, ANFIS and ANN. Fault resistance assumed in this case study is 0.1Ω. Details of implementation and comparative study are discussed in this part.
5.2.1. SVM based fault location approach
The current energy coefficients for numerous fault locations, FIAs, fault impedances and power angles are estimated through simulation studies conducted on MATLAB/SIMULINK platform. Then a database of current energy coefficients and corresponding fault locations distance in kilometer is generated. This database has been utilized for training the multi-class SVM. Radial basis function has been preferred as a kernel function with a sigma value of 0.8. The outcomes of the case studies conducted for LG (AG), LL (AB), LLG (ABG) and LLL (ABC) faults after successful training of SVM are tabulated in Table 5 . Percentage error in the estimation of fault location for all case studies is also included in the tables. It can be noted from the tables that SVM estimates the fault location with an almost zero percent error.
5.2.2. ANFIS based fault location approach
The same database generated for SVM has been utilized for training ANFIS network. Triangular membership functions with three linguistic variables are generated for each set of current energy coefficients. The ANFIS network has been trained for 4,000 epochs with hybrid learning method as an optimization tool. After successful training of ANFIS network, it has been tested for LG (AG), LL (AB), LLG (ABG) and LLL (ABC) faults. The results are tabulated in Table 5 along with the percentage error in the estimation of fault location. From the tables it can be seen that ANFIS estimates the fault location with the maximum percentage error of thirteen.
5.2.3. ANN based fault location approach
The same database utilized for training SVM and ANFIS network with normalized fault location distances has been deployed for training ANN system. Normalized fault location distances are estimated through dividing the fault distance in kilometers by the length of the transmission line (300 km). The ANN system deployed is of four layers with one input layer, two hidden layers of nineteen neurons in each and an output layer with saturated linear function. The system is trained using back propagation algorithm and the estimation error is found to be decreased after two thousand epochs. After training the system, it has been tested for LG (AG), LL (AB), LLG (ABG) and LLL (ABC) faults. The estimation results along with the percentage error in the estimation of fault location are tabulated in Table 5 . It can be understood from the tables that ANN estimates the fault location with the maximum percentage error of forty.
5.3. Comparative studies between SVM, ANFIS and ANN based fault location approaches
Performance comparison of SVM, ANFIS and ANN for estimation of fault location distance has been illustrated in this section. An instance of the above case studies of LL fault that occurred between phases “A” and “B” (AB fault) at 90 km as tabulated in Table 5 has been considered for comparative studies. In this case, ANN estimates the distance fault location from generator bus-1 at 85.39 km. As the estimated location is before actual location, the percentage error becomes a negative value of −1.54%. ANFIS estimates the same location as 92.436 km, which is more than the actual distance, therefore establishing the percentage error as positive with a value of 0.81%. SVM accurately estimates the location and hence percentage error leads to zero. This validates the superiority of SVM based fault location approach over ANFIS and ANNs based approaches.
6. Conclusion
A novel SFDCL methodology based on GPS enabled RTUs for detection, classification and location of faults in transmission lines has been presented in this paper. Coalesced utilization of DOST in conjunction with SVM facilitates the proposed methodology to detect, classify and locate all types of transmission line faults with improved accuracy and utmost robustness. Extensive case studies are performed on transmission lines fed from both ends for validating the proposed methodology. Simulation results confirm that the proposed methodology meets the stringent reliability requirements of WAPs like immunity toward FIA and fault distance. Hence the proposed methodology can significantly aid transmission line protection systems for enhancing overall reliability and continuity of supply by accurately detecting, classifying and localizing the transmission line faults. The proposed methodology may be extended for protection of distribution lines of power system networks as a future work.
References
- [1] S. Liu, P.X. Liu, A. El Saddik; Modeling and stability analysis of automatic generation control over cognitive radio networks in smart grids; IEEE Trans. Syst. Man Cybern, 45 (2) (2015), pp. 223–234
- [2] K. Wang, X. Qiu, S. Guo, F. Qi; Fault tolerance oriented sensors relay monitoring mechanism for overhead transmission line in smart grid; IEEE Sens. J., 15 (3) (2015), pp. 1982–1991
- [3] S. Ananthavel, S. Padmanaban, S. Shanmugham, F. Blaabjerg, A.H. Ertas, V. Fedak; Analysis of enhancement in available power transfer capacity by STATCOM integrated SMES by numerical simulation studies; Int. J. Eng. Sci. Tech, 2215-0986 (2015) in press
- [4] A.S. Dobakhshari, A.M. Ranjbar; A wide-area scheme for power system fault location incorporating bad data detection; IEEE Trans. Power Del, 30 (2) (2015), pp. 800–808
- [5] V. Terzija, Z.M. Radojevic, G. Preston; Flexible synchronized measurement technology-based fault locator; IEEE Trans. Smart Grid, 6 (2) (2015), pp. 866–873
- [6] J. Wu, J. Xiong, Y. Shi; Efficient location identification of multiple line outages with limited PMUs in smart grids; IEEE Trans. Power Sys, 30 (4) (2015), pp. 1659–1668
- [7] J. Zare, F. Aminifar, M. Sanaye-Pasand; Communication-constrained regionalization of power systems for synchrophasor-based wide-area backup protection scheme; IEEE Trans. Smart Grid, 6 (3) (2015), pp. 1530–1538
- [8] S. Gupta, R. Kambli, S. Wagh, F. Kazi; Support-vector-machine-based proactive cascade prediction in smart grid using probabilistic framework; IEEE Trans. Ind. Electr, 62 (4) (2015), pp. 2478–2486
- [9] D. Chanda, N.K. Kishore, A.K. Sinha; Application of wavelet multiresolution analysis for identification and classification of faults on transmission lines; Electr. Power Syst. Res, 73 (3) (2005), pp. 323–333
- [10] A. Ferrero, S. Sangiovanni, E. Zapitelli; A fuzzy set approach to fault type identification in digital relaying; IEEE Trans. Power Del, 10 (1) (1995), pp. 169–175
- [11] T. Takagi, Y. Yamakoshi, M. Yamaura, R. Kondow, T.M. Atsushima; Development of a new type fault locator using the one-terminal voltage and current data; IEEE Trans. Power Apparatus Sys, PAS-101 (8) (1982), pp. 2892–2898
- [12] Q. Jian, C. Xiangxun, Z. Jianchao; Travelling wave fault location of transmission line using wavelet transform; Proc. Int. Conf. IEEE Power System Technology, POWERCON'98', Beijing, Aug. (1998), pp. 533–537 vol.1
- [13] M. Jaya Bharata Reddy, D.K. Mohanta; Adaptive-neuro-fuzzy inference system approach for transmission line fault classification and location incorporating effects of power swings; IET Gen. Trans. Dis, 2 (2) (2008), pp. 235–244
- [14] D. Novosel, B. Bachmann, D. Hart, Y. Hu; Algorithms for locating faults on series compensated lines using neural network and deterministic methods; IEEE Trans. Power Del, 11 (4) (1996), pp. 1728–1736
- [15] T. Funabashi, H. Otoguro, Y. Mizuma, L. Dube, A. Ametani; Digital fault location for parallel double-circuit multi-terminal transmission lines; IEEE Trans. Power Del, 15 (2) (2000), pp. 531–537
- [16] J. Liang, S. Elangovan, J.B.X. Devotta; A wavelet multiresolution analysis approach to fault detection and classification in transmission lines; Electr. Power Energy Sys, 20 (5) (1998), pp. 327–332
- [17] D.A. Countney, T.B. Littlert, J. Livie; Fault location on a distribution network using a decentralized analysis process; Proc. Int. Conf. IET Developments in Power System Protection, Glasgow, Mar. (2008), pp. 349–353
- [18] M. Jaya Bharata Reddy, B. Karthik Chandra, D.K. Mohanta; A DOST based approach for the condition monitoring of 11 kV distribution line insulators; IEEE Trans. Dielectr. Electr. Insul, 18 (2) (2011), pp. 588–595
- [19] Y. Wang, J. Orchard; The discrete orthonormal Stockwell transform for image restoration; Proc. Int. Conf. IEEE Image Processing (ICIP), Cairo, Nov. (2009), pp. 2761–2764
- [20] S. Drabycz, R.G. Stockwell, J.R. Mitchell; Image texture characterization using the discrete orthogonal s-transform; J. Digit. Imaging, 22 (6) (2009), pp. 696–708
- [21] L.S. Moulin, A.P. Alves da Silva, M.A. El-Sharkawi, R.J. Marks II; Support vector machines for transient stability analysis of large-scale power systems; IEEE Trans. Power Sys, 19 (2) (2004)
- [22] J.S.R. Jang; ANFIS: adaptive-network-based fuzzy inference system; IEEE Trans. Syst. Man Cybern, 23 (3) (1993), pp. 665–685
- [23] T. Takagi, M. Sugeno; Derivation of fuzzy control rules from human operators control actions; Proc. IFAC Symposium on Fuzzy Information, Knowledge Representation and Decision Analysis (1983), pp. 55–60
- [24] I. Rojas, J.L. Bernier, R. Rodriguez-Alvarez, Z. Prieto; What are the main functional blocks involved in the design of adaptive neuro-fuzzy inference systems?; Proc. IEEE-INNS-ENNS International Joint Conference on Neural Networks (2000), pp. 551–556 vol. 6
- [25] E.M. Abdelrahim, T. Yahagi; A new transformed input-domain ANFIS for highly nonlinear system modeling and prediction; Proc. Canadian Conference on Electrical and Computer Engineering, May (2001), pp. 655–660 vol. 1
- [26] P.K. Dash, S.R. Samantaray, G. Panda; Fault classification and section identification of an advanced series-compensated transmission line using support vector machine; IEEE Trans. Power Del, 22 (1) (2007)
- [27] P. Janik, T. Lobos; Automated classification of power-quality disturbances using SVM and RBF networks; IEEE Trans. Power Del, 21 (3) (2006)
- [28] G. Loosli; Toolbox SimpleSVM Documentation; http://cbio.ensmp.fr/sirene/documentationSimpleSVM.pdf (2009)
- [29] M. Kezonuic; A survey neural net application to protective relaying and fault analysis; Eng. Intell. Sys, 5 (4) (1997), pp. 185–192
- [30] H. Khorashadi-Zadeh, S. Naveh-Hosseini; An accurate fault locator for cable transmission using ANN; Proc. 12th IEEE Mediterranean Electro Technical Conference, Dubrovnik, Croatia (2004), pp. 901–904 vol. 3
- [31] H. Khorashadi-Zadeh, M.R. Aghaebrahimi; A novel approach to fault classification and fault location for medium voltage cables based on artificial neural network; Int. J. Comput. Intell. Sys, 2 (1) (2005), pp. 90–93
Document information
Published on 10/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?