Abstract
The Open Shop Problem is a Production Scheduling problem where jobs do not have predestined processing routes, which increases the solution space and, therefore, the complexity of the problem. This work proposes a novel mathematical model that addresses the Open Shop theme with worker flexibility and no-wait. We consider the resource constraint of flexible and multiskilled labor. That is, the workers can execute their activities in more than one workstation. Simultaneously, the latter the continued production is contemplated, which hinders the reachability of feasible solutions and therefore increases the problem complexity. To validate the model, we generate several benchmarks, and the results obtained highlight the importance of worker flexibility in achieving greater problem feasibility.
Keywords: Mathematical model, no-wait, open shop, worker flexibility
1. Introduction
Production Scheduling is an area of utmost importance for companies since its primary objective is dealing with the allocation of scarce resources to productive operations in a given period to optimize one or more performance indicators [1,2]. In this sense, it defines when one or more workstations will process the jobs or operations.
This area of knowledge has been studied since the beginning of the last century, resulting from the pioneering work of Henry L. Gantt. However, it was only in the 1950s, with the seminal work of [3], that the area had its importance recognized within Operational Research (OR).
Since 1950, there is a plethora of books, articles, and publications related to the theme of Production Programming. Several concepts underlying it have been widely studied and published in highly renowned journals within the academic universe. Among these concepts, perhaps the most fundamental is related to the manufacturing environment, that is, under which productive logic and flow pattern, the tasks will be processed by the machines.
Concerning this aspect, when studied in its pure form, without the hybridization between two types of productive configuration, five types of productive setups are found. Single Machine, Parallel Machines, Flow Shop, Job Shop, and Open Shop, the last object of study of this paper.
The Open Shop differs from other manufacturing environments due to the lack of previous knowledge of the processing route for jobs and operations on the machines. Although there are several applications of this environment in practice, such as in mechanical workshops [4], quality control centers [5,6], laboratory facilities in medical centers [7], among others, there are fewer publications related to this subject.
A possible reason for this low academic exploitation might be its greater complexity, explained to some extent by its distinctive characteristic. The arbitrariness allowed for processing makes the space for solutions to problems concerning this configuration greater than that seen in other productive logics.
Within this universe, some papers deal with formulations that address the non-infinitude of resources. They are finite, in the case of labor and, or capacitated, in the case of workstations. This class of problems has the name of Open Shop with Resource Constraints (Resource-Constrained Open Shop). Such works are scant in the literature due to their significant complexity.
In an even more restricted spectrum are the jobs that include the possibility of jobs possesses the no-wait constraint, i.e., from the moment of the start of the processing of the job until its completion, it must be uninterruptedly processed along with workstations.
This work aims to present a novel mathematical model, to the best of our knowledge, that simultaneously addresses both the resource constraints, using flexible labor, and the production regime, related to the no-wait production system, whose we validate from the exact resolution of the proposed model, by adding the no-wait constraints to the model presented in [8].
The remainder of the paper is organized as follows. In Section 2, we exhibit the concept of Open Shop and Shop Scheduling with Resource Constraints, giving a brief description of the articles that simultaneously address both themes and published in this century. Section 3 describes the problem to be studied and the mathematical model that will be the basis for the model proposed here. In Section 4, we present and discuss the generation of instances, the resolution of these, evaluating the effects that the degree of flexibility of workers exerts in problem feasibility. Finally, in Section 5, we give some concluding remarks.
2. Literature review
2.1 Open shop
The Open shop is the production environment in which there are no restrictions regarding the processing route of each job throughout the production process ([2]). In this case, the construction of this is carried out during the production of the jobs and, it may differ between them, being part of the decision process related to sequencing [9].
The seminal work on this theme is attributed to [4], which deals with Open Shop with considerations about computational complexity. This paper addresses both the cases in which there is the possibility of interrupting the processing of jobs (preemption) and instances in which the interruption is not part of the scope of the problem. The authors of this study aimed to minimize processing completion time and, for that purpose, developed algorithms for both preemptive and non-preemptive cases.
2.2 No-wait open shop
Problems of this class are those in which the jobs being processed do not wait between workstations. Even the start of production of this job can be shifted to the right (right-shift schedules) so that the start time is different from the release date to meet this no-wait constraint.
One of the reasons for the occurrence of no-wait in productive environments lies in the technological properties of the production. The physical properties of a material, like temperature and viscosity, require the job to be processed continuously. Such examples occur in steel industries, plastic molding, among others. In pharmaceutical or chemical industries, waiting for a job at one of the workstations can mean its degradation.
The other reason is related to the lack of storage capacity between workstations. In this case, two Production Programming Problems arise from this situation. The No-wait problem, the object of study of this work. And the Blocking Problem, in which the job remains on the workstation, even if its execution on this one is finished, until the next machine that processes the job is free. Therefore, the Blocking Problem is less restrictive and, therefore, less complicated than No-wait.
The seminal work on the theme is that of [10], whose objective was to study the complexity of the no-wait problems, not only being restricted to the Open Shop but also addressing the other types of Shop Scheduling. The work consists of several theorems and proofs of these for problems with few workstations (at most 3) and few operations per job.
In the review article of Hall and Sriskandarajah [11], the authors address19 Open Shop problems with the no-wait constraint, accompanied or not by other characteristics, for different optimality criteria. The study also shows the complexity of each of these problems. The focus of this review is to address no-wait and blocking in all Shop Scheduling environments, presenting the complexity of each.
Allahverdi [12] resumes Hall and Sriskandarajah [11], covering all manufacturing environments, with articles on the matter published between mid-1993 and 2016. Of the 231 studies analyzed in that period, only six deal with the No-wait Open Shop, showing the low academic exploration of the theme. Among the works presented in [12] is that of [13]. The authors develop and solve to optimality three types of mathematical models for the no-wait. Then, the authors propose new metaheuristics based on Genetic Algorithms and Variable Neighborhood Search (VNS) to solve larger instances in reasonable computational time.
2.3 Shop scheduling with resource constraint
Among the introductory works of this topic, that of [14] is the most important since it makes the taxonomy of problems with resource constraints analogous to what is done in [15] for classical problems.
In the 3-field notation of Graham et al. (1979), , represents the manufacturing environment in which the jobs are processed; alludes to the job characteristics, that is, which aspects the problem studied differ from the classic model; and is related to the criteria of optimality, that is, which is the objective function or functions that are intended to maximize or minimize.
The notation related to the resource constraint is inserted in the field of the notation of Graham et al. (1979), is represented as follows: , where is relative to the number of resources, is related to the size of the resource, and is allusive to the resource requirements. receives a value of 1 when the number of resources is constant and equal to . can also be used when the number of resources is an integral part of the process and, therefore, is not previously known.
The Greek letter , such as , can take the value 1, when the size of the resource is constant and equal to , and when it is part of the process.
Finally, has a value of 1 when resource requirements have a constant upper limit, and receives when no upper limit is specified.
2.4 Open shop with resource constraints
Open Shop problems with resource constraints are unusual in the literature due to their great computational complexity. In this millennium, in a search made in the Scopus database, of the 796 publications found in the period, among journal articles, congress articles, books, etc., only five deal with the topic. These five studies will be summarized in the following paragraphs.
Oulamara et al. [16] deal with resources from a different viewpoint than those usually found in the literature. From their perspective, the job processing has two phases: preparation and execution. In the first, resources would be used, for example, labor. In execution, these resources would no longer be needed, being available again. The authors work with a problem with two machines and approach different resolution strategies, such as sequencing heuristics, to solve this unusual type of Open Shop.
In Borissova [17], the author integrates the discussion between staff scheduling and Open Shop. The author’s objective is to determine the number of optimal or Pareto-optimal workers for the manufacturing environment in question. To this end, the author develops a mathematical model used to determine the number of team members and their respective work scale. The significant contribution of the model is its easy adaptability to different operational requirements, based on the formulation of optimization steps with adequate objectives. Some of the optimality criteria commonly found in this type of approach are the determination of the least amount of idle staff, determination of the shortest processing time, among others.
In the work of Ciro et al. [18], they also deal with human resources, here with multiple skills, that is, workers can perform operations in more than one workstation, as long as the operator masters the skills required in processing a given operation. The authors work on two fronts: in the development of the mathematical model and the resolution through exact methods of small instances; and in the solution of more extensive benchmarks from the use of the Ant Colony Optimization (ACO) metaheuristic with fuzzy operators to define the parameters of the metaheuristic used.
In Ciro et al. [8], it is proposed for the same model discussed in Ciro et al. [18] the resolution of larger instances. Here, they use a population metaheuristic (Genetic Algorithms) and a constructive metaheuristic (ACO). The authors develop two mathematical models: a non-linear and a linear model, the latter being presented and described in the following chapter. The adaptations proposed in the present study will be made.
In the study by Ciro et al. [19], they use a multiobjective approach to the problem presented in Ciro et al. [18]. In this work, the authors aim to simultaneously optimize the total flow time of the jobs, the balance of workloads related to both man and machine. To this end, the authors use two of the most well-known algorithms for multiobjective optimization: NSGA-II (Non-dominated Sorting Genetic Algorithm II), composed of two main parts, the first being a quick, non-dominated solution and the second is preserving the diversity of the solution; and NSGA-III, which has the principles of NSGA-II, but which is used for problems with more than two objectives to be optimized.
Concisely, we infer from these analyzed studies is that they keep in common the focus on human resources and only them. There has not been researched and studied Open Shop models with more than one resource restriction, like Dual -Resource Constrained (when two types of resources are analyzed and restricted) or Multi-Resource Constrained (with more than two resource types). Such themes are widely explored in other manufacturing environments that make up Shop Scheduling, mainly in the Job Shop. Regarding the resolutive methods used, as the instances become more extensive, the use of methodologies other than the exact one is more significant.
3. Mathematical model for the no-wait open shop with worker flexibility
3.1 Problem description
The Open Shop presented here consists of machines and jobs where each job has at most operations, and the processing order can contain multiple options according to the job to be processed. Each operation must be processed at the designated workstation with a known processing time , a corresponding setup time under additional resource availability constraints (workers, required skills, and mastered skills).
Job preemption is not allowed. Any operation, when started, must be completed without interruption. The processing and setup times are considered separately, so the setup of the machine can be initiated in advance as soon as the machine is free. Besides, some classic assumptions of Production Scheduling are met, such as the exclusivity assumption, in which each workstation must process one job at a time, and each job must be processed by one machine at a time. All machines are continuously available, and items are available according to their respective release dates.
The optimality criterion is the total flowtime measured by the difference between the job completion time and its release date , which shall be minimized.
Regarding resources, each worker can only be assigned to an operation that he has mastered. That is, he has the necessary skills to perform it. Moreover, the worker designated for processing a specific job on a particular workstation must remain on it throughout the whole processing period of the job.
Items must be continuously processed, with no-wait constraint applied between the workstations.
From the taxonomic point of view, the present work in terms of the notation presented in Blazewicz et al. (1983) can be classified as follows: , since both the number of resources (workforce), as the amount of it is predetermined. And there are no limits on the number of hours worked in processing jobs. The machine environment is the Open Shop with arbitrary machines (from 3 to 10 workstations). The field also contains the no-wait constraint, while the optimality criterion is the total flowtime, which must be minimized.
3.2 Mathematical model
The following modeling is inspired by that found in [8]. In this work, the authors deal with an Open Shop with limited resources, represented here by the workers who carry out the activities at the workstations. In addition, workers have multiple skills so that they can operate more than one machine. The model presented also includes the no-wait, something unprecedented, to the best of our knowledge for Open Shop problems with Resource Constraints. The model parameters are as follows:
- , Set of Jobs, ;
- , Set of Machines, ;
- , Set of Workers, ;
- , Set of Skills, ;
- , Job Index, ;
- , Machine Index, ;
- , Worker Index, ;
- , Skill Index, ;
- , Large Positive Number;
- , the Setup time of job on machine ;
- , the Processing time of job on machine ;
- , the release date of job ;
- , if job on machine requires skill ; , otherwise;
- , if worker provides skill ; , otherwise.
The problem variables are as follows:
- , if job precedes job on machine ; , otherwise;
- , if job is executed on machine then on the machine ; , otherwise;
- , if worker executes job on machine ; , otherwise;
- – Completion time of job ; ;
- , if job on machine precedes job on machine ; , otherwise;
- , the start time of job .
The positive number was stipulated as being times the longest possible processing time, whose value is . Therefore, .
The following mathematical formulation is Mixed Integer Linear Programming, with 4 of the 5 component variables of the problem of a binary nature.
Model:
|
|
(1) |
Subject to
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
The objective of the model (Equation (1)) is to minimize the total flowtime, where the completion time of job is greater than the release date of that job, according to Equation (17), so it is guaranteed that the total flowtime will always be positive . Constraint (2) defines the completion time. Constraint (3) establishes the relationship between the time when processing begins and the job release date. Constraint (4) represents the operational sequence constraint for operations processed on the same machine. The setup time of the operation cannot be started until the machine has finished processing the operation . Constraint (5) indicates the relationship between two operations of job , not necessarily consecutive. The start time of must be greater than or equal to the conclusion time of . Constraint (6) expresses the relationship between two operations performed by the same worker, where it is forbidden for the worker to carry out two activities simultaneously. The set (7)-(8) defines the no-wait constraints. Constraint (9) expresses the sequence of pairs of operations performed on the same machine. Constraint (10) expresses the relationship of any two operations of a job . Constraint (11) defines the sequence of any pairs of operations performed by the same worker, all happening while the same worker performs both activities.
The set (12)-(13) guarantees an order for two operations performed by the same worker, regardless of whether they are processed on different machines. The set of restrictions (14)-(16) indicates that only a worker with the correct skill level can perform the required job; each worker performs at least one activity, and, finally, only one worker is assigned to each activity, respectively. Equation (17) establishes the relationship between the setup time and the start time with the release date of each job. Finally, Equation (18) defines the binary decision variables.
In brief, the set (7)-(8) was proposed in this paper and incorporated into the original model. Besides, the variable referring to the time when the job starts to be processed, was added in Constraint (3), which establishes that start time will always be positive. Ultimately, the Constraint (17) was adapted, adding the variable as mentioned earlier to it.
4. Results and discussion
This chapter is divided into two parts—the first being dedicated to how the instances used in the mathematical model validation are built. The second is related to the presentation of the results of the work and its potential aftermath.
4.1 Construction of the benchmarks
Each benchmark used was built randomly, from the combination of four parameters, namely, the number of jobs, machines, workers, and skills. For the first three, the values vary between 3 and 10, while for the last, the values range between 3 and 7. Furthermore, the values for the number of workers and the number of machines must be the same since we assume a resource (worker) per machine. Thus, for each level, represented by the number of jobs to be sequenced, there is a total of 40 benchmarks. As the number of tiers is equal to 8, it is possible to construct 320 examples for the problem studied. A formal description of the process is presented in Figure 1.

|
| Figure 1. Pseudocode of the benchmark generator |
However, in just one generation, we found that many sets were not obtained. Thus, for each generation, 100 replications were performed, making it possible to obtain 320,000 benchmarks. For the tests carried out, we decided to use only one example of the acquired set, according to the oldest generation. Due to this seniority criterion, the first generation of the parameter set is considered, discarding the others.
Concerning the other parameters, the processing times are integers uniformly distributed in the interval . The setup times of the machine are integers uniformly distributed in the interval . The release dates are integers uniformly distributed in the interval . And matrices (worker-skill) and (skill-operation) are generated randomly which 1 means that the operation requires that skill, or the worker masters that skill.
The instances were built and executed on a computer with an Intel Core i7- 5500U CPU and 2.4 GHz, 8 GB of RAM, and a 64-bit Windows 10 operating system. To solve the proposed model, the GUROBI 7.0.2 solver was used in its academic version, the coding of which is implemented in C#.
We divided the benchmark into five groups, namely:
- Group I: in this, there is total flexibility for workers, that is, all of them are qualified to carry out all operations;
- Group II: here, there is a total inflexibility of the workers, i.e., each one master only one of the skills necessary to accomplish the task;
- Group III: in the instances belonging to that group, each worker masters two skills;
- Group IV: here, each worker masters three skills, at most;
- Group V: in the instances in this group, each worker has four skills.
For each group, 3600 seconds was set as the time limit for resolving each benchmark. The following tables will show only the valid instances. An instance is valid when both the worker-skill matrix and the skill-operation matrix do not have null rows and, or columns. In that regard, 269 valid instances were generated for each class studied.
Regarding the presentation of the tables, the results are displayed in them as follows: in the first column is the number of jobs (J) to be sequenced; in the second are the number of valid instances generated (VIG) for that number of jobs specified in the first column; the third shows the number of optimal solutions obtained (OS); the third shows the number of suboptimal solutions (SOS). A suboptimal solution is one that has a gap greater than 0%; The average value of this gap is shown in the fifth column; the sixth and seventh columns are dedicated to showing the number of non-incumbent (INC) and infeasible (INF) benchmarks, respectively. A non-incumbent solution is one that, after reaching the time limit, has not been obtained any valid initial solution.
Table 1 shows the results of Group I.
| J | VIG | OS | SOS | % | INC | INF |
|---|---|---|---|---|---|---|
| 3 | 36 | 20 | 10 | 23.3 | 0 | 0 |
| 4 | 38 | 19 | 19 | 30.2 | 0 | 0 |
| 5 | 33 | 12 | 21 | 39.9 | 0 | 0 |
| 6 | 35 | 12 | 23 | 44.2 | 0 | 1 |
| 7 | 32 | 7 | 21 | 47.1 | 4 | 0 |
| 8 | 33 | 5 | 22 | 46.9 | 6 | 0 |
| 9 | 31 | 3 | 21 | 49.5 | 7 | 0 |
| 10 | 31 | 0 | 14 | 48.4 | 15 | 2 |
In this group, from the 269 valid benchmarks, 78 (29%) achieved the optimal result. If we divide the instances into three subgroups, small with up to 6 jobs, medium with 7 and 8 jobs, and large with 9 and 10 jobs, only three large instances (3.8%) reached the optimum, attesting to the complexity of the problem studied. Regarding the instances in this study classified as non-incumbent or infeasible, there were 32 instances whose result was the first, with 22 (68.8%) of these occurrences verified in large instances. Regarding the second, there were only three infeasibilities (1.1%), two of them found in large instances and one in the small stratum.
Group II, which encompasses the specialized workforce, has the worst results in terms of problem feasibility. In this class, 133 of the 269 valid benchmarks (49.4%) were infeasible, 66 of them encountered in small instances. Another significant result is related to the low number of optimal solutions found, only 23, all of them on the small instances subgroup. Not only optimal but also sub-optimal solutions are scarce. Table 2 summarizes these results, attesting to the increasing complexity of the studied problem when the worker masters only one skill.
| J | VIG | OS | SOS | % | INC | INF |
|---|---|---|---|---|---|---|
| 3 | 36 | 13 | 8 | 26.6 | 1 | 14 |
| 4 | 38 | 4 | 13 | 40.2 | 1 | 20 |
| 5 | 33 | 5 | 9 | 42.1 | 5 | 14 |
| 6 | 35 | 1 | 8 | 43.1 | 8 | 18 |
| 7 | 32 | 0 | 4 | 47.2 | 9 | 19 |
| 8 | 33 | 0 | 5 | 50.2 | 14 | 14 |
| 9 | 31 | 0 | 1 | 20 | 12 | 18 |
| 10 | 31 | 0 | 0 | - | 15 | 16 |
By adding just one more skill to the workforce, Group III presents a considerably lower rate of infeasibility, if compared to the Group II aforementioned. In the 269 benchmarks analyzed, 55 were infeasible, which corresponds to 20.4% of the total amount of computational tests performed here. In this class, more optimal results were found, some of them in medium and large subgroups, contrary to the observed in Group II. 62 of the 269 problems, in the time limit established, did not present any valid solution, being in this paper classified as non-incumbent. Table 3 addresses the results related to this group.
| J | VIG | OS | SOS | % | INC | INF |
|---|---|---|---|---|---|---|
| 3 | 36 | 22 | 11 | 29.7 | 0 | 3 |
| 4 | 38 | 10 | 19 | 31.8 | 0 | 9 |
| 5 | 33 | 6 | 23 | 38.8 | 1 | 3 |
| 6 | 35 | 6 | 19 | 42.1 | 5 | 5 |
| 7 | 32 | 4 | 11 | 50 | 10 | 7 |
| 8 | 33 | 1 | 9 | 52.1 | 14 | 9 |
| 9 | 31 | 2 | 5 | 40.6 | 14 | 10 |
| 10 | 31 | 0 | 4 | 62.5 | 18 | 9 |
In Group IV, only 24 of the 269 problems were infeasible, representing 8.9% of the total, a decrease of 11.5 percentage points if compared to Group III. More than half of the benchmarks are in the suboptimal range (51.3%). The average gap varies between 24.2% in problems with three jobs and 53.1% in those of 10 jobs to be processed. Table 4 presents the observed results of this penultimate variation in the workforce’s skill set.
| J | VIG | OS | SOS | % | INC | INF |
|---|---|---|---|---|---|---|
| 3 | 36 | 25 | 11 | 26.3 | 0 | 0 |
| 4 | 38 | 16 | 20 | 31.8 | 0 | 2 |
| 5 | 33 | 10 | 21 | 41.4 | 1 | 1 |
| 6 | 35 | 6 | 24 | 46.5 | 2 | 3 |
| 7 | 32 | 4 | 16 | 50.7 | 8 | 4 |
| 8 | 33 | 0 | 21 | 48.8 | 7 | 5 |
| 9 | 31 | 1 | 17 | 52 | 9 | 4 |
| 10 | 31 | 1 | 8 | 52.1 | 17 | 5 |
Finally, in Group V, the labor force has four mastered skills. With this amount of abilities, the results obtained were almost as good as those obtained in Group I, when the workforce is totally flexible. From the 269 benchmarks evaluated in the optimization process, only six were deemed infeasible, 2.2%. The quantity of minimum flowtime solutions encountered was the same observed in Group I (78). 31 problems did not present any valid result in the 3600 seconds time limit, verified in medium and large subgroups. Table 5 shows the results linked to this ultimate part of the analysis.
| J | VIG | OS | SOS | % | INC | INF |
|---|---|---|---|---|---|---|
| 3 | 36 | 25 | 11 | 24.2 | 0 | 0 |
| 4 | 38 | 19 | 19 | 30 | 0 | 0 |
| 5 | 33 | 12 | 21 | 40.5 | 0 | 0 |
| 6 | 35 | 10 | 24 | 49.8 | 0 | 1 |
| 7 | 32 | 6 | 22 | 50.1 | 3 | 1 |
| 8 | 33 | 4 | 22 | 48.3 | 7 | 0 |
| 9 | 31 | 2 | 20 | 49.2 | 8 | 1 |
| 10 | 31 | 0 | 15 | 53.1 | 13 | 3 |
In short, the results show that the problem studied has high complexity and, as the operator becomes more specialized, more difficulty in finding feasible solutions is encountered. This result is presented in Figure 2.
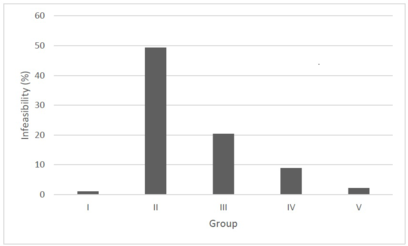
|
| Figure 2. Effect of worker flexibility on problem infeasibility |
Such complexity is expected due to the study of no-wait problems is, per se, hard. Even finding feasibility in models of this type is too computationally expensive.
5. Conclusions
This work aims to present, to the best of our knowledge, a novel Open Shop Scheduling problem since it simultaneously addresses no-wait and resource constraints, something considerably difficult when such subjects are considered individually.
This originality is obtained from the addition of no-wait constraints and the variable related to the start time of the jobs – the main result to be garnered when it comes to the continuous and uninterrupted production of a job –, to the Open Shop model of [8], making the necessary adaptations.
As it is an unprecedented model, it was necessary to develop an instance generator to validate the model. Such a generator can be considered an actual adjacent result of this work since future works may use the presented structure.
After the generation of the instances, the computational tests phase was carried out, whose results can be summarized under two aspects. The first is the amount of sub-optimal results, even with the 3600 seconds time limit, attesting to the non- triviality of the studied problem. And the last, related to the importance that the flexible and multiskilled workforce has for the infeasibility to be mitigated, due to the high number of non-feasible solutions when the workers master only one skill.
In future works, solving methods different from the exact one can be studied, matheuristics being an example of it to address larger instances, up to 100 jobs, to reduce the computational cost linked to its use when studying problems closer to the reality of the manufacturing environment. Another aspect that can be hereafter approached lies in the possibility of a multi-resource problem, evaluating the impact of other inputs beyond the labor force, such as machine capacity, has in the complexity of the problem.
Acknowledgements
We would like to thank CAPES for funding the research.
Referências
[1] Leung J.Y-T.(Ed.) Handbook of scheduling: algorithms, models and performance analysis. Chapman and Hall/CRC, Boca Raton, 2004.
[2] Pinedo M. Scheduling: theory, algorithms and systems. Springer, New York, 2012.
[3] Johnson S.M. Optimal two- and three-stage production schedules with setup times included. Nav. Res. Log. Quarterly, 1:61-68, 1954.
[4] Gonzalez T., Sahni, S. Open shop scheduling to minimize finish time. J. of the ACM, 23:665-679, 1976.
[5] Liu C.B.R. Scheduling ordered open shops. Comp. Oper. Res., 14:257-264, 1987.
[6] Prins C. An overview of scheduling problems arising in satellite communications. J. Oper. Res. Soc., 40:611-623, 1994.
[7] Matta M. A genetic algorithm for the proportionate multiprocessor open shop. Comp. Oper. Res., 36:2601-2618, 2009.
[8] Ciro G.C., Dugardin F., Yalaoui F., Kelly R. Open shop scheduling with a multi-skills resource constraint: a genetic algorithm and an ant colony optimization approach. Int. J. Oper. Res., 54(167):4854-4881, 2016.
[9] Chen B., Potts C.N., Woeginger, G.J. A review of machine scheduling: complexity, algorithms and applications. In Du D.Z., Pardalos, P.M. (Eds.), Handbook of Combinatorial Optimization, 21-169, 1998.
[10] Sahni S., Cho Y. Complexity of scheduling shops with no wait in process. Math. Oper. Res., 4(4):303-477, 1979.
[11] Hall N.G., Sriskandarajah C. A survey of machine scheduling problems with blocking and no-wait in process. Oper. Res., 44:510-525, 1996.
[12] Allahverdi A. A survey of scheduling with no-wait in process. Eur. J. Oper. Res., 255:665-686, 2016.
[13] Naderi B., Zandieh M. Modeling and scheduling no-wait open shop problems. Int. J. Prod. Econ., 158:256-266, 2014.
[14] Blazewicz J., Lenstra J.K., Rinnooy Kan A.H.G. Scheduling subject to resource constraints: classification and complexity. Discr. App. Math., 5(1):11-24, 1983.
[15] Graham R.L., Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Optimization and approximation in deterministic sequencing and scheduling: a survey. Ann. Discr. Math, 5:287-326, 1979.
[16] Oulamara A., Rebaine D., Serairi M. Scheduling the two-machine open shop problem under resource constraints for setting the jobs. Ann. Oper. Res., 211:333-356, 2013.
[17] Borissova D. An optimal staffing and scheduling approach in open shop environment. Comptes Rendus de L’Académie bulgare des Sciences, 60:1295-1300, 2015.
[18] Ciro G.C., Dugardin F., Yalaoui F., Kelly R. A fuzzy ant colony optimization to solve an open shop scheduling problem with multi-skills resource constraint. IFAC – Papers Online, 48:715-720, 2015.
[19] Ciro G.C., Dugardin F., Yalaoui F., Kelly R. A NSGA-II and NSGA-III comparison for solving an open shop scheduling problem with resource constraint. IFAC – Papers Online, 49:1272-1277, 2016.
Document information
Published on 29/04/21
Accepted on 07/04/21
Submitted on 03/12/20
Volume 37, Issue 2, 2021
DOI: 10.23967/j.rimni.2021.04.005
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?