Abstract
This paper proposes a Firefly algorithm based technique to optimize the control variables for simultaneous optimization of real power loss and voltage stability limit of the transmission system. Mathematically, this issue can be formulated as nonlinear equality and inequality constrained optimization problem with an objective function integrating both real power loss and voltage stability limit. Transformers taps, unified power flow controller and its parameters have been included as control variables in the problem formulation. The effectiveness of the proposed algorithm has been tested on New England 39-bus system. Simulation results obtained with the proposed algorithm are compared with the real coded genetic algorithm for single objective of real power loss minimization and multi-objective of real power loss minimization and voltage stability limit maximization. Also, a classical optimization method known as interior point successive linear programming technique is considered here to compare the results of firefly algorithm for single objective of real power loss minimization. Simulation results confirm the potentiality of the proposed algorithm in solving optimization problems.
Keywords
Firefly algorithm (FA) ; Optimal power flow (OPF) ; Continuation power Flow (CPF) ; Interior point successive linear programming (IPSLP) ; Real coded genetic algorithm (RCGA) ; Unified power flow controller (UPFC)
1. Introduction
In recent years, the Optimal Power Flow (OPF) has become an essential tool in power systems planning, operation and control for both integrated and deregulated power industries. OPF is stated as a nonlinear, nonconvex, static optimization problem with both discrete and continuous variables. The OPF problem solution aims to optimize certain objective functions like Real Power Loss (RPL) through optimal adjustment of various control variables, while satisfying both equality and inequality constraints. RPL minimization, generation cost minimization and voltage stability enhancement are the different objectives of OPF problem. The mathematical formulation of OPF problem was firstly presented by Dommel and Tinny [1] and then the issue has been handled by several researchers. In the literature, there are many conventional techniques such as Newton based programming method [2] , Linear programming method [3] and recently Interior point method [4] to solve the OPF problem.
With the development of Flexible AC transmission Systems (FACTS) technology, there is a possibility of controlling power flow to improve power system performance without generation rescheduling and topology changes. Among all the FACTS controllers, Unified Power Flow Controller (UPFC) is a popular device that provides flexibility in OPF by means of shunt and series compensation [5] and [6] . Glanzman and Anderson [7] coordinated several FACTS devices to avoid congestion, to provide secure transmission with reduced RPL. But, it is a well known fact that a secure operation of power system is not possible unless the optimization problem takes into account the system voltage security in its solution. Continuation Power Flow (CPF), a powerful tool, gives the information about the percentage of overloading capability of the system without voltage collapse [8] . In Reference [9] , Milano et al. successfully included CPF problem into an OPF problem to address simultaneously both the security and the voltage collapse issues. voltage stability limit (VSL) is defined as the maximum percentage overloading (λmax ) capability the system can withstand without voltage collapse, which is considered as another objective function along with the RPL minimization, thereby redefining the task as multi-objective optimization problem. The difficulty with the traditional techniques lies in the fact that they are more sensitive to initial points due to non monotonic solution surface and so not able to find the global optimum. To overcome the restrictions of traditional algorithms, meta-heuristic algorithms have been applied to work out OPF problems. Recently, nature inspired meta-heuristic algorithms show a powerful and efficient performance for dealing with high dimension nonlinear OPF problems. In all meta-heuristic search techniques, much effort has been devoted to make an appropriate trade-off between exploration and exploitation in searching for the optimal solutions. Many meta-heuristic algorithms have been applied to solve OPF problems, such as Particle Swarm Optimization (PSO) [10] , Tabu Search (TS) algorithm [11] , Bacteria Foraging Algorithm (BFA) [12] , Differential Evolution (DE) algorithm [13] , and Gravitational Search Algorithm (GSA) [14] . More recently, harmony search algorithm [15] and [16] , Krill Herd (KH) algorithm [17] , [18] , [19] , [20] , [21] and [22] and monarch butterfly optimization [23] perform powerfully and efficiently in solving highly non linear optimization problems.
In the present paper, a meta-heuristic algorithm known as FA is employed to solve the combined OPF and CPF problem of RPL minimization and VSL maximization. The FA is developed by “Xin-She Yang” [24] , [25] , [26] , [27] , [28] , [29] , [30] , [31] and [32] based on the flashing behavior of the fireflies which are available in nature. A comprehensive review of FA and its merits and demerits is given in Reference [27] . In Reference [33] , the authors have applied FA to solve Economic Load Dispatch Problem (ELDP) and recently it has been applied to solve OPF problem, incorporating Thyristor Controlled Series Capacitor (TCSC) to enhance power transfer capability of transmission line [34] . In this work, the control variables like transformer tap positions, UPFC location and its variables are optimized with the FA to optimize the single objective function of RPL minimization and multi-Objective of RPL minimization and VSL maximization, keeping all the variables within the limits. For both cases of single and multiple objectives, the optimization is carried out in three ways. First, only transformer taps are optimized, second UPFC location and its variables are only optimized with fixed optimized tap positions, and finally both the transformer taps and UPFC variables are simultaneously optimized. New England 39-bus system is considered as the test system for simulation purpose. The simulation results are compared with the results of IPSLP method and RCGA method to show the potentiality of the proposed algorithm.
The structure of this paper is organized as follows. Section 2 presents the mathematical formulations of single and multi-objective optimization problems along with principle of operation of UPFC. Section 3 describes global numerical optimization, the FA. The RCGA method is presented in section 4 . Section 5 describes IPSLP technique. In section 6 , the results of the proposed FA are compared with the results of RCGA and IPSLP methods. Finally, section 7 provides the conclusion and points out the path of the future work.
2. Statement of the problem
Problem: To solve single objective function problem of RPL minimization and multi-objective function problem of RPL minimization and maximization of VSL of the New England 39 bus test systems, connected with UPFC by using IPSLP, RCGA and FA. Here, both sequential and simultaneous allocation of transformer taps and UPFC are carried out for comparison.
2.1. Problem formulation of OPF
Mathematically, OPF problem of RPL minimization can be formulated as follows:
|
|
( 1) |
F(x, u) is the fitness function equating to the RPL of the test system. g(x, u ) is a set of non linear equality constraints to represent power flow, and h(x, u ) is a set of nonlinear inequality constraints i.e., bus voltages, transformer tap setting values, line MVA limits, etc. Vector x consists of state variables or dependent variables and vector u consists of independent variables or control variables. In this research work, the control variables are transformer tap values, which can vary in between 0.85 and 1.15 in step of 0.05, series injected voltage magnitude (Vse ) of UPFC with the ranges [0, 0.3 p.u.] and series injected voltage phase angle (δse ) of UPFC with the range [0,2π]. All these control variables are optimized with IPSLP, RCGA and FA to minimize the RPL of the test system. Here, the minimum and the maximum voltages of load buses are considered as 0.9 p.u. and 1.1 p.u. for the test system.
2.2. OPF formulation considering with VSL
The single objective function could be extended further with the inclusion of VSL, results a new fitness function. The VSL can be calculated through continuation power flow (CPF) technique which introduces load parameter (λ) stated as the percentage increase of load and generation from its base value. The resulting load and generation equations in terms of the load parameter are given as follows:
|
|
( 2) |
|
|
( 3) |
|
|
( 4) |
The load parameter (λ) can be increased until the system soon reaches the edge of instability, which is also called as notch point (NP) of the P–V curve. So the maximum value of the load parameter (λmax ) is known as voltage stability limit (VSL). The objective is to
|
|
( 5) |
Since both the RPL and voltage stability limits are in different range of values, the fitness function is formulated as a weighted sum. The reciprocal of VSL is sum to original cost function and overall cost function can be minimized. The fitness function to be optimized now can be represented as follows:
|
|
( 6) |
|
|
|
|
W1 is the weight adjustment for RPL and W2 is the weight adjustment for VSL. Ideally, W1 and W2 are adjusted so that the weighted values of RPL and VSL are similar in value. To find out this critical point in the system, the process of CPF [8] is carried out for each solution generated. The load is increased in steps, and for each increment, the values are calculated by the process of prediction and correction.
2.3. Unified power flow controller
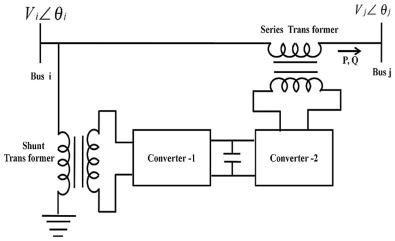
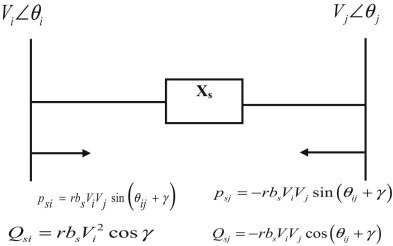
The UPFC structure shown in Fig. 1 basically shares the same dc-link to operate the two switching converters supplied by a common energy stored dc capacitor. The shunt and series transformers are used to couple the switching converter 1 and switching converter 2 to the power system network respectively. The converter 1 is connected in shunt to bus i while the converter 2 is connected in series between bus i and bus j . The series converter injects the necessary control voltage with the desired magnitude and phase angle through the coupling transformer to control the flow of required active and reactive power in the transmission line. The basic function of shunt converter is to interchange the real power with the power system network to maintain the energy stored at the common dc-link capacitor. The shunt converter is also capable to interchange the reactive power with the power system network thereby providing independent control of shunt reactive power compensation. Only one UPFC with injection model [35] and [36] is connected in the test system for simultaneous optimization of RPL and VSL enhancement. The UPFC injection model is shown in Fig. 2 .
|
|
|
Fig. 1. Device basic arrangement. |
|
|
|
Fig. 2. UPFC injection model. |
3. Firefly algorithm
3.1. Overview
Fireflies use flash signals to attract other fireflies for potential mates. Based on this behavior, a metaheuristic algorithm was developed by Xin-She Yang [24] , [25] and [26] . All the fireflies are considered unisexual and their attraction is directly proportional to the intensity of their flash. Therefore, if a firefly particle had the choice of moving toward either of two fireflies, it will be more attracted toward the firefly with higher brightness and moves in that direction. If there are no fireflies nearby, the firefly will move in a random direction. The brightness of flash is associated with the fitness function. The light intensity also obeys the inverse square law as in Equation (7)
|
|
( 7) |
where I(r) is the light intensity at a distance r and Is is the intensity at the source. For a given medium with fixed absorption coefficient γ , the light intensity I varies with the distance r and is given in Equation (8) as
|
|
( 8) |
Here, I0 is the original light intensity, γ is the absorption coefficient and r is the distance between the fireflies. As a fireflys attractiveness is proportional to the light intensity seen by adjacent fireflies, the attractiveness β of a firefly can be defined as
|
|
( 9) |
where β0 is the attractiveness at r = 0 . For two fireflies i and j , r is calculated as
|
|
( 10) |
Equation (10) is the distance between any two fireflies i and j at xi and xj respectively. In each generation, the fireflies move to nearby fireflies having more brightness as determined by Equation (11) as
|
|
( 11) |
where α is the randomization parameter and ε is the vector of random numbers taken from Gaussian distribution. Here controls the step size. The value α is chosen to be 0.3, which controls randomly. Movement of the fireflies at the end of each generation, the fireflies are ranked based on their brightness, and the best firefly in each generation is found. The fireflies are made to move in subsequent generations and in each generation; the light intensities of each firefly is updated with respect to the fitness function. At the end of all the generations, the firefly with the highest brightness, i.e., the best fitness value, is concluded as the optimal solution to the problem. The algorithm is found to be effective in solving noisy problems too. The number of fireflies is usually 20–40; in this case, the number of fireflies is chosen to be 30. The randomness in the movement of the firefly can be controlled by varying the parameter δ. In the problem, the value of δ is chosen to be 0.97. A higher value will facilitate more random movement by the fireflies and assist them in avoiding convergence to a local minimum.
3.2. Main algorithm
The basic steps of the FA can be summarized as the following:
- Step 1: Initialization of the firefly algorithm
- The dimension of the problem
- The number of fireflies
- The maximum number of iterations
- The values of α , β , γ and δ are chosen.
- Iteration counter i = 0
- Step 2: Increment the iteration counter i = i+1
- Step 3: Calculate the fitness of the fireflies in every iteration by using the fitness functions as given in Equations (1) and (6) and associate light intensity of each firefly to the same.
- Step 4: Sort the fireflies with varying intensities and find the best firefly in each iteration.
- Step 5: Vary the light intensity perception of all other fireflies based on the distance between them.
- Step 6: Move the fireflies based on attraction, which depends on light intensities and also control parameters.
- Step 7: If the stopping criteria in not reached, go back to step 2 else go to step 8.
- Step 8: Display the results with the firefly particle of highest light intensity.
The parameters of the FA are given in Table 1 and the flowchart is shown in Fig. 3 .
| S. No. | Parameters | Quantity |
|---|---|---|
| 1 | Number of fireflies | 30 |
| 2 | Maximum iterations | 100 |
| 3 | Randomness (α) | 0.3 |
| 4 | Absorption coefficient (γ) | 1.0 |
| 5 | Attractiveness (β) | 0.2 |
|
|
|
Fig. 3. The flowchart of FA. |
4. Real coded genetic algorithm (RCGA)
4.1. Overview
Real coded Genetic Algorithm is chosen over standard GA owing to its advantages in solving optimization problem with continuous and discrete parameters. RCGA mimics the process of natural selection which results in evolution of organisms with better adaptation to the environment [37] , [38] and [39] . The same behavior is used to solve multi-dimensional complex problems. The method has been proven effective for solving problems than binary coded algorithm. The algorithm considers solutions as genes and performs gene manipulation. The discrete values are stored with preset resolutions, whereas the continuous values are encoded as they are. The control parameters of RCGA are as given in Table 2 .
| S. No. | Parameters | Quantity |
|---|---|---|
| 1 | Population size (NP) | 40 |
| 2 | Number of generations | 30 |
| 3 | Cross over probability (Pc ) | 0.6 |
| 4 | Lambda (λ) | 0.5 |
| 5 | Probability of mutation (Pm ) | 0.12 |
The probability of mutation is valued at 0.12. A higher value will result in chaotic nature and convergence is affected. A lower value results in convergence at local minima. The following steps are performed to solve the fitness function for optimal solution.
4.2. Main algorithm
The basic steps of the RCGA can be summarized as follows:
- Step 1: Initialize the population with random solutions within the limits.
- Step 2: Find the fitness value of the solutions using the fitness functions as given in Equations (1) and (6) .
- Step 3:Crossover: Two random solutions Xi and Xj are chosen and crossover function is performed, in which parts of two parents combine to form a new offspring. Unlike standard GA, in RCGA, this is done with real values as X_new = (1 − λ)*Xi + λ*Xj , where λ is the crossover parameter.
- Step 4:Mutation: A part of the solution is mutated to a new random value. This results in a new value which is different from the previous solution. This is controlled by a probability factor called probability of mutation.
- Step 5:Elitism: The number of members in the population is maintained in every generation. The weakest members are replaced by newer offspring/mutants that have better fitness in every generation
- Step 6: Find the best member in every generation.
- Step 7: Steps 2–6 are repeated until the number of iterations has reached a preset limit.
- Step 8: The results are displayed for the best solution.
5. Interior point successive linear programming (IPSLP) technique
The OPF problem of RPL minimization can be formulated as follows:
|
|
( 12) |
where x0 , u0 are the initial values of x and u ;
- Δx , Δu indicate the step length from initial point
- and g, h indicate the linear approximation of non linear problem.
IPSLP Algorithm:
- Step 1: Solve the power flow problem.
- Step 2: Linearize the Optimal power flow (OPF) problem and formulate it as fitness function.
- Step 3: Linearize the incremental network model.
- Step 4: Compute the linearly constrained OPF by primal–dual interior point method.
- Step 5: Update the control variables by Δu ; solve the exact nonlinear power flow problem.
- Step 6: Evaluate the cost function for the updated control variables.
- Step 7: If the optimality solution is reached, then terminate the algorithm; otherwise, go to step 2 and continue.
6. Simulation results and discussion
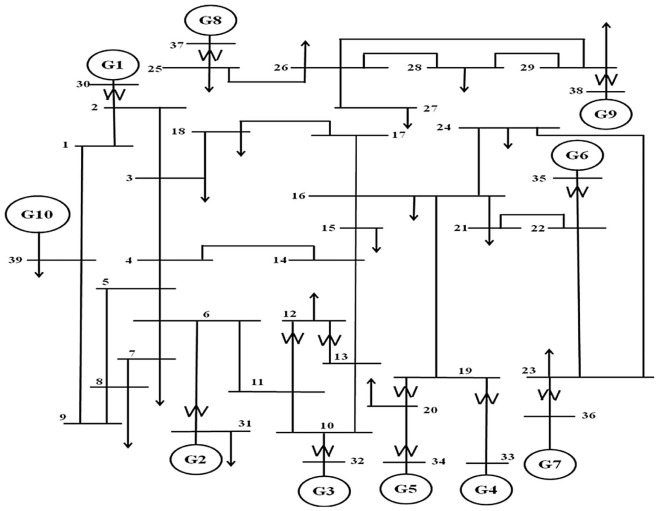
The effectiveness of the proposed method has been tested on the New England 39 bus test system [40] shown in Fig. 4 . The test system characteristics are given in Table 3 . The test system has 10 generators at buses from 30 to 39 and 12 transformers T1 to T12 located in the lines 2–30, 10–32, 12–11, 12–13, 19–33, 19–20, 20–34, 22–35, 23–36, 25–37, 29–38, 31–6 respectively.
|
|
|
Fig. 4. New England 39 bus test system. |
| S. No. | Data | Quantity |
|---|---|---|
| 1 | Number of buses | 39 |
| 2 | Generator buses | 10 |
| 3 | Load buses | 29 |
| 4 | Transmission lines | 46 |
| 5 | Transformers | 12 |
| 6 | Total load (MW) | 6097.10 |
A software program for IPSLP, RCGA and FA has written in MATLAB 8.3 version and run on core i5, 2.50 GHz and 4.0 GB RAM computer. Power flow is solved for the base case to find RPL and the VSL is obtained using CPF technique. For the test system with nominal values of taps, the RPL is 0.4378 p.u. and the VSL is 0.81. Next, the proposed methodology is applied to optimize only RPL (denoted as FAS) and simultaneously optimize the RPL and VSL (denoted as FAM) of power system. Simulation results for different cases are discussed below.
6.1. Case 1: transformer taps only optimized
6.1.1. Case 1.1: optimization of RPL only (single objective case)
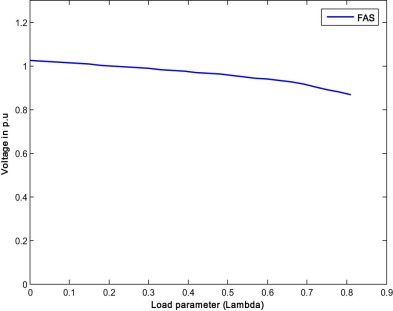
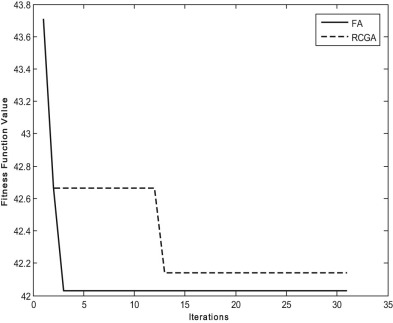
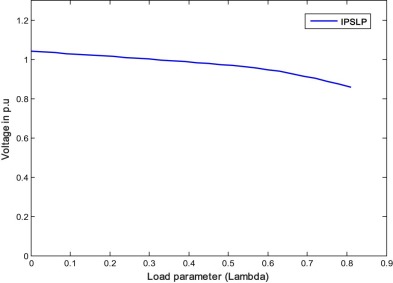
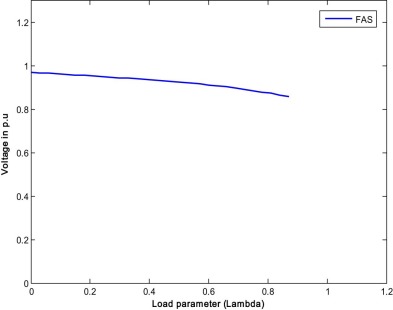
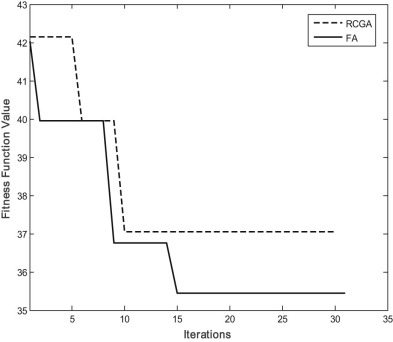
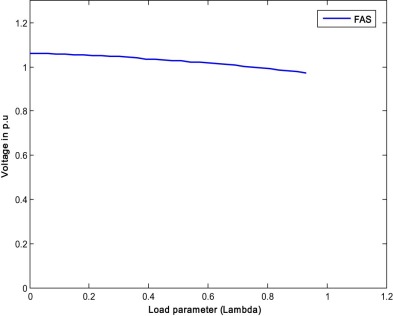
When only transformer taps are optimized with IPSLP technique for single objective of RPL, the loss is reduced from 0.4378 p.u. to 0.4266 p.u. With the optimized taps, the CPF is run for estimating the VSL and found the value of 0.78. For the same case with the RCGA, the RPL and VSL obtained are 0.42141 p.u. and 0.75 respectively. Similarly, the transformer taps are optimized with FA for the same single objective of RPL, the loss are further reduced to 0.4203 p.u. and the VSL is 0.81. The optimized transformer taps along with RPL and VSL are given in Table 4 , which indicates the potentiality of the FA over the IPSLP and RCGA methods in loss reduction. In the single objective case, VSL is not included in the fitness function. Fig. 5 , Fig. 6 and Fig. 7 show the PV curves of the weakest bus for case 1.1 by IPSLP, RCGA and FA respectively. The performance characteristics of RCGA and FA are shown in Fig. 8 .
| Control variables | Optimization of only RPL (single objective case) | Optimization of both RPL and VSL (multi-objective case) | |||
|---|---|---|---|---|---|
| IPSLP | RCGASa | FASb | RCGAMc | FAMd | |
| T1 | 1.10 | 1.05 | 1.15 | 1.10 | 1.10 |
| T2 | 1.10 | 1.15 | 1.10 | 1.05 | 1.05 |
| T3 | 0.95 | 1.10 | 1.05 | 1.10 | 1.05 |
| T4 | 1.10 | 1.05 | 1.05 | 1.05 | 1.05 |
| T5 | 1.10 | 1.05 | 1.15 | 1.00 | 1.10 |
| T6 | 1.00 | 1.05 | 1.10 | 1.10 | 1.10 |
| T7 | 1.10 | 1.05 | 1.10 | 1.00 | 1.05 |
| T8 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 |
| T9 | 1.10 | 1.05 | 1.10 | 1.15 | 1.15 |
| T10 | 1.10 | 1.05 | 1.10 | 1.05 | 1.05 |
| T11 | 1.05 | 1.10 | 1.15 | 1.05 | 1.10 |
| T12 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 |
| RPL | 0.4266 p.u. | 0.42141 p.u. | 0.4203 p.u. | 0.436912 p.u. | 0.43082 p.u . |
| VSL | 0.78 | 0.75 | 0.81 | 0.84 | 0.84 |
Bold font has been used to indicate the proposed algorithm and better performance.
a. RCGA is applied to optimize only RPL denoted as RCGAS.
b. FA is applied to optimize only RPL denoted as FAS.
c. RCGA is applied to optimize both RPL and VSL denoted as RCGAM.
d. FA is applied to optimize both RPL and VSL denoted as FAM.
|
|
|
Fig. 5. P–V curve of the weakest bus for case 1.1 (IPSLP). |
|
|
|
Fig. 6. P–V curve of the weakest bus for case 1.1 (RCGAS). |
|
|
|
Fig. 7. P–V curve of the weakest bus for case 1.1 (FAS). |
|
|
|
Fig. 8. Performance characteristics of RCGA and FA for case 1.1. |
6.1.2. Case 1.2: optimization of both RPL and VSL (multi objective case)
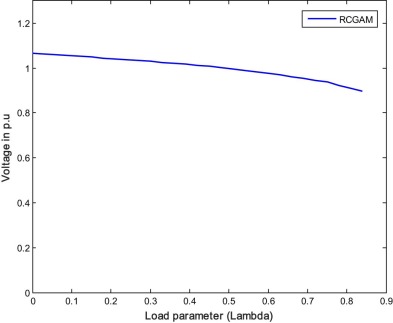
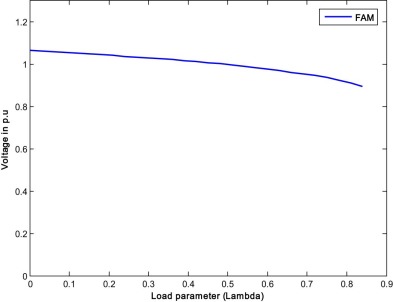
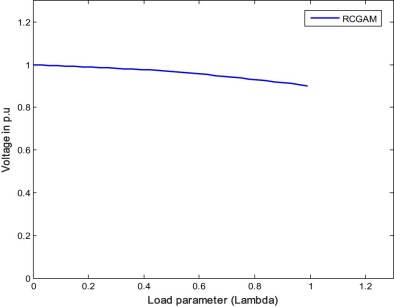
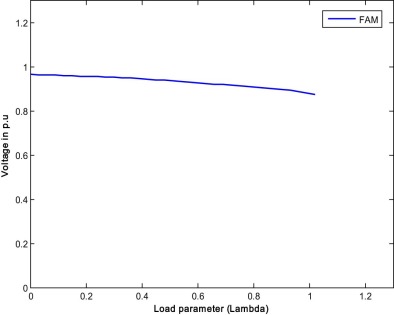
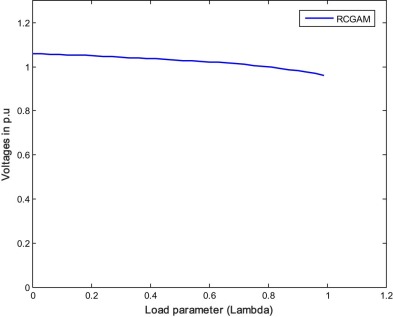
When both RPL and VSL are optimized, the cost function is modified. The reciprocal of VSL is added to the RPL and the optimization is carried out with RCGA and FA methods. Transformer tap values along with RPL and VSL are given in Table 4 . From the results, it is seen that the VSL is improved but losses are increased marginally with both the methods. Even RPL is increased slightly, the overall multi-objective function that is the sum of RPL and reciprocal of VSL is reduced with both the methods compared to single objective case. It is noticed here that with the proposed method the overall multi-objective function (RPL + 1/VSL) is further reduced showing a better performance than the RCGA. Fig. 9 and Fig. 10 show the PV curve of the weakest bus for case 1.2 by RCGA and FA respectively.
|
|
|
Fig. 9. P–V curve of the weakest bus for case 1.2 (RCGAM). |
|
|
|
Fig. 10. P–V curve of the weakest bus for case 1.2 (FAM). |
6.2. Case 2: UPFC location and its variables are optimized by keeping the taps in fixed position
6.2.1. Case 2.1: optimization of RPL only (single objective case)
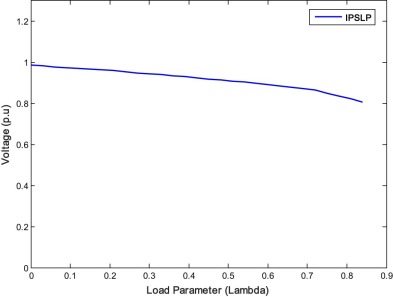
With the optimized transformer tap values, the UPFC location and its parameters are optimized with IPSLP, RCGA and FA techniques. In the test system, only 32 lines were considered for connecting the UPFC as the remaining 14 lines consist transformers and feeding generator powers to the network [39] . In IPSLP technique, the UPFC is connected in all the 32 lines considering one at a time, as it cannot be linearized through perturbation and so it is not a control variable. Here, the RPL are reduced from 0.4266 p.u. to 0.3798 p.u. with the best location and UPFC injection voltage in each succession of linearization. With optimized UPFC variables, the CPF is carried out to calculate the VSL and obtained value is 0.84. In the case of RCGA and FA, the line at which UPFC should be connected is decided randomly out of 32 lines selected in the initial stage. So with RCGA and FA, the line number in which UPFC is to be connected also becomes a control variable along with others. With RCGA and FA methods, the UPFC location and its variables are optimized keeping the optimized transformer taps fixed and found that the losses are reduced from 0.42141 p.u. to 0.37056 p.u. with RCGA and 0.4203 p.u. to 0.3545 p.u. with FA as given in Table 5 along with optimized UPFC location and its parameters. The VSL values calculated from the two methods are also given in Table 5 . From the results, it is clear that when a nonlinear device like UPFC is connected in the system, both RCGA and FA are able to find the global minimum, whereas IPSLP algorithm converges at local minimum only. As UPFC is connected in the system, there is further reduction in the losses obtained with RCGA and FA compared to case 1.1. Moreover, the FA gives global value of RPL showing the strength in optimizing the losses compared to RCGA. Fig. 11 , Fig. 12 and Fig. 13 show the PV curves of the weakest bus for case 2.1 by IPSLP, RCGA and FA methods respectively. The performance characteristics of the RCGA and FA for single objective case are also shown in Fig. 14 .
| Control variables | Optimization of only RPL (single objective case) | Optimization of both RPL and VSL (multi-objective case) | |||
|---|---|---|---|---|---|
| IPSLP | RCGASa | FASb | RCGAMc | FAMd | |
| UPFC series injected voltage (Vse ) | 0.0099 p.u. | 0.0234 p.u. | 0.0294 p.u. | 0.0100 p.u. | 0.0096 p.u. |
| UPFC series injected voltage phase angle (δse ) | 1.040 rad | 1.6774 rad | 1.9330 rad | 1.000 rad | 0.9134 rad |
| UPFC location | 3–4 | 16–19 | 26–29 | 21–22 | 26–27 |
| RPL | 0.3798 p.u. | 0.37056 p.u. | 0.3545 p.u. | 0.390307 p.u. | 0.3742 p.u. |
| VSL | 0.84 | 0.84 | 0.900 | 0.990 | 1.020 |
Bold font has been used to indicate the proposed algorithm and better performance.
a. RCGA is applied to optimize only RPL denoted as RCGAS.
b. FA is applied to optimize only RPL denoted as FAS.
c. RCGA is applied to optimize both RPL and VSL denoted as RCGAM.
d. FA is applied to optimize both RPL and VSL denoted as FAM.
|
|
|
Fig. 11. P–V cure of the weakest bus for case 2.1 (IPSLP). |
|
|
|
Fig. 12. P–V cure of the weakest bus for case 2.1 (RCGAS). |
|
|
|
Fig. 13. P–V curve of the weakest bus for case 2.1 (FAS). |
|
|
|
Fig. 14. Performance characteristics of RCGA and FA for case 2.1. |
6.2.2. Case 2.2: optimization of both RPL and VSL (multi objective case)
With the optimized transformer taps in fixed position, the UPFC location and its parameters are optimized by RCGA and FA for multi objective case of RPL and VSL. Table 5 shows the optimized UPFC location and its parameters along with RPL and VSL. Although the loss in this case is marginally increased compared to single objective case, the overall multi-objective function i.e., the sum of RPL and reciprocal of VSL, is reduced with both RCGA and FA methods. Also, compared to case 1.2, the multi objective function (RPL + 1/VSL) is further reduced because of introduction of the UPFC. It is noticed here from the results that the reduction of RPL and improvement of VSL, i.e., reduction of multi-objective function, is obtained with FA showing the efficacy over the RCGA. The PV curves for the weakest bus of RCGA and FA are shown in Fig. 15 and Fig. 16 .
|
|
|
Fig. 15. P–V curve of the weakest bus for case 2.2 (RCGAM). |
|
|
|
Fig. 16. P–V curve of the weakest bus for case 2.2 (FAM). |
6.3. Case 3: simultaneous optimization of UPFC location and its variables along with taps
6.3.1. Case 3.1: optimization of RPL only (single objective case)
With the IPSLP technique, the UPFC variables along with taps (12 transformer taps, UPFC series injected voltage magnitude and Phase angle) are simultaneously optimized and found that the RPL is 0.3947 p.u. and VSL is 0.87. Similarly, with RCGA and FA techniques, the UPFC location and its variables along with taps are simultaneously optimized. The values of RPL and VSL along with optimized UPFC parameters and transformer taps are given in Table 6 . It is observed from the simulation results that the losses obtained from FA technique are low as compared to IPSLP and RCGA techniques. Also it is noticed from the previous results of case 1.1 and case 2.1 that the losses are further reduced as in this case control variables are simultaneously optimized with RCGA and FA. Fig. 17 , Fig. 18 and Fig. 19 show the PV curves of the weakest bus for single objective case by IPSLP, RCGA and FA respectively. The performance characteristics of RCGA and FA for single objective case are shown in Fig. 20 .
| Control variables | Optimization of only RPL (single objective case) | Optimization of both RPL and VSL (multi-objective case) | |||
|---|---|---|---|---|---|
| IPSLP | RCGASa | FASb | RCGAMc | FAMd | |
| T1 | 1.00 | 1.00 | 1.10 | 1.10 | 1.00 |
| T2 | 1.00 | 0.95 | 1.00 | 1.10 | 1.05 |
| T3 | 1.05 | 0.95 | 1.00 | 1.15 | 1.05 |
| T4 | 1.00 | 1.00 | 1.00 | 0.95 | 1.05 |
| T5 | 1.05 | 1.05 | 1.00 | 1.00 | 1.10 |
| T6 | 1.05 | 1.05 | 1.00 | 1.00 | 1.10 |
| T7 | 1.05 | 1.00 | 1.00 | 1.15 | 1.05 |
| T8 | 1.05 | 1.05 | 1.05 | 0.95 | 1.05 |
| T9 | 1.05 | 1.10 | 1.00 | 1.00 | 1.00 |
| T10 | 1.00 | 1.05 | 1.05 | 1.10 | 1.10 |
| T11 | 1.05 | 0.95 | 1.05 | 1.00 | 1.05 |
| T12 | 1.05 | 1.00 | 1.00 | 0.95 | 1.05 |
| UPFC series injected voltage (Vse ) | 0.010 p.u. | 0.012167 p.u. | 0.0225 p.u. | 0.030000 p.u. | 0.0168 p.u. |
| UPFC series injected voltage phase angle (δse ) | 1.000 rad | 0.937246 rad | 1.2759 rad | 1.000 rad | 1.2544 rad |
| UPFC location | 4–14 | 17–18 | 16–24 | 28–29 | 16–19 |
| RPL | 0.3947 p.u. | 0.3694 p.u. | 0.3463 p.u. | 0.381822 p.u. | 0.3617 p.u. |
| VSL | 0.870 | 0.870 | 0.930 | 0.990 | 1.080 |
Bold font has been used to indicate the proposed algorithm and better performance.
a. RCGA is applied to optimize only RPL denoted as RCGAS.
b. FA is applied to optimize only RPL denoted as FAS.
c. RCGA is applied to optimize both RPL and VSL denoted as RCGAM.
d. FA is applied to optimize both RPL and VSL denoted as FAM.
|
|
|
Fig. 17. P–V curve of the weakest bus for case 3.1 (IPSLP). |
|
|
|
Fig. 18. P–V curve of the weakest bus for case 3.1 (RCGA). |
|
|
|
Fig. 19. P–V curve of the weakest bus for case 3.1 (FAS). |
|
|
|
Fig. 20. Performance characteristics of RCGA and FA for case 3.1. |
6.3.2. Case 3.2: optimization of both RPL and VSL (multi objective case)
With RCGA and FA techniques all the variables are simultaneously optimized for multi-objective case and obtained the values of RPL and VSL given in Table 6 . Here the losses are marginally increased compared to single objective case, but overall multi-objective function i.e., the sum of RPL and reciprocal of VSL, is reduced with both RCGA and FA methods. Compared to case 1.2 and case 2.2, the multi objective function (RPL + 1/VSL) is further reduced as the control variables are simultaneously optimized. Also it is noticed here from the results that the reduction of RPL and improvement of VSL i.e., reduction of multi-objective function, is obtained with FA indicating potentiality and superiority over the RCGA. P–V curves of the weakest bus (multi objective case) are shown in Fig. 21 and Fig. 22 .
|
|
|
Fig. 21. P–V curve of the weakest bus for case 3.2 (RCGAM). |
|
|
|
Fig. 22. P–V curve of the weakest bus for case 3.2 (FAM). |
6.4. Robustness evaluation
To test the robustness of FA, 10 trial runs were performed for New England 39 bus test system. Table 7 , Table 8 and Table 9 show the results of RPL values for case studies 1.1, 2.1 and 3.1. It can be seen here that the optimal RPL obtained by the proposed FA for all the three cases is always nearer to the average value, which is also lesser than RCGA, showing the robustness and superiority of the proposed FA method for the OPF problem of RPL minimization.
| S. No. | Method | RPL | ||
|---|---|---|---|---|
| Best loss value | Worst loss value | Average loss value | ||
| 1 | FA | 0.4203 p.u. | 0.43177 p.u. | 0.42503 p.u. |
| 2 | RCGA | 0.421419 p.u. | 0.426628 p.u. | 0.425843 p.u. |
| 3 | IPSLP | 0.4266 p.u. | NA | NA |
Bold font in Table 7 indicates the results obtained from the proposed algorithm.
| S. No. | Method | RPL | ||
|---|---|---|---|---|
| Best loss value | Worst loss value | Average loss value | ||
| 1 | FA | 0.354563 p.u. | 0.38934 p.u. | 0.37124 p.u. |
| 2 | RCGA | 0.37056 p.u. | 0.39945 p.u. | 0.37685 p.u. |
| 3 | IPSLP | 0.3798 p.u. | NA | NA |
Bold font in Table 8 indicates the results obtained from the proposed algorithm.
| S. No. | Method | RPL | ||
|---|---|---|---|---|
| Best loss value | Worst loss value | Average loss value | ||
| 1 | FA | 0.3463 p.u. | 0.37744 p.u. | 0.36953 p.u. |
| 2 | RCGA | 0.369446 p.u. | 0.38967 p.u. | 0.37374 p.u. |
| 3 | IPSLP | 0.3947 p.u. | NA | NA |
Bold font in Table 9 indicates the results obtained from the proposed algorithm.
7. Conclusion
FA method has been successfully implemented in this paper to find the optimum control variables for OPF problem of RPL minimization (single objective case) and for simultaneous optimization of RPL and VSL (multi-objective case). Transformers tap settings, UPFC location, series injected voltage magnitude and phase angle of UPFC have been considered as control variables. From the results, it is observed that optimization of the control variables for single objective of RPL led to deterioration of VSL, but for multi-objective case, even though the loss has increased slightly, the combined cost function has reduced with significant improvement in VSL. Simulation results of the proposed method are compared with the results of the IPSLP method for single objective of RPL and found that the FA method is superior in loss minimization as the IPSLP technique is not able to find global optimum because non linear device like UPFC is introduced in the system. Also, to compare the simulation results of the proposed algorithm for both single and multi-objective cases, RCGA technique was considered. The results obtained with the FA in all the cases are much better and hence it is concluded that the proposed method has the ability to obtain near global solution with stable convergence characteristics for optimization problems. Thus, the proposed FA may be recommended as a promising algorithm for solving some more complex engineering optimization problems for the future researchers.
Acknowledgement
The authors convey deep sense of gratitude to the management of Annamacharya Institute of Technology and Sciences for helping with required facilities to complete this work.
References
- [1] H.W. Dommel, T.F. Tinny; Optimal power flow solution; IEEE Trans. Power Apparatus Syst, 30 (2002), pp. 469–483
- [2] P. Nagendra, S.H. Dey, T. Datta, S. Paul; Voltage stability assessment of a power system incorporating FACTS controllers using unique network equivalent; Ain Shams Eng. J., 5 (2014), pp. 103–111
- [3] P. Ristanovic; Successive linear programming based optimal power flow solution, optimal power flow solution techniques, requirements and challenges; IEEE Power Eng. Soc (1996)
- [4] J.L. Martinez, A. Ramous, G. Exposito, V. Quintana; Transmission loss reduction by interior point methods: implementation issues and practical experience; IEE Proc. Gener. Transm. Distrib, 152 (2005), pp. 90–98
- [5] L. Gyugyi; The unified power flow controller: a new approach to power transmission control; Presented at; 1994 IEEE Summer Meeting, paper No.94-SM 474-7 (1994)
- [6] M. Noroozian, L. Angquist, M. Ghandhari, G. Anderson; Use of UPFC for optimal power flow controller; IEEE Trans. Power Deliv, 12 (1997), pp. 1629–1634
- [7] G. Glanzman, G. Anderson; Coordinated control of FACTS based on optimal power flow; Proceedings of 37th annual North America Power Symposium Ames, IA, October 23–25 (2005)
- [8] V. Ajjarpu, C. Christy; The continuation power flow: a tool for steady state voltage stability analysis; IEEE Trans. Power Syst, 7 (1992), pp. 416–423
- [9] F. Milano, C.A. Canizares, A.J. Conejo; Sensitivity-based security constrained OPF market clearing model; IEEE Trans. Power Syst, 20 (2005), pp. 2051–2060
- [10] M.A. Abido; Optimal power flow using particle swarm optimization; Electr. Power Energy Syst, 24 (2002), pp. 563–571
- [11] M.A. Abido; Optimal power flow by using tabu search algorithm; Electr. Power Compon. Syst, 30 (2002)
- [12] M. Tripathy, S. Mishra, L.L. Lai, Q.P. Zhang; Transmission loss reduction on FACTS and bacteria foraging algorithm; Parallel Problem Solving from Nature – PPSN IX, vol. 4193 (2006), pp. 222–231
- [13] A.A. Abou El Ela, M.A. Abido, S.R. Spea; Optimal power flow using differential evolution algorithm; Electr. Power Syst. Res, 80 (2010), pp. 878–885
- [14] S. Duman, U. Guvenc, Y. Sonmez, N. Yorukeren; Optimal power flow using gravitational search algorithm; Energy Convers. Manag, 59 (2012), pp. 86–95
- [15] G. Wang, L. Guo, H. Duan, H. Wang, L. Liu, M. Shao; Hybridizing harmony search with biogeography based optimization for global numerical optimization; J. Comput. Theor. Nanosci, 10 (2013), pp. 2312–2322
- [16] G.-G. Wang, A.H. Gandomi, X. Zhao, H. Cheng, E. Chu; Hybridizing harmony search algorithm with cuckoo search for global numerical optimization; Soft Comput (2014) http://dx.doi.org/10.1007/s00500-014-1502-7
- [17] G. Wang, L. Guo, H. Wang, H. Duan, L. Liu, J. Li; Incorporating mutation scheme into krill herd algorithm for global numerical optimization; Neural Comput. Appl, 24 (2014), pp. 853–871
- [18] G.-G. Wang, A.H. Gandomi, A.H. Alavi; An effective krill herd algorithm with migration operator in biogeography based optimization; Appl. Math. Model, 38 (2014), pp. 2454–2462
- [19] G.-G. Wang, L. Guo, A.H. Gandomi, G.-S. Hao, H. Wang; Chaotic krill herd algorithm; Inf. Sci. (Ny), 274 (2014), pp. 17–34
- [20] L. Guo, G.-G. Wang, A.H. Gandomi, A.H. Alavi, H. Duan; A new improved krill herd algorithm for global numerical optimization; Neurocomputing, 138 (2014), pp. 392–402
- [21] G.-G. Wang, A.H. Gandomi, A.H. Alavi; Stud krill herd algorithm; Neurocomputing, 28 (2014), pp. 363–370
- [22] G.G. Wang, A.H. Gandomi, A.H. Alavi, G.S. Hao; Hybrid krill herd algorithm with differential evolution for global numerical optimization; Neural Comput. Appl, 25 (2014), pp. 297–308
- [23] G.-G. Wang, S. Deb, Z. Cui; Monarch butterfly optimization; Neural Comput. Appl (2015) http://dx.doi.org/10.1007/s00521-015-1923-y
- [24] X.S. Yang; Firefly algorithm; Nature Inspired Metaheuristic Algorithms, Luniver Press, Beckington, UK (2008), pp. 81–89
- [25] X.S. Yang; Firefly algorithm: stochastic test functions and design optimization; Int. J. Bioinspired Comput, 2 (2010), pp. 78–84
- [26] X.S. Yang; Firefly algorithm for multimodal optimization; SAGA, 20 (5792) (2009), pp. 169–178
- [27] I. Fister, I. Fister Jr., X.-S. Yang, J. Brest; A comprehensive review of firefly algorithms; Swarm Evol. Comput, 13 (2013), pp. 34–46
- [28] S. Padhan, R.K. Sahu, S. Panda; Application of firefly algorithm for load frequency control of multi-area interconnected power system; Electr. Power Compon. Syst, 42 (2014), pp. 1419–1430
- [29] G.-G. Wang, L. Guo, H. Duan, H. Wang; A new improved firefly algorithm for global numerical optimization; J. Comput. Theor. Nanosci, 11 (2014), pp. 477–485
- [30] S. Shamshirband, D. Petkovic, N.T. Pavlovic, C. Sudheer, T.A. Altameem, A. Gani; Support vector machine firefly algorithm based optimization of lens system; Appl. Opt, 54 (2015), pp. 37–45
- [31] L. Olatomiwa, S. Mekhilef, S. Shamshirband, K. Mohammadi, D. Petkovic, C. Sudheer; A support vector machine-firefly algorithm based model for global solar radiation prediction; Sol. Energy, 115 (2015), pp. 632–644
- [32] I. Fister Jr., M. Perc, S.M. Kamal, I. Fister; A review of chaos-based firefly algorithm: perspectives and research challenges; Appl. Math. Comput, 252 (2015), pp. 155–165
- [33] M.H. Sulaiman, M.W. Mustafa, Z.N. Zakaria, O. Alimano, S.R.A. Rahim; Firefly algorithm technique for solving economic dispatch problem; Power Engineering and Optimization Conference, Melaka, Malaysia, 6–7 June (2012)
- [34] B. Venkateswararao, G. Venakata Nagesh Kumar; Optimal location of Thyristor controlled series capacitor to enhance power transfer capability using firefly algorithm; Electr. Power Compon. Syst, 42 (2014), pp. 1541–1552
- [35] M. Tripathy, S. Mishra; Bacteria foraging based solution to optimize both real power loss and voltage stability limit; IEEE Trans. Power Syst, 22 (2007), p. 1
- [36] E. Acha, C.R. Feurte Esquivel, H. Ambritz-Perez, C. Angeles-Camacho; Modeling and Simulation in Power Network; John Wiley and Sons Ltd. (2004)
- [37] N. Amjady, H. Nasiri; Economic dispatch using an efficient real coded genetic algorithm; IET Gener. Transm. Distrib, 3 (2008), pp. 266–278
- [38] A. Balnco, M. Delgado, M.C. Pegalair; A real coded genetic algorithm for training recurrent neural networks; Neural Netw, 14 (2001), pp. 93–105
- [39] S. Panda, S.C. Swain, A.K. Baliarsingh; Real coded genetic algorithm for robust coordinated design of excitation and SSSC based controller; J. Electr. Eng, 8 (2008), pp. 31–38
- [40] S. Mishra, M. Tripathy, J. Nanda; Multi-machine power system stabilizer design by rule based bacteria foraging; Electr. Power Syst. Res, 77 (2007), pp. 1595–1607
Document information
Published on 10/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?