Abstract
Spectral response measurements of germanium-based triple-junction solar cells were performed under a variety of light and voltage bias conditions. Two of the three junctions exhibited voltage and light bias-dependent artifacts in their measured responses, complicating the true spectral response of these junctions. To obtain more insight into the observed phenomena, a set of current-voltage measurement combinations were also performed on the solar cells under identical illumination conditions, and the data were used in the context of a diode-based analytical model to calculate and predict the spectral response behavior of each junction as a function of voltage. The analysis revealed that both low shunt resistance and low breakdown voltages in two of the three junctions influenced the measured quantum efficiency of all three junctions. The data and the modeling suggest that combination of current-voltage measurements under various light bias sources can reveal important information about the spectral response behavior in multijunction solar cells.
Introduction
With significant advances in high-efficiency multijunction solar cell (MJSC) technologies, the number of subcells within each structure has steadily increased over the years with the goal of maximizing the operating voltage while preserving the other performance parameters such as the short circuit current (Isc) and the fill factor [1-6]. Recently, five-junction solar cells based on semiconductor bonded technology have demonstrated confirmed non-concentrator terrestrial air mass 1.5 global spectrum power conversion efficiency of ≈ 39% [7] and concentrator 4-junction cell efficiencies of 46% [8]. With increased complexities in design and architecture of these types of cells, the task of performing electrical characterization and spectral response (SR) measurements of the cells will also become more involved. Although there are well-established procedures for performing current–voltage (I–V) or spectral response measurements in MJSCs [9, 10], it has been shown previously that certain factors such as low shunt resistance [11-17], low reverse breakdown voltage [10, 18] or luminescence coupling [12, 19-25] can cause artifacts in the spectral response or the quantum efficiency (QE) of the device.
Luminescence coupling is usually a factor between two adjacent junctions and its effects generally appear as an increased QE signal in the wavelength range corresponding to energies above the bandgap of the current-limited junction [24-26]. It has also been reported that luminescence coupling has a light bias intensity dependence, resulting in a decrease in QE of the junction of interest with an increase in the light bias intensity of the junction above it [12]. This reduction factor is substantially dependent on the LC coupling coefficients between the junctions. When considering artifacts originating mostly from shunt and breakdown voltage issues, most of the work reported to-date in QE measurements of MJSCs, particularly 3-junction cells based on a germanium (Ge) bottom cell (BC), has been focused on cases where only a single junction has been found to behave nonideally. If the nonideality is due to a low breakdown voltage only, then an applied voltage bias of enough magnitude is able to fully recover the QE of the junction of interest without much dependence on the light bias intensity [18]. If the junction of interest suffers from a low shunt resistance, increasing the light bias intensity of the nonlimiting junctions and application of a voltage bias is generally needed to achieve a good measurement of the QE signal [14]. There are even reported cases where a combination of luminescence coupling and low shunt resistance affect the QE response of the Ge junction [12].
Although generalized opto-electronic models have been proposed that combine and explain a variety of simultaneous effects in MJSCs measurements [21], it is still very illuminating to consider simpler analytical models to explain the influence of the most severe artifacts in certain devices. Our aim has particularly been focused on cells where two junctions revealed both low shunt resistance and low breakdown voltage effects and when LC has not been a major factor in causing artifacts in the QE response of the junctions. Even though several previous works have been dedicated to this subject and some variations of it [10, 12, 14-18], we found that significant insight can be obtained into the behavior of each junction when we first investigated the I–V response of one of these types of cells under several combinations of light sources where each light source is a high-power light emitting diode (LED) with a unique wavelength emission peak suitable to light bias a single junction. For a triple junction cell, this approach involves eight combinations of measurements (3 single-LED illuminations, 3 double LED combinations, one triple LED illumination, and one with no illumination). These data can then be used within the context of a straight-forward two-diode equivalent circuit (EC) model to determine a set of parameters that will fit all eight data combinations at once. This technique eliminates the need for separate iso-cell measurements for parameter estimates because there are sufficient data to allow for obtaining good fits to the data. After the EC model parameters are determined, the results are used to predict SR and QE of each junction with similar levels of light bias as a function of voltage and compare the findings to the experimental results. We generally find very good agreement between the predicted model results and the experimental data. When more than one junction suffers from nonideal shunt and breakdown voltage effects generally caused during manufacturing or nonoptimal material processing, the ideal diode-like behavior expected from a well-fabricated p-n junction is nonexistent. In these cases, the QE measurement of the intended junction will reveal artifacts originating from all of the nonideal junctions, in a combined way. Furthermore, in almost all cases studied, the magnitude of the measured QE itself, as measured across the two terminals of the entire stack, will be less than the individual junctions’ actual QE response, even under the best voltage bias conditions.
Experimental
For this study, the samples were monolithic, two-terminal triple junction GaInP/GaAs/Ge solar cells of commercial grade with a nominal area of 2.3 cm2 and air mass (AM) 1.5 G 1-sun efficiency of 27% at 25°C [4]. The current-voltage and the spectral response data reported here are representative of multiple solar cells tested within the batch received. Combinations of current-voltage measurements were performed with a source-meter electrometer and three high-power LEDs with projector optics illuminating the entire area of the cell with bright illumination beams of good uniformity. The spectral irradiance of all three LEDs at the incident plane of illumination, was measured by a calibrated spectroradiometer. The irradiance has a Gaussian form, with the three-center wavelengths at 520 nm, 741 nm, and 1077 nm. All three LEDs were operated with battery sources close to their rated source current values for better control over signal-to-noise ratios when performing differential QE measurements. The reported irradiance values for each LED were obtained by integrating the spectral irradiance curves over wavelength. For QE, a dual-light source monochromator set up was used, utilizing the principle of differential spectral response (DSR) measurement as described previously [27] with calibrated monitor detectors from 300 nm to 1900 nm, allowing for simultaneous measurements of the cell photocurrent and the incident monochromatic beam power. The monochromator beam was chopped by a mechanical chopper, hence generating a small AC photocurrent that is collected via a transimpedance preamplifier with the ability to separate AC and DC components of the signal and built-in voltage bias capability. The AC signal of the cell was measured by a lock-in amplifier. The voltage bias was applied in the forward bias direction of the cell operation from 0 V to values slightly higher than the open circuit voltage, Voc, of the cell under the illumination conditions to verify modeling results. Although application of higher voltage amounts is possible, it can lead to significant instability in the recorded AC lock-in signal. The monochromator measurement uncertainty for spectral response measurements under low voltage bias is generally better than 1%. This includes the uncertainty of the reference photodiode and the transfer calibration onto the monitor diode, the repeatability and reproducibility measurements and the standard deviation of the collected data. However, at bias voltages approaching the Voc, it can reach 5% or more, mostly due to signal instability.
The Modeling Framework
In this section, we first describe the mathematical model used to fit the composite I–V curve data under each unique lighting condition. Then, by use of a simplified analysis, we demonstrate how the true value of the spectral response of a given junction is affected by various artifacts.
Mathematical model for each junction
We consider a typical two-diode model for each junction [28], with its corresponding shunt and series resistances. The implicit current density versus voltage J–V curves for each junction can be written in the forward bias direction:
|
|
(1) |
and in reverse bias direction:
|
|
(2) |
where is the photocurrent density of the ith junction, is the saturation current density, is the saturation current density for the depletion region, is the device area, is the ideality factor, is the shunt resistance, is the series resistance, is the Miller index and is the breakdown voltage. In equation (2), a multiplicative factor is added to account for the cells avalanche breakdown in the reverse bias [28]. We define the differential spectral responsivity of each junction as the difference in its short circuit current between the two chopper states of closed and open, r, divided by the power of the incident monochromatic beam. The difference between these two current densities is simply:
|
|
(3) |
Note that in reality, in a MJSC, only the voltage across the entire cell stack can be fixed, say at 0 V, leaving each junction under a different operating voltage. However, this definition is consistent with single-cell measurements where the short circuit current is the quantity of interest for spectral response measurements. For a very small value of r, which is the case for differential monochromator-based measurements, this change is equivalent to a small displacement of the entire curve, in an amount equal to r.
To calculate the composite curve for the entire cell, which constitutes the series sum of the individual junction , first the best fit parameters for each implicit equation corresponding to each junction are selected and the functional form is calculated. Inverting these functions and obtaining curves then allow for summation of the voltages at fixed current values. Finally, this composite curve can be inverted back to the form. As it will be described in 'Discussion and Results', the objective of this modeling was to obtain the best fit parameters from as many combination I–V curves as possible so that a robust estimate of the voltage bias dependence of the spectral responsivity of each junction can be made. Here, by best fit, we mean the best visual fit of the model to the experimental data, that is, no least square calculations were employed.
Factors limiting the spectral response measurements
The mathematical model given by equations (1) and (2) allows for determination of the relationship between the measured spectral response quantity, which is influenced by the whole composite curve and measured at the terminals, and the real increase of the zero-voltage current for the junction of interest. We have observed that in cases where one or more junctions have nonideal diode properties, application of a voltage bias or light bias will not fully recover the entire value r, as desired. Although this concept can be mathematically explained by use of equations (1) and (2), here we present a simplified case that demonstrates this point well.
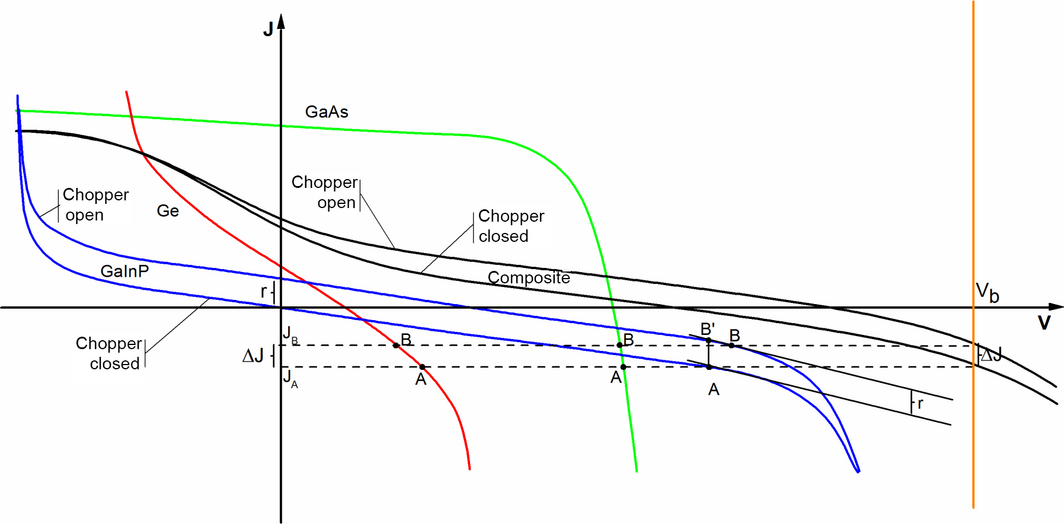
Figure 1 shows an example of an MJSC case with a well-behaved GaAs junction but with faulty Ge and GaInP junctions with low shunt resistances and low breakdown voltages. The plotted J–V curves are representative of the sort of behavior we have seen in our measurement and modeling work. This plot represents a case where the intention is to extract the SR of the GaInP junction by light biasing the Ge junction (with the 1077 nm LED) and the GaAs junction (with the 741 nm LED), while light modulating the GaInP junction with the much weaker 520 nm monochromatic light. For the sake of clarity, the J–V curve corresponding to the open chopper state is drawn in an expanded view with an exaggerated r value, but in reality, r is many orders of magnitude smaller than the other two junctions’ light bias-induced short circuit current values. Given this, the composite J–V curve can be constructed for both chopper states, showing that points A and B represent the actual operating points for each curve as the chopper turns. Points A and B on each versus curve are close enough so that the segments of the curves joining these points are parts of straight lines. Point B’ on the chopper-open GaInP J–V curve is a point that shares the same voltage with point A of the chopper-closed GaInP J–V curve. The effect of opening the chopper can be approximated as an upward shift of the J–V curve equal to r. However, it can be seen from the graphics that the actual operating point for the chopper-open curve is point B for the given . We now can apply equations of straight lines with their corresponding slope and origin intercept to this region. In the low voltage bias range, we can think of the GaInP versus curve (blue curve) for the open chopper state to be equal to the versus curve with the closed chopper case, but being displaced upwards by a value , making the tangents to the points A and B’ parallel. The zero-intercept value of the BB’ line is equal to the line tangent at A plus . We are not interested in B’ but as is so small, we can consider that B and B’ share the same tangent line. So, the following four linear equations for the versus graphics near the points A and B for all 4 curves are evident:
|
|
(4) |
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
|
Figure 1. versus curves for each junction of a triple junction solar cell presenting a good diode-like GaAs junction behavior in contrast to Ge and GaInP junctions exhibiting low shunt resistances and low breakdown voltages. While Ge and GaAs junctions are light biased, the GaInP junction is only light modulated with a chopped monochromatic beam. Its short circuit current density rise is very small, but is exaggerated for demonstration purposes. |
Since the three junctions are in series, the current density through them is the same and we sum the voltages to obtain the versus relations, with the chopper closed and open:
|
|
(8) |
|
|
(9) |
From this set of equations, we calculate the current density that passes through the cell when the chopper is closed and open and when a certain voltage bias applied:
|
|
(10) |
|
|
(11) |
The difference between these two current densities is the amplitude of the AC current density that is actually being measured:
|
|
(12) |
is always lower than the change in the short circuit current density of the junction being measured, but gets close to it only as we tend to certain values for the slopes of the versus curves. This behavior can be easily understood by observing the following limit:
|
|
(13) |
Equation (12) indicates that the measurement of the spectral response of one junction, such as the GaInP junction, can be affected by the J–V characteristics of the other junctions as well. Furthermore, it can be seen from equation (13) that having a higher intensity light bias on the Ge junction would make larger, therefore increasing the closer to the r limit, in essence increasing the measured spectral response of the GaInP junction. The section on 'Voltage bias dependence of spectral response' discusses this issue in detail.
The responsivity of a junction is defined as:
|
|
(14) |
where P is the monochromatic beam power. However, the measurement gives the following value:
|
|
(15) |
Therefore, the ratio of these two quantities, describes a factor that effectively reduces the spectral response from its maximum expected value:
|
|
(16) |
In the section on the 'Voltage bias dependence of spectral response', it will be shown that this ratio is close to 1 for well-behaved junctions and lower than 1 for bad cases of low shunt resistance or breakdown voltages. This ratio can be extracted from combinations of I–V measurements at a representative wavelength for each junction, prior to performing any spectral response measurements.
Discussion and Results
Performing a set of I–V measurements of the cell under all possible combinations of the three LED light sources prior to performing QE measurements can significantly help in determining: (1) which junctions are likely to be affected by artifacts, (2) what level of light and voltage bias should be used to obtain the best measurement results, and finally (3) how the best QE measurement results compare with model predictions for the maximum QE that each junction is able to produce internally.
Combinations of I–V measurements
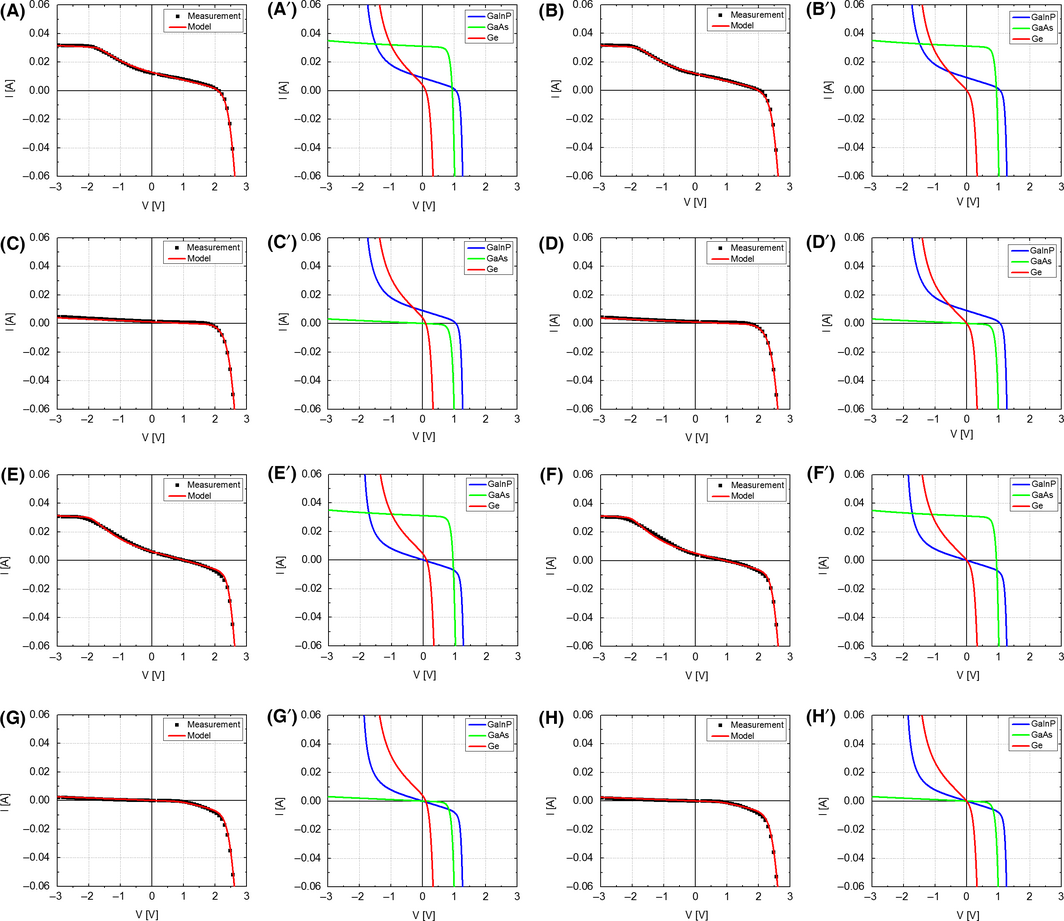
In order to use the mathematical model described in 'Mathematical model for each junction' to predict the SR behavior, the values of all the parameters in equations (1) and (2) need to be determined as accurately as possible. This was accomplished by performing eight combinations of I–V measurements on the solar cell, with three unique LEDs appropriate for generating a photocurrent signal in each of the junctions. These were the 520 nm LED for excitation of the GaInP junction, the 741 nm LED for the GaAs junction, and the 1077 nm LED for the Ge junction. The best fit parameters for each junction are chosen so that the calculated composite I–V curve gives the best fit to the measured cells I–V curve for each of the eight unique measurements. Figure 2(aa’–hh’) show all the eight different combinations of I–V measurements possible, with the modeled and measured composite I–V curves on the left panel and the individual junction I–Vs under the given illumination conditions on the right panel. Note that if the cell has either one or no nonideal junctions, it will suffice to perform just one I–V curve measurement with all three LEDs on to obtain a good estimate of the parameters. However, in a case such as this where two junctions have poor diode qualities, data from additional combinations of I–V measurements significantly improve the estimate of the parameters. The modeling results here indicate that both the GaInP junction and the Ge junction suffer from low shunt resistance and low breakdown voltages [14, 18].
|
|
|
Figure 2. versus curves measured with eight combinations of the three different light biases. For each case, we show the measurement and the models best fit on the left panel and the modeled curves for each junction on the right panel. The eight cases are as follows: (A) All three LEDs on. (B) 520 and 741 nm LEDs on. (C) 520 and 1077 nm LEDs on. (D) 520 nm LED on. (E) 741 and 1077 nm LEDs on. (F) 741 nm LED on. (G) 1077 nm LED on. (H) No LED on. |
The two-diode model seems to provide a reasonably good fit to the various composite I–V curves. However, even a single-diode model may be sufficient for obtaining reasonable fits to the data. The data fitting, especially in the forward bias direction, could potentially be improved further with additional circuit elements and fit parameters, but those additions will add complexities to the simple model presented here.
Table 1 reports the values of the fit parameters for each junction. As expected, the shunt and breakdown voltage values for the GaInP and the Ge junctions are lower than what has typically been reported for solar cells [14] The photocurrent density values correspond to cases where the junctions are illuminated by their respective LEDs, that is, would be zero for an LED off-state for a particular junction. The Miller indices are set to 3, as suggested elsewhere [28].
| Junction | Rs [Ω] | Rsh [Ω] | Jph [A/m2] | J01[A/m2] | J02 [A/m2] | n | nm | Vbd [V] |
|---|---|---|---|---|---|---|---|---|
| GaInP | 0.5 | 145 | 39.1 | 2.2 × 10−19 | 3 × 10−5 | 3.3 | 3 | −2 |
| GaAs | 0.5 | 1000 | 134.8 | 4.3 × 10−15 | 2.2 × 10−4 | 2.8 | 3 | −10 |
| Ge | 0.5 | 45 | 17.4 | 4.3 × 10−8 | 2.2 | 2.5 | 3 | −1.8 |
Voltage bias dependence of spectral response
Once the I–V curve parameters are determined, the measured spectral response behavior as a function of voltage can be calculated and compared to the measured data. This calculation is based on the modeled junction I–Vs and not based on equation (12) which was derived with a simpler explanation of the observed effects. Furthermore, the important ratio can also be plotted as a function of to see the discrepancy between the measured SR of a junction versus the predicted response from the modeled individual I–V curve. Since the SR is a differential measurement, the mechanical motion of the chopper results in a pair of I–V composite curves, one for when the chopper blocks the monochromatic light and one for when it unblocks it. The SR calculations are straightforward. Taking the GaInP junction as an example, the individual I–V curves for GaAs and Ge junctions are simulated under the 741 nm and the 1077 nm LEDs ‘on’, and the I–V curve for GaInP junction is simulated under dark (520 nm LED ‘off’). A second simulation of this case is run again, with the singular difference that a small photocurrent value is picked for the GaInP junction to simulate its response under the open chopper scenario. This value is many orders of magnitude lower than the other two photocurrent values, just as is the case in actual measurements. From this result, the change due to photogenerated current in the GaInP junction at 0 V, r, is calculated from the simulated subcell J–V curve. This of course is proportional to the real responsivity of the junction. However, the actual quantity that is measured, , is proportional to , the difference in the composite current between the two chopper states of on and off, as previously shown in Figure 1. is also obtained from the simulation as a function of bias voltage. Plotting the calculated ratio as a function of voltage is very revealing; for example, it can show whether a true, artifact-free spectral response for a given junction can be obtained from a measurement.
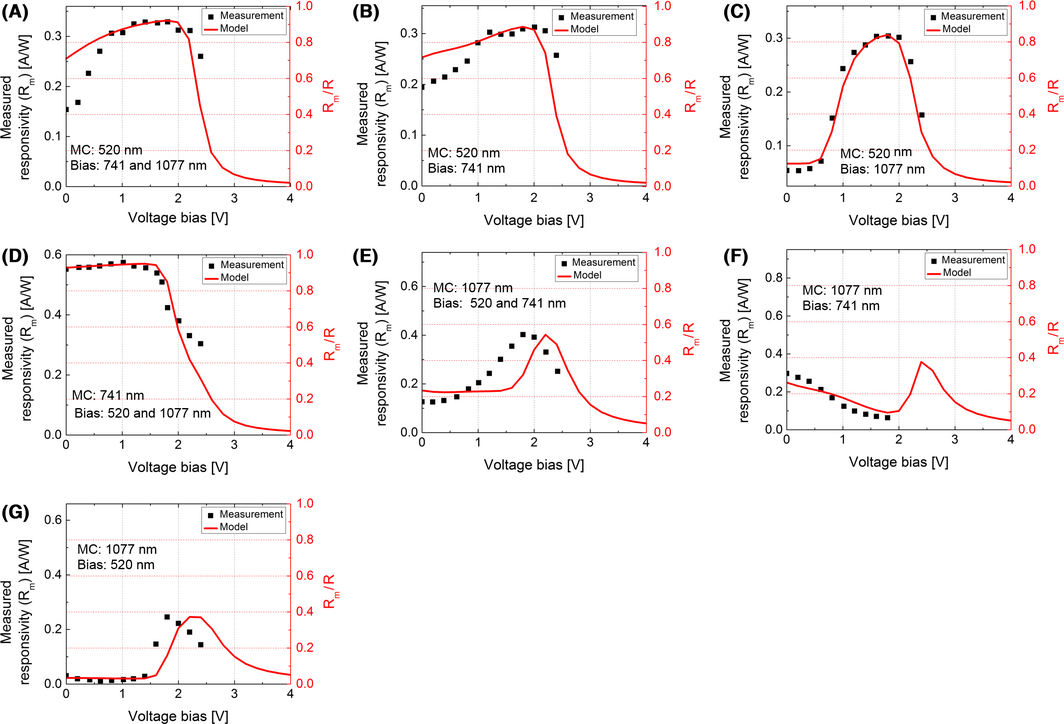
Figures 3A–C show the calculated and measured spectral response as a function of for the GaInP junction with the monochromator (MC) wavelength at 520 nm and the following light bias scenarios: (A) both 741 and 1077 nm LEDs, (B) only the 741 nm LED, and (C) only the 1077 nm LED. The left Y-axis represents the measured and calculated responsivities and the right Y-axis simultaneously shows the ratio , obtained purely from the calculations. Remembering that a ratio means that the measured responsivity is equal to the actual junction responsivity, that is, photocurrent generated in the junction is the photocurrent measured at the terminals, two important observations can be made here: First, the diode-based model predicts the dependence of the responsivity relatively well, predicting a peak response that can be achieved by an application of ≈ 1.8 V in all three cases with the exception that both combinations of the 1077 and 741 nm LEDs are needed to obtain the maximum response. Note that beyond the peak value, the responsivity should drop to 0, as the data also suggest, though the DSR measurement becomes very unstable at higher . The second observation is that in Figure 3A, is reaching a maximum value at 0.92 for the GaInP junction, meaning that no matter what voltage bias is used, 8% of the GaInP-generated photocurrent can never be recovered at the external terminals.
|
|
|
Figure 3. Measurements of the spectral response versus voltage bias for fixed wavelengths corresponding to a region of responsivity of a given junction: (A–C) GaInP junction response with ac monochromatic (MC) wavelength of 520 nm and dc bias lights as labeled. (D) GaAs junction with ac monochromatic wavelength of 741 nm and dc bias wavelengths of 520 and 1077 nm. (E and F) Ge junction response with ac monochromatic wavelength of 1077 nm and dc bias lights as labeled. |
Figure 3D shows the dependence of the responsivities for the GaAs junction, with the monochromator wavelength at 741 nm, and both the light bias 520 and 1077 nm LEDs on. The data and the model are in good agreement here, showing no significant dependence until the responsivity drops at higher voltages. This behavior is consistent with the high breakdown voltage and high shunt resistance of the GaAs junction. Yet, the ratio for this junction is at 0.96, indicating that the poor behavior of the other two junctions slightly affects the maximum measured responsivity of an otherwise ideal junction. The other two light bias cases for this junction were similar and are therefore not shown.
Finally, Figure 3E–G show the dependence of the responsivities for the Ge junction, with the monochromator wavelength at 1077 nm and the light bias scenarios: (E) both 520 and 741 nm LEDs on, (F) with only 741 nm LED on, and (G) with only 520 nm LED on. Although there are small discrepancies between the modeled and measured results, the findings are similar to the GaInP case in that a peak response is achieved at a voltage bias higher than 0 V, typically around 2 V. One notable exception is that unlike the GaInP junction measurements, the maximum for the Ge junction is 0.55, indicating that a much smaller photogenerated current value is extracted at the terminals for this junction. A portion of this 45% photocurrent loss can be recovered for the Ge junction if the 520 nm LED intensity were increased.
We believe that the discrepancies observed between the model and the data, particularly at the low voltage values for Figure 3A and B and the shifts in the peak positions for Figure 3E and F, originate from imperfections of the double-diode I–V model in capturing all the relevant physics inside these imperfect devices. Since we are using the parameters strictly obtained from I–V curve fits, we do not make any alterations or adjustments to the individual ratio plots afterwards. Actual spectral response measurements are differential lock-in based measurements and furthermore, the monochromatic light intensity is very low and hence it is possible that there are nonlinearity or second-order effects present between the monochromator “on” and “off” states that we have not captured in our simulations; that is, it is possible the shape of the I–V curve for the chopper-on and chopper-off states change slightly. There is no way for us to know this, because our instruments are not sensitive to this while there is a large light bias signal present on the other junctions. The purpose of this section is to show that it is possible to understand the voltage bias behavior but the exact source of discrepancy between the model and the data is beyond the scope of this work.
Complete wavelength measurements
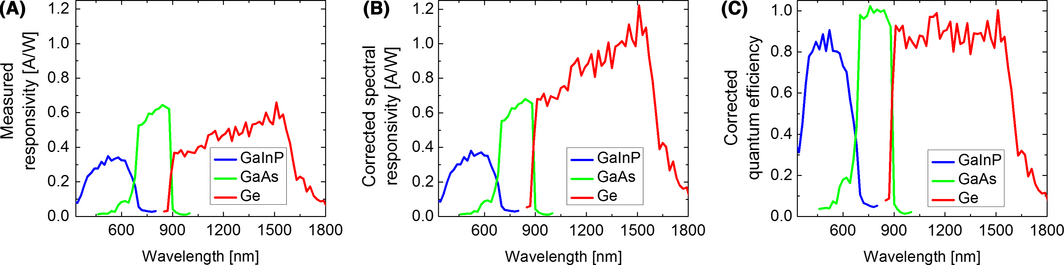
Now that the voltage dependence of the SR has been described at fixed wavelengths within the regions of responsivity of each junction, we now turn our attention to the full wavelength measurements for all three junctions. Figure 4A shows the measured spectral responses of all three junctions under the best voltage bias conditions and light bias conditions corresponding to LED light intensities of 116 , 228 and 31 for the 520 nm, 741 nm, and the 1077 nm LEDs, respectively. Notice that the nonzero photocurrent response for the GaInP top cell in the region is likely due to some leaked photocurrent from the GaAs middle cell due to the low shunt resistance values of the Ge and the GaInP subcells. However, the nonzero response (0.03 A/W) for the Ge junction for is related to LC from the middle junction. The calculated ratios for each junction from the previous section are used as correction factors for each corresponding curve. The corrected spectral response results are plotted as in Figure 4B. The largest correction factor of 1/0.55 for the Ge junction substantially increases the responsivity of that junction, to values expected from a well-behaved Ge junction. In Figure 4C, the corrected QE curves are also shown for reference.
|
|
|
Figure 4. The complete spectral response measurements of all three junctions. (A) Best SR measurements under a given set of bias light and voltage conditions. (B) The corrected spectral responsivity according to the model. GaInP, GaAs and the Ge measured responsivities in (A) are multiplied by the correction factors 1/0.92, 1/0.96, and 1/0.55, respectively. (C) Quantum efficiency obtained after the corrections in (B). |
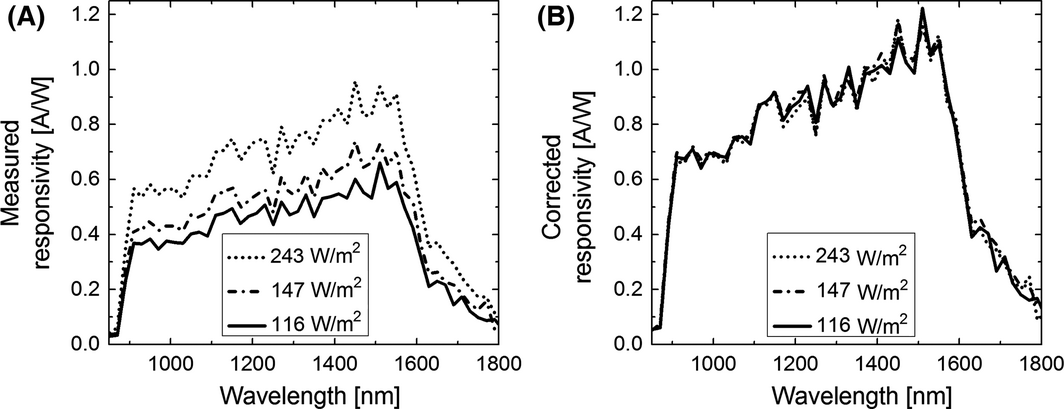
Furthermore, the analytical model allows one to predict the magnitude of the light bias needed to obtain the best QE measurement for the affected junctions. Focusing on the Ge junctions response, we know that the poor diode behavior of the GaInP junction is partially to blame for Ges low SR values. Applying a stronger light bias to the GaInP junction should shift the operating voltage point for that junction farther to the right towards a higher shunt resistance region, that is, , causing , hence approaching the corrected SR curve. To show this trend, the 520 nm LED intensity was progressively increased from the initial value of 116 to 147 and 243 while the 741 nm LED was kept fixed at 228 , partially to maintain the effect of LC between the GaAs and the Ge junctions at a fixed level. To calculate the model predicted ratios, a linear relationship was assumed between the 520 nm LED light intensity and the photogenerated current in the GaInP junction as a result. The predicted ratios for the Ge junction should rise from 0.55 to 0.63 and finally to 0.81 for the three 520 nm LED light intensity settings. Figure 5A and B show the results of these three measurements for the Ge junction, and the corrected Ge responsivities based on these calculated ratios. The plots indicate good agreement between the model and the measurements and show that all three distinct curves can be collapsed onto one curve, within the context of the simple analytical model. Since the 741 nm bias light was kept constant for all three measurements and only the 520 nm light was changed, the luminescence coupling between the middle and the bottom junctions were mostly unchanged as evidenced by the plateau below 870 nm. So the shunt resistance effect is the dominant mechanism affecting the QE response of these devices.
|
|
|
Figure 5. (A) Spectral responsivity of the Ge junction with different intensities of the 520 nm LED light bias, while keeping the 741 nm LED light intensity constant and . (B) Agreement between the measurements after multiplying each curve by the correction factors predicted by our model. |
Conclusions
Combinations of I–V measurements under various types of light bias sources were used within the context of an analytical two-diode I–V curve model to predict the voltage bias and light bias dependence of the differential spectral response measurements in a triple junction solar cell. The solar cells studied for this work were Ge based, with both the GaInP and the Ge junctions presenting severe cases of low shunt resistance and low reverse bias breakdown voltages. We have shown that these conditions can significantly affect the spectral response measurements of all three junctions, with the Ge junction affected the most. Our work suggests that it is valuable to perform these sets of current voltage measurements and subsequent analysis prior to any spectral response measurements so that one can choose a priori how to set up, or what to expect from, the DSR measurements.
Acknowledgments
B. H. Hamadani thanks H. Yoon of NIST for useful discussions and providing reference detectors for calibrations of the spectral response system, J. Roller for writing the computer code needed to run the system, and Matthew Lumb of the Naval Research Laboratory for useful discussions. J. P. Babaro expresses his gratitude to NIST for the hospitality during his stay, while this work was done.
Conflict of Interest
None declared.
References
- Cotal, H., C. Fetzer, J. Boisvert, G. Kinsey, R. King, P. Hebert et al. 2009. III–V multijunction solar cells for concentrating photovoltaics. Energy Environ. Sci.2:174.
- Kurtz, S., and J. Geisz. 2010. Multijunction solar cells for conversion of concentrated sunlight to electricity. Opt. Express18:A73–A78.
- Yamaguchi, M.2003. III-V compound multi-junction solar cells: present and future. Sol. Energy Mater. Sol. Cells75:261–269.
- Yoon, H., J. E. Granata, P. Hebert, R. R. King, C. M. Fetzer, P. C. Colter et al. 2005. Recent advances in high-efficiency III-V multi-junction solar cells for space applications: ultra triple junction qualification. Prog. Photovoltaics Res. Appl.13:133–139.
- Boisvert, J., D. Law, R. King, D. Bhusari, X. Liu, A. Zakaria et al. 2010. Development of advanced space solar cells at Spectrolab. 35th IEEE Photovolt. Spec. Conf., 123–127.
- King, R. R., C. M. Fetzer, D. C. Law, K. M. Edmondson, H. Yoon, G. S. Kinsey et al. 2007. Advanced III-V multijunction cells for space. Conf. Rec. 2006 IEEE 4th World Conf. Photovolt. Energy Conversion, WCPEC-4, 2:1757–1762.
- Chiu, P. T., D. C. Law, R. L. Woo, S. B. Singer, D. Bhusari, W. D. Hong et al. 2014. 35.8% space and 38.8% terrestrial 5J direct bonded cells. IEEE 40th Photovolt. Spec. Conf.
- 2014. Press Release, Fraunhofer Institute for Solar Energy Systems, 1 December 2014.
- ASTM Standard E2236-10: Standard test methods for measurement of electrical performance and spectral response of non-concentrator multijunction photovoltaic cells and modules.
- King, D. L., B. R. Hansen, J. M. Moore, and D. J. Aiken. 2000. New methods for measuring performance of monolithic multi-junction solar cells. Conf. Rec. Twenty-Eighth IEEE Photovolt. Spec. Conf. - 2000 (Cat. No.00CH37036), 1197–1201.
- Li, J.-J., S. H. Lim, and Y.-H. Zhang. 2012. A novel method to eliminate the measurement artifacts of external quantum efficiency of multi-junction solar cells caused by the shunt effect. Proc. SPIE, 8256:825616–825623.
- Li, J.-J., S. H. Lim, C. R. Allen, D. Ding, and Y.-H. Zhang. 2011. Combined effects of shunt and luminescence coupling on external quantum efficiency measurements of multijunction solar cells. IEEE J. Photovolt.1:225–230.
- Li, J.-J., and Y.-H. Zhang. 2013. Elimination of artifacts in external quantum efficiency measurements for multijunction solar cells using a pulsed light bias. IEEE J. Photovolt.3:364–369.
- Meusel, M., C. Baur, G. Letay, A. W. Bett, W. Warta, and E. Fernandez. 2003. Spectral response measurements of monolithic GaInP/Ga(In)As/Ge triple-junction solar cells: measurement artifacts and their explanation. Prog. Photovoltaics Res. Appl.11:499–514.
- Paraskeva, V., M. Hadjipanayi, M. Norton, M. Pravettoni, G. E. Georghiou. 2013. Voltage and light bias dependent quantum efficiency measurements of GaInP/GaInAs/Ge triple junction devices. Sol. Energy Mater. Sol. Cells116:55–60.
- Pravettoni, M., R. Galleano, A. Virtuani, H. Müllejans, and E. D. Dunlop. 2011. Spectral response measurement of double-junction thin-film photovoltaic devices: the impact of shunt resistance and bias voltage. Meas. Sci. Technol.22:045902.
- Siefer, G., C. Baur, and A. W. Bett. 2010. External quantum efficiency measurements of Germanium bottom subcells: Measurement artifacts and correction procedures. Conf. Rec. IEEE Photovolt. Spec. Conf., 704–707.
- Barrigón, E., P. Espinet-González, Y. Contreras, and I. Rey-Stolle. 2015. Implications of low breakdown voltage of component subcells on external quantum efficiency measurements of multijunction solar cells. Prog. Photovolt. Res. Appl.23:1597–1607.
- Allen, C. R., S. H. Lim, J.-J. Li, and Y.-H. Zhang. 2011. Simple method for determining luminescence coupling in multi-junction solar cells. 2011 37th IEEE Photovolt. Spec. Conf., 000452–000453.
- Derkacs, D., D. T. Bilir, and V. A. Sabnis. 2013. Luminescent coupling in GaAs/GaInNAsSb multijunction solar cells. IEEE J. Photovolt.3:520–527.
- Geisz, J. F., M. A. Steiner, I. García, R. M. France, W. E. McMahon, C. R. Osterwald, and D. J. Friedman. 2015. Generalized optoelectronic model of series-connected multijunction solar cells. IEEE J. Photovolt.5:1827–1839.
- Steiner, M. A., S. R. Kurtz, J. F. Geisz, W. E. McMahon, and J. M. Olson. 2012. Using phase effects to understand measurements of the quantum efficiency and related luminescent coupling in a multijunction solar cell. IEEE J. Photovolt.2:424–433.
- Steiner, M. A., and J. F. Geisz. 2012. Non-linear luminescent coupling in series-connected multijunction solar cells Non-linear luminescent coupling in series-connected multijunction solar cells. Appl. Phys. Lett.100:251106.
- Yoon, H., R. R. King, G. S. Kinsey, S. Kurtz, and D. D. Krut. 2003. Radiative coupling effects in GaInP/GaAs/Ge multijunction solar cells. 3rd World Conf. PV Energy Conv.745–748.
- Baur, C., M. Hermle, F. Dimroth, and A. W. Bett. 2007. Effects of optical coupling in III-V multilayer systems. Appl. Phys. Lett.90:13–16.
- Geisz, J. F., S. Kurtz, M. W. Wanlass, J. S. Ward, A. Duda, D. J. Friedman et al. 2007. High-efficiency GaInP/GaAs/InGaAs triple-junction solar cells grown inverted with a metamorphic bottom junction. Appl. Phys. Lett.91:12–15.
- Hamadani, B. H., J. Roller, B. Dougherty, F. Persaud, and H. W. Yoon. 2013. Absolute spectral responsivity measurements of solar cells by a hybrid optical technique. Appl. Opt.52:5184–5193.
- Breitenstein, O.2013. The physics of industrial crystalline silicon solar cells. Adv. Photovolt.89:1–75.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?