Abstract
This article presents the effects of nonlinear thermal radiation and induced magnetic field on viscoelastic fluid flow toward a stagnation point. It is assumed that there exists a kind of chemical reaction between chemical species A and B. The diffusion coefficients of the two chemical species in the viscoelastic fluid flow are unequal. Since chemical species B is a catalyst at the horizontal surface, hence homogeneous and heterogeneous schemes are of the isothermal cubic autocatalytic reaction and first order reaction respectively. The transformed governing equations are solved numerically using Runge–Kutta integration scheme along with Newton’s method. Good agreement is obtained between present and published numerical results for a limiting case. The influence of some pertinent parameters on skin friction coefficient, local heat transfer rate, together with velocity, induced magnetic field, temperature, and concentration profiles is illustrated graphically and discussed. Based on all of these assumptions, results indicate that the effects of induced magnetic and viscoelastic parameters on velocity, transverse velocity and velocity of induced magnetic field are almost the same but opposite in nature. The strength of heterogeneous reaction parameter is very helpful to reduce the concentration of bulk fluid and increase the concentration of catalyst at the surface.
Keywords
Induced magnetic field; Homogeneous–heterogeneous reactions; Nonlinear thermal radiation; Viscoelastic fluid
Nomenclature
u- velocity component in x direction
v- velocity component in y direction
- magnetic components in x and y directions
- magnetic component in free stream flow
- skin friction coefficient
- specific heat at constant pressure
x- distance along the surface
y- distance normal to the surface
f- dimensionless velocity
- local Nusselt number
- Prandtl number
- heat transfer
T- dimensional fluid temperature
- stretching velocity at the wall
- stretching velocity at the free stream
- wall temperature
- ambient temperature
- local Reynolds number
- dimensionless induced magnetic velocities field in y and x directions respectively
- stretching rate at the wall and free stream
- strength of Homogeneous and Heterogeneous reaction parameters
- concentration of Specie A
- conc. gradient of specie A
- conc. of cpecie B
- conc. gradient of specie B
Greek symbols
λ- stretching ratio parameter
Γ- viscoelastic parameter
δ- ratio of diffusion coefficients chemical specie A to B
ε- reciprocal magnetic Prandtl number
κ- thermal conductivity
η- similarity variable
θ- dimensionless temperature
ϑ- kinematics viscosity
α- thermal diffusivity
σ- electrical conductivity
- Stefan–Boltzmann constant
- mean absorption coefficient
β- magnetic parameter
σ- electric conductivity
θ- dimensionless temperature
ψ- stream function
- magnetic permeability
1. Introduction
The study of fluid flow over a horizontal stretchable surface has extensive applications in pharmaceutical companies (i.e. medicinal pharmaceutical technology), production of polythene and paper, polymer extrusion, cooling of elastic sheets, fiber technology, production of plastic materials, science and engineering technology. It is worth mentioning that almost all the fluids mentioned above are materials (fluids) which exhibit viscous and elastic characteristics when undergoing deformation. Viscoelastic fluid flow over a stretching surface was investigated by Rajagopal et al. [1]. Chethan et al. [2] examined the slip condition on viscoelastic liquid flow over an exponentially stretching surface. Rashidi et al. [3] analyzed the effects of Soret and Dufour on magnetohydrodynamic viscoelastic fluid flow past a vertical stretching surface. Singh and Agarwal [4] studied the variable thermal conductivity effect on the flow of viscoelastic fluid over a permeable exponentially stretching surface. Hayat et al. [5] discussed the boundary layer analysis of viscoelastic nanofluid flow over a stretching cylinder. A stagnation point is a point in a flow field where the local velocity is zero. In fluid dynamics, when this occurs at the surface of an object, the fluid flow is often brought to rest. To induce such fluid to flow, Paul Richard Heinrich Blasius in 1908 considered the report of Prandtl Ludwig together with the principle of stretching fluid layers at the free stream [6]. It is pertinent to note that in the work of Blasius, the fluid motion is maintained by the stretching of fluid layers at the free stream. Thereafter, Hiemenz [7] presented two dimensional stagnation-point flow over a flat plate. Abolbashari et al. [8] presented the analysis of non-Newtonian fluid flow induced by stretching sheet. Heat transfer characteristics of viscoelastic fluid past a stretching surface in the presence of thermal radiation and viscous dissipation was presented by Cortell [17]. The dynamics of micropolar fluid at constant vortex viscosity toward a stagnation point formed on a melting stretchable surface can be seen in [9]. Just of recent, Sandeep et al. [10] discussed the dual solutions of governing equation which models Stagnation-point flow of a Jeffrey nanofluid over a stretching surface with induced magnetic field and chemical reaction.
It is a well-known fact that all bodies radiate heat, the higher the temperature the greater the radiation such that when two bodies at different temperatures are within each other the hotter body will supply heat to the colder body until they reach the same temperature. This scientific statement is known as Prevost’s Theory of Exchange, often referred to as the starting point from which the modern physical theory of thermal radiation was developed in the 19th century; for more details, see Putley [11]. Considering this mode of transfer of heat energy, Raju et al. [12] discussed the effect of radiation on the flow past a stretching sheet in the presence of inclined magnetic field. Heat transfer characteristics of MHD flow over a nonlinear stretching sheet in the presence of thermal radiation were studied by Cortell [13]. In the study conducted by Ganji et al. [14] on effects of thermal radiation within magnetohydrodynamics nanofluid flow between two horizontal rotating plates, it was pointed out that Nusselt number has direct relationship with radiation parameter. Heat transfer analysis of magnetohydrodynamic nanofluid flow over a stretching/shrinking surface was scrutinized by Sandeep et al. [15]. Raju et al. [18] analyzed the thermal radiation effect on ferrofluid flow past a flat plate in the presence of aligned magnetic field. It is also important to remark that in most of the studies mentioned above, nonlinear temperature (Rosseland approximation) is simplified by using Taylor series expansion and the higher order terms are truncated. Consequently, the non-dimenzionalization and parametrization of thermal radiation model become a simple task. Physically, the electromagnetic radiation that occurs in the fluid as it flows during some of the industrial processes may not be realistic if interpreted as linear. In addition, the Taylor series expansion may not give full details of the effect. In view of this, nonlinear thermal radiation has been a newly introduced model for accurate explanation. In another related studies on unsteady magnetohydrodynamic typical fluid flow and micropolar fluid flow past a vertical porous plate moving through a binary mixture in an optically thin environment by Animasaun [19] and [20]. The radiative heat flux term that models the thermal radiation in the flow is taken as fourth power of temperature in the energy equation; dimensionless equation was obtained without using Taylor series expansion. Hayat et al. [16] studied the effects of nonlinear thermal radiation on the three-dimensional nanofluid flow past a stretching sheet.
A chemical reaction has occurred when two or more reactants yield product. If the product of a chemical reaction is a catalyst which even speeds up the chemical reaction, then such chemical reaction is said to have passed through autocatalysis. A chain of autocatalytic reactions was first proposed by Lotka [21]. Sapre [22] investigated the problem of simultaneous chemical reaction and diffusion in the presence of catalyst. Williams et al. [23] reported that this kind of reaction can occur between bulk of fluid and surface of a plate in which the boundary layer is formed upon. Merkin [24] adopted an order of magnitude (scaling analysis) together with the same assumptions of large Reynolds number on Navier–Stoke’s equation as reported by Ludwig Prandtl; and then presented a simple model for the interaction between homogeneous (in the bulk of fluid) and heterogeneous (at the surface) reaction involving two chemical species A and B within a thin layer formed on a surface in fluid flow. Explanation on the case of unequal diffusion coefficients of chemical species A and B can be found in Chaudhary and Merkin [25]. Mabood et al. [26] analyzed the flow of chemically reacting fluid over a stretching sheet. Boundary layer analysis of MHD Casson fluid flow over a permeable stretching sheet in the presence of chemical reaction was depicted by Gireesha et al. [27]. Animasaun [28] considered the case of nth order of chemical reaction in Casson fluid flow with temperature dependent plastic dynamic viscosity. Khan and Pop [29] investigated a case of homogeneous–heterogeneous reaction which occurs in viscoelastic fluid flow. A homogeneous–heterogeneous reaction on Powell–Eyring fluid flow over a stretching sheet was analytically discussed by Hayat et al. [30]. Bachok et al. [31] studied the homogeneous–heterogeneous reactions on stagnation-point flow past a stretching surface.
Magnetohydrodynamics (MHD) is the science of motion of electrically conducting fluid in the presence of magnetic field. It was deduced that on 3rd of October 1942, a scientist/Engineer called H. Alfven reported that if a conducting liquid is placed in a constant magnetic field, motion of the liquid may give rise to a force called electromotive force (e.m.f.) which produces electric currents. A kind of electromotive force which induces current and also tends to generate what is called Lorentz force; further reported that owing to the magnetic field, these currents give mechanical forces which change the state of motion of the liquid [32]. Ever since then, Engineers and researchers have reported its application in fusion reactors, dispersion of metals, metallurgy, design of MHD pumps, MHD generator and MHD flow meters, etc. Liron and Wilhelm [33] stated that MHD boundary layer flow of a viscous and electrically conducting fluid in the presence of a transverse magnetic field is observed in various technical systems employing liquid metal and plasma flow. Sandeep and Sulochana [34] illustrated an unsteady micropolar fluid flow over a stretching/shrinking surface in the presence of magnetic field. The heat transfer analysis of Casson fluid flow past a permeable exponentially stretching surface with magnetic field was discussed by Raju et al. [35]. Micropolar fluid flow over a linear stretching surface with magnetic field was analytically studied by Siddheshwar and Mahabaleshwar [36]. Magnetic Reynolds number is an important parameter in the study of effects of induced magnetic field on fluid flow. Rashidi et al. [37] solved a system of nonlinear differential equations modeling the flow of a Newtonian magnetic lubricant squeeze film with magnetic induction and reported the effect of magnetic Reynolds number. Transient magnetohydrodynamics free convection flow of four different types of water based nanofluid past a vertical surface is presented by Freidoonimehr et al. [38].
Motsa and Animasaun [39] considered a case in which the order of magnitude of diffusion-thermo (Dufour effect) is more significant in boundary layer fluid flow in the presence of Lorentz force at initial unsteady stage and final steady stage. Sheikholeslami and Rashidi [40] adopted Control Volume-based Finite Element Method to simulate nanofluid flow in the presence of a non-uniform magnetic field. The aim of the study was extended in [41] and it was concluded that increasing magnetic number leads to augmentation of the Nusselt number. In most cases of electrically conducting fluid flow in the presence of magnetic field, the magnetic Reynolds number of the flow may not be realistic to be assumed small in magnitude; hence, the induced magnetic field is not negligible. Ali et al. [42] examined the induced magnetic effect on stagnation-point flow toward a stretching surface and concluded that the induced magnetic parameter develops the momentum boundary layer thickness. An induced magnetic field effect on stagnation point flow of a nanofluid past a stretching surface was considered by Pal and Mandal [43]. In all the literatures mentioned above, it is worth noticing that little attention has been given to investigate the motion of viscoelastic fluid toward a stretching sheet in the presence of nonlinear thermal radiation. In addition, no attempt has been made to investigate the case of unequal diffusivities of homogeneous–heterogeneous reaction which occurs in the viscoelastic fluid as it flows toward a stagnation point and thereafter. The nonlinear governing equations that model the fluid flow are considered in this study and non-dimensionalized by using suitable similarity variables. The transformed governing equations are solved numerically via Runge–Kutta along with Newton’s method. The influence of selected dimensionless parameters on velocity, induced magnetic field, temperature and concentration profiles along with the friction factor and local Nusselt number is illustrated graphically and presented in tabular form.
2. Mathematical analysis
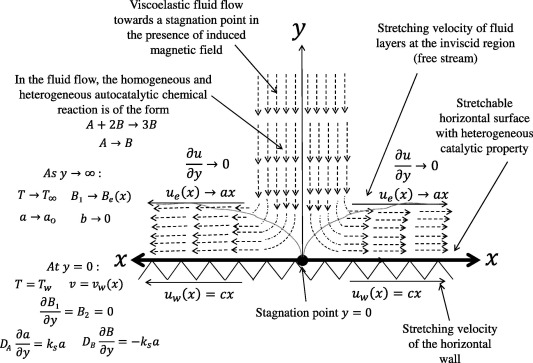
Consider a steady, electrically conducting viscoelastic fluid flow toward a stagnation point and thereafter along a horizontal stretchable surface in the presence of induced magnetic field and homogeneous–heterogeneous reactions.
The physical model along with the coordinate system is shown in Fig. 1. The stretching sheet is considered along the -axis and -axis is normal to it. The magnetic Reynolds number of the viscoelastic flow is not small in magnitude; hence, the induced magnetic field is highly significant. It is assumed that the applied magnetic field is of uniform strength . It is also assumed that an induced magnetic field is applied in -direction and the parallel component approaches the value in the free stream flow. In addition, normal component of the induced magnetic field vanishes near the wall. The temperatures near and far away from the stretching sheet are denoted as and respectively. The stretching and free streams velocities are and respectively, where c and a are positive constants which represent stretching rate. It is assumed that there exists a homogeneous–heterogeneous reaction between chemical species A and B as the viscoelastic fluid flows toward a stagnation point and thereafter. This kind of chemical reaction is referred to as autocatalytic since chemical specie B is known as catalyst. Following Merkin [24], it is assumed that within the boundary layer we have isothermal cubic autocatalytic reaction given by
|
|
(1) |
while on the catalyst surface we have the single, isothermal first order chemical reaction of the form
|
|
(2) |
where a and b are the concentrations of the chemical species A and B respectively. Here, and are known as the reaction rate coefficients which may not be actually referred to as a constant because it includes all the likely parameters that may affect reaction rate except concentration which we have explicitly accounted for in Eqs. (1) and (2). Considering all the assumptions stated above and following the mathematical formulations given by Merkin [24], Chaudhary and Merkin [25], Nazar et al. [42] and Ishak et al. [44], the governing boundary layer equations for
|
|
|
Figure 1. Physical configuration and coordinate system.
|
Continuity equation
|
|
(3) |
Momentum equation
|
|
(4) |
Induced magnetic field equation
|
|
(5) |
|
|
(6) |
Energy equation
|
|
(7) |
Homogeneous–heterogeneous reaction model for the concentrations of reactants A and B, as stated in the reaction scheme Eqs. (1) and (2)
|
|
(8) |
|
|
(9) |
Eqs. (3), (4), (5), (6), (7), (8) and (9) are subject to boundary conditions
|
|
(10) |
|
|
(11) |
The magnetic diffusivity of the fluid is equivalent to . To convert the governing equations into set of nonlinear ordinary differential equations, we now introduce the following similarity transformation:
|
|
|
|
(12) |
Using Rosseland approximation for thermal radiation, the radiative heat flux is
|
|
(13) |
where and are the Stefan–Boltzman constant and the mean absorption coefficient respectively. In this study, it is assumed that the temperature differences within the flow are not sufficiently small. In view of this, it may not be realistic to simplify the radiative heat flux by expanding in a Taylor series about and then neglecting higher order terms. Implicit differentiation may be adopted to simplify Eq. (13) and then substitute into energy Eq. (7)
|
|
(14) |
If we are to consider , the similarity variable related to energy equation is equivalent to
|
|
The new form is adopted to parameterize the nonlinear term of thermal radiation in the energy equation. It is pertinent to remark that the variables defined in Eq. (12) automatically satisfy Eqs. (3) and (5). Upon substituting Eq. (12) into (3), (4), (5), (6), (7), (8), (9), (10) and (11), the following nonlinear coupled ordinary differential equations are obtained
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
|
|
(19) |
The case of homogeneous–heterogeneous chemical reaction in which the diffusion coefficients of chemical species A and B are not of the same magnitude (unequal diffusivities) is considered in this study; hence, it is valid to retain dimensionless governing Eqs. (18) and (19). The dimensionless boundary conditions are now of the form
|
|
(20) |
|
|
(21) |
where Γ is the viscoelastic parameter, M is the magnetic parameter, ε is the reciprocal magnetic Prandtl number, is the Prandtl number, λ is the velocity ratio parameter, is the Schmidt number for chemical specie, is the Schmidt number for chemical specie, is known as the strength of homogeneous reaction, is the strength of heterogeneous reaction, S is the suction parameter and is the ratio of diffusion coefficient, which are represented below.
|
|
|
|
(22) |
Physical quantities of engineering interest are the shear stress coefficient (friction factor) and the local Nusselt number are given by
|
|
(23) |
Here, is the wall shear stress and is the wall heat flux, which are given by
|
|
(24) |
Using the variables in Eq. (12) we obtain
|
|
(25) |
3. Numerical procedure
The nonlinear ordinary differential equations Eqs. (15), (16), (17), (18) and (19) subject to boundary conditions Eqs. (20) and (21) are solved numerically using Runge–Kutta and Newton’s method given by Mallikarjuna et al. [45]. We assumed the unspecified initial conditions for unknown variables, and the transformed first order differential equations are integrated numerically as an initial valued problem to a given terminal point. We can check the accuracy of the assumed missing initial condition, by comparing the calculated value of the different variables at the terminal point with the given value by the existence of the difference in improved values such that the missing initial conditions must be obtained. The calculations are carried out by a program in MATLAB package.
4. Results and discussion
The influence of some pertinent parameters on velocity, induced magnetic field, temperature and concentration profiles along with the friction factor coefficient and local Nusselt number is discussed and presented through graphs and tables. Table 1 depicts the validation of the present results with the already published literature. Table 1 shows that the values of and with variation in M are in favorable agreement with previously published data in the literature by Ali et al. [42]. This proves the validity of the present results along with the accuracy of the numerical technique we used in this study.
| M | Ali et al. [42] | Ali et al. [42] | Present | Present |
|---|---|---|---|---|
| 0.1 | 4.70928 | 0.97902 | 4.70927 | 0.97902 |
| 0.5 | 4.62764 | 0.97617 | 4.62765 | 0.97617 |
| 1 | 4.52158 | 0.97240 | 4.52158 | 0.97240 |
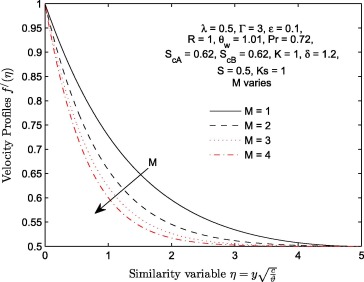
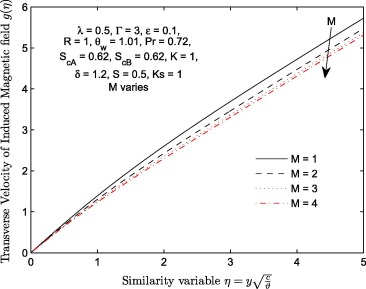
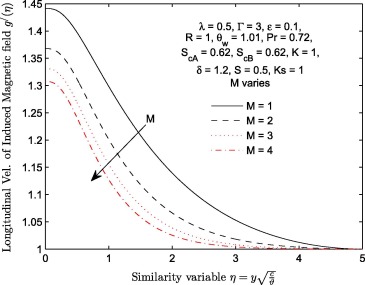
The effect of magnetic field parameter on longitudinal velocity , transverse velocity of induced magnetic field and induced magnetic field profiles of the flow is plotted in Figure 2, Figure 3 and Figure 4 respectively. It can be deduced that an increase in magnetic field parameter (M ) depreciates both velocity and velocity of induced magnetic profiles. The decrease we observed in all these figures can be traced to the presence of lorentz force. As magnitude of parameter M increases, the lorentz force dominates and tends to increase the viscous forces. This effect consequently leads to decrease in the longitudinal velocity of transverse velocity of inducing magnetic field as shown in Fig. 3. A significant decrease in transverse velocity of induced magnetic field with M is highly significant at the free stream. The behavior of with an increase in M is illustrated in Fig. 5. This profile decreases near the wall () only. Table 2 further unravels the effects of increasing the magnitude of M on . It is observed that decreases with M.
|
|
|
Figure 2. Velocity profiles . For different values of magnetic field parameter M.
|
|
|
|
Figure 3. Transverse velocity profiles for different values of magnetic field parameter M.
|
|
|
|
Figure 4. Longitudinal velocity profiles for different values of magnetic field parameter M on.
|
|
|
|
Figure 5. Variation in the magnitude of magnetic field parameter M with .
|
| 1 | 0.002769 | 1.155076 | 1 | 0.419162 | 1.093213 | ||
| 2 | 0.088140 | 1.131197 | 2 | 0.218492 | 1.109898 | ||
| 3 | 0.156035 | 1.118931 | 3 | 0.156035 | 1.118931 | ||
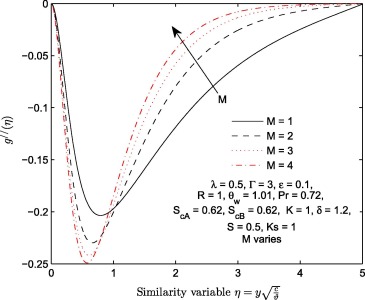
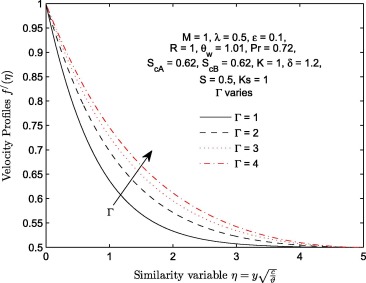
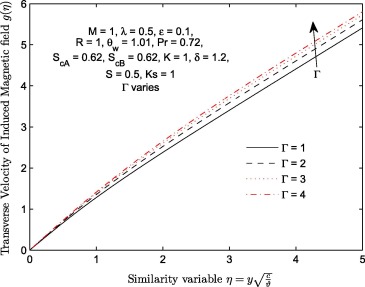
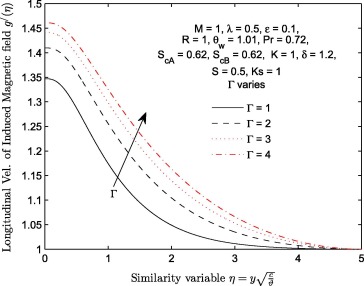
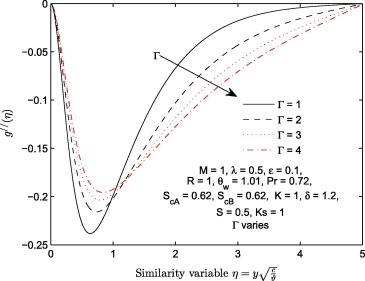
At a constant magnitude of lorentz force (), the effect of viscoelastic parameter (Γ ) on longitudinal velocity , transverse velocity of induced magnetic field and induced magnetic field profiles of the flow is plotted in Figure 6, Figure 7 and Figure 8 respectively. It is shown that an increase in viscoelastic parameter (Γ ) leads to an increase in both velocity and velocity of induced magnetic profiles. The increase we noticed in all these figures can be traced to the reduction in the strength of viscous force. As we all known, fluid with lower viscous forces holding their molecules flow faster than the fluid with high viscous forces. This effect consequently leads to increase in the longitudinal velocity of transverse velocity of induced magnetic field as shown in Fig. 7. The behavior of with an increase in the magnitude of Γ is illustrated in Fig. 9. This profile increases near the wall () only. Table 2 further explains the effects of increasing the magnitude of Γ on . It is observed that increases with Γ.
|
|
|
Figure 6. Velocity profiles for different values of viscoelastic parameter Γ.
|
|
|
|
Figure 7. Transverse velocity profiles for different values of viscoelastic parameter Γ.
|
|
|
|
Figure 8. Longitudinal velocity profiles for different values of viscoelastic parameter Γ.
|
|
|
|
Figure 9. Variation in the magnitude of viscoelastic parameter Γ with .
|
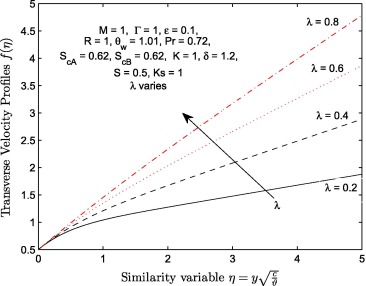
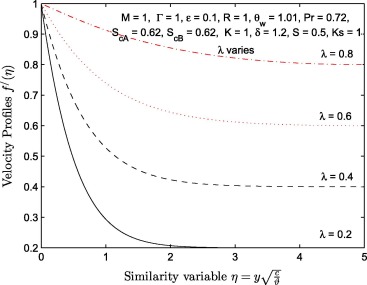
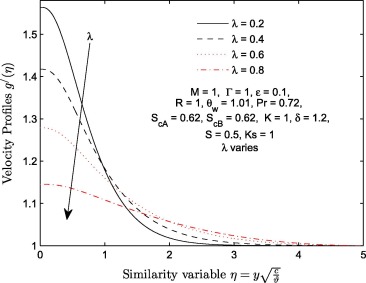
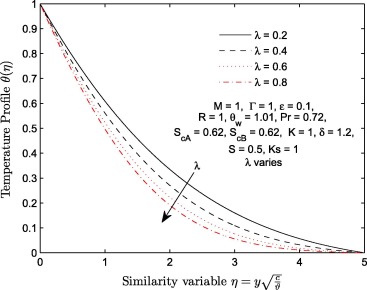
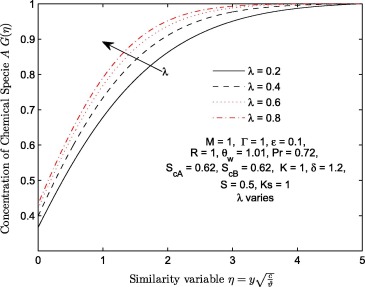
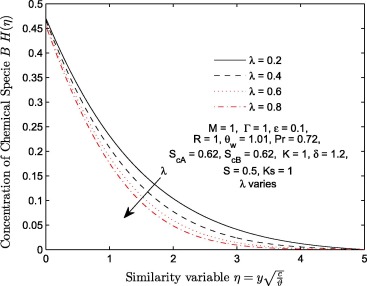
The effects of velocity stretching ratio parameter (λ ) on and are shown in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. Transverse velocity profile increases significantly with λ few distance away from the wall. The longitudinal velocity profiles increase negligibly near the wall () and significantly near the free stream (). Velocity of induced magnetic field decreases with an increase in velocity stretching ratio parameter (λ ) near the wall () and increases negligibly thereafter. The temperature function decreases with λ. Figure 14 and Figure 15 display the effect of λ on concentration of specie A and specie B when ratio of momentum diffusivity to mass diffusivity , strengths of homogeneous and heterogeneous chemical reactions . It is observed that increases with λ while decreases with the same parameter. It is further deduced that increase in the magnitude of λ has negligible effect on and significant effect on .
|
|
|
Figure 10. Transverse velocity profiles for different values of velocity ratio parameter λ.
|
|
|
|
Figure 11. Velocity profiles for different values of velocity ratio parameter λ.
|
|
|
|
Figure 12. Velocity profiles for different values of velocity ratio parameter λ.
|
|
|
|
Figure 13. Temperature profiles for different values of velocity ratio parameter λ.
|
|
|
|
Figure 14. Effects of velocity ratio parameter λ on concentration of chemical specie A .
|
|
|
|
Figure 15. Effects of velocity ratio parameter λ on concentration of chemical specie B (catalyst) .
|
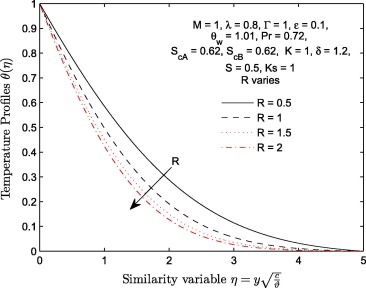
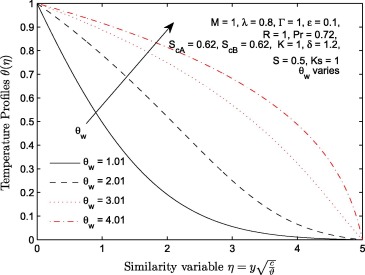
Effects of thermal radiation R and temperature parameter on temperature profiles are illustrated in Figure 16 and Figure 17 respectively. At a constant value of , temperature profile decreases with an increase in the magnitude of R. The effect of radiation parameter R is to reduce the temperature significantly in the flow region. Thermal radiation is found to be energy transfer by the emission of electromagnetic waves which carry heat energy away as the fluid flows. Since the increase in radiation parameter means increase in the rate at which heat energy is released from the flow region, this accounts for decrease in temperature distribution as the magnitude of parameter R increases. It is very important to remark that this effect actually depends on the definition of parameter R ; here, it is defined as the ratio of to . In most published articles, if thermal radiation parameter is defined otherwise, increase in the parameter leads to increase in temperature. Certainly, this is not realistic (i.e. can temperature still increase when energy is transferred out of the fluid domain?). This may depend on the physical model. For more details on this, see [13] and [20]. Also, Fig. 17 depicts an increase in with . The increase we observed in with reduces as grows large.
|
|
|
Figure 16. Temperature profiles for different values of radiation parameter R.
|
|
|
|
Figure 17. Temperature profiles for different values of temperature parameter R.
|
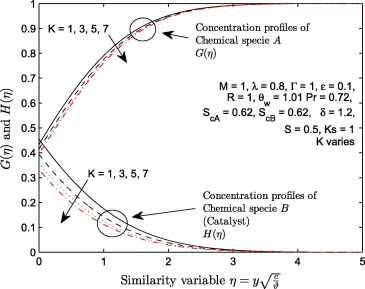
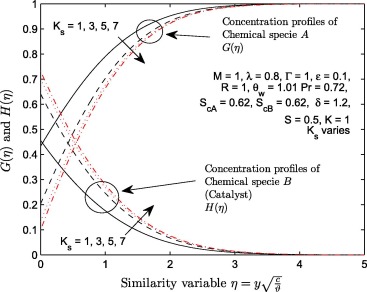
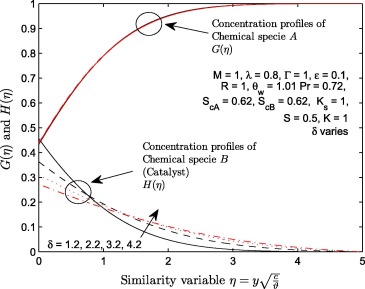
The behavior of concentration of chemical specie A and chemical specie B with an increase in the strength of homogeneous chemical reaction K and strength of heterogeneous chemical reaction is illustrated in Figure 18 and Figure 19. It is noticed that the boundary conditions at the wall and at the free stream are satisfied. The concentration of chemical specie A decreases negligibly with K. This decreasing effect is only near the wall. It is observed that the concentration of chemical specie B (i.e. catalyst) decreases significantly near the wall. This significantly decreasing effect can be traced to the amount of magnitude assigned to parameter δ. This accounts for the reason why δ has no significant effect on the concentration of chemical specie A since magnitude of K and is fixed; see Fig. 20 for more details. As shown in Fig. 19, higher values of the strength of heterogeneous reaction result in the increment of and . It is worth mentioning that at all points of η within , the increase in the magnitude of from 1 to 3 results in a significant increase of and profiles. This significant increase of and reduces as grows larger. At a fixed value of , it is observed that the coefficients of decrease with K; see Table 3. Also, it is observed in Table 3 that the coefficients of increase more significantly with when .
|
|
|
Figure 18. Variation in the strength of homogeneous parameter (K ) with and .
|
|
|
|
Figure 19. Variation in the strength of heterogeneous parameter () with and .
|
|
|
|
Figure 20. Variation in the ratio of diffusion coefficient parameter (δ ) with and .
|
Table 3.
Numerical values of and with variations in K and when and .
| 1 | 0.43296989 | 1 | 0.43296989 | ||
| 2 | 0.55214357 | 2 | 0.42197286 | ||
| 3 | 0.41414673 | 3 | 0.60884911 | ||
5. Conclusions
This study deals with the induced magnetic field effect on viscoelastic fluid flow past a stretching sheet in the presence of nonlinear thermal radiation and homogeneous–heterogeneous reactions. The arising sets of governing nonlinear coupled partial differential equations are transformed into a set of nonlinear coupled ordinary differential equations using self-similarity transformations, which are then solved numerically. The conclusions are as follows:
- the nonlinear thermal radiation improves the temperature profiles and suppresses the rate of heat transfer. At fixed value of R , decrease in temperature distribution from the wall to the free stream is minimum when magnitude of is small compared to maximum pattern of decreasing when magnitude of is large.
- variation in the magnitude of ratio of diffusion coefficient is an increasing function of concentration of the catalyst only within the fluid domain.
- stretching ratio parameter and viscoelastic parameter have tendency to enhance the heat transfer rate. The effects of increasing magnitude of Γ on and are the opposite of the effects of increasing M on the same set of profiles.
- an increase in the magnetic field parameter depreciates the friction factor coefficient and heat transfer rate.
- strength of heterogeneous reaction parameter is very helpful to reduce the concentration of bulk fluid and enlarge the concentration of the catalyst at the surface.
- at a constant value of Γ, transverse velocity profile is an increasing function of velocity ratio λ.
References
- [1] K.R. Rajagopal, T.N. Na, A.S. Guptha; Flow of a viscoelastic fluid over a stretching sheet; Rheol. Acta, 23 (1984), pp. 213–215
- [2] A.S. Chethan, G.N. Sekhar, P.G. Siddheshwar; Flow and heat transfer of an exponential stretching sheet in a viscoelastic liquid with navier slip boundary condition; J. Appl. Fluid Mech., 8 (2015), pp. 223–229
- [3] M.M. Rashidi, M. Ali, B. Rostami, P. Rostami, Gong-Nan Xie, Heat and mass transfer for MHD viscoelastic fluid flow over a vertical stretching sheet with considering soret dufour effects 861065 (2015) 12, http://dx.doi.org/10.1155/2015/861065.
- [4] V. Singh, S. Agarwal; Heat transfer for two types of viscoelastic fluid over an exponentially stretching sheet with variable thermal conductivity and radiation in porous medium; Therm. Sci., 18 (2014), pp. 1079–1093
- [5] T. Hayat, M. Bilal Ashraf, S.A. Shehzad, N.N. Bayomi; Mixed convection flow of viscoelastic nanofluid flow over a stretching cylinder; J. Braz. Soc. Mecha. Sci. Eng., 37 (2014), pp. 849–859
- [6] H. Blasius; Grenzschichten in Fluüssigkeiten mit kleiner Reibung; Z. Math. Phys, 56 (1908), pp. 1–37
- [7] K. Hiemenz; Die Grenzschict neinem in den gleichformigen flussigkeitsstrom eingetauchten geraden Kreiszylinder; Dingler’s Polytech. J., 326 (1911), pp. 321–410
- [8] M.H. Abolbasharia, N. Freidoonimehr, F. Nazari, M.M. Rashidi, Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface, Adv. Powder Technol. (in press) http://dx.doi.org/10.1016/j.apt.2015.01.003.
- [9] S.K. Adegbie, O.K. , I.L. Animasaun, Melting heat transfer effects on stagnation point flow of micropolar fluid with variable dynamic viscosity and thermal conductivity at constant vortex viscosity, J. Nigerian Math. Soc. (in press) http://dx.doi.org/10.1016/j.jnnms.2015.06.004.
- [10] N. Sandeep, C. Sulochana, I.L. Animasaun; Stagnation-point flow of a Jeffrey nano fluid over a stretching surface with induced magnetic field and chemical reaction; Int. J. Eng. Res. Afr., 20 (2016), pp. 93–111
- [11] E.H. Putley; The development of thermal imaging systems; Recent Advances in Medical Thermology, Springer, New York (1984), pp. 151–166
- [12] C.S.K. Raju, N. Sandeep, C. Sulochana, V. Sugunamma, M. Jayachandrababu; Radiation, inclined magnetic field and cross-diffusion effects on flow over a stretching surface; J. Nigerian Math. Soc., 34 (2015), pp. 169–180
- [13] R. Cortell; Fluid flow and radiative nonlinear heat transfer over a stretching sheet; J. King Saud Univ., 26 (2014), pp. 161–167
- [14] D.D. Ganji, M. Sheikholeslami, M. Younus, J.R. Ellahi, Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model, J. Magn. Magnetic Mater. (in press) http://dx.doi.org/10.1016/j.jmmm.2014.08.021.
- [15] N. Sandeep, C. Sulochana, B. Rushikumar; MHD boundary layer flow and heat transfer past a stretching/shrinking sheet in a nanofluid; J. Nanofluids, 4 (2015), pp. 512–517
- [16] T. Hayat, M. Imtiaz, A. Alsaedi, M.A. Kutbi; MHD three-dimensional flow of nanofluid with velocity slip and nonlinear thermal radiation; J. Magn. Mate., 396 (2015), pp. 31–37
- [17] R.B. Cortell; Viscoelastic fluid flow and heat transfer over a stretching sheet under the effects of a non-uniform heat source, viscous dissipation and thermal radiation; Int. J. Heat Mass Transfer, 50 (2007), pp. 3152–3162
- [18] C.S.K. Raju, N. Sandeep, C. Sulochana, V. Sugunamma; Effects of aligned magnetic field and radiation on the flow of ferrofluids over a flat plate with non-uniform heat source/sink; Int. J. Sci. Eng., 8 (2015), pp. 151–158
- [19] I.L. Animasaun; Dynamics of unsteady MHD convective flow with thermophoresis of particles and variable thermo-physical properties past a vertical surface moving through binary mixture; Open J. Fluid Dyn., 5 (2015), pp. 106–120
- [20] I.L. Animasaun; Double diffusive unsteady convective micropolar flow past a vertical porous plate moving through binary mixture using modified Boussinesq approximation; Ain Shams Eng. J. (2015) http://dx.doi.org/10.1016/j.asej.2015.06.010
- [21] A.J. Lotka; Contribution to the theory of periodic reaction; J. Phys. Chem. A, 14 (1910), pp. 271–274
- [22] A.V. Sapre; Diffusional enhancement of autocatalytic reactions in catalyst particles; Am. Inst. Chem. Eng., 35 (1989), pp. 655–657
- [23] W.W. Williams, J. Zhao, L.D. Schmidt; Ignition and extinction of surface and homogeneous oxidation of NH3 and CH4; Am. Inst. Chem. Eng. (AIChE), 37 (1991), pp. 641–649 http://dx.doi.org/10.1002/aic.690370502
- [24] J.H. Merkin; A model for isothermal homogeneous–heterogenous reactions in boundary layer flow; Math. Comput. Modell., 24 (1996), pp. 125–136
- [25] M.A. Chaudhary, J.H. Merkin; A simple isothermal model for homogeneous–heterogeneous reactions in boundary-layer flow. II different diffusivities for reactant and autocatalyst; Fluid Dyn. Res., 16 (1995), pp. 335–359
- [26] F. Mabood, W.A. Khan, A.I. Md. Ismail; MHD stagnation point flow and heat transfer impinging on stretching sheet with chemical reaction and transpiration; Chem. Eng. J., 273 (2015), pp. 430–437
- [27] B.J. Gireesha, B. Mahanthesh, M.M. Rashidi; MHD boundary layer heat and mass transfer of a chemically reacting Casson fluid over a permeable stretching surface with non-uniform heat source/sink; Int. J. Ind. Math., 7 (2015), pp. 247–260
- [28] Animasaun; Effects of thermophoresis, variable viscosity and thermal conductivity on free convective heat and mass transfer of non-darcian MHD dissipative Casson fluid flow with suction and nth order of chemical reaction; J. Nigerian Math. Soc., 34 (2015), pp. 11–31
- [29] W.A. Khan, I.M. Pop; Effect of homogeneous–heterogeneous reactions on the viscoelastic fluid toward a stretching sheet; J. Heat Transfer, 134 (2012), pp. 1–5
- [30] T. Hayat, M. Imtiaz, A. Alsaedi; Effects of homogeneous–heterogeneous reactions in flow of Powell-Eyring fluid; J. Cent. South. Univ., 22 (2015), pp. 3211–3216
- [31] N. Bachok, A. Ishak, I. Pop; On the stagnation-point flow towards a stretching sheet with homogeneous–heterogeneous reactions effects; Commun. Nonlinear Sci. Numeric. Simulat., 16 (2011), pp. 4296–4302
- [32] H. Alfven; Existence of electromagnetic-hydrodynamic waves; Nature Publ. Group, 150 (1942), pp. 405–406 http://dx.doi.org/10.1038/150405d0
- [33] N. Liron, H.E. Wilhelm; Integration of the magnetohydrodynamic boundary-layer equations by Meksins method; J. Appl. Math. Mech. (ZAMM), 54 (1974), pp. 27–37
- [34] N. Sandeep, C. Sulochana; Dual solutions for unsteady mixed flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink; Eng. Sci. Technol. Int., 8 (2015), pp. 1–8
- [35] C.S.K. Raju, N. Sandeep, V. Sugunamma, M. Jayachandrababu, J.V. Ramanareddy; Heat and mass transfer in magneto hydrodynamic Casson fluid over an exponentially permeable stretching surface; Eng. Sci. Technol. Int. J. (2015) http://dx.doi.org/10.1016/j.jestch.2015.05.010
- [36] P.G. Siddheshwar, U.S. Mahabaleshwar; Analytical solution to the MHD flow of micropolar fluid over a linear stretching sheet; Int. J. Appl. Mech. Eng., 20 (2015), pp. 397–406
- [37] M.M. Rashidi, N. Freidoonimehr, E. Momoniat, B. Rostami; Study of nonlinear MHD tribological squeeze film at generalized magnetic reynolds numbers using DTM; PLoS ONE, 10 (2015), p. e0135004
- [38] N. Freidoonimehr, M.M. Rashidi, S. Mahmud; Unsteady MHD free convectiveflow past a permeable stretching vertical surface in a nano-fluid; Int. J. Therm. Sci., 87 (2015), pp. 136–145
- [39] S.S. Motsa, I.L. Animasaun; A new numerical investigation of some thermo-physical properties on unsteady MHD non-Darcian flow past an impulsively started vertical surface; Therm. Sci., 19 (2015), pp. S249–S258 http://dx.doi.org/10.2298/TSCI15S1S49M
- [40] M. Sheikholeslami, M.M. Rashidi; Ferrofluid heat transfer treatment in the presence of variable magnetic field; Eur. Phys. J. Plus, 130 (2015), p. 115
- [41] M. Sheikholeslami1, M.M. Rashidi, Effect of space dependent magnetic field on free convection of Fe3O4–water nanofluid, J. Taiwan Inst. Chem. Eng. (in press) http://dx.doi.org/10.1016/j.jtice.2015.03.035.
- [42] R. Nazar, F.M. Ali, N.M. Arifin, I. Pop; MHD stagnation-point flow and heat transfer towards stretching sheet with induced magnetic field; Appl. Math. Mech. (English Ed.), 32 (2011), pp. 409–418
- [43] D. Pal, G. Mandal; MHD convective stagnation-point flow of nanofluids over a non-isothermal stretching sheet with induced magnetic field; Meccanica, 50 (2015), pp. 2023–2035
- [44] A. Ishak, R. Nazar, I. Pop; Mixed convection boundary layers in the stagnation-point flow towards a vertical stretching sheet; Meccanica, 41 (2006), pp. 509–518
- [45] B. Mallikarjuna, A.M. Rashad, A.J. Chamka, S. Hariprasad Raju; Chemical reaction effects on MHD convective heat and mass transfer flow past a rotating vertical cone embedded in a variable porosity regime; Afr. Math. (2015) http://dx.doi.org/10.1007/s13370-015-0372-1
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?