A new semi-analytical solution of compound KdV-Burgers equation of fractional order

Abstract

This article introduces and illustrates a novel approximation to the compound KdV-Burgers equation. For such a challenge, the q-homotopy analysis transform technique (q-HATM) is a potent approach. The suggested procedure avoids the complexity seen in many other methods and provides an approximation that is extremely near to the exact solution. The uniqueness theorem and convergence analysis of the expected problem are explored with the aid of Banach's fixed-point theory. Through a difference in the fractional derivative, the normal frequency for the fractional solution to this issue changes. All of the discovered solutions are illustrated in the figures and tables.

Keywords: q-Homotopy analysis transform method, convergence analysis, compound KdV-Burgers equation

1. Introduction

Leibnitz conceived the idea of a fraction in derivative, and it was found that fractional calculus is better suited than classical calculus for simulating real-world issues. The theory of fractional calculus offers a practical and methodical analysis of the reality of nature [1–3]. Its capacity to offer accurate descriptions of complicated nonlinear systems has lately piqued interest. Several fields have paid more attention to fractional-order derivatives, e.g. electrodynamics [4], neurophysiology [5], finance, nanotechnology, fluid dynamics [6], etc. Also, fractional differential equations (FDEs) control memory-based systems [7-8]. Arbitrariness in their arrangement offers more degrees of freedom in analysis and design, leading to more precise modeling, improved control robustness, and more flexibility in signal processing. A fractional-order system can better describe electrochemical phenomena like diffusion processes or double-layer charge distribution. As a result, FDEs are used to model the supercapacitors, fuel cells, and lithium present in batteries. Viscoelastic materials, fractal patterns, the characterization of ceramic bodies, the putrefaction rate of meat and fruit, and the investigation of erosion in a metal surface are further intriguing application fields.

The non-local features of fractional differential equation models make them advantageous for use in physical simulations. In contrast to the integer-order derivative, which is local in nature, the fractional-order derivative is non-local. It shows that, in addition to its current state, the physical system's next state will depend on every previous condition it has experienced. As a result, fractional models are more accurate [9-10].

The purpose of this work is to suggest an effective technique for solving some differential equations of fractional order. Liao introduced the homotopy analysis approach [11], which forms an endless mapping from an initial condition to an exact solution after choosing an adjunct linear operator. The auxiliary parameter validates that the solution has converged. The application of semianalytical approaches in conjunction with an appropriate transform shortens the time required to investigate solutions to nonlinear issues representing real-life implementations. The q-homotopy analysis transform technique (q-HATM) [12-15] combines the HAM with the Laplace transform. Its strength is its ability to adapt two powerful computational approaches for investigating FDEs. The convergence area of the solution series may be controlled in a sizable allowable domain by selecting the correct ${\textstyle \hbar }$.

We can consider the compound KdV-Burgers equation as

$\varphi _{\tau }+l\varphi \varphi _{x}+m\varphi ^{2}\varphi _{x}+n\varphi _{xx}-o\varphi _{xxx}=0,$

(1)

where ${\textstyle l,m,n}$ and ${\textstyle o}$ are constants. This is a combination of the KdV, mKdV, and Burgers equations, combining nonlinear, dispersion, and dissipation effects. Eq. (1) includes the following specific significant cases

• If ${\textstyle l\neq {0},m\neq {0},n=0,o\neq {0}}$, Eq (1) becomes the compound ${\textstyle \mathrm {KdV} }$ equation

$\varphi _{\tau }+l\varphi \varphi _{x}+m\varphi ^{2}\varphi _{x}-o\varphi _{xxx}=0.$

(2)

• If ${\textstyle l=0,m\neq {0},n\neq {0},o\neq {0}}$, Eq (1) becomes the mKdV-Burgers equation

$\varphi _{\tau }+m\varphi ^{2}\varphi _{x}+n\varphi _{xx}-o\varphi _{xxx}=0.$

(3)

• If ${\textstyle l\neq {0},m=0,n\neq {0},o\neq {0}}$, Eq (1) becomes the KdV-Burgers equation

$\varphi _{\tau }+l\varphi \varphi _{x}+n\varphi _{xx}-o\varphi _{xxx}=0.$

(4)

• If ${\textstyle n=0}$ in Eqs. (3) and (4), then we obtain the mKdV equation

$\varphi _{\tau }+m\varphi ^{2}\varphi _{x}-o\varphi _{xxx}=0,$

(5)

and the KdV equation

$\varphi _{\tau }+l\varphi \varphi _{x}-o\varphi _{xxx}=0,$

(6)

respectively.

Long-wave propagation in nonlinear media with dispersion and dissipation is modeled using Eq. (1) [16]. Using both an automated technique and the homogeneous balancing technique, a kind solution to Eq. (1) has been discovered [18–19]. A type of Backlund transformation for this system has recently been developed [20]. In the one-dimensional nonlinear lattice [16], the wave propagation of limited particles with a harmonic force may be described by Eq. (2) [17]. In particular, it explains how small-amplitude ion-acoustic waves propagate in plasmas without Landau damping, and it is also used to explain how thermal pulses move through a single crystal of sodium fluoride in solid physics [21-22]. Many studies have been done on this equation [23-25].

2. Preliminaries to FC

Definition I  

The Caputo fractional order derivative of ${\textstyle \varphi (\tau )}$ is defined as [26]

$D_{\tau }^{\varepsilon }\varphi (\tau )={\begin{cases}\displaystyle {\frac {d^{m}\varphi (\tau )}{d\tau ^{m}}},&m=\varepsilon ,\\\displaystyle {\frac {1}{\Gamma \left(m-\varepsilon \right)}}\int _{0}^{\tau }\left(\tau {-\rho }\right)^{m-\varepsilon {-1}}\varphi ^{\left(m\right)}\left(\rho \right)d\rho ,&m-1<\varepsilon {<}m,m\in \mathbb {N} .\end{cases}}$

(7)

Definition II  

The Laplace transform of ${\textstyle \varphi \left(\tau \right)}$ is defined as

$\ell \left\{\displaystyle {\frac {d^{m}}{d\tau ^{m}}};\varphi ;s\right\}=s^{m}\varphi \left(s\right)-\sum _{r}^{m-1}s^{m-r-1}\varphi ^{(r)}\left(0^{+}\right),$

(8)

The formula for the Laplace transform of the Caputo fractional derivative is [7]

$\ell \left\{D_{\tau }^{\varepsilon }\varphi \right\}=s^{\varepsilon }\ell \left\{\varphi \right\}-\sum _{r}^{m-1}s^{\varepsilon {-}r-1}\varphi ^{({\scriptstyle {\scriptscriptstyle r}})}\left(0^{+}\right)\,,\quad m-1<\varepsilon \leq m.$

(9)

3. Proposed q-HATM of the fractional order

The q-HATM will be discussed in full below, see [12-15]. Consider the following nonlinear fractional differential equation:

$D_{\tau }^{\alpha }\varphi \left(x,\tau \right)+{\mathcal {R}}\varphi (x,\tau )+{\mathcal {N}}\varphi (x,\tau )=T(x,\tau )\;,\qquad n-1<\varepsilon \leq n,$

(10)

where ${\textstyle D_{\tau }^{\varepsilon }={\frac {\partial ^{\varepsilon }}{\partial \tau ^{\varepsilon }}}}$ is the Caputo derivative in this case, while ${\textstyle {\mathcal {R}}}$ and ${\textstyle {\mathcal {N}}}$ are linear and nonlinear operators, respectively. The source expression is ${\textstyle T(x,\tau )}$. Using the Laplace transform on Eq. (10) and solving it, we obtain

$s^{\scriptscriptstyle {\textstyle {\scriptstyle \varepsilon }}}{\mathcal {L}}\left\{\varphi \right\}-\sum _{i}^{n-1}s^{\scriptstyle {\scriptscriptstyle {\scriptstyle {\scriptscriptstyle \varepsilon {-}i-1}}}}\varphi ^{\left({\textstyle {\scriptscriptstyle i}}\right)}\left(x,0\right)+{\mathcal {L}}\left\{{\mathcal {R}}\varphi \right\}+{\mathcal {L}}\left\{{\mathcal {N}}\varphi \right\}-{\mathcal {L}}\left\{T(x,\tau )\right\}=0.$

(11)

The nonlinear operator is

$N\left[{\mathit {\Theta }}(x,\tau ;q)\right]={\mathcal {L}}\left\{{\mathit {\Theta }}(x,\tau ;q)\right\}-{\frac {\varphi (x)}{s}}-{\frac {\varphi _{x}(x)}{s^{\scriptscriptstyle 2}}}+{\frac {1}{s^{\varepsilon }}}{\mathcal {L}}\left\{{\mathcal {R}}{\mathit {\Theta }}(x,\tau ;q)\right\}$$+{\frac {1}{s^{\varepsilon }}}{\mathcal {L}}\left\{{\mathcal {N}}{\mathit {\Theta }}(x,\tau ;q)\right\}-{\frac {1}{s^{\varepsilon }}}{\mathcal {L}}\left\{T(x,\tau )\right\},\qquad$

(12)

The embedding parameter ${\textstyle q\in [0,{\frac {1}{n}}]}$ is used here, and the function ${\textstyle {\mathit {\Theta }}(x,\tau ;q)}$ is unknown. Built a homotopy as follows:

$\left[1-nq\right]L\left[{\mathit {\Theta }}(x,\tau ;q)-\varphi _{0}(x,0)\right]=\hbar qH(x,\tau ){\mathcal {N}}\left[\varphi (x,\tau )\right],$

(13)

where ${\textstyle \hbar }$ is an auxiliary nonzero parameter, ${\textstyle \varphi _{0}(x,0)}$ is an initial guess. By increasing ${\textstyle q}$, ${\textstyle {\mathit {\Theta }}}$ converges from ${\textstyle \varphi _{0}}$ to ${\textstyle \varphi }$. As a result of Taylor's theorem, we obtain

${\mathit {\Theta }}(x,\tau ,q)=\varphi _{0}(x,\tau )+\sum _{k=1}^{\infty }\varphi _{k}(x,\tau )q^{k},$

(14)

where

$\varphi _{k}(x,\tau )={\frac {1}{k!}}{\frac {\partial ^{k}{\mathit {\Theta }}(x,\tau ,q)}{\partial q^{k}}}\left.\mid _{q=0}\right..$

(15)

Series (14) converge at ${\textstyle q={\frac {1}{n}}}$, providing a solution, by appropriately selecting an auxiliary linear operator ${\textstyle \varphi _{0}}$, ${\textstyle n}$, ${\textstyle \hbar }$, and ${\textstyle H}$

$\varphi (x,\tau )=\varphi _{0}(x,\tau )+\sum _{k=1}^{\infty }\varphi _{k}(x,\tau )\left({\frac {1}{n}}\right)^{k}.$

(16)

Eq. (13) is now differentiated ${\textstyle m}$ times, then divided by ${\textstyle m!}$ and assuming that ${\textstyle q=0}$

${\mathcal {L}}\left\{\varphi _{k}(x,\tau )-\varsigma _{k}\varphi _{k-1}(x,\tau )\right\}=\hbar H(x,\tau ){\mathfrak {R}}_{k}\left({\overset {\rightarrow }{\varphi }}_{k-1}\right),$

(17)

where the vectors are defined as

${\overset {\rightarrow }{\varphi }}_{k}(x,\tau )=\left\{\varphi _{0}(x,\tau ),\varphi _{1}(x,\tau ),\varphi _{2}(x,\tau ),\cdots ,\varphi _{k}(x,\tau )\right\}$

(18)

By using the inverse transform on Eq. (17)

$\varphi _{k}(x,\tau )=\varsigma _{k}\varphi _{k-1}(x,\tau )+\hbar H(x,\tau ){\mathcal {L}}^{-1}\left\{{\mathfrak {R}}_{k}\left({\overset {\rightarrow }{\varphi }}_{k-1}\right)\right\},$

(19)

where

${\mathfrak {R}}_{k}\left({\overset {\rightarrow }{\varphi }}_{k-1}\right)={\frac {1}{\left(k-1\right)!}}{\frac {\partial ^{k-1}N\left[{\mathit {\Theta }}(x,\tau ,q)\right]}{\partial q^{k-1}}}\left.\mid _{q=0}\right.,$

(20)

and

$\varsigma _{k}={\begin{cases}0,&k\leq {1},\\n,&k>1\end{cases}}$

Lastly, the components of the q-HATM solution may be easily derived by solving Eq. (19).

4. Convergence analysis of q-HATM

We can come to the conclusion that there is only one solution to a given issue that meets a specific initial condition using the concepts of existence and uniqueness.

Theorem I. The acquired solution by using the q-HATM for the compound KdV-Burgers equation is unique wherever $0<\omega {<1}$, where

$\omega =\left(\varsigma _{k}+\hbar \right)+\hbar \left\{o\sigma ^{3}-l\sigma \left(A_{1}+A_{2}\right)-m\sigma \left(A_{1}^{2}-A_{2}^{2}\right)-n\sigma ^{2}\right\}{\mathit {\Omega }}$

(21)

Proof. The compound KdV-Burgers equation described in Eq. (39) has the following analytic solution:

$\varphi (x,\tau )=\sum _{k=0}^{\infty }\varphi _{k}(x,\tau )d^{k},$

(22)

where

${\begin{array}{l}\varphi _{k}(x,\tau )&=&\left(\varsigma _{k}+\hbar \right)\varphi _{k-1}-\hbar \left(1-{\frac {\varsigma _{k}}{n}}\right){\mathcal {L}}^{-1}\left\{{\frac {\varphi \left(x\right)}{s}}\right\}-\hbar {\mathcal {L}}^{-1}{\Biggl \{}\left({\frac {1}{s^{\varepsilon }}}\right){\mathcal {L}}{\biggl [}o\left(\varphi _{k-1}\right)_{3x}\\&&-l\sum _{i=0}^{k-1}\varphi _{\hbox{i}}\left(\varphi _{\hbox{k-1-i}}\right)_{x}-m\sum _{i=0}^{k-1}\,\sum _{h=0}^{i}\varphi _{\scriptscriptstyle h}\varphi _{\scriptscriptstyle i-h}\left(\varphi _{\scriptscriptstyle k-1-i}\right)_{x}-n\left(\varphi _{k-1}\right)_{2x}{\biggr ]}{\Biggr \}}.\end{array}}$

(23)

Let $\varphi$ and ${\overline {\varphi }}$ represent the compound KdV-Burgers equation's two solutions such that $|\varphi |\leq A_{1}$ and $|{\overline {\varphi }}|\leq A_{2}$, using the aforementioned equation, we obtain

${\bigl |}\varphi -{\overline {\varphi }}{\bigr |}={\Biggl |}\left(\varsigma _{k}+\hbar \right)\left(\varphi -{\overline {\varphi }}\right)-\hbar {\mathcal {L}}^{-1}{\Biggl \{}\left({\frac {1}{s^{\varepsilon }}}\right){\mathcal {L}}{\Bigl [}o\left(\varphi _{3x}-{\overline {\varphi }}_{3x}\right)-l\left(\varphi -{\overline {\varphi }}\right)\left(\varphi _{x}-{\overline {\varphi }}_{x}\right)$ $-m\left(\varphi ^{2}-{\overline {\varphi }}^{2}\right)\left(\varphi _{x}-{\overline {\varphi }}_{x}\right)-n\left(\varphi _{2x}-{\overline {\varphi }}_{2x}\right){\Bigr ]}{\Biggr \}}{\Biggr |}.$

(24)

The convolution theorem for the Laplace transform has allowed us to

${\begin{aligned}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}&=\displaystyle \left(\varsigma _{k}+\hbar \right){\bigl |}\varphi -{\overline {\varphi }}{\bigr |}+\hbar \int _{0}^{\tau }{\Bigl \{}o{\bigl |}\varphi _{3x}-{\overline {\varphi }}_{3x}{\bigr |}-l{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}{\bigl |}\varphi _{x}-{\overline {\varphi }}_{x}{\bigr |}\\&\displaystyle -m{\bigl |}\varphi ^{2}-{\overline {\varphi }}^{2}{\bigr |}{\bigl |}\varphi _{x}-{\overline {\varphi }}_{x}{\bigr |}-n{\bigl |}\varphi _{2x}-{\overline {\varphi }}_{2x}{\bigr |}{\Bigr \}}{\frac {(\tau -\rho )^{\varepsilon }}{\Gamma \left(\varepsilon +1\right)}}d\rho .\\&\leq \displaystyle \left(\varsigma _{k}+\hbar \right){\bigl |}\varphi -{\overline {\varphi }}{\bigr |}+\hbar \int _{0}^{\tau }{\Bigl \{}o{\frac {\partial ^{3}}{\partial x^{3}}}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}-l{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}{\frac {\partial }{\partial x}}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}\\&\displaystyle -m\left(A_{1}^{2}-A_{2}^{2}\right){\frac {\partial }{\partial x}}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}-n{\frac {\partial ^{2}}{\partial x^{2}}}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}{\Bigr \}}{\frac {(\tau -\rho )^{\varepsilon }}{\Gamma \left(\varepsilon +1\right)}}d\rho .\\&\leq \displaystyle \left(\varsigma _{k}+\hbar \right){\bigl |}\varphi -{\overline {\varphi }}{\bigr |}+\hbar {\Bigl \{}o{\frac {\partial ^{3}}{\partial x^{3}}}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}-l{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}{\frac {\partial }{\partial x}}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}\\&\displaystyle -m\left(A_{1}^{2}-A_{2}^{2}\right){\frac {\partial }{\partial x}}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}-n{\frac {\partial ^{2}}{\partial x^{2}}}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}{\Bigr \}}\int _{0}^{\tau }{\frac {(\tau -\rho )^{\varepsilon }}{\Gamma \left(\varepsilon +1\right)}}d\rho .\\&\leq \displaystyle \left(\varsigma _{k}+\hbar \right){\bigl |}\varphi -{\overline {\varphi }}{\bigr |}+\hbar {\Bigl \{}o\sigma ^{3}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}-l\sigma \left(A_{1}+A_{2}\right){\bigl |}\varphi -{\overline {\varphi }}{\bigr |}\\&\displaystyle -m\sigma \left(A_{1}^{2}-A_{2}^{2}\right){\bigl |}\varphi -{\overline {\varphi }}{\bigr |}-n\sigma ^{2}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}{\Bigr \}}{\frac {\tau ^{\varepsilon +1}}{\Gamma \left(\varepsilon +2\right)}},\end{aligned}}$

(25)

where ${\textstyle \sigma ^{n}={\frac {\partial ^{n}}{\partial x^{n}}},n=1,2,3}$. The above equation can be simplified by the integral mean value [28] as shown below

${\bigl |}\varphi -{\overline {\varphi }}{\bigr |}\leq \left(\varsigma _{k}+\hbar \right){\bigl |}\varphi -{\overline {\varphi }}{\bigr |}+\hbar {\Bigl \{}o\sigma ^{3}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}-l{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}\sigma {\bigl |}\varphi -{\overline {\varphi }}{\bigr |}$ $-m\sigma \left(A_{1}^{2}-A_{2}^{2}\right){\bigl |}\varphi -{\overline {\varphi }}{\bigr |}-n\sigma ^{2}{\bigl |}\varphi -{\overline {\varphi }}{\bigr |}{\Bigr \}}{\mathit {\Omega }}\leq \omega {\bigl |}\varphi -{\overline {\varphi }}{\bigr |},$

(26)

${\textstyle \therefore \left(1-\omega \right){\bigl |}\varphi -{\overline {\varphi }}{\bigr |}\leq {0}}$. Since ${\textstyle 0<\omega {<1}}$, therefore ${\textstyle {\bigl |}\varphi -{\overline {\varphi }}{\bigr |}=0}$, which gives ${\textstyle \varphi ={\overline {\varphi }}}$, where ${\textstyle {\mathit {\Omega }}={\frac {\tau ^{\varepsilon {+1}}}{\Gamma \left(\varepsilon {+2}\right)}}}$. As a result, the approximate solution is unique.

Theorem II Let ${\textstyle {\mathcal {B}}}$ be a Banach space with the nonlinear map ${\textstyle {\mathcal {F}}:{\mathcal {B}}\rightarrow {\mathcal {B}}}$. Assume that

${\bigl \Vert }{\mathcal {F}}(\varphi )-{\mathcal {F}}(S){\bigr \Vert }\leq \omega {\bigl \Vert }\varphi {-}S{\bigr \Vert },\;\forall \varphi ,S\in {\mathcal {B}},<\omega {<1.}$

(27)

It is determined that there is a fixed point for ${\textstyle {\mathcal {F}}}$ using the prior hypothesis and Banach's fixed-point theory [29]. Also, if the values of ${\textstyle \varphi _{0},S_{0}\in {\mathcal {B}}}$ are chosen at random, the analytical solution using the suggested technique converges to a fixed point of ${\textstyle {\mathcal {F}}}$ and

${\bigl \Vert }\varphi _{\vartheta }-\varphi _{\varphi }{\bigr \Vert }\leq {\frac {\omega ^{\varphi }}{1-\omega }}{\bigl \Vert }\varphi _{1}-\varphi _{0}{\bigr \Vert }{.}$

(28)

Proof. Assume that ${\textstyle {\mathcal {B}}}$ is a Banach space with ${\textstyle (C[K],{\bigl \Vert }{.}{\bigr \Vert })}$ and the norm ${\textstyle {\bigl \Vert }{.}{\bigr \Vert }}$ denoted by ${\textstyle {\bigl \Vert }h\left(x\right){\bigr \Vert }={\underset {\tau \in K}{max}}{\bigl |}h\left(x\right){\bigr |}.}$ We shall now affirm that the Cauchy sequence represented by ${\textstyle \left\{\varphi _{\vartheta }\right\}}$ in the Banach space is the following:

${\bigl \Vert }\varphi _{\vartheta }-\varphi _{\psi }{\bigr \Vert }={\underset {\tau \in K}{max}}{\bigl |}\varphi _{\vartheta }-\varphi _{\psi }{\bigr |}$ $={\underset {\tau \in K}{max}}{\Biggl |}\left(\varsigma _{k}+\hbar \right)\left(\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}\right)-\hbar {\mathcal {L}}^{-1}{\Biggl \{}\left({\frac {1}{s^{\varepsilon }}}\right){\mathcal {L}}{\Biggl [}o\left({\frac {\partial ^{3}\varphi _{\vartheta {-1}}}{\partial x^{3}}}-{\frac {\partial ^{3}\varphi _{\psi {-1}}}{\partial x^{3}}}\right)-l\left(\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}\right)$ $\times \left({\frac {\partial \varphi _{\vartheta {-1}}}{\partial x}}-{\frac {\partial \varphi _{\psi {-1}}}{\partial x}}\right)-m\left({\frac {\partial \varphi _{\vartheta {-1}}^{2}}{\partial x}}-{\frac {\partial \varphi _{\psi {-1}}^{2}}{\partial x}}\right)\left({\frac {\partial \varphi _{\vartheta {-1}}}{\partial x}}-{\frac {\partial \varphi _{\psi {-1}}}{\partial x}}\right)-n\left({\frac {\partial ^{2}\varphi _{\vartheta {-1}}}{\partial x^{2}}}-{\frac {\partial ^{2}\varphi _{\psi {-1}}}{\partial x^{2}}}\right){\Biggr ]}{\Biggr \}}{\Biggr |}$

(29)

$\leq {\underset {\tau \in K}{max}}{\Biggl [}\left(\varsigma _{k}+\hbar \right){\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}-\hbar {\mathcal {L}}^{-1}{\Biggl \{}\left({\frac {1}{s^{\varepsilon }}}\right){\mathcal {L}}{\Biggl [}o{\Biggl |}{\frac {\partial ^{3}\varphi _{\vartheta {-1}}}{\partial x^{3}}}-{\frac {\partial ^{3}\varphi _{\psi {-1}}}{\partial x^{3}}}{\Biggr |}$ $-l{\Biggl |}\left(\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}\right)\times \left({\frac {\partial \varphi _{\vartheta {-1}}}{\partial x}}-{\frac {\partial \varphi _{\psi {-1}}}{\partial x}}\right){\Biggr |}-m{\Biggr |}\left({\frac {\partial \varphi _{\vartheta {-1}}^{2}}{\partial x}}-{\frac {\partial \varphi _{\psi {-1}}^{2}}{\partial x}}\right)$ $\left({\frac {\partial \varphi _{\vartheta {-1}}}{\partial x}}-{\frac {\partial \varphi _{\psi {-1}}}{\partial x}}\right){\Biggr |}-n{\Biggr |}\left({\frac {\partial ^{2}\varphi _{\vartheta {-1}}}{\partial x^{2}}}-{\frac {\partial ^{2}\varphi _{\psi {-1}}}{\partial x^{2}}}\right){\Biggr |}{\Biggr ]}{\Biggr \}}{\Biggr ]}$

(30)

By utilizing the convolution theorem for the Laplace transform, we have

${\bigl \Vert }\varphi _{\vartheta }-\varphi _{\psi }{\bigr \Vert }\leq {\underset {\tau \in K}{max}}{\Biggl [}\left(\varsigma _{k}+\hbar \right){\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}-\hbar \int _{0}^{\tau }{\Biggl \{}o{\Biggl |}{\frac {\partial ^{3}\varphi _{\vartheta {-1}}}{\partial x^{3}}}-{\frac {\partial ^{3}\varphi _{\psi {-1}}}{\partial x^{3}}}{\Biggr |}$ $-l{\Biggl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\Biggl |}{\Biggr |}{\frac {\partial \varphi _{\vartheta {-1}}}{\partial x}}-{\frac {\partial \varphi _{\psi {-1}}}{\partial x}}{\Biggr |}-m{\Biggr |}{\frac {\partial \varphi _{\vartheta {-1}}^{2}}{\partial x}}-{\frac {\partial \varphi _{\psi {-1}}^{2}}{\partial x}}{\Biggr |}{\Biggr |}{\frac {\partial \varphi _{\vartheta {-1}}}{\partial x}}-{\frac {\partial \varphi _{\psi {-1}}}{\partial x}}{\Biggr |}$ $-n{\Biggr |}{\frac {\partial ^{2}\varphi _{\vartheta {-1}}}{\partial x^{2}}}-{\frac {\partial ^{2}\varphi _{\psi {-1}}}{\partial x^{2}}}{\Biggr |}{\Biggr \}}{\frac {(\tau {-\rho })^{\varepsilon }}{\Gamma \left(\varepsilon {+1}\right)}}d\rho {\Biggr ]}$

(31)

$\leq {\underset {\tau \in K}{max}}{\biggl [}\left(\varsigma _{k}+\hbar \right){\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}-\hbar \int _{0}^{\tau }{\Bigl \{}o\sigma ^{3}{\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}-l\sigma {\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}{\bigl |}A-B{\bigr |}$ $-m\sigma {\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}{\bigl |}A-B{\bigr |}{\bigl |}A+B{\bigr |}-n\sigma ^{2}{\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}{\Bigr \}}{\frac {(\tau {-\rho })^{\varepsilon }}{\Gamma \left(\varepsilon {+1}\right)}}d\rho {\biggr ]}.$

(32)

We can use the integral mean value [28] to reduce the previous equation as follows:

${\bigl \Vert }\varphi _{\vartheta }-\varphi _{\psi }{\bigr \Vert }\leq {\underset {\tau \in K}{max}}{\Bigl [}\left(\varsigma _{k}+\hbar \right){\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}+\hbar {\Bigl \{}o\sigma ^{3}{\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}-l\sigma$ ${\bigl |}\left(\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}\right)(A-B){\bigr |}-m\sigma {\bigl |}\left(\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}\right)(A^{2}-B^{2}){\bigr |}-n\sigma ^{2}{\bigl |}\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr |}{\Bigr \}}{\mathit {\Omega }}{\Bigr ]},$ ${\bigl \Vert }\varphi _{\vartheta }-\varphi _{\psi }{\bigr \Vert }\leq \psi {\bigl \Vert }\varphi _{\vartheta {-1}}-\varphi _{\psi {-1}}{\bigr \Vert }{.}$

(33)

Subtracting ${\textstyle \vartheta }$ by ${\textstyle \psi {+1}}$, we find that

${\bigl \Vert }\varphi _{\psi {+1}}-\varphi _{\psi }{\bigr \Vert }\leq \omega {\bigl \Vert }\varphi _{\psi }-\varphi _{\psi {-1}}{\bigr \Vert }\leq \omega ^{2}{\bigl \Vert }\varphi _{\psi {-1}}-\varphi _{\psi {-2}}{\bigr \Vert }\leq \cdots \leq \omega ^{\psi }{\bigl \Vert }\varphi _{1}-\varphi _{0}{\bigr \Vert }{.}$

(34)

By using triangular inequality, we find that

${\bigl \Vert }\varphi _{\vartheta }-\varphi _{\psi }{\bigr \Vert }={\bigl \Vert }\varphi _{\psi {+1}}+\varphi _{\psi {+2}}+\varphi _{\vartheta }-\varphi _{\psi {+1}}-\varphi _{\psi {+2}}-\varphi _{\psi }{\bigr \Vert }$ $={\bigl \Vert }\varphi _{\psi {+1}}+\varphi _{\psi {+2}}+\cdots {+\varphi }_{\vartheta }-\varphi _{\vartheta {-1}}-\cdots {-\varphi }_{\psi {+2}}-\varphi _{\psi {+1}}-\varphi _{\psi }{\bigr \Vert }$ $\leq {\bigl \Vert }\varphi _{\psi +1}-\varphi _{\psi }{\bigr \Vert }+{\bigl \Vert }\varphi _{\psi +2}-\varphi _{\psi +1}{\bigr \Vert }+\cdots +{\bigl \Vert }\varphi _{\vartheta }-\varphi _{\vartheta -1}{\bigr \Vert }$ $\leq \left\{\omega ^{\psi }+\omega ^{\psi {+1}}+\cdots {+\omega }^{\vartheta {-1}}\right\}{\bigl \Vert }\varphi _{1}-\varphi _{0}{\bigr \Vert }$ $\leq \omega ^{\psi }\left\{1+\omega {+\cdots }+\omega ^{\vartheta {-\psi }-1}\right\}{\bigl \Vert }\varphi _{1}-\varphi _{0}{\bigr \Vert }$ $\leq \omega ^{\psi }\left\{{\frac {1-\omega ^{\vartheta {-\psi }-1}}{1-\omega }}\right\}{\bigl \Vert }\varphi _{1}-\varphi _{0}{\bigr \Vert }{.}$

(35)

Since ${\textstyle 0<\omega {<1}}$, so ${\textstyle 1-\omega ^{\vartheta {-\psi }-1}<1}$, therefore, we get

${\bigl \Vert }\varphi _{\vartheta }-\varphi _{\psi }{\bigr \Vert }\leq {\frac {\omega ^{\psi }}{1-\omega }}{\bigl \Vert }\varphi _{1}-\varphi _{0}{\bigr \Vert }{.}$

(36)

Since ${\textstyle {\bigl \Vert }\varphi _{1}-\varphi _{0}{\bigr \Vert }{<\infty }}$, we find that ${\textstyle {\bigl \Vert }\varphi _{\vartheta }-\varphi _{\psi }{\bigr \Vert }\rightarrow {0}}$ when ${\textstyle \vartheta }$ and ${\textstyle \psi \rightarrow \infty }$. Because of this, it can be seen that the sequence $\left\{\varphi _{\vartheta }\right\}$ generated by q-HATM is a Cauchy sequence and is thus convergent.

5. Solution for compound KdV-Burgers equation

We shall employ the fractional q-homotopy analysis transform technique to present the solution to the pertinent problem. To illustrate the reliability of the suggested strategy, we shall give three instances. This section looks at the new fractional compound KdV-Burgers equation, which has the following form:

${\frac {\partial ^{\varepsilon }\varphi }{\partial \tau ^{\varepsilon }}}+l\varphi {\frac {\partial \varphi }{\partial x}}+m\varphi ^{2}{\frac {\partial \varphi }{\partial x}}+n{\frac {\partial ^{2}\varphi }{\partial x^{2}}}-o{\frac {\partial ^{3}\varphi }{\partial x^{3}}}=0,\;0<\varepsilon \leq {1},$

(37)

where $l$, $m$, $n$ and $o$ are nonzero constants, with the initial condition [27]

$\varphi \left(x,0\right)=\varphi \left(x\right).$

(38)

Equation (37) may be expressed in operator form as

$D_{\tau }^{\varepsilon }\varphi (x,\tau )=o\varphi _{3x}-l\varphi \varphi _{x}-m\varphi ^{2}\varphi _{x}-n\varphi _{xx},\;0<\varepsilon \leq {1.}$

(39)

According to the q-HATM, we define the ${\textstyle K^{th}}$-order deformation equation and the nonlinear operator ${\textstyle {\mathcal {N}}}$ as

${\mathcal {N}}\left[{\mathit {\Theta }}(x,\tau ;q)\right]={\mathcal {L}}\left\{{\mathit {\Theta }}(x,\tau ;q)\right\}-\left(1-{\frac {\varsigma _{\hbox{k}}}{n}}\right)\left({\frac {\varphi \left(x\right)}{s}}\right)-{\frac {1}{s^{\varepsilon }}}{\mathcal {L}}{\Bigl \{}o\left({\mathit {\Theta }}(x,\tau ;q)\right)_{3x}$-$l{\mathit {\Theta }}(x,\tau ;q)\left({\mathit {\Theta }}(x,\tau ;q)\right)_{x}$ $-m\left({\mathit {\Theta }}(x,\tau ;q)\right)^{2}\left({\mathit {\Theta }}(x,\tau ;q)\right)_{x}-n\left({\mathit {\Theta }}(x,\tau ;q)\right)_{2x}{\Bigr \}},$

(40)

${\mathcal {L}}\left\{\varphi _{\scriptscriptstyle k}(x,\tau )-\chi _{\scriptscriptstyle k}\varphi _{\scriptscriptstyle k-1}(x,\tau )\right\}=\hbar {\mathfrak {R}}_{\scriptscriptstyle k}\left({\overset {\rightarrow }{\varphi }}_{\scriptscriptstyle k-1}\right),$

(41)

respectively, where

${\mathfrak {R}}_{k}\left({\overset {\rightarrow }{\varphi }}_{k-1}\right)={\mathcal {L}}\left\{\varphi _{k-1}\right\}-\left(1-{\frac {\varsigma _{k}}{n}}\right)\left({\frac {\varphi \left(x\right)}{s}}\right)-{\frac {1}{s^{\varepsilon }}}{\mathcal {L}}{\biggl \{}o\left(\varphi _{k-1}\right)_{3x}-l\sum _{i=0}^{k-1}\varphi _{i}\left(\varphi _{\hbox{k-1-i}}\right)_{x}$ $-m\sum _{i=0}^{k-1}\,\sum _{h=0}^{i}\varphi _{\scriptscriptstyle h}\varphi _{\scriptscriptstyle i-h}\left(\varphi _{\scriptscriptstyle k-1-i}\right)_{x}-n\left(\varphi _{k-1}\right)_{2x}{\biggr \}}.$

(42)

Hence, for ${\textstyle k\geq {1}}$, the generic solutions of Eq. (41) are defined as

$\varphi _{k}(x,\tau )=\varsigma _{k}\varphi _{k-1}+\hbar {\mathcal {L}}^{-1}\left\{{\mathfrak {R}}_{k}\left({\overset {\rightarrow }{\varphi }}_{k-1}\right)\right\}.$

(43)

By utilizing Eq. (43), we can describe the solutions of q-HATM of Eq. (39) as

$\varphi (x,\tau )=\sum _{k=0}^{N}\varphi _{k}\left({\frac {1}{n}}\right)^{k}.$

(44)

6. Arguments and numerical results

By applying the q-HATM, a novel approximate solution to the fractional compound KdV-Burgers equation will be discovered for three different states.

Application 1

We can consider the following rational function solution with the initial condition [27] for equation (39) as

$\left.{\begin{aligned}\varphi \left(x,\tau \right)&={\frac {54}{9x+2\tau }}-{\frac {1}{3}},\\\varphi \left(x,0\right)&={\frac {54}{9x}}-{\frac {1}{3}}.\end{aligned}}\right\}$

(45)

By using the q-HATM technique to solve Eq. (39) under the aforementioned initial condition and ${\textstyle l=m=n=1}$, ${\textstyle o=6}$, we get

$\varphi \left(x,\tau \right)=\left({\frac {54}{9x}}-{\frac {1}{3}}\right)-{\frac {4\hbar \tau ^{\varepsilon }}{3x^{2}\Gamma (\varepsilon {+1)}}}\left({\frac {1}{n}}\right)+\left\{\varphi _{1}(n+\hbar )+{\frac {16\hbar ^{2}\tau ^{2\varepsilon }}{27x^{3}\Gamma (2\varepsilon {+1)}}}\right\}\left({\frac {1}{n}}\right)^{2}$ $+\left\{\left(n+\hbar \right)\left(\varphi _{2}-{\frac {2\varphi _{1}(x+36)\hbar \tau ^{\varepsilon }}{x^{3}\Gamma (\varepsilon {+1)}}}\right)\right.$ $\left.+{\frac {32\hbar ^{3}\tau ^{3\varepsilon }\left((x(x+6)+270)\Gamma (\varepsilon {+1)}^{2}-3(x+45)\Gamma (2\varepsilon {+1)}\right)}{81x^{6}\Gamma (\varepsilon {+1)}^{2}\Gamma (3\varepsilon {+1)}}}\right\}\left({\frac {1}{n}}\right)^{3}+\cdots$

(46)

If ${\textstyle n=1}$ and ${\textstyle \hbar =-1}$, we get

$\varphi \left(x,\tau \right)=\left({\frac {54}{9x}}-{\frac {1}{3}}\right)-{\frac {4\tau ^{\varepsilon }}{3x^{2}\Gamma (\varepsilon {+1)}}}+{\frac {16\tau ^{2\varepsilon }}{27x^{3}\Gamma (2\varepsilon {+1)}}}$ $+{\frac {32\tau ^{3\varepsilon }\left(3(x+45)\Gamma (2\varepsilon {+1)}-(x(x+6)+270)\Gamma (\varepsilon {+1)}^{2}\right)}{81x^{6}\Gamma (\varepsilon {+1)}^{2}\Gamma (3\varepsilon {+1)}}}+\cdots$

(47)

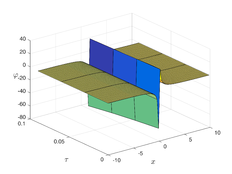
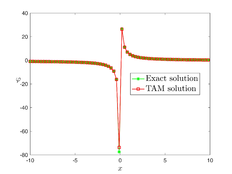
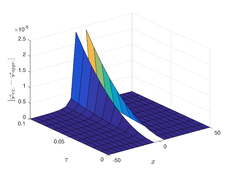
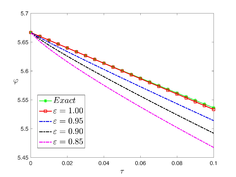
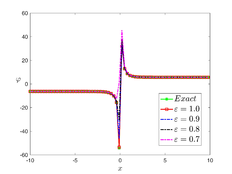
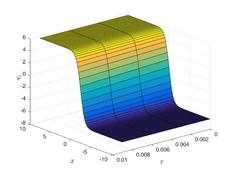
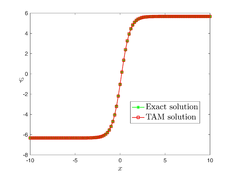
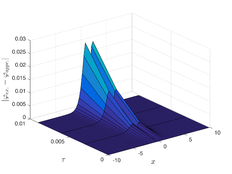
The analytical outcomes show that the approximate solution of Eq. (37) has a general style that is consistent with the exact solution in Eq. (45) for the particular case ${\textstyle \alpha =1}$. As illustrated in Figure 1, the exact solution was contrasted with the third iteration of the approximate solution, in order to understand the geometric behavior of the approximate solution q-HATM of Eq. (37). Also, the third iteration was contrasted to the exact solution when ${\textstyle \alpha =1}$, ${\textstyle \alpha =0.95}$, ${\textstyle \alpha =0.90}$ and ${\textstyle \alpha =0.80}$ respectively. It is clear from Figure 1 that each subfigure behaves in a manner that is comparable and equivalent to the others. We also see that, in terms of precision, the fractional solutions represented by subfigures (C) and (D) correspond and match the exact solution. We observe that the power series solution in Eq. (47) converges to the exact solution when ${\textstyle n\rightarrow \infty }$. The numerical outcomes from the exact solution were contrasted with the numerical outcomes from q-HATM in Table 1. It indicates the superiority of the proposed strategy in obtaining a lower error rate.

(a) 3D graph of the exact solution (b) 3D graph of the q-HATM solution (c) Graphical representation at ${\textstyle \tau =0.01}$ (d) Graphical representation for various values of ${\textstyle \varepsilon }$ (e) Absolute error at ${\textstyle \tau =0.01}$ (f) Graphical representation at ${\textstyle x=1}$

Figure 1. Periodic wave analytical solutions $\varphi \left(x,\tau \right)$ of Eq. (37) with initial condition (48).

Table 1. Comparison of the q-HATM and exact solution for case 1 at $\tau =1$

x	$\varphi _{\scriptscriptstyle Ex}$	$\varphi _{\scriptscriptstyle HATM}\left(\varepsilon =1\right)$	Absolute error	$\varphi _{\scriptscriptstyle HATM}\left(\varepsilon =0.95\right)$	$\varphi _{\scriptscriptstyle HATM}\left(\varepsilon =0.90\right)$
2	2.366670	2.366260	4.11523E-4	2.345170	2.319200
4	1.087720	1.087710	1.35369E-4	1.086100	1.084540
6	0.630952	0.630951	1.81447E-6	0.630284	0.629662
8	0.396396	0.396396	4.34462E-7	0.396015	0.395662
10	0.253623	0.253623	1.43138E-7	0.253375	0.253144
12	0.157576	0.157576	5.77333E-8	0.157401	0.157238
14	0.088541	0.088541	2.67807E-8	0.088411	0.088290
16	0.036529	0.036529	1.37629E-8	0.036429	0.036335
18	-0.004065	-0.004065	7.64909E-9	-0.004144	-0.004219
20	-0.036630	-0.036630	4.52223E-9	-0.036695	-0.036755

Application 2

We can consider the following hyperbolic function solution with the initial condition [27] for Eq. (39) as

$\left.{\begin{aligned}\varphi \left(x,\tau \right)&=6\coth \left(x-{\frac {106\tau }{9}}\right)-{\frac {1}{3}},\\\varphi \left(x,0\right)&=6\coth \left(x\right)-{\frac {1}{3}}.\end{aligned}}\right\}$

(48)

By using the q-HATM technique to solve Eq. 39) under the aforementioned initial condition and $l=m=n=1$, $o=6$, we get

$\varphi \left(x,\tau \right)=\left(6\coth \left(x\right)-{\frac {1}{3}}\right)-{\frac {212\hbar \tau ^{\varepsilon }{\hbox{csch}}^{2}(x)}{3\Gamma (\varepsilon {+1)}}}\left({\frac {1}{n}}\right)+$ $\left\{\varphi _{1}(n+\hbar )+{\frac {44944\hbar ^{2}\tau ^{2\varepsilon }\coth(x){\hbox{csch}}^{2}(x)}{27\Gamma (2\varepsilon {+1)}}}\right\}\left({\frac {1}{n}}\right)^{2}+\cdots$

(49)

If ${\textstyle n=1}$ and ${\textstyle \hbar =-1}$, we get

$\varphi \left(x,\tau \right)=\left(6\coth \left(x\right)-{\frac {1}{3}}\right)+{\frac {212\tau ^{\varepsilon }{\hbox{csch}}^{2}(x)}{3\Gamma (\varepsilon {+1)}}}+{\frac {44944\tau ^{2\varepsilon }\coth(x){\hbox{csch}}^{2}(x)}{27\Gamma (2\varepsilon {+1)}}}+$ ${\frac {22472\tau ^{3\varepsilon }{\hbox{csch}}^{6}(x)}{243\Gamma (\varepsilon {+1)}^{2}\Gamma (3\varepsilon {+1)}}}\left\{\Gamma (\varepsilon {+1)}^{2}(-36\sinh(2x)-1190\cosh(2x)+53\cosh(4x)-2103)\right.$ $\left.+18\Gamma (2\varepsilon {+1)}(\sinh(2x)+36\cosh(2x)+54)\right\}+\cdots$

(50)

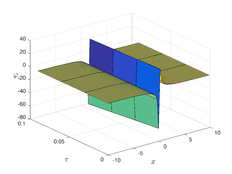
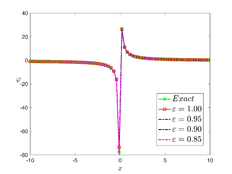
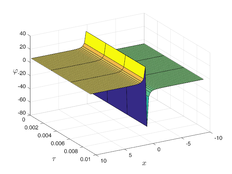
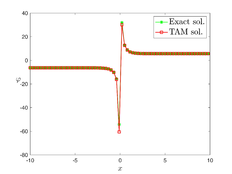
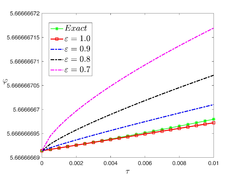
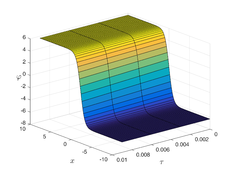
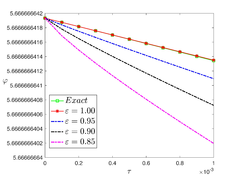
The analytical outcomes show that the approximate solution of Eq. (37) has a general style that is consistent with the exact solution in Eq. (48) for the particular case ${\textstyle \alpha =1}$. As illustrated in Figure 2, the exact solution was contrasted with the third iteration of the approximate solution, in order to understand the geometric behavior of the approximate solution q-HATM of Eq. (37). Also, the third iteration was contrasted to the exact solution when ${\textstyle \alpha =1}$, ${\textstyle \alpha =0.95}$, ${\textstyle \alpha =0.90}$ and ${\textstyle \alpha =0.80}$, respectively. It is clear from Figure 1 that each subfigure behaves in a manner that is comparable and equivalent to the others. We also see that, in terms of precision, the fractional solutions represented by subfigures (c) and (d) correspond and match the exact solution. The numerical outcomes from the exact solution were contrasted with the numerical outcomes from q-HATM in Table 2. It indicates the superiority of the proposed strategy in obtaining a lower error rate.

(a) 3D graph of the exact solution (b) 3D graph of the q-HATM solution (c) Graphical representation at ${\textstyle \tau =0.01}$ (d) Graphical representation for various values of ${\textstyle \varepsilon }$ (e) Absolute error at ${\textstyle \tau =0.01}$ (f) Graphical representation ${\textstyle x=1}$

Figure 2. Periodic wave analytical solutions $\varphi \left(x,\tau \right)$ of Eq. (37) with initial condition (48)

Table 2. Comparison of the q-HATM and exact solution for case 2 at $\tau =1$

x	$\varphi _{\scriptscriptstyle Ex}$	$\varphi _{\scriptscriptstyle HATM}\left(\varepsilon =1\right)$	Absolute error	$\varphi _{\scriptscriptstyle HATM}\left(\varepsilon =0.95\right)$	$\varphi _{\scriptscriptstyle HATM}\left(\varepsilon =0.90\right)$
-30	-6.33333	-6.33333	2.02221E-22	-6.33333	-6.33333
-25	-6.33333	-6.33333	4.45421E-18	-6.33333	-6.33333
-20	-6.33333	-6.33333	9.81104E-14	-6.33333	-6.33333
-15	-6.33333	-6.33333	2.15990E-09	-6.33333	-6.33333
-10	-6.33333	-6.33329	4.75750E-05	-6.33328	-6.33326
10	-6.6862	5.66673	12.35290000	5.66674	5.66675
15	5.68577	5.68577	1.91023E-02	5.66667	5.66667
20	5.66667	5.68577	8.65864E-07	5.66667	5.66667
25	5.66667	5.68577	3.93099E-11	5.66667	5.66667
30	5.66667	5.68577	2.66453E-15	5.66667	5.66667

Application 3

We can consider the following hyperbolic function solution with the initial condition [27] for equation (39) as

$\left.{\begin{aligned}\varphi \left(x,\tau \right)&=6\tanh \left(x-{\frac {106\tau }{9}}\right)-{\frac {1}{3}},\\\varphi \left(x,0\right)&=6\tanh \left(x\right)-{\frac {1}{3}}.\end{aligned}}\right\}$

(51)

By using the q-HATM technique to solve Eq. (39) under the aforementioned initial condition and $l=m=n=1$, $o=6$, we get

$\varphi \left(x,\tau \right)=\left(6\tanh \left(x\right)-{\frac {1}{3}}\right)+{\frac {212\hbar \tau ^{\varepsilon }{\hbox{sech}}^{2}(x)}{3\Gamma (\varepsilon {+1)}}}\left({\frac {1}{n}}\right)+\left\{\varphi _{1}(n+\hbar )-{\frac {44944\hbar ^{2}\tau ^{2\varepsilon }\tanh(x){\hbox{sech}}^{2}(x)}{27\Gamma (2\varepsilon {+1)}}}\right\}\left({\frac {1}{n}}\right)^{2}+\cdots$

(52)

If ${\textstyle n=1}$ and ${\textstyle \hbar =-1}$, we get

$\varphi \left(x,\tau \right)=\left(6\tanh \left(x\right)-{\frac {1}{3}}\right)-{\frac {212\tau ^{\varepsilon }{\hbox{sech}}^{2}(x)}{3\Gamma (\varepsilon {+1)}}}-{\frac {44944\tau ^{2\varepsilon }\tanh(x){\hbox{sech}}^{2}(x)}{27\Gamma (2\varepsilon {+1)}}}-{\frac {22472\tau ^{3\varepsilon }{\hbox{sech}}^{6}(x)}{243\Gamma (\varepsilon {+1)}^{2}\Gamma (3\varepsilon {+1)}}}$ $\left\{\Gamma (\varepsilon {+1)}^{2}(36\sinh(2x)+1190\cosh(2x)+53\cosh(4x)-2103)-18\Gamma (2\varepsilon {+1)}(\sinh(2x)+36\cosh(2x)-54)\right\}+\cdots$

(53)

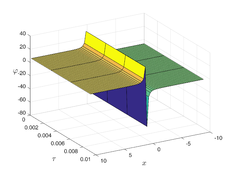
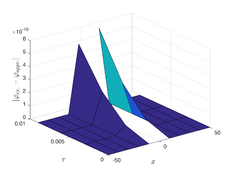
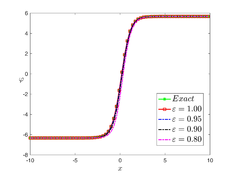
The analytical outcomes show that the approximate solution of Eq. (37) has a general style that is consistent with the exact solution in Eq. (51) for the particular case ${\textstyle \alpha =1}$. As illustrated in Figure 3, the exact solution was contrasted with the third iteration of the approximate solution, in order to understand the geometric behavior of the approximate solution q-HATM of Eq. (37). Also, the third iteration was contrasted to the exact solution when ${\textstyle \alpha =1}$, ${\textstyle \alpha =0.95}$, ${\textstyle \alpha =0.90}$ and ${\textstyle \alpha =0.80}$ respectively. It is clear from Figure 1 that each subfigure behaves in a manner that is comparable and equivalent to the others. We also see that, in terms of precision, the fractional solutions represented by subfigures (c) and (d) correspond and match the exact solution. The numerical outcomes from the exact solution were contrasted with the numerical outcomes from q-HATM in Table 3. It indicates the superiority of the proposed strategy in obtaining a lower error rate.

(a) 3D graph of the exact solution (b) 3D graph of the q-HATM solution (c) Graphical representation at ${\textstyle \tau =0.01}$ (d) Graphical representation for various values of ${\textstyle \varepsilon }$ (e) Absolute error at ${\textstyle \tau =0.01}$ (f) Graphical representation ${\textstyle x=1}$

Figure 3. Periodic wave analytical solutions $\varphi \left(x,\tau \right)$ of Eq. (37) with initial condition (51)

Table 3. Comparison of the q-HATM and exact solution for case 3 at $\tau =1$

x	$\varphi _{\scriptscriptstyle Ex}$	$\varphi _{\scriptscriptstyle NDM}\left(\varepsilon =1\right)$	Absolute error	$\varphi _{\scriptscriptstyle NDM}\left(\varepsilon =0.9\right)$	$\varphi _{\scriptscriptstyle NDM}\left(\varepsilon =0.8\right)$
-30	-6.33333	-6.33333	0	-6.33333	-6.33333
-25	-6.33333	-6.33333	0	-6.33333	-6.33333
-20	-6.33333	-6.33333	1.33227E-14	-6.33333	-6.33333
-15	-6.33333	-6.33333	2.86205E-10	-6.33333	-6.33333
-10	-6.33333	-6.33333	6.30408E-06	-6.33333	-6.33332
10	-6.00007	5.66666	11.66670000	5.66666	5.66666
15	5.64763	5.66667	1.90417E-02	5.66667	5.66667
20	5.66667	5.66667	8.65864E-07	5.66667	5.66667
25	5.66667	5.66667	3.93099E-11	5.66667	5.66667
30	5.66667	5.66667	1.77636E-15	5.66667	5.66667

7. Conclusion

We continually make scientific and technological progress by studying and investigating nonlinear physical models using innovative methodologies. In the proposed framework, we employed HATM to analyze the fractional-order compound KdV-Burgers equation. The uniqueness theorem and convergence analysis of the expected problem are investigated using Banach's fixed-point theory. Three examples are given to show the dependability and applicability of the predicted method. For the distinct fractional order, 2D, and 3D graphs, and tables are supplied with the behaviors for the obtained results. The motivating behaviors of the analogical models are concluded using these graphs. Examining these types of incidents might inspire fresh approaches to researching other real-world happenings. Also, it might spark ideas for an accurate approach to assessing nonlinear models in science and technology. This study clarifies the suggested model, which has a strong historical dependence on time instants and can be clearly shown using fractional ideas. Last but not least, a nonlocal index of memory is what the fractional derivative physically means. This characteristic makes the fractional derivative appropriate for modeling such an issue.

Conflict of Interest: The author declare that there is no conflict of interest.

Data Availability: No data were used to support this study.

Acknowledgments

This research project was funded by the Deanship of Scientific Research, Princess Nourah bint Abdulrahman University, through the Program of Research Project Funding After Publication, grant No (43- PRFA-P-48).

References

[1] He J.H. A tutorial review on fractal spacetime and fractional calculus. International Journal of Theoretical Physics, 53:3698-3718, 2014.

[2] Liu F.J., Liu H.Y., Li Z.B, Le J.H. A delayed fractional model for Cocoon heat-proof property. Thermal Science, 21(4):1867-1871, 2017.

[3] He J.H. Fractal calculus and its geometrical explanation. Results in Physics, 10:272-276, 2018.

[4] Tarasov V.E. Fractional vector calculus and fractional Maxwells equations. Annals of Physics, 323(11):2756-2778, 2008.

[5] Mirzazadeh M. A novel approach for solving fractional Fisher equation using differential transform method. Pramana, 86:957-963, 2016.

[6] Prakash A., Veeresha P., Prakasha D., Goyal M. A new efficient technique for solving fractional coupled NavierStokes equations using q-homotopy analysis transform method. Pramana, 93, 6, 2019.

[7] Podlubny I. Fractional differential equations. Academic Press, New York, pp. 340, 1999.

[8] Kilbas A., Srivastava H., Trujillo J. Theory and applications of fractional differential equations. Elsevier, Vol. 204, pp. 540, 2006.

[9] Prakash A., Goyal M., Gupta S. Fractional variational iteration method for solving time-fractional Newell-Whitehead-Segel equation. Nonlinear Engineering, 8:164-171, 2019.

[10] Prakash A., Goyal M., Gupta S. A reliable algorithm for fractional Bloch model arising in magnetic resonance imaging. Pramana, 92:1-10, 2019.

[11] Liao S. On the homotopy analysis method for nonlinear problems. Applied Mathematics and Computation, 147:499-513, 2004.

[12] Prakash A., Kaur H. Numerical solution for fractional model of Fokker-Planck equation by using q-HATM. Chaos, Solitons & Fractals 105:99-110, 2017.

[13] Srivastava H.M., Kumar D., Singh J. An efficient analytical technique for fractional model of vibration equation. Applied Mathematical Modelling, 45:192-204, 2017.

[14] Kumar D., Singh J., Baleanu D. A new numerical algorithm for fractional FitzhughNagumo equation arising in transmission of nerve impulses. Nonlinear Dynamics, 91:307-317, 2018.

[15] Singh J., Kumar D., Swroop R. Numerical solution of time-and space-fractional coupled Burgers equations via homotopy algorithm. Alexandria Engineering Journal, 55:1753-1763, 2016.

[16] Wadati M. Wave propagation in nonlinear lattice. I. Journal of the Physical Society of Japan, 38:673-680, 1975.

[17] Konno K., Ichikawa Y. A modified Korteweg de Vries equation for ion acoustic waves. Journal of the Physical Society of Japan, 37:1631-1636, 1974.

[18] Wang M. Exact solutions for a compound KdV-Burgers equation. Physics Letters A, 213(5-6):279-287, 1996.

[19] Parkes E.J., Duffy B.R. Travelling solitary wave solutions to a compound KdV-Burgers equation. Physics Letters A, 229(4):217-220, 1997.

[20] Li B., Chen Y., Zhang H. Auto-Bäcklund transformation and exact solutions for compound KdV-type and compound KdVBurgers-type equations with nonlinear terms of any order. Physics Letters A, 305(6):377-382, 2002.

[21] Narayanamurti V., Varma C.M. Nonlinear propagation of heat pulses in solids. Physical Review Letters, 25(16):1105-1108, 1970.

[22] Tappert F.D., Varma C.M. Asymptotic theory of self-trapping of heat pulses in solids. Physical Review Letters, 25(16):1108-1111, 1970.

[23] Gondal M., Arife A., Khan M., Hussain I. An efficient numerical method for solving linear and nonlinear partial differential equations by combining homotopy analysis and transform method. World Appl. Sci. J., 14:1786-1791, 2011.

[24] Khan M., Gondal M.A., Hussain I., Karimi Vanani S. A new comparative study between homotopy analysis transform method and homotopy perturbation transform method on a semi infinite domain. Math. Comput. Model., 55(3-4):1143-1150, 2012.

[25] Alqahtani Z, Hagag AE. A fractional numerical study on a plant disease model with replanting and preventive treatment. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 39(3), 27, 2023.

[26] Gorenflo R., Mainardi F. Fractional Calculus. In: Fractals and Fractional Calculus in Continuum Mechanics, Carpinteri A., Mainardi F. (eds), International Centre for Mechanical Sciences (Courses and Lectures), 378:223-276, Springer, Vienna, 1997.

[27] Naher H., Aini Abdullah F., Bekir A. Abundant traveling wave solutions of the compound KdV-Burgers equation via the improved (G/G)-expansion method. AIP Advances, 2(4), 042163, 2012.

[28] Singh P., Sharma D. Convergence and error analysis of series solution of nonlinear partial differential equation. Nonlinear Engineering, 7(4):303-308, 2018.

[29] Kreyszig E. Introductory functional analysis with applications. Chapter 5: Further applications: Banach fixed point theorems. New York, Wiley Classic Libraries, 299-321, 1989.