Abstract
This work details a methodology to characterize the performance of solar thermal and photovoltaic thermal (PVT) collectors using an indoor solar simulator. In this study, several cases have been compared to show that the methodology can be used to extract fundamental performance characteristics from a solar collector. In the first case, a serpentine collector was compared against a header riser collector using the same mass flow rate. It was found that the header riser was less efficient, with a 34% increase in the overall loss coefficient. The experimental results were compared with commonly used empirical models and showed a close agreement. In the second case, the impact on performance of using a polycarbonate cover is presented. The results show that the optical efficiency of the collector is reduced by 12% when using a cover; however, because the loss coefficient is reduced by 53%, the covered collector performs better when there is a large temperature difference between the absorber and the ambient. The third case investigates the combined performance of a PVT collector, that produces both heat and electricity from a single device. By placing photovoltaic (PV) laminates on top of the serpentine absorber, the thermal efficiency is reduced by 15%. When electricity is generated by laminates, the thermal efficiency is reduced by a further 3.5%; this drop in thermal efficiency is a result of the incident radiation producing electricity before reaching the thermal absorber. The combined efficiency of the PVT collectors was compared at controlled inlet temperatures. The serpentine design had the highest combined efficiency of 61% with 8% electricity at the lowest inlet temperature (21°C). The dominant form of loss in the PVT system is temperature driven; as the thermal efficiency decreases, electricity generation makes up a larger percentage of the combined output. This study highlights the potential for manufacturers of bespoke thermal absorbers and PV devices to combine their products into a single PVT device that could achieve improved efficiency over a given roof area.
Nomenclature
Ac
collector area (m2)
Cb
bond conductance (W/m·K)
Cp
specific heat (J/K·kg)
De
external pipe diameter (m)
Di
internal pipe diameter (m)
FR
heat removal factor
hfi
heat transfer coefficient (W/m2·K)
k
thermal conductivity (W/m·K)
m˙
mass flow rate (kg/sec)
Qu
useful energy per unit time (W)
Ta
ambient temperature (°C)
Tpm
average plate temperature (°C)
UL
overall heat loss coefficient (W/m2·K)
Tm
mean fluid temperature (°C)
Ti
inlet temperature (°C)
To
outlet temperature (°C)
G
irradiance (W/m2)
S
absorbed solar energy (W)
W
fin width (m)
a2
temperature dependence of heat loss coefficient (W/m2K2)
P
electrical power (W)
I
electrical current (A)
R
electrical resistance (Ω)
Kατ
incident angle modifier
v
kinematic viscosity (m2/sec)
L
pipe length (m)
α
absorbtance
δ
thickness (m)
ηt
thermal efficiency
ηe
electrical efficiency
η0
zero loss thermal efficiency
τ
transmittance
β
PV temperature coefficient (%/°C)
Introduction
Solar thermal collectors
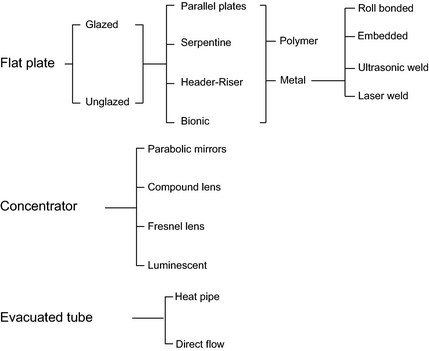
Solar thermal collectors operate by absorbing solar radiation, converting it into thermal energy and then transporting it so that it can be used for heating. A summary of the different designs and materials used in solar thermal collectors is shown in Figure 1.
|
|
|
Figure 1. Summary of main solar thermal technologies. |
Solar thermal collectors can be combined with photovoltaics (PV) to create a hybrid panel that produces both heat and electricity. These devices are called photovoltaic thermal (PVT) collectors. It has been shown that the energy produced by PVT is superior to that produced by the same area of conventional solar thermal and PV installed side by side [1].
PVT collectors
PVT collectors use a similar absorber to those found in conventional thermal collectors, the main difference is that the absorber surface in a PVT collector is behind a layer of encapsulated PV cells. A comprehensive review of different PVT collectors and their applications is given by Chow [2].
As well as extracting useful energy, the heat removal process of PVT also reduces the operating temperature of the PV cells on the absorber surface. The efficiency of a PV cell decreases linearly with temperature [3]; so by removing this excess heat, the PV cells of a PVT device can be maintained at a higher electrical efficiency thus producing more electricity. This is desirable as electricity is a higher grade form of energy than heat, which means that it can be more easily transported and converted into other forms of energy.
Flat plate PVT collectors
PVT collectors are a type of co-generation device that produces both electricity and heat from a single collector. In a PVT device, the PV cells act as the solar absorber and a heat removal fluid is used to recover the excess thermal energy. Many believe that the purpose of a PVT collector is to actively cool PV cells so that they operate at a lower temperature and thus more efficiently; however for nonconcentrator systems this is not always true, as the hot water in the system may be higher than the temperature reached by the PV cells under normal conditions [4]. The most desirable aspect of PVT technology is to be able to use available roof space as efficiently as possible [5]. A study into the layout of series connected PV cells on the surface of the solar absorber had little difference on the thermal and electrical performance [6].
There are several types of PVT system that have been introduced in literature, the design depends on the heat removal fluid that is used:
- Water (PVT/w) [[[#ese375-bib-0007|[7]]], [2], [8]];
- Air (PVT/a) [[[#ese375-bib-0007|[7]]], [2], [8]];
- Refrigerant [[[#ese375-bib-0007|[7]]], [8]];
- Heat pipe [7];
- Dual fluid (PVT/wa) [[[#ese375-bib-0008|[8]]], [9], [10]];
- PVT concentrator [[[#ese375-bib-0011|[11]]], [12], [13]].
A PVT Technology Roadmap was published as part of PV Catapult of the 6th Framework Programme [14]. To reduce system costs associated with conventional solar technologies, the roadmap suggested that the development of PVT systems should be focused on residential systems in an attempt to reduce system costs. As a result, commercially available PVT technologies closely resemble standard solar collectors. A number of priority areas were identified including technical issues, marketing issues, and building integration issues. One aspect was building integration with an emphasis on the development of plug-and-play systems that could be integrated with existing building practices. The PVT forum was a coordination action from the 2003 PVT Catapult Programme which aimed to prepare Europe for the expansion of the PV market [15].
Performance testing of PVT solar collectors
There is currently no standard method to assess the performance of a PVT collector; however, a draft was proposed as part of the PV Catapult Programme [16]. This however, was a combination of existing standards used to determine the performance of conventional solar thermal and PV collectors, EN 12975 and IEC 61215, respectively.
Outdoor testing
In the outdoor testing of solar collectors, there is no control over environmental conditions so they must be accurately monitored throughout the test. Sun et al. carried out experimental performance testing on a roll-bonded collector combined with a heat pump using an outdoor system [17]. Zondag and Devries validated numerical models of PV-T systems using an outdoor testing station that was able to control the temperature to the inlet, measure ambient temperature, irradiance and wind speed [[[#ese375-bib-0001|[1]]], [18]]. Zhang et al. carried out outdoor testing of an evacuated-tube solar collector with and without a heat shield [19]. It was reported that the most difficult part of the study was controlling the working temperatures above 100°C because evacuated tube devices operate at a much higher temperature than flat plate systems. The outdoor testing rigs used in these experiments were used to measure the inputs for the thermal efficiency curve, which provide useful information on collector performance [20].
More recently, Touafek carried out a study of a PVT collector mounted inside a galvanized steel housing with insulation and a glass cover. They found that the device performed better than a serpentine collector and the zero loss efficiency of the novel design was 55% [21]. Another study was carried out by Ibrahim into a flat plate spiral design collector designed for building integration applications and measured a combined efficiency of 62% [22].
Indoor testing
Laboratory testing involves the characterization of the performance under controlled laboratory conditions. This type of test is short term, has well defined parameters and the experimental variables are monitored. It is standard practice to validate the numerical models using experimental methods.
Zondag carried out experimental validation of the numerical models with different dimensional complicity. The results for the one dimensional model, which was found to be adequate, are summarised in Table 1.
| Panel | Zero loss efficiency |
|---|---|
| |
| Thermal collector | 0.84 ± 0.011 |
| PVT without electricity | 0.59 ± 0.015 |
| PVT with electricity | 0.54 ± 0.015 |
The results were then used to estimate the annual thermal efficiency of the PVT collector which was found to be 33% compared to 54% for the conventional solar thermal collector. The electrical efficiency of the PVT collector was 6.7% compared to 7.2% for the conventional PV laminate under the same conditions.
Zakharchecko carried out an experimental test that investigated the use of different types of PV panels and methods of thermal contact in a PVT system. They concluded that a PVT system requires a special type of modified PV panel for efficient heat extraction and commercial panels were not suitable for use in a PVT collector [24].
Tonui and Tripanagnostopoulos validated their steady state numerical model using temperature readings taken from thermocouples placed in the PVT air collector. The collector was tested outdoors and a pyranometer and anemometer were used to record irradiation and wind speed, respectively [25].
Iordanou constructed an experimental system to validate numerical models of a solar collector that contained a porous medium in the flow channels [26]. The models were experimentally validated using an indoor solar simulator that consisted of 110 halogen floodlights, each 150 W. Thermocouples placed on the surface of the solar absorber were used to gather information on surface temperature. Agrawal et al. also used a halogen light source to compare the performance of hybrid PVT tiles and was able to record the electrical and thermal output over a time period. The air-based system incorporated microchannels and the thermal and electrical efficiency was 14.7% and 10.8%, respectively [27]. Halogen lamps, however, produce a high quantity of infrared portion; an early study by Govaer showed that lamps with a non-identical solar spectrum, such as that produced by a halogen lamp, could be used to generate heat in a solar collector [28]. However, metal halide lamps are the preferred choice for testing solar collectors, as their output closely matches that of the solar spectrum. In one study, a large-scale simulator consisting of 35 metal halide lamps (575 W); each fixed into its own parabolic reflector, was used to test a complete solar domestic hot water system [29]. In another study, a light source consisting of 228 halogen lamps and supplemented with 912 LEDs, to ensure spectral match with that of the sun, was used to test a solar-powered refrigeration system [30]. The use of metal halide lamps has also been used to carry out accelerated durability testing of the components in a solar collector [31].
Thermal analysis of a flat-plate collector
The energy generated by any flat plate solar collector can be expressed using equation (1)[20].
|
|
(1) |
|
|
(2) |
where, Ac is the collector area, G is the irradiance, τ is the transmittance of any covers, α is the absorptance of the collector, UL is the overall heat loss coefficient, Tpm is the average plate temperature, and Ta is ambient temperature.
Header riser collectors
Equation (1) was reformulated by Hottel and Whillier-Bliss [32], so that useful energy can be characterized as a function of the fluid temperature entering the collector, Ti. Equation (1) shows that the losses are driven by the temperature difference between Tpm and Ta and equal zero when Tpm = Ta; under these conditions the collector is said to be operating at zero loss efficiency, also known as the optical efficiency. The Hottel and Whillier-Bliss model (HWB) incorporates a heat removal factor, FR which compares Qu to the theoretical energy gain if the entire collector was kept at inlet temperature, see equation (3). The methodology of the HWB model is extensively covered in [20].
|
|
(3) |
where, m˙ is the mass flow rate of the fluid through the collector, Cp is the specific heat of the fluid, and To is the outlet temperature. Once the values of FR and UL have been determined it is possible to calculate the useful energy gain of a collector using equation (6).
|
|
(4) |
Serpentine collectors
In a serpentine collector, there is a single pipe connected to the back of the absorber. Because there is heat transfer between the pipes as they snake across the width of the absorber, the HWB model cannot be used to determine FR. Zhang and Lavan solved the problem of FR for a serpentine collector with N, number of turns using a matrix approach [33]. They showed that the calculation of FR is dependent on a set of nondimensional parameters, F1–F6, shown in equations (5)–(12) [20]. Their findings show that the heat removal factor is at a maximum at N = 1 and a minimum at N = 2. FR then begins to increase with N but at a decreasing rate; and as N reaches infinity, the value of FR begins to reach the value at N = 1. This finding is supported by Dayan, who showed that as the number of turns increases the tube length increases for a given area [34]. When N = 1 the serpentine collector acts as a header riser plate and FR is greatest as there is no heat transfer between tubes [33].
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
PVT collectors
When analyzing the performance of a PVT collector, the additional electricity generation and influence of PV cells mounted onto the absorber surface must be taken into account. Florschuetz modified the HWB model to calculate the combined electrical and thermal output, , of a PVT collector using equation (15) [35].
|
|
(15) |
The terms and are modified terms for the absorbed solar energy, S, and overall heat loss coefficient, UL, respectively. To modify S, the instantaneous electrical efficiency of the PV cells is first calculated by taking into account the effect of temperature on performance see equation (16).
|
|
(16) |
where, ηref is the reference efficiency, Tref, is the reference temperature of the PV cells, Tpv is the temperature of the PV cells, and β is the temperature coefficient of efficiency of the PV cells.
Because the irradiance reaches the PV cells before the thermal absorber, the PV efficiency can be deducted from absorbed solar radiation, S, as shown in equation (17).
|
|
(17) |
where, αPVT is the thermal absorptance of the PVT collector.
UL is then modified to take into account the additional electricity generation. Unlike in a thermal collector; where there are no convective losses when the average absorber temperature reaches ambient, PV cells still have an efficiency limited by how much light they can convert into electricity. To compensate for this, the value of UL is reduced in proportion to the maximum efficiency of the PV cells, see equation (18).
|
|
(18) |
Florchuetz showed that FR differs from by no more than 1% for thermal collectors with an hfi greater than 15 W/m2K [35]. This means that the FR values calculated for serpentine and header riser collectors are applicable to PV-T collectors.
Experimental characterization
Separate guidelines have been developed by ASHRAE and ISO for the performance testing of solar thermal collectors [[[#ese375-bib-0036|[36]]], [37]]. They are very similar in approach but differ in terms of performance characteristics extracted from the results.
In the ASHRAE method, it is possible to determine FR and UL by measuring the steady state thermal efficiency, ηt, of the collector at different inlet temperatures. The graph of equation (19) is then plotted to determine the values of FR and UL for the collector.
|
|
(19) |
In the ISO method, the collector is also tested under steady state conditions but this time the difference between mean fluid temperature, Tm, and the ambient temperature is used. Equation (20) is obtained using second-order curve fitting to determine UL and the temperature dependence of UL, a2.
|
|
(20) |
where,
|
|
(21) |
In this work, the ASHRAE method is the most suitable as it allows validation of FR calculated using the empirical methods.
There is currently no official standard testing for PVT collectors but a series of recommendations were proposed as an outcome from the PV catapult program [16]. These recommendations bridge the gap between PV and solar thermal testing and are based on the existing standards for the individual technologies. Notable differences include:
- Monitoring the thermal resistance introduced by the additional PV laminate;
- Measuring the temperature distribution across the PV-T collector;
- Monitoring the power output of the PV cells mounted onto the surface.
Objective
The objective of this study was to create an experimental system that can characterize the performance of a solar collector. To establish its ability to fulfill this role, several cases are compared in this report. These include:
- A comparison of a header riser and serpentine design using the same mass flow rate;
- The impact of using a polycarbonate cover on the overall heat loss coefficient;
- The combined performance of a PVT collector.
Methodology
An indoor testing system was constructed following the guidelines in the aforementioned standards. The system is comprised of four components:
- Simulation of solar irradiance;
- Temperature control;
- Mass flow rate control;
- Performance monitoring.
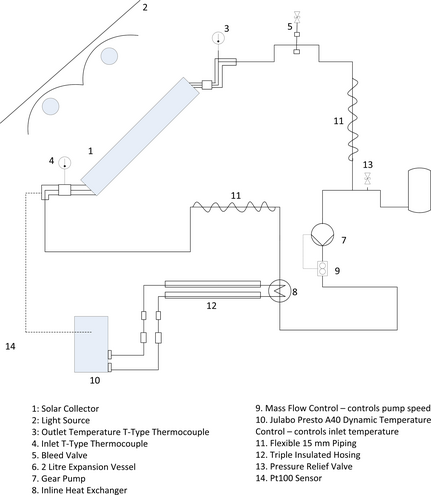
The overall system and schematic are shown in Figures 2 and 3, respectively.
|
|
|
Figure 2. Testing system for the performance characterization of solar collectors. |
|
|
|
Figure 3. Schematic of testing system. |
Collector designs
The collectors compared in this study were constructed using Sunstrip Lazerplate fins (S-Solar, Finspång, Sweden). Each fin consists of a single copper pipe laser welded to an aluminum sheet. The technical data supplied by the manufacturer are shown in Table 2.
| Parameter | Value |
|---|---|
| Fin efficiency 20 L/h | 0.938 |
| Fin efficiency 60 L/h | 0.975 |
| Emissivity (%) | 0.05 ± 2 |
| Absorptivity (%) | 0.95 ± 2 |
| Thickness (mm) | 0.5 |
The bespoke PV laminates used in this study were manufactured by GB-Sol, Cardiff, UK. The laminates are strips measuring 785 × 129 mm and contain a row of 6 series connected monocrystalline PV cells. The PV cells were encapsulated with EVA and sandwiched between 3 mm of glass on the top surface and a Tedlar back sheet. The electrical output for the individual PV cells that make up the laminate is provided in Table 3.
| Efficiency (%) | Pmpp (W) | Vmp (V) | Imp (A) | Voc (V) | Isc (A) | FF (%) |
|---|---|---|---|---|---|---|
| 17.70 | 2.72 | 0.524 | 5.204 | 0.631 | 5.666 | 76.21 |
| Voc temp. coef. %/K | −0.329 | |||||
| Isc temp. coef. %/K | +0.043 | |||||
| Pm temp. coes %/K | −0.42 | |||||
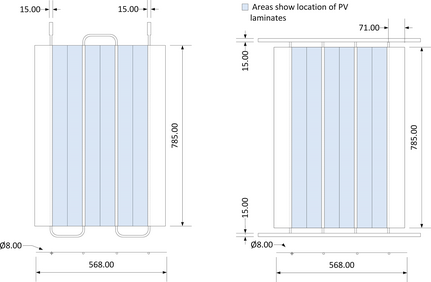
For the PVT test, three laminates were laid on top of the absorber and held in place using spring loaded clips. The collector dimensions and the positions of the PV laminates are shown in Figure 4. The surface area of the absorbers compared in this study is 0.446 m2.
|
|
|
Figure 4. Dimensions (mm) of absorbers compared in this study. |
Simulation of solar irradiance
Metal halide lamps have a spectral output that closely matches that of the solar spectrum [38] and can be used in the simulation of solar irradiance [37].
In this study, the irradiance was generated by four 1000 W metal halide lamps (Hg-Hydroponics, Lincoln, UK) mounted into parabolic reflectors (Alanod-Solar, Ennepetal, Germany) that have high reflectivity across the solar spectral range. To ensure that the light was uniform across the testing surface, a sheet of greased paper was used to disperse the light. The “non-uniformity” [39] of the light across the testing surface was measured at 13.66% using a first class CMP6 pyranometer (Kipp and Zonen, Delft, Netherlands). After a 30 min warm-up period, the lighting system had a “temporal instability” [39] of 0.37%.
A novel method was used to quantify irradiance using the average plate temperature. This method is independent of spectral sensitivity and is detailed in the Results section.
Temperature control
To create a steady state, the inlet temperature was controlled using a dynamic temperature controller (Presto A40; Julabo, Seelbach, Germany). An external pt100 sensor was connected to the controller and positioned at the inlet to enable feedback based control of the inlet temperature. The collectors were characterised using five data points across a temperature range of 21°C to 80°C. The temperature control circuit used silicone oil as the heat transfer fluid, and this was connected to the collector circuit using an inline plate heat exchanger (Bowman, Birmingham, UK).
Mass flow control
The thermal output of the collector is calculated using equation (22).
|
|
(22) |
where, the mass flow rate and cp is the specific heat of the fluid. Control of mass flow rate through the collector was achieved using a Bronkhorst Cori-Flow M15 mass flow controller (Bronkhorst Cori-Tech B.V., Ruurlo, Netherlands) which controls the speed of a Tuthill, DGS series, gear pump (Tuthill, Alsip, USA). The mass flow recommended by ISO [37] is 0.02 kg/sec per m2 of collector and was applied to all cases compared in this study.
Performance monitoring
Thermal performance
The thermal output and performance of the collectors were calculated from temperatures recorded at the inlet, outlet, and ambient. All temperature readings were measured using T-Type thermocouples (Omega Engineering, Manchester, UK) that were calibrated against a high-precision thermometer in a water bath. The thermocouples were found to have an uncertainty of ±0.5%.
To ensure that the temperature readings were representative of the bulk flow, the inlet and outlet sensors were placed downstream of fixings; and the ambient air sensor was sheltered from radiation. The tests were carried out in a large open space with a stable ambient temperature and humidity.
To investigate temperature distribution, 32 thermocouples were attached to the back of the absorber using copper tape. Each thermocouple was placed at the center of an evenly spaced grid comprised of eight columns and four rows.
Electrical performance
The IV curves for the PV laminate were obtained at different inlet temperatures using an electrical source meter (Model 2601B; Keithley, Cleveland, US). The electrical output from the PV cells was measured when the collector reached thermal equilibrium, determined by a steady fluid temperature at the outlet. This was to ensure the thermal losses of the PV cell had stabilised. The electrical output was measured by connecting a fixed resistance of 2Ω. The electrical current through the circuit was measured in series using a digital multimeter (Model DMM4020; Tektronix, Beaverton, US) and the electrical power output calculated using equation (23).
|
|
(23) |
Calculation of uncertainty
The results generated in this study have been subjected to a multivariate uncertainty analysis to determine the total combined uncertainty in the results, ωT- see equation (24). The standard uncertainties associated with experimental measurements are shown in Table 4.
|
|
(24) |
where, y is the output, x is the independent variable, and ωx is the variable uncertainty of x.
| Parameter | Value | Standard uncertainty (%) | Origin |
|---|---|---|---|
| |||
| Mass flow | 0.009 kg/sec | −0.05 | Manufacturer |
| Temperature (inlet, outlet, ambient, mean plate temperature) | Variable | ±0.5 | Manufacturer and confirmed through measurement |
| Collector area | 0.45 m2 | ±0.31 | Measured |
| Absorbtivity | 0.95 | ±2 | Manufacturer |
| Transmittancea | 0.85 | ±2.5 | Manufacturer |
| Emissivity | 0.05 | ±2 | Manufacturer |
| Specific heat of water | Variable | NA | No information available – interpolated from fluid property tables (ThermExcel) |
| Incident angle modifier | 1 | NA | No information available – assumed value |
| Irradiance | Variable | ±0.729 | Measured |
In absence of information claiming otherwise, the datasheet values of uncertainty reported by the manufacturers have been taken as the standard uncertainty. These values were used to determine the combined uncertainty which was then multiplied by a coverage factor of 2 to give a confidence interval of 95%.
Quantification of irradiance
During steady state testing, the average temperature of the thermocouples in contact with the absorber was taken as the mean plate temperature, Tpm. Equation (1) shows that when Tpm − Ta = 0 there are no losses from the collector. At this point the collector is operating at zero-loss efficiency or optical efficiency. It is possible to measure the optical absorption of selective surfaces using spectroscopy techniques [[[#ese375-bib-0040|[40]]], [41]] and is advisable in the characterization of a solar collector; however in this study, datasheet values of absorbtance, α, were used. With knowledge of collector absorbtance, it is possible to calculate the total incident radiation using equation (25)
|
|
(25) |
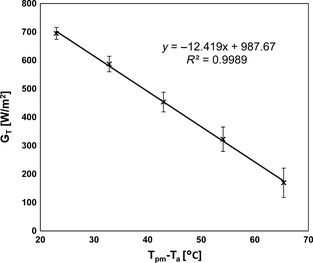
where, Kατ is the incident angle modifier, which in this study was assumed to be unity as there were no covers used; the value of transmittance, τ, was also unity. These figures have been used to plot the graph shown in Figure 5.
|
|
|
Figure 5. Determination of incident radiation using mean plate temperature for the serpentine collector. |
The y-intercept of the equation of the linear trend line shown in Figure 5 is equal to the irradiance on the solar collector. In this example shown in Figure 5 the value of irradiance is 988 W/m2.
Comparison with empirical models
To compare the results with the empirical models the heat transfer coefficient inside the collector pipes, hfi, must be determined.
The Reynolds number is the ratio of inertial forces to viscous forces and is used as an indicator of flow regime. Laminar flow occurs at Reynolds numbers of <2300 and turbulent flow occurs at >4000. Reynolds number is calculated using equation (26).
|
|
(26) |
where, Q is the volumetric flow rate, Di is the hydraulic diameter (for a circular pipe this is equal to the internal diameter), v is the kinematic viscosity (m2/sec), and A is the cross sectional area of the pipe.
The Nusselt number is the ratio of convective to conductive heat transfer across the boundary and its value is dependent on the flow regime in the pipe. Fully developed laminar flow is characterized by stable, constant fluid motion with a maximum velocity at the center of the pipe and zero velocity at the pipe walls. Under these conditions the Nusselt number is constant and can be calculated using equation (27) [42].
|
|
(27) |
where, Ts is the surface temperature of the pipe wall and is heat flux.
If the flow enters a pipe at uniform velocity, the length of pipe for laminar flow to be established is calculated using equation (28)[42].
|
|
(28) |
It has been suggested that because the length of pipe in a solar collector is too short to reach fully developed conditions [43], the collector should be evaluated using the average Nusselt number over internal length of piping in the collector, L. Equation (29) is used to calculate the average Nusselt flow in undeveloped laminar flow [42].
|
|
(29) |
where; Pr, the Prandtl number, is the ratio of kinematic viscosity to thermal diffusivity; μb and μs are the dynamic viscosities for the bulk fluid and surface temperature, respectively.
Once the Nusselt number has been calculated, hfi is calculated using equation (30).
|
|
(30) |
The parameters used to determine the internal heat transfer coefficient for each of the collectors examined in this study are shown in Table 5.
| Characteristics for experimental collectors | |
|---|---|
| |
| Pipe diameter | 0.0075 m |
| Pipe area | 0.000044 m2 |
| Fluid density | 998.2 kg/m3 |
| Fluid dynamic viscosity | 7.98E-04 Pa·sec |
| Mass flow rate serpentine | 0.009 kg/sec |
| Mass flow rate parallela | 0.00225 kg/sec |
| Hydraulic diameter (circular) | 0.0075 m |
| Kinematic viscosity at 20°C | 7.99E-07 m |
| Internal pipe diameter | 0.0075 m |
| External pipe diameter | 0.0080 m |
| Pipe length | 0.79 m |
| Prandtl number at 20°C | 6.00 |
| Thermal conductivity water at 20°C | 0.60 (W/m·K) |
Results
Three cases are presented in this report to highlight the capabilities of the experimental methodology.
Case 1 – header riser versus serpentine
Thermal efficiency curve
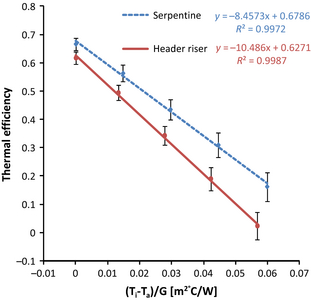
Figure 6 shows a comparison of the thermal efficiency curves for the serpentine and header riser collectors. The graph is a plot of equation (19) and the values of UL and FR have been obtained from the equation of the line and are shown in Table 6.
| Parameter | Serpentine (abs) | Header Riser (abs) |
|---|---|---|
| Zero loss efficiency FR(ατ) | 67.9 ±4.4% | 62.7 ±2.2% |
| ULFR [W/m2 °C] | 8.46 ± 0.14 | 10.49 ± 0.16 |
| FR | 0.71 ± 0.08 | 0.66 ± 0.08 |
| UL [W/m2 °C] | 11.84 ± 1.2 | 15.89 ± 1.68 |
|
|
|
Figure 6. Thermal efficiency curves for the uncovered serpentine and header riser collectors. |
Figure 6 and Table 6 show that both cases have similar values of zero loss efficiency, but as the temperature difference between the inlet and the outlet increases, the performance between the two collectors begins to diverge.
The reason for the increased heat loss coefficient in the header riser collector is because the flow is split between multiple pipes; thus providing a larger surface area for heat exchange to the ambient. As a consequence, the header riser design is a better emitter of thermal energy than the serpentine collector; if the operation of the solar panel was reversed then it would provide a more efficient means of dissipating heat into the environment. It can also be seen that the efficiency of the header riser design would exceed that of the serpentine collector at a point below Ti − Ta/G = 0. In these conditions, the heat transfer would be occurring from the ambient into the collector and, again as a result of the increased surface area, the header riser collector would perform better in this situation.
Temperature distribution
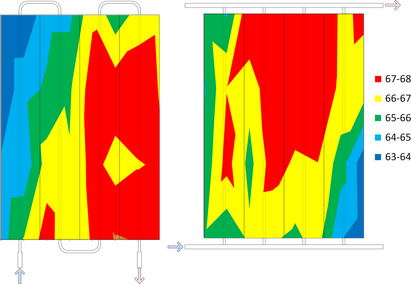
The temperature distribution across the header riser and serpentine collector, as recorded by the thermocouples on the back of the absorber, is shown in Figure 7. In the serpentine collector, the temperature of the absorber increases from left to right and the temperature profile follows the pattern of the pipes.
|
|
|
Figure 7. Temperature comparison of temperature distribution for serpentine (left) and header riser (right) uncovered absorbers at inlet temperature of 50°C. |
For the header riser design, the coldest area of the absorber is located in the bottom right. The pressure drop and flow rate through this riser pipe will be the highest, thus explaining why this area is colder; this finding is in agreement with other studies into the flow distribution of a header riser solar collector [[[#ese375-bib-0044|[44]]], [45], [46]].
Comparison with empirical models
The experimental value for UL was incorporated into the empirical models to validate the calculation of FR. The heat transfer coefficient inside the pipe was calculated and compared for both fully developed and developing laminar flow.
Serpentine collector
The experimental value of FR for the serpentine collector was compared with the values obtained using the Zang and Lavan model. The experimental value of heat loss for the serpentine collector was 11.84 W/m2°C as shown in Table 6. The comparison of calculated and experimental values of FR is shown in Table 7.
| Flow regime | Developing laminar | Fully developed laminar |
|---|---|---|
| Calculated heat transfer coefficient [W/m2 K] | 712.4 | 348.8 |
| Calculated heat removal factor – FR | 0.76 | 0.71 |
| Experimental heat removal factor – FR | 0.71 | |
Header riser collector
The experimental value of FR for the header riser collector was compared with the values obtained using the Hottel and Whillier-Bliss model. The experimental value of heat loss for the header riser collector was 15.89 W/m2°C as shown in Table 8.
| Flow regime | Developing laminar | Fully developed laminar |
|---|---|---|
| Calculated heat transfer coefficient [W/m2 K] | 467.9 | 348.8 |
| Calculated heat removal factor – FR | 0.69 | 0.66 |
| Experimental heat removal factor – FR | 0.66 | |
In both the serpentine and the header riser collectors, it was shown that the exact same heat removal factor was obtained numerically if the flow conditions were treated as fully developed laminar flow. When developing laminar flow was assumed, the value of FR was over estimated. The use of the developing laminar model assumes that the flow is uniform before entering the collector. The collectors tested in this study were part of a closed loop system and this result suggests that flow had already developed a fully laminar flow profile when at the inlet.
Case 2 – covered versus uncovered
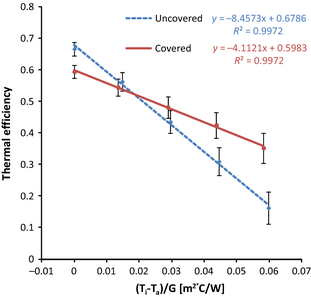
This section details the comparison of the serpentine absorber with and without the use of a poly carbonate covering. To calculate the transmittance of the cover, the reduction in irradiance caused by the cover was measured using a Kipp and Zonen CMP 6 Pyranometer (285–2800 nm). This was measured under the metal halide lamps used to characterize the thermal performance of the collectors. Using this method, transmittance was recorded as 0.85 ± 2.5%; where the error is that quoted by the manufacturer of the pyranometer. The thermal efficiency curves for the covered and uncovered case are shown in Figure 8.
|
|
|
Figure 8. Thermal efficiency curve for covered and uncovered serpentine absorber. |
Figure 8 shows that the uncovered collector has a higher zero loss efficiency (Ti − Ta/G = 0) than the covered collector before being overtaken by the covered collector at around Ti− Ta/G = 0.02. The reduced optical efficiency of the uncovered collector is a result of reflection and transmission losses that occur as light passes through the cover. The use of a cover insulates the collector and as a result the top loss coefficient is reduced. The experimental values of FR and UL for the covered and uncovered cases are shown in Table 9.
| Parameter | Uncovered (abs) | Covered (abs) |
|---|---|---|
| Zero loss efficiency FR(ατ) | 68.9 ±4.4% | 59.8 ±2.4% |
| ULFR [W/m2 °C] | 8.46 ± 0.14 | 4.11 ± 0.16 |
| FR | 0.71 ± 0.08 | 0.74 ± 0.12 |
| UL [W/m2 °C] | 11.84 ± 1.2 | 5.55 ± 0.64 |
Case 3 – PVT performance
Electrical performance at varying inlet temperatures
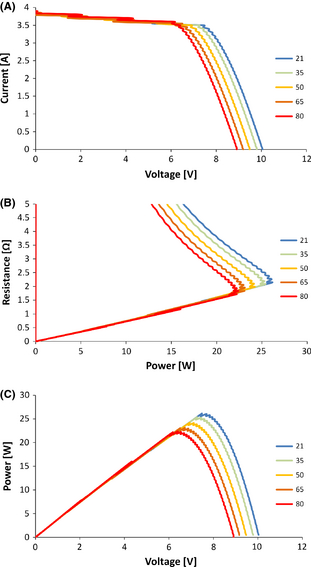
The IV curve of the PV laminate at different inlet temperatures is shown in Figure 9A. The IV plot shows that as inlet temperature increases, the voltage begins to reduce. This reduction in voltage reduces the maximum power possible from the PV system. This effect can be seen more clearly when power, the product of I and V, is plotted against voltage, see Figure 9B. This graph shows that the maximum possible power from the PV is highest when the inlet temperature is at 21°C and lowest when the inlet temperature is 80°C.
|
|
|
Figure 9. (A) IV curve (B) resistance versus power curve (C) power versus voltage curve for PV laminate at different inlet temperatures (°C). |
The power output from a PV system is controlled by the resistance of the load it is supplying. The optimum resistance is dependent on the current and voltage output. Figure 9C shows the plot of resistance versus power. Using this graph it is possible to identify the optimum resistance for each inlet temperature. The optimum resistance for each inlet temperature varies from 1.86 Ω at 21°C inlet to 2.26 Ω at 80°C inlet.
Thermal efficiency curve
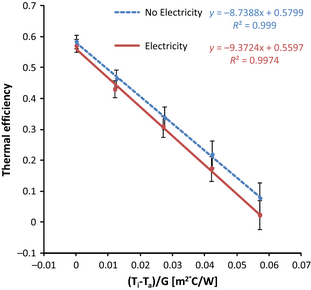
The comparison of thermal efficiency in Figure 10 shows that when electricity is being generated by the panels, the thermal efficiency is reduced, see also Table 10. The reason for this is because incident radiation generates electricity in the PV layer before reaching the absorber. This observation is in agreement with Florchuetzs modification of absorbed solar energy in equation (17). The modification of UL however, shown in equation (18), predicts that higher PV efficiencies decrease the value of UL. The reason for this is that more heat energy is wasted by the PV cells as they become less efficient and this becomes available for thermal energy collection. As a result, the thermal efficiency curves would appear convergent, not divergent as shown in Figure 10. This effect, however, would be relatively small as electricity only makes up a small portion of the overall output.
| Parameter | No electricity (abs) | Electricity (abs) |
|---|---|---|
| Zero loss efficiency FR(ατ) | 58.0 ±3.8% | 56.0 ±4.2% |
| ULFR [W/m2 °C] | 8.74 ± 0.18 | 9.37 ± 0.16 |
| FR | 0.61 ± 0.08 | 0.59 ± 0.06 |
| UL [W/m2 °C] | 14.3 ± 2.0 | 15.9 ± 2.0 |
|
|
|
Figure 10. Thermal efficiency curve for the uncovered serpentine collector with and without electricity generation. |
By placing the laminates on top of the collector, the amount of light reaching the absorber is reduced. From Table 11 it can be seen that the use of PV laminates reduces the zero loss efficiency only slightly more than the polycarbonate glazing; however the value of UL is increased by 21% compared to uncovered. A possible explanation for this is that the low emittance coating of the absorber is not effective when the laminates are placed onto its surface.
| Parameter | Uncovered (abs) | Covered (abs) | PVT (abs) |
|---|---|---|---|
| Zero loss efficiency FR(ατ) | 67.9 ±4.4% | 59.8 ±2.4% | 59.0 ±3.8% |
| ULFR [W/m2 °C] | 8.46 ± 0.14 | 4.11 ± 0.16 | 8.74 ± 0.18 |
| FR | 0.71 ± 0.08 | 0.74 ± 0.12 | 0.6 ± 0.08 |
| UL [W/m2 °C] | 11.8 ± 0.12 | 5.6 ± 0.6 | 14.3 ± 2.0 |
Combined power output of a PVT collector at fixed resistance
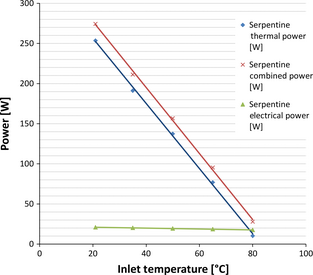
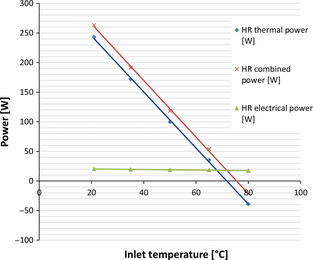
The combined output of the PVT system was plotted by combining the thermal efficiency curve with the electrical power output. A graph of the combined PVT output for the serpentine and header riser collector is shown in Figures 11 and 12, respectively. It can be seen that the impact of inlet temperature on the combined performance for both collector designs is similar.
|
|
|
Figure 11. Combined power output of an uncovered serpentine PVT collector. |
|
|
|
Figure 12. Combined power output of a header riser PVT collector. |
In both cases output is dominated by thermal energy and therefore the biggest loss of combined efficiency is a result of thermal losses from the collector. The electrical efficiency only makes up 8% of the overall efficiency when the inlet temperature is set at 21°C. The drop in electrical performance is less than the drop in thermal performance; this means that electricity makes up an increasing portion of the combined output as inlet temperature is increased. This effect is seen in Table 12. This combined output is in good agreement with the combined output of other PVT collectors reported in literature [2].
| Inlet (°C) | Thermal power (W) | Thermal efficiency (%) | Electrical power (W) | Combined power (W) | Electrical efficiencya (%) | Electrical ratiob | Combined efficiency | |
|---|---|---|---|---|---|---|---|---|
| ||||||||
| Serpentine | 21 | 253.5 | 57.1 | 20.8 | 274.4 | 7.46 | 0.08 | 0.617 |
| 35 | 191.2 | 43.0 | 20.1 | 211.3 | 7.21 | 0.10 | 0.476 | |
| 50 | 137.3 | 30.9 | 19.4 | 156.6 | 6.93 | 0.12 | 0.352 | |
| 65 | 76.8 | 17.3 | 18.5 | 95.4 | 6.63 | 0.19 | 0.215 | |
| 80 | 10.2 | 2.3 | 17.6 | 27.8 | 6.29 | 0.63 | 0.063 | |
| Header riser | 21 | 243.1 | 0.547 | 20.1 | 263.2 | 7.20 | 0.08 | 0.592 |
| 35 | 171.9 | 0.387 | 19.6 | 191.5 | 7.0 | 0.10 | 0.431 | |
| 50 | 99.5 | 0.224 | 18.9 | 118.4 | 6.8 | 0.16 | 0.266 | |
| 65 | 35.3 | 0.079 | 18.5 | 53.8 | 6.6 | 0.34 | 0.121 | |
| 80 | −39.1 | −0.039 | 17.3 | −21.8 | 6.2 | 0.79 | −0.049 | |
Discussion
Comparison with other studies
In this study it was found that combined efficiency of the PVT system was 62% and 59% for the serpentine and header riser collector, respectively. This is in close agreement with reported results from other studies which are summarized in Table 13.
| Type | Efficiency (%) | Electrical fraction | Reference |
|---|---|---|---|
| |||
| Uncovered flat plate – serpentine | 62 (combined) | 0.08a | This study |
| Uncovered flat plate spiral | 69.8 (combined) | 0.15 | [22] |
| Uncovered flat plate web | 60.4 (combined) | 0.19 | [47] |
| Galvanized steel flat plate collector | 55 (thermal only) | NA | [21] |
| Flat plate PVT | 54 (thermal only) | NA | [23] |
| Flat plate PVT | 62 (combined) | 0.17 | [48] |
This table shows the limited amount of information that is published for studies in this area. This makes it very difficult to make useful comparisons in performance. The strength of the methodology set out in this report is therefore highlighted. As a minimum, investigators of PVT systems should provide the electrical, thermal and combined efficiencies as well as the heat removal factor for the collector under investigation. With the comparisons that can be made, it can be seen that the results in this paper are similar to others found in literature.
Conclusion
In this study, an experimental system that can be used to extract fundamental performance characteristics of solar thermal collectors has been detailed. The testing system has been designed to be adaptable and flexible so that different parameters can be isolated and the impact on performance measured. In the cases presented in this paper, the experimental system has been used to: characterize the performance of two different designs of collector; quantify the impact of using a cover to reduce heat loss; quantify the combined efficiency of a PVT collector. The results show that when using the same mass flow rate, the serpentine has superior performance due to reduced heat loss coefficient. It was also shown that the use of a cover reduces the overall heat loss coefficient of the serpentine collector by 50%. In a PVT collector, the thermal efficiency is the biggest contributor to overall output. Because of this, the serpentine collector has the highest combined efficiency.
The development of experimental systems like the one detailed in this study will help researchers better understand the parameters that influence performance and encourage the testing and development of innovative concepts.
Acknowledgments
This work was sponsored by ChapmanBDSP and the Engineering and Physical Research Council, UK. A special thanks to the technicians at Brunel University, particularly Peter Wilson and Clive Barrett, who gave tremendous support throughout the project. Also thanks to the technicians of CEBER, Costas Xanthos, and Eamon Wyse for their help and advice in construction of the experimental system.
Conflict of Interest
None declared.
References
- Zondag, H. A., D. W. De Vries, W. G. J. Van Helden, R. J. C. Van Zolingen, and A. A. Van Steenhoven. 2003. The yield of different combined pv-thermal collector designs. Sol. Energy74:253–269.
- Chow, T. T.2010. A review on photovoltaic/thermal hybrid solar technology. Appl. Energy87:365–379.
- Skoplaki, E., and J. A. Palyvos. 2009. On the temperature dependence of photovoltaic module electrical performance: a review of efficiency/power correlations. Sol. Energy83:614–624.
- Huang, B. J., T. H. Lin, W. C. Hung, and F. S. Sun. 2001. Performance evaluation of solar photovoltaic/thermal systems. Sol. Energy70:443–448.
- Bystrom, J. 2008. Iea shc task 35 subtask ada 1-2 outcome of pv/t market survey interviews. Available at http://archive.iea-shc.org/publications/task.aspx?Task=35 (accessed March 15, 2015).
- Tiwari, G. N., I. M. Al-Helal. 2015. Analytical expression of temperature dependent electrical efficiency of n-pvt water collectors connected in series. Sol. Energy114:61–76.
- Zhang, X., X. Zhao, S. Smith, J. Xu, and X. Yu. 2012. Review of r&d progress and practical application of the solar photovoltaic/thermal (pv/t) technologies. Renew. Sust. Energy Rev.16:599–617.
- Daghigh, R., M. H. Ruslan, and K. Sopian. 2011. Advances in liquid based photovoltaic/thermal (pv/t) collectors. Renew. Sust. Energy Rev.15:4156–4170.
- Prakash, J. 1994. Transient analysis of a photovoltaic-thermal solar collector for co-generation of electricity and hot air/water. Energy Convers. Manage.35:967–972.
- Tripanagnostopoulos, Y.2007. Aspects and improvements of hybrid photovoltaic/thermal solar energy systems. Sol. Energy81:1117–1131.
- Zondag, H. 2006. Commercially available pvt products. http://archive.iea-shc.org/task35/publications/DA2-1_Commercially_Available_PVT_Products_v20070102.pdf (accessed March 15, 2015).
- Bernardo, L. R., B. Perers, H. Håkansson, B. Karlsson. 2011. Performance evaluation of low concentrating photovoltaic/thermal systems: a case study from Sweden. Sol. Energy85:1499–1510.
- Bernardo, R., B. Perers, H. Håkansson, and B. Karlsson. 2008. Evaluation of a parabolic concentrating pvt system. In Eurosun 2008. Curran Associates, Inc.(Apr 2011).
- Affolter, P., W. Eisenmann, H. Fechner, M. Rommel, H. Tripanagnostopoulos, Y. Schaap, et al. 2006. A European guide for the development and market introduction of pv-thermal technology. The 6th Framework Programme.
- WIP. Pv catapult european collaboration for identification of pv research and markets opportunities, socio-economics, studies, performance assessment and dissemination of pv and pv-thermal technology, 03 2015. http://www.wip-munich.de/projects/overviewofallprojects/99-projects/projects/237-pvcatapult.html (accessed March 15, 2015)
- Zondag, H., N. Van der Borg, W. Eisenmann. 2005. D8-6: Pvt performance measurement guidelines: guidelines for performance measurements of liquid-cooled non-concentrating pvt collectors using c-si cells. Petten: ECN & ISFH: Emmerthal.
- Sun, X., J. Wu, Y. Dai, and R. Wang. 2014. Experimental study on roll-bond collector/evaporator with optimized-channel used in direct expansion solar assisted heat pump water heating system. Appl. Therm. Eng.66:571–579.
- De Vries, D. W. 1998. Design of a photovoltaic/thermal combi-panel.
- Zhang, X., S. You, H. Ge, Y. Gao, W. Xu, M. Wang, et al. 2014. Thermal performance of direct-flow coaxial evacuated-tube solar collectors with and without a heat shield. Energy Convers. Manage.84:80–87.
- Duffie, J. A., and W. A. Beckman. 2013. Solar engineering of thermal processes. 4th ed. John Wiley & Sons, New York, USA.
- Touafek, K., A. Khelifa, and M. Adouane. 2014. Theoretical and experimental study of sheet and tubes hybrid pvt collector. Energy Convers. Manage.80:71–77.
- Ibrahim, A., A. Fudholi, K. Sopian, M. Y. Othman, M. H. Ruslan. 2014. Efficiencies and improvement potential of building integrated photovoltaic thermal (bipvt) system. Energy Convers. Manage.77:527–534.
- Zondag, H. A., D. W. De De Vries, W. G. J. Van Helden, R. J. C. Van Zolingen, and A. A. Van Steenhoven. 2002. The thermal and electrical yield of a pv-thermal collector. Sol. Energy72:113–128.
- Zakharchenko, R., L. Licea-Jimenez, S. A. Perez-Garcia, P. Vorobiev, U. Dehesa-Carrasco, J. F. Perez-Robles, et al. 2004. Photovoltaic solar panel for a hybrid pv/thermal system. Sol Energy Mat. Sol. Cells82:253–261.
- Tonui, J. K., and Y. Tripanagnostopoulos. 2007. Air-cooled pv/t solar collectors with low cost performance improvements. Sol. Energy81:498–511.
- Iordanou, G. 2009. Flat-Plate Solar Collectors for Water Heating with Improved Heat Transfer for Application in Climatic Conditions of the Mediterranean Region. Ph.D. thesis, Durham University, Durham, UK.
- Agrawal, S., and A. Tiwari. 2011. Experimental validation of glazed hybrid micro-channel solar cell thermal tile. Sol. Energy85:3046–3056.
- Govaer, D. 1988. Indoor collector testing with an incandescent simulator. Sol. Energy40:363–368.
- Mondol, J. D., D. Smyth, A. Zacharopoulos. 2011. Experimental characterisation of a novel heat exchanger for a solar hot water application under indoor and outdoor conditions. Renew. Energy36:1766–1779.
- Metcalf, S. J., Z. Tamainot-Telto, R. E. Critoph. 2011. Application of a compact sorption generator to solar refrigeration: case study of dakar (senegal). Appl. Therm. Eng.31:2197–2204.
- Köhl, M., G. Jorgensen, S. Brunold, B. Carlsson, M. Heck, and K. Möller. 2005. Durability of polymeric glazing materials for solar applications. Sol. Energy79:618–623.
- Hottel, H., and A. Whillier. 1955. Evaluation of flat-plate solar collector performance. In Trans. Conf. Use ofSol. Energy3:95–100.
- Zhang, M. F., and Z. Lavan. 1983. Thermal performance of a serpentine absorber plate. Proc. Annu. Meet.-Am. Sect. Int. Sol. Energy Soc.;(United States), 6(CONF-830622-).
- Dayan, M. 1997. High performance in low-flow solar domestic hot water systems. Masters thesis, University of Winconsin, Winconsin, MD.
- Florschuetz, L. W.1979. Extension of the hottel-whillier model to the analysis of combined photovoltaic/thermal flat plate collectors. Sol. Energy22:361–366.
- ASHRAE Standard. 2003. Standard 93-2003 “methods of testing to determine the performance of solar collectors”. ashrae, Atlanta.
- ISO. 2013. Iso 9806:2013 (e) solar energy - solar thermal collectors - test methods.
- Codd, D. S., A. Carslon, J. Rees, A. H. Slocum. 2010. A low cost high flux solar simulator. Sol. Energy84:2202–2212.
- IEC Standard. 2007. 60904–9. photovoltaic devices—part 9: solar simulator performance requirements, 2 edn. International Electrotechnical Commission.
- Kennedy, C. E., and H. Price. 2005. Progress in development of high-temperature solar-selective coating. In ASME 2005 International Solar Energy Conference, Pp. 749–755, American Society of Mechanical Engineers.
- Orel, Z. C., and M. K. Gunde. 2001. Spectrally selective paint coatings: preparation and characterization. Sol. Energy Mat. Sol. Cells68:337–353.
- Cengel, Y. A. 1998. Heat transfer a practical approach. McGraw-Hill, New York, USA.
- Jordan, R. C., and B. Y. H. Liu. 1977. Applications of solar energy for heating and cooling of buildings. Technical report, American Society of Heating, Refrigerating and Air Conditioning Engineers, Inc., New York.
- Weitbrecht, V., D. Lehmann, and A. Richter. 2002. Flow distribution in solar collectors with laminar flow conditions. Sol. Energy73:433–441.
- Wang, X. A., and L. G. Wu. 1990. Analysis and performance of flat-plate solar collector arrays. Sol. Energy45:71–78.
- Jones, G. F., and N. Lior. 1994. Flow distribution in manifolded solar collectors with negligible buoyancy effects. Sol. Energy52:289–300.
- Fudholi, A., K. Sopian, M. H. Yazdi, M. H. Ruslan, A. Ibrahim, H. A. Kazem. 2014. Performance analysis of photovoltaic thermal (pvt) water collectors. Energy Convers. Manage.78:641–651.
- Chow, T. T., J. Ji, and W. He. 2007. Photovoltaic-thermal collector system for domestic application. J. Solar Energy Eng.129:205–209.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?