Unaxisymmetric stagnation-point flow and heat transfer of a viscous fluid with variable viscosity on a cylinder in constant heat flux

Abstract

Existing solutions of the problem of axisymmetric stagnation-point flow and heat transfer on either a cylinder or a flat plate are for incompressible fluid. Here, fluid with viscosity proportional to a linear function of temperature is considered in the problem of an unaxisymmetric stagnation-point flow and heat transfer of an infinite stationary cylinder with non-uniform normal transpiration U₀(φ  ) and constant heat flux. The impinging free-stream is steady and with a constant strain rate ${\textstyle {\overline {k}}}$. A reduction of Navier–Stokes and energy equations is obtained by use of appropriate similarity transformations. The semi-similar solution of the Navier–Stokes equations and energy equation has been obtained numerically using an implicit finite-difference scheme. All the solutions aforesaid are presented for Reynolds numbers, ${\textstyle Re={\overline {k}}a^{2}/2{\upsilon }_{\infty }}$, ranging from 0.01 to 100 for different values of Prandtl number and viscosity-variation parameter and for selected values of transpiration rate function, ${\textstyle S(\varphi )=U_{0}(\varphi )/{\overline {k}}a}$, where a is cylinder radius and υ_∞ is the reference kinematic viscosity of the fluid. Dimensionless shear-stresses corresponding to all the cases increase with the increase in Reynolds number and transpiration rate function while dimensionless shear stresses decrease with the increase in viscosity-variation parameter. The local coefficient of heat transfer (Nusselt number) increases with increasing the transpiration rate function and Prandtl number.

Keywords

Unaxisymmetric stagnation-point flow; Heat transfer; Stationary cylinder; Temperature dependent viscosity; Numerical solution; Non-uniform transpiration

Nomenclature

a- cylinder radius

r- radial coordinate

z- axial coordinate

u, w- velocity components along (r, z)-axis

T- temperature

q_W- wall heat flux

T_∞- freestream temperature

S(φ)- transpiration rate function

k- thermal conductivity

${\textstyle {\overline {k}}}$- freestream strain rate

f(η, φ)- function related to u-component of velocity

Nu- Nusselt number

U₀(φ)- transpiration

Re- Reynolds number

Pr- Prandtl number

P- non-dimensional fluid pressure

p- fluid pressure

h- heat transfer coefficient

q_w- heat flow at wall

Greek symbols

η- similarity variable

φ- angular coordinate

α- thermal diffusivity

ρ- fluid density

υ- kinematic viscosity

υ_∞- reference kinematic viscosity

μ- viscosity of the fluid depending on the fluid temperature

μ_∞- viscosity of the ambient fluid

γ- viscosity-variation parameter

θ(η, φ)- non-dimensional temperature

σ- shear stress

1. Introduction

The study of impinging jet problems has been of considerable interest during past decades because of great technical importance in many industrial applications, such as the drying of papers and films, the tempering of glass and metal during processing, the cooling of gas turbine surfaces and electronic components, surface painting, the water show technology and textile technology, pest-citing, de-icing, geology, biology, astrophysics and Chemistry. Existing solutions of the problem of axisymmetric stagnation-point flow and heat transfer on either a cylinder or a flat plate are for viscous, incompressible fluid. These studies were started by Hiemenz [1], who obtained an exact solution of the Navier–Stokes equations governing the two-dimensional stagnation-point flow on a flat plate, and were continued by Homann [2] with an analogous axisymmetric study and by Howarth [3] and Davey [4], whose results for stagnation-point flow against a flat plate for asymmetric cases were presented. Wang [5] and [6] was the first to find an exact solution for the problem of axisymmetric stagnation-point flow on an infinite stationary circular cylinder; this was continued by Gorla’s works [7], [8], [9], [10] and [11], which are a series of steady and unsteady flows and heat transfer over a circular cylinder in the vicinity of the stagnation-point for the cases of constant axial movement and the special case of axial harmonic motion of a non-rotating cylinder. Cunning et al. [12] have considered the stagnation-point flow problem on a rotating circular cylinder with constant angular velocity; Grosch and Salwen [13] as well as Takhar et al. [14] studied special cases of unsteady viscous flow on an infinite circular cylinder. The most works of the same types are the ones by Saleh and Rahimi [15] and Rahimi and Saleh [16] and [17], which are exact solution studies of a stagnation-point flow and heat transfer on a circular cylinder with time-dependent axial and rotational movements, as well as studies by Abbasi and Rahimi [18], [19], [20] and [21], which are exact solutions of stagnation-point flow and heat transfer but on a flat plate. Some existing compressible flow studies but in the stagnation region of bodies and by using boundary layer equations include the study by Subhashini and Nath [22] as well as Kumari and Nath [23] and [24], which are in the stagnation region of a body, and works of Katz [25] as well as Afzal and Ahmad [26], Libby [27], and Gersten et al. [28], which are all general studies in the stagnation region of a body. Recently, Alizadeh et al. [29] and [30] have considered the unaxisymmetric stagnation-point flow and heat transfer of a viscous fluid on a stationary and moving cylinder with time-dependent axial velocity and magnetohydrodynamic effects. Sheikholeslami et al. [31], [32], [33], [34], [35], [36], [37], [38] and [39] have presented the thermal radiation and magnetohydrodynamics and entropy generation and space dependent magnetic field and ferrohydrodynamic of nanofluid and ferrofluid from a plate and between two horizontal parallel plates and in a semi annulus enclosure with viscous dissipation and free and force convection. Also, Kandelousi [40] have considered the effect of spatially variable magnetic field on ferrofluid flow and heat transfer considering constant heat flux boundary condition using finite element method. In a geological context, Ribe and Smooke [41] presented a two-dimensional dynamical model for melt extraction from a mantle plume and indicated that the flow in the melt zone has the form of a stagnation-point flow. Kellogg and Turcotte [42] also modeled the homogenization of the subducted oceanic crust with the depleted mantle considering the combined problem of thinning and diffusion at a stagnation-point flow. Studies of analytical investigation of MHD Jeffery–Hamel nanofluid flow in non-parallel walls were performed by Sheikholeslami et al. [43] who obtained solutions using a fourth order Runge–Kutta method.

All the aforesaid studies were confined to the fluid with constant viscosity. However, it is known that this physical property may change significantly with temperature. To predict accurately the flow behavior, it is necessary to take into account this variation of viscosity. On assuming that the viscosity of the fluid is linear functions of temperature, a semi-empirical formula was proposed by Charraudeau [44] which is appropriate for small Prandtl number. Studies of the effect of variable viscosity on flow and heat transfer to a continuous moving flat plate were performed by Pop et al. [45] and Pantokratoras [46] who obtained similarity solutions considering that viscosity varies as an inverse function of temperature. But Pantokratoras [46] obtained the results considering both viscosity and Prandtl number variables across the boundary layer. Seddeek and Salem [47] studied the case of a variable viscosity with magnetic field on the flow and heat transfer to a continuous moving flat plate.

All the studies mentioned above are regarding the axisymmetric flow and heat transfer and none has considered the effect of flow being unaxisymmetric and temperature dependent viscosity. In the present analysis, the problem of unaxisymmetric stagnation-point flow and heat transfer of a viscous fluid on a stationary cylinder with non-uniform transpiration and viscosity proportional to a linear function of temperature and constant wall heat flux is considered for the first time. A reduction of Navier–Stokes and energy equations is obtained by use of appropriate similarity transformations. The semi-similar solution of these equations is obtained numerically using an implicit finite-difference scheme. All the solutions aforesaid are presented for Reynolds numbers, ${\textstyle Re={\overline {k}}a^{2}/2{\upsilon }_{\infty }}$, ranging from 0.01 to 100 for different values of Prandtl number and viscosity-variation parameter and for selected values of transpiration rate function, ${\textstyle S(\varphi )=U_{0}(\varphi )/{\overline {k}}a}$, where a is cylinder radius and υ_∞ is the reference kinematic viscosity of the fluid. Dimensionless shear-stresses corresponding to all the cases increase with the increase in Reynolds number and transpiration rate function while dimensionless shear-stresses decrease with the increase in viscosity-variation parameter. The local coefficient of heat transfer (Nusselt number) increases with increasing the transpiration rate function and Prandtl number.

2. Problem formulation

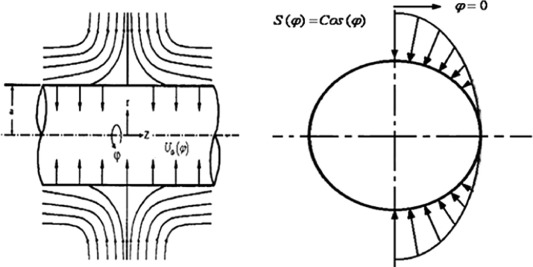
Flow is considered in cylindrical coordinates (r, φ, z) with corresponding velocity components (u, v, w); see Fig. 1. An external axisymmetric radial stagnation-point flow of strain rate ${\textstyle {\overline {k}}}$ impinges on the cylinder of radius a, centered at r = 0. Because of existence of a selected transpiration function shown below, a laminar steady incompressible flow and heat transfer of a viscous fluid in the neighborhood of an unaxisymmetric stagnation-point of a stationary infinite circular cylinder with viscosity proportional to a linear function of temperature and constant wall heat flux form.

Figure 1. Schematic diagram of a stationary cylinder under radial stagnation flow.

The steady Navier–Stokes and energy equations in cylindrical polar coordinates governing the unaxisymmetric incompressible flow and heat transfer with temperature dependent viscosity are as follows.

Mass:

${\frac {\partial u}{\partial r}}+{\frac {u}{r}}+{\frac {\partial w}{\partial z}}=$$0$

(1)

r – Momentum:

$u{\frac {\partial u}{\partial r}}+w{\frac {\partial u}{\partial z}}=$$-{\frac {1}{\rho }}{\frac {\partial p}{\partial r}}+{\frac {1}{\rho }}\left[{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(\mu r{\frac {\partial u}{\partial r}}\right)-\right.$$\left.{\frac {\mu u}{r^{2}}}+{\frac {1}{r^{2}}}{\frac {\partial }{\partial \varphi }}\left(\mu {\frac {\partial u}{\partial \varphi }}\right)\right]$

(2)

z – momentum:

$u{\frac {\partial w}{\partial r}}+w{\frac {\partial w}{\partial z}}=$$-{\frac {1}{\rho }}{\frac {\partial p}{\partial z}}+{\frac {1}{\rho }}\left[{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(\mu r{\frac {\partial w}{\partial r}}\right)+\right.$$\left.{\frac {1}{r^{2}}}{\frac {\partial }{\partial \varphi }}\left(\mu {\frac {\partial w}{\partial \varphi }}\right)\right]$

(3)

Energy:

$u{\frac {\partial T}{\partial r}}+w{\frac {\partial T}{\partial z}}=$$\alpha \left[{\frac {{\partial }^{2}T}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial T}{\partial r}}+\right.$$\left.{\frac {1}{r^{2}}}{\frac {{\partial }^{2}T}{\partial {\varphi }^{2}}}+\right.$$\left.{\frac {{\partial }^{2}T}{\partial z^{2}}}\right]$

(4)

where p, ρ, μ(T), α and T are the fluid pressure, density, viscosity of the fluid depending on the fluid temperature T, fluid thermal diffusivity, and temperature inside the boundary layer and after the impingement has occurred, respectively. The boundary conditions for the velocity field are as follows:

$w=0{\mbox{,}}\quad u=-U_{0}(\varphi )\quad r=a:$

(5)

$r\rightarrow \infty :\quad w=2{\overline {k}}z{\mbox{,}}\quad u=$$-{\overline {k}}\left(r-{\frac {a^{2}}{r}}\right)$

(6)

And the two boundary conditions with respect to φ are as follows:

$u(r{\mbox{,}}0)=u(r{\mbox{,}}2\pi )$

${\frac {\partial u(r{\mbox{,}}0)}{\partial \varphi }}={\frac {\partial u(r{\mbox{,}}2\pi )}{\partial \varphi }}$

(7)

in which Eq. (5) represents no-slip conditions on the cylinder wall, and the relations of Eq. (6) show that the viscous flow solution approaches, in a manner analogous to the Hiemenz flow, the potential flow solution as r → ∞. This can be confirmed by starting from continuity equation as the following:

${\textstyle -{\frac {1}{r}}{\frac {\partial }{\partial r}}(ru)={\frac {\partial w}{\partial z}}=}$${\mbox{Constant}}=2{\overline {k}}z$ and integrating in r and z directions with boundary conditions: w = 0 when z = 0 and u = −U₀(φ) when r = a.

For the temperature field, we have

$r=a:\quad {\frac {\partial T}{\partial r}}=-{\frac {q_{w}}{k}}=$${\mbox{Constant}}$

$r\rightarrow \infty :\quad T\rightarrow T_{\infty }$

(8)

And the two boundary conditions with respect to φ are as follows:

$T(r{\mbox{,}}0)=T(r{\mbox{,}}2\pi )$

${\frac {\partial T(r{\mbox{,}}0)}{\partial \varphi }}={\frac {\partial T(r{\mbox{,}}2\pi )}{\partial \varphi }}$

(9)

where q_w, is the cylinder surface heat flux and T_∞ is the free-stream temperature.

Out of the many forms of viscosity variation, which are available in the literature, we will consider only following form proposed by Charraudeau [44]

$\mu ={\mu }_{\infty }[1+{\gamma }^{_{\ast }}(T-T_{\infty })]$

(10)

where μ_∞ is the viscosity of the ambient fluid and γ^∗ is defined as follows:

${\gamma }^{_{\ast }}={\frac {1}{\mu }}\left({\frac {\partial \mu }{\partial T}}\right)$

(11)

A reduction of the Navier–Stokes equations is obtained by applying the following similarity transformations:

$u=-{\frac {{\overline {k}}a}{\sqrt {\eta }}}f(\eta {\mbox{,}}\varphi ){\mbox{,}}\quad w=$$2{\overline {k}}f^{'}(\eta {\mbox{,}}\varphi )z{\mbox{,}}\quad p=$$\rho {\overline {k}}^{2}a^{2}P$

(12)

where ${\textstyle \eta ={\left({\frac {r}{a}}\right)}^{2}}$ is dimensionless radial variable. Transformations (12) satisfy Eq. (1) automatically and their insertion into Eqs. (2) and (3) yields a coupled system of differential equations in terms of f(η, φ), and an expression for the pressure:

$(1+\gamma \theta )\left[\eta f^{'''}+f^{''}+{\frac {1}{4\eta }}{\frac {{\partial }^{2}f^{'}}{\partial {\varphi }^{2}}}\right]+$$\gamma \left[\eta \cdot {\theta }^{'}\cdot f^{''}+\right.$$\left.{\frac {1}{4\eta }}{\frac {\partial \theta }{\partial \varphi }}{\frac {\partial f^{'}}{\partial \varphi }}\right]+$$Re[1+{ff}^{''}-{\left(f^{'}\right)}^{2}]=0$

(13)

$P-P_{0}=-{\frac {f}{2\eta }}-{\frac {1}{Re}}{\int }_{1}^{\eta }(1+$$\gamma \theta )\left[f^{''}+{\frac {1}{4{\eta }^{2}}}{\frac {{\partial }^{2}f}{\partial {\varphi }^{2}}}\right]d\eta -$${\frac {\gamma }{Re}}{\int }_{1}^{\eta }\left[f^{'}\cdot {\theta }^{'}-\right.$$\left.{\frac {f\cdot {\theta }^{'}}{2\eta }}+{\frac {1}{4{\eta }^{2}}}{\frac {\partial \theta }{\partial \varphi }}{\frac {\partial f}{\partial \varphi }}\right]d\eta -$$2{\left({\frac {z}{a}}\right)}^{2}$

(14)

where ${\textstyle Re={\frac {{\overline {k}}a^{2}}{2{\upsilon }_{\infty }}}}$ is the Reynolds number, ${\textstyle \gamma ={\frac {1}{\mu }}\left({\frac {\partial \mu }{\partial T}}\right)\left({\frac {a.q_{w}}{2k}}\right)}$ is the viscosity-variation parameter and prime indicates differentiation with respect to η. From conditions (5), (6) and (7) the boundary conditions for Eqs. (13) and (14) are as follows:

$\eta =1:\quad f^{'}(1{\mbox{,}}\varphi )=0{\mbox{,}}\quad f(1{\mbox{,}}\varphi )=$$S(\varphi )$

(15)

$\eta \rightarrow \infty :\quad f^{'}(\infty {\mbox{,}}\varphi )=$$1$

(16)

$f(\eta {\mbox{,}}0)=f(\eta {\mbox{,}}2\pi ){\mbox{,}}\quad {\frac {\partial f(\eta {\mbox{,}}0)}{\partial \varphi }}=$${\frac {\partial f(\eta {\mbox{,}}2\pi )}{\partial \varphi }}$

(17)

in which ${\textstyle S(\varphi )={\frac {U_{0}(\varphi )}{{\overline {k}}a}}}$ is the transpiration rate function. Note that Eqs. (13) and (14) are the complete form of Eqs. (9) and (11) in Ref. [15]. These equations are the same if transpiration rate and viscosity are constant.

For the sake of brevity, only results for selected values of S(φ) = Cos(φ) and S(φ) = Ln(φ) are shown in this paper.

To transform the energy equation into a non-dimensional form, we introduce

$\theta (\eta {\mbox{,}}\varphi )={\frac {T(\eta {\mbox{,}}\varphi )-T_{\infty }}{a\cdot q_{w}/2k}}$

(18)

Making use of Eqs. (12) and (18) in the energy equation and with neglecting the small dissipation terms, we have the following:

$\eta {\theta }^{''}+{\theta }^{'}+{\frac {1}{4\eta }}{\frac {{\partial }^{2}\theta }{\partial {\varphi }^{2}}}+$$Re\cdot Pr(f{\theta }^{'})=0$

(19)

With boundary conditions as

${\begin{array}{l}\eta =1:\quad {\theta }^{'}(1{\mbox{,}}\varphi )=-1\\\eta \rightarrow \infty :\quad \theta (\infty {\mbox{,}}\varphi )=0\end{array}}$

(20)

$\theta (r{\mbox{,}}0)=\theta (r{\mbox{,}}2\pi ){\mbox{,}}\quad {\frac {\partial \theta (r{\mbox{,}}0)}{\partial \varphi }}=$${\frac {\partial \theta (r{\mbox{,}}2\pi )}{\partial \varphi }}$

(21)

Note that Eq. (19) is the complete form of Eq. (14) in Ref. [15]. These equations are the same if transpiration rate and viscosity are constant.

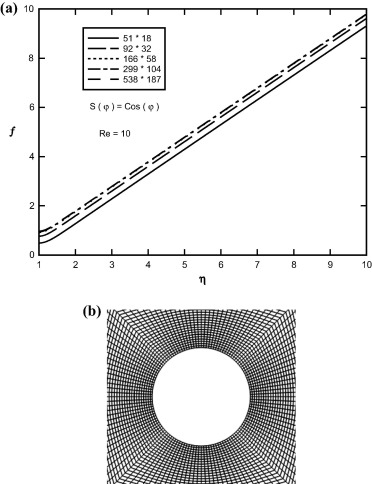
Eqs. (13) and (19), along with boundary conditions (15), (16), (17), (20) and (21), have been solved numerically by an implicit, iterative tri-diagonal finite difference method similar to that discussed by Blottner [48]. To assess the grid independence of the numerical scheme, the distributions of the f(η, φ) function against η on the cylinder were initially tested with different (η, φ) mesh sizes of 51 ∗ 18, 92 ∗ 32, 166 ∗ 58, 299 ∗ 104 and 538 ∗ 187 in Fig. 2(a). In this set of mesh sizes, as can be seen, the coefficient of 1.8 was used in each test to increase the number of mesh grids in both directions of η and φ. It was found that the variations of the f(η, φ) function distributions on the cylinder were not significant, between (η, φ) and mesh sizes of (166 ∗ 58), (299 ∗ 104) and (538 ∗ 187). Hence, a (299 ∗ 104) grid in η − φ directions was applied for the computational domain in the cylinder. Fine, non-uniform grid spacing is used in the η-direction to capture the rapid changes, such as grid lines, being closer packed near the walls. On the other hand, a uniform mesh was implemented in the φ-direction. Fig. 2(b) illustrates a sample of computational meshes used in this investigation.

Figure 2. (a) Sample profiles of f(η, φ) distributions on the cylinder for various mesh sizes at Re = 10, γ = 0 and S(φ) = Cos(φ). (b) Sample of grid system.

Validation in numerical study is very important to ensure accuracy, consistency and reliability of the numerical results obtained. For this reason, comparisons between present and previous results available for various values of η and Re are presented in Table 1 and Table 2 accordingly.

Table 1. Comparison of our results for f(η, φ) and θ(η, φ) with published results for various values of η when Re = 0.1, Pr = 1.0, γ = 0 and S(φ) = 0.

η	f(η, φ)		θ(η, φ)
	Gorla [7]	Present	Gorla [7]	Present
1.0	0.00000	0.00000	1.00000	1.00000
1.5	0.06492	0.06492	0.84610	0.84604
2.0	0.22652	0.22646	0.73715	0.73701
2.5	0.45402	0.45402	0.65311	0.65293

Table 2. Comparison of our results for f(η, φ) and θ(η, φ) with published results for various values of Re when η = 1.6, Pr = 1.0, γ = 0 and S(φ) = 0.

Re	f(η, φ)		θ(η, φ)
	Gorla [7]	Present	Gorla [7]	Present
1.0	0.19836	0.19834	0.62815	0.62815
10	0.39532	0.39532	0.17302	0.17295
100	0.48437	0.48429	0.00000	0.00000

3. Shear-stress

The shear-stress at the cylinder surface is calculated from the following:

$\sigma =\mu {\left[{\frac {\partial w}{\partial r}}\right]}_{r=a}$

(22)

where μ is the viscosity of the fluid depending on the fluid temperature. Using definition (12), the shear stress at the cylinder surface for semi-similar solutions becomes the following:

$\sigma =\mu {\frac {2}{a}}[2{\overline {k}}{zf}^{''}(1{\mbox{,}}\varphi )]\Rightarrow {\frac {\sigma a}{4\mu {\overline {k}}z}}=$$f^{''}(1{\mbox{,}}\varphi )$

(23)

Results for ${\textstyle \sigma a/4\mu {\overline {k}}z}$ against φ for different values of Reynolds numbers and transpiration rate function and viscosity-variation parameter are presented later.

4. Heat transfer coefficient

The local heat transfer coefficient and rate of heat transfer for defined wall heat flux case are given by the following:

$h={\frac {q_{w}}{T_{w}-T_{\infty }}}={\frac {-k{\left({\frac {\partial T}{\partial r}}\right)}_{r=a}}{T_{w}-T_{\infty }}}=$${\frac {2k}{a}}{\frac {1}{\theta (1{\mbox{,}}\varphi )}}$

(24)

where

$q_{w}={\frac {2k}{a}}{\frac {1}{\theta (1{\mbox{,}}\varphi )}}(T_{w}-$$T_{\infty })$

In terms of Nusselt number

$Nu={\frac {h\cdot a}{2k}}={\frac {1}{\theta (1{\mbox{,}}\varphi )}}$

(25)

5. Presentation of results

In this section solution of semi-similar Eqs. (13) and (19) along with surface shear-stresses for prescribed values of surface heat flux for selected values of Reynolds and Prandtl numbers, viscosity-variation parameter and transpiration rate function, is presented. For the sake of brevity, only results for selected values of S(φ) = Cos(φ), S(φ) = Ln(φ) are shown in this paper.

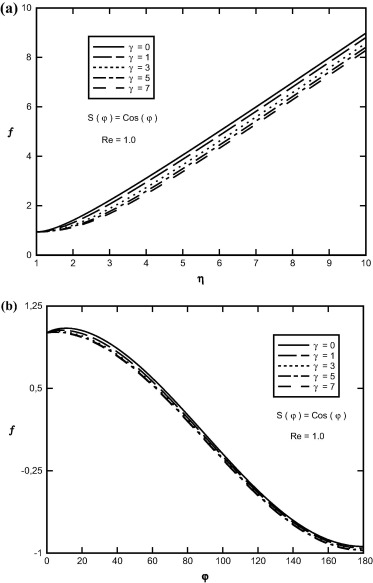
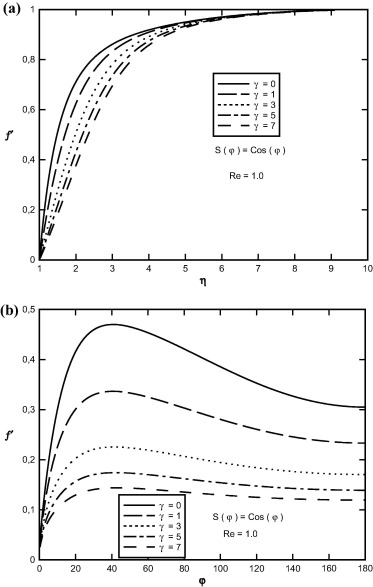
Sample profiles of the f(η, φ) function against η and φ for Pr = 1.0, and for selected values of viscosity-variation parameter are presented in Fig. 3. As viscosity-variation parameter increases, the depth of diffusion of the fluid velocity field in radial and angular directions decreases. It can also be concluded that the velocity boundary layer thicknesses enhance for large values of γ.

Figure 3. Variation of f(η, φ) in terms of (a) η, (b) φ at Re = 1.0, S(φ) = Cos(φ) and for different values of viscosity-variation parameter.

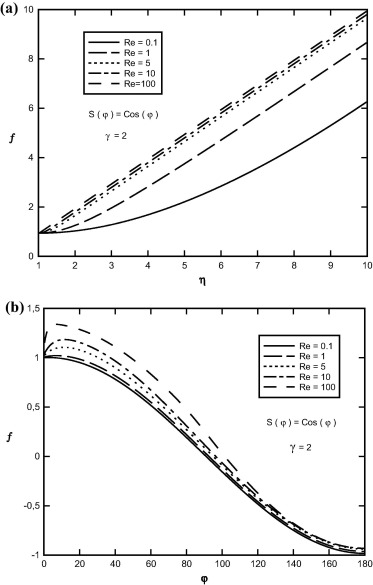
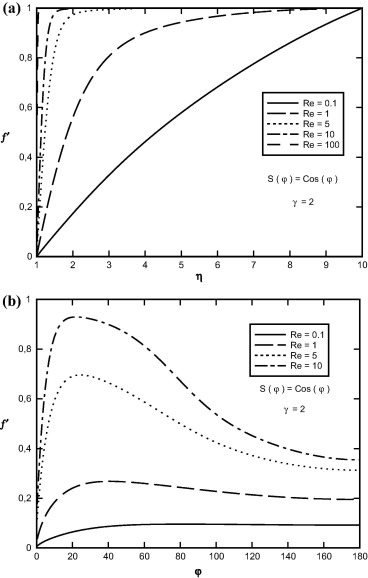
Sample profiles of the f(η, φ) function against η and φ for Re = 1.0, γ = 2.0 and for selected values of Reynolds numbers are presented in Fig. 4. As Reynolds number increases, the depth of diffusion of the fluid velocity field in radial and angular directions increases.

Figure 4. Variation of f(η, φ) in terms of (a) η, (b) φ at γ = 2.0, S(φ) = Cos(φ) and for different values of Reynolds numbers.

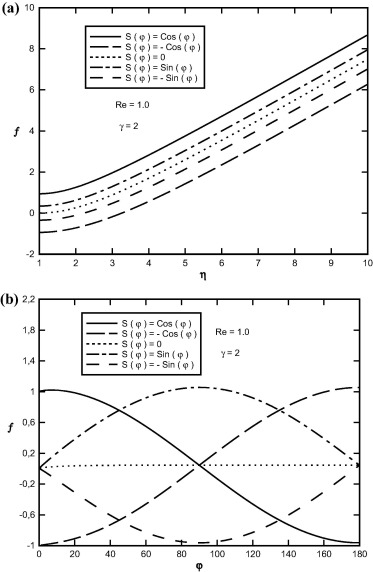
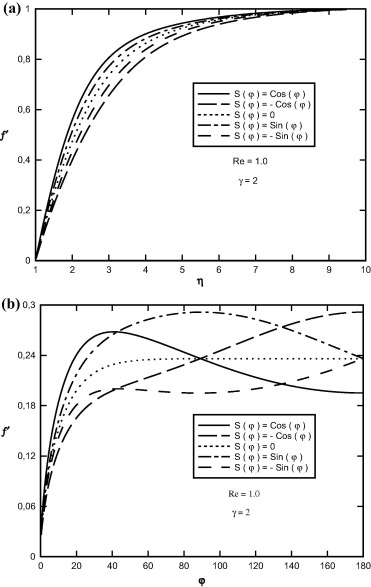
Effects of transpiration rate function on f(η, φ) function against η and φ for Pr = 1.0, γ = 2.0 and selected value of Reynolds number Re = 1.0 are shown in Fig. 5. In this figure negative S(φ) is blowing rate and positive S(φ) is the suction rate. It is evident from this figure that, as transpiration rate function increases, the f function increases and if S(φ) decreases, the f function decreases. It is interesting to note that, as S(φ) increases, the depth of diffusion of the fluid velocity field in radial and angular directions increases. Sample profiles of the f′(η, φ) functions in terms of η and φ are depicted in Figure 6, Figure 7 and Figure 8, for selected values of Reynolds number, viscosity-variation parameter and transpiration rate function. From this figures, the initial slope of the f′ function increases with increasing Reynolds number and transpiration rate function while the initial slope of the f′ function decreases with increasing viscosity-variation parameter. In fact the increase in transpiration rate function and Reynolds number decreases the thickness of the boundary layer.

Figure 5. Variation of f(η, φ) in terms of (a) η, (b) φ at S(φ) = Cos(φ), Re = 1.0, γ = 2.0 and for different values of transpiration rate function.

Figure 6. Variation of f′(η, φ) in terms of (a) η, (b) φ at S(φ) = Cos(φ), Re = 1.0 and for different values of viscosity-variation parameter.

Figure 7. Variation of f′(η, φ) in terms of (a) η, (b) φ at γ = 2.0, S(φ) = Cos(φ) and for different values of Reynolds numbers.

Figure 8. Variation of f′(η, φ) in terms of (a) η, (b) φ at γ = 2.0, Re = 1.0, S(φ) = Cos(φ) and for different values of transpiration rate function.

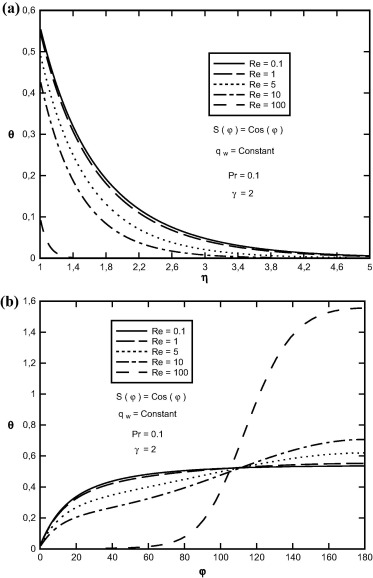
Effect of Reynolds numbers on θ(η, φ) function in terms of η and φ for the case of constant surface heat flux and S(φ) = Cos(φ) is shown in Fig. 9. As Reynolds numbers increase, the depth of diffusion of the thermal boundary layer decreases, and therefore the heat-transfer coefficient increases.

Figure 9. Variation of θ(η, φ) in terms of (a) η, (b) φ at Pr = 0.1, γ = 2.0, S(φ) = Cos(φ) and for different values of Reynolds numbers.

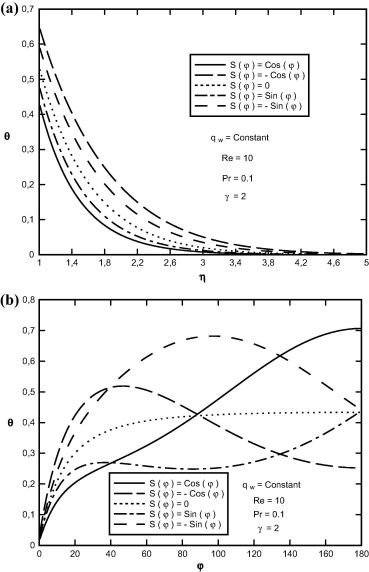
Sample profiles of the θ(η, φ) function in terms of η and φ for Re = 10, γ = 2, Pr = 0.1 are presented in Fig. 10, for selected values of transpiration rate function. It is seen that as the rate of transpiration rate function increases, the depth of diffusion of the temperature field decreases and thus the heat transfer coefficient increases.

Figure 10. Variation of θ(η, φ) in terms of (a) η, (b) φ at Pr = 0.1, γ = 2.0, S(φ) = Cos(φ) and for different values of transpiration rate function.

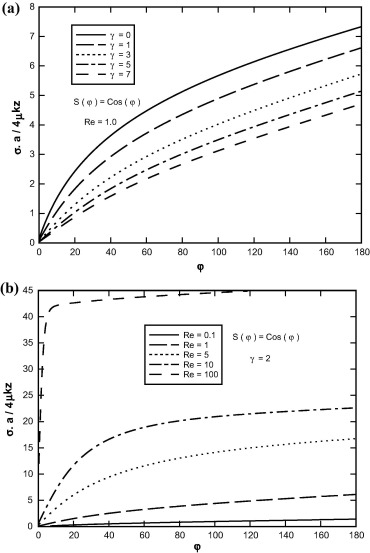
Sample profiles of surface shear stress against φ for Re = 1.0, Pr = 1.0 and S(φ) = Cos(φ) are shown in Fig. 11, for selected values of viscosity-variation parameter and Reynolds numbers. The increase in Reynolds Number and decrease in viscosity-variation parameter increase the wall shear-stress in φ direction and on the other hand cause the value of fluid velocity in this direction to approach its value in inviscid flow, rapidly. In fact the increase in Reynolds number and decrease in viscosity-variation parameter decrease the thickness of the boundary layer.

Figure 11. Variation of shear stress in terms of φ (a) for different values of viscosity-variation parameter, (b) for different values of Reynolds numbers.

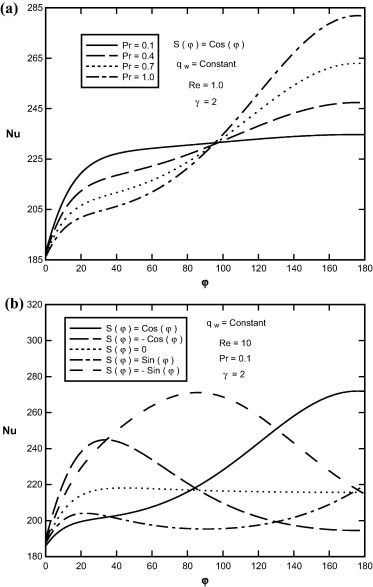
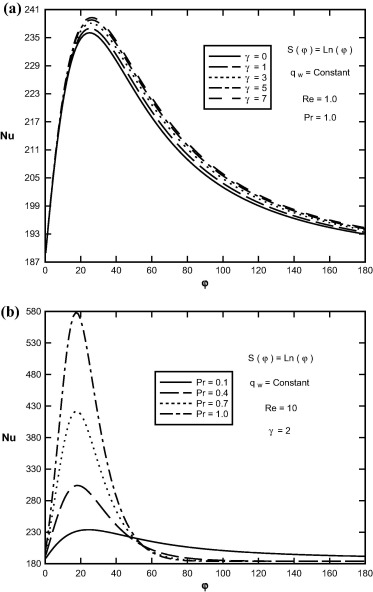
Sample profiles of the Nusselt number (local heat transfer coefficient) for Re = 10, γ = 2 and S(φ) = Cos(φ) are shown in Fig. 12, for selected values of Prandtl number and transpiration rate function. Nusselt number increases as Prandtl number and transpiration rate function increase (see Fig. 13).

Figure 12. Variation of Nusselt number in terms of φ (a) for different values of Prandtl number, (b) for different values of transpiration rate function.

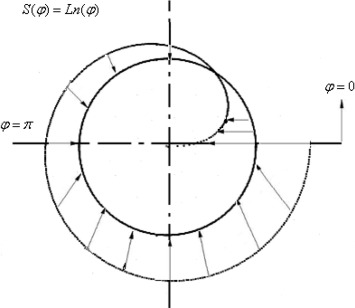
Figure 13. Schematic diagram of the transpiration function S(φ) = Ln(φ).

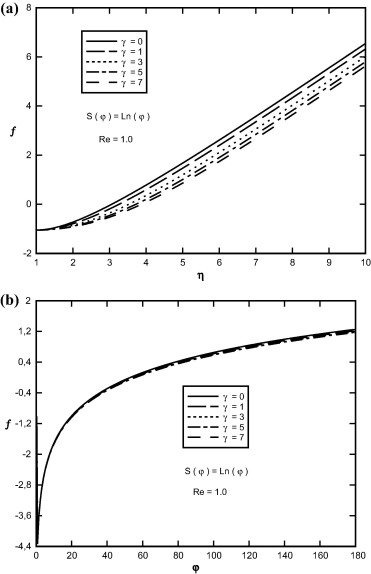
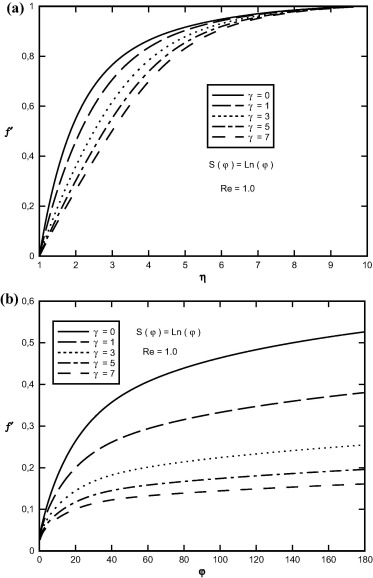
Sample profiles of the f(η, φ) function against η and φ for Re = 1.0, S(φ) = Ln(φ) and for selected values of viscosity-variation parameter are presented in Fig. 14. As viscosity-variation parameter increases, the depth of diffusion of the fluid velocity field in radial and angular direction decreases. Sample profiles of the f′(η, φ) functions in terms of η and φ are depicted in Fig. 15, for selected values of viscosity-variation parameter. From these figures, the initial slope of the f′ function decreases with increasing viscosity-variation parameter. In fact the increase in viscosity-variation parameter increases the thickness of the boundary layer.

Figure 14. Variation of f(η, φ) in terms of (a) η, (b) φ at Re = 1.0, S(φ) = Ln(φ) and for different values of viscosity-variation parameter.

Figure 15. Variation of f′(η, φ) in terms of (a) η, (b) φ at Re = 1.0, S(φ) = Ln(φ) and for different values of viscosity-variation parameter.

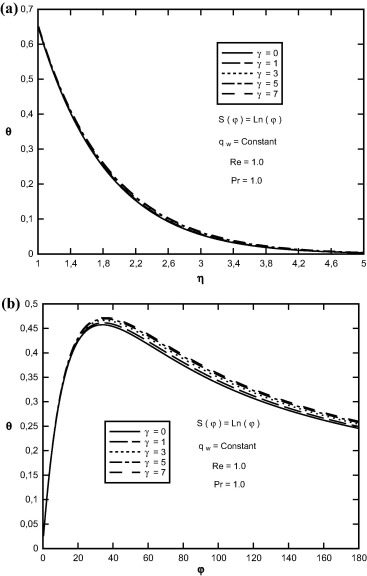
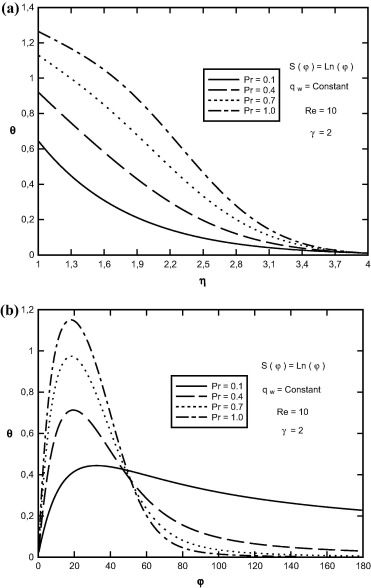
Effect of variation of constant Prandtl number and viscosity-variation parameter on θ(η, φ) function in terms of η and φ for the case of constant surface heat flux and S(φ) = Ln(φ) is shown in Figure 16 and Figure 17. As Prandtl number and viscosity-variation parameter increase, the depth of diffusion of the thermal boundary layer decreases, and therefore the heat-transfer coefficient increases.

Figure 16. Variation of θ(η, φ) in terms of (a) η, (b) φ at Pr = 1.0, S(φ) = Ln(φ) and for different values of viscosity-variation parameter.

Figure 17. Variation of θ(η, φ) in terms of (a) η, (b) φ at Re = 10, S(φ) = Ln(φ) and for different values of Prandtl number.

Sample profiles of the Nusselt number (local heat transfer coefficient) for S(φ) = Ln(φ) are shown in Fig. 18, for selected values of Prandtl number and viscosity-variation parameter. Nusselt number increases as Prandtl number increases while Nusselt number decreases with increase in viscosity-variation parameter.

Figure 18. Variation of Nusselt number in terms of φ. (a) For different values of viscosity-variation parameter. (b) For different values of Prandtl number.

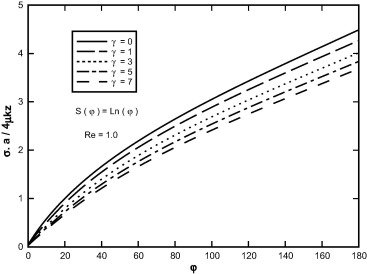
Sample profiles of surface shear stress against φ for Re = 1.0 and S(φ) = Ln(φ) are shown in Fig. 19, for selected values of viscosity-variation parameter. The increase in viscosity-variation parameter decreases the wall shear stress in φ direction and on the other hand causes the value of fluid velocity in this direction to approach its value in inviscid flow, rapidly. In fact the increase in viscosity-variation parameter increases the thickness of the boundary layer.

Figure 19. Variation of shear stress in terms of φ for different values of viscosity-variation parameter.

6. Conclusions

Existing solutions of the problem of axisymmetric stagnation-point flow and heat transfer on either a cylinder or a flat plate are for incompressible fluid. Here, fluid with viscosity proportional to a linear function of temperature is considered in the problem of an unaxisymmetric stagnation-point flow and heat transfer of an infinite stationary cylinder with non-uniform normal transpiration U₀(φ  ) and constant heat flux. The impinging free-stream is steady and with a constant strain rate ${\textstyle {\overline {k}}}$. A reduction of Navier–Stokes and energy equations is obtained by use of appropriate similarity transformations. The semi-similar solution of the Navier–Stokes equations and energy equation has been obtained numerically using an implicit finite-difference scheme. All the solutions aforesaid are presented for Reynolds numbers, ${\textstyle Re={\overline {k}}a^{2}/2{\upsilon }_{\infty }}$, ranging from 0.01 to 100 for different values of Prandtl number and viscosity-variation parameter and for selected values of transpiration rate function, ${\textstyle S(\varphi )=U_{0}(\varphi )/{\overline {k}}a}$, where a is cylinder radius and υ_∞ is the reference kinematic viscosity of the fluid. Dimensionless shear-stresses corresponding to all the cases increase with the increase in Reynolds number and transpiration rate function while dimensionless shear stresses decrease with the increase in viscosity-variation parameter. The local coefficient of heat transfer (Nusselt number) increases with increasing the transpiration rate function and Prandtl number. For the case of axisymmetric stagnation-point flow, f = f(η), f′ = f′(η) and S(φ) = 0, γ = 0 or ${\textstyle {\frac {{\partial }^{2}f}{\partial {\varphi }^{2}}}=0}$, ${\textstyle {\frac {{\partial }^{2}f^{'}}{\partial {\varphi }^{2}}}=}$$0$, ${\textstyle {\frac {{\partial }^{2}\theta }{\partial {\varphi }^{2}}}=}$$0$, ${\textstyle {\frac {\partial f^{'}}{\partial \varphi }}=0}$, ${\textstyle {\frac {\partial \theta }{\partial \varphi }}=0}$ and similarity variables and component of velocity by Wang [5], as well as energy equation by Gorla [7] and Saleh and Rahimi [15] are reached.

Acknowledgment

This research was supported by a grant from Payame Noor University (PNU), Iran.

References

1. [1] K. Hiemenz; Die Grenzschicht an einem in den gleichförmingen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder; Dinglers Polytechnisches J., 326 (1911), pp. 321–410
2. [2] F.Z. Homann; Der Einfluss Grosser Zahighkeit bei der Strmung um den Zylinder und um die Kugel; Zeitschrift für angewandte Mathematik und Mechanik, 16 (1936), pp. 153–164 http://dx.doi.org/10.1002/zamm.19360160304
3. [3] L. Howarth; The boundary layer in three-dimensional flow. Part 2. The flow near stagnation point; Philos. Mag., 42 (7) (1951), pp. 1433–1440
4. [4] A. Davey; Boundary-layer flow at a saddle point of attachment; J. Fluid Mech., 10 (4) (1961), pp. 593–610 http://dx.doi.org/10.1017/S0022112061000391
5. [5] C.Y. Wang; Axisymmetric stagnation flow on a cylinder; Q. Appl. Math., 32 (1974), pp. 207–213
6. [6] C.Y. Wang; Axisymmetric stagnation flow towards a moving plate; Am. Inst. Chem. Eng. J., 19 (5) (1973), pp. 1080–1082 http://dx.doi.org/10.1002/aic.690190540
7. [7] R.S.R. Gorla; Heat transfer in an axisymmetric stagnation flow on a cylinder; Appl. Sci. Res., 32 (5) (1976), pp. 541–553 http://dx.doi.org/10.1007/BF00385923
8. [8] R.S.R. Gorla; Unsteady laminar axisymmetric stagnation flow over a circular cylinder; Develop. Mech., 9 (1977), pp. 286–288
9. [9] R.S.R. Gorla; Non-similar axisymmetric stagnation flow on a moving cylinder; Int. J. Eng. Sci., 16 (6) (1978), pp. 392–400
10. [10] R.S.R. Gorla; Transient response behavior of an axisymmetric stagnation flow on a circular cylinder due to time-dependent free stream velocity; Lett. Appl. Eng. Sci.; Int. J., 16 (7) (1978), pp. 493–502 Doi:10.1016 /0020-7225(78)9008 2-4
11. [11] R.S.R. Gorla; Unsteady viscous flow in the vicinity of an axisymmetric stagnation-point on a cylinder; Int. J. Eng. Sci., 17 (1) (1979), pp. 87–93 http://dx.doi.org/10.1016/0020-7225(79)90009-0
12. [12] G.M. Cunning, A.M.J. Davis, P.D. Weidman; Radial stagnation flow on a rotating cylinder with uniform transpiration; J. Eng. Math., 33 (2) (1998), pp. 113–128 http://dx.doi.org/10.1023/A:1004243728777
13. [13] C.E. Grosch, H. Salwen; Oscillating stagnation point flow; Proc. Royal Soc. London, Ser. A: Math. Phys. Sci., 384 (1786) (1982), pp. 175–190
14. [14] H.S. Takhar, A.J. Chamkha, J. Nath; Unsteady axisymmetric stagnation-point flow of a viscous fluid on a cylinder; Int. J. Eng. Sci., 37 (15) (1999), pp. 1943–1957 http://dx.doi.org/10.1016/S0020-7225(99)00009-9
15. [15] R. Saleh, A.B. Rahimi; Axisymmetric stagnation-point flow and heat transfer of a viscous fluid on a moving cylinder with time-dependent axial velocity and uniform transpiration; J. Fluids Eng., 126 (6) (2004), pp. 997–1005 http://dx.doi.org/10.1115/1.1845556
16. [16] A.B. Rahimi, R. Saleh; Axisymmetric stagnation-point flow and heat transfer of aviscous fluid on a rotating cylinderwith time-dependent angular velocity and uniform transpiration; J. Fluids Eng., 129 (1) (2007), pp. 107–115
17. [17] A.B. Rahimi, R. Saleh; Similarity solution of unaxisymmetric heat transfer in stagnation-point flow on a cylinder with simultaneous axial and rotational movements; J. Heat Transfer, 130 (5) (2008), pp. 054502-1–054502-5
18. [18] A.S. Abbasi, A.B. Rahimi; Non-axisymmetric three-dimensional stagnation-point flow and heat transfer on a flat plate; J. Fluids Eng., 131 (7) (2009), pp. 074501.1–074501.5
19. [19] A.S. Abbasi, A.B. Rahimi; Three-dimensional stagnation-point flow and heat transfer on a flat plate with transpiration; J. Thermophys. Heat Transfer, 23 (3) (2009), pp. 513–521 http://dx.doi.org/10.2514/1.41529
20. [20] A.S. Abbasi, A.B. Rahimi, H. Niazman; Exact solution of three-dimensional unsteady stagnation flow on a heated plate; J. Thermophys. Heat Transfer, 25 (1) (2011), pp. 55–58 http://dx.doi.org/10.2514/1.48702
21. [21] A.S. Abbasi, A.B. Rahimi; Investigation of two-dimensional stagnation-point flow and heat transfer impinging on a flat plate; J. Heat Transfer (2011) (accepted as technical brief)
22. [22] S.V. Subhashini, G. Nath; Unsteady compressible flow in the stagnation region of two-dimensional and axisymmetric bodies; Acta Mech., 134 (3–4) (1999), pp. 135–145 http://dx.doi.org/10.1007/BF01312652
23. [23] M. Kumari, G. Nath; Unsteady compressible 3-dimensional boundary layer flow near an axisymmetric stagnation point with mass transfer; Int. J. Eng. Sci., 18 (12) (1980), pp. 1285–1300 http://dx.doi.org/10.1016/0020-7225(80)90120-2
24. [24] M. Kumari, G. Nath; Self-similar solution of unsteady compressible three-dimensional stagnation-point boundary layers; J. Appl. Math. Phys., 32 (3) (1981)
25. [25] A. Katz; Transformations of the compressible boundary layer equations; SIAM J. Appl. Math., 22 (4) (1972)
26. [26] N. Afzal, S. Ahmad; Effect of transpiration and injection on self- similar solutions of second-order boundary layer equations; Int. J. Heat Mass Transfer, 18 (5) (1975), pp. 607–614 http://dx.doi.org/10.1016/0017-9310(75)90272-0
27. [27] P.A. Libby; Heat and mass transfer at a general three-dimensional stagnation point; AIAA J., 5 (3) (1967), pp. 507–517 http://dx.doi.org/10.2514/3.4008
28. [28] K. Gersten, H.D. Papenfuss, J.F. Gross; Influence of the Prandtl Number on second-order heat transfer due to surface curvature at a three-dimensional stagnation point; Int. J. Heat Mass Transfer, 21 (3) (1978), pp. 275–284 http://dx.doi.org/10.1016/0017-9310(78)90120-5
29. [29] Rasool Alizadeh, Asghar B. Rahimi, Mohammad Najafi; Unaxisymmetric stagnation-point flow and heat transfer of a viscous fluid on a moving cylinder with time-dependent axial velocity; J. Brazilian Soc. Mech. Sci. Eng. (2015), pp. 1–14
30. [30] Rasool Alizadeh, Asghar B. Rahimi, Mohammad Najafi; Magnetohydrodynamic unaxisymmetric stagnation-point flow and heat transfer of a viscous fluid on a stationary cylinder; Alexandria Eng. J., 55 (1) (2016), pp. 37–49
31. [31] Mohsen Sheikholeslami, Davood Domiri Ganji, M. Younus Javed, R. Ellahi; Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model; J. Magn. Magn. Mater., 374 (2015), pp. 36–43
32. [32] Mohsen Sheikholeslami, Davood Domiri Ganji; Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method; Phys. A: Stat. Mech. Appl., 417 (2015), pp. 273–286
33. [33] Mohsen Sheikholeslami, Mohammad Mehdi Rashidi; Effect of space dependent magnetic field on free convection of Fe₃O₄–water nanofluid; J. Taiwan Inst. Chem. Eng., 56 (2015), pp. 6–15
34. [34] Mohsen Sheikholeslami, Shirley Abelman, Davood Domiri Ganji; Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation; Int. J. Heat Mass Transfer, 79 (2014), pp. 212–222
35. [35] Mohsen Sheikholeslami, Davood Domiri Ganji; Ferrohydrodynamic and magnetohydrodynamic effects on ferrofluid flow and convective heat transfer; Energy, 75 (2014), pp. 400–410
36. [36] M. Sheikholeslami, T. Hayat, A. Alsaedi; MHD free convection of Al₂O₃–water nanofluid considering thermal radiation: a numerical study; Int. J. Heat Mass Transfer, 96 (2016), pp. 513–524
37. [37] Mohsen Sheikholeslami, Davood Domiri Ganji, Mohammad Mehdi Rashidi; Ferrofluid flow and heat transfer in a semi annulus enclosure in the presence of magnetic source considering thermal radiation; J. Taiwan Inst. Chem. Eng., 47 (2015), pp. 6–17
38. [38] Mohsen Sheikholeslami, Kuppalapalle Vajravelu, Mohammad Mehdi Rashidi; Forced convection heat transfer in a semi annulus under the influence of a variable magnetic field; Int. J. Heat Mass Transfer, 92 (2016), pp. 339–348
39. [39] Mohsen Sheikholeslami Kandelousi; KKL correlation for simulation of nanofluid flow and heat transfer in a permeable channel; Phys. Lett. A, 378 (45) (2014), pp. 3331–3339
40. [40] Mohsen Sheikholeslami Kandelousi; Effect of spatially variable magnetic field on ferrofluid flow and heat transfer considering constant heat flux boundary condition; Eur. Phys. J. Plus, 129 (11) (2014), pp. 1–12
41. [41] Neil M. Ribe, Michell D. Smooke; A stagnation point flow model for melt extraction from a mantle plume; J. Geophys. Res.: Solid Earth, 92 (B7) (1987), pp. 6437–6443
42. [42] L.H. Kellogg, D.L. Turcotte; Homogenization of the mantle by convective mixing and diffusion; Earth Planet. Sci. Lett., 81 (4) (1987), pp. 371–378
43. [43] M. Sheikholeslami, H. Mollabasi, D.D. Ganji; Analytical investigation of MHD Jeffery-Hamel nanofluid flow in non-parallel walls; Int. J. Nanosci. Nanotechnol., 11 (4) (2015), pp. 241–248
44. [44] Jacques Charraudeau; Influence de gradients de proprietes physiques en convection force – application au cas du tube; Int. J. Heat Mass Transfer, 18 (1) (1975), pp. 87–95
45. [45] Ioan Pop, Rama Subba Reddy Gorla, Majid Rashidi; The effect of variable viscosity on flow and heat transfer to a continuous moving flat plate; Int. J. Eng. Sci., 30 (1) (1992), pp. 1–6
46. [46] A. Pantokratoras; Further results on the variable viscosity on flow and heat transfer to a continuous moving flat plate; Int. J. Eng. Sci., 42 (17) (2004), pp. 1891–1896
47. [47] M.A. Seddeek, A.M. Salem; Further results on the variable viscosity with magnetic field on flow and heat transfer to a continuous moving flat plate; Phys. Lett., A 353 (4) (2006), pp. 337–340
48. [48] F.G. Blottner; Finite-diference methods of solution of the boundary layer equations; AIAA J., 8 (1970), pp. 193–205