Abstract
Magneto-hydrodynamic (MHD) principle is an important interdisciplinary field. One of the most important applications of this effect is pumping of materials that are hard to pump using conventional pumps. In this work, the progress achieved in this field is surveyed and organized according to the type of application. The literature of the past 27 years is searched for the major developments of MHD applications. MHD seawater thrusters are promising for a variety of applications requiring high flow rates and velocity. MHD molten metal pump is important replacement to conventional pumps because their moving parts cannot stand the molten metal temperature. MHD molten salt pump is used for nuclear reactor coolants due to its no-moving-parts feature. Nanofluid MHD pumping is a promising technology especially for bioapplications. Advantages of MHD include silence due to no-moving-parts propulsion. Much progress has been made, but with MHD pump still not suitable for wider applications, this remains a fertile area for future research.
Keywords
Magnetohydrodynamic (MHD) pump; Seawater pump; Molten metal pump; Molten salt pump; Nano-fluid Pump; Micro-pump
1. Introduction
From space ships to military submarines and power generation; high speed electromagnetic propulsion is widely used and studied. For example, some propulsion systems require pumping force without any moving parts. Other systems like space ships have no air and not enough fuel to thrust. Systems with very high temperature like molten metal or liquid can be driven or steered using MHD force. MHD force can provide thrusting force for plasma thruster used in space ships. On the other hand, conductive metals and molten salts can generate power using MHD principle. Therapeutic MHD can be used as a micro-pump for blood pumping to maintain sugar level in blood. MHD micro-pumps have attracted interest from researchers and technology companies, as it can solve most of the problems of moving micro-parts. Some applications of magneto-hydrodynamics are shown in Fig. 1.
|
|
|
Figure 1. Magneto-hydrodynamics applications. |
1.1. Definition
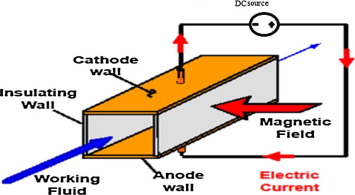
The basic principle of MHD is straightforward; a unidirectional current is established through an electrically conducting fluid such as seawater. Then, a high intensity magnetic field perpendicular to the current is imposed through the fluid. This combination of orthogonal magnetic field, electric field, and a relative motion of ions results in a Lorentz force with direction defined by the cross product of current and magnetic field vectors. If the device containing the electromagnet and the enclosure is fixed, the fluid is essentially pumped. However, if the device is free or has minimal resistance to motion, it will recoil according to Newton’s second law of motion. In this case, the device is referred to as pump-jet or thruster. The major structural components of MHD pump are inlet nozzle, main body, and nozzle diffuser, as shown in Fig. 2. The superconducting magnet and electrodes are arranged in the main body such that electric and magnetic fields are orthogonal. Some advantages and disadvantages of MHD pumps as opposed to conventional pumps are summarized in Table 1.
|
|
|
Figure 2. MHD pump components. |
| Advantages | Disadvantages |
|---|---|
|
|
1.2. Theory of operation
In this section, a simplified mathematical description of an ideal MHD pump is provided. This also serves to introduce some of the basic terms and concepts. Recent research revealed some complications which may reduce the efficiency of an MHD pump. The following equations are applicable to any fluid of scalar electrical conductivity s (S/m) at a given point, and velocity vector V (m/s). If the fluid is subjected to the combination of electric field vector E (V/m), and magnetic flux density vector B (T), then the induced electric current density J (A/m2) is a vector with a magnitude and direction defined by:
|
|
(1) |
The cross product (V × B) in Eq. (1) is manifested as an apparent electric field, which is similar to the back EMF associated with electric motors, where the motor armature is analogous to the flowing fluid. When E, V and B are mutually orthogonal – which is the most favorable situation – the back EMF will be in the direction opposite to the imposed electric field. The magnitude and direction of the current density depends mainly on the relative magnitudes of the imposed electrical field E and the back EMF. The direction of the current density J determines whether the system behaves as a pump or as a generator. It is easy to use Eq. (1) if the directions and the magnitudes of E, V and B are uniform throughout the channel. However, this is difficult to accomplish in the actual design, where Eq. (1) must be integrated over the entire volume of the working fluid.
If the working fluid is gaseous, additional terms must be added to Eq. (1). Those terms have been omitted here because the medium applicable to MHD thrusters is seawater. If the seawater becomes stationary, Eq. (1) reduces to a simple Ohm’s Law used in a DC circuit theory. Assuming that the flow channel does not experience large flow perturbations, or that the electric field does not result in a breakdown event in seawater, the electric current density can be calculated with an acceptable degree of accuracy. Two-phase flow resulting from high gas production on the electrodes, or flow irregularities, requires considerable modeling effort and complicated computer codes to obtain an accurate solution.
When electric current passes through an electrically neutral conducting medium in the presence of a magnetic field, a vector body force per unit volume F (N/m3) affects the medium. F is referred to as Lorentz force and is given by the following:
|
|
(2) |
This force is applied to accelerate seawater in the MHD duct. On the other hand, it will decelerate the water if the resulting direction of J converts the MHD duct into a generator. The total energy input to the MHD pump per unit volume is called electric power density P (W/m3). For a DC circuit, it is expressed as follows:
|
|
(3) |
Part of this power will be used to provide thrust, while the rest will be lost by heating the MHD duct. For MHD pumps, the resistive losses are equal to Joule heating power density Pj (W/m3), where,
|
|
(4) |
The difference between total power input and Joule heating power losses constitutes an ideal effective thrust power density Pt (W/m3). Multiplying both sides of Eq. (1) by J gives the following:
|
|
(5) |
Dividing both sides of Eq. (5) by d and rearranging after substituting Eq. (3) for the power density P, yields the following:
|
|
(6) |
Therefore, the effective thrust power density is given as follows:
|
|
(7) |
Substituting Eq. (2) into Eq. (7), an alternative expression for Pt is found as follows:
|
|
(8) |
The loading parameter K is defined as:
|
|
(9) |
After substituting K into Eq. (1), and using vector magnitudes since the system is orthogonal, the induced electric current density (A/m2) can be written as follows:
|
|
(10) |
The power delivered to the load, per unit volume of the pump, is given as follows:
|
|
(11) |
Eqs. (1) and (11) can be rearranged to give the output voltage and power per unit volume as a function of electric current density. The results are given as follows:
|
|
(12) |
|
|
(13) |
Since the direction of J is reversed, Lorentz force will oppose the fluid motion and is expressed as follows:
|
|
(14) |
Considering a constant diameter MHD duct, for a fluid to move against this force, there must be a pressure difference (dP) across an axial distance dx, given by:
|
|
(15) |
For constant values of B, V, and s, the total pressure drop across the MHD duct (Pin − Pout) is given as follows:
|
|
(16) |
where l is the duct length.
The fluid work rate per unit volume is defined as follows:
|
|
(17) |
The electrical efficiency (Ne) is defined as the ratio of power output to the power delivered by the working fluid, and is given by:
|
|
(18) |
In applications where the working fluid is at high temperature, an MHD generator can be used as an energy topper in conjunction with another energy conversion system. As the Joule losses in MHD pump occur within the working fluid, the energy is still partially useful; however, it represents a departure from thermodynamic reversibility. In MHD channels with constant magnetic fields Lorentz force is constant. If the pump is designed to operate with orthogonal fields, energy conservation can be used to evaluate the velocity as a function of position in the channel. The total output power of the pump is determined by integrating Eq. (8) with respect to the position in the MHD duct.
An MHD pump consists of the following components:
- Flow channel
- Super-conducting magnet
- Electrodes
- Electrical power supply
- Supporting structure
The magnet makes up around 20% of the total mass. The remaining mass is basically a structural support to restrain the magnet together. Field strength of 10 T is achievable using super-conducting magnets. Important parameters of coil configuration for an MHD thruster include weight, efficiency and field leakage. In real operation, the flow may not be uniform, especially during transient operation, as the magnetic field is generally not uniform across the channel. Since J is coupled with V and B, the solution of Eq. (7) for the total delivered power is involved. Therefore, an approximation for quasi-steady magnetic flux is computed using the Biot–Savart Law:
|
|
(19) |
where
- C1: Magnetic permeability divided by 4
- v: Volume of integration
- Jm: Current density in magnetic coils
- Nab: Unit vector from point a to point b
- r: Distance from a to b
Electric field (E) can be calculated using Eq. (1) and the steady-state forms of two of Maxwell’s equations are given as follows:
|
|
(20) |
|
|
(21) |
Provided that the velocity V and the magnetic flux density B are known, Eq. (20) implies the existence of an electric potential satisfying the relation:
|
|
(22) |
Substituting J from Eq. (1) into Eq. (21), and using Eq. (22), results in a second-order partial differential equation in , where magnetic flux can be calculated:
|
|
(23) |
1.3. Overview of MHD pump applications
A review and evaluation of recent advances in micro-scale pumping technologies was conducted by Iverson and Garimella [2]. However, the review did not include the macro-scale applications of MHD pumps. An overview of MHD commercial devices used for industrial applications such as the world largest MHD pump, which is capable of pumping 3500 m3/h of 300 °C Sodium, as well as high temperature pumps and submersible pumps, was presented by Branover and Unger [3]. However, it was done 25 years ago. Das and Wang [4] illustrated certain unique applications of MHD pumps that are relevant to point-of-care diagnostic device design and fabrication. Therefore, there is a need for an up-to-date survey of the progress achieved in MHD pumps applications.
Despite the fact that the basic MHD principle has been known for many years, only few practical applications were investigated. MHD systems still have considerable challenges ahead before it could become practical. The problems may be classified into two categories;
- Technology-specific, concerning physical phenomena of superconductors.
- Practical techniques to examine the possibility of designing and constructing MHD thruster systems.
This investigation focuses on the later kind of problems. It is considered that MHD pump can be designed with the freedom of configuration and size, so that they could have high propulsive performance, as shifting is not required. Some possible configurations of MHD thruster systems have been proposed for ship propulsion [5]. However, it has not been ascertained which configuration of the system is optimal.
MHD generator or pump is simple and compact, and has a high power density. As such, it is especially attractive for military applications. Compactness and the absence of rotating machinery were felt to be important from a viewpoint of reducing noise, especially important in submarine propulsion. The lack of recent publications implies that military applications have caused current MHD developments to be confidential in nature.
The feasibility of MHD propulsion was first demonstrated by Way [6], who published a very complete and mathematically rigorous analysis of an external duct DC propulsion system. In the sixties, few marine models were constructed, but with little success. Recent developments in super-conductivity and superconducting magnets are responsible for intense research in MHD propulsion and generation. The Japanese research group JAFSA has made a major contribution to the development of MHD thrusters for high speed ships [7]. JAFSA constructed a 3 m operable model.
In principle, the relationship between MHD pump and generator is analogous to an electrical motor being driven and operated like a generator. The focus of this work will be on the operation of an MHD pump, because it is less complex, and has known practical applications. Recent research revealed many complications which may significantly reduce the achievable efficiency of an MHD pump. However, projected efficiency is still attractive enough for submarine propulsion applications. The major applications of MHD pumps will be discussed, such as pumping of seawater, molten metal, molten salt, and nanofluid pumping.
2. Seawater pumping
MHD thrusters have long been recognized as potentially attractive candidates for ship propulsion, because such systems eliminate the conventional rotating drive components. The MHD thruster is essentially an electromagnetic (EM) pump operating in seawater. Electrical current is passed directly through the seawater and interacts with an applied magnetic field; the interaction of the magnetic field and the electrode current in the seawater results in a Lorentz force acting on the water, and the reaction to this force propels the vessel forward. The concept of EM propulsion has been examined periodically during the past 35 years as an alternative method of propulsion for surface ships and submersibles.
Magnetic field effect on (CuO) water nanofluid flow was investigated by Sheikholeslami et al. [8]. They studied the heat transfer in an enclosure which is heated from below. Applying Lattice-Boltzmann method to solve the governing equations, the effective thermal conductivity and viscosity of nanofluid were calculated by KKL (Koo–Kleinstreuer–Li) correlation. In their model, the effect of Brownian motion on the effective thermal conductivity was considered. Effect of active parameter such as: Hartmann number, heat source length, nanoparticle volume fraction and Rayleigh numbers on the flow and heat transfer characteristics have been examined. The results revealed that the enhancement in heat transfer increases with Hartmann number and heat source length, and decreases with Rayleigh number. It was also found that the effect of Hartmann number and heat source length is more pronounced at high Rayleigh number.
MHD flow and mixed convective heat transfer of Al2O3–water nanofluid inside a vertical microtube was investigated theoretically by Malvandi and Ganji [9]. A two-phase mixture model was used for nanofluid in the hypothesis that Brownian motion and thermophoretic diffusivities are the only significant slip mechanisms between solid and liquid phases. Due to non-adherence of the fluid–solid interface resulting from microscopic roughness in microtubes, Navier’s slip boundary condition was considered at the surfaces. Assuming a fully developed flow and heat transfer, the basic partial differential equations including continuity, momentum, and energy equations were reduced to two-point ordinary boundary value differential equations with endpoint singularities, which were solved numerically. The results indicated that for smaller nanoparticles, the nanoparticle volume fraction is more uniform and there are no abnormal variations in the heat transfer rate and pressure drop. In addition, heat transfer rate is enhanced in the presence of the magnetic field especially for the smaller nanoparticles. Moreover, as the magnetic field strength (Ha) intensifies, the peak of the velocity profile near the walls is increased; however, the peak of the velocity profile at the core region is decreased.
Performance calculations for torpedo-sized and submarine-sized vehicles operating 30 m beneath sea surface have been done by Lin et al. [10]. It was found that reasonable submarine velocity can be achieved with a magnetic field of about 5 T.
A numerical investigation of the hydro-thermal behavior of a ferrofluid (seawater and 4 vol% Fe3O4) was presented by Aminfar et al. [11]. The ferrofluid was in a rectangular vertical duct subjected to different magnetic fields, while two-phase mixture model and control volume technique were used. Considering the electrical conductivity of the ferrofluid, in addition to the ferrohydrodynamics principles, the magnetohydrodynamic principles have been taken into account. Three cases for magnetic field have been considered to study mixed convection of the ferrofluid: non-uniform axial field (negative and positive gradient), uniform transverse field and the third case when both fields are applied simultaneously. The results indicated that negative gradient axial field and uniform transverse field act similarly and enhance both the Nusselt number and the friction factor, while positive gradient axial field does the opposite. It is also concluded that under the influence of both fields, increasing the intensity of uniform transverse field results in decreasing the effect of non-uniform axial fields.
An active boundary layer control system for marine vehicles is revealed by Meng [12], where the boundary layer control system comprises a plurality of magnets and seawater electrodes placed in circumferential rows around the beam of the hull. The magnets and electrodes are positioned so that a Lorentz force generated by the interacting magnetic and electric fields will drive the boundary layer flow in an axial direction toward the end of the hull. The boundary layer control system reduces turbulence and may relaminarizes boundary layer flow, thereby reducing radiated noise.
An MHD model that couples a one-dimensional flow model to a two-dimensional electrical model was made by Doss and Geyer [13]. Their model has been developed to demonstrate the need for high strength magnetic fields and to investigate the influence of friction and end losses on the performance of MHD thrusters. Parametric studies have been performed using the model that includes the variation of the applied magnetic field (5–20 T), thruster diameter (0.5–2.0 m), wall roughness (0–3 mm), flow velocity (5–20 m/s), and the load factor (1–10). The results indicated that friction and end losses can have a deleterious effect on the thruster efficiency close to a load factor of one. Furthermore, the parameter studies show that the thruster efficiency increases with the strength of the magnetic field and thruster diameter and decreases with wall roughness and flow velocity. Furthermore, it was concluded that careful considerations should be given to the analysis and design of MHD thrusters for load factors close to unity.
Conducting fluid in the micro-channel of MHD micropump was studied by Jang and Lee [14]. The micropump is driven by Lorentz force in the direction perpendicular to both magnetic and electric fields. The performance of the micropump is obtained by measuring the pressure head difference and flow rate as the applied voltage changes from 10 to 60 VDC at 0.19 and 0.44 T (T). The pressure head difference is 18 mm at 38 mA and the flow rate is 63 μl/min at 1.8 mA, while the inside diameter of inlet/outlet tube is 2 mm and the magnetic flux density is 0.44 T. It was noted that bubble generation by the electrolysis of the conducting liquid can be observed.
Bennecib et al. [15] introduced a complete set of basic equations for a new MHD DC pump. The equations presented a simplified MHD flow model based on steady-state, incompressible and laminar flow theory, and were used to investigate the characteristics of the proposed MHD DC pump. Finite volume method was used to solve both electromagnetic and hydrodynamic models. It was concluded that an active part is necessary in the design of the pump. In addition, it was indicated that the thrust performance depends on the electrode length (L2) and channel radius (Rch) and appeared to favor L2 = 0.08 m, Rch = 0.03 m as optimized dimensions. The numerical results of the pump performance characteristics showed that the new concept was capable of delivering bi-directional activation.
Three different thrusters were designed, constructed, and evaluated by Lin et al. [16]. For the first time, videographic and photographic recordings of flow through MHD thrusters were obtained. The MHD-induced flow rate, thrust, and mechanical efficiency were measured and calculated for each thruster at different combinations of electric current and magnetic field strength. Direct determination of thrust, and subsequently of efficiency was not possible. Therefore, the hydraulic resistance of each different thruster was correlated with flow rate. That information was used in conjunction with the measured MHD-induced flow rate to calculate the thrust and efficiency of each thruster. As the experimental results were found repeatable, a theoretical model was developed to predict the performance of each thruster. The results of the model were presented for one thruster at several magnetic field strengths and various electric currents. The predictions corresponded well with the measured and calculated values of MHD-induced flow rate and mechanical efficiency.
The use of MHD to circulate fluids in conduits fabricated with low temperature co-fired ceramic tapes was described by Zhong et al. [17]. Conduits shaped like toroidal and rectangular loops were fabricated. Electrodes printed on the ceramic substrate along the conduits’ walls facilitated transmission of electric currents through the test fluids. When the devices were subjected to a magnetic field, the resulting Lorentz forces propelled the liquids.
A rectangular closed circuit filled with an electrolyte fluid, known as macro-pump was examined by Aoki et al. [18]. A permanent magnet generates magnetic field while electrodes generate electric field in the flow. The fluid conductor moves inside the circuit under MHD effect. The MHD model has been derived from the Navier–Stokes equations and coupled with the Maxwell equations for Newtonian incompressible fluid. Electric and magnetic components engaged in the test chamber assisted in creating the propulsion of the electrolyte fluid. The electromagnetic forces that arose were due to the cross product between the vector density of induced current and the vector density of applied magnetic field, which results in Lorentz force. Results were presented for 3D numerical MHD simulation for Newtonian fluid as well as experimental data. The goal was to relate the magnetic field with the electric field and the amount of movement produced, as well as to calculate the current density and fluid velocity. The flow analysis was performed with the magnetic field fixed, while the electric field is changed. Observing the interaction between the field strengths, and density of the electrolyte fluid, an optimal configuration for the flow velocity was determined and compared with other publications.
An MHD model that coupled one-dimensional flow to two-dimensional electrical model was developed by Doss and Geyer [13]. The model was used to demonstrate the need for high strength magnetic fields and to investigate the influence of friction and end losses on the performance of MHD thrusters. Parametric studies have been performed on the model including the variation of the applied magnetic field from 5–20 T, thruster diameter from 0.5–2.0 m, wall roughness from 0–3 mm, flow velocity from 5–20 m/s, and the load factor from 1–10. The results indicated that friction and end losses can have a deleterious effect on the thruster efficiency close to a load factor equal to unity. Furthermore, parametric studies showed that the thruster efficiency increases with the strength of the magnetic field and thruster diameter and decreases with wall roughness and flow velocity.
The coupling between electrochemistry and hydrodynamics was studied by Boissonneau and Thibault [19]. MHD effect on seawater was used for direct propulsion and flow control. Experimental measurements were carried out in a small seawater tunnel at their laboratory using seawater with a NaCl concentration of 35 g l−1. The first aspect of their study was the effect of electrolysis micro-bubbles on the flow, leading to modification of the turbulent boundary layer or flow on bubble characteristics. The second aspect was the effect of the flow conditions on the electrode working conditions, such as the effective electroactive species and the electrode potential evolution. The main conclusions were that the electrolysis micro-bubbles do not affect the flow in the domain considered. However, in contrast, flow conditions do affect bubble size and distribution. On the other hand, the competition between electroactive species (i.e. anodic reactions) is entirely controlled by the flow. This means, from a practical point of view, that there is no opportunity to select an anode material that enables the selection of oxygen evolution instead of chlorine in the conditions prescribed by seawater MHD applications.
Two-phase seawater MHD flows were recorded at the center of a multi-Tesla solenoid magnet by Lin et al. [20]. A closed seawater loop using a synthetic “sea salt” solution was installed in and around the magnet. The plexi-glass test section consisted of two parallel electrodes that passed the DC current through the seawater. The test section was placed at the center of the magnet with the magnetic field being perpendicular to the current, so that Lorentz force was created in the axial direction of the test section. As a result of electrolysis, hydrogen and chlorine/oxygen gases were produced at the cathode and anode, respectively. In addition to the visualization of the complex two-phase MHD flows, performance of the test section as an MHD pump was studied as well.
The reasons for the renewed interest in the concept of MHD seawater propulsion were discussed by Doss and Geyer [21]. They presented the main advantages of this concept, together with some of the technical challenges that need to be overcome in order to achieve reliability and performance. They discussed in simple terms some of the technical issues and loss mechanisms influencing the thruster performance in terms of its electrical efficiency. These issues include jet losses, nozzle efficiency, Ohmic losses, frictional losses, three-dimensional effects and electrolysis inside the thruster. The studies showed that the frictional and end losses can have strong adverse effects on the thruster performance, and that the thruster efficiency increases with the strength of the magnetic field and thruster diameter, and decreases with the wall roughness and the flow velocity.
In light of advances in high-temperature superconductivity, the feasibility of MHD ship propulsion using superconducting magnets was reviewed by Mitchell and Gubser [22]. The scaling relations for the electrical and hydraulic efficiencies of MHD pump-jets show that overall efficiencies greater than 50% are feasible at speeds of 40 knots and higher, provided that magnetic fields greater than 5 T can be maintained over volumes of the order of 100 m3. The development of large-scale electrical machinery and magnets using high-temperature superconductors could make it practical to construct submersibles for high-speed and silent operation. Low-speed tankers for movement of bulk cargo would be efficient with even lower fields.
Different superconducting MHD systems were described in J. Phys. III France [5], with focus on electromagnetic aspect. Related programs throughout the world were described as well. It was reported that magnetic levitated trains could be the new high speed transportation system for the 21st century. Intensive studies involving MagLev trains using superconductivity have been carried out in Japan since 1970. In 1991 a six year program was launched in the United States to evaluate the performances of MagLev systems for transportation. Japan is also up at the top with the tests of Yamato I, a 260 ton MHD propelled ship.
A small high-temperature superconducting magnet has been produced by Hales et al. [23] as part of an MHD propulsion unit to power a model boat. The magnet was wound from 6 pancake coils of Bi–Sr–Ca–Cu–O HTS tape, and was conduction cooled using an onboard “thermal battery”, containing 3 liters of solid nitrogen. The magnet was racetrack shaped, and aluminum electrodes were placed along the straights of the magnet to pass an electric current through the saltwater, perpendicular to the magnetic field. Power for the magnet and the electrodes was provided by onboard sealed lead acid batteries, resulting in a fully ’stand-alone’ magnet system, which is capable of up to 1.25 h of continuous operation on one battery pack. The system was integrated into a model boat hull, which was successfully launched in 2004. A top speed of ∼30 mm/s was reached during the first trial.
Early studies showed that MHD thrusters were impractical, inefficient, and restricted to fields of 2 T. However, a review performed by Petrick et al. [24] concluded that with the evolution of superconducting magnet technology, later studies investigated the performance of MHD thrusters with much higher magnetic field strengths. They concluded that at higher fields (greater than 6 T), practical MHD propulsion systems appear possible. The feasibility of attaining the requisite higher magnetic fields has increased markedly, because of rapid advances in building high-field superconducting magnets, and the recent evolution of high-temperature superconductors.
A two-Tesla test facility was designed, built, and operated by Picologlou et al. [25] to investigate the performance of MHD seawater thrusters. The results of this investigation were used to validate MHD thruster performance computer models. The facility test loop, its components, and their design were presented in detail. Additionally, the test matrix and its rational were discussed. Finally, representative experimental results of the test program were presented, and compared to pretest computer model predictions. Good agreement between predicted and measured data had served to validate the thruster performance computer models.
The flow characteristics inside MHD plasma generators and seawater thrusters were analyzed and compared by Doss and Roy [26]. They used a three-dimensional computer model that solves the governing partial differential equations for fluid flow and electrical fields. Calculations had been performed for a Faraday plasma generator and for a continuous electrode seawater thruster. The results of the calculations showed that the effects caused by the interaction of the MHD forces with the fluid flow are strongly manifested in the case of the MHD generator, as compared to the flow development in the MHD thruster. The existence of velocity overshoots over the sidewalls confirmed previously published results for MHD generators with strong MHD interaction. For MHD thrusters, the velocity profile was found to be slightly flatter over the sidewall as compared to that over the electrode wall. As a result, distinct enhancement of the skin friction exists over the sidewalls of MHD generators in comparison with that of MHD thrusters.
The working principle of a DC MHD micropump was described by Homsy et al. [27]. The pump can be operated at high current densities in micro-fluidic channels without introducing gas bubbles into the pumping channel. The main design feature for current generation was a micro-machined frit-like structure that connects the pumping channel to side reservoirs, where platinum electrodes were located. Current densities up to 4000 A m−2 could be applied without noticeable Joule heating in the system. Pump performance was studied as a function of current density and magnetic field intensity, as well as buffer ionic strength and pH. Bead velocities up to 1 mm sz1 were observed in buffered solutions using a 0.4 T NdFeB permanent magnet, at an applied current density of 4000 A m−2. The pump was intended for transport of electrolyte solutions having a relatively high ionic strength in a DC magnetic field environment. The application of this pump for the study of biological samples in a miniaturized total analysis system with integrated NMR detection was foreseen.
Recent developments of MHD seawater pumping include the use of Electro-MHD (EMHD) pumping for the recovery of oil spills on seawater, which was discussed by Zhaoa et al. [28]. It is based on the different flow states of oil, air and seawater under the actions of electro-magnetic force, gravity, buoyancy and interphase force. The EMHD thin oil film recovery method is essentially an air-oil-seawater three-phase flow under the action of the electromagnetic field and random waves. The key problems include:
- Mechanism of wave-multiphase flow-electromagnetic field coupling system.
- Dynamic response characteristics of the air-oil-seawater three-phase flow with electromagnetic field and waves.
- Design principles of EMHD marine thin oil film disposal system under real conditions.
After ten years of experiments on air-oil-seawater flow under electromagnetic field, a 35 m3/h prototype has been successfully tested.
3. Molten metal pumping
Liquid metal MHD power conversion has been recently proposed for electrical pumping of various heat sources. This system is based on extension of the Faraday’s law of induction to liquid metal. It contains high density liquid metal and a suitable thermodynamic fluid. A device for transfer of molten metal was invented by Bykhovsky and Panov [29]. The device comprises a centrifugal conduction MHD pump, arranged within a molten metal bath. It is equipped with a metal housing, a cover, a metal rod, as well as a solenoid. These components form a closed magnetic circuit, whereby a magnetic field is produced within the working chamber. The working chamber is hermetically connected with the pipe for discharge of molten metal.
Branover and Unger [3] discussed extensive metallurgical applications of MHD such as:
- MHD devices employing liquid working medium for process applications.
- Electromagnetic (EM) modulation of molten metal flow.
- EM pump performance of superconducting MHD devices.
- Induction EM alkali-metal pumps.
- A physical model for EM-driven flow in channel-induction furnaces.
- Grain refinement in Al alloys via EM vibrational method.
- Dendrite growth of solidifying metal in DC magnetic field.
- MHD for mass and heat transfer in single-crystal melt growth.
- Inverse EM shaping.
- Embrittlement of steel by lead.
- An open cycle MHD disk generator.
- Acceleration of gas–liquid piston flows for molten-metal MHD pumps.
- MHD flow around a cylinder.
- New MHD drag coefficients.
- Liquid–metal MHD two-phase flow.
- And finally, Two-phase liquid gas mixers for MHD energy conversion.
Gailitis et al. [30] used a screw dynamo scheme to model liquid–metal pumping experiments. The experiments were used to study MHD dynamo field generation. The model was filled with liquid sodium. The model was designed for complete utilization of the pump power. The electrodynamics processes in the model were calculated. The input and output were arranged along the same line, reducing the critical Reynolds number. The flow rates responding to an external disturbance were found to correspond to the theory. The experiment suggested that the model can achieve the critical flow rate and observe magnetic field generation.
Electric installations on the base of induction machines were studied by Khristinich et al. [31]. They considered molten metal electromagnetic stirring in mixers, furnaces and ladders, as well as in refining installations and in a liquid phase of continuously casted ingots. Physical simulation of differential and integral installations was performed; as a result, methods were suggested for improving electromagnetic stirrers and technological process intensification within melting-casting units.
New inexpensive electromagnetic equipment was discussed by Hertwich and Foliforov [32]. The equipment was used for moving molten aluminum, which could open up attractive technical and economic perspectives for melting and casting aluminum. Three types of equipment for the transportation of molten aluminum were offered; electromagnetic side channel pump, tube pump, and electro-magnetic launder.
An experimental study of a liquid metal flow in a rectangular channel under the influence of an inhomogeneous magnetic field was presented by Andreev et al. [33]. This was a fundamental problem of liquid metal MHD. The problem is relevant to the technique of electromagnetic braking in the process of continuous casting of steel, as well as for Lorentz force velocimetry. Based on local velocity and electric potential measurements, they identified three distinct flow regions; 1. A turbulence suppression region, 2. A vortical region and 3. A wall jet region. It was shown that in region (1) the applied inhomogeneous magnetic field breaks the incoming flow in its central part and transforms the velocity profile, which was initially flat, into an M-shaped form. In the central part of the flow, the intensity of the velocity fluctuations was found to decrease strongly. In region (2) the magnetic field was the strongest. The flow was characterized by large-scale vortical structures which are time dependent for certain values of the control parameters. In region (3) downstream of the magnetic system, two sidewall boundary layers were observed to generate velocity fluctuations with intensity up to 25% of the mean flow. These boundary layers bear close resemblance to wall jets known from ordinary hydrodynamics. The experimental data provided a comprehensive database against which numerical simulations and turbulence models can be tested.
Results of 3D numerical MHD simulation of DC EM pump were presented by Daoud and Kandev [34]. The pump was used for liquid aluminum at large Reynolds number under externally imposed non-uniform magnetic field. The formulation of the MHD model had been derived from the Reynolds-Averaged Navier–Stokes equations. Standard k–ε turbulence model coupled with Maxwell equations for Newtonian incompressible fluid was implemented. The equations were solved simultaneously using finite element method. A direct electrical current was applied to a pair of electrodes, placed orthogonally to the magnetic field, the current exerted Lorentz force which drove the molten metal through a flat rectangular channel. Several pumping conditions were applied to study the deformations of the flow velocity in the magnetic field region.
Dolezel et al. [35] investigated pumping molten metals and salts (as cooling agents in nuclear reactors) by MHD pumps with permanent magnets. Their focus was on the steady-state movement of these coolants in the closed loops driven by the balance of Lorentz force and hydrodynamic drag force. They illustrated their method using two examples. Their results showed that in nuclear reactors of the type RAPID, it is possible to use MHD pumps for pumping selected cooling media. They found satisfactory results using 2D calculations and concluded that only the final computation should be shown in 3D.
Andreev et al. [36] presented an experimental study of a liquid metal flow in a rectangular channel under the influence of an inhomogeneous magnetic field. This is a fundamental problem of liquid metal MHD that is relevant to the technique of electromagnetic braking in the process of steel casting. Based on velocity and electric potential measurements they identified three distinct flow regions; a turbulence suppression region, a vortical region, and a wall jet region.
Clad steel slabs were developed by Haradaa et al. [37] by suppressing the mixing of molten steels in the mold pool of continuous casting strand. A level DC magnetic field installed in the mold was used. In the process, two molten steels of different chemical composition were discharged by two nozzles into the upper and the lower pools respectively, after that they solidified in the outer and the inner layers as clad steel slabs. The mechanism of separation into two layers had been elucidated by using a three dimensional MHD analysis. The numerical prediction employing Maxwell’s equation, Ohm’s law, and the turbulent flow model showed that the mixing of the steels was suppressed by the EM dividing of the upper and the lower flows. The principle of the new process had also been verified by steel casting trials of the clad steel slabs.
4. Molten salt pumping
Molten salts are used in nuclear reactors for transfer of heat from active zones. Either molten metals and their alloys or molten salts such as fluoride salts can be used. Pumping of these liquid media by classical mechanical radial or axial pumps is rather difficult, and the lifetime of such devices is relatively low. Therefore, electromagnetic pumps without any movable parts can be a good replacement. The simplest devices of this kind are MHD pumps. Their magnetic field is generated either by a system of arranged saddle coils carrying DC or by a system of permanent magnets.
The use of molten fluoride, especially the LiF–BeF2 mixture called “Flibe” was studied by Moriyama et al. [38]. “Flibe” had been suggested as the primary loop coolant because of its inherent advantages such as high temperature stability and low electrical conductivity. The use of molten salts has also been suggested for the chemical processing of tritium.
Takeuchi et al. [39] investigated the effect of MHD force – like in MHD pump – on the flow of molten salt stimulant, potassium hydroxide–water solution in particular. The flow field and heat transfer of turbulent pipe flow was studied. The study was part of benchmark experiment for the flow and heat transfer measurement of electrically conducting fluid under magnetic field. First, water was used as working fluid to obtain reference data. The fully developed turbulent flow was measured using PIV technique, turbulent structure and turbulent statistics. As a result, average flow field was obtained. For heat transfer measurement, higher Reynolds number was chosen so as to reduce the effect of buoyancy. For water tests without magnetic field, both heat transfer and flow field measurements were in good agreement with existing data and provided reference data for the apparatus.
5. Nanofluid pumping
MHD nanofluid flow and heat transfer has been investigated by several authors; Sheikholeslami et al. [40] investigated numerically natural convection in a concentric annulus between a cold outer square and heated inner circular cylinders in the presence of static radial magnetic field. They used lattice Boltzmann method. The inner and outer cylinders were maintained at constant uniform temperatures and it was assumed that all walls are magnetic field proofed. The numerical investigation was carried out for different governing parameters such as; Hartmann number, nanoparticles volume fraction, and Rayleigh number. The effective thermal conductivity and viscosity of nanofluids were calculated using Maxwell–Garnetts (MG) and Brinkman models, respectively. In addition, multi-distribution function (MDF) model was used to simulate the effect of uniform magnetic field. The results revealed that the average Nusselt number is an increasing function of nanoparticle volume fraction as well as Rayleigh number, while it is a decreasing function of Hartmann number.
MHD nanofluid hydrothermal treatment in a cubic cavity heated from below was presented by Sheikholeslami and Ellahi [41]; The mathematical model consists of continuity and momentum equations, while a new model was proposed to find the effect of Brownian motion on the effective viscosity and thermal conductivity of the nanofluid. Lattice Boltzmann method was used to simulate 3-D problems. The Koo–Kleinstreuer–Li correlation was taken into account as well. Numerical calculation was performed for different values of Hartmann number, nanoparticle volume fraction and Rayleigh number. The results were presented graphically as streamlines, isotherms and iso-kinetic energy, as well as Nusselt number. It was noticed that the applied magnetic field results in a force opposite to the flow direction. This force drags the flow and thereby reduces the velocity and consequently the convection currents. In addition, it can be deduced that Nusselt number is an increasing function of Rayleigh number and nanofluid volume fraction while it is a decreasing function of Hartmann number.
Effect of spatially variable magnetic field on ferrofluid flow and heat transfer was investigated by Sheikholeslami and Rashidi [42]. The enclosure is filled with Fe3O4–water nanofluid. Control Volume based Finite Element Method (CVFEM) was used to solve the governing equations. The joint effects of Ferrohydrodynamic and magnetohydrodynamic have been taken into account. The effects of Magnetic number, Hartmann number, Rayleigh number and nanoparticle volume fraction on the flow and heat transfer characteristics have been studied. The results show that heat transfer decreases with Rayleigh number. In addition, Nusselt number is found to be increasing function of Magnetic number, Rayleigh number and nanoparticle volume fraction while being a decreasing function of Hartmann number.
MHD free convection flow of CuO–water nanofluid in a square enclosure with a rectangular heated body was investigated numerically by Sheikholeslami and Ganji [43], where they used Lattice Boltzmann Method (LBM) scheme. Effective thermal conductivity and viscosity of the nanofluid were calculated by Koo–Kleinstreuer–Li correlation. Effects of pertinent parameters such as Hartmann number, nanoparticle volume fraction and Rayleigh number on the flow, heat transfer, and entropy generation had been examined. The results showed that heat transfer rate and entropy generation number increase with Rayleigh number and nanoparticle volume fraction but decrease with Hartmann number.
Effect of external magnetic field on ferrofluid flow and heat transfer in a semi annulus enclosure with sinusoidal hot wall was investigated by Sheikholeslami and Ganji [44]. The governing equations were based on both effects of Ferrohydro-dynamic (FHD) and MHD. Those equations were solved using Control Volume based Finite Element Method (CVFEM). The influences of Rayleigh number, nanoparticle volume fraction, magnetic number and Hartmann number on the flow and heat transfer characteristics had been examined. Results showed that Nusselt number increases with Rayleigh number and nanoparticle volume fraction but decreases with Hartmann number. It can be concluded that for low Rayleigh number, heat transfer is an increasing function of Hartmann number and decreasing function of Magnetic number while opposite trend is observed for high Rayleigh number
Effect of thermal radiation on MHD nanofluid flow between two horizontal rotating plates is studied by Sheikholeslami et al. [45]. The major effects of Brownian motion and thermophoresis had been included in the model of nanofluid. The flow partial differential equations governing heat and mass transfer are reduced to a set of ordinary differential equations using the appropriate velocity, temperature and concentration transformations. Those equations, subjected to the appropriate boundary conditions, were solved numerically using the fourth-order Runge–Kutta method. The effects of magnetic parameter, Reynolds number, rotation parameter, Schmidt number, thermophoretic parameter, Brownian parameter and radiation parameter on heat and mass characteristics were examined. Results showed that Nusselt number increases with radiation parameter and Reynolds number, while it decreases with other active parameters. It was also observed that concentration boundary layer thickness decreases with radiation parameter.
Sheikholeslami and Abelman [46] studied the effects of magnetic field on nanofluid flow and heat and mass transfer between two horizontal coaxial cylinders. They used two-phase model for that purpose. The effect of viscous dissipation was also examined. The basic equations governing the flow and heat and mass transfer were reduced to a set of ordinary differential equations, using the appropriate transformation of the velocity, temperature, and concentration. The equations along with associated boundary conditions were solved numerically using fourth-order Runge–Kutta method. The effects of Hartmann number, Reynolds number, Schmidt number, Brownian parameter, thermophoresis parameter, Eckert number, and aspect ratio on flow and heat and mass transfer were examined. Results revealed that Nusselt number increases with aspect ratio and Hartmann number but decreases with Reynolds number, Schmidt number, Brownian parameter, thermophoresis parameter, and Eckert number.
Nanofluid hydrothermal behavior in the presence of variable magnetic field was investigated by Sheikholeslami and Ganji [47] using Differential Transformation method. The fluid in the enclosure is water containing two types of nanoparticles: Al2O3 and CuO. Effective thermal conductivity and viscosity of the nanofluid were calculated using Koo–Kleinstreuer–Li (KKL) correlation. Influence of Brownian motion on effective thermal conductivity was considered. The results from Differential Transformation Method and previous work were in good agreement, which proved the suitability of this method for solving such problems. The effects of squeeze number, nanofluid volume fraction, Hartmann number and heat source parameter on flow and heat transfer were investigated. The results showed that skin friction coefficient increases with squeeze number and Hartmann number but decreases with nanofluid volume fraction. In addition, Nusselt number increases with nanoparticle volume fraction and Hartmann number and decreases with squeeze number.
MHD pumping performance was predicted by Ho [48] using a steady-state analytical model. Incompressible and fully developed laminar flow theory was utilized in the analysis. Flow characteristics with different scalar dimensions in duct channel were analyzed. In order to make the analytical solution possible, the governing equations were transformed into Poisson equation. Since Lorentz force is interacted by electric current and magnetic flux, it is converted into hydrostatic pressure gradient in the moment equations. Furthermore, the concept of flow circuit, similar to thermal network in conduction, was also proposed. Excellent agreement between flow circuit and experimental results was achieved. Several conclusions are listed as follows:
- For a fully developed MHD flow problem, assuming uniform distribution of Lorentz force along the flow channel will make the analytical solution possible.
- The set up of flow circuit similar to thermal network in heat conduction provides a practical way to evaluate the flow resistance in flow channel.
- By varying the aspect ratio, the duct can be classified as shallower, deeper, narrower or wider, which simplifies the analysis.
- Lower flow resistance can be obtained using a deeper duct. However, current density on the sidewalls will decrease simultaneously; that brings about a gradual decrease of flow rate. Furthermore, higher voltage is needed to keep the current constant in wider duct with lower flow resistance.
- As duct depth goes to zero, flow rate becomes unstable due to retarding bubbles in the flow channel. On the other hand, larger bubbles produced by higher current result in discrepancy between analytical and experimental results.
The effect of Nanofluid properties on the flow field as well as temperature distribution in a MHD pump was numerically investigated by Shahidian et al. [49]. In order to solve the non-linear governing differential equations, a finite difference based code was developed and utilized. Temperature and velocity were calculated by solving energy and Navier–Stokes equations. Results show that temperature stays almost constant with magnetic field. Furthermore, velocity and temperature behave similarly for each period. However, heat transfer inside the MHD pump varies with nanofluid (Al2O3 nanoparticles) in comparison with the NaCl solution.
In microfluidic devices, it is necessary to propel samples from one part of the device to another, stir fluids, and detect the presence of chemical and biological targets [50]. Given the small size of those devices, the above tasks are far from trivial. MHD offers an elegant way to control fluid flow in micro-devices without the need of mechanical components. Qian and Bau [50] reviewed the theory of MHD for low conductivity fluids and described various applications of MHD such as fluid pumping, flow control in fluidic networks, fluid stirring and mixing, circular liquid chromatography, thermal reactors, and micro-coolers. This review however, deals with recent applications of MHD pumps in particular.
Shahidian et al. [51] numerically investigated the flow of blood, as a non-Newtonian fluid, in an MHD pump. A power law model for blood viscosity was utilized. In order to solve the nonlinear governing momentum and Maxwell equations, a computational fluid dynamic (CFD) code based on finite difference was utilized. The simulation results show that the velocity increases with magnetic flux density (B) and current (I).
A micro-MHD pump for the manipulation of fluids in an NMR environment was presented by Homsy [1]. Pumping electrolytic solutions with MHD pump involve the generation of an electric current in such environments. Preliminary studies with simple MHD pump designs have led to an ideal microchannel geometry and DC MHD micropump. It was shown that MHD flow rate is directly proportional to both current density and magnetic field intensity. The micropump utilizes high DC current density across the pumping channel with the help of an array of nanometer deep side-channels. Bubble generation in the channels due to water electrolysis was avoided by placing the electrodes in outer reservoirs in fluidic connection with the system.
6. Conclusion
MHD principle is used for pumping fluids that are hard to pump by conventional pumps. MHD seawater thrusters are promising for a variety of applications requiring high flow rates and velocity, while MHD micro- and nanopumps have a variety of applications, especially in biotechnology. MHD molten metal pump is important replacement to conventional pumps because their moving parts cannot stand the molten metal temperature. MHD molten salt pump is used for nuclear reactor coolants due to its no-moving-parts feature. MHD pump can successfully handle the salty cooling water without being worn out like conventional pumps. The need for MHD pumps is increasing due to its advantages and wide applications. For example, the rise of renewable energy has increased the demand for a way to pump and steer the sun-heated liquid. One of the major obstacles to further applications of MHD is the need for further development of magnetic field generation theory, as the magnetic field proportionally affects the applied force. In addition, the use of less resisting conducting material would enhance the performance of MHD pumps especially in high temperature fluids.
References
- [1] A. Homsy, Design, Microfabrication, and Characterization of MHD Pumps and their Applications in NMR Environments, Docteur ès Sciences Dissertation, The University of Neuchâtel, Switzerland, 2006.
- [2] B.D. Iverson, S. Garimella, Recent advances in microscale pumping technologies: a review and evaluation, J. Microfluid Nanofluid, Birck and NCN Publications, Paper 81, 2008.
- [3] H. Branover, Y. Unger; Metallurgical Technologies, Energy Conversion, and Magnetohydrodynamic Flows; Proceedings of the Sixth Beer-Sheva International Seminar on Magnetohydrodynamic Flows and Turbulence, vol. 148, AIAA, Negev (1990)
- [4] C. Das, G. Wang; Some practical applications of magnetohydrodynamic pumping; J. Sens. Actuat. A: Phys., 201 (2013), pp. 43–48
- [5] P. Tixador; Magnetic levitation and MHD propulsion; J. Phys. III, EDP Sci., 4 (4) (1994), pp. 581–593
- [6] S. Way; Electromagnetic propulsion for cargo submarines; J. Hydronautics, 2 (2) (1968), pp. 49–57
- [7] A.A. Bednarczyk, Nuclear electric magnetohydrodynamic propulsion for submarine, MSc Thesis, MIT, 1989.
- [8] M. Sheikholeslami, M. Bandpy, R. Ellahi, A. Zeeshan; Simulation of MHD CuO–water nanofluid flow and convective heat transfer considering Lorentz forces; J. Magn. Magn. Mater., 369 (2014), pp. 69–80
- [9] A. Malvandi, D.D. Ganji; Magnetohydrodynamic mixed convective flow of Al2O3–water nanofluid inside a vertical microtube; J. Magn. Magn. Mater., 369 (2014), pp. 132–141
- [10] T.F. Lin, J.B. Gilbert, G.D. Roy; Analyses of magnetohydrodynamic propulsion with seawater for underwater vehicles; J. Propul. Power, 7 (1991), pp. 1081–1083
- [11] H. Aminfar, M. Mohammadpourfard, F. Mohseni; Two-phase mixture model simulation of the hydro-thermal behavior of an electrical conductive ferrofluid in the presence of magnetic fields; J. Magn. Magn. Mater., 324 (5) (2012), pp. 830–842
- [12] J.C. Meng, Magnetohydrodynamic boundary layer control system, Patent, Department of the Navy, Washington, DC, 12, 1993.
- [13] E.D. Doss, H.K. Geyer, The need for superconducting magnets for MHD seawater propulsion, The 25th Intersociety Energy Conversion Engineering Conference, Reno, NV, 12–17 Aug. 1990.
- [14] J. Jaesung, S.L. Seung; Theoretical and experimental study of MHD (magnetohydrodinamic) micropump; Sens. Actuat. A: Phys., 99–01 (2000), pp. 302–307
- [15] N. Bennecib, R. Abdessemed, S. Drid; Design and flow simulation for a new DC pump MHD for seawater; J. Appl. Fluid Mech., 2 (2) (2009), pp. 23–28
- [16] T.F. Lin, D.L. Aumiller, J.B. Gilbert, M.J. Coslo, Studies of several small seawater MHD thrusters using the high-field solenoid of MIT’s Bitter Magnet Laboratory, Annual Report, Applied Research Lab, Penn. State Unv., Unv. Park, 1993.
- [17] J. Zhong, M. Yi, H.H. Bau, Magneto hydrodynamic (MHD) pump fabricated with ceramic tapes, Departmental Papers (MEAM), Paper 125, Unv. of Penn., 2002.
- [18] L.P. Aoki, M.G. Maunsell, H.E. Schulz; A magnetohydrodynamic study of behavior in an electrolyte fluid using numerical and experimental solutions; J. Engenharia Térmica (Thermal Engineering), 11 (1–2) (2012), pp. 53–60
- [19] P. Boissonneau, J.P. Thibault; Experimental analysis of couplings between electrolysis and hydrodynamics in the context of MHD in seawater; J. Phys. D: Appl. Phys, 32 (18) (1999), p. 2387
- [20] T.F. Lin, D.L. Aumiller, J.B. Gilbert, M.J. Cosio, B.L. Brandt, L.G. Rubin, Study of the Influence of Electric and Magnetic Fields on Seawater Magnetohydrodinamic Propulsion, International Society of Offshore and Polar Engineers, 1992.
- [21] E.D. Doss, H.K. Geyer, MHD Seawater Propulsion, British Maritime Technology, 1993.
- [22] D.L. Mitchell, D.U. Gubser; Magnetohydrodinamic ship propulsion with super conducting magnets; J. Supercond., 1 (4) (1988), pp. 349–364
- [23] P. Hales, P. Hirst, S. Milward, S. Harrison; A solid-nitrogen cooled high-temperature superconducting magnet for use in magnetohydrodinamic marine propulsion; IEEE Trans., 16 (2) (2006)
- [24] M. Petrick, J. Libera, J.X. Bouillard, E.S. Pierson, D. Hill, Results from a large-scale MHD propulsion experiment, in: The 30th Symposium on Engineering Aspects of Magnetohydrodynamics, Baltimore, MD, 29 Jun.–2 Jul., 1992.
- [25] B. Picologlou, E. Doss, D. Black, W.C. Sikes, Experimental determination of magnetohydrodynamic seawater thruster performance in a two Tesla test facility, in: The 27th Intersociety Energy Conversion Engineering Conference, San Diego, CA, 3–7 Aug. 1992.
- [26] E.D. Doss, G.D. Roy; Flow development and analysis of MHD generators and seawater thrusters; J. Fluids Eng., 114 (1) (1992), pp. 68–72
- [27] A. Homsy, S. Koster, J.C.T. Eijkel, A.V. Berg, F. Lucklum, E. Verpoorte, N.F. Rooij; A high current density DC magnetohydrodinamic (MHD) micropump; Epub (2005), pp. 466–471
- [28] L. Zhaoa, F. Liu, Y. Peng, W. An, C. Sha, Z. Wang, J. Liu, H. Ye; Research development and key scientific and technical problems on EMHD marine oil film recovery technology; J. Aquatic Procedia, 3 (2015), pp. 21–28
- [29] D.G. Bykhovsky, A.N. Panov, Device for transfer of molten metal, US Patent: US 5009399 A, 1991.
- [30] A.K. Gailitis, B.G. Karasev, I.R. Kirillov, O.A. Lielausis, S.M. Luzhanskii, A.P. Ogorodnikov, G.V. Preslitskii; Experiment with a liquid-metal model of an MHD dynamo; J. Magnetohydrodynamics, 23 (4) (1988)
- [31] R.M. Khristinich, V.N. Timofeyev, V.V. Stafievskaya, A.V. Velenteyenko, Molten Metal Electromagnetic Stirring in Metallurgy, International Scientific Colloquium, Hannover, March 24–26, 2003.
- [32] G. Hertwich, V. Foliforov, Electromagnetic Stirring and Pumping of Aluminum Melts, Hertwich Engineering, Austria, Nov., 2001.
- [33] O. Andreev, Y. Kolesnikov, A. Thess; Liquid metal flow under inhomogeneous magnetic field; Phys. Fluids, 18 (2006), p. 065108
- [34] A. Daoud, N. Kandev; Magneto-Hydrodynamic Numerical Study of DC Electromagnetic Pump for Liquid Metal; Institut de recherche des Hydro (LTE), Quebec (2008)
- [35] I. Dolezel, V. Kotlan, B. Ulrych, V. Valenta, Magnetohydrodinamic Pumps with Permanent Magnets for Pumping Molten Metal’s or Salts, Electroscope, 2009.
- [36] O. Andreev, Y. Kolesnikov, A. Thessb; Experimental study of liquid metal channel flow under the influence of a nonuniform magnetic field; J. Phys. Fluids, 18 (2006), p. 065108
- [37] H. Haradaa, E. Takeuchia, M. Zezeb, H. Tanakac; MHD analysis in hydromagnetic casting process of clad steel slabs; Appl. Math. Model., 22 (11) (1998), pp. 873–882
- [38] H. Moriyama, A. Sagara, S. Tanaka, R.W. Moir, D.K. Sze; Molten salts in fusion nuclear technology; Fusion Eng. Des., 39–40 (1998), pp. 627–637
- [39] J. Takeuchi, S. Satake, R. Miraghaie, K. Yuki, T. Yokomine, T. Kunugi, N.B. Morley, M.A. Abdou; Study of heat transfer enhancement/suppression for molten salt flows in a large diameter circular pipe; Fusion Eng. Des., 81 (1) (2006), pp. 601–606
- [40] M. Sheikholeslami, M. Gorji-Bandpay, D.D. Ganji; Magnetic field effects on natural convection around a horizontal circular cylinder inside a square enclosure filled with nanofluid; Int. Comm. Heat Mass Transfer, 39 (2012), pp. 978–986
- [41] M. Sheikholeslami, R. Ellahi; Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid; Int. J. Heat Mass Transfer, 89 (2015), pp. 799–808
- [42] M. Sheikholeslami, M.M. Rashidi; Effect of space dependent magnetic field on free convection of Fe3O4–water nanofluid; J. Taiwan Inst. Chem. Eng. (2015)
- [43] M. Sheikholeslami, D.D. Ganji; Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method; Physica A, 417 (2015), pp. 273–286
- [44] M. Sheikholeslami, D.D. Ganji; Ferrohydrodynamic and Magneto-hydrodynamic effects on ferrofluid flow and convective heat transfer; Energy, 75 (2014), pp. 400–410
- [45] M. Sheikholeslami, D.D. Ganji, M.Y. Javed, R. Ellahi; Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model; J. Magn. Magn. Mater., 374 (2015), pp. 36–43
- [46] M. Sheikholeslami, S. Abelman; Two phase simulation of nanofluid flow and heat transfer in an annulus in the presence of an axial magnetic field; IEEE Trans. Nanotechnol., 14 (3) (2015), pp. 561–569
- [47] M. Sheikholeslami, D.D. Ganji; Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM; Comput. Methods Appl. Mech. Engrg., 283 (2015), pp. 651–663
- [48] J. Ho; Characteristic study of MHD pump with channel in rectangular ducts; J. Marine Sci. Technol., 15 (4) (2007), pp. 315–321
- [49] A. Shahidian, M. Ghassemi, R. Mohammadi; Effect of nanofluid properties on magnetohydrodynamic pump (MHD); Adv. Mater. Res., 403–408 (2012), pp. 663–669
- [50] S. Qian, H.H. Bau; Magneto-hydrodynamics based microfluidics; Mech. Res. Commun., 36 (1) (2009), pp. 10–21
- [51] A. Shahidian, M. Ghassemi, S. Khorasanizade, G. Ahmadi; Flow analysis of non-newtonian blood in a magnetohydrodynamic pump; IEEE Trans. Magn., 45 (6) (2009), pp. 2667–2670
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?