Galoisian and numerical approach of three dimensional linear differential systems with skew symmetric matrices defined in a non- constant differential field

Resumen

Este trabajo contrasta métodos numéricos con métodos algebraicos aplicados ambos a la resolución de un sistema de ecuaciones diferenciales lineales 3-dimensionales con matrices antisimétricas definidas en un cuerpo diferencial no constante. Al mismo sistema se aplican métodos y algorítmos propios de la Teoría de Galois Diferencial, lo que permite resolverlo algebraicamente y métodos numéricos, en particular métodos de la familia de Runge - Kutta. Por último, se calculan los errores absolutos y relativos entre las soluciones Liouvillianas, obtenidas mediante la resolución algebraica y las soluciones obtenidas aplicando métodos numéricos.

Palabras claves: Teoría de Galois diferencial, métodos de la familia de Runge - Kutta, soluciones Liouvillianas, sistemas de ecuaciones diferenciales, matrices antisimétricas, cuerpo diferencial no constante.

Abstract

This work contrasts numerical methods with algebraic methods. These methods are applied to solve a three dimensional linear differential system with skew symmetric matrices defined in a non- constant differential field. Algorithms and methods of Differential Galois Theory, are used to provide an algebraic solution, while numerical methods, in particular, methods from Runge - Kutta family, are applied to the same system. Finally, the absolute and relative errors between Liouvillians solution are calculated comparing the solutions obtained by means of algebraic methods and by means of numerical methods.

1 Introducción

Este trabajo es una versión mejorada de [12], la cual corresponde a la tesis de maestría del segundo autor, dirigida por el primer y el tercer autor en la Universidad del Norte.

El objetivo de este trabajo es contrastar mé todos numéricos con métodos algebraicos en la resolución de sistemas de ecuaciones diferenciales lineales 3-dimensionales con matrices antisimétricas definidas en un cuerpo diferencial no constante.

Para lograr este objetivo se hizo un estudio de las formas de resolución de sistemas de ecuaciones diferenciales lineales cuando la matriz de coeficientes es constante y se muestra que en el caso que los coeficientes del sistema de ecuaciones diferenciales pertenezca a un cuerpo diferencial no constante, el método de solución útil cuando los coeficientes son constantes, sólo es aplicable a un tipo muy restringido de matrices con entradas en un cuerpo diferencial no constante.

Ante esta realidad se hace uso de la Teoría de Galois Diferencial, [1,15]. El sistema original se somete a una serie de transformaciones a trav és de las cuales el sistema se convierte en una ecuación diferencial lineal reducida a la cual puede aplicarse el algoritmo implementado por Jerry Kovacic, [2]. Para el desarrollo de estas transformaciones se aplicaron conceptos expuestos por Emili Picard, Ernest Vessiot y Jean Gaston Darboux, en trabajos relativos a estos temas. Es un hecho conocido que só lo una clase bastante pequeña de ecuaciones diferenciales o de sistemas de las mismas tiene solución mediante métodos analíticos, ante esta circunstancia los métodos numéricos proveen una herramienta poderosa y adecuada que permite una aproximación a la solución bajo ciertas condiciones que debe cumplir el sistema. El estudio del sistema objetivo permitió comprobar que es posible resolverlo mediante la aplicación de métodos numéricos. Al sistema de ecuaciones se le aplicó métodos de la familia de Runge-Kutta, en particular mé todos de cuarto orden que en Matlab [14] se especifican como ODE45, [5,6,7,8,11,13,16]. Recientemente se han aplicado técnicas algebraicas y numéricas usando la algebrización Hamiltoniana para resolver un sistema de ecuaciones no-lineales de primer orden, ver [4].

2 Movimiento de un sólido rígido y la ecuación diferencial objetivo

2.1 Movimiento de un sólido rígido

Un sólido rígido es un conjunto de puntos del espacio que conservan la distancia entre ellos, bajo la acción de fuerzas aplicadas. Cualquier movimiento de un sólido rígido, es un movimiento rígido. Los movimientos rígidos pueden ser traslaciones o rotaciones. En una traslación, dos puntos cualesquiera del conjunto de puntos se mueven siguiendo una trayectoria paralela. Una rotación se realiza alrededor de un eje que bien puede pasar por puntos del sólido o por puntos que no forman parte del mismo, dos puntos cualesquiera que se encuentren sobre el mismo vector, cuyo origen es un punto del eje de rotación se mueven con la misma velocidad angular, en general, el movimiento de un sólido rígido es una combinación de rotación y traslación. Todo movimiento rígido es una isometría y por tanto puede ser descrito mediante transformaciones algebraicas, si V y W son espacios vectoriales, cada uno con un producto interno y dV es la métrica asociada al producto interno en V y dW es la métrica asociada al producto interno en W, una isometría es una función de V en W tal que

$\forall \left(v_{1},v_{2}\right)\in V\times V,d_{V}\left(v_{1},v_{2}\right)=d_{W}\left(\phi \left(v_{1}\right),\phi \left(v_{w}\right)\right)$

Un movimiento de un sólido rígido en el espacio tridimensional se puede describir mediante un grupo de isometrías uniparamétricas, eligiendo como parámetro el tiempo. Sea ${\textstyle {\overrightarrow {\gamma }}:}$ ${\textstyle I\longrightarrow \mathbb {R} ^{3}}$una función analítica, I un intervalo en R, la longitud de arco entre los puntos a y b de I se define como

$s=\int _{a}^{b}\left\Vert {\overrightarrow {\gamma ^{\prime }}}\left(t\right)\right\Vert dt$

El vector tangente unitario de la curva en R3 cuando esta ha sido parametrizada por su longitud de arco es,

${\overrightarrow {\mu }}\left(s\right)={\overrightarrow {\gamma ^{\prime }}}\left(s\right)$

La función de curvatura de ${\textstyle \gamma }$ es

$\kappa \left(s\right)=\left\Vert {\overrightarrow {\mu }}\left(s\right)\right\Vert$

El vector normal principal de ${\textstyle \gamma }$ es

${\overrightarrow {\eta }}\left(s\right)={\dfrac {{\overrightarrow {\mu ^{\prime }}}\left(s\right)}{\left\Vert {\overrightarrow {\mu }}\left(s\right)\right\Vert }}$

y el vector binormal de ${\textstyle \gamma }$ es

${\overrightarrow {b}}\left(s\right)={\overrightarrow {\mu }}\left(s\right)\times {\overrightarrow {\eta }}\left(s\right)$

Además, existe una función escalar ${\textstyle \tau :I\longrightarrow \mathbb {R} }$ llamada la torsión de ${\textstyle \gamma }$, tal que ${\textstyle {\overrightarrow {b^{\prime }}}\left(s\right)=-}$ ${\textstyle \tau \left(s\right){\overrightarrow {\eta }}\left(s\right)}$ . Si e1; e2; e3 son vectores unitarios ortogonales dos a dos, y p ${\textstyle \in }$ R3, un sistema ortonormal de coordenadas con origen en p se simboliza como: (p; e1; e2; e3) y es un sistema de referencia en p.

Los vectores ${\textstyle {\overrightarrow {\mu }}\left(s\right)}$, ${\textstyle {\overrightarrow {\eta }}\left(s\right)}$, ${\textstyle {\overrightarrow {b}}\left(s\right)}$, son vectores unitarios, ortogonales entre si, y junto con ${\textstyle {\overrightarrow {\gamma }}\left(s\right)}$forman un sistema de referencia para la curva ${\textstyle {\overrightarrow {\gamma }}}$ conocido como sistema de referencia de Frenet para la curva. El siguiente teorema enuncia que es posible especificar una curva si se conoce su función de curvatura y su torsión:

Teorema Fundamental de Curvas: Dadas dos funciones diferenciables ${\textstyle \kappa \left(s\right)>0,\tau \left(s\right),s\in I,}$ existe una curva regular ${\textstyle {\overrightarrow {\gamma }}:I\rightarrow \mathbb {R} ^{3}}$tal que ${\textstyle s}$ es la longitud de arco, ${\textstyle \kappa \left(s\right)}$ es la curvatura y y ${\textstyle \tau \left(s\right)}$ es la torsión de ${\textstyle \gamma }$. Además, si otra curva ${\textstyle {\overrightarrow {\chi }}}$ satisface las mismas condiciones, esta difiere de ${\textstyle {\overrightarrow {\gamma }}}$ por un movimiento rígido, esto es, existe una transformacion lineal y ortogonal ${\textstyle T}$ con determinante positivo y un vector ${\textstyle {\overrightarrow {c}}}$ tal que ${\textstyle {\overrightarrow {\chi }}=T{\overrightarrow {\gamma }}+{\overrightarrow {c}}}$, ver [10].

2.2 La ecuación objetivo

El sistema diferencial lineal objeto de nuestro interés es:

$\left({\begin{array}{c}\partial _{x}\gamma _{1}\\\partial _{x}\gamma _{2}\\\partial _{x}\gamma _{3}\end{array}}\right)=\left({\begin{array}{ccc}0&0&-{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}\\0&0&{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}\\{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}&-{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}&0\end{array}}\right)\left({\begin{array}{c}\gamma _{1}\\\gamma _{2}\\\gamma _{3}\end{array}}\right)$

con matriz de coeficientes antisimétrica definida en un cuerpo diferencial no constante, este sistema modela el movimiento de un sólido rígido en el espacio vectorial ${\textstyle \mathbb {C} ^{3}}$ o en un espacio afín. Estamos interesados en mostrar dos enfoques, uno numérico, otro analitico, en la resolución del sistema en cuestión.

2.3 Algebrización y cambio Hamiltoniano de variable

La teoría de Galois establece que es posible encontrar las raices de un polinomio $p$, definido sobre un cuerpo $\Bbbk$, realizando operaciones aritméticas y radicaciones con sus coeficientes, siempre y cuando el grupo de Galois del polinomio sea resoluble, esto es, exista una cadena finita de subgrupos normales,$\left\{e\right\}=G_{0}\triangleleft G_{1}\triangleleft ...\triangleleft Gal_{p}\left(F/\Bbbk \right)$ . El grupo de Galois de un polinomio está formado por los homomorfismos que al actuar sobre las raices del polinomio producen también raices.

La teoría de Galois diferencial establece proposiciones análogas para las ecuaciones diferenciales: permite decidir cuándo una ecuación diferencial se puede resolver a partir de sus coeficientes encontrando el correspondiente grupo resoluble.

Para determinar este grupo, es necesario desarrollar un proceso de algebrización de la ecuación diferencial, el cual consiste en expresar las funciones coeficientes de la ecuación diferencial como funciones racionales, el proceso de algebrización es posible mediante el procedimiento llamado cambio hamiltoniano de variable, [1]. Un cambio de variable $x=x\left(t\right)$ es un cambio Hamiltoniano de variable, si y sólo si $\left(x\left(t\right),\partial _{t}x\left(t\right)\right)$ es una solución del sistema autónomo clásico Hamiltoniano con un grado de libertad, $H=H\left(x,p\right)={\frac {p^{2}}{2}}+V\left(x\right)$, para algún $V$, elemento de un cuerpo diferencial con coeficientes en $\mathbb {C} .$ Si un cambio de variable es Hamiltoniano, existe $\alpha$ tal que $\left(\partial _{t}x\right)^{2}=\alpha \left(x\right)$ y por tanto, ${\widehat {\partial _{t}}}={\sqrt {\alpha }}\partial _{t}$ define una derivación para la nueva variable. Mediante el cambio hamiltoniano de variable $e^{x}=z,$ las funciones transcendentes del sistema diferencial objetivo se transforman en funciones racionales, lo que permite la algebrización del proceso de solución del sistema diferencial, en efecto:

$\partial _{x}z=e^{x}=z={\sqrt {\alpha }}\Rightarrow \alpha =\left(\partial _{x}z\right)^{2}=z^{2}\in \mathbb {C} \left(z\right)$

$\partial _{x}z=z\partial x=e^{x}\partial x={\sqrt {\alpha }}\partial _{x}\gamma _{i}\left(x\right)={\widehat {\partial _{z}}}{\widehat {\gamma }}_{i}\left(z\right)$

además,

$e^{x}+e^{-x}={\dfrac {z^{2}+1}{z}}\wedge e^{x}-e^{-x}={\dfrac {z^{2}-1}{z}}$

entonces, el sistema se transforma en:

$\left({\begin{array}{c}\partial _{z}{\widehat {\gamma }}_{1}\\\partial _{z}{\widehat {\gamma }}_{2}\\\partial _{z}{\widehat {\gamma }}_{3}\end{array}}\right)=\left({\begin{array}{ccc}0&0&-{\dfrac {2{\sqrt {2}}}{z^{2}+1}}\\0&0&{\dfrac {z^{2}-1}{z\left(z^{2}+1\right)}}\\{\dfrac {2{\sqrt {2}}}{z^{2}+1}}&-{\dfrac {z^{2}-1}{z\left(z^{2}+1\right)}}&0\end{array}}\right)\left({\begin{array}{c}{\widehat {\gamma }}_{1}\\{\widehat {\gamma }}_{2}\\{\widehat {\gamma }}_{3}\end{array}}\right)$

Mediante el uso de las coordenadas simétricas de Darboux, [10], para la esfera compleja : ${\textstyle {\widehat {\gamma }}_{1}^{2}\left(z\right)+{\widehat {\gamma }}_{2}^{2}\left(z\right)-{\widehat {\gamma }}_{3}^{2}\left(z\right)=u^{2}\left(z\right)}$, el sistema algebrizado se transforma en una ecuación lineal diferencial reducida.

$u={\dfrac {{\widehat {\gamma }}_{1}\left(z\right)+i{\widehat {\gamma }}_{2}\left(z\right)}{1-{\widehat {\gamma }}_{3}\left(z\right)}}={\dfrac {1+{\widehat {\gamma }}_{3}\left(z\right)}{{\widehat {\gamma }}_{1}\left(z\right)-i{\widehat {\gamma }}_{2}\left(z\right)}}$

$v={\dfrac {{\widehat {\gamma }}_{3}\left(z\right)-1}{{\widehat {\gamma }}_{1}\left(z\right)-i{\widehat {\gamma }}_{2}\left(z\right)}}={\dfrac {{\widehat {\gamma }}_{1}\left(z\right)+i{\widehat {\gamma }}_{2}\left(z\right)}{-\left(1+{\widehat {\gamma }}_{3}\left(z\right)\right)}},z\in \mathbb {C}$

Si se deriva a $u$ con respecto a $z$, se tiene que

${\begin{array}{l}\partial _{z}u&={\dfrac {{\widehat {\gamma }}_{3}}{1-{\widehat {\gamma }}_{3}}}\left(i{\dfrac {z^{2}-1}{z\left(z^{2}+1\right)}}-{\dfrac {2{\sqrt {2}}}{z^{2}+1}}\right)\\&-u{\dfrac {1}{1-{\widehat {\gamma }}_{3}}}\left(-{\dfrac {2{\sqrt {2}}}{z^{2}+1}}{\widehat {\gamma }}_{1}+{\dfrac {z^{2}-1}{z\left(z^{2}+1\right)}}{\widehat {\gamma }}_{2}\right)\end{array}}$

(1)

Teniendo en cuenta que:

${\dfrac {u+v}{u-v}}={\widehat {\gamma }}_{3},1-{\widehat {\gamma }}_{3}={\dfrac {-2v}{u-v}},{\dfrac {{\widehat {\gamma }}_{3}}{1-{\widehat {\gamma }}_{3}}}=-{\dfrac {u+v}{2v}}$ ${\dfrac {1-uv}{u-v}}={\widehat {\gamma }}_{1},{\dfrac {1+uv}{u-v}}i={\widehat {\gamma }}_{2}$

La expresión (1) se transforma en una Riccati:

$\partial _{z}u={\frac {1}{2}}\left({\dfrac {2{\sqrt {2}}}{z^{2}+1}}+{\dfrac {z^{2}-1}{z\left(z^{2}+1\right)}}i\right)u^{2}+{\frac {1}{2}}\left({\dfrac {2{\sqrt {2}}}{z^{2}+1}}-{\dfrac {z^{2}-1}{z\left(z^{2}+1\right)}}i\right)$

(2)

Ahora, mediante el cambio $u=\varepsilon {\dfrac {\partial _{z}y}{y}}=\varepsilon \partial _{z}\left(\ln y\right)$, donde $\varepsilon$ es una función de $z\in \mathbb {C}$, por determinar, se tranformará la ecuación (2) en una ecuación diferencial de segundo orden

$\partial _{z}^{2}y+\left({\frac {\partial _{z}\varepsilon }{\varepsilon }}\right)\partial _{z}y-{\dfrac {\overline {\alpha }}{\varepsilon }}y-\left(1+\alpha \varepsilon \right){\dfrac {\left(\partial _{z}y\right)^{2}}{y}}=0$

(3)

donde $\alpha ={\frac {1}{2}}\left({\dfrac {2{\sqrt {2}}}{z^{2}+1}}+{\dfrac {z^{2}-1}{z\left(z^{2}+1\right)}}i\right)$. Para que (3) sea una ecuación diferencial lineal de segundo orden es necesario que $1+\alpha \varepsilon =0$, por tanto $\varepsilon ={\dfrac {-1}{\alpha }}\wedge \partial _{z}\varepsilon ={\dfrac {\partial _{z}\alpha }{\alpha ^{2}}}$lo que finalmente conduce a:

$\partial _{z}^{2}y-{\frac {\partial _{z}\alpha }{\alpha }}\partial _{z}y+\alpha {\overline {\alpha }}y=0$

(4)

Ahora, la ecuación (4) puede transformarse en una EDLR [1]

${\begin{array}{l}f&=e^{{\frac {1}{2}}\int {\frac {\partial _{z}\alpha }{\alpha }}}=e^{{\frac {1}{2}}\ln \alpha }\Rightarrow f=\alpha ^{\frac {1}{2}},t=y\alpha ^{\frac {1}{2}}\end{array}}$ ${\begin{array}{l}\partial _{z}^{2}t&=\left({\dfrac {1}{2}}{\frac {\partial _{z}^{2}\alpha }{}}{\alpha }-{\frac {1}{4}}\left({\frac {\partial _{z}\alpha }{\alpha }}\right)^{2}-\alpha {\overline {\alpha }}\right)t\end{array}}$

El proceso de algebrización del sistema diferencial lineal ha permitido expresar el coeficiente de $t$, ${\dfrac {1}{2}}{\frac {\partial _{z}^{2}\alpha }{\alpha }}-{\frac {1}{4}}\left({\frac {\partial _{z}\alpha }{\alpha }}\right)^{2}-\alpha {\overline {\alpha }}$, como una función racional, en efecto

${\dfrac {\alpha ^{\prime \prime }\left(z\right)}{2\alpha \left(z\right)}}-\left({\dfrac {\alpha ^{\prime }\left(z\right)}{2\alpha \left(z\right)}}\right)^{2}-\alpha {\overline {\alpha }}=r={\frac {s}{q}}=$ ${\begin{array}{l}={\dfrac {z^{12}+24z^{10}+63z^{8}-128z^{6}-33z^{4}+8z^{2}+1}{2z^{2}\left(z^{2}+1\right)^{2}\left(z^{4}+6z^{2}+1\right)^{2}}}+\end{array}}$ ${\begin{array}{l}+{\dfrac {-2{\sqrt {2}}\left(3z^{11}+21z^{9}+46z^{7}+42z^{5}+15z^{3}+z\right)i}{2z^{2}\left(z^{2}+1\right)^{2}\left(z^{4}+6z^{2}+1\right)^{2}}}\end{array}}$

$r\in \mathbb {C} \left[x\right]$.

Al transformar el sistema de ecuaciones diferenciales lineales con coeficientes no constantes en una EDL o en una EDLR con funciones racionales en $\mathbb {C} \left[x\right]$, como coeficientes, es posible aplicar el Algoritmo de Kovacic para obtener una base de soluciones [3]. El Algoritmo de Kovacic clasifica las EDLR' s en cuatro tipos, éstos están relacionados con los ceros de $s$, los de $q$ y el orden de $r$ en infinito, definido como: $\circ \left(r_{\infty }\right)$ $=grad\left(q\right)-grad\left(s\right)$, además se define el conjunto $\Gamma$ como $\Gamma$ $=\Gamma ^{\prime }\cup \infty$, donde $\Gamma ^{\prime }=\left\{c\in \mathbb {C} :q\left(c\right)=0\right\}$. Para la ecuación que nos ocupa, $s$ y $q$ tienen 12 y 14 ceros, respectivamente, dos de los ceros de $s$ son de multiplicidad algebraica 2 el resto son de orden o multiplicidad algebraíca 1, todos los ceros de $q$ son de orden par, y $\circ \left(r_{\infty }\right)$ es 2, por tanto, si existe una solución para la EDLR debe ser de la forma $y=Pe^{\int w}$ donde $P$ y $w$ se construyen con los pasos del algoritmo, ver [2]. La ecuación:

$\partial _{z}^{2}t=\left({\dfrac {1}{2}}{\frac {\partial _{z}^{2}\alpha }{\alpha }}-{\frac {1}{4}}\left({\frac {\partial _{z}\alpha }{\alpha }}\right)^{2}-\alpha {\overline {\alpha }}\right)t$

cae entonces en el caso 1 del Algoritmo de Kovacic y de existir la solución, tendrá la forma ${\textstyle t=Pe^{\int w}}$y será una solución liouvilliana [9].

Solucionar a mano, mediante el Algoritmo de Kovacic, EDLR es, en general, muy laborioso, normalmente la EDLR se utiliza para conocer el tipo de ecuación y la estructura de su correspondiente grupo de Galois Diferencial. En la práctica, para solucionar la ecuación diferencial, se aplica el programa"kovacicsols", implementado en Maple, a la EDL Las soluciones que se obtienen al aplicar "kovacicsols" a la ecuación $\partial _{z}^{2}y-{\frac {\partial _{z}\alpha }{\alpha }}\partial _{z}y+\alpha {\overline {\alpha }}y=0$ son:

$y_{1}\left(z\right)={\dfrac {{\sqrt {2}}\left(1+i\right)z+2}{2{\sqrt {z^{i}\left(z^{2}+1\right)}}}},y_{2}\left(z\right)={\dfrac {\left({\sqrt {2}}\left(i-1\right)z+2\right){\sqrt {z^{i}}}}{2{\sqrt {z^{2}+1}}}}$

al algoritmo proveer dos soluciones se tiene una base de soluciones, y cualquier solución particular será de la forma:

$C_{1}{\dfrac {{\sqrt {2}}\left(1+i\right)z+2}{2{\sqrt {z^{i}\left(z^{2}+1\right)}}}}+C_{2}{\dfrac {\left({\sqrt {2}}\left(i-1\right)z+2\right){\sqrt {z^{i}}}}{2{\sqrt {z^{2}+1}}}},C_{1},C_{2}\in \mathbb {C}$

La base de soluciones de la EDLR será:

${\begin{array}{l}{\hbox{ }}t_{1}\left(z\right)&={\dfrac {i{\sqrt {z^{3}-4{\sqrt {2}}iz^{2}-\left(9-10i\right)z^{1}-6{\sqrt {2}}+2iz^{-1}}}}{2{\sqrt {z^{i}}}\left(z^{2}+1\right)}}\\t_{2}\left(z\right)&={\dfrac {\sqrt {z^{i}\left(z^{3}-\left({\sqrt {2}}+{\sqrt {2}}i+2i\right)z^{2}-5\left(1-i\right)z+{\sqrt {2}}\left(3-i\right)-iz^{-1}\right)}}{\left(z^{2}+1\right)}}\end{array}}$

La base de soluciones de la Riccati asociada a la EDL, será:

${\begin{array}{l}u_{1}\left(z\right)&={\dfrac {-2iz^{3}-{\sqrt {2}}\left(3-i\right)z^{2}+2\left(2-i\right)z-{\sqrt {2}}\left(1+i\right)}{-2iz^{3}-{\sqrt {2}}\left(5+i\right)z^{2}-2\left(2-3i\right)z+{\sqrt {2}}\left(1+i\right)}}\\u_{2}\left(z\right)&={\dfrac {2iz^{3}+{\sqrt {2}}\left(3+i\right)z^{2}+2\left(2+i\right)z+{\sqrt {2}}\left(1-i\right)}{-2iz^{3}-{\sqrt {2}}\left(5-i\right)z^{2}+2\left(2+3i\right)z+{\sqrt {2}}\left(1+i\right)}}\end{array}}$

Aplicando el hecho que ${\overline {u}}={\dfrac {-1}{v}}$ y que

${\dfrac {u+v}{u-v}}={\widehat {\gamma }}_{3},1-{\widehat {\gamma }}_{3}={\dfrac {-2v}{u-v}},{\dfrac {{\widehat {\gamma }}_{3}}{1-{\widehat {\gamma }}_{3}}}=-{\dfrac {u+v}{2v}}$ ${\dfrac {1-uv}{u-v}}={\widehat {\gamma }}_{1},{\dfrac {1+uv}{u-v}}i={\widehat {\gamma }}_{2}$

es posible reconstruir la curva.

3 Solución mediante métodos numéricos

En las últimas décadas, Matlab [14] se ha convertido en un lenguage cada vez más importante para la computación científica, por ello en esta sección presentamos resultados numéricos, resueltos por medio de un código computacional generado en el lenguaje de Matlab.

Para que sea posible solucionar mediante métodos numéricos un sistema diferencial, es necesario que la función vectorial sea continua, acotada, y satisfaga una condición de Lipschitz con constante de Lipschitz $\beta$ en una región $\Re$ de $\mathbb {R} ^{n+1}$. A continuación se prueba que la función vectorial,

$\left(-{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}\gamma _{3}\left(x\right),{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}\gamma _{3}\left(x\right),{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}\gamma _{1}\left(x\right)-{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}\gamma _{2}\left(x\right)\right)$

cumple estas condiciones, por tanto, si ${\textstyle \left(x_{0},\mathbf {Y} _{0}\right)}$ es un punto cualquiera de ${\textstyle \Re }$, entonces, el problema de valores iniciales

${\begin{array}{l}\partial _{x}\mathbf {Y} =f\left(x,\mathbf {Y} \right)\\\mathbf {Y} \left(x_{0}\right)=\mathbf {Y} _{0}\end{array}}$

tiene solución única sobre el intervalo ${\textstyle \left[a,b\right]}$ y la gráfica de esta solución se encuentra en ${\textstyle \Re }$.

La función es de Lipschitz en $\gamma$

La función $f:\mathbb {R} \times \mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}$, definida mediante,

$\left({\begin{array}{c}\partial _{x}\gamma _{1}\\\partial _{x}\gamma _{2}\\\partial _{x}\gamma _{3}\end{array}}\right)=\left({\begin{array}{ccc}0&0&-{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}\\0&0&{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}\\{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}&-{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}&0\end{array}}\right)\left({\begin{array}{c}\gamma _{1}\\\gamma _{2}\\\gamma _{3}\end{array}}\right)$

es de Lipschitz en su segunda variable, ${\textstyle {\overrightarrow {\gamma }}=\left(\gamma _{1},\gamma _{2},\gamma _{3}\right)^{T}}$, en efecto, sea

$A=\left({\begin{array}{ccc}0&0&-{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}\\0&0&{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}\\{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}&-{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}&0\end{array}}\right)$

$\left\Vert A\left({\begin{array}{c}\gamma _{1}^{\star }\\\gamma _{2}^{\star }\\\gamma _{3}^{\star }\end{array}}\right)-A\left({\begin{array}{c}\gamma _{1}\\\gamma _{2}\\\gamma _{3}\end{array}}\right)\right\Vert _{\infty }=\left\Vert A\left({\begin{array}{c}\gamma _{1}^{\star }-\gamma _{1}\\\gamma _{2}^{\star }-\gamma _{2}\\\gamma _{3}^{\star }-\gamma _{3}\end{array}}\right)\right\Vert _{\infty }$ $\leq \left\Vert A\right\Vert _{\infty }\left\Vert \left({\begin{array}{c}\gamma _{1}^{\star }-\gamma _{1}\\\gamma _{2}^{\star }-\gamma _{2}\\\gamma _{3}^{\star }-\gamma _{3}\end{array}}\right)\right\Vert _{\infty }$

Dado que

$\left\Vert A\right\Vert _{\infty }={\underset {1\leq i\leq 3}{\max }}{\displaystyle \sum \limits _{j=1}^{3}}\left\vert a_{ij}\right\vert \wedge$ ${\displaystyle \sum \limits _{j=1}^{3}}\left\vert a_{1j}\right\vert ={\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}},$ ${\displaystyle \sum \limits _{j=1}^{3}}\left\vert a_{2j}\right\vert ={\dfrac {\left\vert e^{x}-e^{-x}\right\vert }{e^{x}+e^{-x}}},$ ${\displaystyle \sum \limits _{j=1}^{3}}\left\vert a_{3j}\right\vert ={\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}+{\dfrac {\left\vert e^{x}-e^{-x}\right\vert }{e^{x}+e^{-x}}}$ $\Rightarrow \left\Vert A\right\Vert _{\infty }={\dfrac {2{\sqrt {2}}+\left\vert e^{-x}-e^{x}\right\vert }{e^{x}+e^{-x}}}$

Si $x\geq {0}$

$\left\Vert A\right\Vert _{\infty }={\dfrac {2{\sqrt {2}}+\left\vert e^{x}-e^{-x}\right\vert }{e^{x}+e^{-x}}}={\dfrac {e^{2x}+2{\sqrt {2}}e^{x}-1}{e^{2x}+1}}=$ $={\dfrac {e^{2x}-1}{e^{2x}+1}}+{\dfrac {2{\sqrt {2}}e^{x}}{e^{2x}+1}}$

${\dfrac {e^{2x}-1}{e^{2x}+1}}\leq {1}$ $h\left(x\right)={\dfrac {2{\sqrt {2}}e^{x}}{e^{2x}+1}}>0$ $\forall x\in \mathbb {R}$, alcanza su único máximo relativo en $0$ y ${\underset {x\rightarrow \infty }{\lim }}{\dfrac {2{\sqrt {2}}e^{x}}{e^{2x}+1}}=0$, se concluye que $0<{\dfrac {2{\sqrt {2}}e^{x}}{e^{2x}+1}}\leq {\sqrt {2}}\Rightarrow {0}<{\dfrac {e^{2x}-1}{e^{2x}+1}}+{\dfrac {2{\sqrt {2}}e^{x}}{e^{2x}+1}}\leq {1}+{\sqrt {2}}$ $\Rightarrow$ $\left\Vert A\right\Vert _{\infty }\leq {1}+{\sqrt {2}}$ Sea $x<0,\left\vert e^{-x}-e^{x}\right\vert =e^{-x}-e^{x}$ entonces,

$\left\Vert A\right\Vert _{\infty }={\dfrac {2{\sqrt {2}}+\left\vert e^{x}-e^{-x}\right\vert }{e^{x}+e^{-x}}}={\dfrac {2{\sqrt {2}}e^{x}+1-e^{2x}}{e^{2x}+1}}=$ $={\dfrac {2{\sqrt {2}}e^{x}}{e^{2x}+1}}+{\dfrac {1-e^{2x}}{e^{2x}+1}}\leq {\sqrt {2}}+1$

La norma infinito de la matriz $A$ está acotada por $1+{\sqrt {2}},$luego

$\left\Vert A\right\Vert _{\infty }\left\Vert \left({\begin{array}{c}\gamma _{1}^{\star }-\gamma _{1}\\\gamma _{2}^{\star }-\gamma _{2}\\\gamma _{3}^{\star }-\gamma _{3}\end{array}}\right)\right\Vert _{\infty }\leq \left(1+{\sqrt {2}}\right)\left\Vert \left({\begin{array}{c}\gamma _{1}^{\star }-\gamma _{1}\\\gamma _{2}^{\star }-\gamma _{2}\\\gamma _{3}^{\star }-\gamma _{3}\end{array}}\right)\right\Vert _{\infty }$

la función ${\textstyle f:\mathbb {R} \times \mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}}$ satisface una condición de Lipschitz en la variable ${\textstyle \gamma }$con constante de Lipschitz ${\textstyle 1+{\sqrt {2}}}$ en una región

${\begin{array}{l}\Re &=\left\{\left(x,\gamma _{1}\left(x\right),\gamma _{2}\left(x\right),\gamma _{3}\left(x\right):x\in \mathbb {R} \right)\right\}\\\Re &\subseteq \mathbb {R} ^{3+1}\end{array}}$

y cada una de las funciones ${\textstyle \gamma _{1},\gamma _{2},\gamma _{3}}$ son funciones acotadas en ${\textstyle \mathbb {R} }$

El punto $\left(0,\mathbf {\gamma } _{0}\right)^{T}=\left(0,0,0.5,-0.5\right)^{T}$ es un punto de $\Re$, entonces el problema de valores iniciales

$\left({\begin{array}{c}\partial _{x}\gamma _{1}\\\partial _{x}\gamma _{2}\\\partial _{x}\gamma _{3}\end{array}}\right)=\left({\begin{array}{ccc}0&0&-{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}\\0&0&{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}\\{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}&-{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}&0\end{array}}\right)\left({\begin{array}{c}\gamma _{1}\\\gamma _{2}\\\gamma _{3}\end{array}}\right)$ $\left(0,\mathbf {\gamma } _{0}\right)^{T}=\left(0,0,0.5,-0.5\right)^{T}$

tiene solución única en $\Re {.}$

Para encontrar la solución numérica del sistema diferencial

$\left({\begin{array}{c}\partial _{x}\gamma _{1}\\\partial _{x}\gamma _{2}\\\partial _{x}\gamma _{3}\end{array}}\right)=\left({\begin{array}{ccc}0&0&-{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}\\0&0&{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}\\{\dfrac {2{\sqrt {2}}}{e^{x}+e^{-x}}}&-{\dfrac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}&0\end{array}}\right)\left({\begin{array}{c}\gamma _{1}\\\gamma _{2}\\\gamma _{3}\end{array}}\right)$

y de la forma algebrizada del mismo, se usará el método de Runge-Kutta explícito de Dormand y Prince, DOPRI 5(4).

En la figura 1 se presenta la gráfica de la solución del sistema exponencial.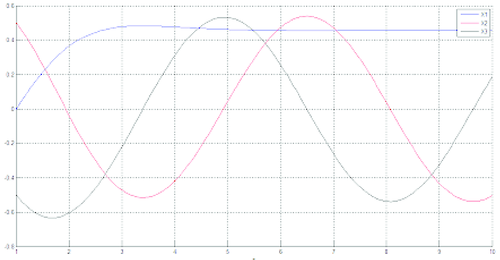

Figura 1: Solución del sistema exponencial.

La figura 2 representan las soluciones numérica y analítica del sistema exponencial.

Figura 2: Sol numérica $\left(X_{i}\right)$ versus Sol analítica $\left(B_{i}\right)$ S. Exp.

El cálculo del error absoluto entre la solución analítica y la numérica del sistema exponencial, produjo los resultados gráficos mostrados en las figuras 3, 4 y 5.

Figura 3: Error absoluto entre $B_{1}$ y $X_{1}$.

Figura 4: Error absoluto entre $B_{2}$ y $X_{2}$.

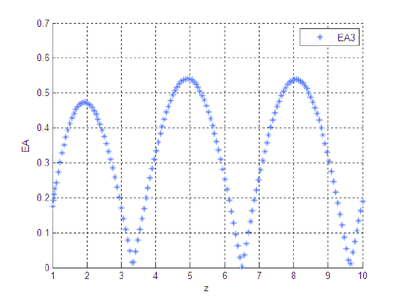
Figura 5: Error absoluto entre $B_{3}$ y $X_{3}$.

Al calcular el error relativo entre las soluciones analíticas y numérica del sistema exponencial se obtuvo la información gráfica que se expone en las figuras 6, 7 y 8.

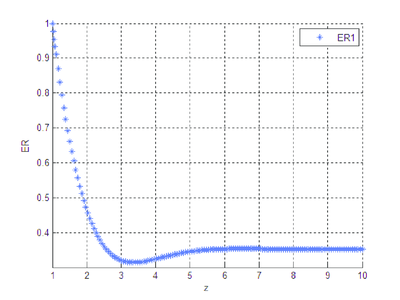
Figura 6: Error relativo entre $B_{1}$ y $X_{1}$.

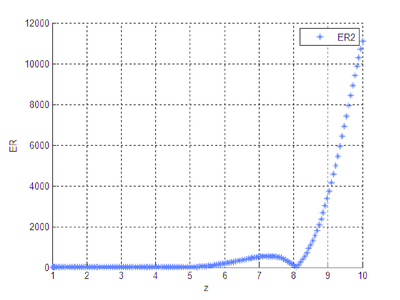
Figura 7: Error relativo entre $B_{2}$ y $X_{2}$.

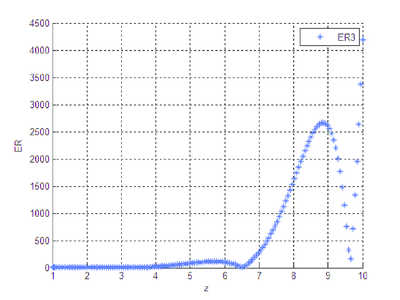
Figura 8: Error relativo entre $B_{3}$ y $X_{3}$.

La representación gráfica de la solución del sistema algebrizado se presenta en la figura 9.

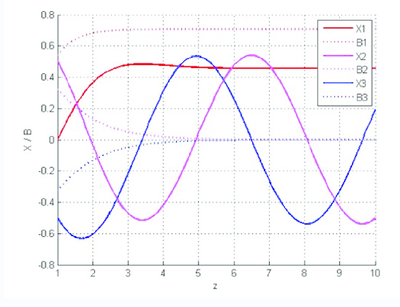
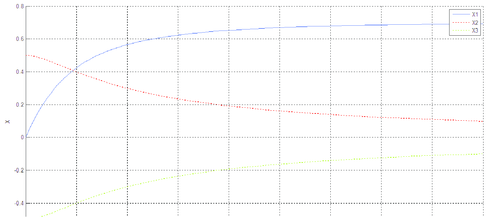
Figura 9: Solución sistema algebrizado.

El programa mediante el cual se comparan la solución numérica y analítica del sistema algebrizado produce los resultados presentados en la figura 10.

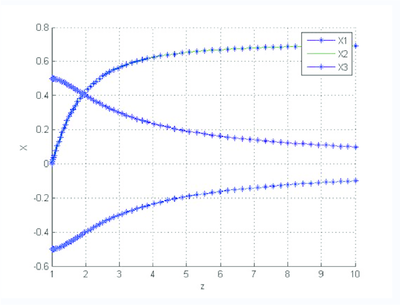
Figura 10: Sol. numérica versus Sol. analítica. S. Algebrizado.

Las figuras 11, 12 y 13 muestran el error absoluto entre la solución numérica y la analítica del sistema algebrizado.

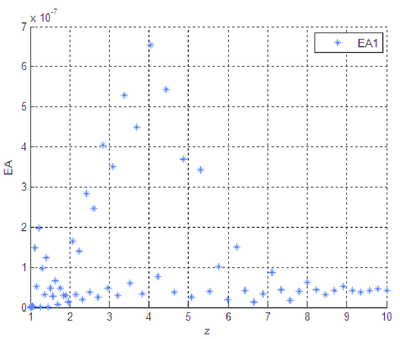
Figura 11: Error absoluto entre $X_{1}$ y $G_{1}$.

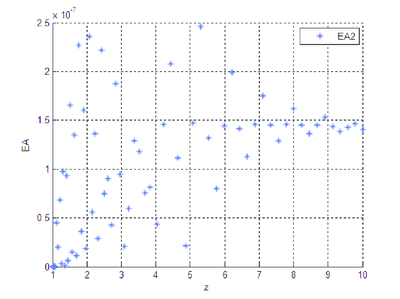
Figura 12: Error absoluto entre $X_{2}$ y $G_{2}$.

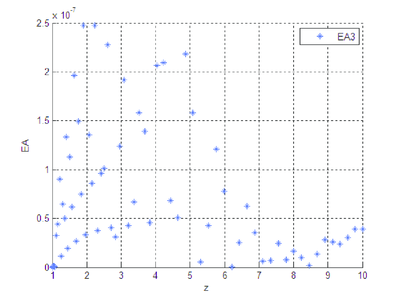
Figura 13: Error absoluto entre $X_{3}$ y $G_{3}$.

En las figuras 14, 15 y 16 se muestran los errores relativos entre las soluciones analítica y numérica del sistema algebrizado:

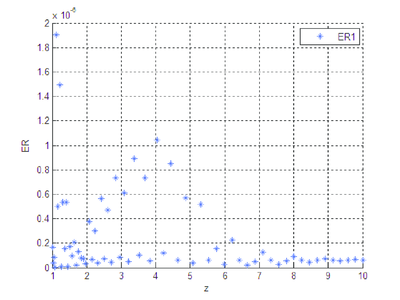
Figura 14: Error relativo entre $X_{1}$ y $G_{1}$.

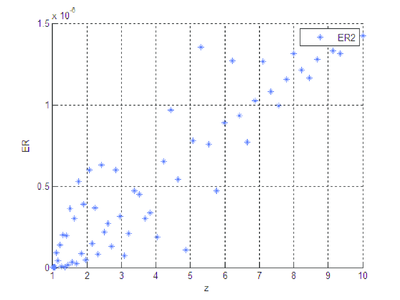
Figura 15: Error relativo entre $X_{2}$ y $G_{2}$.

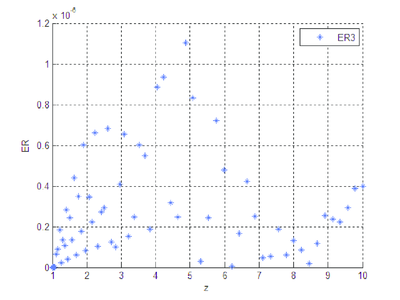
Figura 16: Error relativo entre $X_{3}$ y $G_{3}$.

4 Conclusiones

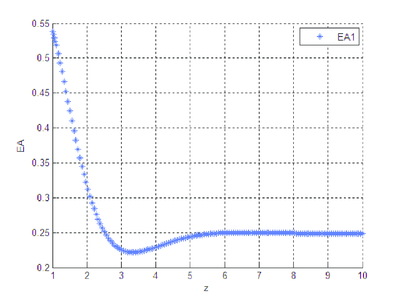
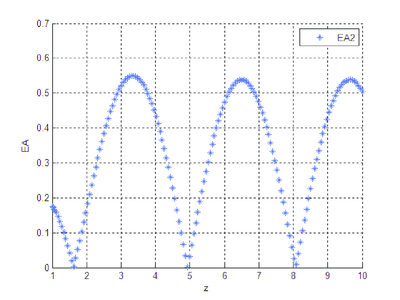
Las gráficas que se obtienen al correr el programa que se diseñó, ponen de manifiesto una diferencia notable entre las soluciones numérica y analítica del sistema diferencial cuando el mismo está en forma exponencial.

Se observa que la diferencia existente entre las soluciones numérica y analítica, cuando se trabaja con la forma algebrizada del sistema diferencial, es imperceptible, gráficamente no hay distinción clara, el orden del error entre las dos soluciones es pequeño.

Al menos para este sistema, es evidente la necesidad de algebrizar previamente el sistema para que la solución numérica obtenida sea la adecuada.

El proceso que permite la algebrización del sistema diferencial hace uso de procesos proyectivos y de las coordenadas simétricas de Darboux, mediante estos procesos se obtuvieron las transformaciones expuestas. Este trabajo, al igual que [4], pone en evidencia que la algebrización Hamiltoniana es una herramienta útil, junto con los métodos numéricos, puesto que permiten minimizar los errores.

Agradecimientos

Los autores agradecen a la oficina de la DIDI de la Universidad del Norte, por el apoyo brindado para la publicación de este artículo. Los autores agradecen también a la Universidad Simón Bolívar. Finalmente los autores agradecen a los árbitros anónimos por su ayuda para mejorar este documento.

Bibliografía

[1] P.B. Acosta-Humánez, Galoisian Approach to Supersymmetric Quantum Mechanics. PhD. Thesis, Technical University of Catalonia, abril 2009.

[2] P.B. Acosta-Humánez, La teoría de Morales-Ramis y el algoritmo de Kovacic. Lecturas Matemáticas, Volumen Especial, pp. 21-56, 2006.

[3] P. B. Acosta-Humánez, E. Suazo, Liouvillian propagators, Riccati equation and diferential theory. Journal of Physics a: Mathematical and Theoretical, 46, 2013.

[4] P. B. Acosta-Humánez, M. Machado, A. V. Sinitsyn A model of anaerobic digestion for biogas production using Abel equations. Far East Journal of Mathematical Sciences (FJMS), 101:1295-1311, 2017.

[5] R. Bulirsch, J. Stoer, Introduction to numerical analisys. Third edition. Springer-Verlag, 2002.

[6] R. L. Burden, J. Douglas Faires, Análisis numérico. Cengage Learning, Séptima edición, 2009.

[7] J. C. Butcher, Numerical methods for ordinary differential equations. John Wiley and Sons, Second edition, 2008.

[8] M. Calvo, J. I. Montijano, L. Rández, Una familia de métodos multirevolución Runge-Kutta explícitos de orden cinco. Departamento Matemática Aplicada, Universidad de Zaragoza, pp. 45-54, 2003.

[9] A. Campos, Cómo obtener ecuaciones reducidas de Riccati invariantes con respecto a un campo de vectores. Lecturas Matemáticas, Volumen Especial, pp. 95-103, 2006.

[10] S. A. Carrillo Torres, Constructibilidad mediante funciones Liouvillianas de curvas espaciales con curvatura y torsión racionales. Trabajo de grado, Universidad Sergio Arboleda, 2009.

[11] W, Cheney, D, Kincaid, Métodos numéricos y computación. Cengage Learning, Sexta edición, 2011.

[12] M. I. Jiménez Niebles, Enfoque Galoisiano y numérico de sistemas diferenciales lineales 3-dimensionales con matrices antisimétricas definidas en un cuerpo diferencial no constante. Tésis de Maestría, Universidad del Norte, 2015.

[13] J. D. Lambert, Numerical methods for Ordinary differential sistems. The initial value problem. John Wiley and Sons, 1991.

[14] Matlab. Available: http://www.mathworks.com

[15] J. J. Morales-Ruiz, Differential Galois Theory and non-integrability of Hamiltonian systems. Birkhaüser, 1999.

[16] T. Sauer, Análisis numérico. Pearson, Segunda edición, 2013.