| Line 84: | Line 84: | ||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| − | | style="vertical-align: | + | | style="vertical-align: center;width: 100%;"|[[Image:Draft_Conde_136208335-image2.png|600px]] |
|} | |} | ||
Revision as of 20:26, 11 May 2020
ABSTRACT: The improvements in monitoring devices result in databases of increasing size showing dam behaviour. Advanced tools are required to extract useful information from such large amounts of data. Machine learning is increasingly used for that purpose worldwide: data-based models are built to estimate the dam response in front of a given combination of loads. The results of the comparison between model predictions and actual measurements can be used for decision support in dam safety evaluations. However, most of the works to date consider each device separately. A different approach is used in this contribution: a set of displacement records are jointly considered to identify patterns using a classification model. First, potential anomaly scenarios are defined and the response of the dam for each of them is obtained with numerical models under a realistic load combination. Then, the resulting displacements are used to generate a machine learning classifier. This model is later used to predict the most probable class of dam behavior corresponding to a new set of records. The methodology is applied to a double-curvature arch dam, showing great potential for anomaly detection.
Keywords: Machine Learning, Random Forest, Arch Dam, Anomaly Detection.
1 Introduction
The tendency towards the installation of automatic data acquisition systems in dam monitoring results in an increasing amount of available data. This has motivated researchers and practitioners to use machine-learning-based predictive models for dam safety assessment, as shown by the number of scientific publications in the field [1].
Most of the published works share the same structure: some period of data measurements is taken, for which both the loads (mainly the reservoir level and the temperature) and the response are known. The displacements in concrete dams are more frequently analyzed, though other variables have also been addressed (e.g. leakage [2]). Some data-based predictive model is fitted to part of the available data (i.e. training set), then the model is applied to predict the dam response for the remaining period (i.e. test or validation set). Prediction accuracy is measured by comparing the model predictions with the actual readings.
The main goal of these approaches is early detection of anomalies, for which some threshold is typically set so that if the deviation of the actual reading from the model prediction is greater than the threshold, some warning is issued.
This approach provides advantages over conventional statistical models such as HST [3], including more flexibility and accuracy [4], therefore, it allows setting more constrained safety thresholds and better control of dam response.
Other works deal with the interpretation of the dam response by analyzing the model. Although machine learning (ML) algorithms are often considered as ‘black box’ models, some tools are available for their analysis, which have been shown to be useful for understanding dam behavior [5-8].
However, these approaches also have an important limitation, namely that each monitoring device is analyzed separately. Thus, the implementation of these models for anomaly detection requires fitting and analyzing as many models as relevant monitoring devices: their predictions need to be compared to the readings, then the results interpreted as regards potential anomalies or failure modes. This interpretation must be based on knowledge of the historical behavior of the dam in different situations.
The simultaneous analysis of a set of monitoring devices by means of an expert system would improve the process of anomaly detection. For example, in the event of some reading error in one device, a prediction model could detect it more or less quickly, but a subsequent analysis is required to determine whether the difference between the prediction and the measurement corresponds to a certain anomaly.
However, the joint analysis of the readings of a set of devices has been much less explored. Mata et al [9] proposed a methodology based on Principal Component Analysis (PCA) and presented an example application with one potential failure scenario under constant hydrostatic load. The idea is to identify patterns among a set of readings to elucidate whether they correspond to a safe state or to some anomaly. For such purpose, the anomaly considered (an unacceptable relative sliding between dam and foundation in the right bank) was simulated with a numerical model.
In this work, we followed a similar approach with the following novelties:
- 1. Several anomaly scenarios were considered.
- 2. Low-relevant anomalies are analyzed, to verify the potential for early detection.
- 3. The thermal load was considered in addition to the hydrostatic load.
- 4. The method was verified for different load combinations.
- 5. The chosen algorithm is capable of dealing with a high amount of input variables (load and monitoring devices), without the need for doing variable selection.
In addition, the proposed methodology can be useful to support the design of the monitoring system: the algorithm automatically computes the relative influence of the inputs (here, the monitoring devices) as regards their usefulness to identify response scenarios, so the most relevant ones can be selected for being automated.
2 Methodology
The proposed methodology includes the following steps:
- 1. Determination of the potential anomalies or failure modes to consider. They need to be susceptible of being reproduced with a numerical model with enough accuracy. In the pilot test, an arch dam was selected and anomalies were defined that reproduce imposed displacements on the abutments and on the foundation. These conditions have been introduced into the model by modifying the corresponding boundary condition.
- 2. Computation of the dam response with the Finite Element Method (FEM). In our implementation, we use an in-house developed code [10] implemented in the Kratos environment [11] and coupled with the pre and post processor GiD [12]. Both the normal and the anomalous scenarios are computed and the predicted response in the monitoring devices is stored. In the case study presented we considered the displacements measured by pendulums. We used real load combinations, according to the actual evolution of the reservoir level and air temperature. If applied before construction, realistic combinations of environmental conditions should be generated.
- 3. Creation of a database including the variable loads (reservoir level and temperature in our case), the dam response at the location of the monitoring devices and the identifier of the corresponding scenario (normal or anomalous).
- 4. Generation of a machine learning classifier, fitted to the data. This model takes the loads and displacements as inputs, together with the identifier of the corresponding scenario, then ‘learns’ patterns associated to each of the simulated states. Once fitted, the model can be used to compute the most probable scenario for a set of readings, given some load combination.
Once the classifier has been trained and verified, it can be used to predict the most probable class of dam behavior corresponding to a new set of records.
3 Case study
3.1 Description of the dam
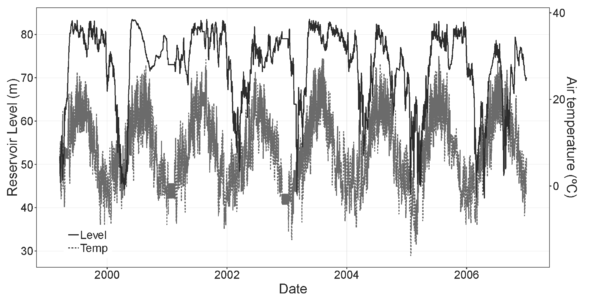
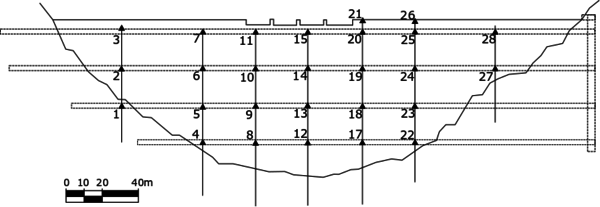
The methodology has been applied to a Spanish double curvature arch dam with 80 m height over foundation and 20 cantilevers. The monitoring data for the period 1999-2006 were considered, including the reservoir level and the air temperature, as well as the displacements in 28 stations of 7 pendulums. Fig. 1 shows the time series of the reservoir level and air temperature in the period analyzed. We considered both the tangential and radial displacements at all the available locations for the analysis. Fig. 2 shows a scheme of the dam and the location of the monitoring devices.
|
Since both the reservoir level and the concrete temperature are influential in the dam displacements, and the latter is dependent on the initial temperature considered, we run a preliminary analysis to obtain a realistic thermal field to be used as initial temperature in the dam body. For that purpose, a transient analysis was run over the period analyzed (1999-2006) with a constant value of the initial temperature (8ºC) and a time step of 12 h. The resulting thermal field at the end of this preliminary computation was taken as the initial temperature for all the scenarios considered. A similar approach was used by Santillán et al. [13].
|
Material properties are included in Table 1. The mesh is formed by tetrahedral linear elements of variable size: a finer mesh was used in the dam body, enough to ensure at least three elements along the radial direction, while increasing size was chosen for the foundation, up to 25 m. This resulted in 33000 nodes forming 173000 tetrahedrons.
| Material properties | Concrete | Foundation | Units |
| Young Modulus | 3e10 | 4.9e10 | Pa |
| Poisson | 0.2 | 0.25 | [-] |
| Density | 2400 | 3000 | Kg/m3 |
3.2 Scenarios considered
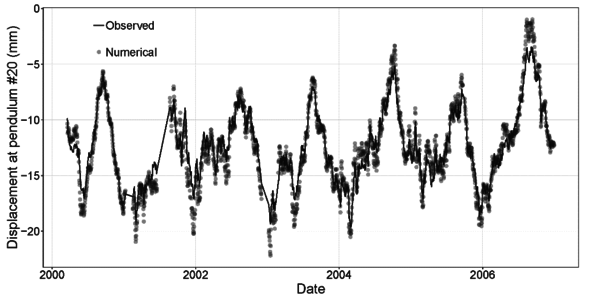
First, we run a transient analysis representing the actual behavior of the dam, to be taken as a reference of the normal or safe state (Scenario 0). We verified that this model sensibly represents the observed dam response by comparing the evolution of displacements in the model with the measurements recorded. Fig. 3 includes this comparison for one of the locations.
|
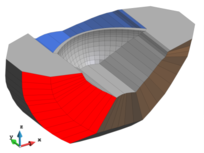
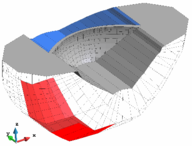
Then we defined modifications with respect to Scenario 0, representing potential anomalies (Table 2 and Fig. 4).
| Scenario | Description | Magnitude |
| 1 | Imposed displacement in the left abutment | 1 mm |
| 2 | 0.5 mm | |
| 3 | Imposed displacement in the right abutment | 1 mm |
| 4 | 0.5 mm | |
| 5 | Imposed displacement in the riverbed | 1 mm |
|
|
|
| (a) | (b) | (c) |
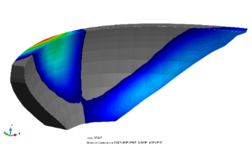
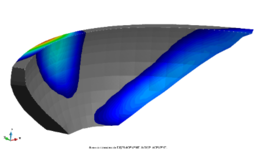
The difference in displacement fields among scenarios is small in general, as seen in the example in Fig. 5.
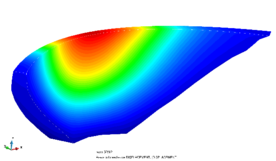
|
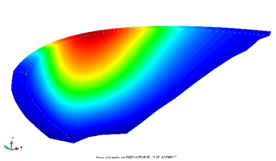
|
|
|
|
|
As a result of these calculations, we obtained a database including 34152 records for the period 1999-2006 for 6 Scenarios. Each record includes reservoir level and air temperature, as well as tangential and radial displacements in 28 locations. The last column contains the identifier of the scenario corresponding to each set of records.
Although time is not explicitly considered, we divided the dataset into a training period corresponding to years 1999-2002, and left the remaining data for validation. This approach represents a realistic application, in which past performance can be used to build a model that can be later applied to real-time safety assessment. In practice, the model could be updated with certain frequency to enlarge the training set and thus the predictive accuracy. The effect of the training set size on the performance of ML models was assessed in a previous work, including criteria for updating the model [4]. In this case, we tested three different periods for training, namely 1999-2000, 1999-2001 and 1999-2002. For validation, we used the data for 2003-2006 for all models.
The data used, generated by numerical models, include no measurement errors. We modified them by adding a random variable with zero mean and a standard deviation of 0.10 mm to simulate errors due to measurement accuracy.
4 Classification task
Among the machine learning algorithms available for classification, we used random forest in this work [14], since it is acknowledged to be appropriate in settings with many highly correlated input variables [15]. The algorithm automatically selects the more relevant variables and discards those with low influence in the results, which in our case are those with low usefulness to identify the response scenario.
The same algorithm was previously employed in regression problems in different applications, e.g. to build dam predictive models [2], to interpret dam response to seismic loads [16] and to better understand the behavior of labyrinth spillways [17].
First, we took all the available inputs. Then, the process was repeated taking only those inputs which showed to have highest relevance for the classification. We used this approach to build models with the 10 and 20 topmost relevant inputs. The availability of an accurate model using a reduced number of inputs can be useful to choose which devices should be automated in an existing dam.
We used the library randomForest [18] and the R software [19]. All the models were run with default training parameters.
5 Results and discussion
The raw outcome of the model is the probability of belonging to each of the defined classes. Then, the predicted scenario is that with the highest probability. Table 3 shows a summary of the results obtained. They correspond to the classification of the validation data, i.e. the period 2003-2006. There is a clear increase in predictive accuracy when 20 inputs are used instead of 10, and a small benefit when all 64 variables are considered.
The size of the training set has a relevant influence in the classification accuracy. The general improvement is low when year 2002 is added, but including data for 2001 results in a decrease of around 30% in average misclassification error. It should be kept in mind that we considered 720 records per year, e.g. two measurements per day. On a different note, the prediction task is challenging, since the validation data includes 17532 sets of measurements to be classified among the scenarios considered. In such setting, the resulting accuracy can be considered as a useful result.
The misclassification rate for Scenario 0 (last column in Table 3) is useful result for practical purposes, since it represents the percentage of normal records that were wrongly classified as potentially anomalous (e.g. false positive rate). The results show that model performance improves as more information (e.g. number of devices) is included.
| Model Id | Inputs | Training set | Average classification error (%) | Scenario with highest error | Classification error for Scenario 0 (%) |
| A | All (64) | 1999-2000 | 4.79 | 2 | 2.09 |
| B | 1999-2001 | 3.48 | 4 | 1.71 | |
| C | 1999-2002 | 3.04 | 3 | 0.86 | |
| D | More relevant (10) | 1999-2000 | 13.93 | 5 | 17.86 |
| E | 1999-2001 | 10.71 | 5 | 15.40 | |
| F | 1999-2002 | 9.29 | 5 | 13.42 | |
| G | More relevant (20) | 1999-2000 | 6.21 | 2 | 8.35 |
| H | 1999-2001 | 4.50 | 0 | 6.37 | |
| I | 1999-2002 | 3.83 | 0 | 5.30 |
Table 4 shows the confusion matrix, i.e., the predicted versus the actual class for each sample, for the case with all inputs and training period 1999-2002. As expected, Scenario 0 is misclassified with Scenarios 2 and 4, which feature the lowest magnitude of the imposed displacement (0.5 mm). All situations for Scenarios 1 and 3 are correctly identified as not pertaining to Scenario 0.
| Actual scenario | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | ||
| Predicted scenario | 0 | 2898 | 0 | 42 | 0 | 97 | 67 |
| 1 | 0 | 2781 | 8 | 0 | 0 | 0 | |
| 2 | 8 | 141 | 2872 | 0 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 2789 | 4 | 0 | |
| 4 | 14 | 0 | 0 | 133 | 2818 | 20 | |
| 5 | 2 | 0 | 0 | 0 | 3 | 2835 | |
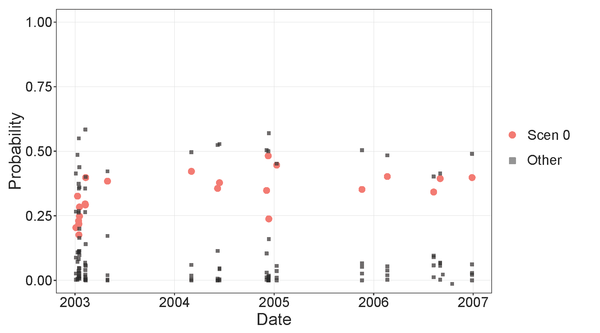
As mentioned before, the default predicted class is the one that obtains the highest probability. However, the results can be analyzed in more detail by observing the probabilities assigned by the model to all classes. As an example, errors in the classification of Scenario 0 of the complete model have been investigated. Fig. 6 shows the probabilities assigned to Scenario 0 (colored circles) and those corresponding to the other scenarios (black squares). Although Scenario 0 does not have the highest probability, the predicted values are clearly different from zero, often close to the highest among the remaining classes, and never the minimum.
The average probability of Scenario 0 in cases erroneously classified as anomalous is 0.33. This value is greater than the average probability assigned to Scenario 0 in truly anomalous scenarios, which are respectively 0.008, 0.13, 0.01, 0.15 and 0.12.
|
Another aspect that can be considered in practice is the temporal evolution of the prediction: in the example considered, every misclassification of Scenario 0 was followed by a correct prediction as normal behavior. Therefore, the reliability of the prediction can be associated to the number of samples consecutively predicted with the same class. From a practical viewpoint, the occurrence of a set of consecutive anomaly predictions can be established as a requirement for the issuance of safety warnings. Similar results were obtained for false negatives, i.e. anomalous scenarios wrongly classified as safe.
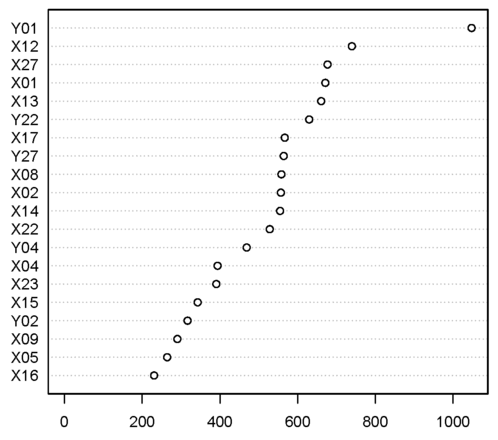
Classification models can be further analyzed to extract useful information. A measure of variable importance is computed for each input during model fitting [14]. The result for the model with all available variables is shown in Fig. 7. It is based on the average result of all scenarios considered.
|
Fig. 8 shows that the most influential devices are located at the bottom part of the dam body. These results are reasonable, since the modifications to the reference case include imposed displacements on the boundary of the foundation, therefore their effect is higher in that area, and tend to be compensated by the monolithic response of the structure. This is in contrast to the conventional practice in dam safety: the displacements in the upper area of the higher cantilevers are more frequently analyzed, because they typically result in higher range of variation.
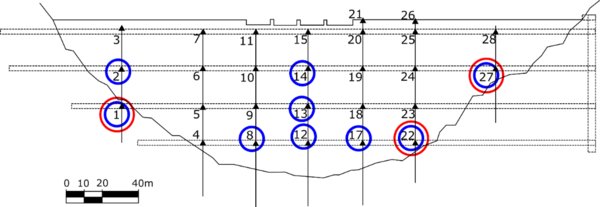
|
These results depend on the nature of the anomaly to detect, but show that when all devices are jointly considered, deviations with respect to normal behavior are more easily detected in areas with lower range of variation in normal operation conditions.
6 Summary and conclusions
A methodology based on machine learning has been presented for the joint analysis of dam monitoring data, which allows classifying the response of the structure among a series of previously defined possible states. The results show that the method can be useful as a support for dam safety analysis, thus allowing the identification of even small deviations from normal behavior.
The main limitation of the approach presented is that it only those scenarios that can be numerically modeled with sufficient precision can be considered. This limits its application to certain situations. However, it could be applied to others not considered in this work, such as the opening of the dam-foundation contact in concrete dams, or the appearance of preferential seepage zones in earth and rock-filldams. The latter would be reflected in certain reading patterns at the piezometers. This line of work is currently underway.
Furthermore, a possible anomaly cannot, in principle, be directly identified if it has not been defined and reproduced beforehand. In such situation, the result of the model could be anomalous in terms of the probability of belonging to the considered scenarios, which could also be useful for identification. This is also a research under development: these situations could be considered by adding an ‘unknown’ scenario to the potential anomalies.
7 Acknowledgements
The authors acknowledge the financial support to CIMNE via the CERCA Programme/Generalitat the Catalunya. This work was also partially funded by the Spanish Ministry of Science, Innovation and Universities (Ministerio de Ciencia, Innovación y Universidades) through the projects NUMA (RTC-2016-4859-5) and TRISTAN (RTI2018-094785-B-I00).
8 References
- 1. Salazar, F., Morán, R., Toledo, M. Á., & Oñate, E. (2017). Data-based models for the prediction of dam behaviour: a review and some methodological considerations. Archives of Computational Methods in Engineering, 24(1), 1-21.
- 2. Salazar, F., Toledo, M. A., Oñate, E., & Morán, R. (2015). An empirical comparison of machine learning techniques for dam behaviour modelling. Structural Safety, 56, 9-17.
- 3. Willm, Beaujoint. Les méthodes de surveillance des barrages au service de la production hydraulique d’Electricité de France, problems anciens et solutions nouvelles. IXth Int. Congr. Large Dams, Istanbul; 1967. p. 529–50.
- 4. Salazar, F., Toledo, M. Á., González, J. M., & Oñate, E. (2017). Early detection of anomalies in dam performance: A methodology based on boosted regression trees. Structural Control and Health Monitoring, 24(11), e2012.
- 5. Mata, J. (2011). Interpretation of concrete dam behaviour with artificial neural network and multiple linear regression models. Engineering Structures, 33(3), 903-910.
- 6. De Granrut, M., Simon, A., &Dias, D. (2019). Artificial neural networks for the interpretation of piezometric levels at the rock-concrete interface of arch dams. Engineering Structures, 178, 616-634.
- 7. Tinoco, J. A. B., Granrut, M. D., Dias, D., Miranda, T. F., & Simon, A. G. (2018). Using soft computing tools for piezometric level prediction. In Third International Dam World Conference (pp. 1-10).
- 8. Salazar, F., Toledo, M. Á., Oñate, E., & Suárez, B. (2016). Interpretation of dam deformation and leakage with boosted regression trees. Engineering Structures, 119, 230-251.
- 9. Mata, J., Leitão, N. S., De Castro, A. T., & Da Costa, J. S. (2014). Construction of decision rules for early detection of a developing concrete arch dam failure scenario. A discriminant approach. Computers & Structures, 142, 45-53.
- 10. Vicente, D. J., San Mauro, J., Salazar, F., & Baena, C. M. (2017). An Interactive Tool for Automatic Predimensioning and Numerical Modeling of Arch Dams. Mathematical Problems in Engineering, 2017.
- 11. Dadvand, P., Rossi, R., & Oñate, E. (2010). An object-oriented environment for developing finite element codes for multi-disciplinary applications. Archives of Computational Methods in Engineering, 17(3), 253-297.
- 12. Ribó, R., Pasenau, M., Escolano, E., Pérez, J., Coll, A., Melendo, A., & González, S. (2008). GiD The Personal Pre and Postprocessor. Reference Manual, version, 9.
- 13. Santillán, D., Salete, E., Vicente, D. J., & Toledo, M. Á. (2014). Treatment of solar radiation by spatial and temporal discretization for modeling the thermal response of arch dams. Journal of Engineering Mechanics, 140(11), 05014001.
- 14. Breiman, L. (2001). Random forests. Machine learning, 45(1), 5-32.
- 15. Díaz-Uriarte, R., & De Andres, S. A. (2006). Gene selection and classification of microarray data using random forest. BMC Bioinformatics, 7(1), 3.
- 16. Salazar, F. and Hariri-Ardebili, M.A., 2019, Machine Learning Based Seismic Stability Assessment of Dams with Heterogeneous Concrete, 3rd Meeting of EWG Dams and Earthquakes, Lisbon, Portugal, May 06-09.
- 17. Salazar, F., & Crookston, B. M. (2019). A Performance Comparison of Machine Learning Algorithms for Arced Labyrinth Spillways. Water, 11(3), 544.
- 18. Liaw, A., & Wiener, M. (2002). Classification and regression by randomForest. R news, 2(3), 18-22.
- 19. R Core Team (2019). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.
Document information
Published on 01/01/2021
DOI: 10.1007/978-3-030-51085-5_48
Licence: CC BY-NC-SA license