| (4 intermediate revisions by the same user not shown) | |||
| Line 556: | Line 556: | ||
<div class="center" style="font-size: 75%;">'''Tabela 2'''. Comparativo entre os métodos desenvolvidos e o ''solver'' Gurobi para os problemas difíceis da BaseSun Fonte: os autores) | <div class="center" style="font-size: 75%;">'''Tabela 2'''. Comparativo entre os métodos desenvolvidos e o ''solver'' Gurobi para os problemas difíceis da BaseSun Fonte: os autores) | ||
</div> | </div> | ||
| − | |||
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
| Line 1,388: | Line 1,387: | ||
</div> | </div> | ||
| − | {| style="width: | + | {| style="width: 70%;margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| rowspan='2' colspan='2' style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|'''Nome e tamanho dos problemas''' | | rowspan='2' colspan='2' style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|'''Nome e tamanho dos problemas''' | ||
| Line 1,508: | Line 1,507: | ||
<div class="center" style="font-size: 75%;">'''Tabela 4'''. Desempenho de heur-3 com relação aos outros métodos aplicado aos problemas fáceis da BaseSun (Fonte: os autores)</div> | <div class="center" style="font-size: 75%;">'''Tabela 4'''. Desempenho de heur-3 com relação aos outros métodos aplicado aos problemas fáceis da BaseSun (Fonte: os autores)</div> | ||
| − | {| style="width: | + | {| style="width: 80%;margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| colspan='3' style="border-top: 2pt solid black;border-bottom: 2pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|'''BT''' | | colspan='3' style="border-top: 2pt solid black;border-bottom: 2pt solid black;border-right: 1pt solid black;text-align: center;vertical-align: bottom;"|'''BT''' | ||
| Line 2,492: | Line 2,491: | ||
==Referências== | ==Referências== | ||
| − | + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | |
| − | |||
| − | [ | + | [1] Hitchcock F.L. The distribution of a product from several sources to númerous facilities. J. Math. Phys., 20:224–230, 1941. |
| − | [ | + | [2] Hirsch W.M., Dantzig G.B. Notes on linear programming. Part XIX : the fixed charge problem. Randon Research, Santa Monica, CA, 1954. |
| − | [ | + | [3] Loch G.V. Uma nova abordagem no processo iterativo de melhoria de solução na resolução do problema de transporte. Universidade Federal do Paraná, 2014. |
| − | [ | + | [4] Yousefi K., Afshari A.J., Hajiaghaei-Keshteli M. Heuristic approaches to solve the fixed-charge transportation problem with discount supposition. J. Ind. Prod. Eng., 35(7):444–470, 2018. |
| − | [ | + | [5] Hirsch W.M., Dantzig G.B. The fixed charge problem. Nav. Res. Logist. Q., 15(3):413–424, 1968. |
| − | [ | + | [6] Sun M., Aronson J.E., McKeown P.G., Drinka D. A tabu search heuristic procedure for the fixed charge transportation problem. Eur. J. Oper. Res., 106(2–3):441–456, 1998. |
| − | [ | + | [7] Glover F., Amini M., Kochenberger G. Parametric ghost image processes for fixed-charge problems: A study of transportation networks. J. Heuristics, 11(4):307–336, 2005. |
| − | [ | + | [8] Aguado J.S. Fixed charge transportation problems: A new heuristic approach based on Lagrangean relaxation and the solving of core problems. Ann. Oper. Res., 172(1):45–69, 2009. |
| − | [ | + | [9] Buson E., Roberti R., Toth P. A reduced-cost iterated local search heuristic for the fixed-charge transportation problem. Oper. Res., 14(1):1095–1106, 2014. |
| − | [ | + | [10] Roberti R., Bartolini E., Mingozzi A. The fixed charge transportation problem: An exact algorithm based on a new integer programming formulation. Manage. Sci., 61(6):1275–1291, 2014. |
| − | [ | + | [11] Mingozzi A., Roberti R. An exact algorithm for the fixed charge transportation problem based on matching source and sink patterns an exact algorithm for the fixed charge transportation problem based on matching source and sink patterns. Transp. Sci., 52(2):229–238, 2018. |
| − | [ | + | [12] Zhao Y., Larsson T., Rönnberg E., Pardalos P.M. The fixed charge transportation problem : a strong formulation based on Lagrangian decomposition and column generation. J. Glob. Optim., 72(3):517–538, 2018. |
| − | [ | + | [13] Othman Z., Delavar M.R.R., Behnam S., Lessanibahri S. Adaptive genetic algorithm for fixed-charge tranportation problem. Proc. Int. MultiConference Eng. Comput. Sci., I:96–101, 2011. |
| − | [ | + | [14] Kennington J. The fixed-charge transportation problem: A computational study with a branch-and-bound code. AIIE Trans., 8(2):241–247, 1976. |
| − | [ | + | [15] Balinski M.L. Fixed-cost transportation problems. Nav. Res. Logist. Q., 8(1):41–54, 1961. |
| − | [ | + | [16] Silva T.C.L. Nova metodologia para resolução de problemas de transporte em casos esparsos. Universidade Federal do Paraná, 2012. |
| − | [ | + | [17] Kowalski K., Lev B., Shen W., Tu Y. A fast and simple branching algorithm for solving small scale fixed-charge transportation problem. Oper. Res. Perspect., 1(1):1–5, 2014. |
| − | [ | + | [18] Loch G.V., Silva A.C.L. A computational experiment in a heuristic for the fixed charge transportation problem. Int. Ref. J. Eng. Sci., 3(4):1–7, 2014. |
| − | [ | + | [19] Loch G.V., Silva A.C.L. A computational study on the number of iterations to solve the transportation problem. Appl. Math. Sci., 8(92):4579–4583, 2014. |
| − | [ | + | [20] Oliveira C.R.V., Schmidt C.E., Silva A.C.L. Análise da resolução do problema de transporte com custo fixo utilizando o Cplex e o Gurobi. In Anais do 1o Simpósio De Métodos Numéricos, 2016, pp. 188–191, 2016. |
| − | [23] GUROBI OPTIMIZATION INC | + | [21] Microsoft Corporation. Visual Basic 2013, 2014. |
| + | |||
| + | [22] Oliveira C.R.V., Schmidt C.E., Silva A.C.L. Comparação entre o desempenho de dois solvers de otimização na resolução de problemas de transporte com custo fixo. CMN 2017 Congress on Numerical Methods in Engineering, 3-5 July Valencia, Spain, pp. 1401–1410, 2017. | ||
| + | |||
| + | [23] GUROBI OPTIMIZATION INC. Gurobi Optimizer, 2016. | ||
| + | |||
| + | [24] IBM Corporation. Ibm ilog cplex interactive optimizer, 2012. | ||
| + | |||
| + | </div> | ||
| − | |||
| − | |||
---- | ---- | ||
<span style="text-align: center; font-size: 75%;"><span id="fn-5"></span>([[#fnc-5|<sup>5</sup>]]) A partir dos problemas de Tipo E, os métodos não foram testados no trabalho de [8], pois segundo o autor, haveria necessidade de alterar os parâmetros para obter bons resultados.</span> | <span style="text-align: center; font-size: 75%;"><span id="fn-5"></span>([[#fnc-5|<sup>5</sup>]]) A partir dos problemas de Tipo E, os métodos não foram testados no trabalho de [8], pois segundo o autor, haveria necessidade de alterar os parâmetros para obter bons resultados.</span> | ||
Revision as of 14:37, 3 March 2020
Abstract
The Fixed Charge Transportation Problem (FCTP) is a Linear Programming (LP) class, whereby the total shipping cost of a product, from a source to a destination, consists of a unit transportation cost, proportional to the amount of sent items and a fixed charge associated with the opening of the route. The FCTP is NP-hard and has a characteristic in which, as far as the difference between the value of the unit cost and the fixed charge increases, the computational time changes, worsening the performance. This paper purpose a matheuristic approach to the FCTP which results were good when compared to other methods available in the Literature.
Keywords: Fixed Charge Transportation Problem, matheuristic, operations research
Resumo
O Problema de Transporte com Custo Fixo (PTCF) é uma classe da Programação Linear (PL), em que o custo total de envio de um produto, de uma origem até um destino, consiste em um custo de transporte unitário proporcional à quantidade de itens enviados e um custo fixo associado à abertura da rota. O PTCF é NP-hard e possui uma característica em que, à medida que a diferença entre o valor do custo unitário e o custo fixo aumenta, o tempo computacional muda, piorando o seu desempenho. Esta pesquisa apresenta abordagem matemática de uma matheurística aplicada ao PTCF cujos resultados foram bons quando comparados a outros métodos disponíveis na literatura.
Palavras-chave: Problema de Transporte com Custo Fixo, matheurística, pesquisa operacional
1. Introdução
O Problema de Transporte (PT), destaca-se entre os típicos problemas da Programação Linear (PL) que em 1941 foi proposto por Hitchcock [1] e tem sua resolução, por meio de algoritmo específico, realizada por Dantzig em 1951. Nele, o custo total de envio de um produto, entre uma origem e um destino, é proporcional à quantidade transportada.
Por outro lado, existem os Problemas Gerais com Custo Fixo (PGCF), e um caso particular é o Problema de Transporte com Custo Fixo (PTCF), que foi proposto por Hirsch and Dantzig [2], e é definido então, como um caso particular dos PGCF e uma generalização do PT [3].
A formulação matemática do PTCF assemelha-se a de um PT, porém agregando o custo fixo, que pode representar, por exemplo, pedágios em rodovias ou o custo de abertura de uma nova rota.
É possível comparar a formulação matemática entre um PT e um PTCF com origens e destinos, destacando as diferenças entre os mesmos, começando pela função objetivo (1), que no PTCF apresenta o acréscimo do custo fixo associado à abertura ou não da ligação de para , definido pela variável binária .
O PT e PTCF devem estar equilibrados, ou seja, a quantidade total de oferta deve ser igual a quantidade total de demanda .
As restrições (2) e (3), comuns a ambos, garantem que não será excedida a capacidade de oferta em cada origem e que todos os destinos serão atendidos.
Para o PTCF, em relação ao PT, é adicionado o conjunto de restrições (4), onde , se implica que e haverá abertura da rota. No caso de variáveis degeneradas e variáveis não básicas temos que . O conjunto de restrições (6) também é acrescentado ao PTCF e indica que as variáveis são binárias (abertura ou não da rota).
No PTCF o conjunto de restrições (4), juntamente com (1) e (5), forçam que se e somente se e por outro lado, se e somente se .
Sendo assim, a formulação matemática para o PTCF é dada por:
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
As aplicações para o PTCF, segundo [3], foram desenvolvidas em diferentes áreas, tais como a alocação de veículos lançadores para missões espaciais, a localização de usinas nucleares, a gestão de resíduos sólidos, a alocação de professores, problemas de controle de estoque, sequenciamento de horário e designação de pessoal.
Desde a sua formulação, em 1951, métodos exatos e heurísticos foram propostos. Muitos deles destinados a pequenos problemas ou apenas mostrando sua aplicação para exemplos didáticos. Yousefi et al. [4] apresenta uma revisão de literatura relacionada ao PTCF relacionando os autores com o tipo de método utilizado.
A pesquisa de Hirsch and Dantzig [5] ressalta que o PTCF é do tipo NP-hard. Na literatura corrente, trabalhos como o de [6,7,8,9,10,11,12] trouxeram avanços para o PTCF, sendo que todos apresentaram resultados para a mesma base de dados utilizada por Sun et al. [6], com problemas de dimensão até e
O PTCF, como já mencionado, pode ser aplicado não só a problemas específicos de transporte, mas também em outras áreas. Othman et al. [13] afirma que os mercados competitivos obrigam as empresas a reduzirem os custos mantendo o nível de serviço ao cliente. Contudo, muitas vezes esperar uma resposta exata, pode levar muito tempo, tal como ocorre na resolução do PTCF. O presente artigo visa apresentar uma matheurística para a resolução do PTCF, pois dessa forma, em vários casos, a substituição de um método exato por uma heurística possibilita encontrar um resultado próximo do valor ótimo global em um período de tempo menor.
Segundo [14], os intervalos de valores atribuídos ao custo fixo, quando comparados ao custo unitário na sua função objetivo, interferem no desempenho do tempo computacional. Os problemas da literatura desenvolvidos por [6] apresentam estas características e serviram de base para as pesquisas posteriores relacionadas ao PTCF. Sendo assim, desenvolver e implementar computacionalmente uma heurística para a resolução dos problemas clássicos do PTCF tem o intuito de minimizar o tempo para a obtenção da resposta.
2. Metodologia
Os métodos a seguir são baseados nos trabalhos de [3,15,16,17] e os problemas da literatura adotados, que foram criados por Sun et al. [6].
2.1. Método de Balinski
O trabalho de Balinski [15] resume-se em relaxar o PTCF e o resolvê-lo como um PT. Essa relaxação na função objetivo envolve o valor do custo unitário de transporte , o custo fixo e o menor valor entre a oferta ( e a demanda (), tal que .
No método em questão, e isolando nessa equação e substituindo na equação da função objetivo resulta em . Uma nova matriz é então gerada e denominada Matriz de Balinski - MB.
A MB é utilizada para resolver o PT e como consequência, obter uma solução aproximada para o PTCF.
2.2. Método de Silva e Loch
O trabalho de Silva [16] trata de PT do tipo Esparso3 e a abordagem utilizada em sua pesquisa, que representa a solução de um PT em árvore, mostra que nessa estrutura, comparada ao quadro, é mais fácil identificar o ciclo ao inserir uma nova variável na base.
No método MODI4, como pode ser visto em [18,19], os cálculos de alguns dos novos valores de custos atualizados permanecem inalterados de uma iteração para a outra. A identificação de um ciclo é facilmente visualizada por meio da estrutura em árvore ao invés do quadro. Observando esse fato na estrutura de árvore, o novo método de Loch [3] para recálculo dos custos atualizados trouxe uma nova abordagem: não era preciso recalcular todos os custos.
Outra contribuição do trabalho de Loch [3] refere-se a uma proposta de Melhoria da Solução (MSL) no processo de resolução do PTCF onde a ideia é armazenar um conjunto de informações para cada variável não básica (vnb), analisando as alterações provocadas caso venha a entrar na base no próximo pivoteamento. Essas informações são:
- = o arco que sai da base;
- = o custo atualizado;
- = o valor que a variável assume caso torne-se básica;
- = o aumento no custo fixo;
- = redução no custo fixo;
- = variação total no valor da função objetivo caso a variável entre na base.
Cada célula associada a uma variável não básica armazena esse conjunto de seis informações. O processo de melhoria ocorre enquanto existir , ou seja, enquanto a solução ainda não é um minimizador local. O fluxograma apresentado na Figura 1 mostra como funciona essa dinâmica para o MSL.
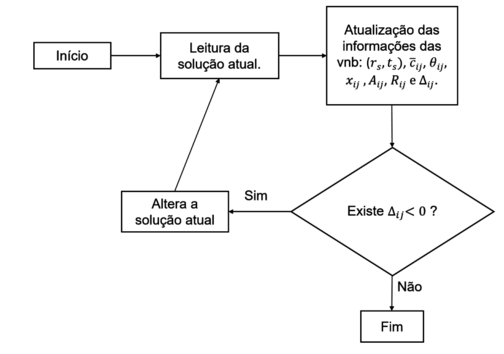
|
| Figura 1. Fluxograma para MSL (Fonte: os autores) |
2.3. Base de dados
A pesquisa de Sun et al. [6] foi responsável por gerar um conjunto de testes voltados ao PTCF. Essa base de dados também foi utilizada por outros pesquisadores como [7,8,9]. O enfoque dessa pesquisa será essa base de dados, que passa a ser denominada “BaseSun”.
A BaseSun está subdividida em uma classe de problemas fáceis e outra de problemas difíceis. Os problemas fáceis contemplam doze instâncias de dimensões variadas ( , , , , , ) em que as demanda totais são de , , , , , , respectivamente. Por outro lado, os problemas difíceis, incluem oito tipos de problemas, classificados de A a H. Para cada tipo, existem problemas com dimensões e demanda total de para cada um deles (totalizando dessa forma, 120 instâncias). Os custos unitários de transporte são valores inteiros que pertencem ao intervalo [3,8]. As diferenças entre os tipos de problemas estão na variação de valores do custo fixo, conforme apresentado no Quadro 1.
Os problemas da BaseSun foram utilizados em um trabalho desenvolvido em [20], onde testes computacionais são realizados no intuito de comparar o desempenho dos solvers Gurobie CPLEXpara essa base de dados da literatura, constatando que o solver Gurobi apresentou um desempenho superior para obtenção de uma melhor resposta da função objetivo, em um tempo pré-fixado de segundos.
| Tipo | Variação do Custo Fixo | |
| Limite inferior | Limite superior | |
| A | 50 | 200 |
| B | 100 | 400 |
| C | 200 | 800 |
| D | 400 | 1600 |
| E | 800 | 3200 |
| F | 1600 | 6400 |
| G | 3200 | 12800 |
| H | 6400 | 25600 |
Buson et al. [9] alertam que existe um erro tipográfico em uma das tabelas de [7] em um problema do TIPO C, mais especificamente o N320-A, onde o valor da função objetivo correto é e não . Sendo assim, esse valor foi corrigido nessa pesquisa.
Outro detalhe percebido é a duplicidade de três problemas da BaseSun, alocados no Tipo F (N350C e N350D), Tipo G (N360C e N360D) e Tipo H (N370C, N370D). Os problemas especificados entre parênteses, após cada tipo mencionado, são iguais. Mesmo assim, foi mantida essa duplicidade na pesquisa para não alterar as comparações entre os métodos.
2.4. Método de Kowalski
O método heurístico de Kowalski et al. [17] é definido como simples e rápido para PTCF de pequenas dimensões. Os autores sugerem que ele pode ser aplicado para grandes problemas.
Em seu trabalho Kowalski et al. [17] apresentam um experimento computacional para uma solução com variáveis degeneradas. Porém, na implementação computacional dessa pesquisa ao usar o Método de Loch, para resolver o PTCF relaxado, o cuidado para tratar uma solução degenerada já é realizado. Sendo assim essa proposta para uma solução degenerada não foi adotada no desenvolvimento desse trabalho.
O Método de Kowalski, apresentado anteriormente e aqui denominado KOWA, foi implementado para realizar testes com a BaseSun, já que em seu artigo o autor apresenta apenas a aplicação para um problema didático. Os passos desse método são apresentados resumidamente no Quadro 2.
Início KOWA
Fim KOWA |
3. Mathaeurística proposta
Ao longo da trajetória histórica do PTCF [6] aplicaram a Busca Tabu - BT e [7] utilizaram a técnica Ghost Image Process - GIP para os problemas da literatura, aqui denominados BaseSun. Comparados com o solver Cplex, ambos os autores encontraram resultados satisfatórios (com pequenas diferenças entre a solução encontrada e o limitante inferior) para esses problemas.
[8] também realizou testes em parte da BaseSun utilizando as heurísticas CORE-2 e CORE-3. Nos problemas do tipo A e B foram aplicados CORE-2 e CORE-3 e nos do tipo C e D apenas CORE-2. A justificativa dada para restringir os testes foi a de que o método é adequado apenas para problemas com uma razão entre o custo unitário e o custo fixo que não seja excessivamente alta, no caso os do tipo A até D. Aplicada aos outros tipos de E até H, os parâmetros da heurística CORE-2 necessitavam ser examinados, pois mostraram-se ineficientes. Além disso, a enumeração em CORE-3 atingiu pouca melhoria.
De acordo com o objetivo do presente artigo, buscou-se desenvolver um método heurístico para resolver o PTCF. A BaseSun será o conjunto de problemas a ser testado, para posteriormente servir de comparação com os outros métodos do estado da arte.
A medida em que o método era implementado, o mesmo foi sofrendo alterações e a cada mudança uma melhoria na obtenção do valor da função objetivo foi observada. Essas alterações deram origem às heurísticas HEUR-1, HEUR-2 e HEUR-3 que serão apresentadas na sequência. Os resultados computacionais encontrados para cada uma, aplicados a BaseSun, serão informados no próximo capítulo.
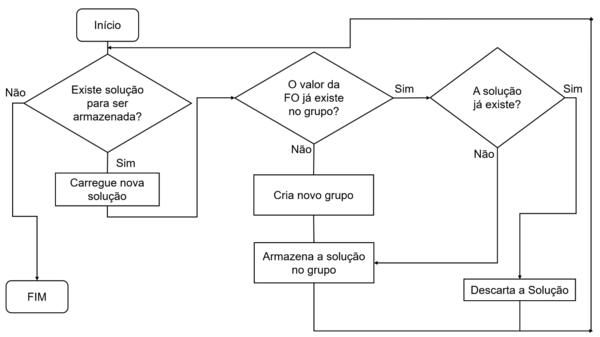
É necessário mencionar previamente que, em todos os métodos implementados neste artigo, o teste para o armazenamento de uma solução encontrada para o PTCF, denominado “TesteSol”, realiza uma otimização no modo de procura, ao verificar se a solução atual já é conhecida. Todas as soluções obtidas são armazenadas em grupos distintos cuja característica é ter o mesmo valor da função objetivo (FO). Ao invés de procurar todas as soluções em uma única lista, primeiramente o valor da FO é localizado nos grupos. Se o valor da FO não existe, a solução é nova e será armazenada, criando neste caso, um novo grupo para esse valor e guardando a solução. Agora, se o valor da FO já existe em um grupo, a procura pela solução que gerou esta resposta é feita apenas neste local específico, para verificar se é conhecida ou não. Se for, a solução é descartada, caso contrário é armazenada. O fluxograma da Figura 2 detalha este procedimento.
| Figura 2. Fluxograma para testesol (Fonte: os autores) |
3.1 HEUR-1
Tendo como ponto de partida os métodos desenvolvidos por Balinski [15] e a proposta para o PTCF feita por Loch [3], uma primeira heurística foi desenvolvida – HEUR-1. Para isso, foram realizadas perturbações randômicas utilizando como solução inicial o método do Custo Mínimo (CM) adaptado ao Método de Balinski (CMBAL). Durante um tempo pré-fixado de 120 segundos, o MSL foi utilizado e valores aleatórios eram gerados para forçar uma variável a entrar na base, a cada solução nova, aqui denominado Perturbação Randômica (PR). Dessa forma, as respostas para a função objetivo passavam pelo TesteSol. O Quadro 3 apresenta o pseudocódigo para o método HEUR-1.
| Início HEUR-1
Obter solução básica inicial - CMBAL Enquanto tempo < 120s MSL (Resolução do PT) PR TesteSol Fim enquanto Fim HEUR-1 |
3.2 HEUR-2
A heurística– HEUR-2, foi gerada retirando-se da HEUR1 a PR e provocando uma pequena alteração no método de Balinski. Essa mudança gerou uma melhoria no valor da função objetivo para os problemas de dimensões menores da BaseSun, mas por outro lado, o resultado foi pior para problemas de maiores dimensões.
A alteração no método de Balinski é pequena e consiste em agregar ao valor do custo unitário de transporte () a quantidade de vezes em que a variável foi básica (aqui denominada ), de modo que essa alteração possa penalizar as variáveis básicas, forçando a entrada de outras que ainda não estiveram na base, gerando a expressão (7):
|
|
(7) |
O Quadro 4 apresenta o pseudocódigo para HEUR-2.
| Início HEUR-2
Obter solução básica inicial por CMBAL Enquanto tempo < 120s Método Balinski Modificado MSL (Resolução do PT) TesteSol Fim enquanto Fim HEUR-2 |
3.3. KOWOLI
No desenvolvimento do método original de Kowalski et al. [17], algumas mudanças na implementação foram realizadas ao longo dessa pesquisa, e esta variação de KOWA foi denominada KOWOLI.
As alterações são pequenas, sendo elas:
- Encontrar o menor valor de custo fixo na linha e subtrair de todos os custos fixos na respectiva linha;
- Ao desbloquear a interseção no processo de ramificação, atribui-se o valor muito alto ao custo fixo nesse ponto.
O pseudocódigo do Quadro 5 apresenta o método KOWOLI com destaque para o que foi alterado, com relação ao método original KOWA.
Início KOWOLI
* Encontrar o Mín (fij)na linha i e subtrair este valor de todos os fij na linha i.
* Valores originais devolvidos na ramificação com interseção = ∞
Fim KOWOLI |
3.4. HEUR-3
Após as variações entre HEUR-1 e HEUR-2; a implementação de KOWA e a variação para KOWOLI, chegou-se ao método heurístico final deste trabalho – HEUR-3.
Para obter uma Solução Básica Factível Inicial - SBFI, o método HEUR-3 utiliza CMBAL. Dentro de um tempo pré-fixado, em segundos, utiliza-se uma rotina baseada em KOWOLI e aliada ao MSL, que aborda o PTCF em uma estrutura em árvore baseado em [16] e resolve o problema relaxado utilizando o método de LOCH. As soluções encontradas são verificadas em TesteSol. O Quadro 6 apresenta o pseudocódigo para o método HEUR-3.
| Início HEUR-3
Obter SBFI por CMBAL Enquanto tempo < 120s KOWOLI MSL TesteSol Fim enquanto Fim HEUR-3 |
Vale ressaltar que os métodos HEUR-1, HEUR-2, KOWA e HEUR-3 foram implementados em linguagem Visual Basic 2013 a partir da plataforma do Visual Studio Ultimate 2013 [21], e processados em uma máquina Dell Inspiron 15, Série 5000 com 8GB SSD, memória RAM de 16GB e processador Intel Core i7.
4. Resultados computacionais
A técnica GIP, implementada por [7] mostra um resultado muito eficiente para os valores da função objetivo encontrados para a BaseSun até o momento, sendo superior à técnica de BT de [6].
O trabalho de Buson et al. [9] foi superior a GIP, mas as comparações apresentadas estão em torno da média por tipo de problema (A – H), não sendo possível comparar cada problema individualmente. Dessa forma, tal comparativo não foi incluído nessa pesquisa.
Cabe ressaltar que, no que diz respeito ao uso de um solver durante a implementação dos métodos da literatura e aos métodos desenvolvidos:
- O método BT, de Sun et al. [6], é uma heurística pura, sem uso de solver em sua rotina;
- A técnica GIP, proposta por [7], e os métodos CORE-2 e CORE-3 de Aguado [8] utilizam o solver Cplex em sua rotina;
- O método RCLIS de [9], faz uso do Cplex nas rotinas ; e ;
- As heurísticas HEUR-1, HEUR-2, KOWA E HEUR-3 são puras, sem uso de um solver em sua rotina.
Esta seção está dividida em duas partes. A primeira compara as heurísticas desenvolvidas para avaliar o seu desempenho aplicado aos problemas da literatura. Definida a melhor heurística, esta será comparada na segunda parte às técnicas do estado da arte: BT, CORE-2 e CORE-3, e GIP, além de um comparativo com o solver Gurobi.
(3) Um modelo do problema de transporte pode ser denso ou esparso. No caso de ser denso, possui todos os custos entre origens e destinos conhecidos e limitados, ou seja, cada origem m está conectada a um destino n. No caso esparso, algumas ou todas as origens se conectam a um número menor de destinos.
(4) Baseado em [3], nesse método, as variáveis duais são utilizadas para calcular o custo atualizado de cada variável não-básica, escolhendo-se a de custo atualizado mais negativo para entrar na base e, apenas para essa variável, identifica-se o
4.1 Comparativo entre os métodos desenvolvidos
Com o objetivo de verificar qual das heurísticas implementadas nessa pesquisa foi superior, nesse primeiro momento, HEUR-1, HEUR-2, KOWA e HEUR-3 são comparadas entre si e, juntamente com elas, o solver Gurobi.
Um estudo desenvolvido por Oliveira et al. [22] compara os solvers Gurobi [23] e CPLEX - [24], para a resolução da BaseSun, foi realizado, pré-fixando o tempo em , , , e . A resolução em mostrou-se eficaz, apesar de não atingir a otimalidade do problema, pois para tempos superiores a esse, o valor do GAP para cada problema não sofria alteração significativa. Sendo assim, o tempo máximo de foi o critério de parada para as heurísticas desenvolvidas nessa pesquisa.
Os métodos HEUR-1, HEUR-2, KOWA, HEUR-3 e o solver Gurobi foram aplicados aos problemas fáceis da BaseSun, em tempo máximo de segundos, e apresentaram os resultados conforme mostrado na Tabela 1.
Os valores da Tabela 1 mostram que em problemas de dimensões até , as heurísticas HEUR-2, KOWA, HEUR-3 e o solver Gurobi atingem o valor ótimo da função objetivo. Para os 4 problemas restantes, de dimensões e , HEUR-3 apresentou o melhor resultado em 3 problemas.
A Tabela 2 reúne todos os resultados para os tipos de problemas de A até H, destacando em negrito o melhor resultado. Observa-se que entre os 120 problemas da BaseSun, HEUR-3 obteve o melhor resultado em 114 problemas, o que corresponde a aproximadamente 95% dos casos, e isto inclui a comparação com o solver Gurobi, que foi superior em apenas 5 instâncias.
| Nome e tamanho dos problemas | Valor Função Objetivo | |||||
| HEUR-1 | HEUR - 2 | KOWA | HEUR-3 | GUROBI | ||
| N104 | 10 x 10 | 40,264 | 40,258 | 40,258 | 40,258 | 40,258 |
| N107 | 42,030 | 42,029 | 42,029 | 42,029 | 42,029 | |
| N204 | 15 x 15 | 54,502 | 54,502 | 54,502 | 54,502 | 54,502 |
| N207 | 53,606 | 53,596 | 53,596 | 53,596 | 53,596 | |
| N304 | 10 x 20 | 56,391 | 56,366 | 56,366 | 56,366 | 56,366 |
| N307 | 49,742 | 49,742 | 49,742 | 49,742 | 49,742 | |
| N504 | 10 x 30 | 57,205 | 57,130 | 57,130 | 57,130 | 57,130 |
| N507 | 52,977 | 52,903 | 52,903 | 52,903 | 52,903 | |
| N1004 | 50 x 50 | 165,633 | 165,192 | 163,653 | 163,658 | 163,688 |
| N1007 | 162,620 | 163,602 | 162,288 | 162,247 | 162,264 | |
| N2004 | 30 x 100 | 104,665 | 107,650 | 104,103 | 104,014 | 104,112 |
| N2007 | 105,468 | 107,313 | 104,242 | 104,231 | 104,172 | |
Com relação ao solver Gurobi, é importante ressaltar que:
- Foi utilizado em suas configurações default;
- O tempo limite de processamento de ;
- Na tentativa de implementar um método híbrido, a partir de uma SBFI, utilizando o resultado obtido em HEUR-3, o solver Gurobi não apresentou, em geral, melhorias no valor da função objetivo. E quando houve melhorias, essas foram muito pequenas, causando pouca variação do GAP, mesmo quando alguns parâmetros do solver eram alterados.
| Tipo | Nome | Heur 1 | Heur 2 | Gurobi | KOWA | Heur-3 | Tipo | Nome | Heur 1 | Heur 2 | Gurobi | KOWA | Heur-3 | Tipo | Nome | Heur 1 | Heur 2 | Gurobi | KOWA | Heur-3 | Tipo | Nome | Heur 1 | Heur 2 | Gurobi | KOWA | Heur-3 |
| A | N3000 | 169,80 | 173,19 | 168,28 | 168,13 | 168,10 | B | N3100 | 181,63 | 186,29 | 179,38 | 179,33 | 179,08 | C | N3200 | 204,64 | 213,45 | 200,18 | 200,49 | 200,32 | D | N3300 | 251,59 | 260,03 | 241,25 | 241,68 | 240,30 |
| N3001 | 168,72 | 171,84 | 166,95 | 166,93 | 166,76 | N3101 | 180,02 | 184,07 | 178,15 | 178,17 | 177,98 | N3201 | 205,46 | 210,68 | 199,99 | 200,13 | 199,82 | N3301 | 251,16 | 259,68 | 241,25 | 241,94 | 240,19 | ||||
| N3002 | 169,45 | 171,98 | 167,98 | 167,93 | 167,81 | N3102 | 181,45 | 186,13 | 179,29 | 179,13 | 178,93 | N3202 | 206,06 | 210,91 | 201,43 | 201,04 | 200,88 | N3302 | 246,90 | 254,75 | 243,13 | 241,92 | 240,97 | ||||
| N3003 | 169,71 | 173,45 | 168,62 | 168,66 | 168,42 | N3103 | 182,17 | 185,94 | 179,70 | 179,58 | 179,12 | N3203 | 202,64 | 207,38 | 200,16 | 200,68 | 199,63 | N3303 | 244,41 | 254,80 | 239,38 | 238,66 | 238,05 | ||||
| N3004 | 169,37 | 174,02 | 167,54 | 167,48 | 167,31 | N3104 | 183,03 | 184,71 | 179,95 | 179,71 | 179,45 | N3204 | 207,07 | 211,35 | 202,21 | 202,22 | 201,80 | N3304 | 249,37 | 257,03 | 245,60 | 242,68 | 242,43 | ||||
| N3005 | 169,43 | 171,98 | 167,84 | 167,96 | 167,85 | N3105 | 181,70 | 185,76 | 178,75 | 178,76 | 178,42 | N3205 | 204,51 | 208,18 | 200,18 | 199,77 | 199,58 | N3305 | 249,01 | 256,07 | 241,07 | 240,55 | 239,75 | ||||
| N3006 | 167,20 | 170,94 | 166,06 | 165,91 | 165,83 | N3106 | 180,40 | 184,07 | 176,89 | 176,92 | 176,49 | N3206 | 203,19 | 207,50 | 198,22 | 198,03 | 197,42 | N3306 | 245,05 | 254,58 | 239,37 | 238,23 | 237,02 | ||||
| N3007 | 169,50 | 172,31 | 167,55 | 167,39 | 167,38 | N3107 | 181,15 | 185,33 | 178,51 | 178,32 | 178,14 | N3207 | 203,63 | 211,46 | 199,57 | 199,02 | 198,66 | N3307 | 248,78 | 252,91 | 238,01 | 237,99 | 236,81 | ||||
| N3008 | 167,01 | 170,51 | 165,90 | 165,91 | 165,70 | N3108 | 179,93 | 183,81 | 176,80 | 176,77 | 176,34 | N3208 | 200,14 | 211,18 | 197,69 | 197,88 | 197,26 | N3308 | 243,71 | 259,36 | 237,44 | 236,54 | 235,76 | ||||
| N3009 | 168,66 | 171,55 | 167,43 | 167,35 | 167,23 | N3109 | 180,89 | 184,94 | 178,14 | 178,14 | 177,79 | N3209 | 202,74 | 208,98 | 199,42 | 198,92 | 198,86 | N3309 | 246,59 | 254,20 | 240,71 | 240,14 | 239,97 | ||||
| N300A | 168,80 | 172,17 | 167,55 | 167,42 | 167,36 | N310A | 182,66 | 186,79 | 179,35 | 179,28 | 179,09 | N320A | 205,14 | 209,54 | 201,89 | 201,48 | 200,95 | N330A | 253,50 | 258,70 | 243,10 | 242,99 | 242,46 | ||||
| N300B | 170,31 | 173,38 | 168,71 | 168,60 | 168,59 | N310B | 183,35 | 186,04 | 179,98 | 180,00 | 179,69 | N320B | 207,38 | 211,99 | 202,02 | 202,21 | 201,23 | N330B | 256,54 | 259,15 | 245,22 | 243,37 | 241,65 | ||||
| N300C | 166,74 | 171,42 | 165,38 | 165,53 | 165,49 | N310C | 177,88 | 182,13 | 176,04 | 176,57 | 176,19 | N320C | 202,23 | 208,42 | 197,86 | 197,36 | 196,99 | N330C | 245,72 | 256,88 | 238,88 | 237,55 | 236,94 | ||||
| N300D | 167,73 | 171,46 | 166,39 | 166,42 | 166,31 | N310D | 179,61 | 184,73 | 177,70 | 177,46 | 177,31 | N320D | 203,42 | 210,73 | 199,60 | 199,20 | 198,76 | N330D | 247,94 | 257,86 | 240,06 | 238,30 | 237,58 | ||||
| N300E | 172,07 | 175,81 | 169,67 | 169,55 | 169,47 | N310E | 182,38 | 188,57 | 180,34 | 180,33 | 179,94 | N320E | 206,48 | 211,65 | 201,81 | 200,97 | 200,77 | N330E | 246,42 | 254,22 | 240,25 | 240,69 | 240,55 | ||||
| Tipo | Nome | Heur 1 | Heur 2 | Gurobi | KOWA | Heur-3 | Tipo | Nome | Heur 1 | Heur 2 | Gurobi | KOWA | Heur-3 | Tipo | Nome | Heur 1 | Heur 2 | Gurobi | KOWA | Heur-3 | Tipo | Nome | Heur 1 | Heur 2 | Gurobi | KOWA | Heur-3 |
| E | N3400 | 327,74 | 340,36 | 318,01 | 316,36 | 314,37 | F | N3500 | 484,83 | 490,33 | 463,12 | 458,42 | 455,70 | G | N3600 | 758,67 | 766,61 | 742,31 | 732,17 | 724,54 | H | N3700 | 1336,91 | 1336,00 | 1281,68 | 1260,67 | 1243,52 |
| N3401 | 324,49 | 330,68 | 317,04 | 315,40 | 312,85 | N3501 | 479,46 | 493,50 | 466,57 | 457,82 | 453,48 | N3601 | 760,98 | 772,05 | 741,09 | 732,60 | 721,17 | N3701 | 1318,40 | 1332,23 | 1283,39 | 1265,82 | 1241,52 | ||||
| N3402 | 327,87 | 338,34 | 320,99 | 318,01 | 316,92 | N3502 | 476,29 | 494,94 | 464,08 | 462,23 | 455,12 | N3602 | 757,92 | 772,66 | 741,34 | 730,80 | 721,88 | N3702 | 1307,13 | 1329,87 | 1269,01 | 1261,58 | 1226,74 | ||||
| N3403 | 318,60 | 320,79 | 314,16 | 310,85 | 309,62 | N3503 | 460,19 | 472,10 | 452,06 | 452,89 | 443,93 | N3603 | 740,70 | 749,66 | 730,71 | 730,57 | 707,11 | N3703 | 1275,61 | 1295,35 | 1262,47 | 1242,35 | 1217,45 | ||||
| N3404 | 332,87 | 342,06 | 322,01 | 319,82 | 318,06 | N3504 | 479,79 | 486,90 | 469,10 | 465,52 | 460,39 | N3604 | 765,34 | 800,08 | 751,69 | 741,68 | 727,92 | N3704 | 1344,07 | 1340,18 | 1302,56 | 1274,28 | 1257,37 | ||||
| N3405 | 327,68 | 339,34 | 318,46 | 318,92 | 316,72 | N3505 | 488,04 | 498,98 | 467,83 | 458,83 | 453,01 | N3605 | 748,47 | 770,11 | 736,29 | 735,09 | 725,68 | N3705 | 1299,31 | 1369,40 | 1294,04 | 1277,73 | 1248,30 | ||||
| N3406 | 322,75 | 335,63 | 316,48 | 312,77 | 310,31 | N3506 | 465,91 | 484,53 | 458,87 | 452,78 | 451,21 | N3606 | 741,65 | 775,21 | 737,73 | 727,35 | 714,36 | N3706 | 1330,96 | 1335,46 | 1284,53 | 1287,73 | 1241,96 | ||||
| N3407 | 318,22 | 324,07 | 312,14 | 309,80 | 307,74 | N3507 | 465,51 | 479,31 | 451,82 | 447,67 | 443,77 | N3607 | 731,53 | 751,27 | 724,37 | 712,47 | 706,82 | N3707 | 1296,31 | 1303,39 | 1247,30 | 1239,99 | 1213,07 | ||||
| N3408 | 325,28 | 330,80 | 312,40 | 314,16 | 309,07 | N3508 | 475,84 | 493,68 | 459,49 | 457,64 | 452,44 | N3608 | 748,17 | 781,37 | 741,93 | 723,23 | 717,07 | N3708 | 1329,90 | 1350,56 | 1274,18 | 1282,09 | 1238,91 | ||||
| N3409 | 331,60 | 336,46 | 321,47 | 313,90 | 314,89 | N3509 | 476,10 | 485,84 | 464,74 | 458,91 | 455,08 | N3609 | 767,13 | 767,98 | 743,34 | 732,78 | 725,27 | N3709 | 1284,40 | 1338,70 | 1298,61 | 1252,32 | 1237,26 | ||||
| N340A | 336,18 | 337,97 | 325,13 | 322,10 | 319,02 | N350A | 478,71 | 495,44 | 470,78 | 465,61 | 462,13 | N360A | 774,93 | 785,01 | 750,14 | 745,68 | 738,06 | N370A | 1344,24 | 1352,75 | 1300,28 | 1298,25 | 1269,31 | ||||
| N340B | 333,66 | 336,23 | 321,98 | 322,74 | 318,65 | N350B | 479,09 | 489,30 | 465,95 | 467,97 | 461,68 | N360B | 776,95 | 813,13 | 756,73 | 742,08 | 729,23 | N370B | 1338,68 | 1383,86 | 1299,71 | 1274,25 | 1256,01 | ||||
| N340C | 328,70 | 336,29 | 315,72 | 312,45 | 310,64 | N350C | 479,59 | 486,30 | 460,66 | 459,73 | 455,72 | N360C | 767,12 | 793,30 | 740,09 | 737,28 | 728,74 | N370C | 1319,06 | 1333,81 | 1288,41 | 1259,26 | 1254,84 | ||||
| N340D | 323,35 | 331,02 | 316,34 | 313,07 | 311,70 | N350D | 477,72 | 486,30 | 460,66 | 459,73 | 455,72 | N360D | 754,82 | 793,30 | 740,09 | 737,28 | 728,74 | N370D | 1294,52 | 1333,81 | 1288,41 | 1259,26 | 1254,84 | ||||
| N340E | 335,04 | 338,20 | 317,17 | 316,52 | 313,76 | N350E | 473,43 | 496,04 | 462,54 | 461,91 | 459,91 | N360E | 758,69 | 765,70 | 742,64 | 731,95 | 724,61 | N370E | 1305,81 | 1327,27 | 1282,26 | 1255,57 | 1232,46 |
4.2. Comparativo entre os métodos da literatura
Tendo em vista que o método HEUR-3 foi superior aos demais implementados (HEUR-1, HEUR-2 e KOWA), nesta seção o mesmo será comparado com os trabalhos do estado da arte de [6,7,8]5 além do solver Gurobi.
Cabe ressaltar que HEUR-3 é uma heurística pura assim como a BT, diferente dos outros métodos que utilizam um solver em algum momento da rotina implementada.
Começando pelos doze problemas fáceis da BaseSun, a Tabela 3 indica que nos problemas de dimensões até , os métodos CORE-3, GUROBI E HEUR-3 atingem a melhor solução em todos os casos.
| Nome e tamanho dos problemas | Valor da Função Objetivo | ||||||
| BT | GIP | CORE-2 | CORE-3 | GUROBI | HEUR-3 | ||
| N104 | 40,258 | 40,258 | 40,258 | 40,258 | 40,258 | 40,258 | |
| N107 | 42,029 | 42,029 | 42,03 | 42,029 | 42,029 | 42,029 | |
| N204 | 54,502 | 54,502 | 54,578 | 54,502 | 54,502 | 54,502 | |
| N207 | 53,601 | 53,601 | 53,610 | 53,596 | 53,596 | 53,596 | |
| N304 | 56,391 | 56,366 | 56,366 | 56,366 | 56,366 | 56,366 | |
| N307 | 49,742 | 49,742 | 49,756 | 49,742 | 49,742 | 49,742 | |
| N504 | 57,130 | 57,130 | 57,152 | 57,130 | 57,130 | 57,130 | |
| N507 | 52,977 | 52,903 | 52,918 | 52,903 | 52,903 | 52,903 | |
| N1004 | 163,793 | 163,585 | 163,787 | 163,692 | 163,688 | 163,658 | |
| N1007 | 162,313 | 162,237 | 162,453 | 162,234 | 162,264 | 162,247 | |
| N2004 | 104,193 | 104,001 | 104,129 | 104,031 | 104,112 | 104,014 | |
| N2007 | 104,341 | 104,256 | 104,313 | 104,254 | 104,172 | 104,231 | |
A Tabela 4 condensa as informações do desempenho de HEUR-3 quando comparada separadamente com cada método, analisando entre os 12 problemas fáceis da BaseSun, quantos tiveram o desempenho igual (=), superior (>) ou inferior (<) a cada método ou ao solver.
| BT | CORE-2 | CORE-3 | GIP | GUROBI | ||||||||||
| = | > | < | = | > | < | = | > | < | = | > | < | = | > | < |
| 5 | 7 | 0 | 2 | 10 | 0 | 8 | 3 | 1 | 7 | 2 | 3 | 8 | 3 | 1 |
A Tabela 5 analisa todos os métodos em questão para todas as instâncias relacionadas aos tipos de problemas de A até H da BaseSun.
| Nome | BT | GIP | Core 2 | Core 3 | Gurobi | HEUR-3 | Tipo | Nome | BT | GIP | Core 2 | Gurobi | HEUR-3 | Tipo | Nome | BT | GIP | Gurobi | HEUR-3 | Tipo | Nome | BT | GIP | Gurobi | HEUR-3 |
| N3000 | 168,46 | 168,06 | 168,21 | 167,96 | 168,28 | 168,10 | C | N3200 | 201,44 | 199,61 | 200,67 | 200,18 | 200,32 | E | N3400 | 314,66 | 312,14 | 318,01 | 314,37 | G | N3600 | 713,87 | 713,20 | 742,31 | 724,54 |
| N3001 | 166,93 | 166,68 | 166,81 | 166,68 | 166,95 | 166,76 | N3201 | 199,72 | 198,84 | 199,80 | 199,99 | 199,82 | N3401 | 314,57 | 309,55 | 317,04 | 312,85 | N3601 | 722,66 | 709,80 | 741,09 | 721,17 | |||
| N3002 | 167,89 | 167,92 | 168,15 | 168,00 | 167,98 | 167,81 | N3202 | 201,73 | 199,99 | 201,59 | 201,43 | 200,88 | N3402 | 317,43 | 314,14 | 320,99 | 316,92 | N3602 | 716,00 | 704,51 | 741,34 | 721,88 | |||
| N3003 | 168,85 | 168,43 | 168,68 | 168,43 | 168,62 | 168,42 | N3203 | 200,65 | 199,34 | 200,06 | 200,16 | 199,63 | N3403 | 306,56 | 305,62 | 314,16 | 309,62 | N3603 | 702,93 | 698,86 | 730,71 | 707,11 | |||
| N3004 | 167,58 | 167,28 | 167,59 | 167,24 | 167,54 | 167,31 | N3204 | 201,75 | 201,09 | 201,41 | 202,21 | 201,80 | N3404 | 316,05 | 314,94 | 322,01 | 318,06 | N3604 | 731,66 | 719,95 | 751,69 | 727,92 | |||
| N3005 | 168,25 | 167,64 | 168,04 | 167,66 | 167,84 | 167,85 | N3205 | 199,58 | 198,76 | 199,96 | 200,18 | 199,58 | N3405 | 314,18 | 311,12 | 318,46 | 316,72 | N3605 | 710,33 | 701,14 | 736,29 | 725,68 | |||
| N3006 | 166,29 | 165,86 | 165,94 | 165,75 | 166,06 | 165,83 | N3206 | 198,31 | 197,38 | 198,19 | 198,22 | 197,42 | N3406 | 308,78 | 308,43 | 316,48 | 310,31 | N3606 | 715,81 | 711,07 | 737,73 | 714,36 | |||
| N3007 | 167,85 | 167,36 | 167,52 | 167,35 | 167,,546 | 167,38 | N3207 | 200,20 | 198,01 | 199,10 | 199,57 | 198,66 | N3407 | 305,78 | 305,44 | 312,14 | 307,74 | N3607 | 701,70 | 696,39 | 724,37 | 706,82 | |||
| N3008 | 165,94 | 165,58 | 165,97 | 165,89 | 165,90 | 165,70 | N3208 | 197,04 | 196,56 | 197,29 | 197,69 | 197,26 | N3408 | 312,40 | 308,18 | 312,40 | 309,07 | N3608 | 705,94 | 709,13 | 741,93 | 717,07 | |||
| N3009 | 167,21 | 167,19 | 167,32 | 167,08 | 167,43 | 167,23 | N3209 | 199,16 | 198,26 | 198,50 | 199,42 | 198,86 | N3409 | 315,37 | 312,06 | 321,47 | 314,89 | N3609 | 717,73 | 713,19 | 743,34 | 725,27 | |||
| N300A | 167,90 | 167,36 | 167,57 | 167,44 | 167,55 | 167,36 | N320A | 201,04 | 200,64 | 201,11 | 201,89 | 200,95 | N340A | 317,23 | 316,34 | 325,13 | 319,02 | N360A | 730,94 | 729,01 | 750,14 | 738,06 | |||
| N300B | 168,81 | 168,50 | 168,73 | 168,63 | 168,71 | 168,59 | N320B | 202,68 | 201,11 | 201,81 | 202,02 | 201,23 | N340B | 316,35 | 314,49 | 321,98 | 318,65 | N360B | 727,06 | 718,44 | 756,73 | 729,23 | |||
| N300C | 165,77 | 165,30 | 165,73 | 165,70 | 165,38 | 165,49 | N320C | 198,74 | 196,26 | 197,33 | 197,86 | 196,99 | N340C | 310,84 | 308,29 | 315,72 | 310,64 | N360C | 725,35 | 716,83 | 740,09 | 728,74 | |||
| N300D | 166,30 | 166,22 | 166,45 | 166,37 | 166,39 | 166,31 | N320D | 199,74 | 198,16 | 199,18 | 199,60 | 198,76 | N340D | 309,50 | 308,48 | 316,34 | 311,70 | N360D | 725,35 | 716,83 | 740,09 | 728,74 | |||
| N300E | 169,87 | 169,38 | 169,96 | 169,49 | 169,67 | 169,47 | N320E | 201,58 | 200,18 | 201,44 | 201,81 | 200,77 | N340E | 316,11 | 311,35 | 317,17 | 313,76 | N360E | 722,01 | 712,12 | 742,64 | 724,61 | |||
| Nome | BT | GIP | Core 2 | Core 3 | Gurobi | HEUR-3 | Tipo | Nome | GIP | Core 2 | Gurobi | HEUR-3 | Gurobi | Tipo | Nome | BT | GIP | Gurobi | HEUR-3 | Tipo | Nome | BT | GIP | Gurobi | HEUR-3 |
| N3100 | 179,67 | 179,02 | 179,08 | 178,93 | 179,38 | 179,08 | D | N3300 | 240,21 | 239,12 | 240,60 | 241,25 | 240,30 | F | N3500 | 457,66 | 450,80 | 463,12 | 455,70 | H | N3700 | 1253,88 | 1217,48 | 1281,68 | 1243,52 |
| N3101 | 178,52 | 177,86 | 178,32 | 177,76 | 178,15 | 177,98 | N3301 | 241,43 | 238,57 | 240,41 | 241,25 | 240,19 | N3501 | 454,37 | 445,77 | 466,57 | 453,48 | N3701 | 1237,13 | 1217,56 | 1283,39 | 1241,52 | |||
| N3102 | 179,02 | 179,01 | 179,27 | 179,27 | 179,29 | 178,93 | N3302 | 240,56 | 239,88 | 242,31 | 243,13 | 240,97 | N3502 | 451,04 | 449,37 | 464,08 | 455,12 | N3702 | 1230,01 | 1211,00 | 1269,01 | 1226,74 | |||
| N3103 | 179,28 | 179,02 | 179,37 | 179,23 | 179,70 | 179,12 | N3303 | 237,27 | 237,20 | 239,02 | 239,38 | 238,05 | N3503 | 439,55 | 438,73 | 452,06 | 443,93 | N3703 | 1213,14 | 1213,20 | 1262,47 | 1217,45 | |||
| N3104 | 179,83 | 179,23 | 179,68 | 179,68 | 179,95 | 179,45 | N3304 | 243,78 | 241,30 | 243,80 | 245,60 | 242,43 | N3504 | 458,95 | 454,24 | 469,10 | 460,39 | N3704 | 1247,73 | 1230,93 | 1302,56 | 1257,37 | |||
| N3105 | 178,71 | 178,16 | 178,84 | 178,76 | 178,75 | 178,42 | N3305 | 241,59 | 237,92 | 240,65 | 241,07 | 239,75 | N3505 | 452,51 | 448,01 | 467,83 | 453,01 | N3705 | 1242,73 | 1223,85 | 1294,04 | 1248,30 | |||
| N3106 | 177,30 | 176,55 | 177,12 | 176,72 | 176,89 | 176,49 | N3306 | 237,46 | 236,06 | 237,43 | 239,37 | 237,02 | N3506 | 447,53 | 442,90 | 458,87 | 451,21 | N3706 | 1240,64 | 1233,66 | 1284,53 | 1241,96 | |||
| N3107 | 178,57 | 177,90 | 178,44 | 178,27 | 178,51 | 178,14 | N3307 | 238,48 | 236,15 | 237,61 | 238,01 | 236,81 | N3507 | 443,38 | 439,88 | 451,82 | 443,77 | N3707 | 1213,41 | 1193,30 | 1247,30 | 1213,07 | |||
| N3108 | 176,54 | 176,27 | 176,96 | 176,86 | 176,80 | 176,34 | N3308 | 236,80 | 234,48 | 236,53 | 237,44 | 235,76 | N3508 | 450,75 | 447,13 | 459,49 | 452,44 | N3708 | 1220,71 | 1222,30 | 1274,18 | 1238,91 | |||
| N3109 | 178,08 | 177,60 | 178,07 | 177,84 | 178,14 | 177,79 | N3309 | 238,96 | 238,23 | 239,29 | 240,71 | 239,97 | N3509 | 453,42 | 451,45 | 464,74 | 455,08 | N3709 | 1220,42 | 1211,78 | 1298,61 | 1237,26 | |||
| N310A | 179,43 | 178,70 | 179,40 | 179,26 | 179,35 | 179,09 | N330A | 242,35 | 242,00 | 242,81 | 243,10 | 242,46 | N350A | 459,30 | 455,81 | 470,78 | 462,13 | N370A | 1255,48 | 1256,83 | 1300,28 | 1269,31 | |||
| N310B | 180,02 | 179,65 | 180,17 | 179,90 | 179,98 | 179,69 | N330B | 243,34 | 241,01 | 242,83 | 245,22 | 241,65 | N350B | 457,23 | 453,74 | 465,95 | 461,68 | N370B | 1243,27 | 1229,57 | 1299,71 | 1256,01 | |||
| N310C | 176,11 | 175,85 | 176,45 | 176,20 | 176,04 | 176,19 | N330C | 237,91 | 235,17 | 237,05 | 238,88 | 236,94 | N350C | 451,83 | 449,02 | 460,66 | 455,72 | N370C | 1243,69 | 1229,67 | 1288,41 | 1254,84 | |||
| N310D | 178,29 | 177,33 | 177,94 | 177,80 | 177,70 | 177,31 | N330D | 237,07 | 236,00 | 239,88 | 240,06 | 237,58 | N350D | 451,83 | 449,02 | 460,66 | 455,72 | N370D | 1243,69 | 1229,67 | 1288,41 | 1254,84 | |||
| N310E | 180,27 | 179,76 | 183,99 | 183,77 | 180,34 | 179,94 | N330E | 241,73 | 238,43 | 243,63 | 240,25 | 240,55 | N350E | 451,83 | 449,55 | 462,54 | 459,91 | N370E | 1219,00 | 1220,29 | 1282,26 | 1232,46 |
A Tabela 6 compara separadamente HEUR-3 com cada método, analisando se o desempenho foi superior (>) ou inferior (<).
Quando comparado ao método BT e CORE-2, HEUR-3 teve um desempenho superior na maioria dos problemas do Tipo A, B, C e D, ou seja, 80% superior com relação ao primeiro e 93% com relação ao segundo. Comparado ao método CORE-3, HEUR-3 foi superior em 70% dos casos.
HEUR-3 teve um desempenho inferior com relação ao método BT para os tipos de problemas E, F, G e H e para todos os tipos quando comparado à técnica GIP.
Os melhores resultados da função objetivo quando comparado ao solver Gurobi foi atingido por HEUR-3, que em todos os tipos de problemas foi superior, totalizando uma marca de aproximadamente 96% de eficácia.
| TIPO | BT | CORE-2 | CORE-3 | GIP | GUROBI | |||||
| > | < | > | < | > | < | > | < | > | < | |
| A | 13 | 2 | 15 | 0 | 8 | 7 | 4 | 11 | 13 | 2 |
| B | 14 | 1 | 15 | 0 | 13 | 2 | 3 | 12 | 14 | 1 |
| C | 11 | 4 | 12 | 3 | - | - | 0 | 15 | 14 | 1 |
| D | 10 | 5 | 14 | 1 | - | - | 0 | 15 | 14 | 1 |
| E | 7 | 8 | - | - | - | - | 0 | 15 | 15 | 0 |
| F | 2 | 13 | - | - | - | - | 0 | 15 | 15 | 0 |
| G | 3 | 12 | - | - | - | - | 0 | 15 | 15 | 0 |
| H | 3 | 13 | - | - | - | - | 0 | 15 | 15 | 0 |
| TOTAL | 63 | 58 | 56 | 4 | 21 | 9 | 7 | 113 | 115 | 5 |
5. Conclusão
No presente trabalho foi apresentado um método matheurístico para a resolução do Problema de Transporte com Custo Fixo. A utilização do algoritmo exato MSL faz com que o PT seja resolvido em tempo computacional muito baixo e possibilita que mais iterações sejam realizadas no algoritmo HEUR-3 para um tempo computacional de limite fixo. Destaca-se que com a utilização do MSL, tem-se a resolução exata do PT sem a necessidade de utilização de qualquer solver para resolução de PL’s.
Além disso, o procedimento computacional de verificar se cada solução já havia acontecido, faz com que os cálculos já realizados em outras iterações não precisem ser realizados novamente.
O PTCF é classificado como um problema do tipo NP-hard e encontrar a solução ótima, em alguns casos, nem sempre é possível. Não se trata apenas do tamanho do problema, mas sim da diferença entre o valor do custo unitário e o valor do custo fixo de transporte. A medida em que essa diferença se torna cada vez maior, a dificuldade em resolver o PTCF fica mais evidente e isso ocorre na BaseSun.
Desta forma, HEUR-3 apresenta soluções rápidas para o PTCF e que em algumas instâncias atinge resultados ainda melhores que os apresentados no estado da arte. Seu desempenho foi superior aos métodos híbridos CORE-2 em 93% e CORE-3 em 70% dos casos. Com relação ao solver Gurobi, atinge os melhores valores da função objetivo em 95,8% dos casos, ambos no tempo limite de 120 segundos. Por outro lado, ao ser comparado ao método BT, que assim como HEUR-3 é uma heurística pura, apresenta superioridade em 52,5% dos casos.
O bom desempenho de HEUR-3 frente ao Gurobi, CORE-2, CORE-3 e BT mostra que a sua utilização se torna viável, uma vez que alcançar uma resposta exata pode exigir muito do tempo computacional. Já a heurística permite atingir resultados próximos do ótimo em um período de tempo menor.
Referências
[1] Hitchcock F.L. The distribution of a product from several sources to númerous facilities. J. Math. Phys., 20:224–230, 1941.
[2] Hirsch W.M., Dantzig G.B. Notes on linear programming. Part XIX : the fixed charge problem. Randon Research, Santa Monica, CA, 1954.
[3] Loch G.V. Uma nova abordagem no processo iterativo de melhoria de solução na resolução do problema de transporte. Universidade Federal do Paraná, 2014.
[4] Yousefi K., Afshari A.J., Hajiaghaei-Keshteli M. Heuristic approaches to solve the fixed-charge transportation problem with discount supposition. J. Ind. Prod. Eng., 35(7):444–470, 2018.
[5] Hirsch W.M., Dantzig G.B. The fixed charge problem. Nav. Res. Logist. Q., 15(3):413–424, 1968.
[6] Sun M., Aronson J.E., McKeown P.G., Drinka D. A tabu search heuristic procedure for the fixed charge transportation problem. Eur. J. Oper. Res., 106(2–3):441–456, 1998.
[7] Glover F., Amini M., Kochenberger G. Parametric ghost image processes for fixed-charge problems: A study of transportation networks. J. Heuristics, 11(4):307–336, 2005.
[8] Aguado J.S. Fixed charge transportation problems: A new heuristic approach based on Lagrangean relaxation and the solving of core problems. Ann. Oper. Res., 172(1):45–69, 2009.
[9] Buson E., Roberti R., Toth P. A reduced-cost iterated local search heuristic for the fixed-charge transportation problem. Oper. Res., 14(1):1095–1106, 2014.
[10] Roberti R., Bartolini E., Mingozzi A. The fixed charge transportation problem: An exact algorithm based on a new integer programming formulation. Manage. Sci., 61(6):1275–1291, 2014.
[11] Mingozzi A., Roberti R. An exact algorithm for the fixed charge transportation problem based on matching source and sink patterns an exact algorithm for the fixed charge transportation problem based on matching source and sink patterns. Transp. Sci., 52(2):229–238, 2018.
[12] Zhao Y., Larsson T., Rönnberg E., Pardalos P.M. The fixed charge transportation problem : a strong formulation based on Lagrangian decomposition and column generation. J. Glob. Optim., 72(3):517–538, 2018.
[13] Othman Z., Delavar M.R.R., Behnam S., Lessanibahri S. Adaptive genetic algorithm for fixed-charge tranportation problem. Proc. Int. MultiConference Eng. Comput. Sci., I:96–101, 2011.
[14] Kennington J. The fixed-charge transportation problem: A computational study with a branch-and-bound code. AIIE Trans., 8(2):241–247, 1976.
[15] Balinski M.L. Fixed-cost transportation problems. Nav. Res. Logist. Q., 8(1):41–54, 1961.
[16] Silva T.C.L. Nova metodologia para resolução de problemas de transporte em casos esparsos. Universidade Federal do Paraná, 2012.
[17] Kowalski K., Lev B., Shen W., Tu Y. A fast and simple branching algorithm for solving small scale fixed-charge transportation problem. Oper. Res. Perspect., 1(1):1–5, 2014.
[18] Loch G.V., Silva A.C.L. A computational experiment in a heuristic for the fixed charge transportation problem. Int. Ref. J. Eng. Sci., 3(4):1–7, 2014.
[19] Loch G.V., Silva A.C.L. A computational study on the number of iterations to solve the transportation problem. Appl. Math. Sci., 8(92):4579–4583, 2014.
[20] Oliveira C.R.V., Schmidt C.E., Silva A.C.L. Análise da resolução do problema de transporte com custo fixo utilizando o Cplex e o Gurobi. In Anais do 1o Simpósio De Métodos Numéricos, 2016, pp. 188–191, 2016.
[21] Microsoft Corporation. Visual Basic 2013, 2014.
[22] Oliveira C.R.V., Schmidt C.E., Silva A.C.L. Comparação entre o desempenho de dois solvers de otimização na resolução de problemas de transporte com custo fixo. CMN 2017 Congress on Numerical Methods in Engineering, 3-5 July Valencia, Spain, pp. 1401–1410, 2017.
[23] GUROBI OPTIMIZATION INC. Gurobi Optimizer, 2016.
[24] IBM Corporation. Ibm ilog cplex interactive optimizer, 2012.
(5) A partir dos problemas de Tipo E, os métodos não foram testados no trabalho de [8], pois segundo o autor, haveria necessidade de alterar os parâmetros para obter bons resultados.
Document information
Published on 03/03/20
Accepted on 14/01/20
Submitted on 11/07/19
Volume 36, Issue 1, 2020
DOI: 10.23967/j.rimni.2020.01.005
Licence: CC BY-NC-SA license