(Created page with "<!-- metadata commented in wiki content <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> <big>'''DYNAMIC BUCKLING OF SHELL-LIKE STRUCTURES UN...") |
|||
| Line 3: | Line 3: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <big>'''DYNAMIC BUCKLING OF SHELL-LIKE STRUCTURES UNDER PRESSURES DUE TO AN EXPLOSION <span id="fnc-1"></span><span style="text-align: center; font-size: 75%;"> | + | <big>'''DYNAMIC BUCKLING OF SHELL-LIKE STRUCTURES UNDER PRESSURES DUE TO AN EXPLOSION <span id="fnc-1"></span><span style="text-align: center; font-size: 75%;"></span> '''</big></div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
Revision as of 21:16, 16 April 2019
Abstract: The nonlinear dynamic response and buckling of a simple, two degree of freedom system is investigated in this work under an impulsive load that simulates a nearby detonation-like explosion. The system includes force and moment springs in much the same way as membrane and bending effects develop in shell structures. The static response is first obtained to evaluate bifurcation states and nonlinear equilibrium paths including geometric imperfections. The dynamic problem is modeled using Lagrange equation of motion. The nonlinear dynamic response under impulsive load is next computed for the perfect configuration under increasing load levels. The presence of quasi-bifurcations is detected using stability coefficients based on second order derivatives of the total potential energy. For a given load level, it is found that one stability coefficient vanishes at the first maximum in the displacement versus time trajectory, at which the system passes through a state of zero velocity. This occurs for the same displacement configuration as in the static buckling mode. The results show that quasi-bifurcation loads thus obtained are independent of the amplitude of the geometric imperfection considered but display high sensitivity to changes in the membrane to bending stiffness ratio.
Keywords : Blast loads; dynamic buckling; nonlinear dynamics; structural stability; vibrations.
Resumen: La respuesta dinámica nolineal y el pandeo de un sistema simple de dos grados de libertad se estudia en este trabajo bajo carga impulsiva que simula una explosión cercana. El sistema incluye resortes de fuerza y momento que representan efectos membranales y flexionales tal como los que se desarrollan en cáscaras. Primero se obtiene la respuesta estatica para evaluar bifurcacion y trayectorias de equilibrio nolineales incluyendo imperfecciones geométricas. El problema dinamico se modela usando las ecuaciones de movimiento de Lagrange. Se computa la respuesta dinamica nolineal bajo cargas impulsivas para la configuracion perfecta bajo niveles crecientes de carga. Se detecta la presencia de cuasi-bifurcaciones mediante coeficientes de estabilidad basados en derivadas segundas de la energía. Para un nivel determinado de carga se encuentra que un coeficiente de estabilidad se anula en el primer maximo en la trayectoria de desplazamiento versus tiempo, en cuyo caso la velocidad es nula, lo cual ocurre para la misma configuracion de desplazamiento que en el modo de pandeo estatico. Los resultados demustran que las cargas de cuasi-bifurcacion son independiente de la imperfeccion geometrica considerada pero muestran gran sensibilidad frente a cambios en la relacion de rigideces membranal versus flexional.
Palabras clave: cargas de impacto; pandeo dinámico; dinámica nolineal; estabilidad estructural; explosiones.
INTRODUCTION
This paper investigates the dynamic buckling of a simple, two degree of freedom (DOF) model, under an impulsive load in order to explore the type of analysis that should be considered when addressing shell problems under blast pressures due to explosions. The specific area of interest of the authors is the response of tanks in oil refineries and oil storage facilities (Godoy 2016).
Explosions have been identified as the most frequent accidents affecting the oil industry. Interest in the behavior of oil storage tanks under blast loads caused by explosions has intensified during the last decade following the notorious accident at a tank farm located in Buncefield, UK (2008) and another one in Bayamon, Puerto Rico (Batista-Abreu and Godoy 2011). Evidence from field observations in Buncefield and other places where explosions occurred indicates that permanent damage takes place in thin walled structures, involving buckling and plasticity (Taveau 2011; Noret et al. 2012).
Understanding and modeling this class of problems requires computation of the nonlinear dynamic response under short duration impulsive loads. Although the nonlinear dynamic analysis of structures under impulsive loads is part of the state of the art in analytical and finite element approaches (Nayfeh 1979; Nayfeh and Balachandran 2004), such studies may sometimes be obscured by the complexity of the problem under consideration, whereas the interpretation of results and the evaluation of stability to identify dynamic buckling are topics still subject to discussion. Thus, to improve our understanding on the mechanics of behavior of shells under blast loads it may be convenient to perform studies on much simpler analogous structural systems, for which the response can be modeled using analytical tools.
The buckling of structures under step or impulsive loading has been the subject of research since the 1960s. Reviews of dynamic buckling criteria were presented for example in the books by Simitses (1990), Amabili (2008), and Kubiak (2013). By analogy with the static case, we shall define that a fundamental motion is the trajectory in a plot of a representative DOF with respect to time, computed at a given load level.
Two forms of dynamic buckling which are relevant to the present study have been identified in the literature:
(a) Instability in the mode of the fundamental motion, associated with large amplitude oscillations. Forced vibrations are investigated in this approach using nonlinear dynamics and a criterion is employed to assess the occurrence of unstable oscillations. The most common criterion employed in the literature was originally proposed by Budiansky and Roth (1962) and refined by Budiansky (1967), in which the dynamic response is first computed for various load levels and a plot of load versus amplitude of a representative DOF is constructed. By analogy with the static case, this plot is here called a pseudo-equilibrium path. Dynamic buckling is identified whenever there is a jump in the pseudo-equilibrium path, i.e. when a small increment in load causes a non-proportional (large) increment in transient displacements. This criterion was originally developed for step loads, but its application to impulsive loads (such as those associated with explosions) is less evident. Other forms of identification of this type of instability use a phase-space diagram (displacement versus velocity).
In some cases, it may be difficult to identify dynamic buckling from changes in displacements. For seismic excitation, Virella et al. (2006) considered changes in the slope of the pseudo-equilibrium path, so that dynamic buckling was said to occur whenever a small increment in load causes a large change in slope. This approach was subsequently employed for example by Buratti and Tavano (2014), and reviewed by Kubiak (2013).
Finally, Kounadis et al. (1989) studied a one DOF system together with an energy criterion to identify dynamic buckling.
(b) Instability in a mode which is orthogonal to the fundamental motion. This behavior is known as quasi-bifurcation from a fundamental trajectory and was originally identified by Lee (1977, 1981). As stated before, the motion of an undisturbed system shows oscillations in a mode here identified as the fundamental mode. But there are cases in which a second mode (which is orthogonal to the fundamental mode) grows at a critical time, leading to a quasi-bifurcation; at first this takes the form of small random oscillations, but a divergent motion is finally achieved. This quasi-bifurcation initially occurs in a mode with the same configuration as that provided by the static critical mode under the same load distribution. Further, Lee (1981) identified that the dynamic post-bifurcation mode may change in time.
The identification of a quasi-bifurcation state may be carried out either:
(i) By establishing conditions at which dynamic bifurcation should occur, such as in the works of Kounadis et al. (1989), and Simitses (1990). The relationship between static and dynamic instability was explored by Simitses (1990) who stated that when the dynamic response along the fundamental motion reaches a deflected configuration which is coincident with the configuration at static buckling, then a jump occurs into another equilibrium state.
(ii) By following stability indicators along the fundamental motion, such as frequencies of vibration, static eigenvalue problems, tangent matrix or, as in the present case, static stability coefficients. Various authors (Kroplin and Dinkle 1986; Kleiber et al. 1987; Burmeister and Ramm 1990; Kratzig and Eller 1992) implemented strategies to evaluate stability along a fundamental motion.
This paper focuses on quasi-bifurcation phenomena which is believed to occur in shells under impulsive loads due to an explosion and which may be instrumental in explaining the failure modes observed in oil industry infrastructure.
CASE-STUDY OF TWO DOF SYSTEM
To illustrate the dynamic instability process under an impulsive loading, a simple two DOF system is considered in this paper. This system was originally proposed by Croll and Walker (1972) to investigate static buckling, and a similar one was studied by Simitses (1990).
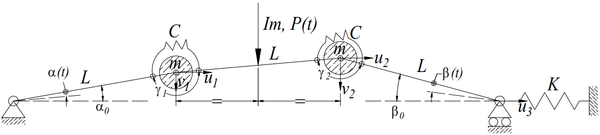
The system is shown in Figure 1, and is formed by three rigid bars of length L with an initial configuration at angles α0 and β0, and with rotational springs of modulus C and a line spring of modulus K. Notice that C and K are representative of bending and membrane action in a shell or arch structure but do not have a direct relationship with them. The mass of the system is assumed to be lumped at the hinges.
|
Two degrees-of-freedom describe the deformation of the structure under static or dynamic loads, and they can be chosen as the angular rotations at the outer hinges, α and β measured with respect to the original configuration of the system. Alternatively, vertical displacement (v1, v2), horizontal displacement (u1, u2), and angular (γ1, γ2) components may be defined at the central hinges as a function of α and β. Taking the inertial forces at u1 and u2into account may be a better choice to address problems of vibrations of shells (Amabili 2008).
The equations of motion are derived from the energy criterion due to Lagrange (see, for example, Baruh 1999)
|
(1) |
where qiare a set of generalized coordinates (in this case q1≡ α and q2≡ β) and Qk are the generalized forces. Dissipation is assumed to satisfy the condition
|
|
(2) |
The kinematic relations are given by
|
(3) |
The kinetic energy may be written as
|
|
(4) |
The total potential energy of the system results in the form
|
|
(5) |
where
|
(6) |
The system of nonlinear ordinary differential-algebraic equations of motion in terms of two unknown has been solved using the IDA algorithm, as available in the SUNDIALS package (Hindmarsh et al. 2005), which is part of Mathematica (2015).
For the static response, eq. (1) reduces to the principle of stationary potential energy for static equilibrium, that is
|
|
(7) |
As shown by Thompson and Hunt (1973), stability coefficients may be obtained from the second derivatives, and a state is said to be stable if the following stability coefficients are positive:
|
(8) |
where E indicates a static equilibrium condition and all derivatives are evaluated at the state being investigated.
NONLINEAR STATIC RESPONSE
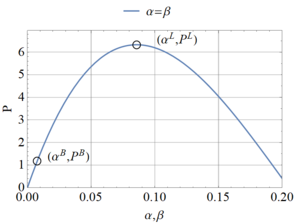
To perform computations, both static and dynamic, values have been assigned to variables by adopting L=1, C=1, K=1000, α0=β0=0.2rad, m=10. For this set of data, Croll and Walker (1972) obtained a static nonlinear equilibrium path (α=β), reaching an unstable limit point, and a bifurcation (unstable, symmetric) at a load well before the limit point. Using the present algorithm, the results indicate a limit point at PL=6.23 in a mode given by αL=βL=0.0857rad, whereas bifurcation is obtained at PB=1.18 with a configuration given by αB=βB=7.64×10-3rad (Figure 2). Static results are in agreement with those obtained by Croll and Walker (1972) using perturbation techniques.
Based on the results of the theory of elastic stability (Croll and Walker 1972, Thompson and Hunt 1973), it is possible to state that, under static load, the present system experiences unstable behavior at PB. Because there are no stable equilibrium states emerging from the bifurcation state, then the system will experience a dynamic jump in search of a stable equilibrium configuration; this dynamic jump is usually associated with large displacements and strains in real systems, with the consequence that plasticity and material failure usually occur before a new equilibrium state is reached.
|
A similar study may next be performed by including a geometric imperfection into the original configuration. Let
|
|
(9) |
be the imperfection parameter.
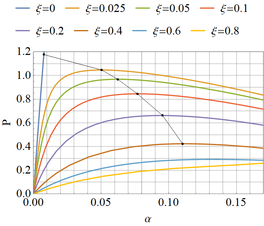
For a perfect configuration, β0 = α0 and ξ = 0. For non-zero values of ξ the Riks (1979) algorithm has been followed to compute the equilibrium paths. Results are plotted in Figure 3 in the form of P versus displacement α; for example, for ξ = 0.025 the equilibrium path departs from bifurcation behavior and a maximum is reached at αM= 0.05rad with PM= 1.04. Unstable behavior (leading to a descending path) is found to occur beyond the maximum, leading to a dynamic jump. For increasing values of ξ the maximum occurs at decreasing values of PM and increasing αM. Also, the values of αM are significantly larger than αB in this case.
Figure 4 shows the maximum load in Figure 3 (normalized with respect to PB) as a function of the imperfection, i.e. a static imperfection-sensitivity plot. Notice that there is a large drop in the maximum load that the system can attain for increasing values of ξ.
The equilibrium path ceases to display a maximum for values of ξ larger than 0.6, so that for values of ξ>0.6 the behavior is no longer associated with bifurcation but represents a set of monotonically increasing stable equilibrium states. The range of interest in our case is for systems that exhibit unstable behavior under static load, and this occurs for ξ<0.6.
|
|
NONLINEAR DYNAMIC RESPONSE OF THE PERFECT SYSTEM
The perfect system, ξ=0, is first considered in this section. Natural frequencies were computed, and the natural periods result in T1=2.22s (for vibrations in a symmetric mode) and T2=6.71s (for vibrations in an asymmetric mode).
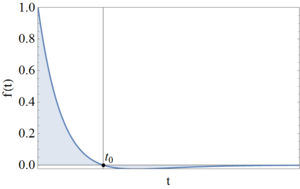
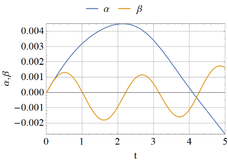
An impulsive loading is next represented using the following variation in time
|
(10) |
as employed by Ameijeiras and Godoy (2016) and shown in Figure 5. To perform computations, the positive phase duration t0 has been initially adopted as 0.05s; however, its influence on the results is explored by means of parametric studies in Section 7.
|
In each case the transient response is shown for a given load level P in terms of the rotations α β and α-β with respect to time.
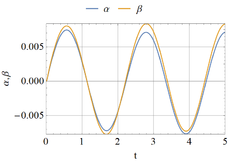
The system response is shown in Figure 6 (a) for P0=1.18 (the bifurcation load which was already computed and shown in Figure 2). In the absence of damping, the oscillations have constant amplitude with a maximum at α≈β≈0.23×10-3. It may be seen that the two DOF system oscillates in-phase and the oscillation are stable.
The stability coefficients have been plotted in Figure 6(b). Although the stability coefficients can be strictly employed for static states only, they are plotted here as a function of time to facilitate visualization, but their value should be considered only at points for zero velocity in the plot, i.e. at maximum or minimum values in Figure 6(a). Because all values are positive, then it may be said that the motion is stable, at least for the states for which a maximum or a minimum occur in Figure 6(a).
|
Results for a perfect system with P0=6.23 (which is the limit load in Figure 2) has oscillations that increase up to a maximum of α ≈ β ≈ 1.4×10-3, but still they are associated with stable coefficients.
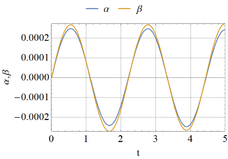
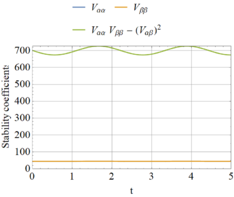
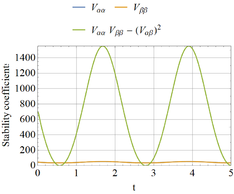
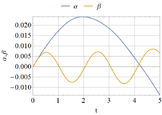
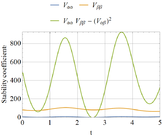
The situation changes for P=34.88, and results are represented in Figure 7. The following remarks can be made in this last case:
- One stability coefficient drops to zero in Figure 7(b), thus indicating the possibility of a singular behavior.
- The time at which this occurs in Figure 7(b) is t = 0.57s, and this corresponds to the first maximum in the α versus time plot in Figure 7(a). This indicates that the stability coefficient is zero at a state with zero velocity, so that the system temporarily passes through a static configuration.
|
* The displacement at t = 0.57s in Figure 7 (a) is α = 7.6×10-3. This α coincides with the static displacement at bifurcation, i.e. αB. This indicates that the system temporarily passes through the same static configuration as in static bifurcation. At this state along the fundamental motion the system displays the same conditions as in the static case and thus exhibits the same unstable behavior.
- These previous remarks are the condition identified by Lee (1977, 1981) for a quasi-bifurcation, and explored using other stability parameters by Kleiber (1987). It may be concluded that the system reaches a quasi-bifurcation at P = 34.88 and departs from the fundamental motion given by α(t) = β(t) to enter into a bifurcated state with α ≠ β (which is the eigenmode in the static problem).
- Because the static bifurcation is unstable, a dynamic jump occurs at this quasi-bifurcation state.
- For higher loads, i.e., P > 34.88, at least one stability coefficient has a negative value.
This mechanism contributes to explain why large deflections and plasticity are observed in real structures under impulsive loads due to an explosion: they are caused by a dynamic jump at a quasi-bifurcation.
Notice that dynamic instability in a mode with α(t) = β(t) (as predicted by the criterion due to Budiansky and Roth (1962), and Budiansky (1967) does not occur for this load level. An investigation of the oscillations along the fundamental motion shows that a much higher load level P is required to reach dynamic instability. Such behavior is of no interest in the present study because a quasi-bifurcation occurs well before an oscillatory instability.
A plot of the DOF at quasi-bifurcation versus the load level is shown in Figure 8. Unlike problems controlled by instability along the fundamental motion, as described by Budianksy (1967), in which a sharp change in maximum displacements is obtained for a small change in the load parameter, in the present case a smooth nonlinear curve is obtained, with a decreasing tangent for increasing values of P.
|
ENERGY CONSIDERATIONS
Energy at bifurcation and quasi-bifurcation states
To better understand ways to estimate dynamic quasi-bifurcations under impulsive loads, it is worth considering the energy involved in the process.
As shown in Figure 7(a), for a peak load P0D = 34.88 the configuration at the critical time tc = 0.57s reaches a displacement field given by α = β = 7.6×10-3rad.
- Because this is the same configuration as in the bifurcation state under static loading, then the strain energy UDis the same as UB, i.e. UD = UB = 4.5×10-3.
- Along the fundamental motion shown in Figure 7(a), energy conservation under impulsive loading requires that T + U = constant. To evaluate the constant we know that at time t = 0, the strain energy is zero, U(t = 0) = 0, and the above expression reduces to T(t = 0) = T0. Thus, conservation reads T + U = T0.
- The velocity is zero at t = tc, and the kinetic energy becomes zero, so that the conservation of energy becomes U (t = tc) = UD = T0.
- Finally, it follows that quasi-bifurcation is reached if
|
|
(11) |
Thus, the kinetic energy TD at the beginning of the transient response for a load level PDmust be equal to the elastic energy UB of the static system evaluated at the static bifurcation state.
Comparison with an energy criterion
An energy-based approach has been proposed in the literature by Simitses (1990), and Doyle (2001) to estimate dynamic buckling loads occurring in the form of quasi-bifurcation. The approach considers the energy imparted by the impulse to the system and evaluates the conditions for which this energy is equal to the energy required to reach the static bifurcation.
Critical conditions are reached when
|
|
(12) |
where UM is the elastic energy of the static system evaluated at one critical state; and TD is the kinetic energy at the beginning of the transient response for a load level PD, which is not yet known.
|
|
(13) |
with the velocity along the motion and mt the total mass.
The impulse given by the initial velocity is:
|
|
(14) |
The impulse of the positive phase of the transient force is given by the time integration:
|
(15) |
Using the impulse-momentum theorem, equating expression (14) and (15):
|
(16) |
From which the initial kinetic energy can be computed as a function of P0. This kinetic energy given to the system can be matched to UM and the critical peak load may be obtained:
|
(17) |
Then, the impulse which produce critical condition is:
|
(18) |
For the present case, the elastic energy at static bifurcation (see equation 5) is UB= 4.5×10-3. This can be used in eq. (17) to predict a quasi-bifurcation load at PD= 29.9. This value is very close (and a lower bound) to what was found in the previous section based on the nonlinear transient response and use of the stability coefficients.
In summary, computation of the elastic energy when the system buckles under a static load can be used to identify the initial velocity and impulse under a blast load and thus estimate a dynamic quasi-bifurcation. This energy approach may be extremely helpful for multi-degree of freedom systems because less computations are required, provided the deformed shape of the systems in static and dynamic behavior are approximately the same.
INFLUENCE OF GEOMETRIC IMPERFECTIONS
Lee states that “when the system is subjected to initial disturbances however small in amplitude but having a component leading to the eigenmode, the component of the deviated motion having the eigenmode grows most rapidly” (Lee 1981). To explore this problem, the initial shape of the two DOF system is modified to include a geometric imperfection with the shape of the static eigenmode. The influence of imperfections in the geometry is explored in this section in a way similar to what was done for the perfect dynamic case in Section 4. The imperfection is again written in terms of the parameter ξ (Eq. 9), taking extreme values between 0 and 0.6.
Consider first an imperfection amplitude ξ = 0.4. According to what was obtained in the static case, this value of ξ is still in the region affected by static unstable bifurcation, and a maximum in the imperfect equilibrium path is reached at PM(ξ = 0.4) = 0.42 with a displacement of αM(ξ = 0.4) = 0.11rad (Figure 3). Notice that for the imperfect system both values of the load and displacement at the maximum in the equilibrium path change with respect to the perfect system. In comparison with the perfect case (for which PB = 1.18 and αB = 7.6×10-3rad), the singularity in the static path appears at a lower load, but with a larger displacement amplitude.
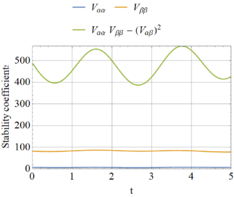
For P0= 6.23 in the imperfect system, the transient response indicates that the two DOF do not oscillate in-phase because they start from different initial values and undergo an amplification of this difference in time, as shown in Figure 9(a). The stability coefficients in Figure 9 (b) are all positive, thus indicating stable behavior at points corresponding to maximum values in Figure 9 (a).
|
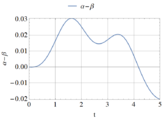
By increasing the load, one finds that the minimum load that produces instability is PD(ξ = 0.4) = 32.5 and the results are plotted in Figure 10. The unstable behavior is shown in Figure 10 (c) and arises for the first time at t = 2.55s, which is in coincidence with a maximum in β in Figure 10 (a). Notice that the difference (α-β) plotted in figure 10 (b) has values even larger than those of α or β, thus indicating that the system oscillates in an asymmetric mode.
|
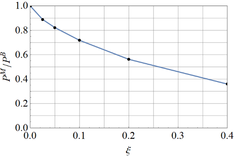
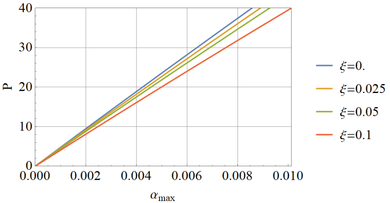
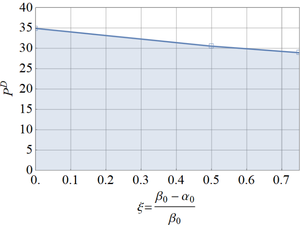
A summary of quasi-bifurcation load versus imperfection amplitude is shown in Figure 11. It may be seen that there is moderate imperfection-sensitivity in the plot, and an important conclusion is that the quasi-bifurcation load is not significantly affected by deviations from the perfect geometry.
|
Result from the energy criterion in Section 5 may be also visualized in Figure 11; it is interesting to notice that the energy approach is a lower bound to the more accurate results based on the transient dynamic response.
INFLUENCE OF PARAMETERS CONTROLLING THE RESPONSE
Results in the previous sections were restricted to one value of pulse duration, t0 = 0.05, and one stiffness ratio K/C = 1000. However, it would be important to consider the influence of changes in these parameters on the quasi-bifurcation results, and this is explored in this section.
Influence of pulse duration (t0)
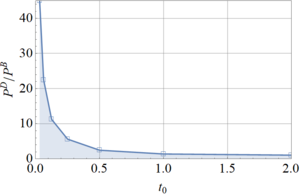
The influence of t0 on the quasi-bifurcation load is explored in this section for several values of t0 and assuming perfect system with ξ = 0. The results are summarized in Figure 12, in which the dynamic quasi-bifurcation loads have been normalized with respect to the static bifurcation load.
|
The case studied in previous sections with t = 0.05s yields large differences between static bifurcation and dynamic quasi-bifurcation; however, the differences reduce considerably for longer values of t0. In the limit, as t0 reaches the fundamental period, the quasi-bifurcation load becomes almost the same as the static bifurcation load. On the contrary, shorter times of positive pulse duration are associated with large differences between static and dynamic results.
The region of the plot in Figure 12 for small t0 is dominated by the impulse, whereas the static response dominates for large values of t0. This means that attention must be given to the choice of t0 in modeling nearby explosions because results are highly sensitive with respect to the positive pulse duration.
Influence of the stiffness ratio (K/C)
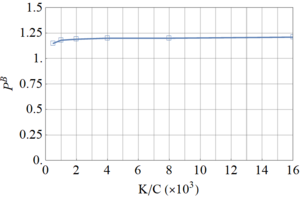
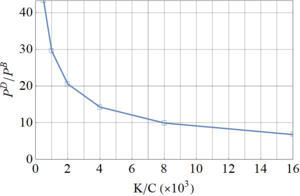
The influence of the elastic constants is studied in this section to understand the dependence of quasi-bifurcation loads on the membrane to bending stiffness ratio. Static bifurcation and dynamic critical loads have been evaluated for several values of K/C ranging from 0.25 to 16×103 for the perfect case (ξ), and results are shown in Figures 13 and 14.
The effect of the K/C ratio in the static bifurcation load is shown in Figure 13. Notice that this load remains almost constant even though the value of K/C exhibit large changes.
|
The situation changes for dynamic quasi-bifurcation, and the influence of K/C ratio is shown in Figure 14. Notice that for K/C lower than the case studied (K/C=1000), leads to higher dynamic critical load. For ratios K/C higher than the case studied, the quasi-bifurcation load reduces dramatically but keeps above the static one.
This trend is also expected to occur in shell analysis, although values of K and C in the two DOF model do not have a direct correlation with membrane and bending stiffness in a metal shell.
|
CONCLUSIONS
The present results for a simple two DOF system attempt to highlight the mechanism by which thin-walled structures may experience plasticity and even collapse under an impulsive load caused by a nearby explosion.
For a system that has an unstable critical state under static load (an unstable symmetric bifurcation in the present study), a quasi-bifurcation has been shown to occur if the static critical displacement configuration is reached at a state with zero velocity in the dynamic motion under an impulse. For the present two DOF model, stability at a point with zero velocity was evaluated by means of static stability coefficients. Other forms of stability evaluation may be more convenient for multiple degrees of freedom systems, such as natural frequencies or singularities in the tangent stiffness matrix.
Studies of imperfection-sensitivity of the present system indicate that there is moderate sensitivity of quasi-bifurcation loads, in the order of less than 20% change between perfect and imperfect response. The sensitivity with respect to changes in the stiffness parameters has also been studied, and one can see that low sensitivity is detected for static bifurcation loads, but significant changes are computed for quasi-bifurcation loads. This design-sensitivity is also expected to occur in thin-walled structures.
Finally, the pulse duration, as reflected by t0, plays a key role in the evaluation of quasi-bifurcation. For t0 in the order of the natural period of vibration, the response is almost the same as in the static case or step loading; but for small values of t0 there are large differences between quasi-bifurcation and bifurcation loads. For example, for t0 = 0.1T1, the value of quasi-bifurcation load is more than 10 times the critical bifurcation load.
Following the work of Simitses (1990), when the initial kinetic energy associated with a blast load reaches the value of the energy of a static unstable equilibrium position, then there is a movement away from equilibrium which is identified as dynamic buckling. This approach has been investigated in the paper and provides results within 15% of those obtained by the nonlinear transient analysis. This is a lower bound to the quasi-bifurcation load, and it has the advantage that it does not require computation of the transient results.
Acknowledgments. This research was supported by a grant CONICET-PIP 0126 (2013-2017), and by a grant awarded to Institute IDIT by CONICET (2016-2021).
REFERENCES
Amabili M. (2008) Nonlinear vibrations and stability of plates and shells. Cambridge University Press, UK.
Ameijeiras M.P. and Godoy L.A. (2016) Simplified analytical approach to evaluate the nonlinear dynamics of elastic cylindrical shells under lateral blast loads. Latin American J of Solids and Structures 13:1281-1298.
Baruh H (1999) Analytical dynamics. McGraw-Hill, Singapore.
Batista-Abreu J. and Godoy L.A. (2011) Investigación de causas de explosiones en una planta de almacenamiento de combustible en Puerto Rico. Revista Internacional de Desastres Naturales, Accidentes e Infraestructura Civil 11(2):109-122 (in Spanish).
Budiansky B. (1967) Dynamic buckling of elastic structures: criteria and estimates. In: G. Herrmann (ed) Dynamic Stability of Structures, Pergamon Press, pp 83-106.
Budiansky B. and Roth R.S. (1962) Axisymmetric dynamic buckling of clamped shallow spherical shells. In: NASA TN D-1510 Collected Papers on Instability of Shell Structures, Washington, DC, pp 597-606.
Buncefield Major Incident Investigation Board (2008) The Buncefield incident, 11 December 2005, the final report of the major incident investigation board, v.11. The Office of Public Sector Information, Richmond, Surrey, UK.
Buratti N. and Tavano M. (2014) Dynamic buckling and seismic fragility of anchored steel tanks by the added mass method. Earthquake Engineering & Structural Dynamics 43(1):1-21.
Burmeister A. and Ramm E. (1990). Dynamic stability analysis of shell structures. In: W. B. Kratzig, E. Oñate (ed) Computational Mechanics of Nonlinear Response of Shells, Springer, pp152-163.
Croll J.G.A. and Walker A.C. (1972) Elements of structural stability. Macmillan, London.
Doyle J.F. (2001) Nonlinear analysis of thin-walled Structures: statics, dynamics and stability. Springer-Verlag, New York.
Godoy L.A. (2016), Buckling of vertical oil storage steel tanks: Review of static buckling studies. Thin-Walled Structures 103:1-21.
Hindmarsh A.C., Brown P.N., Grant K.E. et al. (2005) SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Transactions on Mathematical Software 31(3):363-396.
Kleiber M., Kotula W., Saran M. (1987) Numerical analysis of dynamic quasi-bifurcation. Engineering Computations 4:48-52.
Kounadis A.N., Raftoyiannis J., Mallis J. (1989) Dynamic buckling of an arch model under impact loading. Journal of Sound and Vibration 134(2):193-202.
Kratzig W.B. and Eller C. (1992) Numerical algorithms for nonlinear unstable dynamic shell responses. Computers and Structures 44(1/2):263-271.
Kroplin B. and Dinkle D. (1986) Dynamic versus static buckling analysis of thin walled shell structures. In: T. Hughes and E. Hinton (ed) Finite Element Methods for Plate and Shell Structures V2, Pineridge Press, pp 229–251.
Kubiak T. (2013) Static and dynamic buckling of thin-walled plate structures. Springer, New York.
Lee L.H. (1977) Quasi-bifurcations in dynamics of elasto-plastic continua. J. Applied Mechanics 44(3):413-418.
Lee L.H. (1981) On dynamic stability and quasi-bifurcation. Int. J. Nonlinear Mechanics 16(1):79-87.
Mathematica (2017). Wolfram Research, Champaign, IL.
Nayfeh A.H. and Balachandran B. (2004) Applied nonlinear dynamics. Wiley-VCH, Weinheim.
Nayfeh A.H. and Mook D.T. (1979) Nonlinear oscillations. John Wiley & Sons, New York.
Noret E., Prod’homme G., Yalamas T. et al (2012) Safety of atmospheric storage tanks during accidental explosions. European Journal of Environmental and Civil Engineering 16(9):998–1022.
Riks E. (1979) An incremental approach to the solution of snapping and buckling problems. Int. J. of Solids and Structures 15:529-551.
Simitses G.J. (1990) Dynamic stability of suddenly loaded structures. Springer-Verlag, New York.
Taveau J. (2011) Explosion of fixed roof atmospheric storage tanks, Part 1: Background and review of case histories. Process Safety Progress 30(4):381-392.
Thompson J.M.T. and Hunt G.W. (1973) A general theory of elastic stability. John Wiley, London.
Virella J.C., Godoy L.A., Suárez L.E. (2006) Dynamic buckling of anchored steel tanks subjected to horizontal earthquake excitation. Journal of Constructional Steel Research 62(6):521-531.
(1) Artículo recibido el 28 de Octubre de 2018 y aceptado para publicación el 15 de Noviembre de 2018.
(2) Profesor Adjunto, Departamento de Estructuras. Facultad de Ciencias Exactas Físicas y Naturales, Universidad Nacional de Córdoba. Casilla de Correo 916, 5000 Córdoba, Argentina. E-mail: m.ameijeiras@unc.edu.ar
(3) Investigador Superior, Instituto de Estudios Avanzados en Ingeniería y Tecnología (IDIT UNC-CONICET), Córdoba, Argentina, luis.godoy@unc.edu.ar
Document information
Published on 06/12/18
Accepted on 15/04/19
Submitted on 15/04/19
Volume 18, Issue 2, 2018
Licence: CC BY-NC-SA license