Research on the identification of modulus parameters for rigid pavement panel foundations

Abstract: Based on the Pasternak two-parameter foundation model, this study establishes a dynamic model for analyzing the deflection of slabs under moving loads. The variational method and reciprocal equal work theorem are employed to obtain the deflection solution, while the Matlab program is utilized with practical examples to calculate the foundation response modulus considering transfer shear force, bending moment, and their combined effects. By fitting measured dynamic deflections with theoretical predictions using the least square method, the response modulus K of the foundation is determined, demonstrating that our proposed model effectively captures the realistic behavior of rigid pavements.

Keywords: Pasternak model; Least squares method; Foundation reaction modulus

1 Introduction

With the rapid development of China's civil aviation industry, higher performance and safety requirements for airport pavement are inevitable. Currently, the commonly used foundation models include the E. Winkler foundation model and the elastic half-space foundation model. Although the Winkler foundation model theory is simple and intuitive, requiring only one elastic parameter to express ideal elastic foundation characteristics and relating displacement of any point solely to applied stress at that point, it fails to consider soil-ground continuity. In contrast, the elastic half-space foundation model overemphasizes stress diffusion between soil and ground, making calculations more cumbersome and impractical for engineering applications. Consequently, mechanics experts have developed several more reasonable foundation calculation models through extensive experimentation. Zhang Weigang and Chen Xiangming et al utilized the Kelvin viscoelastic model under moving load conditions to obtain a relatively accurate foundation reaction modulus [1,2]. The viscoelastic Winkler dynamic model verified by Xing Yaozhong better reflects actual airport operations [3]. V. Patil employed Pasternak's two-parameter soil medium as a model to investigate material nonlinearity effects on pavement response in supporting soil medium [4]. Yakshansh Kumar applied a novel finite element-based cyclic response model for rigid pavement design while establishing the period range of moving load within rigid pavement parameters [5]. Airport pavements consist of multiple concrete panels working collectively. This paper selects the Pasternak two-parameter foundation model based on independent parameters: foundation reaction modulus K and shear modulus G; thereby establishing a dynamic rigid pavement model considering joint load transfer capacity.

2.1 The formulation of the equation of motion

Figure 1 The schematic of a two-parameter foundation model

Figure 2 The forces on the shear layer

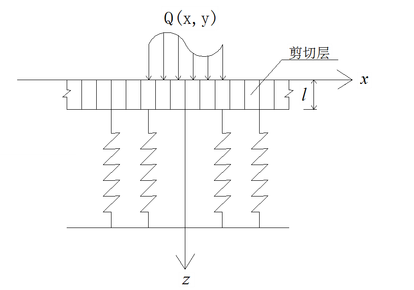
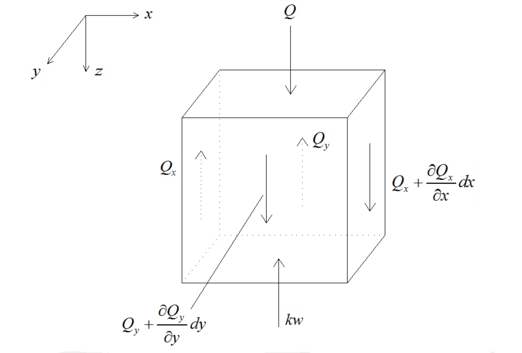
Based on the two-parameter foundation, a dynamic model of rigid thin plate pavement on the two-parameter foundation is established, considering boundary shear and bending under moving load [6]. The dynamic equation of the two-parameter foundation incorporates two independent parameters: reaction modulus K and shear modulus G. Figure 1 illustrates the schematic diagram of the two-parameter foundation, while Figure 2 depicts the forces acting on the shear layer [7].

According to the Kirchhoff thin plate theory [8] and the theory of elastic mechanics, we establish the motion equation for plates subjected to a two-parameter foundation under dynamic loading as follows:

$D{\nabla }^{4}w+M{\frac {{\partial }^{2}w}{\partial t^{2}}}+$$Kw-G{\nabla }^{2}w=P$

$\left(1\right)$

D — the flexural stiffness of the plate, $D={\frac {Eh^{3}}{12(1-{\mu }^{2})}}$

µ —Poisson's ratio

$M=\rho h$ —The areal density

${\nabla }^{2}={\frac {{\partial }^{2}}{\partial x^{2}}}+{\frac {{\partial }^{2}}{\partial y^{2}}}$ —The Laplace operator in two dimensions

K—Foundation reaction modulus

G—Foundation shear modulus

The aforementioned equation represents the differential equation of motion for the track panel system subjected to a general moving load, denoted as $P(x,y,t)$ . In the context of the investigated form of moving load in this study, the equality $P(x,y,t)$ can be expressed as follows

$P(x,y,t)=P_{0}\delta (x-v_{x}t)\delta (y-\eta )$

$\left(2\right)$

The function $\delta$ is represented by $\delta (.)$ , and the uniform gliding speed of the aircraft is denoted by $v_{x}$ .

2.2 Boundary conditions (shear and bending)

The plate dimensions are defined as length a and width b, with simultaneous transfer of shear force and bending moment between the plates in the actual working state. The boundary shear force is generated by the spring support force, where the elastic support rigidity coefficient $k_{1}$ represents the boundary condition parameter. Similarly, the bending moment is generated by the spring-supporting moment, with the elastic supporting rigidity coefficient $k_{2}$ representing another boundary condition parameter. Assuming that $Y=0,b$ corresponds to the side where the seam is located, we can express its general formula for boundary conditions as follows:

${\begin{array}{c}V_{y=0,b}=D{\left[{\frac {{\partial }^{3}w}{\partial y^{3}}}+{\frac {(2-\mu ){\partial }^{3}w}{\partial x^{2}\partial y}}\right]}_{y=0,b}=-k_{1}{\left[w\right]}_{y=0,b}\\M_{y\vert y=0,b}=D\left({\frac {{\partial }^{2}w}{\partial y^{2}}}+\mu {\frac {{\partial }^{2}w}{\partial x^{2}}}\right)\vert {}_{y=0,b}=-k_{2}{\vert {\frac {\partial w}{\partial y}}\vert }_{y=0,b}\end{array}}$

$\left(3\right)$

3 The solution to the equation of motion

3.1 Solving time factors

The variational formulation of equation (1) for plate motion is as follows

${\int }_{0}^{a}{\int }_{0}^{b}\left\{D{\nabla }^{4}w+M{\frac {{\partial }^{2}w}{\partial t^{2}}}+\right.$$\left.Kw-G{\nabla }^{2}w-P\right\}\delta wdxdy=0$ $\left(4\right)$

The lateral load concentration stands out among them. $P=P(x,y,t)$ ， $w=w(x,y,t)$

Select a function in the specified format as the solution for the variational equation mentioned above.

$\lbrace {\begin{array}{c}w(x,y,t)=T(t)W(x,y)\\P(x,y,t)=B(t)W(x,y)\end{array}}$

$\left(5\right)$

The mode function of the plate is represented by $W(x,y)$ , and the coefficients of the deflection function $w(x,y,t)$ and load $P(x,y,t)$ are denoted as $T(t)$ and $B(t)$ respectively. The variation corresponding to the deflection function $w(x,y,t)$ is as follows:

$\delta w=W(x,y)T(t)$

$\left(6\right)$

Substituting equations (5) and (6) into (4) gives:

${\overset {..}{T}}(t)+w_{mn}{}^{2}T(t)={\frac {1}{M}}B(t)$

$\left(7\right)$

Where:

${\begin{array}{c}w_{mn}{}^{2}={\frac {1}{M}}{\frac {I_{1}}{I_{2}}}\\I_{1}={\int }_{0}^{a}{\int }_{0}^{b}\left[D{\nabla }^{4}W(x,y)+KW(x,y)-G{\nabla }^{2}W(x,y)\right]W(x,y)dxdy\\I_{2}={\int }_{0}^{a}{\int }_{0}^{b}W^{2}(x,y)dxdy\end{array}}$

The computable expression for T(t) is as follows:

$T(t)=(c_{1}cosw_{mn}t+c_{2}sinw_{mn}t)+{\frac {1}{Mw_{mn}}}{\int }_{0}^{t}B(\tau )sinw_{mn}(t-$$\tau )d\tau$ $\left(8\right)$

The natural frequency of undamped free vibration of the thin plate, denoted as $w_{mn}$ is considered. In equation (8), the first term represents the intrinsic vibration characteristics of the sheet, while the second term accounts for its response under external excitation.

Where c₁ and c₂ are constants, B(t) is dependent on the initial conditions of motion and the characteristics of the load. In this study, we consider a concentrated load P₀, irrespective of its mass. Consequently, B(t) can be expressed as follows:

$B(t)={\frac {P_{0}W(v_{x}t,\eta )}{{\int }_{0}^{a}{\int }_{0}^{b}W^{2}(x,y)dxdy}}$

$\left(9\right)$

According to formulas (8) and (9), the dynamic deflection of the plate under the influence of a moving concentrated load P, with zero initial conditions (c₁ =c₂), can be determined as follows:

$w\left(x,y,t\right)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {W\left(x,y\right)}{Mw_{mn}{\int }_{0}^{a}{\int }_{0}^{b}W^{2}\left(x,y\right)dxdy}}{\int }_{0}^{t}P_{0}W\left(v_{x}\tau ,\eta \right)sinw_{mn}\left(t-\right.$$\left.\tau \right)d\tau$ $\left(10\right)$

3.2 Solving coordinate factors