Research on the identification of modulus parameters for rigid pavement panel foundations

Abstract

Based on the Pasternak two-parameter foundation model, this study establishes a dynamic model for analyzing the deflection of slabs under moving loads. The variational method and reciprocal equal work theorem are employed to obtain the deflection solution. Additionally, the Matlab program is utilized with practical examples to calculate the foundation response modulus under actual conditions when the pavement panel simultaneously transmits shear and bending forces. By fitting measured dynamic deflections with theoretical predictions using the least square method, the response modulus ${\textstyle K}$ of the foundation is determined. This demonstrates that our proposed model effectively captures the realistic behavior of rigid pavements..

Keywords: Pasternak model, least squares method, foundation reaction modulus

1. Introduction

With the rapid development of China's civil aviation industry, higher performance and safety requirements for airport pavement are inevitable.Currently, the commonly used foundation models include the E.Winkler foundation model and the elastic half-space foundation model. Although the Winkler foundation model theory is simple and intuitive, requiring only one elastic parameter to express ideal elastic foundation characteristics and relating displacement of any point solely to applied stress at that point,it fails to consider soil-ground continuity. In contrast, the elastic half-space foundation model overemphasizes stress diffusion between soil and ground, making calculations more cumbersome and impractical for engineering applications. Consequently, mechanics experts have developed several more reasonable foundation calculation models through extensive experimentation. Zhang et al. [1] and Chen and Liu [2] utilized the Kelvin viscoelastic model under moving load conditions to obtain a relatively accurate foundation reaction modulus. The viscoelastic Winkler dynamic model verified by Xing [3] better reflects actual airport operations. Patil et al. [4] employed Pasternak's two-parameter soil medium as a model to investigate material nonlinearity effects on pavement response in supporting soil medium. Kumar et al. [5] applied a novel finite element-based cyclic response model for rigid pavement design while establishing the period range of moving load within rigid pavement parameters. Airport pavements consist of multiple concrete panels working collectively. This paper selects the Pasternak two-parameter foundation model based on independent parameters:foundation reaction modulus ${\textstyle K}$ and shear modulus ${\textstyle G}$; thereby establishing a dynamic rigid pavement model considering joint load transfer capacity.

2. The formulation of dual-panel motion equations

2.1 The formulation of the equation of motion

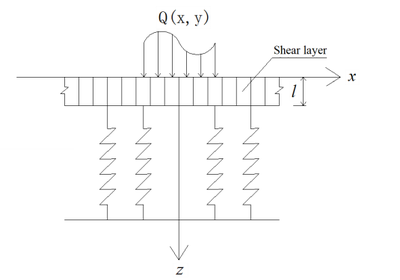
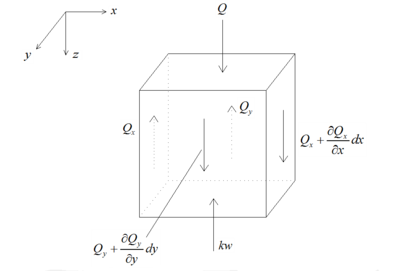
Based on the two-parameter foundation, a dynamic model of rigid thin plate pavement on the two-parameter foundation is established, considering boundary shear and bending under moving load [6], where ${\textstyle {\mathit {\boldsymbol {Q}}}}$ is the foundation reaction force. The dynamic equation of the two-parameter foundation incorporates two independent parameters: reaction modulus ${\textstyle K}$ and shear modulus ${\textstyle G}$. Figure 1 illustrates the schematic diagram of the two-parameter foundation, while Figure 2 depicts the forces acting on the shear layer [7].

Figure 1. Schematic of a two-parameter foundation model

Figure 2. Forces on the shear layer

According to the Kirchhoff thin plate theory [8] and the theory of elastic mechanics, we establish the motion equation for plates subjected to a two-parameter foundation under dynamic loading as follows:

$D{\nabla }^{4}w+M{\frac {{\partial }^{2}w}{\partial {t}^{2}}}+Kw-G{\nabla }^{2}w=P$

(1)

$D={\frac {E{h}^{3}}{12\left(1-{\mu }^{2}\right)}}$

where:

${\textstyle D}$ is the flexural stiffness of the plate,

${\textstyle \mathrm {\mu } }$, the Poisson's ratio

${\textstyle M=\rho h}$, the areal density

${\textstyle {\nabla }^{2}={\frac {{\partial }^{2}}{\partial {x}^{2}}}+{\frac {{\partial }^{2}}{\partial {y}^{2}}}}$, Laplace operator in two dimensions

${\textstyle K}$, foundation reaction modulus

${\textstyle G}$, foundation shear modulus, and

${\textstyle w}$ is the vertical deflection of the pavement panel.

The aforementioned equation represents the differential equation of motion for the track panel system subjected to a general moving load, denoted as ${\textstyle P\left(x,y,t\right)}$. In the context of the investigated form of moving load in this study, the equality ${\textstyle P\left(x,y,t\right)}$ can be expressed as follows:

$P\left(x,y,t\right)={P}_{0}\delta \left(x-{v}_{x}t\right)\delta \left(y-\eta \right)$

(2)

The function ${\textstyle \delta \,}$ is represented by ${\textstyle \delta \left(x\right)}$, and the uniform gliding speed of the aircraft is denoted by ${\textstyle {v}_{x}}$.

2.2 Boundary conditions (shear and bending)

The plate dimensions are defined as length ${\textstyle a}$ and width ${\textstyle b}$, with simultaneous transfer of shear force and bending moment between the plates in the actual working state. The boundary shear force is generated by the spring support force, where the elastic support rigidity coefficient ${\textstyle {k}_{1}\,}$ represents the boundary condition parameter. Similarly, the bending moment is generated by the spring-supporting moment, with the elastic supporting rigidity coefficient ${\textstyle {k}_{2}}$ representing another boundary condition parameter. Assuming that ${\textstyle Y=}$$0,b$ corresponds to the side where the seam is located, we can express its general formula for boundary conditions as follows:

${V}_{y=0,b}=D{\left[{\frac {{\partial }^{3}w}{\partial {y}^{3}}}+{\frac {\left(2-\mu \right){\partial }^{3}w}{\partial {x}^{2}\partial y}}\right]}_{y=0,b}=-{k}_{1}{\left[w\right]}_{y=0,b}$ ${M}_{y\left|y=0,b\right.}=D\left({\frac {{\partial }^{2}w}{\partial {y}^{2}}}+\mu {\frac {{\partial }^{2}w}{\partial {x}^{2}}}\right){\Big |}y=0,\quad b=-{k}_{2}\left|{\frac {\partial w}{\partial y}}\right|_{y=0,b}$

(3)

3. The solution to the equation of motion

3.1 Solving time factors

The variational formulation of Eq. (1) for plate motion is as follows:

$\int _{0}^{a}\int _{0}^{b}\left\{D{\nabla }^{4}w+M{\frac {{\partial }^{2}w}{\partial {t}^{2}}}+Kw-G{\nabla }^{2}w-P\right\}\delta wdxdy=0$

(4)

The lateral load concentration stands out among them. ${\textstyle P=}$$P\left(x,y,t\right)$, ${\textstyle w=w\left(x,y,t\right)}$.

Select a function in the specified format as the solution for the variational equation mentioned above

$\left\{{\begin{matrix}\ w(x,y,t)=T(t)W(x,y)\\P(x,y,t)=B(t)W(x,y)\end{matrix}}\right.$

(5)

The mode function of the plate is represented by ${\textstyle W\left(x,y\right)}$, and the coefficients of the deflection function ${\textstyle w\left(x,y,t\right)}$ and load ${\textstyle P\left(x,y,t\right)}$ are denoted as ${\textstyle T\left(t\right)}$ and ${\textstyle B\left(t\right)}$, respectively. The variation corresponding to the deflection function ${\textstyle w\left(x,y,t\right)}$ is as follows:

$\delta w=W\left(x,y\right)T\left(t\right)$

(6)

Substituting Eqs. (5) and (6) into (4) gives:

$\left(t\right)+{{w}_{mn}}^{2}T\left(t\right)={\frac {1}{M}}B\left(t\right)$

(7)

where

${{w}_{mn}}^{2}={\frac {1}{M}}{\frac {{I}_{1}}{{I}_{2}}}$ ${I}_{1}=\int _{0}^{a}\int _{0}^{b}\left[D{\nabla }^{4}W\left(x,y\right)+KW\left(x,y\right)-G{\nabla }^{2}W\left(x,y\right)\right]W\left(x,y\right)dxdy$ ${I}_{2}=\int _{0}^{a}\int _{0}^{b}{W}^{2}\left(x,y\right)dxdy$

The computable expression for ${\textstyle T(t)}$ is as follows:

$T\left(t\right)=\left({c}_{1}\mathrm {cos} \,{w}_{mn}t+{c}_{2}\mathrm {sin} \,{w}_{mn}t\right)+{\frac {1}{M{w}_{mn}}}\int _{0}^{t}B\left(\tau \right)\mathrm {sin} \,{w}_{mn}\left(t-\tau \right)d\tau$

(8)

where, ${\textstyle {w}_{mn}}$ represents the natural frequency of undamped free vibration for a thin plate. The first term in Eq. (8) denotes the thin plate's free vibration, while the second term represents its forced vibration.

Among them, ${\textstyle c_{1}}$ and ${\textstyle c_{2}}$ are constants that depend on the initial conditions of motion, while ${\textstyle B(t)}$ is dependent on the load characteristics. In this study, the load is considered as a concentrated load ${\textstyle P_{0}}$, neglecting its mass. Consequently, ${\textstyle B(t)}$ can be expressed as follows:

$B\left(t\right)={\frac {{P}_{0}W\left({v}_{x}t,\eta \right)}{\displaystyle \int _{0}^{a}\int _{0}^{b}{W}^{2}\left(x,y\right)dxdy}}$

(9)

According to Eqs. (8) and (9), the dynamic deflection of the plate under the influence of a moving concentrated load P, with zero initial conditions (${\textstyle c_{1}=c_{2}}$), can be determined as follows:

$w\left(x,y,t\right)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {W\left(x,y\right)}{M{w}_{mn}\displaystyle \int _{0}^{a}\int _{0}^{b}{W}^{2}\left(x,y\right)dxdy}}$$\int _{0}^{t}{P}_{0}W\left({v}_{x}\tau ,\eta \right)\mathrm {sin} \,{w}_{mn}\left(t-\tau \right)d\tau$

(10)

3.2 Solving coordinate factors

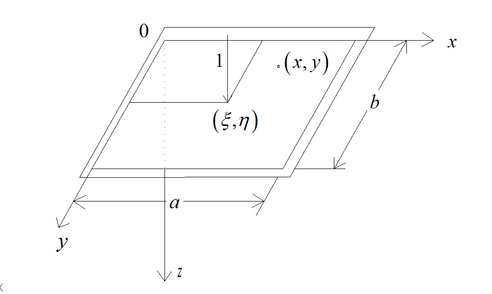
In order to address the analytical solution for the bending behavior of diverse boundary plates subjected to moving loads, a four-sided simply supported rectangular plate with dimensions, geometry, and material properties that precisely match those of the actual system is considered as the fundamental model [9], as depicted in Figure 3.

Figure 3. Basic system of board

The plate is subjected to a unit concentration force at the flow coordinate ${\textstyle \left(\zeta ,\eta \right)}$, and the displacement is solved using a trigonometric series

${w}_{1}={\frac {4}{abD}}\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {\mathrm {sin} \,{k}_{m}\zeta \mathrm {sin} \,{k}_{n}\eta }{({{k}_{m}}^{2}+{{k}_{n}}^{2}{)}^{2}}}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$

(11)

where, ${k}_{m}={\frac {m\pi }{a}},\quad {k}_{n}={\frac {n\pi }{b}}$.

The solution ${\textstyle {w}_{1}}$ is referred to as the fundamental solution corresponding to the rectangular plate system.

The boundary condition can be simplified as a simply supported boundary by incorporating the corresponding support settlement and constraint moment under actual boundary conditions. The additional support settlement is assumed to be:

${W}_{x0}=\sum _{n=1}^{\infty }{A}_{n}\mathrm {sin} \,{k}_{n}y\qquad ,\qquad {W}_{xa}=\sum _{n=1}^{\infty }{B}_{n}\mathrm {sin} \,{k}_{n}y,$ ${W}_{y0}=\sum _{m=1}^{\infty }{C}_{m}\mathrm {sin} \,{k}_{m}x\qquad ,\qquad {W}_{yb}=\sum _{m=1}^{\infty }{D}_{m}\mathrm {sin} \,{k}_{m}x.$

(12)

The additional constraint torque shall be determined as follows:

${M}_{x0}=\sum _{n=1}^{\infty }{E}_{n}\mathrm {sin} \,{k}_{n}y\qquad ,\qquad {M}_{xa}=\sum _{n=1}^{\infty }{F}_{n}\mathrm {sin} \,{k}_{n}y,$ ${M}_{y0}=\sum _{m=1}^{\infty }{G}_{m}\mathrm {sin} \,{k}_{m}x\qquad ,\qquad {M}_{yb}=\sum _{m=1}^{\infty }{H}_{m}\mathrm {sin} \,{k}_{m}x.$

(13)

The reciprocal theorem of work between the fundamental system and the real system can be utilized to derive:

${\begin{aligned}\displaystyle W\left(\xi ,\eta \right)=&\displaystyle \int _{0}^{a}\int _{0}^{b}\left[\left(M{{w}_{mn}}^{2}-K\right)W\left(x,y\right)+G{\nabla }^{2}W\left(x,y\right)\right]{w}_{1}dxdy\\&\displaystyle +\int _{0}^{a}{W}_{y0}{V}_{y0}dx+\int _{0}^{b}{W}_{x0}{V}_{x0}dy-\displaystyle \int _{0}^{a}{W}_{yb}{V}_{yb}dx-\displaystyle \int _{0}^{b}{W}_{xa}{V}_{xa}dy\\&\displaystyle +\int _{0}^{a}{M}_{y0}{\frac {\partial {w}_{1}}{\partial y}}{\Bigg |}y=0dx\int _{0}^{b}{M}_{x0}\displaystyle {\frac {\partial {w}_{1}}{\partial x}}{\Bigg |}x=0dy\\&\displaystyle -\int _{0}^{a}{M}_{yb}{\frac {\partial {w}_{1}}{\partial y}}{\Bigg |}y=bdx-\displaystyle \int _{0}^{b}{M}_{xa}{\frac {\partial {w}_{1}}{\partial x}}{\Bigg |}x=ady\end{aligned}}$

(14)

Set:

$W\left(x,y\right)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{A}_{mn}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$

(15)

Substituting Eqs. (12), (13) and (15) into (14) yields:

${A}_{mn}={\frac {{\frac {2}{a}}{k}_{m}\left\{D\left[{{k}_{m}}^{2}+\left(2-\mu \right){{k}_{n}}^{2}\right]\left({A}_{n}-{B}_{n}\mathrm {cos} \,m\pi \right)+\left({E}_{n}-{F}_{n}\mathrm {cos} \,m\pi \right)\right\}}{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}$ $\qquad +{\frac {{\frac {2}{b}}{k}_{n}\left\{D\left[{{k}_{n}}^{2}+\left(2-\mu \right){{k}_{m}}^{2}\right]\left({C}_{m}-{D}_{m}\mathrm {cos} \,n\pi \right)+\left({G}_{m}-{H}_{m}\mathrm {cos} \,n\pi \right)\right\}}{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}$

(16)

Substituting ${\textstyle {A}_{mn}}$ into ${\textstyle W\left(x,y\right)}$ can obtain the mode function expression of the triangular series type:

$W\left(x,y\right)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {{A}_{n}\left[{{k}_{m}}^{2}+\left(2-\mu \right){{k}_{n}}^{2}\right]{\frac {2}{a}}{k}_{m}D}{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$ $\quad \quad \quad +\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {-{B}_{n}\mathrm {cos} \,m\pi \left[{{k}_{m}}^{2}+\left(2-\mu \right){{k}_{n}}^{2}\right]{\frac {2}{a}}{k}_{m}D}{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$ $\quad \quad \quad +\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {{C}_{m}\left[{{k}_{m}}^{2}+\left(2-\mu \right){{k}_{n}}^{2}\right]{\frac {2}{b}}{k}_{n}D}{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$ $\quad \quad \quad +\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {-{D}_{m}\mathrm {cos} \,n\pi \left[{{k}_{n}}^{2}+\left(2-\mu \right){{k}_{m}}^{2}\right]{\frac {2}{b}}{k}_{n}D}{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$ $\quad \quad \quad +\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {{E}_{n}{\frac {2}{a}}{k}_{m}}{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$ $\quad \quad \quad +\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {-{F}_{n}{\frac {2}{a}}{k}_{m}\mathrm {cos} \,m\pi }{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$ $\quad \quad \quad +\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {{G}_{m}{\frac {2}{b}}{k}_{n}}{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$ $\quad \quad \quad +\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {-{H}_{m}{\frac {2}{b}}{k}_{n}\mathrm {cos} \,n\pi }{D{\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)}^{2}-\left[M{{w}_{mn}}^{2}-K-G\left({{k}_{m}}^{2}+{{k}_{n}}^{2}\right)\right]}}\mathrm {sin} \,{k}_{m}x\mathrm {sin} \,{k}_{n}y$

(17)

Set:

$W\left(x,y\right)={w}_{1}+{w}_{2}+{w}_{3}+{w}_{4}+{w}_{5}+{w}_{6}+{w}_{7}+{w}_{8}$

The mode function of the triangular series can only satisfy the condition that the boundary deflection is zero while ensuring homogeneity in the corresponding boundary shear force and bending moment. Therefore, ${\textstyle {w}_{1}}$, ${\textstyle {w}_{2}}$, ${\textstyle {w}_{3}}$ and ${\textstyle {w}_{4}}$ undergo hyperbolic transformations in one of the following directions. Similarly, ${\textstyle {w}_{5}}$, ${\textstyle {w}_{6}}$, ${\textstyle {w}_{7}}$ and ${\textstyle {w}_{8}}$ are transformed accordingly. We can get:

${\begin{aligned}{w}_{1}=&\sum _{n=1}^{\infty }{\frac {{A}_{n}}{\left({{\alpha }_{n}}^{2}-{{\beta }_{n}}^{2}\right)}}\left\{{\begin{matrix}\quad \left[{\frac {{{\alpha }_{n}}^{2}sh{\alpha }_{n}\left(a-x\right)}{sh{\alpha }_{n}a}}-{\frac {{{\beta }_{n}}^{2}sh{\beta }_{n}\left(a-x\right)}{sh{\beta }_{n}a}}\right]\\\ +\left(2-\mu \right){{k}_{n}}^{2}\left[-{\frac {sh{\alpha }_{n}\left(a-x\right)}{sh{\alpha }_{n}a}}+{\frac {sh{\beta }_{n}\left(a-x\right)}{sh{\beta }_{n}a}}\right]\end{matrix}}\right\}\mathrm {sin} \,{k}_{n}y.\\{w}_{2}=&\sum _{n=1}^{\infty }{\frac {{B}_{n}}{\left({{\alpha }_{n}}^{2}-{{\beta }_{n}}^{2}\right)}}\left\{{\begin{matrix}\quad \left[{\frac {{{\alpha }_{n}}^{2}sh{\alpha }_{n}x}{sh{\alpha }_{n}a}}-{\frac {{{\beta }_{n}}^{2}sh{\beta }_{n}x}{sh{\beta }_{n}a}}\right]\\\ +\left(2-\mu \right){{k}_{n}}^{2}\left[-{\frac {sh{\alpha }_{n}x}{sh{\alpha }_{n}a}}+{\frac {sh{\beta }_{n}x}{sh{\beta }_{n}a}}\right]\end{matrix}}\right\}\mathrm {sin} \,{k}_{n}y.\\{w}_{3}=&\sum _{m=1}^{\infty }{\frac {{C}_{m}}{\left({{\alpha }_{m}}^{2}-{{\beta }_{m}}^{2}\right)}}\left\{{\begin{matrix}\quad \left[{\frac {{{\alpha }_{m}}^{2}sh{\alpha }_{m}\left(b-y\right)}{sh{\alpha }_{m}b}}-{\frac {{{\beta }_{m}}^{2}sh{\beta }_{m}\left(b-y\right)}{sh{\beta }_{m}b}}\right]\\\ +\left(2-\mu \right){{k}_{m}}^{2}\left[-{\frac {sh{\alpha }_{m}\left(b-y\right)}{sh{\alpha }_{m}b}}+{\frac {sh{\beta }_{m}\left(b-y\right)}{sh{\beta }_{m}b}}\right]\end{matrix}}\right\}\mathrm {sin} \,{k}_{m}x.\\{w}_{4}=&\sum _{m=1}^{\infty }{\frac {{D}_{m}}{\left({{\alpha }_{m}}^{2}-{{\beta }_{m}}^{2}\right)}}\left\{{\begin{matrix}\quad \left[{\frac {{{\alpha }_{m}}^{2}sh{\alpha }_{m}y}{sh{\alpha }_{m}b}}-{\frac {{{\beta }_{m}}^{2}sh{\beta }_{m}y}{sh{\beta }_{m}b}}\right]\\\ +\left(2-\mu \right){{k}_{m}}^{2}\left[-{\frac {sh{\alpha }_{m}y}{sh{\alpha }_{m}b}}+{\frac {sh{\beta }_{m}y}{sh{\beta }_{m}b}}\right]\end{matrix}}\right\}\mathrm {sin} \,{k}_{m}x.\\{w}_{5}=&\sum _{n=1}^{\infty }{\frac {{E}_{n}}{D\left({{\alpha }_{n}}^{2}-{{\beta }_{n}}^{2}\right)}}\left[-{\frac {sh{\alpha }_{n}\left(a-x\right)}{sh{\alpha }_{n}a}}+{\frac {sh{\beta }_{n}\left(a-x\right)}{sh{\beta }_{n}a}}\right]\mathrm {sin} \,{k}_{n}y.\\{w}_{6}=&\sum _{n=1}^{\infty }{\frac {{F}_{n}}{D\left({{\alpha }_{n}}^{2}-{{\beta }_{n}}^{2}\right)}}\left[-{\frac {sh{\alpha }_{n}x}{sh{\alpha }_{n}a}}+{\frac {sh{\beta }_{n}x}{sh{\beta }_{n}a}}\right]\mathrm {sin} \,{k}_{n}y.\\{w}_{7}=&\sum _{m=1}^{\infty }{\frac {{G}_{m}}{D\left({{\alpha }_{m}}^{2}-{{\beta }_{m}}^{2}\right)}}\left[-{\frac {sh{\alpha }_{m}\left(b-y\right)}{sh{\alpha }_{m}b}}+{\frac {sh{\beta }_{m}\left(b-y\right)}{sh{\beta }_{m}b}}\right]\mathrm {sin} \,{k}_{m}x.\\{w}_{8}=&\sum _{m=1}^{\infty }{\frac {{H}_{m}}{D\left({{\alpha }_{m}}^{2}-{{\beta }_{m}}^{2}\right)}}\left[-{\frac {sh{\alpha }_{m}y}{sh{\alpha }_{m}b}}+{\frac {sh{\beta }_{m}y}{sh{\beta }_{m}b}}\right]\mathrm {sin} \,{k}_{m}x.\end{aligned}}$

(18)

The coordinate factor after the aforementioned transformation not only satisfies the condition of zero boundary deflection but also fulfills equations (12) and (13). In this scenario, the actual system must adhere to boundary conditions (3). The substitution of ${\textstyle {B}_{n}}$, ${\textstyle {C}_{m}}$, ${\textstyle {D}_{m}}$, ${\textstyle {E}_{n}}$, ${\textstyle {F}_{n}}$, ${\textstyle {G}_{m}}$ and ${\textstyle {H}_{m}}$ into Eq. (3) yields eight equations, the solutions of which provide the corresponding values. Substituting these values into Eq. (17) determines the coordinate factor ${\textstyle W\left(x,y\right)}$.

By substituting the coordinate factor ${\textstyle W\left(x,y\right)}$ into Eq. (10), one can derive the expression for ${\textstyle W\left(x,y,t\right)}$ and obtain an analytical formula for the deflection of the pavement panel

$W\left(x,y,t\right)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {W\left(x,y\right)}{M{w}_{mn}\displaystyle \int _{0}^{a}\displaystyle \int _{0}^{b}{W}^{2}\left(x,y\right)dxdy}}\int _{0}^{t}{P}_{0}W\left({v}_{x}\tau ,\eta \right)\mathrm {sin} \,{w}_{mn}\left(t-\tau \right)d\tau$

(19)

4. The identification of foundation modulus

According to the analytical expression of deflection, the deflection value of the plate can be determined when the reaction modulus ${\textstyle K}$ of the foundation is fixed. Conversely, if the measured deflection at each measuring point is known, a fitting process can be conducted by establishing an objective function to compare and match the measured dynamic deflection with theoretical dynamic deflection. The program [10] is implemented using Matlab for identifying the response modulus of the foundation. During parameter optimization, an objective function is formulated based on the least squares criterion:

$\mathrm {min} \,\epsilon (K)=\mathrm {min} \,{\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}({w}_{i}-{\overline {{w}_{i}}}{)}^{2}}}$

Among them, ${\textstyle \mathrm {min} \,\epsilon (K)}$, for the objective function, ${\textstyle {w}_{i}}$ and ${\textstyle {\overline {{w}_{i}}}}$ represent the theoretically calculated and measured deflection values of the measurement points, respectively, and ${\textstyle n}$ represents the number of measurement points on the pavement. Adjust ${\textstyle K}$ one by one to minimize the objective function, and the ${\textstyle K}$ value at this point is the identified foundation response modulus.

5. Verification of the case

The model and inversion recognition method presented in this paper were utilized to compute the pavement surface of an airport located in Nanjing, with geometric dimensions of ${\textstyle a=6}$m, ${\textstyle b=4}$m, elastic modulus ${\textstyle E=3.5\times 1{0}^{4\,}}$MPa, Poisson ratio ${\textstyle \mu =0.167}$, density ${\textstyle \rho =2500\,{\frac {\rm {kN}}{{\rm {m}}^{2}}}}$, thickness ${\textstyle h=15.75}$mm. Additionally, considered were foundation shear modulus ${\textstyle G=35.17{\frac {\rm {N}}{{\rm {cm}}^{3}}}}$, rigidity coefficients ${\textstyle k1=1.5706\times 1{0}^{4}{\frac {\rm {kN}}{\rm {m}}}}$, ${\textstyle k2=1.5830\times 1{0}^{4}{\frac {\rm {kN}}{\rm {m}}}}$ as well as loading equipment for aircraft (${\textstyle {P}_{0}=215000}$N).

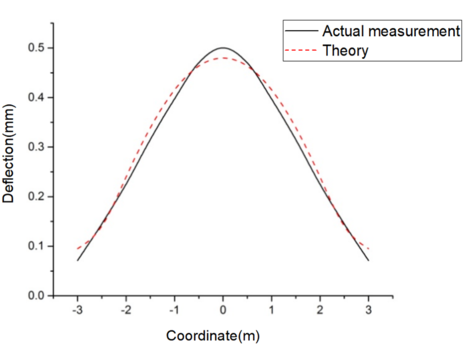
When the velocity reaches ${\textstyle 2.59}$ m/s and ${\textstyle y=1.1}$m, Table 1 presents both the measured and theoretical deflection values, while Figure 4 illustrates the fitting curve.

Table 1. Inversion results of foundation modulus (velocity = ${\textstyle 2.59}$ m/s and ${\textstyle y=1.1}$m)

Coordinate	0.0	0.5	1.0	1.5	2.0	2.5	3.0
Measured deflection(mm)	0.395	0.365	0.335	0.270	0.195	0.115	0.050
Theoretical deflectio(mm)	0.402	0.388	0.349	0.285	0.201	0.104	0.073
Deviation value(mm)	-0.007	-0.023	-0.014	-0.015	-0.006	0.011	-0.023
K(N/cm3)	58.33

Figure 4. Comparison curve between theoretical deflection and measured deflection

When the velocity reaches ${\textstyle 2.79}$ m/s and ${\textstyle y=0.68}$m, Table 2 presents both the measured and theoretical deflection values, while Figure 5 illustrates the corresponding fitting curve.

Table 2. Inversion results of foundation modulus (velocity = ${\textstyle 2.79}$ m/s and ${\textstyle y=0.68}$m)

Coordinate	0.0	0.5	1.0	1.5	2.0	2.5	3.0
Measured deflection(mm)	0.5	0.47	0.397	0.315	0.225	0.145	0.071
Theoretical deflection(mm)	0.485	0.469	0.420	0.343	0.242	0.127	0.060
Deviation value(mm)	0.015	0.001	-0.023	-0.028	-0.017	0.018	0.011
K(N/cm3)	58.40

Figure 5. Comparison curve between theoretical deflection and measured deflection

According to Tables 1 and 2, as well as Figures 4 and 5, it is evident that the theoretical deflection values align closely with the measured deflection values. This demonstrates that the dynamic model established in this paper accurately reflects real-world conditions. Furthermore, the stability and convergence of the parameter inversion method used have been proven.

6. Conclusions

(1) This study established a more accurate dynamic model for airport pavement systems, taking into account reasonable assumptions and simplifications of the foundation, loads, boundary conditions, and pavement panels. The model is a rigid thin plate pavement dynamic model that considers boundary shear and bending dual parameter foundation under moving loads. It accurately reflects the actual working state of rigid pavement and can be applied to the design of asphalt and overlay thickness on aircraft rigid pavement;

(2) The methods of variational method and reciprocal work theorem were used in this study to solve the differential equations of motion of the built dynamic system. An analytical solution for deflection was obtained, and an inversion calculation program based on the principle of least squares was compiled. Structural parameters of the rigid pavement panel were inverted and identified based on measured dynamic deflection. The stability, accuracy, and reliability of the identification method were verified through examples.

Acknowledgments

The authors would like to thank The Youth Innovation Team of Shaanxi Universities (Key Technology Innovation Team for Urban Rail Transit Track Bed); Youth fund project at Xi’an Jiaotong Engineering Institute (2023KY-39) and The Scientific Research Program Funded by Education Department of Shaanxi Provincial Government (Program No.23JK0532). Hui-min Cao and Han-jun Zhao contributed equally to this work.

References

[1] Zhang W., Chen X., Zuo X. Research on airport rigid pavement parameter identification on dynamic loading (in Chinese). Computer Simulation, 29(09):73-76+202, 2012.

[2] Chen X., Liu H. Dynamic identification simulation of foundation response modulus of airport (in Chinese). Computer Simulation, 26(07):54-57, 2009.

[3] Xing Y., Liu H. Foundation parameter identification research of airport rigid pavement (in Chinese). Central South Highway Engineering, (04):52-54, 2006.

[4] Patil V., Sawant V., Deb K. Finite element analysis of rigid pavement on a nonlinear two parameter foundation model. International Journal of Geotechnical Engineering, 6(3):275-286, 2012. DOI: 10.3328/IJGE.2012.06.03.274-286

[5] Kumar Y., Trivedi A., Shukla S.K. Deflections governed by the cyclic strength of rigid pavement subjected to structural vibration due to high-velocity moving loads.  Journal of Vibration Engineering & Technologies, 12:3543–3562, 2024.

[6] Taheri M.R., Zaman M.M . Effects of a moving aircraft and temperature differential on response of rigid pavements. Computers & Structures, 57(3):503-511, 1995. DOI:10.1016/0045-7949(94)00625-D

[7] Worku A., Lulseged A. Kinematic pile-soil interaction using a rigorous two-parameter foundation model. Soil Dynamics and Earthquake Engineering, 165, 107701, 2023.

[8] Li C.J., Zhang Y., Jia Y.M., Chen J. The polygonal scaled boundary thin plate element based on the discrete Kirchhoff theory. Computers & Mathematics with Applications, 97:223-236, 2021.

[9] Alisjahbana S.W., Wangsadinata W. Dynamic response of rigid roadway pavement under moving traffic loads. The 8th International Structural Engineering and Construction Conference, Sydney, Australia, 2015.

[10] Heitmann S., Aburn M.J., Breakspear M. The brain dynamics toolbox for Matlab. Neurocomputing, 315:82-88, 2018. DOI:10.1016/j.neucom.2018.06.026