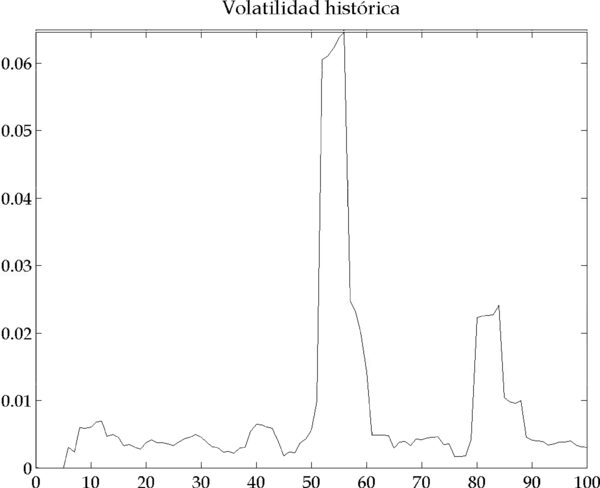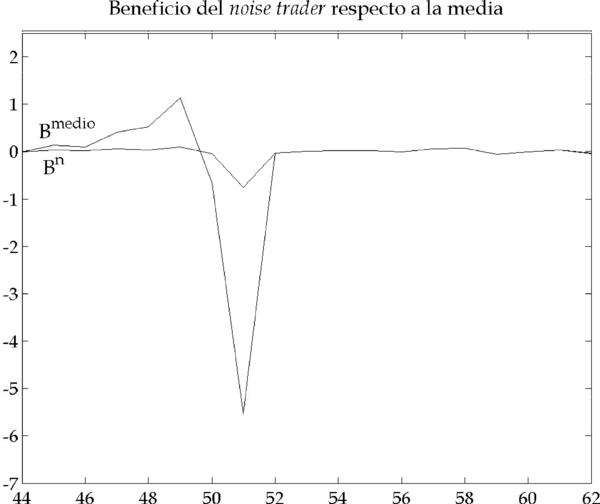(Created page with " <span id='_GoBack'></span> <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> <big>Modelo evolutivo del impacto de técnicas VaR en los </big>...") |
(Tag: Visual edit) |
||
| Line 3: | Line 3: | ||
<span id='_GoBack'></span> | <span id='_GoBack'></span> | ||
| − | < | + | === <big>Modelo evolutivo del impacto de técnicas VaR en los </big><big>mercados financieros<span id="fnc-1"></span><span style="text-align: center; font-size: 75%;">[[#fn-1|<sup>1</sup>]]</span></big> === |
| − | < | + | |
| − | + | ==== B. Llacay, G. Peffer ==== | |
| − | + | <span style="text-align: center; font-size: 75%;">Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE)</span> | |
| − | + | <span style="text-align: center; font-size: 75%;">E-mail: {llacay, [mailto:gilbert}@cimne.upc.es gilbert}@cimne.upc.es]</span><div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <span style="text-align: center; font-size: 75%;">E-mail: {llacay, [mailto:gilbert}@cimne.upc.es gilbert}@cimne.upc.es]</span> | + | |
| − | + | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | |
<span style="text-align: center; font-size: 75%;">'''Abstract'''</span></div> | <span style="text-align: center; font-size: 75%;">'''Abstract'''</span></div> | ||
Revision as of 14:29, 22 November 2016
Modelo evolutivo del impacto de técnicas VaR en los mercados financieros1
B. Llacay, G. Peffer
Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE)
E-mail: {llacay, gilbert}@cimne.upc.es| Recently, some authors have warned of the increasingly widespread use of risk management techniques by financial institutions, arguing that this can cause the market to become more unstable. To analyse these claims, we present a model based on evolutionary game theory of a financial market, where part of the investors use the VaR technique to manage their risk. We study the evolution of this market through simulation, and we confirm that the use of risk management models can induce instability regimes in the market, characterised by sudden changes in the asset price and sharp increases in the volatility. |
Key words: Risk management, VaR, Evolutionary game theory, Financial markets
(1) Artículo presentado en la 7th Spanish-Italian Meeting on Financial Mathematics (Cuenca, 8-9 Julio 2004)
1
Introducción
Durante el verano de 1998, los mercados financieros internacionales se vieron azotados por una de las crisis más importantes de las últimas décadas: la crisis de Rusia/LTCM. El LTCM (Long-Term Capital Management) era un fondo de cobertura especializado en operaciones de arbitraje2, principalmente en renta fija. Contaba entre sus filas con algunos de los más reputados especialistas, que trabajaban con los modelos de inversión y gestión de riesgo más avanzados del momento. Su rentabilidad era excepcionalmente alta, lo que lo puso en el punto de mira de los demás agentes del mercado, entre ellos los principales bancos de inversión del mundo. Sin embargo, pese a su buena gestión, el LTCM se vio sumido en pocos días en una crisis de la que sólo una intervención in extremis de la Reserva Federal de EEUU pudo salvarlo (Perold, 1999).
La crisis del LTCM ha sido objeto de estudio entre los analistas financieros, para llegar a desentrañar las causas que hicieron que uno de los fondos más solventes y con una gestión más cautelosa se viera abocado al borde de la quiebra. La explicación más plausible, proporcionada por MacKenzie (2003), se centra en el comportamiento imitativo de los inversores. Los sobresalientes beneficios del LTCM lo convirtieron en foco de atención de los otros agentes, quienes buscaron imitar sus estrategias de inversión para obtener mejores resultados. De esta manera, las posiciones del LTCM fueron replicadas por otros inversores, lo cual resultó nefasto en verano de 1998. Las medidas de gestión de riesgo – mayoritariamente VaR – empleadas por los agentes tampoco resultaron ajenas al desastre: al bajar el precio de algunos activos, aquellos inversores con un límite de VaR más bajo se vieron obligados a vender parte de su cartera, incluidos activos no directamente afectados por la caída, para evitar rebasar su nivel máximo de riesgo. Sin embargo, estas ventas aceleraron la caída de los precios e incrementaron la volatilidad, de manera que otros inversores con límites superiores de VaR se vieron obligados también a vender. Este proceso se realimentó a sí mismo, provocando caídas en los precios y drenando rápidamente la liquidez del mercado debido a que muchos agentes tenían carteras parecidas y se deshacían de los mismos activos. Esta situación puso en aprietos al LTCM, quien vio que su cartera perdía valor en poco tiempo y además no podía liquidar sus posiciones porque aquellos con los mismos activos en cartera se le habían adelantado, saturando el mercado. Cuando se supo de los problemas del LTCM, los precios de sus activos cayeron y además sus contrapartes, al intentar reducir sus pérdidas ante una posible quiebra del fondo consiguiendo tanto colateral como fuera posible, empujaron los precios en una dirección que precipitó efectivamente al LTCM casi a la quiebra.
Sin llegar a las consecuencias trágicas de la crisis del LTCM, algunos autores han alertado sobre las consecuencias devastadoras que para los mercados financieros puede tener la combinación de la utilización de técnicas de gestión de riesgo con un comportamiento imitativo de los inversores (Persaud, 2000). En los últimos años, mediante iniciativas como el Acuerdo de Basilea II, se ha promovido la adopción de técnicas de gestión de riesgo como el VaR por parte de las instituciones financieras. Con estas iniciativas se pretende estabilizar los mercados financieros frente al considerable número de crisis que los han azotado en las últimas décadas (FMI, 1998). En efecto, sería natural pensar que un mercado donde todos los participantes controlan y acotan el nivel de riesgo que asumen es más robusto frente a los shocks negativos y por ende más estable frente a las crisis. Ahora bien, tal como argumenta Persaud (2000), estas medidas se aplican a un mercado donde los inversores exhiben cada vez más un comportamiento seguidista. Replican la cartera de los otros, por ejemplo para explotar su información, o simplemente para obtener resultados parecidos, puesto que frecuentemente los agentes son recompensados por sus resultados relativos frente al resto de inversores. Si además emplean las mismas técnicas de gestión de riesgo, ante caídas de los precios se ven obligados a vender activos de sus carteras al mismo tiempo. Estas ventas simultáneas crean, de forma temporal, correlaciones superiores entre precios, lo cual incrementa la volatilidad en el mercado. Persaud afirma que en estas circunstancias, aunque parezca contradictorio, el comportamiento de los inversores sería más eficiente y el mercado, más estable, si sólo algunos de los agentes emplearan modelos de gestión de riesgo.
Actualmente nos encontramos por tanto ante la siguiente situación: por un lado, es aconsejable que las instituciones financieras regulen y controlen el riesgo que asumen y le pongan límites. Pero como hemos visto – y el caso del LTCM es un ejemplo palpable de ello –, en un mercado seguidista las medidas de riesgo adoptadas pueden inducir un efecto global desestabilizador, perjudicando a las propias instituciones financieras. Por consiguiente, un mercado donde todos empleen técnicas de gestión de riesgo como el VaR puede, en un contexto de comportamiento imitativo generalizado, no ser robusto, como también puede no serlo un mercado donde nadie gestione su riesgo. La proporción ideal de agentes que gestionen su riesgo con VaR debería oscilar entre estos dos escenarios, puesto que puede dar seguridad y ser beneficioso en un mercado donde pocos agentes lo hacen, pero puede causar inestabilidad cuando la mayoría lo hace. Esta situación un tanto paradójica viene causada no por el uso de medidas de gestión de riesgo en sí, sino por el tipo de medidas empleadas. Las técnicas – como el VaR – que utilizan las entidades financieras son estáticas, en el sentido de que se basan en variables globales históricas, como la volatilidad y las correlaciones entre activos, y no tienen en cuenta el comportamiento de los otros participantes del mercado (Morris y Shin, 1999), que lejos de ser inmutable, reacciona a los cambios y marca el rumbo de la evolución del mercado.
En el marco de este contexto, nos proponemos estudiar el efecto agregado del uso de técnicas de gestión de riesgo como el VaR en mercados donde los inversores pueden exhibir un comportamiento imitativo. Desarrollamos un modelo basado en la teoría de juegos evolutivos que se inspira en las causas de la crisis del LTCM descritas en los parágrafos precedentes. Consideramos un mercado de un solo activo cuyos inversores pueden elegir entre dos estrategias: por un lado pueden emitir sus órdenes basándose en un simple modelo de valoración y un modelo VaR de gestión de riesgo – relative value traders – o bien puede emitir sus órdenes de forma aleatoria – noise traders. Los relative value traders emulan de algún modo entidades como el LTCM y aquéllas que le siguieron, que utilizan los más avanzados modelos de valoración y gestión de riesgo y sus resultados se benefician de ello. El foco de nuestro artículo está en el modelo de gestión de riesgo, por lo que el modelo de valoración que emplean los relative value traders es lo más sencillo posible sin perder la capacidad de reflejar la superioridad de estos inversores frente a los que usan la estrategia aleatoria. Ambos tipos de agente siguen un comportamiento imitativo: cuando una de las estrategias proporciona unos beneficios superiores a los de la otra, una proporción de los inversores que usan la estrategia menos beneficiosa decide imitar a los que obtienen mejores resultados y adoptar su estrategia (esta proporción es tanto mayor cuanto más acusada sea la diferencia de beneficios). Estudiaremos qué efectos globales emergen de la interrelación entre los inversores, entre ellos la formación del precio, la volatilidad y la inestabilidad del mercado. Aunque se trata de un modelo muy estilizado, permite captar la inestabilidad que puede inducir la adopción generalizada de modelos estáticos de gestión de riesgo.
En la siguiente sección revisamos los conceptos de teoría de juegos evolutivos que empleamos en nuestro modelo, y presentamos brevemente la aplicación que se ha hecho hasta el momento de la teoría de juegos evolutivos en modelos de mercados financieros. En la Sección 3 explicamos el modelo que hemos creado, basado fundamentalmente en tres pilares: las estrategias empleadas por los inversores, el proceso de formación del precio y la evolución de la población de agentes. En la Sección 4 presentamos los resultados que hemos obtenido de la simulación del modelo, y analizamos la dinámica desestabilizadora que puede introducir el uso generalizado de medidas de gestión de riesgo. Finalmente, en la Sección 5 exponemos las conclusiones que se siguen de nuestro trabajo.
(2) Esencialmente, operaciones de arbitraje de convergencia y valor relativo (convergence y relative value trades)
2 Teoría de Juegos Evolutivos: Revisión de Conceptos
:2.1 Origen y Objetivos
Durante las últimas décadas, la teoría de juegos se ha aplicado profusamente en la modelización de problemas económicos y también financieros, pero impone hipótesis muy restrictivas, dotando por ejemplo a los agentes de una racionalidad ilimitada. Como reacción a estas limitaciones, y con el deseo de crear una teoría del comportamiento estratégico más cercana a la realidad, se ha desarrollado en los últimos 15 años una nueva línea de investigación dentro de la teoría de juegos, llamada teoría de juegos evolutivos. Ésta cuestiona y relaja algunos de los supuestos de la teoría de juegos tradicional, aportando una nueva visión sobre los problemas económicos y financieros.
La teoría de juegos evolutivos toma su nombre y sus técnicas básicas del trabajo hecho por biólogos en teoría de juegos para estudiar cómo las características de comportamiento que aportan los genes hacen que algunos organismos se adapten mejor a su entorno que otros (Samuelson, 1998). Los jugadores se seleccionan de una gran población de jugadores potenciales – se pueden considerar distintas poblaciones de jugadores si éstos juegan roles diferentes (Young, 1998). En un juego evolutivo no se supone que los agentes gozan de una sofisticada capacidad racional, sino que ésta se suple con un proceso de aprendizaje (Tadj y Touzene, 2003). Se supone que las estrategias empleadas por los jugadores son producto de un proceso de prueba y error en que los actores se dan cuenta de que algunas estrategias proporcionan mejores resultados que otras. De este modo, los jugadores aprenden qué estrategia les conviene usar, pero no lo hacen a través de un cálculo racional ilimitado, sino a partir de heurísticas, comportamiento imitativo, analogías con casos anteriores, etc. (Samuelson, 1998).
La teoría de juegos evolutivos permite salvar además otra de las limitaciones importantes de la teoría de juegos tradicional: el problema de selección de equilibrios. Uno de los conceptos fundamentales de la teoría de juegos es el de equilibrio de Nash3. Ahora bien, cuando un juego tiene más de un equilibrio, no se proporciona ningún criterio para escoger entre ellos. Ante este problema, la teoría de juegos evolutivos explicita el proceso dinámico a través del cual los jugadores ajustan sus acciones a lo largo del juego en respuesta a las acciones de los demás, de manera que se puede ver cómo se llega a un equilibrio a partir de la adaptación de las estrategias empleadas (Kandori et al., 1993).
(3) Una combinación de estrategias se dice que es un equilibrio de Nash si ningún jugador tiene incentivos para cambiar de estrategia si los otros jugadores mantienen la suya (Rasmusen, 1989)
:2.2 Enfoques de la teoría de juegos evolutivos
La teoría de juegos evolutivos presenta dos enfoques para el estudio de un juego. El primer enfoque se basa en el concepto de estrategia evolutivamente estable y el segundo, en la dinámica del modelo (Samuelson, 1998). En nuestro caso, hemos optado por el segundo enfoque, que como veremos se ajusta mejor a nuestras necesidades. A continuación, sin embargo, describimos brevemente ambos enfoques.
Estrategia evolutivamente estable
El enfoque original de la teoría de juegos evolutivos, basado en el trabajo de Maynard Smith y Price (1973) y Maynard Smith (1982) se centra en el concepto de estrategia evolutivamente estable (EEE). Este concepto se asocia a la robustez ante las perturbaciones en un sistema evolutivo. Supongamos que se seleccionan aleatoriamente individuos de una gran población de forma repetida para jugar a un juego de 2 jugadores. Supongamos que estos individuos inicialmente juegan una determinada estrategia. Introduzcamos ahora una proporción de individuos que juegan otra estrategia, llamada estrategia mutante. Se dice que la primera es evolutivamente estable si, para cualquier estrategia mutante, existe una barrera de invasión positiva tal que, si la proporción de individuos que juegan la estrategia mutante cae por debajo de esta barrera, entonces la primera estrategia proporciona unos resultados mejores que la estrategia mutante. Es decir, no es invadible por pequeñas proporciones de estrategias mutantes (Weibull, 1995).
Modelo dinámico
El enfoque alternativo consiste en construir un modelo dinámico que muestre cómo varían las proporciones de distintas estrategias en una población. Normalmente esta dinámica se aproxima por el valor esperado del proceso, que resulta en la llamada dinámica de réplica (Samuelson, 1998). La dinámica de réplica establece que si un tipo de jugador obtiene un payoff que está por encima de la media, entonces su porcentaje en la población aumenta, y éste disminuye si el payoff está por debajo de la media. La dinámica de un juego evolutivo se formaliza como el siguiente sistema de ecuaciones diferenciales ordinarias en caso de que se trabaje en tiempo continuo (Weibull, 1995):
donde es la proporción de la población que juega la estrategia
-ésima en el momento
,
es el payoff esperado para la estrategia
-ésima dada la población
, y
nota el payoff medio de la población
.
Cuando se opta por discretizar el proceso, la dinámica de réplica se formaliza como un sistema de ecuaciones en diferencias. Dado el origen biológico de la dinámica de réplica, se podrían albergar dudas respecto a su aplicabilidad en modelos económicos. Sin embargo (Samuelson, 1998), algunos autores han demostrado que la dinámica de réplica puede obtenerse a partir de modelos sencillos de aprendizaje (ver, por ejemplo, Börgers y Sarin (1997); Cabrales (1993) o Schlag (1994)). También parece natural aplicar la dinámica de réplica en contextos como el nuestro, donde el comportamiento seguidista o imitativo juega un papel importante. Aquellas estrategias que reportan mejores resultados son prontamente imitadas por otros agentes, incrementando por tanto su proporción en la población, de manera similar al proceso biológico de selección natural (Samuelson, 1998).
El enfoque basado en el concepto de estrategia evolutivamente estable y el enfoque dinámico no son absolutamente disjuntos, sino que tienen algunos puntos de encuentro. Por ejemplo, se puede demostrar que toda estrategia evolutivamente estable es un punto de equilibrio de la dinámica de réplica, aunque el recíproco no es cierto (Friedman, 1998).
Como hemos avanzado, nuestro modelo se basa en el segundo enfoque. Nos interesa estudiar la evolución de las estrategias empleadas por los inversores de un mercado financiero y para ello necesitamos emplear un modelo dinámico. El concepto de EEE es tan sólo un concepto de estabilidad. Aunque la idea es dinámica – informa de cuándo una estrategia es robusta frente a la introducción de estrategias mutantes en la población –, la definición es estática – no proporciona ningún indicio de cómo llegar a tal estado (Friedman, 2001).
:2.3 Aplicación de la teoría de juegos evolutivos en las finanzas
La teoría de juegos evolutivos, con su enfoque basado en la dinámica evolutiva y el aprendizaje, presenta buenas perspectivas para ser aplicada al campo de las finanzas. Supone un avance respecto a los estáticos modelos de equilibrio, que no especifican cómo ni cuándo se alcanzan los equilibrios, porque permite estudiar la evolución a lo largo del tiempo de los mercados financieros y analizar cómo se converge o no a los equilibrios propugnados por la teoría. En los últimos años se han desarrollado modelos de adaptación en el contexto de los mercados financieros que se basan cada vez más, de manera explícita o implícita, en la teoría de juegos evolutivos (Friedman, 2001).
En un juego evolutivo estándar, especialmente si se inscribe en el primer enfoque de la teoría de juegos, basado en la estabilidad evolutiva, se asume que los jugadores son seleccionados aleatoriamente y de forma repetida de una gran población para jugar a un juego de 2 jugadores (Samuelson, 1998). Pero esta formalización no acostumbra a tener sentido en un modelo que refleje el comportamiento de un mercado financiero, puesto que en este caso, los agentes ajustan su estrategia de acuerdo con el beneficio que con ella obtienen. Y este beneficio se obtiene del precio de los activos, que se determina por la acción agregada de todos los participantes del mercado. El precio se mueve en función de las órdenes que emite cada uno de los agentes, y éstos a su vez miran el precio para calcular su cartera. Delante de esta realidad, los juegos evolutivos estándares resultan insuficientes, porque no se puede construir un modelo mínimamente realista de un mercado financiero como un juego de sólo dos jugadores (a no ser que se trate de un mercado con pocos participantes lo suficientemente importantes como para mover los precios). En los últimos años se han publicado algunos artículos de modelos de teoría de juegos para mercados financieros donde se consideran juegos de jugadores o incluso se toman mercados formados por un continuo de agentes.
Por ejemplo, se ha estudiado con creciente interés los efectos y la supervivencia de inversores no racionales - con una percepción errónea de la distribución de los precios de los activos - en los mercados financieros (Wang, 2001). Se emplea un modelo de teoría de juegos evolutivos para estudiar cuál es la evolución a largo plazo de una población dinámica compuesta por inversores racionales y noise traders. Una de las primeras aportaciones a esta línea de investigación es (De Long et al., 1990, 1991) y ha recibido sucesivas contribuciones, entre las cuales podemos citar Palomino (1996) o Hirschleifer y Luo (2001).
En nuestro modelo estudiamos también la evolución a largo plazo de una población de inversores compuesta por dos tipos de agentes. Consideramos por un lado relative value traders que calculan los órdenes que emiten al mercado de acuerdo con un simple modelo de valoración y acotan además el nivel de riesgo en que incurren mediante la técnica del VaR. El resto de la población está formado por agentes que emiten órdenes aleatorios sin emplear ningún modelo. Veremos qué efectos causa en la dinámica del mercado el uso de modelos de gestión de riesgo en un entorno seguidista.
3 Descripción del Modelo
:3.1 Contexto general
En este artículo nos proponemos estudiar la influencia que tiene el uso generalizado de modelos de gestión de riesgo en la dinámica del mercado. Para ello desarrollamos un modelo en tiempo discreto basado en la teoría de juegos evolutivos para un mercado donde se negocia un único activo. Consideramos una población de inversores que pueden aplicar dos tipos de estrategia: llamamos relative value traders a aquellos agentes que emplean una estrategia basada en el uso de un simple modelo exógeno de valoración del activo más un modelo de gestión de riesgo, y noise traders a aquéllos que emplean una estrategia basada en una actuación aleatoria. Los agentes se sirven de estas estrategias para decidir qué órdenes emiten al mercado. A partir de las órdenes emitidas se forma un nuevo precio para el activo, que a su vez sirve a los inversores para evaluar su estrategia. Concretamente, los inversores miden los resultados obtenidos con su estrategia a través del beneficio obtenido. De aquellos inversores cuya estrategia les haya reportado peores resultados, algunos optarán por cambiar de estrategia e imitar a los inversores que hayan obtenido beneficios más altos, con lo cual la población de inversores irá evolucionando a través del tiempo en función de la evolución de los precios y de los órdenes emitidos.
Vemos, por tanto, que la dinámica del mercado se basa en tres procesos inextricablemente ligados entre ellos: la emisión de órdenes de acuerdo con una determinada estrategia, la formación de precios y la evolución de la población de inversores. Los tres procesos se relacionan unos con otros de tal manera que cada uno de ellos es necesario para determinar los restantes. Podemos esquematizar el vínculo entre los tres procesos de la forma siguiente:
|
| ||||||||
| Figura 3.1 – Procesos que rigen la dinámica del mercado |
A continuación explicamos cómo hemos modelizado cada uno de los tres procesos.
:3.2 Las estrategias de los agentes
Como ya hemos mencionado, consideramos dos tipos de agente, dependiendo de la estrategia que emplee: relative value trader y noise trader.
Relative value trader
Los relative value traders emiten su orden basándose en un simple modelo exógeno de valoración y un modelo de gestión de riesgo.
Modelo de valoración: suponemos que los relative value traders reciben información - la misma para todos los inversores - acerca de los dividendos que pagará el activo. Con esta información, los inversores se forman una opinión acerca del valor de éste. De acuerdo con este valor, un relative value trader decidirá comprar si considera que el activo está infravalorado, y por contra decidirá vender si considera que está supervalorado. Además, la cantidad de activo que comprará o venderá es proporcional a la diferencia entre precio y valor. Si denota el orden que emite un relative value trader en tiempo
, entonces (Farmer, 1998)
donde es una constante,
es el precio del activo en tiempo
y
es su valor.
El valor se forma a partir de la información
que se recibe acerca de la variación prevista del precio:
. Por tanto,
En nuestro modelo formalizamos tal como sigue:
donde se distribuye bajo una uniforme, y
sigue una distribución de Poisson de parámetro
.
es por tanto un proceso estocástico escalonado, donde cada cierto tiempo los inversores reciben nueva información acerca del valor del activo.
Modelo de gestión de riesgo: el modelo de gestión de riesgo implementado sigue la metodología VaR ('value-at-risk'), que determina la distribución de probabilidad para el beneficio o pérdida de una cartera en un cierto horizonte de tiempo. Se trata de una medida de gestión de riesgo cuyo uso se ha ido extendiendo entre las instituciones financieras. Los relative value traders deben calcular en cada instante de tiempo el nivel de riesgo en que están incurriendo dada su cartera actual y la volatilidad del precio del activo. Para ello, se supone que la diferencia de precios sigue una distribución normal
, donde
es la volatilidad del activo. Bajo esta distribución, se estima que con un 95% de probabilidad, la pérdida que puede sufrir la cartera de un periodo al siguiente es
por cada unidad de activo. Los relative value traders fijan un límite
al riesgo que están dispuestos a asumir. Si la pérdida estimada de la cartera supera
, entonces los relative value traders se verán obligados a reducir sus posiciones y ajustar su cartera hasta alcanzar un nivel de riesgo por debajo del límite máximo permitido.
Como hemos mencionado, los relative value traders necesitan conocer la volatilidad en cada instante de tiempo para poder utilizar el modelo VaR. En nuestro modelo calculamos la volatilidad a tiempo ,
, utilizando el precio de los 5 periodos anteriores, con la fórmula
donde se resta el término en cada periodo para cancelar las tendencias lineales en el precio del activo.
Noise traders
Los noise traders emiten sus órdenes de acuerdo con una distribución uniforme
donde fija el rango dentro del cual un noise trader emite sus órdenes. Este tipo de inversor contribuye a proporcionar liquidez al mercado.
:3.3 Formación del precio
Gran parte de la literatura de modelización de mercados financieros asume que el precio se forma a partir de la condición de equilibrio económico. Los precios se ajustan para que la oferta iguale la demanda, y sólo cuando se alcanza el precio de equilibrio se efectúan las correspondientes transacciones. Sin embargo, este procedimiento no refleja el mecanismo real de la mayoría de mercados financieros modernos (Farmer, 2000).
El proceso de formación de precios que consideramos no se basa en condiciones de equilibrio, sino en el exceso de demanda, es decir, demanda menos oferta. Los agentes emiten sus órdenes de acuerdo con las estrategias detalladas en la sección anterior. El precio se forma a partir del precio anterior, teniendo en cuenta el exceso de demanda del activo. Si más agentes desean comprar que vender, el precio subirá, y viceversa si las órdenes de venta superan en número a las de compra. Así pues, suponemos que el nuevo precio depende del precio anterior y del orden neto de la forma siguiente
donde es la suma de las órdenes emitidas por los dos tipos de agente ponderadas de acuerdo con su proporción correspondiente
y
en el mercado (ver Sección 3.4), y
es una constante que refleja la liquidez del mercado.
:3.4 Evolución de la población
Una vez los agentes han emitido sus órdenes al mercado de acuerdo con sus respectivas estrategias – bien basándose en modelos, bien de forma aleatoria – y se ha formado un nuevo precio para el activo a partir del exceso de demanda, los inversores pueden evaluar el éxito de su estrategia a través de los beneficios obtenidos. La estrategia que haya reportado mejores resultados tenderá a ser adoptada por más agentes, y por consiguiente su proporción en la población aumentará. Por el contrario, la proporción de agentes que empleen la estrategia menos beneficiosa descenderá porque algunos de éstos pasarán a adoptar la otra estrategia. La dinámica de la población puede entenderse como un proceso de imitación, puesto que aquellos agentes que obtienen mejores beneficios con su estrategia son imitados por una parte de la población, que adopta la misma estrategia.
Hemos visto en la Sección 2.2 que la teoría de juegos evolutivos modeliza este tipo de procesos mediante la dinámica de réplica. Nosotros consideramos una dinámica de réplica en tiempo discreto. Denotamos por la proporción de relative value traders en la población a tiempo
. Entonces, formalizamos la evolución de la población mediante la ecuación (Hofbauer y Sigmund, 2003)
donde indica el beneficio obtenido a tiempo
por un relative value trader, y
es el beneficio dado por el empleo de la estrategia aleatoria. Aunque esta ecuación no es el equivalente en tiempo discreto de la ecuación diferencial de la dinámica de réplica (ver Sección 2.2), nos proporciona una formulación alternativa que se comporta mejor.
4 Resultados de la Simulación
Dadas las características del modelo – donde las órdenes se emiten siguiendo modelos estocásticos y se ajustan mediante un modelo de gestión de riesgo –, y la complejidad derivada de la interrelación entre sus distintas componentes, la simulación es la única herramienta para explorar los resultados del modelo. Presentamos a continuación tres casos basados en configuraciones diferentes del modelo, permitiendo explorar las posibilidades y limitaciones de éste, y extraer consecuencias de distinto tipo.
:4.1 Primer caso: modelo de valoración vs. estrategia aleatoria
En esta primera configuración del modelo, la más simple, consideramos que la población está formada por dos tipos de inversores, que se identifican con la estrategia que usan:
* Relative value traders: utilizan una estrategia basada en un simple modelo de valoración (ver Sección 3.2). En este primer caso, supondremos que este tipo de agentes no emplean ningún modelo de gestión de riesgo. Los relative value traders reciben información sobre el cambio en los precios, a partir de la cual emiten sus órdenes acordemente. Modelizamos la información recibida como un proceso escalonado,
, donde
y
. Una vez conocida esta información, los relative value traders emiten sus órdenes:
, donde
.
* Noise traders: emiten sus órdenes de forma aleatoria, siguiendo una distribución uniforme de parámetros fijados: .
Este primer ejemplo no es el foco de atención del artículo, puesto que ninguno de los inversores emplea un modelo de gestión de riesgo, sino que se basan solamente en un modelo de valoración. Sin embargo, creemos oportuno estudiar primero los resultados que se derivan de este caso para mostrar el modelo básico sobre el cual implementaremos un modelo de gestión de riesgo. Familiarizarnos con este modelo de base nos permitirá estudiar qué efectos produce el modelo de valoración empleado por los relative value traders, y seremos capaces por tanto de identificar y aislar después las perturbaciones inducidas por el uso de un modelo de VaR.
|
Figura 4.1 – Información recibida y órdenes emitidos por los relative value traders (Parámetros: |
Cuando los relative value traders reciben una información que le permite prever una tendencia en el precio – sea alcista o bajista -, esta previsión se cumple por su propia naturaleza. Como vemos en la Figura 4.1, estos inversores reciben una información que augura una subida paulatina en los precios. Delante de estas circunstancias, emiten órdenes de compra. Y justamente el precio reacciona al alza (Figura 4.2) frente a las órdenes emitidas en el mercado – de forma tímida en las primeras iteraciones porque las órdenes son de poca magnitud y hay por tanto poco movimiento en el mercado, pero de manera clara cuando el los relative value traders empiezan a emitir órdenes de mayor magnitud como resultado de la información recibida.
|
Figura 4.2 – Evolución del precio (Parámetros: |
Este movimiento de los precios favorece a los relative value traders, ya que coincide con su previsión de variación de precios, y esto les permite hacerse con más beneficios que los inversores que actúan de manera aleatoria (Figura 4.3). Como sus resultados son mejores, por la dinámica de réplica algunos noise traders, que han obtenido beneficios inferiores, les imitan, de manera que el número de relative value traders aumenta a costa del número de noise traders. Cuantos más inversores actúan de acuerdo con la previsión alcista, más peso específico tienen sus órdenes en el mercado y marcan aún más fuertemente la tendencia en el precio, que a su vez les beneficia y les permite extenderse. Como vemos (Figura 4.4), es un proceso que se realimenta a sí mismo, hasta converger en una población dominada completamente por relative value traders, que pueden entonces controlar perfectamente la evolución de precios.
|
Figura 4.3 – Beneficio de los dos tipos de inversor (Parámetros: |
|
Figura 4.4 – Evolución de la población (Parámetros: |
Se llega de esta manera a un mercado estable, porque en esta situación se ha extinguido la posibilidad de cualquier movimiento de signo contrario que pueda desestabilizar la situación. La volatilidad desciende hasta hacerse prácticamente nula4 (Figura 4.5).
|
Figura 4.5 – Volatilidad histórica (Parámetros: |
Se trata de un escenario en general poco realista – aunque, de hecho, el proceso de formación de una burbuja financiera no difiere mucho en esencia de la situación expuesta en el caso de que las expectativas no se alimenten de factores fundamentales. Como ya hemos comentado, el objetivo de este primer caso es introducir una parte del modelo, la correspondiente al modelo de valoración, para estudiar en detalle qué efectos induce en la dinámica del mercado. En el siguiente caso veremos cómo se modifica el escenario cuando los relative value traders usan además un modelo de gestión de riesgo.
(4) Observamos que como la volatilidad se calcula con los precios históricos de los 5 periodos anteriores, no puede computarse en los 5 primeros pasos de tiempo, y como muestra la Figura 4.5,le damos valor cero.
:4.2 Segundo caso: modelo de valoración y VaR vs. estrategia aleatoria
Como hemos mencionado previamente, el objetivo principal de este artículo es estudiar el efecto que produce el empleo de modelos de gestión de riesgo en la estabilidad del mercado. Es en este segundo caso donde acometemos tal objetivo. Para que los resultados sean lo más diáfanos posible y permitan interpretar los efectos derivados del uso de la técnica VaR, consideramos una configuración del modelo sencilla, con dos grupos de inversores, cada uno de los cuales sigue una de las siguientes estrategias:
* Relative value traders: como en el caso anterior (Sección 4.1), reciben información sobre el cambio en los precios, modelizada como un proceso escalonado, a partir de la cual calculan el orden que les convendría emitir:
, donde
(ver Sección 3.2). Pero, y aquí reside la variación respecto al primer caso, emplean un modelo de gestión de riesgo basado en la metodología VaR. Antes de emitir un orden al mercado, comprueban que el nivel de riesgo que comportaría sea asumible. Tal como se expone en la Sección 3.2, los relative value traders estiman en cada iteración, con un 95% de confianza, la pérdida que pueden sufrir en el periodo
con la cartera que poseen:
, donde
es la volatilidad del mercado y
, la posición acumulada por el agente a tiempo
. Los agentes comparan esta pérdida con el límite máximo de riesgo que están dispuestos a asumir,
, y en caso de que supere el límite, se verán obligados a modificar su posición de manera que el nivel de riesgo se mantenga dentro del límite. Esta reducción influirá otras variables, como el precio y la evolución de la población, lo cual introducirá una nueva dinámica en el mercado no presente en el primer caso mostrado.
* Noise traders: como antes, emiten sus órdenes de forma aleatoria, siguiendo una distribución uniforme de parámetros fijados: .
Dependiendo de los valores que se dan a los parámetros – por ejemplo, los parámetros ,
o
de las distribuciones uniformes y de Poisson que siguen los inversores al emitir sus órdenes, o bien el límite de riesgo
– se obtienen regímenes distintos como resultado de las simulaciones. Hemos visto en el caso anterior un ejemplo donde la población convergía a un mercado dominado por el primer tipo de inversor. Si se utiliza un modelo de gestión de riesgo pero se fija un límite
muy alto, de manera que no se alcance nunca, obtendremos un régimen como el mostrado en el caso anterior, porque el modelo VaR, aunque implementado, no se usa efectivamente. Por otro lado, si se fija un límite
muy bajo, se limita extraordinariamente la magnitud de los órdenes que pueden emitir los relative value traders, lo cual los deja en inferioridad de condiciones frente a los noise traders, que a la larga se hacen con el control del mercado.
En un rango intermedio de valores de , el mercado muestra a menudo un régimen de tipo oscilante en la población como el que estudiaremos a continuación. En términos generales, son regímenes donde los relative value traders emiten sus órdenes de acuerdo con su modelo de valoración y controlando en todo momento que no se exceda el límite de riesgo
. Si obtienen beneficios superiores a los noise traders, algunos de éstos adoptarán también un modelo de valoración y un modelo de gestión de riesgo, de manera que cada vez más inversores utilizarán una estrategia basada en modelos. Ahora bien, si se da el caso de que en algún momento se excede el límite de VaR, es decir,
, donde
es la volatilidad del mercado y
, la posición acumulada por el agente a tiempo
, entonces estos inversores se verán obligados a reducir su cartera hasta una posición
tal que el nivel de riesgo asociado quede dentro de los límites, es decir,
. Esta reducción de posiciones impactará en los precios, lo que incrementará la volatilidad. Esta subida puede hacer que los relative value traders tengan que reducir aún más su cartera porque, con las mismas posiciones, un incremento de volatilidad conlleva un incremento de riesgo. De esta manera, se entra en un proceso que puede desembocar en ventas precipitadas5, una caída de precios, un disparo de la volatilidad, pérdidas cuantiosas para los inversores y en consecuencia, una recomposición de la población. Después de este intervalo de inestabilidad, el mercado recupera la calma y poco a poco se vuelve al comportamiento inicial, con el peligro consiguiente de que se repita la situación de inestabilidad.
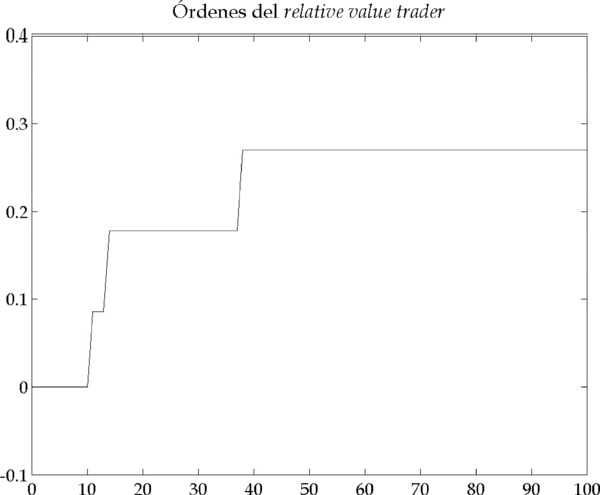
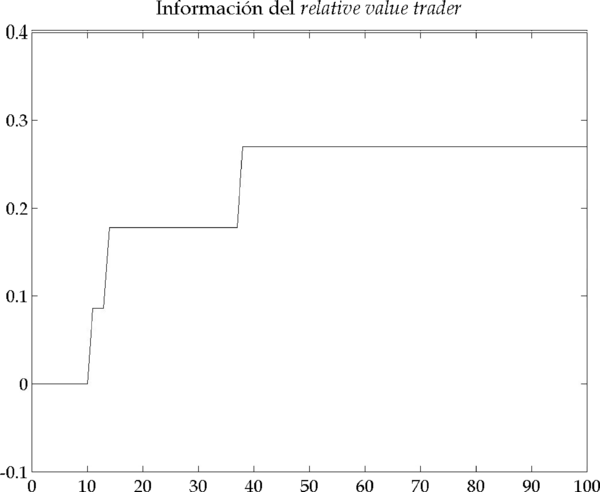
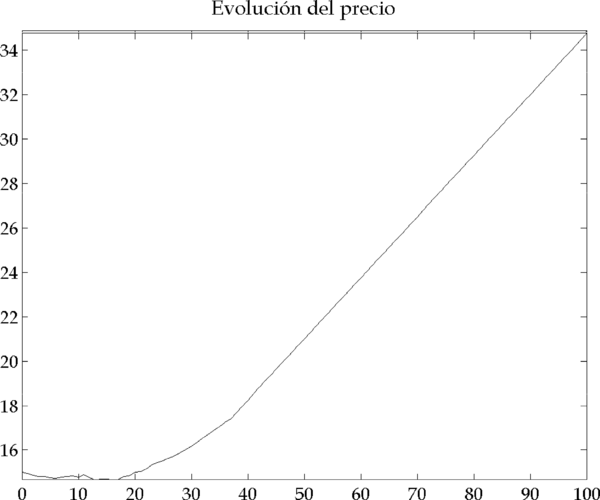
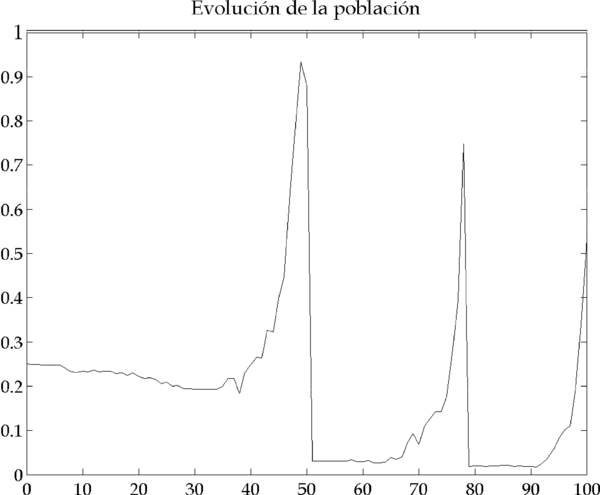
En un caso de estas características, la simulación muestra unos resultados como los de la Figura 4.6, que recogen la dinámica que acabamos de esbozar.
|
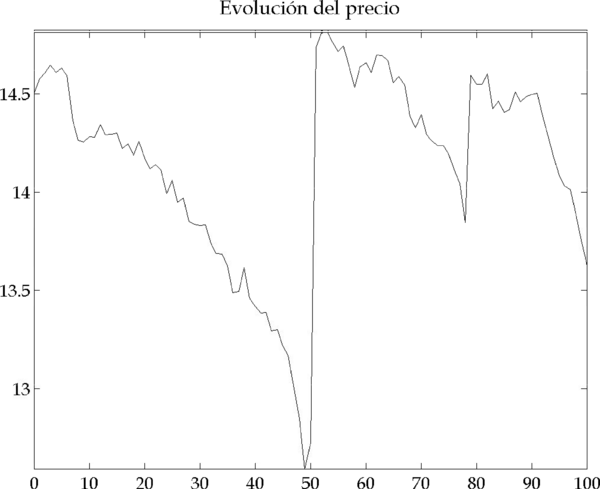
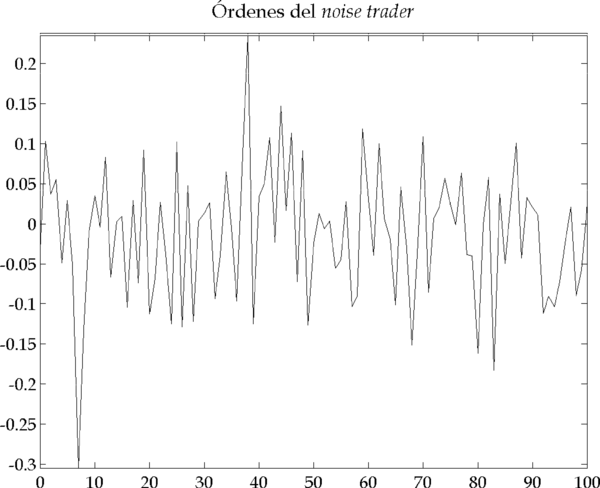
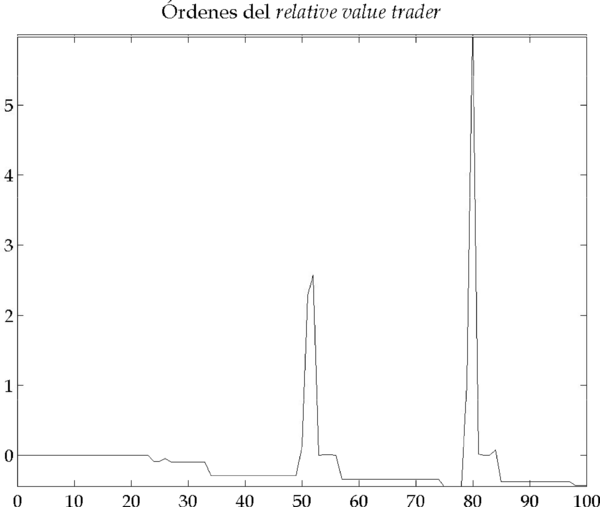
Figura 4.6 – Resultados de la simulación (Parámetros: |
En los gráficos de la Figura 4.6 se identifican con claridad dos picos que corresponden a dos periodos de inestabilidad en el mercado. Veamos ahora en detalle cómo y por qué se originan estos picos, analizando el primero de ellos (el segundo se origina por causas análogas).
Hasta la iteración 49, los relative value traders emiten sus órdenes siguiendo la información que reciben: , donde, en este caso,
. Como la previsión es que los precios bajen, acumulan órdenes de venta que forman una cartera corta (Figura 4.7).
|
Figura 4.7 – Información recibida y órdenes emitidos por los relative value traders (Parámetros: |
Hasta este momento, el nivel de riesgo asumido, , no excede el límite fijado,
. Se acumula una posición
tal que, en la iteración 50, un pequeño aumento de la volatilidad
causado por los movimientos de los noise traders hace que se toque el límite de riesgo, fijado en
(Figura 4.8) y los inversores se vean obligados a reducir su cartera.
|
Figura 4.8 – Volatilidad histórica y nivel de riesgo de los relative value traders (Parámetros: |
|
Figura 4.9 – Evolución del precio (Parámetros: |
Esta reducción de cartera de los relative value traders – orden de compra porque la cartera es corta – causa una subida del precio (Figura 4.9), que incrementa la volatilidad (Figura 4.8).
El incremento de volatilidad hace que la cartera conlleve un mayor nivel de riesgo, de manera que los relative value traders se vuelven a ver obligados a deshacer algunas de sus posiciones. Esta variación en la cartera es más marcada que la anterior, de manera que las otras variables también sufren cambios más bruscos: el precio sube claramente (Figura 4.9) y la volatilidad se dispara (Figura 4.8).
Estos movimientos hacen que los relative value traders incurran en pérdidas y, al ser sus beneficios inferiores a los beneficios medios de la población (Figura 4.10), por el mecanismo de dinámica de réplica (ver Sección 3.4) su porcentaje en la población disminuye en las iteraciones 50-51 (Figura 4.11). Esta disminución podría interpretarse como la desaparición de algunos inversores del mercado, puesto que pérdidas de este calibre pueden llevar algunos agentes a la quiebra financiera. Sin embargo, en nuestro modelo no implementamos de forma explícita este mecanismo.
|
Figura 4.10 – Beneficio de los dos tipos de inversor (Parámetros: |
|
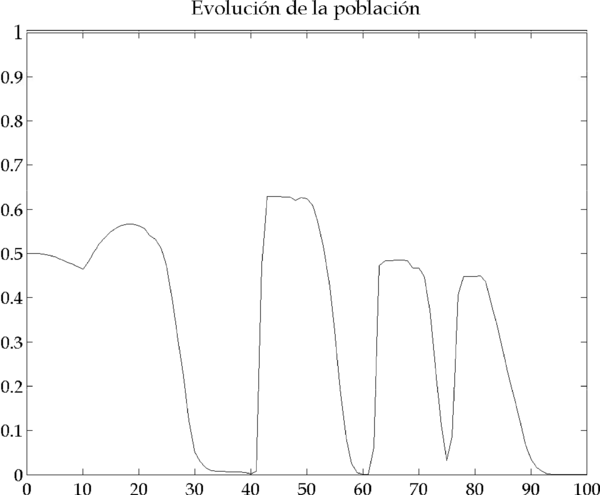
Figura 4.11 – Evolución de la población (Parámetros: |
La alta volatilidad a partir de la iteración 52 hace que los relative value traders sólo puedan emitir órdenes muy pequeños en valor absoluto para no sobrepasar su límite de riesgo . Esta reducción de los órdenes, juntamente con la caída de
, la proporción de relative value traders en la población (Figura 4.11), ayuda a recuperar la estabilidad del mercado, porque los precios varían poco (Figura 4.9) y la volatilidad disminuye (Figura 4.8). Sin embargo, a medida que se estabiliza el mercado, se vuelve al comportamiento previo a la caída de precios, de manera que se puede entrar en un régimen donde se alternan de forma cíclica periodos de estabilidad y crecimiento del mercado con periodos de inestabilidad marcada y pérdidas cuantiosas.
Vemos con este ejemplo paradigmático que la implementación de un modelo de gestión de riesgo puede aportar inestabilidad al mercado, con cambios sustanciales de precios y aumentos indiscriminados de la volatilidad. Esta situación reconfigura la población de inversores, eliminando aquellos inversores con pérdidas más acusadas e incorporando nuevos inversores que optan por una estrategia aleatoria porque les reporta beneficios superiores a la media en estas circunstancias convulsas. Aun siendo un modelo muy simple, permite captar algunas de las dinámicas observadas en los mercados reales, como en la crisis del LTCM.
Sin embargo, cabe observar algunas de las limitaciones de nuestro modelo. La más destacada es la homogeneidad de la población de inversores. La población está formada sólo por dos tipos de inversores, y todos los inversores del mismo tipo son idénticos (reciben la misma información, tienen el mismo límite de VaR, se rigen por la misma distribución de probabilidad). Este hecho no sólo es poco realista, sino que induce una dinámica muy marcada en el modelo. Los inversores del mismo tipo actúan todos a la vez y en la misma dirección, de manera que el resultado de sus acciones se ve magnificado. En un mercado real encontramos gran variedad de inversores. Si bien la mayoría emplean la metodología de VaR, tienen límites distintos, lo cual los hace actuar de formas diferentes. Esto hace que no todos se vean obligados a comprar o vender simultáneamente, sino que en un primer instante sólo aquellos con un límite VaR más bajo se ven abocados a reducir sus posiciones. El impacto que éstos causan en el mercado puede llevar a otros inversores a alcanzar su límite de riesgo y a reducir su cartera, de manera que se entra en una reacción en cadena de efectos devastadores, tal y como sucedió en la crisis del LTCM (MacKenzie, 2003).
Nuestro modelo, al constar únicamente de dos poblaciones, no puede mostrar este proceso en cadena en toda su magnitud. Sin embargo, sí podemos estudiar la dinámica de un mercado donde interactúan dos grupos de inversores que utilizan un modelo de gestión de riesgo con diferentes límites de VaR. Presentamos los resultados de este caso a continuación, como ejemplo final de la sección y puerta abierta a otros modelos con más variedad de inversores.
(5) En caso de que la cartera sea larga. Si ésta es corta, entonces se reacciona con compras precipitadas.
:4.3 Tercer caso: 2 modelos de VaR con límites distintos
Supongamos ahora que la población está constituida por dos grupos de relative value traders. Los dos grupos utilizan un modelo de valoración y un modelo de gestión de riesgo, guiándose por las mismas reglas que los relative value traders del ejemplo anterior (Sección 4.2). Ambos grupos se diferencian únicamente por la información que reciben y su límite de VaR. Como en el ejemplo anterior, modelizamos la información que reciben como un proceso escalonado. Notaremos la información recibida por el primer grupo de relative value traders por , que viene dado por
De forma análoga, utilizaremos la notación para indicar la información recibida por el segundo grupo de relative value traders. Ésta viene dada por
Los dos grupos de inversores calculan los órdenes que les convendría emitir de acuerdo con la información recibida: . Pero antes de emitir este orden al mercado, comprueban que su cartera no supere el nivel máximo de riesgo,
.
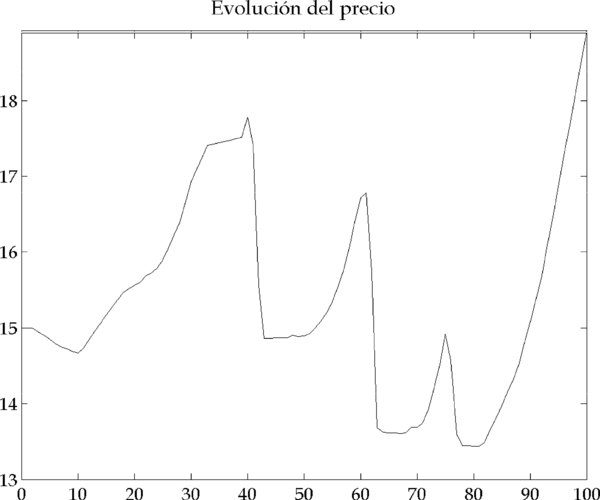
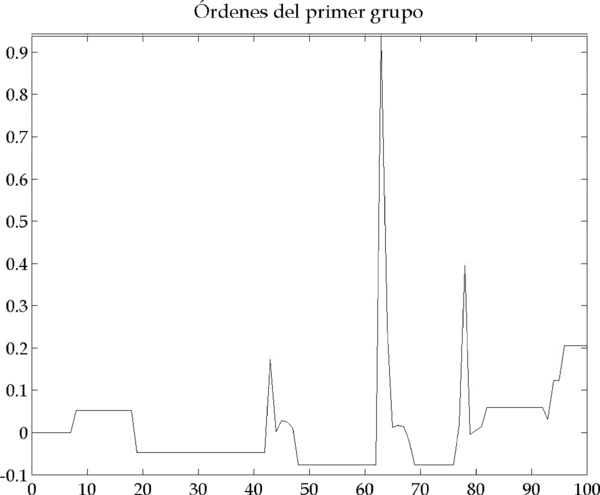
En este caso, los movimientos de un grupo de inversores pueden causar una reacción en el mercado que lleve a los otros inversores a reducir su cartera, acelerando el proceso de inestabilización del mercado. La Figura 4.12 muestra los resultados de un caso de este tipo, que a continuación analizaremos más en detalle.
|
Figura 4.12 – Resultados de la simulación (Parámetros: |
Observamos nuevamente un proceso de tipo cíclico. A modo de ejemplo, estudiaremos en detalle el proceso que lleva a la primera subida marcada de los precios (las causas de éste y los otros ciclos son análogas).
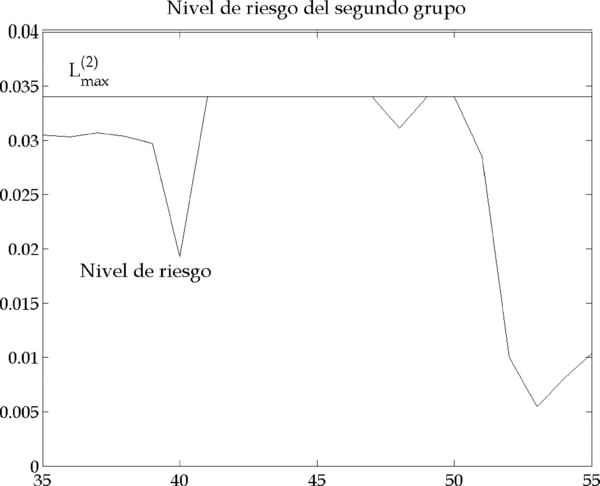
Hasta la iteración 41, ambos grupos de inversores emiten las órdenes que les dicta su información (Figura 4.13 y Figura 4.14), sin ninguna distorsión causada por el modelo de gestión de riesgo. Sin embargo, en las iteraciones 41-42 el segundo grupo de inversores se ve obligado a vender porque ha sobrepasado su límite de VaR (Figura 4.15).
|
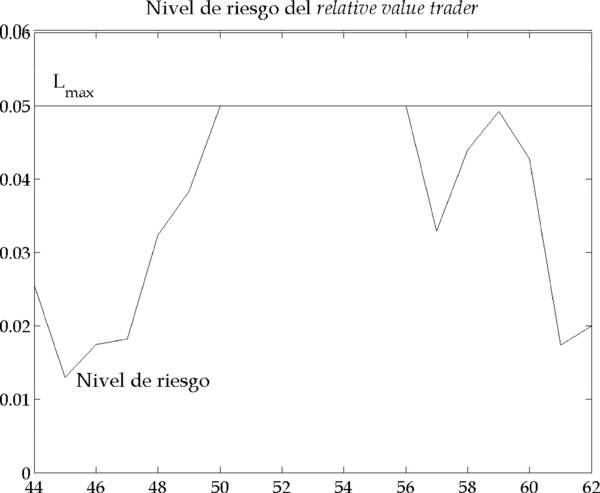
Figura 4.15 – Nivel de riesgo del segundo grupo de relative value traders (Parámetros: |
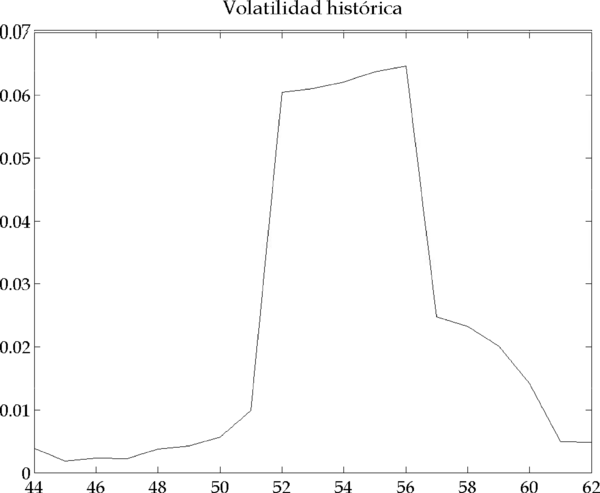
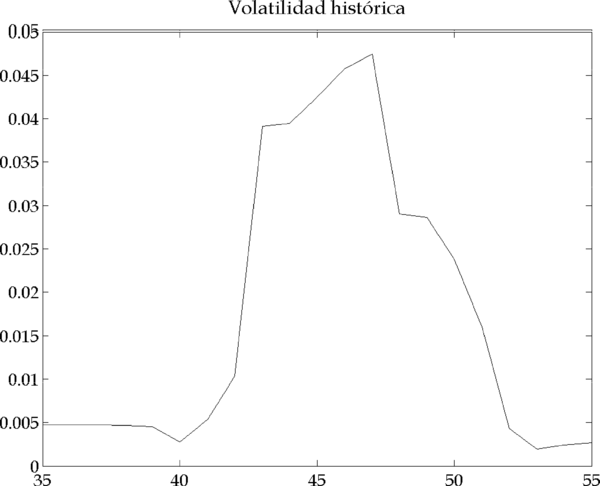
El orden de venta que emite el segundo grupo de inversores en las iteraciones 41-42 hace bajar fuertemente los precios e incrementar por tanto la volatilidad (Figura 4.16).
|
Figura 4.16 – Evolución del precio y volatilidad histórica (Parámetros: |
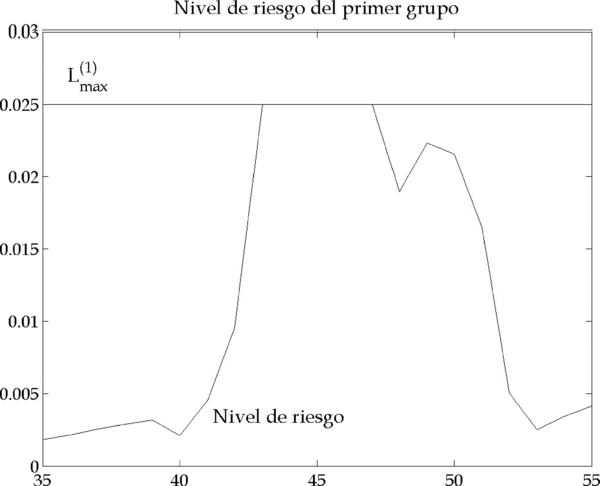
Por el incremento de volatilidad en la iteración 43 (Figura 4.16), la cartera del primer grupo de inversores se vuelve de repente más arriesgada, llegando a rebasar su límite de VaR, , en la iteración 43 (Figura 4.17). Por tanto, también este grupo de inversores se ve obligado a cortar su posición, emitiendo un orden de compra porque su cartera es corta (Figura 4.13).
|
Figura 4.17 – Nivel de riesgo del primer grupo de relative value traders (Parámetros: |
Los órdenes de compra del primer grupo de relative value traders se deben a la alteración en el mercado que causa el segundo grupo en las iteraciones 41-42 al vender por culpa de su modelo de riesgo. De esta manera, vemos que ambos grupos de inversores deben reducir su cartera, lo que impacta en los precios y dispara la volatilidad (Figura 4.16).
Observamos por tanto que los efectos que causa el modelo de gestión de riesgo de una parte de la población se puede contagiar al resto de la población, amplificándose y entrando en una espiral de inestabilidad. Nuestro modelo, al constar sólo de dos poblaciones, muestra en menor medida este efecto de contagio, pero si hubiera más grupos de inversores con otros límites de VaR, se podrían ver arrastrados sucesivamente por esta espiral desestabilizadora, magnificando aún más sus efectos.
5 Conclusiones e Investigaciones Futuras
Hemos visto que la introducción de medidas de gestión de riesgo, aunque está dirigida a hacer el mercado más estable, a veces puede tener justamente el efecto contrario, como sostienen Persaud (2000) o MacKenzie (2003). Hemos constatado que el uso de técnicas como el VaR puede inducir caídas de precios e incrementos de la volatilidad en el mercado. Cuando se transpone esta situación a los mercados reales, se puede traducir en la quiebra de instituciones financieras que, en caso de propagarse a otros agentes, nos situaría frente a una crisis financiera.
Ahora bien, tal como hemos comentado anteriormente, nuestro modelo es muy simple y uno de sus puntos débiles es la homogeneidad de sus inversores. Por un lado, nuestro modelo sólo admite dos grupos distintos de inversores. Por tanto, el modelo podría enriquecerse con la inclusión de más grupos de inversores con comportamientos distintos. Por ejemplo, en la Sección 4.3 hemos presentado los resultados de un modelo donde la población está formada por dos grupos de relative value traders con distinto límite de riesgo. Aunque este modelo, a pesar de su sencillez, nos permite vislumbrar cómo los efectos de las acciones de un grupo pueden contagiarse al otro, si la población de inversores estuviera formada por más tipos de agentes, el comportamiento del mercado se vería enriquecido y permitiría estudiar una situación más realista – no tan estilizada – de contagio entre los distintos grupos de agentes, y de amplificación de las perturbaciones en el mercado causadas por uno de los grupos.
Por otro lado, el modelo adolece de una excesiva uniformidad entre los componentes de un mismo grupo de inversores. Esta limitación viene impuesta por la propia naturaleza de la teoría de juegos evolutivos. Tal como hemos dicho en la Sección 2.1, en un juego evolutivo los jugadores se seleccionan de una gran población de jugadores potenciales. Estos jugadores son homogéneos, tan sólo se diferencian por la estrategia que eligen. Y no hay ninguna manera de distinguir dos jugadores que empleen la misma estrategia. Por tanto, todo modelo basado en la teoría de juegos evolutivos debe tratar con grupos de agentes idénticos, lo que de manera inevitable influye en la dinámica del modelo. Para superar esta limitación, podríamos recurrir a otro paradigma de modelización, como los modelos multi-agentes, que permiten trabajar con poblaciones de agentes tan heterogéneos como se desee (ver, por ejemplo, (LeBaron, 1998); o (Tesfatsion, 2002)).
También debemos admitir que el perfil de los noise traders, que actúan aleatoriamente, es demasiado estilizado. Se ha pretendido construir un modelo tan simple como fuera posible que a la vez captara y pusiera de relieve los efectos de la adopción de medidas de riesgo de un entorno seguidista. Sin embargo, de cara al futuro se contempla la construcción de una modelización más realista de los distintos tipos de inversores.
Como conclusión final de nuestro trabajo, queremos lanzar una nota de advertencia sobre el uso indiscriminado de técnicas de gestión de riesgo como el VaR. Aunque en determinados entornos su empleo puede reportar seguridad a los agentes financieros y estabilidad y robustez al mercado, ante determinadas circunstancias su efecto puede ser pernicioso, haciendo peor el remedio que la enfermedad. De esto no se deduce que sea mejor que nadie emplee ninguna medida de gestión de riesgo, sino que se pone el acento en el tipo de medida usada. El VaR, como muchas otras medidas de riesgo, se basa en datos históricos y no tiene en consideración el efecto que las acciones del propio inversor tendrán en el mercado ni –de forma más importante –, el efecto que tendrán las reacciones de los demás inversores. Es por tanto esencial, desarrollar modelos de gestión de riesgo que contemplen el aspecto estratégico, es decir, la interrelación entre los distintos agentes de mercado y la incidencia de las acciones de unos sobre los otros.
Referencias
Börgers, T. y Sarin, R. (1997). “Learning Through Reinforcement and Replicator Dynamics.” Journal of Economic Theory, Vol. 77, pp. 1-14.
Cabrales, A. (1993). “Stochastic Replicator Dynamics.” Documento de Trabajo UPF 54.
De Long, J.B., Shleifer, A., Summers, L.H. y Waldmann, R.J. (1990) “Noise Trader Risk in Financial Markets.” Journal of Political Economy, Vol. 98, pp. 703-738.
De Long, J.B., Shleifer, A., Summers, L.H. y Waldmann, R.J. (1991) “The Survival of Noise Traders in Financial Markets.” Journal of Business, Vol. 64, Nº 1, pp. 1-19.
Farmer, J.D. (1998). “Market Force, Ecology and Evolution.” Documento de Trabajo del Instituto de Santa Fe 08-12-117.
FMI (1998). “World Economic Outlook.” Washington, D.C.
Friedman, D. (1998). “On economic applications of evolutionary games.” Journal of Evolutionary Economics, Vol. 8, pp. 15-43.
Friedman, D. (2001). “Towards Evolutionary Game Models of Financial Markets.” Quantitative Finance, Vol. 1, pp. 177-185.
Hirshleifer, D. y Luo, G.Y. (2001). “On the Survival of Overconfident Traders in a Competitive Securities Market.” Journal of Financial Markets, Vol. 4, pp. 73-84.
Hofbauer, J. y Sigmund, K. (2003). “Evolutionary Game Dynamics.” Bulletin of the American Mathematical Society, Vol. 40, Nº 4, pp.479-519.
Kandori, M., Mailath, G.J. y Rob. R. (1993). “Learning, Mutation, and Long Run Equilibria in Games.” Econometrica, Vol. 61, Nº 1, pp. 29-56.
LeBaron, B. (1998). “Agent Based Computational Finance: Suggested Readings and Early Research.” Journal of Economic Dynamics and Control Vol.24, pp. 679-702.
MacKenzie, D. (2003). “Long-Term Capital Management and the Sociology of Arbitrage.”, Economy and Society, Vol. 32, pp.349-380.
Maynard Smith, J. (1982). “Evolution and the Theory of Games.” Cambridge University Press, Cambridge.
Maynard Smith, J. y Price, G.R. (1973). “The Logic of Animal Conflict.” Nature, Vol. 246, pp. 15-18.
Morris, S. y Shin, H.S. (1999). “Risk Management with Interdependent Choice.” Oxford Review of Economic Policy, Vol. 15, pp. 52.62.
Palomino, F. (1996). “Noise Trading in Small Markets.” Journal of Finance, Vol. 51, Nº 4, pp. 1537-1550.
Perold, A.F. (1999). “Long-Term Capital Management, L.P.” Harvard Business School Publishing, Boston, MA.
Persaud, A. (2000) “Sending the herd off the cliff edge: The disturbing interaction between herding and market-sensitive risk management practices.” Erisk, December 2000.
Rasmusen, E. (1989). “Games and Information.” Basil Blackwell, Oxford.
Samuelson, L. (1998). “Evolutionary Games and Equilibrium Selection.” The MIT Press, Cambridge.
Schlag, K.H. (1994). “Why Imitate, and if so, How ? Exploring a Model of Social Evolution.” SFB 303, Universidad de Bonn, Artículo de Discusión Nº B-296.
Tadj, L. y Touzene, A. (2003). “A QBD approach to evolutionary game theory.” Applied Mathematical Modelling, Vol. 27, pp. 913-927.
Tesfatsion, L. (2002). “Agent-Based Computational Economics.” ISU Economics Working Paper No. 1, Iowa State University.
Wang, F.A. (2001). “Overconfidence, Investor Sentiment, and Evolution.” Journal of Financial Intermediation, Vol. 10, pp. 138-170.
Weibull, J.W. (1995). “Evolutionary Game Theory.” The MIT Press, Cambridge.
Young, H. P. (1998). “Individual Strategy and Social Structure. An Evolutionary Theory of Institutions.” Princeton University Press, Princeton.
Document information
Published on 01/01/2004
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?