| (67 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
==Resumen== | ==Resumen== | ||
| Line 18: | Line 14: | ||
Desde principios del presente siglo se han incrementado notablemente los esfuerzos por coordinar y sincronizar grupos de robots que forman redes para el trabajo colaborativo. Estas ''Redes de Robots'' (RR´s) se justifican en misiones que no son posibles llevarlas a cabo con robots actuando de forma individual por razones de su propia capacidad. Entre los aspectos de estudio de mayor interés destaca la propuesta de ''leyes de control'' que gobiernen el comportamiento colectivo. Para muchas misiones de estas RR´s, la etapa primaria es su ''formación'' con un patrón geométrico o una distribución determinada [1]. La formación consiste en un posicionamiento relativo espacial con respecto a una o más referencias, fijas o móviles, para cada uno de los robots que forman parte de la red [2]. Para este problema de formación se han utilizado distintas metodologías [2-8]. La mayor parte de estas metodologías se fundamenta en la teoría de grafos cuyos inicios están documentados desde el siglo XVIII y que en la década de 1960 se extiende para aplicaciones en redes complejas [9-15]. Mediante la teoría de grafos es posible expresar interacciones entre sistemas dinámicos de manera general y organizada, facilitando la formulación de leyes de control para gobernar el comportamiento entero de una red. | Desde principios del presente siglo se han incrementado notablemente los esfuerzos por coordinar y sincronizar grupos de robots que forman redes para el trabajo colaborativo. Estas ''Redes de Robots'' (RR´s) se justifican en misiones que no son posibles llevarlas a cabo con robots actuando de forma individual por razones de su propia capacidad. Entre los aspectos de estudio de mayor interés destaca la propuesta de ''leyes de control'' que gobiernen el comportamiento colectivo. Para muchas misiones de estas RR´s, la etapa primaria es su ''formación'' con un patrón geométrico o una distribución determinada [1]. La formación consiste en un posicionamiento relativo espacial con respecto a una o más referencias, fijas o móviles, para cada uno de los robots que forman parte de la red [2]. Para este problema de formación se han utilizado distintas metodologías [2-8]. La mayor parte de estas metodologías se fundamenta en la teoría de grafos cuyos inicios están documentados desde el siglo XVIII y que en la década de 1960 se extiende para aplicaciones en redes complejas [9-15]. Mediante la teoría de grafos es posible expresar interacciones entre sistemas dinámicos de manera general y organizada, facilitando la formulación de leyes de control para gobernar el comportamiento entero de una red. | ||
| − | Dentro del campo de la teoría de grafos y redes complejas, el ''acoplamiento difusivo estático'' es una estrategia ampliamente utilizada para realizar la interconexión entre los nodos (robots) de la red [16,17]. El principio de acoplamiento difusivo estático es un esquema de retroalimentación constante [17] entre los robots que forman parte de la red, pudiendo ser esta conectividad global o parcial (respectivamente: todos los robots se conectan con el resto de robots o sólo parte de ellos). La retroalimentación consiste en insertar como parte de la entrada del sistema dinámico del robot una señal que es la diferencia entre las variables de salida del robot de interés y las variables de salida del resto de robots en la red [18]. De este tipo de acoplamiento se han derivado distintas metodologías con el propósito de forzar una respuesta deseada en los robots, denominada estado de ''sincronía''[14]; ó bien, una respuesta de sincronía natural, denominada ''consenso'' [19-21]. Una modalidad de estrategia de control que destaca para redes de gran dimensión es el control ''pinning ''(líderes referentes), que propone una acción de control en sólo un reducido número de sistemas dinámicos de la red y que inducen a la red entera hacia un estado de sincronía [11,14-15,22]. Estas estrategias se pueden llevar a cabo tanto mediante el control centralizado como con el control distribuido [23]. Con el control centralizado el procesamiento reside en un procesador que se encarga de monitorear las variables de estado de cada robot y de comunicar las acciones de control necesarias para alcanzar el objetivo de movimiento. Con el control distribuido el procesamiento reside en dos o más procesadores con acceso total o parcial a la información de variables de estado de la red; típicamente los robots llevan sus | + | Dentro del campo de la teoría de grafos y redes complejas, el ''acoplamiento difusivo estático'' es una estrategia ampliamente utilizada para realizar la interconexión entre los nodos (robots) de la red [16,17]. El principio de acoplamiento difusivo estático es un esquema de retroalimentación constante [17] entre los robots que forman parte de la red, pudiendo ser esta conectividad global o parcial (respectivamente: todos los robots se conectan con el resto de robots o sólo parte de ellos). La retroalimentación consiste en insertar como parte de la entrada del sistema dinámico del robot una señal que es la diferencia entre las variables de salida del robot de interés y las variables de salida del resto de robots en la red [18]. De este tipo de acoplamiento se han derivado distintas metodologías con el propósito de forzar una respuesta deseada en los robots, denominada estado de ''sincronía''[14]; ó bien, una respuesta de sincronía natural, denominada ''consenso'' [19-21]. Una modalidad de estrategia de control que destaca para redes de gran dimensión es el control ''pinning ''(líderes referentes), que propone una acción de control en sólo un reducido número de sistemas dinámicos de la red y que inducen a la red entera hacia un estado de sincronía [11,14-15,22]. Estas estrategias se pueden llevar a cabo tanto mediante el control centralizado como con el control distribuido [23]. Con el control centralizado el procesamiento reside en un procesador que se encarga de monitorear las variables de estado de cada robot y de comunicar las acciones de control necesarias para alcanzar el objetivo de movimiento. Con el control distribuido el procesamiento reside en dos o más procesadores con acceso total o parcial a la información de variables de estado de la red; típicamente los robots llevan sus procesadores a bordo. |
| − | La formación de robots es aún un problema abierto [3-5], especialmente para RR´s de gran dimensión y RR´s heterogéneas. Las redes heterogéneas de robots están integradas por robots con distintos modelos dinámicos, con distintas dimensiones de vectores de variables de estado, con distinta dimensión de variables de salida o una combinación de las condiciones anteriores [16,17]. Las soluciones propuestas aún son parciales y requieren una integración para resolver problemas íntimamente relacionados. Tales problemas, además de los ya mencionados, son la evasión de obstáculos, la no colisión entre robots, las saturaciones en los accionamientos para el control, la diversidad de escenarios y las limitaciones en los enlaces de comunicación para el control[14-15]. | + | La formación de robots es aún un problema abierto [3-5], especialmente para RR´s de gran dimensión y RR´s heterogéneas. Las redes heterogéneas de robots están integradas por robots con distintos modelos dinámicos, con distintas dimensiones de vectores de variables de estado, con distinta dimensión de variables de salida o una combinación de las condiciones anteriores [16,17]. Las soluciones propuestas aún son parciales y requieren una integración para resolver problemas íntimamente relacionados. Tales problemas, además de los ya mencionados, son la evasión de obstáculos, la no colisión entre robots, las saturaciones en los accionamientos para el control, la diversidad de escenarios y las limitaciones en los enlaces de comunicación para el control [14-15]. |
Las contribuciones del presente trabajo se aplican en la ''formación ''de una RR´s utilizando herramientas derivadas de la teoría de grafos. Estas contribuciones son: (i) un tutorial para la formulación de RR´s mediante el acoplamiento difusivo estático en el que se describen de manera detallada los elementos y variables que intervienen en la red, (ii) una ley de control para una formación deseada de la RR´s bajo esta formulación y (iii) un procedimiento para la no colisión entre los robots que forman la red utilizando la misma topología de la RR´s. La metodología desarrollada se ejemplifica con simulaciones y experimentos mediante la construcción de una red de ''Robots Móviles Terrestres a base de Ruedas ''(RMTR’s). | Las contribuciones del presente trabajo se aplican en la ''formación ''de una RR´s utilizando herramientas derivadas de la teoría de grafos. Estas contribuciones son: (i) un tutorial para la formulación de RR´s mediante el acoplamiento difusivo estático en el que se describen de manera detallada los elementos y variables que intervienen en la red, (ii) una ley de control para una formación deseada de la RR´s bajo esta formulación y (iii) un procedimiento para la no colisión entre los robots que forman la red utilizando la misma topología de la RR´s. La metodología desarrollada se ejemplifica con simulaciones y experimentos mediante la construcción de una red de ''Robots Móviles Terrestres a base de Ruedas ''(RMTR’s). | ||
| − | El resto de este documento está organizado como sigue. En la sección 2 se expone un tutorial que describe paso a paso | + | El resto de este documento está organizado como sigue. En la sección 2 se expone un tutorial que describe paso a paso la formulación de una RR´s basado en el modelo para cada <math display="inline">i</math>-ésimo robot que forma parte de la red y la estrategia de acoplamiento difusivo estático. En la sección 3 se propone la ley de control para la formación de una red de robots construida con robots tipo uniciclo. La efectividad de la ley de control se demuestra utilizando la teoría de estabilidad de Lyapunov. En la sección 4 se presentan los resultados de simulación y experimentación. En la sección 5 se describe un procedimiento para evitar las colisiones entre robots de la red ejemplificada en la sección 4 y se presentan resultados de simulación y experimentación. Finalmente, en la sección 6 se presentan las conclusiones generales. |
==2. Formulación de una red de robots== | ==2. Formulación de una red de robots== | ||
| Line 54: | Line 50: | ||
| [[Image:draft_Aparicio Nogué_723966060-image1.jpeg|300px]] [[Image:draft_Aparicio Nogué_723966060-image2.jpeg|96px]] | | [[Image:draft_Aparicio Nogué_723966060-image1.jpeg|300px]] [[Image:draft_Aparicio Nogué_723966060-image2.jpeg|96px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 1 | + | | colspan="1" | '''Figura 1.''' (a) Diagrama a bloques de un robot individual, (b) Representación simplificada |
|} | |} | ||
| − | ===2.2 Modelo del | + | ===2.2 Modelo del i-ésimo robot en una red de robots=== |
Para un robot <math display="inline">{R}_{i}</math> que pertenece a una red se puede proponer un nuevo vector de entrada <math display="inline">{\mathit{\boldsymbol{\vartheta }}}_{i}\mathit{\boldsymbol{\in \, }}{\mathit{\mathbb{R}}}^{{p}_{{\vartheta }_{i}}}</math>, de manera que su modelo quedaría como | Para un robot <math display="inline">{R}_{i}</math> que pertenece a una red se puede proponer un nuevo vector de entrada <math display="inline">{\mathit{\boldsymbol{\vartheta }}}_{i}\mathit{\boldsymbol{\in \, }}{\mathit{\mathbb{R}}}^{{p}_{{\vartheta }_{i}}}</math>, de manera que su modelo quedaría como | ||
| Line 65: | Line 61: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>{\overset{\cdot}{\mathit{\boldsymbol{x}}}}_{i}={\mathit{\boldsymbol{f}}}_{i}(t,{\mathit{\boldsymbol{x}}}_{i},{\mathit{\boldsymbol{u}}}_{i}) | + | | style="text-align: center;" | <math>{\overset{\cdot}{\mathit{\boldsymbol{x}}}}_{i}={\mathit{\boldsymbol{f}}}_{i}(t,{\mathit{\boldsymbol{x}}}_{i},{\mathit{\boldsymbol{u}}}_{i})</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>{\mathit{\boldsymbol{y}}}_{i}={\mathit{\boldsymbol{h}}}_{i}(t,{\mathit{\boldsymbol{x}}}_{i},{\mathit{\boldsymbol{u}}}_{i}) | + | | style="text-align: center;" | <math>{\mathit{\boldsymbol{y}}}_{i}={\mathit{\boldsymbol{h}}}_{i}(t,{\mathit{\boldsymbol{x}}}_{i},{\mathit{\boldsymbol{u}}}_{i})</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>{\mathit{\boldsymbol{u}}}_{i}={\mathit{\boldsymbol{\Upsilon }}}_{i}\left( t,\mathit{\boldsymbol{y}},{\mathit{\boldsymbol{\vartheta }}}_{i}\right) | + | | style="text-align: center;" | <math>{\mathit{\boldsymbol{u}}}_{i}={\mathit{\boldsymbol{\Upsilon }}}_{i}\left( t,\mathit{\boldsymbol{y}},{\mathit{\boldsymbol{\vartheta }}}_{i}\right)</math>, |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(2) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(2) | ||
|} | |} | ||
| Line 83: | Line 79: | ||
| [[Image:draft_Aparicio Nogué_723966060-image3.jpeg|150px]] | | [[Image:draft_Aparicio Nogué_723966060-image3.jpeg|150px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 2 | + | | colspan="1" | '''Figura 2.''' Modelo de un <math display="inline">i</math>-ésimo robot que pertenece a una red. |
|} | |} | ||
| Line 95: | Line 91: | ||
| [[Image:draft_Aparicio Nogué_723966060-image4.jpeg|306px]] | | [[Image:draft_Aparicio Nogué_723966060-image4.jpeg|306px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 3 | + | | colspan="1" | '''Figura 3.''' Diagrama a bloques de una red de robots. |
|} | |} | ||
| Line 107: | Line 103: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">G=(R,\varepsilon )</math>, | + | | style="text-align: center;" | <math display="inline">\mathit{\cal G}=(R,\varepsilon)</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" |(3) | | style="width: 5px;text-align: right;white-space: nowrap;" |(3) | ||
|} | |} | ||
|} | |} | ||
| − | donde <math display="inline">R=</math><math>\left\{ {R}_{i}:i=1,2,\ldots ,N\right\}</math> es el conjunto de <math display="inline">N</math> robots y <math display="inline">\varepsilon=</math><math>\left\{ {\varepsilon}_{ij}({\mathit{\boldsymbol{y}}}_{j}):i,j=1,2,\ldots ,N\right\}</math> es el conjunto de <math display="inline"> | + | donde <math display="inline">R=</math><math>\left\{ {R}_{i}:i=1,2,\ldots ,N\right\}</math> es el conjunto de <math display="inline">N</math> robots y <math display="inline">\varepsilon=</math><math>\left\{ {\varepsilon}_{ij}({\mathit{\boldsymbol{y}}}_{j}):i,j=1,2,\ldots ,N\right\}</math> es el conjunto de <math display="inline">N\times N</math> conexiones dirigidas de la red. Una conexión dirigida <math display="inline">\, {\varepsilon}_{ij}({\mathit{\boldsymbol{y}}}_{j})\in {\mathit{\mathbb{R}}}^{{p}_{i}}</math> es una función que corresponde a un par de robots <math display="inline">({R}_{i},{R}_{j})</math> siendo la salida <math display="inline">{\mathit{\boldsymbol{y}}}_{j}\in {\mathit{\mathbb{R}}}^{{s}_{j}}</math> (salida del robot <math display="inline">{R}_{j}</math>) el vector de información que se transfiere al robot <math display="inline">{R}_{i}</math> mediante una transformación <math display="inline">{\varepsilon}_{ij}:\, {\mathit{\mathbb{R}}}^{{s}_{j}}\rightarrow {\mathit{\mathbb{R}}}^{{p}_{i}}</math>. La Figura 4 muestra las conexiones dirigidas de manera generalizada para un par de robots <math display="inline">{R}_{i}</math> y <math display="inline">{R}_{j}</math>. |
<div id='img-4'></div> | <div id='img-4'></div> | ||
| Line 119: | Line 115: | ||
| [[Image:draft_Aparicio Nogué_723966060-image5.jpeg|336px]] | | [[Image:draft_Aparicio Nogué_723966060-image5.jpeg|336px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 4 | + | | colspan="1" | '''Figura 4.''' Grafo o esquema generalizado de conexiones dirigidas en los robots <math display="inline">{R}_{i}</math> y <math display="inline">{R}_{j}</math> de una red. |
|} | |} | ||
| Line 129: | Line 125: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{\varepsilon}}}_{i}(\mathit{\boldsymbol{y}})=c\sum _{j=1}^{N}{\mathit{\boldsymbol{\varepsilon}}}_{ij}({\mathit{\boldsymbol{y}}}_{j})</math> | + | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{\varepsilon}}}_{i}(\mathit{\boldsymbol{y}})=c\sum _{j=1}^{N}{\mathit{\boldsymbol{\varepsilon}}}_{ij}({\mathit{\boldsymbol{y}}}_{j})</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" |(4) | | style="width: 5px;text-align: right;white-space: nowrap;" |(4) | ||
|} | |} | ||
|} | |} | ||
| − | donde <math display="inline">c>0</math> es la denominada fuerza global de acoplamiento, <math display="inline">{\mathit{\boldsymbol{\varepsilon}}}_{ij}({\mathit{\boldsymbol{y}}}_{j})=</math><math>{g}_{ij}{\mathit{\boldsymbol{\Gamma }}}_{ij}{\mathit{\boldsymbol{y}}}_{j}</math>, con <math display="inline">{g}_{ij}</math> elemento de la matriz de configuración externa de red <math display="inline">\mathit{\boldsymbol{\, G}}\in {\mathit{\mathbb{R}}}^{ | + | donde <math display="inline">c>0</math> es la denominada fuerza global de acoplamiento, <math display="inline">{\mathit{\boldsymbol{\varepsilon}}}_{ij}({\mathit{\boldsymbol{y}}}_{j})=</math><math>{g}_{ij}{\mathit{\boldsymbol{\Gamma }}}_{ij}{\mathit{\boldsymbol{y}}}_{j}</math>, con <math display="inline">{g}_{ij}</math> elemento de la matriz de configuración externa de red <math display="inline">\mathit{\boldsymbol{\, G}}\in {\mathit{\mathbb{R}}}^{N\times N}</math> obtenida mediante |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 141: | Line 137: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\mathit{\boldsymbol{G}}=\mathit{\boldsymbol{\cal A}}-{\Delta }_{ent}</math> | + | | style="text-align: center;" | <math display="inline">\mathit{\boldsymbol{G}}=\mathit{\boldsymbol{\cal A}}-{\Delta }_{ent}</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" |(5) | | style="width: 5px;text-align: right;white-space: nowrap;" |(5) | ||
|} | |} | ||
|} | |} | ||
| − | donde <math display="inline">\mathit{\boldsymbol{\cal A}}{\mathit{\boldsymbol{\, \, }}\in \mathit{\mathbb{R}}}^{ | + | donde <math display="inline">\mathit{\boldsymbol{\cal A}}{\mathit{\boldsymbol{\, \, }}\in \mathit{\mathbb{R}}}^{N\times N}</math> es la matriz de adyacencia ponderada con sus elementos <math display="inline">{a}_{ij}>0</math> si existe una conexión entre el robot <math display="inline">{R}_{i}</math> y el robot <math display="inline">{R}_{j}</math> y <math display="inline">{a}_{ij}=</math><math>0</math> si no existe la conexión (<math display="inline">{a}_{ij}</math> es la magnitud de la conexión y en particular <math display="inline">{a}_{ii}=</math><math>0</math>); <math display="inline">{\Delta }_{ent}=</math><math>diag\lbrace {d}_{ii}\rbrace {\mathit{\boldsymbol{\, \, }}\in \mathit{\mathbb{R}}}^{N\times N}</math> es la matriz de grado de entrada con <math display="inline">{d}_{ii}=</math><math>\sum _{j=1}^{N}{a}_{ij}</math> la suma de los pesos de las conexiones que ingresan a cada robot <math display="inline">{R}_{i}</math> (note que de esta forma <math display="inline">\mathit{\boldsymbol{G}}</math> es difundida puesto que la suma de sus elementos por renglón es nula); y <math display="inline">{\mathit{\boldsymbol{\Gamma }}}_{ij}\in {\mathit{\mathbb{R}}}^{{p}_{i}\times {s}_{j}}</math> es la matriz de configuración interna que expresa las proporciones de contribución de las variables de salida <math display="inline">{\mathit{\boldsymbol{y}}}_{j}</math> hacia <math display="inline">{\mathit{\boldsymbol{u}}}_{i}</math> y en consecuencia, define la relación interna entre las variables del robot <math display="inline">{R}_{j}</math> hacia las variables del robot <math display="inline">{R}_{i}</math>. |
De esta manera el acoplamiento difusivo estático para generar <math display="inline">{\mathit{\boldsymbol{u}}}_{i}</math> es | De esta manera el acoplamiento difusivo estático para generar <math display="inline">{\mathit{\boldsymbol{u}}}_{i}</math> es | ||
| Line 155: | Line 151: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{u}}}_{i}=c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\Gamma }}}_{ij}{\mathit{\boldsymbol{y}}}_{j}+</math><math>{\mathit{\boldsymbol{\vartheta }}}_{i},\quad i=1,2,\ldots ,N</math> | + | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{u}}}_{i}=c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\Gamma }}}_{ij}{\mathit{\boldsymbol{y}}}_{j}+</math><math>{\mathit{\boldsymbol{\vartheta }}}_{i},\quad i=1,2,\ldots ,N</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" |(6) | | style="width: 5px;text-align: right;white-space: nowrap;" |(6) | ||
|} | |} | ||
| Line 167: | Line 163: | ||
| [[Image:draft_Aparicio Nogué_723966060-image6.jpeg|600px]] | | [[Image:draft_Aparicio Nogué_723966060-image6.jpeg|600px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 5 | + | | colspan="1" | '''Figura 5.''' Diagrama a bloques para una red de robots con acoplamiento difusivo estático. |
|} | |} | ||
| Line 175: | Line 171: | ||
| [[Image:draft_Aparicio Nogué_723966060-image7.jpeg|426px]] | | [[Image:draft_Aparicio Nogué_723966060-image7.jpeg|426px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 6 | + | | colspan="1" | '''Figura 6.''' Esquema generalizado de conexiones dirigidas equivalente al diagrama a bloques de la Figura 5. |
|} | |} | ||
| Line 187: | Line 183: | ||
| [[Image:draft_Aparicio Nogué_723966060-image8.jpeg|174px]] | | [[Image:draft_Aparicio Nogué_723966060-image8.jpeg|174px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 7 | + | | colspan="1" | '''Figura 7.''' Grafo para el ejemplo de formulación de red de robots. Observe que las autoconexiones en cada robot no son mostradas. |
|} | |} | ||
| Line 195: | Line 191: | ||
| [[Image:draft_Aparicio Nogué_723966060-image9.jpeg|234px]] | | [[Image:draft_Aparicio Nogué_723966060-image9.jpeg|234px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 8 | + | | colspan="1" | '''Figura 8.''' Detalle de los <math display="inline">N=</math><math>4</math> robots distintos para el ejemplo de formulación de red. |
|} | |} | ||
| Line 205: | Line 201: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\mathit{\boldsymbol{A=}}\left[ \begin{matrix}0\\0\\2\\0\end{matrix}\, \, \begin{matrix}3\\0\\0\\5\end{matrix}\, \, \begin{matrix}0\\4\\0\\1\end{matrix}\, \, \begin{matrix}0\\0\\0\\0\end{matrix}\right]</math>, y <math display="inline">{\Delta }_{ent}=</math><math>diag\lbrace 3,4,2,6\rbrace</math> | + | | style="text-align: center;" | <math display="inline">\mathit{\boldsymbol{A=}}\left[ \begin{matrix}0\\0\\2\\0\end{matrix}\, \, \begin{matrix}3\\0\\0\\5\end{matrix}\, \, \begin{matrix}0\\4\\0\\1\end{matrix}\, \, \begin{matrix}0\\0\\0\\0\end{matrix}\right]</math>, y <math display="inline">{\Delta }_{ent}=</math><math>diag\lbrace 3,4,2,6\rbrace</math>. |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 234: | Line 230: | ||
|} | |} | ||
| − | con <math display="inline">{\mathit{\boldsymbol{\Gamma }}}_{ij}{\mathit{\boldsymbol{\, \, }}\in \mathit{\mathbb{R}}}^{{r}_{i} | + | con <math display="inline">{\mathit{\boldsymbol{\Gamma }}}_{ij}{\mathit{\boldsymbol{\, \, }}\in \mathit{\mathbb{R}}}^{{r}_{i}\times {s}_{j}}</math> cada matriz de configuración interna y con <math display="inline">\mathit{\boldsymbol{0}}</math> una matriz cero de dimensión adecuada; es decir |
| Line 249: | Line 245: | ||
con cada <math display="inline">{\gamma }_{ij,kl}\geq 0</math> según la proporción de contribución de las variables <math display="inline">{\mathit{\boldsymbol{y}}}_{j}</math> hacia <math display="inline">{\mathit{\boldsymbol{u}}}_{i}</math>. | con cada <math display="inline">{\gamma }_{ij,kl}\geq 0</math> según la proporción de contribución de las variables <math display="inline">{\mathit{\boldsymbol{y}}}_{j}</math> hacia <math display="inline">{\mathit{\boldsymbol{u}}}_{i}</math>. | ||
| − | De esta manera, se completa (6) para la red de la | + | De esta manera, se completa (6) para la red de la Figura 7 y la Figura 9 muestra su diagrama a bloques equivalente |
<div id='img-9'></div> | <div id='img-9'></div> | ||
| Line 256: | Line 252: | ||
| [[Image:draft_Aparicio Nogué_723966060-image10.jpeg|600px]] | | [[Image:draft_Aparicio Nogué_723966060-image10.jpeg|600px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 9 | + | | colspan="1" | '''Figura 9.''' Diagrama a bloques equivalente para el ejemplo de red heterogénea con 4 robots. |
|} | |} | ||
| Line 268: | Line 264: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}\mathit{\boldsymbol{q}}=\left[ \begin{matrix}cos{(\theta }_{R})&- | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}\mathit{\boldsymbol{q}}=\left[ \begin{matrix}\text {cos}{(\theta }_{R})&-l\text {sen}{(\theta }_{R})\\ \text {sen}{(\theta }_{R})&l\text {cos}{(\theta }_{R})\end{matrix}\right] \left[ \begin{matrix}{v}_{R}\\{\omega }_{R}\end{matrix}\right]</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|- | |- | ||
| Line 283: | Line 279: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}\mathit{\boldsymbol{q}}=\mathit{\boldsymbol{u}}</math> | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}\mathit{\boldsymbol{q}}=\mathit{\boldsymbol{u}}</math>. |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(11) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(11) | ||
|} | |} | ||
| Line 293: | Line 289: | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | | [[Image:draft_Aparicio Nogué_723966060-image11.jpeg| | + | | [[Image:draft_Aparicio Nogué_723966060-image11.jpeg|250px]] |
| + | | [[Image:draft_Aparicio Nogué_723966060-image12.jpeg|250px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figura 10.''' (a) Robot tipo uniciclo de tracción diferencial, (b) Vista superior del robot. |
|} | |} | ||
| Line 305: | Line 302: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}\mathit{\boldsymbol{q}}_{\mathit{\boldsymbol{i}}}=</math><math>{\mathit{\boldsymbol{u}}}_{\mathit{\boldsymbol{i}}}</math> | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}\mathit{\boldsymbol{q}}_{\mathit{\boldsymbol{i}}}=</math><math>{\mathit{\boldsymbol{u}}}_{\mathit{\boldsymbol{i}}}</math>, |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(12) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(12) | ||
|} | |} | ||
| Line 316: | Line 313: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{u}}}_{i}=c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{q}}}_{j}{+\mathit{\boldsymbol{\vartheta }}}_{i},\quad i=</math><math>1,2,\ldots ,N</math> | + | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{u}}}_{i}=c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{q}}}_{j}{+\mathit{\boldsymbol{\vartheta }}}_{i},\quad i=</math><math>1,2,\ldots ,N</math>, |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(13) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(13) | ||
|} | |} | ||
| Line 330: | Line 327: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\text{lim}_{t\rightarrow\infty}\,\|\mathit{\boldsymbol{e}}_{i}(t)\|=0,\quad i=</math><math>1,2,\ldots ,N</math> | + | | style="text-align: center;" | <math display="inline">\text{lim}_{t\rightarrow\infty}\,\|\mathit{\boldsymbol{e}}_{i}(t)\|=0,\quad i=</math><math>1,2,\ldots ,N</math>, |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(14) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(14) | ||
|} | |} | ||
|} | |} | ||
| − | donde <math display="inline">{\mathit{\boldsymbol{e}}}_{i}=</math><math>{[{e}_{ix}\, {e}_{iy}]}^{T}={\mathit{\boldsymbol{q}}}_{i}-\mathit{\boldsymbol{s}}-</math><math>{\mathit{\boldsymbol{\varphi }}}_{i}</math>es el error de formación y se ha insertado un líder virtual (sistema de referencia de red) con sistema dinámico <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{s}}}=</math><math>\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{s}})</math> y un vector de posiciones finales deseadas constantes <math display="inline">{\mathit{\boldsymbol{\varphi }}}_{i}=</math><math>{[{\varphi }_{ix}\, \, {\varphi }_{iy}]}^{T}\, \in \, {\mathit{\mathbb{R}}}^{2}</math> para cada <math display="inline"> | + | donde <math display="inline">{\mathit{\boldsymbol{e}}}_{i}=</math><math>{[{e}_{ix}\, {e}_{iy}]}^{T}={\mathit{\boldsymbol{q}}}_{i}-\mathit{\boldsymbol{s}}-</math><math>{\mathit{\boldsymbol{\varphi }}}_{i}</math> es el error de formación y se ha insertado un líder virtual (sistema de referencia de red) con sistema dinámico <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{s}}}=</math><math>\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{s}})</math> y un vector de posiciones finales deseadas constantes <math display="inline">{\mathit{\boldsymbol{\varphi }}}_{i}=</math><math>{[{\varphi }_{ix}\, \, {\varphi }_{iy}]}^{T}\, \in \, {\mathit{\mathbb{R}}}^{2}</math> para cada <math display="inline">{i}</math>-ésimo robot respecto al líder. El vector <math display="inline">\mathit{\boldsymbol{s}}=</math><math>{[{s}_{x}\, \, {s}_{y}]}^{T}</math> puede ser un punto fijo o una trayectoria [11]. La derivada de <math display="inline">{\mathit{\boldsymbol{e}}}_{i}</math> es <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i}}=</math> <math>{\overset{\cdot}{\mathit{\boldsymbol{q}}}}_{i}-\overset{\cdot}{\mathit{\boldsymbol{s}}}</math> o bien sustituyéndole (12) |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 342: | Line 339: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i}}={\mathit{\boldsymbol{u}}}_{i}-</math><math>\overset{\cdot}{\mathit{\boldsymbol{s}}}</math>. |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(15) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(15) | ||
|} | |} | ||
| Line 356: | Line 353: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{\vartheta }}}_{i}=-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-</math><math>c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}+\overset{\cdot}{\mathit{\boldsymbol{s}}},\quad i=</math><math>1,2,\ldots ,N</math> | + | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{\vartheta }}}_{i}=-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-</math><math>c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}+\overset{\cdot}{\mathit{\boldsymbol{s}}},\quad i=</math><math>1,2,\ldots ,N</math>, |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(16) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(16) | ||
|} | |} | ||
|} | |} | ||
| − | donde <math display="inline">{d}_{i}</math> es la ganancia del controlador para el <math display="inline"> | + | donde <math display="inline">{d}_{i}</math> es la ganancia del controlador para el <math display="inline">{i}</math>-ésimo robot. Así (13), luego de sustituirle (16) resulta |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 368: | Line 365: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{u}}}_{i}=c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{q}}}_{j}-</math><math>c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}+</math><math>\overset{\cdot}{\mathit{\boldsymbol{s}}},\quad i=1,2,\ldots ,N</math> | + | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{u}}}_{i}=c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{q}}}_{j}-</math><math>c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}+</math><math>\overset{\cdot}{\mathit{\boldsymbol{s}}},\quad i=1,2,\ldots ,N</math>. |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(17) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(17) | ||
|} | |} | ||
| Line 380: | Line 377: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_ | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i}}=</math><math>c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{e}}}_{j}-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i},\quad i=</math><math>1,2,\ldots ,N</math>, |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(18) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(18) | ||
|} | |} | ||
| Line 392: | Line 389: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{e}}}=-\mathit{\boldsymbol{Fe}}</math> | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{e}}}=-\mathit{\boldsymbol{Fe}}</math>, |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(19) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(19) | ||
|} | |} | ||
| Line 403: | Line 400: | ||
Para demostrar el cumplimiento del objetivo de formación (14) con la ley de control (16) en el sistema expresado por (13)-(12), considérense los siguientes lemas: | Para demostrar el cumplimiento del objetivo de formación (14) con la ley de control (16) en el sistema expresado por (13)-(12), considérense los siguientes lemas: | ||
| − | ''Lema 1'' [25]. Un sistema homogéneo <math display="inline">\mathit{\boldsymbol{ | + | ''Lema 1'' [25]. Un sistema homogéneo <math display="inline">\mathit{\boldsymbol{Ay}}=</math><math>\mathit{\boldsymbol{0}}</math>, donde <math display="inline">\mathit{\boldsymbol{A}}\in {\mathit{\mathbb{R}}}^{r\times r}</math>, posee una solución única (la solución trivial <math display="inline">\mathit{\boldsymbol{y}}=</math><math>\mathit{\boldsymbol{0}}</math>) si y sólo si el <math display="inline">rank\left( \mathit{\boldsymbol{A}}\right) =</math><math>r</math>. |
| − | ''Lema 2'' [26]. Sea <math display="inline">\mathit{\boldsymbol{A}}\in {\mathit{\mathbb{R}}}^{ | + | ''Lema 2'' [26]. Sea <math display="inline">\mathit{\boldsymbol{A}}\in {\mathit{\mathbb{R}}}^{m\times n}</math> con valores singulares <math display="inline">{\sigma }_{1}\geq \ldots \geq {\sigma }_{r}>0</math> y <math display="inline">\mathit{\boldsymbol{B}}\in {\mathit{\mathbb{R}}}^{p\times q}</math> con valores singulares <math display="inline">{\delta }_{1}\geq \ldots \geq {\delta }_{s}>0</math>. Entonces <math display="inline">\mathit{\boldsymbol{A}}\otimes \mathit{\boldsymbol{B}}</math> (ó <math display="inline">\mathit{\boldsymbol{B}}\otimes \mathit{\boldsymbol{A}}</math>) tiene <math display="inline">rs</math> valores singulares <math display="inline">{\sigma }_{1}{\delta }_{1}\geq \ldots \geq {\sigma }_{r}{\delta }_{s}>0</math> y <math display="inline">rank\left( \mathit{\boldsymbol{A}}\otimes \mathit{\boldsymbol{B}}\right) =</math><math>rank\left( \mathit{\boldsymbol{B}}\otimes \mathit{\boldsymbol{A}}\right) =</math><math>rank\left( \mathit{\boldsymbol{A}}\right) rank\mathit{\boldsymbol{(B)}}</math>. NOTA: Si las matrices son cuadradas puede intercambiarse "valores singulares" por "valores característicos". |
| − | ''Lema 3'' [27]. Sea <math display="inline">\mathit{\boldsymbol{P}}\in {\mathit{\mathbb{R}}}^{ | + | ''Lema 3'' [27]. Sea <math display="inline">\mathit{\boldsymbol{P}}\in {\mathit{\mathbb{R}}}^{N\times N}</math> una matriz cuadrada y haciendo <math display="inline">\mathit{\boldsymbol{A}}=</math><math>\frac{1}{2}[\mathit{\boldsymbol{P}}+{\mathit{\boldsymbol{P}}}^{T}]</math>, el Teorema de Silvester establece que <math display="inline">\mathit{\boldsymbol{P}}</math> es definida positiva (<math display="inline">\mathit{\boldsymbol{P}}>0</math>) si y sólo si: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 414: | Line 411: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\mathrm{{\Delta }_{1}=det}\,\left[ {a}_{11}\right] >0,\, \, {\Delta }_{2}=</math><math>det\left[ \begin{matrix}{a}_{11}&{a}_{12}\\{a}_{21}&{a}_{22}\end{matrix}\right] >0,\ldots ,\mathrm{{\Delta }_{N}=det}\,\left[ \mathit{\boldsymbol{A}}\right] >0</math> | + | | style="text-align: center;" | <math display="inline">\mathrm{{\Delta }_{1}=det}\,\left[ {a}_{11}\right] >0,\, \, {\Delta }_{2}=</math><math>det\left[ \begin{matrix}{a}_{11}&{a}_{12}\\{a}_{21}&{a}_{22}\end{matrix}\right] >0,\ldots ,\mathrm{{\Delta }_{N}=det}\,\left[ \mathit{\boldsymbol{A}}\right] >0</math>. |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"| | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"| | ||
|} | |} | ||
|} | |} | ||
| − | NOTA: Si <math display="inline">\mathit{\boldsymbol{P}}</math> es definida positiva (<math display="inline">\mathit{\boldsymbol{P}}>0</math>) entonces <math display="inline" | + | NOTA: Si <math display="inline">\mathit{\boldsymbol{P}}</math> es definida positiva (<math display="inline">\mathit{\boldsymbol{P}}>0</math>) entonces <math display="inline">\mathit{\boldsymbol{-P}}</math> es definida negativa (<math display="inline">\mathit{\boldsymbol{-P}}<0</math>). Si <math display="inline">\mathit{\boldsymbol{P}}</math> es semidefinida positiva (<math display="inline">\mathit{\boldsymbol{P}}\geq 0</math>) entonces <math display="inline">\mathit{\boldsymbol{-P}}</math> es semidefinida negativa (<math display="inline">\mathit{\boldsymbol{-P}}\leq 0</math>). |
| − | ''Lema 4 ''[28]. Sean <math display="inline">\mathit{\boldsymbol{P}}\in {\mathit{\mathbb{R}}}^{ | + | ''Lema 4 ''[28]. Sean <math display="inline">\mathit{\boldsymbol{P}}\in {\mathit{\mathbb{R}}}^{N\times N}</math> y <math display="inline">\mathit{\boldsymbol{\Gamma }}\in {\mathit{\mathbb{R}}}^{n\times n}</math> matrices definidas (semidefinidas) positivas, entonces <math display="inline">\mathit{\boldsymbol{P}}\otimes \mathit{\boldsymbol{\Gamma }}\in {\mathit{\mathbb{R}}}^{Nn\times Nn}</math> es una matriz definida (semidefinida) positiva. |
| − | Ahora, | + | Ahora, considere el punto de equilibrio <math display="inline">\mathit{\boldsymbol{e}}=</math><math>\mathit{\boldsymbol{0}}</math> de (19) y, para el análisis de su estabilidad, considérese la siguiente función candidata de Lyapunov |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 430: | Line 427: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\mathit{\boldsymbol{V}}=\frac{1}{2}{\mathit{\boldsymbol{e}}}^{T}\mathit{\boldsymbol{e}}>0\, \forall \, \mathit{\boldsymbol{e}}\not =0</math> | + | | style="text-align: center;" | <math display="inline">\mathit{\boldsymbol{V}}=\frac{1}{2}{\mathit{\boldsymbol{e}}}^{T}\mathit{\boldsymbol{e}}>\mathit{\boldsymbol{0}}\, \forall \, \mathit{\boldsymbol{e}}\not =\mathit{\boldsymbol{0}}</math>, |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(20) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(20) | ||
|} | |} | ||
| Line 442: | Line 439: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{V}}}={\mathit{\boldsymbol{e}}}^{T}\overset{\cdot}{\mathit{\boldsymbol{e} | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{V}}}={\mathit{\boldsymbol{e}}}^{T}\overset{\cdot}{\mathit{\boldsymbol{e}}}</math>. |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(21) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(21) | ||
|} | |} | ||
| Line 454: | Line 451: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{V}}}=-{\mathit{\boldsymbol{e}}}^{T}\mathit{\boldsymbol{Fe}}</math> | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{V}}}=-{\mathit{\boldsymbol{e}}}^{T}\mathit{\boldsymbol{Fe}}</math>. |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(22) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(22) | ||
|} | |} | ||
|} | |} | ||
| − | De manera que si <math display="inline">\mathit{\boldsymbol{F}}>0</math> entonces <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{V}}}\mathit{\boldsymbol{<}}0</math> <math display="inline">\forall \, e\not =0</math>, significando que <math display="inline">\mathit{\boldsymbol{e}}=</math><math>0</math> es un punto de equilibrio asintóticamente estable y con esto queda demostrado el cumplimiento del objetivo de formación (14). | + | De manera que si <math display="inline">\mathit{\boldsymbol{F}}>0</math> entonces <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{V}}}\mathit{\boldsymbol{<}}0</math> <math display="inline">\forall \, \mathit{\boldsymbol{e}}\not = \mathit{\boldsymbol{0}}</math>, significando que <math display="inline">\mathit{\boldsymbol{e}}= </math><math>\mathit{\boldsymbol{0}}</math> es un punto de equilibrio asintóticamente estable y con esto queda demostrado el cumplimiento del objetivo de formación (14). |
Como ejemplos considérense las siguientes topologías típicas para una red con <math display="inline">N</math> robots. | Como ejemplos considérense las siguientes topologías típicas para una red con <math display="inline">N</math> robots. | ||
| Line 492: | Line 489: | ||
| [[Image:draft_Aparicio Nogué_723966060-image13.jpeg|216px]] | | [[Image:draft_Aparicio Nogué_723966060-image13.jpeg|216px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 11 | + | | colspan="1" | '''Figura 11.''' Una red de <math display="inline">N</math> robots con Topología Estrella. |
|} | |} | ||
| − | |||
Se ha considerado <math display="inline">\mathit{\boldsymbol{D}}=</math><math>diag\lbrace {d}_{1},0,\ldots ,0\rbrace</math> ya que el robot en la raíz (<math display="inline">{R}_{1}</math>) de la red es el único viable para ser líder, pues es el único que mantiene conexiones direccionadas con el resto de los robots. Obsérvese que (24) es una matriz triangular, por lo que si <math display="inline">{d}_{1}\not =0</math> su rango es completo (<math display="inline">rank(\mathit{\boldsymbol{D}}-</math><math>\mathit{\boldsymbol{G}})=N</math>). De esta manera, si <math display="inline">{d}_{1}\not =0</math> y apoyándonos en los ''Lemas 1'' y'' 2'' , <math display="inline">\mathit{\boldsymbol{e}}=</math><math>0</math> es el único punto de equilibrio de (19). | Se ha considerado <math display="inline">\mathit{\boldsymbol{D}}=</math><math>diag\lbrace {d}_{1},0,\ldots ,0\rbrace</math> ya que el robot en la raíz (<math display="inline">{R}_{1}</math>) de la red es el único viable para ser líder, pues es el único que mantiene conexiones direccionadas con el resto de los robots. Obsérvese que (24) es una matriz triangular, por lo que si <math display="inline">{d}_{1}\not =0</math> su rango es completo (<math display="inline">rank(\mathit{\boldsymbol{D}}-</math><math>\mathit{\boldsymbol{G}})=N</math>). De esta manera, si <math display="inline">{d}_{1}\not =0</math> y apoyándonos en los ''Lemas 1'' y'' 2'' , <math display="inline">\mathit{\boldsymbol{e}}=</math><math>0</math> es el único punto de equilibrio de (19). | ||
| Line 510: | Line 506: | ||
|} | |} | ||
| − | de forma que <math display="inline">{\Delta }_{1}=</math><math>{d}_{1}</math> ( | + | de forma que <math display="inline">{\Delta }_{1}=</math><math>{d}_{1}</math> (<math display="inline">{\Delta }_{1}>0</math> si <math display="inline">{d}_{1}>0</math>), <math display="inline">{\Delta }_{2}=</math><math>{d}_{1}-\frac{1}{4}</math> (<math display="inline">{\Delta }_{2}>0</math> si <math display="inline">{d}_{1}>\frac{1}{4)}</math>,…, <math display="inline">{\Delta }_{i}=</math><math>{d}_{1}-\frac{i-1}{4}</math> (<math display="inline">{\Delta }_{i}>0</math> si <math display="inline">{d}_{1}>\frac{i-1}{4}</math>),…, <math display="inline">{\Delta }_{N}=</math><math>{d}_{1}-\frac{N-1}{4}</math> (<math display="inline">{\Delta }_{N}>0</math> si <math display="inline">{d}_{1}>\frac{N-1}{4}</math>). |
De manera que apoyándonos en el ''Lema 4'', entonces si | De manera que apoyándonos en el ''Lema 4'', entonces si | ||
| Line 519: | Line 515: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{d}_{1}>\frac{ | + | | style="text-align: center;" | <math display="inline">{d}_{1}>\frac{N-1}{4}</math>, |
| style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(26) | | style="text-align: right;vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(26) | ||
|} | |} | ||
| Line 555: | Line 551: | ||
| [[Image:draft_Aparicio Nogué_723966060-image14.jpeg|150px]] | | [[Image:draft_Aparicio Nogué_723966060-image14.jpeg|150px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 12 | + | | colspan="1" | '''Figura 12.''' Una red de <math display="inline">N</math> robots con Topología Anillo. |
|} | |} | ||
| − | Nótese que <math display="inline">rank(\mathit{\boldsymbol{G}})=N-</math><math>1</math> (lo cual puede comprobarse directamente al aplicar el procedimiento de eliminación de Gauss). Para que <math display="inline">rank\left( \mathit{\boldsymbol{D-G}}\right)</math> sea completo, por la simetría de la topología, resulta suficiente cualquier <math display="inline">{d}_{i}\not =0</math> | + | Nótese que <math display="inline">rank(\mathit{\boldsymbol{G}})=N-</math><math>1</math> (lo cual puede comprobarse directamente al aplicar el procedimiento de eliminación de Gauss). Para que <math display="inline">rank\left( \mathit{\boldsymbol{D-G}}\right)</math> sea completo, por la simetría de la topología, resulta suficiente cualquier <math display="inline">{d}_{i}\not =0.</math> Supóngase <math display="inline">\mathit{\boldsymbol{D=}}diag\mathit{\boldsymbol{\lbrace }}{d}_{1}\mathit{\boldsymbol{,\, }}0,\ldots ,0\rbrace</math> de manera que si <math display="inline">{d}_{1}\not =0</math> y apoyándose en los ''Lemas 1'' y ''2'', <math display="inline">\mathit{\boldsymbol{e}}=</math><math>0</math> es el único punto de equilibrio de (19). |
| − | Ahora, sustituyendo la <math display="inline">\mathit{\boldsymbol{D}}</math> supuesta en (28) y aplicando el'' Lema 3 ''con <math display="inline">\mathit{\boldsymbol{A}}=</math><math>\left[ \left( \mathit{\boldsymbol{D-G}}\right) {+\left( \mathit{\boldsymbol{D-G}}\right) }^{T}\right] /2</math>se tiene | + | Ahora, sustituyendo la <math display="inline">\mathit{\boldsymbol{D}}</math> supuesta en (28) y aplicando el'' Lema 3 ''con <math display="inline">\mathit{\boldsymbol{A}}=</math><math>\left[ \left( \mathit{\boldsymbol{D-G}}\right) {+\left( \mathit{\boldsymbol{D-G}}\right) }^{T}\right] /2</math> se tiene |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 571: | Line 567: | ||
|} | |} | ||
|} | |} | ||
| − | |||
de forma que <math display="inline">{\Delta }_{i}=</math><math>a{d}_{1}+b</math>, donde <math display="inline">a=</math><math>\frac{i}{{2}^{i-1}}</math> para <math display="inline">i=</math><math>1,2,\ldots ,N</math>, <math display="inline">b=</math><math>\frac{(i+1)}{{2}^{i}}</math> para <math display="inline">i=1,2,\ldots ,N-</math><math>1</math> y <math display="inline">b=</math><math>0</math> para <math display="inline">i=</math><math>N</math>, siendo cada <math display="inline">{\Delta }_{i}>0</math> si <math display="inline">{d}_{1}>0</math>. Por lo tanto, apoyándonos en el ''Lema 4'', entonces si <math display="inline">{d}_{1}>0</math> se cumple que <math display="inline">\mathit{\boldsymbol{F}}>0</math> y el objetivo de formación (14) es satisfecho de forma global. | de forma que <math display="inline">{\Delta }_{i}=</math><math>a{d}_{1}+b</math>, donde <math display="inline">a=</math><math>\frac{i}{{2}^{i-1}}</math> para <math display="inline">i=</math><math>1,2,\ldots ,N</math>, <math display="inline">b=</math><math>\frac{(i+1)}{{2}^{i}}</math> para <math display="inline">i=1,2,\ldots ,N-</math><math>1</math> y <math display="inline">b=</math><math>0</math> para <math display="inline">i=</math><math>N</math>, siendo cada <math display="inline">{\Delta }_{i}>0</math> si <math display="inline">{d}_{1}>0</math>. Por lo tanto, apoyándonos en el ''Lema 4'', entonces si <math display="inline">{d}_{1}>0</math> se cumple que <math display="inline">\mathit{\boldsymbol{F}}>0</math> y el objetivo de formación (14) es satisfecho de forma global. | ||
| Line 603: | Line 598: | ||
| [[Image:draft_Aparicio Nogué_723966060-image15.jpeg|180px]] | | [[Image:draft_Aparicio Nogué_723966060-image15.jpeg|180px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 13 | + | | colspan="1" | '''Figura 13.''' Una red de <math display="inline">N</math> robots con Topología Malla. |
|} | |} | ||
| Line 620: | Line 615: | ||
|} | |} | ||
| − | donde <math display="inline">{{\Delta }_{i}=(N}^{i-1}-</math><math>\left( i-1\right) {N}^{i-2}){d}_{1}+{N}^{i}-i{N}^{i-1},\quad i=1,2,\ldots ,N</math>. De manera que para que cada <math display="inline">{\Delta }_{i}>0</math>, <math display="inline">{d}_{1}>\frac{(i{N}^{i-1}-{N}^{i})}{\left( {N}^{i-1}-\left( i-1\right) {N}^{i-2}\right) =N(i-N)/(N-i+1) | + | donde <math display="inline">{{\Delta }_{i}=(N}^{i-1}-</math><math>\left( i-1\right) {N}^{i-2}){d}_{1}+{N}^{i}-i{N}^{i-1},\quad i=1,2,\ldots ,N</math>. De manera que para que cada <math display="inline">{\Delta }_{i}>0</math>, <math display="inline">{d}_{1}>\frac{(i{N}^{i-1}-{N}^{i})}{\left( {N}^{i-1}-\left( i-1\right) {N}^{i-2}\right) } =N(i-N)/(N-i+1) </math> para <math display="inline">i=</math><math>1,2,\ldots ,N</math>, es decir, <math display="inline">{d}_{1}>0</math>. Por lo tanto, apoyándonos en el ''Lema 4'', entonces si <math display="inline">{d}_{1}>0</math> se cumple que <math display="inline">\mathit{\boldsymbol{F}}>0</math> y el objetivo de formación (14) es satisfecho de forma global. |
==4. Simulación y experimento== | ==4. Simulación y experimento== | ||
| Line 633: | Line 628: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\mathit{\boldsymbol{G}}=\left[ \begin{matrix}0\\{g}_{21}\\{g}_{31}\\0\\0\end{matrix}\quad \begin{matrix}0\\{g}_{22}\\0\\{g}_{42}\\0\end{matrix}\quad \begin{matrix}0\\0\\{g}_{33}\\{g}_{43}\\{g}_{53}\end{matrix}\quad \begin{matrix}0\\0\\{g}_{34}\\{g}_{44}\\0\end{matrix}\quad \begin{matrix}0\\0\\0\\0\\{g}_{55}\end{matrix}\right] | + | | style="text-align: center;" | <math display="inline">\mathit{\boldsymbol{G}}=\left[ \begin{matrix}0\\{g}_{21}\\{g}_{31}\\0\\0\end{matrix}\quad \begin{matrix}0\\{g}_{22}\\0\\{g}_{42}\\0\end{matrix}\quad \begin{matrix}0\\0\\{g}_{33}\\{g}_{43}\\{g}_{53}\end{matrix}\quad \begin{matrix}0\\0\\{g}_{34}\\{g}_{44}\\0\end{matrix}\quad \begin{matrix}0\\0\\0\\0\\{g}_{55}\end{matrix}\right]=\left[ \begin{matrix}0\\1\\1\\0\\0\end{matrix}\quad \begin{matrix}0\\-1\\0\\1\\0\end{matrix}\quad \begin{matrix}0\\0\\-2\\1\\1\end{matrix}\quad \begin{matrix}0\\0\\1\\-2\\0\end{matrix}\quad \begin{matrix}0\\0\\0\\0\\-1\end{matrix}\right]</math> |
| − | + | | style="text-align: right;vertical-align: center;width: 5px;text-align: right;white-space: nowrap;"|(33) | |
| − | + | ||
| − | + | ||
| − | | style="text-align: right;vertical-align: | + | |
|} | |} | ||
|} | |} | ||
| Line 646: | Line 638: | ||
| [[Image:draft_Aparicio Nogué_723966060-image16.jpeg|162px]] | | [[Image:draft_Aparicio Nogué_723966060-image16.jpeg|162px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 14 | + | | colspan="1" | '''Figura 14.''' Topología externa de una RR´s no típica con 5 robots tipo uniciclo de tracción diferencial. |
|} | |} | ||
| Line 673: | Line 665: | ||
Para la simulación de la red formada por cinco robots se utilizó MATLAB R2011b. El experimento se realizó con cinco robots tipo uniciclo modelo YSR-A de la empresa Yujin que reciben las consignas de velocidad mediante módulos de comunicación inalámbrica operando a 418 MHz y a una tasa de 19.2 Kbps. Los módulos de comunicación se conectan a un procesador central vía puerto serie. Este procesador central ejecuta una aplicación de tiempo real en ambiente RTLinux, auxiliado de una tarjeta de video Leonardo de la empresa Arvoo y con programación basada en [33]. Para efectos de identificar la postura de los robots se colocaron dos puntos marca sobre cada robot, uno para la posición objetivo y el otro como auxiliar para el cálculo de su orientación. Las imágenes se registran mediante una cámara UF-1000CL de la empresa UNIQ cuyo eje óptico apunta perpendicularmente al plano de movimiento de los robots (ver Figura 10). La cámara es de alta velocidad y se configuró a razón de 200 cuadros por segundo, obteniéndose un periodo estricto de muestreo en los experimentos de 0.005 s. | Para la simulación de la red formada por cinco robots se utilizó MATLAB R2011b. El experimento se realizó con cinco robots tipo uniciclo modelo YSR-A de la empresa Yujin que reciben las consignas de velocidad mediante módulos de comunicación inalámbrica operando a 418 MHz y a una tasa de 19.2 Kbps. Los módulos de comunicación se conectan a un procesador central vía puerto serie. Este procesador central ejecuta una aplicación de tiempo real en ambiente RTLinux, auxiliado de una tarjeta de video Leonardo de la empresa Arvoo y con programación basada en [33]. Para efectos de identificar la postura de los robots se colocaron dos puntos marca sobre cada robot, uno para la posición objetivo y el otro como auxiliar para el cálculo de su orientación. Las imágenes se registran mediante una cámara UF-1000CL de la empresa UNIQ cuyo eje óptico apunta perpendicularmente al plano de movimiento de los robots (ver Figura 10). La cámara es de alta velocidad y se configuró a razón de 200 cuadros por segundo, obteniéndose un periodo estricto de muestreo en los experimentos de 0.005 s. | ||
| − | En la Tabla 1 se muestran las condiciones iniciales y posiciones finales deseadas para el control de formación de la red de la Figura 14; utilizando un líder virtual con dinámica <math display="inline">\mathit{\boldsymbol{s}} | + | En la Tabla 1 se muestran las condiciones iniciales y posiciones finales deseadas para el control de formación de la red de la Figura 14; utilizando un líder virtual con dinámica <math display="inline">\overset{\cdot}\mathit{\boldsymbol{s}}=</math><math>0</math> y con condición inicial <math display="inline">\mathit{\boldsymbol{s}}(0)=</math><math>{[0\, \, 0]}^{T}</math> m, una fuerza global de acoplamiento <math display="inline">c=</math><math>1.8</math>, ganancias <math display="inline">\mathit{\boldsymbol{D}}=</math><math>diag\lbrace 2\, \, 0\, \, 0\, \, 0\, \, 0\rbrace</math> y una distancia <math display="inline">l=</math><math>0.036</math> m entre marcas sobre cada robot. Obsérvese que se desea una formación en línea recta con un ángulo de |
<math display="inline">\pi /4</math> rad respecto al marco global <math display="inline">{\Sigma }_{W}</math>. | <math display="inline">\pi /4</math> rad respecto al marco global <math display="inline">{\Sigma }_{W}</math>. | ||
| − | < | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| + | '''Tabla 1'''. Condiciones de simulación y experimentación para la RR´s de la Figura 14.</div><br> | ||
| − | {| style="border-collapse: collapse; width: 80%; margin: 0 auto; text-align: center;" | + | {| style="border-collapse: collapse; width: 80%; margin: 0 auto; text-align: center;font-size:85%;" |
|- | |- | ||
| style="border: 1pt solid black;vertical-align: top; width: 25px"| <math>i</math> | | style="border: 1pt solid black;vertical-align: top; width: 25px"| <math>i</math> | ||
| Line 721: | Line 714: | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|-0.30 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|-0.30 | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|-0.30 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|-0.30 | ||
| − | |} | + | |}<br /> |
| + | |||
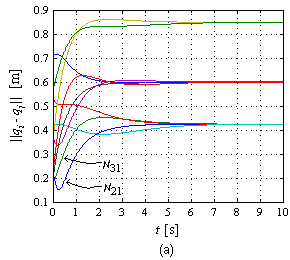
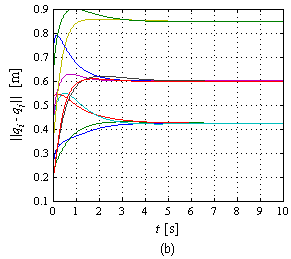
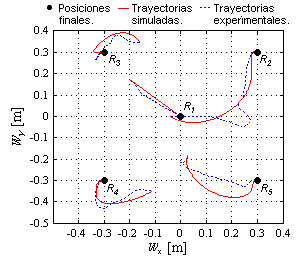
| − | La Figura 15(a) muestra la evolución de los errores en simulación, los cuales tienden a cero a medida que el tiempo transcurre. Una apreciación visual simple destaca que es suficiente <math display="inline">t\approx 5</math> s para que el error pueda considerarse prácticamente cero. En la Figura 15(b) se presentan las gráficas de los errores en el experimento. Cabe destacar que el umbral de reacción de los robots se encuentra por encima de 0.0156 m/s de manera que debajo de dicho valor no hay movimiento del robot. Lo anterior es lo que justifica que en el experimento exista un error en estado estacionario, es decir, cuando la ley de control demanda velocidades pequeñas (pues el robot está cerca del objetivo) se cae dentro del umbral de no reacción del robot deteniendo su movimiento. La norma de error más grande lo presenta <math display="inline">{R}_{5}</math> con <math display="inline">\left\| {e}_{5}\right\| =</math><math>0.0105</math> m. | + | La Figura 15(a) muestra la evolución de los errores en simulación, los cuales tienden a cero a medida que el tiempo transcurre. Una apreciación visual simple destaca que es suficiente <math display="inline">t\approx 5</math> s para que el error pueda considerarse prácticamente cero. En la Figura 15(b) se presentan las gráficas de los errores en el experimento. Cabe destacar que el umbral de reacción de los robots se encuentra por encima de <math display="inline">0.0156</math> m/s de manera que debajo de dicho valor no hay movimiento del robot. Lo anterior es lo que justifica que en el experimento exista un error en estado estacionario, es decir, cuando la ley de control demanda velocidades pequeñas (pues el robot está cerca del objetivo) se cae dentro del umbral de no reacción del robot deteniendo su movimiento. La norma de error más grande lo presenta <math display="inline">{R}_{5}</math> con <math display="inline">\left\| {e}_{5}\right\| =</math><math>0.0105</math> m. |
| Line 731: | Line 725: | ||
| [[Image:draft_Aparicio Nogué_723966060-image17.png|312px]] [[Image:draft_Aparicio Nogué_723966060-image18.png|318px]] | | [[Image:draft_Aparicio Nogué_723966060-image17.png|312px]] [[Image:draft_Aparicio Nogué_723966060-image18.png|318px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 15 | + | | colspan="1" | '''Figura 15.''' Evolución de los errores: (a) En simulación, (b) En experimento. |
|} | |} | ||
| Line 741: | Line 735: | ||
| [[Image:draft_Aparicio Nogué_723966060-image19.png|372px]] | | [[Image:draft_Aparicio Nogué_723966060-image19.png|372px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
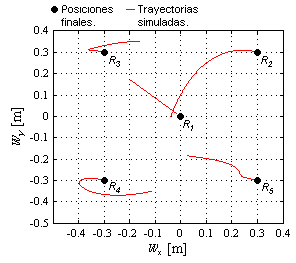
| − | | colspan="1" | '''Figura 16 | + | | colspan="1" | '''Figura 16.''' Trayectorias para la formación en línea recta en el marco global <math display="inline">{\Sigma }_{W}</math>. |
|} | |} | ||
| Line 749: | Line 743: | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | | [[Image:draft_Aparicio Nogué_723966060-image20.png|312px]] [[Image:draft_Aparicio Nogué_723966060-image21.png|312px]] | + | | [[Image:draft_Aparicio Nogué_723966060-image20.png|312px]] |
| + | | [[Image:draft_Aparicio Nogué_723966060-image21.png|312px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figura 17.''' Gráficas de velocidades lineales de los robots: (a) Simulación, (b) Experimento. |
|} | |} | ||
| + | |||
<div id='img-18'></div> | <div id='img-18'></div> | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | | [[Image:draft_Aparicio Nogué_723966060-image22.png|312px]] [[Image:draft_Aparicio Nogué_723966060-image23.png|312px]] | + | | [[Image:draft_Aparicio Nogué_723966060-image22.png|312px]] |
| + | | [[Image:draft_Aparicio Nogué_723966060-image23.png|312px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figura 18.''' Gráficas de velocidades angulares de los robots: (a) Simulación, (b) Experimento. |
|} | |} | ||
| Line 775: | Line 772: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{\vartheta }}}_{i}=-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-</math><math>c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}+\overset{\cdot}{\mathit{\boldsymbol{s}}}+</math><math>{\mathit{\boldsymbol{u}}}_{ri}</math>, <math display="inline">i=</math><math>1,2,\ldots N</math> | + | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{\vartheta }}}_{i}=-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-</math><math>c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}+\overset{\cdot}{\mathit{\boldsymbol{s}}}+</math><math>{\mathit{\boldsymbol{u}}}_{ri}</math>, <math display="inline">i=</math><math>1,2,\ldots N</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" |(35) | | style="width: 5px;text-align: right;white-space: nowrap;" |(35) | ||
|} | |} | ||
|} | |} | ||
| − | donde <math display="inline">{\mathit{\boldsymbol{u}}}_{ri}=</math><math>{h}_{i}{[-{e}_{iy}\, \, {e}_{ix}]}^{T}</math>con <math display="inline">{h}_{i}\, \in \, \mathit{\mathbb{R}}</math>un factor de repulsión. De esta manera (13) resulta | + | donde <math display="inline">{\mathit{\boldsymbol{u}}}_{ri}=</math><math>{h}_{i}{[-{e}_{iy}\, \, {e}_{ix}]}^{T}</math>con <math display="inline">{h}_{i}\, \in \, \mathit{\mathbb{R}}</math> un factor de repulsión. De esta manera (13) resulta |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 787: | Line 784: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{u}}}_{i}=c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{q}}}_{j}-</math><math>c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}+</math><math>\overset{\cdot}{\mathit{\boldsymbol{s}}}+{h}_{i}{\left[ -{e}_{iy}\, \, {e}_{ix}\right] }^{T},\quad i=</math><math>1,2,\ldots N</math> | + | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{u}}}_{i}=c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{q}}}_{j}-</math><math>c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}+</math><math>\overset{\cdot}{\mathit{\boldsymbol{s}}}+{h}_{i}{\left[ -{e}_{iy}\, \, {e}_{ix}\right] }^{T},\quad i=</math><math>1,2,\ldots N</math>. |
| style="width: 5px;text-align: right;white-space: nowrap;" |(36) | | style="width: 5px;text-align: right;white-space: nowrap;" |(36) | ||
|} | |} | ||
| Line 799: | Line 796: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i}}=</math><math>c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{e}}}_{j}-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}+</math><math>{h}_{i}{\left[ -{e}_{iy}\, \, {e}_{ix}\right] }^{T},\quad i=1,2,\ldots N</math>. |
| style="width: 5px;text-align: right;white-space: nowrap;" |(37) | | style="width: 5px;text-align: right;white-space: nowrap;" |(37) | ||
|} | |} | ||
| Line 811: | Line 808: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{V}}}=-c{\mathit{\boldsymbol{e}}}^{T}\lbrace [\mathit{\boldsymbol{D-G}}]\otimes {\mathit{\boldsymbol{I}}}_{2}\rbrace \mathit{\boldsymbol{e}}+</math><math>c{\mathit{\boldsymbol{e}}}^{T}[\mathit{\boldsymbol{H}}\otimes {\mathit{\boldsymbol{I}}}_{2}]{\mathit{\boldsymbol{e}}}^{\bot}</math> | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{V}}}=-c{\mathit{\boldsymbol{e}}}^{T}\lbrace [\mathit{\boldsymbol{D-G}}]\otimes {\mathit{\boldsymbol{I}}}_{2}\rbrace \mathit{\boldsymbol{e}}+</math><math>c{\mathit{\boldsymbol{e}}}^{T}[\mathit{\boldsymbol{H}}\otimes {\mathit{\boldsymbol{I}}}_{2}]{\mathit{\boldsymbol{e}}}^{\bot}</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" |(38) | | style="width: 5px;text-align: right;white-space: nowrap;" |(38) | ||
|} | |} | ||
| Line 818: | Line 815: | ||
donde <math display="inline">\mathit{\boldsymbol{\, H}}=</math><math>diag\lbrace {h}_{1},{h}_{2},\ldots {h}_{N}\rbrace</math> y <math display="inline">{\mathit{\boldsymbol{e}}}^{\bot}=</math><math>{[-{e}_{1y}\, \, {e}_{1x}\, \, -{e}_{2y}\, \, {e}_{2x}\ldots \, -{e}_{Ny}\, \, {e}_{Nx}]}^{T}</math>. | donde <math display="inline">\mathit{\boldsymbol{\, H}}=</math><math>diag\lbrace {h}_{1},{h}_{2},\ldots {h}_{N}\rbrace</math> y <math display="inline">{\mathit{\boldsymbol{e}}}^{\bot}=</math><math>{[-{e}_{1y}\, \, {e}_{1x}\, \, -{e}_{2y}\, \, {e}_{2x}\ldots \, -{e}_{Ny}\, \, {e}_{Nx}]}^{T}</math>. | ||
| − | La contribución<math display="inline">c\mathit{\boldsymbol{e}}^{T}[\mathit{\boldsymbol{H}}\otimes \mathit{\boldsymbol{I}}_{2}]\mathit{\boldsymbol{e}}^{\bot}</math> en (38) es | + | La contribución <math display="inline">c\mathit{\boldsymbol{e}}^{T}[\mathit{\boldsymbol{H}}\otimes \mathit{\boldsymbol{I}}_{2}]\mathit{\boldsymbol{e}}^{\bot}</math> en (38) es |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 825: | Line 822: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>c{\mathit{\boldsymbol{e}}}^{T}[\mathit{\boldsymbol{H}}\otimes {\mathit{\boldsymbol{I}}}_{2}]{\mathit{\boldsymbol{e}}}^{\bot}</math> <math display="inline">=c{\left[ {e}_{1x}\ | + | | style="text-align: center;" | <math>c{\mathit{\boldsymbol{e}}}^{T}[\mathit{\boldsymbol{H}}\otimes {\mathit{\boldsymbol{I}}}_{2}]{\mathit{\boldsymbol{e}}}^{\bot}</math> <math display="inline">=c{\left[ \begin{matrix}{e}_{1x}\\{e}_{1y}\\{e}_{2x}\\{e}_{2y}\\\vdots \\{e}_{Nx}\\{e}_{Ny}\end{matrix}\right]}^{T}\,\left[ \begin{matrix}{h}_{1}\\0\\0\\0\\\vdots \\0\\0\end{matrix}\, \, \begin{matrix}0\\{h}_{1}\\0\\0\\\vdots \\0\\0\end{matrix}\, \, \begin{matrix}0\\0\\{h}_{2}\\0\\\vdots \\0\\0\end{matrix}\, \, \begin{matrix}0\\0\\0\\{h}_{2}\\\vdots \\0\\0\end{matrix}\, \, \begin{matrix}\ldots \\\ldots \\\ldots \\\ldots \\\ddots \\0\\0\end{matrix}\, \, \begin{matrix}0\\0\\0\\0\\\vdots \\{h}_{N}\\0\end{matrix}\, \, \begin{matrix}0\\0\\0\\0\\\vdots \\0\\{h}_{N}\end{matrix}\right] \,\left[ \begin{matrix}-{e}_{1y}\\{e}_{1x}\\-{e}_{2y}\\{e}_{2x}\\\vdots \\-{e}_{Ny}\\{e}_{Nx}\end{matrix}\right]</math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|- | |- | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">=c\lbrace -{h}_{1}{e}_{1x}{e}_{1y}+{h}_{1}{e}_{1x}{e}_{1y}-</math><math>{h}_{2}{e}_{2x}{e}_{2y}+{h}_{2}{e}_{2x}{e}_{2y}\ldots -{h}_{N}{e}_{Nx}{e}_{Ny}+{h}_{N}{e}_{Nx}{e}_{Ny}\rbrace | + | | style="text-align: center;" | <math display="inline">=c\lbrace -{h}_{1}{e}_{1x}{e}_{1y}+{h}_{1}{e}_{1x}{e}_{1y}-</math><math>{h}_{2}{e}_{2x}{e}_{2y}+{h}_{2}{e}_{2x}{e}_{2y}\ldots -{h}_{N}{e}_{Nx}{e}_{Ny}+{h}_{N}{e}_{Nx}{e}_{Ny}\rbrace =0</math>, |
| − | + | | style="text-align: right;vertical-align: center;width: 5px;text-align: right;white-space: nowrap;"|(39) | |
| − | + | ||
| − | + | ||
| − | | style="text-align: right;vertical-align: | + | |
|} | |} | ||
|} | |} | ||
| Line 839: | Line 833: | ||
y (38) resulta equivalente a (22). Con esto se demuestra que el objetivo de formación (14) se sigue satisfaciendo. | y (38) resulta equivalente a (22). Con esto se demuestra que el objetivo de formación (14) se sigue satisfaciendo. | ||
| − | ===5.2. Cálculo de la matriz de repulsión | + | ===5.2. Cálculo de la matriz de repulsión '''H'''=== |
Considérese la Figura 19 en la que se representa el plano <math display="inline">{\Sigma }_{W}</math> de movimiento de los robots. Obsérvese la posición final deseada <math display="inline">{\mathit{\boldsymbol{\varphi }}}_{i}</math> para el punto objetivo <math display="inline">{\mathit{\boldsymbol{q}}}_{i}</math> del robot <math display="inline">{R}_{i}</math>, y obsérvese el punto objetivo <math display="inline">{\mathit{\boldsymbol{q}}}_{j}</math> del robot <math display="inline">{R}_{j}</math>. El espacio físico que ocupa cada robot se delimita por un círculo de radio <math display="inline">r</math>. Ahora note el punto <math display="inline">{\mathit{\boldsymbol{O}}}_{ij}\in \, {\mathit{\mathbb{R}}}^{2}</math> a una distancia <math display="inline">2r</math> de la posición del robot <math display="inline">{R}_{j}</math> sobre la línea que une los puntos <math display="inline">{\mathit{\boldsymbol{q}}}_{i}</math> y <math display="inline">{\mathit{\boldsymbol{q}}}_{j}</math>, el cual expresa la mínima distancia permitida al robot <math display="inline">{R}_{i}</math>para no colisionar con el robot <math display="inline">{R}_{j}</math>; es decir | Considérese la Figura 19 en la que se representa el plano <math display="inline">{\Sigma }_{W}</math> de movimiento de los robots. Obsérvese la posición final deseada <math display="inline">{\mathit{\boldsymbol{\varphi }}}_{i}</math> para el punto objetivo <math display="inline">{\mathit{\boldsymbol{q}}}_{i}</math> del robot <math display="inline">{R}_{i}</math>, y obsérvese el punto objetivo <math display="inline">{\mathit{\boldsymbol{q}}}_{j}</math> del robot <math display="inline">{R}_{j}</math>. El espacio físico que ocupa cada robot se delimita por un círculo de radio <math display="inline">r</math>. Ahora note el punto <math display="inline">{\mathit{\boldsymbol{O}}}_{ij}\in \, {\mathit{\mathbb{R}}}^{2}</math> a una distancia <math display="inline">2r</math> de la posición del robot <math display="inline">{R}_{j}</math> sobre la línea que une los puntos <math display="inline">{\mathit{\boldsymbol{q}}}_{i}</math> y <math display="inline">{\mathit{\boldsymbol{q}}}_{j}</math>, el cual expresa la mínima distancia permitida al robot <math display="inline">{R}_{i}</math>para no colisionar con el robot <math display="inline">{R}_{j}</math>; es decir | ||
| Line 848: | Line 842: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{O}}}_{ij}={\mathit{\boldsymbol{q}}}_{j}+</math><math>2r\frac{{\mathit{\boldsymbol{q}}}_{i}-{\mathit{\boldsymbol{q}}}_{j}}{\left\| {\mathit{\boldsymbol{q}}}_{i}-{\mathit{\boldsymbol{q}}}_{j}\right\| }</math> | + | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{O}}}_{ij}={\mathit{\boldsymbol{q}}}_{j}+</math><math>2r\frac{{\mathit{\boldsymbol{q}}}_{i}-{\mathit{\boldsymbol{q}}}_{j}}{\left\| {\mathit{\boldsymbol{q}}}_{i}-{\mathit{\boldsymbol{q}}}_{j}\right\| }</math>. |
| style="width: 5px;text-align: right;white-space: nowrap;" |(40) | | style="width: 5px;text-align: right;white-space: nowrap;" |(40) | ||
|} | |} | ||
| Line 858: | Line 852: | ||
| [[Image:draft_Aparicio Nogué_723966060-image24.png|246px]] | | [[Image:draft_Aparicio Nogué_723966060-image24.png|246px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 19 | + | | colspan="1" | '''Figura 19.''' Esquema para la evasión de obstáculos. |
|} | |} | ||
| − | Considérese además una matriz <math display="inline">{\mathit{\boldsymbol{H}}}_{r}\in \, {\mathit{\mathbb{R}}}^{ | + | Considérese además una matriz <math display="inline">{\mathit{\boldsymbol{H}}}_{r}\in \, {\mathit{\mathbb{R}}}^{N\times N}</math> con componentes del factor de repulsión <math display="inline">{h}_{ij}>0 </math> (para <math display="inline">i,j=</math><math>1,2,\ldots ,N</math> con <math display="inline">i\not =j</math>) si existe una trayectoria direccionada desde <math display="inline">{R}_{j}</math> hasta <math display="inline">{R}_{i}</math>, tal que el robot <math display="inline">{R}_{i}</math> disponga de la información de las variables de salida del robot <math display="inline">{R}_{j}</math> de forma directa o a través de otro robot en dicha trayectoria; <math display="inline">{h}_{ij}=</math><math>0</math> en caso contrario. Los elementos <math display="inline">{h}_{ii}=</math><math>0</math> (los componentes del factor de repulsión en la diagonal de <math display="inline">{\mathit{\boldsymbol{H}}}_{r}</math> son nulos). De esta manera, los componentes no nulos del factor de repulsión estarían dados por |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 868: | Line 862: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{h}_{ij}=\frac{\alpha \mathrm{tanh}\,(\lambda \lbrace {q}_{iy}-L({q}_{ix})\rbrace \lbrace {\varphi }_{ix}-{q}_{jx}\rbrace )}{\left\| {q}_{i}-{O}_{ij}\right\| +\sigma }</math> | + | | style="text-align: center;" | <math display="inline">{h}_{ij}=\frac{\alpha \mathrm{tanh}\,(\lambda \lbrace {q}_{iy}-L({q}_{ix})\rbrace \lbrace {\varphi }_{ix}-{q}_{jx}\rbrace )}{\left\| {q}_{i}-{O}_{ij}\right\| +\sigma }</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" |(41) | | style="width: 5px;text-align: right;white-space: nowrap;" |(41) | ||
|} | |} | ||
| Line 880: | Line 874: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">L\left( {q}_{ix}\right) =\frac{{\varphi }_{iy}-{q}_{jy}}{{\varphi }_{ix}-{q}_{jx}}\left( {q}_{ix}-\right. </math><math>\left. {q}_{jx}\right) +{q}_{jy}</math> | + | | style="text-align: center;" | <math display="inline">L\left( {q}_{ix}\right) =\frac{{\varphi }_{iy}-{q}_{jy}}{{\varphi }_{ix}-{q}_{jx}}\left( {q}_{ix}-\right. </math><math>\left. {q}_{jx}\right) +{q}_{jy}</math>. |
| style="width: 5px;text-align: right;white-space: nowrap;" |(42) | | style="width: 5px;text-align: right;white-space: nowrap;" |(42) | ||
|} | |} | ||
| Line 905: | Line 899: | ||
En la Tabla 2 se muestran las condiciones iniciales y posiciones finales deseadas. Para el control de esta red se utilizó un líder virtual fijo en el origen del marco global, una fuerza global de acoplamiento <math display="inline">c=</math><math>1.25</math>, ganancia <math display="inline">\mathit{\boldsymbol{D}}=</math><math>diag\lbrace 1\, \, 0\, \, 0\, \, 0\, \, 0\rbrace</math>, <math display="inline">\alpha =</math><math>0.25,\, \, \lambda =12</math> y <math display="inline">\sigma =</math><math>0.001</math>. El radio de delimitación <math display="inline">r</math> fue igual a <math display="inline">0.1</math> m, el cual incluye una tolerancia de <math display="inline">0.02</math> m. | En la Tabla 2 se muestran las condiciones iniciales y posiciones finales deseadas. Para el control de esta red se utilizó un líder virtual fijo en el origen del marco global, una fuerza global de acoplamiento <math display="inline">c=</math><math>1.25</math>, ganancia <math display="inline">\mathit{\boldsymbol{D}}=</math><math>diag\lbrace 1\, \, 0\, \, 0\, \, 0\, \, 0\rbrace</math>, <math display="inline">\alpha =</math><math>0.25,\, \, \lambda =12</math> y <math display="inline">\sigma =</math><math>0.001</math>. El radio de delimitación <math display="inline">r</math> fue igual a <math display="inline">0.1</math> m, el cual incluye una tolerancia de <math display="inline">0.02</math> m. | ||
| − | |||
| − | {| style="border-collapse: collapse;" | + | <div class="auto" style="width: auto; text-align: center; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| + | '''Tabla 2'''. Condiciones de simulación y experimentación para la RR´s de la Figura 14 que incluye la ley con procedimiento para la no colisión.</div><br /> | ||
| + | |||
| + | {| style="border-collapse: collapse; width: 80%; margin: 0 auto; text-align: center;font-size:85%;" | ||
|- | |- | ||
| style="border: 1pt solid black;vertical-align: top;"| <math>i</math> | | style="border: 1pt solid black;vertical-align: top;"| <math>i</math> | ||
| Line 950: | Line 946: | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.3 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|0.3 | ||
| style="border: 1pt solid black;text-align: center;vertical-align: top;"|-0.3 | | style="border: 1pt solid black;text-align: center;vertical-align: top;"|-0.3 | ||
| − | |} | + | |}<br /> |
En el proceso de simulación y experimentación se han calculado las normas de separación <math display="inline">{N}_{ij}=</math><math>\left\| {q}_{i}-{q}_{j}\right\|</math> entre todos los robots con la finalidad de apreciar el desempeño del procedimiento para evitar colisiones en conjunto con la ley para la formación. La Figura 20 presenta las magnitudes de las normas <math display="inline">{N}_{ij}</math> de separación. Debe esperarse que ninguna norma resulte menor a <math display="inline">2\left( r-\right. </math><math>\left. 0.02\right) =0.16</math> m. En la Figura 20(a), obtenida mediante simulación sin incluir el procedimiento para evitar colisiones, se muestra que existe un conflicto de colisión entre los robots <math display="inline">{R}_{1}</math> y <math display="inline">{R}_{2}</math> (en algún momento <math display="inline">{N}_{21}<0.16</math> m). La Figura 20(b), también mediante simulación, muestra que este conflicto se elimina al incluir la acción para la no colisión. Nótese además que entre <math display="inline">{R}_{1}</math> y <math display="inline">{R}_{3}</math> existe una condición inicial cercana a <math display="inline">2(r-</math><math>0.02)</math> sin causar colisión en la evolución de las trayectorias de los robots. La Figura 20(c), obtenida mediante el experimento, muestra que con las ganancias utilizadas se resuelve la colisión entre <math display="inline">{R}_{1}</math> y <math display="inline">{R}_{2}</math> y no se genera ninguna otra colisión. | En el proceso de simulación y experimentación se han calculado las normas de separación <math display="inline">{N}_{ij}=</math><math>\left\| {q}_{i}-{q}_{j}\right\|</math> entre todos los robots con la finalidad de apreciar el desempeño del procedimiento para evitar colisiones en conjunto con la ley para la formación. La Figura 20 presenta las magnitudes de las normas <math display="inline">{N}_{ij}</math> de separación. Debe esperarse que ninguna norma resulte menor a <math display="inline">2\left( r-\right. </math><math>\left. 0.02\right) =0.16</math> m. En la Figura 20(a), obtenida mediante simulación sin incluir el procedimiento para evitar colisiones, se muestra que existe un conflicto de colisión entre los robots <math display="inline">{R}_{1}</math> y <math display="inline">{R}_{2}</math> (en algún momento <math display="inline">{N}_{21}<0.16</math> m). La Figura 20(b), también mediante simulación, muestra que este conflicto se elimina al incluir la acción para la no colisión. Nótese además que entre <math display="inline">{R}_{1}</math> y <math display="inline">{R}_{3}</math> existe una condición inicial cercana a <math display="inline">2(r-</math><math>0.02)</math> sin causar colisión en la evolución de las trayectorias de los robots. La Figura 20(c), obtenida mediante el experimento, muestra que con las ganancias utilizadas se resuelve la colisión entre <math display="inline">{R}_{1}</math> y <math display="inline">{R}_{2}</math> y no se genera ninguna otra colisión. | ||
| Line 958: | Line 954: | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | | [[Image:draft_Aparicio Nogué_723966060-image25.png| | + | | [[Image:draft_Aparicio Nogué_723966060-image25.png|300px]] |
| + | | [[Image:draft_Aparicio Nogué_723966060-image26.png|300px]] | ||
| + | |- | ||
| + | | colspan="2" | [[Image:draft_Aparicio Nogué_723966060-image27.png|300px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figura 20.''' Normas <math display="inline">\left\| {q}_{i}-\right. </math><math>\left. {q}_{j}\right\|</math> : (a) Simulada sin incluir el procedimiento para evitar colisiones, (b) Simulada incluyendo el procedimiento para evitar colisiones y (c) Experimento incluyendo el procedimiento para evitar colisiones. |
|} | |} | ||
| − | La Figura 21 grafica la evolución de los errores de formación. La Figura 21(a) muestra el comportamiento de la evolución de los errores en simulación y sugiere un tiempo de <math display="inline">t\approx</math> | + | La Figura 21 grafica la evolución de los errores de formación. La Figura 21(a) muestra el comportamiento de la evolución de los errores en simulación y sugiere un tiempo de <math display="inline">t\approx 8</math> s para alcanzar prácticamente el objetivo de formación fijado. La Figura 21(b) presenta la gráfica obtenida mediante el experimento. |
<div id='img-21'></div> | <div id='img-21'></div> | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | | [[Image:draft_Aparicio Nogué_723966060-image28.png|312px]] [[Image:draft_Aparicio Nogué_723966060-image29.png|312px]] | + | | [[Image:draft_Aparicio Nogué_723966060-image28.png|312px]] |
| + | | [[Image:draft_Aparicio Nogué_723966060-image29.png|312px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figura 21.''' Evolución de los errores: (a) En simulación, (b) En el experimento. |
|} | |} | ||
| Line 978: | Line 978: | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | | [[Image:draft_Aparicio Nogué_723966060-image30.png|318px]] [[Image:draft_Aparicio Nogué_723966060-image31.png|318px]] | + | | [[Image:draft_Aparicio Nogué_723966060-image30.png|318px]] |
| + | | [[Image:draft_Aparicio Nogué_723966060-image31.png|318px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figura 22.''' (a) Trayectorias para la formación simuladas sin incluir el procedimiento para evitar colisiones, (b) Trayectorias para la formación en simulación y experimentación incluyendo el procedimiento para evitar colisiones. |
|} | |} | ||
| Line 998: | Line 999: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i}}={\mathit{\boldsymbol{u}}}_{i}-</math><math>\overset{\cdot}{\mathit{\boldsymbol{s}}}</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 1,010: | Line 1,011: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i}}=c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{q}}}_{j}+</math><math>{\mathit{\boldsymbol{\vartheta }}}_{i}-\overset{\cdot}{\mathit{\boldsymbol{s}}}</math>. |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 1,022: | Line 1,023: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" |<math>\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i | + | | style="text-align: center;" |<math>\begin{array}{l}\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i}} & \displaystyle =c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{q}}}_{j}-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}+\overset{\cdot}{\mathit{\boldsymbol{s}}}-\overset{\cdot}{\mathit{\boldsymbol{s}}},\\ |
| − | + | & \displaystyle =c\sum _{j=1}^{N}{g}_{ij}({\mathit{\boldsymbol{e}}}_{j}+\mathit{\boldsymbol{s}}+{\mathit{\boldsymbol{\varphi }}}_{j})-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j},\\ | |
| − | + | \displaystyle & =c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{e}}}_{j}+c\sum _{j=1}^{N}{g}_{ij}\mathit{\boldsymbol{s}}+c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j}-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}-c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{\varphi }}}_{j},\\ | |
| − | + | \displaystyle & =c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{e}}}_{j}+c\sum _{j=1}^{N}{g}_{ij}\mathit{\boldsymbol{s}}-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}.\end{array}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 1,044: | Line 1,038: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_ | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{{\mathit{\boldsymbol{e}}}_{i}}=</math><math>c\sum _{j=1}^{N}{g}_{ij}{\mathit{\boldsymbol{e}}}_{j}-c{d}_{i}{\mathit{\boldsymbol{e}}}_{i}</math>. |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
|} | |} | ||
| − | El desarrollo de <math display="inline">{\mathit{\boldsymbol{e | + | El desarrollo de <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{e}}}_{i}</math> para <math display="inline">i=</math><math>1,2,\ldots ,N</math> es |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,056: | Line 1,050: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" |<math display="inline">{\mathit{\boldsymbol{e | + | | style="text-align: center;" |<math display="inline">\overset{\cdot}{\mathit{\boldsymbol{e}}}_{1}=c\left\{ {g}_{11}{e}_{1}+\right. </math><math>\left. {g}_{12}{e}_{2}+\ldots +{g}_{1N}{e}_{N}\right\} -c{d}_{1}{e}_{1}</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|- | |- | ||
|- | |- | ||
| − | | style="text-align: center;" |<math display="inline">{\mathit{\boldsymbol{e | + | | style="text-align: center;" |<math display="inline">\overset{\cdot}{\mathit{\boldsymbol{e}}}_{2}=c\left\{ {g}_{21}{e}_{1}+\right. </math><math>\left. {g}_{22}{e}_{2}+\ldots +{g}_{2N}{e}_{N}\right\} -c{d}_{2}{e}_{2}</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|- | |- | ||
| Line 1,066: | Line 1,060: | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">{\mathit{\boldsymbol{e | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}{\mathit{\boldsymbol{e}}}_{N}=c\left\{ {g}_{N1}{e}_{1}+\right. </math><math>\left. {g}_{N2}{e}_{2}+\ldots +{g}_{NN}{e}_{N}\right\} -c{d}_{N}{e}_{N}</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 1,078: | Line 1,072: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\left[ \begin{matrix}{\overset{\cdot}{\mathit{\boldsymbol{e}}}}_{1}\\{\overset{\cdot}{\mathit{\boldsymbol{e}}}}_{2}\\\vdots \\{\overset{\cdot}{\mathit{\boldsymbol{e}}}}_{N}\end{matrix}\right] =</math><math>c\left[ \begin{matrix}{g}_{11}\\{g}_{21}\\\vdots \\{g}_{N1}\end{matrix}\quad \begin{matrix}{g}_{12}\\{g}_{22}\\\vdots \\{g}_{N2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}{g}_{1N}\\{g}_{2N}\\\vdots \\{g}_{NN}\end{matrix}\right] \left[ \begin{matrix}{\mathit{\boldsymbol{e}}}_{1}\\{\mathit{\boldsymbol{e}}}_{2}\\\vdots \\{\mathit{\boldsymbol{e}}}_{N}\end{matrix}\right] -</math><math>c\left[ \begin{matrix}{d}_{1}\\0\\\vdots \\0\end{matrix}\quad \begin{matrix}0\\{d}_{2}\\\vdots \\0\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}0\\0\\\vdots \\{d}_{N}\end{matrix}\right] \left[ \begin{matrix}{\mathit{\boldsymbol{e}}}_{1}\\{\mathit{\boldsymbol{e}}}_{2}\\\vdots \\{\mathit{\boldsymbol{e}}}_{N}\end{matrix}\right]</math> | + | | style="text-align: center;" | <math display="inline">\left[ \begin{matrix}{\overset{\cdot}{\mathit{\boldsymbol{e}}}}_{1}\\{\overset{\cdot}{\mathit{\boldsymbol{e}}}}_{2}\\\vdots \\{\overset{\cdot}{\mathit{\boldsymbol{e}}}}_{N}\end{matrix}\right] =</math><math>c\left[ \begin{matrix}{g}_{11}\\{g}_{21}\\\vdots \\{g}_{N1}\end{matrix}\quad \begin{matrix}{g}_{12}\\{g}_{22}\\\vdots \\{g}_{N2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}{g}_{1N}\\{g}_{2N}\\\vdots \\{g}_{NN}\end{matrix}\right] \left[ \begin{matrix}{\mathit{\boldsymbol{e}}}_{1}\\{\mathit{\boldsymbol{e}}}_{2}\\\vdots \\{\mathit{\boldsymbol{e}}}_{N}\end{matrix}\right] -</math><math>c\left[ \begin{matrix}{d}_{1}\\0\\\vdots \\0\end{matrix}\quad \begin{matrix}0\\{d}_{2}\\\vdots \\0\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}0\\0\\\vdots \\{d}_{N}\end{matrix}\right] \left[ \begin{matrix}{\mathit{\boldsymbol{e}}}_{1}\\{\mathit{\boldsymbol{e}}}_{2}\\\vdots \\{\mathit{\boldsymbol{e}}}_{N}\end{matrix}\right]</math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|- | |- | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">=c\left( \left[ \begin{matrix}{g}_{11}\\{g}_{21}\\\vdots \\{g}_{N1}\end{matrix}\quad \begin{matrix}{g}_{12}\\{g}_{22}\\\vdots \\{g}_{N2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}{g}_{1N}\\{g}_{2N}\\\vdots \\{g}_{NN}\end{matrix}\right] -\right. </math><math>\left. \left[ \begin{matrix}{d}_{1}\\0\\\vdots \\0\end{matrix}\quad \begin{matrix}0\\{d}_{2}\\\vdots \\0\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}0\\0\\\vdots \\{d}_{N}\end{matrix}\right] \right) \left[ \begin{matrix}{\mathit{\boldsymbol{e}}}_{1}\\{\mathit{\boldsymbol{e}}}_{2}\\\vdots \\{\mathit{\boldsymbol{e}}}_{N}\end{matrix}\right]</math> | + | | style="text-align: center;" | <math display="inline">=c\left( \left[ \begin{matrix}{g}_{11}\\{g}_{21}\\\vdots \\{g}_{N1}\end{matrix}\quad \begin{matrix}{g}_{12}\\{g}_{22}\\\vdots \\{g}_{N2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}{g}_{1N}\\{g}_{2N}\\\vdots \\{g}_{NN}\end{matrix}\right] -\right. </math><math>\left. \left[ \begin{matrix}{d}_{1}\\0\\\vdots \\0\end{matrix}\quad \begin{matrix}0\\{d}_{2}\\\vdots \\0\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}0\\0\\\vdots \\{d}_{N}\end{matrix}\right] \right) \left[ \begin{matrix}{\mathit{\boldsymbol{e}}}_{1}\\{\mathit{\boldsymbol{e}}}_{2}\\\vdots \\{\mathit{\boldsymbol{e}}}_{N}\end{matrix}\right]</math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 1,094: | Line 1,088: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\left[ \begin{matrix}{\overset{\cdot}{e}}_{11}\\{\overset{\cdot}{e}}_{12}\\{\overset{\cdot}{e}}_{21}\\\vdots \\{\overset{\cdot}{e}}_{N2}\end{matrix}\right] =</math><math>c\left( \left[ \begin{matrix}{g}_{11}{I}_{2}\\{g}_{21}{I}_{2}\\\vdots \\{g}_{N1}{I}_{2}\end{matrix}\quad \begin{matrix}{g}_{12}{I}_{2}\\{g}_{22}{I}_{2}\\\vdots \\{g}_{N2}{I}_{2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}{g}_{1N}{I}_{2}\\{g}_{2N}{I}_{2}\\\vdots \\{g}_{NN}{I}_{2}\end{matrix}\right] -\right. </math><math>\left. \left[ \begin{matrix}{d}_{1}{I}_{2}\\0{I}_{2}\\\vdots \\0{I}_{2}\end{matrix}\quad \begin{matrix}0{I}_{2}\\{d}_{2}{I}_{2}\\\vdots \\0{I}_{2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}0{I}_{2}\\0{I}_{2}\\\vdots \\{d}_{N}{I}_{2}\end{matrix}\right] \right) \left[ \begin{matrix}{e}_{11}\\{e}_{12}\\{e}_{21}\\\vdots \\{e}_{N2}\end{matrix}\right]</math> | + | | style="text-align: center;" | <math display="inline">\left[ \begin{matrix}{\overset{\cdot}{e}}_{11}\\{\overset{\cdot}{e}}_{12}\\{\overset{\cdot}{e}}_{21}\\\vdots \\{\overset{\cdot}{e}}_{N2}\end{matrix}\right] =</math><math>c\left( \left[ \begin{matrix}{g}_{11}{I}_{2}\\{g}_{21}{I}_{2}\\\vdots \\{g}_{N1}{I}_{2}\end{matrix}\quad \begin{matrix}{g}_{12}{I}_{2}\\{g}_{22}{I}_{2}\\\vdots \\{g}_{N2}{I}_{2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}{g}_{1N}{I}_{2}\\{g}_{2N}{I}_{2}\\\vdots \\{g}_{NN}{I}_{2}\end{matrix}\right] -\right. </math><math>\left. \left[ \begin{matrix}{d}_{1}{I}_{2}\\0{I}_{2}\\\vdots \\0{I}_{2}\end{matrix}\quad \begin{matrix}0{I}_{2}\\{d}_{2}{I}_{2}\\\vdots \\0{I}_{2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}0{I}_{2}\\0{I}_{2}\\\vdots \\{d}_{N}{I}_{2}\end{matrix}\right] \right) \left[ \begin{matrix}{e}_{11}\\{e}_{12}\\{e}_{21}\\\vdots \\{e}_{N2}\end{matrix}\right]</math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 1,106: | Line 1,100: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\left[ \begin{matrix}{\overset{\cdot}{e}}_{11}\\{\overset{\cdot}{e}}_{12}\\{\overset{\cdot}{e}}_{21}\\\vdots \\{\overset{\cdot}{e}}_{N2}\end{matrix}\right] =</math><math>c\left( \left( \left[ \begin{matrix}{g}_{11}\\{g}_{21}\\\vdots \\{g}_{N1}\end{matrix}\quad \begin{matrix}{g}_{12}\\{g}_{22}\\\vdots \\{g}_{N2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}{g}_{1N}\\{g}_{2N}\\\vdots \\{g}_{NN}\end{matrix}\right] -\right. \right. </math><math>\left. \left. \left[ \begin{matrix}{d}_{1}\\0\\\vdots \\0\end{matrix}\quad \begin{matrix}0\\{d}_{2}\\\vdots \\0\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}0\\0\\\vdots \\{d}_{N}\end{matrix}\right] \right) \otimes {I}_{2}\right) \left[ \begin{matrix}{e}_{11}\\{e}_{12}\\{e}_{21}\\\vdots \\{e}_{N2}\end{matrix}\right]</math> | + | | style="text-align: center;" | <math display="inline">\left[ \begin{matrix}{\overset{\cdot}{e}}_{11}\\{\overset{\cdot}{e}}_{12}\\{\overset{\cdot}{e}}_{21}\\\vdots \\{\overset{\cdot}{e}}_{N2}\end{matrix}\right] =</math><math>c\left( \left( \left[ \begin{matrix}{g}_{11}\\{g}_{21}\\\vdots \\{g}_{N1}\end{matrix}\quad \begin{matrix}{g}_{12}\\{g}_{22}\\\vdots \\{g}_{N2}\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}{g}_{1N}\\{g}_{2N}\\\vdots \\{g}_{NN}\end{matrix}\right] -\right. \right. </math><math>\left. \left. \left[ \begin{matrix}{d}_{1}\\0\\\vdots \\0\end{matrix}\quad \begin{matrix}0\\{d}_{2}\\\vdots \\0\end{matrix}\quad \begin{matrix}\ldots \\\ldots \\\ddots \\\ldots \end{matrix}\quad \begin{matrix}0\\0\\\vdots \\{d}_{N}\end{matrix}\right] \right) \otimes {I}_{2}\right) \left[ \begin{matrix}{e}_{11}\\{e}_{12}\\{e}_{21}\\\vdots \\{e}_{N2}\end{matrix}\right]</math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 1,118: | Line 1,112: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math display="inline">\ | + | | style="text-align: center;" | <math display="inline">\overset{\cdot}\mathit{\boldsymbol{e}}= c\left( \left( \mathit{\boldsymbol{G}}-\right. \right. </math><math>\left. \left. \mathit{\boldsymbol{D}}\right) \otimes {\mathit{\boldsymbol{I}}}_{2}\right) \mathit{\boldsymbol{e}}</math>, |
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 1,130: | Line 1,124: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\overset{\cdot}{\mathit{\boldsymbol{e}}} | + | | style="text-align: center;" | <math>\begin{array}{ll}\overset{\cdot}{\mathit{\boldsymbol{e}}} & =-c\left( \left( \mathit{\boldsymbol{D}}-\mathit{\boldsymbol{G}}\right) \otimes {\mathit{\boldsymbol{I}}}_{2}\right) \mathit{\boldsymbol{e}},\\ |
| − | + | & =-\mathit{\boldsymbol{F}}\mathit{\boldsymbol{e}}.\blacksquare \end{array}</math> | |
| − | + | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | | | style="width: 5px;text-align: right;white-space: nowrap;" | | ||
|} | |} | ||
| Line 1,142: | Line 1,135: | ||
==Referencias== | ==Referencias== | ||
| + | <div class="auto" style="width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
[1] T. M. Cheng, A. V. Savkin, Decentralized control of multi-agent systems for swarming with a given geometric pattern, Computers and Mathematics with Applications, 61(4) (2011) 731–744. | [1] T. M. Cheng, A. V. Savkin, Decentralized control of multi-agent systems for swarming with a given geometric pattern, Computers and Mathematics with Applications, 61(4) (2011) 731–744. | ||
| Line 1,208: | Line 1,202: | ||
[33] E. Bugarín, R. Kelly, RTSVC: Real-Time System for Visual Control of Robots, Wiley Periodicals, Inc. Int J Imaging Syst Technol, Vol. 18, 251–256 (2008). | [33] E. Bugarín, R. Kelly, RTSVC: Real-Time System for Visual Control of Robots, Wiley Periodicals, Inc. Int J Imaging Syst Technol, Vol. 18, 251–256 (2008). | ||
| + | </div> | ||
Latest revision as of 15:23, 16 March 2018
Resumen
En este artículo se describe una propuesta de control para un objetivo de formación de una red de robots en trabajo colaborativo con acoplamiento difusivo estático utilizando herramientas derivadas de la teoría de grafos. Dicha propuesta se garantiza mediante la teoría de estabilidad de Lyapunov y se valida con resultados en simulación y en experimentación. Como parte importante de este trabajo, se detalla a manera de tutorial el procedimiento para la formulación de la red de robots abordada y también se propone una ley de control de formación con procedimiento para la no colisión entre los robots que forman la red utilizando la misma topología de red.
Palabras clave: Formación de redes de robots, acoplamiento difusivo estático, teoría de estabilidad de Lyapunov, validación experimental, no colisión.
Abstract
This article describes a control proposal for a formation objective of a robot network in collaborative work with static diffusive coupling using tools derived from graph theory. This proposal is guaranteed by the stability theory of Lyapunov and it is validated with results in simulation and experimentation. As an important part of this work, it is detailed like a tutorial the procedure for the formulation of the robot network addressed and also it is proposed a formation control law with procedure for non-collision between the robots that form the network using the same network topology.
1. Introducción
Desde principios del presente siglo se han incrementado notablemente los esfuerzos por coordinar y sincronizar grupos de robots que forman redes para el trabajo colaborativo. Estas Redes de Robots (RR´s) se justifican en misiones que no son posibles llevarlas a cabo con robots actuando de forma individual por razones de su propia capacidad. Entre los aspectos de estudio de mayor interés destaca la propuesta de leyes de control que gobiernen el comportamiento colectivo. Para muchas misiones de estas RR´s, la etapa primaria es su formación con un patrón geométrico o una distribución determinada [1]. La formación consiste en un posicionamiento relativo espacial con respecto a una o más referencias, fijas o móviles, para cada uno de los robots que forman parte de la red [2]. Para este problema de formación se han utilizado distintas metodologías [2-8]. La mayor parte de estas metodologías se fundamenta en la teoría de grafos cuyos inicios están documentados desde el siglo XVIII y que en la década de 1960 se extiende para aplicaciones en redes complejas [9-15]. Mediante la teoría de grafos es posible expresar interacciones entre sistemas dinámicos de manera general y organizada, facilitando la formulación de leyes de control para gobernar el comportamiento entero de una red.
Dentro del campo de la teoría de grafos y redes complejas, el acoplamiento difusivo estático es una estrategia ampliamente utilizada para realizar la interconexión entre los nodos (robots) de la red [16,17]. El principio de acoplamiento difusivo estático es un esquema de retroalimentación constante [17] entre los robots que forman parte de la red, pudiendo ser esta conectividad global o parcial (respectivamente: todos los robots se conectan con el resto de robots o sólo parte de ellos). La retroalimentación consiste en insertar como parte de la entrada del sistema dinámico del robot una señal que es la diferencia entre las variables de salida del robot de interés y las variables de salida del resto de robots en la red [18]. De este tipo de acoplamiento se han derivado distintas metodologías con el propósito de forzar una respuesta deseada en los robots, denominada estado de sincronía[14]; ó bien, una respuesta de sincronía natural, denominada consenso [19-21]. Una modalidad de estrategia de control que destaca para redes de gran dimensión es el control pinning (líderes referentes), que propone una acción de control en sólo un reducido número de sistemas dinámicos de la red y que inducen a la red entera hacia un estado de sincronía [11,14-15,22]. Estas estrategias se pueden llevar a cabo tanto mediante el control centralizado como con el control distribuido [23]. Con el control centralizado el procesamiento reside en un procesador que se encarga de monitorear las variables de estado de cada robot y de comunicar las acciones de control necesarias para alcanzar el objetivo de movimiento. Con el control distribuido el procesamiento reside en dos o más procesadores con acceso total o parcial a la información de variables de estado de la red; típicamente los robots llevan sus procesadores a bordo.
La formación de robots es aún un problema abierto [3-5], especialmente para RR´s de gran dimensión y RR´s heterogéneas. Las redes heterogéneas de robots están integradas por robots con distintos modelos dinámicos, con distintas dimensiones de vectores de variables de estado, con distinta dimensión de variables de salida o una combinación de las condiciones anteriores [16,17]. Las soluciones propuestas aún son parciales y requieren una integración para resolver problemas íntimamente relacionados. Tales problemas, además de los ya mencionados, son la evasión de obstáculos, la no colisión entre robots, las saturaciones en los accionamientos para el control, la diversidad de escenarios y las limitaciones en los enlaces de comunicación para el control [14-15].
Las contribuciones del presente trabajo se aplican en la formación de una RR´s utilizando herramientas derivadas de la teoría de grafos. Estas contribuciones son: (i) un tutorial para la formulación de RR´s mediante el acoplamiento difusivo estático en el que se describen de manera detallada los elementos y variables que intervienen en la red, (ii) una ley de control para una formación deseada de la RR´s bajo esta formulación y (iii) un procedimiento para la no colisión entre los robots que forman la red utilizando la misma topología de la RR´s. La metodología desarrollada se ejemplifica con simulaciones y experimentos mediante la construcción de una red de Robots Móviles Terrestres a base de Ruedas (RMTR’s).
El resto de este documento está organizado como sigue. En la sección 2 se expone un tutorial que describe paso a paso la formulación de una RR´s basado en el modelo para cada -ésimo robot que forma parte de la red y la estrategia de acoplamiento difusivo estático. En la sección 3 se propone la ley de control para la formación de una red de robots construida con robots tipo uniciclo. La efectividad de la ley de control se demuestra utilizando la teoría de estabilidad de Lyapunov. En la sección 4 se presentan los resultados de simulación y experimentación. En la sección 5 se describe un procedimiento para evitar las colisiones entre robots de la red ejemplificada en la sección 4 y se presentan resultados de simulación y experimentación. Finalmente, en la sección 6 se presentan las conclusiones generales.
2. Formulación de una red de robots
En esta sección se describe a manera de tutorial una metodología para la formulación de una RR´s. En la sección 2.1 se presenta el modelo de un robot individual. En la sección 2.2 se describe el modelo del -ésimo robot en una red de robots considerando la contribución de todos los robots que pertenecen a la red sobre las entradas de dicho robot. En la sección 2.3 se muestra un esquema de red general de robots. En la sección 2.4 se explican los elementos necesarios para la formulación de una red de robots mediante el acoplamiento difusivo estático y la sección 2.5 expone un ejemplo detallado para la formulación de una red de robots con la estrategia descrita.
2.1 Modelo de un robot individual
El modelo de un robot individual resulta por lo general en una o más ecuaciones diferenciales no lineales que pueden expresarse de la forma
|
donde es el vector de variables de estado, es el vector de variables de salida, denota la variable tiempo continuo, es el vector de variables de entrada. y son funciones continuas. En la Figura 1 se muestra el diagrama a bloques de un robot individual en correspondencia con (1).
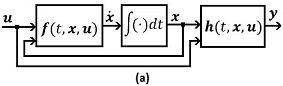 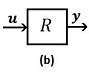
|
| Figura 1. (a) Diagrama a bloques de un robot individual, (b) Representación simplificada |
2.2 Modelo del i-ésimo robot en una red de robots
Para un robot que pertenece a una red se puede proponer un nuevo vector de entrada , de manera que su modelo quedaría como
|
donde es un mapeo de y hacia el vector de excitación con la concatenación de vectores de variables de salida de cada robot de la red, y la cantidad de robots que integran la red. La Figura 2 muestra el modelo de (2) de manera simplificada.
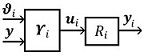
|
| Figura 2. Modelo de un -ésimo robot que pertenece a una red. |
2.3 Modelo de una red de robots
En consecuencia, de acuerdo a (2), la Figura 3 muestra el diagrama a bloques de una red de robots.
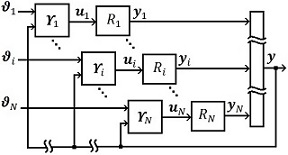
|
| Figura 3. Diagrama a bloques de una red de robots. |
2.4 Estrategia de acoplamiento difusivo estático
Una red de robots también puede ser expresada mediante el conjunto de robots y de conexiones que la conforman mediante
|
donde es el conjunto de robots y es el conjunto de conexiones dirigidas de la red. Una conexión dirigida es una función que corresponde a un par de robots siendo la salida (salida del robot ) el vector de información que se transfiere al robot mediante una transformación . La Figura 4 muestra las conexiones dirigidas de manera generalizada para un par de robots y .
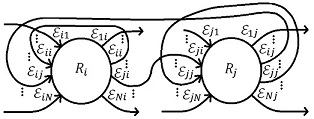
|
| Figura 4. Grafo o esquema generalizado de conexiones dirigidas en los robots y de una red. |
De esta forma, una estrategia común para la construcción de la función relacionada con (2) [11,15-17], corresponde a un sistema lineal de acoplamiento difusivo estático donde el conjunto de conexiones de todos los robots respecto al robot se expresa como
|
donde es la denominada fuerza global de acoplamiento, , con elemento de la matriz de configuración externa de red obtenida mediante
|
donde es la matriz de adyacencia ponderada con sus elementos si existe una conexión entre el robot y el robot y si no existe la conexión ( es la magnitud de la conexión y en particular ); es la matriz de grado de entrada con la suma de los pesos de las conexiones que ingresan a cada robot (note que de esta forma es difundida puesto que la suma de sus elementos por renglón es nula); y es la matriz de configuración interna que expresa las proporciones de contribución de las variables de salida hacia y en consecuencia, define la relación interna entre las variables del robot hacia las variables del robot .
De esta manera el acoplamiento difusivo estático para generar es
|
donde se ha considerado en forma aditiva la nueva entrada de control . La Figura 5 muestra el diagrama a bloques para una red formulada utilizando la estrategia (6), mientras que la Figura 6 presenta el esquema generalizado de conexiones dirigidas equivalente.
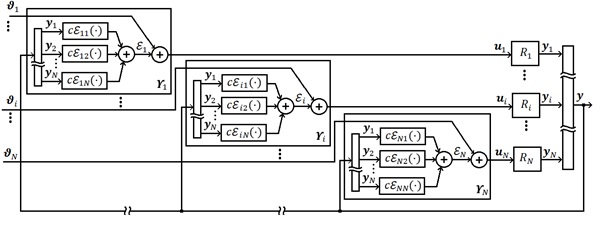
|
| Figura 5. Diagrama a bloques para una red de robots con acoplamiento difusivo estático. |
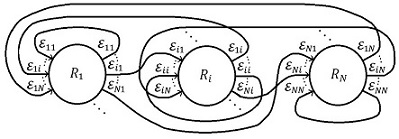
|
| Figura 6. Esquema generalizado de conexiones dirigidas equivalente al diagrama a bloques de la Figura 5. |
2.5 Ejemplo de formulación de una RR´s con acoplamiento difusivo estático
Ejemplo 2.1: Considérese la topología descrita en el grafo de la Figura 7 con los 4 robots distintos (red heterogénea) mostrados en la Figura 8.
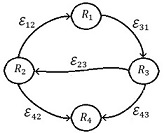
|
| Figura 7. Grafo para el ejemplo de formulación de red de robots. Observe que las autoconexiones en cada robot no son mostradas. |
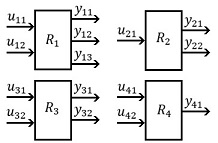
|
| Figura 8. Detalle de los robots distintos para el ejemplo de formulación de red. |
Considere las siguientes magnitudes de conexión: , , , y ; tal que
|
De este modo, según (5), la matriz de conexión externa resulta
|
Ahora bien, la matriz de matrices de configuración interna debe ser
|
con cada matriz de configuración interna y con una matriz cero de dimensión adecuada; es decir
|
con cada según la proporción de contribución de las variables hacia .
De esta manera, se completa (6) para la red de la Figura 7 y la Figura 9 muestra su diagrama a bloques equivalente
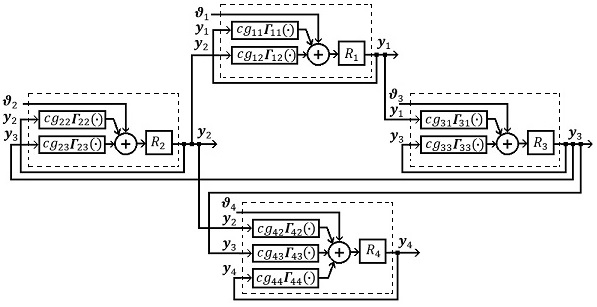
|
| Figura 9. Diagrama a bloques equivalente para el ejemplo de red heterogénea con 4 robots. |
3. Formación de una red de robots
En esta sección se presenta la propuesta para la formación de una red de robots construida con RMTR’s tipo uniciclo de tracción diferencial como el que se muestra en la Figura 10. Los robots se han modelado para expresar la cinemática de un punto objetivo colocado en la parte superior del robot, centrado en referencia al eje que une sus ruedas en el punto pero desplazado una distancia en dirección perpendicular a dicho eje (ver Figura 10). La cinemática de tal punto objetivo puede expresarse como [24]
|
donde denota la orientación del robot en referencia al marco global , es la variable de entrada correspondiente a la velocidad lineal del robot y su otra variable de entrada correspondiente a su velocidad angular. Note que es invertible si , de manera que si esto se cumple (10) en forma simplificada quedaría
|
donde representa el vector de entrada correspondiente a las velocidades lineales en direcciones y como se muestra en la Figura 10(b). La ecuación (11) es el modelo de nuestro robot individual, significando que en relación a (1): , , y .
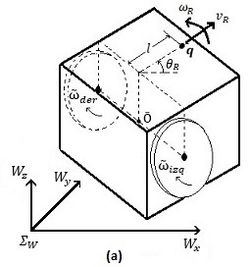
|
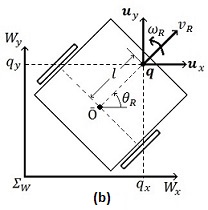
|
| Figura 10. (a) Robot tipo uniciclo de tracción diferencial, (b) Vista superior del robot. | |
Ahora, considérense robots en red con acoplamiento difusivo estático con dinámica (11), de tal modo que para el -ésimo robot sería
|
y de acuerdo a (6)
|
donde se ha sustituido y por ser una red homogénea.
El objetivo de formación se propone como
|
donde es el error de formación y se ha insertado un líder virtual (sistema de referencia de red) con sistema dinámico y un vector de posiciones finales deseadas constantes para cada -ésimo robot respecto al líder. El vector puede ser un punto fijo o una trayectoria [11]. La derivada de es o bien sustituyéndole (12)
|
3.1 Ley de control propuesta
La ley de control propuesta para el objetivo de formación es
|
donde es la ganancia del controlador para el -ésimo robot. Así (13), luego de sustituirle (16) resulta
|
Ya que y que la matriz es difundida, la dinámica (15) del error resulta
|
y en forma matricial (ver Apéndice A)
|
donde , , y expresa el producto Kronecker [26].
3.2 Punto de equilibrio y prueba de estabilidad
Para demostrar el cumplimiento del objetivo de formación (14) con la ley de control (16) en el sistema expresado por (13)-(12), considérense los siguientes lemas:
Lema 1 [25]. Un sistema homogéneo , donde , posee una solución única (la solución trivial ) si y sólo si el .
Lema 2 [26]. Sea con valores singulares y con valores singulares . Entonces (ó ) tiene valores singulares y . NOTA: Si las matrices son cuadradas puede intercambiarse "valores singulares" por "valores característicos".
Lema 3 [27]. Sea una matriz cuadrada y haciendo , el Teorema de Silvester establece que es definida positiva () si y sólo si:
|
NOTA: Si es definida positiva () entonces es definida negativa (). Si es semidefinida positiva () entonces es semidefinida negativa ().
Lema 4 [28]. Sean y matrices definidas (semidefinidas) positivas, entonces es una matriz definida (semidefinida) positiva.
Ahora, considere el punto de equilibrio de (19) y, para el análisis de su estabilidad, considérese la siguiente función candidata de Lyapunov
|
por lo que la derivada temporal de es
|
Tomando de (19) y sustituyendo en (21) se tiene
|
De manera que si entonces , significando que es un punto de equilibrio asintóticamente estable y con esto queda demostrado el cumplimiento del objetivo de formación (14).
Como ejemplos considérense las siguientes topologías típicas para una red con robots.
Ejemplo 3.1: La red direccionada y no ponderada (magnitud de conexión unitaria) de la Figura 11 en configuración estrella con el robot en la raíz. Su matriz de configuración externa resulta
|
Propóngase
|
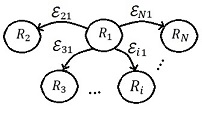
|
| Figura 11. Una red de robots con Topología Estrella. |
Se ha considerado ya que el robot en la raíz () de la red es el único viable para ser líder, pues es el único que mantiene conexiones direccionadas con el resto de los robots. Obsérvese que (24) es una matriz triangular, por lo que si su rango es completo (). De esta manera, si y apoyándonos en los Lemas 1 y 2 , es el único punto de equilibrio de (19).
Ahora, partiendo de (24) y aplicando el Lema 3 con se tiene
|
de forma que ( si ), ( si ,…, ( si ),…, ( si ).
De manera que apoyándonos en el Lema 4, entonces si
|
entonces ; cumpliéndose el objetivo de formación (14) de forma global.
Ejemplo 3.2: La red direccionada y no ponderada de la Figura 12 en configuración anillo. Su matriz de configuración externa resulta
|
Propóngase
|
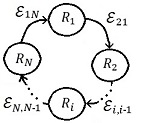
|
| Figura 12. Una red de robots con Topología Anillo. |
Nótese que (lo cual puede comprobarse directamente al aplicar el procedimiento de eliminación de Gauss). Para que sea completo, por la simetría de la topología, resulta suficiente cualquier Supóngase de manera que si y apoyándose en los Lemas 1 y 2, es el único punto de equilibrio de (19).
Ahora, sustituyendo la supuesta en (28) y aplicando el Lema 3 con se tiene
|
de forma que , donde para , para y para , siendo cada si . Por lo tanto, apoyándonos en el Lema 4, entonces si se cumple que y el objetivo de formación (14) es satisfecho de forma global.
Ejemplo 3.3: La red direccionada y no ponderada de la Figura 13 en configuración malla. Su matriz de configuración externa resulta
|
Propóngase
|
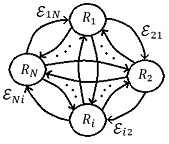
|
| Figura 13. Una red de robots con Topología Malla. |
Nótese que (lo cual puede comprobarse al aplicar el procedimiento de eliminación de Gauss). Para que sea completo resulta suficiente cualquier . Supóngase de manera que si y apoyándose en los Lemas 1 y 2, es el único punto de equilibrio de (19).
Ahora, sustituyendo la supuesta en (31) y aplicando el Lema 3 con se tiene
|
donde . De manera que para que cada , para , es decir, . Por lo tanto, apoyándonos en el Lema 4, entonces si se cumple que y el objetivo de formación (14) es satisfecho de forma global.
4. Simulación y experimento
4.1. Caso particular de una red con 5 robots tipo uniciclo
La Figura 14 muestra una RR’s direccionada, no típica y no ponderada, compuesta por cinco robots tipo uniciclo con dinámica de sus puntos objetivo (12) y para la cual resulta su matriz de configuración externa
|
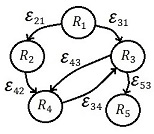
|
| Figura 14. Topología externa de una RR´s no típica con 5 robots tipo uniciclo de tracción diferencial. |
Nótese que ya que su renglón 1 es nulo. Se propone la matriz debido a que tiene trayectorias direccionadas hacia el resto de los robots. Para que sea completo resulta suficiente (lo que se comprueba con el procedimiento de eliminación de Gauss) y apoyándose en los Lemas 1 y 2, es el único punto de equilibrio de (19).
Ahora, aplicando el Lema 3 en con se tiene
|
donde resulta
( si ), ( si ), , ( si ), ( si ) y ( si ).
Por lo tanto, apoyándonos en el Lema 4, entonces si se cumple que y el objetivo de formación (14) es satisfecho de forma global.
4.2. Simulación y experimento
Para la simulación de la red formada por cinco robots se utilizó MATLAB R2011b. El experimento se realizó con cinco robots tipo uniciclo modelo YSR-A de la empresa Yujin que reciben las consignas de velocidad mediante módulos de comunicación inalámbrica operando a 418 MHz y a una tasa de 19.2 Kbps. Los módulos de comunicación se conectan a un procesador central vía puerto serie. Este procesador central ejecuta una aplicación de tiempo real en ambiente RTLinux, auxiliado de una tarjeta de video Leonardo de la empresa Arvoo y con programación basada en [33]. Para efectos de identificar la postura de los robots se colocaron dos puntos marca sobre cada robot, uno para la posición objetivo y el otro como auxiliar para el cálculo de su orientación. Las imágenes se registran mediante una cámara UF-1000CL de la empresa UNIQ cuyo eje óptico apunta perpendicularmente al plano de movimiento de los robots (ver Figura 10). La cámara es de alta velocidad y se configuró a razón de 200 cuadros por segundo, obteniéndose un periodo estricto de muestreo en los experimentos de 0.005 s.
En la Tabla 1 se muestran las condiciones iniciales y posiciones finales deseadas para el control de formación de la red de la Figura 14; utilizando un líder virtual con dinámica y con condición inicial m, una fuerza global de acoplamiento , ganancias y una distancia m entre marcas sobre cada robot. Obsérvese que se desea una formación en línea recta con un ángulo de rad respecto al marco global .
| [m] | [m] | [rad] | [m] | [m] | |
| 1 | 0.1511 | 0.2286 | -1.1802 | 0.30 | 0.30 |
| 2 | 0.4243 | 0.0891 | -1.1310 | 0.15 | 0.15 |
| 3 | -0.2135 | -0.0247 | -0.7598 | 0 | 0 |
| 4 | 0.0496 | -0.0717 | -0.3286 | -0.15 | -0.15 |
| 5 | 0.1259 | -0.2499 | 2.8198 | -0.30 | -0.30 |
La Figura 15(a) muestra la evolución de los errores en simulación, los cuales tienden a cero a medida que el tiempo transcurre. Una apreciación visual simple destaca que es suficiente s para que el error pueda considerarse prácticamente cero. En la Figura 15(b) se presentan las gráficas de los errores en el experimento. Cabe destacar que el umbral de reacción de los robots se encuentra por encima de m/s de manera que debajo de dicho valor no hay movimiento del robot. Lo anterior es lo que justifica que en el experimento exista un error en estado estacionario, es decir, cuando la ley de control demanda velocidades pequeñas (pues el robot está cerca del objetivo) se cae dentro del umbral de no reacción del robot deteniendo su movimiento. La norma de error más grande lo presenta con m.
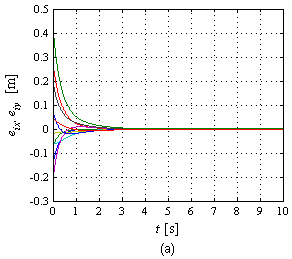 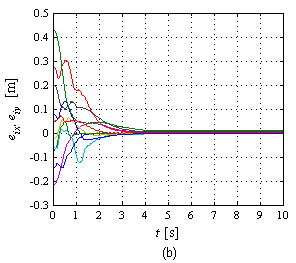
|
| Figura 15. Evolución de los errores: (a) En simulación, (b) En experimento. |
La Figura 16 muestra las trayectorias seguidas por los robots. Las trayectorias experimentales descritas difieren un tanto de las trayectorias simuladas, esto debido a factores no modelados, como deslizamientos, derrapes y umbrales de reacción. El objetivo final, sin embargo, se alcanza satisfactoriamente.
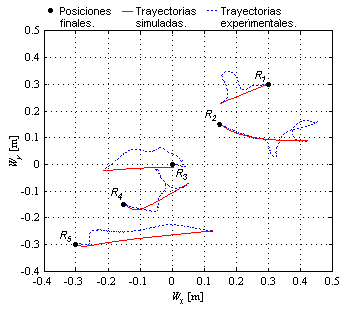
|
| Figura 16. Trayectorias para la formación en línea recta en el marco global . |
Las gráficas en las Figuras 17 y 18 muestran respectivamente la evolución de las velocidades lineales () y angulares () de los robots en simulación (17(a) y 18(a)) y en experimentación (17(b) y 18(b)). Las trayectorias experimentales muestran que luego de s permanece un pequeño valor constante y un pequeño valor oscilatorio incapaces de causar movimiento práctico en los robots.
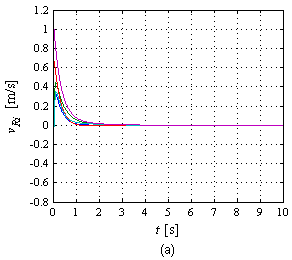
|
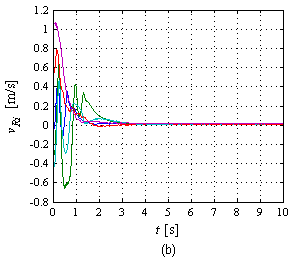
|
| Figura 17. Gráficas de velocidades lineales de los robots: (a) Simulación, (b) Experimento. | |
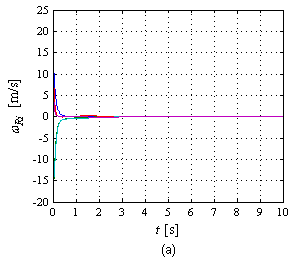
|
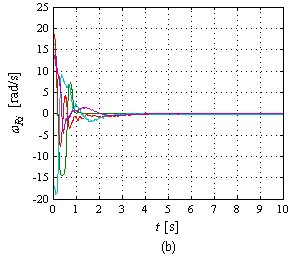
|
| Figura 18. Gráficas de velocidades angulares de los robots: (a) Simulación, (b) Experimento. | |
5. Ley de control con procedimiento para evitar colisiones
La evasión de obstáculos y la no colisión entre los robots de una red aún es un problema abierto, especialmente cuando se tiene un número elevado de robots en áreas reducidas. En la literatura pueden encontrarse estudios que abordan esta problemática [24,29-32].
5.1. Ley de control
Se propone que la ley de control (16) contenga además, en forma aditiva, una acción de repulsión como procedimiento para evitar colisiones entre los robots. Para el planteamiento formulado en la Sección 3, la propuesta, inspirada en [31], es la siguiente (la cual incluye el vector adicional de acciones de control ):
|
donde con un factor de repulsión. De esta manera (13) resulta
|
Manteniendo como objetivo el control de formación expresado por (14), la derivada del error es
|
Obsérvese que sigue siendo un punto de equilibrio. Ahora, considérese la función candidata de Lyapunov (20) y su derivada (21), entonces para este caso puede escribirse como
|
donde y .
La contribución en (38) es
|
y (38) resulta equivalente a (22). Con esto se demuestra que el objetivo de formación (14) se sigue satisfaciendo.
5.2. Cálculo de la matriz de repulsión H
Considérese la Figura 19 en la que se representa el plano de movimiento de los robots. Obsérvese la posición final deseada para el punto objetivo del robot , y obsérvese el punto objetivo del robot . El espacio físico que ocupa cada robot se delimita por un círculo de radio . Ahora note el punto a una distancia de la posición del robot sobre la línea que une los puntos y , el cual expresa la mínima distancia permitida al robot para no colisionar con el robot ; es decir
|

|
| Figura 19. Esquema para la evasión de obstáculos. |
Considérese además una matriz con componentes del factor de repulsión (para con ) si existe una trayectoria direccionada desde hasta , tal que el robot disponga de la información de las variables de salida del robot de forma directa o a través de otro robot en dicha trayectoria; en caso contrario. Los elementos (los componentes del factor de repulsión en la diagonal de son nulos). De esta manera, los componentes no nulos del factor de repulsión estarían dados por
|
donde son ganancias para ponderar la magnitud de la repulsión, es un escalar positivo (muy pequeño sólo para evitar singularidades) y es la evaluación en el punto de la ecuación de la línea recta que une los puntos y ; es decir
|
Finalmente, los elementos de la diagonal en la matriz son para .
5.3. Simulación y experimento considerando el procedimiento para evitar colisiones
Considérese la red mostrada en la Figura 14 y descrita en la Sección 4.2, de tal forma que su matriz de componentes del factor de repulsión es
|
Por lo que la matriz donde , , y .
En la Tabla 2 se muestran las condiciones iniciales y posiciones finales deseadas. Para el control de esta red se utilizó un líder virtual fijo en el origen del marco global, una fuerza global de acoplamiento , ganancia , y . El radio de delimitación fue igual a m, el cual incluye una tolerancia de m.
| [m] | [m] | [rad] | [m] | [m] | |
| 1 | -0.1955 | 0.1706 | 0.0568 | 0 | 0 |
| 2 | -0.0390 | -0.0020 | -0.0267 | 0.3 | 0.3 |
| 3 | -0.1620 | 0.3492 | -3.0882 | -0.3 | 0.3 |
| 4 | -0.1135 | -0.3512 | 3.0847 | -0.3 | -0.3 |
| 5 | 0.0261 | -0.1846 | -0.0542 | 0.3 | -0.3 |
En el proceso de simulación y experimentación se han calculado las normas de separación entre todos los robots con la finalidad de apreciar el desempeño del procedimiento para evitar colisiones en conjunto con la ley para la formación. La Figura 20 presenta las magnitudes de las normas de separación. Debe esperarse que ninguna norma resulte menor a m. En la Figura 20(a), obtenida mediante simulación sin incluir el procedimiento para evitar colisiones, se muestra que existe un conflicto de colisión entre los robots y (en algún momento m). La Figura 20(b), también mediante simulación, muestra que este conflicto se elimina al incluir la acción para la no colisión. Nótese además que entre y existe una condición inicial cercana a sin causar colisión en la evolución de las trayectorias de los robots. La Figura 20(c), obtenida mediante el experimento, muestra que con las ganancias utilizadas se resuelve la colisión entre y y no se genera ninguna otra colisión.
La Figura 21 grafica la evolución de los errores de formación. La Figura 21(a) muestra el comportamiento de la evolución de los errores en simulación y sugiere un tiempo de s para alcanzar prácticamente el objetivo de formación fijado. La Figura 21(b) presenta la gráfica obtenida mediante el experimento.
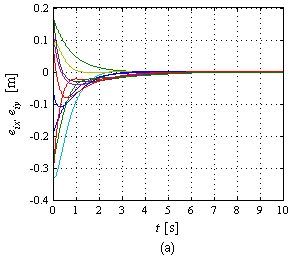
|
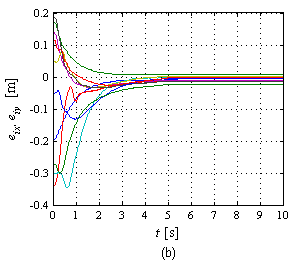
|
| Figura 21. Evolución de los errores: (a) En simulación, (b) En el experimento. | |
En la Figura 22 se observan las posiciones iniciales y finales para cada robot; así como las trayectorias seguidas por cada uno de ellos. En la Figura 22(a) se muestran las trayectorias en simulación sin incluir la ley para la no colisión. En la Figura 22(b) se presentan las trayectorias de los robots cuando se incluye la ley para la no colisión, obsérvese que en el experimento el robot no sigue una línea recta (como en la simulación) debido a que se hace presente la acción para no colisionar con el robot , mismo que describe una trayectoria en arco para evitar colisionar tanto con el robot como con el robot . El movimiento inicial del robot en dirección opuesta a su posición final deseada se debe a la dependencia con los estados de , que al acercarse a incrementa la acción de no colisión en este último. En general, las trayectorias de los cinco robots han sufrido cambios con la ley de no colisión en virtud de la naturaleza de la repulsión entre todos ellos. Para las trayectorias de este experimento y de igual manera que para las de la Figura 16, es notable el logro en una medida satisfactoria del objetivo propuesto.
6. Conclusiones
Se ha presentado un tutorial para formular una red de robots mediante la estrategia de acoplamiento difusivo estático, típica en teoría de grafos. Se ha propuesto una ley de control para lograr el objetivo de formación de una red homogénea de robots utilizando la metodología descrita. Se ha realizado la experimentación para demostrar la validez de la ley de control propuesta y se ha demostrado el cumplimiento del objetivo de formación mediante la teoría de estabilidad de Lyapunov. Se ha particularizado en la inserción de la ganancia de control en tan solo un robot que recibe la información de estados de un líder virtual con la condición de que exista una trayectoria direccionada desde tal robot hacia todos los robots restantes de la red. Finalmente, utilizando la misma topología externa de la red se ha propuesto y validado experimentalmente el objetivo de formación con procedimiento para evitar colisiones entre los robots.
Apéndice A
Detalle de la forma matricial de
Para y de acuerdo a (15) se tiene
|
y considerando (13)
|
Ahora, sustituyéndole la ley de control propuesta (16) tenemos (note que )
|
|
Dado que es difundida
|
El desarrollo de para es
|
ó bien en forma matricial
|
|
y dado que el acoplamiento corresponde a una red homogénea con para
|
|
o bien
|
|
que resulta en
|
es decir
|
|
Agradecimientos
Se agradece el apoyo financiero del Tecnológico Nacional de México, del Instituto Tecnológico de Ensenada, del PRODEP y del CONACYT (Proyecto 166654).
Referencias
[1] T. M. Cheng, A. V. Savkin, Decentralized control of multi-agent systems for swarming with a given geometric pattern, Computers and Mathematics with Applications, 61(4) (2011) 731–744.
[2] H. García, B. Jayawardhana, M. Cao, Distributed Rotational and Translational Maneuvering of Rigid Formations and Their Applications, IEEE Transactions on Robotics, 32(3) (2016) 684-697.
[3] G. Antonelli, F. Arrichiello, F. Caccavale, A. Marino, Decentralized Centroid and Formation Control for Multi-Robot Systems, IEEE International Conference on Robotics and Automation (ICRA), (2013) 3511-3516.
[4] M. Aranda, G. López-Nicolás, C. Sagüés, M. M. Zavlanos, Distributed Formation Stabilization Using Relative Position Measurements in Local Coordinates, IEEE Transactions on Automatic Control. DOI 10.1109/TAC.2016.2527719.
[5] S. Fuady, A. Ravi, R. Bambbang, Distributed Formation Control of Multi-Robot System with Obstacle Avoidance, International Conference on Robotics, Biomimetics, Intelligent Computational Systems (ROBIONETICS) (2013) 94-98.
[6] Z. Han, L. Wang, Z. Lin, Local Formation Control Strategies with Undetermined and Determined Formation Scales for Co-leader Vehicle Networks, IEEE 52nd Conference on Decision and Control (Dec 2013) 7339-7344.
[7] J. Jin, Y. Kim, S. Wee, N. Gans, Decentralized Cooperative Mean Approach to Collision Avoidance for Nonholonomic Mobile Robots, IEEE International Conference on Robotics and Automation, (May 2015) 35-41.
[8] Y.-H. Chang, C.-W. Chang, C.-L. Chen, C.-W. Tao, Fuzzy Sliding-Mode Formation Control for Multirobot Systems: Design and Implementation, IEEE Transactions on Systems, Man and Cybernetics, Part B: Cybernetics, 42(2) (Apr 2012). 444-457.
[9] R. Cohen, S. Havlin, Complex Networks, Structure, Stability and Function, Cambridge University Press, (2007).
[10] J. Cao, G. Chen, P. Li, Global Synchronization in an Array of Delayed Neural Networks With Hibrid Coupling, IEEE Transactions on Systems, Man, and Cybernetics—part b: Cybernetics, 38(2) (2008) 488-498.
[11] G. Chen, Pinning Control and Synchronization on Complex Dynamical Networks, International Journal of Control, Automation, and Systems, 12(2) (2014) 221-230.
[12] X. Guo, J. Li, Stochastic Adaptive Synchronization for Time-Varying Complex Delayed Dynamical Networks with Heterogeneous Nodes, Elsevier Applied Mathematics and Computation 222 (2013) 381-390.
[13] R. V. D. Hofstad, Random Graphs and Complex Networks, Departament of Mathematics and Computer Science, Eindhoven University of Technology, (2013).
[14] C. Hu, J. Yu, H. Jiang, Z. Teng, Pinning Synchronization of Weigthed Complex Networks with Variable Delays and Adaptive Coupling Weights, Springer Nonlinear Dyn, 67 (2012) 1373-1385.
[15] W. Yu, G. Chen, J. Lü, J. Kurts, Synchronization Via Pinning Control on General Complex Networks, SIAM J. Control Optimization. 51(2) (2013) 1395-1416.
[16] G. S. Seyboth, D. V. Dimarogonas, K. H. Johansson, F. Allgöwer, Static diffusive couplings in heterogeneous linear networks, IFAC Proceedings Volumes, 45(26) (2012) 258-263.
[17] P. Wieland, From Static to Dynamic Couplings in Consensus and Synchronization Among Identical and Non-Identical Systems, Ph. D. Thesis, Institute for Systems Theory and Automatic Control, University of Stuttgart (2010).
[18] P. Wieland, F. Allgöwer, On Consensus among Identical Linear Systems using Input-Decoupled Functional Observers, American Control Conference, (Jun 2010) 1641-1646.
[19] R. Olfati-Saber, R. Murray, Consensus Problems in Networks of Agents With Switching Topology and Time-Delays, IEEE Transactions on Automatic Control, 49(9) (sep 2004) 1520-1533.
[20] Q. Song, F. Liu, J. Cao, W. Yu, M-Matrix Strategies for Pinning-Controlled Leader-Following Consensus in Multiagent Systems with Nonlinear Dynamics, IEEE Transactions on Cybernetics, 43(6) (Dec 2013) 1688-1697.
[21] W. Zhong, G. Liu, C. Thomas, Global Bounded Consensus of Multiagent Systems With Nonidentical Nodes and Time Delays, IEEE Transactions on Systems, Man and Cybernetics, 42(5) (Oct 2012) 1480-1488.
[22] Q. Song, J. Cao, On Pinning Synchronization of Directed and Undirected Complex Dynamical Networks, IEEE Transactions on Circuits and Systems-I, 57(3) (Mar 2010) 672-680.
[23] F. Bullo, J. Cortés, S. Martínez, Distributed Control of Robotic Networks: a Mathematical Approach to Motion Coordination Algorithms, Princeton University Press. (2009).
[24] A.Y. Aguilar-Bustos, E. Bugarín, Robot Móvil con Desplazamientos Caóticos Delimitados y Evasión de Obstáculos, XV Congreso Latinoamericano de Control Automático, Lima-Perú (Oct 2012).
[25] C. D. Meyer, Matrix Analysis and Applied Linear Algebra, SIAM, Philadelphia, PA, (2000).
[26] A.J. Laub, Matrix Analysis for Scientists & Engineers , Society for Industrial and Applied Mathematics (SIAM). (2005).
[27] R. Kelly, V. Santibañez, Control de Movimiento de Robots Manipuladores, Ed. Pearson Education. Madrid, España. (2003).
[28] K. Schäcke, On the Kronecker Product, Master´s Thesis, University of Waterloo, (2004).
[29] A. Y. Aguilar-Bustos, E. Bugarín, Robots Móviles en Colaboración con Desplazamientos Caóticos. XVI Congreso Latinoamericano de Control Automático, Cancún, Quintana Roo, México, (Oct 2014).
[30] D. E. Chang, S. C. Shadden, J. E. Marsden, R. Olfati-Saber, Collision Avoidance for Multiple Agent Systems, Proceedings of the 42nd IEEE Conference on Decision and Control. Maui, Hawaii USA, (Dec 2003).
[31] M. A. El Kamel, L. Beji, A. Abichou, S. Mammar, A Novel Obstacle Avoidance Approach for Mobile Robot System Including Target Capturing, Intelligent Systems and Automation, 2nd Mediterranean Conference, (2009) 249-253.
[32] O. Khatib, Real-Time Obstacle Avoidance for Manipulators and Mobile Robots, The International Journal of Robotics Research, 5(1) (1986) 90-98.
[33] E. Bugarín, R. Kelly, RTSVC: Real-Time System for Visual Control of Robots, Wiley Periodicals, Inc. Int J Imaging Syst Technol, Vol. 18, 251–256 (2008).
Document information
Published on 03/01/18
Accepted on 07/05/17
Submitted on 12/12/16
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.7.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?