JuanGracia (talk | contribs) m (JuanGracia moved page Draft Igelmo 876210239 to Review 967396518541) |
JuanGracia (talk | contribs) (Tag: Visual edit) |
||
| Line 27: | Line 27: | ||
<div style="text-align: right; direction: ltr; margin-left: 1em;"> | <div style="text-align: right; direction: ltr; margin-left: 1em;"> | ||
| − | <math display=" | + | <math display="block">\frac{{h}_{2}}{{h}_{1}}=\sqrt{\frac{{E}_{1}}{{E}_{2}}} </math>Ec. 1</div> |
donde ''h<sub>1</sub>'', ''E<sub>1</sub>'' y ''h<sub>2</sub>'', ''E<sub>2</sub>'' son los espesores y los módulos de flexión de los sub-laminados. | donde ''h<sub>1</sub>'', ''E<sub>1</sub>'' y ''h<sub>2</sub>'', ''E<sub>2</sub>'' son los espesores y los módulos de flexión de los sub-laminados. | ||
| Line 44: | Line 44: | ||
<div style="text-align: right; direction: ltr; margin-left: 1em;"> | <div style="text-align: right; direction: ltr; margin-left: 1em;"> | ||
| − | <math display=" | + | <math display="block">{\lambda }^{2}=3\frac{{s}_{1}+{s}_{2}}{{d}_{1}+{d}_{2}}</math> Ec. ''2''</div> |
Donde ''d<sub>i</sub>'' y ''s<sub>i</sub>'' son las flexibilidades de flexión y cortadura de los sub-laminados, respectivamente. | Donde ''d<sub>i</sub>'' y ''s<sub>i</sub>'' son las flexibilidades de flexión y cortadura de los sub-laminados, respectivamente. | ||
| Line 53: | Line 53: | ||
<div style="text-align: right; direction: ltr; margin-left: 1em;"> | <div style="text-align: right; direction: ltr; margin-left: 1em;"> | ||
| − | <math display=" | + | <math display="block">{G}_{I}=\frac{{F}^{2}}{2\omega }\left[ \frac{1}{3}\left( {d}_{1}+\right. \right.\left. \left. {d}_{2}\right) \left( 3{a}^{2}+2a\lambda \right) +\left( {s}_{1}+{s}_{2}\right) \left( 1+\right. \right.\left. \left. \frac{2a}{\lambda }\right) \right] </math> Ec. ''3''</div> |
==Ensayo AENF== | ==Ensayo AENF== | ||
| Line 70: | Line 70: | ||
<div style="text-align: right; direction: ltr; margin-left: 1em;"> | <div style="text-align: right; direction: ltr; margin-left: 1em;"> | ||
| − | <math display=" | + | <math display="block">{Y}_{0}=\frac{Y}{\frac{1}{2}F}=\frac{{a}^{2}{d}_{2}+3{s}_{2}}{{a}^{2}\left( {d}_{1}+{d}_{2}\right) +3\left( {s}_{1}+{s}_{2}\right) }</math> Ec. ''4''</div> |
Aplicando el teorema de Engesser-Castigliano se calcula el desplazamiento en el punto de aplicación de la carga y la flexibilidad en función de la longitud de grieta. Igualando la flexibilidad analítica a la obtenida en el ensayo experimental se puede calcular el valor de la longitud de grieta equivalente en cada punto del ensayo. | Aplicando el teorema de Engesser-Castigliano se calcula el desplazamiento en el punto de aplicación de la carga y la flexibilidad en función de la longitud de grieta. Igualando la flexibilidad analítica a la obtenida en el ensayo experimental se puede calcular el valor de la longitud de grieta equivalente en cada punto del ensayo. | ||
| Line 77: | Line 77: | ||
<div style="text-align: right; direction: ltr; margin-left: 1em;"> | <div style="text-align: right; direction: ltr; margin-left: 1em;"> | ||
| − | <math display=" | + | <math display="block">{G}_{II}=\frac{{F}^{2}}{8\omega }\left[ \left( {a}^{2}{d}_{2}+\right. \right.\left. \left. {s}_{2}\right) \left( 1-{Y}_{0}\right) -{a}^{2}d-s\right] </math> Ec. ''5''</div> |
Donde d y s son las flexibilidades de flexión y cortadura del material hibrido, respectivamente. | Donde d y s son las flexibilidades de flexión y cortadura del material hibrido, respectivamente. | ||
| Line 129: | Line 129: | ||
En la <span id='cite-_Ref195178214'></span>[[#_Ref195178214|Fig. 4]] se pueden observar tanto la gráfica carga-desplazamiento como la curva de resistencia. En el cálculo del desplazamiento se incluye la flexibilidad de la propia máquina de ensayos. El método analítico descrito permite obtener la tasa de liberación de energía para cada par de datos (P, δ). En la <span id='cite-_Ref195178492'></span>[[#_Ref195178492|Tabla 2]] se pueden observar los valores críticos correspondientes tanto al punto de pérdida de linealidad como al 5%MAX. | En la <span id='cite-_Ref195178214'></span>[[#_Ref195178214|Fig. 4]] se pueden observar tanto la gráfica carga-desplazamiento como la curva de resistencia. En el cálculo del desplazamiento se incluye la flexibilidad de la propia máquina de ensayos. El método analítico descrito permite obtener la tasa de liberación de energía para cada par de datos (P, δ). En la <span id='cite-_Ref195178492'></span>[[#_Ref195178492|Tabla 2]] se pueden observar los valores críticos correspondientes tanto al punto de pérdida de linealidad como al 5%MAX. | ||
| − | [[ | + | [[File:Ensayo ADCB. a) Curva de carga-desplazamiento. b) Curva de resistencia.jpg|600x600px]] |
<div id="_Ref195178214" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_Ref195178214" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 139: | Line 139: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[ | + | [[File:Ensayo AENF. a) Curva de carga-desplazamiento. b) Curva de resistencia.jpg|600x600px]] </div> |
<div id="_Ref195515224" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_Ref195515224" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
Revision as of 11:44, 11 July 2025
1. Introducción
La caracterización de la tenacidad a la fractura interlaminar de laminados compuestos unidireccionales, así como de uniones adhesivas en los modos I y II de fractura se realiza, de forma general, mediante ensayos de doble viga en doble voladizo (Double Cantilever Beam, DCB) y Flexión con Entalla Final (End Notched Flexure, ENF). Los ensayos normalizados (ISO 15024, ISO 25217 y ASTM D7905) se realizan sobre configuraciones simétricas (idénticos laminados a ambos lados de la grieta), coincidiendo, en este caso, la tenacidad a fractura (Gc) con la tenacidad de los modos puros de fractura. Sin embargo, si existe una asimetría geométrica y/o material entre los dos sub-laminados que forman la probeta ensayada, se produce la fractura en modo mixto I/II dificultando la caracterización en los modos puros. En este caso, los ensayos se denominan Asymmetric Double Cantilever Beam (ADCB) y Asymmetric End Notched Flexure (AENF).
El objetivo del presente trabajo es conseguir calcular experimentalmente la tenacidad a la fractura en modos puros I y II de un material híbrido a partir de su curva carga-desplazamiento en los ensayos ADCB y AENF, partiendo del conocimiento de las propiedades mecánicas de los sub-laminados que lo componen.
2. Aproximación analítica
Condiciones de modo puro
Mujika et al. [1] estudiaron las condiciones para conseguir modos puros de fractura en los ensayos ADCB y AENF a una muestra compuesta por dos materiales. La condición en el caso ADCB se obtuvo imponiendo desplazamientos tangenciales nulos entre las caras de los sub-laminados junto a la punta de la grieta, mientras que la condición en AENF se obtuvo imponiendo que las tensiones normales entre los sub-laminados en la punta de la grieta deben ser nulas. La relación obtenida es la misma en ambos casos:
donde h1, E1 y h2, E2 son los espesores y los módulos de flexión de los sub-laminados.
Ensayo ADCB
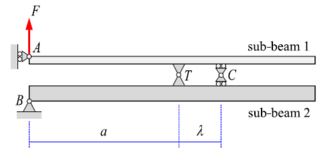
En este trabajo se van a usar las aproximaciones analíticas desarrolladas en [2]. La Fig. 1 muestra un modelo estáticamente determinado del ensayo ADCB basado en cargas puntuales. Este modelo consta de dos juntas en los puntos T (frente de la grieta) y C (a una distancia desconocida λ del punto T). Se supone que en la junta T ambos sub-laminados están sometidas a fuerzas de tracción opuestas y en la junta C están sometidas a fuerzas de compresión opuestas. La junta en el punto T impide los desplazamientos relativos normal y tangencial, y la junta en el punto C impide el desplazamiento relativo normal.
Teniendo en cuenta las fuerzas y momentos de sección del modelo se puede calcular la energía complementaria de deformación en función de la fuerza F aplicada, la longitud de grieta a y la distancia λ, mientras que dicha distancia se puede determinar imponiendo la condición de estado estacionario de la energía complementaria respecto a dicho parámetro, siendo:
Donde di y si son las flexibilidades de flexión y cortadura de los sub-laminados, respectivamente.
Aplicando el teorema de Engesser-Castigliano en el modelo de la figura se calcula el desplazamiento entre los puntos A y B y por tanto la flexibilidad. Si se iguala dicha flexibilidad analítica a la obtenida en el ensayo experimental se puede calcular el valor de la longitud de grieta en cada punto del ensayo. De esta manera se obtiene una longitud de grieta equivalente, que incluye todos los factores que tienen influencia en la flexibilidad del sistema.
Una vez obtenida la longitud de la grieta, la tenacidad a la fractura se obtiene mediante la siguiente expresión:
Ensayo AENF
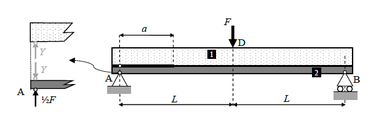
La Fig. 2 muestra el modelo del ensayo AENF. En el caso de existir modo II puro, se asume que la interacción entre los sub-laminados en la zona agrietada se produce a la altura del soporte A, en forma de la fuerza vertical de contacto Y.
Como en el caso anterior, se puede calcular la energía complementaria de deformación, en este caso en función de la fuerza F aplicada, la longitud de grieta a, la luz utilizada en el ensayo (L) y la fuerza en el contacto Y.
Dicha fuerza Y se calcula imponiendo la condición de que el desplazamiento relativo entre los sub-laminados en el punto de apoyo A en nulo. En su expresión normalizada la fuerza en el contacto es:
Aplicando el teorema de Engesser-Castigliano se calcula el desplazamiento en el punto de aplicación de la carga y la flexibilidad en función de la longitud de grieta. Igualando la flexibilidad analítica a la obtenida en el ensayo experimental se puede calcular el valor de la longitud de grieta equivalente en cada punto del ensayo.
La tenacidad a la fractura se obtiene derivando la energía de deformación complementaria respecto a la longitud de grieta, obteniendo:
Donde d y s son las flexibilidades de flexión y cortadura del material hibrido, respectivamente.
3. Procedimiento experimental
En los ensayos se ha utilizado un laminado fabricado a partir de dos pre-impregnados de la misma resina epoxi. En un caso los pre-impregnados están reforzados con fibra larga de carbono mientras que en el otro están reforzados con fibra larga de vidrio. El laminado fabricado es unidireccional y de 24 capas. Aplicando la Ec. 1, para lograr modos puros de fractura, se compone de 16 capas reforzadas con fibra de vidrio y 8 capas reforzadas con fibra de carbono. Durante el proceso de fabricación se utiliza una lámina de teflón para crear la grieta inicial. Esta grieta se encuentra en el plano que separa los dos tipos de capas.
Se han obtenido las propiedades elásticas Ef y GLT de los materiales que componen el material híbrido y también del propio material híbrido mediante ensayos de flexión a tres puntos con diferentes luces. Estos datos están recogidos en la Tabla 1. Los ensayos de flexión del material híbrido se han realizado tanto aplicando la carga en una cara de la probeta como en la otra, obteniendo resultados similares.
| Carbon | Glass | Hybrid [G016/C08] | |
| Ef (MPa) | 85590 | 30657 | 43510 |
| GLT (MPa) | 1819 | 3795 | 5597 |
Para realizar los ensayos ADCB se han pegado unas bisagras metálicas a las probetas y se ha utilizado una máquina universal INSTRON 5967 con una célula de carga de 500N, mientras que para los ensayos AENF se ha utilizado una máquina universal MTS con una célula de carga de 10KN (Fig. 3).
Los efectos de la deformación local se han tenido en cuenta, incluyéndolos en la flexibilidad del sistema.

|

|
4. Resultados
Se ha realizado el ensayo ADCB al material de estudio. Visualmente, se observa que la inclinación de la probeta durante el ensayo es mínima, lo cual indica la prevalencia del modo I respecto del II, que era el efecto buscado con la secuencia de apilamiento propuesta.
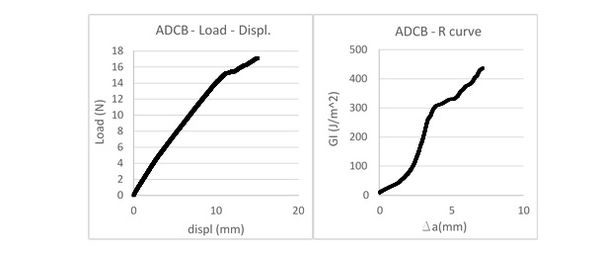
En la Fig. 4 se pueden observar tanto la gráfica carga-desplazamiento como la curva de resistencia. En el cálculo del desplazamiento se incluye la flexibilidad de la propia máquina de ensayos. El método analítico descrito permite obtener la tasa de liberación de energía para cada par de datos (P, δ). En la Tabla 2 se pueden observar los valores críticos correspondientes tanto al punto de pérdida de linealidad como al 5%MAX.
En cuanto al ensayo AENF se ha realizado con una luz de 120mm y se han incluido en el cálculo del desplazamiento las deformaciones locales debidas a la flexibilidad de la máquina de ensayos.
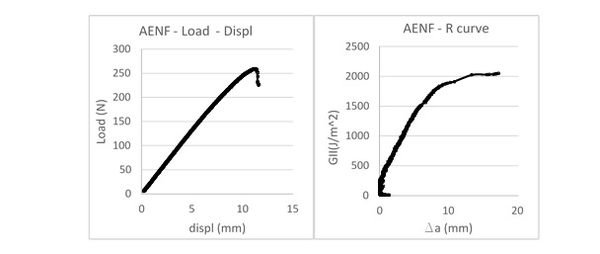
En la Fig. 5 se pueden observar tanto la gráfica carga-desplazamiento como la curva de resistencia. Al igual que en el caso anterior, el método utilizado permite obtener la tasa de liberación de energía de forma continua para cada par de datos de la máquina de ensayos. (P, δ). Los datos críticos de tasa de liberación de energía se observan en la Tabla 2.
| Punto NL | Punto 5 %/max | |
| GIC (J/m2) | 303 | 314 |
| GIIC (J/m2) | 1440 | 1520 |
Se han realizado simulaciones numéricas por el método de los elementos finitos para validar los resultados obtenidos mediante la aproximación analítica y los ensayos experimentales. Se ha creado un modelo para cada probeta utilizando el software ABAQUS Standard. Para el modelado se han empleado elementos del tipo CPS4I con un tamaño de elemento de 0,1mm. Estos elementos son adecuados en los casos de flexión simple por incorporar los efectos del cortante.
Las simulaciones numéricas confirman que los porcentajes de modo puro en cada ensayo es superior al 99% con la secuencia de apilado utilizada en este trabajo.
5. Conclusiones
Se ha fabricado un laminado híbrido compuesto de pre-impregnado de fibra de carbono y de fibra de vidrio utilizando una secuencia de apilado que permita obtener modos de fractura puros en los ensayos ADCB y AENF. Tanto la observación visual como la simulación numérica confirman prevalencia de dichos modos puros en los ensayos.
En cuanto a la obtención de las curvas de resistencia a partir de los datos de las máquinas de ensayos, se han utilizado aproximaciones analíticas basadas en modelos estáticamente determinados de los ensayos.
6. Bibliografía
[1] F. Mujika, P. Tsokanas, A. Arrese, P. S. Valvo, and L. F. M. da Silva, “Mode decoupling in interlaminar fracture toughness tests on bimaterial specimens,” Eng. Fract. Mech., vol. 290, Sep. 2023, doi: 10.1016/j.engfracmech.2023.109454.
[2] F. Mujika, P. Tsokanas, A. Arrese, and L. F. M. da Silva, “Energy release rate in bimaterial specimens tested in pure modes I and II,” Eng. Fract. Mech., vol. 301, no. January, p. 110012, 2024, doi: 10.1016/j.engfracmech.2024.110012.
Document information
Published on 21/01/26
Accepted on 14/07/25
Submitted on 02/07/25
Volume 09 - Comunicaciones MatComp25 (2025), Issue Núm. 3 - Caracterización Experimental, 2026
DOI: 10.23967/r.matcomp.2025.09.24
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?