Latest revision as of 11:52, 3 October 2022

ABSTRACT

In this work, a finite element scheme is proposed using a method of Euler-Taylor-Galerkin described in Páez et al. (2016), for a non-linear model which describes the behavior of a new chemo-fluidic oscillator, Donea (1984). This model is expressed by the coupling of an ordinary differential equation describing the hydrogel dynamics, the non-linear transport equation and an auxiliary equation determining the flux volume. The numerical solution is constructed by taking a semi-discretization in time of the transport equation, employing forward-time Taylor series expansions including time derivatives of second order and third order, avoiding instabilities problems. In this semi discrete equation, the spatial variable is approximated by the finite element formulation according to Galerkin. Some simulations are carried out taking different initial conditions for the concentration of the hydrogel. The numerical results describe the oscillatory behavior of the system as in Donea (1984), where MatLab tools are used as black box.

Keywords: [New chemo-fluidic oscillator], [Non-linear model], [Finite element], [the hydrogel dynamics].

RESUMEN

En este trabajo se propone un esquema de elementos finitos utilizando un método de Euler-Taylor-Galerkin descrito en Páez et al. (2016), para un modelo no lineal que describe el comportamiento de un nuevo oscilador quimio-fluídico (Donea, 1984). Este modelo se expresa mediante el acoplamiento de una ecuación diferencial ordinaria que describe la dinámica del hidrogel, la ecuación del transporte no lineal y una ecuación auxiliar que determina el volumen del flujo. La solución numérica se construye tomando una semi discretización en el tiempo de la ecuación del transporte, empleando expansiones de series de Taylor en el tiempo hacia adelante que incluye derivadas en el tiempo de segundo y tercer orden, evitando problemas de inestabilidad. En esta ecuación semi discreta, la variable espacial se aproxima mediante una formulación de elementos finitos según Galerkin. Algunas simulaciones se realizan tomando diferentes condiciones iniciales para la concentración del hidrogel. Los resultados numéricos describen el comportamiento oscilatorio del sistema como en Donea (1984), en donde las herramientas de Matlab se utilizan como caja negra.

Palabras clave: [Nuevo Oscilador quimio-fluídico], [Modelo no lineal], [Elementos finitos], [Dinámica del hidrogel].

Introducción ¹

Los sistemas auto oscilantes juegan un papel importante tanto en las ciencias naturales (biología o química) como en la tecnología (sistemas micro electromecánicos o electrónicos) porque pueden acoplarse a otros sistemas, una de sus aplicaciones más importantes es el uso como reloj del sistema para desencadenar eventos regulares como por ejemplo en el ritmo circadiano o en sistemas electrónicos.

Este trabajo se refiere al uso de un método de Taylor-Galerkin para la aplicación de elemento finitos al sistema no lineal que controla el comportamiento del nuevo oscilador quimio-fluídico y determinar su modelado numérico. El problema matemático fue planteado por Páez ${\textstyle \left[1\right]}$ que realizó una aproximación numérica de la EDP del transporte utilizando el conocido Método de líneas, sin embargo, el sistema de EDOS proporciona una aproximación muy rudimentaria de la solución de la ecuación del transporte.

En primer lugar, esto se debe a la discretización de primer orden en el espacio y en segundo lugar porque puede propagar cambios bruscos o frentes empinados, que es un problema computacional bien conocido en la solución numérica de EDP hiperbólicas.

Con el fin de describir la dinámica del oscilador quimio-fluídico se utilizó un conjunto de modelos matemáticos, que planteó un desafío debido a la complejidad del sistema, ya que el oscilador se ve afectado por varias no linealidades que provienen de las características del hidrogel y el acoplamiento bidireccional entre los dominios químico y fluídico. El hidrogel está diseñado de tal manera que un incremento de la concentración de alcohol reduce su tamaño y viceversa. Por lo tanto, a bajas concentraciones de alcohol, la válvula de hidrogel está cerrada, mientras que las altas concentraciones de alcohol abren la válvula. Un canal de derivación está conectado a la entrada de la válvula, para permitir un flujo continuo de líquido unidireccional cerca del hidrogel independiente de si la válvula de hidrogel está abierta o cerrada.

Por lo tanto para facilitar el proceso de modelado , el sistema se dividió en el dominio fluídico que describe el comportamiento de los flujos volumétricos y las presiones del sistema durante la operación y el dominio químico que a su vez se dividió en dos partes la descripción de la dinámica de hidrogel y el modelado de la línea de retardo , dando como resultado un sistema acoplado compuesto por la EDP del transporte unidimensional, la EDO que modela el comportamiento dinámico del hidrogel y la ecuación que determina el volumen en el buffer.

Para realizar este trabajo siguiendo muy de cerca lo realizado por Donea ${\textstyle \left[2\right]}$ se semi-discretiza la ecuación del transporte no lineal usando expansiones en serie de Taylor en el tiempo de primer, segundo y tercer orden para obtener una ecuación diferencial de segundo orden en el espacio en la que aplicamos la formulación variacional de Galerkin para utilizar el método de elementos finitos y obtener el sistema de ecuaciones lineales que necesita del valor de la variable que determina el tamaño del hidrogel que se lo obtiene para cada instante de tiempo aplicando el método de Runge-Kutta 4 y el volumen del buffer que se lo encontramos usando métodos de integración numérica.

Analizar con más detalle su modelaje matemático y la solución numérica de este Nuevo Oscilador químico-fluidico basado en hidrogeles inteligentes fue uno de los motivos de la realización del presente trabajo además de extender el método lineal usado por Donea [2] para la ecuación del transporte no lineal y brindar una metodología de solución para modelos de nuevos osciladores que involucren la ecuación de transporte unidimensional no lineal.

1. Diseño de un oscilador quimio-fluídico

El nuevo oscilador quimio-fluídico se basa en un circuito de retroalimentación negativa que contiene una linea de retardo, donde la retroalimentación negativa es proporcionada por una válvula de hidrogel que tiene la capacidad de cambiar su tamaño dependiendo de la temperatura y la concentración de la solución acuosa que está en contacto directamente con el hidrogel. En este nuevo oscilador la temperatura se mantiene constante por lo que el único parámetro que produce un cambio en el tamaño del hidrogel es la concentración de alcohol.

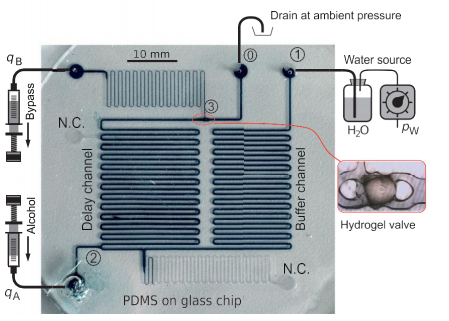
Figura 1. Fotografía del circuito oscilador quimio-fluídico fabricado, lleno con una solución muy teñida para una mejor visibilidad de los canales. Las fuentes externas de flujo constante y presión se muestran esquemáticamente. Circuito fluídico equivalente. La válvula de hidrogel está representada por una fuente de flujo controlado.

El oscilador es alimentado por tres fuentes constantes. La primera es una fuente de flujo constante ${\textstyle {q}_{A}}$ que suministra al sistema una solución de concentración de alcohol ${\textstyle {c}_{alc}}$ . Una segunda fuente proporciona agua desionizada a una presión constante ${\textstyle {p}_{W}}$ ubicada en el nodo 1. El agua fluye a través de un canal largo denominado linea de amortiguamiento para después mezclarse en el nodo 2 con la solución de alcohol proporcionada por ${\textstyle {q}_{A}}$ , para después la solución mixta ingresa al canal del fluido largo que actúa como una linea de retardo. Usando este canal, la solución se transporta a una velocidad determinada por el caudal a través de la linea de retardo ${\textstyle {q}_{2}\left(t\right)}$ y su sección transversal. El extremo de este canal está conectado a la entrada de la válvula de hidrogel, cuya conducta fluídica está controlada por la concentración de alcohol de la solución. Finalmente, un canal de derivación se conecta al nodo 3 para drenar el líquido a un caudal constante ${\textstyle {q}_{B}}$ elegido convenientemente.

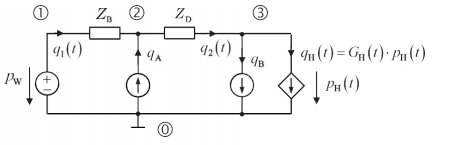
El sistema de micro fluidos se modelará por medio de las leyes de Kirchhoff, dentro del marco de la teoría de redes para un circuito. Este enfoque se lo utiliza por lo pequeñas que son las dimensiones de las magnitudes que gobiernan el funcionamiento del oscilador dentro del estudio de los micro fluidos dado que están en un rango de micro nano y pico litro, por lo tanto, la presión se considera análoga a la tensión y el caudal volumétrico a la corriente eléctrica, así como las líneas de retardo a las resistencias. En este contexto, el oscilador puede describirse por la red de fluidos presentada en la figura 2.

Figura 2. Circuito fluídico equivalente. La válvula de hidrogel está representada por una fuente de flujo controlado.

2. Modelo matemático del oscilador químico-fluídico

El problema matemático a estudiar fue planteado por Páez et al. en ${\textstyle \left[1\right]}$ , y consiste en encontrar funciones ${\textstyle {l}_{v}}$ : ${\textstyle \left[0,T\right]\times \left[0,1\right]\rightarrow {R}_{+}}$ tales que:

{\begin{matrix}{\frac {d{l}_{v}}{dt}}\left(t\right)=\gamma \left[C\left(t,1\right)\right]\left\{{l}_{eq}\left[C\left(t,1\right)-{l}_{v}\left(t\right)\right]\right.\\{l}_{v}\left(0\right)={l}_{v}^{0}\end{matrix}}\Longrightarrow {\begin{matrix}{l}_{v}^{0}\,,\,{C}^{0}\left(x\right)={C}_{ini}\left(x\right)\,\,\forall x\in \left(0\,,\,\left.1\right]\right.\quad \quad \quad \,\,\left(1\right)\\{l}_{v}^{n+1}=F\left({l}_{v}^{n}\,,{C}^{n}\left(1\right);\Delta t\right),n=0,1,2,...,N\end{matrix}}

{\begin{matrix}{\frac {\partial C}{\partial t}}\left(t,x\right)+v\left({l}_{v}\left(t\right)\right){\frac {\partial C}{\partial x}}\left(t,x\right)=0\,\,,\,\forall \left(t,x\right)\in \left(0,\left.T\right]\times \left(0,\left.1\right]\right.\right.\,;\quad \\C\left(0,x\right)={C}_{ini}\left(x\right)\,,\quad \forall x\in \left[0,{L}_{d}\right];\\C\left(t,0\right)={C}_{a}\left(t\right)\,,\quad \quad \forall t\geq \left[0,T\right];\end{matrix}}\quad (2)\quad

Los datos en este problema son las funciones ${\textstyle \Upsilon }$ , ${\textstyle {l}_{eq}}$ , ${\textstyle \,v}$ , ${\textstyle \,{C}_{ini}}$ , ${\textstyle \,{C}_{a}}$ , ${\textstyle {l}_{v}^{0}}$ y donde ${\textstyle C\left(t,1\right)}$ es el valor desconocido que debe determinarse de la función ${\textstyle C\left(t,x\right)}$ en el extremo ${\textstyle x=}$ $1$ ; que también debe determinarse de manera simultánea, en este problema, se determinará la función ${\textstyle {V}_{buff}\left(t\right)}$ : ${\textstyle \left[0,T\right]\rightarrow {R}^{+}}$ definida por:

Donde ${\textstyle {q}_{2}}$ es una función conocida y ${\textstyle {q}_{A}}$ es una constante también conocida.

2.1 Semi - discretización en el tiempo del problema (2)

Se considera la ecuación del transporte

Si se denota por ${\textstyle {C}^{n}\left(x\right)}$ el valor de la función ${\textstyle C\left(t,x\right)}$ evaluada en el nodo ${\textstyle t=}$ ${t}^{n}$ , entonces un esquema en diferencias finitas bien simple para aproximar la derivada temporal en ${\textstyle \left(4\right)}$ sería el que se obtiene mediante la expansión en serie de Taylor, a primer orden, en torno al punto ${\textstyle {t}^{n+1}=}$ ${t}^{n}+\Delta t$ :

De acá, despreciando el ${\textstyle O\left(\Delta t\right)}$ se tiene que:

que es el conocido esquema tipo forward -time (Euler).

Si ahora se evalúa la EDP ${\textstyle \left(4\right)}$ en ${\textstyle t=}$ ${t}^{n}$ se tiene para cada ${\textstyle n=}$ $0,1,...,N\,$ la EDO:

Ahora, usando el esquema tipo forward-time la expresión ${\textstyle \left(5\right)}$ se transforma en:

Aquí ${\textstyle {l}_{v}^{n}}$ es el valor de ${\textstyle {l}_{v}(t)}$ en ${\textstyle t=}$ ${t}^{n}$ que se determina utilizando Ruge-Kutta 4 aplicado al problema inicial ${\textstyle \left(1\right)}$

Donde, en general, ${\textstyle {C}^{n}\left(1\right)}$ es el valor desconocido ${\textstyle C\left(t\right)=}$ $1$ en la frontera ${\textstyle x=}$ $1$ para el tiempo ${\textstyle t=}$ ${t}^{n}$ . Para este esquema, la constante conocida ${\textstyle {l}_{v}^{0}}$ es el iterado inicial. En el contexto del método de diferencias finitas, la expresión ${\textstyle \left(6\right)}$ produce un esquema numérico inestable al aproximar el término de derivada espacial empleando un esquema centrado, es decir

La inestabilidad surge porque la derivada parcial respecto a la coordenada espacial, se evalúa en un nivel de tiempo ${\textstyle n}$ anterior al nivel de tiempo ${\textstyle n}$ donde se evalua el termino de derivada temporal. Por lo tanto, un esquema estable se puede obtener si los dos términos de derivadas ${\textstyle {\frac {\partial C}{\partial t}}}$ y ${\textstyle {\frac {\partial C}{\partial x}}}$ se evalúan en el mismo nivel de tiempo ${\textstyle n}$ (al menos a segundo orden en ${\textstyle \Delta t}$ ). En este orden de ideas, Donea ${\textstyle \left[1\right]}$ afirma que la manera más fácil de hacer la evaluación de ambos términos de la expresión ${\textstyle \left(6\right)}$ en el mismo nivel de tiempo ${\textstyle n}$ es expresando la aproximación en diferencia para el término de derivada temporal en el nivel de tiempo ${\textstyle n}$ .Una manera de lograr esto es por medio de una expansión en serie de Taylor hacia adelante en el tiempo, incluyendo derivadas de segundo y tercer orden. Es decir, de la expansión

Se despeja el término ${\textstyle {\left.\left[{\frac {\partial C}{\partial x}}\right]\left(t,x\right)\right|}_{t={t}^{n}}}$ y (considerando nuevamente la notación que se introdujo para el esquema forward-time) despreciando el término ${\textstyle O\left(\Delta {t}^{3}\right)}$ y usando la discretización en el tiempo ${\textstyle \left(5\right)}$ , para la ecuacion del transporte ${\textstyle \left(4\right)}$ se puede remplazar por la siguiente:

${\textstyle {\frac {{C}^{n+1}\left(x\right)-{C}^{n}\left(x\right)}{\Delta t}}-}$ ${\frac {\Delta {t}^{2}}{6}}\,{\left[{\frac {{\partial }^{3}C}{\partial {t}^{3}}}\right]}^{n}\left(x\right)=$ $-v\left({l}_{v}^{n}\right){\frac {\partial {C}^{n}}{\partial x}}\left(x\right)+$ ${\frac {\Delta t}{2}}\left[{\frac {{\partial }^{2}{C}^{n}}{\partial {t}^{2}}}\right]\left(x\right)\,,\,\forall x\,\left(0\,,\left.1\right]\right.\quad \quad \quad \quad \,\left(9\right)$

Para cada ${\textstyle n=}$ $0,1,...,N$ . Los términos de segunda y tercera derivada que aparecen en esta expresión se pueden determinar en primer lugar por diferenciación sucesiva de la ecuación ${\textstyle \left(4\right)}$ y luego evaluando en el tiempo ${\textstyle t=}$ ${t}^{n}$ . A continuación, se ilustra el cálculo para la segunda derivada. Por un lado:

${\textstyle {\frac {{\partial }^{3}C}{\partial {t}^{3}}}={v}^{2}{\frac {{\partial }^{2}}{\partial {t}^{2}}}\cdot \left({\frac {\partial C}{\partial t}}\right)+}$ $3v{\frac {dv}{dt}}\left({\frac {{\partial }^{2}C}{\partial {x}^{2}}}\right)-{\frac {\partial C}{\partial x}}\cdot \left({\frac {{d}^{2}v}{d{t}^{2}}}\right)\quad \quad \quad \quad \,\,\left(11\right)$

Ahora, combinando ${\textstyle \left(10\right)}$ y ${\textstyle \left(11\right)}$ , evaluadas en ${\textstyle t=}$ ${t}^{n}$ , con la ecuación ${\textstyle \left(9\right)}$ se tiene

${\textstyle {\frac {{C}^{n+1}\left(x\right)-{C}^{n}\left(x\right)}{\Delta t}}-}$ ${\frac {\Delta {t}^{2}}{6}}\,{\left[v\left({l}_{v}^{n}\right){\frac {{\partial }^{2}}{\partial {x}^{2}}}\left({\frac {\partial {C}^{n}}{\partial t}}\right)\left(x\right)+3v\left({l}_{v}^{n}\right){\frac {dv\left({l}_{v}^{n}\right)}{dt}}\cdot {\frac {{\partial }^{2}{C}^{n}}{\partial {x}^{2}}}\left(x\right)-{\frac {{d}^{2}v\left({l}_{v}^{n}\right)}{d{t}^{2}}}\cdot {\frac {{\partial C}^{n}}{\partial x}}\left(x\right)\right]}^{1}=$ $-v\left({l}_{v}^{n}\right){\frac {\partial {C}^{n}}{\partial x}}\left(x\right)+$ ${\frac {\Delta t}{2}}\left[v\left({l}_{v}^{n}\right){\frac {{\partial }^{2}{C}^{n}}{\partial {t}^{2}}}\left(x\right)-\right.$ $\left.{\frac {dv\left({l}_{v}^{n}\right)}{dt}}\cdot {\frac {\partial {C}^{n}}{\partial x}}\left(x\right)\right]\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\left(12\right)\quad \quad \quad \quad$

${\textstyle Para\,todo\,x\in \left(0\,,\left.1\right]\right.\,y\,cada\,n=}$ $0,1,...,N\quad \quad \quad \quad \quad$

La expresión (12) es similar a la que propone Leveque cuando genera métodos numéricos estabilizados mediante la adicción de un término difusivo ${\textstyle \epsilon {\frac {{\partial }^{2}{C}^{n}}{\partial {x}^{2}}}}$ a la ecuación del transporte no lineal. Sin embargo, debe de advertirse que en ${\textstyle \left(12\right)}$ el término ${\textstyle {\frac {{\partial }^{2}{C}^{n}}{\partial {x}^{2}}}}$ aparece es como parte de la aproximación en diferencia para la derivada parcial de C respecto del tiempo, evaluada en el nivel n. Por otro lado, siguiendo de cerca lo sugerido por Donea ${\textstyle \left[1\right]}$ el término de la derivada parcial de tercer orden que aparece en la expansión en serie de Taylor se expresa apropósito en una forma mixta espacio-temporal. Esta forma mixta de la derivada permitirá el uso de elementos finitos tipo ${\textstyle {C}^{0}}$ con una simple modificación de la usual y consistente matriz de masa de manera bastante similar como se hace en el contexto de residuos ponderados de petrov-Galerkin ${\textstyle \left[5\right]}$ .

Desarrollando los productos especificados y agrupando los términos tenemos que el problema planteado en (11) se semi discretiza en el tiempo y para cada ${\textstyle n}$ se plantea el siguiente problema,

Dado ${\textstyle \left[0,1\right]\ni x\,\rightarrow {C}^{0}\left(x\right)=}$ ${C}_{ini}\left(x\right)$ , encontrar ${\textstyle {C}^{n}{\left(x\right)}_{0\leq n\leq N},\forall x\in \left[0,1\right]}$ , tal que:

Para poder resolver la ecuación diferencial de segundo orden planteada en (15) necesitamos de 2 condiciones, pero el problema solo nos proporciona una condición por lo que fue necesario imponer una segunda condición para resolver el problema, la cual la deducimos del modelo matemático para el problema del transporte propia del oscilador quimio-fluídico:

\left\{{\begin{matrix}{\frac {d{l}_{v}}{dt}}\left(t\right)=\gamma \left[C\left(t,1\right)\right]\left\{{l}_{eq}\left[C\left(t,1\right)-{l}_{v}\left(t\right)\right]\right.\\{l}_{v}\left(0\right)={l}_{v}^{0}\end{matrix}}\Longrightarrow {\begin{matrix}{l}_{v}^{0}\,,\,{C}^{0}\left(x\right)={C}_{ini}\left(x\right)\,\,\forall x\in \left(0\,,\,\left.1\right]\right.\quad \quad \quad \,\,\left(14\right)\\{l}_{v}^{n+1}=F\left({l}_{v}^{n}\,,{C}^{n}\left(1\right);\Delta t\right),n=0,1,2,...,N\end{matrix}}\right.

Deducción de la condición en ${\textstyle x=}$ $1$

De la EDP:

de la semi - discretización de ${\textstyle {\frac {\partial C}{\partial t}}\,\Longrightarrow {\frac {{C}^{n+1}\left(x\right)-{C}^{n}\left(x\right)}{\Delta t}}}$

Que al evaluarla en ${\textstyle x=}$ $1$ , tenemos una Condición de Robin.

2.2 Método de Taylor-Galerkin

Considerando el producto interno ${\textstyle {L}_{2}}$ sobre el intervalo ${\textstyle \left(0,1\right)}$ :

Aplicando la definición del producto interno en los espacios ${\textstyle {L}_{2}}$ ,con condiciones de frontera de Dirilecht y de Robin, aplicando la fórmula de integración por partes y remplazando las funciones de forma en ${\textstyle \left(18\right)}$ tenemos para el problema: ${\textstyle \sum _{j=1}^{M}{c}_{j}^{n+1}{\frac {{d\varphi }_{j}\left(1\right)}{dx}}{\varphi }_{i}\left(1\right)-}$ $\sum _{j=1}^{M}{c}_{j}^{n+1}\int _{0}^{1}{\frac {d{\varphi }_{j}\left(x\right)}{dx}}{\frac {d{\varphi }_{i}\left(x\right)}{dx}}dx\,+$ ${\alpha }_{1}\int _{0}^{1}\left(\sum _{j=1}^{M}{c}_{j}^{n+1}{\varphi }_{j}\left(x\right)\right)\,{\varphi }_{i}\left(x\right)dx\quad =$ $-{\alpha }_{2}\sum _{j=1}^{M}{c}_{j}^{n}{\frac {d{\varphi }_{j}\left(1\right)}{dx}}_{j}{\varphi }_{i}\left(1\right)\,+$ ${\alpha }_{2}\sum _{j=1}^{M}{c}_{j}^{n}\int _{0}^{1}{\frac {d{\varphi }_{j}\left(x\right)}{dx}}{\frac {d{\varphi }_{i}\left(x\right)}{dx}}dx\quad +$ ${\alpha }_{3}\sum _{j=1}^{M}{c}_{j}^{n}{\frac {d{\varphi }_{j}\left(x\right)}{dx}}{\varphi }_{i}\left(x\right)dx\,\,-$ ${\alpha }_{1}\sum _{j=1}^{M}{c}_{j}^{n}\int _{0}^{1}{\varphi }_{i}\left(x\right){\varphi }_{j}\left(x\right)dx\quad \quad \quad \,\,\forall {\varphi }_{i},{\varphi }_{j}\in {V}_{h}\quad \quad \quad \left(19\right)$

2.3 Método de Runge Kutta de 4 orden

Estado Inicial

${\textstyle {\mathit {\boldsymbol {t}}}_{\mathit {\boldsymbol {1}}}=}$ ${\mathit {\boldsymbol {0}}}\,$

${\textstyle {l}_{v}\left({t}_{1}\right)={l}_{v}\left(1\right)={l}_{ch}=}$ $1.19$

${\textstyle {V}_{buff}\left({t}_{1}\right)=\,{V}_{buff}\left(1\right)=}$ $0$

${\textstyle h\left({t}_{1}\right)=h\left(1\right)={\frac {1}{2}}\left({l}_{ch}-\right.}$ $\left.{l}_{v}\left({t}_{1}\right)\right)H\left({l}_{ch}-{l}_{v}\left({t}_{1}\right)\right)=$ $0$

${\textstyle L\left({t}_{1}\right)=}$ $L\left(1\right)=2{l}_{ch}-h\left({t}_{1}\right)-{\sqrt {2}}{w}_{dl}$

${\textstyle {G}_{H}({t}_{1})=}$ ${G}_{H}(1)={\frac {{h\left({t}_{1}\right)}^{3}{d}_{ch}}{6nL\left({t}_{1}\right)}}\left(1-\right.$ $\left.0.63{\frac {h\left({t}_{1}\right)}{{d}_{ch}}}\right)$

${\textstyle {q}_{H}\left({t}_{1}\right)=}$ ${q}_{H}\left(1\right)={\frac {{p}_{Eq}{G}_{H}\left({t}_{1}\right)}{{G}_{H}\left({t}_{1}\right){Z}_{Eq}+1}}$

${\textstyle {q}_{2}\left({t}_{1}\right)=}$ ${q}_{2}\left(1\right)={q}_{H}\left({t}_{1}\right)+{q}_{B}$

${\textstyle {q}_{1}\left({t}_{1}\right)=}$ ${q}_{2}\left(1\right)=-{q}_{A}+{q}_{2}\left({t}_{1}\right)$

${\textstyle v\left({t}_{1}\right)=}$ $\,v\left(1\right)={\frac {{q}_{2}\left({t}_{1}\right)}{{d}_{ch}\cdot {w}_{dl}}}$

${\textstyle c\left(1;\,:\right)=}$ $2,26$ ${\textstyle \left(c\left(x,t\right)\,para\,x=1\,es\,al\,final\,de\,la\,l{\acute {\imath }}nea\,de\,retardo\right)}$

${\textstyle {l}_{v}^{,}\left(t\right)=\Upsilon \left(c\right)\left({l}_{eq}\left(c\right)-\right.}$ $\left.{l}_{v}\left(t\right)\right)\quad \quad \quad \quad$

${\textstyle {\frac {d{l}_{v}\left(t\right)}{dt}}=f\left(t,{l}_{v}\right)}$

${\textstyle f\left(t,{l}_{v}\left(t\right)\right)=}$ ${l}_{v}^{,}\left(t\right)=\Upsilon \left(c\left(k,end\right)\right)\left({l}_{eq}c\left(k,end\right)-\right.$ $\left.{l}_{v}\left(t\right)\right)\quad \quad$

${\textstyle {l}_{v}^{,}\left({t}_{k}\right)=\Upsilon \left(c\left({t}_{k}\right)\right)\left({l}_{eq}\left(c\left({t}_{k}\right)\right)-\right.}$ $\left.{l}_{v}\left({t}_{k}\right)\right)\quad \quad \quad \quad \quad \quad$

${\textstyle {k}_{1}=}$ $f\left({t}_{k},{lv}_{k}\right)=f\left(t\left(k\right),{l}_{v}\left(k\right)\right)=$ $\gamma \left(c\left({t}_{k}\right)\right)\left({l}_{eq}\left(c\left({t}_{k}\right)\right)-\right.$ $\left.\left({l}_{vk}\right)\right)$

${\textstyle {k}_{2}=f\left({t}_{k}+{\frac {\Delta t}{2}},{l}_{vk}+{\frac {\Delta t}{2}}{k}_{1}\right)=}$ $\gamma \left(c\left({t}_{k}\right)\right)\left({l}_{eq}\left(c\left({t}_{k}+\right.\right.\right.$ $\left.\left.\left.{\frac {\Delta t}{2}}\right)\right)-\left({l}_{vk}+\right.\right.$ $\left.\left.\Delta t{\frac {{k}_{1}}{2}}\right)\right)$

${\textstyle {k}_{3}=f\left({t}_{k}+{\frac {\Delta t}{2}},{l}_{vk}+{\frac {\Delta t}{2}}{k}_{2}\right)=}$ $\gamma \left(c\left({t}_{k}\right)\right)\left({l}_{eq}\left(c\left({t}_{k}+\right.\right.\right.$ $\left.\left.\left.{\frac {\Delta t}{2}}\right)\right)-\left({l}_{vk}+\right.\right.$ $\left.\left.\Delta t{\frac {{k}_{2}}{2}}\right)\right)$

${\textstyle {k}_{4}=}$ $f\left({t}_{k}+\Delta t,{l}_{vk}+\Delta t\right)=\gamma \left(c\left({t}_{k}\right)\right)\left({l}_{eq}\left(c\left({t}_{k}\right)\right)-\right.$ $\left.\left({l}_{vk}+\Delta t{k}_{3}\right)\right)$

${\textstyle {l}_{vk+1}^{,}={l}_{v}^{,}\left({t}_{k+1}\right)={l}_{vk}+}$ ${\frac {\Delta t}{6}}\left({k}_{1}+{2k}_{2}+2{k}_{3}+{k}_{4}\right)$

El determinar el valor de ${\textstyle {l}_{v}\left({t}_{k}\right)}$ para cada instante de tiempo nos permite encontrar los valores de cada una de las variables del sistema para ese instante de tiempo y alimentar con esas variables la ecuación ${\textstyle \left(3.2\right)}$ discretizada en el espacio específicamente ${\textstyle {\propto }_{1}}$ , ${\textstyle {\propto }_{2}}$ y ${\textstyle {\propto }_{3}}$

${\textstyle h\left({t}_{k+1}\right)={\frac {1}{2}}\left({l}_{ch}-{l}_{v}\left({t}_{k}\right)\right)H\left({l}_{ch}-\right.}$ $\left.{l}_{v}\left({t}_{k}\right)\right)$

${\textstyle L\left({t}_{k+1}\right)=}$ $2{l}_{ch}-h\left({t}_{k}\right)-{\sqrt {2}}{w}_{dl}$

${\textstyle {G}_{H}({t}_{k+1})=}$ ${\frac {{h\left({t}_{k}\right)}^{3}{d}_{ch}}{6nL\left({t}_{i}\right)}}\left(1-\right.$ $\left.0.63{\frac {h\left({t}_{k}\right)}{{d}_{ch}}}\right)$

${\textstyle {q}_{H}\left({t}_{k+1}\right)=}$ ${\frac {{p}_{Eq}{G}_{H}\left({t}_{k}\right)}{{G}_{H}\left({t}_{k}\right){Z}_{Eq}+1}}$

${\textstyle {q}_{2}\left({t}_{k+1}\right)=}$ ${q}_{H}\left({t}_{k}\right)+{q}_{B}$

${\textstyle {q}_{1}\left({t}_{k+1}\right)=}$ $-{q}_{A}+{q}_{2}\left({t}_{k}\right)$

${\textstyle {V}_{buff}\left({t}_{k+1}\right)=}$ ${V}_{buff}\left({t}_{k}\right)-\left({\frac {{q}_{1}\left({t}_{k+1}\right)-{q}_{1}\left({t}_{k}\right)}{2}}\right)h$

${\textstyle v\left({t}_{k+1}\right)=}$ ${\frac {{q}_{2}\left({t}_{k}\right)}{{d}_{ch}\cdot {w}_{dl}}}$

Valores de ${\textstyle {\propto }_{1}\,,\,{\propto }_{2\,\,}\,y\,\,{\propto }_{3}}$ en la ecuación del transporte discretizada en el tiempo usando el método de Euler-Taylor-Galerkin para después resolverla en el espacio aplicando el método de elementos finitos.

${\textstyle {\propto }_{1}={\frac {-6}{{dt}^{2}\cdot {v}_{\left(k\right)}}}}$

${\textstyle {\propto }_{2}=}$ $-\left(2+{\frac {3\Delta t}{{v}_{\left(k\right)}}}\cdot \left({\frac {dv}{dt}}\right)\right)$

${\textstyle {\propto }_{3}=}$ $-{\frac {\Delta t}{{v}^{2}}}\cdot {\frac {{d}^{2}v}{{dt}^{2}}}-{\frac {3}{{v}^{2}}}{\frac {dv}{dt}}-$ ${\frac {6}{\Delta t\cdot v}}$

2.3 Método de Elementos Finitos

Consideraremos una discretización de elementos finitos tal como se explicó anteriormente, pero adaptada al intervalo de trabajo ${\textstyle \left[0,1\right]}$ . En efecto la partición de este intervalo corresponde a la discretización longitudinal del canal de la línea de retardo en ${\textstyle \left(M-\right.}$ $\left.1\right)\,$ elementos ${\textstyle {I}_{j}=}$ $\left[{x}_{j},{x}_{j+1}\right]$ de longitud ${\textstyle {h}_{j}=}$ ${x}_{j+1}-{x}_{j}$ para ${\textstyle j=}$ $1,2,3,...,M.$ Siendo ${\textstyle {h}_{i}=}$ $h$ , la partición representa una malla de puntos ${\textstyle {x}_{j}}$ que denotaremos por ${\textstyle {\tau }_{h}}$ .

Si escribimos ${\textstyle \left(19\right)}$ utilizando la formulación elemental tendríamos:

${\textstyle \left[{\begin{matrix}{\frac {d{\varphi }_{i}^{,}\left(1\right)}{dx}}\cdot {\varphi }_{i}\left(1\right)&{\frac {d{\varphi }_{i}^{,}\left(1\right)}{dx}}\cdot {\varphi }_{i+1}\left(1\right)\\{\frac {d{\varphi }_{i+1}^{,}\left(1\right)}{dx}}\cdot {\varphi }_{i}\left(1\right)&{\frac {d{\varphi }_{i+1}^{,}\left(1\right)}{dx}}\cdot {\varphi }_{i+1}\left(1\right)\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n+1}\\{c}_{i+1}^{n+1}\end{matrix}}\right]-}$ $\left[{\begin{matrix}{\frac {d{\varphi }_{i}^{,}\left(0\right)}{dx}}\cdot {\varphi }_{i}\left(1\right)&{\frac {d{\varphi }_{i}^{,}\left(0\right)}{dx}}\cdot {\varphi }_{i+1}\left(1\right)\\{\frac {d{\varphi }_{i+1}^{,}\left(0\right)}{dx}}\cdot {\varphi }_{i}\left(1\right)&{\frac {d{\varphi }_{i+1}^{,}\left(0\right)}{dx}}\cdot {\varphi }_{i+1}\left(1\right)\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n+1}\\{c}_{i+1}^{n+1}\end{matrix}}\right]+$ ${\frac {1}{{h}_{i}}}\left[{\begin{matrix}1&-1\\-1&1\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n+1}\\{c}_{i+1}^{n+1}\end{matrix}}\right]+$ ${\frac {{\alpha }_{1}}{6}}{h}_{i}\left[{\begin{matrix}2&1\\1&2\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n+1}\\{c}_{i+1}^{n+1}\end{matrix}}\right]+$ ${\frac {-{\propto }_{311}}{2}}\left[{\begin{matrix}-1&1\\-1&1\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n+1}\\{c}_{i+1}^{n+1}\end{matrix}}\right]\left[{c}_{M}^{n+1}\right]=$ ${\propto }_{2}\left[{\begin{matrix}{\frac {d{\varphi }_{i}^{,}\left(1\right)}{dx}}\cdot {\varphi }_{i}\left(1\right)&{\frac {d{\varphi }_{i}^{,}\left(1\right)}{dx}}\cdot {\varphi }_{i+1}\left(1\right)\\{\frac {d{\varphi }_{i+1}^{,}\left(1\right)}{dx}}\cdot {\varphi }_{i}\left(1\right)&{\frac {d{\varphi }_{i+1}^{,}\left(1\right)}{dx}}\cdot {\varphi }_{i+1}\left(1\right)\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n}\\{c}_{i+1}^{n}\end{matrix}}\right]-$ ${\propto }_{2}\left[{\begin{matrix}{\frac {d{\varphi }_{i}^{,}\left(0\right)}{dx}}\cdot {\varphi }_{i}\left(0\right)&{\frac {d{\varphi }_{i}^{,}\left(0\right)}{dx}}\cdot {\varphi }_{i+1}\left(0\right)\\{\frac {d{\varphi }_{i+1}^{,}\left(0\right)}{dx}}\cdot {\varphi }_{i}\left(0\right)&{\frac {d{\varphi }_{i+1}^{,}\left(1\right)}{dx}}\cdot {\varphi }_{i+1}\left(0\right)\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n}\\{c}_{i+1}^{n}\end{matrix}}\right]+$ ${\frac {-{\propto }_{2}}{{h}_{i}}}\left[{\begin{matrix}1&-1\\-1&1\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n}\\{c}_{i+1}^{n}\end{matrix}}\right]+$ ${\frac {{\propto }_{322}}{2}}\left[{\begin{matrix}-1&1\\-1&1\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n}\\{c}_{i+1}^{n}\end{matrix}}\right]+$ ${\frac {{\propto }_{1}{h}_{i}}{6}}\left[{\begin{matrix}2&1\\1&2\end{matrix}}\right]\left[{\begin{matrix}{C}_{i}^{n}\\{c}_{i+1}^{n}\end{matrix}}\right]\quad \quad \quad \quad \quad \quad \left(20\right)$

3. Experimentación numérica

Después de plantear la parte matemática para el modelo y obtener el sistema de ecuaciones se diseñó un programa en Matlab para el sistema acoplado donde se realizaron varios ensayos con sus respectivos ajustes numéricos en función de las definiciones teóricas explicadas en los capítulos 2 y 3.

Cada experimento detalla el cambio en la concentración inicial ${\textstyle C\left(0,x\right)=}$ ${c}_{ini}\left(x\right)$ que es un valor experimental único para el funcionamiento del hidrogel que no consta como dato en Páez ${\textstyle \left[1\right]}$ y se lo ha impuesto en función del modelo físico.

Experimento 1

Se toman los valores en el espacio de ${\textstyle M=}$ $20$ (nodos); ${\textstyle dx=}$ ${\frac {1}{M-1}}$ ; ${\textstyle Courant=}$ ${\frac {dt}{dx}}$ ; ${\textstyle dt=}$ $courant\cdot dx$ ; Courant= 0.1

Se tomó como condición ${\textstyle C\left(0,x\right)=}$ ${c}_{ini}\left(x\right)$ un valor constante que en este caso es el valor experimental con el que trabajaron la parte numérica en el estudio inicial ${\textstyle {c}_{ini}\left(x\right)=}$ $2.2635$

Los valores de las de las derivadas de la concentración que se encuentran en ${\textstyle {\alpha }_{3}}$ se remplazan por diferencias hacia adelante (Euler) para ${\textstyle t\geq 0}$ .

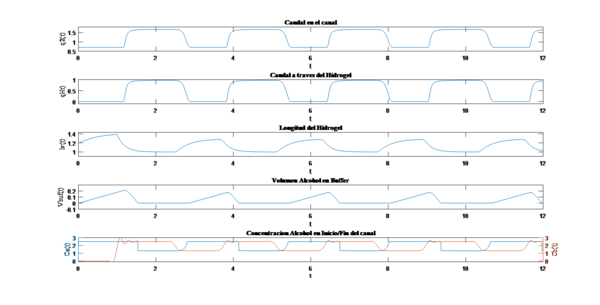
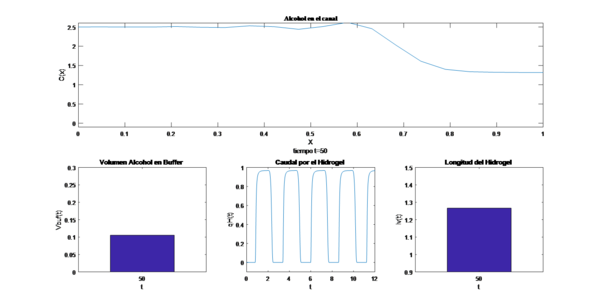
Figura 3. Respuesta del oscilador quimio-fluídico modelado por el sistema.

Se puede observar un comportamiento periódico en el Hidrogel que es lo que permite que el dispositivo funcione como un oscilador con retroalimentación negativa producto del aumento y disminución de la mezcla de alcohol en la cámara del hidrogel, pero al inicio del flujo de mezcla de alcohol y agua se produce inestabilidad en los frentes de onda que luego se regularizan conforme avanza el proceso de abrir y cerrar de la válvula que debido a que el hidrogel sufre una deformación mayor a la longitud de la cámara.

Figura 4. Respuesta del oscilador quimio-fluídico modelado por las variables de estado.

Experimento 2

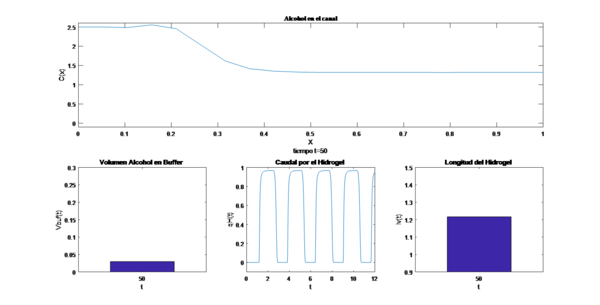
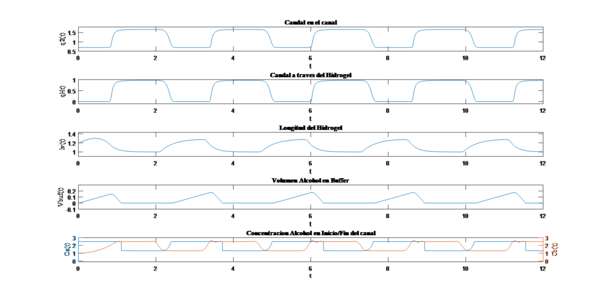
En este ensayo se tomó como condición inicial un perfil cuadrático dado que en el canal existe una mezcla de agua y alcohol producto de los flujos de agua desionizada y alcohol, pero que no que alcanza el nivel mínimo de concentración para que reaccione el hidrogel y comience a comprimirse debido al aumento de alcohol, se presenta un comportamiento periódico, pero con menor perturbación al inicio del proceso lo que permite un flujo de concentración más estable y suave en los frentes de onda.

Figura 5. Respuesta del oscilador quimio-fluídico modelado por las variables de estado.

Figura 6. Respuesta del oscilador quimio-fluídico modelado por el sistema.

4. Conclusiones y recomendaciones

La primera observación que se puede realizar es que el método aplicado al sistema compuesto por las ecuaciones ${\textstyle (15),\left(16\right)\,y\,\left(17\right)\,}$ reproduce la dinámica del Modelo numérico original de Páez ${\textstyle \left[1\right]}$ , con pequeñas diferencias en la amplitud y el periodo, pero que es capaz de producir señales periódicas estables para la configuración de parámetros sin necesitar ningún forzamiento externo, lo que nos quiere decir que el comportamiento oscilatorio es auto excitado.

La segunda observación es que a partir de una aproximación numérica de la ecuación de transporte lineal (velocidad constante) basada en el método de Euler-Taylor-Galerkin para la discretización en el tiempo y el Método de Elementos Finitos para la discretización en el espacio planteado por Donea, al aplicar el mismo método con algunas variaciones en las condiciones iniciales y de frontera en la ecuación del transporte del sistema no lineal que además esta acoplado a una ecuación diferencial ordinaria no lineal que gobierna el comportamiento del hidrogel y otra ecuación que controla el volumen del buffer dándonos como resultado un sistema complejo de resolver, se obtuvieron resultados satisfactorios en relación a su oscilación y su movimiento periódico y acotado . Es muy importante notar que este modelo numérico permite observar que si cambiamos el valor inicial ${\textstyle {C}_{ini}}$ se producirá una variación al inicio del funcionamiento del hidrogel que sería en el régimen estacionario pero que después de este régimen inicial el hidrogel muestra un comportamiento oscilatorio y periódico propio del análisis inicial de Páez.

La tercera observación es que este análisis numérico aplicado al oscilador quimio-fluídico de forma analítica contribuye a la comprensión de que la válvula compuesta por el hidrogel es extremadamente sensible a la variación de los parámetros, es decir tiene la capacidad de cambiar drásticamente su volumen bajo pequeñas variaciones de parámetros termodinámicos especiales.

En esta investigación se pudo dar otra opción para modelar matemáticamente los dominios del oscilador, en el dominio fluídico dada por la red de flujos, el transporte de la concentración a través de la línea de retardo y en el dominio químico dada por el comportamiento del hidrogel y la concentración de alcohol que producen un sistema dinámico suave por partes.

Se recomienda utilizar para futuros estudios un método de refinamiento matemático como por ejemplo el método de Galerkin-Discontinuo para poder modelar de manera más detallada el comportamiento del Oscilador quimio-fluídico.

5. Referencias

${\textstyle \left[1\right]}$ Páez Chávez, J.; Voigt, A.; Schreiter, J.; Marschner, U.; Siegmund, S.; and Richter, A. (2016). A New Self-Excited Chemo-Fluidic Oscillator Based on Stimuli-Responsive Hydrogels: Mathematical Modeling and Dynamic Behavior. Applied Mathematical Modelling, vol. 40(23-24), 9719-9738.

${\textstyle \left[2\right]}$ J. Donea. (1984). A Taylor-Galerkin Method for convective transport problems, International Journal for Numerical Methods in Engineering, vol. 20(1), 101-119.

${\textstyle \left[3\right]}$ P. D Lax and B. Wendroff. (1962). On the Stability of Difference Schemes, Communications on Pure and Applied Mathematics, vol. XV, 363-371.

${\textstyle \left[4\right]}$ P. D Lax and B. Wendroff. (1964). Difference schemes for hyperbolic equations with high order of accuracy, Communications on Pure and Applied Mathematics, vol. XVII, 381-398.

${\textstyle \left[5\right]}$ C. E. Leith. (1965). Methods in Computational Physics, Vol. 4. Academic Press, New York.

${\textstyle \left[6\right]\,}$ J. K. Dukowics and J. D. Ramshow. (1979). Tensor Viscosity Method For Convection in Numerical fluid dynamics. Journal of Computational Physics. Vol.32(1), 71-79.

${\textstyle \left[7\right]}$ D. Kuzmin. (2009). Explicit and implicit FEM -FCT algorithms with flux linearization, Journal of Computational Physics, vol. 228(7), 2517-2534.

${\textstyle \left[8\right]}$ F. Mesinger. (1977). Forward-backward Scheme and its use in a limited area model, Beiträge zur Physik der Atmosphäre, vol 50, 200-210.

${\textstyle \left[9\right]}$ A. Lenk, R. G. Ballas, R. Werthschützky, G. Pfeifer. (2010). Electromechanical Systems in Microtechnology and Mechatronics: Electrical, Mechanical and Acoustic, their Interactions and Aplications. Springer-Verlag, Berlin.

${\textstyle \left[10\right]\,}$ R. K. Gary, A. Dixit, P. Yadav. (2009). Basic Electronics, Laxmi Publications , New Delhi.

${\textstyle \left[11\right]}$ A. Richter, J. Wenzel, K. Kristchmer. (2007). Mechanically adjustable chemostats based on stimuli-responsive polymers, Sensors and Actuators B: Chemical, vol.25(2), 569 -573 .

${\textstyle \left[12\right]\,}$ K. W. Morton and A. K. Parrott. (1980). Generalised Galerkin methods for hyperbolic equations. Journal of Computational Physics, vol.36(2), 249-270.

${\textstyle \left[13\right]}$ J. Leveque. (2007). Finite Difference Methods for Ordinary and Partial Differential Equations. Society for Industrial and Applied Mathematics.

${\textstyle \left[14\right]\,}$ I. Christies, D.F. Griffiths, A.R. Mitchell and O.C. Zienkicwicz. (1976). Finite element methods for second order differential equations with significant first derivatives. International journal for numerical methods in engineering, vol. 10, 1389-1396.