(→4. Validación de la varianza de los costos de incertidumbre mediante simulación) |
|||
| (48 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
Frente al problema de la variabilidad de la velocidad del viento en la generación eólica y la dificultad que esto conlleva en el despacho económico de energía eléctrica, en este se presentan desarrollos formulaciones matemáticas (funciones), denominadas costos de incertidumbre(UCF). El término se utiliza en un modelo compuesto de dos partes, uno implica costos de penalización por sobrestimación y el otro debido a la subestimación de una potencia programada. Mediante formulación matemática analítica y simulaciones de Montecarlo, se ha encontrado el valor esperado de los costos de incertidumbre, considerando la estocasticidad del recurso primario (viento) mediante distribuciones de probabilidad. Sin embargo, no se pueden evaluar con exactitud los resultados desde un punto de vista analítico, sin tener en cuenta la variabilidad alrededor del valor promedio. En este artículo se calcula la función analítica de la varianza, entendida como medida de dispersión de los valores esperados de los costos de incertidumbre para el caso concreto de los operadores eólicos; asimismo, se valida esta formulación mediante simulaciones de Montecarlo. La función encontrada es usada para observar la dispersión de los datos en torno a su valor medio esperado, mediante la aplicación de la desviación estándar que es sencillo determinar a partir de la varianza obtenida. | Frente al problema de la variabilidad de la velocidad del viento en la generación eólica y la dificultad que esto conlleva en el despacho económico de energía eléctrica, en este se presentan desarrollos formulaciones matemáticas (funciones), denominadas costos de incertidumbre(UCF). El término se utiliza en un modelo compuesto de dos partes, uno implica costos de penalización por sobrestimación y el otro debido a la subestimación de una potencia programada. Mediante formulación matemática analítica y simulaciones de Montecarlo, se ha encontrado el valor esperado de los costos de incertidumbre, considerando la estocasticidad del recurso primario (viento) mediante distribuciones de probabilidad. Sin embargo, no se pueden evaluar con exactitud los resultados desde un punto de vista analítico, sin tener en cuenta la variabilidad alrededor del valor promedio. En este artículo se calcula la función analítica de la varianza, entendida como medida de dispersión de los valores esperados de los costos de incertidumbre para el caso concreto de los operadores eólicos; asimismo, se valida esta formulación mediante simulaciones de Montecarlo. La función encontrada es usada para observar la dispersión de los datos en torno a su valor medio esperado, mediante la aplicación de la desviación estándar que es sencillo determinar a partir de la varianza obtenida. | ||
| − | '''Palabras | + | '''Palabras clave''': Energía eólica controlable, costos de incertidumbre, estudios probabilísticos, simulaciones de Monte Carlo |
==Abstract== | ==Abstract== | ||
| Line 12: | Line 12: | ||
==1. Introducción== | ==1. Introducción== | ||
| − | En los países desarrollados del mundo se ha venido cambiando el método de generación de energía, dejando atrás la generación con energías provenientes de fuentes fósiles y nucleares, y dando paso a la implementación de la generación con energías renovables. Esta transición se ha notado con la construcción de grades parques de generación de tipo eólico. Sin embargo debido a la estocasticidad del recurso primario, este tipo de generación se considera como no programable en el despacho económico óptimo <span id='citeF-1'></span>[[#cite-1|[1]]]. El desarrollo de modelos de despacho económico teniendo en cuenta la estocasticidad de las fuentes primarias se empieza a estudiar en artículos como el desarrollado en el 2008 por | + | En los países desarrollados del mundo se ha venido cambiando el método de generación de energía, dejando atrás la generación con energías provenientes de fuentes fósiles y nucleares, y dando paso a la implementación de la generación con energías renovables. Esta transición se ha notado con la construcción de grades parques de generación de tipo eólico. Sin embargo debido a la estocasticidad del recurso primario, este tipo de generación se considera como no programable en el despacho económico óptimo <span id='citeF-1'></span>[[#cite-1|[1]]]. El desarrollo de modelos de despacho económico teniendo en cuenta la estocasticidad de las fuentes primarias se empieza a estudiar en artículos como el desarrollado en el 2008 por Hetzer et al. <span id='citeF-2'></span>[[#cite-2|[2]]], en el que plantean la necesidad de incorporar sistemas de conversión de energía eólica (WECS) en el problema de despacho económico. Este documento introduce los términos de costos de sobreestimación y subestimación de la potencia eólica disponible, añadiéndolos como factores al despacho económico clásico; para ello caracterizan la variabilidad del viento mediante la función de probabilidad de densidad de Weibull. Más adelante, en 2012, Zhao et al., en un artículo publicado por la IEEE <span id='citeF-3'></span>[[#cite-3|[3]]], proponen una función de distribución de la potencia eólica a partir del comportamiento de la velocidad del viento según la distribución de Rayleigh, desarrollan así un algoritmo de optimización basándose en un método de decodificación de Enjambre de Partículas Discreto (PSO) para solucionar el problema de despacho. Los artículos anteriores incorporan métodos heurísticos a la solución del despacho en generación eólica; en el mismo sentido el siguiente articulo (Haddi and Tarek <span id='citeF-4'></span>[[#cite-4|[4]]]) expone el método ABC- Weighted-Sum, aplicándolo para obtener una mejor configuración que relacione los costos de generación con las emisiones en la generación térmica a gas, implementando la generación eólica para observar la disminución total en las emisiones. |
| − | Para hacer posible la implementación de (WEG) | + | Para hacer posible la implementación de (WEG), Arévalo et al. introducen la formulación analítica del valor esperado de los costos de incertidumbre, los cuales determinan costos de penalización por subestimar o sobrestimar la potencia programada, lo que permite al operador incluir estos costos en el valor de operación del generador eólico <span id='citeF-1'></span>[[#cite-1|[1]]]. |
El articulo mencionado anteriormente valida la función analítica del valor esperado con simulaciones de Montecarlo obteniendo resultados con bajo error. La velocidad del viento utilizada como variable aleatoria y la cantidad de datos utilizados en este estudio, hacen que esta medida de tendencia central sea insuficiente para describir el conjunto de datos, por ello se hace necesario elaborar un análisis estadístico de la dispersión de estos datos respecto al valor medio evaluado. Una medida de dispersión utilizada en este artículo es la varianza, que describe la esperanza del cuadrado de la desviación de cada variable respecto a la media de los datos. En los capítulos siguientes se hará el planteamiento de la función analítica de varianza a partir de su definición expresada en términos del valor esperado que se obtuvo en <span id='citeF-1'></span>[[#cite-1|[1]]]. Esta función analítica se validará con la simulación de Montecarlo de un generador eólico, teniendo en cuenta como variable aleatoria la velocidad del viento modelada como una función de probabilidad ya usada en WEG, la función de Weibull. Se presenta también un estudio de optimización teniendo en cuenta que potencia programada puede tener tanto un menor costo de incertidumbre así como una menor variabilidad de los datos, dicha optimización se propone de forma estadística utilizando la desviación estándar calculada a partir de la función de varianza encontrada para finalmente obtener conclusiones del trabajo realizado. | El articulo mencionado anteriormente valida la función analítica del valor esperado con simulaciones de Montecarlo obteniendo resultados con bajo error. La velocidad del viento utilizada como variable aleatoria y la cantidad de datos utilizados en este estudio, hacen que esta medida de tendencia central sea insuficiente para describir el conjunto de datos, por ello se hace necesario elaborar un análisis estadístico de la dispersión de estos datos respecto al valor medio evaluado. Una medida de dispersión utilizada en este artículo es la varianza, que describe la esperanza del cuadrado de la desviación de cada variable respecto a la media de los datos. En los capítulos siguientes se hará el planteamiento de la función analítica de varianza a partir de su definición expresada en términos del valor esperado que se obtuvo en <span id='citeF-1'></span>[[#cite-1|[1]]]. Esta función analítica se validará con la simulación de Montecarlo de un generador eólico, teniendo en cuenta como variable aleatoria la velocidad del viento modelada como una función de probabilidad ya usada en WEG, la función de Weibull. Se presenta también un estudio de optimización teniendo en cuenta que potencia programada puede tener tanto un menor costo de incertidumbre así como una menor variabilidad de los datos, dicha optimización se propone de forma estadística utilizando la desviación estándar calculada a partir de la función de varianza encontrada para finalmente obtener conclusiones del trabajo realizado. | ||
| Line 53: | Line 53: | ||
|} | |} | ||
| − | siendo <math display="inline">c_{o,i}</math> un coeficiente de penalización por subestimar | + | siendo <math display="inline">c_{o,i}</math> un coeficiente de penalización por subestimar. |
| − | Finalmente, los costos de incertidumbre corresponden al valor esperado de las funciones de costos de penalización por subestimar y sobrestimar E(X), donde X son las variables: <math display="inline">W_{av,i}</math> potencia disponible y <math display="inline">W_{s,i}</math> potencia programada, <span id='citeF-5'></span>[[#cite-5|[5]]], para este caso aplicados a la generación eólica se tiene: | + | Finalmente, los costos de incertidumbre corresponden al valor esperado de las funciones de costos de penalización por subestimar y sobrestimar <math>E(X)</math>, donde <math>X</math> son las variables: <math display="inline">W_{av,i}</math> potencia disponible y <math display="inline">W_{s,i}</math> potencia programada, <span id='citeF-5'></span>[[#cite-5|[5]]], para este caso aplicados a la generación eólica se tiene: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 84: | Line 84: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>E\left[C_{o,i\left(W_{s,i},W_{av,i}\right)}\right | + | | style="text-align: center;" | <math>E\left[C_{o,i\left(W_{s,i},W_{av,i}\right)}\right]=\int \limits _{0}^{W_s,i} c_{o,i}\left(W_{s,i}-W_{av,i}\right)\cdot f_W\left(W{av,i}\right)dW_{w,i} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (5) | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
| Line 94: | Line 94: | ||
* <math display="inline">v_{r}</math> '''Velocidad Nominal '''(''rated speed''): la velocidad del viento para la cual se alcanza la potencia nominal del generador. | * <math display="inline">v_{r}</math> '''Velocidad Nominal '''(''rated speed''): la velocidad del viento para la cual se alcanza la potencia nominal del generador. | ||
* <math display="inline">v_{o}</math> '''Velocidad de desconexión '''(''cut out speed''): la velocidad del viento para la que el rotor del generador se detiene por acción de los sistemas de regulación para evitar sufrir daños. | * <math display="inline">v_{o}</math> '''Velocidad de desconexión '''(''cut out speed''): la velocidad del viento para la que el rotor del generador se detiene por acción de los sistemas de regulación para evitar sufrir daños. | ||
| − | * <math display="inline">W_{r}</math> '''Potencia nominal.''' | + | * <math display="inline">W_{r}</math> '''Potencia nominal.'''<br /> |
| + | |||
Ademas, las constantes: | Ademas, las constantes: | ||
| Line 167: | Line 168: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>E[C_{w,o,i}(W_{w,s,i},W_{w,i})]=c_{w,o,i}W_{w,s,i} \cdot (1-e^{-\frac{V_{i}^2}{2 \sigma ^2}} + e^{ | + | | style="text-align: center;" | <math>E\left[C_{w,o,i}\left(W_{w,s,i},W_{w,i}\right)\right]=c_{w,o,i}W_{w,s,i} \cdot \left(1-e^{-\frac{V_{i}^2}{2 \sigma ^2}} + e^{\frac{V_{0}^2}{2 \sigma ^2}} + e^{-\frac{\kappa ^2}{2 \rho ^2 \sigma ^2}}\right) -</math> |
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" |<math>-\frac{\sqrt{2\pi } c_{w,o,i}\rho \sigma }{2}\left( erf \left(\frac{W_{w,s,i}-\kappa }{\sqrt{2} \rho \sigma }\right) - erf\left(\frac{-\kappa }{\sqrt{2} \rho \sigma }\right)\right)</math> |
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (10) | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
| Line 203: | Line 202: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>Var[C_{w,u,i}(W_{w,s,i},W_{w,i})]=</math> | + | | style="text-align: center;" | <math>Var\left[C_{w,u,i}\left(W_{w,s,i},W_{w,i}\right)\right]=</math> |
|- | |- | ||
| − | | style="text-align: center;" | <math>E[C_{w,u,i}(W_{w,s,i},W_{w,i})^2]</math> | + | | style="text-align: center;" | <math>E\left[C_{w,u,i}\left(W_{w,s,i},W_{w,i}\right)^2\right]</math> |
|- | |- | ||
| style="text-align: center;" | – | | style="text-align: center;" | – | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>E[C_{w,u,i}(W_{w,s,i},W_{w,i})]^2 </math> | + | | style="text-align: center;" | <math>E\left[C_{w,u,i}\left(W_{w,s,i},W_{w,i}\right)\right]^2 </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (12) | | style="width: 5px;text-align: right;white-space: nowrap;" | (12) | ||
| Line 221: | Line 220: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>Var[C_{w,o,i}(W_{w,s,i},W_{w,i})]=</math> | + | | style="text-align: center;" | <math>Var\left[C_{w,o,i}\left(W_{w,s,i},W_{w,i}\right)\right]=</math> |
|- | |- | ||
| − | | style="text-align: center;" | <math>E[C_{w,o,i}(W_{w,s,i},W_{w,i})^2]</math> | + | | style="text-align: center;" | <math>E\left[C_{w,o,i}\left(W_{w,s,i},W_{w,i}\right)^2\right]</math> |
|- | |- | ||
| style="text-align: center;" | – | | style="text-align: center;" | – | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>E[C_{w,o,i}(W_{w,s,i},W_{w,i})]^2 </math> | + | | style="text-align: center;" | <math>E\left[C_{w,o,i}\left(W_{w,s,i},W_{w,i}\right)\right]^2 </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (13) | | style="width: 5px;text-align: right;white-space: nowrap;" | (13) | ||
| Line 251: | Line 250: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>Var[C_{w,u,i}(W_{w,s,i},W_{w,i})\pm C_{w,o,i}(W_{w,s,i},W_{w,i})]=</math> | + | | style="text-align: center;" | <math>Var\left[C_{w,u,i}\left(W_{w,s,i},W_{w,i}\right)\pm C_{w,o,i}\left(W_{w,s,i},W_{w,i}\right)\right]=</math> |
|- | |- | ||
| − | | style="text-align: center;" | <math>Var[C_{w,u,i}(W_{w,s,i},W_{w,i})]</math> | + | | style="text-align: center;" | <math>Var\left[C_{w,u,i}\left(W_{w,s,i},W_{w,i}\right)\right]</math> |
|- | |- | ||
| style="text-align: center;" | <math>+</math> | | style="text-align: center;" | <math>+</math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>Var[C_{w,o,i}(W_{w,s,i},W_{w,i})]</math> | + | | style="text-align: center;" | <math>Var\left[C_{w,o,i}\left(W_{w,s,i},W_{w,i}\right)\right]</math> |
|- | |- | ||
| style="text-align: center;" | <math>\pm </math> | | style="text-align: center;" | <math>\pm </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>2Cov[C_{w,u,i}(W_{w,s,i},W_{w,i}), C_{w,o,i}(W_{w,s,i},W_{w,i})] </math> | + | | style="text-align: center;" | <math>2Cov\left[C_{w,u,i}\left(W_{w,s,i},W_{w,i}\right), C_{w,o,i}\left(W_{w,s,i},W_{w,i}\right)\right] </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (15) | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) | ||
| Line 275: | Line 274: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>Var[C_{w,u,i}(W_{w,s,i},W_{w,i})]=a_{u}-b_{u} </math> | + | | style="text-align: center;" | <math>Var\left[C_{w,u,i}\left(W_{w,s,i},W_{w,i}\right)\right]=a_{u}-b_{u} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (16) | | style="width: 5px;text-align: right;white-space: nowrap;" | (16) | ||
| Line 296: | Line 295: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>I_{1}=</math> | + | | style="text-align: center;" | <math>I_{1}=c_{w,u,i}^2\cdot \left( 2\rho ^2\sigma ^2\left(e^{-\left(\frac{W_{w,s,i}- \kappa }{\sqrt{2} \rho \sigma }\right)^2}-e^{-\left(\frac{W_{r}- \kappa }{\sqrt{2} \rho \sigma }\right)^2}\right)-\left(W_{r}-W_{w,s,i}\right)^2 e^{-\left(\frac{W_{r}- \kappa }{\sqrt{2} \rho \sigma }\right)^2} \right.</math> |
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | |style="text-align: center;" |<math> \left.+ \sqrt{2\pi}\rho\sigma \left(\kappa - W_{w,s,i}\right) \left( erf \left(\frac{W_{r}- \kappa }{\sqrt{2} \rho \sigma }\right)-erf \left(\frac{W_{w,s,i}- \kappa }{\sqrt{2} \rho \sigma }\right)\right)\right)</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (17) | | style="width: 5px;text-align: right;white-space: nowrap;" | (17) | ||
| Line 312: | Line 307: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>I_{2}=c_{w,u,i}^2(W_{r}-W_{w,s,i})^2 \cdot (e^{-(\frac{v_{r}^2}{2\sigma ^2})} - e^{-(\frac{v_{0}^2}{2\sigma ^2})}) </math> | + | | style="text-align: center;" | <math>I_{2}=c_{w,u,i}^2\left(W_{r}-W_{w,s,i}\right)^2 \cdot \left(e^{-\left(\frac{v_{r}^2}{2\sigma ^2}\right)} - e^{-\left(\frac{v_{0}^2}{2\sigma ^2}\right)}\right) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (18) | | style="width: 5px;text-align: right;white-space: nowrap;" | (18) | ||
| Line 322: | Line 317: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>b_{u} =(</math> | + | | style="text-align: center;" | <math>b_{u} =\left(\frac{c_{w,u,i}}{2}\left( \sqrt{2\pi } \rho \sigma \left(erf\left(\frac{W_{w,s,i}-\kappa }{\sqrt{2} \rho \sigma }\right)-erf \left(\frac{W_{r}-\kappa }{\sqrt{2} \rho \sigma }\right)\right)+2\left(W_{w,s,i}-W_r\right)e^{- \left(\frac{W_{r}-\kappa }{\sqrt{2} \rho \sigma }\right)^2} \right)\right. </math> |
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" |<math>\left.+\frac{c_{w,u,i}}{2}\left(e^{-\frac{V_{r}^2}{2\sigma ^2}}-e^{-\frac{V_{0}^2}{2\sigma ^2}}\right)\left(W_{r}-W_{w,s,i}\right)\right)^2 </math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (19) | | style="width: 5px;text-align: right;white-space: nowrap;" | (19) | ||
| Line 342: | Line 333: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>Var[C_{w,o,i}(W_{w,s,i},W_{w,i})]=a_{o}-b_{o} </math> | + | | style="text-align: center;" | <math>Var\left[C_{w,o,i}(W_{w,s,i},W_{w,i})\right]=a_{o}-b_{o} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (20) | | style="width: 5px;text-align: right;white-space: nowrap;" | (20) | ||
| Line 363: | Line 354: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>I_{o1}=c_{w,o,i}^2W_{w,s,i}^2\cdot (1-e^{-\frac{v_{i}^2}{2 \sigma ^2}} + e^{-\frac{v_{o}^2}{2 \sigma ^2}}) </math> | + | | style="text-align: center;" | <math>I_{o1}=c_{w,o,i}^2W_{w,s,i}^2\cdot \left(1-e^{-\frac{v_{i}^2}{2 \sigma ^2}} + e^{-\frac{v_{o}^2}{2 \sigma ^2}}\right) </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (21) | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) | ||
| Line 373: | Line 364: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>I_{o2}=c_{w,o,i}^2( (W_{w,s,i}^2+2\rho ^2\sigma ^2+\kappa ^2)</math> | + | | style="text-align: center;" | <math>I_{o2}=c_{w,o,i}^2\left( \left(W_{w,s,i}^2+2\rho ^2\sigma ^2+\kappa ^2\right) \cdot e^{-\left(\frac{-\kappa }{\sqrt{2} \rho \sigma }\right)^2}-\left(2\rho ^2\sigma ^2\right)\cdot e^{-\left(\frac{W_{w,s,i}-\kappa }{\sqrt{2} \rho \sigma }\right)^2}\right)</math> |
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | |style="text-align: center;" | <math>+\sqrt{2\pi }\rho \sigma \left( \kappa{-}W_{w,s,i}\right)\cdot \left(erf\left(\frac{W_{w,s,i}-\kappa }{\sqrt{2} \rho \sigma }\right)-erf\left(\frac{-\kappa }{\sqrt{2} \rho \sigma }\right)\right) </math> |
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (22) | | style="width: 5px;text-align: right;white-space: nowrap;" | (22) | ||
| Line 387: | Line 376: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>b_{o}= | + | | style="text-align: center;" | <math>b_{o}=\left(c_{w,o,i}W_{w,s,i} \cdot \left(1-e^{-\frac{V_{i}^2}{2 \sigma ^2}} + e^{-\frac{V_{0}^2}{2 \sigma ^2}} + e^{-\frac{\kappa ^2}{2 \rho ^2 \sigma ^2}}\right) -\frac{\sqrt{2\pi } c_{w,o,i}\rho \sigma }{2}\left(erf \left(\frac{W_{w,s,i}-\kappa }{\sqrt{2} \rho \sigma }\right) - erf \left(\frac{-\kappa }{\sqrt{2} \rho \sigma }\right)\right)\right)^2 </math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (23) | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) | ||
| Line 410: | Line 393: | ||
|} | |} | ||
| − | Por definición <span id='citeF-2'></span>[[#cite-2|[2]]] los costos de penalización por subestimar ocurren cuando los de sobrestimar no están, solo existe una posibilidad de que se encuentren y es en un solo punto (<math display="inline">W_{w,s,i}</math>), al desarrollar matemáticamente este punto el resultado es cero; es decir que E[XY] se puede considerar como la suma de los valores esperados, con esto ya se tienen todos los valores analíticos. | + | Por definición <span id='citeF-2'></span>[[#cite-2|[2]]] los costos de penalización por subestimar ocurren cuando los de sobrestimar no están, solo existe una posibilidad de que se encuentren y es en un solo punto (<math display="inline">W_{w,s,i}</math>), al desarrollar matemáticamente este punto el resultado es cero; es decir que <math display="inline">E[XY]</math> se puede considerar como la suma de los valores esperados, con esto ya se tienen todos los valores analíticos. |
==4. Validación de la varianza de los costos de incertidumbre mediante simulación == | ==4. Validación de la varianza de los costos de incertidumbre mediante simulación == | ||
| − | Con el objetivo de validar la fórmula encontrada analíticamente se plantea la simulación de Montecarlo para un generador eólico utilizando los parámetros de la | + | Con el objetivo de validar la fórmula encontrada analíticamente se plantea la simulación de Montecarlo para un generador eólico utilizando los parámetros de la [[#tab-1|Tabla 1]], la simulación consiste en 100000 datos aleatorios de la velocidad del viento teniendo en cuenta la distribución de Weibull adaptada específicamente a la Raylegh, estos datos se encuentran acumulados alrededor del valor del viento nominal dado en la tabla de parámetros, 15 m/s, <span id='citeF-6'></span><span id='citeF-7'></span>[[#cite-6|[6,7]]]. |
<div class="center" style="font-size: 75%;">'''Tabla 1'''. Datos de entrada para la simulación de generador eólico | <div class="center" style="font-size: 75%;">'''Tabla 1'''. Datos de entrada para la simulación de generador eólico | ||
</div> | </div> | ||
| − | + | <div id='tab-1'></div> | |
| − | + | ||
{| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size:85%;" | {| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size:85%;" | ||
|- | |- | ||
| − | | colspan='3' | Entradas | + | | colspan='3' | '''Entradas''' |
|- | |- | ||
| − | | Variable | + | | '''Variable ''' |
| − | | Descripción y Unidad | + | | '''Descripción y Unidad''' |
| − | | Valor | + | | '''Valor''' |
|- | |- | ||
| <math display="inline">W_{w,s,i}</math> | | <math display="inline">W_{w,s,i}</math> | ||
| Line 473: | Line 455: | ||
|} | |} | ||
| − | A continuación, en la Figura 1 se muestra la distribución de los datos, donde se muestra que sigue la función Raylegh, además se muestra la potencia disponible en el generador basado en las condiciones de potencia del generador definidas en (6), (7) y (8). | + | |
| + | A continuación, en la [[#img-1|Figura 1]] se muestra la distribución de los datos, donde se muestra que sigue la función Raylegh, además se muestra la potencia disponible en el generador basado en las condiciones de potencia del generador definidas en (6), (7) y (8). | ||
<div id='img-1'></div> | <div id='img-1'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto%;max-width: auto%;" |
|- | |- | ||
| − | |[[Image:Draft_Rivera_142488066-Ps.png| | + | |[[Image:Draft_Rivera_142488066-Ps.png|450px|Velocidad del viento, Potencia disponible y Potencia programada]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 1 | + | | colspan="1" style="padding:10px;"| '''Figura 1'''. Velocidad del viento, Potencia disponible y Potencia programada |
|} | |} | ||
| − | Luego, en la | + | Luego, en la [[#img-2|Figura 2]] se presenta la cantidad de escenarios en los cuales se subestima y se sobrestima la potencia programada, como se definió en (1) y (2). |
<div id='img-2'></div> | <div id='img-2'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width:auto;" |
|- | |- | ||
| − | |[[Image:Draft_Rivera_142488066-Sub-sob.png| | + | |[[Image:Draft_Rivera_142488066-Sub-sob.png|450px|Histograma costos por subestimar y sobrestimar]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 2 | + | | colspan="1" style="padding:10px;"| '''Figura 2'''. Histograma costos por subestimar y sobrestimar |
|} | |} | ||
| − | Posteriormente, en el histograma de la | + | |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | |
| + | Posteriormente, en el histograma de la [[#img-3|Figura 3]] se muestra la acumulación de escenarios de costos de incertidumbre producto de la suma de los costos por sobreestimar y subestimar. El valor esperado de estos costos que se obtienen en el histograma es de <math display="inline"> 2.0879e+04</math>, y el valor esperado de los costos de incertidumbre que se obtiene por la formula encontrada analíticamente en (9 y 10) es de <math display="inline">2.0850e+04</math> obteniendo un error de <math display="inline">6.9162e-04</math>. | ||
| + | |||
| + | <div id='img-3'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width:auto;" | ||
|- | |- | ||
| − | |[[Image:Draft_Rivera_142488066-UFC.png| | + | |[[Image:Draft_Rivera_142488066-UFC.png|450px|Histograma UCF]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 3 | + | | colspan="1" style="padding:10px;" | '''Figura 3'''. Histograma UCF |
|} | |} | ||
| − | En la | + | |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | |
| + | En la [[#img-4|Figura 4]] se observa el cambio de los costos de incertidumbre al cambiar la potencia programada para el mismo generador con las características de la Tabla 1, variando de 0 MW a la potencia nominal del generador 150 MW. Esta gráfica permite encontrar el valor óptimo de potencia que se debe programar para que los UCF sean mínimos. | ||
| + | |||
| + | <div id='img-4'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | |[[Image:Draft_Rivera_142488066-UCFvsPS.png| | + | |[[Image:Draft_Rivera_142488066-UCFvsPS.png|450px|UCF al variar la potencia programada]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 4 | + | | colspan="1" style="padding:10px;"| '''Figura 4'''. UCF al variar la potencia programada |
|} | |} | ||
Finalmente se procede a calcular la varianza mediante simulación de Montecarlo al igual que se simulo los UCF, obteniendo (<math display="inline">3.141e+08</math>), al compararlo con el valor obtenido analíticamente <math display="inline">3.0012e+08</math> se obtuvo un error de 0.0043. | Finalmente se procede a calcular la varianza mediante simulación de Montecarlo al igual que se simulo los UCF, obteniendo (<math display="inline">3.141e+08</math>), al compararlo con el valor obtenido analíticamente <math display="inline">3.0012e+08</math> se obtuvo un error de 0.0043. | ||
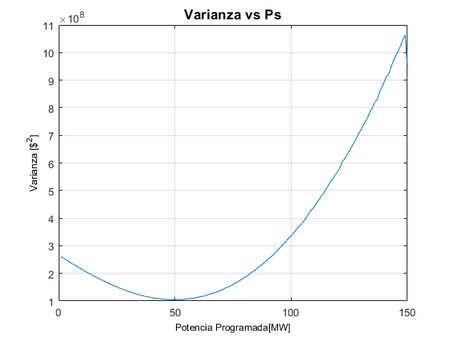
| − | Además, se hace el mismo análisis que con los costos de incertidumbre variando la potencia programada <span id='citeF-8'></span> | + | Además, se hace el mismo análisis que con los costos de incertidumbre variando la potencia programada <span id='citeF-8'></span><span id='citeF-8'></span>[[#cite-8|[8,9]]], observando que cuando este tiene una menor varianza significa una menor dispersión para la cantidad de escenarios, como se observa en la [[#img-5|Figura 5]]. |
<div id='img-5'></div> | <div id='img-5'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | |[[Image:Draft_Rivera_142488066-Var.png| | + | |[[Image:Draft_Rivera_142488066-Var.png|450px|Varianza al cambiar la Potencia programada]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 5 | + | | colspan="1" style="padding:10px;" | '''Figura 5'''. Varianza al cambiar la Potencia programada |
|} | |} | ||
| − | ==5 Conclusiones== | + | ==5. Conclusiones== |
Este articulo propone la formulación matemática de la varianza de los costos de incertidumbre, que representa la medida de dispersión de los valores esperados de los UCF para el caso específico de los generadores eólicos. Su importancia radica en que muestra la variabilidad de los costos de incertidumbre al analizar distintos escenarios de la potencia programada, específicamente en sistemas de generación eólicos donde la fuente de energía primaria (velocidad del viento) tiene asociada una gran incertidumbre. | Este articulo propone la formulación matemática de la varianza de los costos de incertidumbre, que representa la medida de dispersión de los valores esperados de los UCF para el caso específico de los generadores eólicos. Su importancia radica en que muestra la variabilidad de los costos de incertidumbre al analizar distintos escenarios de la potencia programada, específicamente en sistemas de generación eólicos donde la fuente de energía primaria (velocidad del viento) tiene asociada una gran incertidumbre. | ||
| Line 528: | Line 519: | ||
Se encuentra una aplicación en la optimización despacho, al relacionar tanto (UCF) como varianza de (UCF) con la potencia programada, su importancia radica en que muestra los valores mínimos y máximos de costos de incertidumbre y la variabilidad de este valor esperado, además se incluye para este estudio un análisis de varianza exponiendo el bajo error. | Se encuentra una aplicación en la optimización despacho, al relacionar tanto (UCF) como varianza de (UCF) con la potencia programada, su importancia radica en que muestra los valores mínimos y máximos de costos de incertidumbre y la variabilidad de este valor esperado, además se incluye para este estudio un análisis de varianza exponiendo el bajo error. | ||
| − | Pensando en el desarrollo y la alta penetración que comienzan a tener las energías renovables, el desarrollo de UFC presenta una gran aplicación en la optimización del despacho económico, pues minimiza riesgos tanto económicos como técnicos por sobrestimar o subestimar la potencia programada. Asimismo, el desarrollo matemático que se muestra de la varianza de UFC, añade un valor de validez y confianza a la optimización del despacho de generadores eólicos(WEG).El riguroso estudio presentado en el texto presenta gran aplicabilidad en los sistemas de potencia, debido a la alta penetración de energías renovables no convencionales, sin embargo su trascendencia radica en su complementariedad con sistemas de almacenamiento o generadores convencionales. | + | Pensando en el desarrollo y la alta penetración que comienzan a tener las energías renovables, el desarrollo de UFC presenta una gran aplicación en la optimización del despacho económico, pues minimiza riesgos tanto económicos como técnicos por sobrestimar o subestimar la potencia programada. Asimismo, el desarrollo matemático que se muestra de la varianza de UFC, añade un valor de validez y confianza a la optimización del despacho de generadores eólicos(WEG). El riguroso estudio presentado en el texto presenta gran aplicabilidad en los sistemas de potencia, debido a la alta penetración de energías renovables no convencionales, sin embargo su trascendencia radica en su complementariedad con sistemas de almacenamiento o generadores convencionales. |
| − | Finalmente el proceso matemático para obtener la varianza de UFC en WEG planteado, sirve como punto de partida para el futuro desarrollo de funciones matemáticas para varianza de UFC de otros sistemas de generación. Estos son sistemas de energías renovables o sistemas presentes en microgrids de generación distribuida, en los cuales ya se desarrollo un valor esperado de los costos de incertidumbre, como son generación fotovoltaica (PVG), vehículos eléctricos conectados a la red (PEV) y pequeñas centrales hidroeléctricas (PCHs)<span id='citeF-6'></span> | + | Finalmente el proceso matemático para obtener la varianza de UFC en WEG planteado, sirve como punto de partida para el futuro desarrollo de funciones matemáticas para varianza de UFC de otros sistemas de generación. Estos son sistemas de energías renovables o sistemas presentes en microgrids de generación distribuida, en los cuales ya se desarrollo un valor esperado de los costos de incertidumbre, como son generación fotovoltaica (PVG), vehículos eléctricos conectados a la red (PEV) y pequeñas centrales hidroeléctricas (PCHs) <span id='citeF-6'></span><span id='citeF-7'></span>[[#cite-6|[6,7]]]. |
| − | + | ==Acknowledgements== | |
| − | The authors would like to thank the Cyted Network: RED | + | The authors would like to thank the Cyted Network: RED IBEROAMERICANA PARA EL DESARROLLO Y LA INTEGRACION DE PEQUENOS GENERADORES EOLICOS(MICRO-EOLO) for the continued support during thedevelopment of this work. |
| − | === | + | ==Referencias== |
| + | |||
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[1]]] Arevalo, J. C., Santos, F., Rivera S. R. Uncertainty cost functions for solar photovoltaic generation, wind energy generation, and plug-in electric vehicles: mathematical expected value and verification by Monte Carlo simulation. International Journal of Power and Energy Conversion, 10(2):171-207, 2019. | |
<div id="cite-2"></div> | <div id="cite-2"></div> | ||
| − | + | [[#citeF-2|[2]]] Hetzer, J., Yu, D. C., Bhattarai K. An Economic dispatch model incorporating wind power. IEEE Transactions on Industrial Informatics, Volume 23:101-110, 2008. | |
<div id="cite-3"></div> | <div id="cite-3"></div> | ||
| − | + | [[#citeF-3|[3]]] Zhao, J., Fushuan, W., Zhao, Y., Yusheng, X., Kit P. W. (2012) Optimal dispatch of electric vehicles and wind power using enhanced particle swarm optimization. IEEE Transactions on Industrial Informatics, 8:263-275, 2012. | |
<div id="cite-4"></div> | <div id="cite-4"></div> | ||
| − | + | [[#citeF-4|[4]]] Haddi, S., Tarek, B. Economic/emission dispatch including wind power using ABC-Weighted-Sum. International Journal of Engineering and Technical Research (IJETR), 3:891-896, 2015. | |
<div id="cite-5"></div> | <div id="cite-5"></div> | ||
| − | + | [[#citeF-5|[5]]] Arevalo, J. C., Santos, F., Rivera S. R. Application of analytical uncertainty costs of solar, wind and electric vehicles in optimal power dispatch. Revista Ingeniería, 22:324-346, 2017. | |
<div id="cite-6"></div> | <div id="cite-6"></div> | ||
| − | + | [[#citeF-6|[6]]] Molina, F. S., Perez, S. J., Rivera S. R. Uncertainty cost function formulation in small hydropower plants inside microgrid. Ingenierías USBMed, 8:41-49, 2017. | |
<div id="cite-7"></div> | <div id="cite-7"></div> | ||
| − | + | [[#citeF-7|[7]]] Yao, Y., Wenzhong, G., James Momoh. Economic dispatch for microgrid containing electric vehicles via probabilistic modeling. National Renewable Energy Laboratory (NREL), 3:21-28, 2015. | |
<div id="cite-8"></div> | <div id="cite-8"></div> | ||
| − | + | [[#citeF-8|[8]]] Peña A., Romero D., Rivera S. Generation and demand scheduling in a micro-grid with battery-based storage systems, hybrid renewable systems and electric vehicle aggregators. WSEAS Transaction on Power Systems, 14(2):8-23, 2019. | |
<div id="cite-9"></div> | <div id="cite-9"></div> | ||
| − | + | [[#citeF-9|[9]]] Ñustes W., Rivera S. Colombia: territorio de inversión en fuentes no convencionales de energía renovable para la generación eléctrica. Revista Ingeniería, Investigación y Desarrollo, 17:37-48, 2017. | |
| + | </div> | ||
Latest revision as of 12:35, 28 May 2021
Resumen
Frente al problema de la variabilidad de la velocidad del viento en la generación eólica y la dificultad que esto conlleva en el despacho económico de energía eléctrica, en este se presentan desarrollos formulaciones matemáticas (funciones), denominadas costos de incertidumbre(UCF). El término se utiliza en un modelo compuesto de dos partes, uno implica costos de penalización por sobrestimación y el otro debido a la subestimación de una potencia programada. Mediante formulación matemática analítica y simulaciones de Montecarlo, se ha encontrado el valor esperado de los costos de incertidumbre, considerando la estocasticidad del recurso primario (viento) mediante distribuciones de probabilidad. Sin embargo, no se pueden evaluar con exactitud los resultados desde un punto de vista analítico, sin tener en cuenta la variabilidad alrededor del valor promedio. En este artículo se calcula la función analítica de la varianza, entendida como medida de dispersión de los valores esperados de los costos de incertidumbre para el caso concreto de los operadores eólicos; asimismo, se valida esta formulación mediante simulaciones de Montecarlo. La función encontrada es usada para observar la dispersión de los datos en torno a su valor medio esperado, mediante la aplicación de la desviación estándar que es sencillo determinar a partir de la varianza obtenida.
Palabras clave: Energía eólica controlable, costos de incertidumbre, estudios probabilísticos, simulaciones de Monte Carlo
Abstract
Faced with the problem of wind speed in generation and the difficulty that this entails in the economic future of electric power, mathematical formulations (functions), called uncertainty costs, have been developed. The term is used in a model composed of two parts, an implication of penalization costs for overestimation and the other due to the underestimation of a programmed power. Through analytical mathematics and Monte Carlo simulations, we have found the expected value of the costs of uncertainty, the stability of primary resources through the distribution of probability. However, the results can not be evaluated accurately from an analytical point of view, without taking into account the variability around the average value. In this article we calculate the analytical function of the variance, we understand as a measure of dispersion of the expected values of uncertainty costs for the specific case of wind operators; Likewise, this formulation has been validated through Monte Carlo simulations. The function found is used to observe the dispersion of the data around its expected average value, by applying the standard deviation.
Keywords: Controllable wind energy, uncertainty costs, probabilistic studies, Monte Carlo simulation
1. Introducción
En los países desarrollados del mundo se ha venido cambiando el método de generación de energía, dejando atrás la generación con energías provenientes de fuentes fósiles y nucleares, y dando paso a la implementación de la generación con energías renovables. Esta transición se ha notado con la construcción de grades parques de generación de tipo eólico. Sin embargo debido a la estocasticidad del recurso primario, este tipo de generación se considera como no programable en el despacho económico óptimo [1]. El desarrollo de modelos de despacho económico teniendo en cuenta la estocasticidad de las fuentes primarias se empieza a estudiar en artículos como el desarrollado en el 2008 por Hetzer et al. [2], en el que plantean la necesidad de incorporar sistemas de conversión de energía eólica (WECS) en el problema de despacho económico. Este documento introduce los términos de costos de sobreestimación y subestimación de la potencia eólica disponible, añadiéndolos como factores al despacho económico clásico; para ello caracterizan la variabilidad del viento mediante la función de probabilidad de densidad de Weibull. Más adelante, en 2012, Zhao et al., en un artículo publicado por la IEEE [3], proponen una función de distribución de la potencia eólica a partir del comportamiento de la velocidad del viento según la distribución de Rayleigh, desarrollan así un algoritmo de optimización basándose en un método de decodificación de Enjambre de Partículas Discreto (PSO) para solucionar el problema de despacho. Los artículos anteriores incorporan métodos heurísticos a la solución del despacho en generación eólica; en el mismo sentido el siguiente articulo (Haddi and Tarek [4]) expone el método ABC- Weighted-Sum, aplicándolo para obtener una mejor configuración que relacione los costos de generación con las emisiones en la generación térmica a gas, implementando la generación eólica para observar la disminución total en las emisiones.
Para hacer posible la implementación de (WEG), Arévalo et al. introducen la formulación analítica del valor esperado de los costos de incertidumbre, los cuales determinan costos de penalización por subestimar o sobrestimar la potencia programada, lo que permite al operador incluir estos costos en el valor de operación del generador eólico [1].
El articulo mencionado anteriormente valida la función analítica del valor esperado con simulaciones de Montecarlo obteniendo resultados con bajo error. La velocidad del viento utilizada como variable aleatoria y la cantidad de datos utilizados en este estudio, hacen que esta medida de tendencia central sea insuficiente para describir el conjunto de datos, por ello se hace necesario elaborar un análisis estadístico de la dispersión de estos datos respecto al valor medio evaluado. Una medida de dispersión utilizada en este artículo es la varianza, que describe la esperanza del cuadrado de la desviación de cada variable respecto a la media de los datos. En los capítulos siguientes se hará el planteamiento de la función analítica de varianza a partir de su definición expresada en términos del valor esperado que se obtuvo en [1]. Esta función analítica se validará con la simulación de Montecarlo de un generador eólico, teniendo en cuenta como variable aleatoria la velocidad del viento modelada como una función de probabilidad ya usada en WEG, la función de Weibull. Se presenta también un estudio de optimización teniendo en cuenta que potencia programada puede tener tanto un menor costo de incertidumbre así como una menor variabilidad de los datos, dicha optimización se propone de forma estadística utilizando la desviación estándar calculada a partir de la función de varianza encontrada para finalmente obtener conclusiones del trabajo realizado.
2. Descripción matemática de los costos de incertidumbre para generación eólica
En los sistemas eólicos la variabilidad del viento determina la potencia disponible de un generador, por tanto, dada una potencia programada existe la posibilidad de que la potencia disponible sea mayor o menor. Esta incertidumbre de potencia tiene asociado un costo: Si se tiene mayor potencia disponible de la que se programó, se desperdicia el recurso primario disponible, pues no se evaluó con exactitud el valor real de la velocidad del viento y por otro lado si por razones meteorológicas la velocidad de viento es baja junto con una potencia obtenida menor a la programada, significa que se evaluó por encima de la capacidad real que tiene el generador, entonces la potencia faltante para alcanzar la programada se ve traducida en un costo [1,5].
Como se mencionó, el costo de incertidumbre(UCF) puede tener dos valores, uno donde hay un excedente de potencia que no se despacho y otro en el que hace falta para cumplir con lo programado, a cada uno de estos escenarios se los define como costos por subestimar y costos por sobrestimar, respectivamente.
Siendo la potencia disponible y la potencia programada se definen los costos por subestimar y sobrestimar de la siguiente manera:
1. Costos por subestimar Existen cuando definidos como:
|
|
(1) |
siendo un coeficiente de penalización por subestimar
2. Costos por sobrestimar Existen cuando definidos como:
|
|
(2) |
siendo un coeficiente de penalización por subestimar.
Finalmente, los costos de incertidumbre corresponden al valor esperado de las funciones de costos de penalización por subestimar y sobrestimar , donde son las variables: potencia disponible y potencia programada, [5], para este caso aplicados a la generación eólica se tiene:
|
|
(3) |
donde UCF es la función de costos de incertidumbre. Para cada caso es desarrollada una integral:
|
|
(4) |
|
|
(5) |
donde es la PDF de la potencia WEG del generador i, teniendo en cuenta que la función de probabilidad sigue la distribución de Weibull, se puede relacionar esta distribución con la potencia de salida de un generador eólico en función de su velocidad , de modo que las condiciones de generación son definidas por:
- Velocidad de arranque (cut in speed): la velocidad del viento para la que el generador comienza a entregar potencia útil.
- Velocidad Nominal (rated speed): la velocidad del viento para la cual se alcanza la potencia nominal del generador.
- Velocidad de desconexión (cut out speed): la velocidad del viento para la que el rotor del generador se detiene por acción de los sistemas de regulación para evitar sufrir daños.
- Potencia nominal.
Ademas, las constantes:
- : Factor de forma de la PDF.
Con lo anterior se definen los límites o condiciones en las que se cumplen los costos de penalización por subestimar o sobrestimar de acuerdo a la curva de potencia, [1] y [5] definen estos limites de la siguiente manera:
- Condición A: para o
|
|
(6) |
- Condición B: para
|
|
(7) |
- Condición C: para
|
|
(8) |
Aplicando estas condiciones se obtienen las siguientes funciones de costos de penalización por subestimar y sobrestimar [1]:
|
|
(9) |
|
|
(10) |
Este resultado será fundamental para el planteamiento y desarrollo de la varianza. [1,5].
3. Formulación de la varianza en los costos de incertidumbre
La varianza es una medida de dispersión definida como la esperanza del cuadrado de la desviación respecto a la media y puede ser definida de la siguiente forma:
|
|
(11) |
Siendo E[X] el valor esperado de una función de distribución de probabilidad X.
Específicamente en este caso, E[X] es una función de costos de penalización por subestimar y sobrestimar; es decir, se tendrán dos resultados de varianza, uno debido a los costos de penalización por subestimar y otro por sobrestimar:
- Varianza por subestimar:
|
(12) |
- Varianza por sobrestimar:
|
(13) |
Para hallar la varianza total se debe tener en cuenta que los costos de penalización por subestimar y sobrestimar son eventos dependientes, como consecuencia se utilizó la siguiente formula:
|
|
(14) |
es decir:
|
|
(15) |
3.1 Varianza de costos de penalización por subestimar
Como se puede ver en la ecuación (13) la varianza se puede dividir en dos partes, de la siguiente forma:
|
|
(16) |
se soluciona a partir de metodos de sustitución simple y se puede deducir de (11). El resultado de la varianza por subestimar es el siguiente:
|
|
|
|
(17) |
|
|
(18) |
|
|
(19) |
3.2 Varianza de costos de penalización por sobrestimar
De forma similar al planteamiento y solución de la varianza de costos de penalización por subestimar, se obtiene:
|
|
(20) |
Al igual que en el caso anterior, a partir de sustituciones simples y resultado de (8) es posible encontrar la solución, obteniendo el siguiente resultado:
|
|
|
|
(21) |
|
|
(22) |
|
|
(23) |
Para la varianza total de los costos de incertidumbre como ya se mencionó se utilizó la covarianza, la cual es obtenida con la siguiente formula:
|
|
(24) |
Por definición [2] los costos de penalización por subestimar ocurren cuando los de sobrestimar no están, solo existe una posibilidad de que se encuentren y es en un solo punto (), al desarrollar matemáticamente este punto el resultado es cero; es decir que se puede considerar como la suma de los valores esperados, con esto ya se tienen todos los valores analíticos.
4. Validación de la varianza de los costos de incertidumbre mediante simulación
Con el objetivo de validar la fórmula encontrada analíticamente se plantea la simulación de Montecarlo para un generador eólico utilizando los parámetros de la Tabla 1, la simulación consiste en 100000 datos aleatorios de la velocidad del viento teniendo en cuenta la distribución de Weibull adaptada específicamente a la Raylegh, estos datos se encuentran acumulados alrededor del valor del viento nominal dado en la tabla de parámetros, 15 m/s, [6,7].
| Entradas | ||
| Variable | Descripción y Unidad | Valor |
| Potencia programada al generador eólico [MW] | 100 | |
| Velocidad de inicio de generación [m/s] | 5 | |
| Velocidad nominal del viento [m/s] | 15 | |
| Velocidad de parada de generador [m/s] | 45 | |
| Potencia nominal de salida [MW] | 150 | |
| Constante lineal [MW/m/s] | 15 | |
| Constante independiente [MW] | -75 | |
| Parámetro de escala Raylegh [m/s] | 15.9577 | |
| Costo de penalización por sub estimar al generador [$ /MW] | 300 | |
| Costo de penalización por sobre estimar al generador [$ /MW] | 700 | |
| N | Número de iteraciones | 100000 |
A continuación, en la Figura 1 se muestra la distribución de los datos, donde se muestra que sigue la función Raylegh, además se muestra la potencia disponible en el generador basado en las condiciones de potencia del generador definidas en (6), (7) y (8).
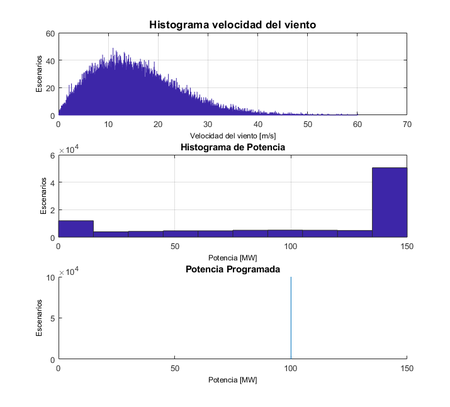
|
| Figura 1. Velocidad del viento, Potencia disponible y Potencia programada |
Luego, en la Figura 2 se presenta la cantidad de escenarios en los cuales se subestima y se sobrestima la potencia programada, como se definió en (1) y (2).
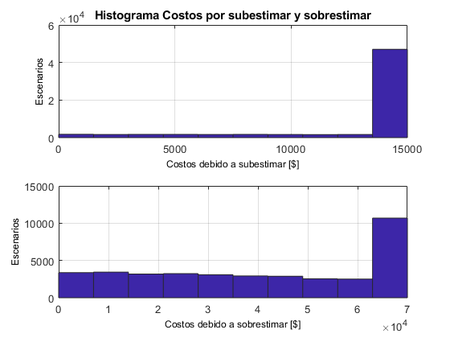
|
| Figura 2. Histograma costos por subestimar y sobrestimar |
Posteriormente, en el histograma de la Figura 3 se muestra la acumulación de escenarios de costos de incertidumbre producto de la suma de los costos por sobreestimar y subestimar. El valor esperado de estos costos que se obtienen en el histograma es de , y el valor esperado de los costos de incertidumbre que se obtiene por la formula encontrada analíticamente en (9 y 10) es de obteniendo un error de .
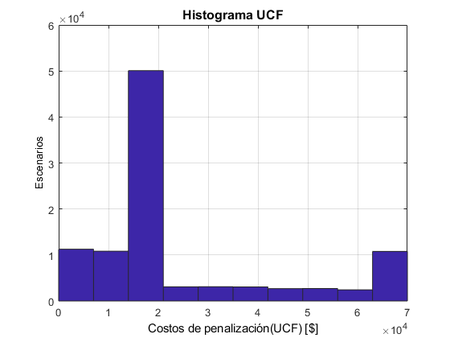
|
| Figura 3. Histograma UCF |
En la Figura 4 se observa el cambio de los costos de incertidumbre al cambiar la potencia programada para el mismo generador con las características de la Tabla 1, variando de 0 MW a la potencia nominal del generador 150 MW. Esta gráfica permite encontrar el valor óptimo de potencia que se debe programar para que los UCF sean mínimos.
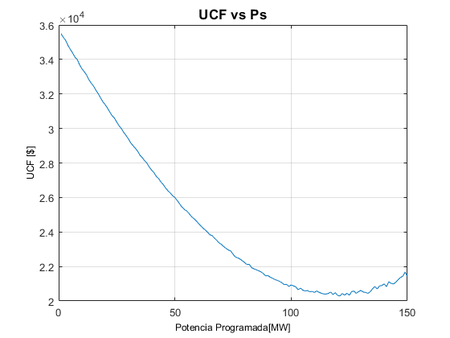
|
| Figura 4. UCF al variar la potencia programada |
Finalmente se procede a calcular la varianza mediante simulación de Montecarlo al igual que se simulo los UCF, obteniendo (), al compararlo con el valor obtenido analíticamente se obtuvo un error de 0.0043.
Además, se hace el mismo análisis que con los costos de incertidumbre variando la potencia programada [8,9], observando que cuando este tiene una menor varianza significa una menor dispersión para la cantidad de escenarios, como se observa en la Figura 5.
|
| Figura 5. Varianza al cambiar la Potencia programada |
5. Conclusiones
Este articulo propone la formulación matemática de la varianza de los costos de incertidumbre, que representa la medida de dispersión de los valores esperados de los UCF para el caso específico de los generadores eólicos. Su importancia radica en que muestra la variabilidad de los costos de incertidumbre al analizar distintos escenarios de la potencia programada, específicamente en sistemas de generación eólicos donde la fuente de energía primaria (velocidad del viento) tiene asociada una gran incertidumbre.
La varianza analítica es exitosamente validada mediante simulaciones de Montecarlo usando variables aleatorias, mostrando el bajo error de los resultados al comparar los resultados simulados con los analíticos.
Se encuentra una aplicación en la optimización despacho, al relacionar tanto (UCF) como varianza de (UCF) con la potencia programada, su importancia radica en que muestra los valores mínimos y máximos de costos de incertidumbre y la variabilidad de este valor esperado, además se incluye para este estudio un análisis de varianza exponiendo el bajo error.
Pensando en el desarrollo y la alta penetración que comienzan a tener las energías renovables, el desarrollo de UFC presenta una gran aplicación en la optimización del despacho económico, pues minimiza riesgos tanto económicos como técnicos por sobrestimar o subestimar la potencia programada. Asimismo, el desarrollo matemático que se muestra de la varianza de UFC, añade un valor de validez y confianza a la optimización del despacho de generadores eólicos(WEG). El riguroso estudio presentado en el texto presenta gran aplicabilidad en los sistemas de potencia, debido a la alta penetración de energías renovables no convencionales, sin embargo su trascendencia radica en su complementariedad con sistemas de almacenamiento o generadores convencionales.
Finalmente el proceso matemático para obtener la varianza de UFC en WEG planteado, sirve como punto de partida para el futuro desarrollo de funciones matemáticas para varianza de UFC de otros sistemas de generación. Estos son sistemas de energías renovables o sistemas presentes en microgrids de generación distribuida, en los cuales ya se desarrollo un valor esperado de los costos de incertidumbre, como son generación fotovoltaica (PVG), vehículos eléctricos conectados a la red (PEV) y pequeñas centrales hidroeléctricas (PCHs) [6,7].
Acknowledgements
The authors would like to thank the Cyted Network: RED IBEROAMERICANA PARA EL DESARROLLO Y LA INTEGRACION DE PEQUENOS GENERADORES EOLICOS(MICRO-EOLO) for the continued support during thedevelopment of this work.
Referencias
[1] Arevalo, J. C., Santos, F., Rivera S. R. Uncertainty cost functions for solar photovoltaic generation, wind energy generation, and plug-in electric vehicles: mathematical expected value and verification by Monte Carlo simulation. International Journal of Power and Energy Conversion, 10(2):171-207, 2019.
[2] Hetzer, J., Yu, D. C., Bhattarai K. An Economic dispatch model incorporating wind power. IEEE Transactions on Industrial Informatics, Volume 23:101-110, 2008.
[3] Zhao, J., Fushuan, W., Zhao, Y., Yusheng, X., Kit P. W. (2012) Optimal dispatch of electric vehicles and wind power using enhanced particle swarm optimization. IEEE Transactions on Industrial Informatics, 8:263-275, 2012.
[4] Haddi, S., Tarek, B. Economic/emission dispatch including wind power using ABC-Weighted-Sum. International Journal of Engineering and Technical Research (IJETR), 3:891-896, 2015.
[5] Arevalo, J. C., Santos, F., Rivera S. R. Application of analytical uncertainty costs of solar, wind and electric vehicles in optimal power dispatch. Revista Ingeniería, 22:324-346, 2017.
[6] Molina, F. S., Perez, S. J., Rivera S. R. Uncertainty cost function formulation in small hydropower plants inside microgrid. Ingenierías USBMed, 8:41-49, 2017.
[7] Yao, Y., Wenzhong, G., James Momoh. Economic dispatch for microgrid containing electric vehicles via probabilistic modeling. National Renewable Energy Laboratory (NREL), 3:21-28, 2015.
[8] Peña A., Romero D., Rivera S. Generation and demand scheduling in a micro-grid with battery-based storage systems, hybrid renewable systems and electric vehicle aggregators. WSEAS Transaction on Power Systems, 14(2):8-23, 2019.
[9] Ñustes W., Rivera S. Colombia: territorio de inversión en fuentes no convencionales de energía renovable para la generación eléctrica. Revista Ingeniería, Investigación y Desarrollo, 17:37-48, 2017.
Document information
Published on 16/09/19
Accepted on 11/09/19
Submitted on 18/01/19
Volume 35, Issue 3, 2019
DOI: 10.23967/j.rimni.2019.09.003
Licence: CC BY-NC-SA license