Abstract
The distribution of resistance coefficients of heat supply pipe networks is the key data guiding the hydraulic balance adjustment of heat networks. Since the heat supply pipe network is composed of many pipe segments and the resistance coefficient of each pipe segment is different during heat supply operation, the identification of the resistance coefficient of the heat supply pipe network is an optimization problem with multiple objective functions. In this paper, a high-dimensional multi-objective differential evolutionary algorithm based on global sorting is developed as a method to identify the resistance coefficients of the heat network and the multi-objective algorithm is applied to the resistance identification of the heat network, and the computational process of resistance identification is improved. The fuzzy mathematical method is applied to the process of resistance identification, and a set of optimal solution sets are generated through the identification of each pipe segment and the optimal solutions are selected from the optimal solution sets based on the fuzzy degree of subordination to solve the problem of determining the optimal solutions. The problem of determining the optimal solution is solved. The results show that compared with the single-objective algorithm, the high-dimensional multi-objective differential evolutionary algorithm based on global sorting produces a uniform and concentrated optimal solution set, and the optimal solution accuracy is higher.
Keywords: Heating pipe network, resistance identification, high-dimensional multi-objective optimization, differential evolutionary algorithm
1. Introduction
Heating systems are critical infrastructure for cities in northern China. With the rapid development of Internet of Things (IoT) technology, the urban centralized heat supply system is transforming into a new type of heat supply system that is jointly composed of a heat supply physical equipment network, heat supply IoT, and heat supply information management platform. In the new heating system, intelligent regulation devices with communication functions and heat metering instruments were installed at the heat inlets of heat consumers. The application of intelligent regulating devices allows heat users to actively adjust hot water flow according to their room temperature demand, realizing accurate heat supply. However, the independent adjustment of many heat users will lead to real-time changes in the resistance distribution of the pipeline network, which will also make the flow regulation of the heat station face greater difficulties. If the flow rate adjustment of the heat station can not adapt to the heating needs of the heat users, it will lead to system hydraulic imbalance, resulting in energy waste [1]. To realize the accurate flow regulation of the heat station, it is necessary to grasp the changes in the resistance distribution of the heat network in real time.
The continuous development of the heat metering system and the application of a large number of intelligent heat metering instruments make it possible to obtain real-time changes in the flow rate of each user through the heat supply information management platform, which provides a data basis for the real-time identification of the resistance distribution of the heat network. Lin [2], Wang et al. [3] calculated the resistance coefficients of the pipe network based on the generalized inverse matrix theory by using multiple sets of hydraulic conditions. Bekibayev et al. [4] determined the resistance coefficients of the pipes by comparing the results of hydraulic calculations with the actual data from the SCADA system. Kaltenbacher et al. [5] proposed a method for identifying the resistance coefficients of individual pipes in a water supply network using the inverse of the steady-state hydraulic equations of the network. Zecchin et al. [6] used a particle swarm algorithm to identify the resistance of pipe networks. Dini and Tabesh [7] completed the identification of resistance coefficients of pipe networks using an ant colony optimization algorithm. Savic and Walters [8], Lingireddy and Ormsbee [9], Fan et al. [10], Liang [11] and Liu et al. [12] successfully applied genetic algorithms to the resistance identification of heating pipe network. Sherri et al. [13], Lv [14], Zhou et al. [15] used the improved genetic algorithm to improve the efficiency of resistance coefficient optimization identification of heat supply network.
In the above literature, the deviation between the measured value of each flow or pressure measurement point and the calculated value of the corresponding theoretical model is treated with the weighted sum of squares, and the weighted sum of squares is used as the objective function for the identification of the resistance distribution of the pipe network. When this method is used for optimization, there will be several sets of solutions that satisfy the objective function and the only solution cannot be determined [16,17,18,19]. To solve this problem, Greco and Giudice [20] and Wang et al. [21] calculated the identification results that could meet the application requirements of hydraulic calculation by using the multi-condition iterative identification algorithm. Xu et al. [22] used multiple hydraulic conditions to control the relative error of the impedance identification value. However, the above literature still uses genetic algorithms and other single-objective algorithms to solve the problem. The single-objective algorithm only considers the convergence of solutions, which makes the total objective function value lower than the convergence accuracy and fails to consider the uniformity of the distribution of solutions, resulting in an uneven distribution of solutions [23,24]. In other words, when the convergence accuracy of the total objective function is satisfied, the solution is not distributed evenly. The calculated values of the theoretical model of some measuring points are close to the observed values, while the calculated values of the theoretical model of some measuring points are different from the observed values.
The resistance identification of the heating network is a multi-objective optimization problem, whose goal is to find a set of resistance coefficients that make the calculated flow value in the hydraulic model equal to the actual observed value. The resistance coefficient of each pipe section is the decision variable, and the sub-objective function is the error function between the measured value of the flow or pressure measurement point and the calculated value of the theoretical model. In summary, this paper proposes a high-dimensional multi-objective differential evolution algorithm based on global ranking for pipe network resistance identification. The high-dimensional multi-objective differential evolution algorithm is applied to the resistance identification of the pipe network, which improves the uniformity of the distribution of the identification results and realizes the resistance identification with high convergence, high accuracy, and high stability. The optimal solution is obtained by the method based on fuzzy mathematics, which makes the calculated value of the theoretical model and the observed value of all the measurement points close to each other.
The rest of the paper is arranged as follows: Section 2 describes the mathematical description of the resistance identification of the heating system. In Section 3, the resistance identification of heating system is regarded as a multi-objective optimization problem, the process of multi-objective resistance identification is introduced and the calculation process of resistance identification is improved. The fuzzy mathematics method is applied to the resistance identification process, a group of optimal solution sets is generated by identifying each pipe section, and the optimal solution is selected from the optimal solution set according to the fuzzy membership degree, the problem of determining the optimal solution is solved. In Section 4, the multi-objective differential evolution algorithm based on global ranking is applied to practical engineering and compared with the single-objective differential evolution algorithm. The conclusions of this paper are discussed in Section 5.
2. Mathematical description of the drag coefficient optimization identification problem
In the identification process of the resistance coefficient of the pipe network, since the actual resistance coefficient in the pipe network cannot be obtained by measurement, it is impossible to compare the difference between the actual resistance value and the identification value to determine whether the identification is accurate. With the wide application of heat metering meters with remote communication functions in the heating pipe network, the flow at the heating inlet of each user in the heating pipe network can be measured in real-time. Therefore, after the resistance coefficient distribution of the pipe network is identified, the calculated flow at each user inlet of the heating network can be calculated by solving the hydraulic model [25] by the basic circuit method. Comparing the calculated flow with the measured flow, we can judge whether the identification result is accurate or not. According to this scheme, the heating pipe network resistance identification is based on the known pipe network topology, through the intelligent optimization algorithm, to find a set of appropriate resistance values to minimize the difference between the calculated flow value and the measured value of each measurement point, where the resistance coefficient of each pipe section is the decision variable, and the difference function of the calculated flow value and the measured value of each measurement point is the objective function. Since the number of measurement points in a heating pipe network is often less than the number of pipe segments, the identification of resistance in a heating pipe network involves -dimensional decision variables and -dimensional objective functions, forming a multi-objective optimization problem as shown in Eq. (1):
|
|
(1) |
where:
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
In Eq. (2), is the calculated flow rate value of the th measurement point, m/h; is the measured flow rate value of the th measurement point, m/h. In Eq. (3), is the resistance coefficient of the recognized pipe section, Pa/(m/h); is the n-dimensional decision space. In Eq. (4), is the lower limit of the resistance coefficient of the pipe section, Pa/(m/h); is the upper limit of the resistance coefficient of the pipe section, Pa/(m/h). In Eq. (5), is called the objective function, and is the m-dimensional objective space [26].
Affected by the system running time, the thermal user's self-regulation and other factors, the actual resistance coefficient of the pipe section will deviate from the design resistance coefficient to a certain extent, so there are two situations in determining the search range of the resistance coefficient of each pipe section.
1) There is no variable resistance attachment on the pipe section. When there is no variable resistance attachment on the pipe section, the actual resistance coefficient of the pipe section will only deviate from the design resistance coefficient to a certain extent. The resistance search range in this case is calculated as shown in Eq. (6):
|
|
(6) |
|
|
(7) |
where is the design resistance coefficient of the pipe; is the friction resistance coefficient of the pipe; is the diameter of the pipe section, mm; is the length of the pipe section, m; is the local resistance coefficient of the pipe; is the density of the fluid in the pipe section, kg/m; is the resistance search range; 0.8, 1.2 for the search range coefficients, based on the practical experience of the project to determine.
2) There are attachments on the pipe section. When there are variable resistance accessories such as valves on the pipe section, the range of resistance coefficient of the pipe is calculated according to the method in case 1), and then the range of resistance variation of the valve is calculated according to the valve opening range. Finally, the total resistance system search range of the pipe section is determined by adding the two resistance coefficient ranges.
3. Resistance recognition process of high-dimensional multi-objective differential evolutionary algorithm based on global sorting
The heating pipe network system is complex and the number of flow measurement points is large, so the number of objective functions is usually greater than four. According to the definition of a high-dimensional multi-objective optimization problem [27], the heating pipe network resistance identification problem is a high-dimensional multi-objective optimization problem.
Based on the multi-objective and high latitude characteristics of the resistance identification problem, the use of single-objective optimization algorithms for resistance identification is prone to problems such as poor convergence and low accuracy of results. In this paper, the high-dimensional multi-objective optimization algorithm is applied to the resistance identification problem of the heat supply pipe network, and a high-dimensional multi-objective differential evolution (Global Ranking based Many-objective Differential Evolution (GR-MODE)) algorithm based on Global Ranking is proposed to optimize the identification of resistance coefficients of the heat supply system. The GR-MODE algorithm is used to obtain the optimal solution set by identifying the resistance of the pipe network, and a fuzzy mathematical method based on the optimal solution set is used to select the solution with the highest degree of satisfaction as the optimal solution. The optimal solution is the final result of the resistance identification of the pipe network.
GR-MODE algorithm, which improves the evaluation method of individual fitness of single-objective algorithm, the evaluation criterion of optimizing populations for comparative ranking to adapt to high-dimensional multi-objective optimization problems, and adopts differential evolutionary algorithm as the evolutionary strategy of the algorithm, which improves the algorithm's global search ability and convergence. The resistance identification process based on the GR-MODE algorithm is shown in Figure 1.
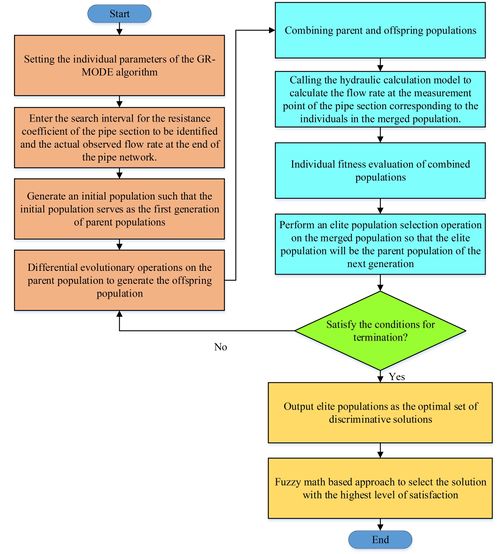
|
| Figure 1. Flowchart for the optimization and identification of drag coefficient based on the GR-MODE algorithm |
3.1 Hydraulic calculation model
After determining and obtaining the resistance coefficient of the pipe network, the hydraulic calculation model is invoked to calculate the flow rate values at each measurement point and compare them with the observed values to determine whether the termination conditions are satisfied. Based on nodal pressure balance and loop pressure drop, the hydraulic mathematical model of the heating pipe network shown in Eq. (8) is obtained according to the principle of graph theory and Kirchhoff's law:
|
|
(8) |
where is the basic association matrix of the pipe network; is the flow rate column vector of each branch pipe section of the pipe network of order ; is the node flow rate column vector of order ; is the independent loop matrix of the pipe network; is the pressure drop column vector of each branch pipe section of the pipe network of order ; is the diagonal matrix of resistance coefficients of order ; is the absolute value of the flow rate of the pipe sections of order diagonal matrix; is the potential energy difference between the two nodes of the branches of order ; is the pump head column vector of the .
3.2 Evaluation method based on global sorting of individual fitness
Due to the heating pipe network resistance identification problem having the characteristics of multi-objective high latitude, using the single-objective algorithm of the fitness evaluation method is prone to cause the uniformity of the distribution of the population to be poor to produce the phenomenon of non-convergence or fall into the local optimum, GR-MODE algorithm adopts the calculation method of individual fitness to take into account the convergence and distribution of the individual indicators within the population, the value of its global fitness () is shown in Eq. (9):
|
|
(9) |
where and are weight coefficients to harmonize the weights of convergence and distribution, which are taken here to be 1.5 and 0.5, respectively; is the global ranking value, defined as the sum of the differences between each in the population and the corresponding target values of other individuals on all targets. The specific calculation can be done as Eq. (10):
|
|
(10) |
Among them:
|
|
(11) |
where is the target dimension; is any individual in the population different from ; is the value of the individual's function on the th target; is the Harmonic average distance of each in the population [27] whose role is to estimate the global density of individuals in the population so that the approximate optimal solution set can have better distribution in the target space, assuming that the Euclidean distance of the closest individuals in the target space [28] is , , , . The Harmonic mean distance of individual is shown in Eq. (12):
|
|
(12) |
In Eq. (12), takes the value , where is the number of individuals in the population; that is, the density of an individual is estimated to cover the effects of all other individuals except itself.
3.3 Evolutionary strategy selection for populations
At present, intelligent optimization algorithms such as genetic algorithms, particle swarm optimization algorithms, cuckoo search algorithms, and differential evolution algorithms are all used as evolutionary strategies for high-dimensional multi-objective optimization algorithms. However, the resistance identification problem of the heating pipe network requires an evolutionary strategy with strong global search ability due to its high dimension and large population. The differential evolution algorithm is considered to be the best evolutionary strategy with its strong global search ability [29]. Therefore, the differential evolution algorithm is adopted in this paper as the evolutionary strategy of the high-dimensional multi-objective evolutionary algorithm to improve the computational performance of the high-dimensional multi-objective evolutionary algorithm. To ensure the excellent performance of the algorithm, it is necessary to set the parameters and strategies of the differential evolution algorithm reasonably according to the actual situation.
The main parameters of the algorithm include the population size (taking the value of , is the individual dimension), the variation operator (taking the value between ), and the crossover operator (taking the value between ). To select suitable parameters, each parameter is combined and several cases are selected for trial calculations to obtain the parameter settings that optimize the performance of the algorithm. Through the trial calculations, the value of , value of , value of , variation strategy of , and crossover strategy of binomial crossover are set for the secondary heating network having to pipe segments.
3.4 Determination of the optimal solution
When the global fitness function value of the algorithm is less than , it terminates and outputs an optimal solution set. The purpose of resistance identification of the heating pipe network is to find a set of resistance values to guide the hydraulic calculation of the heating pipe network, so it is necessary to select the optimal solution from the optimal solution set to achieve the optimal solution for as many sub-targets as possible. Therefore, this paper adopts a method based on fuzzy mathematics to find the optimal solution set and select the solution with the highest satisfaction. The process is as follows:
1) Calculation of fuzzy sets
The fuzzy set is determined by the affiliation function shown in Eq. (13):
|
|
(13) |
where is the maximum value of the absolute value of the difference between the th calculated flow rate and the observed flow rate in the optimal solution set; is the minimum value of the absolute value of the difference between the th calculated flow rate and the observed flow rate in the optimal solution set.
2) Calculate the fuzzy affiliation degree
For the th solution in the set of optimally identified solutions, its normalized fuzzy affiliation degree can be calculated by Eq. (14):
|
|
(14) |
The compromise solution is the solution corresponding to the maximum value in the set and is the number of flow measurement points.
4. Application ase
A community in Luoyang City, China, is selected as a real case to identify the resistance coefficients of its heat network using the GR-MODE algorithm and the single-objective algorithm, respectively, in order to test the feasibility of this study in real engineering and the superior performance of the GR-MODE algorithm.
Differential evolution algorithm (DE) is an efficient optimization algorithm proposed by Kenneth Price et al. after improving evolutionary algorithms such as genetic algorithm. Due to its advantages of fewer control parameters and high operating efficiency, DE has been widely used in optimization processes such as resistance identification of heat supply networks [30]. Therefore, this paper chooses the DE algorithm as a comparison algorithm to show the performance superiority of the GR-MODE algorithm.
4.1 Case overview
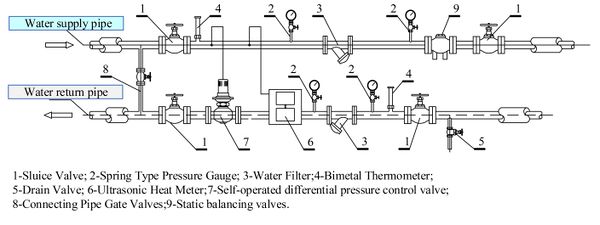
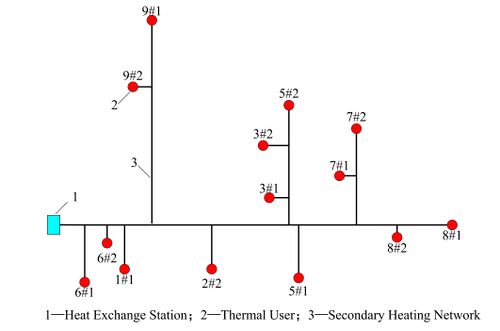
The heating network in this case has been running for about 10 years since it was put into use, and the heat inlet is equipped with self-operated pressure differential valve, remote heat meter, and temperature control valve in the household. The flow observation data of each household are collected through the heat meter and uploaded to the heating monitoring platform. Figure 2 shows the heat inlet device diagram of the case plot, Figure 3 shows the plan view of the heat supply pipe network of the case plot, and Figure 4 shows the topology of the heat supply system of the case plot, containing 1 heat exchange station and 14 heat inlets. To simplify the identification process, this paper simplifies the pipe section after the heat inlet into a pipe segment for identification, the solid line represents the water supply pipe segment, the dotted line represents the return pipe segment, and the dotted line represents the heat exchange station or the heating system in the building.
| Figure 2. Schematic diagram of thermal inlet device |
| Figure 3. Plan view schematic of district heating network |
| Figure 4. Spatial topological structure of district heating network |
4.2 Analysis of results
To verify the feasibility and good performance of the GR-MODE algorithm in practical engineering, GR-MODE algorithm and the DE algorithm are respectively used to identify the resistance of the case pipe network. In order to avoid the chance of identifying results, the pump frequency needs to be changed to create different hydraulic conditions for identification. However, the actual project cannot arbitrarily change the pump frequency, so this paper selects four times of 2:00, 8:00, 14:00 and 20:00 on February 1, 2023 in the case community as the test conditions, and the pump operating frequency is 30Hz and runs at a fixed frequency, the corresponding water pump pressure difference is 82000 Pa. The temperature difference between day and night is large and the thermal demand of users at the four selected times is quite different, and the heat user engaged in self-regulating behavior so different hydraulic conditions can be created to test the applicability of the GR-MODE algorithm.
In order to simplify the identification of the object, it is assumed that the supply and return pipe networks of the heating system are mirror symmetrical, that is, the resistance coefficient of the water supply section and the return section are considered to be the same. The information of pipe diameter and the search range of resistance coefficient of each pipe section is shown in Table 1.
| Pipe segment number | Tube length (m) |
Pipe diameter (mm) |
Resistance search lower limit (Pa/(t/h)2) |
Resistance search high limit (Pa/(t/h)2) |
|---|---|---|---|---|
| E1 | 4 | DN200 | 0.019 | 0.03 |
| E2 | 54.2 | DN80 | 31.712 | 49.502 |
| E3 | 17.9 | DN200 | 0.085 | 0.133 |
| E4 | 23.3 | DN80 | 13.658 | 21.32 |
| E5 | 14.1 | DN200 | 0.067 | 0.105 |
| E6 | 46.3 | DN80 | 27.117 | 42.328 |
| E7 | 21.5 | DN200 | 0.103 | 0.16 |
| E8 | 109 | DN100 | 19.776 | 30.87 |
| E9 | 61.6 | DN80 | 36.076 | 56.313 |
| E10 | 20.3 | DN80 | 11.902 | 18.579 |
| E11 | 47.4 | DN200 | 0.226 | 0.353 |
| E12 | 37.3 | DN80 | 21.813 | 34.05 |
| E13 | 61 | DN200 | 0.291 | 0.454 |
| E14 | 21.5 | DN125 | 1.21 | 1.888 |
| E15 | 41.7 | DN100 | 7.558 | 11.798 |
| E16 | 37.8 | DN80 | 22.147 | 34.572 |
| E17 | 22.1 | DN80 | 12.926 | 20.177 |
| E18 | 23.9 | DN80 | 13.985 | 21.831 |
| E19 | 7.7 | DN150 | 0.167 | 0.26 |
| E20 | 47.1 | DN80 | 27.577 | 43.047 |
| E21 | 45.7 | DN150 | 0.985 | 1.538 |
| E22 | 38.8 | DN100 | 7.04 | 10.99 |
| E23 | 44.2 | DN80 | 25.847 | 40.347 |
| E24 | 21 | DN80 | 12.271 | 19.154 |
| E25 | 32.1 | DN100 | 5.828 | 9.098 |
| E26 | 24.2 | DN80 | 14.167 | 22.114 |
| E27 | 52.4 | DN80 | 30.694 | 47.912 |
| u1 | 185.179 | 2311.437 | ||
| u2 | 187.904 | 2485.103 | ||
| u3 | 176.291 | 5190.842 | ||
| u4 | 193.432 | 2673.524 | ||
| u5 | 180.213 | 4238.581 | ||
| u6 | 167.218 | 5205.427 | ||
| u7 | 184.869 | 2530.211 | ||
| u8 | 197.56 | 5001.832 | ||
| u9 | 197.786 | 4795.671 | ||
| u10 | 189.219 | 1771.339 | ||
| u11 | 197.604 | 2662.436 | ||
| u12 | 173.837 | 3727.313 | ||
| u13 | 188.283 | 2799.541 | ||
| u14 | 185.472 | 7157.587 |
In order to better evaluate the performance of the algorithm, the convergence of the algorithm and the distribution of the results are evaluated by using Generational Distance (GD) and Spread Performance (SP) [26]. GD is a convergence evaluation metric used to evaluate the degree to which the near-optimal solution set obtained by the algorithm approximates the desired optimal solution set, and SP is a distributional evaluation metric to assess the uniformity of the obtained near-optimal solution set.
(1) Generational distance is calculated as shown in Eq. (15):
|
|
(15) |
where is the size of the near-optimal solution set; is the Euclidean distance between the th solution in the near-optimal solution set and the ideal optimal solution set.
(2) The spatial measure is calculated as shown in Eq. (16)
|
|
(16) |
where is the minimum Euclidean distance from the th individual in the solution set to the other individuals in the solution set.
For the solution sets generated by the algorithm runs, the smaller the GD value of the solution set indicates that the near-optimal solution set obtained by the algorithm is closer to the ideal optimal solution set, and the smaller the SP value nearly indicates that the near-optimal solution set is more uniform. The statistics of GD and SP corresponding to the optimal solution set obtained by the GR-MODE algorithm and the same number of solution sets obtained by the DE algorithm in multiple runs are shown in Table 2. The results show that the distribution uniformity of the near-optimal solution sets obtained by the GR-MODE algorithm as well as the degree of approximation to the ideal optimal solution set are better than that of the DE algorithm.
| Norm | Arithmetic | Working condition 1 | Working condition 2 | Working condition 3 | Working condition 4 |
|---|---|---|---|---|---|
| GD | DE | ||||
| MODE | |||||
| SP | DE | ||||
| MODE |
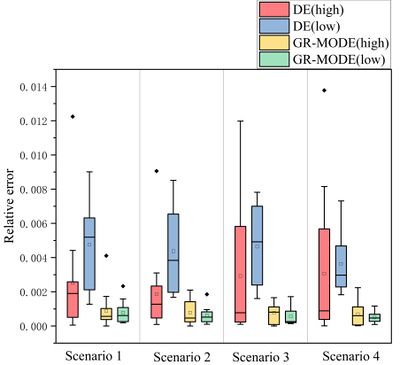
The performance of the optimal solutions obtained by the GR-MODE algorithm and the DE algorithm is compared in terms of the minimum value and distribution of the relative error obtained for the flow rate. The solutions with maximum and minimum fuzzy affiliation are selected from the set of optimal solutions for the cases generated by the algorithms and analyzed with the help of box plots for visual comparison. In Figure 5, DE (high) and DE (low) represent the solutions with the largest and smallest fuzzy affiliation in the set of optimal solutions generated by DE algorithm in several runs, and GR-MODE (high) and GR-MODE (low) represent the solutions with the largest and smallest fuzzy affiliation in the set of optimal solutions generated by GR-MODE algorithm in many runs, respectively. As can be seen from the figure, the distribution of the relative error of the flow obtained by the GR-MODE algorithm in the case is more concentrated than that of the DE algorithm, and the GR-MODE algorithm is capable of obtaining relatively better identification results for each subgoal as far as possible.
| Figure 5. Flow rate error statistics |
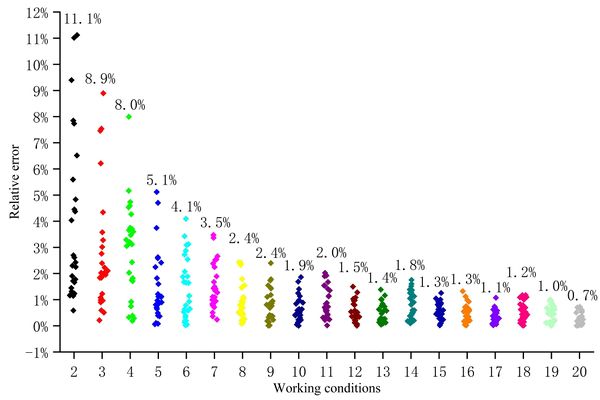
After obtaining the optimal solution set, the optimal solution is found in the optimal solution set by fuzzy mathematical methods, and in order to improve the reliability of the results, multiple working conditions are used for calculation, and the average value is taken as the final calculation result. The more the number of conditions used in the identification process, the more reliable the results of resistance identification will be, but the time required for identification will also increase. In order to make full use of the number of working conditions to identify the resistance coefficient of the pipe section within a limited time, a restriction is added to the number of working conditions: when the relative change between the average value of the identification result under the current working condition and the average value of the identification result under the previous working condition of any pipe section is less than 1%, the optimal identification of the resistance coefficient of the pipe section is stopped, and the average value of which is taken as the final identification result. The scatter point in each column in Figure 6 corresponds to the error between the average value of the resistance under the current working condition and the average value of the resistance under the previous working condition of the pipe section, as shown in the figure the case in the 20th working condition stops the identification, and the figure outputs the identification results as shown in Table 3.
| Figure 6. Scatter plot of relative errors by generation for operating conditions |
| Serial number | Resistance coefficient (Pa/(t/h)2) |
Serial number | Resistance coefficient (Pa/(t/h)2) |
Serial number | Resistance coefficient (Pa/(t/h)2) |
|---|---|---|---|---|---|
| E1 | 0.024 | E15 | 9.599 | U2 | 501.091 |
| E2 | 40.507 | E16 | 28.307 | U3 | 864.900 |
| E3 | 0.106 | E17 | 16.527 | U4 | 529.917 |
| E4 | 17.510 | E18 | 17.863 | U5 | 1068.557 |
| E5 | 0.085 | E19 | 0.213 | U6 | 821.867 |
| E6 | 34.618 | E20 | 35.093 | U7 | 246.768 |
| E7 | 0.129 | E21 | 1.254 | U8 | 295.601 |
| E8 | 24.720 | E22 | 8.967 | U9 | 396.599 |
| E9 | 45.968 | E23 | 33.167 | U10 | 412.076 |
| E10 | 15.257 | E24 | 15.687 | U11 | 872.400 |
| E11 | 0.283 | E25 | 7.414 | ||
| E12 | 27.828 | E26 | 18.176 | ||
| E13 | 0.365 | E27 | 39.254 | ||
| E14 | 1.548 | U1 | 438.436 |
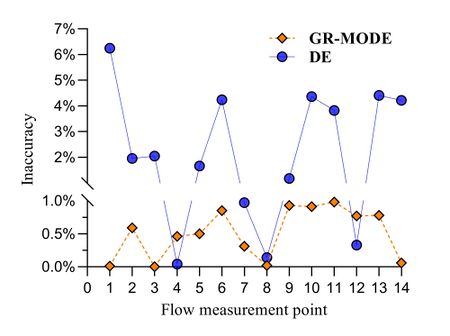
The optimal solutions obtained by the GR-MODE algorithm and the solutions obtained by the DE algorithm, which are brought into the hydraulic model, are shown in Figure 7 for the errors between the calculated and measured values of the theoretical model of the flow measurement points. From the figure, it can be seen that the errors of the GR-MODE algorithm are less than 1%, with a maximum error of 0.98%. The errors of the DE algorithm are mostly between 1% and 5%, with a maximum error of 6.25%, which indicates that the optimal solution obtained by the GR-MODE algorithm has a higher accuracy.
| Figure 7. Discrepancy between theoretical model calculations and measured values |
5. Conclusions
For the problem of multi-objective identification of pipe network resistance, this paper applies a high-dimensional multi-objective differential evolutionary algorithm based on global sorting to the problem of identifying resistance coefficients of heat supply pipe network to achieve high-precision and high-convergence resistance identification and uses fuzzy mathematical methods to find the optimal solution of resistance coefficients in the optimal solution set, which solves the problem of single-objective algorithms being unable to determine the optimal solution of the same pipe section for multiple identifications so that the identification of the resistance coefficient can better guide the operation and regulation of the pipe network. The following conclusions are obtained through the verification of actual cases:
- The resistance identification of a high-dimensional multi-objective differential evolution algorithm based on global sorting has high accuracy and good convergence performance.
- The distribution of the solutions in the solution set obtained by the high-dimensional multi-objective differential evolutionary algorithm based on global sorting is very uniform, and it has excellent performance in heat supply pipe network resistance identification, and the optimal solution found in the optimal solution set by the method of fuzzy mathematics is very high in accuracy, and it can be applied in practical engineering.
Acknowledgments
This paper is based on the project funded by the Chinese Government/World Bank/Global Environment Facility-China Renewable Energy Scale-Up Phase II (QUT-2017-ZX-0010).
Conflict of interest statement: The authors declare that there are no conflict of interests, we do not have any possible conflicts of interest.
Data availability statement: The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
[1] Wang Z.J., Dong L.H., Jiang Y.C., Fang X.-M. Dynamic hydraulic misalignment and control of outdoor pipe network for heat metering variable flow heating system. Journal of Harbin Institute of Technology, 42(02):218-222+258, 2010.
[2] Lin R.Q. Research on non-similar hydraulic working condition construction and pipe resistance coefficient identification of branch heating pipe network. Harbin Institute of Technology, 2021.
[3] Wang N., You S.J., Wang Y., et al. Hydraulic resistance identification and optimal pressure control of district heating network. Energy and Buildings, 170:83-94, 2018.
[4] Bekibayev T., Zhapbasbayev U., Ramazanova G., Bossinov D., Pham D.T. Oil pipeline hydraulic resistance coefficient identification. Cogent Engineering, 8(1):1950303, 2021.
[5] Kaltenbacher S., Steinberger M., Horn M. Pipe roughness identification of water distribution networks: The full turbulent case. Applied Mathematical Modelling, 80:879-894, 2020.
[6] Zecchin A.C., Lambert M.F., Simpson A.R., White L.B. Parameter identification in pipeline networks: transient-based expectation-maximization approach for systems containing unknown boundary conditions. Journal of Hydraulic Engineering, 140(6):04014020, 2014.
[7] Dini M., Tabesh M. A new method for simultaneous calibration of demand pattern and Hazen-Williams coefficients in water distribution systems. Water Resources Management, 28:2021-2034, 2014.
[8] Savic D.A., Walters G.A. Genetic algorithm techniques for calibrating network models. Report, 95:12, 1995.
[9] Lingireddy S., Ormsbee L.E. Optimal network calibration model based on genetic algorithms. WRPMD'99: Preparing for the 21st Century, 1-8, 1999.
[10] Fan Q., Zhou X., Han H., Zhang W. Resistance coefficient identification of a heating pipe network based on a heuristic three-parent genetic algorithm. Engineering Optimization, 55(6):930-945, 2023.
[11] Liang H.B. Heat supply pipe network resistance coefficient identification and leakage diagnosis. North China Electric Power University (Beijing), 2018.
[12] Liu Y.X., Zou P. H., Ma Y.X. Identification of resistance coefficient of water supply pipe network based on genetic algorithm. China Water Supply and Drainage, 30(23):113-116, 2014.
[13] Sherri F., Mahvi A.H., Eshlagy A.T., Hassani A.H. A new approach in the simultaneous calibration of Hazen-Williams coefficients and demand of nodes in water distribution systems. Desalination Water Treat, 74:137-148, 2017.
[14] Lv K. Optimization of pipe network impedance identification based on hybrid genetic algorithm. Boiler Manufacturing, 233(03):61-64, 2012.
[15] Zhou Z.G., Zou P.H., Tan H.P., et al. Recognition of heat network resistance characteristics based on genetic and hybrid algorithm. Journal of Harbin Institute of Technology, 40(11):1761-1765, 2008.
[16] Jiang F. Hybrid intelligent optimization algorithm and its application. Xi'an University of Electronic Science and Technology, 2011.
[17] Gao Y., Shi L., Yao P. Study on multi-objective genetic algorithm. Proceedings of the 3rd World Congress on Intelligent Control and Automation (Cat. No.00EX393), Hefei, Vol. 1, pp. 646-650, 2000.
[18] Augusto O.B., Bennis F., Caro S. A new method for decision making in multi-objective optimization problems. Pesquisa Operacional, 32:331-369, 2012.
[19] Konak A., Coit D.W., Smith A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliability Engineering & System Safety, 91(9):992-1007, 2006.
[20] Greco M., Giudice G.D. New approach to water distribution network calibration. Journal of Hydraulic Engineering, 125(8):849-854, 1999.
[21] Wang H., Wang H.Y., Zhou W.G. Identification method of resistance coefficients of pipe segments in heat supply pipe networks. Computational Physics, 30(3):422-432, 2013.
[22] Xu G., Zhang T.Q., Lv Mou., et al. Genetic algorithm for correcting pipe resistance coefficients under multiple working conditions. China Water Supply and Drainage, (08):50-53, 2004.
[23] Liu Q.Q. Multi-objective problem optimization based on artificial bee colony algorithm. Shenzhen University, 2016.
[24] Xie C.W., Pan J.M., Guo H., et al. A large-scale multi-objective evolutionary algorithm using hybrid strategies. Journal of Computing, 1-21, 2023.
[25] Fu X.Z., Xiao Y.M. Fluid transmission and distribution pipe network (Fourth Edition). China Construction Industry Press, 2018.
[26] Xiao J., Xu X.K., Zhang Y.J., et al. Differential evolutionary algorithm and its application to high-dimensional multi-objective optimization. People's Posts and Telecommunications Press: Academic Monographs on Information and Communication Innovation, 2018.
[27] Xiao J., Bi X. J., Wang K.J. Research on high-dimensional multi-objective optimization based on global ranking. Journal of Software, 26(07):1574-1583, 2015.
[28] Ding Y., Yang J. Comparison of Euclidean distance and normalized Euclidean distance in k-nearest neighbor algorithm. Software, 41(10):135-136+140, 2020.
[29] Montano A.A., Coello A.C., Mezura-Montes E. A novel differential evolution algorithm incorporating local dominance and scalar selection mechanisms for multi-objective optimization. IEEE Congress on Evolutionary Computation, 1-8, 2010.
[30] Wu X.F. Research on impedance identification and variable differential pressure optimal control method of heating pipe network based on differential evolution algorithm. Qingdao University of Technology, 2023.
Document information
Published on 22/04/24
Accepted on 14/04/24
Submitted on 13/12/23
Volume 40, Issue 2, 2024
DOI: 10.23967/j.rimni.2024.04.001
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?