Abstract
The overall stability of hydraulic tainter steel gate decrease seriously, and they are caused by improper structure layout of the two-way eccentric compression of struts. Chinese and American specification method, structural mechanics method and finite element method are respectively used to study rational structural layout of strut arms in vertical frame. First of all, a unified method for rational layout of struts of tainter gate in vertical frame is deduced by using structural mechanics method that simplifies curve girder as straight girder on the basis of zero rotation in vertical girder. Second, rational layouts of struts were researched by utilizing spatial finite element method according to zero rotation in vertical girder. The 756 groups rational layout results of the above three methods with different water heads, different number of struts and different unit stiffness ratios were researched. The differences of struts stress and material dosages of various rational layout methods were evaluated. From the point of view of the forces of tainter gate struts in vertical frame, as the results shown, the layouts of struts by Chinese and American specification method, straight beam method and finite element method are large eccentric compression, small eccentric compression and axial compression respectively. The layout of struts with specification method in lower head is quite different from straight beam method and finite element method, and the layouts of deep water head with straight beam method and finite element method are tend to be consistent. Unit stiffness ratio between vertical girder and strut has little effect on layout of tainter gate struts, but has a great influence on material dosages of tainter gate. Compared with specification method, layout of tainter gate with two struts and three struts by using straight beam method and finite element method can improve stability of struts and save materials of overall tainter gate structure, and the material saving rates of tainter gate with two struts and three struts with finite element method are respectively [32.63, 47.58] (%) and [21.61, 30.01] (%). Rational layout concise charts of tainter gate with two struts and three struts by specification method, straight beam method and finite element method are given, which can be used directly for projects designs. Compared with specification method, the layout of struts of straight beam method and finite element method is not only security and economy, but also method and mechanics concept are simple, which can provide the theoretical basis for specification revision of Chinese and American.
Introduction
Tainter gates are widely used in discharge structures due to simplicity, light weight, smooth flow and low hoist-capacity requirements. Rational layout of struts is directly relate to the safety and economy of the whole tainter gate structure [1]. The vertical girder tainter gates are widely used in deep water all over the world, especially in China. For the layout problems of struts of tainter gate, Design code for steel gate in water resources and hydropower projects [2] in China provides the principles: loads of girders or struts are equal. There have been some problems in existing tainter gates projects that were designed according to the Chinese specification. Such as: 1) The upper cantilever length of vertical girder is long, which leads to the decrease of overall stiffness of tainter gate, and 2) The cross section angle of vertical girder in intersection of strut is larger so that the struts produce larger bending moment in vertical plane and two-way eccentric compression, thereby reducing overall stability of tainter gate. The arrangement principle of struts of tainter gate in Design of hydraulic steel structures [3] and Design of spillway tainter gates[4] is consistent with the Chinese code. In order to overcome the shortcomings of the principles of Chinese and American specification, and guarantee the struts only bear axial forces in vertical frame, Wang [5,6,7] according to structural mechanics method simplified vertical curved girder as straight girder and proposed a layout method that end angle displacement of struts equal zero for surface and deep hole tainter gates. The approach of Wang's also has disadvantages: 1) Simplify vertical curved girder as a continuous straight girder, 2) Hydrostatic load in vertical curve girder is no longer linear load [8], 3) Interaction between vertical girder and strut cannot be considered, and 4) Only two typical special cases of surface and deep hole tainter gates are given, but the layout of submerged tainter gates under different water heads are still not given. Therefore, it is necessary to establish spatial finite element structure models of vertical frame of tainter gate and to research rational layout of strut structures of tainter gates under any water head based on the principle of zero moment in end of strut in vertical frame. The research also can provide the theoretical basis for specification revision of Chinese and American. The most important is to ensure the safety and economy of the hydraulic tainter gate.
1 Layout of specification method
To ensure cross section of upper and lower girders or upper and lower struts are equal and easy to manufacture in practical projects, girders of tainter gate are arranged under the condition of equal loads according to the current Chinese and American specification. According to the relation between water head and height of tainter gate, tainter gates are divided into surface tainter gate and submerged tainter gate, and deep hole tainter gate is a special case of submerged tainter gate. Assuming the distance from the k(k=1,2,…,n) girder to the surface of water is Zk, then the position of k girder can be calculate by following equations [9].
The surface tainter gate:
|
|
(1) |
where n is the number of main girder; H is the distance from surface of water to the sill (m).
The submerged tainter gate:
|
|
(2) |
|
|
(3) |
where a is the distance from surface of water to the top of tainter gate (m).
To arrange the structure of struts more specific, and according to the relation between the water head and the height of tainter gate, the gates are further subdivided into surface, submerged and deep hole tainter gate. When the a/H is equal to zero, the tainter gate is surface hole tainter gate; the a/H is in interval (0,0.9], the tainter gate is submerged hole tainter gate; and the a/H is in interval (0.9,1], the tainter gate is deep hole tainter gate. It is considered that the submerged hole tainter gates which are less than 10% of hydrostatic load between the top and the bottom of gate can be considered as the deep hole tainter gates.
2 Layout of straight beam method
The structural mechanics method of simplifying vertical curved girder as a continuous straight girder is called the straight beam method. In order to overcome the shortcomings of the principles of Chinese specification and the specific and feasible layout methods of American specification and guarantee the struts only bear axial forces in vertical frame (or make the struts are more close to one-way eccentric compression in vertical frame), Wang [5,6] according to structural mechanics method simplified vertical curved girder as straight girder and proposed a layout method that end angle displacement of struts equal zero for surface and deep hole tainter gates. To make up for the disadvantages of Wang's, layout method of straight beam method is utilized to derive the unified theoretical equation of submerged hole tainter gate with two struts or three struts. Surface hole and deep hole tainter gates are the two typical special cases of submerged tainter gates.
Tainter gate bears hydrostatic loads, hydrodynamic loads, seismic loads, self weight and opening and closing forces in actual operation[10]. In order to quantitatively analyze the rational layout structures of tainter gate struts, the main and long-term hydrostatic loads is considered. For the sake of deriving theoretical equation of the layout of tainter gate struts, the straight beam method is used.
2.1 Layout of tainter gate with two struts
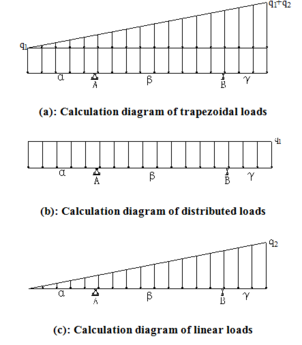
Hydrostatic loads of vertical girders of submerged hole tainter gate with two struts are trapezoidal distribution along the skin plate. The trapezoid distributed loads can be equivalent to the superposition of uniform distributed loads and linear loads , is the unit weight of water. Vertical girders directly rigid connect with struts form plane rigid frame. Without bending moment on the point of intersection of strut and girder can be simplified as hinge support according to straight beam method. The plane rigid frame is composed of vertical girder and strut, which can be simplified as a continuous beam. Computational models of tainter gate with two struts are shown in Figure 1.
Assuming that flexural rigidity (EI) of vertical girder is constant. To simplify calculation, length of girder is regarded as 1. Length coefficient of upper , middle and lower section of vertical girder is respectively, that is the point of intersection of the strut and girder can be determined. Then:
|
|
(4) |
According to equilibrium conditions, the support reactions of uniform distributed loads and linear loads are respectively:
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
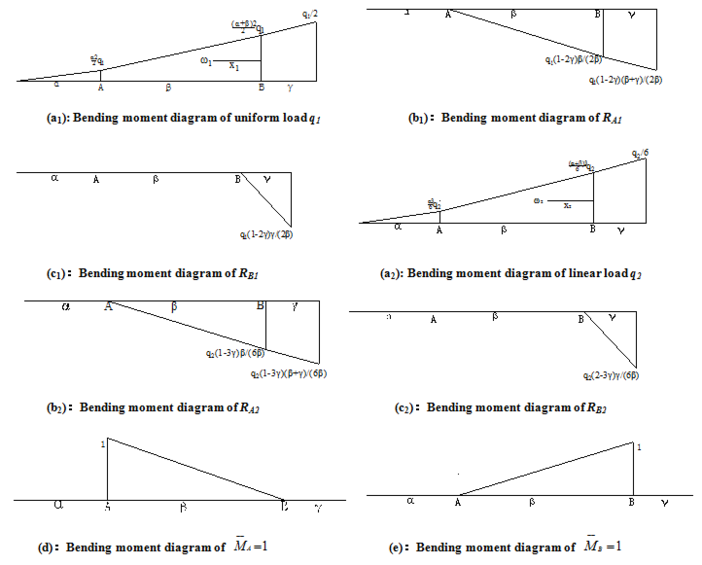
The vertical girder is considered as cantilever beam with one end fixed, and the moment diagrams of uniform distributed loads and linear loads can be drawn. Then bending moment diagrams of the trapezoidal loads can be obtained by superposition. The rotation angle () of cross sections of A and B can be obtained by using graph multiplication method [11]. Bending moment diagrams of and are shown in Figure 2.
The middle part areas of bending moment diagrams and the distance between centroid of middle part areas of bending moment diagrams of linear loads and B in Figures 2a1 and 2a2 as shown in following:
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
Using graph multiplication method:
|
|
(13) |
|
|
(14) |
Equations (4)-(12) are put into equations (13) and (14) , and simplified as:
|
|
(15) |
|
|
(16) |
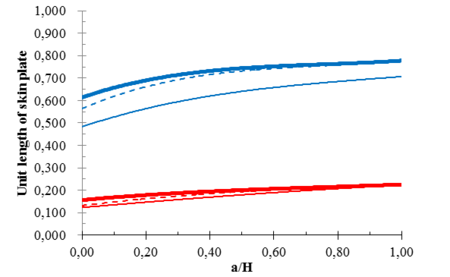
Equations (1), (15) and (16) are set up, and then the relationships between q1 and q2 arecombined when a/H is in interval [0,1] with step length 0.05. Then MATHEMATICA programming [12] is used to solve equations and the values of are obtained. Arrangement results of tainter gates with two struts are gained as shown in Figure 7.
2.2 Layout of tainter gate with three struts
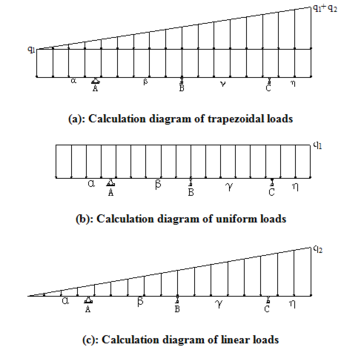
Hydrostatic loads of vertical girders of submerged hole tainter gate with three struts are trapezoidal distribution along the skin plate. The trapezoid distributed loads can be equivalent to the superposition of uniform distributed loads and linear loads , is the unit weight of water. Assuming that the flexural rigidity (EI) of vertical girder is constant. Compared with two struts structure, three struts structure is statically indeterminate structure, and besides static equilibrium equation, the deformation compatibility equation must be added. The B support as a redundant constraint, and deflection of B in deformation compatibility equation is equal to zero. To simplify calculation, the length of girder is regarded as 1. Length coefficient of upper, upper middle, lower middle and lower section of vertical girder is respectively, that is the point of intersection of the strut and girder can be determined. The counterforce of each support is RA、RB and RC. Computational models of tainter gate with three struts are shown in Figure 3
|
|
(17) |
Static equilibrium equations under uniform distributed loads:
|
|
(18) |
|
|
(19) |
Static equilibrium equations under linear loads:
|
|
(20) |
|
|
(21) |
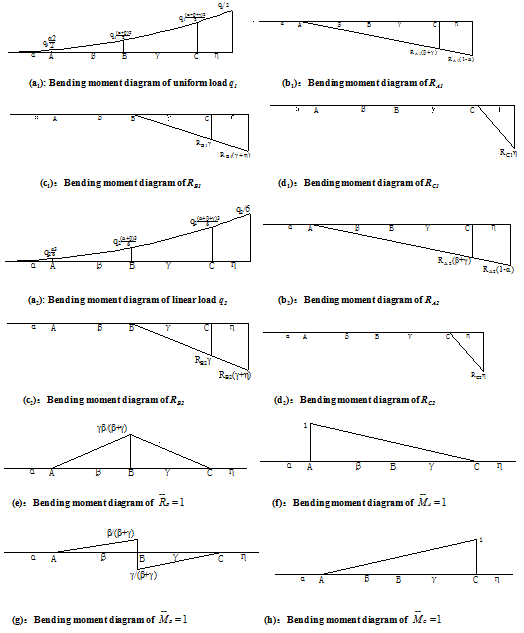
The vertical girder is considered as cantilever beam with one end fixed, and the moment diagrams of uniform distributed loads and linear loads can be drawn. Then bending moment diagrams of the trapezoidal loads can be obtained by superposition. Deflection at the supports of B and rotation angle () of cross section of at the supports of A, B and C can be gained using graph multiplication method. Unit concentrated load and unit moment of force are applied in basic structure. The bending moment diagrams under uniform distributed loads and linear loads are shown in Figure 4.
The area (AC) of bending moment diagram and the distance between centroid of area (AC) of bending moment diagram of uniform distributed loads and C in Figure 4a1 as shown in following:
|
|
(22) |
|
|
(23) |
The area (AB) of bending moment diagram and the distance between centroid of area (AB) of bending moment diagram of uniform distributed loads and B in Figure 4a1 as shown in following:
|
|
(24) |
|
|
(25) |
The area (BC) of bending moment diagram and the distance between centroid of area(BC) of bending moment diagram of uniform distributed loads and C in Figure 4a1 as shown in following:
|
|
(26) |
|
|
(27) |
The area (AC) of bending moment diagram and the distance between centroid of area (AC) of bending moment diagram of linear loads and C in Figure 4a2 as shown in following:
|
|
(28) |
|
|
(29) |
The area (AB) of bending moment diagram and the distance between centroid of area(AB) of bending moment diagram of linear loads and B in Figure 4a2 as shown in following:
|
|
(30) |
|
|
(31) |
The area (BC) of bending moment diagram and the distance between centroid of area (BC) of bending moment diagram of linear loads and C in Figure 4a2 as shown in following:
|
|
(32) |
|
|
(33) |
Deformation compatibility equations of uniform distributed loads and linear loads are supplemented by deflection () of B that equals to zero, and the following formulas are got by graph multiplication method:
|
|
(34) |
|
|
(35) |
Equations (34) and (35) are simplified by the conditions of fB1=0 and fB2=0:
|
|
(36) |
|
|
(37) |
The rotation angles () of cross section at supports of A,B and C under uniform distributed loads and linear loads are obtained by graph multiplication method. Then the equations of rotation angle at supports of A,B and C under trapezoidal loads are got by superposition method:
|
|
(38) |
|
(39) |
|
(40) |
Equations (38)-(40) are simplified by the conditions of rotation angles( ) of cross section at supports of A, B and C that equal to zero:
|
|
(41) |
|
(42) |
|
(43) |
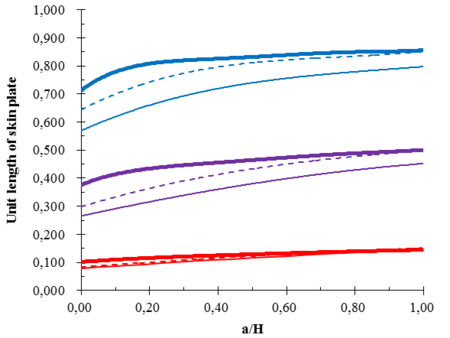
Equations (17)-(21), (36), (37), (41), (42) and (43) are set up, and then equations (22)-(33) are put into the above equation sets. The relationships between q1 and q2arecombined when a/H is in interval [0,1] with step length 0.05. Then MATHEMATICA programming is used to solve equations and the values of are obtained. Arrangement results of tainter gates with three struts are gained as shown in Figure 8.
3 Layout of finite element method
Finite element models of vertical frame structure of tainter gate were established by using the APDL language programming in three-dimensional finite element software. The detailed analysis procedures were as follows: 1) Beam188 element was selected [13,14], and the cross section of struts is box section and vertical girder is I-shaped section. Finite element models of two struts and three struts with vertical girder were established [15,16] as shown in Figures 5 and 6; 2) Material properties were determined: Elastic modulus and Poisson's ratio are 2.06 x 105MPa and 0.3 respectively; 3) Constraints were imposed: trunnion of tainter gate is hinged joint, and vertical upward constraint at the bottom of the girder; 4) Loads were applied: hydrostatic loads were applied to the skin plate of the tainter gate, and the density of water is 9.8KN/m3; 5) Results were solved and analyzed. Taking a hydropower station with radius of skin plate is 32 m and normal storage level is 23.8 m as an example, and the layout results of 21 groups different water heads of two struts and 21 groups different water heads of three struts respectively under the conditions of 756 groups of different unit stiffness ratio between girder and strut by using the above steps. Regarding layout results of the Chinese and American specification as the initial value and the point of intersection of the strut and girder as variable, APDL language of ANSYS14.0 calculation program was utilized. The bending moment at the end of the strut was extracted, and stop calculation when the values of bending moment is zero(that is zero rotation in vertical girder). Then the arrangement results of the strut are the rational arrangement results of finite element method.
4 Comparative analysis of three kinds of layout results
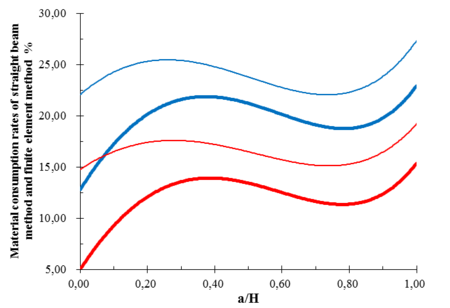
Taking a hydropower station with radius of skin plate is 32 m and normal storage level is 23.8 m as an example, The rational layout results of tainter gates in different water heads were respectively obtained by the method of Chinese and American specification, straight beam method and finite element method. Non dimensional results are shown in Figures 7 and 8, respectively.
Notes: Heavy line represents the layout results of straight beam method, thin line represents the layout results of Chinese and American specification method, dotted line represents the layout results of finite element method. blue line represents the upper strut, red line represents the lower strut, purple line represents the middle strut in Figures 7 and 8.
Firstly, the layouts of tainter gate with two struts and three struts of the three kinds of methods under any water head are respectively obtained from Figures 7 and 8. The layout results of finite element method are between the specification method and the straight beam method. The layout results of straight beam method and finite element method are tend to be consistent for deep hole tainter gates. The layout results of three kinds of methods are close for the lower strut of tainter gates. The layout results of straight beam method and finite element method are very close for the surface tainter gates and the upper or upper middle struts of the submerged tainter gates. However, the differences of layout results between former two and the Chinese specification method are quite large. Secondly, with the increase of water heads, the struts of tainter gates are move up, but the magnitudes of lower struts moving up are minimal. The rational arrangement results of the tainter gates that can be applied in practical projects according to Figures 7 and 8. To save length of the paper, Results of bending moment of the end struts under the conditions of the unit stiffness ratio between vertical girder and strut and the water heads are fixed are obtained by finite element method as shown in Table 1. Table 1 lists the calculation results of finite element method under the three layout methods.
| Strut type | Specification | Straight beam method | Finite element method | |
| Two struts | Surface | 126.21 | -45.76 | 0.00 |
| -42.03 | -20.44 | 0.00 | ||
| Submerged | 652.40 | -54.53 | 0.00 | |
| -295.43 | -3.25 | 0.00 | ||
| Deep | 6876.30 | -504.00 | 0.00 | |
| -3567.33 | 449.50 | 0.00 | ||
| Three struts | Surface | 69.22 | -19.53 | 0.00 |
| -4.38 | -2.97 | 0.00 | ||
| -14.97 | -9.74 | 0.00 | ||
| Submerged | 374.47 | -70.25 | 0.00 | |
| -8.46 | -3.74 | 0.00 | ||
| -99.80 | 34.45 | 0.00 | ||
| Deep | 4176.60 | -504.90 | 0.00 | |
| -133.30 | -17.47 | 0.00 | ||
| -1369.67 | 466.25 | 0.00 | ||
From Table 1 seen, the absolute values of bending moments of the end struts that arranged with straight beam method and finite element method are less than that arranged with the specification method, and the bending moments of the end struts that arranged with finite element method are zero. Further analysis shows that: The struts which are arranged with the specification method are large eccentric compression in the vertical frame. The struts which are arranged with straight beam method are small eccentric compression in the vertical frame. The struts which are arranged with finite element method are axial compression in the vertical frame. Therefore, using straight beam method and finite element method to carry out the layout of struts can improve the overall stability bearing capacity of tainter gates.
5 Comparison of amounts of strut materials
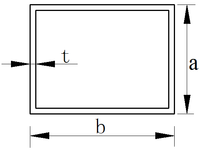
Taking a hydropower station with radius of skin plate is 32 m and normal storage level is 23.8 m as an example. Using finite element software ANSYS14.0 [17] to compare consumption of strut structure materials according to two struts and three struts in six groups unit stiffness ratio (5, 6, 7, 8, 9, 10) of vertical girder and strut under the layout results. Box section is selected as shown in Figure 9. In order to facilitate comparison the amounts of strut materials, width (b) and height (a) of box section remain unchanged, and only change the wall thickness (t) of the section. The struts which are arranged with Chinese and American specification method and straight beam method are eccentric compression in the vertical frame. However, The struts which are arranged with finite element method are axial compression in the vertical frame. Section sizes of the struts are determined according to eccentric compression and axial compression under the premise of strength, stiffness and stability. And then the struts material dosages in the case of three kinds of arrangement methods are compared.
The stability of tainter gates are mainly determined by the stability of the struts. Section design of the struts are carried out by using integral stability equation of eccentric compression and axial compression, such as the equations (44) and (45):
|
|
(44) |
|
|
(45) |
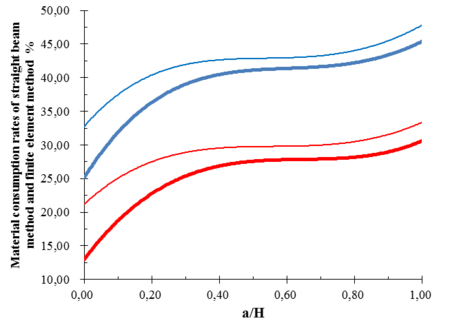
where is the Euler critical force that considers the resistance factor, and rest of the parameters are detailed introduced in the specification. Compared with the Chinese and American specification method, the calculation results show that two struts and three struts can be save material dosages by using straight beam method and finite element method. And the change rules of material saving rate with the unit stiffness ratio between vertical girder and strut are obvious. To save length of paper, the material savings rates of straight beam method and finite element method are given under the circumstances of unit stiffness ratio are respectively 5 and 10 as shown in Figures 10 and 11.
Notes: Heavy line represents the layout results of straight beam method, thin line represents the layout results of finite element method, blue line represents the unit stiffness ratio is 5, red line represents the unit stiffness ratio is 10 in Figures 10 and 11.
From Figures 10 and 11 can be obtained: when the unit stiffness ratios between vertical girder and strut of the two struts structure are constant, material savings rates under the layout results of straight beam method and finite element method increase with the increase of the water head. The material savings rates of deep hole tainter gate reaches the maximum [24.69, 45.31] (%) and [32.63, 47.58] (%), respectively. Material savings rates of three struts under the layout results of straight beam method and finite element method increase with the increase of a/H in interval [0, 0.23], decrease with the increase of a/H is in interval (0.23, 0.95], and increase with the increase of is a/H in interval (0.95, 1]. The material savings rates of deep hole tainter gate reaches the maximum [12.51, 25.98](%) and [21.61, 30.01](%), respectively. The material savings rates of the two struts structure are larger than the three struts structure’s. The material savings rates of the layout results of straight beam method and finite element method decrease with the increase of the unit stiffness ratios between vertical girder and strut, and the material savings rates of finite element method is larger. Considering the economy, the unit stiffness ratio of vertical girder and strut should be taken a smaller value as far as possible within the prescribed ranges that required in the Chinese specification.
In addition, A conclusion is that unit stiffness ratios between vertical girder and strut have little effect on the layout of struts. The reason is that the layout of finite element method based on the theory of bending moment of end struts equal to zero, and in this case the moment cannot transfer between vertical girder and strut.
6 Conclusions
The following conclusions can be drawn through the research by means of specification method of Chinese and American, straight beam method and finite element method:
1) A unified method for arranging the struts of any tainter gates under any water head according to the straight beam method with zero rotation in vertical girder is put forward, which is used for arranging the struts of any tainter gate that are small eccentric compression member in vertical frame.
2) That spatial finite element method with zero end angle displacement of struts(that is zero rotation in vertical girder) utilized to arrange the struts of any tainter gate is proposed, which is used for arranging the struts of tainter gates that are axial compression member in vertical frame.
3) Unit stiffness ratios between vertical girder and strut have little effect on the rational layout of struts. However, considering the economy, the unit stiffness ratio of vertical girder and strut should be taken a smaller value as far as possible within the prescribed ranges that required in the Chinese specification.
4) The layout results of struts are quite different between specification method of Chinese and American, straight beam method and spatial finite element method. For tainter gates under lower water head, the layout results of Chinese and American specification method near the lower sill, straight beam method near the top girder and finite element method between the above. For deep water head tainter gates, the layout results of straight beam method and spatial finite element method are tend to be consistent.
5) Rational layout concise chart of Chinese and American specification, straight beam method and finite element method is proposed, which can be used directly for projects design. Compared with the specification the layout of strut structure of straight beam method and finite element method are not only security and economy, but also method and mechanics concept are simple, which can provide the theoretical basis for specification revision of Chinese and American.
6) Providing a specific and feasible method that carry out the layout of strut arms of tainter gates for design of hydraulic steel structures and design of spillway tainter gates of American.
Acknowledgements
The author would like to gratefully acknowledge the support of NSFC, and the Associate professor Wei Ning for help.
References
[1] Zhang Jiguang, Liu Gongren. Accident analysis and research on light radial steel gate[J]. Journal of hydroelectric power generation, 1992, 11(3):49-57.
[2] Ministry of Water Resources of the People's Republic of China. Specification for design of steel gate in hydraulic and hydroelectric projects(SL74-2013)[S]. Beijing: China Water & Power Press, 2013.
[3] USACE.Design of hydraulic steel structures.CECW-CE Engineer Manual,1110-2-584[S].U.S.Army Corps of Engineers(USACE),Washington,D.C., 2014.
[4] USACE.Design of spillway tainter gates.CECW-ET Engineer Manual,1110-2-2702[S].U.S.Army Corps of Engineers(USACE),Washington,D.C., 2000.
[5] Wang Zhengzhong, Lou Zongke, Li zongli. Rational structure layout of three arm surface radial sluice gate[J]. Journal of Northwestern Agricultural University, 1995, 23(3): 230-233.
[6] Wang Zhengzhong. Discussion on rational structure layout and calculation scheme of large and middle scale radial steel gate[J]. Yangtze River, 1995,26 (1): 54-58.
[7] Liu Jiliang, Wang Zhengzhong, Jia Shikai. Optimization design of main frame of radial gate with three arms based on rational layout[J]. Journal of Zhejiang University (Projects Science), 2011, 45(11):1985-1990.
[8] Liu Lihua, Zeng Youlin, DuanKerang. Optimal analysis and design on radial gates with three supporting legs[J]. Journal of Hydraulic Projects, 1996, 27(7): 9-15.
[9] Ministry of water resources and hydropower planning and Design General Institute. Hydraulic Design Handbook: sluice and dam building (Second Edition) [M]. Beijing: China Water Conservancy and Hydropower Press, 2014, 402-405.
[10] Gao Shizhao, Xu Guobin. Calculation method for vertical hydrodynamic force of hydraulic gate[J]. Projects mechanics, 2015,32 (7):236-242.
[11] Long Yuqiu, Bao Shihua et al. Structural mechanics (Second Edition) [M]. Beijing: Higher Education Press, 2006, 174-180.
[12] Li Genqiang. MATLAB and MATHEMATICA software application [M]. Beijing: People's Posts and Telecommunications Publishing House, 2016, 188-190.
[13] Tamara Nestorovic • Dragan Marinkovic, SomuShabadi • Miroslav Trajkov. User defined finite element for modeling and analysis of active piezoelectric shell structures[J]. Meccanica, 2014,49(8):1763-1774.
[14] P. Pegios, S. Papargyri-Beskou, D. E. Beskos. Finite element static and stability analysis of gradient elastic beam structures[J]. Acta Mechanica, 2015, 226(3):745-768.
[15] YANG Yong, GUO Zixiong, NIE Jianguo, et al. Study on numerical simulation technology of steel reinforced concrete structures using ANSYS[J]. Projects Mechanics, 2006, 23(4):79-85.
[16] YAO Yuntao, XIAO Rucheng. The 3-D finite element analysis method of box girders with coarse mesh[J]. Projects Mechanics, 2010, 27(3):67-75.
[17] Ling Guilong . ANSYS 14 from entry to the master [M]. Beijing: Tsinghua University press, 2016.
Document information
Published on 03/01/18
Accepted on 06/06/17
Submitted on 10/01/17
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.6.003
Licence: CC BY-NC-SA license