How similar are annual and summer temperature variability in central Sweden?

Abstract

Tree-ring based temperature reconstructions have successfully inferred the past inter-annual to millennium scales summer temperature variability. A clear relationship between annual and summer temperatures can provide insights into the variability of past annual mean temperature from the reconstructed summer temperature. However, how similar are summer and annual temperatures is to a large extent still unknown. This study aims at investigating the relationship between annual and summer temperatures at different timescales in central Sweden during the last millennium. The temperature variability in central Sweden can represent large parts of Scandinavia which has been a key region for dendroclimatological research. The observed annual and summer temperatures during 1901–2005 were firstly decomposed into different frequency bands using ensemble empirical mode decomposition (EEMD) method, and then the scale-dependent relationship was quantified using Pearson correlation coefficients. The relationship between the observed annual and summer temperatures determined by the instrumental data was subsequently used to evaluate 7 climate models. The model with the best performance was used to infer the relationship for the last millennium. The results show that the relationship between the observed annual and summer temperatures becomes stronger as the timescale increases, except for the 4–16 years timescales at which it does not show any relationship. The summer temperature variability at short timescales (2–4 years) shows much higher variance than the annual variability, while the annual temperature variability at long timescales (>32 years) has a much higher variance than the summer one. During the last millennium, the simulated summer temperature also shows higher variance at the short timescales (2–4 years) and lower variance at the long timescales (>1024 years) than those of the annual temperature. The relationship between the two temperatures is generally close at the long timescales, and weak at the short timescales. Overall the summer temperature variability cannot well reflect the annual mean temperature variability for the study region during both the 20th century and the last millennium. Furthermore, all the climate models examined overestimate the annual mean temperature variance at the 2–4 years timescales, which indicates that the overestimate could be one of reasons why the volcanic eruption induced cooling is larger in climate models than in proxy data.

Keywords

Annual temperature; Summer temperature; Central Sweden; Climate model simulation; Scale-dependent similarity

1. Introduction

Annual mean temperature is a traditionally-used indicator for global climate change, since it reflect a mean state of the Earth surface temperature, and can be more directly linked to Earth energy balance than seasonal mean temperature (Sutton et al., 2015). To improve our understanding of climate change and variability prior to the industrial revolution, as well as set the current warming in a long-term context, many efforts have been made to reconstruct annual mean temperature back in time (Mann et al., 2009). However, most existing annual mean temperature reconstructions have difficulty to infer precise annual-decadal-resolution variability due to the leak of proxy data which can be precisely dated and can reflect annual mean temperature (Marcott et al., 2013).

Tree-ring data is one of the most widely used high-resolution climate proxies due to its annual resolution and exact dating. Compared to other proxies, tree-ring data from high latitudes/altitudes provides precise inter-annual to multi-centurial changes of growing seasonal/summer temperatures, which are used to further our understanding of local to regional climate change and variability during the last several thousand years (Grudd et al., 2002 and Helama et al., 2002). However, tree-ring data can only reflect the growing seasonal/summer temperature variability.

If summer temperature are similar with annual mean temperature at some timescales regarding some features (e.g. variability, variance), we may use reconstructed summer temperature to infer some features of past annual mean temperature at these timescales, which will further our knowledge of past climate variability. Therefore, to what extent can summer temperature variability represent the variability of mean state of surface air temperature (i.e. annual mean temperature) is important for gaining deep insights into past mean climate variability. The question is even more important for regions where large amounts of temperature-sensitive tree-ring proxies exist, since the past summer mean temperatures in the regions have been already inferred.

Fennoscandia is one of the key regions for dendroclimatic research due to its large areas of forests with climate-sensitive trees and limited human influence (Linderholm et al., 2010). Recently, a millennium-long reconstruction of warm-seasonal temperatures in central Scandinavia was presented, and it was shown that the reconstruction represented the temperature variability for a large part of Fennoscandia (Zhang et al., 2015). A clear relationship between annual and summer temperatures in this region may help to increase our understanding of the past temperature in Scandinavia.

In central Scandinavia, instrumental temperature records cover more than 100 years. However, the lengths of these records are still too short to explore the relationship between the annual and summer temperatures beyond the industrial period. In order to go further back in time and have the possibility to investigate variation at longer timescales, we need to use the data from paleoclimate model simulations. Paleoclimate Modelling Intercomparison Project Phase III (PMIP3, Braconnot et al., 2012) has recently released data from a series of last millennium simulations which date back to 850 CE. However, initially the climate models must be evaluated on their capabilities in replicating the observed relationship between the annual and summer temperatures.

This study focused on improving our understanding of the relationship between the annual and summer temperatures in central Scandinavia at different timescales during the last millennium. Specifically, the objectives of this study are 1) to investigate the relationship between observed annual and summer temperatures at different timescales in central Sweden during 1901–2005; 2) to validate the performance of 7 PMIP3 atmosphere-ocean general circulation models (AOGCMs) in replicating the observed scale-dependent relationships between the annual and summer temperatures and the variance percentage of the annual and summer temperatures at different timescales; 3) to investigate the scale-dependent relationship between the two temperatures for the last millennium using simulations of the most reliable model evaluated. This paper is organised as follows. Section 2 describes the study area; Section 3 documents the data and methods used; results are presented in Section 4; the results are discussed in Section 5, and lastly a summary and conclusions are provided in Section 6.

2. Study region

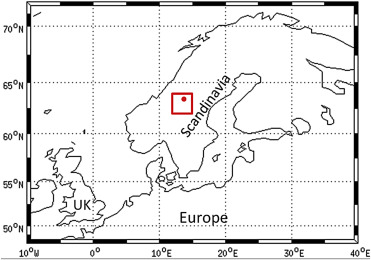
The study region is located at central Sweden as shown in Fig. 1. The region is one of the key areas for dendroclimatological studies in the world. In this area, summer temperature has been reconstructed for the past 3600 years based on Pinus sylvestris L. (Scots pine) tree-ring width data ( Linderholm and Gunnarson, 2005) and warm-season (April–September) temperature has been reconstructed for the past 1200 years using tree-ring density data from the same tree species (Zhang et al., 2015). The climate in this area is strongly influenced by the North Atlantic Oscillation (NAO) throughout the year ( Chen and Hellström, 1999, Busuioc et al., 2001 and Folland et al., 2009) as well as the proximity to the North Atlantic Ocean (Sutton and Dong, 2012). The annual total precipitation is 857 mm in the west (Storlien, 583 m a.s.l.) and 628 mm in the east (Duved, 400 m a.s.l.), and the annual mean temperature is 1.1 °C (Storlien) in the west and 1.3 °C in the east (Duved) based on the statistics during 1961–1990 (Alexandersson et al., 1991). The leading mode of Atlantic sea surface temperature (Atlantic Multi-decadal Oscillation (AMO)) has been found to have impacts on the temperature variability in this region at multi-decadal to century timescales (Sutton and Dong, 2012). The summer temperature variability in this region is quite homogenous. The correlation decay distance of 500–800 km during 1901–2001 is at r = 0.71 ( Björklund, 2014).

Fig. 1. A map showing the selected grid cell (the red dot) of CRU TS 3.22 dataset 2.5° longitude × 2.5° latitude and the area of 12–15°E, 62–64°N (marked by red frame).

3. Data and methods

3.1. Instrumental data

The observed annual and summer temperatures used in this study are derived from monthly mean temperatures at the area of 12–15°E, 62–64°N from CRU TS 3.22 gridded (2.5° longitude × 2.5° latitude) monthly temperature dataset. The area contains 1 grid cell (13.75°E, 63.75°N, the red dot in Fig. 1). The CRU TS 3.22 dataset was based on an archive provided by more than 4000 weather stations distributed around the world and covers the period 1901–2013 (Harris et al., 2014). The latest central Scandinavian temperature reconstructions were derived within the area around the selected grid cell. We selected this area as a case study is due to not only that the scale-dependent analysis makes more sense at the place where tree-ring proxy exists, but also the central Scandinavian temperature variability represents the temperature variability at a large part of the whole Scandinavia. We chose the 2.5° longitude × 2.5° latitude resolution dataset, because the resolution is more comparable with the spatial resolution of PMIP3 climate models than the 0.5° longitude × 0.5° latitude resolution dataset.

3.2. Model simulations

The model data is collected from historical and last millennium simulations performed by 7 climate models under Coupled Model Intercomparison Project Phase 5 (CMIP5). We selected these models, because all the models also have been used to perform last millennium simulations that simulate the global climate variability during the last millennium (850–1850) under PMIP3 using reconstructed forcing data (Schmidt et al., 2012). The detailed information of the climate models was summarised in Table 1. The aim of historical simulations is to simulate true global climate evolution during 1850–2005 by incorporating observed climate forcings following the CMIP5 protocol (Taylor et al., 2012). To facilitate the comparison with observed data, we selected the modelled data from grid cells in the same area (12–15°E, 62–64°N) where the observational data was extracted. Most of the models have only 1 grid cell in the selected area, while models with relatively high-resolution have more than 1 grid cell in the area. The number of grid cells selected in each model was given in Table 1. For the models with more than 1 grid cell, modelled data was derived from the mean value of the data from all selected grid cells. The ensemble mean from the 7 models was calculated by averaging the output (e.g. the relationship between the annual and summer temperatures) from all the models.

Table 1. Information of the 7 CMIP5 climate models.

Model	Institute/Country	Atmosphere resolution	Number of grids in selected area
bcc-csm1.1	BCC/China	128 × 64	1
CCSM4	NCAR/USA	288 × 192	6
GISS-E2-R	NASA GISS/USA	144 × 90	1
HadCM3	MOHC/UK	96 × 73	1
MIROC-ESM	MIROC/Japan	128 × 64	1
MPI-ESM-P	MPI-M/Germany	196 × 98	2
MRI-CGCM3	MRI/Japan	320 × 160	6

Note: The resolution of the atmosphere of the models expressed by the number of longitudinal grids × the number of latitudinal grids.

3.3. Ensemble empirical mode decomposition (EEMD) and correlation analysis

In order to investigate the relationship between the annual and summer temperatures' variability at different timescales, we firstly decomposed the original time series into time-frequency domains using ensemble empirical mode decomposition (EEMD) method (Wu and Huang, 2009), and then quantify the relationship of the two temperatures in each characteristic frequency band using Pearson correlation coefficient (Pearson, 1895).

EEMD is built on empirical mode decomposition (EMD). EMD is an adaptive time-frequency data analysis method. Using this method, a data generated with nonlinear and non-stationary process can be decomposed into a series of empirical modes and a residual. Each of the empirical modes, defined as an intrinsic mode function (IMF), was sifted out using a iteration process when it satisfying the following conditions: 1) in the whole dataset, the number of extrema and the number of zero-crossings (values changes from positive to negative, or from negative to positive) must either equal or differ at most by 1; 2) at any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero (Huang et al., 1998). This method is adaptive and posteriori, so the mode components reflect intrinsic scale characteristics of the original data, and have meaningful physical interpretations (Huang et al., 1998). However, a major drawback of this method is that an IMF which is supposed to reflect the variation at one characteristic scale often consists of signals of widely disparate scale, or a characteristic scale resides in different IMF components (Wu and Huang, 2009). This will weaken the characteristic scale in each IMF. The EEMD is a method further developed from EMD, which overcome the scale separation problem. In this method, the original data is preprocessed by adding white noise, and then is decomposed into IMFs. After many times repetition, the ensemble means of the corresponding IMFs were the final IMFs. Both EMD and EEMD methods have been widely used in geophysical studies (Huang and Wu, 2008 and Ji et al., 2014).

In this study, EEMD was implemented by adding white noise that has 20% of the standard deviation of the original data. The trial was run by 200 times. We chose these parameters since they have been previously demonstrated to possess a good property on decomposition and overcoming mode mixing (Wu and Huang, 2009). The annual and summer temperatures were decomposed into a number of characteristic modes and residuals. The number of the modes depends on the length of the time series. According to the definition of IMF, the mode component is not restricted to a narrow band signal. It can be non-stationary. Despite frequency modulated, each IMF is still located at a relatively narrow frequency band. Since IMFs reflect intrinsic modes of a non-stationary signal, this makes the scale-dependent study having physical meanings. In this study, observed temperature series and historical modelled temperature series were decomposed into 6 IMFs and 1 residual which represent the following frequency bands: 2–4 years, 4–8 years, 8–16 years, 16–32 years, 32–64 years, >64 years. Last millennium temperature series were decomposed into 9 IMFs and 1 residual which represent the following frequency bands: 2–4 years, 4–8 years, 8–16 years, 16–32 years, 32–64 years, 64–128 years, 128–256 years, 256–512 years, 512–1024 years and >1024 years.

3.4. Evaluation approaches

In order to infer the relationship between the annual and summer temperatures during the last millennium, we need the simulated temperature data from a proper model. The model was selected by evaluating its capabilities in replicating 1) the relationship between the observed annual and summer temperatures and 2) the variance of the observed annual and summer temperatures at different timescales during 1901–2005. To quantify the model comparison, three indices were calculated based on the observational and modelled data, and were subsequently used to quantitatively compare the performance of the models. In addition, significance levels of the correlations between the simulated annual and summer temperatures at different timescales were calculated, and then were used to qualitatively evaluate the performance of the models.

The first index, called differences of the correlation coefficients (DCC), was defined as the absolute differences between the modelled and observed annual and summer temperatures' correlation coefficients at different timescales. The closer to zero is the index, the better is the performance of the model. The second index, called differences of variance percentage for annual mean temperature (DVPA), was defined as the absolute differences between the modelled and observed variance percentage of annual mean temperature at different timescales. This index quantifies the performance of a model in replicating the variance percentage at a timescale of annual mean temperature. The variance percentage represents the proportion of the variance of each timescale in the total variance of all timescales. The closer to zero is the index, the better is the performance of the model. The third index, called differences of variance percentage for summer temperature (DVPS), was the same as the second index, but for evaluating the performance for summer temperature. To quantify the mean performance of each index, the ‘absolute mean value’ was defined for each of the three indices. The ‘absolute mean value’ was calculated by averaging the absolute values of all the individual indices (e.g. the indices at all the timescales) for each model. The calculations of the absolute mean values were based on 7 individual indices (6 indices for the 6 timescales and 1 index for raw series before decomposition) for each model. However, all the DVPA and DVPS indices for raw series are 0. Therefore, we did not show these values in Table 4 and Table 5.

The significance levels of the correlations were calculated using Monte-Carlo method. In this method, correlation coefficient was calculated based on two random time series which have the same length and the similar first autocorrelations with the annual and summer temperature series respectively. The procedure was repeated 1000 times to find out the threshold of the correlation coefficient at 5% and 1% significance levels. Using this method, the autocorrelation of the temperature series was considered when calculating the significance level thresholds. Thus, the significance level will be more reliable comparing with the method when only sample size was considered in the calculation, especially for the temperature series at decadal to centurial timescales which have high autocorrelation.

4. Results

4.1. Observed relationships between the annual and summer temperatures

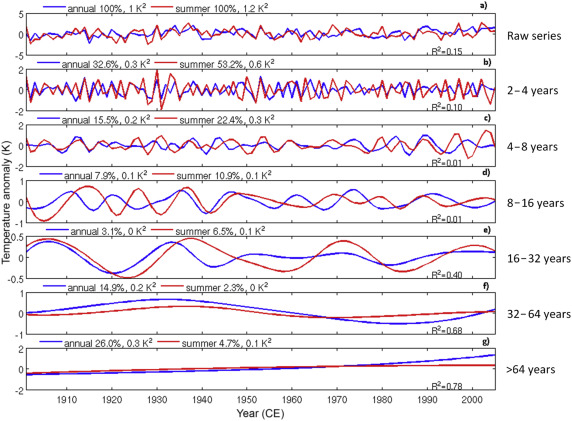
Fig. 2 shows the temporal evolution of the annual and summer temperatures during 1901–2005 in various frequency bands. The raw data before the decomposition are also displayed, which shows that the summer temperature overall has a slightly higher variance than the annual temperature (Fig. 2a). The inter-annual variations of the two temperatures have a pretty low similarity, indicating the overall poor representation of the summer temperature for the annual mean temperature.

Fig. 2. Comparison of the annual mean and summer mean (June–August) temperatures during 1901–2005 at different timescales. Anomalies are relative to 1961–1990 mean. The variances and variance percentages of the annual and summer temperatures were given for each timescale band. The explained variances between the annual and summer temperatures are also given at bottom-right corner for each timescale band.

Looking at the variances at different timescale bands, it becomes clear that the summer temperature has a much higher (93.0% of the total variance) variability in the band 2–32 years than the annual temperature (59.1% of the total variance). On the longer timescales, however, the annual temperature shows higher variability than that of the summer temperature. In the band of >32 years, the summer temperature occupies 7.0% of the total variance, while the annual temperature takes 40.9%, indicating that the long-term (almost equivalent to a linear trend in this case) changes of the annual temperatures are much more important than the changes in the summer temperatures.

The timescale-dependent relationships between the two temperatures are shown in Fig. 2b–g. There is an overall increasing trend in the linkages with the timescales, although exception exists for the 4–16 years timescales which are less than but close to decadal scale. For the 4–8 years timescales, the two time series have opposite variation during 1920–1950, while some out of phase variations can be observed during 1965–1985. For the 8–16 years timescales, the two time series are rarely in phase. On the 2–16 years timescales, the summer shares of the total variances are all greater than those for the annual mean. On the >16 years timescales, the variations become pretty similar although the percentages of the variances are very different. For the 16–32 years timescales, the portion of the summer variability is larger than that of the annual mean, whereas the annual variation has a much larger share of the total variable than that of summer for the >32 years timescales.

These results show that the summer variation dominates the temperature variability on the short timescales, while the annual variation has larger contribution to the long timescales. There is a very low similarity in the band 4–16 years. Much of the similarity between the two temperatures is in the band 2–4 years at which the highest variability exist. On the longer timescales (starting from 16 years), the similarity increases with the increasing timescales. Although the degree of freedom of the data decreases with the increasing timescales, the increasing trend of the similarity can still be considered robust. Thus, the long-term changes of the two temperatures are pretty similar, although the magnitudes can be different.

4.2. Climate model evaluation

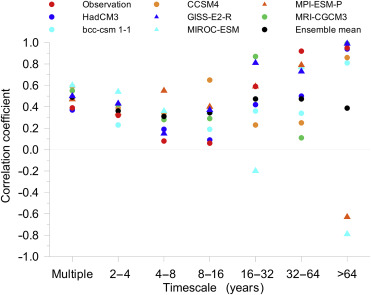
Fig. 3 shows the correlation coefficients as a function of timescales for the observed and simulated annual and summer temperatures. The models show different correlation coefficients between the two temperatures at different timescales. The ranges of the differences overall increase in the linkages with the timescales, which implicates the models have more divergent capabilities in replicating the relationships at the long timescales than that at the short timescales. The model MIROC-ESM and MPI-ESM-P even show opposite trends between the annual and summer temperatures which is not the case in reality. The model MIROC-ESM shows also a weak capability in replicating the relationship at the 16–32 years timescales. At the 4–16 years timescales, all the models overestimate the relationship between the annual and summer temperatures, while at the 32–64 years timescales all the models underestimate the relationship. The model ensemble mean (black dots) does not show a superior performance in replicating the relationships at different timescales.

Fig. 3. Correlation coefficients between the decomposed annual and summer temperature series.

The results of significance test are shown in Table 2. The observed annual and summer temperatures show positively and significantly correlations (at 1% significance level) at the 2–4 years, >32 years and multiple (the raw series before decomposition) timescales. All the models show the same significance level with the observations at the multiple timescales. However, no model shows the same significance level with the observations at all the individual timescales. In addition to the models of MIROC-ESM and MPI-ESM-P which show negative relationship between the annual and summer temperatures, and the model of HadCM3 which does not show significant correlation at any individual timescales, it is difficult to judge the performance of the rest of the models in the significance test.

Table 2. Significance test between the annual and summer temperatures at different timescales.

Data resource	Timescale (years)
	2–4	4–8	8–16	16–32	32–64	>64	Raw
Observation	***				***	***	***
bcc-csm1.1	*	*				*	***
CCSM4	***	***	*			***	***
GISS-E2-R	***			***		***	***
HadCM3							***
MIROC-ESM	***	***		−	*	−	***
MPI-ESM-P	***	***			*	*−	***
MRI-CGCM3	***	*		***		***	***

Note: *** indicates 1% significance levels; * indicates 5% significance levels; −indicates negative correlation.

The DCC index in Table 3 indicate that the models of GISS-E2-R, bcc-csm1.1, HadCM3 and MRI-CGCM3 have better performance in replicating the observed annual and summer temperature relationships comparing with other 3 models. The mean absolute differences of the correlation coefficients in the 4 models are 0.15, 0.20, 0.21 and 0.26 respectively. However, looking at the performance at the individual timescales, the 4 models show different expertise. The model GISS-E2-R shows good performance at the 4–8 years and >64 years timescales; the model bcc-csm1.1 shows good performance at the 2–4 years and multiple timescales; the model HadCM3 shows good performance at the 4–8 years, 16–32 years and multiple timescales; the model MRI-CGCM3 shows good performance at the 2–4 years and >64 years timescales.

Table 3. Differences of the correlation coefficients (DCC) between the modelled and observed annual and summer temperatures.

Models	Timescale (years)
	2–4	4–8	8–16	16–32	32–64	>64	Raw	Abs mean
bcc-csm1.1	−0.09	0.26	0.13	−0.23	−0.58	−0.14	0.00	0.20
CCSM4	0.07	0.26	0.59	−0.36	−0.67	−0.09	0.20	0.32
GISS-E2-R	0.11	0.07	0.31	0.22	−0.19	0.04	0.11	0.15
HadCM3	−0.14	0.07	0.10	0.06	−0.60	−0.47	−0.06	0.21
MIROC-ESM	0.22	0.28	0.29	−0.79#	−0.15	−1.74#	0.21	0.53
MPI-ESM-P	0.02	0.47	0.34	0.00	−0.13	−1.58#	0.08	0.37
MRI-CGCM3	0.10	0.20	0.23	0.28	−0.81	0.04	0.16	0.26

Note: # indicates the differences are different in signs. The closer to zero is the index, the better is the performance of the model. ‘Abs mean’ means absolute mean value.

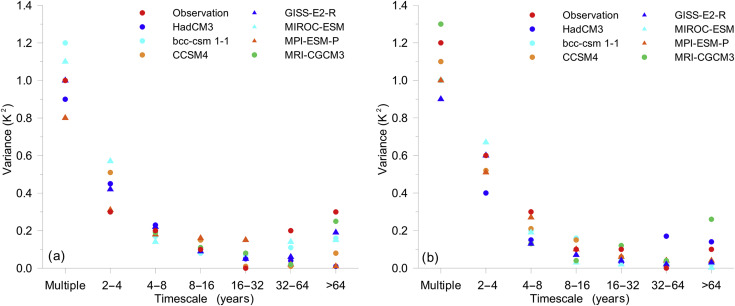
Fig. 4 shows the variance of the observed and modelled annual and summer mean temperatures as a function of timescales. Comparing with the variance of the observed annual mean temperature, the simulated temperature in all the models underestimate the variance at the >32 years timescales. At the 4–16 years timescales and multiple timescales (raw series), the models either overestimate or underestimate the variance. At the 2–4 years and 16–32 years timescales, all the models overestimate the variance. For the summer temperature, most of the models underestimate the variance of the temperature at the 2–32 years and multiple timescales, and all the models overestimate the variance at the 32–64 years timescales.

Fig. 4. Observed and simulated variance of the (a) annual and (b) summer temperatures as a function of timescales.

To quantify the performance of the models in replicating the observed temperature variance at different timescales, the indices of DVPA and DVPS were calculated for each model at different timescales. The results were summarised in Table 4 and Table 5. In average, the model GISS-E2-R, bcc-csm1.1, MRI-CGCM3 and MIROC-ESM have better performance in replicating the observed annual temperature variance percentage at different timescales comparing with other 3 models. However, GISS-E2-R shows better performance at the 8–32 years timescales than the other timescales; bcc-csm1.1 shows better performance at the 4–16 years timescales; MRI-CGCM3 shows better performance at the >64 years, 2–4 years and 8–16 years timescales; MIROC-ESM shows better performance at the 8–32 years timescales. For replicating observed summer temperature variance percentage at the different timescales, the model MPI-ESM-P, CCSM4, bcc-csm1.1 and GISS-E2-R have better performance. However, MPI-ESM-P is good at replicating the variance percentage at the 16–32 years and >64 years timescales; CCSM4, bcc-csm1.1 and GISS-E2-R are all good at replicating the variance percentage at the 16–64 years timescales.

Table 4. Differences of variance percentage (DVPA) at each timescale between the modelled and observed annual mean temperatures.

Model	Timescale (years)
	2–4	4–8	8–16	16–32	32–64	>64	Abs mean
bcc-csm1.1	12.5	−0.1	−1.6	2.9	−4.5	−9.2	4.4
CCSM4	19.2	4.7	6.8	−1.8	−13.1	−15.7	8.8
GISS-E2-R	7.0	5.5	0.2	1.4	−8.8	−5.3	4.0
HadCM3	14.5	9.1	7.7	2.2	−10.2	−23.4	9.6
MIROC-ESM	15.6	−3.3	−0.4	1.1	−2.4	−10.7	4.8
MPI-ESM-P	2.8	6.4	10.8	15.2	−12.4	−22.7	10.0
MRI-CGCM3	−2.6	4.5	2.6	5.6	−12.3	2.3	4.4

Note: The closer to zero is the index, the better is the performance of the model. ‘Abs mean’ means absolute mean value. DVPA for raw series does not show in the table, since all of them are 0.

Table 5. Differences of variance percentage (DVPS) at each timescale between the modelled and observed summer temperatures.

Model	Timescale (years)
	2–4	4–8	8–16	16–32	32–64	>64	Abs mean
bcc-csm1.1	4.6	−4.5	4.0	−2.0	0.4	−2.4	2.6
CCSM4	−4.0	−3.2	2.9	−0.1	−0.5	4.8	2.2
GISS-E2-R	15.1	−8.8	−3.3	−1.1	−0.6	−1.3	4.3
HadCM3	−11.2	−8.4	−0.8	−3.3	14.4	9.3	6.8
MIROC-ESM	18.9	−3.4	−7.9	−4.3	1.0	−4.3	5.7
MPI-ESM-P	−2.7	3.5	−1.5	−0.5	1.6	−0.4	1.5
MRI-CGCM3	−2.4	−12.3	−7.4	4.0	0.5	17.6	6.3

Note: The closer to zero is the index, the better is the performance of the model. ‘Abs mean’ means absolute mean value. DVPS for raw series does not show in the table, since all of them are 0.

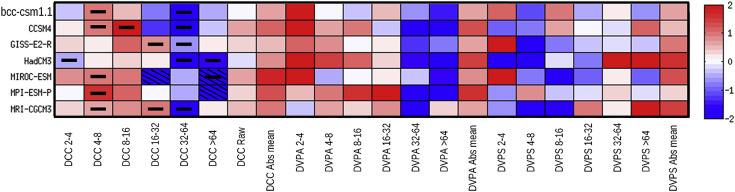
To facilitate comparison of the model performance, the three evaluation indices were standardised, and then summarised in Fig. 5. The results of the significance-test comparison were also presented in Fig. 5. The standardisation which was done by rescaling the evaluation indices enable putting the three indices in one colour table. However, the standardisation did not change the sign of the indices, so the direction diverse from observational values can also be judged according to the colour table. Hatched area (with oblique lines) in Fig. 5 indicates the correlation between the modelled annual and summer temperatures at that timescale is negative. The significance level of the correlation between the modelled annual and summer temperatures was compared with the significance level of the observed relationship at the different timescales. If the modelled (observed) relationship is at 5% significance level and the observed (modelled) relationship is below 5% significance level, then the corresponding DDC index grid in Table 5 was marked by a bold short line.

Fig. 5. Three standardised indices and the significance-test results of the model performance. Rows and columns represent individual models and indices, respectively. Hatched area (with oblique lines) means the correlation between the annual and summer temperatures is negative at that timescale. Bold short lines indicate that the significance-test result in that model at that timescale is different from the observations (e.g. the modelled relationship are significant (non-significant), but the observed relationship are non-significant (significant)). The closer to zero is the index, the better is the performance of the model. The values of the DCC index (given in Table 3), DVPA index (given in Table 4) and DVPS index (given in Table 5) were standardised respectively by being divided by the mean of the absolute mean DCC values (the last column in Table 3), the mean DVPA values (the last column in Table 4) and the mean DVPS values (the last column in Table 5).

From Fig. 5, we see that no model has superior performance for all the evaluation criterions. However, regarding DCC index, GISS-E2-R has the best performance since the value of ‘DCC absolute mean’ is the smallest among all the models. According to the same criterion, GISS-E2-R has the best performance in replicating the variance percentage of the annual mean temperature, and MPI-ESM-P has the best performance in replicating the variance percentage of the summer temperature. However, the fatal disadvantage of MPI-ESM-P is that its modelled annual and summer temperature trends are different in sign which is seriously misestimate the observed annual and summer temperature relationship. Beside MPI-ESM-P, CCSM4, bcc-csm1.1 and GISS-E2-R also have relatively good performance in replicating the summer temperature variance percentage. Therefore, GISS-E2-R was chosen to infer the annual and summer temperature relationship for the last millennium.

4.3. Simulated relationships between the annual and summer temperatures during the last millennium

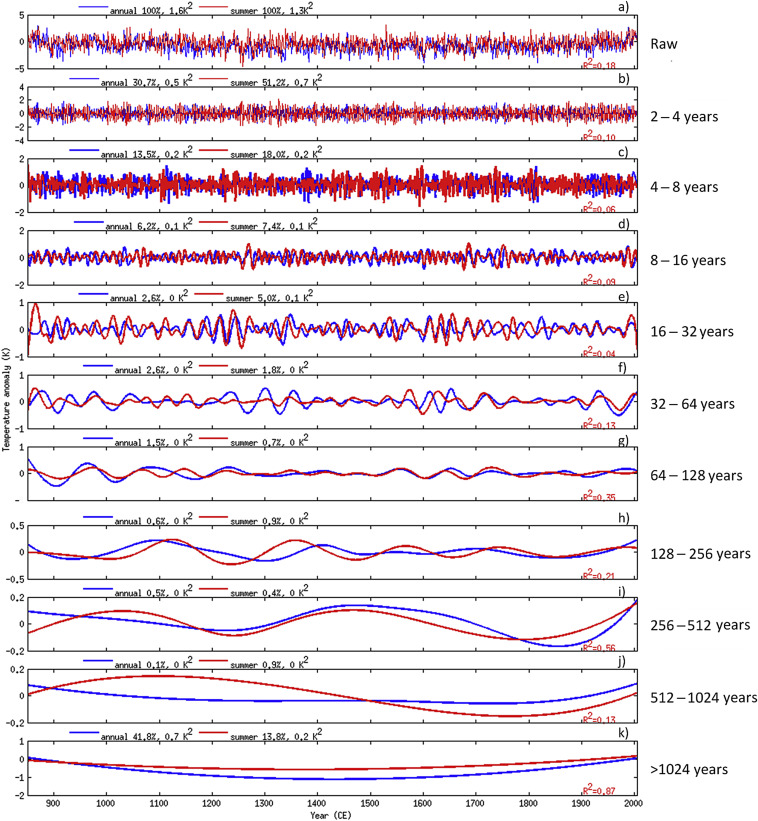
Fig. 6 shows the temporal evolution of the modelled (using GISS-E2-R Model r1i1p121 simulation with all available forcings under PMIP3 (Schmidt et al., 2006 and Schmidt et al., 2012)) annual and summer temperatures during 850–2005 in various frequency bands. The raw data before the decomposition shows that the annual temperature overall has a slightly higher variance than the summer temperature. This result is different from those based on the observed annual and summer temperatures during 1901–2005, in which summer temperature has higher variance than annual mean temperature. The inter-annual variations of the two temperatures still have a pretty low similarity, indicating the overall poor representation of the summer temperature for the annual mean temperature during the last millennium.

Fig. 6. Comparison of the annual and summer (June–August) GISS-E2-R modelled temperatures (anomalies relative to 1961–1990 means) during 850–2005 at different timescales.

Looking at the variances as a function of frequency band, we see that, during the last millennium, the summer temperature has also a much higher (81.6% of the total variance) variability in the band of 2–32 years than the annual temperature (53.0% of the total variance). At the 32–1024 years timescales, both the annual and summer temperatures have relatively low variability. At the >1024 years timescales, however, the annual temperature shows much higher variability than that of the summer temperature. The summer temperature occupies 13.8% of the total variance, while the annual temperature takes 41.8%, indicating that the long-term (almost equivalent to a linear trend in this case) changes of the annual temperatures are much more significant than the changes in the summer temperatures during the last millennium.

The timescale-dependent relationships between the two temperatures are shown in Fig. 6b–k. Relatively high correlations still appear at the long timescales such as 64–128 years, 256–512 years and >1024 years than at the short timescales such as 2–64 years. For the 512–1024 years timescales, the two time series have opposite variation during 850–1500. For the 128–256 years timescales, both of the two temperatures show mismatch to each other during the whole millennium. For the 32–64 years timescales, the summer temperature has higher variance than the annual mean temperature during 1100–1200, while the annual mean temperature has much higher variance than the summer temperature during 1200–1400. For the 16–32 years timescales, distinguished variability appear during 1200–1300 and 1600–1700, and there is also obvious mismatch between the two temperatures during 1700–1850. For the 4–32 years timescales, there are rather low relationships between the annual and summer temperatures during the last millennium.

These results also show that the summer variation dominates the temperature variability on short timescales, while the annual variation has larger contribution to the long timescales for the last millennium. There is a very low similarity in the bands of 4–32 years. Much of the similarity between the two temperatures is in the band of 2–4 years at which the highest variability exist. On the longer timescales (starting from 32 years), relatively high similarity appear at the 64–128 years, 256–512 years and >1024 years timescales, while at the 32–64 years, 128–256 years and 512–1024 years timescales, the similarity is quite low.

5. Discussion

5.1. The weak relations at the 4–16 years timescales

The correlations between the annual and summer temperatures during the 20th century have an overall increasing trend in the linkages with the timescales. This can be partly explained by a decrease of degree of freedom due to increasing temperature autocorrelation at the longer timescales. However, at the 4–16 years timescales, the annual and summer temperatures show really weak relationships. Previous studies indicate that the temperature variability in central Sweden is mainly controlled by NAO with its strongest influences in winter and weakest influences in summer (Chen and Hellström, 1999, Busuioc et al., 2001, Rodwell et al., 1999 and Rodwell and Folland, 2002). Therefore, the NAO-related temperature variability at inter-annual to decadal timescales in summer may have lowest variance comparing with the NAO-related temperature variability at other seasons. Moreover, Folland et al. (2009) analysed summertime extratropical North Atlantic sea level pressure, and found a new robust synoptic circulation pattern (SNAO) which has some influences on summer temperature variability in central Sweden. The circulation pattern (SNAO) is parallel to but different from the NAO (Folland et al., 2009). Therefore, it may cause more divergent variability between the annual and summer temperatures at inter-annual to decadal timescales.

Actually, not only the divergence between the annual and summer temperatures, temperature variability in Sweden at different months can also be different. Moberg and Alexandersson (1997) found that there is no correlation after lags longer than 2 months for the temperature variability over Sweden, and thus a poor persistence in the region. Chen and Hellström (1999) analysed sequential 2-month correlation of temperature data in Sweden, and found that the persistence of the synoptic circulation in central Sweden is generally lower than for the southern part. Therefore, to fully understand the temperature variability at the short timescales (e.g. 2–32 years) in Sweden, more detailed studies on the relationship between the temperature variability and circulation patterns need to be done (Chen, 2000).

5.2. The climate model evaluation

In this study, seven climate models were evaluated regarding their capabilities in replicating the relationship between the annual and summer temperatures in central Sweden and the variance percentage of the temperatures at different timescales. To intercompare the capabilities of the climate models, three indices were defined to quantify the performance of the climate models. Although the GISS-E2-R overall has the best performance, it does not always show the best performance at every timescale. For instance, it shows much closer relationship between the annual and summer temperatures at the 8–32 years timescales, and much weaker relationship at the 32–64 years timescales than the observed data. Therefore, caution is needed when using the modelled data to interpolate the relationships between these timescales.

Previous studies have confirmed that climate models are able to capture the general spatial and temporal features of NAO (Gerber et al., 2008), but there are substantial differences in the spatial patterns among different models (Casado and Pastor, 2012 and Handorf and Dethloff, 2012). Moreover, some aspects of NAO features may misestimate by some models, such as northward shift of low-pressure center of NAO (Zhou et al., 2000). Some climate models may substantially overestimate persistence of the circulation pattern at sub-seasonal and seasonal timescales (Gerber et al., 2008). All these studies indicate the deficiency of climate models on simulating the circulation variability (Osborn et al., 1999). From our results, we infer that the high correlations between the two temperatures at the 8–32 years timescales is due to the close relationship between the summer temperature and the NAO index in the GISS-E2-R model simulation. We should also notice that the overestimation of the strength in the relationships between the annual and summer temperatures at inter-annual to decadal timescales exhibit not only in GISS-E2-R model simulation, but also in all other 6 models. At the 32–64 years timescales, all the models underestimate the relationships between the annual and summer temperatures. The temperature variability in central Sweden at multi-decadal timescale is supposed to be controlled by the long-term variability of Atlantic sea surface temperature (AMO) (Sutton and Dong, 2012). We infer that the underestimate of the relationship between the annual and summer temperatures reflects either a deficiency of the models in simulating the temporal pattern of AMO or an inadequate representation of AMO with regard to the linkage with the temperature variability in central Sweden. From the views of model development, it is also interesting to find out the reason why the two temperatures show a negative relationship at the 16–32 years timescales in MIROC-ESM and >64 years timescales in MIROC-ESM and MPI-ESM-P. The significance-test results also support that most of the models overestimate the strength of the relationship between the annual and summer temperatures at the 4–8 years timescales.

The variance of the modelled annual mean temperature was compared with the variance of the observed annual mean temperature at the different timescales. In this study, all the models show higher variances than the observed ones at the 2–4 years timescales. The 2–4 years is a typical timescale when the global temperature response to a volcanic eruption. Linderholm et al. (2014) have noted that the cooling response in Fennoscandia following a volcanic eruption could remain for up to 4 years. Moreover, previous studies have shown that volcanic eruption induced surface cooling derived from climate model simulations is much stronger than the cooling seen in tree-ring proxies. The reasons were attributed to both underestimate of cooling in proxies (Mann et al., 2012 and Büntgen et al., 2014) and overestimate of modelled volcanic eruption forcings (Marotzke and Forster, 2015). However, the results in this study suggest that the mismatch should be partly attributed to the overestimate of the annual mean temperature variance at the 2–4 years timescales in climate models, at least for the temperature response in central Sweden, although a recent study suggests the excluding of nonlinear aerosol microphysics could be the reason for a unusual-cooling response to volcanic eruptions in climate models (Stoffel et al., 2015). Therefore, more convincing explanations for the overestimate remain to be the tasks for the future research. Another interesting point of our results is that all the models underestimate the variance of the annual mean temperature at >32 years timescales. This result is also in line with the previous findings that the variability of proxy-based temperature reconstructions are usually larger than the variability of the modelled temperature variation at centurial to multi-centurial timescales (IPCC, 2013).

6. Summary and conclusions

The observed annual and summer temperatures from central Sweden were decomposed into IMFs and residuals at the different timescales which were subsequently used to investigate the linkage between the two temperatures during 1901–2005. Using the established timescale-dependent characteristics, seven AOGCMs were evaluated regarding their capabilities in replicating variance percentages at the different timescales for both the annual and summer temperatures and the relationships between the annual and summer temperatures. Using the model GISS-E2-R which has the best performance regarding these criterions, the relationships between the annual and summer temperatures in central Sweden during the last millennium (850–2005) were investigated.

Based on the analyses, the following conclusions can be drawn:

• The linkage between the observed annual and summer temperatures during 1901–2005 strongly depends on timescales. The relationship is generally weak for the short timescales and strong for the long timescales. Closer relationships between the two observed temperatures exist for the long timescales (>32 years) than those shorter than 16 years. Practically no relationship is found for the 4–16 years timescales. This indicates that mechanisms dominating the summer variability at the 4–16 years timescales are significantly different from those for the rest of the year.
• The observed annual and summer temperatures have dominant variances at the 2–4 years timescales, but the summer temperature variability at that timescale is much higher than the annual variability. For the long timescales (>32 years), the difference in the variance between the two temperatures are fairly large too, but the variances of the annual temperature are much larger than those of the summer temperature.
• The climate models examined generally overestimate the linkage between the annual and summer temperatures at the 2–16 years timescales and underestimate the linkage at >32 years timescales. The climate models overestimate the variance of the annual mean temperature at the 2–4 years timescales in this region; this could be one of the reasons why the present climate models have larger annual mean temperature cooling in response to major volcanic eruptions than the cooling found in proxy data. All the models underestimate the annual mean temperature variance at >32 years timescales, which is in line with the previous findings that climate models usually have smaller variances of global mean temperature at centurial to multi-centurial timescales than proxy-based temperature reconstructions.
• The relationship between the annual and summer temperatures during the last millennium (850–2005) is also generally weak for the short timescales and strong for the long timescales. Closer relationships between the two temperatures exist for the 64–128 years, 256–512 years and >1024 years timescales than those <32 years. The summer temperature has dominant variance at the 2–4 years timescales, while the annual temperature has dominant variance at the millennium timescales. The annual and summer temperatures show variable relationship along the time, which could implicate changes of climate regime in central Sweden during the last millennium.
• Overall, summer temperature variability does not seem to be a good reflection of the annual mean temperature variability for the study region.

Acknowledgements

We acknowledge the World Climate Research Programmes Working Group on Coupled Modelling for making available the modelling output. We also thank for the U.S. Department of Energys Program for Climate Model Diagnosis and Intercomparison providing coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. We acknowledge Dr. Wu Zhao-Hua for his Matlab code for EEMD processing. We also acknowledge two anonymous referees for helpful comments which help to improve the quality of this paper a lot. This research contributes to the strategic research areas Modelling the Regional and Global Earth system (MERGE), and Biodiversity and Ecosystem services in a Changing Climate (BECC) and to the PAGES2K initiative.

References

1. Alexandersson et al., 1991 H. Alexandersson, C. Karlström, S. Larsson-McCann; Temperature and Precipitation in Sweden 1961–90. Smhi Meteorologi. 81; (1991), pp. 1–88
2. Björklund, 2014 J. Björklund; Tree-rings and Climate-Standardization, Proxy-development, and Fennoscandian Summer Temperature History; University of Gothenburg, Sweden (2014)
3. Braconnot et al., 2012 P. Braconnot, S.P. Harrison, M. Kageyama, et al.; Evaluation of climate models using palaeoclimatic data; Nat. Clim. Change, 2 (6) (2012), pp. 417–424
4. Busuioc et al., 2001 A. Busuioc, D. Chen, C. Hellström; Temporal and spatial variability of precipitation in Sweden and its link with the large scale atmospheric circulation; Tellus Ser. A-Dynamic Meteorol. Oceanogr., 53 (3) (2001), pp. 348–367
5. Büntgen et al., 2014 U. Büntgen, L. Wacker, K. Nicolussi, et al.; Extraterrestrial confirmation of tree-ring dating; Nat. Clim. Change, 4 (6) (2014), pp. 404–405
6. Casado and Pastor, 2012 M.J. Casado, M.A. Pastor; Use of variability modes to evaluate AR4 climate models over the Euro-Atlantic region; Clim. Dyn., 38 (2012), pp. 225–237
7. Chen, 2000 D. Chen; A monthly circulation climatology for Sweden and its application to a winter temperature case study; Int. J. Climatol., 20 (10) (2000), pp. 1067–1076
8. Chen and Hellström, 1999 D. Chen, C. Hellström; The influence of the North Atlantic Oscillation on the regional temperature variability in Sweden: spatial and temporal variations; Tellus, 51 (4) (1999), pp. 505–516
9. Folland et al., 2009 C.K. Folland, J. Knight, H.W. Linderholm, et al.; The summer North Atlantic Oscillation: past, present, and future; J. Clim., 22 (5) (2009), pp. 1082–1103
10. Gerber et al., 2008 E.P. Gerber, L.M. Polvani, D. Ancukiewicz; Annular mode time scales in the Intergovernmental Panel on Climate Change Fourth Assessment Report models; Geophys. Res. Lett., 35 (22) (2008), pp. 113–130
11. Grudd et al., 2002 H. Grudd, K.R. Briffa, W. Karlén, et al.; A 7400-year tree-ring chronology in northern Swedish Lapland: natural climatic variability expressed on annual to millennial timescales; Holocene, 12 (6) (2002), pp. 657–665
12. Handorf and Dethloff, 2012 D. Handorf, K. Dethloff; How well do state-of-the-art atmosphere-ocean general circulation models reproduce atmospheric teleconnection patterns?; Tellus Ser. A-Dynamic Meteorol. Oceanogr., 64 (12) (2012), pp. 1449–1458
13. Harris et al., 2014 I. Harris, P.D. Jones, T.J. Osborn, et al.; Updated high-resolution grids of monthly climatic observations–the CRU TS3.10 Dataset; Int. J. Climatol., 34 (3) (2014), pp. 623–642
14. Helama et al., 2002 S. Helama, M. Lindholm, M. Timonen, et al.; The supra-long Scots pine tree-ring record for Finnish Lapland: part 2, interannual to centennial variability in summer temperatures for 7500 years; Holocene, 12 (6) (2002), pp. 681–687
15. Huang and Wu, 2008 N.-E. Huang, Z. Wu; A review on Hilbert-Huang transform: method and its applications to geophysical studies; Rev. Geophys., 46 (2) (2008), p. 2008
16. Huang et al., 1998 N.-E. Huang, Z. Shen, S.-R. Long, et al.; The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis; Proc. R. Soc. Lond. A Math. Phys. Eng. Sci., 454 (1971) (1998), pp. 903–995
17. IPCC, 2013 IPCC; Climate Change 2013: The Physical Science Basis; Cambridge University Press, Cambridge (2013)
18. Ji et al., 2014 F. Ji, Z. Wu, J. Huang, et al.; Evolution of land surface air temperature trend; Nat. Clim. Change, 4 (6) (2014), pp. 462–466
19. Linderholm and Gunnarson, 2005 H.W. Linderholm, B.E. Gunnarson; Summer temperature variability in central Scandinavia during the last 3600 years; Geogr. Ann., 87 (1) (2005), pp. 231–241
20. Linderholm et al., 2010 H.W. Linderholm, J.A. Björklund, K. Seftigen, et al.; Dendroclimatology in Fennoscandia–from past accomplishments to future potential; Clim. Past, 6 (1) (2010), pp. 93–114
21. Linderholm et al., 2014 H.W. Linderholm, J. Björklund, K. Seftigen, et al.; Fennoscandia revisited: a spatially improved tree-ring reconstruction of summer temperatures for the last 900 years; Clim. Dyn., 45 (3) (2014), pp. 933–947
22. Mann et al., 2012 M.E. Mann, J.D. Fuentes, S. Rutherford; Underestimation of volcanic cooling in tree-ring-based reconstructions of hemispheric temperatures; Nat. Geosci., 5 (3) (2012), pp. 202–205
23. Mann et al., 2009 M.E. Mann, Z. Zhang, S. Rutherford, et al.; Global signatures and dynamical origins of the Little Ice Age and Medieval Climate Anomaly; Science, 326 (5957) (2009), pp. 1256–1260
24. Marcott et al., 2013 S.A. Marcott, J.D. Shakun, P.U. Clark, et al.; A reconstruction of regional and global temperature for the past 11,300 years; Science, 339 (6124) (2013), pp. 1198–1201
25. Marotzke and Forster, 2015 J. Marotzke, P.M. Forster; Forcing, feedback and internal variability in global temperature trends; Nature, 517 (7536) (2015), pp. 565–570
26. Moberg and Alexandersson, 1997 A. Moberg, H. Alexandersson; Homogenization of Swedish temperature data. Part II: homogenized gridded air temperature compared with a subset of global gridded air temperature since 1861; Int. J. Climatol., 17 (1) (1997), pp. 35–54
27. Osborn et al., 1999 T.J. Osborn, K.R. Briffa, S.F. Tett, et al.; Evaluation of the North Atlantic Oscillation as simulated by a coupled climate model; Clim. Dyn., 15 (9) (1999), pp. 685–702
28. Pearson, 1895 K. Pearson; Notes on regression and inheritance in the case of two parents; Proc. R. Soc. Lond., 58 (1895), pp. 240–242
29. Rodwell and Folland, 2002 M. Rodwell, C. Folland; Atlantic air–sea interaction and seasonal predictability; Q. J. R. Meteorol. Soc., 128 (583) (2002), pp. 1413–1443
30. Rodwell et al., 1999 M. Rodwell, D. Rowell, C. Folland; Oceanic forcing of the wintertime North Atlantic Oscillation and European climate; Nature, 398 (6725) (1999), pp. 320–323
31. Schmidt et al., 2006 G.A. Schmidt, R. Ruedy, J.E. Hansen, et al.; Present-day atmospheric simulations using GISS ModelE: comparison to in situ, satellite, and reanalysis data; J. Clim., 19 (2) (2006), pp. 153–192
32. Schmidt et al., 2012 G.A. Schmidt, J.H. Jungclaus, C.M. Ammann, et al.; Climate forcing reconstructions for use in PMIP simulations of the Last Millennium (v1. 1); Geosci. Model Dev., 5 (2012), pp. 185–191
33. Stoffel et al., 2015 M. Stoffel, M. Khodri, C. Corona, et al.; Estimates of volcanic-induced cooling in the Northern Hemisphere over the past 1,500 years; Nat. Geosci., 8 (2015), pp. 784–788
34. Sutton and Dong, 2012 R.T. Sutton, B. Dong; Atlantic Ocean influence on a shift in european climate in the 1990s; Nat. Geosci., 5 (11) (2012), pp. 788–792
35. Sutton et al., 2015 R. Sutton, E. Suckling, E. Hawkins; What does global mean temperature tell us about local climate?; Philos. Trans. R. Soc. A, 373 (2054) (2015), p. 20140426
36. Taylor et al., 2012 K.E. Taylor, R.J. Stouffer, G.A. Meehl; An overview of CMIP5 and the experiment design; Bull. Am. Meteorol. Soc., 93 (4) (2012), pp. 485–498
37. Wu and Huang, 2009 Z. Wu, N.-E. Huang; Ensemble empirical mode decomposition: a noise-assisted data analysis method; Adv. Adapt. Data Anal., 1 (01) (2009), pp. 1–41
38. Zhang et al., 2015 P. Zhang, H.W. Linderholm, B.E. Gunnarson, et al.; 1200 years of warm-season temperature variability in central Fennoscandia inferred from tree-ring density; Clim. Past Discuss., 11 (1) (2015), pp. 489–519
39. Zhou et al., 2000 T. Zhou, X. Zhang, Y. Yu, et al.; The North Atlantic Oscillation simulated by versions 2 and 4 of IAP/LASG GOALS Model; Adv. Atmos. Sci., 17 (4) (2000), pp. 601–616