Removing non visible objects in scenes of clusters of particles

Resumen

El objeto de este trabajo es resolver, en parte, la problemática de la visualización de conglomerados de partículas resultantes de métodos numéricos en la ingeniería. Se han desarrollado dos métodos para la eliminación de partículas no visibles desde cualquier punto de observación de la cámara. Estos se distinguen según el tipo de información disponible: modelos de partículas con información del contorno (malla de superficie) y modelos sin información del contorno (métodos sin mallas). En ambos casos, los resultados son buenos, pues se logra eliminar gran cantidad de partículas que no influyen en la imagen final.

Abstract

The aim of this paper is to partially solve the problem of visualization of clusters of particles resulting from numerical methods in engineering. Two methods for removing non-visible particles from some view point of the camera were developed. These are divided depending on the type of information available: particle systems with contour information (surface mesh) and particle systems without contour information (methods without mesh). In both cases, the results are very good, it is achieved removing large amount of particles that do not affect the final image, permitting interact with the results of numerical methods.

Palabras clave

Métodos numéricos ; Visualización ; Conglomerados de partículas ; Técnicas de aceleración de la visualización

Keywords

Numerical methods ; Visualization ; Clusters of particles ; Speed-up techniques

1. Introducción

En la aplicación del método de los elementos discretos (DEM) es necesario realizar una fase previa, denominada fase de empaquetamiento . En esta etapa se generan partículas por todo el dominio objeto de estudio. Las cantidades de partículas obtenidas para realizar simulaciones a escala microestructural son significativas en cuanto a su cantidad. Los datos obtenidos de la aplicación de estos métodos pueden llegar a ser del orden de los millones de partículas y, en espacio de disco, gigas de información.

Antes de desarrollar una simulación utilizando el DEM, es necesario analizar el comportamiento de ciertas propiedades del empaquetamiento, tales como la densidad local y global o la distribución espacial, el radio máximo o mínimo, o si la generación se ajusta a la geometría del medio estudiado, entre otras, y tras la simulación es necesario estudiar los resultados.

La gran cantidad de datos de las generaciones obtenidas dificulta, en gran medida, la visualización de propiedades, por lo que es útil aplicar filtros con el objetivo de eliminar datos sin repercusión visual, y con ello mejorar el tiempo requerido para la obtención de las imágenes y lograr interaccionar, en tiempo real, con la representación del modelo de partículas. La determinación de la visibilidad y/o la simplificación de una escena es un problema fundamental en la computación gráfica desde sus inicios.

2. Aceleración de la visualización de grandes volúmenes de partículas

El desafío principal que afrontan los sistemas de generación de imágenes¹ en tiempo real es proporcionar un frame rate adecuado, ² incluso para los modelos más complejos en 3D. El hardware se ha desarrollado enormemente en los últimos años, permitiendo la generación de imágenes de varios millones de primitivas gráficas en segundos. Además, el hardware gráfico cada vez es más programable, con lo cual ofrece más realismo en las representaciones. Por otra parte, debido al interés creciente por lograr un mayor detalle y realismo, la complejidad de los modelos es cada vez mayor, de modo que las representaciones son tan complejas que no pueden ser visualizadas de manera interactiva o incluso en tiempo real. Por tales motivos, la aceleración de la visualización sigue siendo un tema muy tratado en computación gráfica [1] .

Una manera de obtener un frame rate elevado consiste en reducir la complejidad de la imagen a representar. Existen muchos algoritmos y todos se basan en algunas de las estrategias siguientes [1] :

• La optimización de los cuellos de botella en el proceso de visualización, como resultado de la complejidad del comportamiento de los drivers y hardwares gráficos, puede agilizar la visualización.
• El cálculo de visibilidad permite eliminar partes de la representación invisibles desde el punto de vista del observador, que no tendrán que ser procesadas por el hardware gráfico.
• La simplificación de la geometría cuando partes de la representación se encuentran a una distancia tal que no contribuyen mucho a la imagen final.
• Pueden utilizarse las representaciones basadas en imágenes si no es factible simplificar la geometría.

Los algoritmos para acelerar el proceso de visualización de los gráficos en las computadoras se presentan y explican en [2] . Las técnicas para eliminar objetos dentro de una representación, la utilización de impostores gráficos y las técnicas de nivel de detalle son de las más conocidas y aplicadas al efecto.

2.1. Técnicas para seleccionar objetos visibles a partir de una representación

Cuando miramos un objeto desde un ángulo determinado, solo podemos observar parte de este. Si tomamos como ejemplo un cubo, de sus 6 caras solo podemos observar 3 como máximo. Además de que no es posible observar todas las caras de un objeto, también existen objetos en la representación que no son visibles ya que permanecen ocultos tras otros o, sencillamente, no se encuentran en nuestro ángulo de visión.

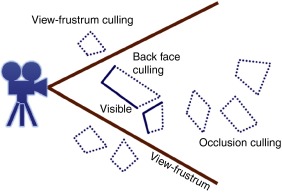
Estos 3 sencillos aspectos son ampliamente utilizados en computación gráfica con la finalidad de acelerar la generación de las imágenes: determinar qué caras o qué partes de las caras que conforman un sólido no son visibles y qué objetos permanecen ocultos tras otros más cercanos a la cámara, o no se ven desde la posición de esta, con el fin de solucionar, en parte, el problema de la visibilidad. Las técnicas más utilizadas y conocidas son el back-face culling , el hierarchical view-frustum culling , el portal culling , el detail culling y el occlusion culling ( fig. 1 ).

Figura 1. Algunas de las técnicas para determinar la visibilidad. (i) View-Frustum Culling . (ii) Back-Face Culling . (iii) Occlusion Culling . (Fuente: [3] )

Mediante la técnica de eliminación de polígonos no orientados al observador,³ es posible determinar cuándo una parte de la superficie de un objeto es visible dependiendo de la posición de la cámara. Esto reduce considerablemente el número de primitivas a dibujar. Este criterio de selección se aplica a objetos cerrados, y la determinación de la visibilidad o no de una parte del objeto se realiza comprobando la disposición de esa parte con respecto a la cámara, eso es, si está de frente o no, ya que la porción del objeto que está contraria al observador es invisible. Matemáticamente, se traduce a una comparación del ángulo formado por el vector que indica la dirección de la cámara y la normal de la superficie del objeto: si este ángulo es inferior a 90°, el polígono puede ser descartado. Podemos encontrar aplicaciones eficientes de esta técnica en [4] , [5]  and [6] .

La técnica de eliminación de objetos fuera del ángulo de visión⁴ consiste en determinar qué primitivas se encuentran dentro o parcialmente dentro del ángulo de visión y necesitan ser visualizadas. Para ello, se utilizan estructuras de datos tales como AABB, OBB, octrees , BSP trees , que presentan un buen desempeño en las representaciones dinámicas y en las estáticas [2] .

Los algoritmos para la eliminación de objetos ocultos⁵ se utilizan fundamentalmente en modelos de arquitectura en que las paredes o los muros son buenos objetos capaces de ocultar otros más pequeños. Los objetos en la representación son explorados de varias formas, buscando el conjunto potencialmente visible⁶ desde distintos puntos de visión. El PVS se forma tomando la representación completa y, partiendo del conjunto de puntos de visión, se van excluyendo aquellas partes de la representación que no contribuirán a la imagen final [2]  and [3] .

La técnica de eliminación de objetos ocultos consiste en seleccionar los objetos de una representación que no pueden verse desde la posición de la cámara porque permanecen ocultos tras otros y pueden despreciarse a la hora de generar la imagen [2]  and [3] . Encontramos información y aplicaciones eficientes de esta técnica en [7] , [8]  and [9] . La eficacia de esta técnica se basa en que en la representación existan objetos que sean «buenos»ocultadores, es decir, objetos relativamente grandes, capaces de ocultar tras de sí varios objetos más pequeños.

El problema de la visibilidad puede resolverse con hardware utilizando el z-buffering o buffering de profundidad. ⁷ Sin embargo, no es un mecanismo suficientemente eficaz. Por ejemplo, imaginemos que el observador está mirando a través de 10 esferas alineadas; una imagen generada a partir de este observador mostrará una sola esfera, pues todas las esferas son comparadas con el z-buffer y potencialmente escritas para el color buffer y el z-buffer , lo cual da lugar a que 9 esferas sean dibujadas innecesariamente.

2.2. Utilización de impostores gráficos

Son usualmente entidades basadas en imágenes, adquiridas a partir de la generación de partes de la representación y que se utilizan como representaciones alternativas de esa misma representación para acelerar el proceso de visualización. Este tipo de primitiva es mucho más eficiente cuando el objeto y el observador se mueven lentamente. Una característica identificativa es que un impostor ha de ser más rápido de dibujar que el objeto que representa y ha de tener las mismas características visuales [1]  and [2] .

Un impostor puede generarse en una etapa previa al proceso, el denominado impostor estático , o dinámicamente en el tiempo de ejecución, el llamado impostor dinámico . Durante el proceso de visualización, se muestra el impostor en lugar de partes de la representación original. El tiempo de visualización depende básicamente de su tamaño en pantalla y no de la complejidad de la parte de la representación que va a representar. Permite una representación rápida de objetos de gran complejidad geométrica [1] .

A la hora de generar un impostor, se adquieren tanto la apariencia como la estructura geométrica del objeto real, a partir de un punto de visión (punto del observador), llamado punto de visión de referencia . Existen diferentes tipos de técnicas para obtener impostores, en función del tipo y del volumen de los datos geométricos. El caso más simple de impostor gráfico es cuando parte de una representación es generada a partir una textura y se combina con un cuadrilátero para colocarla dentro de la representación.

La ventaja principal de los impostores frente a la simplificación de geometrías es que el proceso de generación no requiere ningún conocimiento de la estructura geométrica del objeto real. Esto permite utilizarlos en representaciones de cualquier tipo. Si la diferencia entre un impostor y el objeto original no es detectable, se trata de un impostor válido [1] .

Entre las desventajas de su uso, destaca que requieren mucha memoria o actualización, dependiendo de si es el impostor es estático o dinámico, respectivamente.

2.3. Técnicas de nivel de detalle

Los algoritmos de nivel de detalle permiten obtener múltiples representaciones de un modelo, algunas de alta resolución (donde se necesitan muchas primitivas) y otras de baja resolución (pocas primitivas), dependiendo de la distancia a que se encuentre el observador. Se denominan a menudo técnicas de multirresolución .

El modelado multirresolución representa un objeto con múltiples aproximaciones y permite extraer la más adecuada de todas ellas, según los criterios de la aplicación. Un modelo multirresolución está formado por los datos que representan el objeto y los algoritmos de extracción de estos. Los criterios para determinar la mejor aproximación dependen de cada aplicación en particular [10] .

El fin del modelado multirresolución es enviar al sistema gráfico únicamente la información que describe mejor un objeto en cada momento. Usualmente, en un modelo multirresolución, tanto las estructuras de datos como el algoritmo de extracción del nivel de detalle se basan en el uso de primitivas básicas [10] .

Utilizar primitivas gráficas que aprovechen la información de conectividad entre los triángulos de una malla, como las tiras o los abanicos de los triángulos, reduce notablemente la cantidad de información necesaria para dibujar la malla [11] .

Existen 3 planteamientos básicos para gestionar el nivel de detalle: un planteamiento discreto, uno continuo y otro dependiente de la vista [11] .

El planteamiento tradicional, propuesto en [12] , donde se exponen los principios básicos de esta técnica, es conocido como de nivel de detalle discreto y en la actualidad se utiliza en múltiples aplicaciones gráficas. Consiste en crear múltiples versiones de cada objeto, cada una con su nivel de detalle, previamente al proceso. En tiempo de ejecución, se elige el nivel más apropiado para representar el objeto. A medida que el observador se aleja del objeto, el número total de polígonos se reduce y la velocidad de generación de las imágenes se incrementa. Debido a que las versiones de los objetos son calculadas previamente, el proceso de simplificación no puede predecir a partir de qué dirección el objeto será observado y esto provoca una reducción o ampliación uniforme de cada objeto, que es llamado isotrópico o independiente de la vista [11] .

El nivel de detalle discreto tiene muchas ventajas: la mayoría de los cálculos se realizan en una etapa previa a la generación de la imagen y el algoritmo gráfico simplemente necesita determinar cuál es el nivel recomendado para cada objeto. Además, muchos hardwares gráficos permiten cargar múltiples versiones de un modelo.

El planteamiento continuo también proporciona niveles de detalles individuales durante una etapa previa al proceso, y así se crea una estructura de datos que contiene un rango de colores continuo. El nivel de detalle deseado es extraído de esta estructura en tiempo de ejecución. La ventaja principal es que se obtiene una mejor granularidad y ello permite un mejor uso de recursos y una mayor fidelidad en la cantidad de polígonos. Cuando debe cargarse un modelo grande desde disco o a través de la red, un nivel de detalle continuo proporciona una generación de la imagen progresiva y una carga ininterrumpida, propiedades que a menudo resultan muy útiles.

El nivel de detalle «dependiente de la vista» extiende el continuo usando un criterio de simplificación para seleccionar dinámicamente el más apropiado. Además, es anisótropo; un objeto sencillo puede abarcar múltiples niveles de simplificación, y permite una mayor granularidad: mucha más fidelidad y una mejor optimización de los escasos recursos.

A pesar de las ventajas de los niveles de detalle continuo y dependiente de la vista, el planteamiento discreto es más común en la práctica. El procesamiento extra que se requiere para las evaluaciones, las simplificaciones y el refinamiento del modelo en tiempo real, así como la memoria extra que se requiere para la estructura de datos utilizada, llevan a muchos investigadores a decantarse por el planteamiento tradicional [10] . Estas técnicas se explican con más detalle en [2]  and [10] .

Esta técnica es bastante común en aplicaciones en que el observador está en movimiento en la representación. En este caso, los pequeños detalles contribuyen poco o nada, eliminar estos detalles, sacrificando calidad en la representación para ganar en velocidad de generación de la imagen. Si nos encontramos en una posición fija, usualmente esta técnica se deshabilita.

3. Aceleración de la visualización de modelos de partículas

Los empaquetamientos de partículas generados en la primera fase del DEM presentan una serie de características y/o particularidades que pueden tenerse en cuenta a la hora de hacer una representación visual. A continuación se presentan las más significativas para el cálculo de la visibilidad.

• Están formados por grandes cantidades de pequeñas partículas (muy pequeñas en relación con el objeto que pertenece la generación) y que, en general, no difieren significativamente en tamaño.
• Generalmente, los empaquetamientos son aglomeraciones de partículas cuya densidad puede alcanzar valores de entre el 40 y el 55 %.
• Los empaquetamientos representan volúmenes (en el caso de 3D), por lo que, en conjunto, pueden considerarse como cuerpos cerrados, ya que se generan partículas por todo el medio de estudio.

Si se tiene en cuenta la primera característica, la utilización de una técnica de oclusión resulta sumamente costosa e ineficiente. No obstante, existen algunos casos en que se ha aplicado el DEM para realizar simulaciones utilizando partículas que difieren considerablemente en sus dimensiones, como en [13] . En estos casos, cabría estudiar la utilización de las partículas más grandes como ocultadores de objetos más pequeños.

Sin embargo, si se analiza la segunda propiedad, puede observarse que un porcentaje bastante alto de partículas no influye en modo alguno en la imagen final. Dada la alta densidad del empaquetamiento, solo serán visibles aquellas partículas que se encuentren más cercanas a la superficie del objeto.

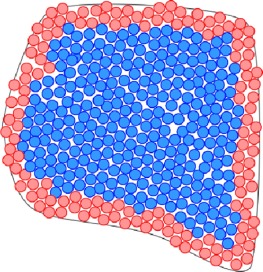
Esta es una característica que puede ser utilizada a favor de reducir la cantidad de partículas a procesar en cada paso de la visualización. En la figura 2 se muestra un ejemplo en 2D de las partículas en un empaquetamiento. A partir de este momento, este conjunto de partículas señalado en rojo se denominará corteza del empaquetamiento .

Figura 2. Representación figurada de un empaquetamiento donde las partículas interiores (color azul) quedan ocultas tras las partículas más cercanas a la superficie (color rojo).

La idea se basa en no considerar las partículas que no pertenecen a la corteza a la hora de generar las imágenes. Sin embargo, estas partículas no pueden descartarse del todo ya que, en caso de realizar cortes volumétricos a los empaquetamientos, sería necesario reconstruir parcialmente la corteza. La obtención de las partículas de la corteza se realiza en una etapa previa a la visualización ya que, en los empaquetamientos estáticos, las partículas nunca cambian de posición y, por tanto, la corteza siempre es la misma. En otras situaciones, como en algunas etapas posteriores al proceso, sí es necesario reencontrar/recalcular las partículas que pertenecen a la corteza.

Lo ideal es tener una corteza constituida únicamente por aquellas partículas que influyen en la imagen final desde alguna posición de la cámara. Sin embargo, teniendo en cuenta la gran cantidad de partículas que forman los empaquetamientos es sumamente costoso determinar de forma exacta la corteza del empaquetamiento.

La idea práctica se basa en obtener una aproximación de la corteza mediante un método poco costoso. En este caso, se consideran solo aquellas partículas que se encuentren a la distancia d de la superficie. La selección de esta distancia depende de la fracción de volumen local y del radio mínimo y máximo de las partículas. El éxito fundamental de este método radica en realizar una aproximación bastante buena de la corteza. Una distancia demasiado pequeña provoca agujeros en la representación del empaquetamiento desde algunas posiciones de la cámara y, por tanto, se pierde la integridad de la imagen. En cambio, una distancia demasiado grande implica una corteza demasiado gruesa y tiene en cuenta demasiadas partículas que no van a influir en la imagen final.

3.1. Algoritmos para el cálculo de la visibilidad en representaciones de conglomerados de partículas con información del contorno

Cuando se dispone de información del contorno del conglomerado de partículas, puede ser más fácil calcular las partículas que serán visibles desde la posición de la cámara. Contar con la malla de superficie permite obtener la corteza del conglomerado de partículas y también aquellas partes de esta que serán visibles desde el punto de visión del observador de manera sencilla.

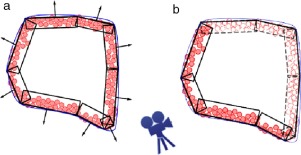
Considerando la tercera propiedad, pudieran no dibujarse aquellas partículas de la corteza que se encuentren próximas a las partes de la superficie que no están frente a la cámara. Considerando la corteza del empaquetamiento como una forma rústica de superficie y asociando normales en dependencia de la parte de la superficie a la que corresponda, es posible obtener las partículas potencialmente visibles (fig. 3 ). Se asocia a las partículas correspondientes a cada rectángulo (caso 2D) la normal correspondiente a la región de la corteza a la cual pertenecen. Nótese que una partícula puede pertenecer a más de una región.

Figura 3. Orientación de las regiones en la corteza del empaquetamiento en 2D. a) Asociación de normales a sectores de la corteza en función de su correspondencia con la superficie. b) Selección de las esferas visibles a partir de la posición de la cámara.

Una vez asociadas las normales a cada una de las regiones de la corteza, se puede verificar si estas regiones se encuentran frente a la cámara o no y, por tanto, si sus partículas son visibles (fig. 3 ). Es deseable que una partícula pueda pertenecer a más de una región de la corteza ya que su visibilidad viene determinada por la disyunción entre las visibilidades de las regiones a que pertenece. Esto favorece que no surjan agujeros cuando no se dibuja una región que no se encuentre enfrente y que sea adyacente a otra que sí es visible.

La normal asociada a cada una de las caras de la corteza se calcula utilizando el plano obtenido a partir de los 3 puntos que definen cada una de las caras. Para encontrar la corteza, se construyen figuras geométricas situando la base en las caras de la malla orientadas hacia el interior y con una profundidad d , esto es, en el caso de mallas de superficies de triángulos utilizadas para definir la corteza, un prisma triangular orientado hacia el interior de la malla. Se obtienen así las partículas interiores a la figura geométrica formada. Las partículas que se van a dibujar se obtienen comparando la normal de la corteza con el vector formado por la posición de la cámara y su dirección.

3.2. Algoritmos para el cálculo de la visibilidad en representaciones de conglomerados de partículas sin información de contorno

Los métodos libres de mallas y de partículas tienen el inconveniente que no disponen de información del contorno. En este caso, no es posible aplicar el algoritmo tratado anteriormente para eliminar todas las partículas que no son visibles desde cualquier punto de mira. No disponer de una forma, aunque sea rústica, del contorno dificulta la obtención de una corteza suave ya que no es posible proyectar hacia el interior y escoger como visibles las partículas que quedan en el rango de proyección.

En este caso, el algoritmo propuesto utiliza una división por celdas o rejilla, que contiene información de las partículas y sirve también para el cálculo de la visibilidad en la representación. El algoritmo se formula de la manera siguiente:

• Construir una caja uniforme contenedora de partículas (PUCB). En cada celda, se tiene información de la posición en el espacio de cada una de las partículas e información relacionada con la cantidad de partículas que contiene.
• A partir del PUCB, construir un mapa de numeración por distancias en que cada posición guarda la distancia discreta de las partículas que contiene la rejilla con el exterior, esto es, una celda que no contenga partículas tendrá una distancia 0, pues claramente está en el exterior del conglomerado; las celdas con partículas en su interior tendrán la siguiente distancia con respecto al exterior:
• Inicialmente, todas las celdas tienen valor o distancia 0.
• El mapa se construye por niveles de la manera siguiente: en cada iteración, se verifica el nivel i y se asignan valores de distancias que incluso duplican el nivel estudiado. Para asignar los valores de las distancias, se sigue esta ley: una celda tiene valor n si el valor máximo de sus vecinas ⁸ es n  − 1.
• Una vez asignadas todas las distancias «calculables» en un nivel, se pasa al siguiente hasta que no quedan celdas sin asignar.
• Con el mapa de distancias completo, es posible obtener las partículas visibles para una distancia d , la cual determina hasta qué nivel de profundidad son visibles.

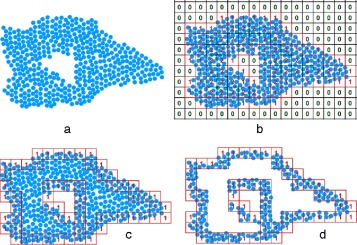
Gráficamente, puede representarse como en la figura 4 .

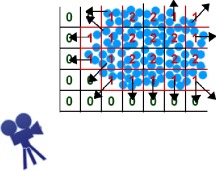
Figura 4. Algoritmo gráfico para la obtención de las partículas potencialmente visibles en un conglomerado. a) Modelo de partículas. b) División por celdas (rejilla) y mapa de distancias «discreta». c y d) Elección de celdas de la rejilla a partir del mapa de distancia y una profundidad dada. En esta muestra, se escogen las partículas con un nivel de profundidad o distancia «1».

También puede calcularse la visibilidad en un punto de visión específico asignando normales a las celdas y comparándolas con la dirección en que mira la cámara o el observador. El valor de las normales puede calcularse considerando la dirección de los niveles de profundidad hacia el interior del conglomerado de partículas, esto es, la normal de una celda apunta hacia el valor de distancia menor entre las celdas vecinas (fig. 5 ).

Figura 5. Cálculo de las normales asociadas a cada una de las celdas de la rejilla considerando la distancia discreta como indicador de dirección.

4. Resultados

La visualización científica de conglomerados de partículas es de gran importancia para el estudio de sucesos en ingeniería, pero la gran cantidad de información que contienen no permite interaccionar con la imagen resultante. El desarrollo de técnicas de aceleración para facilitar la visualización, como las técnicas de obtención de visibilidad, permite descartar, en este caso, gran cantidad de partículas. Esto podría formar parte de una fase previa al procesamiento de los datos para luego aplicar técnicas más afines a la visualización u otras relacionadas con la aceleración en sí.

Como se puede deducir, la visualización de grandes volúmenes de datos es un problema incluso para las computadoras más sofisticadas y potentes. El número de partículas gestionadas en el DEM puede llegar a varios millones, lo cual puede requerir, además, varios Gb de almacenamiento. Analizando las características de los empaquetamientos, se puede concluir que no es necesaria la visualización completa de todo el modelo de partículas, ya que la gran mayoría no son visibles desde ningún punto de vista.

Se han implementado 2 técnicas para eliminar elementos potencialmente no visibles desde la posición de la cámara en los modelos de partículas. Se han analizado 5 modelos de partículas diferentes para ver sus diferencias de comportamiento: un cubo geométrico, una cuchilla o herramienta de corte del terreno, 2 estructuras óseas (fémur y cráneo) y una estructura de ingeniería (estructura de un edificio). Para la generación del medio, se ha seguido el procedimiento de empaquetamiento de partículas genéricas para el DEM propuesto en [14] .

En la tabla 1 se muestran los resultados obtenidos tras la aplicación de este método. Estos resultados están expresados en función de la cantidad de partículas que se tuvieron en cuenta a la hora de generar las imágenes tras utilizar las técnicas de visibilidad mencionadas. La profundidad de la corteza para esta implementación se determinó a partir del radio máximo de las partículas, pero es preciso utilizar otros parámetros del modelo de partículas. La figura 6 muestra los empaquetamientos referidos en la tabla 1 .

Tabla 1. Cantidades de partículas por etapas en la aceleración de la visualización de conglomerados de partículas con información de la corteza

Objeto de estudio	Número de partículas	Partículas en la corteza (%)	Partículas a dibujar (%)
Cubo	132.681	51,69	10,83
			28,98
			20,35
Cuchilla de corte de terreno	352.203	45,21	13,48
			26,94
			30,58
Fémur	211.599	72,52	36,35
			36,89
			40,70
Estructura de un edificio	3.368.687	82,27	39,85
			45,22
			57,04
Cráneo	1.101.920	85,55	59,90
			60,26
			60,72

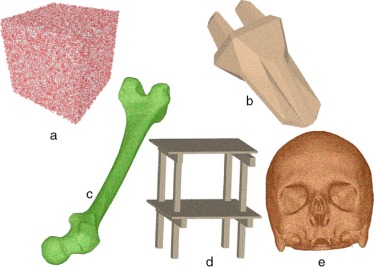
Figura 6. Ejemplos de empaquetamientos: a) Cubo, 132.681 partículas. b) Cuchilla de corte de terreno, 352.203 partículas. c) Estructura ósea (fémur), 12.605 partículas. d) Estructura ingenieril (edificio), 3.368.687 partículas. e) Cráneo humano, 1.101.920 partículas.

La columna «Partículas en la corteza» muestra la cantidad de partículas que pueden ser visibles desde cualquier posición de la cámara. Constituye una simplificación inicial del conjunto de partículas a dibujar. Por su parte, la columna «Partículas dibujadas» muestra la cantidad de partículas que finalmente se dibujaron para obtener la imagen desde 3 posiciones arbitrarias del observador. En este caso el criterio de selección fue eliminar aquellas partículas de la corteza que no se encontraran frente a la cámara. Se muestran 3 valores, tomados desde posiciones arbitrarias del observador que ilustran el mejor caso y el peor caso posibles, dependiendo del problema de que se trate.

La cantidad de partículas eliminadas, utilizando los algoritmos propuestos, para desarrollar el proceso de visualización varía según la forma geométrica de los cuerpos y la relación existente entre el tamaño de la partícula y el volumen total del cuerpo. Como puede apreciarse, los mejores resultados se obtienen en el caso del cubo y la cuchilla, que son objetos que no tienen partes estrechas o delgadas, como el fémur y la estructura. El cráneo, aunque visualmente no lo sea, es también un «objeto» delgado, pues solo se tomó la capa fina que constituye el hueso para generar el modelo de partículas. En definitiva, con la utilización del método propuesto se logra disminuir la cantidad de partículas considerablemente, con lo cual se acelera el proceso de visualización.

Cuando no se dispone de datos del contorno, los resultados pueden variar sustancialmente. En este caso, es más complejo obtener una corteza más suave y uniforme, por las características mencionadas en el capítulo anterior. A continuación se muestran los resultados asociados a la aplicación de esta metodología (tabla 2 ).

Tabla 2. Resultados asociados al cálculo de las partículas visibles cuando no se tiene información del contorno

Objeto	Tamaño celda	Celdas	Prof. corteza	Part. corteza	%
Cubo	3	27.000	1	19.184	17,20
	3	27.000	2	40.456	36,28
	5	5.832	1	26.421	23,69
	6	4.913	1	40.077	35,94
	10	1.000	1	57.640	51,69
Cuchilla	3	284.316	1	78.591	22,31
de corte	3	284.316	2	172.378	48,93
de terreno	5	72.576	1	80.104	22,74
	6	44.640	1	88.000	24,98
	10	12.160	1	123.607	35,09
Fémur	3	284.130	1	69.015	32,61
	3	284.130	1	137.216	64,84
	5	72.358	2	89.694	42,38
	6	46.460	1	101.080	47,76
	10	13.230	1	136.588	64,54

La tabla muestra, en este orden:

• El tamaño de celda, que en un principio puede ser cualquier valor real positivo. Sin embargo, tomar un valor pequeño puede hacer que aparezcan celdas interiores vacías, lo cual no es bueno para la visibilidad, mientras que un factor muy grande puede también arrojar resultados no deseados, pues se toman en consideración partículas muy alejadas de la corteza. En este caso, está calculado con respecto al radio máximo de las partículas.
• La cantidad de celdas a recorrer en la celosía y en el mapa de distancia.
• La profundidad de la corteza, que es la profundidad tomada en el mapa de distancia para obtener las partículas visibles, en que «2» significa tomar todas las celdas de profundidad 1 y 2.
• La cantidad de partículas en la corteza y que potencialmente influirán en la imagen final.
• El porcentaje de partículas potencialmente visibles con respecto al total.

En estos casos, solo se han calculado las partículas potencialmente visibles pues la idea es aplicar posteriormente alguna técnica para la visualización, como impostores gráficos o nivel de detalle. Las partículas que quedan frente al observador y que realmente son visibles pueden calcularse comparando la dirección de los vectores asociados a la dirección en que observa la cámara y la dirección de la profundidad en el mapa de distancias discretas (fig. 5 ).

Un estudio de la relación coste-beneficio a partir del uso de los algoritmos presentados señala un ahorro significativo de tiempo por cada imagen generada y en cada análisis posterior al proceso, ya que en el peor de los casos estudiados se logró eliminar hasta el 40 % de las partículas. La mayoría de las veces, este cálculo solo se efectúa una vez y las pruebas realizadas muestran que los resultados finales de la visualización y el análisis no difieren en gran medida de si se trabaja con el conglomerado completo o con parte de este.

Para lograr un uso eficiente de los algoritmos presentados, es necesario organizar las partículas en clústeres o rejillas.

5. Conclusiones

A partir de los datos mostrados en la tabla 2 , se puede llegar a conclusiones con respecto a la profundidad más conveniente de la corteza y que, para obtener una buena imagen, quizás sea más ventajoso fijarla poco profunda y aumentar el tamaño de las celdas en la rejilla, lo cual es más costoso en tiempo pero evita huecos en la imagen y solo hay que hacerlo una vez. Si estos datos se comparan con los resultados del método en que se tiene información del contorno (tabla 1 ), se puede ver que, con una profundidad de 10 veces el radio máximo (este fue el valor tomado para la tabla 1 ), la cantidad de esferas en la corteza aumenta. (Véase el porcentaje asociado.)

El algoritmo permite también representar partes interiores de la nube de partículas en función de los niveles de profundidad calculados.

Sobre el porcentaje de fallos del algoritmo, eso es, cuando no se dibuja una esfera que realmente sería visible, no se hace un estudio riguroso, sino que solo se muestran los resultados en que no hay huecos en la imagen. Esto puede influir en los beneficios de los algoritmos propuestos, pero los ejemplos estudiados indican que, incluso en el peor de los casos, se reduce considerablemente la cantidad de partículas a dibujar.

El valor asociado al tamaño de celda es más conveniente tomarlo a partir de un estudio del modelo de partículas relativo no solo al radio máximo, sino también a la densidad, a la porosidad, al radio mínimo y máximo y a otras propiedades de la nube de partículas. Este trabajo no aborda este tema y solo tiene en cuenta el radio máximo a la hora de calcular la profundidad de la corteza.

Es conveniente mencionar las ventajas de los algoritmos propuestos frente a las últimas tendencias de los métodos de elementos discretos en que cada vez es más común el uso de partículas no esféricas, como conglomerados de esferas, elipsoides, ovoides, poliedros, supercuádricas, esferocilindros, entre otras, ya que la aplicación de estas técnicas es casi transparente en estos casos, pues solo se tiene en cuenta la posición de la partícula con respecto al modelo.

References

1. [1] S. Jeschke; Accelerating the rendering process using impostors, Ph.D. thesis; Institute of Computer Graphics and Algorithms, Vienna University of Technology, Favoritenstrasse 9-11/186, A-1040 Vienna, Austria (2005 Mar) URL http://www.cg.tuwien.ac.at/research/publications/2005/jeschke-05-ARI/
2. [2] T. Akenine-Moller, E. Haines, N. Hoffman; Real-Time Rendering; (3rd Edition)A. K. Peters, Ltd, Natick, MA, USA (2008)
3. [3] D. Cohen-Or, Y.L. Chrysanthou, C.T. Silva, F. Durand; A survey of visibility for walkthrough applications; IEEE Transactions on Visualization and Computer Graphics, 9 (3) (2003), pp. 412–431 doi:10.1109/TVCG.2003.1207447. URL http://dx.doi.org/10.1109/TVCG.2003.1207447
4. [4] U. Assarsson, T. Moller; Optimized view frustum culling algorithms for bounding boxes; Journal of Graphics, GPU, and Game Tools, 5 (1) (2000), pp. 9–22
5. [5] S. Kumar, D. Manocha, W. Garrett, M. Lin; Hierarchical back-face computation; en: Proceedings of the eurographics workshop on Rendering techniques, Springer-Verlag, London, UK (1996), p. 235-ff URL http://portal.acm.org/citation.cfm?id=275458.275483
6. [6] M. Slater, Y. Chrysanthou; View volume culling using a probabilistic caching scheme; Proceedings of the ACM symposium on Virtual reality software and technology, VRST ’97, ACM, New York, NY, USA (1997), pp. 71–77 doi:http://doi.acm.org/10.1145/261135.261150. URL http://doi.acm.org/10.1145/261135.261150
7. [7] H.C. Batagelo, S.-T. Wu; Dynamic scene occlusion culling using a regular grid.; in: SIBGRAPI, IEEE Computer Society (2002), pp. 43–50 URL http://dblp.uni-trier.de/db/conf/sibgrapi/sibgrapi2002.html#BatageloW02
8. [8] G. Papaioannou, A. Gaitatzes, D. Christopoulos; Efficient occlusion culling using solid occluders (2006) URL http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.110.8306&rep=rep1&type=pdf
9. [9] I. Pantazopoulos, S. Tzafestas; Occlusion culling algorithms: A comprehensive survey; J. Intell. Robotics Syst., 35 (2002), pp. 123–156 DOI:10.1023/A:1021175220384. URL http://portal.acm.org/citation.cfm?id=585420.585445
10. [10] P. Heckbert, M. Garland; Multiresolution modeling for fast rendering; Proceedings of Graphics Interface (1994), pp. 43–50
11. [11] D. Luebke, B. Watson, J.D. Cohen, M. Reddy, A. Varshney; Level of Detail for 3D Graphics; Elsevier Science Inc., New York, NY, USA (2002)
12. [12] J.H. Clark; Hierarchical geometric models for visible surface algorithms; Commun. ACM, 19 (10) (1976), pp. 547–554 doi:10.1145/360349.360354. URL http://doi.acm.org/10.1145/360349.360354
13. [13] H. He, Z. Guo, P. Stroeven, M. Stroeven, L.J. Sluys; Self-healing capacity of concrete-computer simulation study of unhydrated cement structure.; Image Analysis and Stereology, 26 (2007), pp. 137–143
14. [14] I. Perez Moralez, R. Rosello Valera, Y. Perez Brito, H. Diaz Guzman, C. Recarey Morfa; Procedure for packing generic particles for the discrete element method; Rev. Int. Mét. Num. Cálc. Dis. Ing., 25 (2009), pp. 95–110

1

En inglés, render .

2

En inglés, frames per second (FPS) o frame rate o frame frequency . En informática, es conocido como real-time computing (RTC).

3

En inglés, back-face culling .

4

En inglés, view-frustum culling .

5

En inglés, occlusion culling .

6

En inglés, potentially visible set (PVS).

7

El z-buffering es la parte de la memoria de un adaptador de vídeo encargada de gestionar las coordenadas de profundidad de las imágenes en los gráficos en 3 dimensiones (3-D), normalmente calculados por hardware y algunas veces por software.

8

Se consideran celdas vecinas aquellas que comparten algún nodo entre ellas.