Abstract
We describe a spectrum splitting solar module design approach using ensembles of 2–20 subcells with bandgaps optimized for the AM1.5D spectrum. Device physics calculations and experimental data determine radiative efficiency parameters for III-V compound semiconductor subcells and enable modification of conventional detailed balance calculations to predict module efficiency while retaining computational speed for a wide search of the design space. Accounting for nonideal absorption and recombination rates due to realistic material imperfections allows us to identify the minimum subcell quantity, quality, electrical connection configuration, and concentration required for 50% module efficiency with realistic optical losses and modeled contact resistance losses. We predict a module efficiency of 50% or greater will be possible with 7–10 electrically independent subcells in a spectral splitting optic at 300–500 suns concentration, assuming a 90% optical efficiency and 98% electrical efficiency, provided the subcells can achieve an average external radiative efficiency of 3–5% and a short circuit current that is at least 90% of the ideal. In examining spectrum splitting solar cells with both series-connected and electrically independent subcells, we identify a new design trade-off independent of the challenges of fabricating optimal bandgap combinations. Series-connected ensembles, having a single set of electrical contacts, are less sensitive to lumped series resistance losses than ensembles where each subcells are contacted independently. By contrast, ensembles with electrically independent subcells can achieve lower radiative losses when the subcells are designed for good optical confinement. Distributing electrically independent subcells in a concentrating receiver module allows flexibility in subcell selection and fabrication, and can achieve ultra-high efficiency with conventional III-V cell technology.
Introduction
A wide variety of photovoltaic cell technologies have shown dramatic performance improvements over the past decade, yet the prospect of a practical module capable of 50% efficiency remains remote. Experimentally achieved single-cell devices have achieved a record efficiency of 28.8% [1], which is close to the theoretical limit of 33.8% for such devices [2]. However, the single-cell limit is far below the fundamental efficiency limit for solar energy conversion of 74.0% for global illumination and 92.8% for direct [2] because a single pn junction can only efficiently convert photons with energy close to the value of its energy bandgap. The best single junction cell will lose more than 40% of the energy in the incident light to transmission of subbandgap photons and thermalization of carriers with photon energy in excess of the bandgap [3]. Spectrum splitting, which divides the solar spectrum into spectral bands of different energy and directs the bands onto multiple subcells with bandgap values matched to the energy of their photon allocation, is a necessary feature of any photovoltaic design capable of achieving >33.8% efficiency. The use of multiple subcells to increase conversion efficiency is well known. In these designs, the subcells are grown monolithically in a stacked configuration and are electrically in series. The incident spectrum is divided among the subcells by sequential absorption, with the top subcells absorbing and converting high energy photons while transmitting lower energy photons to the subcells below. State-of-the-art high-efficiency solar cells using this monolithic multijunction stack technology have achieved efficiency as high as 46% [4-8].
While the 46% record efficiency for monolithic multijunction solar cells (MJSCs) appears close to 50%, the performance of these cells is measured under high-intensity illumination that simulates an ideal optical concentration system. Once practical high-efficiency devices are installed in the necessary concentrating optics, the overall module efficiency drops, with the record module achieving only 38.9% [9, 10] with commercial optics and 43.3% with ultra-high-efficiency optics in a minimodule [11, 12]. This suggests that an integrated module efficiency of 50% or greater will not be achieved by a commercially practical module through continued incremental improvements to the monolithic MJSC architecture, such as material quality improvements or adjustment of the subcell bandgaps. Prospective designs incorporating 4, 5, and 6 subcells into the monolithic MJSC stack are projected to raise the photovoltaic cell efficiency as high as 50.91% under ideal concentrating optics [13], which will result in a module efficiency well below 50% once integrated with realistic optics and electronics.
An alternative approach to the monolithic MJSC uses a separate optical element to split the incident light among subcells that are electrically independent from one another and may be physically isolated [14-17]. While the addition of the spectrum splitting optic increases the complexity of these designs, removing the requirement for monolithically integrated subcells confers benefits that may be overall advantageous. First, the subcells no longer need to be grown on the same substrate, which allows a wider variety of materials and bandgaps to be combined. Secondly, the subcells can be optimized independently to maximize electrical performance. Thirdly, isolated subcells that are not connected in series electrically are not constrained to collect equal numbers of photons for current matching, and consequently can better match the target spectrum. To date, all designs using separate spectrum splitting optics have used six or fewer subcells. The highest demonstrated efficiency is 38.5% for a minimodule with two physically separated dual-junction subcells [18]. A hybrid approach using a monolithic triple junction and an electrically independent, isolated fourth subcell in a submodule achieved 40.4% efficiency [19].
Both types of spectrum splitting modules lack an obvious path of incremental improvements that could enable them to achieve 50% efficiency. If photovoltaics are to reach that efficiency target, they will require designs that are much more ambitious.
Here, we present a systematic investigation of the design requirements for photovoltaic modules capable of achieving 50% efficiency with multijunction architecture based on established single-junction cell technology. We consider spectrum splitting module designs that include many more bandgap combinations than previously demonstrated designs and we specifically analyze the effect in series electrical connection as well as concentration. By incorporating performance parameters representing realistic material performance for the subcells, and by accounting for a realistic amount of loss in the optical and electrical systems required by a spectrum splitting module, we identify the number of subcells, degree of concentration, cell quality, and electrical configuration required to achieve 50% module efficiency for designs with up to 20 subcells.
The efficiencies predicted by this design approach represent a large improvement over current state-of-the-art designs, but do not require disruptive innovation in cell technology. Recent advances in cell material growth, epitaxial liftoff and transfer of cells, and pick-and-place automation all set the stage for this design approach that features the use of many high-quality independent subcells [20-22]. Combined with optical systems capable of splitting and concentrating the solar spectrum into desirable subbands with high efficiency [23], a module incorporating many subcells has realistic potential to achieve the ultra-high-efficiency target of 50%.
Methods
Exploring the design space for multijunction photovoltaics requires a mechanism for predicting the realistic performance of a large number of designs. The detailed balance calculation is the standard tool for evaluating potential solar cell designs because it presents the ideal limiting efficiency for the combination of energy bandgaps and concentration level [24]. The calculation determines an ideal J-V relationship for a cell by balancing the number of absorbed photons with the combined number of collected carriers and radiatively emitted photons. Radiative emission is assumed to consist of the temperature-dependent black body spectrum of the cell, plus luminescence caused by recombination of excited carriers, which depends on the degree of quasi-Fermi-level splitting present in the cell. Conventional detailed balance calculations assume no carriers are lost to nonradiative recombination. In addition, the calculation typically assumes perfect absorption of photons with energy greater than the cell energy bandgap. The detailed balance calculation allows rapid assessment of a potential cell design, enabling a wide search of the design space.
To explore the benefit of designs with multiple subcells, we start by calculating the conventional detailed balance efficiency of ensembles with 2–20 subcells, both electrically in-series and independent. The set of bandgaps in each ensemble was optimized. In the case of the series-connected cells, this optimization is constrained by the current-matching requirement and the technique is straightforward, see ref [25]. The systems with electrically independent cells are not constrained by the need for each cell to absorb an equal number of photons, and consequently the design space for these ensembles grows exponentially with the number of subcells. For the electrically independent ensembles, a computational technique termed “simulated annealing” identified the optimal sets of bandgaps for each number of subcells [26]. The simulated annealing algorithm used consists of two stages of optimization: first, a randomly seeded search allows all subcell bandgaps to vary over a wide range; secondly, a subsequent search is seeded with the best candidate identified in previous search and allows one subcell bandgap at a time to vary over a narrow range. This process was repeated multiple times for each ensemble in search of repeated optimum values, which suggest a global optimum.
The conventional detailed balance calculation informs us of the limiting efficiency of these spectrum splitting designs, however, the practical efficiency of any device falls far short of this limiting efficiency value [27]. At present computationally intensive device physics and optical simulations are required for a realistic performance estimate, and these techniques require a fully specified design for every device under consideration. Because data on the optical and electrical properties of materials at every possible energy bandgap value are not documented, and because the computational costs and design effort required for each device physics calculation are large, device physics techniques are not practical for a comprehensive search of the photovoltaic system design space. To address the shortcomings of conventional detailed balance calculation while retaining the speed of calculation, we introduce three parameters, the external radiative efficiency (ERE), absorption efficiency, and a lumped series resistance as key parameters for modified detailed balance calculations, which together capture a large portion of the nonideal behavior. We use this modified detailed balance approach to identify systems whose designed efficiency exceeds 50% in the presence of realistic material performance and optical and electrical system losses.
It is straightforward to incorporate these ERE and absorption efficiency parameters into the detailed balance calculation. The modified equation balances the incident flux as modified by the absorption efficiency (abs) with the collected carriers and the radiative and nonradiative recombination. Radiative emission from the cell is assumed to follow the same modified Kirchhoff relation as in the unmodified calculation, but that quantity is now assumed to be a percentage – equal to the ERE – of the total recombination. With these assumptions we calculate a new J-V relation for each cell and determine its fill factor and maximum power point under illumination by its particular spectral slice.
|
|
(1) |
Note that we assume unity absorptivity for photons with energy at or above the cell bandgap value, and zero absorptivity for lower energy photons. This allows us to disregard the cell thickness in these calculations and allows us to treat the absorption efficiency and ERE as independent parameters. The J-V curve produced by the modified detailed balance calculation captures the performance of the cell with perfect current collection and will therefore overestimate the fill factor of the cell. Incorporating a lumped series resistance captures the loss in voltage due to contact and other resistances. With these three parameters, the ERE, absorption efficiency, and series resistance (Rs), the modified detailed balance approach can accurately reproduce the performance of realistic cells while retaining computational speed.
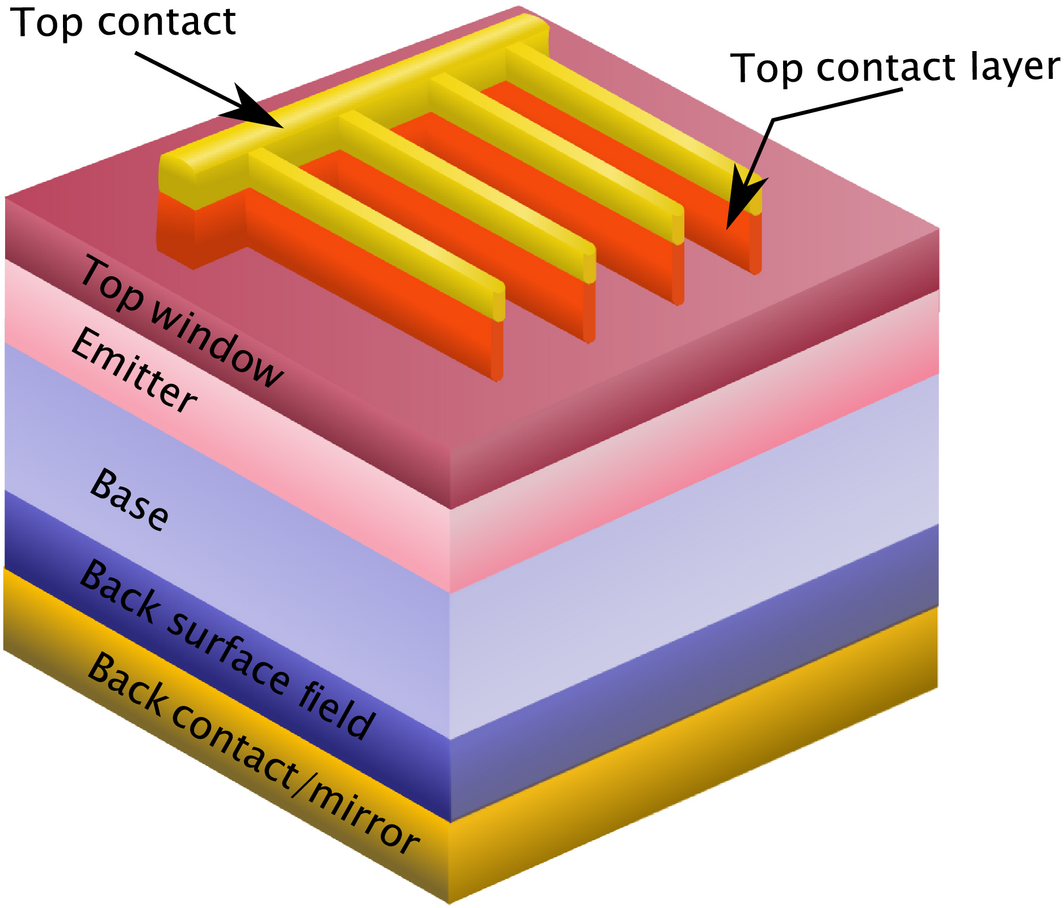
To determine realistic values for the absorption and ERE parameters to use in the detailed balance calculations, we selected seven materials that span a large range of bandgap values and performed one-dimensional device physics simulations on candidate designs of cells made from these materials using AFORS-HET [28, 29]. We incorporated realistic doping-dependent mobility and lifetime data for the candidate materials [30-33] to optimize device designs for each cell, including doping and thicknesses for emitter, base, front and back window layers, and contact layers. A schematic of the cell design showing the layers included for each material is shown in Figure 1. The design did not account for top contact shadowing losses and the top contact layer was treated as optically transparent. Table 1 summarizes the layer thicknesses, compositions, and doping levels for the Afors-Het simulations. In all cases, the cells were optimized both for performance on the growth wafer and for performance after epitaxial liftoff (ELO) or substrate removal, which allows the use of back reflectors to improve light trapping and allow thinner absorption layers. The epitaxial liftoff cells were modeled assuming perfect back reflectors. Because ERE and absorption efficiency are effected by the interaction of cell design, material quality, and optical environment, the AFORS-HET simulations serve to bound realistic values of ERE and absorption efficiency for subsequent modified detailed balance optimizations and to illustrate the possible degree of variation in these parameter values between subcells.
|
|
|
Figure 1. Schematic of basic solar cell design optimized through 1D device simulations using AFORS-Het. Layer thickness, doping, and device polarity were optimized based on material parameters from literature. |
| Subcell | Bottom contact | Bottom window | Base | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Composition | t (nm) | N | Composition | t (nm) | N | Composition | t (nm) | N | |
| InGaAs ELO | n++ InGaAs | 300 | 1.0E+19 | n+ InP | 15 | 1.0E+19 | n InGaAs | 2000 | 1.0E+17 |
| InGaAs wafer | n++ InGaAs | 300 | 1.0E+19 | n+ InP | 15 | 1.0E+19 | n InGaAs | 4000 | 1.0E+17 |
| InGaAsP 1 ELO | p++ InP | 200 | 1.0E+19 | p+ InP | 100 | 3.0E+18 | p In0.71 Ga0.29As0.62P0.38 | 3000 | 5.0E+17 |
| InGaAsP 1 wafer | p++ InP | 200 | 1.0E+19 | p+ InP | 100 | 3.0E+18 | p In0.71 Ga0.29As0.62P0.38 | 5000 | 5.0E+17 |
| InGaAsP 2 ELO | p++ InP | 300 | 1.0E+19 | p+ InAlAs | 10 | 1.0E+18 | p In0.87 Ga0.13As0.28P0.72 | 3000 | 5.0E+17 |
| InGaAsP 2 wafer | p++ InP | 300 | 1.0E+19 | p+ InAlAs | 10 | 1.0E+18 | p In0.87 Ga0.13As0.28P0.72 | 5000 | 5.0E+17 |
| GaAs ELO | n++ GaAs | 300 | 5.0E+18 | n+ Ga0.73In0.63P | 30 | 3.0E+18 | n GaAs | 2000 | 2.0E+17 |
| GaAs wafer | n++ GaAs | 300 | 5.0E+18 | n+ Ga0.73In0.63P | 30 | 3.0E+18 | n GaAs | 4000 | 2.0E+17 |
| AlGaAs ELO | n++ GaAs | 300 | 5.0E+18 | n+ Ga0.37In0.63P | 30 | 3.0E+18 | n Al0.1 Ga0.9As | 1000 | 2.0E+17 |
| AlGaAs wafer | n++ GaAs | 300 | 5.0E+18 | n+ Ga0.37In0.63P | 30 | 3.0E+18 | n Al0.1 Ga0.9As | 2000 | 2.0E+17 |
| InGaP ELO | p++ GaAs | 250 | 1.0E+19 | p+ Al0.2 Ga0.32In0.48P | 30 | 2.0E+17 | p Ga0.37In0.63P | 800 | 5.0E+17 |
| p+ Ga0.37In0.63P | 10 | 5.0E+18 | |||||||
| InGaP wafer | p++ GaAs | 250 | 1.0E+19 | p+ Al0.2 Ga0.32In0.48P | 30 | 2.0E+17 | p Ga0.37In0.63P | 1400 | 5.0E+17 |
| p+ Ga0.37In0.63P | 10 | 5.0E+18 | |||||||
| AlGaAsP ELO | p++ Ga0.52In0.48P | 10 | 5.0E+18 | p+ Al0.5In0.5P | 20 | 2.0E+17 | p Al0.2 Ga0.32In0.48P | 700 | 5.0E+17 |
| p++ GaAs | 300 | 1.0E+19 | |||||||
| AlGaAsP wafer | p++ Ga0.52In0.48P | 10 | 5.0E+18 | p+ Al0.5In0.5P | 20 | 2.0E+17 | p Al0.2 Ga0.32In0.48P | 1200 | 5.0E+17 |
| p++ GaAs | 300 | 1.0E+19 | |||||||
| Subcell | Emitter | Top window | Top contact | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Composition | t (nm) | N | Composition | t (nm) | N | Composition | t (nm) | N | |
| InGaAs ELO | p+ InGaAs | 350 | 1.0E+18 | p++ InP | 15 | 1.0E+19 | p++ InGaAs | 300 | 1.0E+19 |
| InGaAs wafer | p+ InGaAs | 350 | 1.0E+18 | p++ InP | 15 | 1.0E+19 | p++ InGaAs | 300 | 1.0E+19 |
| InGaAsP 1 ELO | n+ In0.71 Ga0.29As0.62P0.38 | 270 | 8.0E+17 | n+ InP | 200 | 5.0E+18 | n++ InGaAs | 300 | 1.0E+19 |
| InGaAsP 1 wafer | n+ In0.71 Ga0.29As0.62P0.38 | 270 | 8.0E+17 | n+ InP | 200 | 5.0E+18 | n++ InGaAs | 300 | 1.0E+19 |
| InGaAsP 2 ELO | n+ In0.87 Ga0.13As0.28P0.72 | 200 | 1.0E+18 | n+ InAlAs | 10 | 5.0E+18 | n++ InGaAs | 300 | 1.0E+19 |
| InGaAsP 2 wafer | n+ In0.87 Ga0.13As0.28P0.72 | 200 | 1.0E+18 | n+ InAlAs | 10 | 5.0E+18 | n++ InGaAs | 300 | 1.0E+19 |
| GaAs ELO | p+ A Al0.2 Ga0.8As | 250 | 2.0E+18 | p+ Ga0.37In0.63P | 50 | 8.0E+18 | p++ GaAs | 250 | 1.0E+19 |
| GaAs wafer | p+ Al0.2 Ga0.8As | 250 | 2.0E+18 | p+ Ga0.37In0.63P | 50 | 8.0E+18 | p++ GaAs | 250 | 1.0E+19 |
| AlGaAs ELO | p+ Al0.1 Ga0.9As | 300 | 2.0E+18 | p+ Ga0.37In0.63P | 50 | 8.0E+18 | p++ GaAs | 250 | 1.0E+19 |
| AlGaAs wafer | p+ Al0.1 Ga0.9As | 300 | 2.0E+18 | p+ Ga0.37In0.63P | 50 | 8.0E+18 | p++ GaAs | 250 | 1.0E+19 |
| InGaP ELO | n+ Ga0.37In0.63P | 60 | 3.0E+18 | n+ Al0.2 Ga0.32In0.48P | 10 | 5.0E+18 | n++ GaAs | 300 | 5.0E+18 |
| InGaP wafer | n+ Ga0.37In0.63P | 60 | 3.0E+18 | n+ Al0.2 Ga0.32In0.48P | 10 | 5.0E+18 | n++ GaAs | 300 | 5.0E+18 |
| AlGaAsP ELO | n+ Al0.2 Ga0.32In0.48P | 50 | 5.0E+18 | n+ Al0.5In0.5P | 10 | 5.0E+18 | GaAs n | 300 | 5.0E+18 |
| AlGaAsP wafer | n+ Al0.2 Ga0.32In0.48P | 50 | 5.0E+18 | n+ Al0.5In0.5P | 10 | 5.0E+18 | GaAs n | 300 | 5.0E+18 |
The performance results for these simulations are summarized in Table 2. In all cases the simulated power production of each cell was substantially lower than the ideal detailed balance power, as expected. However, the lowest bandgap cells exhibited the largest departure from the ideal efficiency. This trend suggested the need to reoptimize the bandgaps for the ensembles to account for realistic material behavior. Table 2 also includes the ERE values extracted from the simulated open circuit voltage and short circuit current for each cell material [34] and the absorption efficiency (abs), which is the short circuit current as a percentage of the value predicted by ideal detailed balance. The values for the InGaP and GaAs epitaxial liftoff cells are taken from record cell performance reported in the literature [21] and [34], respectively. Comparing the ERE values for the simulated epitaxial liftoff cells to the values for on-wafer cells shows the tremendous value of epitaxial liftoff for improving cell performance. These ELO cells benefit from improved optical confinement with the back reflector, which prevents photons from escaping the cell into the growth substrate, and from thinner absorber layers, which reduces bulk nonradiative recombination. Table 2 shows that epitaxial liftoff is an essential component of high external radiative efficiency for the III–V cells considered for spectrum splitting PV.
| Cell | Eg | Detailed balance prediction | Device physics simulation | Extracted parameters | Experiment | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Jsc (mA/cm2) | Voc (mV) | FF (%) | Jsc (mA/cm2) | Voc (mV) | FF (%) | Absorption | ERE | ERE | ||
| InGaAs ELO | 0.74 | 6.68 | 399 | 77.2 | 6.24 | 417 | 76.0 | 0.938 | 0.147 | |
| InGaAs wafer | 0.74 | 5.97 | 366 | 75.1 | 0.897 | 0.021 | 0.0095 | |||
| InGaAsP 1 ELO | 0.94 | 8.57 | 595 | 82.7 | 8.56 | 566 | 80.4 | 0.993 | 0.024 | |
| InGaAsP 1 wafer | 0.94 | 8.41 | 540 | 79.2 | 0.975 | 0.009 | 0.017 | |||
| InGaAsP 2 ELO | 1.15 | 9.75 | 798 | 86.1 | 9.36 | 769 | 84.6 | 0.958 | 0.025 | |
| InGaAsP 2 wafer | 1.15 | 9.17 | 741 | 83.2 | 0.940 | 0.008 | 0.004 | |||
| GaAs ELO | 1.42 | 32 | 1154 | 89.5 | 29.43 | 1107 | 87.6 | 0.920 | 0.225 | |
| GaAs wafer | 1.42 | 11.48 | 1034 | 87.4 | 0.923 | 0.026 | 0.018 | |||
| AlGaAs ELO | 1.58 | 7 | 1449 | 91.3 | 5.82 | 1220 | 86.9 | 0.925 | 0.123 | |
| AlGaAs wafer | 1.58 | 5.36 | 1199 | 86.9 | 0.898 | 0.082 | 0.00175 | |||
| InGaP ELO | 1.84 | 19.7 | 1506 | 91.4 | 16.00 | 1458 | 88.8 | 0.816 | 0.080 | |
| InGaP wafer | 1.84 | 5.80 | 1345 | 88.6 | 0.975 | 0.001 | 0.0065 | |||
| InAlGaP ELO | 2.13 | 6.13 | 1733 | 92.4 | 5.81 | 1642 | 91.0 | 0.629 | 0.0022 | |
| InAlGaP wafer | 2.13 | 5.81 | 1639 | 91.0 | 0.629 | 0.0019 | 2.1E-6 | |||
The ERE values for the ELO cells in Table 2 vary over a wide range among the cells. Because the cell open circuit voltage decreases linearly with the natural logarithm of ERE [35], a direct average of ERE values will overstate the expected average performance of these cells. Instead, taking the geometric mean of the ERE values incorporates their logarithmic scaling and results in an average ERE of 4.7%. The performance of an ensemble of cells with these bandgaps and that average ERE value will have the same total efficiency as the ensemble with the cell-specific ERE values. While this value is higher than the simulated value for most of the cells, the highest ERE values included in the average come from experimentally realized cells, suggesting that optimization of growth and other device parameters can produce III–V devices with very high radiative efficiency. The arithmetic mean of the absorption efficiency values is 90.6%. For simulation purposes, the value 90% was chosen as a conservative yet realistic derating value. Table 2 also shows the experimentally verified ERE values for cells on their growth substrates. These values differ from the simulated ERE values, with five of the seven cells having lower ERE compared to the simulation. The geometric mean ERE for the on-wafer experimental cells is 0.22%, whereas the geometric mean for the simulated cells is 0.97%, with the highest bandgap cell contributing most of the difference. The gap between simulated and experimental cells suggests a range of expected realistic performance after additional work on cell development.
With realistic values for the ERE and absorption parameters determined, we reoptimized the bandgaps for the spectrum splitting ensembles with both series-connected and electrically independent subcells using the modified detailed balance calculation to determine whether the nonideal material behavior would change the desired bandgap combinations. We used the appropriate mean values for the ERE and absorption because the optimization allowed bandgap values to range freely between 0.3 and 4 eV, and because the effects of the ERE and absorption on cell performance are independent. Finally, we varied the ERE value and concentration for the system to map out the full design space for ultra-high-efficiency spectrum splitting photovoltaics.
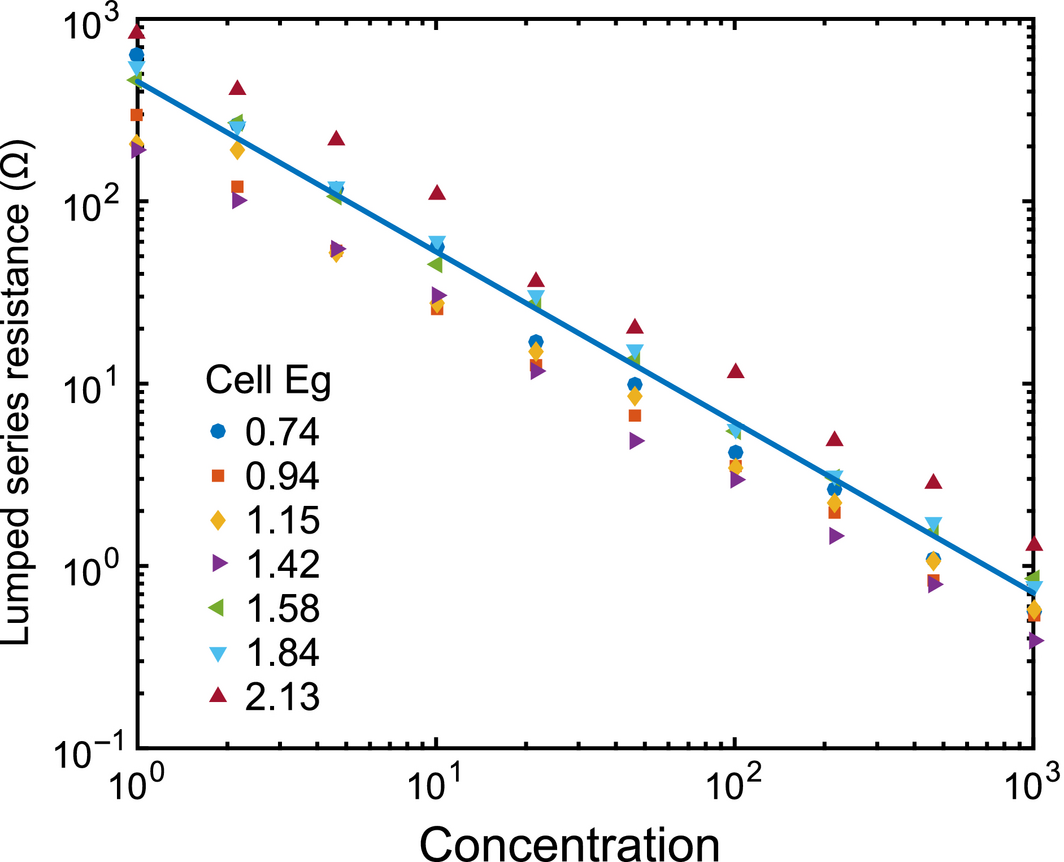
As with the ERE and absorption parameters, the value for the lumped series resistance parameter, Rs, was determined from the geometric mean value of lumped resistance from a set of electrical simulations. For each of the bandgaps in Table 2, a distributed circuit model was built with dark current and short circuit current densities determined by the corresponding ERE and absorption parameters from Table 2 [36]. The circuit model was used to optimize an inverted square contact grid for 1 mm2 square cells at concentrations ranging from 1 sun to 1000 suns. Because the loss due to series resistance is proportional to the square of the current, higher concentrations require much lower series resistances for optimal performance. The lumped Rs for each concentration for the seven cells is plotted in Figure 2.
|
|
|
Figure 2. Optimized series resistance for simulated subcells with bandgaps ranging from 0.74 to 2.13 eV at concentrations from 1 to 1000 suns. The blue line shows the trend for the optimized values. |
Once the lumped series resistance, the ERE, and the absorption efficiency are incorporated into the modified detailed balance calculation it can reproduce the short circuit current and open circuit voltage of the cells modeled by the distributed circuit model to within 1% (relative) and the modified detailed balance can reproduce the fill factor to within 2.5%. Overall the efficiency of the modified detailed balance model of each cell captures the efficiency predicted by the lumped circuit model to within 2%. While this does constitute a loss of accuracy relative to the more physically detailed lumped circuit model, the computational speed of the modified detailed balance approach makes it more practical for searching the large design space.
The series resistance values plotted in Figure 2 are optimized for the specific cells and performance parameters in Table 2. An average lumped series resistance, analog to the average ERE and absorption values is extracted from fitting the geometric mean versus concentration for all data points in Figure 2. The dependence of the average Rs on concentration, C, is described by a power law:
|
|
(2) |
The individual lumped series resistances plotted in Figure 2 vary over a wide range for any particular concentration and the performance of individual cells modeled using the average Rs value will differ from the performance using the optimized Rs value by as much as 12%. However, the total performance of the entire ensembles of cells modeled using the average Rs value is within 2% of the ensemble performance modeled with the optimized Rs values for each cell, which validates the utility of the average for modeling ensemble behavior.
Results
Figure 3 shows the conventional detailed balance efficiencies of optimized spectral splitting ensembles with 2–20 subcells at different concentration values. The plot shows the increase in efficiency with increasing number of subcells is primarily due to the increase in spectral efficiency, which we define as
|
|
(3) |
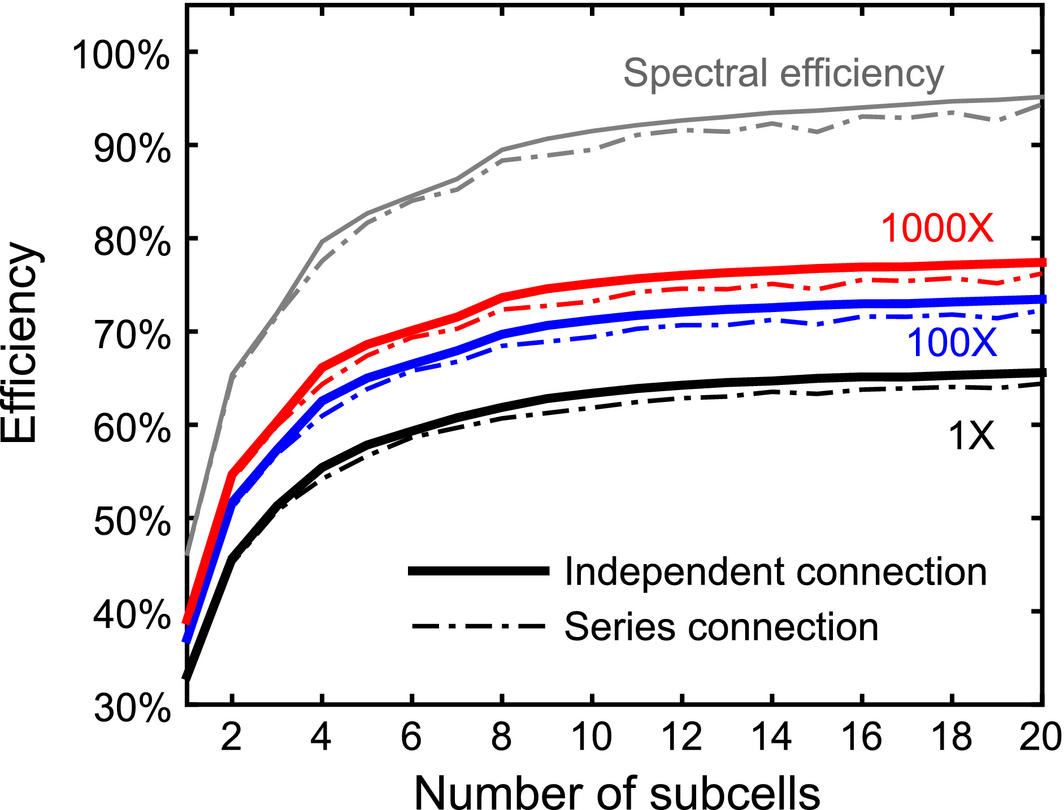
where dn/dE is the spectral flux density of the AM1.5D standard spectrum in photons/cm2-s-eV and Egi is the bandgap value of the ith subcell in the ensemble. The spectral efficiency is percentage of energy in the incident spectrum not lost to thermalization or subbandgap transmission. The increase in spectral efficiency is most dramatic (17 percentage points) up to eight cells, with only four percentage points of efficiency gained by increasing from 8 to 20 cells. Achieving a spectral efficiency of 90%, which corresponds to reducing the combined thermalization and transmission losses to 10% of the incident power, requires an ensemble of at least eight cells. Figure 2 also shows that increasing the concentration on the system from 1 sun to 1000 suns results in approximately 10 percentage points in efficiency improvement. This suggests that a combination of concentration and spectrum splitting will be valuable in exceeding 50% system efficiency. Finally, the dashed lines for the series-connected spectrum splitting ensembles are consistently 1–2 percentage points lower than those for the independently connected designs. This is a consequence of the current-matching constraint forcing the selection of bandgap combinations with a lower spectral efficiency in order to ensure that all subcells absorb an equal number of photons.
|
|
|
Figure 3. The ideal detailed balance efficiency for spectral splitting ensembles with 2–20 cells, both series connected and electrically independent at concentrations of 1, 100, and 1000 suns. The spectral efficiency of the independently connected and series-connected ensembles is also plotted showing the source of the efficiency improvement with increasing cell number. |
The efficiencies in Figure 3 suggest that 50% efficiency can be exceeded by a three-cell ensemble at any concentration. However, these conventional detailed balance calculations assume ideal behavior for photon absorption and radiation and perfect carrier collection. Practical cells have less than ideal absorption due to finite thickness, as well as reflection and transmission losses and will have some nonradiative recombination due to material imperfections. In order to understand the efficiency trends for cells with realistic material quality, we repeated the optimization and efficiency calculations for ensembles with 2–20 subcells (both series connected and with electrically independent subcells) using nonunity values for the ERE and absorption efficiency.
Including nonunity ERE and absorption efficiency did not change the optimal bandgaps for the series-connected ensembles. The constraint of series electrical connection and the need to maximize spectral efficiency dominate the subcell bandgap selection regardless of material quality. However, the bandgaps for the independently connected designs did change upon the inclusion of nonideal material behavior. The designs of ensembles with fewer than 10 cells exhibited the strongest dependence on material quality. Once optimized with nonunity ERE and absorption efficiency, the electrically independent designs uniformly increased the bandgap energy of the lowest energy subcell. This trend is a result of low bandgap cells being particularly sensitive to decreases in ERE. At low bandgap energies the loss of voltage due to nonunity ERE consumes a greater percentage of the open circuit voltage and the fill factor also degrades more significantly, which combine to eliminate the benefit of capturing more low energy photons. Ensembles with more than 10 cells did not have large changes in subcell bandgap values after optimization with nonideal material parameters. The expected efficiencies with 3% ERE and 90% absorption efficiency are ~10 percentage points lower than the ideal detailed balance efficiencies.
While the modified detailed balance approach gives a realistic prediction of the efficiency of an ensemble of cells, the total system has additional losses that must be taken into account. A practical spectrum splitting photovoltaic system will require some optical system to split and concentrate the incident spectrum into the desired spectral range for each subcell in the design. Such a system will inevitably introduce inefficiency through misallocation of photons to the wrong cell and reflections. In addition, an electrical system to combine the power of the subcells at a single output voltage will add electrical losses. In order to accommodate these optical and electrical losses and still produce module efficiency <50%, the ensemble of subcells must have a combined efficiency of much <50%. In our analysis we have assumed an optical system that concentrates the light and divides the spectrum with 90% optical efficiency, including losses from reflection and photon misallocation. The optical efficiency of the spectrum splitting optic is assumed to be equal for the electrically independent and series-connected designs. We assume an electrical system of 98% efficiency for designs with electrically independent subcells to account for losses in a DC–DC voltage combination circuit. The contact resistance losses for both the series-connected subcells and electrically independent subcells are accounted for by the lumped series resistance parameter.
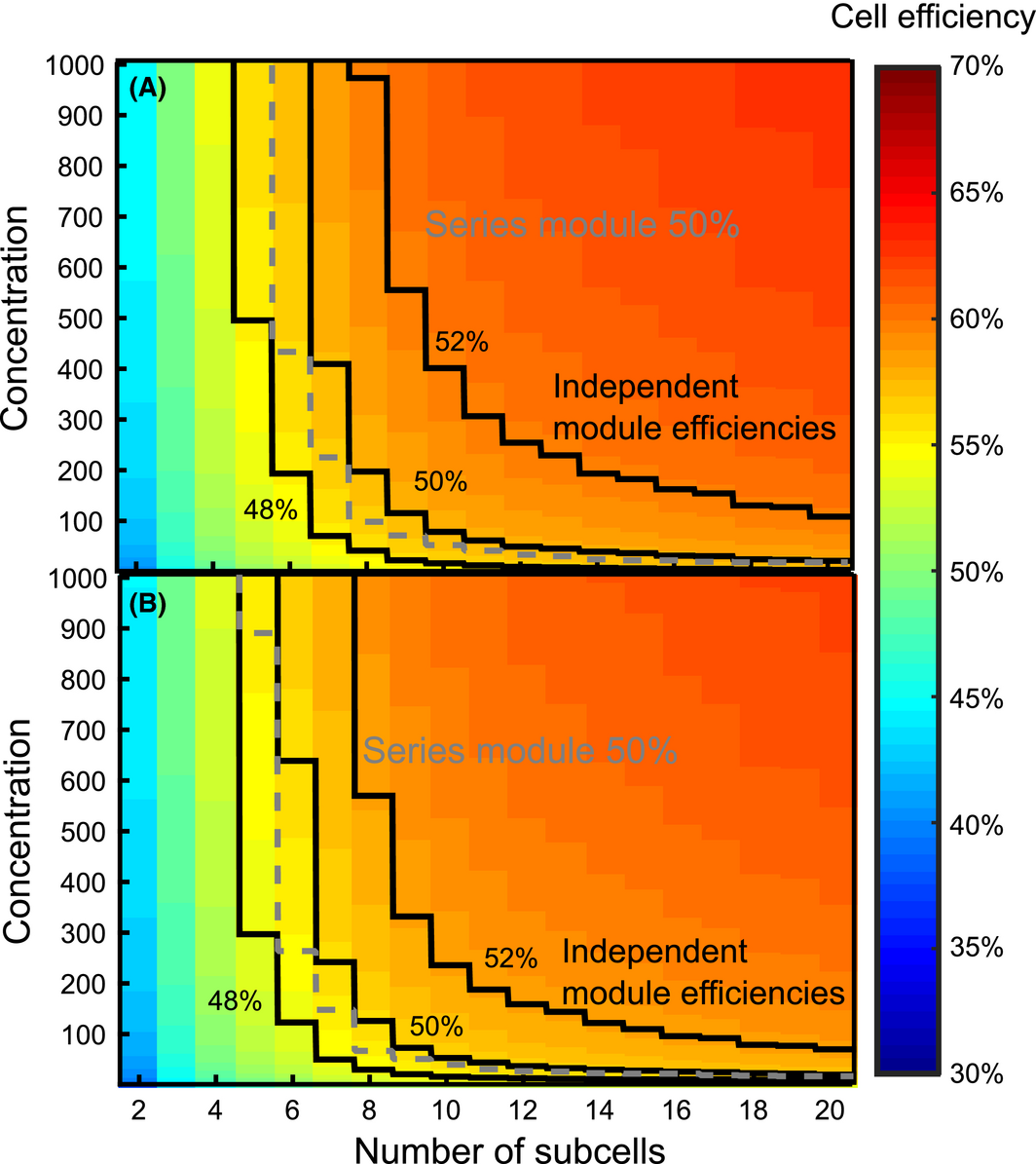
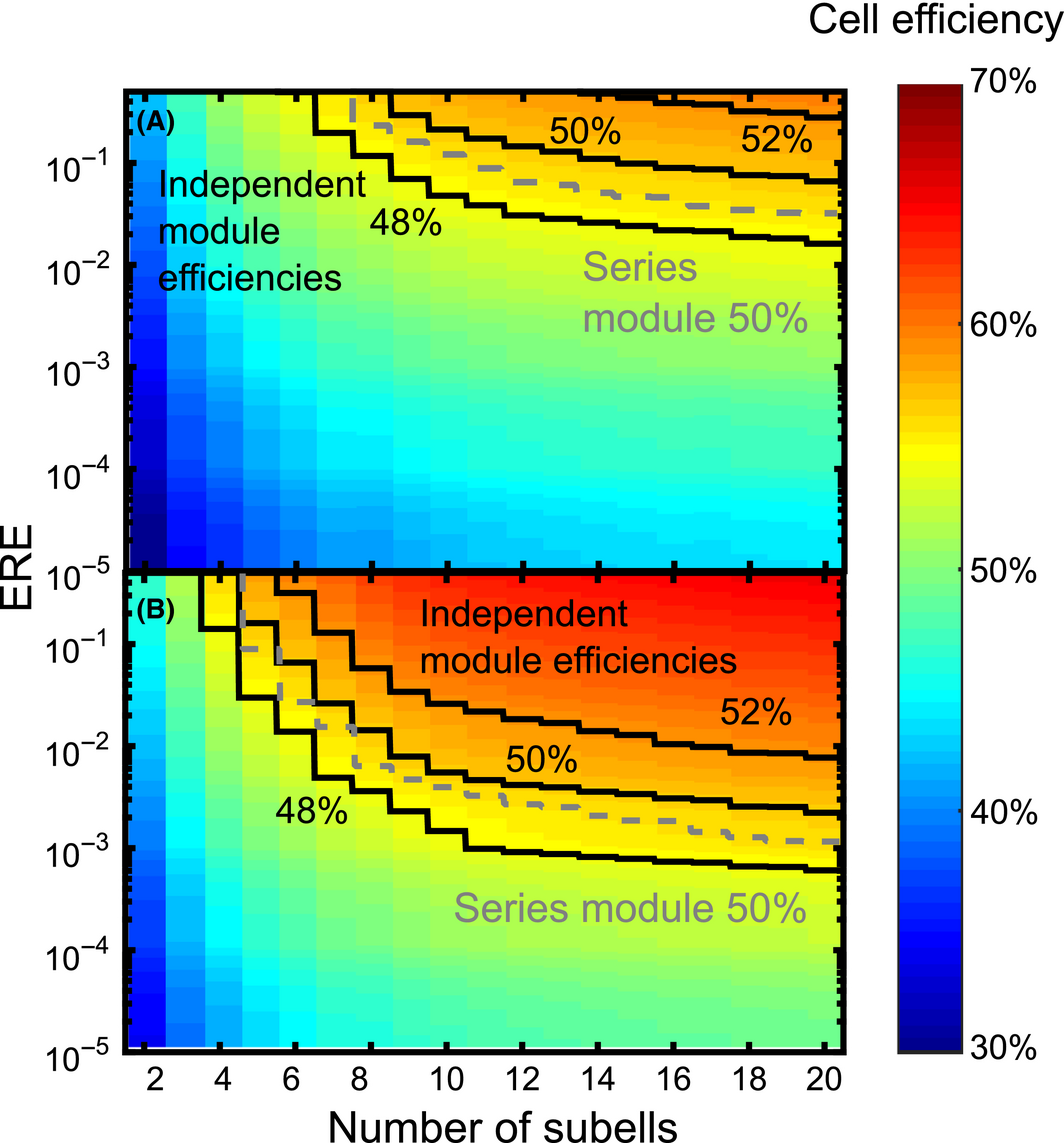
Figure 4 shows the two-dimensional plot of efficiency versus number of cells and concentration for independently connected modules with 2–20 subcells. The two panels of the figure show the cell ensemble efficiency under two different material parameters: (1) 3% ERE and 90% absorption efficiency; and (2) 5% ERE and 90% absorption efficiency. Marked on each plot are contours showing total module efficiency with a spectrum splitting optic with 90% optical efficiency and electrical system of 98% efficiency. Also included in Figure 4 are dashed contours showing the required concentration for a 50% efficient module with electrically series-connected subcells and a 90% optical efficiency (series-connected cell efficiency not shown on this 2D plot). The color scale corresponds to the efficiency of the photovoltaic cell under ideal illumination, analog to the flash test efficiency used to evaluate current monolithic MJSCs [37]. As the color scale indicates, both 3% and 5% ERE cells with four or more subcells can achieve 50% cell efficiency even at one sun concentration, in contrast to the current record four-junction cell efficiency of 46% at 508 suns. The higher efficiency predicted for the four subcell ensembles in Figure 4 is due in part to the higher spectral efficiency of the four optimal independent bandgaps (79.6%) compared to record cell spectral efficiency (77.8%).
|
|
|
Figure 4. Efficiency maps for independent cell spectrum splitting ensembles with 2–20 cells at different concentrations and in panel (A) 3% external radiative efficiency (ERE), 90% absorption, and panel (B) 5% ERE and 90% absorption. The color maps indicate the efficiency of the independent photovoltaic cell ensemble under ideal illumination and with series resistance losses. The solid contours indicate the minimum concentration required for an overall module efficiency assuming electrically independent subcells, an optical system with 90% efficiency and a 98% efficient electrical system. The dashed contours indicate the minimum concentration required for a 50% efficient module with series-connected subcells and 90% optical efficiency. |
These plots show the importance of ERE for achieving a high module efficiency. With the lower external radiative efficiency, as shown in panel (A), it requires at least seven subcells at a concentration of 400 suns to achieve a total module power conversion efficiency of 50% with 90% efficient optics and 98% efficient electronics. By contrast, the set of designs with 5% ERE and 90% absorption efficiency can achieve 50% module efficiency with realistic optical and electrical losses using a design with six subcells at 620 suns concentration. The concentration required decreases with larger numbers of subcells, and only 59 suns are required to achieve 50% module efficiency with 10 subcells at 5% ERE. This highlights the trade-off in complexity between the optical design and the cell design in achieving very high module efficiency.
The dashed contour showing the minimum concentration required for a module with series-connected subcells to achieve 50% efficiency shows the advantage conferred by series electrical connection for the subcells. The series-connected module assumes 90% optical efficiency and no additional electrical losses to account for the easier task of routing and combining power for cells that are already series connected [38]. Despite the disadvantage in spectral efficiency the series-connected ensembles have higher performance than the corresponding independent ensembles once the losses due to contact resistance are accounted for. This efficiency advantage for contacted systems is due to the electrical configuration. Monolithic series-connected cells have one set of contacts for the entire ensemble and consequently the voltage loss due to contact resistance is applied once to the entire ensembles voltage. By contrast, ensembles with independent subcells require unique contacts for each subcell, which in turn cause a loss of voltage for each subcell. Because we expect the lumped series resistance for series-connected ensembles to be similar to that for independent ensembles, the loss due to lumped series resistance will increase with the number of subcells for the independent ensembles while remaining relatively constant across all series-connected designs, for a given concentration.
However, the contours in Figure 4 assume that monolithic series-connected subcells are capable of achieving the same ERE as physically separated cells. In fact, as Table 2 shows, the ERE of a subcell is highly dependent on its optical environment, as well as dependent on the material quality of the cell [39, 40]. Placing the subcells on high-quality back reflectors, as is possible for the electrically independent subcells, improves the cell ERE by preventing light from escaping through the back of the cell and by allowing thinner absorber layers, which reduces bulk recombination. Monolithic series-connected MJSCs cannot incorporate back reflectors between the subcells, and consequently must use thicker absorber layers to achieve the equivalent light path through the material. Monolithic cells exhibit lower radiative efficiency due to the larger amount of nonradiative bulk recombination in the thicker absorber layers and due to the loss of radiatively recombined photons that escape into the surrounding material. For a monolithic MJSC to achieve the ERE values in Figure 4, the material would require a much lower defect density than an ensemble of electrically independent subcells placed on back reflectors. This is consistent with the fact that practical series-connected MJSCs with four subcells require substantial concentration to achieve efficiencies over 45% [7, 11]. Finally, this analysis has assumed that the optimal bandgap combinations for series-connected ensembles can be grown monolithically, a feat that has not yet been achieved for ensembles with more than three subcells.
Figure 5 presents another view of the interaction among number of cells, concentration, and ERE in determining overall module efficiency. This plot shows the efficiency of independently connected cell ensembles at 10 suns and 500 suns concentration with different ERE values. The solid contours again show total module efficiency with 90% efficient optics and a 98% efficient electrical system for electrically independent subcells and the dashed contour shows the module efficiency for series-connected subcells with 90% efficient optics. Considering second panel (B), the plot at 500 suns concentration, at 1% ERE, this plot indicates that nine independent subcells will be required to achieve 50% module efficiency. The steepness of the contours in the region from 4 to 10 cells highlights the value of improvements in ERE. An increase from 1% to 2% ERE reduces the number of independent subcells required to achieve 50% from nine to eight, which would constitute a reduction in potential cost and complexity. By contrast, the plot for 10 suns shows that low concentration modules will require 10 or more independent subcells with average radiative efficiency of roughly 20%, equal to current record performance devices [34].
|
|
|
Figure 5. Efficiency map for independently connected spectrum splitting ensembles with 2–20 cells at (A) 10 suns and (B) 500 suns at different external radiative efficiency (ERE) values. The solid contours show the minimum ERE required for overall module efficiency for ensembles with electrically independent subcells with 90% optical efficiency and 98% DC electrical combination efficiency. The dashed contours show the minimum ERE required for modules with series-connected subcells and 90% optical efficiency. |
The contour showing the minimum ERE for series-connected modules to achieve 50% highlights the challenge for designs with monolithic cells to achieve ultra-high efficiency. The reduced loss from series resistance does translate to a lower minimum ERE required for the series-connected ensembles. However, note that 0.2% ERE, the average value for the experimental on-wafer cells in Table 2, corresponds to a need for an ensemble with 13 series-connected subcells with optimal bandgaps at 500 suns to achieve 50% module efficiency. At 1% ERE, a series-connected ensemble with seven subcells at the optimal bandgaps can achieve 50% efficiency at 500 suns. Achieving an ERE of 1% in a monolithic ensemble that lacks optical confinement will require exceptionally high material quality. Identifying materials for the optimal bandgaps of these subcells that can be grown or assembled while maintaining that material quality adds to the challenge and mitigates the efficiency advantage of the lower series resistance losses.
Conclusion
Achieving very high module efficiency (>50%) for photovoltaic solar conversion requires a combination of a large number of high-quality cells, an efficient optical system to split the incident spectrum correctly among those cells and a moderate-to-high degree of concentration. The radiative quality of the cells will determine the optimum bandgaps of the cells in an ensemble and the radiative and absorption efficiencies together with a lumped series resistance determine how far the cell performance departs from the ideal detailed balance limit. By including these three parameters into the detailed balance calculation, we have predicted that a module efficiency of 50% or greater will be possible with 7–10 electrically independent subcells in a spectral splitting optic at 300–500 suns concentration, assuming a 90% optical efficiency and 98% electrical efficiency. Alternatively, a series-connected cell with 6–8 subcells at 100–300 suns could achieve this efficiency if the cells can reach an ERE of 3% or greater and can be manufactured with the optimal bandgaps.
While this analysis has been presented as an exploration of the minimum requirements for the photovoltaic cells, it is important to note that it also contains some aggressive requirements for the quality of the optical and electrical systems. This analysis has not presented any specific optical spectrum splitting concepts. Instead, the 90% optical efficiency used to predict module performance serves as a baseline performance requirement for any spectrum splitting concept under consideration. This value is consistent with reported spectrum splitting optical efficiencies [15, 41]. Similarly, the 98% efficiency of the DC electrical system serves as a target for power management systems [38]. This approach was used to develop specific implementations of spectrum splitting with practically achievable cells and optics. These designs are being developed as prototypes and are detailed in other publications [42-44].
Conflict of Interest
None declared.
References
- Green, M. A., K. Emery, Y. Hishikawa, W. Warta, and E. D. Dunlop. 2012. Solar cell efficiency tables (version 40). Prog. Photovoltaics Res. Appl.20:606–614.
- Green, M. A.2011. Limiting photovoltaic efficiency under new ASTM International G173-based reference spectra. Prog. Photovoltaics Res. Appl.19: Pp 954–959.
- Polman, A., and H. A. Atwater. 2012. Photonic design principles for ultrahigh-efficiency photovoltaics. Nat. Mater.11:174–177.
- King, R. R., D. C. Law, C. M. Fetzer, R. A. Sherif, K. M. Edmondson, S. Kurtz et al. 2005. Pathways to 40% efficient concentrator photovoltaics. Pp. 6–10in20th European Photovoltaic Solar Energy Conference and Exhibition.
- Chiu, P., S. Wojtczuk, X. Zhang, C. Harris, D. Pulver, and M. Timmons. 2011. 42.3% Efficient InGaP/GaAs/InGaAs concentrators using bifacial epigrowth. Pp. 000771–000774in37th IEEE Photovoltaic Specialists Conference.
- Wesoff, E.2013. Sharp hits record 44.4% efficiency for triple-junction solar cell: greentech media. Greentech Media. Available at http://www.greentechmedia.com/articles/read/Sharp-Hits-Record-44.4-Efficiency-For-Triple-Junction-Solar-Cell (accessed 27 June 2013).
- Green, M. A., K. Emery, Y. Hishikawa, W. Warta, and E. D. Dunlop. 2015. Solar cell efficiency tables (Version 45). Prog. Photovoltaics Res. Appl.23:1–9.
- Colthorpe, A.Soitec-Fraunhofer ISE multi-junction CPV cell hits world record 46% conversion efficiency | PV-Tech. Available at http://www.pv-tech.org/news/soitec_fraunhofer_ise_multi_junction_cpv_cell_hits_world_record_46_conversi (accessed 15 July 2015).
- Gifford, J.2015. Soitec hits 38.9% with four-junction CPV cell: pv-magazine. PV Magazine. Available at http://www.pv-magazine.com/news/details/beitrag/soitec-hits-389-with-four-junction-cpv-cell_100019952/#axzz3lGi8yNcg (accessed 9 September 2015).
- Green, M. A., K. Emery, Y. Hishikawa, W. Warta, and E. D. Dunlop. 2015. Solar cell efficiency tables (version 46). Prog. Photovoltaics Res. Appl.23:805–812.
- Steiner, M., G. Siefer, T. Schmidt, M. Wiesenfarth, F. Dimroth, and A. W. Bett. 2016. 43% sunlight to electricity conversion efficiency using CPV. IEEE J. Photovolt.6:1020–1024.
- Green, M. A., K. Emery, Y. Hishikawa, W. Warta, and E. D. Dunlop. 2016. Solar cell efficiency tables (version 47). Prog. Photovoltaics Res. Appl.24:3–11.
- King, R. R., D. Bhusari, D. Larrabee, X. Liu, E. Rehder, K. Edmondson et al. 2012. Solar cell generations over 40% efficiency. Prog. Photovoltaics Res. Appl.20:801–815.
- Moon, R. L., L. W. James, H. A. VanderPlas, and N. J. Nelson. 1978. Performance of an Al0.92 Ga0.08As/Al0.14 Ga0.86As solar cell in concentrated sunlight. Appl. Phys. Lett.33:196.
- Barnett, A., D. Kirkpatrick, C. Honsberg, D. Moore, M. Wanlass, K. Emery et al. 2009. Very high efficiency solar cell modules. Prog. Photovoltaics Res. Appl.17:75–83.
- Imenes, A. G., and D. R. Mills. 2004. Spectral beam splitting technology for increased conversion efficiency in solar concentrating systems: a review. Sol. Energy Mater. Sol. Cells84:19–69.
- Gross, B., G. Peharz, G. Seifer, M. Peters, J. C. Goldschmidt, M. Steiner et al. 2009. Highly efficient light splittig photovoltaic receiver. Pp. 21–25in24th European Photovoltaic Solar Energy Conference.
- Wang, X., N. Waite, P. Murcia, K. Emery, M. Steiner, F. Kiamilev et al. 2012. Lateral spectrum splitting concentrator photovoltaics: direct measurement of component and submodule efficiency. Prog. Photovoltaics Res. Appl.20:149–165.
- Green, M. A., M. J. Keevers, I. Thomas, J. B. Lasich, K. Emery, and R. R. King. 2015. 40% efficient sunlight to electricity conversion. Prog. Photovoltaics Res. Appl.23:685–691.
- Kayes, B. M., H. Nie, R. Twist, S. G. Spruytte, F. Reinhardt, I. C. Kizilyalli et al. 2011. 27.6% Conversion efficiency, a new record for single-junction solar cells under 1 sun illumination. Pp. 000004–000008inConference Record of the IEEE Photovoltaic Specialists Conference.
- Geisz, J. F., M. A. Steiner, I. García, S. R. Kurtz, and D. J. Friedman. 2013. Enhanced external radiative efficiency for 20.8% efficient single-junction GaInP solar cells. Appl. Phys. Lett.103:41118.
- Yoon, J., S. Jo, I. S. Chun, I. Jung, H.-S. Kim, M. Meitl et al. 2010. GaAs photovoltaics and optoelectronics using releasable multilayer epitaxial assemblies. Nature465:329–333.
- Eisler, C. N., E. D. Kosten, E. C. Warmann, and H. A. Atwater. 2013. Spectrum splitting photovoltaics: polyhedral specular reflector design for ultra-high efficiency modules. Pp. 1848–1851inIEEE 39th Photovoltaic Specialists Conference.
- Shockley, W., and H. J. Queisser. 1961. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys.32:510.
- Henry, C. H.1980. Limiting efficiencies of ideal single and multiple energy-gap terrestrial solar cells. J. Appl. Phys.51:4494–4500.
- Kirkpatrick, S., C. D. Gelatt, and M. P. Vecchi. 1983. Optimization by simulated annealing. Science220:671–680.
- Kurtz, S., D. Myers, W. E. McMahon, J. Geisz, and M. Steiner. 2008. A comparison of theoretical efficiencies of multi-junction concentrator solar cells. Prog. Photovolt.16:537–546.
- Froitzheim, A., R. Stangl, L. Elstner, M. Kriegel, and W. Fuhs. 2003. AFORS-HET: a computer-program for the simulation of heterojunction solar cells to be distributed for public use. Pp. 279–282inProceedings of the 3rd world conference on photovoltaic energy conversion.
- Varache, R., C. Leendertz, M. E. Gueunier-Farret, J. Haschke, D. Muñoz, and L. Korte. 2015. Investigation of selective junctions using a newly developed tunnel current model for solar cell applications. Sol. Energy Mater. Sol. Cells141:14–23.
- Ahrenkiel, R. K., R. Ellingson, S. Johnston, J. Webb, J. Carapella, and M. Wanlass. 1999. Recombination lifetime of In[sub x]Ga[sub 1−x]As alloys used in thermophotovoltaic converters. AIP Conference Proceedings460:282–288.
- Vurgaftman, I., J. R. Meyer, and L. R. Ram-Mohan. 2001. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys.89:5815.
- Sermage, B., J. L. Benchimol, and G. M. Cohen. 1998. Carrier lifetime in p-doped InGaAs and InGaAsP. Pp. 758–760in1998 International Conference on Indium Phosphide and Related Materials (Cat. No. 98CH36129), 2.
- King, R. R., C. M. Fetzer, K. M. Edmondson, D. C. Law, P. C. Colter, H. L. Cotal et al. 2004. Metamorphic III-V materials, sublattice disorder, and multijunction solar cell approaches with over 37% efficiency. in19th European Photovoltaic Solar Energy Conference and Exhibition.
- Green, M. A.2012. Radiative efficiency of state-of-the-art photovoltaic cells. Prog. Photovoltaics Res. Appl.20:472–476.
- Ross, R. T.1967. Some thermodynamics of photochemical systems. J. Chem. Phys.46:4590–4593.
- Steiner, M., S. P. Philipps, M. Hermle, A. W. Bett, and F. Dimroth. 2011. Validated front contact grid simulation for GaAs solar cells under concentrated sunlight. Prog. Photovoltaics Res. Appl.19:73–83.
- Fanetti, E.1981. Flash technique for GaAs concentrator solar cell measurement. Electron. Lett.00:469–470.
- Flowers, C. A., C. N. Eisler, and H. A. Atwater. 2014. Electrically independent subcircuits for a seven-junction spectrum splitting photovoltaic module. Pp. 1339–1343inIEEE 40th Photovoltaic Specialist Conference, PVSC 2014.
- Braun, A., E. A. Katz, D. Feuermann, B. M. Kayes, and J. M. Gordon. 2013. Photovoltaic performance enhancement by external recycling of photon emission. Energy Environ. Sci.6:1499.
- Kosten, E. D., J. H. Atwater, J. Parsons, A. Polman, and H. A. Atwater. A path to a 40% efficient single junction solar cell by limiting light emission angle.
- Eisler, C. N., E. C. Warmann, C. A. Flowers, M. Dee, E. D. Kosten, and H. A. Atwater. 2014. Design improvements for the polyhedral specular reflector spectrum-splitting module for ultra-high efficiency (>50%). Pp. 2224–2229inIEEE 40th Photovoltaic Specialist Conference (PVSC).
- Eisler, C. N., C. A. Flowers, P. Espinet, S. Darbe, E. C. Warmann, J. Lloyd et al. 2015. Designing and prototyping the polyhedral specular reflector, a spectrum-splitting module with projected >50% efficiency. inIEEE 42nd Photovoltaic Specialist Conference (PVSC).
- Xu, Q., Y. Ji, B. Riggs, A. Ollanik, N. Farrar-foley, H. Jim et al. 2016. A transmissive, spectrum-splitting concentrating photovoltaic module for hybrid photovoltaic-solar thermal energy conversion. Sol. Energy137:585–593.
- Escarra, M. D., S. Darbe, E. C. Warmann, and H. A. Atwater. 2013. Spectrum-splitting photovoltaics: holographic spectrum splitting in eight-junction, ultra-high efficiency module. Pp. 1852–1855inIEEE 39th Photovoltaic Specialist Conference.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?