Energy production advantage of independent subcell connection for multijunction photovoltaics

Abstract

Increasing the number of subcells in a multijunction or “spectrum splitting” photovoltaic improves efficiency under the standard AM1.5D design spectrum, but it can lower efficiency under spectra that differ from the standard if the subcells are connected electrically in series. Using atmospheric data and the SMARTS multiple scattering and absorption model, we simulated sunny day spectra over 1 year for five locations in the United States and determined the annual energy production of spectrum splitting ensembles with 2–20 subcells connected electrically in series or independently. While electrically independent subcells have a small efficiency advantage over series-connected ensembles under the AM1.5D design spectrum, they have a pronounced energy production advantage under realistic spectra over 1 year. Simulated energy production increased with subcell number for the electrically independent ensembles, but it peaked at 8–10 subcells for those connected in series. Electrically independent ensembles with 20 subcells produce up to 27% more energy annually than the series-connected 20-subcell ensemble. This energy production advantage persists when clouds are accounted for.

Introduction

The most efficient photovoltaic devices under the AM1.5 spectrum use the design concept of dividing the solar spectrum among multiple photovoltaic subcells, or “spectrum splitting” to improve performance beyond the capabilities of single junction designs [1-3]. However, tailoring the selection of subcell band gaps to the specific design spectrum raises the possibility of increased sensitivity of efficiency to spectral variation as experienced by systems operating under natural sunlight, which in turn has the potential to compromise integrated energy production [4, 5]. While efficiency measurements under the AM1.5 spectrum provide an essential means of standardized comparison between different photovoltaic technologies, the true product of photovoltaics is cumulative energy production over days and months with conditions that can vary widely from the standard test. The photovoltaics community has an increasing interest in predicting both the standard test efficiency and the energy production behavior of different photovoltaic technologies, in particular identifying the effects of design decisions on energy production [6-8]. Here, we present an examination of the relative effect on energy production for spectrum splitting designs with 2–20 subcells that are either connected electrically in series or are electrically independent of one another.

The most common form of spectrum splitting photovoltaics at present consists of cells with two to four subcells that are monolithically integrated and connected in series electrically [1, 9, 10]. The incident sunlight is divided among the subcells by sequential absorption, with high band gap junctions filtering out the high-energy photons and transmitting the lower energy light for absorption by the subcells below. The electrical series connection forces all subcells to generate the same current, which in turn determines the optimal combination of band gaps for a given spectrum. An alternate configuration for spectrum splitting uses a separate optical element to direct photons in different energy ranges onto physically isolated subcells [11-13]. In this approach, the subcells can be electrically independent from one another, removing the current matching requirement and constraint on band gap selection. Most of the efficiency difference between spectrum splitting photovoltaic cells will be determined by the number of subcells and how close their band gap energies are to the optimum values for the AM1.5 spectrum [2, 14]. Cells with electrically independent subcells have a small efficiency advantage over series-connected cells with the same number of junctions because they can achieve a better match between band gap energies and the spectrum when relieved of the need to match currents in all subcells [15].

While the monolithic, series-connected spectrum splitting configuration sacrifices only a small amount of efficiency under the design spectrum in exchange for simplified optical and electrical integration requirements, the series connection makes the device sensitive to illumination conditions that differ from the standard [4, 16]. All subcells will absorb an equal number of photons under the AM1.5 spectrum, but under the varying spectrum of natural sunlight, some subcells may be over illuminated relative to the others, and this excess energy cannot be collected. More damaging to cell performance, a subcell that is under illuminated will constrain the current through the entire device and can substantially reduce total device efficiency [17]. The degree to which field performance resembles performance under the standard will be determined by how much the photon density in the spectral bands for each subcell of natural sunlight tends to vary from the AM1.5 spectrum. Currently deployed spectrum splitting photovoltaics use only 2–4 spectral bands, which may reduce sensitivity to fine variations [4]. However, designs with increasing numbers of subcells are under consideration for higher cell efficiencies and may suffer more strongly from this effect in the series-connected configuration [10]. Previous efforts to predict the energy production of spectrum splitting photovoltaics have examined multijunction solar cells with up to six series-connected subcells and a variety of three subcell, electrically independent band gap combinations [18-21]. This paper extends the analysis to large numbers of subcells and locations that exhibit wider variation in atmospheric conditions, which are important areas of inquiry as spectrum splitting photovoltaics become increasingly ambitious in terms of subcell number and deployment scope.

Determining the impact of electrical configuration and number of subcells on energy production requires analyzing the performance of different designs under a set of spectra that have a degree and type of variation comparable to that experienced in the field. The spectrum of natural sunlight at a particular location on earth and a point in time varies depending on the emission of the sun, the composition-dependent transmission properties of the atmosphere, and the path length through the atmosphere [22]. The suns spectrum is comparatively stable relative to the other factors, and accounts for only 0.3% of the spectral variation [23]; consequently, this analysis omits this source of variation. The atmospheric path length is determined by location, elevation, and time of day and year, making 1 year a logical length of time over which to simulate energy production [24]. The absorptivity of the atmosphere depends on the concentration of water, CO₂, O₃, and other gaseous pollutants as well as the absorption and scattering of suspended aerosols [25]. While spectrally resolved irradiance data are not typically available at most locations, the spectrum can be simulated using extensive existing databases of typical atmospheric conditions and aerosol optical depth [26]. Although the actual spectrum at a particular location and point in time will likely differ from the simulation based on average conditions, the simulated spectra can reproduce the typical degree of spectral variation for the location and times of year considered. In turn, these spectra can be used to predict the typical performance of photovoltaic systems under that locations varying illumination conditions. This analysis compares the energy production of spectrum splitting ensembles with 2–20 subcells in both electrically independent and in series configurations under one years worth of simulated spectra for five locations in the United States.

Methods

Spectrum splitting ensembles with 2–20 subcells connected electrically in series and independently and optimized for the AM1.5D spectrum were analyzed by detailed balance calculation under spectra simulated to represent the typical annual range of variation for multiple locations in the United States [27]. The detailed balance calculation assumed ideal cells operating at 300 K and under 500 suns concentration, and the series-connected cells were constrained to pass the same current through all subcells, using Henrys method [28]. The electrically independent cells allowed each subcell to operate at its individual max power point subject to the illumination conditions. The independently connected ensembles were optimized through a simulated annealing process. The band gap combinations for series and independent ensembles are tabulated in the supplemental information. The calculation assumed perfect spectral splitting among the subcells. The assumption of ideal cells will result in higher predictions of energy production than is realistic, however, many common cell nonidealities such as nonradiative recombination are not spectrally sensitive, and consequently, the relative behavior of nonideal cells will follow the same patterns as ideal cells.

Sunny day spectra

Simulated spectra were generated at hourly intervals from 8 am to 5 pm for 365 days to account for the most productive photovoltaic energy production hours of the day. These hours will neglect some period of illumination in the morning and evening of the summer months, however, the analysis will show that these hours cumulatively account for a small portion of the annual irradiance. In addition, neglecting these low-light hours will reduce the effect of the electrical connection difference and understate the advantage of the electrically independent ensembles. Consequently, this limitation of the input spectra is conservative in terms of estimating the effect size. For each spectrum, the air mass was determined by geographic location, date and time, and the temperature, pressure, and dew point were taken from hourly normal values published by NOAA [29]. Daily values for aerosol optical depth and precipitable water were generated using monthly normal and standard deviation values for each location as published from the AERONET data set [30]. CO₂ was set to 370 ppm, the annual average value for the year 2000, and O₃ was set to 0.3438 cm, the value in the U.S. Standard Atmosphere [31]. These atmospheric conditions were used as inputs to the Simple Model of the Atmospheric Radiative Transfer of Sunshine (SMARTS) multiple scattering and absorption model, which then calculated the direct spectral irradiance over wavelengths from 280 to 4000 nm [32]. Spectra were simulated for Phoenix, AZ, Albuquerque, NM, Houston, TX, Tulsa, OK and Knoxville, TN. Phoenix was selected as a location with high direct irradiance (DNI) where concentration photovoltaics (CPV) is already of interest, and because high-quality data on atmospheric conditions were available for input to the SMARTS program. The other locations were selected for the availability of atmospheric data and to explore the effects of elevation, latitude, and climate. Together these locations span a wide range of climate conditions and latitude in the portion of the United States with a high solar resource. The power production under each spectrum was then multiplied by 1 h to integrate energy production per square meter of aperture area over the course of 1 year.

The simulated spectra will not exactly reproduce the irradiance conditions at any location and time because they use average values for the atmospheric conditions. In addition, the method of generating aerosol optical depth and precipitable water values will not capture the full degree of correlation between those values. However, the range of spectral variation and overall distribution of spectral irradiances generated should resemble the variability experienced at these locations, as with previous analysis efforts [18, 20, 21, 33]. Finally, the simulated spectra all assume an absence of cloud cover at the time and date for which they are generated. Consequently, the simulated spectra will overestimate the total irradiance and energy production for these locations.

Cloud correction

While the sunny day spectra are a good way to investigate the sensitivity of spectrum splitting photovoltaic efficiency to changing atmospheric conditions, all locations experience some amount of cloud cover that will reduce the direct normal irradiance. The prevalence of clouds at a given location can vary greatly with time due to the local climate, and therefore they may interact with the spectral variation to have an unpredictable effect on energy production. Unfortunately, it is difficult to obtain spectrally resolved data that account for cloud cover and identify the direct and diffuse components of the total irradiance. To explore the effect of clouds on energy production for these specific locations, we used data from the National Solar Radiation Database from NREL to determine the average percentage of expected DNI transmission for every hour over the course of the year. The data consist of simulated total DNI, global horizontal, and diffuse total irradiance hourly for every day for years from 1991 to 2010 as obtained from the METSTAT model based on local weather station data, local and satellite-based measurements of aerosol optical depth, ozone and precipitable water, and automated local and satellite-based observations of cloud cover and ground albedo [34]. In addition, the data include expected DNI, global horizontal, and diffuse total irradiance as determined by a sunny day model incorporating the same measurements of AOD, ozone, CO₂, precipitable water, local pressure, and humidity for the location but with the assumption of no cloud cover. For each hour considered in the energy production simulation, we calculated the ratio of DNI modeled including cloud observations to the sunny day model prediction of DNI over each year for all locations. We adopted this percentage as the hourly average DNI transmission for that particular hour. We then averaged the hourly DNI transmission over the 20 years of data for each location and multiplied the expected energy production for each hour by that percentage.

It is important to note two assumptions here. First, this method of derating the DNI transmission assumes that clouds have a uniform spectral impact on transmission. This assumption may be reasonable for circumstances with intermittent clouds that eliminate direct transmission for some percentage of each hour, but it is not likely to be valid for thin, persistent clouds that partially screen the sun while allowing some fraction of direct irradiance. Unfortunately, we were unable to identify a way to distinguish these circumstances in the data or to determine the spectral transmission of clouds in general. The decision to treat the cloud transmission as spectrally uniform may reduce the degree of variation in the simulated spectra relative to a model for cloud transmission with spectral resolution. However, to the best of our knowledge, there are no comprehensive data on the spectral transmission of clouds that would be useful to this analysis. Therefore, our assumption of spectrally uniform transmission is conservative in that it will most likely underestimate the true sensitivity of energy production to atmospheric conditions. Second, the decision to scale the energy production by the DNI transmission ignores any decrease in efficiency due to deconcentration of the light on the solar cells. Because the cells are simulated to operate at 500 suns, the effect on efficiency will be negligible except at very low transmission values, where the effect on cumulative energy production difference will be small.

Results and Discussion

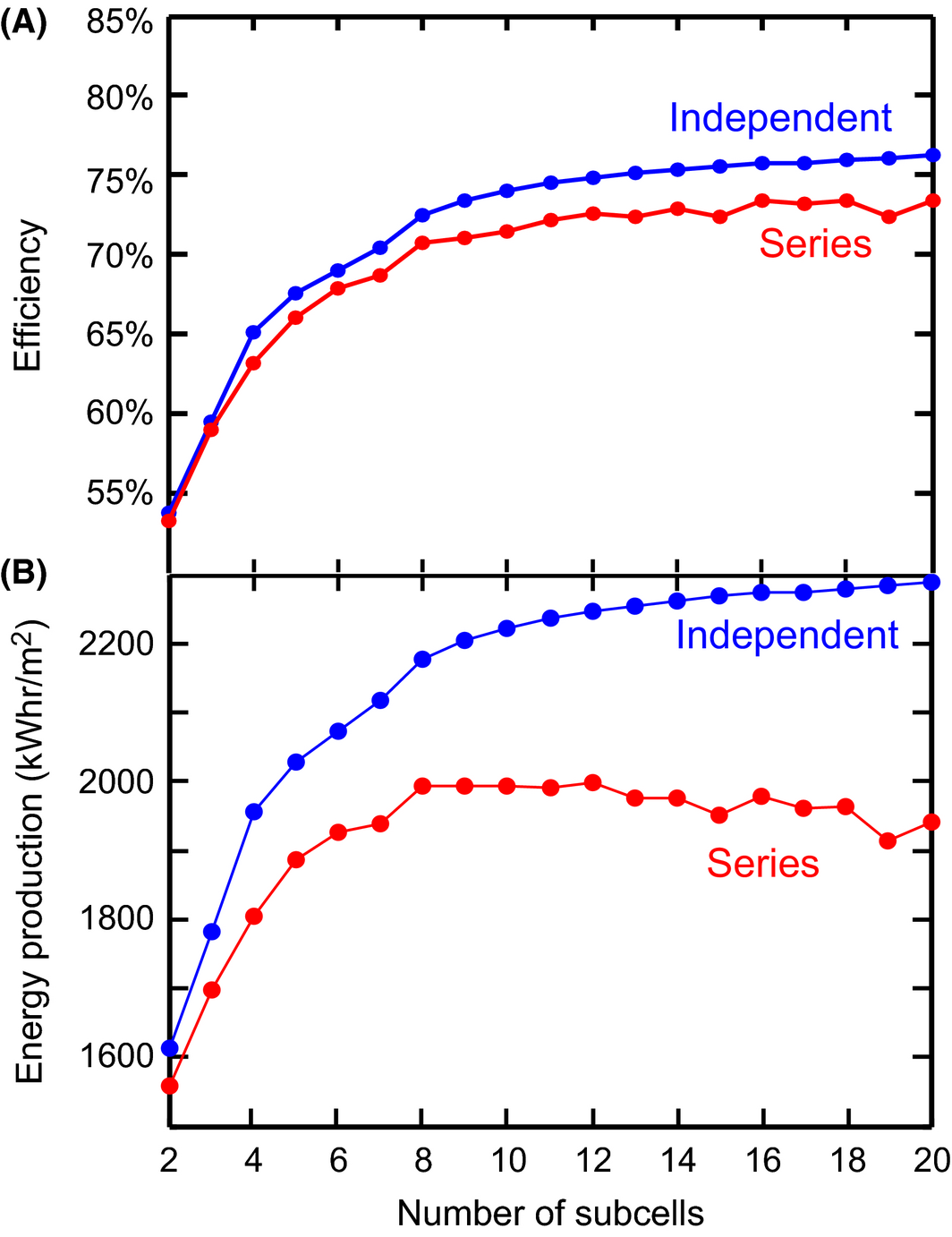
The efficiency of spectrum splitting ensembles with electrically independent subcells is only slightly greater than the efficiency of series-connected ensembles under the design spectrum of AM1.5D as shown in Figure 1(A). The two-cell series ensemble exhibits 99% of the power efficiency of the independent ensemble under AM1.5D, while the 20-subcell series ensemble exhibits 98.4% of the independent power. The efficiency of both sets of ensembles increases with the number of subcells, with some deviation for the 15-subcell series-connected ensemble, which suffers from the current matching constraint aligning poorly with the absorption bands in the AM1.5D spectrum. However, the electrically independent ensembles have a significant energy production advantage that increases with the number of subcells. Taking Phoenix, AZ as the first case, Figure 1 panel (B) shows the two subcell series ensemble produces 3.4% less energy than the electrically independent two subcell ensemble. For 20 subcells, the series connection reduces energy production by 14.8% relative to the electrically independent design. In addition, the simulated annual energy production of independent ensembles increases as the number of subcells increases from 2 to 20 while the series connected energy production peaks with 12 subcells and declines as more subcells are added, despite the higher design efficiency of the ensembles with more subcells. The discrepancy between the energy production and design efficiency trends indicates a greater difference in efficiency between the series and independent ensembles over some portion of the year.

Figure 1. (A) Efficiency versus number of subcells for ideal spectrum splitting ensembles with electrically in series and independent subcells at 500 suns concentration under the AM1.5D spectrum. (B) Simulated annual energy production for Phoenix, AZ for electrically independent and in series spectrum splitting ensembles operating at 500 suns concentration. The energy production units are kWh/m2 of aperture area.

Performance under varying irradiance levels

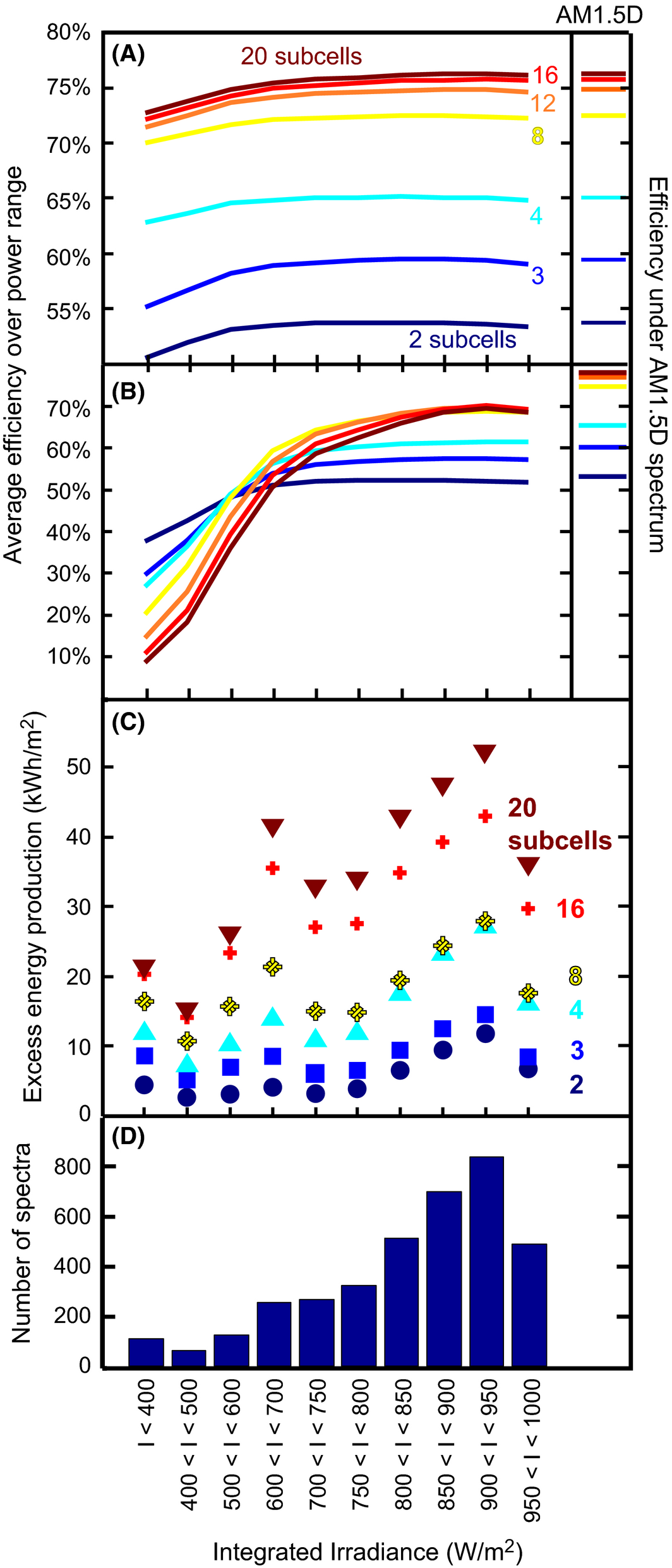
A closer examination of the simulated spectra and efficiency trends for Phoenix is useful for identifying the cause of this efficiency deviation. The simulated spectra exhibit a large amount of variation over the course of a day and year. This variation includes both spectral composition and total irradiance level. Figure 2 panel (D) shows the number of spectra that have integrated direct irradiance levels falling in 10 different ranges. While many of the simulated spectra have a total irradiance similar to the 900 W/m² set by the AM1.5D standard, 485 spectra (13% of the total) have irradiance greater than 950 W/m² and 1126 (31%) have irradiance less than 800 W/m². The spectra that fall in these 10 irradiance ranges are plotted in the supplemental information. Figure 2 panels (A) and (B) show the efficiency of a subset of independent and series ensembles averaged over all the spectra in the power ranges shown in panel (D). The small inset panel at the right shows the efficiency of the ensembles under the AM1.5D design spectrum.

Figure 2. (A) Efficiency of electrically independent spectrum splitting ensembles averaged over all spectra in 10 different irradiance level ranges. The far right panel shows efficiency of the independent ensembles under the AM1.5D spectrum. (B) Efficiency of series-connected spectrum splitting ensembles averaged over all spectra in the irradiance level ranges. The far right panel shows the series-connected efficiency under AM1.5D. Note the difference in efficiency range for panels (A) and (B). (C) The cumulative energy produced by the electrically independent ensembles in excess of that produced by the series-connected ensembles over the then different irradiance level ranges. (D) Histogram of spectra showing the relative prevalence of the different irradiance levels.

Panel (A) shows the efficiency of the independent ensembles is on average very consistent over a wide range of irradiance levels. The average efficiency at the lowest irradiance range is 5.7% lower than the efficiency over the 900–950 W/m² range for two cells and 4.7% lower for 20 cells. At every power range, the average efficiency increases with increasing subcell number, and overall, the average efficiencies are close to the efficiency under AM1.5D.

By contrast, panel (B) shows the efficiency of the series-connected ensembles averaged over the spectra in the same power bins. Again, the inset panel at right shows the efficiency of the ensembles under the AM1.5D spectrum. The series-connected ensembles show a much larger sensitivity to the irradiance level in their average efficiency. The two-cell ensemble efficiency in the lowest power range is only 72% of the average efficiency in the 900–950 W/m² range. Ensembles with larger numbers of subcells exhibit a larger decrease in efficiency as the irradiance level deviates from the 900 W/m² level, including a strong decrease in efficiency at the highest irradiance levels.

The decrease in efficiency with declining irradiance becomes steeper as more subcells are incorporated into the ensembles, and at irradiance levels less than 500 W/m², the average efficiency decreases as the number of subcells increases. In addition, the peak average efficiency for the series-connected ensembles does not correspond to the 20-subcell ensemble. Instead, the 16-subcell ensemble has the highest average efficiency in the 900–950 W/m² range. Finally, at all irradiance levels, all series-connected ensembles have an average efficiency that is substantially lower than the efficiency under the AM1.5D spectrum, indicating significant differences between the standard spectrum and the realistic spectra regardless of irradiance level. For these ensembles, the design efficiency is not a good predictor of efficiency under the changing conditions in deployment.

Figure 2 panel (C) shows the combined energy production advantage of the independent ensembles relative to the series-connected ensembles for the different irradiance ranges. The energy production advantage increases with number of subcells at all irradiance levels, and the relative magnitude of the advantage compared to the combined irradiance at the different ranges suggests that the independent ensembles enjoy two slightly different advantages over the series ensembles. First, note that averaged over all numbers of subcells, 60% of the excess energy of the independent ensembles is generated under spectra with more than 750 W/m² irradiance. The spectra in this range constitute 84% of the total irradiance over the year. This additional energy production at high irradiance levels can be considered an efficiency advantage for independent ensembles due to improved spectral utilization. At the low-power level, spectra with less than 750 W/m² constitute 16% of the cumulative annual irradiance. Series-connected ensembles exhibit low average efficiency levels under these low irradiance spectra and produce little energy. Compared to the low energy production of the series-connected ensembles, the energy production of the independent ensembles under these low-power spectra can be considered an extended capacity factor allowing the independent ensembles to generate power under illumination conditions that are unfavorable to series-connected ensembles. Averaged over all numbers of subcells, this extended capacity factor accounts for 40% of the excess energy generated by the independent ensembles (on average 7% of the total annual energy production).

Performance over course of year

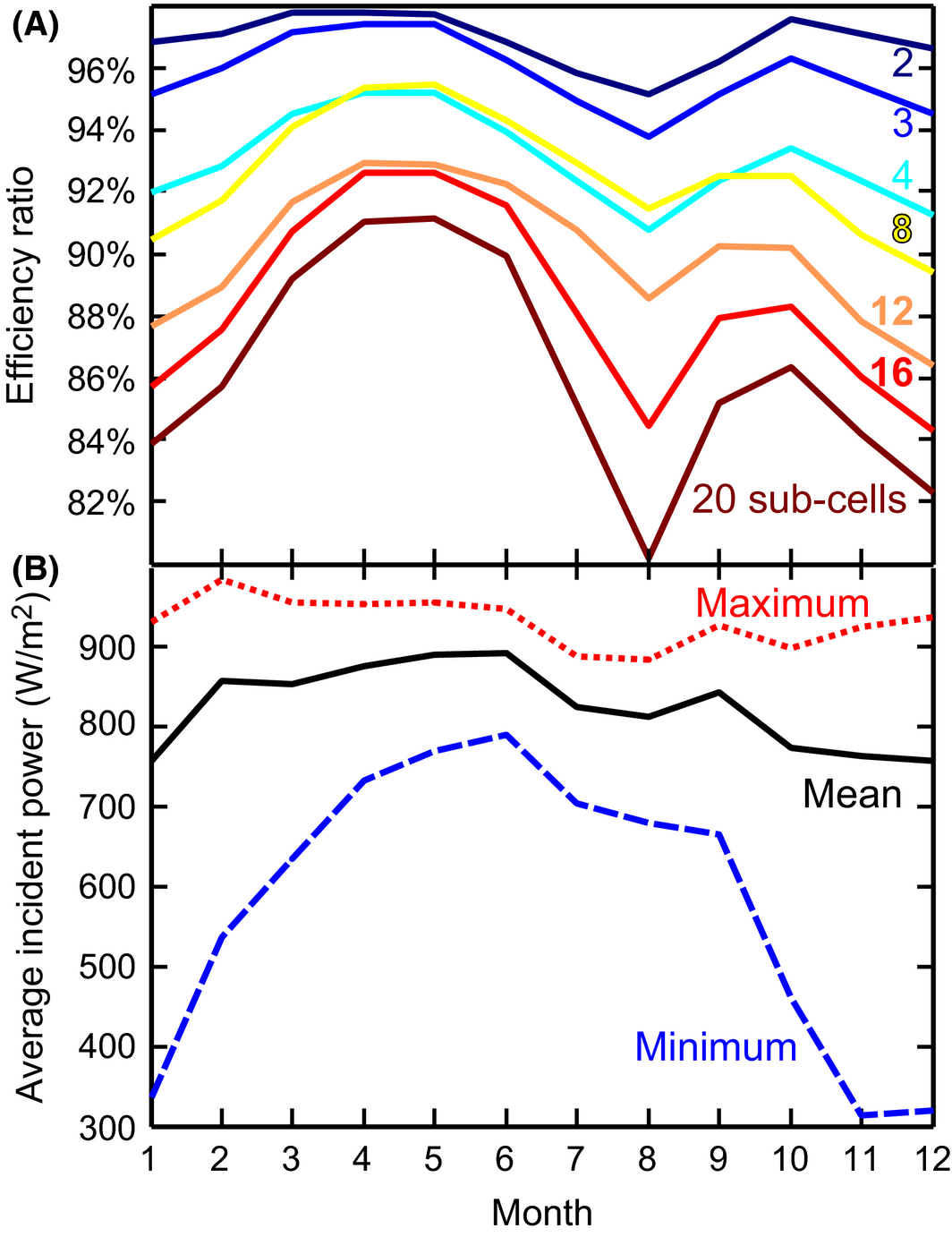
In addition to understanding the energy production advantage of independent ensembles relative to series-connected ensembles at different irradiance levels, it is also interesting to examine their relative performance over the course of a year. Figure 3 panel (A) shows the monthly average relative efficiency of series-connected ensembles normalized to the independent ensemble efficiency, again for Phoenix, AZ. Panel (B) shows the monthly mean, maximum, and minimum irradiance level. While the relative performance generally tracks the monthly average irradiance levels, the seasonal variation is not simply connected to day length. The series ensembles have a strong relative performance dip in the months of July, August, and September, most likely due to higher aerosol optical depth and precipitable water presence during the monsoon season.

Figure 3. (A) Efficiency ratio of series-connected to electrically independent spectrum splitting ensembles averaged over all spectra in each month of the year in Phoenix, AZ. (B) Minimum, mean, and maximum irradiance level for each month of the year in Phoenix, AZ.

Performance at different locations

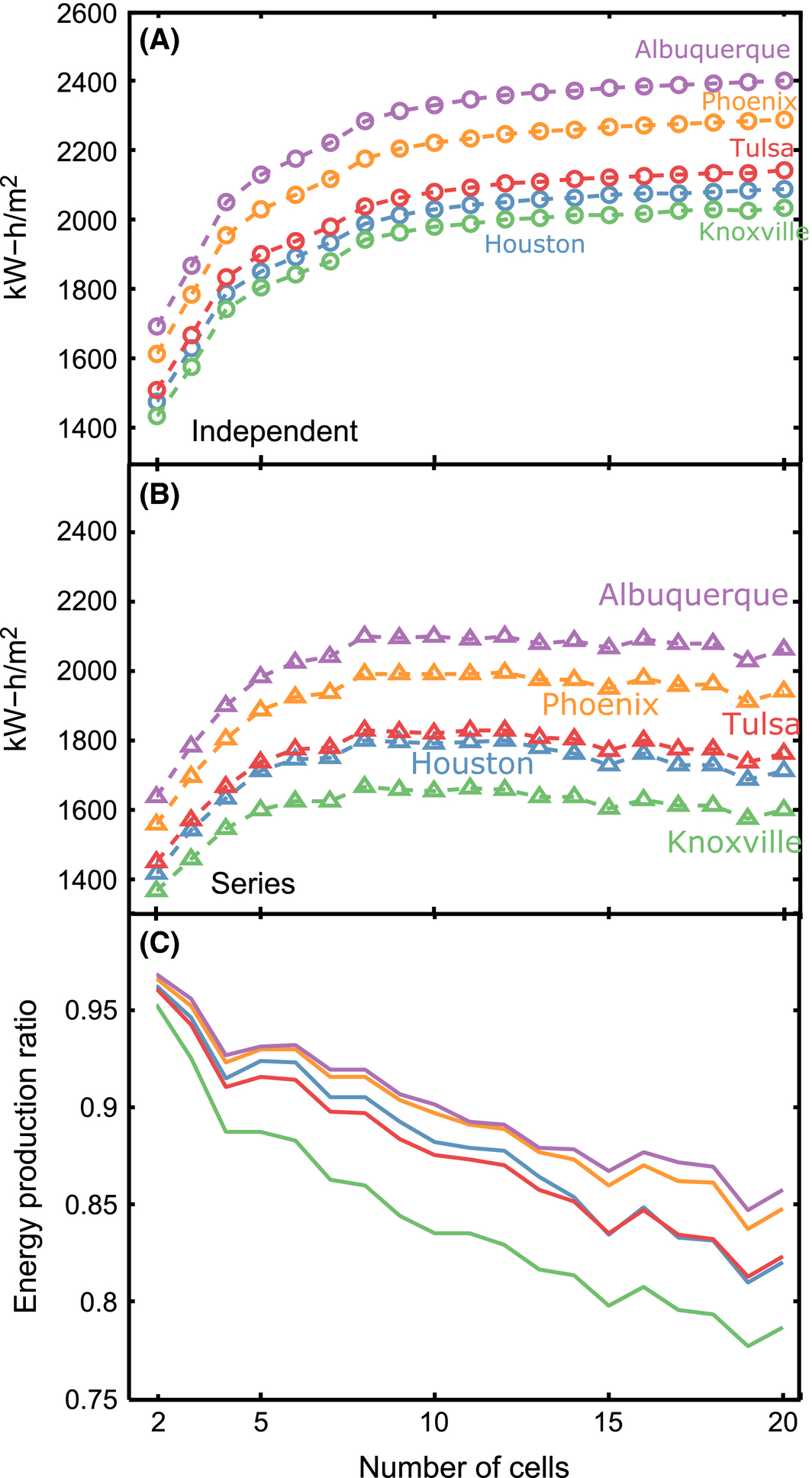
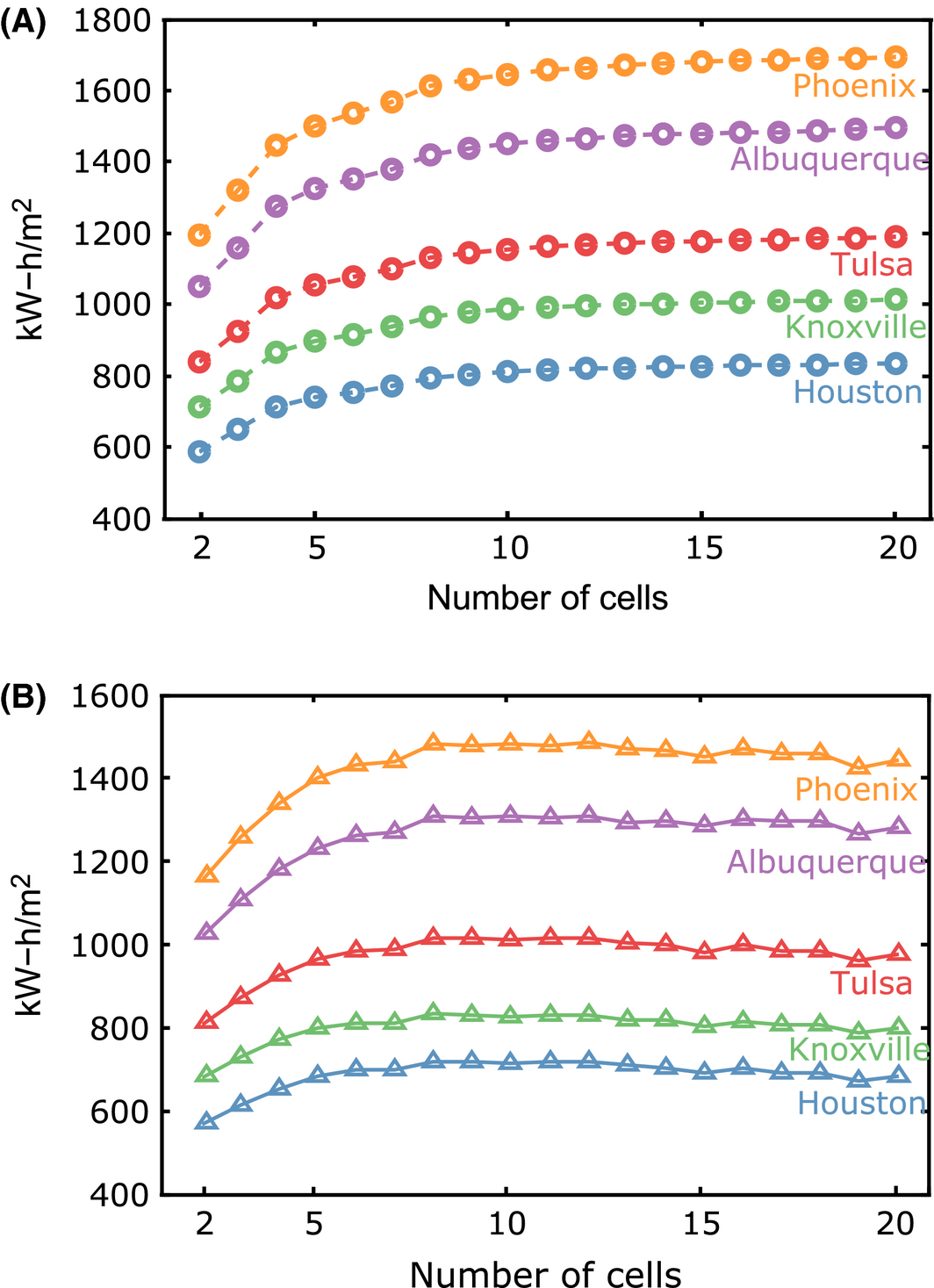
The particular performance penalty of series relative to independent ensembles in the summer months for Phoenix appears to be specific to the climate of that location. To explore the effect of geographic location on the relative performance of spectrum splitting ensembles with electrically in series and independent subcells, the annual energy production simulation was duplicated for a variety of different locations: Houston, TX, Albuquerque, NM, Tulsa, OK, and Knoxville, TN. Figure 4 panel (A) shows the annual energy production for the independent ensembles at all five locations and panel (B) shows the annual energy production for the series ensembles. The broad trend of energy production as a function of subcell number is the same at all locations, though the expected energy production varies based on differences in the total sunny day irradiance simulated for the various cities. Importantly, the series-connected ensembles all exhibit the same maximum energy production with 8–12 subcells and declining energy production with larger ensembles, consistent with the performance for Phoenix.

Figure 4. (A) Simulated annual energy production for ideal spectrum splitting ensembles with electrically independent subcells operating at 500 suns in Phoenix, AZ, Albuquerque, NM, Tulsa, OK, Knoxvile, TN, and Houston, TX. All simulated spectra are for sunny days. (B) Simulated annual energy production for spectrum splitting ensembles with series-connected subcells. (C) Ratio of series-connected energy production to electrically independent energy production.

Figure 4 panel (C) shows the ratio of series-connected to independent energy production for all five locations versus the number of subcells per ensemble. The series-connection penalty ranges from 2.5% to 5% of independent energy production for ensembles with two cells. The penalty increases to range from 14% to 22% for the 20-cell ensembles, which suggests that not all locations experience an equal amount of spectral deviation over the course of the year. The unequal series-connection penalty among different locations raises an important point. First, it is current practice to target concentrating photovoltaic (CPV) installations with series-connected subcells in locations with a high percentage of direct irradiance, which helps ensure most incident spectra resemble the AM1.5D standard and cell performance is close to specification, as indicated in Figure 3. However, as CPV expands into more marginal locations with higher latitude or more atmospheric absorption and scattering, systems with series-connected cells will underperform their specification, with this effect worsening for ensembles with larger numbers of subcells. By contrast, CPV systems with electrically independent subcells will produce power that is a more consistent percentage of the total direct irradiance.

Energy production with cloud correction

Figure 5 shows the expected annual energy production for independent (panel A) and series-connected (panel B) ensembles exposed to cloud-adjusted direct normal irradiance at 500 suns concentration. While the baseline energy production levels for the different cities is significantly different from the levels shown in Figure 4, the relative performance of series and independent ensembles at a given location are preserved. All locations project increasing energy production with increasing number of subcells for independently connected ensembles, and all locations show annual energy production peaking with 8–12 subcells for the series-connected ensembles. In addition, the series-connected energy production as a percentage of independent energy production is not substantially different from the trends shown in Figure 4(C). The consistency of this behavior with and without cloud correction and across multiple locations with differing climates suggests that the energy production advantage of independent ensembles is not tied to local climate effects other than the degree of spectral variability. While the behavior does neglect the impact of clouds on the direct spectrum, the efficiency trends shown in Figure 2(A) and (B) suggest that accounting for spectral transmission through screening clouds will increase the energy production advantage of the independent ensembles, making the projections in Figure 5 conservative.

Figure 5. (A) Simulated annual energy production of ideal spectrum splitting ensembles with electrically independent subcells under 500 suns. Simulated spectra have intensity uniformly decreased by the average percent cloud coverage for each hour. (B) Simulated annual energy production of ideal spectrum splitting ensembles with series-connected subcells under cloud-adjusted spectra.

Conclusions

While the efficiency of spectrum splitting ensembles with electrically independent subcells is only slightly higher than the efficiency of ensembles with the same number of subcells connected in series under the AM1.5D design spectrum, the energy production potential of the two electrical configurations differs widely under varying spectral conditions. The energy production advantage of ensembles with electrically independent cells results from the consistency of the efficiency of these ensembles under spectra that differ from the design spectrum. By contrast, the series-connected ensembles decrease in efficiency rapidly as the incident spectrum deviates from the AM1.5D irradiance level, and the efficiency decreases faster with increasing subcell number.

The energy production advantage of independent ensembles can be roughly broken into two components. A total of 60% of the additional energy comes from better performance under high illumination conditions and will appear as additional peak power production. The other 40% comes from energy production at low irradiance conditions when the series-connected ensembles produce negligible power. While the power production of the independent ensembles under these conditions is low, it does constitute an extended capacity factor that adds up over the course of the year and may have considerable economic value.

While the energy production advantage of independent ensembles is consistent for a wide variety of locations both with and without accounting for the effects of clouds reducing direct transmission, the relative advantage throughout the year for a particular location will be sensitive to local climate trends. This may result in the series-connected ensembles producing less power than expected at different times of the year, as in the case of Phoenix, AZ. Combining the local power production trends with energy pricing trends for specific installation locations can give a clearer evaluation of the relative economic benefit of independent electrical connection for spectrum splitting ensembles.

Finally, as the cost of concentrating photovoltaic tracking and optical systems decreases, the range of territory where these types of installations can produce cost-competitive power will increase. For example, if a generation plant with series-connected subcells can produce cost-effective power in Albuquerque, NM, Figure 5 suggests that a similar plant with independent subcells will be economically feasible in Tulsa, OK, assuming comparable costs for the system components. The independent electrical connections spectral insensitivity and improved performance have the potential to increase the scope of the market for CPV into areas previously considered uneconomical.

The energy production advantage of electrically independent spectrum splitting ensembles relative to series-connected ensembles is significant and consistent for all numbers of band gaps and all locations. This performance advantage is a powerful argument for pursuing new designs with electrically independent subcells. Historically, the small efficiency advantage of electrically independent subcells was not considered to justify the additional technical complexity required to achieve those connections or optically distribute the spectrum among the subcells. The comparative simplicity of monolithic series-connected designs has made them more practical for systems with small numbers of subcells. However, as efforts turn to larger numbers of subcells, this analysis shows that the energy production advantage of independently connected cell designs will increase and potentially justify the pursuit of more complex systems.

Conflict of Interest

None declared.

References

1. Dimroth, F., M. Grave, P. Beutel, U. Fiedeler, C. Karcher, T. N. D. Tibbits, et al. 2014. Wafer bonded four-junction GaInP/GaAs//GaInAsP/GaInAs concentrator solar cells with 44. 7% efficiency. Prog. Photovoltaics22:277–282.
2. Marti, A., and G. L. Araujo. 1996. Limiting efficiencies for photovoltaic energy conversion in multigap systems. Sol. Energy Mater. Sol. Cells43:203–222.
3. King, R. R., D. C. Law, C. M. Fetzer, R. A. Sherif, K. M. Edmondson, S. Kurtz, et al. 2005. Pathways to 40% -efficient concentrator photovoltaics. 20th European Photovoltaic Solar Energy Conference and Exhibition, June, 6–10.
4. Kurtz, S. R., J. M. Olson, and P. Faine. 1991. The difference between standard and average efficiencies of multijunction compared with single-junction concentrator cells. Sol. Cells30:501–513.
5. Philipps, S. P., G. Peharz, R. Hoheisel, T. Hornung, N. M. Al-Abbadi, F. Dimroth, et al. 2010. Energy harvesting efficiency of III-V multi-junction concentrator solar cells under realistic spectral conditions. AIP Conf. Proc.1277:294–298.
6. Hoang, P., V. Bourdin, Q. Liu, G. Caruso, and V. Archambault. 2014. Coupling optical and thermal models to accurately predict PV panel electricity production. Sol. Energy Mater. Sol. Cells125:325–338.
7. Chan, N. L. A., H. E. Brindley, and N. J. Ekins-Daukes. 2014. Impact of individual atmospheric parameters on CPV system power, energy yield and cost of energy. Prog. Photovoltaics Res. Appl.22:1080–1095.
8. Leloux, J., E. Lorenzo, B. García-Domingo, J. Aguilera, and C. A. Gueymard. 2014. A bankable method of assessing the performance of a CPV plant. Appl. Energy118:1–11.
9. Chiu, P., S. Wojtczuk, X. Zhang, C. Harris, D. Pulver, and M. Timmons. 2011. 42.3% Efficient InGaP/GaAs/InGaAs concentrators using bifacial epigrowth. 2011 37th IEEE Photovolt. Spec. Conf.000771–000774.
10. King, R. R., D. Bhusari, D. Larrabee, X. Liu, E. Rehder, K. Edmondson, et al. 2012. Solar cell generations over 40% efficiency. Prog. Photovoltaics:801–815.
11. Barnett, A., D. Kirkpatrick, C. Honsberg, D. Moore, M. Wanlass, K. Emery, et al. 2009. Very high efficiency solar cell modules. Prog. Photovoltaics Res. Appl.17:75–83.
12. Imenes, A. G., and D. R. Mills. 2004. Spectral beam splitting technology for increased conversion efficiency in solar concentrating systems: a review. Sol. Energy Mater. Sol. Cells84:19–69.
13. Mitchell, B., G. Peharz, G. Siefer, M. Peters, T. Gandy, J. C. Goldschmidt, et al. 2011. Four-junction spectral beam-splitting photovoltaic receiver with high optical efficiency. Prog. Photovoltaics19:61–72.
14. Kurtz, S., D. Myers, W. E. McMahon, J. Geisz, and M. Steiner. 2008. A comparison of theoretical efficiencies of multi-junction concentrator solar cells. Prog. Photovoltaics16:537–546.
15. Tobias, I., and A. Luque. 2002. Ideal efficiency of monolithic, series-connected multijunction solar cells. Prog. Photovoltaics10:323–329.
16. Faine, P., S. R. Kurtz, C. Riordan, and J. M. Olson. 1991. The influence of spectral solar irradiance variations on the performance of selected single-junction and multijunction solar cells. Sol. Cells31:259–278.
17. Kinsey, G. S., A. Nayak, M. Liu, V. Garboushian, and S. Beach. 2011. Increasing power and energy in amonix solar power plants. IEEE J. Photovolt.1:3–4.
18. Mols, Y., L. Zhao, G. Flamand, M. Meuris, and J. Poortmans. 2012. Annual energy yield: A comparison between various monolithic and mechanically stacked multijunction solar cells BT - 38th IEEE Photovoltaic Specialists Conference, PVSC 2012, June 3, 2012 – June 8, 2012. 2092–2095.
19. Dimroth, F., S. P. Philipps, G. Peharz, E. Welser, R. Kellenbenz, T. Roesener, et al. 2010. Promises of advanced multi-junction solar cells for the use in CPV systems. 1231–1236.
20. Philipps, S. P., G. Peharz, R. Hoheisel, T. Hornung, N. M. Al-Abbadi, F. Dimroth, et al. 2010. Energy harvesting efficiency of III-V multi-junction concentrator solar cells under realistic spectral conditions. Sol. Energy Mater. Sol Cells94:877–897.
21. Wang, X., A. Barnett, and L. Fellow. 2012. The effect of spectrum variation on the energy production of triple-junction solar cells. IEEE J. Photovoltaics2:417–423.
22. Wild, M., H. Gilgen, A. Roesch, A. Ohmura, C. N. Long, E. G. Dutton, et al. 2005. From dimming to brightening: decadal changes in solar radiation at Earths surface. Science308:847–850.
23. Foukal, P., C. Fröhlich, H. Spruit, and T. M. L. Wigley. 2006. Variations in solar luminosity and their effect on the Earths climate. Nature443:161–166.
24. Myers, D. R., and K. E. Emery. 2002. Terrestrial solar spectral modeling tools and applications for photovoltaic devices preprint. 29th IEEE PV Specialists Conference Conference.
25. Dubovik, O., and M. D. King. 2000. A flexible inversion algorithm for retrieval of aerosol optical properties from Sun and sky radiance measurements. J. Geophys. Res.105:20673.
26. Tossa, A. K., Y. M. Soro, Y. Azoumah, and D. Yamegueu. 2014. A new approach to estimate the performance and energy productivity of photovoltaic modules in real operating conditions. Sol. Energy110:543–560.
27. Warmann, E. C., C. Eisler, E. Kosten, M. Escarra, and H. A. Atwater. 2013. Spectrum splitting photovoltaics: Materials and device parameters to achieve ultrahigh system efficiency. 2013 IEEE 39th Photovolt. Spec. Conf.1922–1925.
28. Henry, C. H.1980. Limiting efficiencies of ideal single and multiple energy gap terrestrial solar cells. J. Appl. Phys.51:4494.
29. 1981-2010 U.S. Climate Normals | National Climatic Data Center (NCDC). [Online]. Available at http://www.ncdc.noaa.gov/data-access/land-based-station-data/land-based-datasets/climate-normals/1981-2010-normals-data (accessed 10 March 2015).
30. Buis, J. P., A. Setzer, B. N. Holben, T. F. Eck, I. Slutsker, D. Tanre, et al. 1998. AERONET — a federated instrument network and data archive for aerosol characterization. Remote Sensing of Environment66:1–16.
31. Gueymard, C. A., D. Myers, and K. Emery. 2002. Proposed reference irradiance spectra for solar energy systems testing. Sol. Energy73:443–467.
32. Myers, D. R., and C. A. Gueymard. 2004. Description and availability of the SMARTS spectral model for photovoltaic applications Proc. SPIE 5520, Organic Photovoltaics V, 56.
33. Kinsey, G. S.2015. Spectrum sensitivity, energy yield, and revenue prediction of PV modules. IEEE J. Photovoltaics5:258–262.
34. NSRDB: 1991–2010 update. [Online]. Available at http://rredc.nrel.gov/solar/old_data/nsrdb/1991-2010/. (accessed 10 March 2015).