Dynamic model and numerical simulation for a new eccentric rotary multiphase pump

Abstract

In order to simplify the manufacture of multiphase pump and improve the operating flexibility for gas void fraction (GVF) of the multiphase fluids that the pump transported, an eccentric rotary multiphase pump (ERMP) is presented. In this study, the structural characteristics and working principle of the ERMP are presented first. Then, the kinematic and force models are established for the key components- sliding vane and rotor. The velocity, acceleration, and force equations with shaft rotation angle are derived for each component. Based on the established models, simulations are performed for an ERMP prototype. The simulated results show that the areas opposite the sliding vane and apart from the center of the rotor have larger velocities and wear problem. Moreover, the binding force, pressure difference induced force and the normal force exercise a negative effect on the friction at the sliding vane sides and rotor. Lower shaft speed and smaller eccentric distance of the crankshaft are helpful to reduce this effect. The findings confirm that the proposed ERMP is suitable for multiphase transportation and has a higher mechanical efficiency for its advanced structure and working principle.

Key words: multiphase pump, ERMP, sliding vane, rotor, kinematic and force behavior

1. Introduction

Multiphase fluid transportation, which enables the transfer of multiphase fluid in a single pipeline, is considered to be an efficient and economical technology in the petrochemical industry. Due to the elimination of conventional transportation facilities such as bulky separators, fluid pumps, gas compressors and extra pipelines, the cost of the multiphase transportation technology is only about 70% of the conventional transportation technology [1].

Moreover, the multiphase transportation technology is especially helpful in the exploration of the petroleum resources at remote areas for this technology provides a simpler and more compact system. More and more petrochemical companies worldwide are attracted to the use of multiphase pumps for boosting multiphase flow and many investigations on multiphase pumps have been carried out [2–8]. According to the boosting principles of developed pumps, the multiphase pumps can be classified as the rotodynamic pump and positive displacement pump. Rotodynamic pump, such as the helicon-axial pump, transform the mechanical input power into kinetic energy of multiphase fluid by displacing it along suitable designed channels within the pumps and then converted into working pressure [9]. The rotodynamic pump can provide a large flow but is not suitable for handling multiphase fluids that gas void fraction (GVF) is more than 50%. Positive displacement pump, such as the twin-screw pump, works on the principle of enclosing a defined volume on the suction side and moving it to the discharge end [10]. The positive displacement pump can handle the multiphase fluids with a large difference in the inlet GVFs. Several multiphase boosting applications demonstrated that positive displacement pump could operate for multiphase duties successfully [11-15]. However, the rotors of the positive displacement pump are geometrically complex and require higher machining precision that results in a higher manufacture cost.

In order to simplify the manufacture of multiphase pump and improve its operating flexibility for GVF, a novel positive displacement multiphase pump names eccentric rotary multiphase pump (ERMP) is presented. The major components of the proposed ERMP are all geometry simple and easy to manufacture. Due to the synchronically movement of the rotor and the cylinder of the pump, the frictional loss between the major components are largely minimized and the mechanical efficiency of the proposed pump is higher than that of the conventional rotary mechanisms.

In this investigation, the structural characteristics and working process of the proposed ERMP are particularly introduced. Its kinematic behaviors as well as the dynamic behaviors are theoretically formulated and discussed. In addition, the effects of the eccentric distance of the crankshaft on the kinematic and dynamic behaviors of key components of the pump are theoretically analyzed.

2. Structural characteristics and working principle

Shown as in Figure 1, the proposed ERMP consists of a rotor, a sliding vane, a housing case, and a crankshaft. The rotor is eccentrically assembly in the cylinder that is assembly with the housing case. Due to the outside wall of the rotor and the inside wall of the cylinder are tangent to each other, a crescent-shaped working chamber is formed by the inside wall of the cylinder and the outside wall of the rotor. The upper end the sliding vane is inserted in the groove of the housing case while the lower end is assembly with the rotor by a joint. In such case, the formed crescent-shaped chamber is divided into an intake chamber and a discharge chamber by the sliding vane. The intake port and discharge port of the pump are connected to the intake chamber and discharge chamber, respectively.

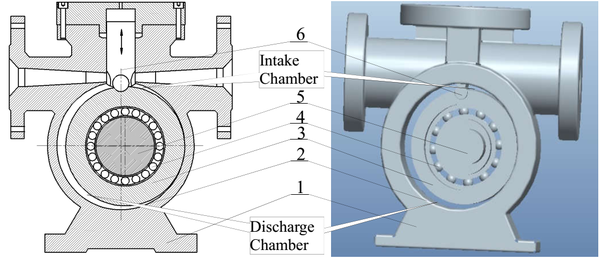
1-housing case, 2-cylinder, 3-rotor, 4-rotor bearing, 5-crankshaft, 6-sliding vane

Figure 1. Structure of the proposed ERMP

During the operation of the pump, the rotor is driven by the crankshaft, which is rotate clockwise around its geometrical axis, to swing in the cylinder and change the volume of the crescent-shaped working chamber. At the same time, the sliding vane reciprocate straightly in the vane slot. Due to the compound motion of the vane, the volumes of the divided intake chamber and discharge chamber vary gradually, and thus the intake -discharge process is resulted, shown as in Figure 2. The volume of the intake chamber increase with the crankshaft angle of $\theta$ and result in a vacuum in this area during the intake process. Meanwhile, the volume of the discharge chamber decrease with the crankshaft angle of $\theta$ during the discharge process. In such case, the pump inhales the multiphase fluid continuously into the intake chamber through the intake port of the pump during the intake process and discharge the multiphase fluid out of the pump through the discharge port during the discharge process.

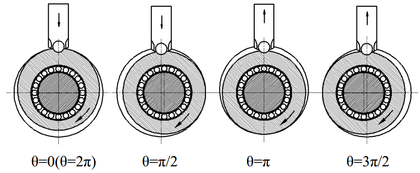
Figure 2. Schematic diagram of the working process

3. Kinematic model for the sliding vane and rotor

3.1 Velocity and acceleration of the sliding vane

The rotor driven by the crankshaft, which rotates at a uniform speed, exhibits a composite planar motion. Simultaneously, the sliding vane driven by the rotor reciprocates along the vane slot. In order to analyze the kinematic characteristics of the sliding vane and the rotor, a fixed coordinate system and a rotational coordinate system have been established. Shown as in Figure 3, the fixed coordinate system $XOY$ locates the origin point at the centrum of pump’s cylinder and $Y$-axis crossing through the centerline of sliding vane. The rotational coordinate system $X_{1}O_{1}Y_{1}$ locates the origin point at the centrum of the rotor and $Y_{1}$-axis crossing the center of round end of the sliding vane. The established rotational coordinate system $X_{1}O_{1}Y_{1}$ rotates synchronously with the rotor based on the radius of the eccentric distance of the crankshaft.

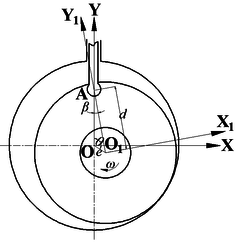
Figure 3. Coordinate systems of the analysis model

The extension length of the sliding vane, l_s, can be expressed as,

$l_{s}=e(1-cos\theta )+{\frac {e^{2}}{4r}}(1-cos2\theta )$

(1)

where $e$ is the eccentric distance of the crankshaft and $r$ is the radius of the rotor. Shown as in Figure 2, the minimum extension length of the sliding vane is zero when the crankshaft angle, $\theta$, equals to zero or $2\pi$ while its maximum value is $2e$ when the crankshaft angle equals to $\pi$. By differentiating the equation (1), the velocity of the sliding vane, $v_{s}$, and acceleration of the sliding vane, $a_{s}$, can be expressed as,

$v_{s}=e\omega \left(sin\theta +{\frac {e}{2r}}sin2\theta \right)$

(2)

$a_{s}=e{\omega }^{2}\left(cos\theta +{\frac {e}{r}}cos2\theta \right)$

(3)

where $\omega$ is the angular speed of the crankshaft which can be obtained as $\omega =n\pi /30$, where $n$ is the rotation rate of the pump. Shown as in Figure 3, the round end of the sliding vane that hinged into the rotor rotates reversely along with the rotor. Its relative angular velocity, $\omega _{r}$, can be expressed as,

${\omega }_{r}={\frac {-e\omega cos(\theta +\beta )}{d}}$

(4)

where $d$ is the distance from $O_{1}$ to point $A$, and $\beta$ is the intersection angle between the center line of the sliding vane and line $AO_{1}$. The value of $\beta$ is vary with crankshaft angle $\theta$ and it can be obtained as,

$\beta =arcsin\left({\frac {esin\theta }{d}}\right)$

(5)

3.2 Velocity and acceleration of the rotor

The rotor of the pump is restrained by both the sliding vane and crankshaft. The movements of the pump include the rotation around the center of the cylinder $O$ and rotation around its own center $O_{1}$. As the sliding vane and the rotor hinged at the round end, the absolute velocity of the rotor at the round end equals to the velocity of the sliding vane. Based on the rotation of the entrained movement of the rotor, the direction of the entrained velocity, $v_{e}$, is vertical to $OO_{1}$ and can be obtained as,

$v_{e}=e\omega$

(6)

The movement at point $A$ is rotating around the rotational coordinate system $X_{1}O_{1}Y_{1}$ (Figure 4). Then, the relative velocity at point $A$ is vertical to $O_{1}A$ and its value can be obtained as,

$v_{r}=\left(r-r_{0}\right){\omega }_{p}$

(7)

where $r_{0}$ is the radius of the round end of the sliding vane, $w_{p}$ is the rotor’s angular velocity around its own center. According to the velocity vector at point $A$, the relative velocity can be expressed as,

$v_{r}={\frac {-e\omega \left(r-r_{0}\right)cos\theta }{\sqrt {{\left(r-r_{0}\right)}^{2}-{\left(esin\theta \right)}^{2}}}}$

(8)

Then, the angular velocity $w_{p}$ can be expressed as,

${\omega }_{p}={\frac {-e\omega cos\theta }{\sqrt {{\left(r-r_{0}\right)}^{2}-{\left(esin\theta \right)}^{2}}}}$

(9)

The coordinate value of point on the head surface of the rotor can be expressed under the rotational coordinate system $X_{1}O_{1}Y_{1}$ as,

$\left\{{\begin{array}{c}x_{1}=l_{B}cos\alpha \\y_{1}=l_{B}sin\alpha \end{array}}\right.$

(10)

where $l_{B}$ is the distance between point on the head surface and the center of the rotor, $\alpha$ is the intersection angle between the coordinate axis $x_{1}$ and line $BO_{1}$.

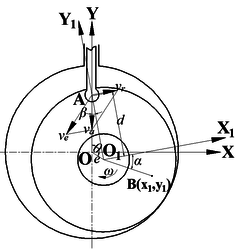
Figure 4. Coordinate systems of the analysis model

Based on the geometry relationship between the fixed coordinate system XOY and the rotational coordinate system $X_{1}O_{1}Y_{1}$, the coordinate value of point on the head surface of the rotor can be expressed under the fixed coordinate system $XOY$ as,

${\textstyle \left\{{\begin{array}{l}x=l_{B}cos\left(\alpha +\beta \right)+esin\theta \\y=l_{B}sin\left(\alpha +\beta \right)+ecos\theta \end{array}}\right.}$

(11)

Then, the velocity of the head surface on the rotor can be obtained by differentiating the above equation as,

${\textstyle \left\{{\begin{array}{l}x=\omega \left(ecos\theta -l_{B}sin(\alpha +\beta ){\frac {ecos\theta }{\sqrt {d^{2}-e^{2}{sin}^{2}\theta }}}\right)\\y=\omega \left(-esin\theta -l_{B}cos(\alpha +\beta ){\frac {ecos\theta }{\sqrt {d^{2}-e^{2}{sin}^{2}\theta }}}\right)\end{array}}\right.}$

(12)

4. Force model for sliding vane and rotor

The force model established in this research include not only the principle forces but also the often-neglected pressure difference induced force between intake chamber and discharge chamber. In these models, we assume the following:

1. The pressure pulsation of the intake and discharge processes is ignored, which means that the intake and discharge pressures are regarded as constants.
2. The effect of oil film thickness change on friction coefficient is neglected.

4.1 Force model for sliding vane

The forces acting on the sliding vane are defined to be positive when their directions are the same as the positive direction of the $X$-axis or $Y$-axis of the established coordinate system $XOY$, shown as in Figure 5. The forces acting on the sliding vane include:

• The normal force ($F_{n}$) and tangential force ($F_{t}$) at the round end of the sliding vane.

• The binding forces ($F_{R1}$ and $F_{R2}$) caused by the groove that the sliding vane inserted.

• The friction forces ($F_{f1}$ and $F_{f2}$) caused by the movement of the sliding vane.

• The inertia force ($F_{Iv}$) of the sliding vane.

• The force ($F_{pb}$) caused by the pressure difference between the intake chamber and the discharge chamber.

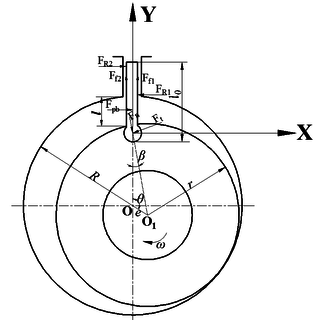
Figure 5. Forces acting on the sliding vane

The friction forces acting on the sliding vane can be obtained as,

${\textstyle \left\{{\begin{array}{c}F_{f1}=u_{s}F_{R1}\\F_{f2}=u_{s}F_{R2}\end{array}}\right.}$

(13)

where $u_{s}$ is the friction coefficient between the sliding vane and groove. The pressure difference induced force acing on the sliding vane can be obtained as,

$F_{pb}=Hl\left(p_{c}-p_{d}\right)$

(14)

where $H$ is the thickness of the sliding vane, $l$ is the extension length of the sliding vane, $p_{c}$ is the discharge pressure of the pump, $p_{d}$ is the intake pressure of the pump.

Based on the rotation of the rotor, the tangential force at the round end of the sliding vane can be obtained as,

$F_{t}={\frac {M_{c}-M_{JZ}}{r-r_{0}}}$

(15)

where $r$ is the radius of the rotor, $r_{0}$ is the radius of the round end of the sliding vane, $M_{c}$ is the friction torque between the rotor and crankshaft, $M_{JZ}$ is the inertia moment acting on the rotor.

According to the conditions of force equilibrium and moment equilibrium on the sliding vane with a fixed axis, the equilibrium equations of the sliding vane can be expressed as,

$\left\{{\begin{array}{l}F_{pb}-F_{R1}+F_{R2}+F_{n}sin\beta -F_{t}cos\beta =0\\F_{f1}+F_{f2}-F_{n}cos\beta -F_{t}sin\beta -F_{Iv}=0\\(F_{f1}-F_{f2})H-F_{R1}(l_{0}-2l)-F_{R2}l_{0}+F_{pb}(l_{0}-l)+F_{n}l_{0}sin\beta -F_{t}l_{0}cos\beta =0\end{array}}\right.$

(16)

where $l_{0}$ is the length of the sliding vane.

4.2 Force model for rotor

The force acting on the rotor include the normal force and tangential force induced by the sliding vane, force ($F_{pg}$) induced by the pressure difference of the multiphase flow, inertia force ($F_{Ip}$) of the rotor.

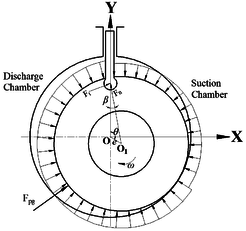
Figure 6. Forces acting on the rotor

Different pressure exist between the intake chamber and discharge chamber of the pump during its application. The pressure difference induced force would loaded on the rotor during the application of the pump, shown as in Figure 6. The value of the force can be obtained as,

$F_{p{\mbox{g}}}=2rH(p_{c}-p_{d})sin{\frac {\theta +\beta }{2}}$

(17)

The resistance moment ($M_{pg}$) caused by the force mentioned above can be expressed as,

$M_{pg}=2F_{pg}sin{\frac {\theta +\beta }{2}}$

(18)

The inertia force of the rotor can be obtained as,

$F_{Ip}=me{\omega }^{2}$

(19)

where $m$ is the weight of the rotor.

In this research, the friction torque ($M_{c}$) between the rotor and crankshaft is considered. Based on the lubrication theory, the friction torque between the rotor and crankshaft can be obtained as,

$M_{c}={\frac {2\pi \mu \left(\omega -{\omega }_{p}\right)R_{e}^{3}l_{e}}{{\delta }_{e}}}$

(20)

where $R_{e}$ is the radius of the crankshaft, $\delta _{e}$ is the interstice between the rotor and crankshaft, $l_{e}$ is the length of the crankshaft, $\mu$ is the frictional coefficient.

The resistance moment ($M_{n}$) caused by the normal force at round end of the sliding vane can be expressed as,

$M_{n}=eF_{n}sin\left(\beta +\theta \right)$

(21)

Based on the research mentioned above, the radial force acting on the rotor can be obtained as,

$F={\sqrt {F_{x}^{2}+F_{y}^{2}}}$

(22)

where $F_{x}$ and $F_{y}$ are the radial components on the $X$-axis and $Y$-axis, and can be obtained as,

$\left\{{\begin{array}{c}F_{x}=F_{t}cos\beta -F_{n}sin\beta +F_{pg}cos{\frac {\beta +\theta }{2}}\\F_{y}=F_{n}cos\beta +F_{t}sin\beta -F_{pg}sin{\frac {\beta +\theta }{2}}\end{array}}\right.$

(23)

The resistance moment ($M_{z}$) acting on the rotor can be obtained as,

$M_{z}=M_{c}+M_{n}+M_{pg}$

(24)

Then, the capacity of the multiphase pump can be obtained as,

$P={\frac {n}{60}}{\int }_{0}^{2\pi }M_{z}d\theta$

(25)

5. Simulation results and discussions

In this investigation, the ERMP porotype with rated flow of 6$m^{3}/h$ is designed for multiphase transportation, where its main dimensions are given in Table 1. Based on the established model, kinematic characteristics of rotor’s components and forces acting on them can be simulated.

Table 1. Operating specifications and main dimensions of the ERMP porotype

Operating specifications		Main dimensions
Rated flow	6m$m^{3}/h$	Length of sliding vane	136mm
Rated speed	200/min	Width of sliding vane	20mm
Working fluid	Gas-oil multiphase flow	Cylinder radius	90mm
Intake pressure	0.1$\sim$0.3MPa	Rotor radius	82mm
Discharge pressure	0.3$\sim$3.0MPa	Radius of vane joint	7mm

5.1 Simulation results for kinematics of sliding vane

In this study, the eccentric distance of the crankshaft is set to be 0.007m, 0.008m and 0.009m to evaluate the kinematic characteristics of sliding vane. Figure 7 shows the simulation results of kinematics for sliding vane. From Figure 7, it can be noted that the movement, velocity, acceleration of the sliding vane and the angular velocity of the round end of sliding vane increase with the eccentric distance. Shown as in Figure 7 (a), the sliding vane reaches its maximum values when the crankshaft rotates to the $\pi$ position. The angular velocity of the round end of the sliding vane has the same variation of the movement of sliding vane, shown as in Figure 7 (d). The velocity of the sliding vane vary with degree of crankshaft in sine form, shown as in Figure 7 (b). On the country, the acceleration of the sliding vane vary with degree of crankshaft in cosine form, shown as in Figure 7 (c).

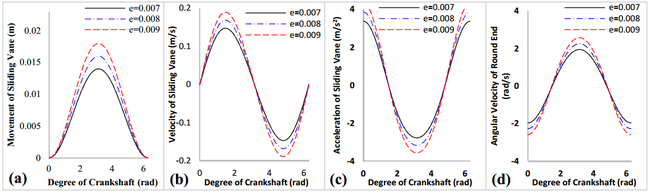
Figure 7. Kinematic analysis for sliding vane

5.2 Simulation results for kinematics of rotor

Based on the established fixed coordinate system ($XOY$) and rotational coordinate system ($X_{1}O_{1}Y_{1}$), movements of points on the end surface of rotor can be obtained. Shown as in Figure 8, the motion path of the points are ellipses in different size, except the motion path of the rotor’s center which represents as a circle.

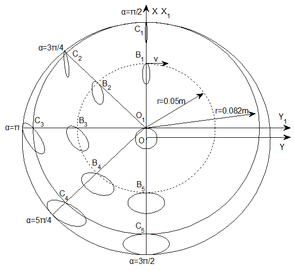
Figure 8. Movements of points on end surface of rotor

In this study, four points on the contour of rotor ($C_{2}$, $C_{3}$, $C_{4}$ and $C_{5}$) and four points on the middle position of end surface of rotor ($B_{2}$, $B_{3}$, $B_{4}$ and $B_{5}$) are selected to simulate velocity of rotor on the end surface, shown as in Figure 8. Figure 9 shows the velocity variations of each selected points on the end surface of rotor. The velocities of each selected points vary with the rotation of the crankshaft in a same trend. The points located at $3\pi /2$ position of the rotor, such as points $C_{5}$ and $B_{5}$, have larger velocities compared with the points in other area. Besides, the more the points approach to the center of the rotor, the smaller velocities they have. Then, the area located at opposite of the sliding vane ($3\pi /2$ position of the rotor) and located at contour part of the rotor, such as area of point $C_{5}$, have wear problem during application of the pump and attention need to be paid.

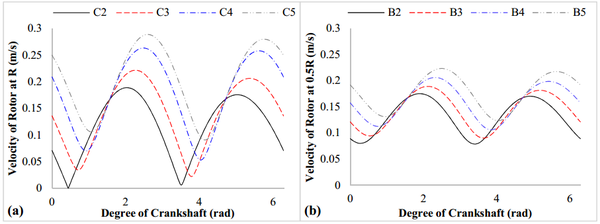
Figure 9. Velocity variations of rotor under different position

Besides, different value of eccentric distance are set to evaluate the effects of eccentric distance on the kinematic behavior of the rotor, as shown in Figure 10. It can noted in Figure 10, the rotor rotates at a faster velocity, a larger angular velocity and angular acceleration when selecting a larger value of the eccentric distance.

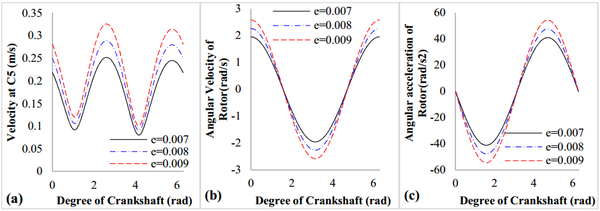
Figure 10. Variation of kinematic behavior of rotor</

5.3 Simulation results for forces on sliding vane

Figure 11 shows the forces acting on the sliding vane. It can be noted that the binding force between the groove ($F_{R1}$) neutralized most of the pressure difference induced force ($F_{pg}$). The tangential force ($F_{t}$) acting on the sliding vane is much less than the pressure difference induced force for the reason that it mainly rest on the rotational inertia of the rotor. Besides, the normal force ($F_{n}$), which mainly affected by the friction forces ($F_{f1}$ and $F_{f2}$) caused by the movement of the sliding vane, increase with rotation of the crankshaft at the first period and decrease at the last period. Moreover, compared with other forces acting on the sliding vane, the binding force ($F_{R1}$), pressure difference induced force ($F_{pg}$), the normal force ($F_{n}$) and friction forces ($F_{f1}$) are much larger and need to be carefully analyzed.

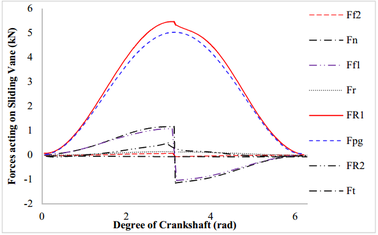
Figure 11. Forces acting on the sliding vane

Figure 12 shows the frictional force and radial force acting on the rotor. Compared with the frictional force acting on the sliding vane, the frictional force acting on the rotor is much smaller, shown as in Figure 12 (a). The radial force acting on the rotor is also much larger than the frictional force acting on the rotor, shown as in Figure 12 (b). The radial force increase with rotation of the crankshaft until reach its maximum value at π position.

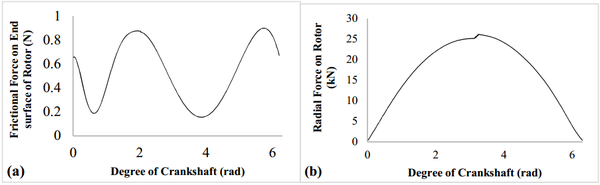
Figure 12. Frictional force and radial force acting on the rotor

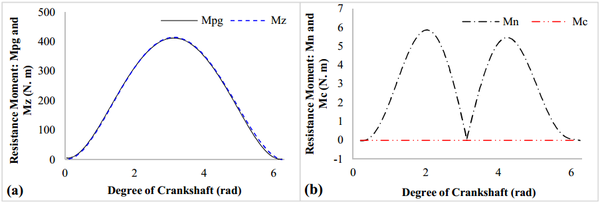
Figure 13 shows the resistance moment acting on the rotor. It can be noted that the total resistance moment ($M_{z}$) is mainly composed by the resistance moment ($M_{pg}$) caused by the pressure difference induced force, for the reason that the values of these two resistances are almost the same, shown as in Figure 13 (a). Meanwhile, the values of the resistance moment caused by the normal force at round end of the sliding vane ($M_{n}$) and the friction moment between the rotor and crankshaft ($M_{c}$) are much smaller than that of the resistance moment ($M_{pg}$) caused by the pressure difference induced force, shown as in Figure 13 (b). Then, the resistance moment $M_{n}$ and $M_{c}$ acting on the rotor can be neglected during the analysis of the pump for the resistance moment is mainly contributed by the resistance moment of $M_{pg}$ which need carefully analyzed.

Figure 13. Resistance moment acting on the rotor

6. Conclusion

The structural characteristics and working process of the proposed ERMP are introduced. The mathematic models of the kinematic and dynamic behaviors of key components of the pump are established. Based on the work done in this research, the following results and conclusions were obtained:

1. The velocity and acceleration of the sliding vane vary with degree of crankshaft in sine and cosine form, respectively. The sliding vane reaches its maximum value when the crankshaft rotates to the $\pi$ position.
2. The areas on the surface of rotor located opposite the sliding vane and apart from the center have larger velocities and wear problem during application of the pump.
3. The binding force, pressure difference induced force, the normal force and friction forces are much larger than other forces and need to be carefully analyzed.
4. The resistance moment is mainly contributed by the resistance moment of $M_{pg}$ induced by the pressure difference of the multiphase flow.

Acknowledgements

The authors acknowledge the support of grant No. 2017QHZ010 from the scientific research-starting project of SWPU China.

References

[1] Porto F., Larson A. Multiphase pump field trials demonstrate practical applications for the technology. SPE Prod. Facil., 12(3):159–164, 1996.

[2] Chynoweth E. Twin screw pump is developed for multiphase applications. Process Eng. London, 67(12):27, 1986.

[3] Neumann W. Efficient multiphase pump station for onshore application and prospects for offshore application. Proceedings of the Eighth International Pump Users Symposium, Texas A&M Univ., College Station, TX, 43–48, 1991.

[4] Beran W.T. On the threshold: subsea multiphase pumping. Proceedings of the 1994 SPE Annual Technical Conference and Exhibition, SPE, New Orleans, 569–581, 1994.

[5] Salis D.J., Cordner M., Birnov M. Multiphase pumping comes of age. World Pumps, 384:53–54, 1998.

[6] Leporcher E., Delaytermoz A., Renault J.F., Gerbier A., Burger O. Deployment of multiphase pumps on a north sea field. Proceedings of the 2001 SPE Annual Technical Conference and Exhibition, SPE, New Orleans, 1755–1766, 2001.

[7] Dogru A.H., Hamoud A.A., Barlow S.G. Multiphase pump recovers more oil in a mature carbonate reservoir. J. Petrol. Technol., 56(2):64–67, 2004.

[8] Bornemann P. Multiphase pumps – the path to success. World Pumps, 511:18–20, 2009.

[9] Cao S., Peng G., Yu Z. Hydrodynamic design of rotodynamic pump impeller for multiphase pumping by combined approach of inverse design and cfd analysis. ASME J. Fluids Eng., 127(2):330–338, 2005.

[10] Cao F., Peng X., Xing Z., Shu P. Thermodynamic performance simulation of a twin-screw multiphase pump. Proc. Inst. Mech. Eng., Part E, 215(2):157–163, 2001.

[11] Chynoweth E. Twin screw pump is developed for multiphase applications. Process Eng. London, 67(12):27–31, 1986.

[12] Dal P.D., Larson L.A. Multiphase pump field trials demonstrate practical applications for the technology. SPE Prod. Facilities. 12(3):159–164, 1996.

[13] Ryazantsev V.M., Plyasov V.V., Shumakov N.D. Twin-screw pumps for transferring petroleum-water-gas multiphase mixture or diesel fuel. Chem. Petrol. Eng., 40(8):407–410, 2004.

[14] Nakashima C. Y., Oliveira S. Heat transfer in a twin-screw multiphase pump: thermal modeling and one application in the petroleum industry. Energy, 31(15):3415–3425, 2006.

[15] Muller L.D., Rohlfing G., Spelter H. Twin screw pumps help improving oil recovery in mature fields and transfer heavy crude oil over long distances. Oil Gas Eur. Mag., 35(3):127–131, 2009.