Resumen

En este trabajo se presenta un método para la optimización de forma de modelos bidimensionales sometidos a casos de carga simple o múltiple. La optimización se realiza aplicando iterativamente reglas evolutivas, basadas en el nivel de esfuerzos. Dichas reglas determinan zonas de la frontera en las que el material es subutilizado o sobreutilizado con el objetivo de que el modelo evolucione a un modelo más ligero y con un nivel de esfuerzos alto y homogéneo. La evolución se lleva a cabo modificando la frontera del modelo lentamente. Dado que la frontera se define con curvas paramétricas B-spline los cambios generados resultan en una frontera suave. La principal propuesta del método es que la modificación de la frontera está dada por un conjunto de desplazamientos que toman en cuenta, en su magnitud y dirección, la información geométrica de la vecindad, a diferencia de otros métodos que simplemente generan desplazamientos perpendiculares a la frontera. Al final del trabajo se presenta el diseño de un marco de bicicleta para mostrar el buen desempeño del método.

Abstract

This paper presents a method for shape optimization of two-dimensional models subjected to simple or multiple load cases. The optimization is performed iteratively using evolutionary rules, based on the stress level. These rules determine regions on the boundary where the material is underused or overused; the objective is that the model evolves to a minimum weight model with a high and homogeneous stress level. The evolution is performed by modifying the boundary of the model slowly. Since the boundary is defined by parametric B-spline curves, generated changes result in a smooth boundary. The main proposal of the method is that boundary modifications are given by a set of displacements that, its magnitude and direction, take into account the geometrical information of the neighborhood, unlike other methods that simply generate displacement perpendicular to the boundary. Finally, the paper presents the design of a frame bike in order to show the good performance of the method.

Palabras clave

Diseño mecánico ; Diseño óptimo ; Optimización estructural ; Optimización de forma ; Métodos evolutivos

Keywords

Mechanical design ; Optimal design ; Structural optimization ; Shape optimization ; Evolutionary methods

1. Introducción

Tradicionalmente, la calidad de la solución a un problema de diseño depende de la experiencia diseñador. El tiempo de diseño y sus costos son una función de la experiencia del diseñador y su equipo de trabajo, así como de su conocimiento de metodologías efectivas de diseño. En este sentido puede pensarse que, entre mayor sea la experiencia mejor será el diseño; sin embargo, es imposible que un diseñador pueda proponer y analizar todas las posibles soluciones a un problema de diseño pues, en general, estos son problemas con múltiples soluciones. Por otra parte, el número de variables de diseño que pueden ser consideradas por una persona y su equipo es limitado. Lo anterior trae como consecuencia que es casi imposible obtener de manera tradicional la solución óptima a un problema de diseño, entendida como la mejor solución posible al problema.

Los métodos de optimización se caracterizan por su capacidad de abordar problemas con múltiples: variables, escenarios y soluciones. Dadas estas características, estos métodos son ideales para la solución de problemas de diseño. El primero en aplicar optimización en el diseño de estructuras fue Maxwell [1] a finales del siglo xix , seguido por Michell [2] con su Optimal Layout Theory. Con la segunda mitad del siglo xx comenzó el desarrollo de métodos de búsqueda basados en Inteligencia Artificial (AI por sus siglas en inglés), métodos poderosos de análisis como el Método de los Elementos Finitos (FEM) y el Método de los Elementos Frontera (BEM), y de equipos de cómputo cada vez más veloces y con mayor capacidad. Esta conjunción de desarrollos ha permitido en los últimos años la aparición de poderosos métodos de optimización aplicados en o creados para diferentes áreas de la ingeniería.

Una de estas áreas es la ingeniería de estructuras para la cual se han desarrollado varios métodos que se engloban con el nombre de métodos de optimización estructural. Los métodos más sobresalientes son aquellos que simulan la manera en la que los seres se adaptan a su medio en la naturaleza, esto es, métodos que lenta e iterativamente cambian las características de una estructura de tal forma que ésta mejora su desempeño en cada iteración. En este sentido, se puede decir que dichos métodos emplean reglas evolutivas para tomar decisiones durante el proceso de diseño lo cual, en cierta medida, sustituye la experiencia de los diseñadores

Cada uno de los métodos emplea reglas o estrategias y criterios similares para provocar que las estructuras evolucionen hacia un óptimo. Lo que verdaderamente distingue a los métodos es la manera en que modifican a las estructuras. Por ejemplo, en el método Evolutionary Structural Optimization o ESO (Xie [3] , Steven [4] , Querin [5] ) la evolución se logra quitando y añadiendo segmentos de material en zonas sub y sobre utilizadas, respectivamente. Métodos que emplean motores de búsqueda inteligentes como Algoritmos Genéticos (GA por sus siglas en inglés) y que tiene muchos exponentes (Velázquez [6] y Annicchiarico [7] solo por mencionar un par) combinan las características de soluciones diversas a lo largo de muchas iteraciones hasta lograr la convergencia en el desempeño de la estructura. En estos no hay una adición o remoción de material como tal. No así en los desarrollados por Mattheck [8]  and [9] , Sethian [10] , Ramm [11] , Maute [12] , Cerver a[13] , entre otros, en los cuales se modifica la forma de una estructura con base en cambios en su frontera, definidos por la aplicación de reglas evolutivas en los puntos que la constituyen.

En estos últimos casos, en los que propiamente se habla de optimización de forma, la frontera de una estructura cambia con base en su respuesta ante una situación dada de cargas. Dicha respuesta puede estar dada en términos de esfuerzo, deformación, energía de distorsión, características geométricas como curvatura, etc., calculados sobre los puntos de la frontera. En general, la optimización de la forma se genera aplicando, sobre dichos puntos, desplazamientos en dirección perpendicular a la frontera y cuya magnitud es calculada de manera diferente por cada método.

Aunque la manera descrita de llevar a cabo la optimización ha demostrado ser efectiva pues genera buenos resultados, puede ser mejorada. El desplazar perpendicularmente punto a punto la frontera, en general, pierde la información geométrica importante de los puntos vecinos. Es decir, la respuesta en un punto de una estructura depende en gran medida de las características de su vecindad, por lo que desplazar la frontera solo en dirección perpendicular no toma en cuenta dicha dependencia.

En este trabajo se presenta un método de optimización de forma que iterativamente modifica la forma de una estructura, modelada con curvas paramétricas, tomando en cuenta la respuesta de la estructura en los puntos de su frontera y su relación geométrica con su vecindad. Como se describe más adelante, la información de las relaciones geométricas se logra a través de las funciones de interpolación que definen las curvas paramétricas con las que se modela el contorno de la estructura. Dichas funciones se utilizan para calcular valores de ponderación que miden la influencia de la vecindad sobre un punto dado, para calcular la dirección que debe tener el desplazamiento aplicado durante cada iteración del proceso de optimización.

2. Modelado paramétrico

Una característica que es requerida en la forma de una estructura es que su contorno no presente cambios bruscos de dirección que puedan resultar, por ejemplo, en concentradores de esfuerzos. Por lo tanto, durante el proceso de optimización es necesario evitar que el contorno de la estructura forme zonas de curvatura elevada. El uso de curvas paramétricas adecuadas puede ayudar para tal situación, en particular aquellas diseñadas especialmente para comportarse «suavemente» ante los cambios.

En el diseño el uso de las curvas paramétricas, tales como las B-splines, es muy socorrido debido a que presentan propiedades deseables en dicha actividad (Shene [14] ):

  • Intuitivas- los cambios realizados en ellas tienen una interpretación geométrica que puede intuirse
  • Flexibles- la forma de crearlas y editarlas es muy sencilla y se tiene gran control sobre dichos cambios
  • Manejo unificado- la creación de diferentes curvas no requiere técnicas distintas de manipulación
  • Invariantes- la curva no cambia su geometría bajo transformaciones tales como traslación y rotación
  • Eficiencia y estabilidad numérica- la ejecución de cálculos sobre la curva no provocan distorsión de su forma

Sean los puntos P1,P2,…,Pm de control de un polígono y 0=u1≤u2≤…≤ um=1 valores del parámetro u que define m-1 segmentos. La curva B-spline C(u) , formada por m-1 segmentos polinomiales de grado p cada uno, contenida por el polígono de control se define como:

( 1)

donde Ni,p(u) son funciones de interpolación de grado p definidas por:

( 2)

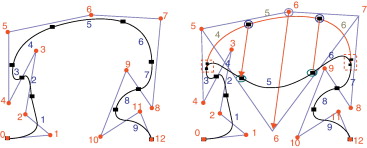
De las ecuaciones anteriores y de la figura 1 se destaca que el cambio en la forma de una curva B-spline es resultado del cambio de posición de los puntos de control y que dicho cambio genera cambios solo en una región bien definida de la curva.


Curva B-spline y su polígono de control. a) curva original, b) el punto de ...


Figura 1.

Curva B-spline y su polígono de control. a) curva original, b) el punto de control 6 es desplazado lo cual genera que la forma de una región bien definida cambie; fuera de dicha región la curva permanece sin cambios.

En cuanto a la optimización de forma, si el análisis en un punto indica que la forma de una estructura debe cambiar, entonces dicho cambio afecta una región bien definida de la curva B-spline que modela la frontera y, por lo tanto, dicho cambio no debe estar basado únicamente en la información del punto de análisis.

3. Método

3.1. Regiones modificables y reglas evolutivas

El método propuesto en este trabajo emplea reglas evolutivas para determinar aquellas regiones, con base en el análisis de los nodos, que deben ser modificadas. En particular, se presenta el método aplicado a problemas de estructuras de mínimo peso con nivel de esfuerzo homogéneo; sin embargo, el método no está restringido solo a este tipo de problemas. Las reglas evolutivas para determinar las regiones modificables son dos: la primera identifica aquellas regiones en las que la estructura está subutilizada, ecuación (3); la segunda identifica las regiones que son sobreutilizadas, ecuación (4).

( 3)
( 4)

donde σi es el esfuerzo de von Mises calculado en un punto i de la frontera, σr es un esfuerzo de referencia (el máximo o el medio de von Mises en la estructura), σy es el esfuerzo de fluencia del material del modelo, TR y TA son tasas de rechazo y adición de material respectivamente. TR y TA marcan los límites en el valor de esfuerzo inferior y superior respectivamente; esto es, regiones subutilizadas son aquellas en que el material es excesivo para la situación de esfuerzos generada y por ello debe retirarse material de ellas, mientras que regiones sobreutilizadas representan una amenaza para la integridad del modelo y deben ser reforzadas agregando material.

La optimización de una estructura se lleva a cabo en un proceso iterativo, evaluando en cada iteración lo siguiente: si alguna de las reglas o ambas se cumplen, la estructura es modificada antes de iniciar una nueva iteración; si las reglas no son satisfechas entonces se dice que se ha llegado a un estado permanente, es decir se ha generado una estructura que no será modificada para los valores dados de TR y TA. En este punto TR y TA cambian de manera que la evolución continúe hacia una estructura con menor peso y un nivel de esfuerzos más alto y homogéneo. El cambio en los valores de TR y TA está dado por:

( 5)
( 6)

donde j representa el j -ésimo estado permanente, TER y TEA son las tasas evolutivas de rechazo y adición respectivamente.

En el caso de estructuras sometidas a N casos de carga, las ecuaciones (3) y (4) se modifican de la siguiente forma:

( 7)
( 8)

donde σi,k y σr,k son los esfuerzos de von Mises en el punto i de la frontera para el k -ésimo caso de carga.

La ecuaciones (7) y (8) representan reglas con lógica AND y OR respectivamente (Li [15] ); esto es, se remueve material siempre y cuando se cumpla la ecuación (7) para todos los casos de carga mientras que se añade material cuando al menos para un caso de carga se cumple (8).

3.2. Relación entre nodos y puntos de control

La optimización de forma se lleva a cabo alterando la geometría de la frontera del modelo o estructura a optimizar, lo cual se logra desplazando los nodos que componen a la curva B-spline que la modela. El desplazamiento de los nodos es resultado de cambiar la posición de los puntos de control de la curva, de acuerdo con la ecuación (1). Como fue mencionado anteriormente, en este trabajo se propone un método para cambiar la forma de la frontera de un modelo empleando la información no solo de los nodos en particular sino también de su vecindad.

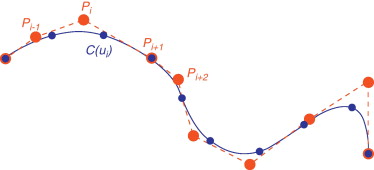
La posición de un nodo C(ui) de una curva B-spline depende de la posición de p+1 puntos de control, es decir: Pi-1, Pi, Pi+1,…,Pi+p-1 (Shene [14] ). En la figura 2 se muestra, para un polinomio de grado p=3 , cuáles son los puntos de control que definen la posición de un punto C(ui) . Para la curva mostrada en la figura, la ecuación (1) adquiere la forma de la ecuación (9).

( 9)


La posición de un nodo sobre la curva paramétrica está definida por un conjunto ...


Figura 2.

La posición de un nodo sobre la curva paramétrica está definida por un conjunto de puntos de control.

En forma matricial, la ecuación (9) es:

( 10)

Por otra parte, las funciones de interpolación tienen la propiedad de unicidad, ecuación (11). la cual indica que los puntos de control Pi-1,Pi,Pi+1,…,Pi+p-1 contribuyen en la posición del nodo C(ui) con porcentajes Ni-1(ui),Ni(ui),Ni+1(ui),…,Ni+p-1(ui) .

( 11)

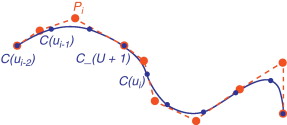
En este mismo sentido, un punto de control Pi influye en la posición de los nodos C(ui-p+1),C(ui-p+2),…,C(ui),C(ui+1) siendo Ni(ui-p+1),Ni(ui-p+2),…,Ni(ui),Ni(ui+1) los valores de dicha influencia, respectivamente, tal como se muestra en la figura 3 . Es importante señalar que en este caso la propiedad de unicidad no se satisface, es decir:

( 12)


La posición de un punto de control está definida por un conjunto de nodos sobre ...


Figura 3.

La posición de un punto de control está definida por un conjunto de nodos sobre la curva paramétrica.

De las relaciones entre nodos, puntos de control y las ecuaciones (11) y (12) se concluyen dos cosas: en primer lugar, la posición de un nodo está dada por un conjunto de puntos de control los cuales contribuyen de manera porcentual a dicha posición; en segundo lugar, la posición de un punto de control está dada por un conjunto de nodos sobre una curva B-spline cuyas funciones de interpolación no cumplen con la propiedad de unicidad y, por lo tanto, no pueden considerarse como valores porcentuales o fraccionarios de influencia. Esto último es de gran importancia para las ideas que se presentan a continuación.

Si el nodo C(ui)   debe cambiar su posición por un desplazamiento , entonces Pi-1,Pi,Pi+1,…,Pi+p-1 cambiarán la suya por los desplazamientos , respectivamente. Ahora bien, si dos nodos vecinos C(ui) y C(ui+1)   deben cambiar su posición, respectivamente, por desplazamientos y independientes entre sí, entonces para los puntos de control relacionados con estos nodos deben calcularse los conjuntos de desplazamientos, también independientes entre sí, y , donde el primer subíndice corresponde al punto de control a desplazar y el segundo al nodo que provoca el desplazamiento.

Se observa que, para que ambos desplazamientos nodales sean posibles, varios puntos de control deberían sufrir dos desplazamientos independientes lo cual, claramente, no produciría las posiciones deseadas de los nodos. La explicación de esto es simple: una de las características principales de las curvas B-spline, como se explicó anteriormente, es que al desplazar un punto de control se cambia la geometría de una región y no solo de un nodo. Como consecuencia, satisfacer desplazamientos nodales independientes y simultáneos no es posible.

En el caso general, es decir que todos los nodos de la curva deban cambiar de posición, los desplazamientos simultáneos que debería sufrir un punto de control Pi son: . Cada uno de estos desplazamientos, todos ellos independientes entre sí, indica que el punto de control debe cambiar su posición para que un nodo cambie parcialmente la suya.

En este punto es importante señalar lo siguiente. A pesar de que la ecuación (10) aparentemente indica una manera de calcular los puntos de control para un conjunto de nodos dado, simplemente premultiplicando por la inversa de la matriz, en realidad no es lo mejor en el caso descrito. Lo anterior se debe a que, de acuerdo con la ecuación (2), las funciones de interpolación Ni,p(u) dependen de relaciones entre valores discretos del parámetro (u1, u2, …, um) , los cuales a su vez dependen de la geometría de la curva B-spline. Dada una curva, se pueden calcular los parámetros con base en los métodos: espaciado uniforme, longitud de cuerda, centrífugo, entre otros, obteniendo resultados muy diferentes con cada uno de ellos. En este trabajo se empleó el método Centrífugo debido a que es el que genera menores “rizos” en las curvas B-spline (Shene[14] ).

Si la posición de cada nodo es modificada directamente, en lugar de hacerlo a través de los puntos de control, las relaciones entre los valores u1, u2, …, um cambia y, por lo tanto, las funciones de interpolación también deberían cambiar, esto es, ser recalculadas. Como consecuencia, la matriz de funciones de interpolación cambiaría. Es por esto que en los sistemas CAD la forma de una curva B-spline, en la mayoría de los casos, es modificada desplazando los puntos de control.

De lo anterior, resulta evidente que es imposible cumplir exactamente con el desplazamiento requerido sobre cada punto de control que, de manera independiente, cada nodo requiere. Dicho de otra manera, el optimizar la forma de un modelo requiere que su frontera sea modificada con base en el valor de una o varias características de la misma; por ejemplo, en el caso de este trabajo, el nivel de esfuerzos. Dichas características no solo dependen de la geometría del modelo, sino de muchas otras variables. Esta complejidad inherente provoca que los desplazamientos nodales necesarios en la optimización sean independientes entre sí y, por lo tanto, imposibles de satisfacer simultáneamente si se desea conservar las bondades de las curvas B-spline.

Para remediar lo anterior, en este trabajo se propone utilizar la información de la influencia del punto de control sobre la posición de los nodos, es decir, los valores de las funciones de interpolación, para determinar la prioridad de los desplazamientos. Así, las funciones de interpolación se convierten en valores de ponderación en el cálculo de los desplazamientos que un punto de control debería realizar en cada iteración del proceso de optimización. En la siguiente sección se describe detalladamente este punto.

3.3. Cálculo de los desplazamientos ponderados

El cálculo de los desplazamientos de los puntos de control se realiza en tres pasos:

  • Determinar los desplazamientos nodales
  • Calcular la dirección de los desplazamientos de los puntos de control
  • Calcular la magnitud de los desplazamientos de los puntos de control.

Paso 1. Los desplazamientos nodales se calculan para aquellos nodos que satisfacen las ecuaciones (3) y (4) en el caso de un solo caso de carga, o las ecuaciones (7) y (8) para múltiples casos de carga. Su magnitud está dada por el valor del esfuerzo calculado en el nodo y el valor del esfuerzo de referencia. En el caso de carga simple, la ecuación (13) corresponde a los nodos que cumplen con la ecuación (3), mientras que la (14) corresponde a los que satisfacen la (4).

( 13)
( 14)

Para múltiples casos de carga, a las ecuaciones (7) y (8) les corresponden las ecuaciones (15) y (16) respectivamente:

( 15)
( 16)

donde k indica cada uno de los casos de carga.

La dirección de los desplazamientos nodales está dada por el vector unitario perpendicular y externo de la frontera en el nodo ( ). La dirección es:

  • , si las ecuaciones (3) o (7) se satisfacen
  • , si las ecuaciones (4) u (8) se cumplen

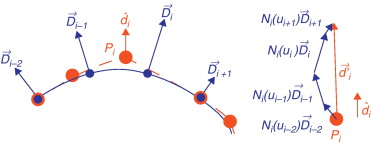
Paso 2. La dirección de los desplazamientos de los puntos de control se basa en los desplazamientos nodales calculados y las funciones de interpolación. La posición de un punto de control Pi cambia si los nodos C(ui-p+1),C(ui-p+2),…,C(ui),C(ui+1)   son modificados por desplazamientos . La relación que existe entre nodos y el punto de control está dada por los valores de las funciones de interpolación Ni(ui-p+1),Ni(ui-p+2),…,Ni(ui),Ni(ui+1)   , las cuales son empleadas como valores de ponderación para calcular la dirección del vector , figura 4 , de acuerdo con la siguiente ecuación:

( 17)


La dirección del vector de desplazamiento necesario para un punto de control se ...


Figura 4.

La dirección del vector de desplazamiento necesario para un punto de control se calcula con base en los valores de las funciones de interpolación y los desplazamientos nodales de la frontera.

Paso 3.   El cálculo de la magnitud del vector depende de la magnitud del desplazamiento ( ) que corresponde al nodo que tiene mayor influencia en la posición del punto de control Pi , es decir, q corresponde al subíndice del parámetro u de:

( 18)

De tal forma que la magnitud de está dada por:

( 19)

donde esize es el tamaño promedio de los elementos finitos en la malla del modelo y f es un factor de corrección para evitar que la frontera del modelo se distorsione debido a los desplazamientos acumulados (Cervera [13] , Yang [16] ). Por lo tanto, combinando los resultados de (17) y (19), el vector de desplazamiento de cada punto de control, en una iteración dada del proceso de optimización, se calcula como:

( 20)

3.4. Criterio de paro

El criterio de paro empleado busca la convergencia en el nivel de esfuerzos del modelo (Cervera [13] ). El nivel de esfuerzos NS en una malla con ne elementos finitos está dado por:

( 21)

Con base en este valor, el criterio de paro está dado por:

( 22)

donde t y t+1 corresponden al número de las iteraciones consideradas en el cálculo.

4. Caso de estudio

En este apartado se aplica el algoritmo de optimización propuesto en la optimización de un marco de bicicleta, modelado con un material con módulo de Young 200 GPa y coeficiente de Poisson de 0,3, sujeto a tres casos de carga definidos de acuerdo con el tipo de esfuerzo que realiza el ciclista (ver tabla 1 ). El peso considerado del ciclista fue 75 kg (∼ 750 N).

Tabla 1. Casos de carga considerados en el diseño óptimo del marco de bicicleta (Tom Compton [17] )
Caso Descripción Cond. Avance Velocidad m/s Dirección de la carga Fuerza Asiento (N) Fuerza Manubrio (N) Fuerza pedal (N)
LC1 Avance en una superficie plana de pendiente 0̊ a velocidad moderada Ligero 10 x 0 0 0
y −800 0 −104
LC2 Avance con pendiente ligera (1/10) y velocidad moderada Moderado 8 x 80 0 52
y −796 0 −512
LC3 Avance con pendiente grande (1/25) y baja velocidad. El ciclista no está sentado en el asiento Fuerte 4 x 0 400 414
y 0 0 −1.655

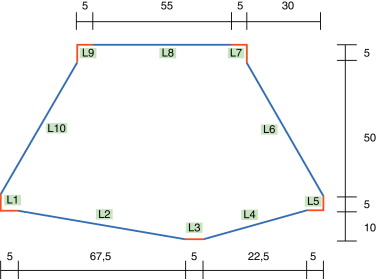
El diseño inicial del marco se muestra en la figura 5 , el cual está modelado con 10 curvas: L1, L3, L4, L5, L7, L9 y L10 son líneas fijas que pueden modificarse, mientras que L2, L6 y L8 son curvas B-spline de grado 3.


Diseño inicial.


Figura 5.

Diseño inicial.

Los valores de los parámetros de optimización empleados son TR = 0,2, TA = 0,95, TRE = 0,01 y TAE = 0,001. Los valores del análisis por elementos finitos calculados para el diseño inicial son los mostrados en la tabla 2 .

Tabla 2. Esfuerzos calculados por medio de análisis por elementos finitos en el diseño incial
Caso de carga Esfuerzo máximo de von Mises (kPa) Esfuerzo promedio de von Mises (kPa)
LC1 623,7 37,6
LC2 658,7 53,7
LC3 600,5 86,9

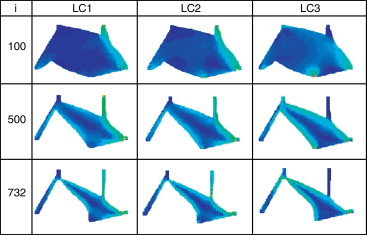
El proceso de optimización se llevó a cabo en 732 iteraciones durante las cuales se eliminó material lentamente del marco mientras la distribución de esfuerzos se homogeneizaba para emplear más eficientemente el material, tal como se muestra en la figura 6 . El diseño final del marco de bicicleta generado por el proceso de optimización es el mostrado en la figura 7 , el cual presenta los valores de esfuerzo de von Mises mostrados en la tabla 3 . En esta misma tabla se muestra una comparación entre los valores de los diseños inicial y final.


Distribuciones de esfuerzos de von Mises de cada caso de carga para diferentes ...


Figura 6.

Distribuciones de esfuerzos de von Mises de cada caso de carga para diferentes iteraciones.


Marco de bicicleta óptimo generado por el método propuesto.


Figura 7.

Marco de bicicleta óptimo generado por el método propuesto.

Tabla 3. Esfuerzos calculados por medio de análisis por elementos finitos en el diseño final (óptimo)
Caso de carga Esfuerzo máximo de von Mises (kPa) Incremento respecto del inicial (%) Esfuerzo promedio de von Mises (kPa) Incremento respecto del inicial (%)
LC1 627,7 0,6 188,9 402,4
LC2 1183,4 79,7 274,2 410,6
LC3 1.602,9 166,9 442,6 409,3

El marco obtenido muestra una mejor utilización del material lo cual se refleja en los valores y porcentajes comparativos mostrados en la tabla 3 , sobre todo en cuanto a los datos del esfuerzo promedio. Por otra parte, este diseño es similar al generado por Mevdev [18] (fig. 8 ) para un marco de bicicleta empleado para una competencia de velocidad.


Bicicleta comercial cuyo diseño fue generado por Mevdev.


Figura 8.

Bicicleta comercial cuyo diseño fue generado por Mevdev.

5. Conclusiones

Existe un número considerable de métodos de optimización de forma en la literatura. Sin embargo, la manera de modificar la geometría de los modelos o estructuras optimizadas de estos métodos no considera la información completa de la región que se está optimizando, sobre todo aquella relacionada con la geometría de la vecindad y su relación con los puntos que se modifican. El método presentado en este trabajo solventa esta deficiencia empleando las características de las curvas paramétricas, en particular las B-spline, las cuales están dadas por las funciones de interpolación que les dan forma. El método así concebido demostró ser capaz de optimizar una estructura sometida a múltiples casos de carga, al grado que el diseño obtenido es similar a uno existente comercialmente.

Agradecimientos

A la Universidad Nacional Autónoma de México por el apoyo proporcionado para la realización de este trabajo a través del proyecto IN108909 «Herramientas Computacionales para el Diseño Óptimo en Proyectos de Ingeniería e Innovación Tecnológica» del Programa de Apoyo a Proyectos de Investigación e Innovación Tecnológica (PAPIIT) de la Dirección General de Asuntos de Personal Académico (DGAPA).

Bibliografía

  1. [1] J.C. Maxwell; On Reciprocal Figures, Frames and Diagrams of Force; Trans Roy Soc Edinburgo, 26 (1872)
  2. [2] A.G.M. Michell; The limits of economy of material in frame structures; Philosophical Magazine, 8 (1904), pp. 589–597
  3. [3] Y.M. Xie, G.P. Steven; Evolutionary Structural Optimization (ESO); (First Edition)Springer, London (1997)
  4. [4] G.P. Steven, Y.M. Xie; Evolutionary Structural Optimization with FEA; Computational Mechanics, 1 (1993), pp. 27–34
  5. [5] O. Querin; Evolutionary Structural Optimisation: Stress Based Formulation and Implementation. Ph. D. Dissertation; Department of Aeronautical Engineering, University of Sydney, Australia (April 1997)
  6. [6] F. Velázquez, S. Santillán; Diseño Óptimo Evolutivo; Ingeniería, Investigación y Tecnología, VII 3 (2006), pp. 139–150
  7. [7] W. Annicchiarico, M. Cerrolaza; Structural Shape Optimization 3D Finite-Element Models Based on Genetic Algorithms and Geometric Modeling; Finite Elements in Analysis and Design, 37 (2001), pp. 403–415
  8. [8] C. Mattheck, S. Burkhardt; A new method of structural shape optimization based on biological growth; Intn. J. Fatigue, 12 (1990), pp. 185–190
  9. [9] C. Mattheck; Design in Nature- Learning from Trees; (First Edition)Springer Verlag, Germany (1998)
  10. [10] J.A. Sethian, A. Wiegmann; Structural Boundary Design via Level Set and Immersed Interface Methods; J. Comp. Phys., 163 (Sep 2000), pp. 489–528
  11. [11] E. Ramm, K. Maute, S. Schwarz; Adaptative Topology and Shape Optimization; Computational Mechanics – New Trends and Applications, CIMNE, Barcelona, Spain (1998)
  12. [12] K. Maute, E. Ramm; Adaptative Topology Optimization; Structural Optimizaction, 10 (1995), pp. 100–112
  13. [13] E. Cervera, J. Trevelyan; Evolutionary structural optimization based on boundary representation of NURBS: Part II: 3D algorithms; Computers & Structures, 83 (23–24) (2005), pp. 1917–1929
  14. [14] C. Shene, Introduction to computing with geometry. Course Notes. [WWW document; consultado 15 Ene 2010]. Disponible en: http://www.cs.mtu.edu/∼shene/COURSES/cs3621/NOTES/ , 1998, July 1
  15. [15] Q. Li, G.P. Steven, Y.M. Xie; On equivalence between stress criterion and stiffness criterion in evolutionary structural optimization; Structural Multidisciplinary Optimisation, 18 (1999), pp. 67–73
  16. [16] H. Yang, W. Wang, J. Sun; Control Point adjustment for B-Spline Curve Approximation; Cumputer – Aided Design, 36 (2004), pp. 639–652
  17. [17] Tom Compton, “Analytic Cycling – Forces on Rider” [documento WWW; consultado 10 Jul 2010], Disponible en: http://www.analyticcycling.com/ForcesPower_Page.html , 2001.
  18. [18] J.J. Mevdev; Design and Optimization of a Carbon Monocoque Bicycle Frame; 4th year Thesis, Department of Aeronautical Engineering, University of Sydney, Australia (1995)
Back to Top
GET EPUB

Document information

Published on 01/09/12
Accepted on 22/06/11
Submitted on 03/05/11

Volume 28, Issue 3, 2012
DOI: 10.1016/j.rimni.2012.03.009
Licence: Other

Web of Science Core Collection® Times cited: 0
Crossref Cited-by Times cited: 1
OpenCitations.net Times cited: 1

Document Score

0

Views 38
Recommendations 0

Share this document

Keywords

• • • •

claim authorship

Are you one of the authors of this document?

I am an author