Resumen
Los programas de ordenador específicos para identificación en análisis modal de estructuras, no son nada económicos; y no siempre se puede disponer de ellos.
En este trabajo se presenta una técnica de optimización simple, que consigue rapidez y calidad de los resultados, en la estimación de las razones de amortiguamiento para cada modo por separado. Y que se puede resolver con una versión de demostración (que se descarga de la red de forma gratuita) de un programa informático comercial de optimización.
Es apropiado para niveles bajos de amortiguamiento estructural (o amortiguamiento independiente de la frecuencia), que son los que se presentan en grandes estructuras. Así mismo, no es necesario que los modos estén bien separados, ni siquiera que la magnitud de los modos próximos sea menor de la propia de aquellos con los que se está trabajando; dentro del algoritmo unos complementos residuales móviles optimizan su posición según los ejes de frecuencias y de ordenadas (magnitud de la respuesta), para tener en cuenta la influencia de los modos fuera del rango bajo estudio. Además, es poco sensible a la presencia de ruido en la señal.
Palabras clave: Amortiguamiento estructural, análisis modal, identificación, optimización
Abstract
Specific computer programs for identification in modal analysis of structures are not economical, and they may not always be available.
This paper presents a technique for simple optimization, getting fast and quality results, in the estimation of the damping ratios for each separate mode, and that can be resolved with a demo version (downloadable for free from the internet) of commercial optimization software.
It is suitable for low levels of structural damping (or non-frequency-dependent damping), which are those that appear in large structures. Likewise, it is not necessary for the modes to be separate, or even that the magnitude of the near modes be less than that of those with which we are working; within the algorithm movable residual complements optimize their position according to the frequency and vertical axes (the response magnitude), to take into account the influence of the modes outside the considered range. In addition, it is not very sensitive to the presence of noise in the signal.
Keywords: Structural damping, modal analysis, identification, optimization
1. Introducción
El análisis modal clásico, frente al operacional, tiene la ventaja de alcanzar una mayor precisión en la identificación de ciertas magnitudes, como son las razones de amortiguamiento. No se trata solo de que la excitación (artificial) sea conocida; sino que se dispone de más procedimientos para estimar los parámetros modales, con el fin de lograr caracterizar el comportamiento estructural [1-4].
A diferencia de las propiedades de rigidez y masa de una estructura, las homólogas de amortiguamiento no pueden determinarse a partir de la geometría de la misma, y de las dimensiones de los elementos estructurales; solo es viable hacerlo experimentalmente, por medio de ensayos, ya que no es posible identificar todos los procesos que intervienen en la disipación de la energía de vibración en las estructuras reales.
Incluso dentro del intervalo de deformaciones lineal, delimitado por el límite elástico de toda la estructura, el amortiguamiento determinado mediante pruebas experimentales puede variar con la amplitud de las deformaciones [5,6]. Esta no linealidad, en general, no se considera en los análisis dinámicos de una forma explícita, esto es, con claridad y determinación.
Dentro del análisis modal operacional, las acciones ambientales constituyen generalmente excitaciones de baja amplitud, por ello la estimación del amortiguamiento es menos precisa, ya que la influencia del ruido se hace más notable, debido a que las oscilaciones de la estructura son más reducidas (y sus resultados por tanto presentan una mayor dispersión) llegando incluso a ser del mismo orden de magnitud que el ruido presente en la señal.
Por consiguiente, la amplitud de la aceleración se ve afectada por el nivel de carga, y esta última altera el amortiguamiento de cada modo (que de hecho no es una magnitud constante); este comportamiento ha sido documentado en [5,6], por ejemplo. Una mayor excitación, produce un mayor amortiguamiento; manifestándose incluso un cierto comportamiento no lineal entre ambos.
La consideración del supuesto de amortiguamiento viscoso como hipótesis de partida en el análisis dinámico de estructuras, puede introducir un error apreciable en los cálculos, ya que la energía disipada por la estructura en su oscilación, en ese caso, es dependiente de la frecuencia, mientras experimentalmente se pone de manifiesto lo contrario, si se atiende al amortiguamiento estructural o histerético. Otros nombres utilizados para referirse a este último mecanismo de amortiguamiento interno son:
- Fricción sólida.
- Amortiguamiento estructural.
- Amortiguamiento material.
- Amortiguamiento independiente de la frecuencia.
- Amortiguamiento histerético o de histéresis.
Este último puede inducir a error, ya que la histéresis es una propiedad de todos los sistemas estructurales, y por ende, de sus materiales constituyentes, que disipan energía.
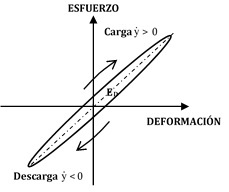
Las cargas alternativas producen un cierto retardo entre las deformaciones y las cargas, por lo que la representación gráfica de los esfuerzos frente a las deformaciones adopta la forma indicada en la Figura 1, denominada ciclo de histéresis.
| Figura 1. Ciclo de histéresis en materiales metálicos estructurales sometidos a cargas alternativas |
En las estructuras metálicas la disipación de energía ocurre debido a imperfecciones en el comportamiento elástico de los materiales sometidos a deformación vibratoria. Este fenómeno, básicamente es debido a:
- Fricción entre las moléculas.
- Deformación permanente si se ha superado el límite elástico.
En la Figura 1, el área del diagrama representa la energía disipada por el sistema en un ciclo de oscilación. Por su parte, el modelo viscoso da lugar a una elipse cuyo tamaño crece con la frecuencia, debido a su dependencia con ella, como ya se ha comentado.
En otro orden de cosas, es sobradamente conocido que en un sistema de varios grados de libertad (en adelante g.d.l.), su comportamiento puede ser descrito como la suma de las contribuciones de varios sistemas independientes de un g.d.l., para cada uno de sus modos de vibración, con lo que la energía disipada en total sería la suma de la correspondiente a cada uno de sus modos de oscilación.
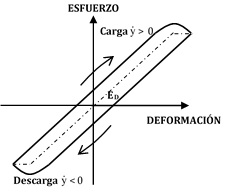
Si a continuación se incrementa la magnitud de la solicitación externa, manteniéndose bajas las frecuencias de excitación, la curva se modifica de la forma siguiente (Figura 2).
| Figura 2. Curva de histéresis de un material metálico. Efecto de la disipación en las fisuras del material |
Por otra parte, entre las ventajas del amortiguamiento histerético estarían:
- Se ajusta de una forma más exacta al comportamiento exhibido por la mayoría de las estructuras reales.
- El análisis de sistemas de varios g.d.l. de forma analítica, es mucho más simple.
La influencia del amortiguamiento en el comportamiento estructural ha sido objeto de estudio en los últimos años, debido a ello, su estimación con la máxima exactitud posible ha cobrado gran importancia. En Montalvão et al. [7] se utiliza la variación en el factor de amortiguamiento como el parámetro principal para la localización del daño estructural. En Montalvão and Silva [8] se efectúa un análisis centrado en la energía disipada por ciclo de vibración, dando lugar a un procedimiento alternativo para la identificación del factor de amortiguamiento; sin embargo, solo es útil si el sistema estructural tiene sus modos de vibración razonablemente separados y poco amortiguados.
Los programas de ordenador comerciales, para análisis dinámico de estructuras en sus dos vertientes: análisis modal clásico y operacional, no son nada económicos, y no siempre se puede disponer de ellos (o quizás de todas las licencias de sus correspondientes módulos); en este trabajo se presenta un procedimiento de optimización sencillo, que opera sobre cada modo por separado, y que se puede resolver con una versión de demostración (descargable de la red de forma gratuita) de un programa informático comercial de optimización.
Trabaja solo con el intervalo correspondiente al pico de cada curva, es decir, el modo de interés en cualquiera de las formas del modelo de respuesta (en lo que sigue se ha expuesto y resuelto para la receptancia). De esta forma, en la función de respuesta en frecuencia (en adelante FRF) analizada, el número de puntos necesarios para definir el pico de cada curva son muy reducidos, así como sus variables asociadas, por lo que una versión de demostración gratuita del programa Gams es suficiente para resolver el modelo matemático de optimización. Eso sí, como contrapartida, son necesarios algunos conocimientos sobre fundamentos de optimización.
2. Determinación de la razón de amortiguamiento aplicando técnicas de optimización
En un sistema de varios g.d.l., la respuesta completa es suma de las contribuciones de cada modo de vibración individual. El conjunto de datos para la extracción de resultados, está constituido por cada una de las FRF, las cuales contienen una parte real y otra compleja.
En el caso general de amortiguamiento estructural (no proporcional), se verifica, para la receptancia (analíticamente es habitual trabajar con ella) [1]:
|
|
(1) |
El modelo modal está constituido por autovalores complejos , razones de amortiguamiento y N autovectores también complejos (en el caso de normalización, de estos últimos, respecto de la matriz de masa). Siendo [1]
|
|
(2) |
Además, representa el residuo y la frecuencia natural, ambas para el modo , siendo la unidad imaginaria.
En la representación gráfica de las mismas, se definen los intervalos que se identifican manualmente (picos de las curvas), en donde se encuentran cada uno de los modos en los que se quiere estimar la razón de amortiguamiento.
En las proximidades de una resonancia , la magnitud resultante de la ecuación (1) está principalmente influida por el modo . Por tanto la ecuación anterior se puede aproximar por
|
|
(3) |
En donde son los complementos residuales móviles (no constantes como se verá posteriormente), para los modos bajos y altos, que tienen en cuenta el efecto, respectivamente, de los modos por debajo y por encima del rango de frecuencias considerado en el análisis. Es decir el efecto de todos los modos (a la izquierda y a la derecha), fuera del rango de análisis se sustituye, mutuamente, por ambas expresiones a ambos lados de la receptancia
|
|
(4) |
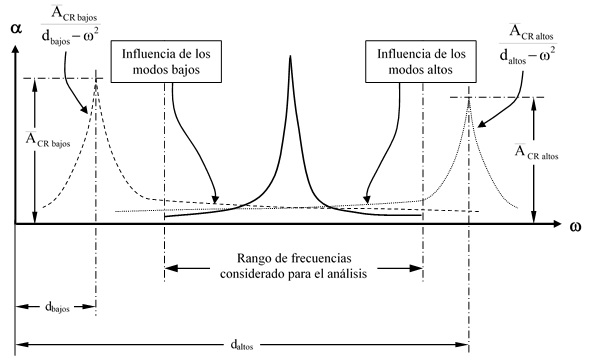
Evidentemente, como ya se ha citado más arriba, estos complementos residuales no son constantes, son funciones que dependen de dos variables; siendo, el desplazamiento horizontal de los a lo largo del eje de frecuencias (para los modos altos y bajos) y, el valor de pico del complemento residual, también (Figura 3) para los modos altos y bajos (la designación de móviles para estos complementos virtuales, hace referencia a que el valor de todas estas variables se ajusta durante el proceso iterativo de optimización).
| Figura 3. Influencia de los modos bajos y altos en el rango de frecuencias bajo estudio |
Nótese que estos residuos tienen partes real e imaginaria, al igual que el de la receptancia (quebrado central), cuya descomposición no es tan inmediata como en el caso de aquellos.
|
|
(5) |
Por consiguiente, dado que en la expresión de la receptancia el numerador y el denominador tienen parte real e imaginaria; una vez que se racionaliza la fracción se hace ineludible separar ambas partes real y compleja en el numerador, con el fin de realizar las estimaciones de las mismas por separado, ya que los programas de optimización comerciales no funcionan con magnitudes imaginarias, solo reales. Después de realizar varias operaciones se llega a [9]
|
|
(6) |
|
|
(7) |
lo que representa la partición buscada.
Cada uno de los intervalos (picos de las curvas en las FRF), deben ser ajustados utilizando un análisis de regresión, para ello se utiliza el método de estimación del mínimo valor absoluto [10]
|
|
(8) |
Los parámetros modales se estiman resolviendo el siguiente problema de programación no lineal
|
|
(9) |
El conjunto de soluciones admisibles, queda definido, por el conjunto de restricciones no lineales del problema
|
|
(10) |
donde es el número de muestras o de puntos en los que se ha medido la respuesta, y son la magnitud de la misma (son datos: ordenadas de las FRF), y , la estimación, respectivamente, de la parte real e imaginaria del intervalo de la receptancia considerada (ec.(5)).
Este trabajo se ha resuelto empleando el lenguaje de programación para optimización GAMS por la familiaridad del autor con el mismo. Pero existen otros paquetes comerciales de características similares en el mercado, como el AMPL y el AIMS; en principio todos ellos serían válidos para el fin propuesto.
Con esto finaliza la exposición del procedimiento analítico de estimación, seguidamente, para ilustrar el mismo, se aplica a un ejemplo numérico mediante un modelo analítico simulado numéricamente con el programa Matlab, y a continuación se aplica a un puente actualmente en servicio.
3. Validación sobre modelo numérico
En este apartado se muestran el análisis y resultados de la aplicación del procedimiento descrito en el apartado 2 sobre un modelo numérico simulado en ordenador; para ello, se ha escogido para esta muestra un modelo de edificio simple de 4 g.d.l. (caso de amortiguamiento histerético general) cuyas matrices de masa y rigidez , son las siguientes
|
|
(11) |
|
|
(12) |
Con el citado programa Matlab de cálculo numérico, se resuelve el problema directo para obtener los autovectores y autovalores (modos de vibración, frecuencias naturales y razones de amortiguamiento respectivamente), que posteriormente -estas dos últimas- sirven de referencia en el proceso de optimización para comprobar la bondad del resultado obtenido (Tabla 1).
| Modo nº | Magnitudes de referencia | Razón de amortig. |
Frecuencia natural [rad/s] |
Intervalo de frecuencias en la identificación [rad/s] | ||
|---|---|---|---|---|---|---|
| Razón amortig. |
Frecuencia [rad/s] |
Ruido ±15% | Ruido ±15% | Mín. | Máx. | |
| 1 | 0.0619 | 7.6654 | 0.0662 | 7.6588 | 2.0 | 12.5 |
| 2 | 0.0508 | 24.8401 | 0.0522 | 24.8751 | 16.5 | 31.5 |
| 3 | 0.1333 | 38.1779 | 0.1554 | 37.9200 | 31.5 | 44.5 |
| 4 | 0.0464 | 50.9901 | 0.0450 | 51.0251 | 44.5 | 62.0 |
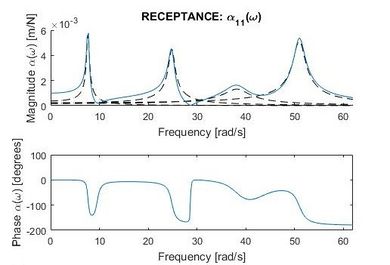
Con los resultados obtenidos, a continuación se simulan numéricamente la matriz [] de FRF, para ilustrar el presente apartado se escoge una de sus componentes (Figura 4), y se aplica el procedimiento descrito en el Apartado 2.
Con todo ello se observa que se alcanzan plenamente los resultados teóricos de referencia (Tabla 1): razones de amortiguamiento y frecuencias naturales.
| Figura 4. Función de respuesta en frecuencia genérica |
Finalmente, para validar el ejemplo numérico, se introduce en la FRF de estudio un ruido blanco artificial de magnitud ±15%, obteniéndose los resultados que se muestran en la Tabla 1. Obsérvese que las diferencias en el modo número 3, se deben a que su contribución a la respuesta es mucho menor (Figura 4).
4. Características del puente analizado
El puente de La Cartuja está ubicado en el Meandro de San Jerónimo, en Sevilla (España), sobre el río Guadalquivir [11,12]. Se trata de un puente de tipo viga cajón continua de sección variable, con tablero ortótropo, totalmente metálico, que respeta la visibilidad del entorno mediante una estructura discreta y elegante.
Consta de 3 vanos, con una longitud total de 238 m: 42.5 m en el vano lado Expo, 170 m en el vano central, y 25.5m en el vano lado Sevilla. La viga cajón o viga principal del puente, está rigidizada mediante marcos de rigidización transversal cada 4.25 m, los cuales dividen el puente en 56 módulos. El peso acabado del puente es de 1869 t, equivalente a 714 kp/m2 (Figuras 4 y 5).
| Figura 5. Vista en alzado, de la viga principal del Puente de la Cartuja |
El ancho del tablero es de 11 m y el canto de la viga variable: desde los 1.92m del estribo lado Expo que aumenta progresivamente hasta llegar a los 6 m en la pila del mismo margen, para disminuir hasta alcanzar los 3 m manteniéndose prácticamente constante en buena parte del vano central y vano lateral lado Sevilla; lo cual representa una relación luz/canto de 56.6: este valor en su día fue el menor registrado en un puente, por lo que se convirtió en el puente más esbelto del mundo. Haciendo gala de una elegancia inédita hasta entonces. Figura desde el año 2007 en el Libro Guinnes de los records.
La continuidad de la viga del puente en los tres vanos, permite alcanzar esta esbeltez, gracias a los vanos laterales relativamente cortos y a las ménsulas ubicadas en el tablero y en los estribos, a través de los cuales se trasmiten reacciones negativas (Figura 4).
| Figura 6. Vista, en primer término, del Puente de la Cartuja |
5. Análisis de resultados
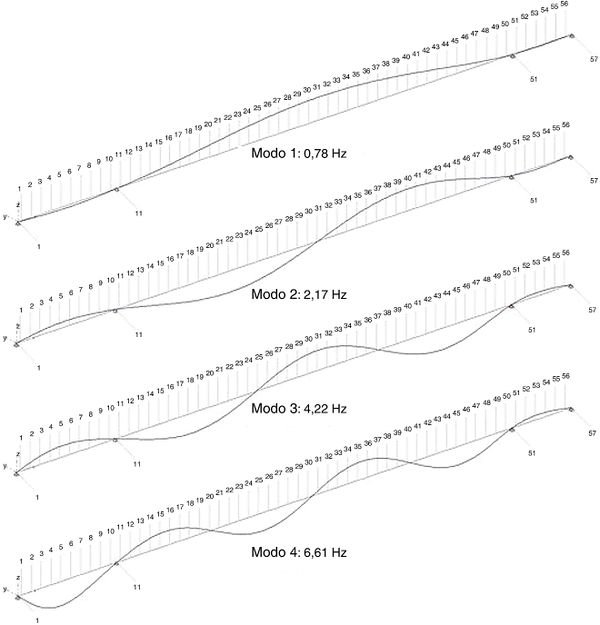
En la Tabla 2, se presenta un resumen de los resultados alcanzados. Las magnitudes de referencia, se han extraído del conjunto de parámetros modales, que caracterizan el comportamiento dinámico del puente analizado, correspondientes a un trabajo anterior [13]. En donde se ajustó su modelo de respuesta, según un patrón independiente de la frecuencia (amortiguamiento estructural). Así mismo, para la exposición de resultados, se utilizan los cuatro primeros modos en flexión vertical (Figura 7), que fueron identificados en el citado trabajo [13].
| Modo de flexión vertical nº |
Magnitudes de referencia | Razón de amortiguamiento |
Frecuencia natural [rad/s] |
Intervalo de frecuencias en la identificación [rad/s] | ||||
|---|---|---|---|---|---|---|---|---|
| Razón amortig. |
Frecuencia [rad/s] |
Sin ruido | Ruido ±15% | Sin ruido | Ruido ±15% | Mín. | Máx. | |
| 1 | 0.0173 | 4.9264 | 0.0173 | 0.0169 | 4.9262 | 4.9342 | 4.6 | 5.2 |
| 3 | 0.0098 | 13.6487 | 0.0113 | - | 13.6986 | 14.3082 | 12.6 | 14.6 |
| 4 | 0.0165 | 26.5091 | 0.0165 | 0.0163 | 26.5091 | 26.5065 | 26.4 | 26.6 |
| 6 | 0.0072 | 41.5143 | 0.0072 | 0.0065 | 41.5100 | 41.5034 | 41.0 | 42.0 |
| Figura 7. Flexión vertical: primeros cuatro modos de oscilación |
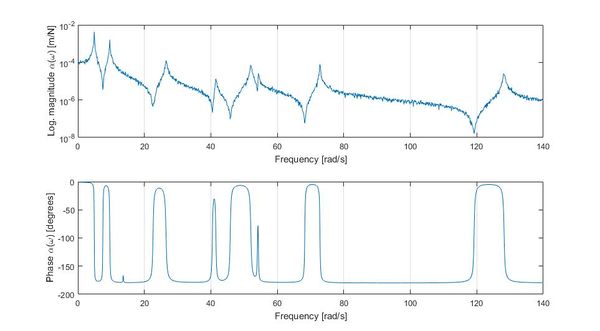
La Figura 8 muestra una parte del modelo de respuesta del mismo: una de las componentes de la matriz de FRF (magnitud y fase), perteneciente a su diagonal principal, con un nivel de ruido en la señal del , para un g.d.l. vertical, en las cercanías de la posición intermedia del vano central del puente, y muy próximo a la clave del mismo; ubicado en la sección nº 32 de la viga principal del puente.
| Figura 8. Componente perteneciente a la diagonal principal (magnitud y fase) de la matriz de FRF, con un nivel de ruido en la señal de , correspondiente a la sección 32 del puente (g.d.l. vertical) |
Es necesario no perder de vista, que en el gráfico del párrafo anterior (Figura 8), los modos de flexión vertical y horizontal están mezclados. En la Tabla 2, se muestran los resultados de las razones de amortiguamiento y las frecuencias naturales, identificadas ambas, para los cuatro primeros modos de flexión vertical según se ha dicho, para su comparación con las magnitudes de referencia [13]: en lo que respecta a la frecuencia natural y la razón de amortiguamiento (ambas correspondientes a cada nº de modo ), sin ruido, y con un nivel adicional de ruido en la señal de 15%; así mismo, se muestran también los intervalos de frecuencias en la identificación (picos de cada curva pertenecientes a cada modo de interés), que se han utilizado para su introducción en el algoritmo de optimización, modelado con el programa informático Gams: sistema de modelado para la programación matemática y la optimización [14].
El nivel de ruido se ha ido incrementando de forma progresiva, en distintas etapas del cálculo de optimización. En el caso del modo 3 -en la numeración mixta de los modos-, llega un momento, en el que el optimizador ya no es capaz de llegar a la solución (en el caso del amortiguamiento), aunque sí le es posible estimar la frecuencia de resonancia. Ello es debido a que la contribución a la respuesta de este segundo modo de flexión vertical (13.6487 rad/s) es muy reducida en la ubicación de referencia (sección nº 32 del puente: Figura 7).
Es de destacar el caso del modo de flexión vertical nº 4 (Tabla 2), su deformada en flexión vertical (vector modal o autovector), contiene también algo de deformación horizontal (Figura 7); y su frecuencia natural 26.5091 rad/s, tiene el modo 5 (de flexión horizontal) muy próximo, a 26.6802 rad/s. Sin embargo, el algoritmo permite obtener una estimación sólida a pesar de la interferencia entre modos próximos. A diferencia de [8], con este procedimiento no es necesario que los modos de vibración se encuentren convenientemente separados.
Los complementos residuales móviles optimizan su posición según los ejes de frecuencias y de ordenadas (magnitud de la respuesta), para tener en cuenta la influencia de todos los modos fuera del rango bajo estudio. Siendo además el algoritmo, poco sensible a la presencia de ruido en la señal.
Las diferencias entre el presente trabajo. con [9] (caso de amortiguamiento histerético general) y [15] (caso de amortiguamiento viscoso general), radica en que en ambos se realiza un ajuste global mediante optimización de toda la matriz FRF (se requiere un tiempo de cálculo elevado y una potencia computacional de procesamiento notable) y en un análisis/ancho de frecuencias que comprende varias frecuencias naturales y modos de vibración simultáneamente; mientras que en el presente trabajo, se coge solo una de las componentes de esa matriz (una única curva) y se analiza un intervalo de la misma que contiene el pico de interés (modo de vibración) de esa curva, de forma que el tiempo de cálculo y la potencia requeridos, son ridículos, abordables con cualquier ordenador personal común. A este respecto, nótese el paso de la expresión (1) a la (3), o por ende a la (4).
Ya en otro orden de cosas, con el lenguaje de programación Gams, los procesos de modelado y resolución del problema están separados; esto tiene la virtud de que el operador se centra solo en el primero, y se olvida de la marcha del algoritmo interno que precisa para resolverlo; para alcanzar la solución del modelo, se utiliza un optimizador de programación no lineal, denominado nlp. Finalmente, en la Tabla 3 se muestra información sobre la convergencia de los resultados: nº de iteraciones, tiempo empleado, y valor alcanzado por la función objetivo z.
| Modo de flexión vertical nº |
Optimizador de programación no lineal (nlp) | ||
|---|---|---|---|
| nº iteraciones | Tiempo [s] | Función objetivo z | |
| 1 | 95 | 0.08 | 0.934·10-5 |
| 3 | 77 | 0.08 | 1.140·10-5 |
| 4 | 42 | 0.02 | 0.053·10-5 |
| 6 | 51 | 0.14 | 1.303·10-5 |
6. Conclusiones
Con este procedimiento, se puede determinar la razón de amortiguamiento según un patrón estructural (independiente de la frecuencia) en estructuras ligeramente amortiguadas, para cada modo por separado en las proximidades del mismo, independientemente de la interferencia y magnitud de los modos próximos con un razonable grado de exactitud. Por tanto, tampoco es necesario para que el algoritmo converja, que los modos próximos sean de una magnitud menor al resonante bajo estudio.
Se trata de una técnica de optimización simple, que permite rapidez en las estimaciones de los factores de amortiguamiento, con una buena exactitud. Es poco sensible a la presencia de ruido en la señal y se puede implementar, en una versión de demostración gratuita de un programa informático de optimización.
Referencias
[1] Mendes N.M., Montalvão J.M. Theoretical and experimental modal analysis. Research Studies Press Ltd. – John Wiley Sons Inc., New York, 1997.
[2] Sitarz P., Powałka B. Modal parameters estimation using ant colony optimisation algorithm. Mechanical Systems and Signal Processing, 76-77:531–554, 2016. DOI: http://dx.doi.org/10.1016/j.ymssp.2016.01.013
[3] Lardiès J. Modal parameter identification by an iterative approach and by the state space model. Mechanical Systems and Signal Processing, 95:239–251, 2017. DOI: http://dx.doi.org/10.1016/j.ymssp.2017.03.010
[4] Cacho-Pérez M., Frechilla N., Lorenzana A. Estimación de parámetros modales de estructuras civiles a partir de la función de respuesta en frecuencia. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 33(3-4):197-203, 2017. DOI: http://dx.doi.org/10.1016/j.rimni.2016.02.001
[5] Sebastián J., Díaz I.M., Casado C.M., Poncela A.V., Lorenzana A. Evaluación de la predicción de aceleraciones debidas al tránsito peatonal en una pasarela en servicio. Informes de la Construcción, 65-531:335-348, 2013. DOI: 10.3989/ic.12.025
[6] A. Cappellini, S. Manzoni, M. Vanali, Experimental and numerical studies of the people effects on a structure modal parameters. Proc. 30th International Modal Analysis Conference IMAC XXX, Jacksonville, USA, (2012).
[7] Montalvão D., Cláudio R.A.L.D., Ribeiro R.A.L.D., Duarte-Silva J. A method for the localization of damage in a CFRP plate using damping. Mechanical Systems and Signal Processing, 23:1846–1854, 2009. DOI: http://dx.doi.org/10.1016/j.compstruct.2012.10.050
[8] Montalvão D., Silva J.M.M. An alternative method to the identification of the modal damping factor based on the dissipated energy. Mechanical Systems and Signal Processing, 54-55:108–123, 2015. DOI: http://dx.doi.org/10.1016/j.ymssp.2014.08.025
[9] Villa L.M., Application of optimization techniques for determining modal parameters by means of frequency response functions. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 23-4:395-414, 2007.
[10] Castillo E., Hadi A. S., Lacruz B. Regresión Diagnostic for the Least Absolute Value and the Minimax Methods. Communications in Statistics, Theory and Methods, 30:381-395, 2001.
[11] Asensio Cerver F. Bridges. Atrium, Barcelona, 1st ed., 1992.
[12] Sevilla: Puentes del 92, Colegio de Ingenieros de Caminos, Canales y Puertos de Andalucía (Sección de Publicaciones), 1992.
[13] Villa L.M., Comparison of the estimated modal parameters of structures from classical and operational modal analysis with mass changes. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 33(3-4):188–196, 2017. DOI: http://dx.doi.org/10.1016/j.rimni.2016.04.003
[14] Castillo E., Conejo J. A., Pedregal P., García R., Alguacil N. Building and Solving Mathematical Programming Models in Engineering and Science. Research Studies Press Ltd., 2001.
[15] Villa L.M., Application of optimization techniques to the determination of modal parameters in civil structures by the identification method. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 35(3):1–12, 2019. DOI: 10.23967/j.rimni.2019.09.010
Document information
Published on 04/06/20
Accepted on 28/05/20
Submitted on 04/03/20
Volume 36, Issue 2, 2020
DOI: 10.23967/j.rimni.2020.06.002
Licence: CC BY-NC-SA license