Improved procedure for determining the ductility of buildings under seismic loads

Abstract

Displacement ductility is a parameter that characterizes the seismic response of structures. Moreover, displacement ductility can be used in order to determine whether a structural design, performed according to a specific seismic code or not, may achieve the main goal of the seismic design: to develop energy dissipation in a stable manner. Determination of displacement ductility is not an easy task, because the structural response usually does not show a clear location of the points that define yield and ultimate displacements. In this paper, some of the main procedures for ductility displacement are revised and compared, and then improvements are performed to such procedures in order to compute the displacement ductility. A new procedure is then introduced, leading to determine the ultimate displacement using the seismic collapse threshold and the yield displacement, achieving the balance of dissipated energy. The procedure has been used to calculate displacement ductility of reinforced concrete framed buildings.

1. Introduction

Displacement ductility is an important characteristic that lead to determine whether seismic response of structures meet the early goals for which they were designed. Displacement ductility is also important because some of the most relevant seismic codes worldwide prescribe modal-spectral analysis for which the response reduction factors are estimated based on displacement ductility [1,2]. This procedure is also present in seismic codes in Latin American countries [3,4,5]. The components of response reduction factors are defined in [6] allowing to determine the response reduction factors following Eq.(1).

${\textstyle R={R}_{\mu }{\Omega }_{d}{R}_{R}}$

(1)

where ${\textstyle {R}_{\mu }}$, ${\textstyle {\Omega }_{d}}$ and ${\textstyle {R}_{R}}$ are the ductility reduction factor, the overstrength factor and the redundancy, respectively. There are several procedures to determine values of displacement ductility, but each produce values with high variability, then does not exist consensus among engineers and researchers about how to choose suitable values of displacement ductility for design [7,8,9].

The concept used to determine displacement ductility is too simple: to stablish any relationship between the elastic and plastic behavior through specific displacements. Since Freeman et al. [1975], scientific and engineering community have accepted the pseudo-static analysis procedure with lateral forces, also called Pushover Analysis.

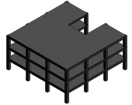
The problem with the definition of displacement ductility arise when its components must be defined. First, there are some ways to determine the yield displacement (${\textstyle {\Delta }_{y}}$) of the whole structure (Fig. 1, adapted from [10]). Fig.1a show the definition of yield displacement at the point of occurrence of the first yield in any of the reinforcement bars of the structure. Fig. 1b show the criteria based on the tangent stiffness, defined by the elastic stiffness. In Fig. 1c, the yield displacement is obtained from the secant stiffness, defined by equalizing the dissipated energy of the capacity curve and the idealized bi-linear shape. Finally, Fig. 1d show the yield displacement defined by [11]. Note that according to this procedure, the secant stiffness corresponds to a line from the origin to a point on the capacity curve with 75% of the maximum base shear capacity. Although the convenience of whether use tangent or secant stiffness has not be concluded yet [12], the preference for the latter has been increasing, because it was included in the seismic assessment procedure N2 [13], adopted in Eurocode 8 [2].

Figure 1. Alternatives for global yield displacement determination. Source: adapted from [10]

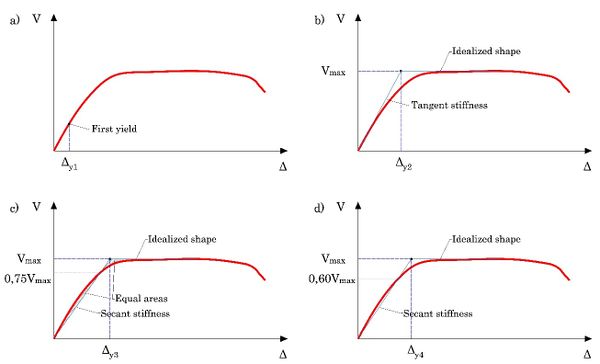
Determination of the ultimate displacement (${\textstyle {\Delta }_{u}}$) is also controversial. One of the most popular criterion is to assume that the ultimate displacement corresponds to the point where the structure reaches the maximum base shear (Fig. 2a). Another used criterion to determine the ultimate displacement assumes that the ultimate displacement correspond to the point in which compressive strain in concrete or the fracture or buckling in transversal reinforcement in any structural member is achieved (Figs. 2b and 2c). The criterion showed in Fig2d is also very popular among researchers. This criterion leads to obtain the ultimate displacement from the point in which the maximum base shear capacity drops a fixed value (usually 10 or 20%). Fig. 2e summarizes ductility calculations based on the above-mentioned criteria.

Once both displacements are calculated, displacement ductility is determined according to Eq.(2).

${\textstyle \mu ={\frac {{\Delta }_{u}}{{\Delta }_{y}}}}$

(2)

Figure 2 summarizes ductility calculations based on the above-mentioned criteria. Note the difference among resulting values, consequently, the need to develop a procedure in order to objectively determine reliable displacement ductility factors. Similar comparison about the referred ultimate displacements can be found in [7].

Figure 2. Alternatives for global ultimate displacement determination. Source: adapted from [10]

Finally, another representative coefficient of the seismic behavior is the over- strength Ωd. This coefficient is obtained from the values of the ultimate base shear ${\textstyle {V}_{u}}$ versus the base shear computed from elastic analysis prescribed by codes, ${\textstyle {V}_{d}}$.

2. Proposed procedure

The new procedure is based in some of the relevant features discussed in the introduction. The procedure to determine the displacement ductility based on non-linear analysis consist in three steps defined as follows:

• First step. The first segment consists in a line from the origin to the point in which the structure presents the first yielding in any bar of the structural members. The latter point will serve as a pivot point to find the yield displacement.

• Second step. Determine the ultimate displacement. To this end, it is necessary to find the base shear for which ultimate rotation capacity in the extremes of the beams and the inferior extremes of the columns of any level are achieved.

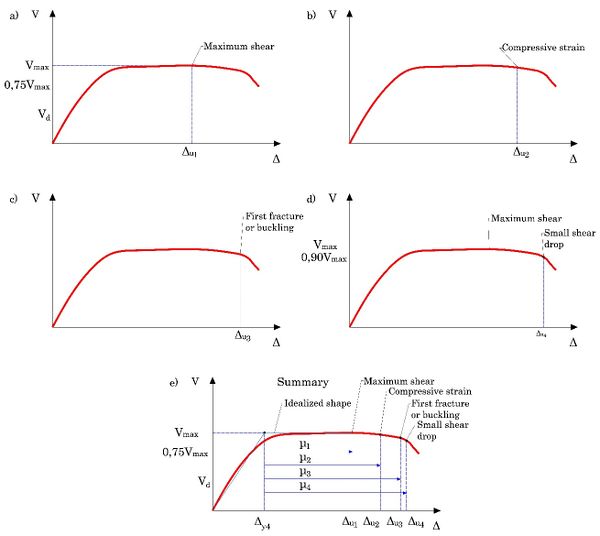
• Third step. Obtain the yield displacement equalizing the areas under the capacity curve and the generated tri-linear idealized shape. This step is performed by means of a couple of curves obtained from the integration of the capacity curve and the tri-linear idealized shape. The point where these two curves intersect, is compared with the point for the ultimate rotation displacement, if the difference between the abscissas of both points was lower than 1%, the chose value of the abscissa for the yield point is accepted, and on the contrary, the yield point must move horizontally in order to adjust the dissipated energy. This way leads to obtain a balance of the dissipated energy of the capacity curve and the idealized bi-linear shape (Fig. 3).

Figure 3. Description of the objective procedure for displacement ductility determination.

2.1. Collapse threshold

Determination of the seismic collapse threshold or the ultimate displacement is performed following the failure mode of the structure analyzed. For this purpose, the adopted criterion is that the whole structure has been reached its ultimate displacement when all the extreme elements of the beams and the lower elements in columns of any story achieve a rotation greater than the ultimate rotation capacity, defined by according to [14]:

${\textstyle {\theta }_{u}={\alpha }_{st}({0,3}^{\nu }){\left[{\frac {\mathrm {max} \,(0,01,w')}{\mathrm {max} \,(0,01,w)}}{f}_{c}\right]}^{0,2}{\left({\frac {Ls}{h}}\right)}^{0,425}{25}^{\left(\alpha {\rho }_{sx}\,{\frac {{f}_{yw}}{{f}_{c}}}\right)}}$

(4)

where: ${\textstyle Ls}$ : Moment-shear ratio at the member end

${\textstyle w}$, ${\textstyle w'}$: Mechanic reinforcement ratio

${\textstyle \nu }$ : Normalized axial load ratio

${\textstyle {\rho }_{sx}}$: Ratio of transverse steel

${\textstyle \alpha }$ : Confinement effectiveness factor

${\textstyle {\alpha }_{st}}$: Coefficient for longitudinal reinforcement, 0.016 for ductile Steel and 0.0105 for non-ductile steel.

The confinement effectiveness factor ${\textstyle \alpha }$ is determined with the cross sections dimensions, following:

${\textstyle \alpha =\left({\frac {1-{S}_{h}}{2{b}_{0}}}\right)\left({\frac {1-{S}_{h}}{2{h}_{0}}}\right)\left(1-\right.}$$\left.{\frac {\sum _{}^{}{b}_{i}^{2}}{6{b}_{0}{h}_{0}}}\right)$

(5)

${\textstyle {b}_{0}}$, ${\textstyle {h}_{0}}$: dimensions of the confined core

${\textstyle {b}_{i}}$: distance between bars

Figure 4. Load step for the collapse, controlled by the ultimate rotations at the end of first-floor beams and columns (ductile failure).

The procedure is carried out by assigning an ultimate chord rotation to each structural element, according to the results of Eq.(2). In this way, for every increment of applied lateral load, computed chord rotations were compared versus the assigned values of ultimate rotation capacity, indicating whether an element has achieved its ultimate rotation [15] (Fig. 4). When all elements located at the ends of the beams belonging to one story and the lower ends of the columns of the immediately below story, exceeded their ultimate chord rotations, then, it is assumed that the structure is not be able to sustain additional lateral forces, so it has been reached the collapse threshold displacement. Then, the ultimate base shear corresponds to the sum of the reactions in supports opposing to lateral forces in the indicated load step.

2.2. Rotation ductility demand

The rotation ductility demand is another parameter that allows to evaluate the seismic behavior of the structures, but in a local level. This coefficient is determined following [16]:

${\textstyle {\mu }_{\theta }=1-{\frac {\theta }{{\theta }_{y}}}}$

(6)

where ${\textstyle \theta }$ is the current rotation at the structural member end, and ${\textstyle {\theta }_{y}}$ is the yield rotation. The latter is determined according to:

${\textstyle {\theta }_{y}={\frac {{\varphi }_{y}{d}_{bL}{f}_{yL}}{8{\sqrt {{f}_{c}^{'}}}}}}$

(7)

In this equation φy is the yield curvature, obtained from Eq.(8); ${\textstyle {d}_{bL}}$ is the diameter of longitudinal reinforcement bars, ${\textstyle {f}_{yL}}$ is the yield strength of the steel, and ${\textstyle {f}_{c}^{'}}$ is the characteristic strength of the concrete. Yield curvature can be approximated to:

${\textstyle {\varphi }_{y}={\frac {{\epsilon }_{c}}{{\xi }_{y}d}}\approx {\frac {1,8\,{f}_{c}}{{{E}_{c}\,\xi }_{y}d}}}$

(8)

where ${\textstyle {E}_{c}}$ is the elastic module of the concrete, ${\textstyle {\xi }_{y}}$ is the normalized neutral axis depth, and ${\textstyle d}$ is the distance between the steel deformed in traction and the most compressed concrete fibre.

3. Cases studied

The relevance of formulating a new procedure to obtain the displacement ductility resides into capture an objective value, regardless of the possibility to reach a fragile, mixed or ductile structural failure mode [17]. In order to test the procedure, it was applied to a set of buildings with different plan configurations. The set consist in seven low-rise reinforced concrete buildings, designed for high seismic hazard zone (design acceleration of 0.3g) and located in a very stiff soil (soil type S2), with a response reduction factor R=6.

Buildings have different plan configurations with three 3.00m high stories. The structures of the buildings consist in special moment-resisting frames, with three 6.00m length spans in each direction. Buildings are endowed with 25cm width RC solid slabs. Fig. 5 summarizes the plan configurations of the seven cases considered herein. Note that cases 2 to 7 are plan irregular because the presence re-entrants in the slabs, but cases 2, 4 and 6 are provided with coupling beams in the open side, avoiding the loss of stiffness in such frames, also avoiding the stress concentration in frames and adjacent zones of the slabs, which can occur during the application of lateral loads. The specifications set for the materials are shown in Table 1.

Table 1. Materials characteristics used for design.

Material	Strength (MPa)
Concrete	f ’c = 25
Steel	Fy= 420

Archetype 1	Archetype 2	Archetype 4	Archetype 6
	Archetype 3	Archetype 5	Archetype 7
Figure 5. Plan configurations of the archetypes studied.

The analysis, design and detailing of the buildings was performed according to the current Venezuelan seismic code [2001] for residential use. However, interstory drift check was performed using an alternative energy-based procedure [18,19], thereby producing stiffer structures than the obtained according to the standard code procedure.

3.1. Non-linear analysis

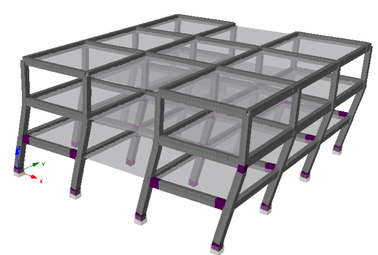
For non-linear analysis, designed buildings were modeled using v-7 of SeismoStruct software [20]. Each structural member was split into four elements, in order to capture the chord rotations in the special zones in which the concentration of the seismic damage is expected. Cross-sections obtained from the design process, were modeled using fibre elements, with the accurate location of every reinforcing bar, and taking into account the effect on the enhancement of the concrete confinement, provided by transversal and longitudinal reinforcement bars (Fig. 6).

Transverse reinforcement have not been directly modeled, but its influence on the enhancement of the strength characteristics of the confined concrete have been taken in account through the modifications factors computed according to [21].

Once the structures were modeled, standard pseudo-static non-linear analyses (Pushover) were performed, with a linear distribution shape of lateral forces, with a target roof displacement estimated as 4% of the total building height.

The analyses were performed for both directions of the buildings, in order to account the influence of the plan irregularity in the capacity curve determination, and in the damage distribution for each structural member. According to the criterion expressed in [7], no relocation of center of mass produced by accidental eccentricity was performed.

4. Results

The capacity curves obtained for each building were processed according the Park’s procedure and the new procedure reported herein, in order to find the idealized shapes in both analysis directions and to determine the values of displacement ductility ( ${\textstyle \mathrm {\mu } }$) and structural overstrength (${\textstyle {\Omega }_{d}}$). The values of both coefficients are summarized in Tables

Figure 6. Discretization of beam and column cross sections using fibre elements.

Table 2. Values of displacement ductility and overstrength of cases studied, computed according to Park’s procedure.

Case	µ (x)	Ωd (x)	µ (y)	Ωd (y)
1	2.89	3.46	2.89	3.46
2	2.77	3.92	2.70	3.87
3	3.43	3.52	3.25	3.99
4	2.95	3.71	2.98	3.66
5	3.16	3.41	3.04	3.70
6	2.91	3.98	3.10	3.91
7	3.47	3.49	2.98	3.99

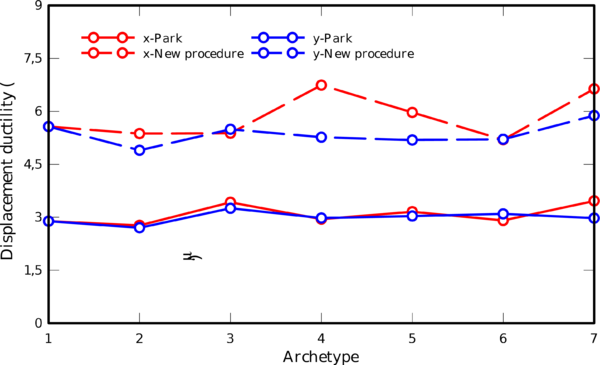
In general, calculated values of displacement ductility using the proposed procedure, show small variations, despite on the plan irregularity of the buildings. For analysis performed in the irregular direction of the cases (x direction) resulting values are less than 6, with the exception of cases 4 and 7, in which the values are near to 7 (Fig. 7). It can be observed the uniformity of the displacement ductility values, which are slightly less than 6.

Figure 7. Displacement ductility of cases studied

Values obtained using the proposed procedure are consistent with those expected for the used structural typology combined with the seismic hazard level. Further- more, the use of the new procedure may serve for the calculation of the inherent response reduction factor of the cases studied according to Eq.(1). The inherent response reduction factor, also called response reduction factor supply [10], may serve as a reference value in order to evaluate the seismic design obtained through the response reduction factor prescribed by the seismic code (also called response reduction factor demand [10].

Table 3. Values of displacement ductility and overstrength of cases studied, computed according to proposed procedure.

Case	µ (x)	Ωd (x)	µ (y)	Ωd (y)
1	5.57	3.36	5.57	3.36
2	5.37	3.84	4.90	3.79
3	5.38	3.49	5.49	3.92
4	6.78	3.58	5.27	3.58
5	5.97	3.34	5.19	3.63
6	5.20	3.90	5.21	3.85
7	6.64	3.39	5.88	3.91

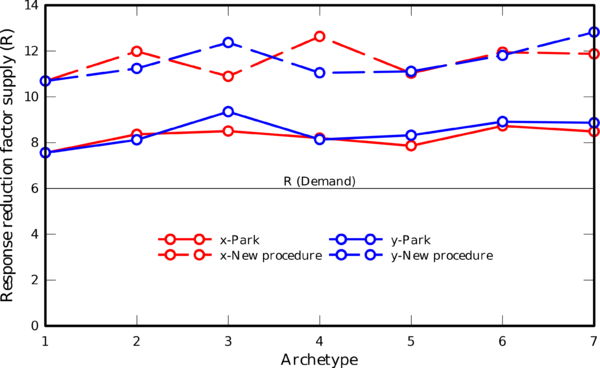
Figure 8. Response reduction factors (supply) computed using Park’s procedure vs. proposed procedure

Both procedures used in this paper have produced values of the response reduction factor (${\textstyle {R}_{Supply}}$) which are greater than the response reduction factor value prescribed by code (${\textstyle {R}_{Demand}}$) (Fig. 8). In spite of this, values calculated from the proposed procedure are consistent with the values reported in recent works, obtained using incremental dynamic analysis (IDA) in framed structures, designed in high seismic-prone regions [22,23,24,25].

Finally, Figs. 9 and 10 show a graphical representation of the values of rotation ductility demands, computed following Eq.(6) for the ultimate displacement, obtained according to the proposed procedure. Distribution of rotation ductility demands is an important issue of the seismic behavior of the structure, because it synthetizes the failure mode under lateral loads. Note that the maximum values of rotation ductility demands correspond to higher ends and lower ends of columns of stories 2 and 1, respectively and both ends of fist floor beams, indicating that such kind of structures have an intermediate type of failure, according to [17].

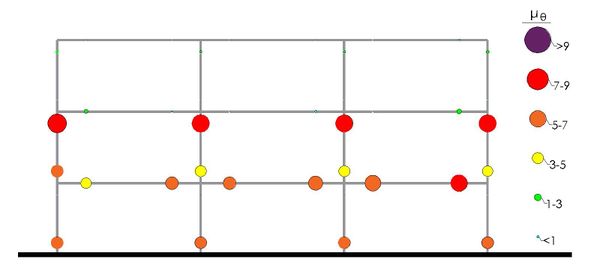
Figure 9. Rotation ductility demands in external frame of the case 1.

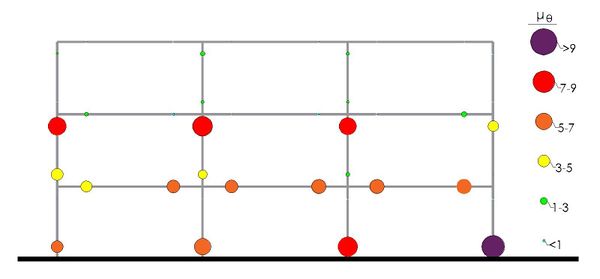
Figure 10. Rotation ductility demands in internal frame of the case 1.

4. CONCLUSIONS

The proposed procedure combines the main goals of previous works in the field, with the end to obtain objectives values of displacement ductility, regardless the structural type, failure mode or even the structural irregularities. This procedure is also simple, thereby enabling in displacement ductility determination using standard pseudo-static non-lineal analysis.

Resulting values of the displacement ductility calculated according the proposed procedure are, in general, nearly uniform in the regular direction of case studied, and have values that lightly vary according the irregular direction of analysis. These values are greater than the ductility values the designer expect the structures develop during a severe earthquake, and are also consistent with values of response reduction factors computed from most refined, and consequently time-consuming analysis, applied in recent works.

Further research should be performed in order to verify the benefit to apply the proposed methodology to different structural typologies with plan irregularities variations, or to irregular in elevation buildings.

The collapse threshold also allows to obtain the instant to determine the last rotations in the elements that make up the structure. From these rotations, the rotation ductility demands can be obtained, which is a measure to evaluate the seismic behavior at the local level and also allows to determine the global failure mode of the structure.

Acknowledgements

First author would acknowledge to Pontificia Universidad Católica de Valparaíso, for the support to the preparation of this paper. Authors also acknowledge the support of CDCHT of the Universidad Centroccidental Lisandro Alvarado and the Network of the CIMNE Classrooms, where this research was developed.

References

[1]	ASCE/SEI, ASCE/SEI 7-10 Minimum Design Loads for Buildings and Other, Reston, 2010.
[2]	CEN, Eurocode 8 Design of Structures for Earthquake Resistance, CEN Eurocode 8, Brussels, 2002.
[3]	FONDONORMA, Covenin 1756-2001. Code for earthquake-resistant buildings, Caracas, 2001.
[4]	ACIS, Colombian code for earthquake-resistant constructions, Bogota, 2010.
[5]	ACHISINA, Seismic design of buildings, NCh433.Of1996, Santiago de Chile, 2012.
[6]	Applied Technology Center (ATC), A critical review of current approaches to earthquake resistant design, Redwood City, 1995.
[7]	M. N. J. Priestley, G. M. Calvi y M. Kowalski, Displacement-based seismic design of structures, Pavia: IUSS Press, 2007.
[8]	J. C. Vielma, A. H. Barbat y S. Oller, «Comparison between the response reduction factors of the Spanish code NCSE-02 and Eurcode-8,» Hormigon y Acero, vol. 246, pp. 79-95, 2007.
[9]	J. C. Vielma, A. H. Barbat y S. Oller, «Response reduction factors: state of the art and code’s comparative study,» Revista Internacional de Ingeniería de Estructuras, vol. 11, nº 1, pp. 79-106, 2007.
[10]	A. Elnashai y L. Di Sarno, Fundamentals of earthquake engineering, Chichester: John Willey and Sons, 2008.
[11]	R. Park, «Ductility evaluation from laboratory and analytical testing,» de in Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo- Kyoto, 1988.
[12]	T. J. Sullivan, G. M. Calvi y M. N. J. Priestley, «Initial stiffness versus secant stiffness,» de in Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, 2004.
[13]	M. Kreslin y P. Fajfar, «The extended N2 method considering higher mode effects in both plan and elevation,» Bulletin of Earthquake Engineering, vol. 10, nº 2, pp. 695-715, 2011.
[14]	T. a. F. M. Panagiotakos, «Seismic Performance of RC Frames Designed to Eurocode 8 or to the Greek Codes 2000,» Bulletin of Earthquake Engineering, vol. 2, pp. 221-259, 2004.
[15]	G. Magliulo, G. Maddaloni y E. Cosenza, «Extension of N2 method to plan irregular buildings considering accidental eccentricity,» Soil Dynamics and Earthquake Engineering, vol. 43, pp. 69-84, 2012.
[16]	M. Fardis, Seismic design, assessment and retrofitting of concrete buildings, Heildelberg: Springer, 2009.
[17]	J. Moehle, Seismic design of reinforced concrete buildings, New York: McGraw-Hill, 2015.
[18]	J. C. Vielma, A. H. Barbat y S. Oller, «Seismic sizing of RC buildings using displacement factors based on energy balance,» Hormigon y Acero, vol. 63, 83-96.
[19]	J. C. Vielma, A. H. Barbat y S. Oller, «Non-linear structural analysis. Application to evaluating the seismic safety.,» de Structural Analysis, E. Camilleri, Ed., New York, Nova Science Publishers, 2010, pp. 101-128.
[20]	SEISMOSOFT, «SeismoStruct v7.0, a computer program for static and dynamic nonlinear analysis of framed structures,» 2014. [En línea].
[21]	J. B. Mander, M. J. N. Priestley y R. Park, «Observed stress-strain behaviour of confined concrete,» Journal of Structural Engineering (ASCE), vol. 114, pp. 1827-1849, 1988.
[22]	J. C. Vielma, A. H. Barbat y S. Oller, «Seismic safety of low ductility structures used in Spain,» Bulletin of Earthquake Engineering, vol. 8, nº 1, pp. 135-155, 2010.
[23]	J. C. Vielma, A. H. Barbat y S. Oller, «Seismic response of the RC framed buildings designed according to Eurocodes,» de Computational methods in Earthquake Engineering, M. Papadrakakis, M. Fragiadakis y N. Lagaros, Edits., Heidelberg, Springer, 2010, pp. 201-220.
[24]	J. C. Vielma, A. H. Barbat, R. Ugel y R. I. Herrera, «Seismic evaluation of low rise RC framed building designed according to Venezuelan codes,» de Engineering Seismology, Geotechnical and Structural Earthquake Engineering, D. A. S., Ed., Rijeka, InTech Publishers, 2012, pp. 283-300.
[25]	R. I. Herrera, J. C. Vielma, R. Ugel, A. Alfaro, A. H. Barbat y L. Pujades, «Seismic response and torsional effects of RC structure with irregular plant and variations in diaphragms, designed with Venezuelan codes,» de in Earthquake resistant Engineering Structures, B. C. y S. Hernandez, Edits., Southampton, WIT Press, 2013, pp. 85-96.