Elastoplastic Analysis of Framed Structures with Interaction Surfaces Obtained for Multiple Linear Regression

Resumo

Os critérios de estado limite último (superfícies de interação) aplicados para projetos estruturais são de melhor utilidade quando são resultantes de tensões. Existem muitas dificuldades para gerar superfícies de interação com 6 esforços seccionais obtidos por modelos numéricos ou experimentais de uma análise de pórtico espacial. O enfoque, na literatura, para a análise não linear de estruturas com vigas 3D é o uso de superfícies de interação com somente 3 esforços combinados na secção transversal. Portanto, uma melhor compreensão do tipo de carga, das interações entre os 6 esforços e da estabilidade global e local da estrutura são necessárias. As superfícies de interação com 3 esforços são apresentadas em formas planas, quádricas, complexas ou mistas, de modo que as técnicas que usam formulações analíticas com esforços combinados e várias formas de secções são mais ou menos complexas. O modelo de regressão linear múltipla permite tratar esforços resultantes de várias análises para obter uma superfície de escoamento com esforços combinados. Neste trabalho, a formulação para obter superfícies e suas aplicações nas análises de estruturas elastoplásticas de pórticos espaciais são apresentadas.

Abstract

The ultimate limit state criteria (yielding surfaces) applied to structural designs are easier in stress resultants. There are many difficulties to generating interaction surfaces with six sectional efforts obtained through to numerical or experimental models of a space-frame analysis. The approach, in the literature, to nonlinear analysis of structures with 3D beams is use of interaction surfaces with only three combined efforts in the cross-section. Therefore, a better understanding of load types, of interactions between the six efforts and of local and global stability of structure are necessary. The interaction surfaces with three efforts are presented in planes, quadrics, more complex, or a mixture of them shapes, so that techniques which use analytical formulations with combined efforts and several section shapes are more or less complex. Multiple linear regression allows to treat the resultant efforts of several analyses for obtaining a yielding surface with the combined efforts. In this paper, the formulation to obtaining of the surfaces and their applications in the analysis of elasto-plastic frame structures are presented.

Palavras-chave

Funções de escoamento ; Curvas de interação ; Vigas de Timoshenko 3D ; Regressão linear múltipla ; Esforços seccionais

Keywords

Yield functions ; Interaction curves ; 3D Timoshenko beams ; Multiple linear regression ; Sectional efforts

1. Introdução

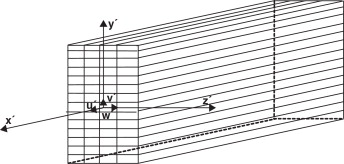
Quando é feita uma análise elastoplástica com modelos de viga 3D (fig. 1 ), necessita-se de uma função da superfície de escoamento que controlará o término da fase elástica e o estado plástico da estrutura. O limite entre a zona elástica e a plástica estabelece-se mediante a superfície de fluência ou superfície de descontinuidade e, a partir deste limite, esta superfície adquire mobilidade no espaço de tensões, seguindo a evolução do processo plástico, transformando-se na denominada superfície de carga plástica. Para estabelecer, durante o processo de carga, o início do comportamento inelástico e a posterior evolução das fronteiras do domínio elástico dentro do espaço, adota-se o critério de fluência ou descontinuidade como visto na equação (1) . A teoria de viga de Timoshenko 3D e seus detalhes é apresentada, por exemplo, em Hanganu [1] . A formulação do modelo de dano e seus detalhes são discutidos, por exemplo, por Vieira [2] , Oller [3] e Hanganu [1] .

$F={\overline {\sigma }}-f_{c}\leq 0$

( 1)

onde: ${\textstyle {\overline {\sigma }}}$ = tensão efetiva e f_c = limite de dano.

Figura 1. Barra 3D com secção dividida mediante uma malha retangular. Eixos locais.

Foi utilizado o programa da tese doutoral de Hanganu que trata da metodologia de avaliação da degradação em estruturas de concreto armado (Hanganu [1] ), adaptado para o caso de estruturas de aço. A formulação de viga de Timoshenko 3D com o modelo de dano usada pelo programa permite o tipo de análise necessária para a obtenção das superfícies (curvas) de interação, levando em conta a não linearidade física do material com resultados em resultantes de tensão. Uma representação da superfície de degradação é vista na figura 2 (Hanganu [1] ). Foram feitas análises, para a validação do programa, de cada esforço seccional de forma a verificar a carga de colapso de cada esforço de forma independente, ou seja, sem levar em conta a interação entre eles. Comprovou-se que o programa pode ser utilizado na proposição de usar a regressão linear múltipla com dados de entrada oriundos destas análises de viga de Timoshenko 3D. Esta abordagem é apresentada em detalhes por Vieira [2] .

Figura 2. Função limite de dano no plano principal σ1  − σ2[1] .

2. Formulação para a obtenção das superfícies

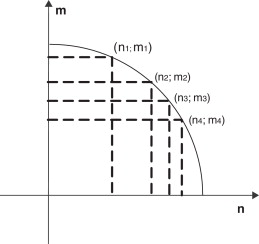
As curvas de interação em resultantes de tensões facilitam as análises de sistemas estruturais evitando o processo de integração numérica ao longo da secção transversal. Para a obtenção das curvas, em resultantes de tensões, foram utilizados os resultados dos esforços seccionais da análise numérica 3D, apresentados em Vieira [2] . Várias combinações de carregamentos foram usadas para gerar pontos (combinações de esforços) que pertencem a superfície proposta, ou seja, que tenham atingido o escoamento. Para um dado carregamento, obtém-se um ponto, como o ponto 1, cujas coordenadas (n₁ , m₁ ) são o esforço axial e o momento fletor, respetivamente, na figura (3 ). A regressão linear múltipla (Montgomery [4] ), trata os pontos obtidos pelas diversas análises e obtém a superfície que passa por estes pontos. Isto é retratado, por exemplo, na figura (3 ). Procura-se obter os valores dos coeficientes constantes das funções, como por exemplo β₁ e β₂ da superfície a ser gerada, como é demonstrado na equação (2) :

$f={\beta }_{1}n^{2}+{\beta }_{2}m-1=0$

( 2)

onde:

• n e m são os esforços normal e fletor adimensionalizados;
• β₁ e β₂ são os coeficientes obtidos através da regressão.

Figura 3. Pontos gerados para criar a função de escoamento.

Para tal, é apresentado um exemplo com resultados de análises (tabela 1 ) obtidas para a equação (2) .

Tabela 1. Tipo de observações para nm

Observações
n	m
0, 956445	0, 040370
0, 956445	0, 040370
0, 301715	0, 679861
0, 301718	0, 679855
0, 783473	0, 210572
0, 783473	0, 210570
0, 990255	0, 008484
0, 990255	0, 008484
0, 080420	0, 899851
0, 080422	0, 899851
0, 064067	0, 915098
0, 064068	0, 915098

Estes dados são tratados pela regressão, de maneira a encontrar os coeficientes β . Com esta formulação, existe a possibilidade de gerar vários tipos de superfícies de interação em resultantes de tensões.

Nesta secção, será apresentada a formulação que trata os dados obtidos até chegar à condição em que possam ser usados pela regressão linear múltipla.

É mais conveniente expressar o modelo com operações matemáticas na forma matricial (Vieira [2] ). Suponha-se que existem k variáveis de regressão e n   observações ${\textstyle \left(x_{i1},x_{i2},\ldots ,x_{ik},y_{i}\right)}$ , com i  = 1, 2, …, n e j  = 1, 2, …, k , e em que o modelo que relaciona os regressores (x_ik ) com a resposta (y ) seja:

$y={\beta }_{0}+{\beta }_{1}x_{i1}+{\beta }_{2}x_{i2}+\cdots {\beta }_{k}x_{ik}+$${\in }_{i},\quad i=1,2,\ldots ,n$

( 3)

Este modelo é um sistema de n equações que pode expressar-se em notação matricial como:

${\boldsymbol {\mbox{y}}}={\boldsymbol {\mbox{X}}}\beta +$${\boldsymbol {\in }}$

( 4)

onde:

${\boldsymbol {\mbox{y}}}=\left[{\begin{array}{c}y_{1}\\y_{2}\\\vdots \\y_{n}\end{array}}\right],\quad {\boldsymbol {\mbox{X}}}=\left[{\begin{array}{ccccc}1&x_{11}&x_{12}&\cdots &x_{1k}\\1&x_{21}&x_{22}&\cdots &x_{2k}\\\vdots &\vdots &\vdots &&\vdots \\1&x_{n1}&x_{n2}&\cdots &x_{nk}\end{array}}\right]$

( 5)

${\boldsymbol {\beta }}=\left[{\begin{array}{c}{\beta }_{0}\\{\beta }_{1}\\\vdots \\{\beta }_{k}\end{array}}\right]\quad e\quad \in =\left[{\begin{array}{c}{\in }_{1}\\{\in }_{2}\\\vdots \\{\in }_{n}\end{array}}\right]$

( 6)

Em geral, y é um vetor de observações de ${\textstyle \left(n\times 1\right)}$ , X é um tensor (matriz) de ${\textstyle \left(n\times p\right)}$ dos níveis das variáveis independentes, β é um vetor de (p  × 1) formado pelos coeficientes de regressão e ∈ é um vetor (n  × 1) dos erros aleatórios.

Deve-se encontrar o vetor dos estimadores dos mínimos quadrados, ${\textstyle {\overset {\mbox{ˆ}}{\beta }}}$ , que minimiza

${\boldsymbol {\mbox{L}}}=\sum _{i=1}^{n}{\in }_{i}^{2}={\boldsymbol {\in }}^{T}{\boldsymbol {\in }}=$${\left({\boldsymbol {\mbox{y}}}-{\boldsymbol {\mbox{X}}}{\boldsymbol {\beta }}\right)}^{T}\left({\boldsymbol {\mbox{y}}}-\right.$$\left.{\boldsymbol {\mbox{X}}}\beta \right)$

( 7)

O estimador de mínimos quadrados ${\textstyle {\overset {\mbox{ˆ}}{\beta }}}$ é a solução para β nas equações

${\frac {\partial {\boldsymbol {\mbox{L}}}}{\partial \beta }}=$${\boldsymbol {0}}$

( 8)

Desenvolvendo-se a equação (8 ), chega-se a:

${\boldsymbol {\mbox{X}}}^{T}{\boldsymbol {\mbox{X}}}{\overset {\mbox{ˆ}}{\beta }}=$${\boldsymbol {\mbox{X}}}^{T}{\boldsymbol {\mbox{y}}}$

( 9)

As equações (9 ) são as equações normais dos mínimos quadrados em forma matricial e são idênticas à forma escalar, como é apresentado em (10) :

$n{\overset {\mbox{ˆ}}{\beta }}_{0}+{\overset {\mbox{ˆ}}{\beta }}_{1}\sum _{i=1}^{n}x_{i1}+$${\overset {\mbox{ˆ}}{\beta }}_{2}\sum _{i=1}^{n}x_{i2}+$$\cdots +{\overset {\mbox{ˆ}}{\beta }}_{k}\sum _{i=1}^{n}x_{ik}=$$\sum _{i=1}^{n}y_{i}$ ${\overset {\mbox{ˆ}}{\beta }}_{0}\sum _{i=1}^{n}x_{i1}+$${\overset {\mbox{ˆ}}{\beta }}_{1}\sum _{i=1}^{n}x_{i1}^{2}+$${\overset {\mbox{ˆ}}{\beta }}_{2}\sum _{i=1}^{n}x_{i1}x_{i2}+$$\cdots +{\overset {\mbox{ˆ}}{\beta }}_{k}\sum _{i=1}^{n}x_{i1}x_{ik}=$$\sum _{i=1}^{n}x_{i1}y_{i}$ $\vdots \quad \quad \quad \vdots \quad \quad \quad \vdots \quad \quad \quad \vdots \quad \quad \quad \vdots$ ${\overset {\mbox{ˆ}}{\beta }}_{0}\sum _{i=1}^{n}x_{ik}+$${\overset {\mbox{ˆ}}{\beta }}_{1}\sum _{i=1}^{n}x_{ik}x_{i1}+$${\overset {\mbox{ˆ}}{\beta }}_{2}\sum _{i=1}^{n}x_{ik}x_{i2}+$$\cdots +{\overset {\mbox{ˆ}}{\beta }}_{k}\sum _{i=1}^{n}x_{ik}^{2}=$$\sum _{i=1}^{n}x_{ik}y_{i}$

( 10)

Para que sejam resolvidas as equações normais, multiplicam-se ambos os membros da equação (9 ) pela inversa de X^TX . Por conseguinte, o estimador de mínimos quadrados de β é:

${\overset {\mbox{ˆ}}{\beta }}={\left({\boldsymbol {\mbox{X}}}^{T}{\boldsymbol {\mbox{X}}}\right)}^{-1}{\boldsymbol {\mbox{X}}}^{T}{\boldsymbol {\mbox{y}}}$

( 11)

Note-se que existem p  = k  + 1 equações normais e p  = k  + 1 incógnitas, ou seja, os valores de ${\textstyle {\overset {\mbox{ˆ}}{\beta }}_{0},{\overset {\mbox{ˆ}}{\beta }}_{1},\cdots ,{\overset {\mbox{ˆ}}{\beta }}_{k}}$ . Por outro lado, a matriz X^TX não é singular, de modo que se pode empregar os métodos de inversão de matrizes que existem na literatura.

A forma matricial das equações normais de (10 ) é apresentada na equação (12 ):

$\left[{\begin{array}{ccccc}n&\sum _{i=1}^{n}x_{i1}&\sum _{i=1}^{n}x_{i2}&\cdots &\sum _{i=1}^{n}x_{ik}\\\sum _{i=1}^{n}x_{i1}&\sum _{i=1}^{n}x_{i1}^{2}&\sum _{i=1}^{n}x_{i1}x_{i2}&\cdots &\sum _{i=1}^{n}x_{i1}x_{ik}\\\vdots &\vdots &\vdots &&\vdots \\\sum _{i=1}^{n}x_{ik}&\sum _{i=1}^{n}x_{ik}x_{i1}&\sum _{i=1}^{n}x_{ik}x_{i2}&\cdots &\sum _{i=1}^{n}x_{ik}^{2}\end{array}}\right]\left[{\begin{array}{c}{\overset {\mbox{ˆ}}{\beta }}_{0}\\{\overset {\mbox{ˆ}}{\beta }}_{1}\\\vdots \\{\overset {\mbox{ˆ}}{\beta }}_{k}\end{array}}\right]$ $=\left[{\begin{array}{c}\sum _{i=1}^{n}y_{i}\\\sum _{i=1}^{n}x_{i1}y_{i}\\\vdots \\\sum _{i=1}^{n}x_{ik}y_{i}\end{array}}\right]$

( 12)

Pode-se observar que a matriz X^TX é uma matriz simétrica de (p  × p ) e que X^Ty é um vetor coluna de (p  × 1). Os elementos diagonais da matriz de X^TX são as somas dos quadrados dos elementos nas colunas de X , enquanto que os elementos que estão fora da diagonal principal são as somas dos produtos cruzados dos elementos das colunas de X (Montegomery [4] ). Os elementos de X^Ty são as somas dos produtos cruzados das colunas de X e as observações de y .

O modelo de regressão ajustado tem a seguinte forma:

${\overset {\mbox{ˆ}}{y}}_{i}={\overset {\mbox{ˆ}}{\beta }}_{0}+$$\sum _{j=1}^{n}{\overset {\mbox{ˆ}}{\beta }}_{j}x_{ij},i=$$1,2,\cdots ,n$

( 13)

A forma matricial do modelo é:

${\overset {\mbox{ˆ}}{\boldsymbol {\mbox{y}}}}={\boldsymbol {\mbox{X}}}{\overset {\mbox{ˆ}}{\beta }}$

( 14)

A diferença entre a observação y_i e o valor ajustado ${\textstyle {\overset {\mbox{ˆ}}{y}}_{i}}$ é um resíduo, ${\textstyle e_{i}=y_{i}-{\overset {\mbox{ˆ}}{y}}_{i}}$ . O vetor de resíduos de ${\textstyle \left(n\times 1\right)}$ denota-se por:

${\boldsymbol {\mbox{e}}}={\boldsymbol {\mbox{y}}}-{\overset {\mbox{ˆ}}{\boldsymbol {\mbox{y}}}}$

( 15)

Aplicando a formulação apresentada, tem-se que os dados obtidos (ver tabela 1 ) são os pontos x_ij (ver equação (13 )) que fazem parte da superfície a obter. Analisando a figura 3 , pode-se observar que existem uma quantidade de pontos cujas coordenadas são em função do n (normal) e do m (fletor). Os esforços seccionais são apresentados, na forma matricial como na equação (5) , para os esforços normal, torçor e fletores com combinações adimensionais na equação (17) :

$x_{1j}=\left[{\begin{array}{cccccc}1&\left({\left({\frac {N}{N_{xp}}}\right)}^{\alpha 1}\right)&\left({\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 2}\right)&\left({\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 3}\right)&\left({\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 4}\right)&\cdots \end{array}}\right]$

( 16)

$=\left[{\begin{array}{ccccc}1&\left(n^{\alpha 1}\right)&\left(m_{x}^{\alpha 2}\right)&\left(m_{y}^{\alpha 3}\right)&\left(m_{z}^{\alpha 4}\right)\end{array}}\cdots \right]$

( 17)

com j  = 1, 2, ⋯ , k

onde:

• N e N_xp são o esforço axial atuante e plástico; M_x e M_xp são o momento torçor atuante e plástico (direção x ); M_y e M_yp são o momento fletor atuante e plástico (direção y ), e M_z e M_zp são o momento fletor atuante e plástico (direção z );
• α_m são os expoentes dos termos de x_1j .

As superfícies de interação podem ser feitas com as mais diversas possibilidades de interação entre esforços. Para o entendimento do processo, é descrito um modelo que leva em conta combinações dos esforços seccionais independentes para pórticos espaciais:

$f={\beta }_{1}{\left({\frac {N}{N_{xp}}}\right)}^{\alpha 1}+$${\beta }_{2}{\left({\frac {M_{x}}{M_{x_{p}}}}\right)}^{{\alpha }_{2}}+$${\beta }_{3}{\left({\frac {M_{y}}{M_{y_{p}}}}\right)}^{{\alpha }_{3}}+$${\beta }_{4}{\left({\frac {M_{z}}{M_{z_{p}}}}\right)}^{{\alpha }_{4}}$ $+{\beta }_{6}{\left({\frac {N}{N_{xp}}}\right)}^{\alpha 5}{\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 6}+$${\beta }_{7}{\left({\frac {N}{N_{xp}}}\right)}^{\alpha 7}{\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 8}+$${\beta }_{8}{\left({\frac {N}{N_{xp}}}\right)}^{\alpha 9}{\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 10}$ $+{\beta }_{9}{\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 13}{\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 14}+$${\beta }_{10}{\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 15}{\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 16}-$$1=0$

( 18)

com

$x_{i1}={\left({\frac {N}{N_{xp}}}\right)}^{\alpha 1},x_{i2}=$${\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 2},x_{i3}=$${\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 3},x_{i4}=$${\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 4},$ $x_{i5}={\left({\frac {N}{N_{xp}}}\right)}^{\alpha 5}{\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 6},x_{i6}=$${\left({\frac {N}{N_{xp}}}\right)}^{\alpha 7}{\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 8},$ $x_{i7}={\left({\frac {N}{N_{xp}}}\right)}^{\alpha 9}{\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 10},x_{i8}=$${\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 11}{\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 12},$ $x_{i9}={\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 13}{\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 14}\quad e\quad x_{i10}=$${\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 15}{\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 16}$

( 19)

onde: i  = 1, 2, ⋯ , n (análises) e j  = 1, 2, ⋯ , k (combinações de esforços).

As observações de (19 ) são apresentadas para a regressão linear múltipla, forma matricial, na equação (20) :

${\boldsymbol {\mbox{X}}}=\left[{\begin{array}{ccccc}1&x_{11}&x_{12}&\cdots &x_{1k}\\1&x_{21}&x_{22}&\cdots &x_{2k}\\\vdots &\vdots &\vdots &&\vdots \\1&x_{n1}&x_{n2}&\cdots &x_{nk}\end{array}}\right]$

( 20)

onde os termos x_ij são os esforços seccionais adimensionais (19 ), vistos anteriormente. Os α_i são as constantes que determinam o grau da função; ${\textstyle \left\{{\begin{array}{c}N\\M_{x}\\M_{y}\\M_{z}\end{array}}\right\}}$ e ${\textstyle \left\{{\begin{array}{c}N_{xp}\\M_{xp}\\M_{yp}\\M_{zp}\end{array}}\right\}}$ são os esforços de cálculo e limites elastoplasticos, respetivamente.

Reapresentando a equação (18) e adotando os seguintes processos:

${\overline {x}}_{1}={\left({\frac {N}{N_{xp}}}\right)}^{\alpha 1},\quad {\overline {x}}_{2}=$${\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 2},\quad {\overline {x}}_{3}=$${\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 3},\quad {\overline {x}}_{4}=$${\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 4},$ ${\overline {x}}_{5}={\left({\frac {N}{N_{xp}}}\right)}^{\alpha 5}{\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 6},\quad {\overline {x}}_{6}=$${\left({\frac {N}{N_{xp}}}\right)}^{\alpha 7}{\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 8},$ ${\overline {x}}_{7}={\left({\frac {N}{N_{xp}}}\right)}^{\alpha 9}{\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 10},\quad {\overline {x}}_{8}=$${\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 11}{\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 12},$ ${\overline {x}}_{9}={\left({\frac {M_{x}}{M_{xp}}}\right)}^{\alpha 13}{\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 14}\quad e\quad {\overline {x}}_{10}=$${\left({\frac {M_{y}}{M_{yp}}}\right)}^{\alpha 15}{\left({\frac {M_{z}}{M_{zp}}}\right)}^{\alpha 16}$

( 21)

com ${\textstyle \left({\frac {N}{N_{xp}}}\right)=}$$n$ , ${\textstyle \left({\frac {M_{x}}{M_{xp}}}\right)=}$$m_{x}$ , ${\textstyle \left({\frac {M_{y}}{M_{yp}}}\right)=}$$m_{y}$ e ${\textstyle \left({\frac {M_{z}}{M_{zp}}}\right)=}$$m_{z}$

$1={\beta }_{0}+{\beta }_{1}n+{\beta }_{2}m_{x}+{\beta }_{3}m_{y}+$${\beta }_{4}m_{z}+{\beta }_{5}{nm}_{x}$ $+\quad {\beta }_{6}{nm}_{y}+{\beta }_{7}{nm}_{z}+{\beta }_{8}m_{x}m_{y}+$${\beta }_{9}m_{x}m_{z}+{\beta }_{10}m_{y}m_{z}$

Chega-se à equação (22 ):

Na forma corrente de regressão, obtém-se:

$1={\beta }_{0}+{\beta }_{1}{\overline {x}}_{1}+{\beta }_{2}{\overline {x}}_{2}+$${\beta }_{3}{\overline {x}}_{3}+{\beta }_{4}{\overline {x}}_{4}+$${\beta }_{5}{\overline {x}}_{5}$ $+\quad {\beta }_{6}{\overline {x}}_{6}+{\beta }_{7}{\overline {x}}_{7}+$${\beta }_{8}{\overline {x}}_{8}+{\beta }_{9}{\overline {x}}_{9}+$${\beta }_{10}{\overline {x}}_{10}$

( 22)

A equação (22 ) mostra uma curva de interação no formato que pode ser utilizado pela regressão linear múltipla (ver eq. (13 )).

3. Processo numérico de obtenção das superfícies

Para obtenção das curvas de interação, foram feitas análises numa viga engastada com diversos tipos de carregamentos. Como resultados das diversas análises, encontram-se pontos que alcançam a superfície de escoamento com resultados em resultantes de tensões. Os diversos grupos de esforços adimensionais são tratados pelo método de regressão múltipla, visto anteriormente, para obter uma função de escoamento correspondente às observações. As funções obtidas pelo processo numérico são comparadas com as apresentadas na literatura para verificar a aplicabilidade do método (Vieira [2] ). As propriedades da viga engastada (ver fig. 4 e tabela 2 ), como dimensões da secção transversal e comprimento, foram padronizadas para se obter uma comparação entres as funções obtidas. Os limites plásticos para a secção foram obtidos em função das fórmulas da literatura. O nível de dano ${\textstyle \left(d\right)}$ do elemento, em que foram retirados os esforços, variou de 60 a 99%. Esta variação do nível do dano dependeu da convergência de cada análise. O elemento em que foram retiradas as observações (esforços seccionais) e observados os níveis de plastificação da secção foi o que tem a condição de contorno engastada. Para cada análise, foram extraídos os esforços adimensionais dos 2 (dois) pontos de Gauss como em Vieira [2] . A função f é a apresentada pela literatura e função f_u é a obtida no presente trabalho. Foram geradas várias malhas de acordo com a necessidade do exemplo tratatado. O número de elementos foi obtido através de testes para verificar a convergência da solução. O exemplo 3.1 foi a base das funções usadas nas análises elastoplásticas.

Figura 4. Viga engastada.

Tabela 2. Propriedades do elemento engastado

Propriedades do elemento engastado
Descrição	Valor adotado	Unidade
Módulo de Young	2, 1e6	kgf/cm2
Módulo de Poisson	0, 3	−
Densidade	7, 85e−6	kgf/cm3
Limite de compressão	2, 4e3	kgf/cm2
Limite de tração	2, 4e3	kgf/cm2
Energia de fratura (dano)	1, 0e7	kgf.cm
Largura da secção (b)	4, 2	cm
Altura da secção (h)	8, 0	cm
Comprimento (l)	200, 0	cm
Nxp compressão	18410, 959	kgf
Nxp tração	80640, 0	kgf
Mxp	80660, 916	kgf.cm
Myp	161280, 0	kgf.cm
Mzp	84600, 0	kgf.cm

3.1. Exemplo 3.1

Neste caso, procura-se uma função que estabeleça a interação entre os esforços seccionais: axial ${\textstyle \left(N\right)}$ e fletores ${\textstyle \left(M_{y},M_{z}\right)}$ . Considera-se a viga engastada, vista na figura 4 , com as propriedades padrões da tabela 2 . Foram aplicadas várias combinações de translações e rotações impostas no nó 1 (ver fig. 4 ) para a obtenção dos grupos de esforços seccionais adimensionais da curva de interação. Foram testadas interações nas duas direções dos momentos. As propriedades particulares do exemplo são apresentadas na tabela 3 .

Tabela 3. Propriedades particulares do exemplo modelo.

Propriedades do exemplo 3.1
Descrição	Valor adotado
Número de elementos	50
Número de nós da malha	101
Número de divisões seccionais	8
Número de análises	6

Deslocamentos impostos (cm)
ux	uz
0,10	10,00
0,20	12,00
0,30	14,00
0,60	18,00
0,90	18,00
0,50	20,00

ux	uy
0,24	7,68
1,33	82,34
1,40	69,52
0,03	13,77
0,06	14,41
0,45	37,44

Foram testadas análises com os dados conjuntos das 2 direções e verificou-se que se pode propor as funções a seguir, analisadas de maneira mais completa em [2] .

• n²  × m

$f_{u}=1,007n^{2}+1,025m-1=0$

( 23)

• n × m²

$f_{u}=1,063n+0,907m^{2}-1=0$

( 24)

• n²  × m²desacoplado

$f_{u}=1,164n^{2}+1,127m^{2}-1=0$

( 25)

• n²  × m²  acoplado

$f_{u}=1,035n^{2}+0,880nm+0,812m^{2}-1=0$

( 26)

4. Análise elastoplástica de estruturas aporticadas

Foram feitas aplicações baseadas na teoria da elastoplasticidade em estruturas aporticadas com o objetivo de analisar o comportamento das superfícies geradas. A seguir, é mostrada a teoria envolvida na utilização de superfícies em resultantes de tensão.

Uma superfície de interação define o estado último de uma secção transversal e depende dos seguintes fatores:

• Forma geométrica da secção transversal;
• Combinação dos esforços seccionais que atuam na secção transversal;
• Teoria de viga utilizada.

Encontram-se soluções analíticas fechadas para determinados tipos de secções (I, retangular, etc.) com casos especiais de combinações de esforços, tais como momentos fletores e esforço normal (Horne [5] , Neal [6] ). Neste trabalho, assume-se uma superfície descrita em função dos esforços seccionais (Silva [7] ), com base na equação (ver eq. (27 )), apresentada com as seguintes combinações de esforços seccionais:

$f={\beta }_{1}{\left({\frac {\vert F_{x}\vert }{F_{x_{p}}}}\right)}^{{\alpha }_{1}}+$${\beta }_{2}{\left({\frac {\vert F_{y}\vert }{F_{y_{p}}}}\right)}^{{\alpha }_{2}}+$${\beta }_{3}{\left({\frac {\vert F_{z}\vert }{F_{z_{p}}}}\right)}^{{\alpha }_{3}}+$${\beta }_{4}{\left({\frac {\vert M_{x}\vert }{M_{x_{p}}}}\right)}^{{\alpha }_{4}}+$${\beta }_{5}{\left({\frac {\vert M_{y}\vert }{M_{y_{p}}}}\right)}^{{\alpha }_{5}}$ $+{\beta }_{6}{\left({\frac {\vert M_{z}\vert }{M_{z_{p}}}}\right)}^{{\alpha }_{6}}+$${\beta }_{7}{\left({\frac {\vert F_{x}\vert }{F_{x_{p}}}}\right)}^{{\alpha }_{7}}{\left({\frac {\vert M_{y}\vert }{M_{y_{p}}}}\right)}^{{\alpha }_{8}}+$${\beta }_{8}{\left({\frac {\vert F_{x}\vert }{F_{x_{p}}}}\right)}^{{\alpha }_{9}}{\left({\frac {\vert M_{z}\vert }{M_{z_{p}}}}\right)}^{{\alpha }_{10}}-$$1=0$

( 27)

onde F_x é o esforço axial, F_y e F_z são os esforços cortantes, M_x é o momento torçor e M_y e M_z são os momentos fletores. ${\textstyle F_{x_{p}}}$ é o esforço normal de plastificação puro, ${\textstyle F_{y_{p}}}$ e ${\textstyle F_{z_{p}}}$ são os esforços cortantes de plastificação puros, ${\textstyle M_{x_{p}}}$ é o momento torçor de plastificação puro, ${\textstyle M_{y_{p}}}$ e ${\textstyle M_{z_{p}}}$ são os momentos fletores de plastificação puros. As constantes β_i reais positivas são obtidas de observações oriundas das análises do modelo de dano em viga de Timoshenko 3D que levam em conta as propriedades da forma geométrica da secção transversal. Os expoentes α_i  ≥ 1 são arbitrados em função do tipo de função desejada. Dentro do contexto da análise elastoplástica perfeita de estruturas, Silva [7] considera que:

• Os esforços seccionais contidos no interior da superfície de interação geram somente deformações elásticas;
• Os esforços seccionais que estejam na superfície de interação geram deformações plásticas;
• Os esforços seccionais fora da superfície de interação representam estados de tensões inadmissíveis porque não se leva em conta o caso do endurecimento.

Durante o processo de aplicação do carregamento em passos de carga, os esforços seccionais em alguns nós dos elementos da estrutura poderão sair da superfície de interação. Para trazer estes esforços seccionais de volta à superfície, utiliza-se o método de Backward Euler, que necessita das derivadas primeira e segunda da superfície em relação aos esforços seccionais.

4.1. Derivadas de primeira ordem

Com base na equação (27 ), obtêm-se as derivadas de primeira ordem da superfície de interação (Silva [7] ), em relação aos esforços seccionais:

${\frac {\partial f}{\partial F_{x}}}={\beta }_{1}{\alpha }_{1}{\frac {\vert F_{x}\vert ^{{\alpha }_{1}-1}}{F_{x_{p}}^{{\alpha }_{1}}}}sign\_f_{x}+$${\beta }_{7}{\alpha }_{7}{\frac {\vert F_{x}\vert ^{{\alpha }_{7}-1}}{F_{x_{p}}^{{\alpha }_{7}}}}sign\_f_{x}{\left({\frac {\vert M_{y}\vert }{M_{y_{p}}}}\right)}^{{\alpha }_{8}}$ $+\quad {\beta }_{8}{\alpha }_{9}{\frac {\vert F_{x}\vert ^{{\alpha }_{9}-1}}{F_{x_{p}}^{{\alpha }_{9}}}}sign\_f_{x}{\left({\frac {\vert M_{z}\vert }{M_{z_{p}}}}\right)}^{{\alpha }_{10}}$ ${\frac {\partial f}{\partial F_{y}}}={\beta }_{2}{\alpha }_{2}{\frac {\vert F_{y}\vert ^{{\alpha }_{2}-1}}{F_{y_{p}}^{{\alpha }_{2}}}}sign\_f_{y}$ ${\frac {\partial f}{\partial F_{z}}}={\beta }_{3}{\alpha }_{3}{\frac {\vert F_{z}\vert ^{{\alpha }_{3}-1}}{F_{z_{p}}^{{\alpha }_{3}}}}sign\_f_{z}$ ${\frac {\partial f}{\partial M_{x}}}={\beta }_{4}{\alpha }_{4}{\frac {\vert M_{x}\vert ^{{\alpha }_{4}-1}}{M_{x_{p}}^{{\alpha }_{4}}}}sign\_m_{x}$ ${\frac {\partial f}{\partial M_{y}}}={\beta }_{5}{\alpha }_{5}{\frac {\vert M_{y}\vert ^{{\alpha }_{5}-1}}{M_{y_{p}}^{{\alpha }_{5}}}}sign\_m_{y}+$${\beta }_{7}{\alpha }_{8}{\left({\frac {\vert F_{x}\vert }{F_{x_{p}}}}\right)}^{{\alpha }_{7}}sign\_m_{y}{\frac {\vert M_{y}\vert ^{{\alpha }_{8}-1}}{M_{y_{p}}^{{\alpha }_{8}}}}$ ${\frac {\partial f}{\partial M_{z}}}={\beta }_{6}{\alpha }_{6}{\frac {\vert M_{y}\vert ^{{\alpha }_{6}-1}}{M_{y_{p}}^{{\alpha }_{6}}}}sign\_m_{z}+$${\beta }_{8}{\alpha }_{10}{\left({\frac {\vert F_{x}\vert }{F_{x_{p}}}}\right)}^{{\alpha }_{9}}sign\_m_{z}{\frac {\vert M_{z}\vert ^{{\alpha }_{10}-1}}{M_{z_{p}}^{{\alpha }_{10}}}}$

( 28)

onde ${\textstyle sign\_f_{i}={\frac {\vert F_{i}\vert }{F_{i_{p}}}}}$ e ${\textstyle sign\_m_{i}={\frac {\vert M_{i}\vert }{M_{i_{p}}}}}$ denotam os sinais das componentes do vetor de esforços nodais com ${\textstyle F_{i}=\left\{{\begin{array}{c}F_{x}\\F_{y}\\F_{z}\end{array}}\right\}}$ e ${\textstyle F_{i_{p}}=\left\{{\begin{array}{c}F_{x_{p}}\\F_{y_{p}}\\F_{z_{p}}\end{array}}\right\};}$${\textstyle M_{i}=\left\{{\begin{array}{c}M_{x}\\M_{y}\\M_{z}\end{array}}\right\}}$ e ${\textstyle M_{i_{p}}=\left\{{\begin{array}{c}M_{x_{p}}\\M_{y_{p}}\\M_{z_{p}}\end{array}}\right\}}$ .

A superfície de interação é assumida como um potencial plástico (Lubliner [8] ). As componentes são apresentadas na forma matricial para cada nó do elemento e definem o fluxo plástico nos nós do elemento durante o processo de carga. Têm-se, a seguir, os vetores para cada nó do elemento:

${\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}=$$\left\{{\begin{array}{c}{\frac {\partial f}{\partial F_{x_{1}}}}\\{\frac {\partial f}{\partial F_{y_{1}}}}\\{\frac {\partial f}{\partial F_{z_{1}}}}\\{\frac {\partial f}{\partial M_{x_{1}}}}\\{\frac {\partial f}{\partial M_{y_{1}}}}\\{\frac {\partial f}{\partial M_{z_{1}}}}\\{\boldsymbol {0}}\end{array}}\right\};\quad {\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}=$$\left\{{\begin{array}{c}{\boldsymbol {0}}\\{\frac {\partial f}{\partial F_{x_{2}}}}\\{\frac {\partial f}{\partial F_{y_{2}}}}\\{\frac {\partial f}{\partial F_{z_{2}}}}\\{\frac {\partial f}{\partial M_{x_{2}}}}\\{\frac {\partial f}{\partial M_{y2}}}\\{\frac {\partial f}{\partial M_{z_{2}}}}\end{array}}\right\}$

( 29)

onde 0 é um vetor nulo de 6 × 1.

4.2. Derivadas de segunda ordem

O gradiente do vetor de fluxo plástico é obtido através da diferenciação de cada componente do vetor da equação (29) em relação aos esforços seccionais. Desenvolvendo-se as derivadas em função da equação (28 ), são apresentadas, a seguir, as segundas derivadas:

Para ∂F_xF_k

${\frac {{\partial }^{2}f}{\partial F_{x}\partial F_{x}}}={\beta }_{1}\left({\alpha }_{1}^{2}-\right.$$\left.{\alpha }_{1}\right){\frac {\vert F_{x}\vert ^{{\alpha }_{1}-2}}{F_{x_{p}}^{{\alpha }_{1}}}}+$${\beta }_{7}\left({\alpha }_{7}^{2}-{\alpha }_{7}\right){\frac {\vert F_{x}\vert ^{{\alpha }_{7}-2}}{F_{x_{p}}^{{\alpha }_{7}}}}{\frac {\vert M_{y}\vert ^{{\alpha }_{8}}}{M_{y_{p}}^{{\alpha }_{8}}}}$ $+\quad {\beta }_{8}\left({\alpha }_{9}^{2}-{\alpha }_{9}\right){\frac {\vert F_{x}\vert ^{{\alpha }_{9}-2}}{F_{x_{p}}^{{\alpha }_{9}}}}{\frac {\vert M_{y}\vert ^{{\alpha }_{10}}}{M_{y_{p}}^{{\alpha }_{10}}}}$ ${\frac {{\partial }^{2}f}{\partial F_{x}\partial F_{y}}}=0;\quad {\frac {{\partial }^{2}f}{\partial F_{x}\partial F_{z}}}=$$0;\quad {\frac {{\partial }^{2}f}{\partial F_{x}\partial M_{x}}}=$$0$ ${\frac {{\partial }^{2}f}{\partial F_{x}\partial M_{y}}}={\beta }_{7}{\alpha }_{7}{\alpha }_{8}{\frac {\vert F_{x}\vert ^{{\alpha }_{7}-1}}{F_{x_{p}}^{{\alpha }_{7}}}}sign\_f_{x}{\frac {\vert M_{y}\vert ^{{\alpha }_{8}-1}}{M_{y_{p}}^{{\alpha }_{8}}}}sign\_m_{y}$ ${\frac {{\partial }^{2}f}{\partial F_{x}\partial M_{z}}}={\beta }_{8}{\alpha }_{9}{\alpha }_{10}{\frac {\vert F_{x}\vert ^{{\alpha }_{9}-1}}{F_{x_{p}}^{{\alpha }_{9}}}}sign\_f_{x}{\frac {\vert M_{z}\vert ^{{\alpha }_{10}-1}}{M_{z_{p}}^{{\alpha }_{10}}}}sign\_m_{z}$

( 30)

Para ∂F_yF_k

${\frac {{\partial }^{2}f}{\partial F_{y}\partial F_{x}}}=0$ ${\frac {{\partial }^{2}f}{\partial F_{y}\partial F_{y}}}={\beta }_{2}\left({\alpha }_{2}^{2}-\right.$$\left.{\alpha }_{2}\right){\frac {\vert F_{y}\vert ^{{\alpha }_{2}-2}}{F_{y_{p}}^{{\alpha }_{2}}}}$ ${\frac {{\partial }^{2}f}{\partial F_{y}\partial F_{z}}}=0;\quad {\frac {{\partial }^{2}f}{\partial F_{y}\partial M_{x}}}=$$0;\quad {\frac {{\partial }^{2}f}{\partial F_{y}\partial M_{y}}}=$$0;\quad {\frac {{\partial }^{2}f}{\partial F_{y}\partial M_{z}}}=$$0$

( 31)

Para ∂F_zF_k

${\frac {{\partial }^{2}f}{\partial F_{z}\partial F_{x}}}=0;\quad {\frac {{\partial }^{2}f}{\partial F_{z}\partial F_{y}}}=$$0;$ ${\frac {{\partial }^{2}f}{\partial F_{z}\partial F_{z}}}={\beta }_{3}\left({\alpha }_{3}^{2}-\right.$$\left.{\alpha }_{3}\right){\frac {\vert F_{z}\vert ^{{\alpha }_{3}-2}}{F_{z_{p}}^{{\alpha }_{3}}}}$ ${\frac {{\partial }^{2}f}{\partial F_{z}\partial M_{x}}}=0;\quad {\frac {{\partial }^{2}f}{\partial F_{z}\partial M_{y}}}=$$0;{\frac {{\partial }^{2}f}{\partial F_{z}\partial M_{z}}}=$$0$

( 32)

Para ∂M_xF_k

${\frac {{\partial }^{2}f}{\partial M_{x}\partial F_{x}}}=0;\quad {\frac {{\partial }^{2}f}{\partial M_{x}\partial F_{y}}}=$$0;\quad {\frac {{\partial }^{2}f}{\partial M_{x}\partial F_{z}}}=$$0$ ${\frac {{\partial }^{2}f}{\partial M_{x}\partial M_{x}}}={\beta }_{4}\left({\alpha }_{4}^{2}-\right.$$\left.{\alpha }_{4}\right){\frac {\vert M_{x}\vert ^{{\alpha }_{4}-2}}{M_{x_{p}}^{{\alpha }_{4}}}}$ ${\frac {{\partial }^{2}f}{\partial M_{x}\partial M_{y}}}=0;\quad {\frac {{\partial }^{2}f}{\partial M_{x}\partial M_{z}}}=$$0$

( 33)

Para ∂M_yF_k

${\frac {{\partial }^{2}f}{\partial M_{y}\partial F_{x}}}={\beta }_{7}{\alpha }_{7}{\alpha }_{8}\quad {\frac {\vert F_{x}\vert ^{{\alpha }_{7}-1}}{F_{x_{p}}^{{\alpha }_{7}}}}sign\_f_{x}{\frac {\vert M_{y}\vert ^{{\alpha }_{8}-1}}{M_{y_{p}}^{{\alpha }_{8}}}}sign\_m_{y}$ ${\frac {{\partial }^{2}f}{\partial M_{y}\partial F_{y}}}=0;\quad {\frac {{\partial }^{2}f}{\partial M_{y}\partial F_{z}}}=$$0;\quad {\frac {{\partial }^{2}f}{\partial M_{y}\partial M_{x}}}=$$0;$ ${\frac {{\partial }^{2}f}{\partial M_{y}\partial M_{y}}}={\beta }_{5}\left({\alpha }_{5}^{2}-\right.$$\left.{\alpha }_{5}\right){\frac {\vert M_{y}\vert ^{{\alpha }_{5}-2}}{M_{y_{p}}^{{\alpha }_{5}}}}+$${\beta }_{7}\left({\alpha }_{8}^{2}-{\alpha }_{8}\right){\frac {\vert F_{x}\vert ^{{\alpha }_{7}}}{F_{x_{p}}^{{\alpha }_{7}}}}{\frac {\vert M_{y}\vert ^{{\alpha }_{8}-2}}{M_{y_{p}}^{{\alpha }_{8}}}}$ ${\frac {{\partial }^{2}f}{\partial M_{y}\partial M_{z}}}=0$

( 34)

Para ∂M_zF_k

${\frac {{\partial }^{2}f}{\partial M_{z}\partial F_{x}}}={\beta }_{8}{\alpha }_{9}{\alpha }_{10}\quad {\frac {\vert F_{x}\vert ^{{\alpha }_{9}-1}}{F_{x_{p}}^{{\alpha }_{9}}}}sign\_f_{x}{\frac {\vert M_{z}\vert ^{{\alpha }_{10}-1}}{M_{z_{p}}^{{\alpha }_{10}}}}sign\_m_{z}$ ${\frac {{\partial }^{2}f}{\partial M_{z}\partial F_{y}}}=0;{\frac {{\partial }^{2}f}{\partial M_{z}\partial F_{z}}}=$$0;\quad {\frac {{\partial }^{2}f}{\partial M_{z}\partial M_{x}}}=$$0;{\frac {{\partial }^{2}f}{\partial M_{z}\partial M_{y}}}=$$0$ ${\frac {{\partial }^{2}f}{\partial M_{z}\partial M_{z}}}={\beta }_{6}\left({\alpha }_{6}^{2}-\right.$$\left.{\alpha }_{6}\right){\frac {\vert M_{z}\vert ^{{\alpha }_{6}-2}}{M_{z_{p}}^{{\alpha }_{6}}}}+$${\beta }_{8}\left({\alpha }_{10}^{2}-{\alpha }_{10}\right){\frac {\vert F_{x}\vert ^{{\alpha }_{9}}}{F_{x_{p}}^{{\alpha }_{9}}}}{\frac {\vert M_{z}\vert ^{{\alpha }_{10}-2}}{M_{z_{p}}^{{\alpha }_{10}}}}$

( 35)

As segundas derivadas na forma matricial representam o gradiente do fluxo plástico para cada nó do elemento (Silva [7] ):

${\boldsymbol {\mbox{A}}}_{1}=\left[{\begin{array}{c}{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial F_{x_{1}}\partial F_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{1}}\partial F_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{1}}\partial F_{z_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{1}}\partial M_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{1}}\partial M_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{1}}\partial M_{z_{1}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial F_{y_{1}}\partial F_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{1}}\partial F_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{1}}\partial F_{z_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{1}}\partial M_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{1}}\partial M_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{1}}\partial M_{z_{1}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial F_{z_{1}}\partial F_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{1}}\partial F_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{1}}\partial F_{z_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{1}}\partial M_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{1}}\partial M_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{1}}\partial M_{z_{1}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial M_{x_{1}}\partial F_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{1}}\partial F_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{1}}\partial F_{z_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{1}}\partial M_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{1}}\partial M_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{1}}\partial M_{z_{1}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial M_{y_{1}}\partial F_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{1}}\partial F_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{1}}\partial F_{z_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{1}}\partial M_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{1}}\partial M_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{1}}\partial M_{z_{1}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial M_{z_{1}}\partial F_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{1}}\partial F_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{1}}\partial F_{z_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{1}}\partial M_{x_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{1}}\partial M_{y_{1}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{1}}\partial M_{z_{1}}}}\end{array}}\end{array}}\right]$

( 36)

${\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}=$$\left[{\begin{array}{cc}{\boldsymbol {\mbox{A}}}_{1}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {0}}\end{array}}\right]$

( 37)

${\boldsymbol {\mbox{A}}}_{2}=\left[{\begin{array}{c}{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial F_{x_{2}}\partial F_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{2}}\partial F_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{2}}\partial F_{z_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{2}}\partial M_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{2}}\partial M_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{x_{2}}\partial M_{z_{2}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial F_{y_{2}}\partial F_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{2}}\partial F_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{2}}\partial F_{z_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{2}}\partial M_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{2}}\partial M_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{y_{2}}\partial M_{z_{2}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial F_{z_{2}}\partial F_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{2}}\partial F_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{2}}\partial F_{z_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{2}}\partial M_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{2}}\partial M_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial F_{z_{2}}\partial M_{z_{2}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial M_{x_{2}}\partial F_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{2}}\partial F_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{2}}\partial F_{z_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{2}}\partial M_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{2}}\partial M_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{x_{2}}\partial M_{z_{2}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial M_{y_{2}}\partial F_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{2}}\partial F_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{2}}\partial F_{z_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{2}}\partial M_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{2}}\partial M_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{y_{2}}\partial M_{z_{2}}}}\end{array}}\\{\begin{array}{cccccc}{\frac {{\partial }^{2}f}{\partial M_{z_{2}}\partial F_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{2}}\partial F_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{2}}\partial F_{z_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{2}}\partial M_{x_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{2}}\partial M_{y_{2}}}}&{\frac {{\partial }^{2}f}{\partial M_{z_{2}}\partial M_{z_{2}}}}\end{array}}\end{array}}\right]$

( 38)

${\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{2}=$$\left[{\begin{array}{cc}{\boldsymbol {0}}&{\boldsymbol {0}}\\{\boldsymbol {0}}&{\boldsymbol {\mbox{A}}}_{2}\end{array}}\right]$

( 39)

onde 0 é uma matriz 6 × 6 com elementos nulos.

4.3. Algoritmo de retorno

Na aplicação do carregamento da estrutura, os esforços seccionais atingem, num ou em ambos os nós do elemento de viga, um estado que sai da superfície de interação, formando-se rótulas plásticas. Neste caso, aplica-se o método de Backward Euler para trazer de volta os esforços seccionais à superfície de interação. Portanto, assume-se, inicialmente, que exista uma combinação de esforços seccionais num dos nós do elemento que esteja fora da superfície de interação (visto em Silva [7] ). Utilizando-se o método de backward Euler, corrige-se o vetor de forças nodais da forma seguinte:

${\overset {\mbox{ˆ}}{F}}_{i}=F_{i}^{trial}-{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}$

( 40)

onde ${\textstyle F_{i}^{trial}={\overline {F}}_{i}+}$$K_{ij}{dU}_{j}$ corresponde a um vetor de forças nodais estimado. Este vetor é obtido através de uma solução elástica dos incrementos de deslocamentos dU_j e da matriz de rigidez linear elástica K_ij do elemento de viga 3D (fig. 1 ). ${\textstyle {\overline {F}}_{i}}$ é o vetor de forças nodais do último passo de carga convergido. O vetor ${\textstyle {\overline {F}}_{i}}$ está dentro ou fora da superfície de interação. Por outro lado, ${\textstyle {\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}}$ é o vetor de fluxo plástico definido em relação aos esforços seccionais que estão fora da superfície de interação e λ₁ é o multiplicador plástico, tal que λ₁  ≥ 0.

Geralmente, os vetores de forças nodais, estimado ${\textstyle F_{i}^{trial}}$ e corrigido ${\textstyle {\overset {\mbox{ˆ}}{F}}_{i}}$ , não satisfazem o critério de escoamento, isto é, não estão sobre a superfície de interação. Assim, torna-se necessário um tipo de processo iterativo para trazer o estado de tensão (esforços seccionais) de volta à superfície de interação (ver fig. 5 ).

Figura 5. Retorno à superfície com um vetor (ver Silva [7] ).

4.3.1. Algoritmo de retorno com 1 (um) vetor

Ao ocorrer a situação de somente uma rótula plástica no elemento de viga, emprega-se somente um vetor de fluxo plástico correspondente aos esforços seccionais que se encontra fora da superfície de interação (ver fig. 5 ).

O processo iterativo utiliza vetores de fluxo plástico atualizados para se aproximar da superfície. Este procedimento é chamado de algoritmo de retorno, sendo que, neste caso, é feito com um vetor. Na figura 5 , encontra-se a interpretação geométrica do algoritmo de retorno (Silva [7] ). Admite-se que os vetores de força nodais F_i (atual) e ${\textstyle {\overset {\mbox{ˆ}}{F}}_{i}}$ (corrigido) não cumprem o critério de escoamento, ou seja, ${\textstyle f\left(F_{i}\right)>1}$ e ${\textstyle f\left({\overset {\mbox{ˆ}}{F}}_{i}\right)>1}$ . Com isso, o vetor de forças residuais r_i , baseado na equação (40) , é definido como:

$r_{i}=F_{i}-{\overset {\mbox{ˆ}}{F}}_{i}=F_{i}-\left(F_{i}^{trial}-\right.$$\left.{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}\right)$

( 41)

Expandindo a equação (41) numa série de Taylor até os termos de primeira ordem e mantendo o vetor de forças nodais de partida ${\textstyle F_{i}^{trial}}$ fixo, obtém-se um novo vetor de forças residuais ${\textstyle r_{i}^{new}}$ . Este novo vetor é apresentado da forma seguinte:

$r_{i}^{new}=r_{i}^{old}+{dF}_{i}+d{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}+$${\lambda }_{1}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}{dF}_{k}$

( 42)

onde dF_i é uma variação em F_i , dλ₁ é uma variação em λ₁ e ${\textstyle \left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]{dF}_{k}}$ é uma variação em ${\textstyle {\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}}$ . Aplicando a condição: ${\textstyle r_{i}^{new}=0}$ , a equação (42) é reapresentada a seguir:

$0=r_{i}^{old}+d{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}+$$\left({\delta }_{ik}+{\lambda }_{1}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}\right){dF}_{k}$

( 43)

Definindo a matriz Q_ik como segue:

$Q_{ik}={\delta }_{ik}+{\lambda }_{1}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}$

( 44)

Aplicam-se manipulações indiciais nas equações (43) e (44) para determinar a correção do vetor de forças nodais, dF_i , na iteração atual, chegando a:

$Q_{li}{dF}_{i}=-\left(r_{l}^{old}+d{\lambda }_{1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}\right)$

( 45)

${dF}_{i}=-Q_{il}^{-1}\left(r_{l}^{old}+d{\lambda }_{1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}\right)$

( 46)

Expandindo a função de escoamento (interação), f , numa série de Taylor até os termos de primeira ordem em torno do vetor de forças nodais final F_i , tem-se que

$f_{1}^{new}=f_{1}^{old}+{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}{dF}_{i}$

( 47)

Impondo que ${\textstyle f_{1}^{new}=0}$ na equação (47) e usando a equação (46) , obtém-se a correção do multiplicador plástico, na iteração atual, como segue:

${\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}{dF}_{i}=$$-f_{1}^{old}$

( 48)

${\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}\left[-\right.$$\left.Q_{il}^{-1}\left(r_{l}^{old}+d{\lambda }_{1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}\right)\right]=$$-f_{1}^{old}$

( 49)

$-{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}Q_{il}^{-1}\left(d{\lambda }_{1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}\right)=$$-f_{1}^{old}+{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}Q_{il}^{-1}r_{i}^{old}$

( 50)

$d{\lambda }_{1}={\frac {f_{1}^{old}-{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}Q_{il}^{-1}r_{i}^{old}}{{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}Q_{il}^{-1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}}}$

( 51)

Este procedimento iterativo termina quando são alcançados os critérios de parada adotados:

$r^{norm}={\sqrt {\frac {\Vert r_{i}\Vert }{\Vert F_{i}^{trial}\Vert }}}\quad <TOL\quad f^{norm}=$$\vert f-1,0\vert <TOL$

( 52)

onde ||r_i || é a norma euclidiana do vetor de forças residuais, ${\textstyle \Vert F_{i}^{trial}\Vert }$ é a norma euclidiana do vetor de forças estimado e TOL é a tolerância para a convergência.

4.3.2. Algoritmo de retorno com 2 (dois) vetores

Para o caso da formação de 2 rótulas plásticas no elemento de viga, são utilizados 2 vetores de fluxo plástico com um vetor para cada nó, ou seja, ${\textstyle {\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}}$ e ${\textstyle {\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}}$ . Os vetores de fluxo são os esforços seccionais de cada nó, que estão fora da superfície de interação, isto é, ${\textstyle f_{1}\left(F_{j}\right)>1}$ e ${\textstyle f_{2}\left(F_{j}\right)>1}$ . Durante o processo iterativo utilizam-se esses vetores de fluxo plástico atualizados para a aproximação da superfície de interação. Este procedimento é chamado algoritmo de retorno com 2 (dois) vetores. A interpretação geométrica do algoritmo é vista na figura 6 . Define-se o vetor de forças nodais de partida como: ${\textstyle F_{i}^{trial}={\overline {F}}_{i}+}$$K_{ij}{dU}_{j}$ , onde ${\textstyle {\overline {F}}_{i}}$ é o vetor de forças nodais do último passo de carga convergido. O vetor ${\textstyle {\overline {F}}_{i}}$ estará dentro ou fora da superfície de interação, ou seja, ${\textstyle f\left({\overline {F}}_{i}\right)<1}$ ou ${\textstyle f\left({\overline {F}}_{i}\right)=}$$1$ , respetivamente. O vetor de forças nodais corrigido expressa-se como:

${\overset {\mbox{ˆ}}{F}}_{i}=F_{i}^{trial}-{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-$${\lambda }_{2}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}$

( 53)

onde λ₁ e λ₂ são os multiplicadores plásticos, sendo que λ₁  ≥ 0 e λ₂  ≥ 0. Admite-se que os vetores de forças nodais atual (F ) e corrigido (${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{F}}}}}$ ) não cumprem a condição de escoamento com ${\textstyle f\left(F_{i}\right)>1}$ e ${\textstyle f\left({\overset {\mbox{ˆ}}{F}}_{i}\right)>1}$ . Define-se o vetor de forças nodais r como:

$r_{i}=F_{i}-{\overset {\mbox{ˆ}}{F}}_{i}=F_{i}-\left(F_{i}^{trial}-\right.$$\left.{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-\right.$$\left.{\lambda }_{2}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}\right)$

( 54)

Figura 6. Retorno a superfície com 2 vetores (Silva [7] ).

Expandindo a equação (54) em série de Taylor até os termos de primeira ordem e mantendo fixo o vetor de forças nodais ${\textstyle F_{i}^{trial}}$ , obtém-se um novo vetor de forças residuais ${\textstyle r_{i}^{new}}$ , que é apresentado na equação (55) :

$r_{i}^{new}=r_{i}^{old}+{dF}_{i}+d{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}+$${\lambda }_{1}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}{dF}_{k}$ $+d{\lambda }_{2}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}+$${\lambda }_{2}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{2}{dF}_{k}$

( 55)

Impondo-se a condição ${\textstyle r_{i}^{new}=0}$ , a equação (55) pode ser reescrita como:

$0=r_{i}^{old}+d{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}+$$d{\lambda }_{2}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}$ $+\left({\delta }_{ik}+{\lambda }_{1}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}+\right.$$\left.{\lambda }_{2}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{2}\right){dF}_{k}$

( 56)

Define-se a matriz Q_ik como:

$Q_{ik}={\delta }_{ik}+{\lambda }_{1}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}+$${\lambda }_{2}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{2}$

( 57)

Aplicam-se, como anteriormente, manipulações indiciais nas equações (55) , (56) e (57) para a obtenção do vetor de forças nodais da iteração atual:

$Q_{li}{dF}_{i}=-\left(r_{l}^{old}+d{\lambda }_{1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}+\right.$$\left.d{\lambda }_{2}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}\right)$

( 58)

${dF}_{i}=-\quad Q_{il}^{-1}\left(r_{l}^{old}+d{\lambda }_{1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}+\right.$$\left.d{\lambda }_{2}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}\right)$

( 59)

Expandindo-se as funções de escoamento no nó 1, f₁ , e no nó 2, f₂ , em série de Taylor até aos termos de primeira ordem em torno do vetor de forças nodais final F_k , chega-se a:

$f_{1}^{new}=f_{1}^{old}+{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}{dF}_{i},f_{2}^{new}=$$f_{2}^{old}+{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}{dF}_{i}$

( 60)

Aplicando a equação (59) nas funções da equação (60) e impondo que ${\textstyle f_{1}^{new}=0}$ e ${\textstyle f_{2}^{new}=0}$ , tem-se que:

$f_{m}^{old}-{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{m}Q_{il}^{-1}r_{l}^{old}=$$d{\lambda }_{1}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{m}Q_{il}^{-1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}+$$d{\lambda }_{2}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{m}Q_{il}^{-1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}$

( 61)

com m  = 1, 2

As incógnitas são as correções dos multiplicadores plásticos dλ₁ e dλ₂ durante o processo iterativo (Silva [7] ). Colocando as equações (61) no sistema matricial:

$\left[{\begin{array}{cc}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}Q_{il}^{-1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}&{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}Q_{il}^{-1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}\\{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}Q_{il}^{-1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}&{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}Q_{il}^{-1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}\end{array}}\right]\left\{{\begin{array}{c}d{\lambda }_{1}\\d{\lambda }_{2}\end{array}}\right\}=\left\{{\begin{array}{c}f_{1}^{old}-{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}Q_{il}^{-1}r_{l}^{old}\\f_{2}^{old}-{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}Q_{il}^{-1}r_{l}^{old}\end{array}}\right\}$

( 62)

Reapresentado a equação (62) da seguinte forma:

$\left[{\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}}\right]\left\{{\begin{array}{c}d{\lambda }_{1}\\d{\lambda }_{2}\end{array}}\right\}=\left\{{\begin{array}{c}b_{1}\\b_{2}\end{array}}\right\}$

( 63)

Solucionando o sistema da equação (63) , obtém-se que:

${\boldsymbol {\mbox{a}}}{\boldsymbol {\lambda }}={\boldsymbol {\mbox{b}}}$

( 64)

${\boldsymbol {\lambda }}={\boldsymbol {\mbox{a}}}^{-1}{\boldsymbol {\mbox{b}}}$

( 65)

com

${\boldsymbol {\mbox{a}}}^{-1}=\left[{\begin{array}{cc}{\frac {a_{22}}{a_{11}a_{22}-a_{12}a_{21}}}&-{\frac {a_{12}}{a_{11}a_{22}-a_{12}a_{21}}}\\-{\frac {a_{21}}{a_{11}a_{22}-a_{12}a_{21}}}&{\frac {a_{11}}{a_{11}a_{22}-a_{12}a_{21}}}\end{array}}\right]$

( 66)

${\boldsymbol {\lambda }}=\left[{\begin{array}{c}{\frac {a_{22}b_{1}-a_{12}b_{2}}{a_{11}a_{22}-a_{12}a_{21}}}\\{\frac {a_{11}b_{2}-a_{21}b_{1}}{a_{11}a_{22}-a_{12}a_{21}}}\end{array}}\right]$

( 67)

$\left[{\begin{array}{c}d{\lambda }_{1}\\d{\lambda }_{2}\end{array}}\right]=\left[{\begin{array}{c}{\frac {a_{22}\left(f_{1}^{old}-{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}Q_{il}^{-1}r_{l}^{old}\right)-a_{12}\left(f_{2}^{old}-{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}Q_{il}^{-1}r_{l}^{old}\right)}{a_{11}a_{22}-a_{12}a_{21}}}\\{\frac {a_{11}\left(f_{2}^{old}-{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}Q_{il}^{-1}r_{l}^{old}\right)-a_{21}\left(f_{1}^{old}-{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}Q_{il}^{-1}r_{l}^{old}\right)}{a_{11}a_{22}-a_{12}a_{21}}}\end{array}}\right]$

( 68)

O processo iterativo termina quando são cumpridos os seguintes critérios de parada:

$r^{norm}={\sqrt {\frac {\Vert r_{i}\Vert }{\Vert F_{i}^{trial}\Vert }}}\quad <TOL,f_{1}^{norm}=$$\vert f_{1}-1,0\vert <TOL,f_{2}^{norm}=\vert f_{2}-1,0\vert <TOL$

( 69)

4.4. Matriz de rigidez consistente

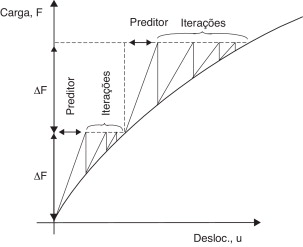
No processo incremental-iterativo, é utilizado, na fase corretora, o método de Newton-Raphson para determinar a configuração de equilíbrio do sistema estrutural (Silva [7] ). Para não destruir a convergência quadrática do método, há necessidade da obtenção de uma matriz de rigidez consistente de forma que sejam apresentados os casos para 1 (um) vetor e 2 (dois) vetores. Na situação de uma rótula plástica, utiliza-se o algoritmo com um vetor e, para duas, o algoritmo com dois vetores. Ao alcançar a convergência atendendo aos critérios adotados nas equações (52) e (69) , atualiza-se a matriz de rigidez consistente ao início de cada passo de carga (ver fig. 7 ).

Figura 7. Procedimento incremental-iterativo de Newton-Raphson como visto em Crisfield [9] .

4.4.1. Algoritmo de retorno com um vetor

Para trazer os esforços seccionais à superfície de interação, no final do processo iterativo, define-se a seguinte correção:

$F_{i}=F_{i}^{trial}-{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1},com\quad {\lambda }_{1}>0$

( 70)

e para o vetor de forças nodais de partida (inicial), define-se como:

$F_{i}^{trial}={\overline {F}}_{i}+K_{ij}{dU}_{j}$

( 71)

Aplicando-se o diferencial total na equação (70) , eq. (42) , chega-se a:

${dF}_{i}=K_{ij}{dU}_{j}-d{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-$${\lambda }_{1}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}{dF}_{k}$

( 72)

Desenvolvendo a equação (72) , obtém-se que:

$\left({\delta }_{ik}+{\lambda }_{1}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}\right){dF}_{k}=$$K_{ij}{dU}_{j}-d{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}$

( 73)

Utilizando a matriz Q_ik definida na equação (44) e definindo que a matriz de redução plástica seja igual a:

$R_{ij}=Q_{il}^{-1}K_{lj}$

( 74)

Com isso, reescreve-se a equação (73) da seguinte forma:

${dF}_{i}=R_{ij}\left({dU}_{j}-d{\lambda }_{1}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}\right)$

( 75)

A equação (75) é semelhante à forma não consistente, sendo diferente no termo K_ij em relação ao ${\textstyle R_{ij}=Q_{il}^{-1}K_{lj}}$ e no facto de o vetor de fluxo plástico ser avaliado no ponto de retorno à superfície de interação (Silva [7] ). Como o vetor de forças nodais final, F_i tem de cumprir a condição ${\textstyle f\left(F_{i}\right)=0}$ , diferencia-se esta condição e tem-se por base a equação (75) , de maneira que

${\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}{dF}_{i}=$$0$

( 76)

${\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}\left({dU}_{j}-\right.$$\left.d{\lambda }_{1}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}\right)=$$0$

( 77)

Desenvolvendo a equação anterior para a obtenção do multiplicador plástico (dλ₁ ), obtém-se:

$d{\lambda }_{1}={\frac {{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}{dU}_{j}}{{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}}}$

( 78)

A matriz de rigidez elastoplástica consistente é obtida em função das equações (75) e (78) , Silva [7] :

$K_{ij}^{AL}=R_{ij}-{\frac {R_{im}{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{1}{\left\{{\frac {\partial f}{\partial F_{n}}}\right\}}_{1}R_{nj}}{{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{1}R_{mn}{\left\{{\frac {\partial f}{\partial F_{n}}}\right\}}_{1}}}$

4.4.2. Algoritmo de retorno com 2 vetores

Para a situação em que existam 2 rótulas plásticas, assume-se que ${\textstyle f_{1}\left(F_{i}\right)=0}$ e ${\textstyle f_{2}\left(F_{i}\right)=0}$ , e a correção para trazer os esforços seccionais de ambos nós para a superfície de interação, ao final do processo iterativo, é apresentada a seguir:

$F_{i}=F_{i}^{trial}-{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-$${\lambda }_{2}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2},com\quad {\lambda }_{1}>0\quad e\quad {\lambda }_{2}>0$

( 79)

Utilizando o vetor de forças nodais de partida, ${\textstyle F_{i}^{trial}={\overline {F}}_{i}+}$$K_{ij}{dU}_{j}$ , na equação anterior e aplicando o diferencial total, chega-se a:

${dF}_{i}=K_{ij}{dU}_{j}-d{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-$${\lambda }_{1}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{1}{dF}_{k}$ $-\quad d{\lambda }_{2}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}-$${\lambda }_{2}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{2}{dF}_{k}$

( 80)

Semelhantemente, as equações (56) e (57) desenvolvem a equação (80) da seguinte forma:

${\left({\delta }_{ik}+{\lambda }_{1}K_{ij}\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]+{\lambda }_{2}K_{ij}{\left[{\frac {{\partial }^{2}f}{\partial F_{j}\partial F_{k}}}\right]}_{2}\right)}_{2}{dF}_{k}$ $=K_{ij}{dU}_{j}-d{\lambda }_{1}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-$$d{\lambda }_{2}K_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}$

( 81)

Usando a matriz Q_ik (ver equação (57 )) e definindo a matriz de redução plástica como ${\textstyle R_{ij}=Q_{il}^{-1}K_{lj}}$ , apresenta-se a equação (81) da seguinte forma:

$Q_{li}{dF}_{i}=K_{lj}{dU}_{j}-d{\lambda }_{1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-$$d{\lambda }_{2}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}$ $\Rightarrow {dF}_{i}=Q_{il}^{-1}(K_{lj}{dU}_{j}-d{\lambda }_{1}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-$$d{\lambda }_{2}K_{lj}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}$ $\Rightarrow {dF}_{i}=R_{ij}\left({dU}_{j}-d{\lambda }_{1}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-\right.$$\left.d{\lambda }_{2}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}\right)$

( 82)

Como o vetor de forças nodais final F_i cumpre as condições ${\textstyle f_{1}\left(F_{i}\right)=0}$ e ${\textstyle f_{2}\left(F_{i}\right)=0}$ , diferenciam-se estas condições com base na equação (82) , (Silva [7] ). Com isso, chega-se a:

${\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{m}{dF}_{i}=$$0$ $\Rightarrow {\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{m}R_{ij}\left({dU}_{j}-\right.$$\left.d{\lambda }_{1}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}-\right.$$\left.d{\lambda }_{2}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}\right)=$$0$ $\Rightarrow {\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{m}R_{ij}{dU}_{j}=$${\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{m}R_{ij}d{\lambda }_{1}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}+$${\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{m}R_{ij}d{\lambda }_{2}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}$

( 83)

com m  = 1,2.

Reescrevendo as equações de (83) em função dos multiplicadores plásticos, na forma matricial, obtém-se:

$\left[{\begin{array}{cc}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}&{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}\\{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}R_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{1}&{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}R_{ij}{\left\{{\frac {\partial f}{\partial F_{j}}}\right\}}_{2}\end{array}}\right]\left\{{\begin{array}{c}d{\lambda }_{1}\\d{\lambda }_{2}\end{array}}\right\}=\left\{{\begin{array}{c}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}{dU}_{j}\\{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}R_{ij}{dU}_{j}\end{array}}\right\}$

( 84)

De forma semelhante ao sistema da equação (63) , a solução do sistema é:

$\left[{\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}}\right]\left\{{\begin{array}{c}d{\lambda }_{1}\\d{\lambda }_{2}\end{array}}\right\}=\left\{{\begin{array}{c}b_{1}\\b_{2}\end{array}}\right\}$

( 85)

${\boldsymbol {\mbox{a}}}{\boldsymbol {\lambda }}={\boldsymbol {\mbox{b}}}$

( 86)

${\boldsymbol {\lambda }}={\boldsymbol {\mbox{a}}}^{-1}{\boldsymbol {\mbox{b}}}$

( 87)

com

${\boldsymbol {\mbox{a}}}^{-1}=\left[{\begin{array}{cc}{\frac {a_{22}}{a_{11}a_{22}-a_{12}a_{21}}}&-{\frac {a_{12}}{a_{11}a_{22}-a_{12}a_{21}}}\\-{\frac {a_{21}}{a_{11}a_{22}-a_{12}a_{21}}}&{\frac {a_{11}}{a_{11}a_{22}-a_{12}a_{21}}}\end{array}}\right]$

( 88)

${\boldsymbol {\lambda }}=\left[{\begin{array}{c}{\frac {a_{22}b_{1}-a_{12}b_{2}}{a_{11}a_{22}-a_{12}a_{21}}}\\{\frac {a_{11}b_{2}-a_{21}b_{1}}{a_{11}a_{22}-a_{12}a_{21}}}\end{array}}\right]$

( 89)

Assim, tem-se que:

$d{\lambda }_{1}={\frac {a_{22}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}{dU}_{j}-a_{12}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}R_{ij}{dU}_{j}}{a_{11}a_{22}-a_{12}a_{21}}}$ $d{\lambda }_{2}={\frac {a_{11}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}R_{ij}{dU}_{j}-a_{21}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}{dU}_{j}}{a_{11}a_{22}-a_{12}a_{21}}}$

( 90)

Convém comentar que, se qualquer multiplicador plástico assume valores negativos, ou seja, dλ₁  < 0 ou dλ₂  < 0, atribui-se valor zero e desativa-se a rótula plástica correspondente ao multiplicador plástico negativo.

Reescrevendo a equação anterior, obtém-se:

${\begin{array}{c}d{\lambda }_{1}=\left({\frac {a_{22}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}}{a_{11}a_{22}-a_{12}a_{21}}}-{\frac {a_{12}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}R_{ij}}{a_{11}a_{22}-a_{12}a_{21}}}\right){dU}_{j}\\d{\lambda }_{2}=\left({\frac {a_{11}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}R_{ij}}{a_{11}a_{22}-a_{12}a_{21}}}-{\frac {a_{21}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}}{a_{11}a_{22}-a_{12}a_{21}}}\right){dU}_{j}\end{array}}\Rightarrow$ $\Rightarrow {\begin{array}{c}d{\lambda }_{1}=\left(c_{1}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}-c_{2}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}R_{ij}\right){dU}_{j}\\d{\lambda }_{2}=\left(c_{3}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{2}R_{ij}-c_{4}{\left\{{\frac {\partial f}{\partial F_{i}}}\right\}}_{1}R_{ij}\right){dU}_{j}\end{array}}\Rightarrow$ $\Rightarrow {\begin{array}{c}d{\lambda }_{1}=\left(c_{1}{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{1}R_{mn}-c_{2}{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{2}R_{mn}\right){dU}_{n}\\d{\lambda }_{2}=\left(c_{3}{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{2}R_{mn}-c_{4}{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{1}R_{mn}\right){dU}_{n}\end{array}}$

( 91)

Com base nas equações (82) e (91) , obtém-se a matriz de rigidez elastoplástica consistente ${\textstyle K_{ij}^{AL}}$ (Silva [7] ):

$K_{ij}^{AL}=R_{ij}-\left(c_{1}R_{im}{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{1}{\left\{{\frac {\partial f}{\partial F_{n}}}\right\}}_{1}R_{nj}-\right.$$\left.c_{2}R_{im}{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{1}{\left\{{\frac {\partial f}{\partial F_{n}}}\right\}}_{2}R_{nj}\right)$ $-\left(c_{3}R_{im}{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{2}{\left\{{\frac {\partial f}{\partial F_{n}}}\right\}}_{2}R_{nj}-\right.$$\left.c_{4}R_{im}{\left\{{\frac {\partial f}{\partial F_{m}}}\right\}}_{2}{\left\{{\frac {\partial f}{\partial F_{n}}}\right\}}_{1}R_{nj}\right)$

( 92)

5. Exemplos numéricos

5.1. Introdução

Os exemplos 5.1 e 5.2 são aplicações para análise de resultados utilizando algumas superfícies obtidas pelo método proposto neste trabalho.

5.2. Exemplo 5.1

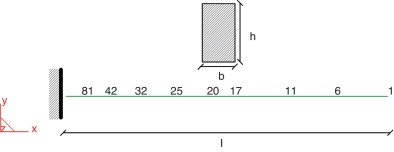
Neste exemplo, são apresentadas aplicações baseadas na teoria de análise elastoplástica utilizando o conceito de rótula plástica e método Backward Euler como em Silva [7] . Utilizam-se algumas funções obtidas pelo modelo apresentado para comparações com o exemplo « Two bay asymetric frame »de Argyris [10] . A figura 8 mostra a geometria de exemplo e a tabela 4 apresenta as suas propriedades.

Figura 8. Geometria e dados da secção transversal (Two bay asymetric frame) [10] .

Tabela 4. Propriedades do material (Two bay asymetric frame).

Propriedades do material (Two bay asymetric frame)
Elemento no	Secção transversal		Dados gerais
1, 2, 3, 6	a-a	A=800, 00cm2
		Iy=106667, 00cm4
		Fxp=290,299×106kgf
		Myp=290,299×107kgf/cm	E=907, 184×105kgf/cm
4, 5	b-b	A=1391, 50cm2	σ0=45, 360×104kgf/cm
		Iy=245368, 00cm4	L=600 cm
		Fxp=504,848×106kgf
		Myp=580,598×107kgf/cm

Para cada função, são observados: 1) O processo de formação das rótulas plásticas; e 2) Como são atingidas as superfícies de interação em função dos deslocamentos, rótulas plásticas e multiplicadores plásticos (λ ). A notação dos gráficos tem o seguinte significado: elemento = e_i com i  = 1, n e nó = n_j com j  = 1, m . Foram usadas as seguintes funções para as análises elastoplásticas:

• Funçãon²m  : f_u  = 1, 007n²  + 1, 025m  − 1 =0 (equação (23 ));
• Funçãonm²  : f_u  = 1, 063n  + 0, 907m²  − 1 =0 (equação (24 ));
• Funçãon²m²  : f_u  = 1, 164n²  + 1, 127m²  − 1 =0 (equação (25 ));
• Funçãon²nmm²  : f_u  = 1, 035n²  + 0, 880nm  + 0, 812m²  − 1 =0 (equação (26 )).

São apresentados, na tabela (5 ), os respetivas das respectivas funções quanto à formação das rótulas plásticas e cargas limite atingidas.

Tabela 5. Rótulas plásticas para as funções analisadas - Two bay asymetric frame

n2m (23 )			nm2(24)			n2m2(25)			n2nmm2(26)
e	nó	λ	e	nó	λ	e	nó	λ	e	nó	λ
Rótulas plásticas
1	1	2,987E+08	1	1	1,610E+06	1	1	1,589E+08	1	1	1,631E+08
2	3	7,243E+08	2	2	5,422E+08	1	2	1,369E+07	2	2	4,007E+05
4	5	3,922E+09	2	3	3,790E+08	2	2	1,364E+06	2	3	3,815E+08
5	5	8,430E+06	3	4	3,350E+06	2	3	3,762E+08	3	4	4,962E+06
6	6	9,999E+08	4	5	2,033E+09	4	5	1,995E+09	4	5	2,124E+09
			5	5	2,885E+06	5	5	7,750E+05	5	5	6,813E+05
			6	6	5,556E+11	6	6	5,247E+08	6	6	5,445E+08
Carga limite
1,81733E+07 kgf			1,90760E+07 kgf			1,75814E+07 kgf			2,01494E+07 kgf
43894,70kp			44986,50kp			41469,80kp			47515,80kp

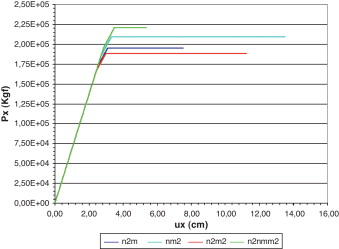
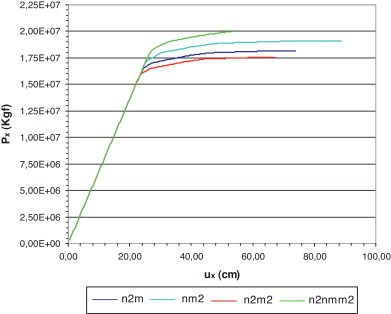
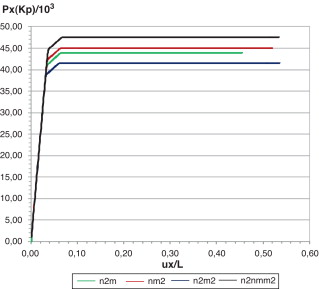
Os resultados obtidos (ver figs. 9 e 10 e tabela 5 ) pelas funções apresentadas são semelhantes à solução dada por Argyris [10] . Os processos de formação das rótulas plásticas foram parecidos para as funções das equações 24 e 26 . Todas as funções possuem semelhanças, sendo que as de resultados mais próximos entre si foram as equações (23) e (25) ; (24) e (26) . Cabe lembrar que a melhor solução do ponto de vista estatístico foi a equação (23) (mais detalhes em Vieira [2] ).

Figura 9. Gráfico carga × deslocamento para o nó 2 - função n2m (Two bay asymetric frame) - unidade: kgf.

Figura 10. Gráfico carga × deslocamento para o nó 2 - função n2m (Two bay asymetric frame) - unidade: kp.

5.3. Exemplo 5.2

Neste exemplo, são utilizadas funções de interação semelhantes ao exemplo de Argyris: « Two beam structure », Argyris [10] . As propriedades do exemplo são apresentadas na tabela 6 e a figura 11 mostra a sua geometria e o nó monitorado n^o 2.

Tabela 6. Propriedades do material - Two beam structure

Propriedades do material (Two beam structure)
Elemento n . o	Secção transversal		Dados gerais
1			E=317, 515×106kgf/cm2
			σ0=125, 282×104kgf/cm2
			Fxp=587,992×104kgf
	a - a	A=4, 85cm2	Myp=280,774×104kgf/cm
2, 3		Iy=1, 475cm4	E=317, 515×106kgf/cm2
			σ0=153, 087×104kgf/cm2
			Fxp=742,667×104kgf
			Myp=354,616×104kgf/cm

Figura 11. Geometria e dados da secção transversal do « Two beam structure »[10] .

Para cada função, são observados: 1) O processo de formação das rótulas plásticas; e 2) Como são atingidas as superfícies de interação em função dos deslocamentos, rótulas plásticas e multiplicadores plásticos (λ ). A notação dos gráficos tem o seguinte significado: elemento = e_i com i  = 1, n e nó = n_j com j  = 1, m .

Foram usadas as seguintes funções para as análises elastoplásticas:

• Funçãon²m  : f_u  = 1, 007n²  + 1, 025m  − 1 =0 (equação (23 ));
• Funçãonm²  : f_u  = 1, 063n  + 0, 907m²  − 1 =0 (equação (24 ));
• Funçãon²m²  : f_u  = 1, 164n²  + 1, 127m²  − 1 =0 (equação (25 ));
• Funçãon²nmm²  : f_u  = 1, 035n²  + 0, 880nm  + 0, 812m²  − 1 =0 (equação (26 )).

São apresentados, na tabela (7 ), os resultados das respetivas funções quanto à formação das rótulas plásticas e cargas limite atingidas. Os resultados obtidos por Argyris [10] estão apresentados na tabela (8 ).

Tabela 7. Rótulas plásticas para as funções analisadas - Two beam structure

n2m (23 )			nm2(24)			n2m2(25)			n2nmm2(26)
e	nó	λ	e	nó	λ	e	nó	λ	e	nó	λ
Rótulas plásticas
1	1	3,495E04	1	1	6,693E+04	1	1	3,818E+04	1	1	3,401E+04
2	4	1,519	3	3	1,013E+05	3	3	7,141E+04	2	4	1,505
3	4	0,769							3	4	0,796
3	3	2,526E04							3	3	2,710E+04
Carga limite
1,95225E+05 kgf			2,09059E+05 kgf			1,88502E+05 kgf			2,20945E+05 kgf
10073,50 kp			9615,61 kp			9496,01 kp			9954,66 kp

Tabela 8. Resultados obtidos por Argyris - Two beam Structure

Curvas de Argyris
Identificação	Curva	Carga crítica (kp)
BESCOP, 30 elementos	0-1	9250,00
BECOEP, 2 elementos	0-2	10100,00
BECOEP, 6 elementos	0-3	9100,00
BECOEP, 30 elementos	0-4-5	9000,00

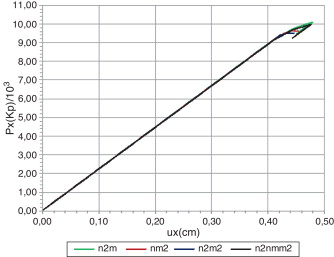
Os resultados obtidos pelas funções apresentadas são semelhantes às soluções das cargas críticas dadas por Argyris [10] . O processo de formação das rótulas plásticas foram parecidos para os pares de funções das equações {(24) , (25) } e {(23) , (26) }. O comportamento das funções (ver figs. 12 e 13 ) foram semelhantes, sendo que a função de melhor resultado elastoplástico comparada com Argyris foi a superfície da equação (23) . Esta, também, foi a melhor solução do ponto de vista estatístico.

Figura 12. Gráfico carga × deslocamento para o nó 2 - (Two beam structure)-unidade: kgf.

Figura 13. Gráfico carga × deslocamento para o nó 2 - (Two beam structure)-unidade: kp.

6. Conclusões

• As superfícies de escoamento em resultantes de tensões facilitam o processo de análise sem a necessidade da integração numérica, de maneira que o modelo baseado nas formulações de viga de Timoshenko 3D e a regressão linear múltipla permitiu a geração destas superfícies por processo numérico;
• As aplicações demonstram que a formulação apresentada consegue gerar boas funções de escoamento que retratam os fenómenos físicos;
• A formulação permite tratar por processo numérico dados obtidos por análises numéricas e/ou experimentais;
• As pesquisas futuras terão o intuito de gerar funções de escoamento para outros tipos de secções transversais com outros materiais;
• Pretende-se também desenvolver um método que obtenha os melhores índices α para as funções de escoamento propostas.

Agradecimentos

Aos professores do PECC/UnB/Brasil, CIMNE/UPC/Espanha e à CAPES pelo fomento.

References

1. [1] A.D. Hanganu, Metodologia de Evaluación del Deterioro en Estructuras de Hormigón Armado, Monografia CIMNE n^o 39, Barcelona, Espanha, 1997.
2. [2] P.C. dos S. Vieira, Geração de Superfícies de Interação pelo Método da Regressão Linear Múltipla com o Modelo de Dano em Vigas de Timoshenko 3D, Publicação no E.TD- 006A/04, Departamento de Engenharia Civil e Ambiental, Universidade de Brasília, Brasília, DF, 150p, 2004.
3. [3] S. Oller; Fractura Mecánica. Un enfoque global; CIMNE, Barcelona, Espanha (2001)
4. [4] D.C. Montegomery, G.C. Runger; Probabilidad y Estadística Aplicadas a la Ingeniería; McGraw-Hill Interamericana Editores, S. A., D. F, México (1998)
5. [5] M.R. Horne; Plastic theory of structures; (2d ed)Pergamon Press’, Oxford, Inglaterra (1972)
6. [6] B.G. Neal; The plastic methods of structural analysis; Chapman and Hall’, Inglaterra (1977)
7. [7] W.T.M. Silva; Análise Elastoplástica de Pórticos Espaciais Utilizando o Conceito de Rótula Plástica e o Método de Backward Euler; Métodos Computacionais em Engenharia, Lisboa, Portugal (2004)
8. [8] J. Lubliner; Plasticity Theory; Macmillan Publishing Company, New York, USA (1990)
9. [9] M.A. Crisfield; A Consistent Co-rotational Formulation for Non-linear, Three-dimensional, Beam-elements; Comp. Methods Appl. Mech. Engrg., 81 (1990), pp. 131–150
10. [10] J. Argyris; Finite Element Analysis of Two and Three-Dimensional Elasto-Plastic Frames-The Natural Approach, Comp; Methods Appl. Mech. Engrg., 35 (1982), pp. 221–248