Elastoplastic analysis of steel frames with interaction surfaces in stress resultants obtained for multiple linear regression

Resumo

As superfícies de interação em resultantes de tensão podem ser de grande utilidade nos processos de análise estrutural, mas sua obtenção para pórticos planos ou espaciais, geralmente, é em esforços combinados de momentos fletores e normais. A literatura apresenta as superfícies em formas planas, quadriculares, complexas ou mistas para análise não linear de estruturas que apresentam os problemas de instabilidade local e global na execução. O modelo de regressão linear múltipla é um método que permite a obtenção de superfícies de interação em resultantes de tensão a partir de análises de elementos sólidos 3D. As análises elastoplásticas de pórticos planos ou espaciais usando estas superfícies facilitam os processos de análise estrutural para a execução de projetos com melhor segurança estrutural. Neste trabalho, a abordagem será para estruturas metálicas com superfícies em resultantes de tensão obtidas por análises não lineares do modelo de dano de vigas de Timoshenko 3D.

Palavras-chave: Superfícies de interação, vigas de Timoshenko 3D, regressão linear múltipla, resultantes de tensões, pórticos metálicos, análise elastoplástica

Abstract

The interaction surfaces in stress resultants can be of great use in the structural analysis processes, but their obtaining for plane or space frames, generally, is in combined efforts of bending moments and normal. The literature presents the surfaces in plane, quadric, complex or mixed forms for nonlinear analysis of structures that have the problems of local and global instability in the executing. The multiple linear regression model is a method that permit obtain interaction surfaces in the stress resultants from 3D solid element analysis. The plane and space frames elastoplastic analysis using these surfaces facilitate the structural analysis processes for the execution of projects with better structural safety. In this work, the approach will be for metallic structures with stress resultants surfaces obtained by Timoshenko 3D beams damage model non-linear analysis.

Keywords: Interaction curves, 3D Timoshenko beams, multiple linear regression, stress resultants, steel frame, elastoplastic analysis

1. Introdução

A análise elastoplástica com pórticos espaciais ou planos necessita da função de escoamento que controla o término da fase elástica e o estado plástico da estrutura. Usar superfícies de interação em resultantes de tensões é de mais fácil entendimento para os projetistas porque geralmente os esforços seccionais são apresentados nestas resultantes, a saber, momentos, cortantes e axial. O modelo de dano em vigas de Timoshenko em vigas 3D permite obter os esforços em resultantes de tensões com a versatilidade de poder usá-lo para estruturas de concreto armado ou aço, de acordo com os parâmetros adotados. No trabalho de Vieira [1] faz-se a aplicação da tese doutoral de Hanganu [2] para o caso de estruturas de aço com a definição do limite de dano quando o valor da função de endurecimento (${\textstyle k\left(d\right))}$ for igual a máxima resistência ao cortante octaédrica (${\textstyle {\tau }_{oct}^{m{\acute {a}}x}(d)}$). As verificações realizadas demonstraram que os limites plásticos foram atendidos. Este trabalho fará a aplicação das superfícies de interação em pórticos planos e espaciais, de modo que seja verificado se a regressão linear múltipla consegue demostrar se a função é de boa utilidade ou não na análise elastoplástica.

2. Métodos

A pesquisa foi desenvolvida com as formulações apresentadas nas Seções 2.1 a 2.6 e 3 (três) estudos de casos na Seção 2.7.

2.1 Funções de Escoamento

Na literatura, as funções de escoamento de uma seção retangular para combinações de esforços seccionais de momento fletor, axial, cortante e torção para pórticos planos e espaciais são apresentadas por Lubliner [3], Mrázik [4] e Crisfield [5] de forma resumida como:

$f={n}^{2}+{m}_{i}-1=0\,com\,i=x,y$

(1)

onde:

${\textstyle n={\frac {N}{{N}_{xp}}}}$; ${\textstyle {m}_{i}=}$${\frac {{M}_{i}}{{M}_{ip}}}$

(2)

com

${\textstyle N}$ = esforço normal atuante;

${\textstyle {N}_{xp}}$ = esforço axial de plastificação;

${\textstyle {M}_{i}}$ = esforço de momento atuante;

${\textstyle {M}_{ip}}$ = esforço de momento de plastificação;

${\textstyle x\,e\,y}$ = direções dos esforços no sistema de referência.

Outras funções apresentam as interações de esforços seccionais como segue:

$f={n}^{2}+{\frac {s}{\sqrt {3}}}{m}_{i}n+{m}_{i}^{2}-1=0\,$

(3)

$f={n}^{2}+3s{m}_{i}n+{\frac {9}{4}}{m}_{i}^{2}-1=0\,$

(4)

com

$s={\frac {{M}_{i}}{\left|{M}_{ip}\right|}}\,$	(5)
$f={m}_{z}+{\frac {3}{4}}{m}_{y}^{2}-1=0$	(6)

$f={m}_{i}^{2}+{f}_{i}^{2}-1=0$

(7)

com

${f}_{i}={\frac {{F}_{i}}{{F}_{ip}}}$

onde ${\textstyle {F}_{i}}$ = força cortante atuante; ${\textstyle {F}_{ip}}$ = força cortante de plastificação.

Existem dificuldades para a obtenção das funções de escoamento por ensaios experimentais, assim como por modelos computacionais porque as mesmas dependem da geometria da seção transversal e das propriedades do material. A abordagem baseada no modelo de dano em vigas de Timoshenko 3D para a obtenção das superfícies com regressão linear múltipla é apresentada em Vieira e Silva [6] e com mais detalhes em Vieira [1].

2.2 Modelo de dano

Hanganu [2] desenvolve o modelo de dano isotrópico para problemas termicamente estáveis, na configuração material lagrangiana com pequenas deformações e deslocamentos com a descrição do dano pela variável ${\textstyle d}$ em função de uma superfície elementar com um volume de material degradado como na Figura 1:

$d={\frac {{S}_{n}-{\overline {S}}_{n}}{{S}_{n}}}=1-{\frac {{\overline {S}}_{n}}{{S}_{n}}}$

(8)

onde ${\textstyle {S}_{n}}$ = área total da seção; ${\textstyle {\overline {S}}_{n}}$= área resistente efetiva; ${\textstyle {S}_{n}-{\overline {S}}_{n}\,}$ = área ocupada pelas aberturas.

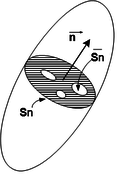
Figura 1. Superfície com dano

A relação de equilíbrio entre a tensão de Cauchy ${\textstyle {\mathit {\boldsymbol {\sigma }}}}$ e a tensão efetiva ${\textstyle {\overline {\mathit {\boldsymbol {\sigma }}}}}$ é mostrada pela equação (9) e a Figura 2:

$\sigma S=\,{\overline {\sigma }}{\boldsymbol {\,}}{\overline {S}}$

(9)

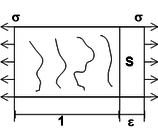
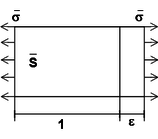
(a) Região real com dano	(b) Região equivalente sem dano
Figura 2. Tensão de Cauchy ${\textstyle \sigma }$ e tensão efetiva ${\textstyle {\overline {\sigma }}}$

Fazendo as relações entre as equações (8) e (9) obtém-se:

${\textstyle {\mathit {\boldsymbol {\sigma }}}=\,{\overline {\mathit {\boldsymbol {\sigma }}}}{\boldsymbol {\,}}\left(1-\right.}$$\left.d\right)=\left(1-d\right){\mathit {\boldsymbol {E}}}\epsilon$

(10)

onde ${\textstyle E}$ = módulo de elasticidade do material; ${\textstyle \epsilon }$ = deformação do material.

Para problemas termicamente estáveis é válida a inequação de Clasius-Planck para representar a dissipação (${\textstyle {\Xi }_{m}}$), sempre crescente, com a potência dissipativa ${\textstyle {\overset {\cdot }{{\Xi }_{m}}}}$ sendo positiva em um ponto para a forma lagrangiana seguinte:

${\overset {\cdot }{{\Xi }_{m}}}={\frac {1}{{m}_{0}}}\,{\mathit {\boldsymbol {\sigma }}}^{T}{\overset {\cdot }{\mathit {\boldsymbol {\epsilon }}}}-$${\overset {\cdot }{\boldsymbol {\Psi }}}=\left({\frac {1}{{m}_{o}}}{\mathit {\boldsymbol {\sigma }}}^{T}-\right.$$\left.{\frac {\partial {\boldsymbol {\Psi }}}{\partial {\mathit {\boldsymbol {\epsilon }}}}}\right){\overset {\cdot }{\mathit {\boldsymbol {\epsilon }}}}-$${\frac {\partial {\boldsymbol {\Psi }}}{\partial d}}{\overset {\cdot }{d}}\geq 0$

(11)

com

${\textstyle {\Psi }_{0}}$ = energia livre elástica de Helmholtz do material sem danos;

${\textstyle \Psi }$ = energia livre de Helmholtz para um modelo com dano isotérmico;

${\textstyle {m}_{0}}$= densidade na configuração material.

O termo ${\textstyle \left({\frac {1}{{m}_{o}}}{\mathit {\boldsymbol {\sigma }}}^{T}-\right.}$$\left.{\frac {\partial {\boldsymbol {\Psi }}}{\partial {\mathit {\boldsymbol {\epsilon }}}}}\right){\overset {\cdot }{\mathit {\boldsymbol {\epsilon }}}}-$${\frac {\partial {\boldsymbol {\Psi }}}{\partial d}}{\overset {\cdot }{d}}\geq 0$ necessita cumprir-se em qualquer variação temporal arbitrária da variável independente ${\textstyle \epsilon }$ . Assim, ${\textstyle {\overset {\cdot }{\epsilon }}}$ pode ser “zero” ou

$\left({\frac {1}{{m}_{o}}}{\mathit {\boldsymbol {\sigma }}}^{T}-{\frac {\partial {\boldsymbol {\Psi }}}{\partial {\mathit {\boldsymbol {\epsilon }}}}}\right)=$$0$

(12)

Desenvolvendo a equação (12) chega-se a:

${\mathit {\boldsymbol {\sigma }}}={m}_{o}{\left({\frac {\partial {\boldsymbol {\Psi }}}{\partial \epsilon }}\right)}^{T}=$$\left(1-d\right){\mathit {\boldsymbol {C}}}^{0}{\mathit {\boldsymbol {\epsilon }}}={\mathit {\boldsymbol {C}}}^{s}{\mathit {\boldsymbol {\epsilon }}}$

(13)

onde ${\textstyle {\mathit {\boldsymbol {C}}}^{s}=\left(1-d\right){\mathit {\boldsymbol {C}}}^{0}}$ é a matriz constitutiva secante do material com dano.

Por consequência o termo restante da equação (11) torna-se em

${\overset {\cdot }{{\Xi }_{m}}}={-{\frac {\partial {\boldsymbol {\Psi }}}{\partial d}}{\overset {\cdot }{d}}{\boldsymbol {=\Psi }}}_{0}{\overset {\cdot }{d}}\geq 0$

(14)

Pelas equações (11) e (14) o dano nunca pode diminuir, ou seja, ${\textstyle {\overset {\cdot }{d}}\geq 0}$.

A função equivalente utilizada no modelo de Hanganu [2] é mostrada na Figura 3 com ${\textstyle {\acute {{f}_{t}}}}$ e ${\textstyle {\acute {{f}_{c}}}}$ como resistências de tração e compressão, respectivamente.

O termo ${\textstyle n}$ é

$n={\frac {{f}_{c}}{{f}_{t}}}$

(15)

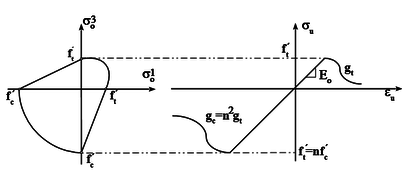
Figura 3. Função limite de dano no plano principal ${\textstyle {\sigma }_{1}-}$${\sigma }_{2}$

A equação que a representa é a seguinte:

${\textstyle {\overline {F}}=\,G\left({\overline {\sigma }}\right)-G({f}_{c})\leq 0}$

(16)

onde ${\textstyle G\left(\chi \right)}$ = função escalar, inversível, positiva e derivada positiva, a determinar.

A função de evolução do limite de dano, Hanganu [2], é mostrada na Figura 4.

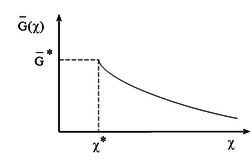
Figura 4. Representação da função ${\textstyle G\left({\overline {\sigma }}\right)}$

O presente trabalho foi focado em estruturas de aço. Desta feita, adotou-se o critério de von Mises que depende de somente um parâmetro, ou seja, a máxima resistência ao cortante octaédrica ${\textstyle {\tau }_{oct}^{m{\acute {a}}x}}$, considerando somente o 2º invariante do tensor desviador de tensões ${\textstyle \,{J}_{2}}$, desprezando a influência do 1º invariante do tensor de tensões e do 3º invariante do tensor desviador de tensões ${\textstyle {J}_{3}}$. De acordo com este critério, se alcança o limite do dano quando o valor da função de endurecimento ${\textstyle \kappa \,(d)}$ alcança a máxima resistência ao cortante octaédrico ${\textstyle {\tau }_{oct}^{m{\acute {a}}x}\,(d)}$

$\kappa \,(d)={\tau }_{oct}^{m{\acute {a}}x}(d)$

(17)

Este critério é representado na equação (18):

$F\left({\mathit {\boldsymbol {J}}}_{\mathit {\boldsymbol {2}}};{\overline {\sigma }}\right)=$$f\left({J}_{2}\right)-{\overline {\sigma }}d={\sqrt {3{\mathit {\boldsymbol {J}}}_{\mathit {\boldsymbol {2}}}}}-$${\overline {\sigma }}d=0$

(18)

2.3 Superfícies de interação por regressão linear múltipla

Na obtenção das superfícies foram feitas várias combinações de carregamentos de forma a ter um grupo de pontos para gerar a superfície proposta, ou seja, pontos que tenham alcançado a superfície de escoamento. Para um dado carregamento, obtém-se um ponto, como por exemplo o ponto 1 da Figura 5, cujas coordenadas (n1, m1) são o esforço axial e momento fletor respectivamente. Mais detalhes sobre os processos de obtenção das superfícies podem ser lidos em Vieira [1].

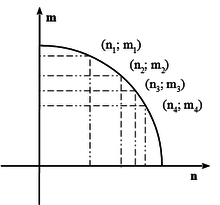
Figura 5. Pontos gerados para criar a função de escoamento (caso uniaxial)

A superfície para o caso da Figura 5 tem a seguinte descrição no formato do modelo de regressão linear múltipla:

$f={\beta }_{1}{n}^{2}+{\beta }_{2}m-1=0$

(19)

onde ${\textstyle n\,e\,m}$ = esforços normal e fletor adimensionais, respectivamente; ${\textstyle {\beta }_{1}\,e\,{\beta }_{2}}$ = coeficientes obtidos pela regressão linear múltipla.

Muitas aplicações da análise de regressão envolvem situações em que há mais de uma variável de regressão. Um modelo de regressão que contém mais de um regressor recebe o nome de modelo de regressão múltipla como por exemplo em Montgomery [7].

O modelo desenvolvido para a formulação pretendida tem a seguinte forma:

$f={\beta }_{1}{{\overline {n}}_{x}}^{{\beta }_{13}}+{\beta }_{2}{{\overline {f}}_{y}}^{{\beta }_{14}}+$${\beta }_{3}{{\overline {f}}_{z}}^{{\beta }_{15}}+{\beta }_{4}{{\overline {m}}_{x}}^{{\beta }_{16}}+$${\beta }_{5}{{\overline {m}}_{y}}^{{\beta }_{17}}+{\beta }_{6}{{\overline {m}}_{z}}^{{\beta }_{18}}+$${\beta }_{7}{{{\overline {n}}_{x}}^{{\beta }_{19}}\,{\overline {m}}_{x}}^{{\beta }_{20}}+$${\beta }_{8}{{{\overline {n}}_{x}}^{{\beta }_{21}}{\overline {m}}_{y}}^{{\beta }_{22}}+$${\beta }_{9}{{{\overline {n}}_{x}}^{{\beta }_{23}}{\overline {m}}_{z}}^{{\beta }_{24}}+$${\beta }_{10}{\,{\overline {m}}_{x}}^{{\beta }_{25}}{{\overline {m}}_{y}}^{{\beta }_{26}}+$${\beta }_{11}{\,{\overline {m}}_{x}}^{{\beta }_{27}}{{\overline {m}}_{z}}^{{\beta }_{28}}+$${\beta }_{12}{{\overline {m}}_{y}}^{{\beta }_{29}}{{\overline {m}}_{z}}^{{\beta }_{30}}-1=$$0$

(20)

onde:

${\textstyle {\overline {n}}_{x}={\frac {{n}_{x}}{{n}_{xp}}}}$ com ${\textstyle {n}_{x}}$ e ${\textstyle {n}_{xp}}$ como o esforço axial atuante e plástico;

${\textstyle {\overline {f}}_{y}={\frac {{f}_{y}}{{f}_{yp}}}}$ com ${\textstyle {f}_{y}}$ e ${\textstyle {f}_{yp}}$ como o esforço cortante atuante e plástico;

${\textstyle {\overline {f}}_{z}={\frac {{f}_{z}}{{f}_{zp}}}}$ com ${\textstyle {f}_{z}}$ e ${\textstyle {f}_{zp}}$ como o esforço cortante atuante e plástico;

${\textstyle {\overline {m}}_{x}={\frac {{m}_{x}}{{m}_{xp}}}}$ com ${\textstyle {m}_{x}}$ e ${\textstyle {m}_{xp}}$ como o momento torçor atuante e plástico;

${\textstyle {\overline {m}}_{y}={\frac {{m}_{y}}{{m}_{yp}}}}$ com ${\textstyle {m}_{y}}$ e ${\textstyle {m}_{yp}}$ como o momento fletor atuante e plástico;

${\textstyle {\overline {m}}_{z}={\frac {{m}_{z}}{{m}_{zp}}}}$ com ${\textstyle {m}_{z}}$ e ${\textstyle {m}_{zp}}$ como o momento fletor atuante e plástico.

Na regressão as observações da equação (20) podem ser apresentadas como

$Y={\beta }_{0}+{\beta }_{1}{x}_{i1}+{\beta }_{2}{x}_{i2}+\cdots +{\beta }_{k}{x}_{ik}+$${\epsilon }_{i}=0\qquad i=1,2,\,\cdots ,n$

(21)

onde

${\textstyle n}$ = número de observações (ensaios);

${\textstyle {\beta }_{k}}$ = coeficientes de regressão da resposta ${\textstyle Y}$;

${\textstyle k\,}$ = variáveis independes (regressores): ${\textstyle {\overline {f}}_{x}}$; ${\textstyle {\overline {f}}_{y}}$; ${\textstyle {\overline {f}}_{z}}$; ${\textstyle \,{\overline {m}}_{x}}$; ${\textstyle \,{\overline {m}}_{y}}$; ${\textstyle {\overline {m}}_{z}}$ e suas combinações;

${\textstyle {\epsilon }_{i}}$ = erros do modelo.

O enfoque matricial da formulação é mostrado como segue:

${\mathit {\boldsymbol {Y}}}={\mathit {\boldsymbol {X\beta }}}+{\mathit {\boldsymbol {\epsilon }}}=$$0$

(22)

com

${\mathit {\boldsymbol {Y=\,}}}\left[{\begin{matrix}{\begin{matrix}{y}_{1}\\{y}_{2}\\\vdots \end{matrix}}\\{y}_{n}\end{matrix}}\right];{\mathit {\boldsymbol {\,X}}}=$$\left[{\begin{matrix}1\\1\\{\begin{matrix}\vdots \\1\end{matrix}}\end{matrix}}{\begin{matrix}{x}_{11}\\{x}_{21}\\{\begin{matrix}\vdots \\{x}_{n1}\end{matrix}}\end{matrix}}{\begin{matrix}{x}_{12}\\{x}_{22}\\{\begin{matrix}\vdots \\{x}_{n2}\end{matrix}}\end{matrix}}{\begin{matrix}\cdots \\\cdots \\{\begin{matrix}\vdots \\\cdots \end{matrix}}\end{matrix}}{\begin{matrix}{x}_{1k}\\{x}_{2k}\\{\begin{matrix}\vdots \\{x}_{nk}\end{matrix}}\end{matrix}}\right]$

(23)

${\mathit {\boldsymbol {\beta =\,}}}\left[{\begin{matrix}{\begin{matrix}{\beta }_{0}\\{\beta }_{1}\\\vdots \end{matrix}}\\{\beta }_{k}\end{matrix}}\right];{\mathit {\boldsymbol {\epsilon }}}=$$\left[{\begin{matrix}{\epsilon }_{1}\\{\epsilon }_{2}\\{\begin{matrix}\vdots \\{\epsilon }_{n}\end{matrix}}\end{matrix}}\right]$

(24)

onde

${\textstyle {\mathit {\boldsymbol {Y}}}}$ = é o vetor de observações de dimensão ${\textstyle (n\times 1)}$;

${\textstyle {\mathit {\boldsymbol {X}}}}$ = é o tensor (matriz) de dimensão ${\textstyle (n\times p)}$ dos níveis das variáveis independentes;

${\textstyle {\mathit {\boldsymbol {\beta }}}}$ = é o vetor dos coeficientes de regressão de dimensão ${\textstyle (p\times 1)}$;

${\textstyle {\mathit {\boldsymbol {\epsilon }}}}$ = é o vetor dos erros aleatórios de dimensão ${\textstyle (n\times 1)}$.

Deve-se encontrar o vetor dos estimadores dos mínimos quadrado, ${\textstyle {\hat {\mathit {\boldsymbol {\beta }}}}}$, que minimiza

${\mathit {\boldsymbol {L}}}=\sum _{i=1}^{n}{\mathit {\boldsymbol {\epsilon }}}_{\mathit {\boldsymbol {i}}}^{\mathit {\boldsymbol {2}}}=$${\mathit {\boldsymbol {\epsilon }}}^{T}{\mathit {\boldsymbol {\epsilon }}}={\left({\mathit {\boldsymbol {Y}}}-{\mathit {\boldsymbol {X\beta }}}\right)}^{T}\left({\mathit {\boldsymbol {Y}}}-\right.$$\left.{\mathit {\boldsymbol {X\beta }}}\right)$

(25)

Desenvolvendo os cálculos chega-se a:

${\hat {\mathit {\boldsymbol {\beta }}}}={\left({\mathit {\boldsymbol {X}}}^{\mathit {\boldsymbol {T}}}{\mathit {\boldsymbol {X}}}\right)}^{-1}{\mathit {\boldsymbol {X}}}^{T}{\mathit {\boldsymbol {Y}}}$

(26)

Mais detalhes dos processos de cálculo podem ser lidos em Montgomery [7].

O modelo ajustado passa a ter a seguinte forma;

${\textstyle {\hat {Y}}_{i}={\hat {\beta }}_{0}+\sum _{j=1}^{n}{\hat {\beta }}_{j}{x}_{ij}}$

(27)

Com ${\textstyle i=1,\,2,\,\cdots ,n}$.

Os testes de hipóteses utilizados são o estatístico de prova “F” e os de coeficientes individuais “t” que podem ser compreendidos com detalhes em Montgomery [7].

As superfícies e seus os resultados estatísticos (Tabelas 1 a 6) que serão usados nas análises elastoplásticas, obtidos em Vieira [1], são as seguintes:

${\textstyle {f}_{1}=1,010{n}^{2}+0,968{m}_{y}^{2}+0,981{m}_{z}^{2}+}$$0,514n{m}_{y}+0,43n{m}_{z}-1=0$

(28)

${\textstyle {f}_{2}=1,158{n}^{2}+1,118{m}_{y}^{2}+1,124{m}_{z}^{2}-1=}$$0$

(29)

${\textstyle {f}_{3}=1,\,014{n}^{2}+0,966{m}_{y}^{2}+0,982{m}_{z}^{2}+}$$0,506n{m}_{y}+0,404n{m}_{z}+0,038{m}_{y}{m}_{z}-1=0$

(30)

${\textstyle {f}_{4}=1,012{n}^{2}+1,027{m}_{z}^{2}-1=0}$

(31)

${\textstyle {f}_{5}=1,\,242{n}^{2}+1,\,087{m}_{z}^{2}-1=0}$

(32)

${\textstyle {f}_{6}=1,089n+\,0,929{m}_{z}^{2}-1=0}$

(33)

Tabela 1. Prova de significância da superfície ${\textstyle {f}_{1}}$

Fonte de variação	Soma dos quadrados	Graus de liberdade	Média dos quadrados	$F$	$P>F$
Regressão	23,860	3	7,953	1183,674	0,000
Erro (resíduo)	0,1400	21	0,007
Total	24,000	24
Prova dos coeficientes individuais
Variáveis	Estimado	Erro	$t$	$P>\left|t\right|$
${n}^{2}$	1,1580	0,0377	30,740	0,000
${m}_{y}^{2}$	1,1180	0,0387	28,900	0,000
${m}_{z}^{2}$	1,1240	0,0381	29,530	0,000

Tabela 2. Prova de significância da superfície ${\textstyle {f}_{2}}$

Fonte de variação	Soma dos quadrados	Graus de liberdade	Média dos quadrados	$F$	$P>F$
Regressão	24,000	5	4,800	55913,754	0,000
Erro (resíduo)	0,000	19	0,000
Total	24,000	24
Prova dos coeficientes individuais
Variáveis	Estimado	Erro	$t$	$P>\left|t\right|$
${n}^{2}$	1,0100	0,0056	179,500	0,000
${m}_{y}^{2}$	0,9680	0,0086	113,100	0,000
${m}_{z}^{2}$	0,9810	0,0085	115,500	0,000
$n{m}_{y}$	0,5140	0,0312	16,500	0,000
$n{m}_{z}$		0,0305	14,100	0,000

Tabela 3. Prova de significância da superfície ${\textstyle {f}_{3}}$

Fonte de variação	Soma dos quadrados	Graus de liberdade	Média dos quadrados	$F$	$P>F$
Regressão	24,000	6	4,000	53308,230	0,000
Erro (resíduo)	0,000	18	0,000
Total	24,000	24
Prova dos coeficientes individuais
Variáveis	Estimado	Erro	$t$	$P>\left|t\right|$
${n}^{2}$	1,0140	0,00552	183,500	0,000
${m}_{y}^{2}$	0,9660	0,00806	119,800	0,000
${m}_{z}^{2}$	0,9820	0,00795	123,500	0,000
$n{m}_{y}$	0,5060	0,02951	17,100	0,000
$n{m}_{z}$	0,4040	0,03146	12,800	0,000
${m}_{y}{m}_{z}$	0,0380	0,01980	1,900	0,000

Tabela 4. Prova de significância da superfície ${\textstyle {f}_{4}}$

Fonte de variação	Soma dos quadrados	Graus de liberdade	Média dos quadrados	$F$	$P>F$
Regressão	12,000	2	6,000	84325,969	0,000
Erro (resíduo)	0,000	10	0,000
Total	12,000	12
Prova dos coeficientes individuais
Variáveis	Estimado	Erro	$t$	$P>\left|t\right|$
${n}^{2}$	1,0120	0,0043	235, 300	0,000
${m}_{z}^{2}$	1,0270	0,0044	233, 800	0,000

Tabela 5. Prova de significância da superfície ${\textstyle {f}_{5}}$

Fonte de variação	Soma dos quadrados	Graus de liberdade	Média dos quadrados	$F$	$P>F$
Regressão	11,960	2	5,979	1455,211	0,000
Erro (resíduo)	0,040	10	0,004
Total	12,000	12
Prova dos coeficientes individuais
Variáveis	Estimado	Erro	$t$	$P>\left|t\right|$
${n}^{2}$	1,2420	0,0309	40,220	0,000
${m}_{z}^{2}$	1,0870	0,0355	30,610	0,000

Tabela 6. Prova de significância da superfície ${\textstyle {f}_{6}}$

Fonte de variação	Soma dos quadrados	Graus de liberdade	Média dos quadrados	$F$	$P>F$
Regressão	11,990	2	5,996	8547,240	0,000
Erro (resíduo)	0,010	10	0,001
Total	12,000	12
Prova dos coeficientes individuais
Variáveis	Estimado	Erro	$t$	$P>\left|t\right|$
$n$	1,0890	0,0112	97,600	0,000
${m}_{z}^{2}$	0,9290	0,0150	62,040	0,000

2.4 Análise elastoplástica de estruturas de pórticos

Uma superfície de interação define o estado último de uma seção transversal e depende dos seguintes fatores:

1. Forma geométrica da seção transversal;

2. Combinação dos esforços seccionais que atuam na seção transversal;

3. Teoria de viga utilizada.

Encontram-se soluções analíticas fechadas para determinados tipos de seções (I, Retangular, etc) com casos especiais de combinações de esforços, tais como momentos fletores e esforço normal Horne [8], Lubliner [3] e Neal [9]. Neste trabalho, assume-se uma superfície descrita na equação (20) em função dos esforços seccionais.

A análise elastoplástica segue os conceitos apresentados no trabalho de Silva [10] com as seguintes considerações;

1) Os esforços seccionais contidos no interior da superfície de interação geram somente deformações elásticas;

2) Os esforços seccionais que estejam na superfície de interação geram deformações plásticas;

3) Os esforços seccionais fora da superfície de interação representam estados de tensões inadmissíveis porque não se leva em conta o caso do endurecimento.

Durante o processo de aplicação do carregamento em passos de carga os esforços seccionais em alguns nós dos elementos da estrutura poderão sair da superfície de interação. Para trazer estes esforços seccionais de volta a superfície utiliza-se o método de Backward Euler que necessita das derivadas primeira e segunda da superfície em relação aos esforços seccionais.

2.4.1 Derivadas de primeira ordem

Baseando-se na equação (20) são obtidas as derivadas de primeira ordem da superfície de interação em relação aos esforços seccionais:

$f={\beta }_{1}{{\overline {f}}_{x}}^{{\beta }_{13}}+{\beta }_{2}{{\overline {f}}_{y}}^{{\beta }_{14}}+$${\beta }_{3}{{\overline {f}}_{z}}^{{\beta }_{15}}+{\beta }_{4}{{\overline {m}}_{x}}^{{\beta }_{16}}+$${\beta }_{5}{{\overline {m}}_{y}}^{{\beta }_{17}}+{\beta }_{6}{{\overline {m}}_{z}}^{{\beta }_{18}}+$${\beta }_{7}{{{\overline {f}}_{x}}^{{\beta }_{19}}\,{\overline {m}}_{x}}^{{\beta }_{20}}+$${\beta }_{8}{{{\overline {f}}_{x}}^{{\beta }_{21}}{\overline {m}}_{y}}^{{\beta }_{22}}+$${\beta }_{9}{{{\overline {f}}_{x}}^{{\beta }_{23}}{\overline {m}}_{z}}^{{\beta }_{24}}+$${\beta }_{10}{\,{\overline {m}}_{x}}^{{\beta }_{25}}{{\overline {m}}_{y}}^{{\beta }_{26}}+$${\beta }_{11}{\,{\overline {m}}_{x}}^{{\beta }_{27}}{{\overline {m}}_{z}}^{{\beta }_{28}}+$${\beta }_{12}{{\overline {m}}_{y}}^{{\beta }_{29}}{{\overline {m}}_{z}}^{{\beta }_{30}}-1=$$0$

${\frac {\partial f}{{f}_{x}}}={\frac {1}{{f}_{x}}}\left(s{f}_{x}\left({\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{19}}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{20}\,}s{m}_{x}{\beta }_{7}{\beta }_{19}+\right.\right.$$\left.\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{\beta 21}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{\beta 22}s{m}_{y}{\beta }_{8}{\beta }_{21}\,+\right.\right.$$\left.\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{23}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{24}}s{m}_{z}{\beta }_{9}{\beta }_{23}+\right.\right.\left.\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{13}}{\beta }_{1}{\beta }_{13}\right)\right)$

(34)

${\frac {\partial f}{{f}_{y}}}={\frac {s{f}_{y}{\beta }_{2}{\left({\frac {{f}_{y}}{{f}_{yp}}}\right)}^{{\beta }_{14}}{\beta }_{14}}{{f}_{y}}}$

(35)

${\frac {\partial f}{{f}_{z}}}={\frac {s{f}_{z}{\beta }_{3}{\left({\frac {{f}_{z}}{{f}_{zp}}}\right)}^{{\beta }_{15}}{\beta }_{15}}{{f}_{z}}}$

(36)

${\frac {\partial f}{{m}_{x}}}={\frac {1}{{m}_{x}}}\left(s{m}_{x}\left({\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{25}}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{26}}s{m}_{y}{\beta }_{10}{\beta }_{25}+\right.\right.$$\left.\left.{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{27}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{28}}s{m}_{z}{\beta }_{11}{\beta }_{27}+\right.\right.$$\left.\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{19}}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{20}}s{f}_{x}{\beta }_{7}{\beta }_{20}+\right.\right.\left.\left.{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{16}}{\beta }_{4}{\beta }_{16}\right)\,\right)\,\,$

(37)

${\frac {\partial f}{{m}_{y}}}={\frac {1}{{m}_{y}}}\left(s{m}_{y}\left({\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{25}}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{26}}s{m}_{x}{\beta }_{10}{\beta }_{26}+\right.\right.$$\left.\left.{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{29}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{30}}s{m}_{z}{\beta }_{12}{\beta }_{29}+\right.\right.$$\left.\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{21}}\,{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{22}}s{f}_{x}{\beta }_{8}{\beta }_{22}+\right.\right.\left.\left.{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{\beta 17}{\beta }_{5}{\beta }_{17}\right)\right)\,\,$

(38)

${\frac {\partial f}{{m}_{z}}}={\frac {1}{{m}_{z}}}\left(s{m}_{z}\left({\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{27}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{28}}s{m}_{x}{\beta }_{11}{\beta }_{28}+\right.\right.$$\left.\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{23}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{24}}s{f}_{x}{\beta }_{9}{\beta }_{24}+\right.\right.$$\left.\left.{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{29}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{30}}s{m}_{y}{\beta }_{12}{\beta }_{30}+\right.\right.\left.\left.{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{18}}{\beta }_{6}{\beta }_{18}\right)\,\right)\,$

(39)

onde ${\textstyle s{f}_{i}={\frac {{f}_{i}}{\left|{f}_{i}\right|}}}$ = sinal do esforço seccional de forças; ${\textstyle s{m}_{i}={\frac {{m}_{i}}{\left|{m}_{i}\right|}}}$ = sinal do esforço seccional de momentos.

A superfície de interação é assumida como um potencial plástico. As componentes são apresentadas na equação (40) na forma matricial para cada nó do elemento do fluxo plástico no nós do elemento durante o processo de carga

${\textstyle {\left\{{\frac {\partial f}{\partial {F}_{j}}}\right\}}_{1}=}$$\left\{{\begin{matrix}{\frac {\partial f}{\partial {F}_{x1}}}\\{\frac {\partial f}{\partial {F}_{y1}}}\\{\frac {\partial f}{\partial {F}_{z1}}}\\{\frac {\partial f}{\partial {M}_{x1}}}\\{\frac {\partial f}{\partial {M}_{y1}}}\\{\frac {\partial f}{\partial {M}_{z1}}}\\{\mathit {\boldsymbol {0}}}\end{matrix}}\right\}$ ; ${\textstyle {\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{2}=}$$\left\{{\begin{matrix}{\mathit {\boldsymbol {0}}}\\{\frac {\partial f}{\partial {F}_{x2}}}\\{\frac {\partial f}{\partial {F}_{y2}}}\\{\frac {\partial f}{\partial {F}_{z2}}}\\{\frac {\partial f}{\partial {M}_{x2}}}\\{\frac {\partial f}{\partial {M}_{y2}}}\\{\frac {\partial f}{\partial {M}_{z2}}}\end{matrix}}\right\}$

(40)

onde ${\textstyle {\mathit {\boldsymbol {0}}}}$ é o vetor nulo de dimensão ${\textstyle (6\times 1)}$.

2.4.2 Derivadas de segunda ordem

As derivadas de segunda ordem expressam o gradiente do vetor de fluxo plástico, obtido pela diferenciação de cada componente do vetores da equação (40). Desenvolvendo-se as derivadas, chega-se a:

Para ${\textstyle \partial {F}_{x}{F}_{k}}$

${\frac {{\partial }^{2}f}{\partial {F}_{x}\partial {F}_{x}}}={\frac {1}{{f}_{x}^{2}}}s{f}_{x}\left({\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{19}}{\beta }_{19}^{2}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{20}}s{m}_{x}{\beta }_{7}+\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{23}}{\beta }_{23}^{2}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{24}}\quad s{m}_{z}{\beta }_{9}+\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{21}}{\beta }_{21}^{2}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{22}}s{m}_{y}{\beta }_{8}-\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{19}}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{20}}s{m}_{x}{\beta }_{7}{\beta }_{19}-\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{23}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{24}}s{m}_{z}{\beta }_{9}{\beta }_{23}-\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{21}}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{22}}s{m}_{y}{\beta }_{8}{\beta }_{21}+\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{13}}{\beta }_{13}^{2}{\beta }_{1}-\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{13}}{\beta }_{1}{\beta }_{13}\right)\quad$

(41)

${\frac {{\partial }^{2}f}{\partial {F}_{x}\partial {F}_{y}}}=0\quad$

(42)

${\frac {{\partial }^{2}f}{\partial {F}_{x}\partial {F}_{z}}}=0\quad$

(43)

${\frac {{\partial }^{2}f}{\partial {F}_{x}\partial {M}_{x}}}={\frac {s{f}_{x}{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{19}}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{20}}{\beta }_{20}s{m}_{x}{\beta }_{7}{\beta }_{19}}{{f}_{x}{m}_{x}}}$

(44)

${\frac {{\partial }^{2}f}{\partial {F}_{x}\partial {M}_{y}}}={\frac {s{f}_{x}{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{21}}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{22}}{\beta }_{22}s{m}_{y}{\beta }_{8}{\beta }_{21}}{{f}_{x}{m}_{y}}}$

(45)

${\frac {{\partial }^{2}f}{\partial {F}_{x}\partial {M}_{z}}}={\frac {s{f}_{x}{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{23}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{24}}{\beta }_{24}s{m}_{z}{\beta }_{9}{\beta }_{23}}{{f}_{x}{m}_{z}}}$

(46)

Para ${\textstyle \partial {F}_{y}{F}_{k}}$

${\frac {{\partial }^{2}f}{\partial {F}_{y}\partial {F}_{x}}}=0\quad$

(47)

${\frac {{\partial }^{2}f}{\partial {F}_{y}\partial {F}_{y}}}={\frac {s{f}_{y}{\beta }_{2}{\left({\frac {{f}_{y}}{{f}_{yp}}}\right)}^{{\beta }_{14}}{\beta }_{14}({\beta }_{14}-1)}{{f}_{y}^{2}}}\quad$

(48)

${\frac {{\partial }^{2}f}{\partial {F}_{y}\partial {F}_{z}}}=0\quad$

(49)

${\frac {{\partial }^{2}f}{\partial {F}_{y}\partial {M}_{x}}}=0\quad$

(50)

${\frac {{\partial }^{2}f}{\partial {F}_{y}\partial {M}_{y}}}=0\quad$

(51)

${\frac {{\partial }^{2}f}{\partial {F}_{y}\partial {M}_{z}}}=0\quad$

(52)

Para ${\textstyle \partial {F}_{z}{F}_{k}}$

${\frac {{\partial }^{2}f}{\partial {F}_{z}\partial {F}_{x}}}=0\quad$

(53)

${\frac {{\partial }^{2}f}{\partial {F}_{z}\partial {F}_{y}}}=0\quad$

(54)

${\frac {{\partial }^{2}f}{\partial {F}_{z}\partial {F}_{z}}}={\frac {s{f}_{z}{\beta }_{3}{\left({\frac {{f}_{z}}{{f}_{zp}}}\right)}^{{\beta }_{15}}{\beta }_{15}({\beta }_{15}-1)\,}{{f}_{z}^{2}}}\,\,$

(55)

${\frac {{\partial }^{2}f}{\partial {F}_{z}\partial {M}_{x}}}=0\quad$

(56)

${\frac {{\partial }^{2}f}{\partial {F}_{z}\partial {M}_{y}}}=0\quad$	(57)
${\frac {{\partial }^{2}f}{\partial {F}_{z}\partial {M}_{z}}}=0\quad$	(58)

Para ${\textstyle \partial {M}_{x}{F}_{k}}$

${\frac {{\partial }^{2}f}{\partial {M}_{x}\partial {F}_{x}}}={\frac {s{f}_{x}{\left({\frac {{f}_{x}}{{f}_{xp}\,\,}}\right)}^{{\beta }_{19}}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{\beta 20}\beta 20\,s{m}_{x}\beta 7\beta 19}{{f}_{x}{m}_{x}}}\quad$

(59)

${\frac {{\partial }^{2}f}{\partial {M}_{x}\partial {F}_{y}}}=0\quad$

(60)

${\frac {{\partial }^{2}f}{\partial {M}_{x}\partial {F}_{z}}}=0\,\,$

(61)

${\frac {{\partial }^{2}f}{\partial {M}_{x}\partial {M}_{x}}}={\frac {1}{{m}_{x}^{2}}}s{m}_{x}\left({\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{25}}{\beta }_{25}^{2}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{26}}s{m}_{y}{\beta }_{10}+\right.$$\left.{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{27}}{\beta }_{27}^{2}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{28}}s{m}_{z}{\beta }_{11}+\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{19}}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{20}}{\beta }_{20}^{2}s{f}_{x}{\beta }_{7}-\right.$$\left.{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{25}}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{26}}s{m}_{y}{\beta }_{10}{\beta }_{25}-\right.$$\left.{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{27}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{28}}s{m}_{z}{\beta }_{11}{\beta }_{27}-\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{19}}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{20}}s{f}_{x}{\beta }_{7}{\beta }_{20}+\right.$$\left.{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{16}}{\beta }_{16}^{2}{\beta }_{4}-\right.$$\left.{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{16}}{\beta }_{4}{\beta }_{16}\right)\,\,$

(62)

${\frac {{\partial }^{2}f}{\partial {M}_{x}\partial {M}_{y}}}={\frac {s{m}_{x}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{25}}\,{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{26}}{\beta }_{26}s{m}_{y}{\beta }_{10}{\beta }_{25}}{{m}_{x}{m}_{y}}}$

(63)

${\frac {{\partial }^{2}f}{\partial {M}_{x}\partial {M}_{z}}}={\frac {s{m}_{x}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{27}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{28}}{\beta }_{28}s{m}_{z}{\beta }_{11}{\beta }_{27}}{{m}_{x}{m}_{z}}}$

(64)

Para ${\textstyle \partial {M}_{y}{F}_{k}}$

${\frac {{\partial }^{2}f}{\partial {M}_{y}\partial {F}_{x}}}={\frac {s{f}_{x}{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{21}}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{22}}{\beta }_{22}s{m}_{y}{\beta }_{8}{\beta }_{21}}{{f}_{x}{m}_{y}}}\,\,$

(65)

${\frac {{\partial }^{2}f}{\partial {M}_{y}\partial {F}_{y}}}=0\quad$

(66)

${\frac {{\partial }^{2}f}{\partial {M}_{y}\partial {F}_{z}}}=0\,\,$

(67)

${\frac {{\partial }^{2}f}{\partial {M}_{y}\partial {M}_{x}}}={\frac {s{m}_{x}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{25}}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{26}}{\beta }_{26}s{m}_{y}{\beta }_{10}{\beta }_{25}}{{m}_{x}{m}_{y}}}\,\,$

(68)

${\frac {{\partial }^{2}f}{\partial {M}_{y}\partial {M}_{y}}}={\frac {1}{{m}_{y}^{2}}}s{m}_{y}\left({\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{25}}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{26}}{\beta }_{26}^{2}s{m}_{x}{\beta }_{10}+\right.$$\left.{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{29}}{\beta }_{29}^{2}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{30}}s{m}_{z}{\beta }_{12}+\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{21}}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{22}}{\beta }_{22}^{2}s{f}_{x}{\beta }_{8}-\right.$$\left.\left({\frac {{m}_{x}}{{m}_{xp}}}\right){\beta }_{25}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{26}}s{m}_{x}{\beta }_{10}{\beta }_{26}-\right.$$\left.{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{29}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{30}}s{m}_{z}{\beta }_{12}{\beta }_{29}-\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{21}}\left({\frac {{m}_{y}}{{m}_{yp}}}\right){\beta }_{22}s{f}_{x}{\beta }_{8}{\beta }_{22}+\right.$$\left.{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{17}}{\beta }_{17}^{2}{\beta }_{5}-\right.$$\left.{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{17}}{\beta }_{5}{\beta }_{17}\right)$

(69)

${\frac {{\partial }^{2}f}{\partial {M}_{y}\partial {M}_{z}}}={\frac {s{m}_{y}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{29}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{30}}{\beta }_{30}s{m}_{z}{\beta }_{12}{\beta }_{29}}{{m}_{y}{m}_{z}}}$

(70)

Para ${\textstyle \partial {M}_{z}{F}_{k}}$

${\frac {{\partial }^{2}f}{\partial {M}_{z}\partial {F}_{x}}}=\,{\frac {s{f}_{x}{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{23}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{24}}{\beta }_{24}s{m}_{z}{\beta }_{9}{\beta }_{23}}{{f}_{x}{m}_{z}}}$

(71)

${\frac {{\partial }^{2}f}{\partial {M}_{z}\partial {F}_{y}}}=0\quad$

(72)

${\frac {{\partial }^{2}f}{\partial {M}_{z}\partial {F}_{z}}}=0\,\,$

(73)

${\frac {{\partial }^{2}f}{\partial {M}_{z}\partial {M}_{x}}}={\frac {s{m}_{x}{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{27}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{28}}{\beta }_{28}s{m}_{z}{\beta }_{11}{\beta }_{27}}{{m}_{x}{m}_{z}}}\quad$

(74)

${\frac {{\partial }^{2}f}{\partial {M}_{z}\partial {M}_{y}}}={\frac {s{m}_{y}{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{29}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{30}}{\beta }_{30}s{m}_{z}{\beta }_{12}{\beta }_{29}}{{m}_{y}{m}_{z}}}$

(75)

${\frac {{\partial }^{2}f}{\partial {M}_{z}\partial {M}_{z}}}={\frac {1}{{m}_{z}^{2}}}s{m}_{z}\left({\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{27}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{28}}{\beta }_{28}^{2}s{m}_{x}{\beta }_{11}+\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{23}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{24}}{\beta }_{24}^{2}s{f}_{x}{\beta }_{9}+\right.$$\left.{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{29}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{30}}{\beta }_{30}^{2}s{m}_{y}{\beta }_{12}-\right.$$\left.{\left({\frac {{m}_{x}}{{m}_{xp}}}\right)}^{{\beta }_{27}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{28}}s{m}_{x}{\beta }_{11}{\beta }_{28}-\right.$$\left.{\left({\frac {{f}_{x}}{{f}_{xp}}}\right)}^{{\beta }_{23}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{24}}s{f}_{x}{\beta }_{9}{\beta }_{24}-\right.$$\left.{\left({\frac {{m}_{y}}{{m}_{yp}}}\right)}^{{\beta }_{29}}{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{30}}s{m}_{y}{\beta }_{12}{\beta }_{30}+\right.$$\left.{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{18}}{\beta }_{18}^{2}{\beta }_{6}-\right.$$\left.{\left({\frac {{m}_{z}}{{m}_{zp}}}\right)}^{{\beta }_{18}}{\beta }_{6}\,{\beta }_{18}\right)$

(76)

As 2ª derivadas na forma matricial podem ser expressas como

${A}_{1}=\left[{\begin{matrix}{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {F}_{x1}\partial {F}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{x1}\partial {F}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{x1}\partial {F}_{z1}}}\\{\frac {{\partial }^{2}f}{\partial {F}_{y1}\partial {F}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{y1}\partial {F}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{y1}\partial {F}_{z1}}}\end{matrix}}&{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {F}_{x1}\partial {M}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{x1}\partial {M}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{x1}\partial {M}_{z1}}}\\{\frac {{\partial }^{2}f}{\partial {F}_{y1}\partial {M}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{y1}\partial {M}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{y1}\partial {M}_{z1}}}\end{matrix}}\\{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {F}_{z1}\partial {F}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{z1}\partial {F}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{z1}\partial {F}_{z1}}}\\{\frac {{\partial }^{2}f}{\partial {M}_{x1}\partial {F}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{x1}\partial {F}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{x1}\partial {F}_{z1}}}\end{matrix}}&{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {F}_{z1}\partial {M}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{z1}\partial {M}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {F}_{z1}\partial {M}_{z1}}}\\{\frac {{\partial }^{2}f}{\partial {M}_{x1}\partial {M}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{x1}\partial {M}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{x1}\partial {M}_{z1}}}\end{matrix}}\\{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {M}_{y1}\partial {F}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{y1}\partial {F}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{y1}\partial {F}_{z1}}}\\{\frac {{\partial }^{2}f}{\partial {M}_{z1}\partial {F}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{z1}\partial {F}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{z1}\partial {F}_{z1}}}\end{matrix}}&{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {M}_{y1}\partial {M}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{y1}\partial {M}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{y1}\partial {M}_{z1}}}\\{\frac {{\partial }^{2}f}{\partial {M}_{z1}\partial {M}_{x1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{z1}\partial {M}_{y1}}}&{\frac {{\partial }^{2}f}{\partial {M}_{z1}\partial {M}_{z1}}}\end{matrix}}\end{matrix}}\right]$

(77)

${\left[{\frac {{\partial }^{2}{\mathit {\boldsymbol {f}}}}{\partial {F}_{j}\partial {F}_{k}}}\right]}_{1}=$$\left[{\begin{matrix}{\mathit {\boldsymbol {A}}}_{\mathit {\boldsymbol {1}}}&{\mathit {\boldsymbol {0}}}\\{\mathit {\boldsymbol {0}}}&{\mathit {\boldsymbol {0}}}\end{matrix}}\right]$

(78)

${A}_{2}=\left[{\begin{matrix}{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {F}_{x2}\partial {F}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{x2}\partial {F}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{x2}\partial {F}_{z2}}}\\{\frac {{\partial }^{2}f}{\partial {F}_{y2}\partial {F}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{y2}\partial {F}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{y2}\partial {F}_{z2}}}\end{matrix}}&{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {F}_{x2}\partial {M}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{x2}\partial {M}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{x2}\partial {M}_{z2}}}\\{\frac {{\partial }^{2}f}{\partial {F}_{y2}\partial {M}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{y2}\partial {M}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{y2}\partial {M}_{z2}}}\end{matrix}}\\{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {F}_{z2}\partial {F}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{z2}\partial {F}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{z2}\partial {F}_{z2}}}\\{\frac {{\partial }^{2}f}{\partial {M}_{x2}\partial {F}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{x2}\partial {F}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{x2}\partial {F}_{z2}}}\end{matrix}}&{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {F}_{z2}\partial {M}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{z2}\partial {M}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {F}_{z2}\partial {M}_{z2}}}\\{\frac {{\partial }^{2}f}{\partial {M}_{x2}\partial {M}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{x2}\partial {M}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{x2}\partial {M}_{z2}}}\end{matrix}}\\{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {M}_{y2}\partial {F}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{y2}\partial {F}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{y2}\partial {F}_{z2}}}\\{\frac {{\partial }^{2}f}{\partial {M}_{z2}\partial {F}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{z2}\partial {F}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{z2}\partial {F}_{z2}}}\end{matrix}}&{\begin{matrix}{\frac {{\partial }^{2}f}{\partial {M}_{y2}\partial {M}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{y2}\partial {M}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{y2}\partial {M}_{z2}}}\\{\frac {{\partial }^{2}f}{\partial {M}_{z2}\partial {M}_{x2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{z2}\partial {M}_{y2}}}&{\frac {{\partial }^{2}f}{\partial {M}_{z2}\partial {M}_{z2}}}\end{matrix}}\end{matrix}}\right]$

(79)

${\left[{\frac {{\partial }^{2}{\mathit {\boldsymbol {f}}}}{\partial {F}_{j}\partial {F}_{k}}}\right]}_{2}=$$\left[{\begin{matrix}{\mathit {\boldsymbol {0}}}&{\mathit {\boldsymbol {0}}}\\{\mathit {\boldsymbol {0}}}&{\mathit {\boldsymbol {A}}}_{\mathit {\boldsymbol {2}}}\end{matrix}}\right]$

(80)

onde ${\textstyle {\mathit {\boldsymbol {0}}}}$ é uma matriz de dimensão ${\textstyle (6\times 6)}$ com elementos nulos.

2.5 Algoritmo de Retorno

O algoritmo de retorno proposto por Silva [10] servirá para trazer de volta os esforços seccionais inadmissíveis, ou seja, os que saem da superfície de interação. O método de backward Euler será utilizado para trazer de volta a superfície estes esforços seccionais. Quando os esforços atingem a superfície se formam as rótulas plásticas.

Assume-se que exista uma combinação de esforços seccionais em um dos nós do elemento que esteja fora da superfície de interação. Usando o método de backward Euler para corrigir o vetor de forças nodais tem-se a seguinte forma:

${\hat {\mathit {\boldsymbol {F}}}}_{i}={\mathit {\boldsymbol {F}}}_{i}^{trial}-{\lambda }_{1}{K}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}$

(81)

onde

${\textstyle {\hat {\mathit {\boldsymbol {F}}}}_{i}}$= vetor de forças nodais corrigido;

${\textstyle {\mathit {\boldsymbol {F}}}_{i}^{trial}}$ = vetor de força nodais estimado;

${\textstyle {\lambda }_{1}}$= multiplicador plástico do nó 1, de forma ${\textstyle {\lambda }_{1}\geq 0}$;

${\textstyle {\mathit {\boldsymbol {K}}}_{ij}}$= matriz de rigidez do elemento;

${\textstyle {\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}}$= vetor de fluxo plástico do nó 1.

O vetor de forças nodais estimado é expressado por:

${\mathit {\boldsymbol {F}}}_{i}^{trial}={\overline {\mathit {\boldsymbol {F}}}}_{i}+{\mathit {\boldsymbol {K}}}_{ij}d{\mathit {\boldsymbol {U}}}_{j}$

(82)

onde ${\textstyle {\overline {\mathit {\boldsymbol {F}}}}_{i}}$ = vetor de forças nodais do último passo de carga convergido; ${\textstyle d{\mathit {\boldsymbol {U}}}_{j}}$ = incrementos do campo de deslocamentos do nó.

O vetor ${\textstyle {F}_{i}^{trial}}$ é obtido da solução elástica dos incrementos de deslocamentos ${\textstyle d{U}_{j}}$ e da matriz de rigidez ${\textstyle {K}_{ij}}$ linear elástica do elemento de viga 3D. O vetor ${\textstyle {\overline {F}}_{i}}$ pode estar dentro, fora ou tocando a superfície de interação. Geralmente, os vetores de forças nodais, estimado (${\textstyle {F}_{i}^{trial}}$) e o corrigido (${\textstyle {\hat {F}}_{i}}$) não estão sobre a superfície de interação quando atingem a fase de escoamento. Usar-se-á um método iterativo para trazer os esforços seccionais a um estado de tensão que esteja na superfície de interação.

O algoritmo irá trabalhar com 2 (duas) possibilidades de formação de rótulas plásticas, ou seja, para 1 (um) nó ou os 2 (dois) nós.

2.5.1 Algoritmo de retorno com 1 (um) vetor

O caso de formação de somente uma rótula plástica no elemento de viga emprega-se um vetor de fluxo plástico correspondente aos esforços seccionais que se encontra fora da superfície de interação, conforme Figura 6.

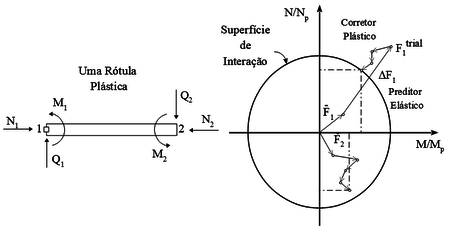
Figura 6. Retorno à superfície com um vetor

O processo iterativo utiliza vetores de fluxo plástico atualizados para aproximar-se da superfície. Este procedimento é chamado de algoritmo de retorno.

Admite-se que os vetores de força nodais ${\textstyle {F}_{i}}$ (atual) e o corrigido ${\textstyle {\hat {F}}_{i}}$ não cumprem o critério de escoamento, ou seja, ${\textstyle f({F}_{i})>1}$ e ${\textstyle f({\hat {F}}_{i})>1.}$

O vetor de forças residuais ${\textstyle {\mathit {\boldsymbol {r}}}_{i}}$ do processo iterativo será como

${\mathit {\boldsymbol {r}}}_{i}={\mathit {\boldsymbol {F}}}_{i}-{\hat {\mathit {\boldsymbol {F}}}}_{i}=$${\mathit {\boldsymbol {F}}}_{i}-\left({\mathit {\boldsymbol {F}}}_{i}^{trial}-{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}\right)$

(83)

Desenvolvendo a equação (83) numa série de Taylor até os termos de 1ª ordem e mantendo o vetor de forças nodais de partida ${\textstyle {\mathit {\boldsymbol {F}}}_{i}^{trial}}$ fixo, obtém-se um novo vetor de forças residuais ${\textstyle {\mathit {\boldsymbol {r}}}_{i}^{n+1}}$, apresentado da seguinte forma:

${\mathit {\boldsymbol {r}}}_{i}^{n+1}={\mathit {\boldsymbol {r}}}_{i}^{n}+d{\mathit {\boldsymbol {F}}}_{i}+$$d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+$${\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{1}d{\mathit {\boldsymbol {F}}}_{k}$

(84)

onde

${\textstyle n=0,1,2,\ldots }$ = passo do processo iterativo.

${\textstyle d{\mathit {\boldsymbol {F}}}_{i}}$ = variação do vetor de forças;

${\textstyle d{\lambda }_{1}}$= variação do multiplicador plástico;

${\textstyle {\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{1}d{\mathit {\boldsymbol {F}}}_{k}}$ = variação do vetor de fluxo (gradiente).

Aplicando a condição de que ${\textstyle {\mathit {\boldsymbol {r}}}_{i}^{n+1}=}$${\mathit {\boldsymbol {0}}}$, a equação (84) torna-se em

${\mathit {\boldsymbol {0}}}={\mathit {\boldsymbol {r}}}_{i}^{n}+d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+$$\left({\delta }_{ik}+{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{1}\right)d{\mathit {\boldsymbol {F}}}_{k}$

(85)

onde ${\textstyle {\delta }_{ik}}$ = Delta de Kronecker.

Definindo-se o termo

${\mathit {\boldsymbol {Q}}}_{ik}=\left({\delta }_{ik}+{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{1}\right)$

(86)

A equação (85), torna-se:

${\mathit {\boldsymbol {0}}}={\mathit {\boldsymbol {r}}}_{i}^{n}+d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+$${Q}_{ik}d{\mathit {\boldsymbol {F}}}_{k}$

(87)

Obtendo os termos da variação do vetor de força, chega-se a:

${Q}_{ik}d{\mathit {\boldsymbol {F}}}_{k}=-\left({\mathit {\boldsymbol {r}}}_{i}^{n}+d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}\right)$

(88)

$d{\mathit {\boldsymbol {F}}}_{k}=-{Q}_{ik}^{-1}\left({\mathit {\boldsymbol {r}}}_{i}^{n}+d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}\right)$

(89)

Expandindo a superfície de interação, ${\textstyle {\mathit {\boldsymbol {f}}}}$, numa série de Taylor até os termos de 1ª ordem entorno do vetor do vetor de forças nodais final (${\textstyle {F}_{k})}$, obtém-se:

${\mathit {\boldsymbol {f}}}_{1}^{n+1}={\mathit {\boldsymbol {f}}}_{1}^{n}+{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}d{\mathit {\boldsymbol {F}}}_{k}$

(90)

Tomando-se ${\textstyle {\mathit {\boldsymbol {f}}}_{1}^{n+1}={\mathit {\boldsymbol {0}}}}$ e desenvolvendo a equação (89) paro obter o multiplicador plástico, chega-se a:

${\mathit {\boldsymbol {f}}}_{1}^{n}=-{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}d{\mathit {\boldsymbol {F}}}_{k}$

(91)

${\mathit {\boldsymbol {f}}}_{1}^{n}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}\left[{Q}_{ik}^{-1}\left({\mathit {\boldsymbol {r}}}_{i}^{n}+d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}\right)\right]$

(92)

${\mathit {\boldsymbol {f}}}_{1}^{n}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}{\mathit {\boldsymbol {r}}}_{i}^{n}+$${\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}$

(93)

${\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}=$${\mathit {\boldsymbol {f}}}_{1}^{n}-{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}{\mathit {\boldsymbol {r}}}_{i}^{n}$

(94)

$d{\lambda }_{1}={\frac {{\mathit {\boldsymbol {f}}}_{1}^{n}-{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}{\mathit {\boldsymbol {r}}}_{i}^{n}}{{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}}}$

(95)

O processo iterativo termina quando são alcançados os critérios de parada adotados:

${r}^{norm}={\sqrt {\frac {\left\|{\mathit {\boldsymbol {r}}}_{i}\right\|}{\left\|{\mathit {\boldsymbol {F}}}_{i}^{trial}\right\|}}}<Tol$ ${\textstyle {\mathit {\boldsymbol {f}}}^{norm}=\left|{\mathit {\boldsymbol {f}}}-\right.}$$\left.1\right|<Tol$

(96)

onde

${\textstyle \left\|{\mathit {\boldsymbol {r}}}_{i}\right\|}$ = norma euclidiana do vetor de forças nodais;

${\textstyle \left\|{\mathit {\boldsymbol {F}}}_{i}^{trial}\right\|}$ = norma euclidiana do vetor de forças estimado;

${\textstyle {\mathit {\boldsymbol {f}}}^{norm}}$= vetor resíduo da superfície de interação;

${\textstyle Tol}$ = tolerância adotada.

2.5.2 Algoritmo de retorno com 2 (dois) vetores

O caso da existência de duas rótulas plástica no elemento de viga usa 2 (dois) vetores de fluxo plástico, um para cada nó. O vetores seguem a premissa de que

${\textstyle {\mathit {\boldsymbol {f}}}_{\mathit {\boldsymbol {1}}}({F}_{j})>1;\,{\mathit {\boldsymbol {f}}}_{\mathit {\boldsymbol {2}}}({F}_{j})>1}$

(97)

Durante o processo iterativo, usa-se dois vetores de fluxo para se aproximar da superfície de interação. Este procedimento é chamado algoritmo de retorno com 2 (dois) vetores. A interpretação geométrica é vista na Figura 7.

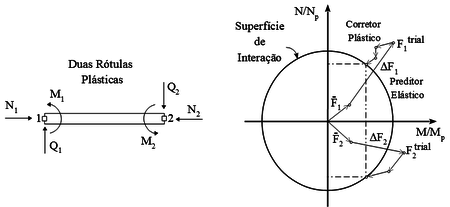
Figura 7. Retorno à superfície com dois vetores

O vetor nodal de partida é similar a equação (82). O vetor de forças nodais para os dois nós corrigido é expressado como

${\hat {\mathit {\boldsymbol {F}}}}_{i}={\mathit {\boldsymbol {F}}}_{i}^{trial}-{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}-$${\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{2}$

(98)

onde ${\textstyle {\lambda }_{1}}$ e ${\textstyle {\lambda }_{2}}$ são os multiplicadores plásticos.

O vetor resíduo das forças tem a forma seguinte:

${\mathit {\boldsymbol {r}}}_{i}={\mathit {\boldsymbol {F}}}_{i}-{\hat {\mathit {\boldsymbol {F}}}}_{i}={\mathit {\boldsymbol {F}}}_{i}-\left(({\mathit {\boldsymbol {F}}}_{i}^{trial}-{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}-{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{2}\right)$

(99)

O vetor novo em função da série de Taylor com termos de 1ª ordem e ${\textstyle {\mathit {\boldsymbol {F}}}_{i}^{trial}}$ fixo é apresentado:

${\mathit {\boldsymbol {r}}}_{i}^{n+1}={\mathit {\boldsymbol {r}}}_{i}^{n}+d{\mathit {\boldsymbol {F}}}_{i}+$$d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+$${\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{1}d{\mathit {\boldsymbol {F}}}_{k}+$$d{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}+$${\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{2}d{\mathit {\boldsymbol {F}}}_{k}$

(100)

Com a condição que ${\textstyle {\mathit {\boldsymbol {r}}}_{i}^{n+1}=}$${\mathit {\boldsymbol {0}}}$, chega-se a:

${\mathit {\boldsymbol {0}}}={\mathit {\boldsymbol {r}}}_{i}^{n}+d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+$$d{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}+$$\left({\delta }_{ik}+{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{1}+\right.$$\left.{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{2}\right)d{\mathit {\boldsymbol {F}}}_{k}$

(101)

Adotando-se:

${\mathit {\boldsymbol {Q}}}_{ik}=\left({\delta }_{ik}+{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{1}+\right.$$\left.{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{\mathit {\boldsymbol {2}}}{\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}\partial {\mathit {\boldsymbol {F}}}_{k}}}\right\}}_{2}\right)$

(102)

Isolando o termo ${\textstyle d{\mathit {\boldsymbol {F}}}_{k}}$ da equação (101), obtém-se:

$d{\mathit {\boldsymbol {F}}}_{k}=-{Q}_{ik}^{-1}\left({\mathit {\boldsymbol {r}}}_{i}^{n}+d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+d{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}\right)$

(103)

Os termos iterativos da função de escoamento (superfícies) são apresentados como

${\mathit {\boldsymbol {f}}}_{1}^{n+1}={\mathit {\boldsymbol {f}}}_{1}^{n}+{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}d{\mathit {\boldsymbol {F}}}_{k}$ $\,{\mathit {\boldsymbol {f}}}_{2}^{n+1}={\mathit {\boldsymbol {f}}}_{2}^{n}+{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}d{\mathit {\boldsymbol {F}}}_{k}$

(104)

Impondo o critério de que ${\textstyle {\mathit {\boldsymbol {f}}}_{1}^{n+1}=}$${\mathit {\boldsymbol {0}}}$ e ${\textstyle \,{\mathit {\boldsymbol {f}}}_{2}^{n+1}=}$${\mathit {\boldsymbol {0}}}$ e desenvolvendo a equação (102), chega-se a:

${\mathit {\boldsymbol {f}}}_{1}^{n}=-{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}d{\mathit {\boldsymbol {F}}}_{k}$ ${\mathit {\boldsymbol {f}}}_{2}^{n}=-{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}d{\mathit {\boldsymbol {F}}}_{k}$

(105)

${\mathit {\boldsymbol {f}}}_{1}^{n}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}\left[{Q}_{ik}^{-1}\left({\mathit {\boldsymbol {r}}}_{i}^{n}+d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+d{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}\right)\right]$ ${\mathit {\boldsymbol {f}}}_{2}^{n}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}\left[{Q}_{ik}^{-1}\left({\mathit {\boldsymbol {r}}}_{i}^{n}+d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+d{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}\right)\right]$

(106)

${\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+$${\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}d{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}=$${\mathit {\boldsymbol {f}}}_{1}^{n}-{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}{\mathit {\boldsymbol {r}}}_{i}^{n}$

(107)

${\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}{Q}_{ik}^{-1}d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}+$${\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}{Q}_{ik}^{-1}d{\lambda }_{2}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}=$${\mathit {\boldsymbol {f}}}_{2}^{n}-{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}{Q}_{ik}^{-1}{\mathit {\boldsymbol {r}}}_{i}^{n}$

(108)

Desenvolvendo o sistema de equações (107) e (108) no sistema matricial, obtêm-se os seguintes temos:

$\left[{\begin{matrix}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}&{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}\\{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}{Q}_{ik}^{-1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}&{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}{Q}_{ik}^{-1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}\end{matrix}}\right]\left\{{\begin{matrix}d{\lambda }_{1}\\d{\lambda }_{2}\end{matrix}}\right\}=$$\left\{{\begin{matrix}{\mathit {\boldsymbol {f}}}_{1}^{n}-{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{1}{Q}_{ik}^{-1}{\mathit {\boldsymbol {r}}}_{i}^{n}\\{\mathit {\boldsymbol {f}}}_{2}^{n}-{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{\mathit {\boldsymbol {j}}}}}\right\}}_{2}{Q}_{ik}^{-1}{\mathit {\boldsymbol {r}}}_{i}^{n}\end{matrix}}\right\}$

(109)

Reapresentando a equação (109) na forma sintética:

$\left[{\begin{matrix}{a}_{11}&{a}_{12}\\{a}_{21}&{a}_{22}\end{matrix}}\right]\left\{{\begin{matrix}d{\lambda }_{1}\\d{\lambda }_{2}\end{matrix}}\right\}=$$\left\{{\begin{matrix}{b}_{1}\\{b}_{2}\end{matrix}}\right\}$

(110)

A solução do sistema da equação (110) é a seguinte:

$\left\{{\begin{matrix}d{\lambda }_{1}\\d{\lambda }_{2}\end{matrix}}\right\}=\left[{\begin{matrix}{\frac {{a}_{22}{b}_{1}-{a}_{12}{b}_{2}}{{a}_{11}{a}_{22}-{a}_{12}{a}_{21}}}\\{\frac {{a}_{11}{b}_{2}-{a}_{21}{b}_{1}}{{a}_{11}{a}_{22}-{a}_{12}{a}_{21}}}\end{matrix}}\right]$

(111)

O processo iterativo segue procedimentos similares ao caso com um 1 (um) vetor:

${r}^{norm}={\sqrt {\frac {\left\|{\mathit {\boldsymbol {r}}}_{i}\right\|}{\left\|{\mathit {\boldsymbol {F}}}_{i}^{trial}\right\|}}}<Tol$ ${\mathit {\boldsymbol {f}}}_{1}^{norm}=\left|{\mathit {\boldsymbol {f}}}_{\mathit {\boldsymbol {1}}}-\right.$$\left.1\right|<Tol$ ${\textstyle {\mathit {\boldsymbol {f}}}_{2}^{norm}=\left|{\mathit {\boldsymbol {f}}}_{\mathit {\boldsymbol {2}}}-\right.}$$\left.1\right|<Tol$

(112)

2.6 Matriz de rigidez consistente

O processo iterativo utiliza o método de Newton-Raphson para determinar a configuração de equilíbrio do sistema estrutural. A manutenção da convergência quadrática faz necessário a obtenção de uma matriz de rigidez consistente para os 2 (dois) vetores. Uma rótula plástica usará o algoritmo com um vetor e para 2 (duas) o algoritmo com dois vetores.

2.6.1 Algoritmo de retorno com um vetor

Usando a equação (81) e (82) como ponto de partida:

${\mathit {\boldsymbol {F}}}_{i}={\mathit {\boldsymbol {F}}}_{i}^{trial}-{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{1}$ ${\mathit {\boldsymbol {F}}}_{i}^{trial}={\overline {\mathit {\boldsymbol {F}}}}_{i}+{\mathit {\boldsymbol {K}}}_{ij}d{\mathit {\boldsymbol {U}}}_{j}$ com ${\textstyle {\lambda }_{1}>0}$

(113)

Aplicando-se o diferencial total na equação (113), chega-se a:

$d{\mathit {\boldsymbol {F}}}_{i}=d({\overline {F}}_{i}+{\mathit {\boldsymbol {K}}}_{ij}d{\mathit {\boldsymbol {U}}}_{j})-$$d\left({\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{1}\right)d{F}_{k}$

(114)

$d{\mathit {\boldsymbol {F}}}_{i}=d{\overline {F}}_{i}+{\mathit {\boldsymbol {K}}}_{ij}d{\mathit {\boldsymbol {U}}}_{j}-$$d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{1}-$${\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{2}{\mathit {\boldsymbol {f}}}}{\partial {F}_{j}\partial {F}_{k}}}\right\}}_{1}d{F}_{k}$

(115)

Adotando ${\textstyle \,d{\overline {F}}_{i}={\mathit {\boldsymbol {0}}}}$

${\mathit {\boldsymbol {0}}}={\mathit {\boldsymbol {K}}}_{ij}d{\mathit {\boldsymbol {U}}}_{j}-$$d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{1}-$$d{F}_{i}-{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{2}{\mathit {\boldsymbol {f}}}}{\partial {F}_{j}\partial {F}_{k}}}\right\}}_{1}d{F}_{k}$

(116)

Isolando o termo ${\textstyle d{F}_{k}}$

${\mathit {\boldsymbol {0}}}={\mathit {\boldsymbol {K}}}_{ij}d{\mathit {\boldsymbol {U}}}_{j}-$$d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{1}-$$\left({\delta }_{ik}+{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {{\partial }^{2}{\mathit {\boldsymbol {f}}}}{\partial {F}_{j}\partial {F}_{k}}}\right\}}_{1}\right)d{F}_{k}$

(117)

Usando ${\textstyle {Q}_{ik}}$ (equação (86)):

${\mathit {\boldsymbol {0}}}={\mathit {\boldsymbol {K}}}_{ij}d{\mathit {\boldsymbol {U}}}_{j}-$$d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{1}-$${\mathit {\boldsymbol {Q}}}_{ik}d{F}_{k}$

(118)

Isolando o termo ${\textstyle d{F}_{k}}$:

$d{F}_{k}={\mathit {\boldsymbol {Q}}}_{ik}^{-1}\left({\mathit {\boldsymbol {K}}}_{ij}d{\mathit {\boldsymbol {U}}}_{j}-d{\lambda }_{1}{\mathit {\boldsymbol {K}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{1}\right)$

(119)

Adotando o termo:

${\mathit {\boldsymbol {R}}}_{ij}={\mathit {\boldsymbol {Q}}}_{ik}^{-1}{\mathit {\boldsymbol {K}}}_{ij}$

(120)

A equação (119) torna-se em:

$d{\mathit {\boldsymbol {F}}}_{i}={\mathit {\boldsymbol {R}}}_{ij}\left(d{\mathit {\boldsymbol {U}}}_{j}-d{\lambda }_{1}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}\right)$

(121)

O vetor de forças nodais final tem que cumprir a condição ${\textstyle {\mathit {\boldsymbol {f}}}_{\mathit {\boldsymbol {1}}}\left({F}_{i}\right)=}$${\mathit {\boldsymbol {0}}}$. Desta maneira, diferencia-se a equação (121) e obtém-se:

${\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}d{\mathit {\boldsymbol {F}}}_{i}=$${\mathit {\boldsymbol {0}}}$

(122)

${\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}d{F}_{i}=$${\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}{\mathit {\boldsymbol {R}}}_{ij}\left(d{\mathit {\boldsymbol {U}}}_{j}-d{\lambda }_{1}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{1}\right)$

(123)

Isolando o termo ${\textstyle d{\lambda }_{1}}$:

$d{\lambda }_{1}={\frac {{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{i}}}\right\}}_{1}{\mathit {\boldsymbol {R}}}_{ij}d{\mathit {\boldsymbol {U}}}_{j}}{{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{i}}}\right\}}_{1}{\mathit {\boldsymbol {R}}}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{j}}}\right\}}_{1}}}$

(124)

A matriz de rigidez consistente é obtida, trabalhando com as equações (124) e (121):

$d{\mathit {\boldsymbol {F}}}_{i}=\left({\mathit {\boldsymbol {R}}}_{ij}-{\frac {{\mathit {\boldsymbol {R}}}_{im}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{m}}}\right\}}_{1}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{n}}}\right\}}_{1}{\mathit {\boldsymbol {R}}}_{nj}}{{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{m}}}\right\}}_{1}{\mathit {\boldsymbol {R}}}_{mn}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{n}}}\right\}}_{1}}}\right)d{\mathit {\boldsymbol {U}}}_{j}$

(125)

com

${\mathit {\boldsymbol {K}}}_{ij}^{AL}=\left({\mathit {\boldsymbol {R}}}_{ij}-{\frac {{\mathit {\boldsymbol {R}}}_{im}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{m}}}\right\}}_{1}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{n}}}\right\}}_{1}{\mathit {\boldsymbol {R}}}_{nj}}{{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{m}}}\right\}}_{1}{\mathit {\boldsymbol {R}}}_{mn}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {F}_{n}}}\right\}}_{1}}}\right)$

(126)

2.6.2 Algoritmo com dois vetores de retorno

Os procedimentos similares são realizados para obter a matriz de rigidez consistente para dois vetores como por exemplo Silva [10] e Vieira [6].

A formulação para os dois vetores tem a seguinte forma:

$d{\mathit {\boldsymbol {F}}}_{i}={\mathit {\boldsymbol {R}}}_{ij}\left({\begin{matrix}d{\mathit {\boldsymbol {U}}}_{j}-d{\lambda }_{1}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}\\-d{\lambda }_{2}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{2}\end{matrix}}\right)$

(127)

As condições do vetor de forças nodais final são que

${\textstyle {\mathit {\boldsymbol {f}}}_{\mathit {\boldsymbol {1}}}\left({F}_{i}\right)=}$${\mathit {\boldsymbol {0}}}$ e ${\textstyle {\mathit {\boldsymbol {f}}}_{\mathit {\boldsymbol {2}}}\left({F}_{i}\right)=}$${\mathit {\boldsymbol {0}}}$

(128)

Os termos dos multiplicadores plásticos são os seguintes:

$\left\{{\begin{matrix}d{\lambda }_{1}\\d{\lambda }_{2}\end{matrix}}\right\}=\left[{\begin{matrix}{\frac {{c}_{1}{b}_{22}-{c}_{2}{b}_{12}}{{b}_{11}{b}_{22}-{b}_{12}{b}_{21}}}\\{\frac {{c}_{2}{b}_{11}-{c}_{1}{b}_{21}}{{b}_{11}{b}_{22}-{b}_{12}{b}_{21}}}\end{matrix}}\right]$

(129)

com

${c}_{1}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{i}}}\right\}}_{1}{R}_{ij}d{U}_{j}$ ${c}_{2}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{i}}}\right\}}_{2}{R}_{ij}d{U}_{j}$ ${b}_{11}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{i}}}\right\}}_{1}{R}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}$ ${b}_{12}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{i}}}\right\}}_{1}{R}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{2}$ ${b}_{21}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{i}}}\right\}}_{2}{R}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{1}$ ${b}_{22}={\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{i}}}\right\}}_{2}{R}_{ij}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{j}}}\right\}}_{2}$

(130)

Se ocorrer o caso dos multiplicadores plásticos for ${\textstyle d{\lambda }_{1}<0}$ ou ${\textstyle d{\lambda }_{2}<0}$ será atribuído o valor zero e desativa-se a rótula plástica correspondente ao caso negativo.

Desenvolvendo os termos das equações (127) e (129):

${\mathit {\boldsymbol {K}}}_{ij}^{AL}={\mathit {\boldsymbol {R}}}_{ij}-\left({d}_{1}{R}_{im}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{m}}}\right\}}_{1}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{n}}}\right\}}_{1}{\mathit {\boldsymbol {R}}}_{nj}-\right.$$\left.{d}_{2}{R}_{im}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{m}}}\right\}}_{1}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{n}}}\right\}}_{2}{\mathit {\boldsymbol {R}}}_{nj}\right)-$$\left({d}_{3}{R}_{im}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{m}}}\right\}}_{2}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{n}}}\right\}}_{2}{\mathit {\boldsymbol {R}}}_{nj}-\right.$$\left.{d}_{4}{R}_{im}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{m}}}\right\}}_{2}{\left\{{\frac {\partial {\mathit {\boldsymbol {f}}}}{\partial {\mathit {\boldsymbol {F}}}_{n}}}\right\}}_{1}{\mathit {\boldsymbol {R}}}_{nj}\right)$

(131)

com

${d}_{1}={\frac {{b}_{22}}{{b}_{11}{b}_{22}-{b}_{12}{b}_{21}}}$ ${d}_{2}={\frac {{b}_{12}}{{b}_{11}{b}_{22}-{b}_{12}{b}_{21}}}$ ${d}_{3}={\frac {{b}_{11}}{{b}_{11}{b}_{22}-{b}_{12}{b}_{21}}}$ ${d}_{4}={\frac {{b}_{21}}{{b}_{11}{b}_{22}-{b}_{12}{b}_{21}}}$

(132)

2.7 Caracterização dos casos

Os casos abordam a formulação apresentada com o intuito de verificar a viabilidade das superfícies de interação obtidas pelo modelo de dano com a regressão linear múltipla. Também, pretende-se usar as informações estatísticas para comparar a qualidade das funções obtidas e suas análises elastoplásticas.

O caso 1 é baseado nos dados do trabalho de Thai e Kim [11] que trata de um pórtico plano, conforme Figura 8 e Tabelas 7 a 10 que apresentam as características do caso como coordenadas, características físicas, propriedades do material e cargas aplicadas, respectivamente.

Propriedades do Pórtico Plano (PP)

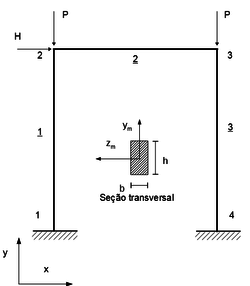
Figura 8. Pórtico Plano de Thai e Kim

Tabela 7. Coordenadas do pórtico plano - Thai e Kim

Nó	X (cm)	Y (cm)	Z (cm)
1	0,000	0,000	0,000
2	0,000	1000,000	0,000
3	1000,000	1000,000	0,000
4	1000,000	0,000	0,000

Tabela 8. Características físicas do pórtico plano - Thai e Kim

Elem.	No I	No F	E (kN/cm$^{\bf {2}}$)	${\boldsymbol {\sigma }}_{y}$ (kN/cm$^{\bf {2}}$)	${\boldsymbol {\nu }}$
1	1	2	1961,3	9,8	0,170
2	2	3
3	3	4

Os termos da Tabela 8 tem a seguinte descrição: ${\textstyle E}$ = módulo de elasticidade; ${\textstyle \nu }$ = coeficiente de Poisson; ${\textstyle {\sigma }_{y}}$= tensão de escoamento.

Tabela 9. Propriedades do material do pórtico plano - Thai e Kim

Elemento	Seção transversal
1,2,3 e 4	$A=800,000\,c{m}^{2}$
	${\textstyle b=20\,cm}$ e ${\textstyle h=}$$40\,cm$
	${I}_{z}=106666,667\,c{m}^{4}$
	${F}_{xp}=7840,000\,kN$
	${M}_{zp}=78400,000\,kN\times cm$

As cargas aplicadas são as seguintes:

Tabela 10. Cargas aplicadas do pórtico plano - Thai e Kim

Nó	Dir	Valor (kN)
2	${F}_{X}$	1,000
2	${F}_{y}$	-1,000
3	${F}_{y}$	-1,000

As funções utilizadas no caso são as ${\textstyle {f}_{4}}$, ${\textstyle {f}_{5}}$ e ${\textstyle {f}_{6}}$, equações (31), (32) e (33), respectivamente.

O caso 2 é baseado no pórtico espacial com dados dos trabalhos de Thai e Kim [11] e Argyris [12], conforme a Figura 9.

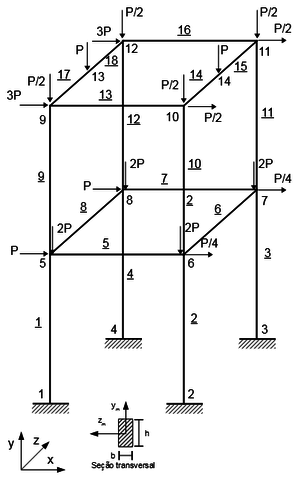
Figura 9 – Pórtico espacial de 2 (dois) pavimentos

As propriedades do caso são apresentadas nas Tabela 11 a Tabela 13.

Tabela 11. Coordenadas do pórtico espacial - Thai e Kim

Nó	X (cm)	Y (cm)	Z (cm)
1	0,000	0,000	0,000
2	400,000	0,000	0,000
3	400,000	0,000	300,000
4	0,000	0,000	300,000
5	0,000	400,000	0,000
6	400,000	400,000	0,000
7	400,000	400,000	300,000
8	0,000	400,000	300,000
9	0,000	800,000	0,000
10	400,000	800,000	0,000
11	400,000	800,000	300,000
12	0,000	800,000	300,000
13	0,000	800,000	150,000
14	400,000	800,000	150,000

Tabela 12. Características físicas do pórtico espacial - Thai e Kim

Elem.	No I	No F	E (kN/cm$^{2}$)	${\boldsymbol {\sigma }}_{y}$ (kN/cm$^{2}$)	${\boldsymbol {\nu }}$
1	1	5	1961,3	9,8	0,170
2	2	6
3	3	7
4	4	8
5	5	6
6	6	7
7	7	8
8	8	5
9	5	9
10	6	10
11	7	11
12	8	12
13	9	10
14	10	14
15	14	11
16	11	12
17	9	13
18	12	13

Tabela 13. Propriedades do material do pórtico espacial - Thai e Kim

Elemento	Seção transversal
1 a 18	$A=800,000\,c{m}^{2}$
	${\textstyle b=20\,cm}$ e ${\textstyle h=}$$40\,cm$
	${I}_{z}=1,067\times {10}^{5}\,c{m}^{4}$
	${I}_{x}=1,067\times {10}^{5}\,c{m}^{4}$
	${I}_{y}=2,667\times {10}^{4}\,c{m}^{4}$
	${M}_{zp}=7,840\times {10}^{4}\,kN\times cm$
	${M}_{xp}=6,533\times {10}^{4}\,kN\times cm$
	${M}_{yp}=3,920\times {10}^{4}\,kN\times cm$
	${F}_{zp}=4,526\times {10}^{3}\,kN$
	${F}_{xp}=7,840\times {10}^{3}\,kN$
	${F}_{yp}=4,526\times {10}^{3}\,kN$

As cargas aplicadas são as seguintes:

Tabela 14. Cargas aplicadas do pórtico espacial - Thai e Kim

Nó	${\boldsymbol {F}}_{\boldsymbol {x}}$ (kN)	${\textstyle {\boldsymbol {F}}_{\boldsymbol {y}}}$ (kN)	${\boldsymbol {F}}_{\boldsymbol {z}}$ (kN)
5	1,000	-2,000	0,000
6	0,250	-2,000	0,000
7	0,250	-2,000	0,000
8	1,000	-2,000	0,000
9	3,000	-0,500	0,000
10	0,500	-0,500	0,000
11	0,500	-0,500	0,000
12	3,000	-0,500	0,000
13	0,000	-1,000	0,000
14	0,000	-1,000	0,000

As funções utilizadas no caso são as ${\textstyle {f}_{1}}$, ${\textstyle {f}_{2}}$ e ${\textstyle {f}_{3}}$, equações (28), (29) e (30), respectivamente.

O caso 3 é baseado no pórtico espacial com dados dos trabalhos de Argyris et al [12] e Park e Lee [13], conforme a Figura 10.

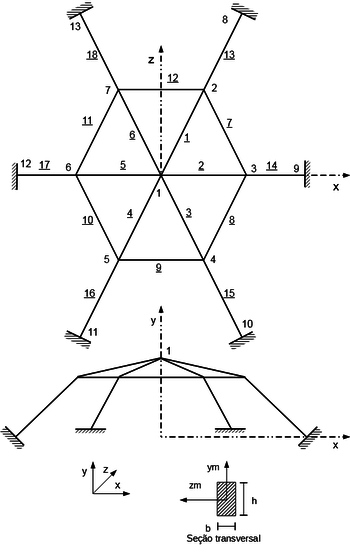
Figura 10. Pórtico em domo - Argyris et al.

As propriedades do caso são apresentadas nas Tabela 15 a Tabela 18.

Tabela 15. Coordenadas do pórtico em domo - Argyris et al.

Nó	X (cm)	Y (cm)	Z (cm)
1	0,000	610,000	0,000
2	628,500	455,000	1088,500
3	1257,000	455,000	0,000
4	628,500	455,000	-1088,500
5	-628,500	455,000	-1088,500
6	-1257,000	455,000	0,000
7	-628,500	455,000	1088,500
8	1219,000	0,000	2111,500
9	2438,000	0,000	0,000
10	1219,000	0,000	-2111,500
11	-1219,000	0,000	-2111,500
12	-2438,000	0,000	0,000
13	-1219,000	0,000	2111,500

Tabela 16. Características físicas do pórtico em domo - Argyris et al.

Elem.	No I	No F	E (kN/cm$^{2}$)	${\boldsymbol {\sigma }}_{y}$ (kN/cm$^{2}$)	${\boldsymbol {\nu }}$
1	1	2	2068,0	8,0	0,1716
2	1	3
3	1	4
4	1	5
5	1	6
6	1	7
7	2	3
8	3	4
9	5	4
10	5	6
11	6	7
12	7	2
13	2	8
14	3	9
15	4	10
16	5	11
17	6	12
18	7	13

Tabela 17. Propriedades do material do pórtico em domo - Argyris et al.

Elemento	Seção transversal
1 a 18	$A=9272,000\,c{m}^{2}$
	${\textstyle b=76\,cm}$ e ${\textstyle h=}$$122\,cm$
	${I}_{z}=1,150\times {10}^{7}\,c{m}^{4}$
	${I}_{x}=1,596\times {10}^{7}\,c{m}^{4}$
	${I}_{y}=4,463\times {10}^{6}\,c{m}^{4}$
	${M}_{zp}=2,262\times {10}^{6}\,kN\times cm$
	${M}_{xp}=6,533\times {10}^{9}\,kN\times cm$
	${M}_{yp}=1,409\times {10}^{6}\,kN\times cm$
	${F}_{zp}=4,282\times {10}^{4}\,kN$
	${F}_{xp}=7,416\times {10}^{4}\,kN$
	${F}_{yp}=4,282\times {10}^{4}\,kN$

As cargas aplicadas são as seguintes:

Tabela 18. Cargas aplicadas do pórtico em domo - Argyris et al.

Nó	${\boldsymbol {F}}_{\boldsymbol {x}}$ (kN)	${\textstyle {\boldsymbol {F}}_{\boldsymbol {y}}}$ (kN)	${\boldsymbol {F}}_{\boldsymbol {z}}$ (kN)
1	0,000	-1,000	0,000

As funções utilizadas no caso são as ${\textstyle {f}_{1}}$, ${\textstyle {f}_{2}}$ e ${\textstyle {f}_{3}}$, equações (28), (29) e (30), respectivamente.

3. Resultados e discussão

Os resultados e discussões dos estudos de caso 1 a 3 são apresentados.

3.1 Caso 1

Os resultados dos estudos, s. O número de elementos plastificados foram 3 (três) para todas as funções e a quantidade de rótulas 5 (cinco). Os caminhos da formação das rótulas são apresentados na Tabela 19 e Figura 11, com as 3 (três) funções ${\textstyle {f}_{4},\,{f}_{5}\,e\,{f}_{6}\,\,}$ mostram que os resultados estão mais próximos da solução do ABAQUS de 20 elementos de Thai e Kim [11] que teve o fator de carga entre 1 e 1,2. Do ponto de vista estatístico, a melhor solução seria a função ${\textstyle {f}_{4}}$, depois ${\textstyle {f}_{6}}$ e por último ${\textstyle {f}_{5}}$. No entanto, a carga limite de ${\textstyle {f}_{5}}$ é que se aproxima melhor aos resultados de Thai e Kim [11] com fatores de carga próximos a 0,8. Se levarmos em conta a solução de 20 elementos do ABACUS de Thai e Kim [11], a função ${\textstyle {f}_{4}}$ foi de fato a melhor corroborando com os resultados estatísticos. O número de elementos plastificados foram 3 (três) para todas as funções e a quantidade de rótulas 5 (cinco). Os caminhos da formação das rótulas são apresentados na Tabela 19.

Tabela 19. Rótulas plásticas – pórtico plano - Thai e Kim.

Função ${\textstyle {f}_{4}}$
Elemento	Nó	${\mathit {\boldsymbol {\lambda }}}$	Carga limite (kN)
1	1	$0,108246\times {10}^{5}$	$309,146$
	2	$0,841207\times {10}^{4}$
2	2	$0,227389\times {10}^{2}$
3	3	$0,844737\times {10}^{4}$
	4	$0,108410\times {10}^{5}$

Função ${\textstyle {f}_{5}}$
Elemento	Nó	${\mathit {\boldsymbol {\lambda }}}$	Carga limite (kN)
1	1	$0,106273\times {10}^{5}$	$300,431$
	2	$0,208395\times {10}^{4}$
2	2	$0,626480\times {10}^{4}$
3	3	$0,836829\times {10}^{4}$
	4	$0,106452\times {10}^{5}$

Função ${\textstyle {f}_{6}}$
Elemento	Nó	${\mathit {\boldsymbol {\lambda }}}$	Carga limite (kN)
1	1	$0,114845\times {10}^{5}$	$318,103$
	2	$0,254762\times {10}^{4}$
2	2	$0,604007\times {10}^{4}$
3	3	$0,899557\times {10}^{4}$
	4	$0,117705\times {10}^{5}$

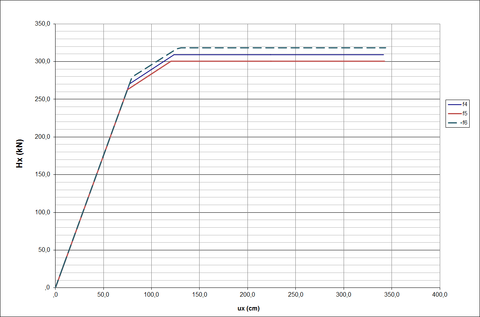
Figura 11. Gráfico carga versus deslocamento horizontal (${\textstyle {H}_{x})-n{\acute {o}}\,2}$) - pórtico plano - Thai e Kim

3.2 Caso 2

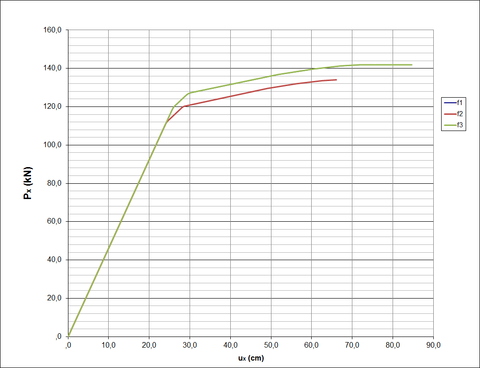
Os resultados dos estudos, Tabela 20 e Figura 12, com as 3 (três) funções ${\textstyle {f}_{2},\,{f}_{3}\,e\,{f}_{1}\,\,}$ mostram que os resultados das cargas limites estão mais elevados do que os de Thai e Kim [11] que teve o valor de 128,82 ${\textstyle kN}$. Do ponto de vista estatístico, a melhor solução seria a função ${\textstyle {f}_{2}}$, depois ${\textstyle {f}_{3}}$ e por último ${\textstyle {f}_{1}}$. Neste caso, a carga limite de ${\textstyle {f}_{2}}$ é a que realmente se aproxima melhor aos resultados de Thai e Kim [11], confirmando os resultados estatísticos com uma diferença relativa de 4,08% ((${\textstyle {f}_{2}-}$$Thai)/Thai\,\times 100)$. Esta diferença pode ter ocorrido porque os esforços plásticos limites (momentos, cortantes e axial) não existem nos dados de Thai e Kim [11], porém são necessários na teoria apresentada. O número de elementos plastificados foram 10 (dez) para todas as funções e a quantidade de rótulas 12 (doze). Os caminhos da formação das rótulas são apresentados na Tabela 20.

Tabela 20. Rótulas plásticas – pórtico espacial - Thai e Kim

Função ${\textstyle {f}_{1}}$
Elemento	Nó	${\mathit {\boldsymbol {\lambda }}}$	Carga limite (kN)
1	1	$0,345728\times {10}^{4}$	$141,886$
2	2	$0,353734\times {10}^{4}$
3	3	$0,348667\times {10}^{4}$
4	4	$0,350863\times {10}^{4}$
5	5	$0,308873\times {10}^{4}$
	6	$0,307316\times {10}^{4}$
7	7	$0,306402\times {10}^{4}$
	8	$0,309575\times {10}^{4}$
9	9	$0,899973\times {10}^{3}$
10	10	$0,933775\times {10}^{3}$
11	11	$0,984856\times {10}^{3}$
12	12	$0,849066\times {10}^{3}$

Função ${\textstyle {f}_{2}}$
Elemento	Nó	${\mathit {\boldsymbol {\lambda }}}$	Carga limite (kN)
1	1	$0,321786\times {10}^{4}$	$134,077$
2	2	$0,326692\times {10}^{4}$
3	3	$0,326692\times {10}^{4}$
4	4	$0,321786\times {10}^{4}$
5	5	$0,299500\times {10}^{4}$
	6	$0,298730\times {10}^{4}$
7	7	$0,298730\times {10}^{4}$
	8	$0,299500\times {10}^{4}$
9	9	$0,106747\times {10}^{4}$
10	10	$0,107793\times {10}^{4}$
11	11	$0,107793\times {10}^{4}$
12	12	$0,106747\times {10}^{4}$

Função ${\textstyle {f}_{3}}$
Elemento	Nó	${\mathit {\boldsymbol {\lambda }}}$	Carga limite (kN)
1	1	$0,345110\times {10}^{4}$	$141,900$
2	2	$0,353048\times {10}^{4}$
3	3	$0,348312\times {10}^{4}$
4	4	$0,349939\times {10}^{4}$
5	5	$0,309236\times {10}^{4}$
	6	$0,307839\times {10}^{4}$
7	7	$0,306698\times {10}^{4}$
	8	$0,309736\times {10}^{4}$
9	9	$0,905438\times {10}^{3}$
10	10	$0,938623\times {10}^{3}$
11	11	$0,983798\times {10}^{3}$
12	12	$0,855577\times {10}^{3}$

Figura 12. Gráfico carga versus deslocamento horizontal (${\textstyle {P}_{x})-n{\acute {o}}\,12}$ - pórtico espacial - Thai e Kim

3.3 Caso 3

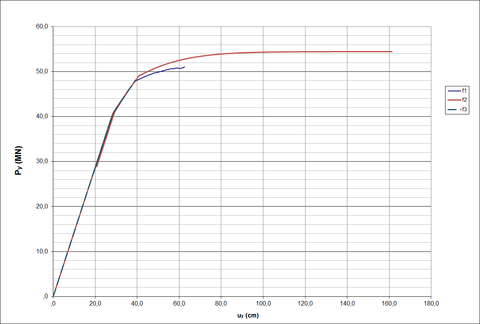
Os resultados dos estudos, Tabela 21 e Figura 13, com as 3 (três) funções ${\textstyle {f}_{2},\,{f}_{3}\,e\,{f}_{1}\,\,}$ mostram que os resultados das cargas limites estão próximos de Argyris et al [12], visualmente, porque o valor exato não é apresentado. Do ponto de vista estatístico, a melhor solução seria a função ${\textstyle {f}_{2}}$, depois ${\textstyle {f}_{3}}$ e por último ${\textstyle {f}_{1}}$. Neste caso, a carga limite de ${\textstyle {f}_{3}}$ é a que realmente se aproxima melhor aos resultados de Argyris et al [12], visualmente. Porém, esta função não conseguiu avançar o caminho de deslocamento em relação aos demais. Se avaliarmos a trajetória de deslocamento, a função ${\textstyle {f}_{2}}$ será a melhor e corroborará com os resultados estatísticos. O número de elementos plastificados foram 6 (seis) para as funções ${\textstyle {f}_{1}}$ e ${\textstyle {f}_{2}}$ e a quantidade de rótulas 12 (doze). Já a função ${\textstyle {f}_{3}}$ foram 6 (seis) elementos e 6 (seis) rótulas. Os caminhos da formação das rótulas são apresentados na Tabela 21.

Tabela 21. Rótulas plásticas – pórtico espacial - pórtico espacial - Argyris et al.

Função ${\textstyle {f}_{1}}$
Elemento	Nó	${\mathit {\boldsymbol {\lambda }}}$	Carga limite (kN)
1	1	$0,549351$	$51,0815$
	2	$0,891167$
2	1	$0,552499$
	3	$0,861987$
3	1	$0,564206$
	4	$0,883022$
4	1	$0,569621$
	5	$0,885590$
5	1	$0,556237$
	6	$0,862806$
6	1	$0,541887$
	7	$0,934919$

Função ${\textstyle {f}_{2}}$
Elemento	Nó	${\mathit {\boldsymbol {\lambda }}}$	Carga limite (kN)
1	1	$2,63534$	$54,4497$
	2	$2,62747$
2	1	$2,64188$
	3	$2,63063$
3	1	$2,64561$
	4	$2,63270$
4	1	$2,64226$
	5	$2,63100$
5	1	$2,63496$
	6	$2,62711$
6	1	$2,63079$
	7	$2,62451$

Função ${\textstyle {f}_{3}}$
Elemento	Nó	${\mathit {\boldsymbol {\lambda }}}$	Carga limite (kN)
1	1	$0,227607$	$48,0914$
2	1	$0,227118$
3	1	$0,226262$
4	1	$0,224668$
5	1	$0,224136$
6	1	$0,225236$

Figura 13. Gráfico carga versus deslocamento horizontal (${\textstyle {P}_{y})-n{\acute {o}}\,1}$ - pórtico espacial - Argyris et al.

4. Conclusões

* As superfícies de escoamento em resultantes de tensões aplicadas para pórticos planos e espaciais obtiveram resultados satisfatórios tendo em vista os exemplos apresentados;

* Os resultados estatísticos conseguiram detectar as melhores funções, a saber, ${\textstyle {f}_{2}}$ e ${\textstyle {f}_{4}}$ para as análises desenvolvidas;

* O método apresentado permitiu o uso do modelo de dano de viga de Timoshenko 3D com bons resultados para estruturas de aço;

* A regressão linear múltipla se apresenta como uma solução viável para obter funções por análises numéricas e/ou experimentais;

* O processo de formação de rótulas plásticas foi similares para os casos 1 e 2, porém o caso 3 apresentou distinções entre as funções apresentadas com ${\textstyle {f}_{1}}$ e ${\textstyle {f}_{2}}$ similares e diferente para ${\textstyle {f}_{3}}$. Isto impactou nos resultados das cargas limites e trajetória de deslocamento do caso 3.

Agradecimentos

À UFOB, CIMNE/UPC, PECC/UnB e a CAPES.

Referências

[1]	Vieira, P.C.S. Geração de superfícies de interação pelo método da regressão linear múltipla com o modelo de dano em vigas de Timoshenko 3D. Pub. E.TD- 006A/04. Departamento de Engenharia Civil e Ambiental, Universidade de Brasília, Brasília, 2004.
[2]	Hanganu, A.D. Metodologia de evaluación del deterioro en estructuras de hormigón armado. Monografia CIMNE nº 39, CIMNE, Barcelona, 1997.
[3]	Lubliner, J. Plasticity theory. Macmillan Publishing Company, Nova Iorque, 1990.
[4]	Mrázik A., Éskaloud M., Tocháécek M. Plastic design of steel structures. E. Horwood: Halsted Press, Nova Iorque, 1987.
[5]	Crisfield, M.A. A consistent co-rotational formulation for non-linear, three-dimensional. Comp. Methods Appl. Mech. Engrg., 81:131-150, 1990.
[6]	Vieira P.C.S., Silva W.T.M. Análise elastoplástica de estruturas aporticadas com superfícies de interação obtidas por regressão linear múltipla. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 3:175–187, 2013.
[7]	Montgomery D.C., Runger G.C. Estatística aplicada e probabilidade para engenheiros. LTC, Rio de Janeiro, 2016.
[8]	Horne, M.R. Plastic theory of structures. 2ª ed., Pergamon Press, Oxford, 1972.
[9]	Neal, B.G. The plastic methods of structural analysis. Chapman and Hall, Inglaterra, 1977.
[10]	Silva, W. T. M. Análise elastoplástica de pórticos espaciais utilizando o conceito de rótula plástica e o método de backward Euler. Métodos Computacionais em Engenharia, [s.n.], Lisboa, 2004.
[11]	Thai H.T., Kim S.E. Nonlinear inelastic analysis of space frames. Journal of Constructional Steel Research, 67:585–592, 2011.
[12]	Argyris, J.H. et al. Finite element analysis of two and three-dimensional elasto-plastic frames - the natural approach. Comp. Method. in Applied Mechanics and Engineering, 35:221-248, 1982.
[13]	Park M.S., Lee B.C. Geometrically non-linear and elastoplastic three-dimensional shear flexible beam element of von-Mises-type hardening material. International Journal for Numerical Methods in Engineering, 39:383-408, 1996.